Adaptive Risk-Driven Control Strategy for Enhancing Highway Renewable Energy System Resilience Against Extreme Weather
Abstract
1. Introduction
| Aspect | Existing Studies | Proposed Framework | Novelty Emphasis |
|---|---|---|---|
| Control Focus | Predominantly economic optimization under normal conditions [9]. | Dynamic, risk-driven optimization shifting between economy, resilience, and recovery objectives. | Hierarchical use of risk levels; shifts from passive economic operation to proactive resilience management [9]; focuses on scheduling under uncertainty, not dynamic priority-shifting. |
| Risk Handling | Often static reliability constraints; reactive response to failures [10]. | Proactive, adaptive hierarchical control based on continuous quantitative risk assessment. | Risk-driven adaptive control; moves beyond static “N − 1” reliability to a predictive, graded response system [10]; reviews reliability optimization but not dynamic risk adaptation. |
| Traffic Integration | Treated as exogenous, stochastic load demand [10]. | Endogenous, controllable variable within a holistic “source–grid–load–storage–road” co-optimization model. | Integration of traffic as an endogenous variable; enables active shaping of traffic flow (e.g., via guidance) to alleviate energy stress, not just passive load forecasting [10]; models EV charging as an exogenous input. |
| Optimization Approach | Often single-objective (cost) or dual-objective (cost and emissions) [4]. | Multi-objective explicit trade-off among resilience (f1), cost (f2), and traffic impact (f3). | Multi-objective co-optimization; introduces and quantifies traffic impact (f3) as a core objective, capturing the socio-economic cost of energy dispatch decisions on transportation [4]; uses a four-objective framework but does not include traffic impact. |
| Algorithm | Conventional optimization or standard algorithms (e.g., standard NSGA-II) [13]. | Enhanced NSGA-II-DE hybrid algorithm combining global exploration (DE) and local exploitation (NSGA-II). | Combination of NSGA-II with differential evolution (DE). The DE mutation operator enhances the ability to escape local optima and find a better-distributed Pareto front under high-dimensional, complex constraints [13]; is the standard NSGA-II algorithm. |
2. Methodology
2.1. Hierarchical Synergistic Control Framework
2.2. Multi-Objective Optimization Model
2.2.1. Objective Functions
- (1)
- Objective 1: Minimize the weighted power loss (f1)
- (2)
- Objective 2: Minimize the overall operating costs (f2)
- (3)
- Objective 3: Minimize the impact of the traffic network (f3)
2.2.2. Key Constraints
- (1)
- Power system constraints
- (2)
- Traffic system constraints
- (3)
- Electricity—traffic coupling constraints
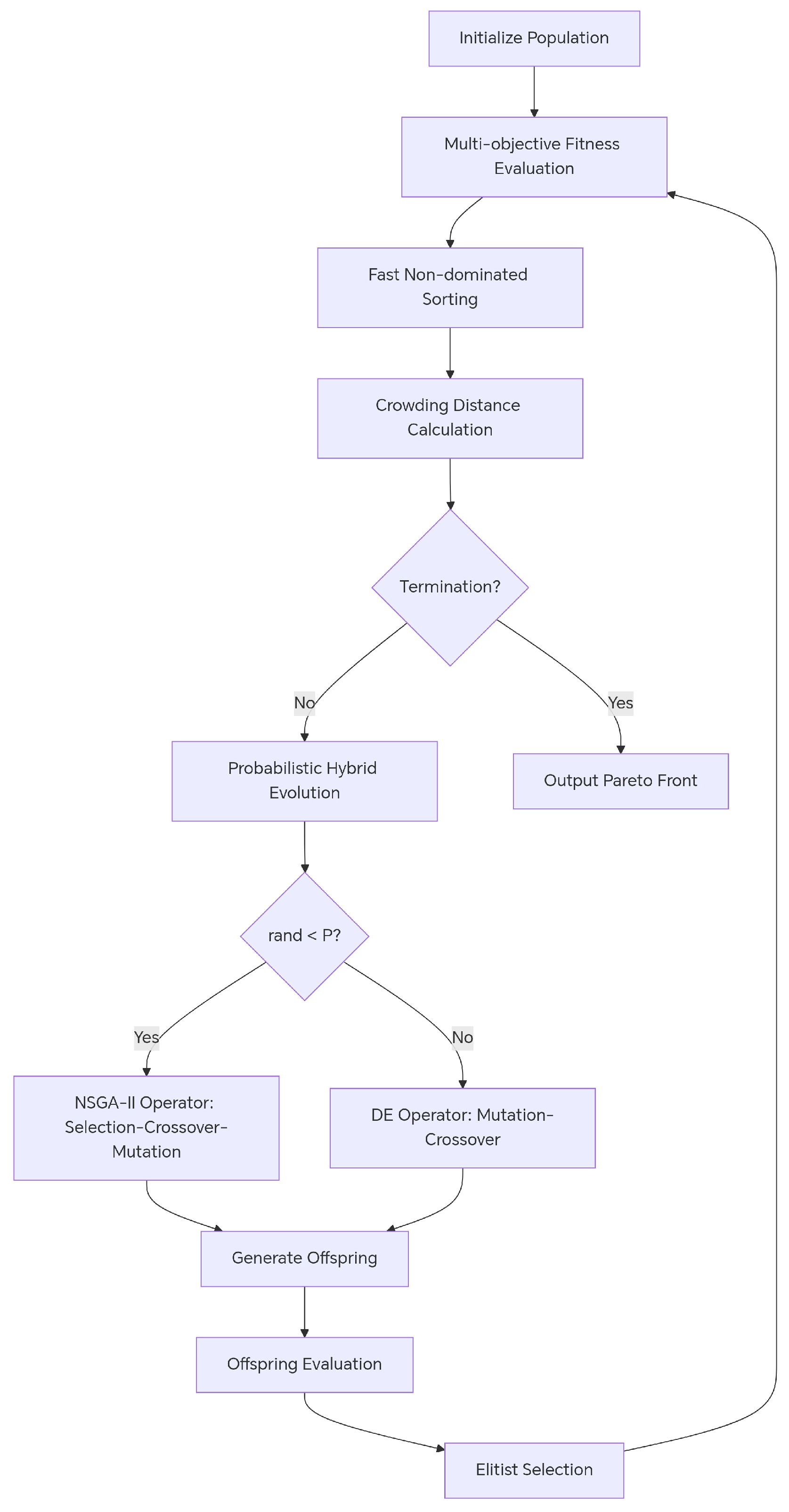
2.3. Optimization Algorithm Based on Improved NSGA-II
2.4. Assumptions
3. Verification Analysis
4. Results and Discussion
4.1. Calculation Scenarios and Parameter Settings
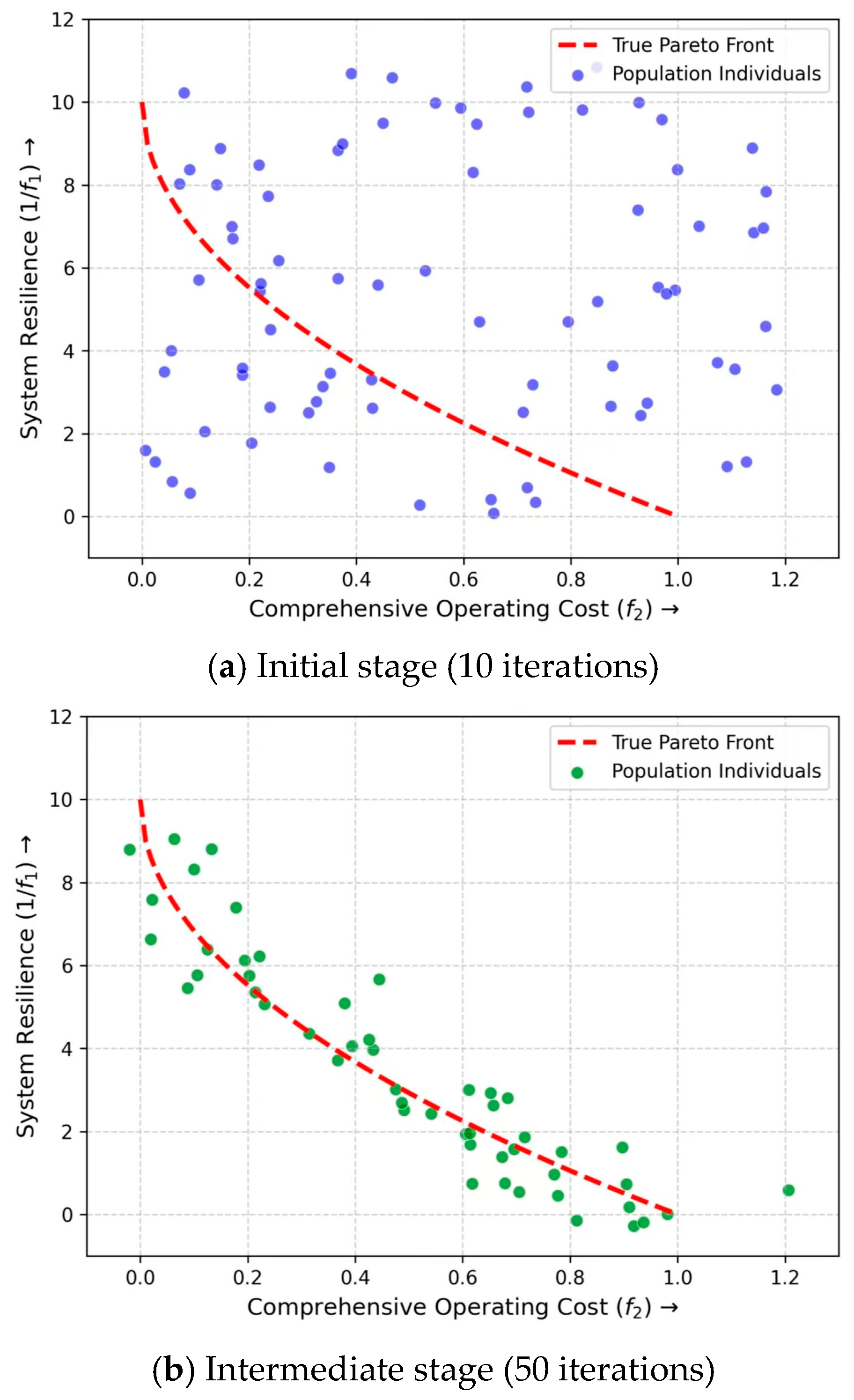
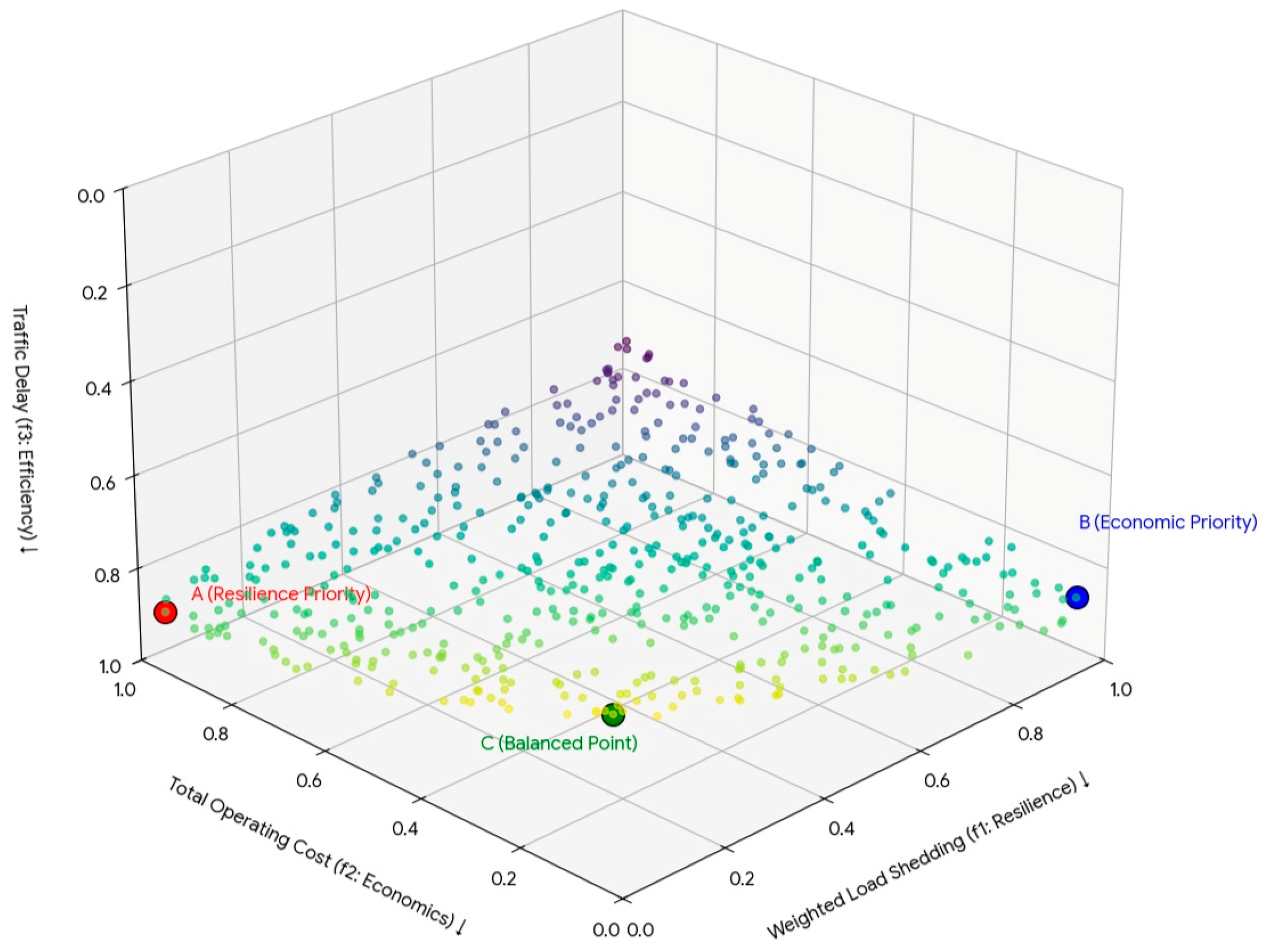
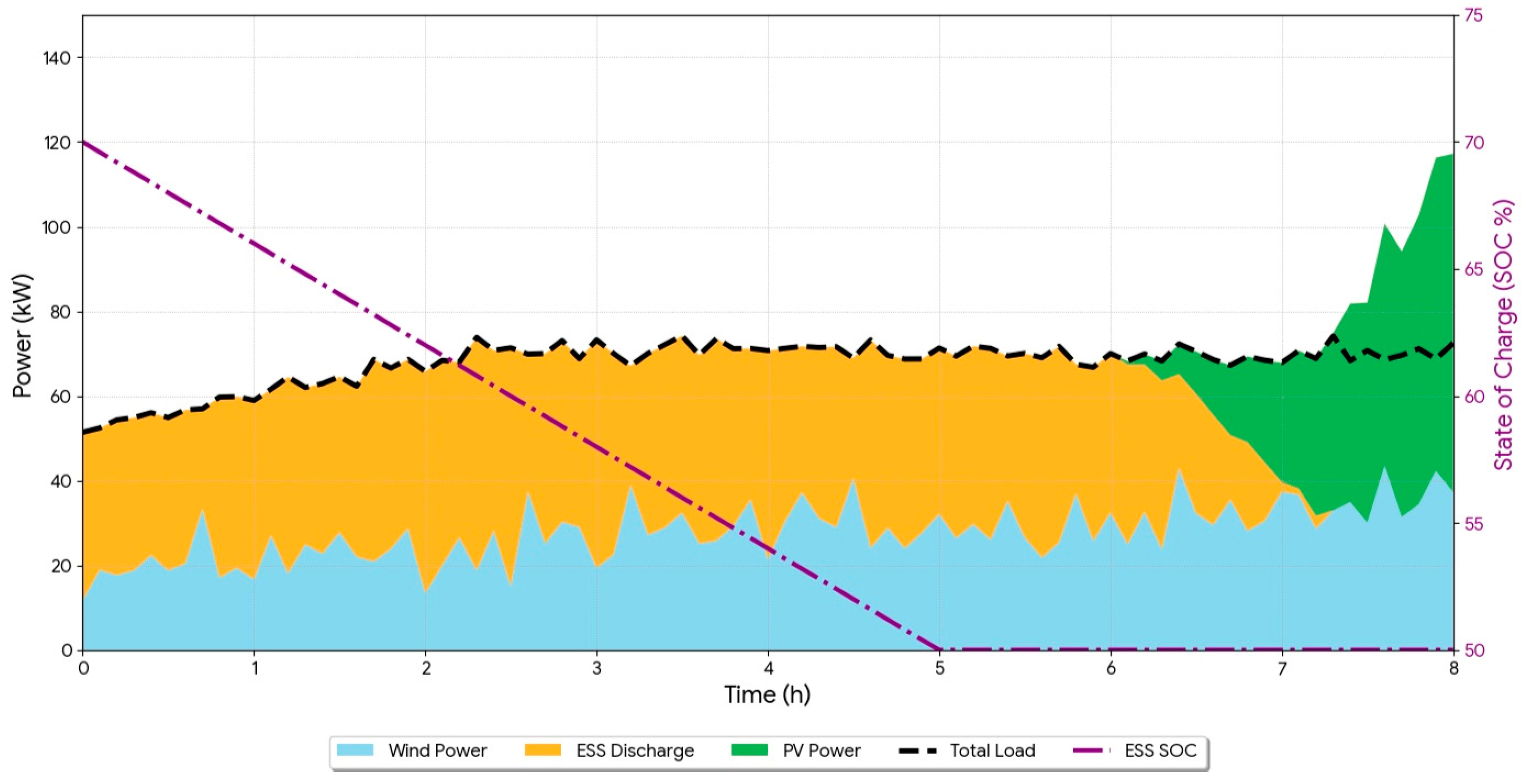
4.2. Control Strategy Performance Analysis
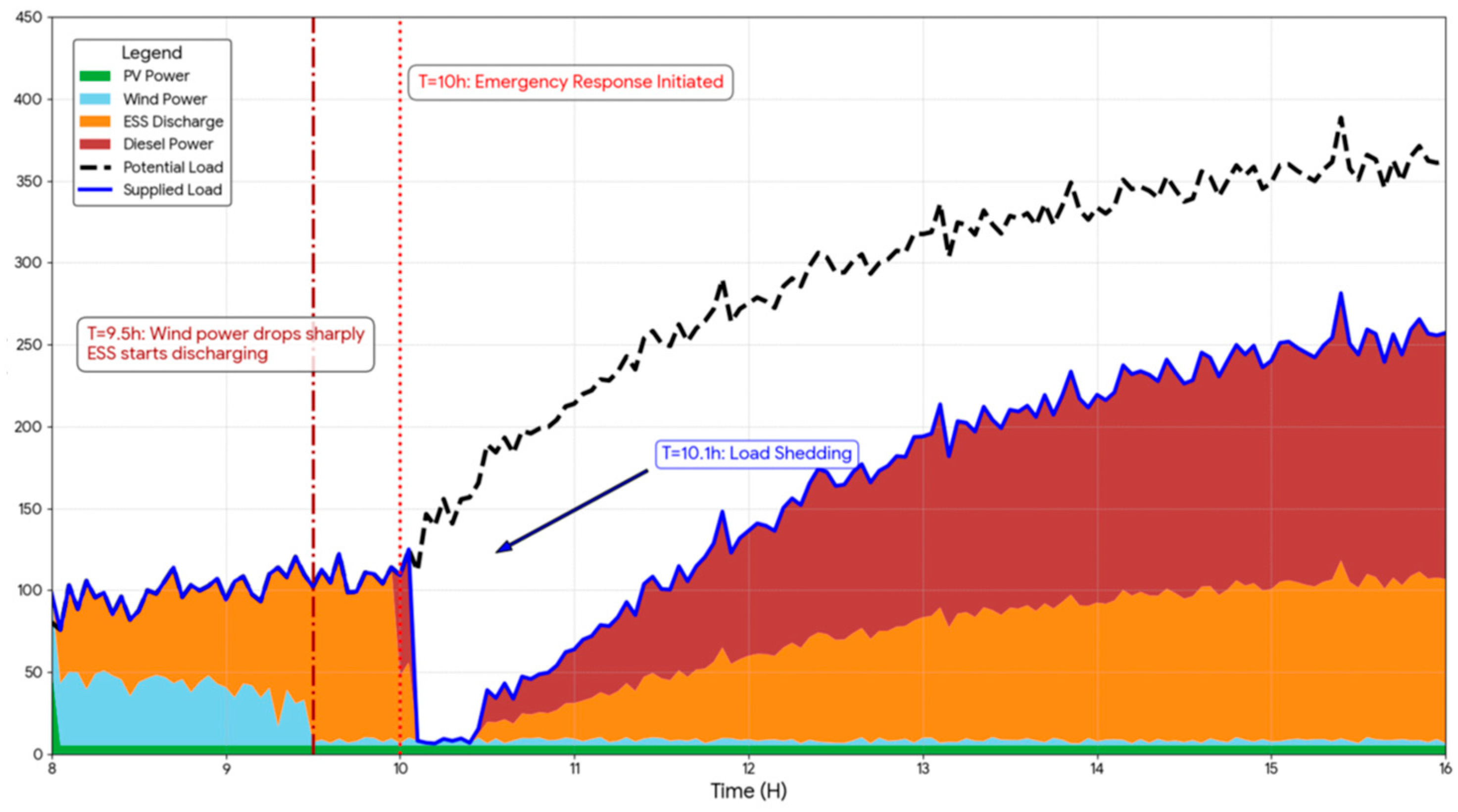
4.3. Control Strategies Under Different Risk Levels
- (1)
- Low-risk scenario simulation (economic operation mode)
- (2)
- High-risk scenario simulation (emergency response mode)
- (3)
- Recovery control mode
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency (IEA). Transport; IEA: Paris, France, 2022; Available online: https://www.iea.org/reports/transport (accessed on 8 September 2025).
- Creutzig, F.; Niamir, L.; Bai, X.; Callaghan, M.; Cullen, J.; Díaz-José, J.; Figueroa, M.; Grubler, A.; Lamb, W.F.; Leip, A.; et al. Demand-side solutions to climate change mitigation focusing on transport sector. Nat. Clim. Change 2022, 12, 240–248. [Google Scholar] [CrossRef]
- Brazilian Institute of Applied Economics. Energy infrastructure collapse during extreme flood events. Sustain. Prod. Consum. 2024, 38, 45–58. [Google Scholar]
- Fathy, A.; Rezk, H.; Ferahtia, S.; Ghoniem, R.M.; Alkanhel, R. An efficient honey badger algorithm for scheduling the microgrid energy management. Energy Rep. 2023, 9, 2058–2074. [Google Scholar] [CrossRef]
- Niu, M.B.; Wang, H.C.; Li, J.; Liu, H.; Yin, R. Coordinated energy dispatch of highway microgrids with mobile storage system based on DMPC optimization. Electr. Power Syst. Res. 2023, 217, 109119. [Google Scholar] [CrossRef]
- Karimi, H.; Jadid, S.; Hasanzadeh, S. Optimal-sustainable multi-energy management of microgrid systems considering integration of renewable energy resources: A multi-layer four-objective optimization. Sustain. Prod. Consum. 2023, 36, 126–138. [Google Scholar] [CrossRef]
- Luo, L.; Abdulkareem, S.S.; Rezvani, A.; Miveh, M.R.; Samad, S.; Aljojo, N.; Pazhoohesh, M. Optimal scheduling of a renewable-based microgrid considering photovoltaic system and battery energy storage under uncertainty. J. Energy Storage 2020, 28, 101306. [Google Scholar] [CrossRef]
- Lei, B.; Ren, Y.; Luan, H.; Dong, R.; Wang, X.; Liao, J.; Fang, S.; Gao, K. A review of optimization for system reliability of microgrid. Mathematics 2023, 11, 822. [Google Scholar] [CrossRef]
- Richardson, P.; Flynn, D.; Keane, A. Optimal charging of electric vehicles in low-voltage distribution systems. IEEE Trans. Power Syst. 2012, 27, 268–279. [Google Scholar] [CrossRef]
- Shao, C.; Wang, X.; Shahidehpour, M.; Li, K. An MILP-based optimal power and transportation coordination model for electrified highways. IEEE Trans. Smart Grid 2020, 3, 1904–1916. [Google Scholar]
- Li, Y.; Chai, S.; Zhang, X.; Wang, G.; Zhu, R.; Chung, E. STPNet: Quantifying the Uncertainty of Electric Vehicle Charging Demand via Long-Term Spatiotemporal Traffic Flow Prediction Intervals. IEEE Trans. Intell. Transp. Syst. 2023, 24, 15018–15034. [Google Scholar] [CrossRef]
- Kotegov, R.; Abokersh, M.; Mateu, C.; Shobo, A.; Boer, D.; Vallès, M. Multi-method optimization of solar district energy systems with battery and thermal energy storage via real-time TRNSYS-Python coupling. Appl. Energy 2025, 400, 126528. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Yang, J.; Su, C. Robust optimization of microgrid based on renewable distributed power generation and load demand uncertainty. Energy 2021, 223, 120043. [Google Scholar] [CrossRef]
- Dey, B.; Bhattacharyya, B.; Márquez, F.P.G. A hybrid optimization-based approach to solve environment constrained economic dispatch problem on microgrid system. J. Clean. Prod. 2021, 307, 127196. [Google Scholar] [CrossRef]
- Liu, R.; He, G.; Wang, X.; Mallapragada, D.; Zhao, H.; Shao-Horn, Y.; Jiang, B. A cross-scale framework for evaluating flexibility values of battery and fuel cell electric vehicles. Nat. Commun. 2024, 15, 280. [Google Scholar] [CrossRef] [PubMed]
- Das, G.; De, M.; Mandal, K.K. Multi-objective optimisation of hybrid renewable energy system by using novel autonomic soft computing techniques. Comput. Electr. Eng. 2021, 94, 107350. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. In Proceedings of the 2002 Congress on Evolutionary Computation—CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 825–830. [Google Scholar] [CrossRef]




| Risk Level | Control Level | Core Optimization Objectives | Synergistic Control Dimension |
|---|---|---|---|
| Low-risk | Tier 1 control: Economic operation | Minimization of integrated operating costs | Source–grid–load–storage |
| Medium-risk | Tier 2 control: Preventive control | Maximize system resilience margin | Source–grid–storage–road |
| High-risk | Tier 3 control: Emergency response | Power loss minimization | Source–load–storage–road |
| Severe-risk | Tier 4 control: Restorative control | Minimization of system recovery time | Grid–source–load |
| Test Functions | Algorithm | Generation Distance (GD) | Inverse Generation Distance (IGD) | Hypervolume (HV) |
|---|---|---|---|---|
| ZDT1 | NSGA-II | 0.0015 | 0.0144 | 0.8523 |
| MOPSO | 0.0004 | 0.0088 | 0.8625 | |
| NSGA-II-DE | 0.0003 | 0.0047 | 0.8700 | |
| ZDT3 | NSGA-II | 0.0011 | 0.1903 | 1.2456 |
| MOPSO | 0.0006 | 0.1956 | 1.3197 | |
| NSGA-II-DE | 0.0006 | 0.1917 | 1.3279 | |
| DTLZ2 | NSGA-II | 0.0090 | 0.0791 | 0.6422 |
| MOPSO | 0.0142 | 0.1082 | 0.5841 | |
| NSGA-II-DE | 0.0080 | 0.0550 | 0.6935 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, P.; Li, H.; Zhao, W.; Tian, X.; Liu, J.; Qin, W.; Hai, L.; Wu, F. Adaptive Risk-Driven Control Strategy for Enhancing Highway Renewable Energy System Resilience Against Extreme Weather. Energies 2025, 18, 5417. https://doi.org/10.3390/en18205417
Cui P, Li H, Zhao W, Tian X, Liu J, Qin W, Hai L, Wu F. Adaptive Risk-Driven Control Strategy for Enhancing Highway Renewable Energy System Resilience Against Extreme Weather. Energies. 2025; 18(20):5417. https://doi.org/10.3390/en18205417
Chicago/Turabian StyleCui, Peiqiang, Hongde Li, Wenwu Zhao, Xiaowu Tian, Jin Liu, Weijie Qin, Liya Hai, and Fan Wu. 2025. "Adaptive Risk-Driven Control Strategy for Enhancing Highway Renewable Energy System Resilience Against Extreme Weather" Energies 18, no. 20: 5417. https://doi.org/10.3390/en18205417
APA StyleCui, P., Li, H., Zhao, W., Tian, X., Liu, J., Qin, W., Hai, L., & Wu, F. (2025). Adaptive Risk-Driven Control Strategy for Enhancing Highway Renewable Energy System Resilience Against Extreme Weather. Energies, 18(20), 5417. https://doi.org/10.3390/en18205417






