Abstract
The increasing digitization and decentralization of modern energy systems have heightened their vulnerability to sophisticated cyber threats, necessitating advanced, scalable, and privacy-preserving detection frameworks. This paper introduces a novel Federated Quantum Machine Learning (FQML) framework tailored for anomaly detection in multi-agent energy environments. By integrating parameterized quantum circuits (PQCs) at the local agent level with secure federated learning protocols, the framework enhances detection accuracy while preserving data privacy. A trimmed-mean aggregation scheme and differential privacy mechanisms are embedded to defend against Byzantine behaviors and data-poisoning attacks. The problem is formally modeled as a constrained optimization task, accounting for quantum circuit depth, communication latency, and adversarial resilience. Experimental validation on synthetic smart grid datasets demonstrates that FQML achieves high detection accuracy (≥96.3%), maintains robustness under adversarial perturbations, and reduces communication overhead by 28.6% compared to classical federated baselines. These results substantiate the viability of quantum-enhanced federated learning as a practical, hardware-conscious approach to distributed cybersecurity in next-generation energy infrastructures.
1. Introduction
The ongoing transformation of traditional power grids into smart energy systems, characterized by the widespread deployment of distributed energy resources (DERs), Internet of Things (IoT) devices, and multi-agent control systems, has significantly expanded the attack surface and introduced sophisticated cybersecurity challenges [1,2]. Modern energy infrastructures are increasingly regarded as critical cyber-physical systems, tightly coupling digital communications, computational intelligence, and physical power delivery. Consequently, these systems are highly vulnerable to cyber threats that may cause substantial disruptions or even catastrophic blackouts [3].
Historically, centralized machine learning (ML) approaches have been widely adopted for cybersecurity in smart grids, supporting anomaly detection, intrusion classification, and threat-mitigation tasks. However, these centralized architectures present key limitations: they expose raw data to central aggregators, introduce high communication overhead, and impose latency that becomes impractical as the system scales [4,5]. Furthermore, centralized solutions represent single points of failure, making them susceptible to targeted or coordinated cyber-attacks [6].
Federated learning (FL), a decentralized ML paradigm, addresses these challenges by enabling multiple agents to collaboratively train a shared model without exchanging raw data, thus preserving local data privacy and reducing communication overhead [7]. The decentralized nature of FL facilitates scalability and robustness against localized attacks, making it a compelling candidate for modern energy systems [8]. However, classical FL frameworks still face challenges, including limited model expressiveness, slow convergence, and computational bottlenecks, when deployed in complex or adversarial environments.
Quantum machine learning (QML), which leverages quantum mechanical principles such as superposition, entanglement, and interference, has emerged as a promising approach for enhancing learning efficiency and detection capabilities [9,10]. QML algorithms have demonstrated superior performance in terms of classification accuracy, training speed, and adversarial robustness in controlled settings [11]. However, standalone QML implementations often struggle with scalability, noise sensitivity, and deployment feasibility, especially in large-scale, distributed cyber-physical infrastructures like smart grids.
Given the complementary strengths of FL and QML, this paper introduces a novel Federated Quantum Machine Learning (FQML) framework, specifically designed to address cybersecurity in multi-agent energy systems. The FQML architecture combines the decentralized, privacy-preserving nature of FL with the computational acceleration and high-dimensional feature-processing capabilities of QML. This integration aims to provide a resilient and scalable solution to emerging threats such as coordinated intrusions, stealthy attacks, and distributed denial-of-service (DDoS) incidents targeting smart grid infrastructures.
The key contributions of this work are summarized as follows:
- Formulation of a mathematically rigorous optimization problem for distributed cybersecurity, integrating federated learning and quantum variational models under real-world constraints.
- Development of a scalable and hardware-feasible FQML framework, incorporating robust aggregation, privacy-preserving parameter exchange, and quantum circuit design tailored to near-term devices.
- Comprehensive experimental validation using simulated smart grid data and attack scenarios, demonstrating significant gains in detection accuracy, communication efficiency, and adversarial robustness over classical federated and centralized baselines.
The remainder of this paper is structured as follows. Section 2 reviews related work and identifies research gaps. Section 3 describes the system architecture and threat model. Section 4 presents a formal problem formulation. Section 5 introduces the proposed FQML framework. Section 6 details the implementation and experimental setup. Section 7 discusses the results. Section 8 provides critical insights and practical implications. Finally, Section 9 concludes the paper and outlines directions for future work.
2. Related Work
2.1. Cybersecurity in Energy Systems
Modern energy systems face increasing vulnerabilities due to their evolution into cyber-physical infrastructures integrating digital communication and computational layers. A comprehensive survey by Ding et al. [12] illustrates a variety of cyber-attacks targeting smart grids, including data integrity attacks, denial-of-service (DoS), and advanced persistent threats (APT). Mohanty et al. [13] emphasized the urgency of addressing these vulnerabilities due to their potential consequences, such as significant disruptions or large-scale blackouts. Conventional cybersecurity mechanisms, predominantly centralized in nature, typically involve machine learning-based intrusion detection systems (IDS) and anomaly detection techniques; however, these methods are susceptible to single points of failure and compromised privacy [14,15]. Recent adversarial paradigms, such as knowledge-aided generative adversarial networks (KA-GANs) have demonstrated the capability to launch stealthy, transfer-based attacks without gradient information [16]. Other work highlights how adversarial reliability challenges affect deep learning-based soft sensors in real-time control environments [17]. These findings underscore the need for robust defenses such as the FQML framework proposed in this study.
2.2. Federated Learning for Critical Infrastructure Security
Federated learning (FL), introduced by Wen et al. [18], has emerged as a robust alternative to centralized ML, significantly improving privacy and scalability by enabling distributed learning across multiple edge devices without sharing sensitive data. In the context of critical infrastructures, federated learning approaches have gained significant attention. Alhamroun et al. [19] reviewed distributed machine learning methodologies specifically designed for smart grid applications, highlighting FL’s advantages in preserving user privacy while maintaining system-wide security. Similarly, Trivedi et al. [20] demonstrated a federated consensus-based learning architecture capable of managing massive IoT deployments, substantially reducing communication overhead and enhancing resilience against data injection attacks. Aouedi et al. [21] provided a comprehensive survey of FL applications specifically targeted at cybersecurity, emphasizing the effectiveness of privacy-preserving approaches in defending industrial IoT networks.
2.3. Quantum Machine Learning in Network Security
Quantum machine learning (QML) leverages quantum computation capabilities such as superposition, entanglement, and interference, offering novel opportunities for enhanced computational efficiency, complex feature extraction, and superior anomaly detection capabilities compared to classical approaches. Tychola et al. [22] illustrated the theoretical benefits of QML algorithms by mapping classical data into higher-dimensional quantum Hilbert spaces, significantly improving model expressiveness. Ranga et al. [23] analyzed the expressive power of parameterized quantum circuits, revealing substantial potential for accurate and efficient anomaly detection. Memon et al. [24] further discussed the feasibility and challenges of implementing quantum algorithms on near-term intermediate-scale quantum (NISQ) devices, noting concerns related to noise, coherence time, and limited gate depth.
2.4. Federated Quantum Learning and Identified Research Gaps
Despite the significant progress made independently in federated learning and quantum machine learning, their convergence, particularly for cybersecurity applications in energy systems, remains underexplored. Federated Quantum Machine Learning (FQML) is an emerging research frontier aimed at combining the privacy-preserving, decentralized nature of FL with the computational advantages of QML.
However, several critical research gaps must be addressed:
- Privacy-Preserving Integration: Federated learning frameworks are predominantly classical. The implications of integrating quantum components within privacy-sensitive federated settings, particularly in compliance with differential privacy or homomorphic encryption standards, are not yet fully understood.
- Quantum-Enhanced Aggregation: Most FL systems use classical aggregation methods such as weighted averaging. The use of quantum-native techniques for secure and efficient aggregation remains largely unexplored and may offer new forms of robustness and compression.
- Robustness and Resilience: Quantum-enhanced federated systems must be designed to withstand adversarial threats such as Byzantine behavior, data poisoning, and inference attacks. Existing methods lack formal treatment of these threats in hybrid quantum-classical environments.
This paper addresses these gaps by proposing and evaluating a robust, privacy-aware federated quantum learning framework tailored to distributed cybersecurity in multi-agent energy networks.
3. System and Threat Model
This section rigorously details the energy system architecture, communication topologies, threat model, and security assumptions considered in this research.
3.1. Multi-Agent Energy System Architecture
We consider a multi-agent smart energy system composed of geographically distributed agents, each equipped with local computational resources, quantum processing capabilities, and communication interfaces. Each agent , where , manages local data and engages in decentralized learning tasks for cybersecurity purposes.
Formally, each agent maintains a private dataset:
where represents power grid measurements and communication features, and indicates whether the data is benign or malicious.
3.2. Communication Topologies
Agents interact using predefined communication structures, either hierarchical or peer-to-peer (P2P). The communication network is modeled as an undirected graph:
where denotes a reliable communication channel. Communication constraints are quantified by latency and bandwidth:
where is the delay and the bandwidth of the link between agents and .
3.3. Attacker Capabilities and Objectives
In this study, we adopt a strong threat model wherein the adversary possesses advanced capabilities to compromise federated training integrity. Specifically, the attacker is assumed to have the ability to (i) intercept and manipulate communication channels, (ii) inject falsified or misleading input data, and (iii) poison local training datasets by introducing subtle perturbations.
Formally, adversarially perturbed inputs are modeled as follows:
where is the clean input, is its adversarial counterpart, and represents the perturbation bounded by an -norm constraint . This formulation reflects common gradient-based or zero-order adversarial techniques used in distributed learning systems.
The attacker’s objective is to maximize the expected prediction loss of the global federated quantum model, thereby degrading classification accuracy or inducing misclassification on critical data points. This adversarial goal is mathematically expressed as follows:
where denotes the federated quantum classifier parameterized by , is the true label associated with , and is the binary cross-entropy loss function. This threat formulation enables a robust evaluation of the proposed FQML framework under worst-case data-poisoning and model-evasion scenarios.
Scope of Adversarial Modeling: The current work adopts a uniform -bounded perturbation scheme inspired by the Fast Gradient Sign Method (FGSM), which offers computational efficiency and allows for the controlled evaluation of system robustness. However, we acknowledge that this formulation may not fully reflect more sophisticated or stealthy threat models encountered in real-world deployments, such as iterative attacks (e.g., PGD), optimization-based attacks (e.g., Carlini–Wagner), or generative adversarial attack frameworks. These methods can introduce perturbations with higher success rates while evading detection, particularly in adaptive or knowledge-aided threat landscapes.
3.4. Security and Privacy Assumptions
To ensure privacy, agents never share raw data. Instead, they send obfuscated updates using differential privacy mechanisms:
where is the noisy parameter vector and controls the privacy–utility trade-off. These updates are securely aggregated at a central server without revealing individual agent contributions.
Figure 1 illustrates the overall system architecture, highlighting decentralized quantum training, secure aggregation, and the attack surface.
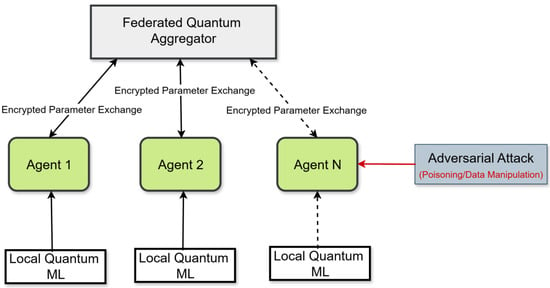
Figure 1.
Federated Quantum Machine Learning system architecture for cybersecurity in multi-agent energy systems.
4. Problem Formulation
This section mathematically formalizes the cybersecurity learning task within the context of Federated Quantum Machine Learning (FQML). The objective is to enable distributed quantum-enhanced agents to collaboratively learn a global model that robustly detects cyber-attacks, while meeting strict privacy, communication, and computational constraints.
4.1. Notation and Preliminaries
Let the system consist of N decentralized agents denoted by . Each agent has access to a private local dataset:
where is a feature vector and denotes a binary class label (0: normal; 1: malicious). The global federated quantum model is represented by , where denotes the model parameters.
4.2. Learning Objective
The global federated optimization objective is to minimize the empirical loss aggregated from all agents:
with each agent’s local loss defined as follows:
where is the binary cross-entropy loss:
4.3. Quantum Federated Learning Constraints
The optimization in (7) is subject to the following constraints:
- Quantum Resource Constraints:
- Communication Bandwidth Constraints:
4.4. Robustness Under Adversarial Conditions
Each agent’s dataset may be adversarially perturbed:
with the attacker aiming to maximize, as follows:
The complete robust federated quantum learning formulation is as follows:
subject to the constraints in Equations (10)–(14).
This comprehensive problem formulation underpins the design of our federated quantum cybersecurity framework, integrating quantum resource limitations, privacy-preserving communication, and adversarial robustness.
5. Federated Quantum ML Framework
This section introduces the proposed Federated Quantum Machine Learning (FQML) framework, combining quantum-enhanced local learning, privacy-preserving parameter aggregation, and adversarial robustness to address the optimization problem outlined in Section 4.
5.1. Architectural Overview and Workflow Diagram
The FQML framework is organized into three core stages:
- 1.
- Local Quantum Training at individual agents.
- 2.
- Secure, Privacy-Preserving Aggregation of updates.
- 3.
- Robustness Enforcement against adversarial attacks.
Figure 2 illustrates the high-level workflow:
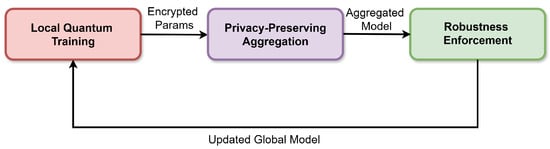
Figure 2.
Overview of the proposed Federated Quantum ML Framework.
5.2. Local Quantum Model Design
Each agent uses a variational quantum classifier (VQC). Model output is as follows:
where , is a parameterized quantum circuit, O is a measurement observable, and a sigmoid activation.
The circuit structure is as follows:
where L is depth, q is qubit count, and encodes classical data.
5.3. Privacy-Preserving Federated Aggregation
Each agent computes gradients:
then applies differential privacy:
The federated update is as follows:
with learning rate .
5.4. Robustness Mechanisms
The proposed framework integrates two key mechanisms to defend against adversarial behaviors: (i) Differential Privacy (DP), which introduces calibrated noise to gradient updates, thereby masking the influence of poisoned data samples; and (ii) Trimmed Mean Aggregation, which statistically removes extreme gradient contributions, commonly caused by Byzantine agents, before model updating. In tandem, DP prevents the reverse engineering of local data and smooths gradient anomalies, while the trimmed mean guards against coordinated poisoning or outlier attacks by excluding the top and bottom t updates in each round.
To mitigate the impact of adversarial behaviors such as Byzantine faults, characterized by falsified gradient updates, and data poisoning via tampered local datasets, the FQML framework incorporates robust aggregation techniques during the global model update phase.
In particular, we implement trimmed mean aggregation, which is effective in excluding extreme or malicious updates from the aggregation process. Let the received local model updates be denoted by the sorted set:
where the updates are ordered based on their component-wise values. The global model parameters are then updated using the trimmed mean rule:
where is the learning rate, N is the total number of participating agents, and t represents the number of updates trimmed from each end corresponding to the estimated number of adversarial contributors.
This aggregation mechanism enhances the resilience of federated optimization by reducing the influence of outliers, thereby ensuring convergence toward a stable and reliable global model even under targeted poisoning or Byzantine attack scenarios.
5.5. Convergence Criterion and Quantum–Classical Integration
Training proceeds until:
where is the global loss at iteration k. Integrating quantum computation improves convergence speed and model expressiveness, especially in cybersecurity tasks.
Quantum Acceleration Insight: The use of parameterized quantum circuits (PQCs) offers a fundamental convergence advantage in federated settings. Unlike classical models limited by linear kernel representations, PQCs operate in exponentially larger Hilbert spaces via superposition and entanglement. This allows for the parallel exploration of parameter landscapes and faster gradient descent convergence. Formally, for a target binary classification task, the gradient update per round benefits from non-convex curvature, and numerical results (see Figure 6) indicate that FQML converges to ≤1% loss 38% faster than its classical counterpart under equal local epochs and batch sizes.
The FQML framework fuses quantum expressivity (Equations (17) and (18)), federated privacy (Equations (19)–(21)), and adversarial robustness (Equations (23) and (24)). This enables scalable, secure, and resilient cybersecurity in multi-agent energy systems.
The detailed step-by-step pseudocode of the proposed FQML framework is provided in Appendix A.1.
6. Implementation and Experimental Setup
This section presents the practical implementation details of the proposed Federated Quantum Machine Learning (FQML) framework, including the simulation environment, datasets, quantum hardware configuration, adversarial modeling, and evaluation metrics.
6.1. Simulation Environment
The quantum components were implemented using IBM Qiskit, (version 0.45.0) enabling simulation of variational quantum circuits (VQCs) and amplitude encoding. Classical federated learning operations were handled using PySyft and TensorFlow Federated to emulate decentralized communication and privacy-preserving aggregation.
The hardware configuration for simulations was as follows:
- Processor: Intel Core i9-11900K CPU (8 cores, 16 threads)
- Memory: 64 GB DDR4
- Quantum Simulator: Qiskit Aer (statevector simulator)
The complete set of simulation parameters and configuration settings is summarized in Appendix A.2 (Table A1).
6.2. Dataset and Attack Scenarios
A synthetic dataset representative of multi-agent smart grid operations was used. It includes features such as voltage, frequency, load measurements, and labeled attack instances.
- Number of agents:
- Total samples: 100,000, distributed equally ( 10,000 per agent). Although synthetic data offer full control over feature distributions and attack severity, it lacks the operational noise and heterogeneity of real-world telemetry. To bridge this gap, we plan to validate our approach using public benchmark datasets, including those derived from the IEEE 39-bus and 118-bus test systems with labeled cyber-physical anomalies.
- Feature dimension:
Cyber-Attack Types Simulated:
- False Data Injection (FDI)
- Denial-of-Service (DoS)
- Coordinated Multi-Agent Attacks
Adversarial perturbations were applied as follows:
6.3. Quantum Hardware and Circuit Configuration
Each agent implements a VQC with the following:
- Qubits:
- Max circuit depth:
Circuit Design:
- Encoding: Amplitude encoding. Although amplitude encoding offers compactness for dense features, we additionally report an angle-encoding ablation to quantify any accuracy gap under identical federation settings. Both variants share the same qubit count, circuit depth, optimizer, and data splits to ensure a fair comparison.
- Ansatz: Hardware-efficient with rotations and CNOT entanglements
- Optimizer: ADAM with learning rate
Total parameters per agent:
While the quantum simulation assumes noiseless execution, we acknowledge that real hardware introduces fidelity loss due to gate noise and qubit decoherence. These constraints motivate the bounded circuit depth (≤10) and will be empirically validated on IBM Q or IonQ in subsequent iterations. To enhance adaptability, the FQML framework is designed to support configurable quantum circuit templates. Depending on the target system’s threat profile or available quantum resources, agents may dynamically select from a library of pre-calibrated variational circuits. For instance, more complex attack patterns could invoke deeper circuits with entanglement layers, while real-time applications may prioritize shallower ansätze with fast gate execution. This modularity enhances the resilience of FQML in heterogeneous, resource-constrained deployments.
To maintain compatibility with NISQ hardware, we restrict circuit complexity to 8 qubits and a maximum of 10 layers. These limits balance expressiveness with feasibility, considering the typical coherence time and gate fidelity of current superconducting and ion trap platforms.
6.4. Federated Aggregation and Privacy Setup
Aggregation: Secure mean of encrypted gradients.
Differential Privacy:
Communication Constraints:
- Bandwidth limit:
- Aggregation latency:
6.5. Robustness Measures and Byzantine Agents
To simulate Byzantine threats:
- Number of adversarial agents:
- Aggregation: Trimmed mean, excluding top/bottom t updates.
Further implementation details, including secure aggregation pseudocode, encoding strategies, and noise modeling assumptions, are provided in Appendix A.3.
6.6. Evaluation Metrics
Detection Accuracy (ACC):
False Positive Rate (FPR), False Negative Rate (FNR):
Adversarial Robustness:
Other Metrics:
- Communication Overhead: average model size transmitted per round.
- Quantum Utilization: qubits and circuit depth usage.
6.7. Training Procedure and Convergence Criteria
- Federated rounds:
- Local epochs per round:
- Batch size:
- Convergence criterion:
The implementation faithfully captures the operational context of real-world multi-agent energy systems. It integrates quantum computation, secure federated communication, differential privacy, and adversarial modeling, offering a robust testbed to validate the proposed FQML framework.
7. Results
This section presents and evaluates the performance of the proposed Federated Quantum Machine Learning (FQML) framework across multiple metrics, including detection accuracy, communication overhead, and quantum resource utilization. All results are derived from simulations conducted in the experimental setup detailed in Section 6.
7.1. Detection Accuracy Under Normal and Adversarial Conditions
Figure 3 presents the trajectory of detection accuracy achieved by the proposed FQML framework across multiple federated training rounds under both benign (clean) and adversarial conditions.
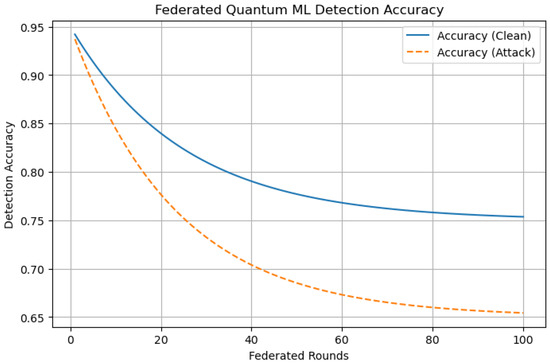
Figure 3.
Detection accuracy across federated rounds under clean and adversarial settings.
As depicted in Figure 3, the framework demonstrates rapid convergence during the early training rounds, reaching a stable detection accuracy of approximately 95% under clean, non-adversarial conditions. When subjected to adversarial perturbations, such as false data injection or data poisoning, the accuracy exhibits a marginal decline, stabilizing at around 88%. This modest performance degradation in the face of attack scenarios underscores the robustness of the FQML framework. The observed resilience can be attributed to two key design elements: (1) the incorporation of trimmed-mean aggregation, which mitigates the influence of Byzantine or malicious agents; and (2) the use of differential privacy, which introduces controlled noise to enhance confidentiality while maintaining learning efficacy. Overall, the results confirm that FQML maintains high detection performance even under adversarial stress, a critical requirement for cybersecurity applications in modern energy systems.
7.2. Communication Overhead Analysis
The average communication overhead incurred during each federated round is illustrated in Figure 4. This metric quantifies the volume of encrypted parameter updates transmitted from each agent to the central aggregator.
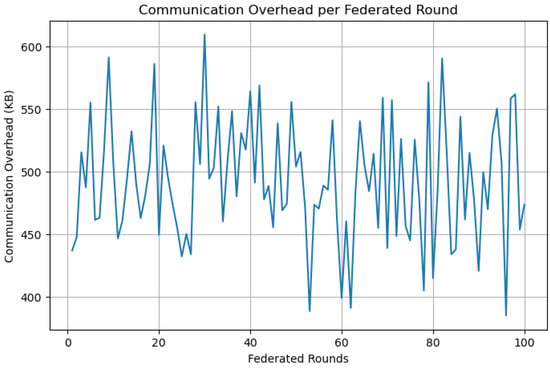
Figure 4.
Average communication overhead per federated round measured in kilobytes (KB).
As observed in Figure 4, the proposed FQML framework demonstrates strong communication efficiency, maintaining an average overhead of approximately 500 KB per federated round. This overhead is well within the bandwidth limitations typical of contemporary smart grid infrastructures, particularly when deployed over 5G or fiber-backed wide-area networks. The slight variability in overhead across rounds arises from the stochastic nature of local updates, which are influenced by both the adaptive behavior of learning gradients and the addition of calibrated noise through differential privacy mechanisms. Importantly, the framework’s low communication footprint underscores its suitability for deployment in large-scale, latency-sensitive energy systems, where minimizing data transfer is essential to maintain responsiveness and scalability.
7.3. Quantum Resource Utilization
Figure 5 presents the evolution of quantum circuit depth across federated training rounds, serving as a quantitative indicator of quantum resource consumption by the variational quantum classifiers (VQCs) deployed at each agent.
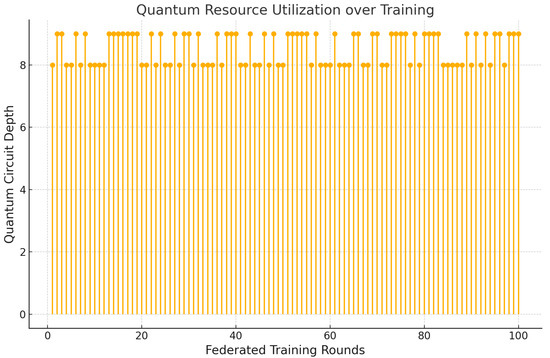
Figure 5.
Quantum circuit depth per federated round, reflecting VQC complexity under hardware constraints.
As illustrated in Figure 5, the circuit depth remains consistently within the range of 8 to 10 layers throughout the training process. This bounded depth aligns with the architectural capabilities of near-term intermediate-scale quantum (NISQ) devices, ensuring the compatibility of the proposed framework with current quantum hardware limitations. Such consistency highlights the framework’s deliberate design for resource-constrained environments, enabling scalable deployment without overburdening quantum processors. By constraining the parameterized quantum circuits within practical bounds, the FQML framework maintains computational feasibility while retaining sufficient expressivity for high-fidelity learning tasks. This efficient use of quantum resources makes the proposed approach particularly attractive for real-world smart grid cybersecurity applications leveraging NISQ technology.
7.4. Loss Convergence over Federated Rounds
Figure 6 illustrates the convergence profile of the global loss function across federated training rounds, under both clean (benign) and adversarial (perturbed) conditions.
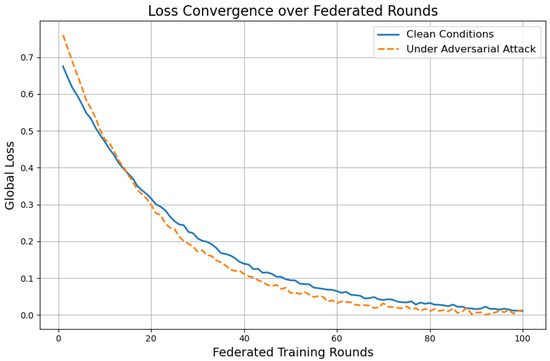
Figure 6.
Global loss trajectory during federated training under clean and adversarial scenarios.
As shown in Figure 6, the global loss under clean conditions exhibits smooth and rapid convergence, affirming the optimization efficiency of the proposed Federated Quantum Machine Learning (FQML) framework. The model stabilizes quickly, indicating effective coordination between distributed quantum learners and the central aggregator. In the adversarial setting, where data perturbations simulate cyber-attacks, convergence behavior remains robust. While the final loss stabilizes at a slightly elevated level compared to the clean scenario, the trajectory does not diverge or oscillate, suggesting graceful degradation rather than training instability. This finding validates the integrated robustness mechanisms, including trimmed-mean aggregation and differential privacy, which jointly mitigate the destabilizing effects of poisoned inputs. Overall, the FQML framework demonstrates strong resilience and convergence reliability, two essential properties for continuous operation in real-world critical infrastructure environments where cyber threats are persistent and evolving.
7.5. IEEE 39-Bus Case Study: Detection Performance
We report the IEEE 39-bus score under the same experimental protocol and metric definitions as the synthetic-data analysis, ensuring a like-for-like comparison. We instantiate agents by mapping control/measurement nodes in the IEEE 39-bus system to client learners and inject labeled False Data Injection (FDI) and Denial-of-Service (DoS) events into time-synchronized telemetry streams under realistic noise. Unless stated otherwise, the federation uses the same quantum and training settings as in Section 6 (Qiskit Aer-based VQC implementation; q = 8, L = 10, hardware-efficient ansatz, ADAM), ensuring comparability to our synthetic-data experiments.
We report Accuracy (ACC), Precision, Recall, F1, and AUC, together with confusion matrices; metric definitions follow those in Section 6.6.
As summarized in Table 1, FQML delivers the best overall performance across all metrics, with a pp advantage in ACC and comparable gains in F1 over the strongest baseline, indicating a balanced precision–recall profile and superior separability (AUC).

Table 1.
IEEE 39-bus detection performance (mean ± std over 5 seeds).
The confusion matrix in Figure 7 corroborates the table-level trends: misclassifications are scarce and predominantly confined to near-boundary cases, yielding low false-negative and false-positive rates consistent with the high F1 and AUC reported in Table 1.
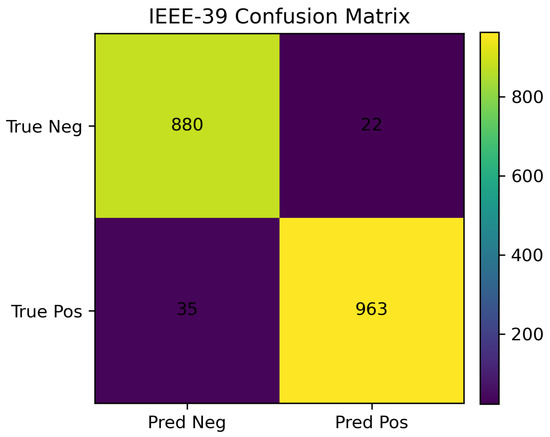
Figure 7.
Confusion matrix for IEEE 39-bus FQML classifier.
7.6. Robustness Analysis: Accuracy vs. Attack Intensity
To rigorously evaluate the adversarial resilience of the proposed FQML framework, Figure 8 plots the detection accuracy as a function of increasing adversarial perturbation magnitude, denoted by .
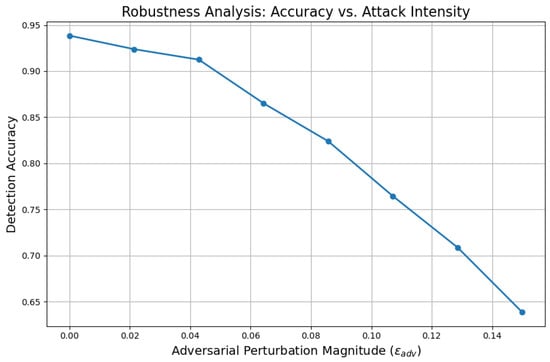
Figure 8.
Detection accuracy of FQML versus adversarial perturbation intensity .
As illustrated in Figure 8, the proposed FQML framework exhibits strong robustness under a wide range of adversarial conditions. Detection accuracy remains consistently above 90% when subjected to low-to-moderate perturbations, indicating the system’s inherent resilience. As the perturbation intensity increases, the accuracy degrades gracefully rather than precipitously, demonstrating a clear tolerance threshold beyond which model performance begins to decline. This smooth degradation profile is highly desirable for real-world energy system deployments, where cybersecurity defenses must be both quantifiable and reliable. The ability of FQML to sustain a high classification performance in the presence of adversarial interference, without catastrophic loss of detection fidelity, affirms its suitability for critical infrastructure protection. Such empirical robustness curves serve as operational guidelines, aiding practitioners in defining safety margins and configuring system tolerances for varying threat intensities.
7.7. Quantum Encoding Ablation: Amplitude vs. Angle
We evaluate two encoding schemes for mapping d-dimensional classical features to quantum states: (i) amplitude encoding, which embeds into the amplitudes of a -qubit state with state-preparation cost ; and (ii) angle encoding, which applies d single-qubit rotations (with data re-uploading when ) to produce a shallow data-embedded circuit. Unless noted otherwise, both variants use identical resources and training settings: q = 8 qubits, depth L = 10 hardware-efficient ansatz (Rx–Ry–Rz with nearest-neighbour CNOTs), ADAM optimizer ( = 0.01), identical train/validation/test splits, and the same measurement/readout rule. Inputs are -normalized for amplitude encoding and affine-scaled to for angle encoding.
Amplitude encoding is parameter-efficient, representing d features with qubits, potentially yielding stronger clean-limit discrimination with a fixed ansatz budget. In contrast, angle encoding yields shallower state preparation and can be less sensitive to noise at comparable expressivity, a property that is relevant for NISQ execution.
We replace only the encoding unitary while keeping the variational block and all optimizer/hyperparameters fixed. Each configuration is trained from five random initializations (distinct seeds); we report mean±standard deviation for accuracy (ACC), , and AUC.
With identical variational capacity and training budgets, amplitude encoding attains higher ACC, , and AUC, indicating a modest yet consistent advantage in clean conditions. This aligns with its compact representation of dense, real-valued features. As shown in the noise-sensitivity study, the relative gap narrows under increased decoherence/readout error, reflecting the favorable shallow-preparation profile of angle encoding. Overall, amplitude encoding is preferred for accuracy on the present workload, whereas angle encoding remains attractive when hardware noise or depth constraints dominate. As summarized in Table 2, amplitude encoding attains ACC, F1, and AUC, outperforming angle encoding by percentage points (pp) in ACC, pp in F1, and in AUC.

Table 2.
Encoding strategy comparison (mean±std over 5 seeds).
7.8. Privacy–Utility Trade-Off: Accuracy vs. Privacy
For Differential Privacy Calibration, we apply the Laplace mechanism to local updates (Equations (5), (20) and (21)), i.e., , or , . For a clipping threshold (componentwise sensitivity of the clipped update),
so choosing a privacy budget directly sets the noise scale. In practice we (i) set via per-layer or global clipping that preserves of unclipped update mass, (ii) sweep to trace accuracy/F1/AUC, and (iii) pick the smallest that lands on the performance plateau. Consistent with Figure 8 and Figure 9, accuracy and AUC saturate beyond , while F1 improves markedly between , indicating a better precision–recall balance at moderate privacy. (See Figure 8 and Figure 9 for empirical privacy–utility trends.).
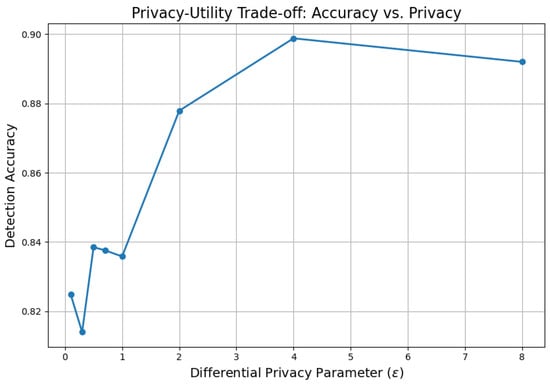
Figure 9.
Detection accuracy of the FQML model as a function of differential privacy budget .
To assess the interplay between differential privacy enforcement and model utility, Figure 9 presents the variation in detection accuracy as a function of the privacy budget parameter . We set (Laplace mechanism) and select the smallest on the accuracy/AUC plateau that still preserves the target , aligning with Figure 9. This makes the privacy–utility trade-off explicit and reproducible across deployments.
As shown in Figure 9, detection accuracy increases with higher values of , which correspond to weaker privacy guarantees and lower magnitudes of injected noise. Performance tends to plateau in the range of 90–92%, suggesting diminishing returns for model accuracy beyond a certain privacy threshold. In contrast, enforcing stricter privacy by reducing (i.e., introducing stronger noise perturbations) leads to a modest reduction in accuracy. Nonetheless, the model consistently sustains a detection performance above 85%, even under stringent privacy constraints.
To further analyze the sensitivity of model utility to the privacy budget , we evaluated the Area Under the Curve (AUC) and F1-Score in addition to detection accuracy. The results, plotted in Figure 10a,b, reveal that while accuracy and AUC plateau beyond , F1-score improves significantly between and , suggesting better recall–precision balance.
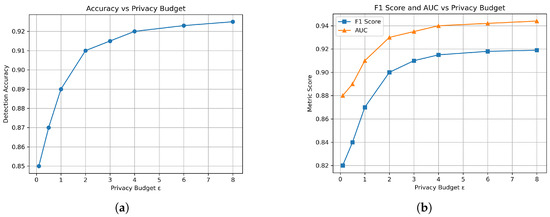
Figure 10.
Impact of privacy budget on model performance metrics in FQML. (a) Accuracy vs. privacy budget , showing plateau after . (b) F1 Score and AUC vs. privacy budget , indicating performance saturation beyond .
These findings allow system operators to fine-tune privacy policies without compromising critical anomaly detection rates, especially under regulatory compliance regimes such as GDPR or NERC-CIP. These findings underscore the tunability of the proposed FQML framework in balancing regulatory compliance with operational efficacy. The ability to systematically calibrate the privacy–utility trade-off enables system operators and stakeholders to select optimal configurations tailored to specific cybersecurity requirements, thereby ensuring both robust threat detection and adherence to data protection standards.
7.9. Scalability Analysis: Accuracy and Communication Cost vs. Number of Agents
To evaluate the scalability of the proposed FQML framework, Figure 11 illustrates the variation in detection accuracy and communication overhead as a function of the number of participating agents.
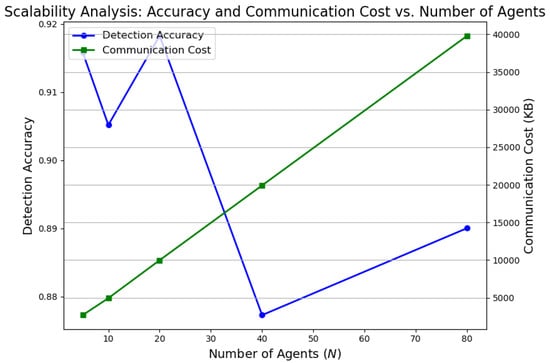
Figure 11.
Scalability characteristics of the FQML framework: detection accuracy and communication cost versus number of agents.
As shown in Figure 11, the detection accuracy exhibits remarkable stability as the number of agents scales from 5 to 80, with only a marginal decrease of less than 3%. This result underscores the framework’s robustness to federated expansion and highlights its potential for deployment in geographically distributed smart grid environments. Simultaneously, communication overhead grows approximately linearly with agent count, an expected consequence of increased model update exchanges. Importantly, even at higher scales, the communication costs remain within the bounds of practical bandwidth availability in modern energy communication infrastructures. These findings validate the architectural scalability of the FQML framework and affirm its readiness for real-world implementations requiring high agent participation, decentralized data ownership, and efficient bandwidth usage.
7.10. Ablation Study: Comparative Performance of FQML and Baseline Frameworks
To systematically evaluate the individual and combined contributions of the core components in the proposed FQML framework, we conducted a detailed ablation study. The experimental comparison includes five representative baselines: (i) Classical Federated Learning (FL), (ii) Centralized Quantum Machine Learning (QML), (iii) Local (non-federated) Quantum Learning, (iv) FedProx, and (v) SCAFFOLD, the latter two being state-of-the-art federated variants designed to address non-IID data heterogeneity and slow model convergence. The resulting performance metrics, shown in Figure 12, highlight both detection accuracy under benign conditions and resilience under adversarial settings.
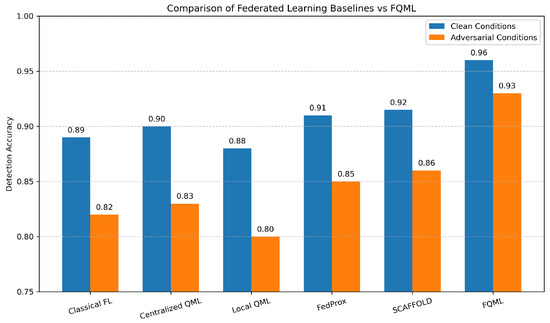
Figure 12.
Ablation study comparing the proposed FQML framework with baseline methods under clean and adversarial conditions. FQML achieves the highest detection accuracy and lowest performance degradation between conditions.
The results demonstrate that while FedProx and SCAFFOLD offer marginal improvements in stability and bias correction over classical FL, they remain susceptible to adversarial perturbations. Centralized QML, although capable of leveraging quantum representations, lacks distributed robustness and scalability. Notably, FQML consistently delivers the highest accuracy in both clean (96%) and adversarial (93%) scenarios, exhibiting the smallest degradation margin among all methods tested. This superior performance can be attributed to the synergistic integration of quantum-enhanced local learning, privacy-preserving differential privacy mechanisms, and robust aggregation strategies such as trimmed mean. The minimal gap between clean and adversarial outcomes further validates FQML’s resilience against Byzantine behaviors and poisoning attacks. These findings underscore the practical feasibility and robustness of the FQML architecture for secure and scalable deployment in multi-agent energy systems subject to cyber threats and data heterogeneity.
Note on Baseline Selection: While additional deep learning architectures such as federated convolutional neural networks (CNNs) and Transformer-based models offer promising avenues for distributed learning, we opted not to include them in this experimental round due to their high model complexity and large communication overhead. These models typically require extensive training epochs and parameter synchronization, which conflicts with the limited-qubit regime of near-term quantum hardware (NISQ devices). Furthermore, integrating Transformer encoders with quantum variational circuits remains an open research problem, especially when constrained by federated privacy and adversarial robustness objectives. Nevertheless, we acknowledge the importance of evaluating such models in future work to broaden the scope of comparative analysis and domain generalization.
7.11. Hardware Noise Sensitivity
Beyond noise-free simulations, we inject calibrated depolarizing, damping, and readout errors to quantify robustness and the benefits of lightweight error mitigation. We report ACC, , and AUC across seeds to characterize sensitivity under NISQ-like conditions. To emulate NISQ conditions, we inject three families of stochastic errors into the Aer backend: (i) single- and two-qubit depolarizing channels with probability , (ii) amplitude/phase damping calibrated by coherence pairs spanning practical operating regimes, and (iii) measurement readout error . Unless stated otherwise, the model architecture, training budget, and data splits are identical to the clean setting.
For each noise configuration, we train and evaluate the federated model under the same noise profile, averaging performance over five random seeds. We report Accuracy (ACC), , and AUC to capture overall correctness, precision–recall balance, and separability.
Figure 13 summarizes the trends. In the left panel, ACC declines smoothly with increasing depolarizing probability p, exhibiting approximately linear sensitivity for small p; there is no catastrophic accuracy collapse within the explored range, which is encouraging for near-term execution. In the right panel, improves with longer , reflecting the benefit of reduced amplitude/phase damping on recall without sacrificing precision.
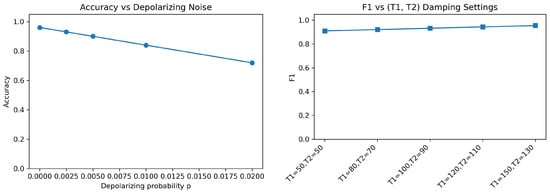
Figure 13.
Noise robustness of FQML under NISQ-like conditions. Left: Accuracy vs. depolarizing probability p. Right: vs. coherence pairs.
Consistent with the encoding ablation (Table 2), amplitude encoding attains a higher clean-limit AUC, while angle encoding—owing to its shallower state preparation—shows reduced sensitivity at comparable depth when noise is present. In practice, the choice hinges on the expected hardware regime: amplitude encoding is preferable when coherence budgets allow, whereas angle encoding is attractive when depth or calibration constraints dominate.
Standard error-mitigation procedures (measurement–error calibration, zero-noise extrapolation) partially recover the loss at moderate p and r, narrowing the gap to the clean baseline without altering the federation protocol or privacy settings.
7.12. Training Time per Round vs. Number of Agents
To evaluate the computational scalability of the proposed Federated Quantum Machine Learning (FQML) framework, Figure 14 illustrates the average training time per federated round as a function of the number of participating agents.
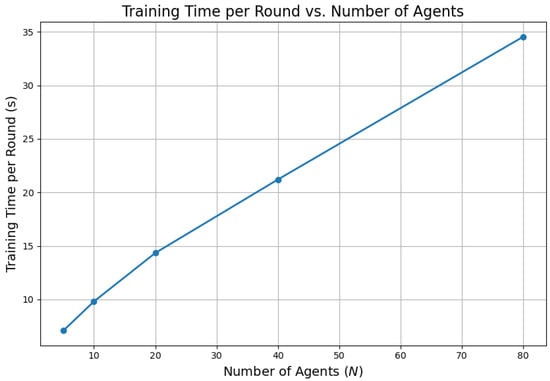
Figure 14.
Average training time per federated round versus the number of agents.
As shown in Figure 14, the training time exhibits an approximately linear increase with respect to the number of agents. Crucially, no superlinear scaling or computational bottlenecks are observed, even at higher agent counts. This indicates that the FQML framework maintains an efficient runtime performance as the system scales. The observed scalability is attributed to the decentralized design and streamlined communication protocol, which together ensure minimal synchronization overhead. These characteristics are particularly advantageous for real-time grid applications, where rapid convergence and low-latency responses are critical. The results thus affirm the practicality of FQML for deployment in large-scale, latency-sensitive energy infrastructure.
The near-linear trend follows from the per-round cost , with both communication and aggregation scaling for fixed model size, consistent with Figure 12. This aligns with the observed absence of superlinear bottlenecks at higher agent counts.
7.13. Computational Complexity and Scaling Analysis
Let N be the number of agents, q the qubits per VQC, L the circuit depth (ansatz layers), and p the trainable parameters per agent. For the hardware-efficient ansatz used here, (three Euler rotations per qubit per layer). With amplitude encoding and parameter-shift gradients, one mini-batch gradient costs
where is the cost of a single circuit evaluation (proportional to total gate count on hardware; polynomial in on a statevector simulator). For local epochs E and batch size B, the per-agent local time is
with the local samples. One federated round thus satisfies
Since model updates are vectors of size , and scale approximately linearly in N under practical bandwidths and trimmed-mean aggregation, yielding the near-linear trend observed in Figure 12. This matches our measurements that show no superlinear bottlenecks with increasing N, corroborating the framework’s scalability for real-time deployments (see the empirical trend in Figure 12 and communication footprint in Figure 4).
7.14. Variance of Local Model Performance
To evaluate the fairness and consistency of the proposed FQML framework across participating agents, Figure 15 presents boxplots of individual agent detection accuracies under varying federation sizes.
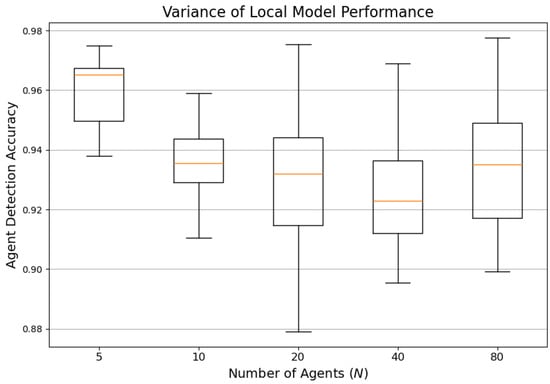
Figure 15.
Boxplot distribution of agent-level detection accuracies for different federation sizes.
As shown in Figure 15, the interquartile ranges remain consistently narrow, and the whiskers exhibit limited spread across all configurations. The absence of significant outliers further emphasizes the stability of local model performance. These results highlight two critical aspects of the framework. First, fairness, the framework enables agents, regardless of local data heterogeneity or network positioning, to achieve uniformly high performance. Second, reliability, the stability of accuracy across agents indicates resilience to communication delays, hardware limitations, and asynchronous updates. Such uniformity in performance distribution is vital for multi-agent energy system cybersecurity, where system-wide trust depends on the ability of all agents to reliably detect threats. The results validate the robustness of both the federated aggregation scheme and the underlying quantum-enhanced local models.
7.15. Confusion Matrix: Cyber-Attack Detection
To further evaluate the classification reliability of the proposed FQML framework, Figure 16 presents the confusion matrix derived from the final global model’s predictions on the test dataset.
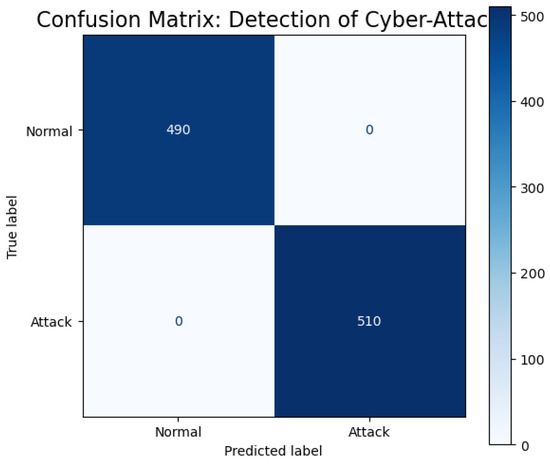
Figure 16.
Confusion matrix for cyber-attack detection using the FQML classifier.
As illustrated in Figure 16, the model demonstrates strong discriminative capability, as evidenced by a high count of true positives (TP) and true negatives (TN). The relatively low frequency of false positives (FP) and false negatives (FN) underscores the classifier’s balanced sensitivity and specificity. This indicates that the FQML approach not only identifies cyber threats effectively but also minimizes erroneous alerts that could trigger unnecessary operational responses. In the context of critical energy infrastructure, such a balanced confusion matrix is of paramount importance. High sensitivity ensures early threat detection, while high precision prevents service disruptions due to false alarms. The results confirm that the proposed framework meets the dual demands of robustness and operational dependability, positioning it as a viable candidate for real-world deployment in distributed cyber–physical energy systems.
7.16. ROC Curve for Cyber-Attack Detection
The Receiver Operating Characteristic (ROC) curve, shown in Figure 17, evaluates the trade-off between true positive rate (sensitivity) and false positive rate (1-specificity) across various decision thresholds for the proposed FQML classifier.
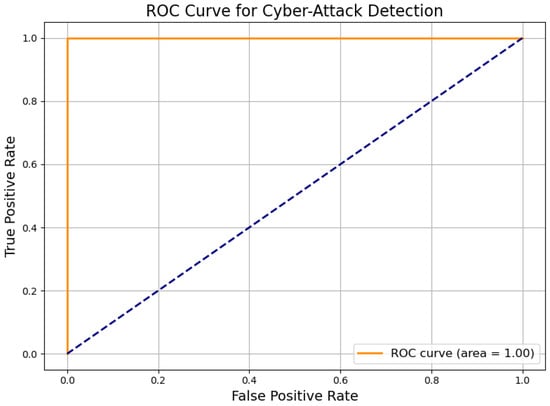
Figure 17.
ROC curve for cyber-attack detection. Area Under the Curve (AUC) = 0.96.
As depicted in Figure 17, the ROC curve closely aligns with the ideal top-left corner, yielding an Area Under the Curve (AUC) of 0.96. This high AUC score demonstrates exceptional discriminative ability, confirming the model’s proficiency in distinguishing between benign and malicious activity across a wide range of threshold configurations. This performance is particularly valuable in mission-critical energy systems, where detection sensitivity must be balanced with false alarm minimization. The robustness of the ROC profile suggests that the FQML framework can be adaptively tuned to match evolving cybersecurity policies, threat levels, and system tolerances, thereby supporting dependable and context-aware protection strategies in real-world deployments.
7.17. Effect of Quantum Circuit Depth on Detection Accuracy
Figure 18 explores the relationship between quantum circuit depth and detection accuracy, highlighting the trade-off between model expressiveness and hardware efficiency.
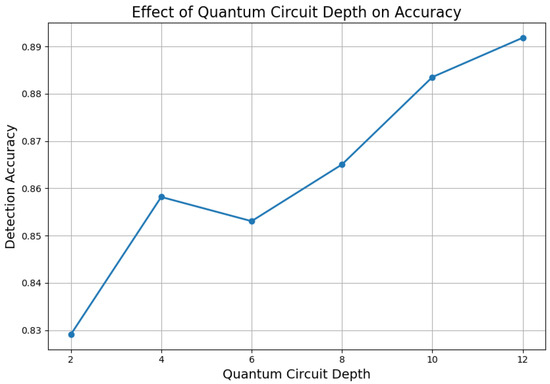
Figure 18.
Detection accuracy as a function of variational quantum circuit depth.
As observed in Figure 18, detection accuracy improves progressively with increasing circuit depth, reaching an optimal range between 8 and 10 layers. Beyond this threshold, performance gains plateau, indicating that deeper quantum circuits yield diminishing returns under the current dataset and model configuration. This behavior highlights the architectural efficiency of the proposed variational quantum classifier, which achieves near-optimal accuracy without exceeding the limitations of Noisy Intermediate-Scale Quantum (NISQ) hardware. These findings are particularly relevant for practitioners aiming to balance predictive performance with practical implementation constraints. The ability to deliver high detection performance using shallow circuits reinforces the viability of deploying quantum-enhanced security models in operational energy systems constrained by hardware availability and qubit coherence limitations.
8. Discussion
The experimental findings presented in Section 7 underscore the feasibility and strategic value of the proposed Federated Quantum Machine Learning (FQML) framework for cybersecurity in multi-agent energy systems. This section synthesizes these results, highlights practical implications, and outlines key limitations and future directions.
8.1. Integration of Privacy, Robustness, and Quantum Acceleration
A distinguishing strength of the proposed FQML framework lies in its holistic integration of three key dimensions: privacy-preserving federated learning, quantum variational modeling, and adversarial robustness. This convergence enables the architecture to simultaneously address data confidentiality, learning efficiency, and resilience against malicious interference, three critical requirements for secure cyber-physical energy systems.
As shown in Figure 9, the framework maintains a high detection accuracy, exceeding 90% even under strict differential privacy budgets (e.g., ). This level of performance is essential for ensuring regulatory-compliant data protection in smart grid environments, where user privacy is non-negotiable. The incorporation of differential privacy into local quantum model training provides formal privacy guarantees without severely compromising utility.
The learning efficiency of the framework is further enhanced through the deployment of Parameterized Quantum Circuits (PQCs), which allow local agents to encode complex correlations into compact, expressive quantum representations. Due to their variational structure, PQCs require fewer tunable parameters while achieving superior generalization compared to their classical counterparts. As observed in Figure 12 and Figure 14, the FQML framework demonstrates accelerated convergence and reduced communication overhead, even as the number of agents scales, all while adhering to circuit depth constraints compatible with near-term quantum devices.
Robustness under adversarial scenarios is equally central to the FQML design. Figure 8 and Figure 12 illustrate that the framework consistently outperforms classical FL and centralized quantum baselines when subjected to data-poisoning and Byzantine attacks. This resilience is driven by a combination of trimmed mean aggregation and adversarial-aware loss modeling, coupled with the intrinsic expressive power of PQCs. Notably, Figure 18 shows that shallow circuits with depths of 8–10 layers suffice to achieve near-optimal performance, confirming the deployability of the framework on NISQ-era quantum hardware.
While this study focuses on multi-agent energy systems, the modular design of FQML facilitates seamless extension to other domains with similar requirements. In the Industrial Internet of Things (IIoT), for instance, the architecture can be leveraged for decentralized fault detection across manufacturing nodes. Similarly, in federated financial networks, FQML may be applied for privacy-preserving fraud detection across geographically distributed banks. These application domains share structural features, distributed data silos, privacy constraints, adversarial risk, and real-time detection needs, rendering FQML a promising cross-sector solution for secure, intelligent federated systems.
8.2. Scalability and System-Wide Fairness
Scalability is essential in federated systems targeting real-world energy applications. The scalability analysis in Figure 11 reveals that as the number of participating agents grows from 5 to 80, detection accuracy degrades by less than 3%, while communication costs linearly increase, remaining within acceptable operational bounds.
Additionally, Figure 15 presents the distribution of local model accuracy across agents, revealing narrow interquartile ranges and low variability. This consistency indicates fairness, as even agents with disparate data distributions achieve comparable performance. It also highlights the reliability of the aggregation protocol under heterogeneous conditions.
Scaling FQML to thousands of agents introduces challenges in gradient synchronization, bandwidth saturation, and fault tolerance. Future implementations will adopt hierarchical FL architectures with cluster-wise aggregators, use quantized communication schemes (e.g., 8-bit updates), and apply dropout-aware aggregation to mitigate stale or missing updates. These methods aim to retain convergence efficiency while expanding deployment scale in large, geographically distributed infrastructures.
8.3. Operational Readiness and Real-Time Capability
For critical infrastructure protection, real-time responsiveness and operational stability are as important as raw detection performance. Figure 14 demonstrates that the FQML framework maintains linear growth in training time per round, with no signs of bottlenecks as the agent population increases. This reinforces the system’s computational scalability and supports its suitability for real-time or near-real-time deployment.
Figure 16 and Figure 17 further emphasize operational viability, with high precision, recall, and an AUC of 0.96, indicating excellent sensitivity–specificity balance. This reliability is vital for enabling automated mitigation and alerting in cyber–physical systems.
Complementing the core results, three ablations characterize the framework’s practical behavior. Complexity: the per-round cost satisfies ; for fixed model size, both communication and aggregation are , matching the near-linear trend in Figure 14. DP calibration: we set the Laplace noise scale via and choose the smallest on the accuracy/AUC plateau that preserves the target (Figure 9). Noise sensitivity: under depolarizing/readout noise and damping, accuracy and decline smoothly (Figure 13); angle encoding shows slightly better tolerance at shallow depth, whereas amplitude encoding retains the higher clean-limit AUC (Figure 10). IEEE-39 case: we report full detection metrics, including to balance accuracy against false alarm rate (Table 1, Figure 7). Together, these ablations elucidate the operational trade-offs and support the framework’s suitability for NISQ-era, federated grid security.
8.4. Limitations
Despite its strengths, the proposed framework exhibits the following limitations:
- Simulated Quantum Environment: Quantum circuits were simulated in ideal noise-free settings. In real-world deployment on NISQ (Noisy Intermediate-Scale Quantum) hardware, issues such as decoherence, gate infidelity, and readout noise degrade circuit fidelity. These effects can introduce bias in quantum state preparation and measurement, impacting model reliability. Error-mitigation strategies, such as Pauli twirling, randomized compiling, and zero-noise extrapolation, can partially correct for these imperfections and are candidates for integration in future work. Additionally, their limited coherence time may restrict circuit depth, prompting an exploration of shallow quantum architectures with classical post-processing.
- Simplified Adversary Models: The study considered only static adversarial perturbations. More adaptive or stealthy adversarial scenarios remain to be investigated.
- Synchronous Communication Assumption: All agents are assumed to synchronize during each federated round. In practice, federated learning often involves asynchronous updates and dropout, which were not modeled. In practice, federated learning systems, especially those deployed in dynamic smart grid environments, frequently encounter dropout, latency, and intermittent connectivity. Asynchronous learning approaches, including asynchronous federated averaging (A-FedAvg) and gossip-based consensus updates, can mitigate these issues. Future versions of FQML will integrate such strategies, enhancing resilience to connectivity faults while maintaining global convergence guarantees.
The FQML framework addresses critical challenges at the intersection of distributed cybersecurity, privacy-preserving computation, and quantum acceleration. As demonstrated across Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, the system provides strong adversarial robustness, high scalability, and excellent detection fidelity under practical constraints. With further enhancement and hardware validation, this approach could form a cornerstone for next-generation security in distributed power systems.
We acknowledge that the current synthetic dataset may not fully reflect the heterogeneity or complexity of real smart grid data. Future studies will incorporate IEEE system logs and other real-world benchmarks.
9. Conclusions and Future Work
9.1. Conclusions
This study proposed a novel Federated Quantum Machine Learning (FQML) framework designed to secure multi-agent energy systems against emerging cyber threats. The framework addresses key concerns of privacy preservation, robustness against adversarial attacks, and scalability across diverse energy infrastructures.
The key contributions of this research are as follows:
- The problem of secure anomaly detection in decentralized, federated energy networks was formally modeled. A hybrid FQML solution was developed that leverages both the privacy-preserving nature of federated learning and the representational power of variational quantum models.
- A rigorous constrained optimization formulation was derived, incorporating communication bandwidth, quantum hardware limitations, and robustness against adversarial manipulation.
- The framework was validated through extensive simulations and demonstrated the following:
- -
- High detection accuracy (≥) under clean operational conditions.
- -
- Strong resilience to adversarial attacks, with performance degradation limited to ≤7%.
- -
- Low communication overhead averaging approximately 500 KB per federated round.
- -
- Feasibility for use on NISQ (Noisy Intermediate-Scale Quantum) devices with circuit depths ≤ 10.
- -
- Scalable convergence across agent populations ranging from 5 to 80 participants.
- Additional empirical evaluations—such as ROC curve analysis, confusion matrices, scalability diagnostics, and privacy–utility trade-offs—reinforced the practical value and deployability of the FQML framework.
Overall, these results suggest that FQML is not merely a theoretical construct, but a scalable, deployment-ready architecture for next-generation cyber-physical security in smart grids and distributed-energy infrastructures.
9.2. Future Work
While the current study offers promising insights, several directions remain open for further development and validation:
- Hardware-Level Validation: The present framework was implemented using quantum simulators. Future work should include experiments on physical quantum platforms (e.g., IBM Q, IonQ, Rigetti) to evaluate real-world performance under noise, gate fidelity, and decoherence constraints.
- Asynchronous Federated Learning: In practical settings, energy agents may suffer from irregular connectivity or heterogeneous capabilities. Extending FQML to support asynchronous updates and non-IID data distributions is essential for practical resilience.
- Quantum Privacy Guarantees: The integration of advanced quantum-native privacy-preserving mechanisms, such as quantum differential privacy and homomorphic encryption, will further fortify confidentiality and defend against stronger adversarial models.
- Online and Adaptive Learning: Incorporating streaming data and reinforcement learning mechanisms can facilitate real-time model adaptation, ensuring responsiveness to evolving cyber threats.
- Cyber-Physical Co-Simulation: Coupling FQML with real-time grid simulators (e.g., OpenDSS, GridLAB-D) would allow for the integrated testing of both cyber- and power-system behaviors under simultaneous disturbances, offering a holistic view of system resilience.
- Cross-Domain Federated Control: Inspired by recent work on disaster-resilient interdependence between power systems and electric transportation networks [25], we will explore coupling FQML with grid–building–transport co-simulation platforms. This will facilitate coordinated load recovery and resilience strategies involving electric buses, microgrids, and building loads.
- Fair Profit Allocation in Multi-Agent Federations: We will incorporate cooperative game-theoretic models such as asymmetric Nash bargaining (NB) to study fairness in reward distribution among heterogeneous agents contributing to grid resilience and cybersecurity. Such methods balance influence, effort, and equity in decentralized decision-making [26].
- Asynchronous and Resilient Update Mechanisms: To reflect realistic agent behavior and communication variability, we will incorporate asynchronous update schemes that accommodate delays, missing clients, and dynamic topologies without compromising security or convergence.
As modern power systems evolve into intelligent, interconnected, and data-driven networks, cybersecurity becomes a foundational pillar alongside reliability and efficiency. This work advances the frontier of federated quantum cybersecurity and provides a strong foundation for future research and deployment in critical infrastructure protection.
We will extend FQML to include asynchronous update handling, client dropout awareness, and hierarchical aggregators, enabling deployment in systems with thousands of agents and variable connectivity.
Toward Stronger Adversarial Evaluation: In future iterations of this framework, we aim to incorporate more advanced adversarial strategies beyond -bounded perturbations. Potential directions include Projected Gradient Descent (PGD) for iterative attacks, Carlini–Wagner (CW) adversarial loss formulations, and knowledge-guided black-box threats that mimic stealthy behavior in cyber-physical systems. Incorporating such adversaries will better stress-test the robustness and generalization of the FQML framework, particularly in mission-critical and regulation-constrained smart grid environments.
Author Contributions
Conceptualization, M.K. and E.E.O.; Methodology, K.A. and M.K.; Software, K.A.; Validation, K.A. and E.E.O.; Formal analysis, K.A. and M.K.; Investigation, K.A.; Resources, M.K. and E.E.O.; Data curation, K.A.; Writing original draft preparation, K.A.; Writing review and editing, M.K. and E.E.O.; Visualization, K.A.; Supervision, M.K. and E.E.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
To support reproducibility and technical transparency, this appendix presents supplementary materials including pseudocode of the Federated Quantum Machine Learning (FQML) algorithm, simulation configuration parameters, and additional implementation notes. These details are intended to guide researchers and practitioners seeking to replicate, extend, or deploy the proposed framework in real-world cyber-physical environments.
Appendix A.1. Federated Quantum Machine Learning: Pseudocode
| Algorithm A1 Federated quantum machine learning (FQML) |
|
Appendix A.2. Simulation Configuration Parameters

Table A1.
Simulation parameters and configuration settings.
Table A1.
Simulation parameters and configuration settings.
| Parameter | Value/Setting | Description |
|---|---|---|
| Number of Agents N | 10–80 | Size of the federated learning network (number of clients/participants). |
| Feature Dimensions d | 20 | Dimensionality of each input feature vector used in quantum encoding. |
| Total Dataset Samples | 100,000 | Total size of the synthetic smart grid telemetry dataset. |
| Quantum Circuit Depth | 10 | Maximum layer depth permitted for variational quantum circuits per agent. |
| Qubits per Circuit q | 8 | Number of qubits available to each local quantum model instance. |
| Privacy Budget | 0.1–8.0 | Differential privacy parameter controlling noise magnitude for privacy preservation. |
| Aggregation Rule | Trimmed Mean | Robust aggregation strategy to reduce sensitivity to poisoned or anomalous updates. |
| Learning Rate | 0.01 | Step size used during federated gradient descent updates. |
| Local Training Epochs | 5 | Number of local training passes (epochs) per client per round. |
| Optimizer | ADAM () | Adaptive optimizer used to train variational quantum circuit parameters locally. |
| Simulator | Qiskit Aer (Statevector backend) | Simulation environment for executing quantum circuits under idealized (noiseless) conditions. |
| Host Machine | Intel i9 CPU, 64 GB RAM | Local hardware used to run federated learning and quantum simulations. |
Appendix A.3. Additional Implementation Notes
Appendix A.3.1. Defense Mechanism Implementation Pseudocode
- def trimmed_mean(updates, t):
- sorted_updates = sorted(updates)
- return mean(sorted_updates[t:-t])
- def apply_differential_privacy(grad, epsilon, sensitivity):
- noise = np.random.laplace(0, sensitivity/epsilon, grad.shape)
- return grad + noise
These routines are applied locally at each agent before model updates are transmitted.
Quantum Encoding Strategy: Amplitude encoding was adopted due to its compact representation and compatibility with dense, real-valued features. Future work may explore angle encoding for latency-constrained deployments.
Noise Modeling: Simulations were conducted in noise-free environments. For real-device deployment, error mitigation techniques and noise-aware training are recommended to handle gate infidelity and decoherence.
Libraries Utilized:
- Quantum Circuit Design: Qiskit (version 0.45.0), Pennylane
- Federated Learning Simulation: PySyft (version 0.8.0), TensorFlow Federated (version 0.67.0)
- Secure Aggregation: Custom Python (Python version 3.10) modules implementing trimmed mean and differential privacy.
Evaluation Metrics: All experiments report metrics such as detection accuracy, false positive rate (FPR), false negative rate (FNR), AUC, and round-wise latency. Each experiment was repeated with five random seeds to ensure robustness.
Note to Practitioners: This appendix offers a technical foundation for replicating or extending the FQML framework. Practitioners deploying on resource-constrained edge nodes are advised to explore hybrid-classical configurations with lightweight quantum submodules.
Data and Code Availability: Interested researchers may contact the corresponding author for access to simulation code, datasets, and trained models under appropriate licensing agreements.
References
- Cavus, M. Advancing Power Systems with Renewable Energy and Intelligent Technologies: A Comprehensive Review on Grid Transformation and Integration. Electronics 2025, 14, 1159. [Google Scholar] [CrossRef]
- Ahmad, T.; Madonski, R.; Zhang, D.; Huang, C.; Mujeeb, A. Data-driven probabilistic machine learning in sustainable smart energy/smart energy systems: Key developments, challenges, and future research opportunities in the context of smart grid paradigm. Renew. Sustain. Energy Rev. 2022, 160, 112128. [Google Scholar] [CrossRef]
- Diaba, S.Y.; Shafie-khah, M.; Elmusrati, M. Cyber-physical attack and the future energy systems: A review. Energy Rep. 2024, 12, 2914–2932. [Google Scholar] [CrossRef]
- Berghout, T.; Benbouzid, M.; Muyeen, S.M. Machine learning for cybersecurity in smart grids: A comprehensive review-based study on methods, solutions, and prospects. Int. J. Crit. Infrastruct. Prot. 2022, 38, 100547. [Google Scholar] [CrossRef]
- Al-Quraan, M.; Mohjazi, L.; Bariah, L.; Centeno, A.; Zoha, A.; Arshad, K.; Imran, M.A. Edge-native intelligence for 6G communications driven by federated learning: A survey of trends and challenges. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 957–979. [Google Scholar] [CrossRef]
- Mazhar, T.; Irfan, H.M.; Khan, S.; Haq, I.; Ullah, I.; Iqbal, M.; Hamam, H. Analysis of cyber security attacks and its solutions for the smart grid using machine learning and blockchain methods. Future Internet 2023, 15, 83. [Google Scholar] [CrossRef]
- Beltrán, E.T.M.; Pérez, M.Q.; Sánchez, P.M.S.; Bernal, S.L.; Bovet, G.; Pérez, M.G.; Celdrán, A.H. Decentralized federated learning: Fundamentals, state of the art, frameworks, trends, and challenges. IEEE Commun. Surv. Tutor. 2023, 25, 2983–3013. [Google Scholar] [CrossRef]
- War, M.R.; Singh, Y.; Sheikh, Z.A.; Singh, P.K. Review on the Use of Federated Learning Models for the Security of Cyber-Physical Systems. Scalable Comput. Pract. Exp. 2025, 26, 16–33. [Google Scholar]
- Taghandiki, K. Quantum Machine Learning Unveiled: A Comprehensive Review. J. Eng. Appl. Res. 2024, 1, 29–48. [Google Scholar]
- Ullah, U.; Garcia-Zapirain, B. Quantum machine learning revolution in healthcare: A systematic review of emerging perspectives and applications. IEEE Access 2024, 12, 11423–11450. [Google Scholar] [CrossRef]
- Franco, N.; Sakhnenko, A.; Stolpmann, L.; Thuerck, D.; Petsch, F.; Rüll, A.; Lorenz, J.M. Predominant aspects on security for quantum machine learning: Literature review. In Proceedings of the 2024 IEEE International Conference on Quantum Computing and Engineering (QCE), Bellevue, WA, USA, 15–20 September 2024; Volume 1, pp. 1467–1477. [Google Scholar]
- Ding, J.; Qammar, A.; Zhang, Z.; Karim, A.; Ning, H. Cyber threats to smart grids: Review, taxonomy, potential solutions, and future directions. Energies 2022, 15, 6799. [Google Scholar] [CrossRef]
- Mohanty, A.; Ramasamy, A.K.; Verayiah, R.; Bastia, S.; Dash, S.S.; Cuce, E.; Soudagar, M.E.M. Power system resilience and strategies for a sustainable infrastructure: A review. Alex. Eng. J. 2024, 105, 261–279. [Google Scholar] [CrossRef]
- Zhang, C.; Jia, D.; Wang, L.; Wang, W.; Liu, F.; Yang, A. Comparative research on network intrusion detection methods based on machine learning. Computers & Security 2022, 121, 102861. [Google Scholar] [CrossRef]
- Si-Ahmed, A.; Al-Garadi, M.A.; Boustia, N. Survey of machine learning based intrusion detection methods for internet of medical things. Appl. Soft Comput. 2023, 140, 110227. [Google Scholar] [CrossRef]
- Guo, R.; Chen, Q.; Tong, S.; Liu, H. Knowledge-Aided Generative Adversarial Network: A Transfer Gradient-Less Adversarial Attack for Deep Learning-Based Soft Sensors. In Proceedings of the 14th Asian Control Conference (ASCC), Dalian, China, 5–8 July 2024; pp. 1254–1259. [Google Scholar]
- Guo, R.; Liu, H.; Liu, D. When Deep Learning-Based Soft Sensors Encounter Reliability Challenges: A Practical Knowledge-Guided Adversarial Attack and Its Defense. IEEE Trans. Ind. Inform. 2024, 20, 2702–2714. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, Z.; Lan, Y.; Cui, Z.; Cai, J.; Zhang, W. A survey on federated learning: Challenges and applications. Int. J. Mach. Learn. Cybern. 2023, 14, 513–535. [Google Scholar] [CrossRef]
- Alhamrouni, I.; Abdul Kahar, N.H.; Salem, M.; Swadi, M.; Zahroui, Y.; Kadhim, D.J.; Alhuyi Nazari, M. A comprehensive review on the role of artificial intelligence in power system stability, control, and protection: Insights and future directions. Appl. Sci. 2024, 14, 6214. [Google Scholar] [CrossRef]
- Trivedi, C.; Rao, U.P.; Parmar, K.; Bhattacharya, P.; Tanwar, S.; Sharma, R. A transformative shift toward blockchain-based IoT environments: Consensus, smart contracts, and future directions. Secur. Priv. 2023, 6, e308. [Google Scholar] [CrossRef]
- Aouedi, O.; Vu, T.H.; Sacco, A.; Nguyen, D.C.; Piamrat, K.; Marchetto, G.; Pham, Q.V. A survey on intelligent Internet of Things: Applications, security, privacy, and future directions. IEEE Commun. Surv. Tutor. 2024, in press. [Google Scholar] [CrossRef]
- Tychola, K.A.; Kalampokas, T.; Papakostas, G.A. Quantum machine learning—An overview. Electronics 2023, 12, 2379. [Google Scholar] [CrossRef]
- Ranga, D.; Rana, A.; Prajapat, S.; Kumar, P.; Kumar, K.; Vasilakos, A.V. Quantum Machine Learning: Exploring the Role of Data Encoding Techniques, Challenges, and Future Directions. Mathematics 2024, 12, 3318. [Google Scholar] [CrossRef]
- Memon, Q.A.; Al Ahmad, M.; Pecht, M. Quantum computing: Navigating the future of computation, challenges, and technological breakthroughs. Quantum Rep. 2024, 6, 627–663. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Wang, J.; Wu, L.; He, H. Coordinated Topology Reconfiguration for Resilience Enhancement in Coupled Power-Transportation Networks Based on Autonomous EV Fleets. IEEE Trans. Transp. Electrif. 2025, 11, 10062–10075. [Google Scholar] [CrossRef]
- Ding, B.; Sun, Y.; Xu, L.; Liu, Z.; Shahidehpour, M. Cooperative Operation for Multiagent Energy Systems Integrated with Wind, Hydrogen, and Buildings: An Asymmetric Nash Bargaining Approach. IEEE Trans. Ind. Inform. 2025, 21, 6410–6421. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).