Improved Polar Lights Optimizer Based Optimal Power Flow for ADNs with Renewable Energy and EVs
Abstract
1. Introduction
2. Methodology
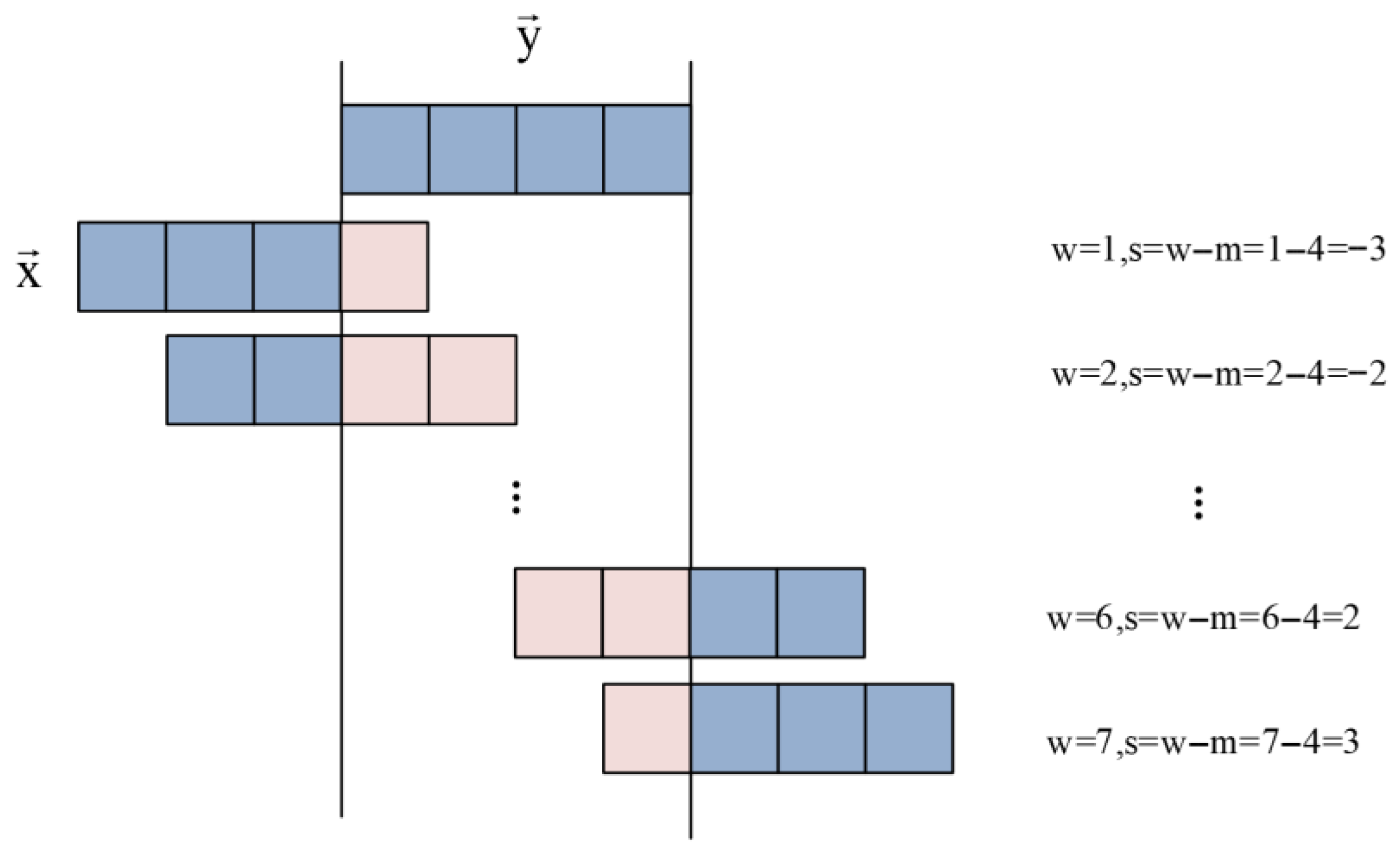
2.1. K-Shape Clustering
2.2. Demand Response Modeling
2.3. The BESS Modeling
2.4. Optimazation Model
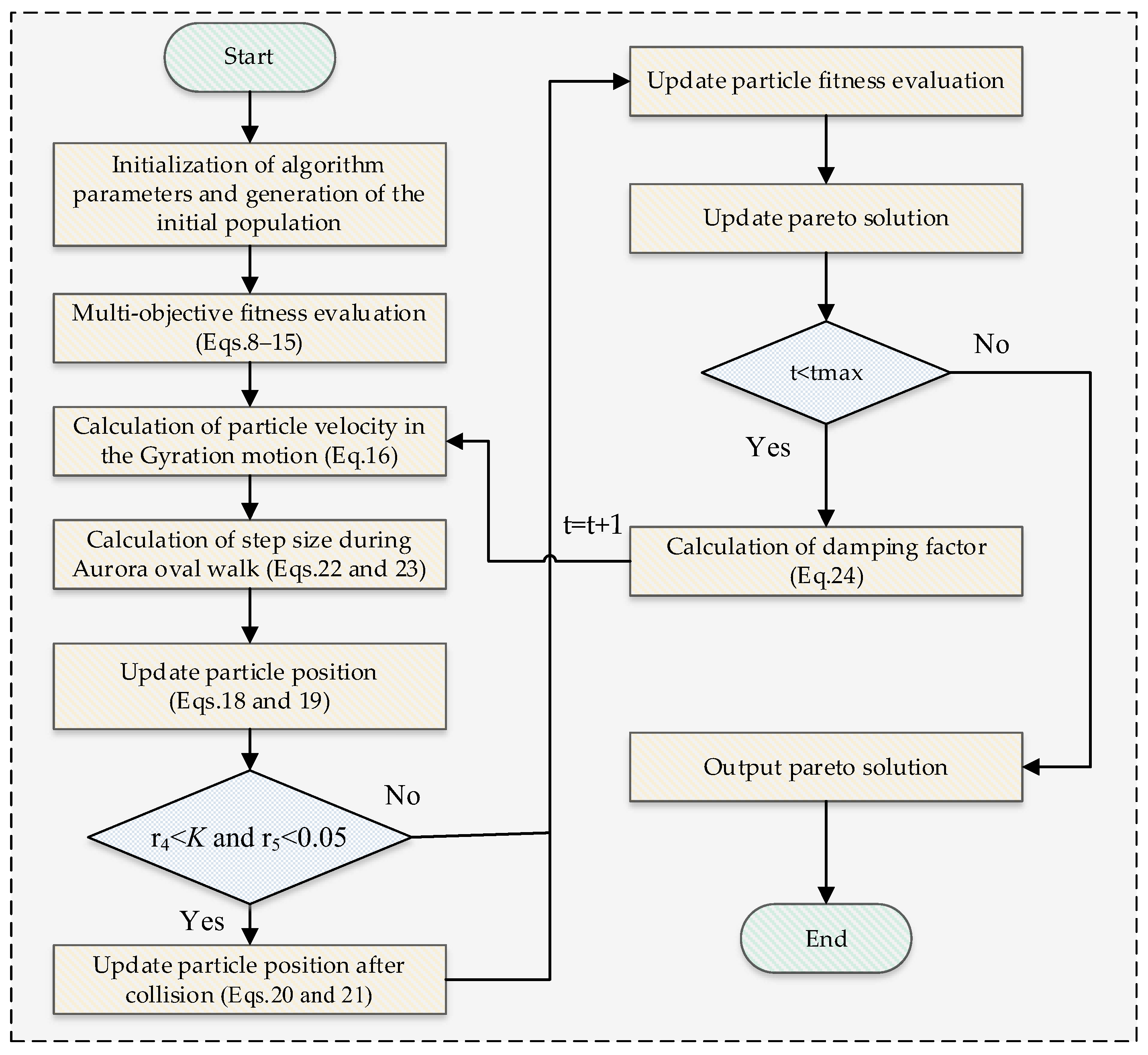
3. Model Solution Based on Polar Lights Optimizer
3.1. Polar Lights Optimizer
3.1.1. Gyration Motion
3.1.2. Aurora Oval Walk
3.1.3. Particle Collision
3.2. Improved Polar Lights Optimizer
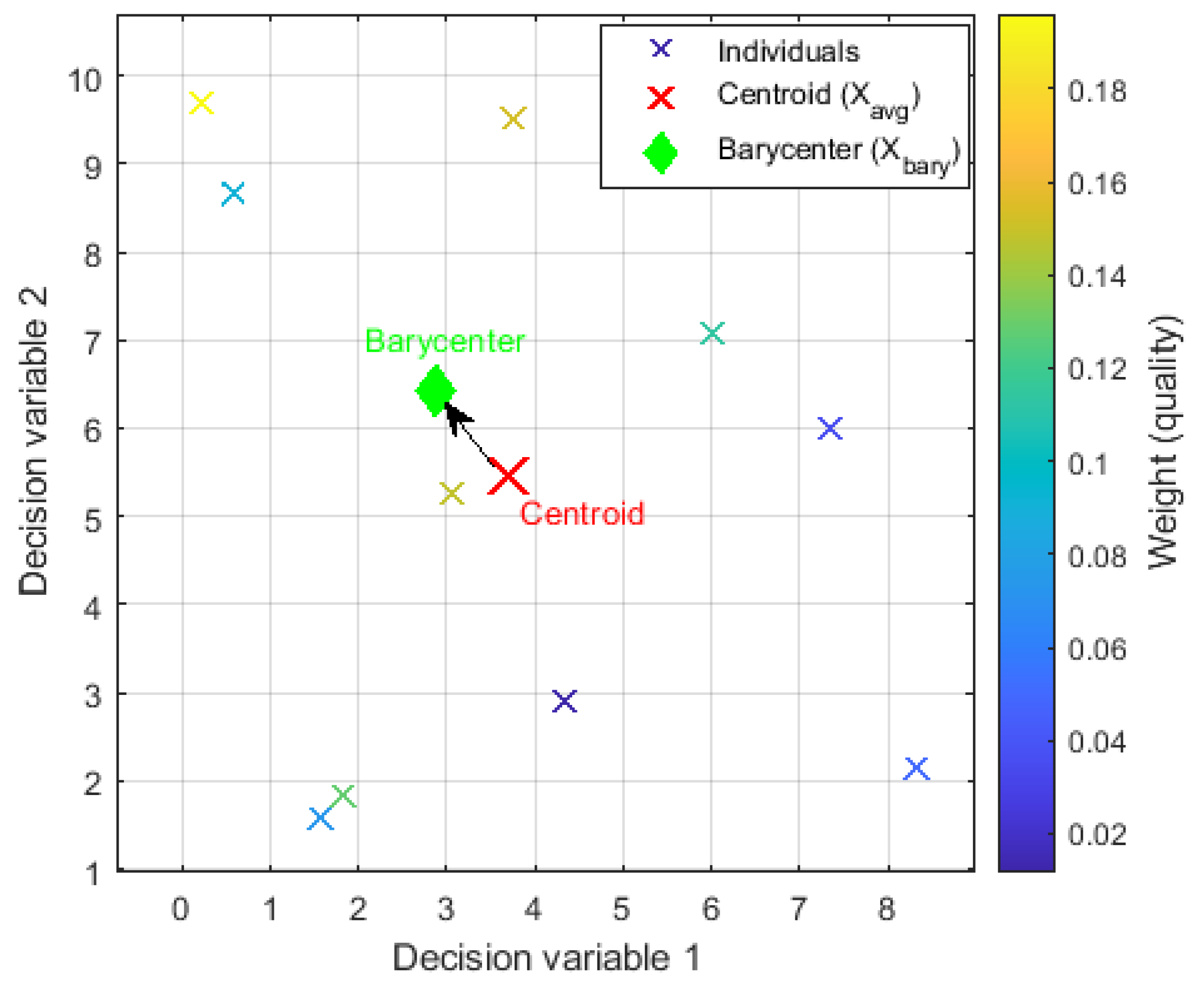
3.2.1. Barycenter-Guided Oval Walk
3.2.2. Dynamically Adaptive Damping Factor
4. Case Study
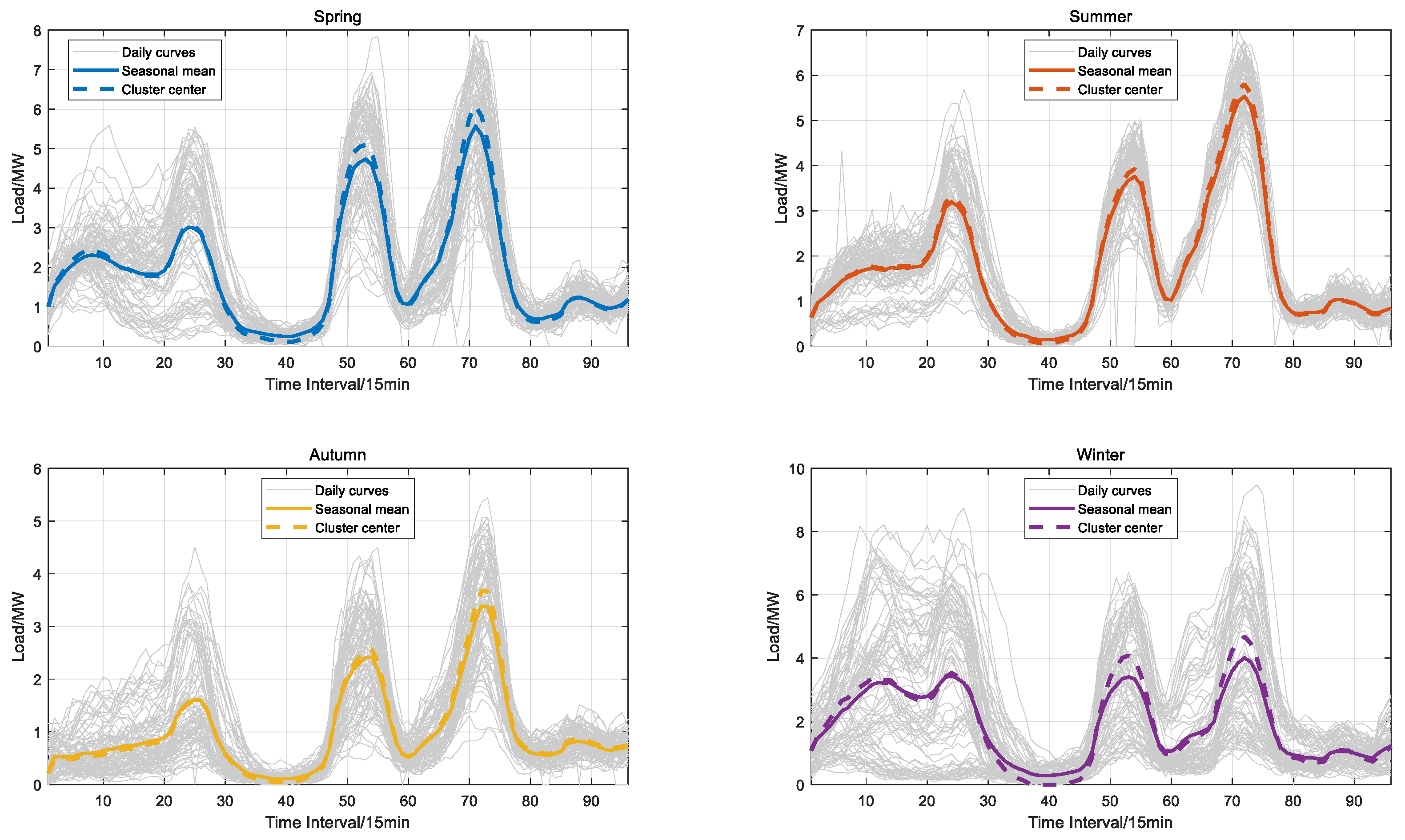
4.1. K-Shape Clustering Result
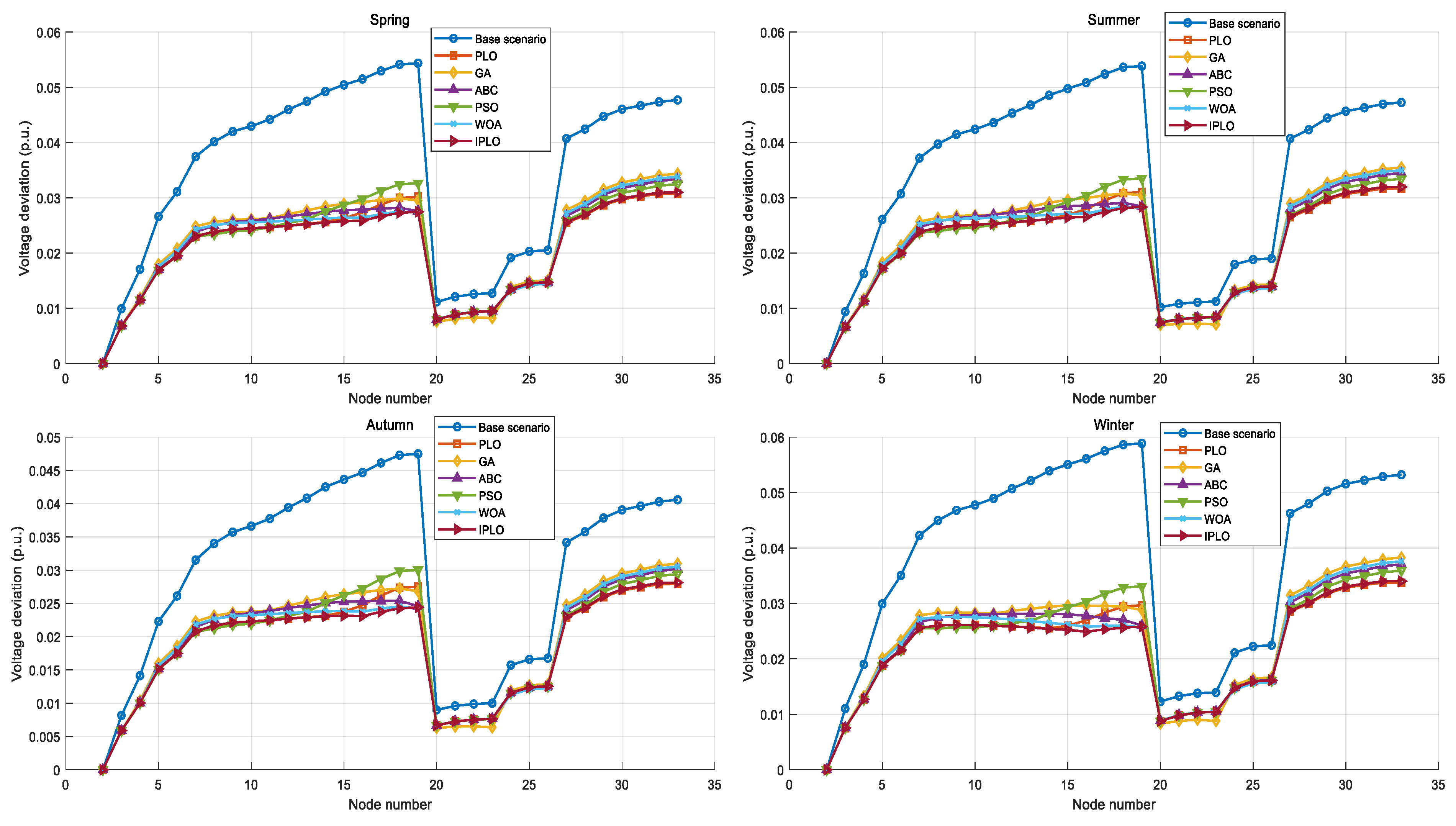
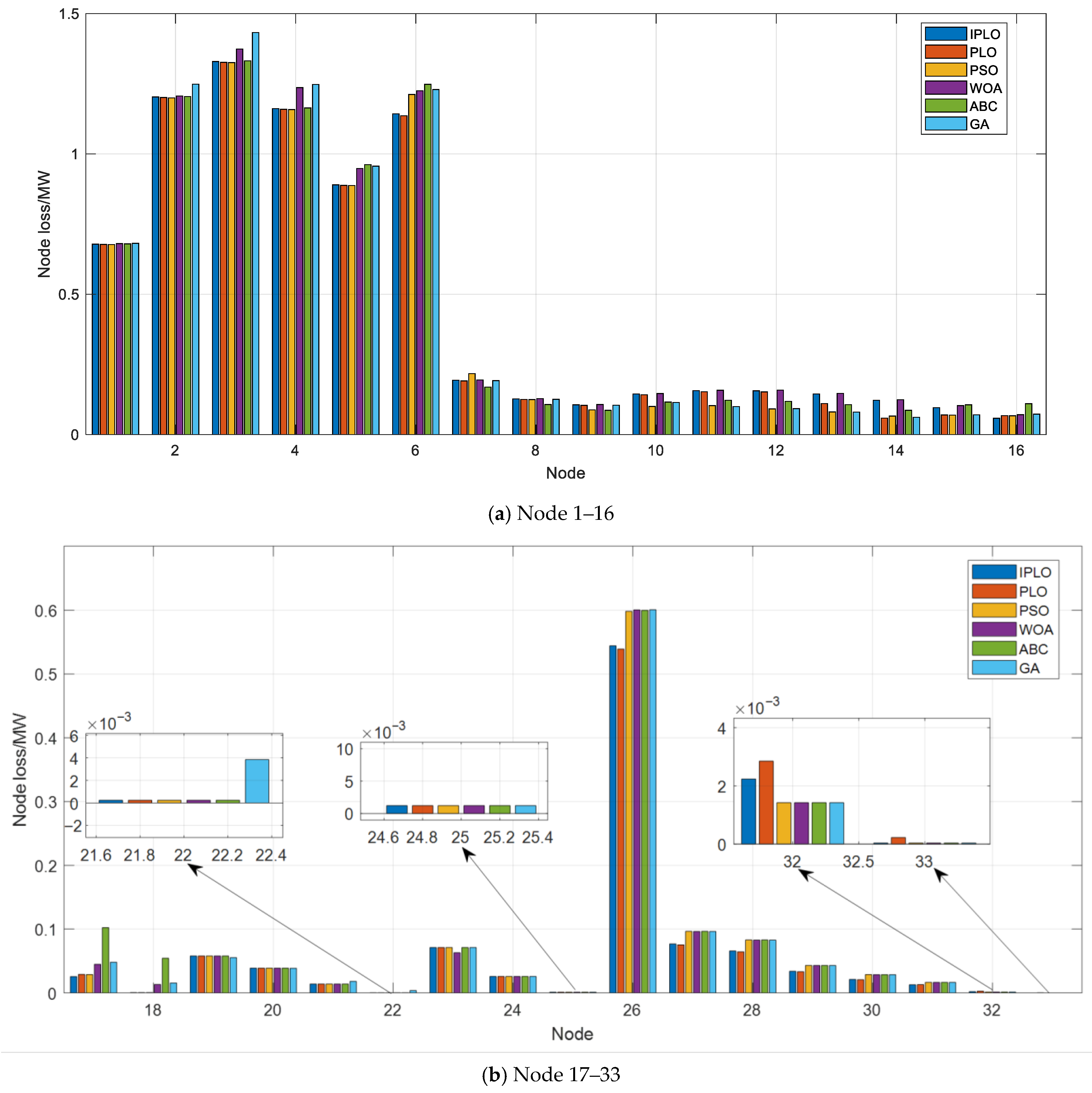
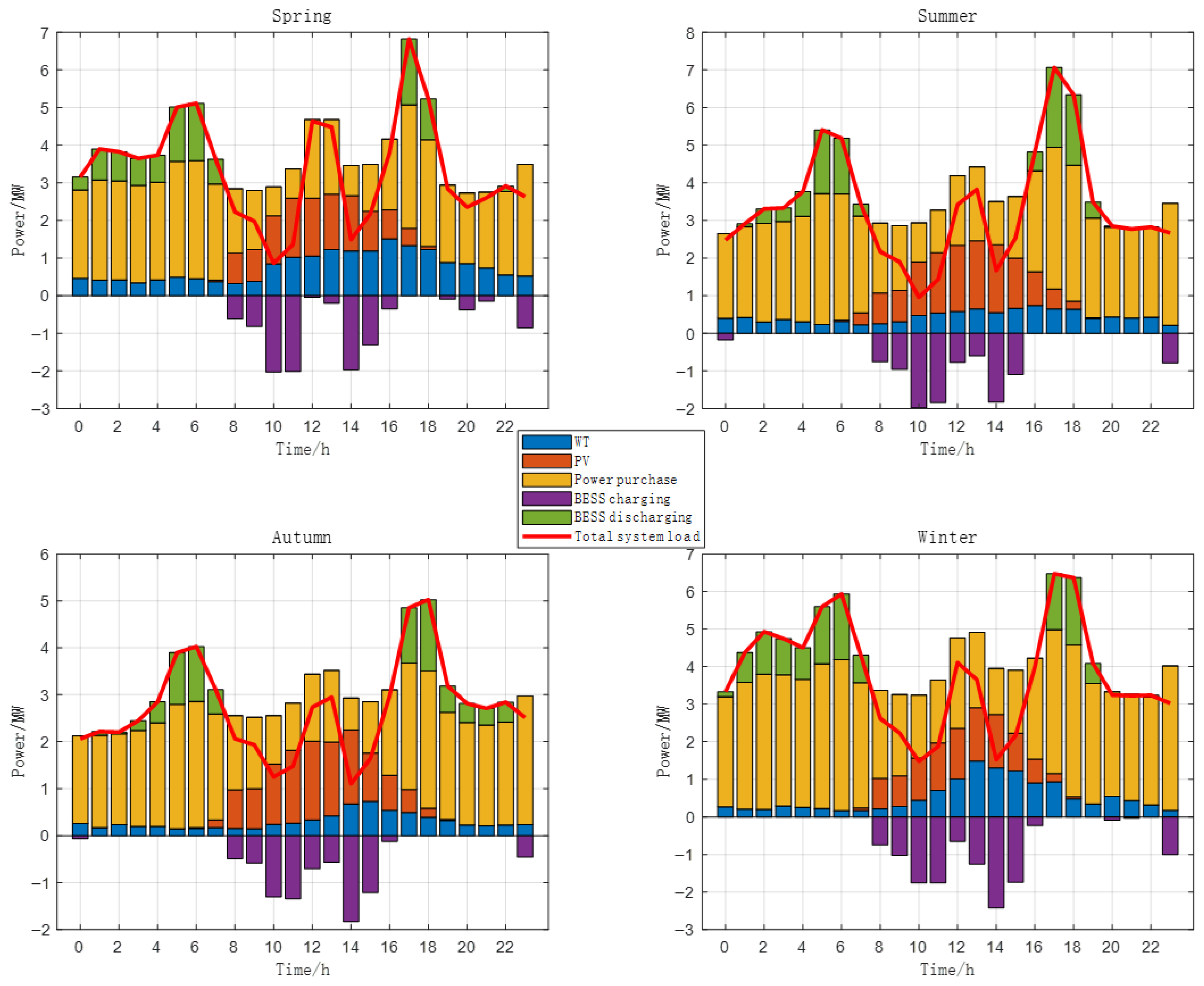
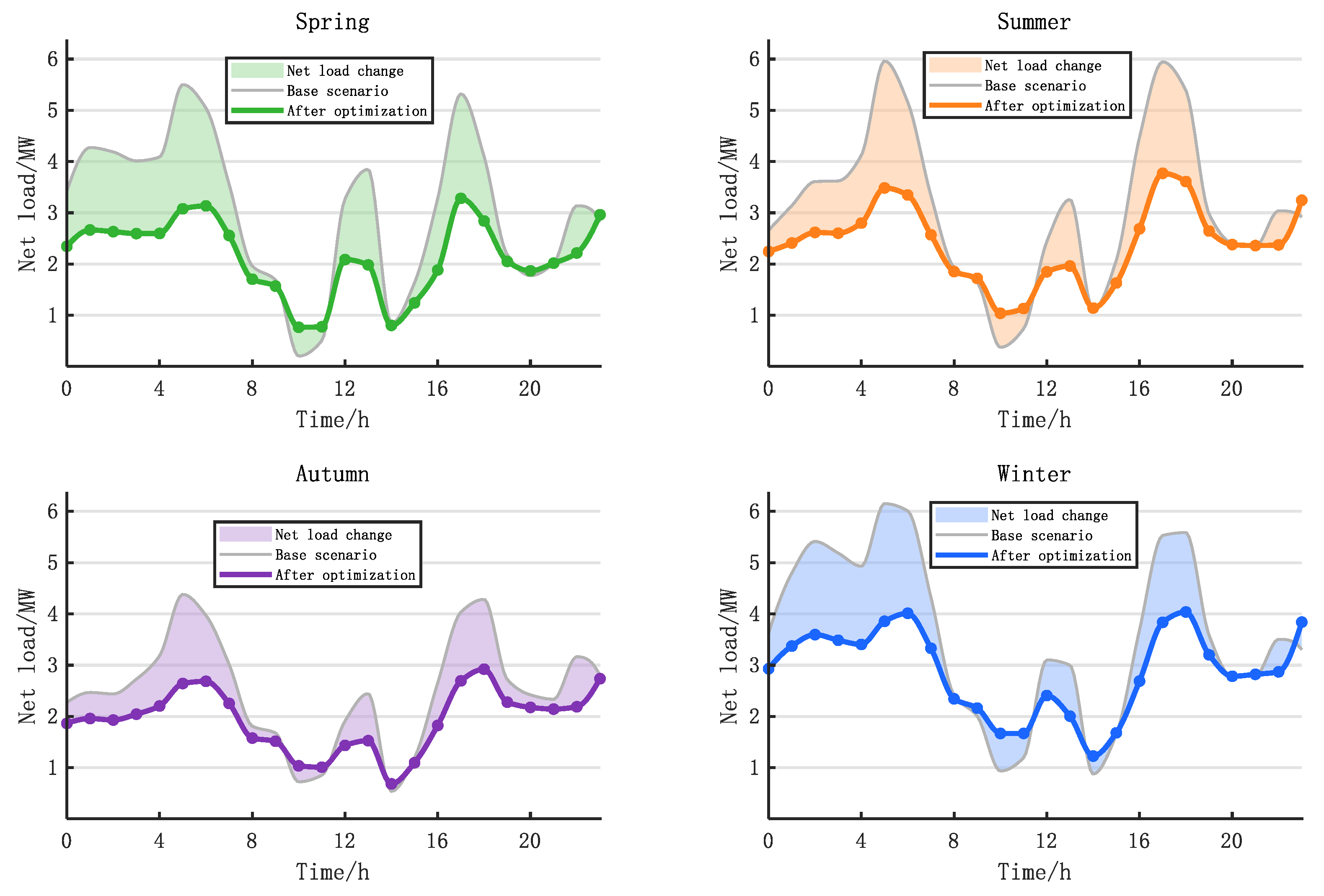
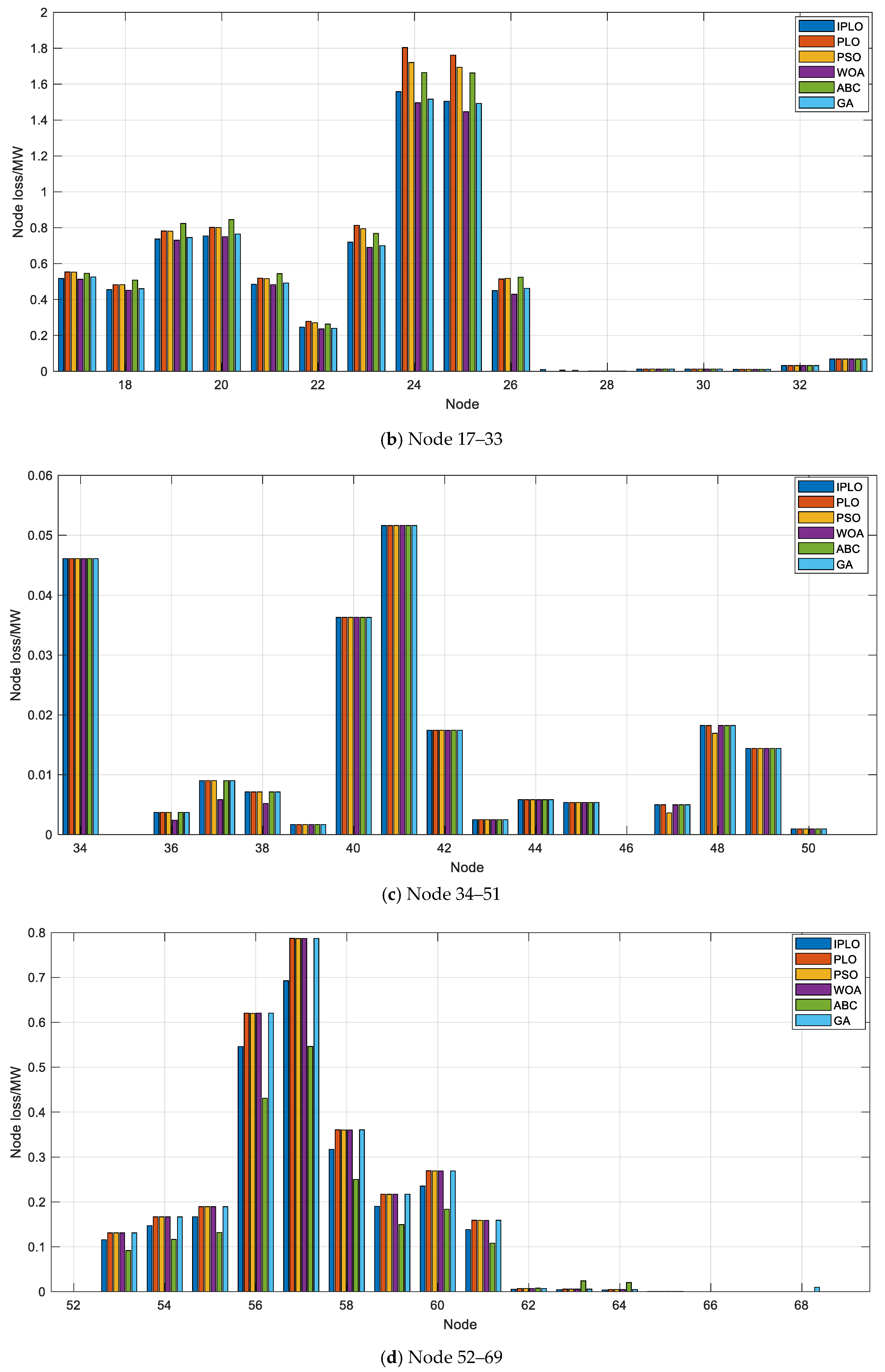
4.2. Analysis of MOOPF Results
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| ABC | artificial bee colony |
| BESS | battery energy storage system |
| ADN | active distribution network |
| EV | electric vehicle |
| LCC | life cycle cost |
| GA | genetic algorithm |
| IPLO | improved polar light optimizer |
| MOOPF | multi-objective optimal power flow |
| SBD | shape-based distance |
| SOC | state of charge |
| OPF | optimal power flow |
| PLO | polar light optimizer |
| PSO | particle swarm optimization |
| PV | photovoltaic |
| WT | wind turbine |
| WOA | whale optimization algorithm |
| Parameters | |
| correlation between two time series | |
| electricity prices | |
| peak, flat, and valley time periods | |
| energy stored in the BESS | |
| charging and discharging power of BESS | |
| charging and discharging efficiencies of BESS | |
| depreciation period | |
| state of charge of BESS | |
| rated capacity of BESS | |
| total load power of the ADN | |
| PV and wind power generation | |
| the number of nodes in the ADN | |
| power output or input of BESS | |
| baseline load power of the ADN | |
| charging load power of EV | |
| node voltage | |
| unit cost of the battery and converter | |
| random number of Lévy distribution | |
| upper and lower bounds | |
| particle speed | |
| weighting coefficient | |
| random number | |
References
- Li, H.; Yu, H.Y.; Liu, Z.J.; Wu, X.; Cao, B.R.; Zhang, C.; Liu, D. Long-term scenario generation of renewable energy generation using attention-based conditional generative adversarial networks. Energy Convers. Econ. 2024, 5, 15–27. [Google Scholar] [CrossRef]
- Hou, H.; Wang, Z.; Zhao, B.; Zhang, L.Q.; Shi, Y.; Xie, C.J.; Dong, Z.Y.; Yu, K.R. Distributed optimization for joint peer-to-peer electricity and carbon trading among multi-energy microgrids considering renewable generation uncertainty. Energy Convers. Econ. 2024, 5, 116–131. [Google Scholar] [CrossRef]
- Wang, J.B.; Wen, J.F.; Wang, J.R.; Yang, B.; Lin, J. Water electrolyzer operation scheduling for green hydrogen production: A review. Renew. Sustain. Energy Rev. 2024, 203, 114779. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, H.Y.; Liao, W.L.; Bak, C.L.; Chen, Z. Protection challenges and solutions for AC systems with renewable energy sources: A review. Prot. Control. Mod. Power Syst. 2025, 10, 18–39. [Google Scholar] [CrossRef]
- Jiang, C.X.; Lin, Z.; Liu, C.X.; Chen, F.X.; Shao, Z.G. MADDPG-Based active distribution network dynamic reconfiguration with renewable energy. Prot. Control. Mod. Power Syst. 2024, 9, 143–155. [Google Scholar] [CrossRef]
- Yang, B.; Li, J.L.; Shu, H.C.; Cai, Z.L.; Tang, B.; Huang, X.Y.; Zhu, M.M. Recent advances of optimal sizing and location of charging stations: A critical overview. Int. J. Energy Res. 2022, 46, 17899–17925. [Google Scholar] [CrossRef]
- Yang, B.; Yu, L.; Chen, Y.X.; Ye, H.Y.; Shao, R.N.; Shu, H.C.; Yu, T.; Zhang, X.S.; Sun, L.M. Modelling, applications, and evaluations of optimal sizing and placement of distributed generations: A critical state-of-the-art survey. Int. J. Energy Res. 2020, 45, 3615–3642. [Google Scholar] [CrossRef]
- Jisoo, K.; Jean, M. Development of coordinated control method based on Graph search method between EV and DG for voltage regulation. Int. J. Electr. Power Energy Syst. 2024, 162, 110295. [Google Scholar] [CrossRef]
- Nibeditha, N.; Rajan Singaravel, M.M. Optimal sizing of PV–Wind generators with a smart EV charging framework to build grid friendly Net Zero Energy Campus. Sustain. Cities Soc. 2024, 111, 105575. [Google Scholar] [CrossRef]
- Tayenne, D.D.L.; Luis, G.G.; João, S.; Franco, J.F. Optimal probabilistic framework for grid cost operation considering voltage probability constraints and high penetration of EVs, wind and PV generation. J. Clean. Prod. 2025, 521, 146241. [Google Scholar] [CrossRef]
- Yuan, W.Q.; Li, Y.L.; Chen, X.L.; Zhang, S.F.; Wan, J.; Tian, H.L. Research on distance protection scheme for single-phase to ground faults in active distribution networks with gap-grounded transformers. Prot. Control. Mod. Power Syst. 2025, 10, 123–141. [Google Scholar] [CrossRef]
- Gao, H.J.; Wang, R.J.; He, S.J.; Wang, Z.Q.; Liu, J.Y. Bi-level stackelberg game-based distribution system expansion planning model considering long-term renewable energy contracts. Prot. Control. Mod. Power Syst. 2023, 8, 1031–1045. [Google Scholar] [CrossRef]
- Vaishya, S.R. An AC optimal power flow framework for active–reactive power scheduling considering generator capability curve. Energy Convers. Econ. 2023, 4, 425–438. [Google Scholar] [CrossRef]
- Ahmed, B.; Sulaiman, S.A.; Ijaz, A.; Khalid, M.; Abido, M.A.; AI-Ismail, F.S. Optimal power flow: A review of state-of-the-art techniques and future perspectives. IEEE Access 2025, 13, 60012–60039. [Google Scholar]
- Subhrajyoti, S.; Ajit, K.B.; Abhishek, K. Multi-objective optimal power flow with DG placement using TLBO and MIPSO: A comparative study. Energy Procedia 2017, 117, 236–243. [Google Scholar] [CrossRef]
- Zhu, J.H.; Yu, X.B.; Wang, F.; Mao, Y.Q. Multi-objective optimal power flow problem using constrained dynamic multitasking multi-objective optimization algorithm. Swarm Evol. Comput. 2025, 93, 101850. [Google Scholar] [CrossRef]
- Masoud, A.; Zaipatimah, A.; Vigna, K.R.; Ridha, H.M. A memory-guided Jaya algorithm to solve multi-objective optimal power flow integrating renewable energy sources. Appl. Soft Comput. 2024, 164, 11924. [Google Scholar]
- Ravi, K.A.; Vinod, K.D.M.; Anil, K.A.; Reddy, N.N. A TOPSIS based multi-objective optimal power flow approach using the artificial hummingbird algorithm for renewable energy and PEV integrated system. Measurement 2025, 256, 118337. [Google Scholar] [CrossRef]
- Aljaidi, M.; Jangir, P.; Arpita; Agrawal, S.P.; Pandya, S.B.; Parmar, A.; Gulothungan, G.; Alkoradees, A.F.; Khishe, M.; Jangid, R. Polar lights optimizer: A novel algorithm for accurate parameter estimation in proton exchange membrane fuel cells. Results Eng. 2025, 27, 106571. [Google Scholar] [CrossRef]
- Sikder, N.; Das, D. Optimal planning of microgrid with integrated QV bus and energy storage system considering uncertainties in load, renewable power generation, failure rates, and repair times of branches. J. Energy Storage 2025, 127, 116915. [Google Scholar] [CrossRef]
- Datta, U.; Kalam, A.; Shi, J. Smart control of BESS in PV integrated EV charging station for reducing transformer overloading and providing battery-to-grid service. J. Energy Storage 2020, 28, 101224. [Google Scholar] [CrossRef]
- Bhatia, A.A.; Das, D. Demand response strategy for microgrid energy management integrating electric vehicles, battery energy storage system, and distributed generators considering uncertainties. Sustain. Energy Grids Netw. 2025, 41, 101594. [Google Scholar] [CrossRef]
- Cao, T.W.; Xu, Y.L.; Liu, G.W.; Tao, S.Y.; Tang, W.J.; Sun, H.B. Feature-enhanced deep learning method for electric vehicle charging demand probabilistic forecasting of charging station. Appl. Energy 2024, 371, 123751. [Google Scholar] [CrossRef]
- Chen, S.J.; Wang, P.; Lü, J.H. k-Shape clustering enhances group lasso for gene selection and sample classification. IEEE Trans. Comput. Biol. Bioinform. 2025, 22, 1176–1188. [Google Scholar]
- Zhu, J.; Miao, Y.; Dong, H.; Li, S.L.; Chen, Z.Y.; Zhang, D. Short-term residential load forecasting based on K-shape clustering and domain adversarial transfer network. J. Mod. Power Syst. Clean Energy 2024, 12, 1239–1249. [Google Scholar]
- Zhang, W.; Cheng, M.; Xiang, Q.; Li, Q.M. Enhancing short-term load forecasting through K-Shape clustering and deep learning integration. IEEE Access 2025, 13, 30817–30832. [Google Scholar] [CrossRef]
- Yang, H.; Yan, C.; Chen, Z.; Wang, P. A K-shape clustering based transformer-decoder model for predicting multi-step potentials of urban mobility field. IEEE Trans. Intell. Transp. Syst. 2024, 25, 10298–10312. [Google Scholar]
- Yang, L.; Zhang, Z. A deep attention convolutional recurrent network assisted by K-shape clustering and enhanced memory for short term wind speed predictions. IEEE Trans. Sustain. Energy 2022, 13, 856–867. [Google Scholar] [CrossRef]
- Song, Y.Q.; Shangguan, L.Z.; Li, G.J. Simulation analysis of flexible concession period contracts in electric vehicle charging infrastructure public-private-partnership (EVCI-PPP) projects based on time-of-use (TOU) charging price strategy. Energy 2021, 228, 120328. [Google Scholar] [CrossRef]
- He, B.; Yang, B.; Han, Y.M.; Zhou, Y.M.; Hu, Y.W.J.; Shu, H.C.; Su, S.; Yang, J.; Huang, Y.P.; Li, J.L.; et al. Optimal EVCS planning via spatial-temporal distribution of charging demand forecasting and traffic-grid coupling. Energy 2024, 313, 133885. [Google Scholar] [CrossRef]
- Chen, C.Y.; Hu, B.; Xie, K.G.; Xiang, B. A peak-valley TOU price model considering power system reliability and power purchase risk. Power Syst. Technol. 2014, 38, 2141–2148. [Google Scholar]
- Zhang, W.Z.; Xu, C.B. Capacity configuration optimization of photovoltaic-battery-electrolysis hybrid system for hydrogen generation considering dynamic efficiency and cost learning. Energy Convers. Econ. 2024, 5, 78–92. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.T.; Chen, Y.X.; Li, D.Y.; Zeng, C.Y.; Chen, Y.J.; Guo, Z.X.; Shu, H.C.; Zhang, X.S.; Yu, T.; et al. Optimal sizing and placement of Energy storage system in power grids: A state-of-the-art one-stop handbook. J. Energy Storage 2020, 32, 101814. [Google Scholar] [CrossRef]
- Sharma, J.; Sundarabalan, C.K.; Balasundar, C. Advanced energy management strategy for enhancing battery lifespan in solar PV-powered EV charging stations with hybrid energy storage systems. Renew. Energy 2025, 251, 123443. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H.L. Polar lights optimizer: Algorithm and applications in image segmentation and feature selection. Neurocomputing 2024, 607, 128427. [Google Scholar] [CrossRef]
- Li, S.B.; Guo, L.; Zhu, J.Z.; Liu, M.L.; Chen, J.X.; Meng, Z.H. Short-term multi-step wind speed forecasting with multi-feature inputs using variational mode decomposition, a novel artificial intelligence network, and the polar lights optimizer. Renew. Energy 2026, 256, 123965. [Google Scholar] [CrossRef]
- Shao, J.C.; Zhou, X.N.; Shao, Q.K.; Chen, H.L.; Pan, B.J. A novel lymph node metastasis prediction method for gastric cancer: Enhanced support vector machine with polar lights optimization. Biomed. Signal Process. Control. 2026, 111, 108349. [Google Scholar] [CrossRef]
- Ekariansyah, A.S.; Muwonge, M.; Saefuttamam, M.R.; Dikaimana, Y.; Nasruddin. Energy, exergy, and exergy-economic optimization of a multigeneration system driven by geothermal primary heat source using multi-objective genetic algorithm (MOGA). Energy 2025, 330, 136653. [Google Scholar] [CrossRef]
- Du, P.; Ye, Y.X.; Wu, H.; Wang, J.Z. Study on deterministic and interval forecasting of electricity load based on multi-objective whale optimization algorithm and transformer model. Expert Syst. Appl. 2025, 268, 126361. [Google Scholar] [CrossRef]
- Nkalo, U.K.; Inya, O.O.; Ifeanyi, O.P.; Ifeanyi, P.; Bola, A.U.; Ewean, D.I. A modified multi-objective particle swarm optimization (M-MOPSO) for optimal sizing of a solar–wind–battery hybrid renewable energy system. Sol. Compass 2024, 12, 100082. [Google Scholar] [CrossRef]
- Cao, Q.F.; Wang, H.L.; Hui, Z.J.; Chen, L.Y. Optimal location and sizing of multi-resource distributed generator based on multi-objective artificial bee colony algorithm. Energy Eng. 2024, 121, 499–521. [Google Scholar] [CrossRef]
- Zhu, X.H.; Hu, X.; Shi, N.; Zhang, Y.; Zhong, J.W. Multi-layer embedded optimization of micro-grid capacity considering price and incentive/compensation coupling mechanisms. Electr. Power 2023, 56, 173–186. [Google Scholar]


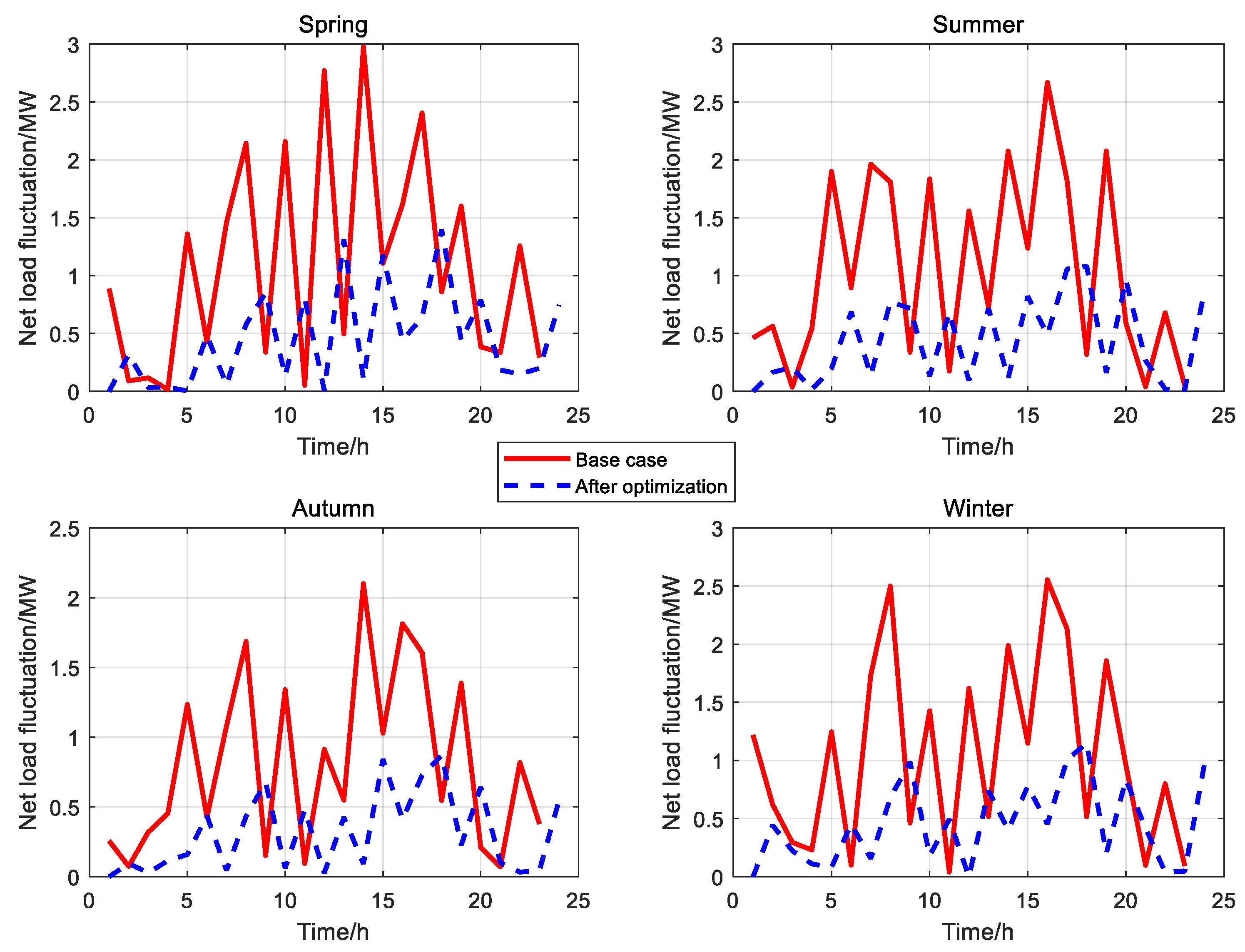
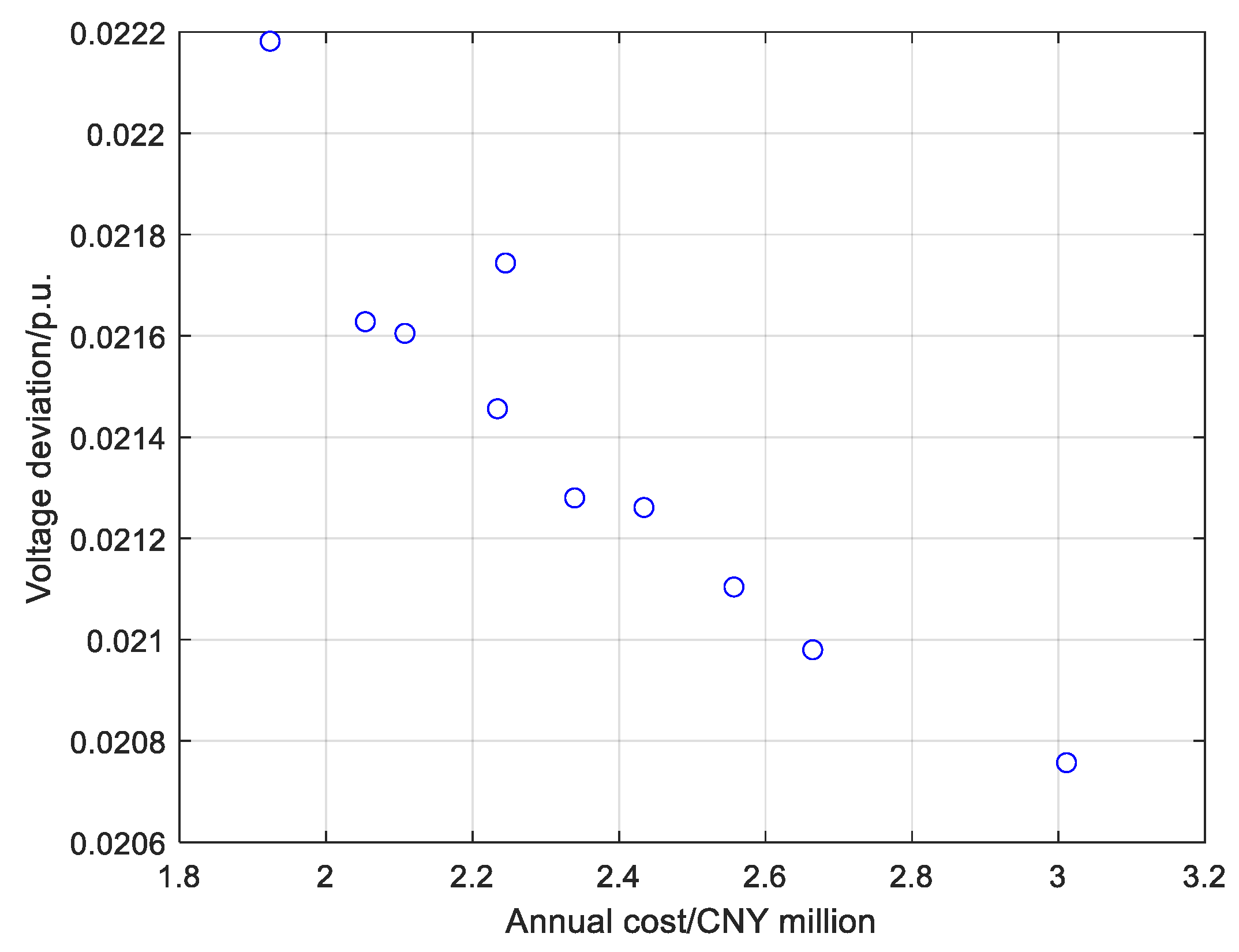
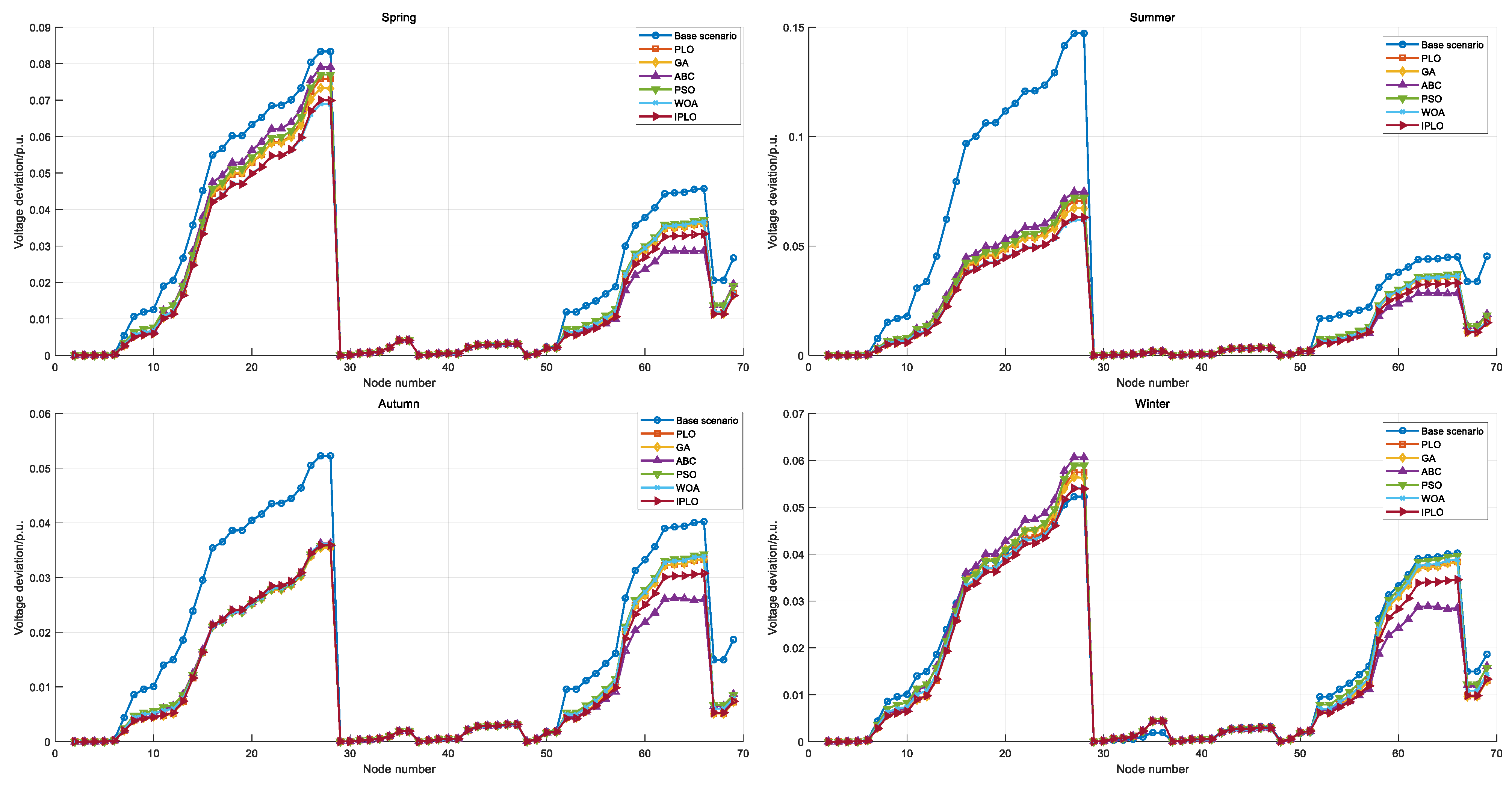
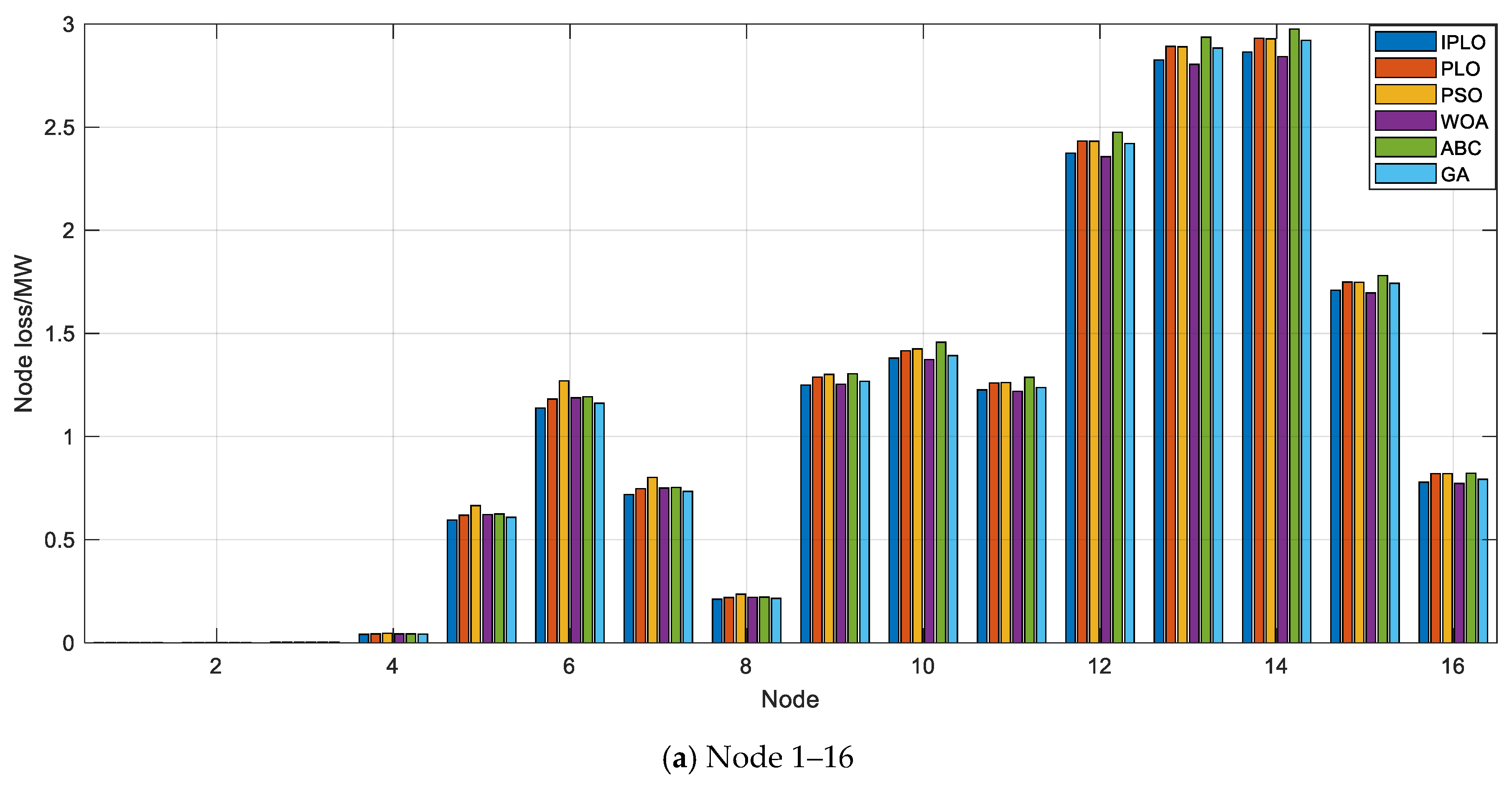
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| WT capacity | 0.5 MW/unit | SOC range | 0.1–0.9 |
| PV capacity | 1.6 MW/unit | Charge/discharge efficiency | 0.96, 1/0.96 |
| Monte Carlo simulation runs | 100 | BESS power range | −4~4 MW |
| Valley electricity price [42] | (1:00–6:00, 23:00–24:00): 290.5 CNY/MWh | BESS capacity range | 0–4 MWh |
| Peak electricity price [42] | (11:00–13:00, 18:00–22:00): 1443.5 CNY/MWh | Single line failure probability | 0.01 |
| Flat electricity price [42] | (7:00–10:00, 14:00–17:00): 1023.0 CNY/MWh |
| Algorithm | Parameter | Value |
|---|---|---|
| Global parameters | Max iterations | 200 |
| Population size | 10 | |
| Pareto solution size | 10 | |
| IPLO and PLO | Initial damping factor | 1.25 |
| Levy exponent | 1.50 | |
| Balance parameter | 0.50 | |
| GA | Crossover probability | 0.7 |
| Mutation probability | 0.01 | |
| PSO | Inertia weight | 0.80 |
| Individual learning factor | 1.00 | |
| Popular learning factor | 1.00 | |
| ABC | Scout limit | 10 |
| Noise perturbation | 0.01 | |
| WOA | Initial convergence factor | 1.00 |
| Spiral coefficient | 0.10 | |
| Convergence factor | 0.10 | |
| Random acceptance rate | 0.05 |
| Algorithm | Annual Costs (CNY Million/Year) | Voltage Deviation (p.u.) | Average Voltage Level (p.u.) | Network Losses (MWh/Year) | Run Time (s) |
|---|---|---|---|---|---|
| Base scenario | - | 0.03491 | 0.9989 | 1119.63 | - |
| IPLO | 2.3614 | 0.02107 | 0.9997 | 737.89 | 13,216 |
| PLO | 2.4236 | 0.02137 | 0.9997 | 742.15 | 13,143 |
| PSO | 1.9879 | 0.02185 | 0.9996 | 770.77 | 12,803 |
| WOA | 2.1107 | 0.02178 | 0.9996 | 752.36 | 12,100 |
| ABC | 1.9251 | 0.02214 | 0.9996 | 787.57 | 29,144 |
| GA | 1.8415 | 0.02219 | 0.9995 | 767.81 | 11,627 |
| Algorithm | Annual Costs (CNY Million/Year) | Voltage Deviation (p.u.) | Average Voltage Level (p.u.) | Network Losses (MWh/Year) | Run Time (s) |
|---|---|---|---|---|---|
| Base scenario | - | 0.02686 | 0.9757 | 3809.98 | - |
| IPLO | 3.0650 | 0.01521 | 0.9769 | 2504.59 | 23,789 |
| PLO | 3.0099 | 0.01611 | 0.9767 | 2660.45 | 22,817 |
| PSO | 3.0237 | 0.01689 | 0.9767 | 2664.02 | 23,250 |
| WOA | 2.9593 | 0.01579 | 0.9769 | 2520.58 | 23,931 |
| ABC | 2.8095 | 0.01608 | 0.9767 | 2592.57 | 38,141 |
| GA | 3.4237 | 0.01606 | 0.9768 | 2562.85 | 23,983 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Zhou, Y.; Zhao, F.; Ruan, X.; Huang, W.; He, Y.; Yang, B. Improved Polar Lights Optimizer Based Optimal Power Flow for ADNs with Renewable Energy and EVs. Energies 2025, 18, 5403. https://doi.org/10.3390/en18205403
Zhang P, Zhou Y, Zhao F, Ruan X, Huang W, He Y, Yang B. Improved Polar Lights Optimizer Based Optimal Power Flow for ADNs with Renewable Energy and EVs. Energies. 2025; 18(20):5403. https://doi.org/10.3390/en18205403
Chicago/Turabian StyleZhang, Peng, Yifan Zhou, Fuyou Zhao, Xuan Ruan, Wei Huang, Yang He, and Bo Yang. 2025. "Improved Polar Lights Optimizer Based Optimal Power Flow for ADNs with Renewable Energy and EVs" Energies 18, no. 20: 5403. https://doi.org/10.3390/en18205403
APA StyleZhang, P., Zhou, Y., Zhao, F., Ruan, X., Huang, W., He, Y., & Yang, B. (2025). Improved Polar Lights Optimizer Based Optimal Power Flow for ADNs with Renewable Energy and EVs. Energies, 18(20), 5403. https://doi.org/10.3390/en18205403






