Enhanced-Dueling Deep Q-Network for Trustworthy Physical Security of Electric Power Substations
Abstract
1. Introduction
2. Problem Formulation and Modeling
2.1. Markov Decision Process (MDP)
2.2. Modeling of Reinforced Learning Algorithm
2.2.1. Deep Q-Networks (DQNs)
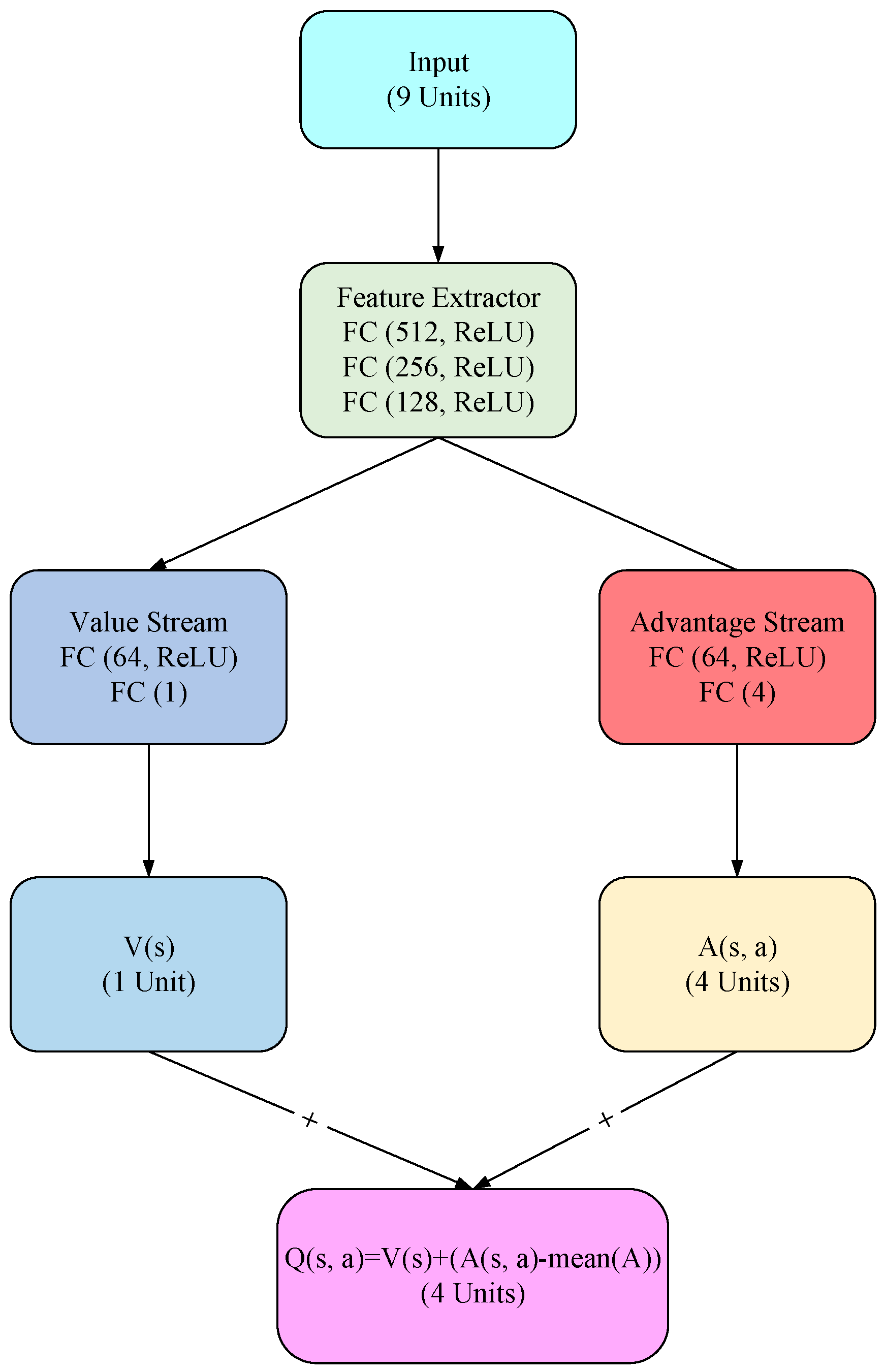
2.2.2. Dueling Deep Q-Networks (Dueling DQNs)
2.2.3. Enhanced-Dueling Deep Q-Network (EDDQN) for Trustworthy Security Policies
3. Case Study and Simulation
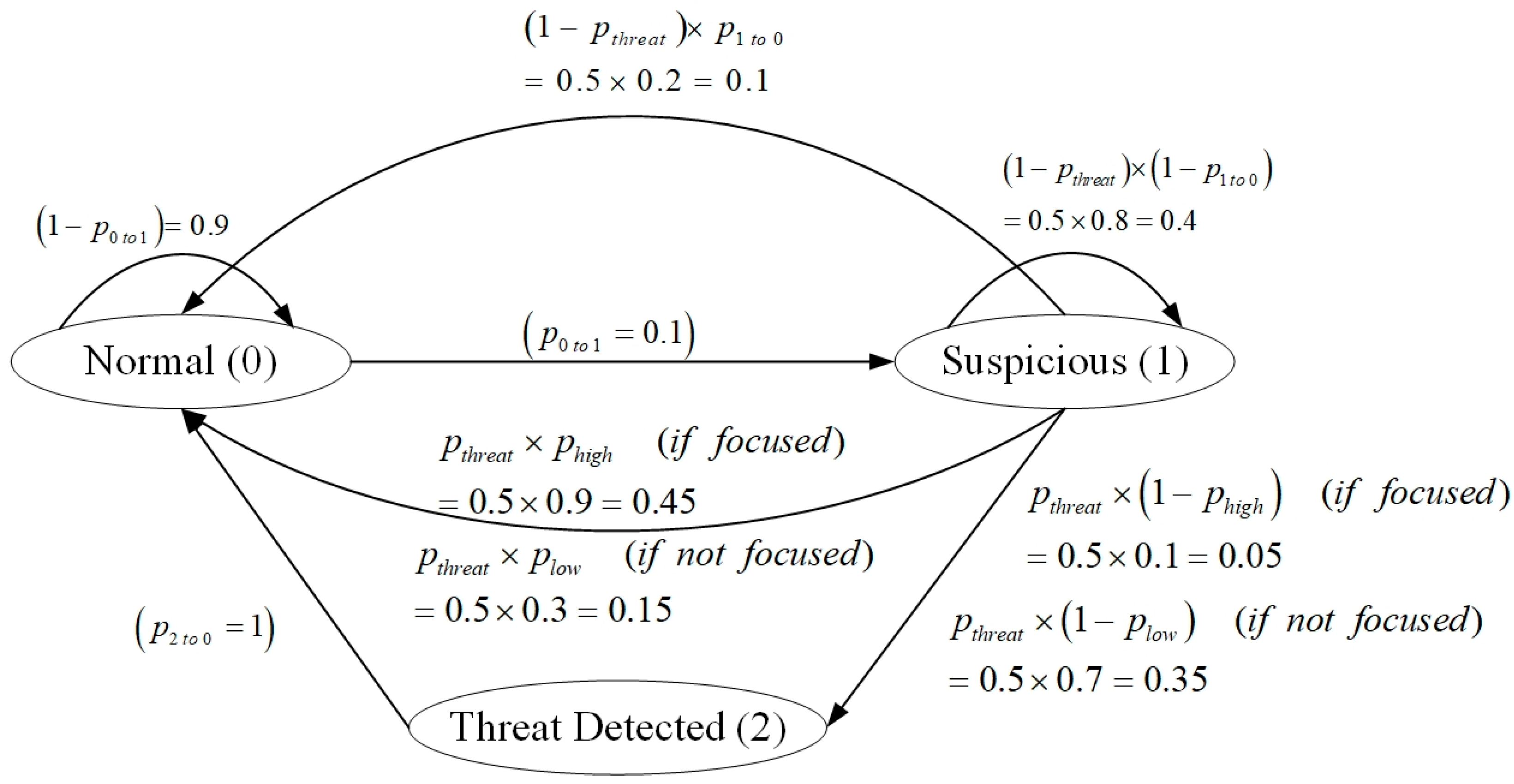
3.1. Synthetic Dataset Generation
- (a)
- Firstly, each zone’s state evolves based on predefined transition probabilities derived from the OE-417 statistics and adjusted to reflect plausible threat dynamics, which are as follows:
- : the probability of transitioning from normal to suspicious.
- : the probability of a threat occurring when a zone is suspicious.
- : the probability of a suspicious zone returning to normal if no threat occurs.
- : the probability of preventing a threat when focusing on the correct zone.
- : the probability of preventing a threat when not focusing on the zone.
- (b)
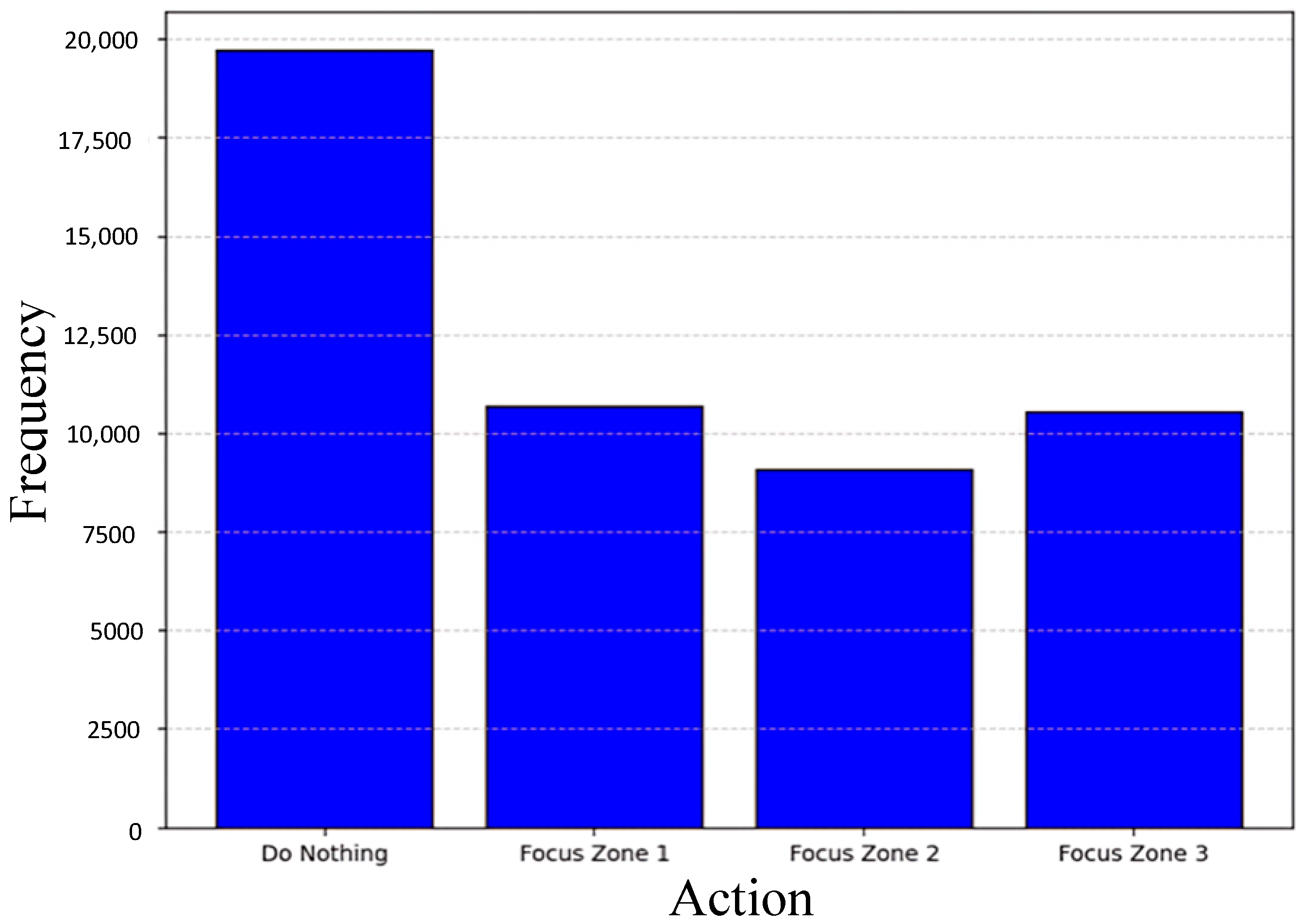
- Then, an action is chosen randomly from the action space: either do nothing (0) or focus on a specific zone (1 to 3).
- (c)
- Then after, rewards are assigned based on outcomes:
- : the reward for preventing a threat.
- : the cost of failing to prevent a threat.
- : the penalty for the false alarm when focusing on a suspicious zone that does not escalate.
3.2. Experimental Settings for Simulation of EDDQN
3.3. Computational Efficiency Analysis
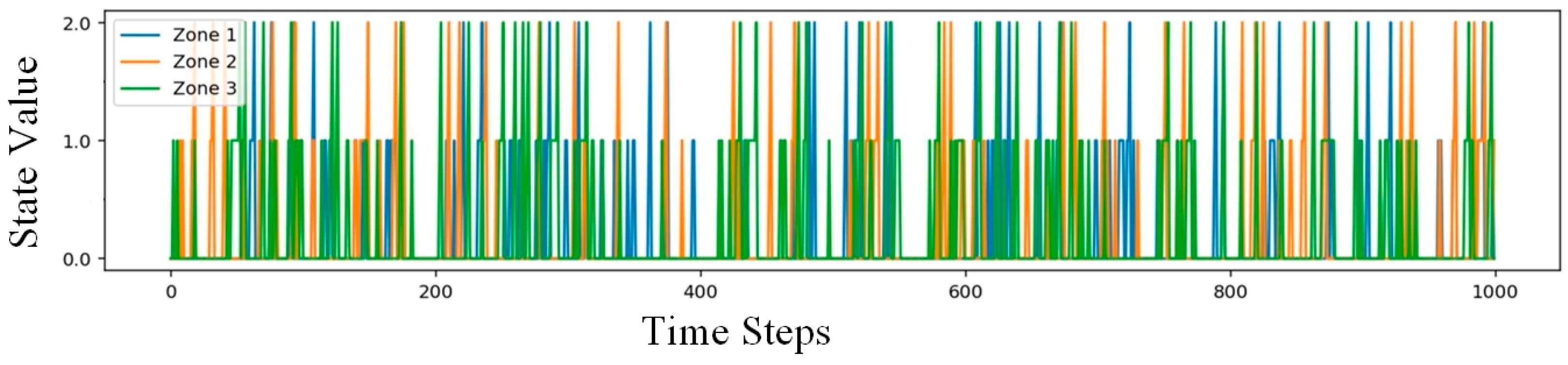
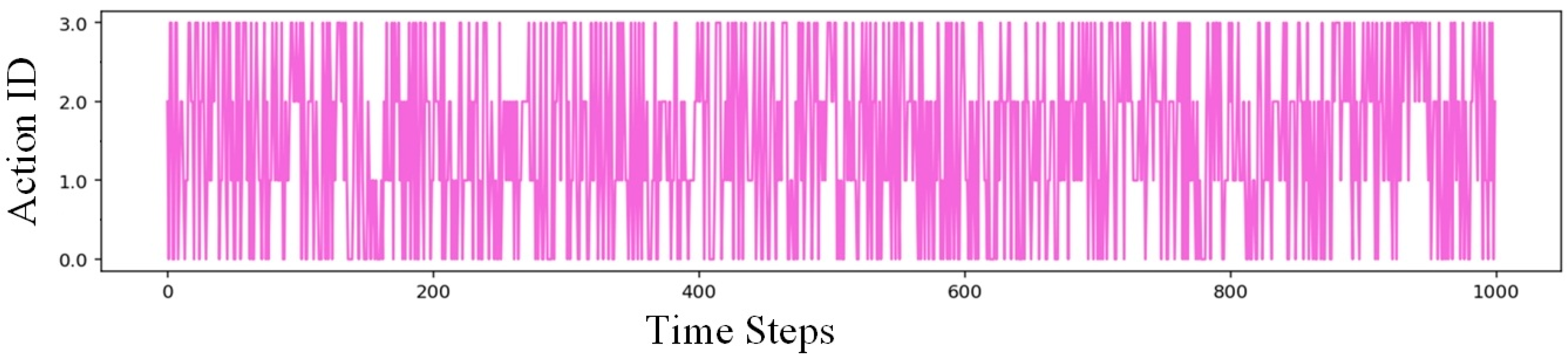
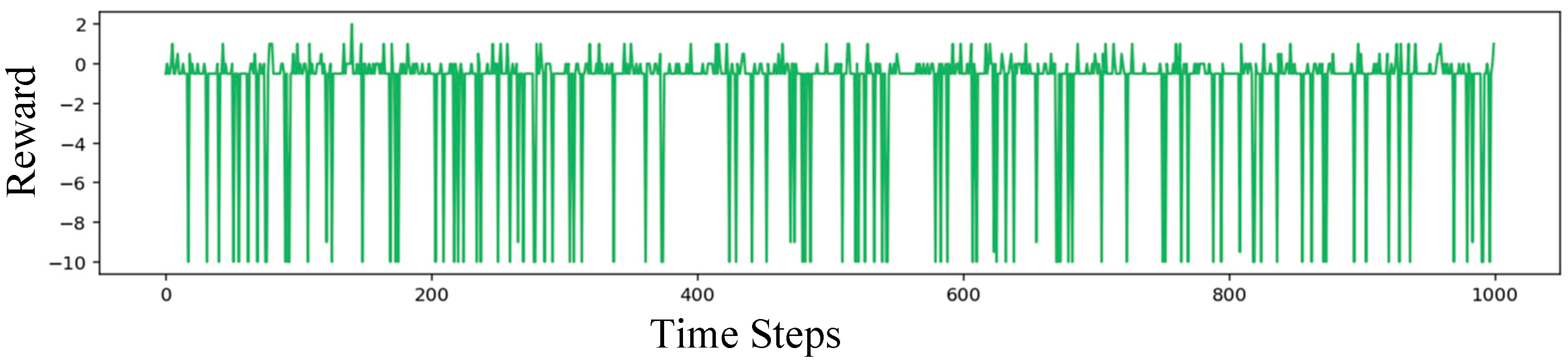
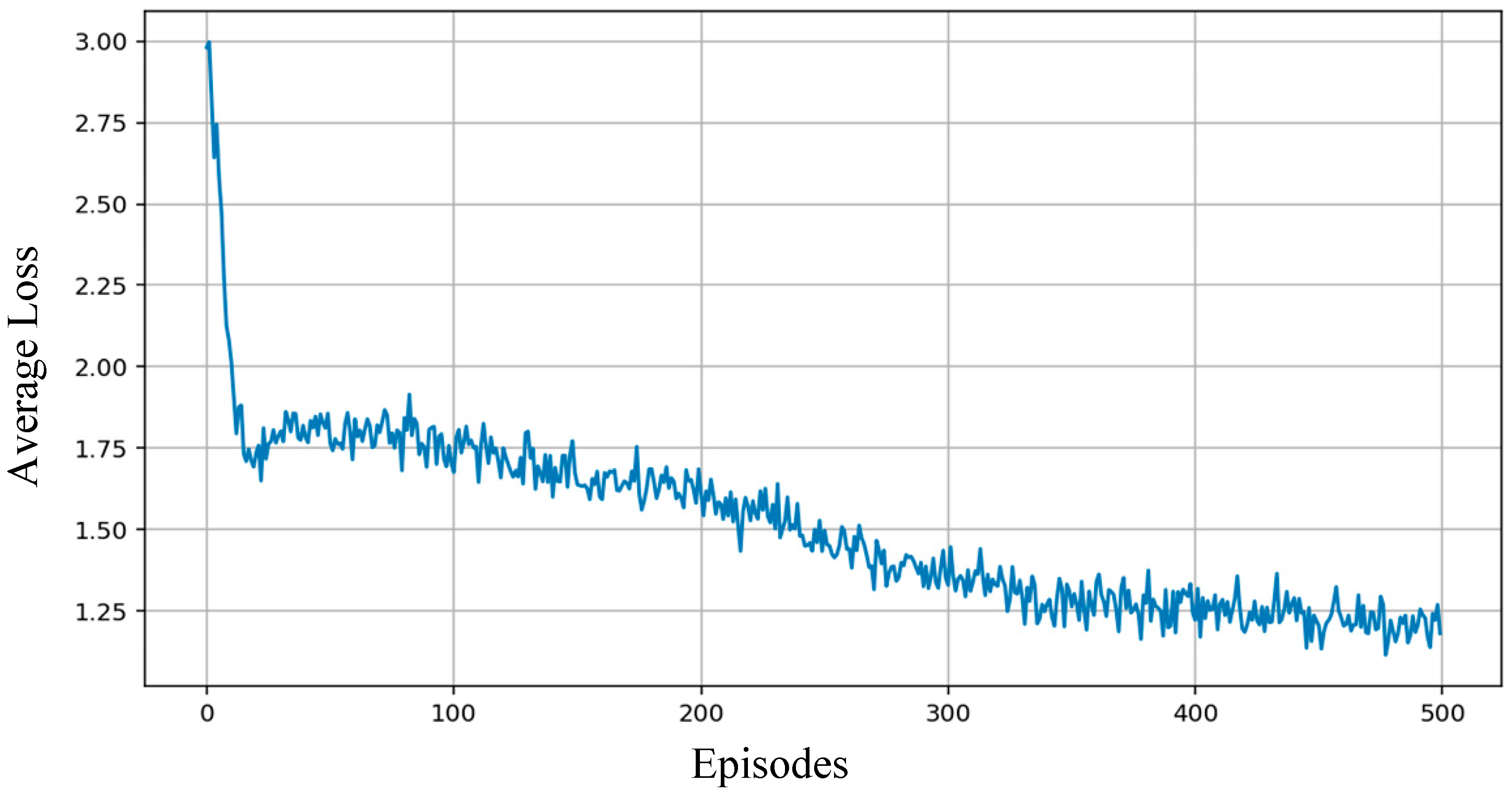
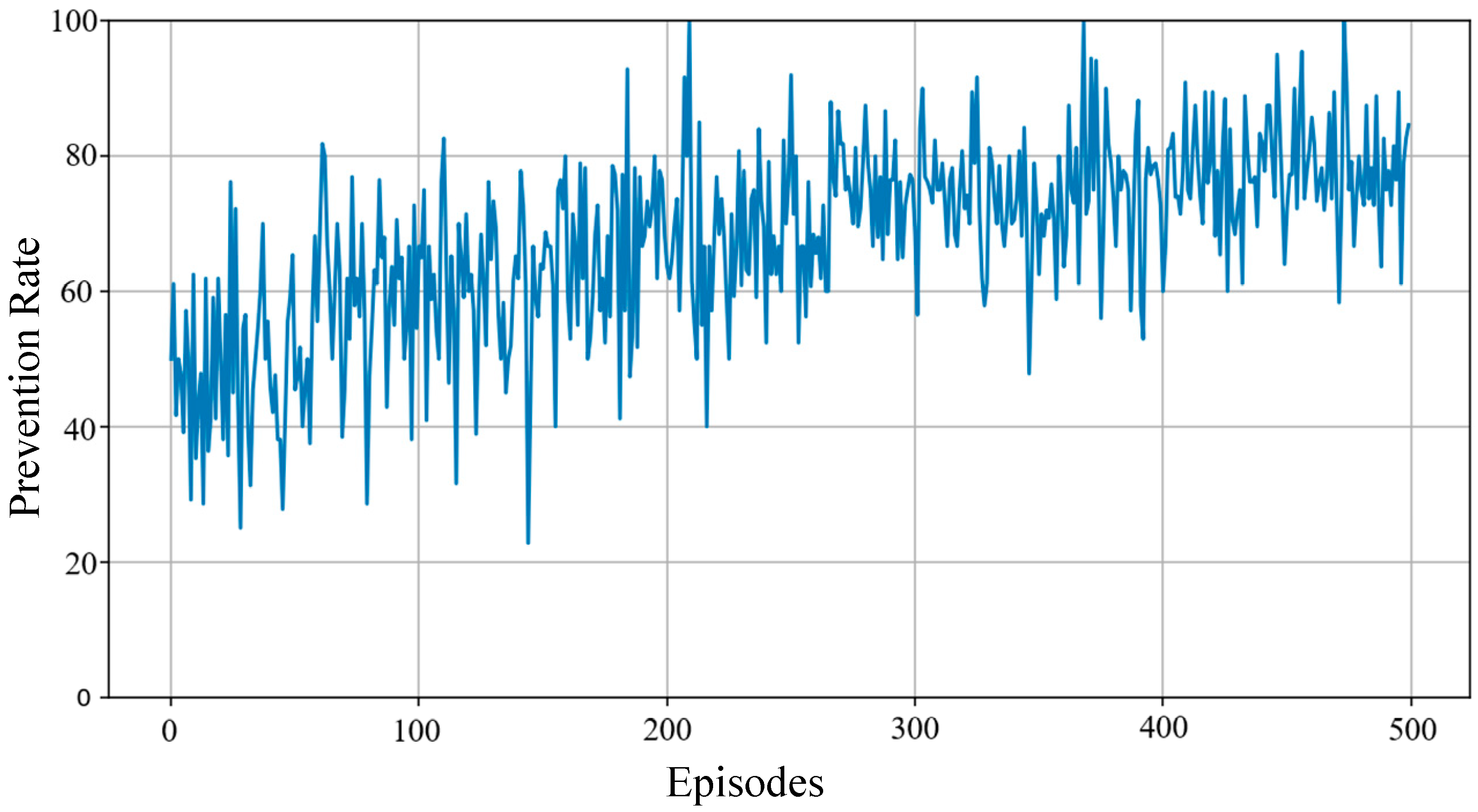
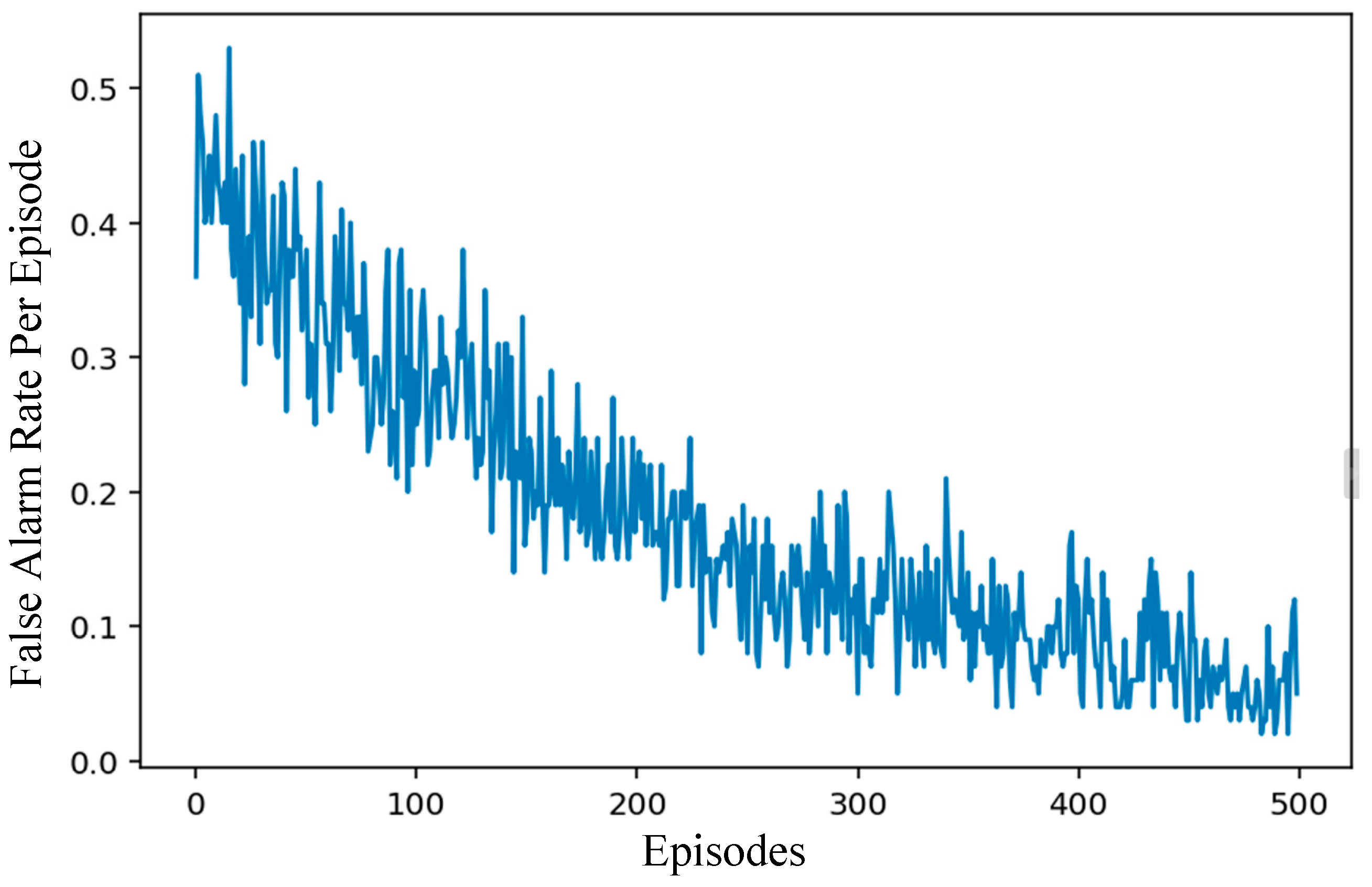
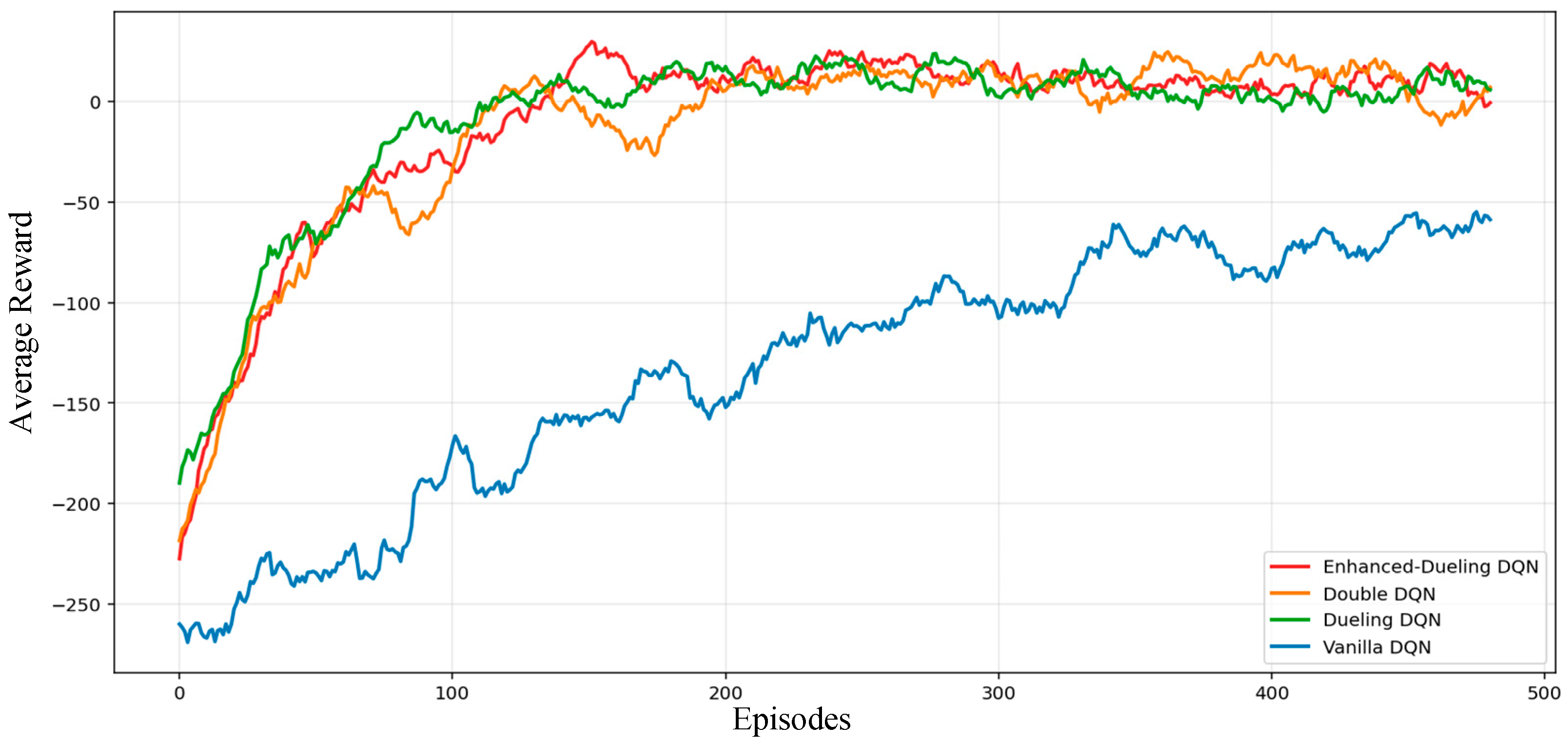
3.4. Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, M.; Li, F.; Pang, Y.; Zhang, W.; Chen, Z. Research on the Electronic Replacement of Substation Physical Security Measures. Shandong Electr. Power 2020, 47, 59–62. [Google Scholar]
- Kelley, B.P. Perimeter Substation Physical Security Design Options for Compliance with NERC CIP 014-1. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016; pp. 1–4. [Google Scholar]
- Mahato, N.K.; Yang, J.; Sun, Y.; Yang, D.; Zhang, Y.; Gong, G.; Hao, J. Physical Security of Electric Power Substations: Threats and Mitigation Measures. In Proceedings of the 2023 3rd International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Nanjing, China, 21 July 2023; pp. 434–438. [Google Scholar]
- Xu, P.; Tian, W. Design and realization of digital video surveillance system for power substation. Electr. Power Autom. Equip. 2005, 25, 66. [Google Scholar]
- Jiangtao, H. Discussion on The Construction of Substation Security Video Surveillance System. IOP Conf. Ser. Mater. Sci. Eng. 2019, 563, 032004. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Reddi, V.J. Deep Reinforcement Learning for Cyber Security. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 3779–3795. [Google Scholar] [CrossRef] [PubMed]
- Tiong, T.; Saad, I.; Teo, K.T.K.; bin Lago, H. Deep Reinforcement Learning with Robust Deep Deterministic Policy Gradient. In Proceedings of the 2020 2nd International Conference on Electrical, Control and Instrumentation Engineering (ICECIE), Kuala Lumpur, Malaysia, 28 November 2020; pp. 1–5. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction. IEEE Trans. Neural Netw. 1998, 9, 1054. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Lan, J.; Dong, X. Improved Q-Learning-Based Motion Control for Basketball Intelligent Robots Under Multi-Sensor Data Fusion. IEEE Access 2024, 12, 57059–57070. [Google Scholar] [CrossRef]
- Jäger, J.; Helfenstein, F.; Scharf, F. Bring Color to Deep Q-Networks: Limitations and Improvements of DQN Leading to Rainbow DQN. In Reinforcement Learning Algorithms: Analysis and Applications; Belousov, B., Abdulsamad, H., Klink, P., Parisi, S., Peters, J., Eds.; Studies in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2021; Volume 883, pp. 135–149. ISBN 978-3-030-41187-9. [Google Scholar]
- Sharma, A.; Pantola, D.; Kumar Gupta, S.; Kumari, D. Performance Evaluation of DQN, DDQN and Dueling DQN in Heart Disease Prediction. In Proceedings of the 2023 Second International Conference On Smart Technologies For Smart Nation (SmartTechCon), Singapore, 18 August 2023; pp. 5–11. [Google Scholar]
- Feng, L.-W.; Liu, S.-T.; Xu, H.-Z. Multifunctional Radar Cognitive Jamming Decision Based on Dueling Double Deep Q-Network. IEEE Access 2022, 10, 112150–112157. [Google Scholar] [CrossRef]
- Ban, T.-W. An Autonomous Transmission Scheme Using Dueling DQN for D2D Communication Networks. IEEE Trans. Veh. Technol. 2020, 69, 16348–16352. [Google Scholar] [CrossRef]
- Han, B.-A.; Yang, J.-J. Research on Adaptive Job Shop Scheduling Problems Based on Dueling Double DQN. IEEE Access 2020, 8, 186474–186495. [Google Scholar] [CrossRef]
- Lv, P.; Wang, X.; Cheng, Y.; Duan, Z. Stochastic Double Deep Q-Network. IEEE Access 2019, 7, 79446–79454. [Google Scholar] [CrossRef]
- Chen, X.; Hu, R.; Luo, K.; Wu, H.; Biancardo, S.A.; Zheng, Y.; Xian, J. Intelligent Ship Route Planning via an A∗ Search Model Enhanced Double-Deep Q-Network. Ocean Eng. 2025, 327, 120956. [Google Scholar] [CrossRef]
- Zeng, L.; Liu, Q.; Shen, S.; Liu, X. Improved Double Deep Q Network-Based Task Scheduling Algorithm in Edge Computing for Makespan Optimization. Tsinghua Sci. Technol. 2024, 29, 806–817. [Google Scholar] [CrossRef]
- Doanis, P.; Spyropoulos, T. Sample-Efficient Multi-Agent DQNs for Scalable Multi-Domain 5G+ Inter-Slice Orchestration. IEEE Trans. Mach. Learn. Commun. Netw. 2024, 2, 956–977. [Google Scholar] [CrossRef]
- Ouchani, S. A Security Policy Hardening Framework for Socio-Cyber-Physical Systems. J. Syst. Archit. 2021, 119, 102259. [Google Scholar] [CrossRef]
- Lang, Q.; Zhu, L.B.D.; Ren, M.M.C.; Zhang, R.; Wu, Y.; He, W.; Li, M. Deep Reinforcement Learning-Based Smart Grid Resource Allocation System. In Proceedings of the 2023 IEEE International Conferences on Internet of Things (iThings) and IEEE Green Computing & Communications (GreenCom) and IEEE Cyber, Physical & Social Computing (CPSCom) and IEEE Smart Data (SmartData) and IEEE Congress on Cybermatics (Cybermatics), Danzhou, China, 17 December 2023; pp. 703–707. [Google Scholar]
- Hao, Y.; Wang, M.; Chow, J.H. Likelihood Analysis of Cyber Data Attacks to Power Systems with Markov Decision Processes. IEEE Trans. Smart Grid 2018, 9, 3191–3202. [Google Scholar] [CrossRef]
- Herrmann, B.; Li, C.C.; Somboonyanon, P. The Development of New IEEE Guidance for Electrical Substation Physical Resilience. In Proceedings of the 2024 IEEE Power & Energy Society General Meeting (PESGM), Seattle, WA, USA, 21–25 July 2024; pp. 1–5. [Google Scholar]
- Sganga, N. Physical Attacks on Power Grid Rose by 71% Last Year, Compared to 2021. CBS News, 22 February 2023. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Qayoom, A.; Khuhro, M.A.; Kumar, K.; Waqas, M.; Saeed, U.; Ur Rehman, S.; Wu, Y.; Wang, S. A Novel Approach for Credit Card Fraud Transaction Detection Using Deep Reinforcement Learning Scheme. PeerJ Comput. Sci. 2024, 10, e1998. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H.; Dayan, P. Q-Learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, Y.; Ogai, H.; Inujima, H.; Tateno, S. Tactical Decision-Making for Autonomous Driving Using Dueling Double Deep Q Network with Double Attention. IEEE Access 2021, 9, 151983–151992. [Google Scholar] [CrossRef]
- Sovrano, F.; Raymond, A.; Prorok, A. Explanation-Aware Experience Replay in Rule-Dense Environments. IEEE Robot. Autom. Lett. 2022, 7, 898–905. [Google Scholar] [CrossRef]
- Electric Disturbance Events (OE-417) Annual Summaries. Available online: https://openenergyhub.ornl.gov/explore/dataset/oe-417-annual-summaries/information/ (accessed on 5 September 2024).


| Project | Environment |
|---|---|
| System | Windows 11 Pro N for Workstations |
| Memory (RAM) | 16 GB + 16 GB (DDR5-5600) |
| CPU | 13th Gen Intel(R) Core(TM) i7-13700H 2.40 GHz |
| Programming environment | Spyder 6.0.1 |
| GPU | NVIDIA RTX4060 |
| Python | Python 3.11 |
| PyTorch | 2.3.1 + cu118 |
| Learning Rate | Batch Size | Average Reward | Prevention Rate | False Alarm Rate | Training Loss |
|---|---|---|---|---|---|
| 0.00001 | 32 | −103.5 | 84.90 | 35.25 | 15.48 |
| 64 | −68.00 | 81.85 | 29.30 | 13.12 | |
| 128 | −239.5.00 | 60.49 | 56.10 | 18.96 | |
| 0.00002 | 32 | −75.65 | 85.28 | 5.20 | 3.51 |
| 64 | 7.50 | 91.11 | 0.50 | 1.59 | |
| 128 | −50.25 | 86.60 | 4.60 | 5.53 | |
| 0.00005 | 32 | −96.70 | 86.10 | 7.60 | 10.30 |
| 64 | 13.3.00 | 86.50 | 0.61 | 2.51 | |
| 128 | −87.70 | 88.00 | 10.11 | 6.35 |
| Parameters | Value | Description |
|---|---|---|
| Learning rate | 0.00002 | Step size for updating the neural network weights. |
| Batch size | 64 | No. of transactions sampled from replay buffer training step. |
| Discount factor | 0.99 | This balances the immediate and future rewards. |
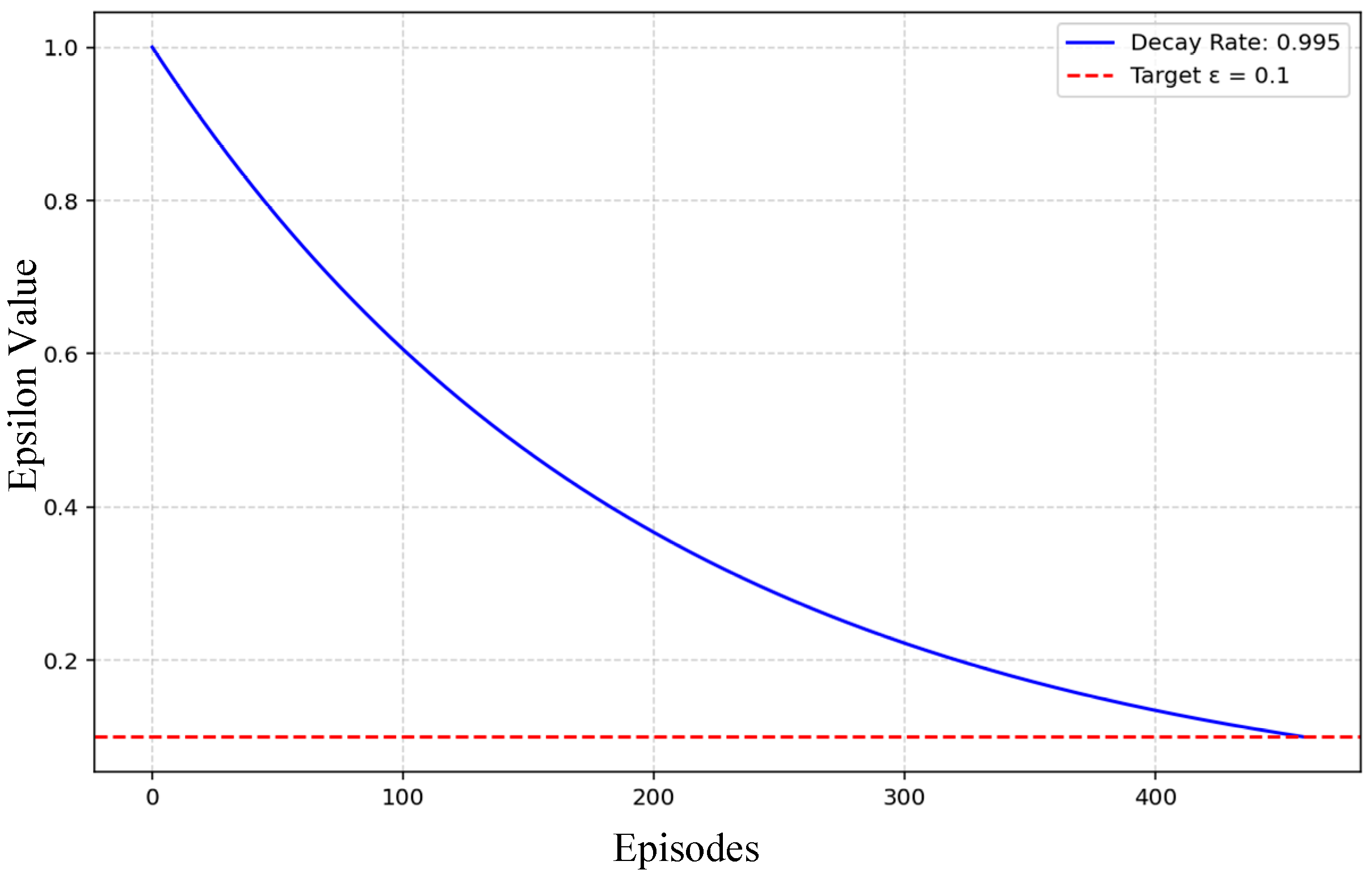
| Epsilon start value | 1.0 | Initial value of epsilon for the epsilon-greedy exploration strategy. |
| Epsilon decay | 0.995 | This is the rate at which epsilon decays per episode, which controls the exploration duration. |
| Epsilon minimum | 0.01 | This is minimum value of epsilon, which ensures some exploration throughout the training. |
| Target network update | Every 50 steps | This is the frequency of updating the target network in order to stabilize the Q-value estimation. |
| PER alpha | 0.7 | Prioritization exponent for sampling transitions in Prioritized Experience Replay. |
| PER beta | 0.5 | This is importance-sampling correction factor in Prioritized Experience Replay. |
| Optimizer | Adam | Optimization algorithm used for training the neural network. |
| Episodes | 500 | Total number of training episodes to learn the policy. |
| States per episode | 100 | Maximum number of steps per episode in the simulation environment. |
| Performance Metrics | Enhanced-Dueling DQN | Dueling DQN | Double DQN | Vanilla DQN |
|---|---|---|---|---|
| Average Reward | 7.5 | 6.6 | 6.1 | −47.7 |
| Prevention Rate | 91.1% | 89.1% | 88.3% | 81.6% |
| False Alarm Rate | 0.5% | 0.8% | 0.7% | 15.0% |
| Training Loss (20-Episode Moving Average) | 1.59 | 12.94 | 12.98 | 20.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahato, N.K.; Yang, J.; Yang, J.; Gong, G.; Hao, J.; Sun, J.; Liu, J. Enhanced-Dueling Deep Q-Network for Trustworthy Physical Security of Electric Power Substations. Energies 2025, 18, 3194. https://doi.org/10.3390/en18123194
Mahato NK, Yang J, Yang J, Gong G, Hao J, Sun J, Liu J. Enhanced-Dueling Deep Q-Network for Trustworthy Physical Security of Electric Power Substations. Energies. 2025; 18(12):3194. https://doi.org/10.3390/en18123194
Chicago/Turabian StyleMahato, Nawaraj Kumar, Junfeng Yang, Jiaxuan Yang, Gangjun Gong, Jianhong Hao, Jing Sun, and Jinlu Liu. 2025. "Enhanced-Dueling Deep Q-Network for Trustworthy Physical Security of Electric Power Substations" Energies 18, no. 12: 3194. https://doi.org/10.3390/en18123194
APA StyleMahato, N. K., Yang, J., Yang, J., Gong, G., Hao, J., Sun, J., & Liu, J. (2025). Enhanced-Dueling Deep Q-Network for Trustworthy Physical Security of Electric Power Substations. Energies, 18(12), 3194. https://doi.org/10.3390/en18123194









