Current Controlled AC/DC Converter and Its Performance—A Mathematical Model
Abstract
1. Introduction
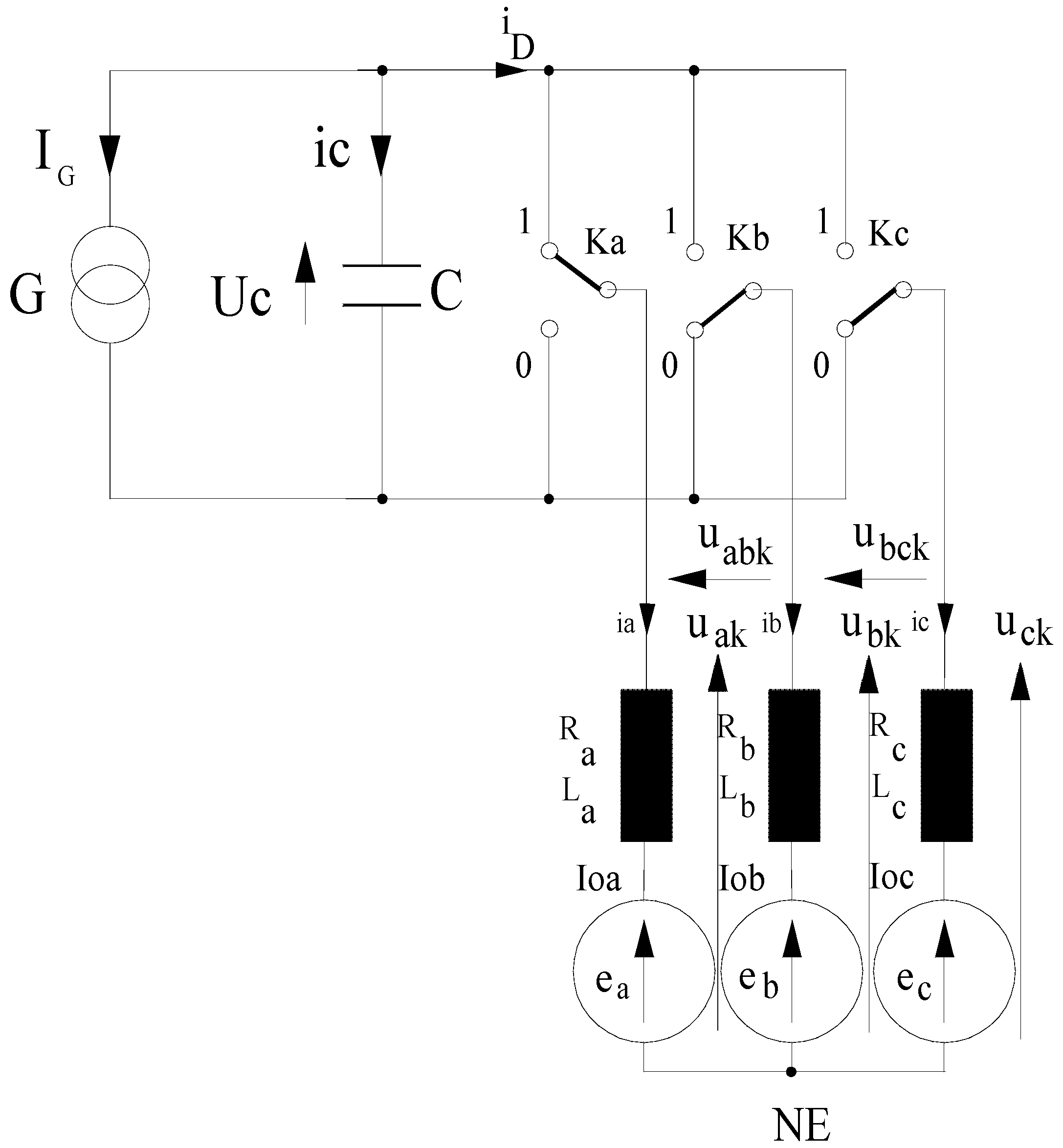
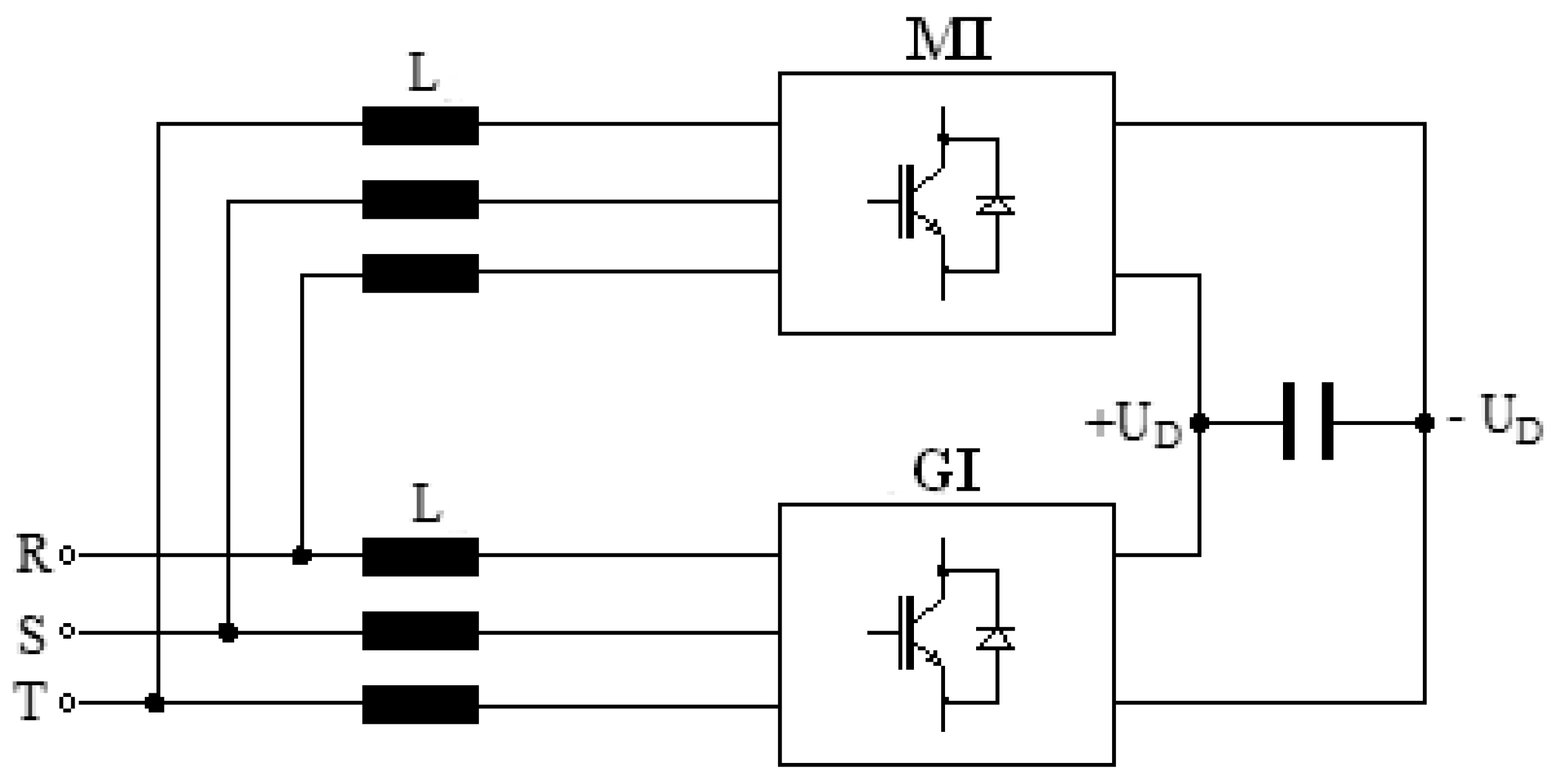
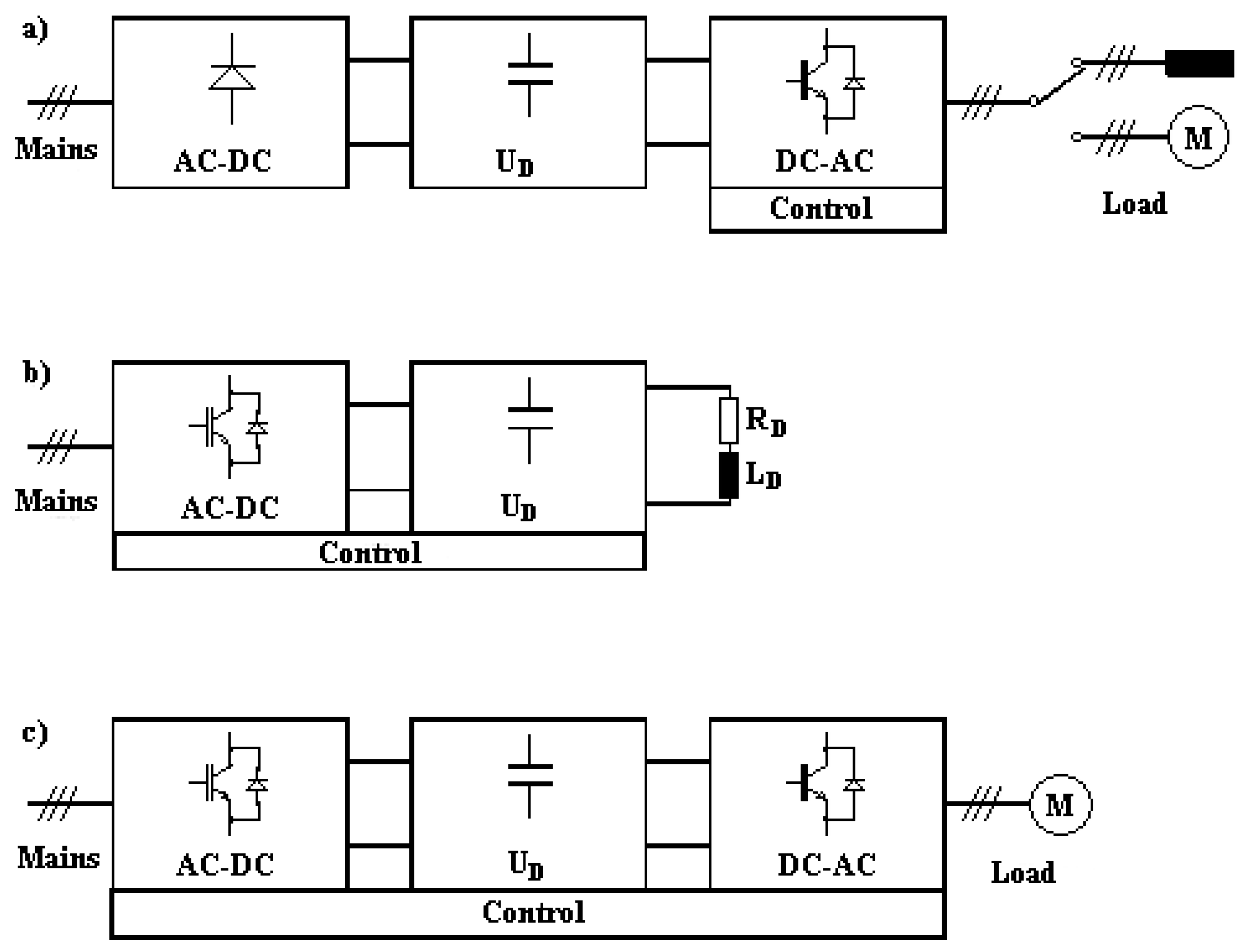
2. Mains Converter
2.1. Model of Mains Converter
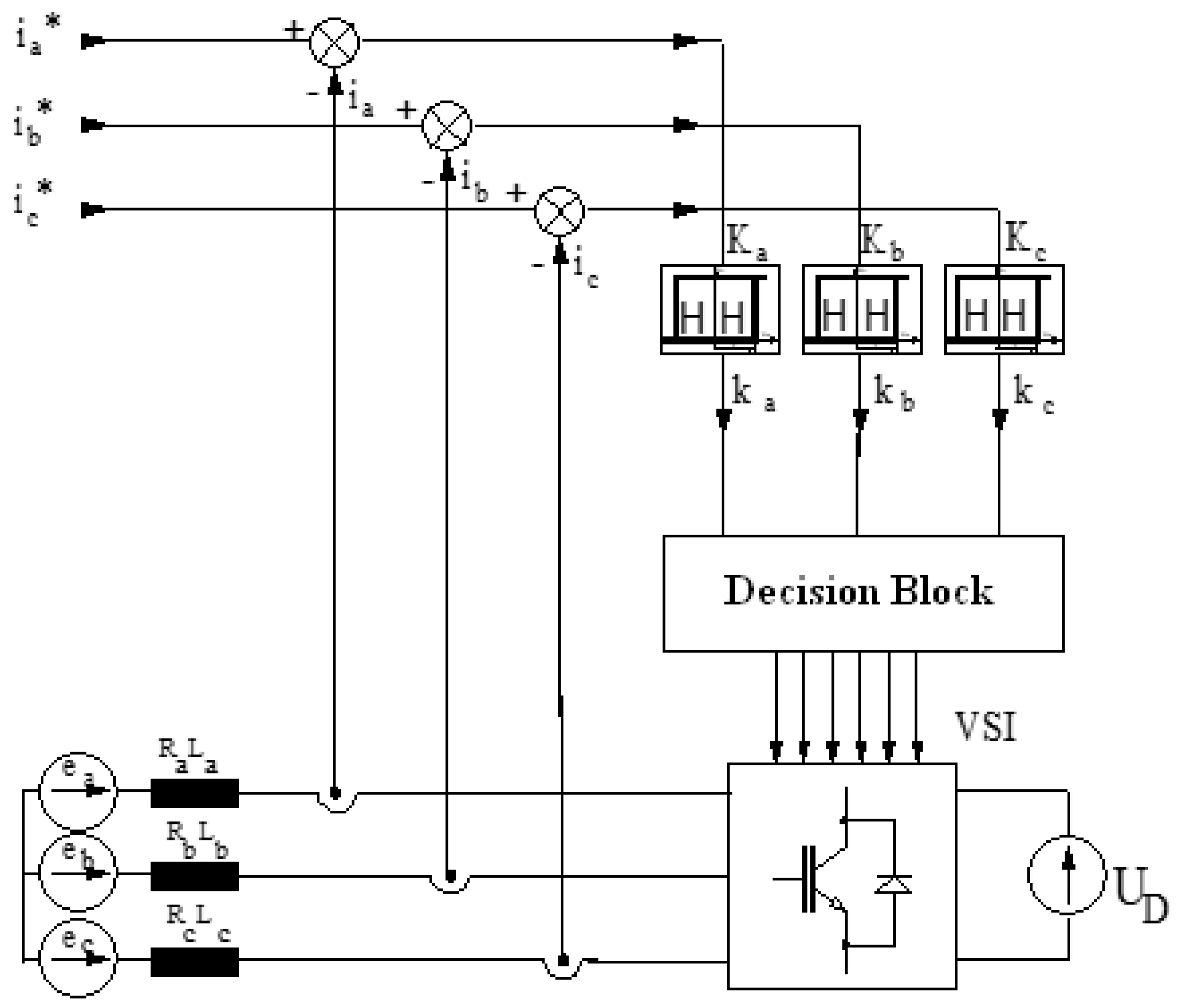
2.2. Converter Control Algorithm
| h | content factor of output current harmonics |
| minimal time between switches of inverter terminals | |
| maximal time between switches of inverter terminals | |
| Tśr | average time between switches |
| vnum | number of vector switches in one period of current |
| average value of the DC voltage source current | |
| amplitude of the set current value | |
| I | RMS value of the phase current |
| H | width of the current control error hysteresis zone |
| SH | width of the auxiliary current control hysteresis zone |
| frequency of the fundamental harmonic of the set inverter current | |
| period of the fundamental harmonic of the set inverter output current | |
| frequency of digital sampling of the inverter control system | |
| period of digital sampling of the inverter control system | |
| intermediate circuit voltage | |
| load circuit reactance | |
| load circuit resistance | |
| phase shift between the current waveform and the electromotive force |
- -
- The machine rotor circuit: ,
- -
- The set waveform of rotor current
- -
- -
- The electromotive force
- -
- Converter supply voltage
- -
- cos;
- -
- Current waveform hysteresis zone: H = 20 A;
- -
- Auxiliary hysteresis zone: SH = 10 A.
2.2.1. Structure of Control Systems
- -
- If > H then the non-zero vector is activated;
- -
- If < H then the zero vector is activated.
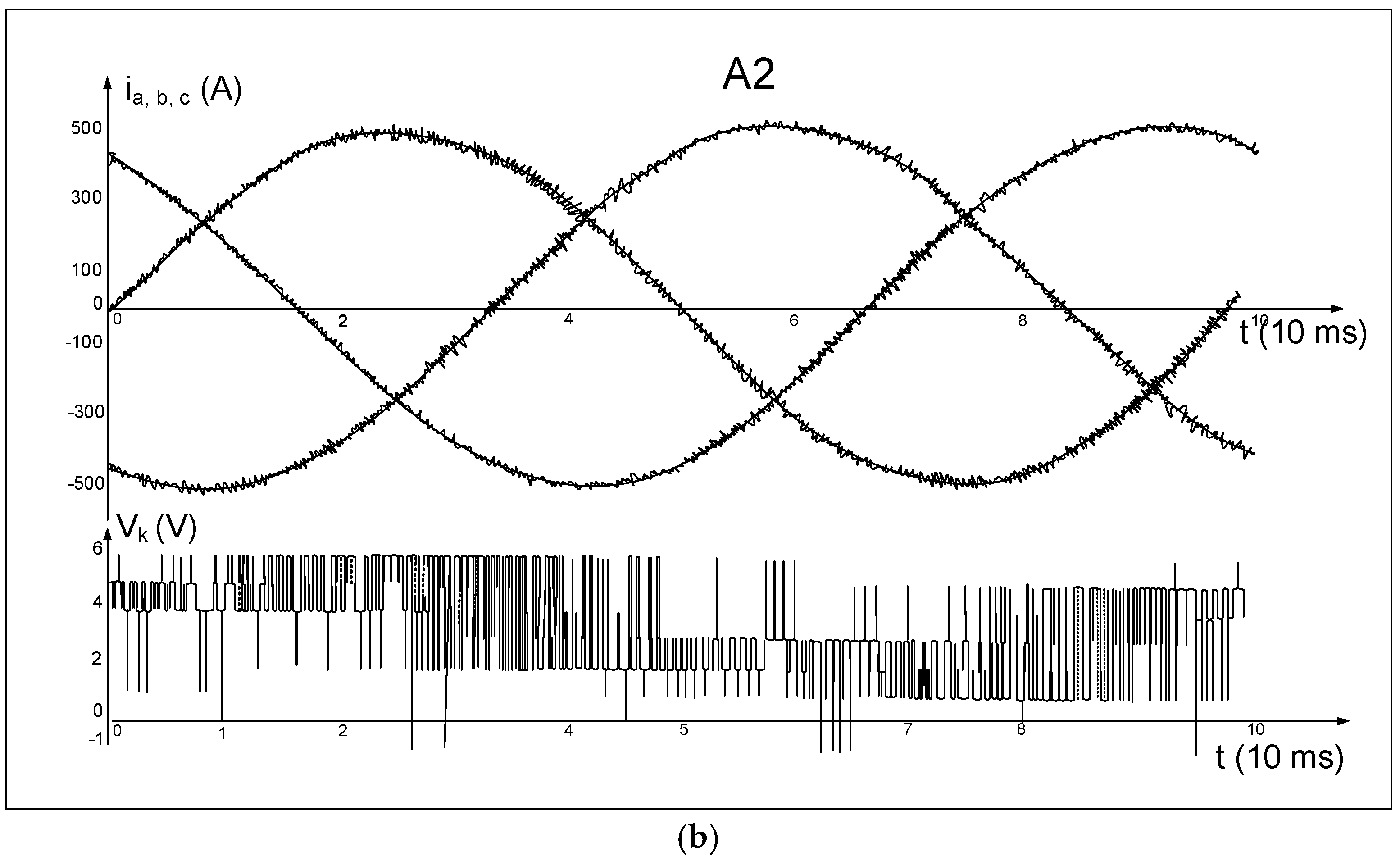
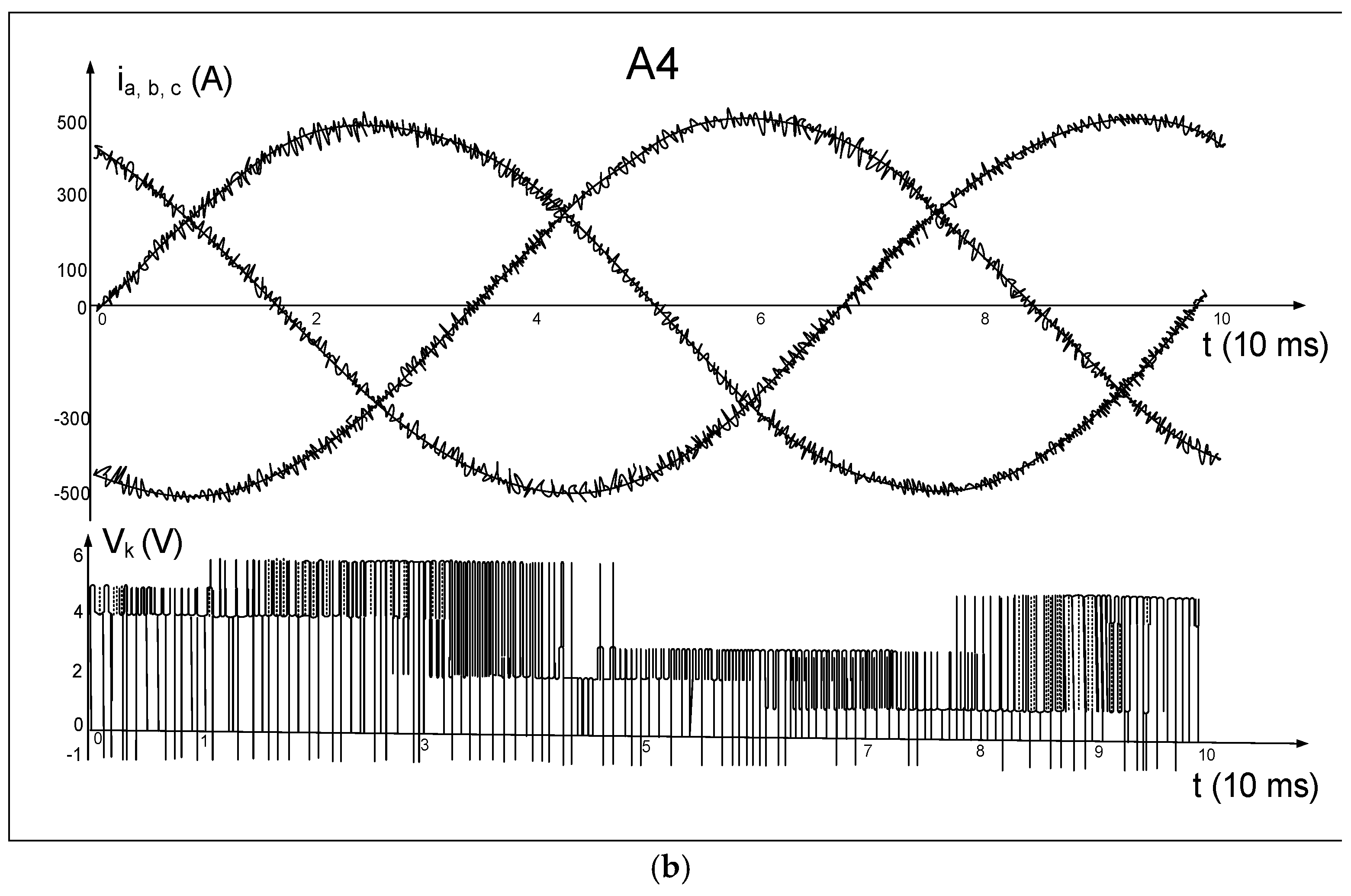
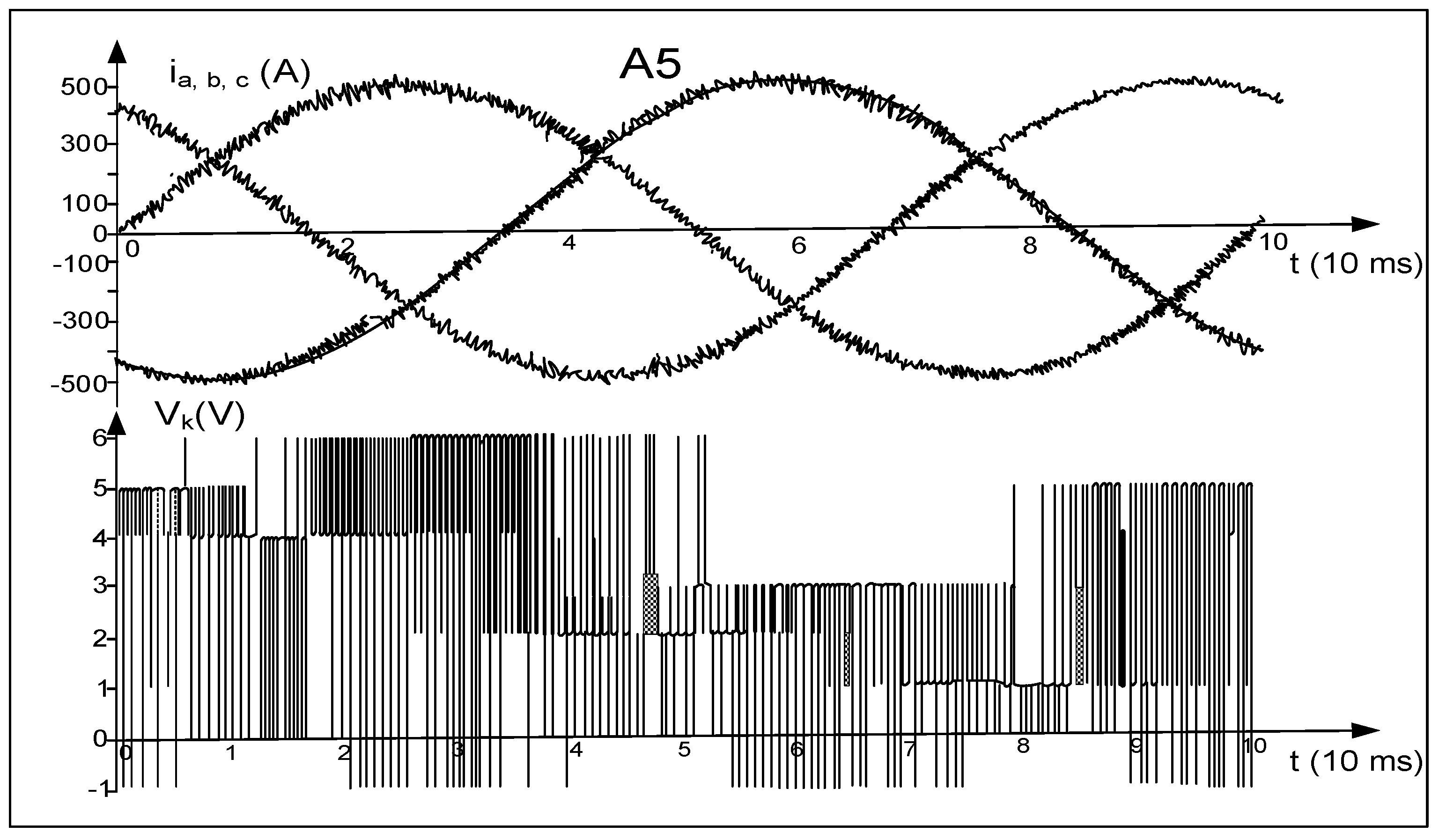
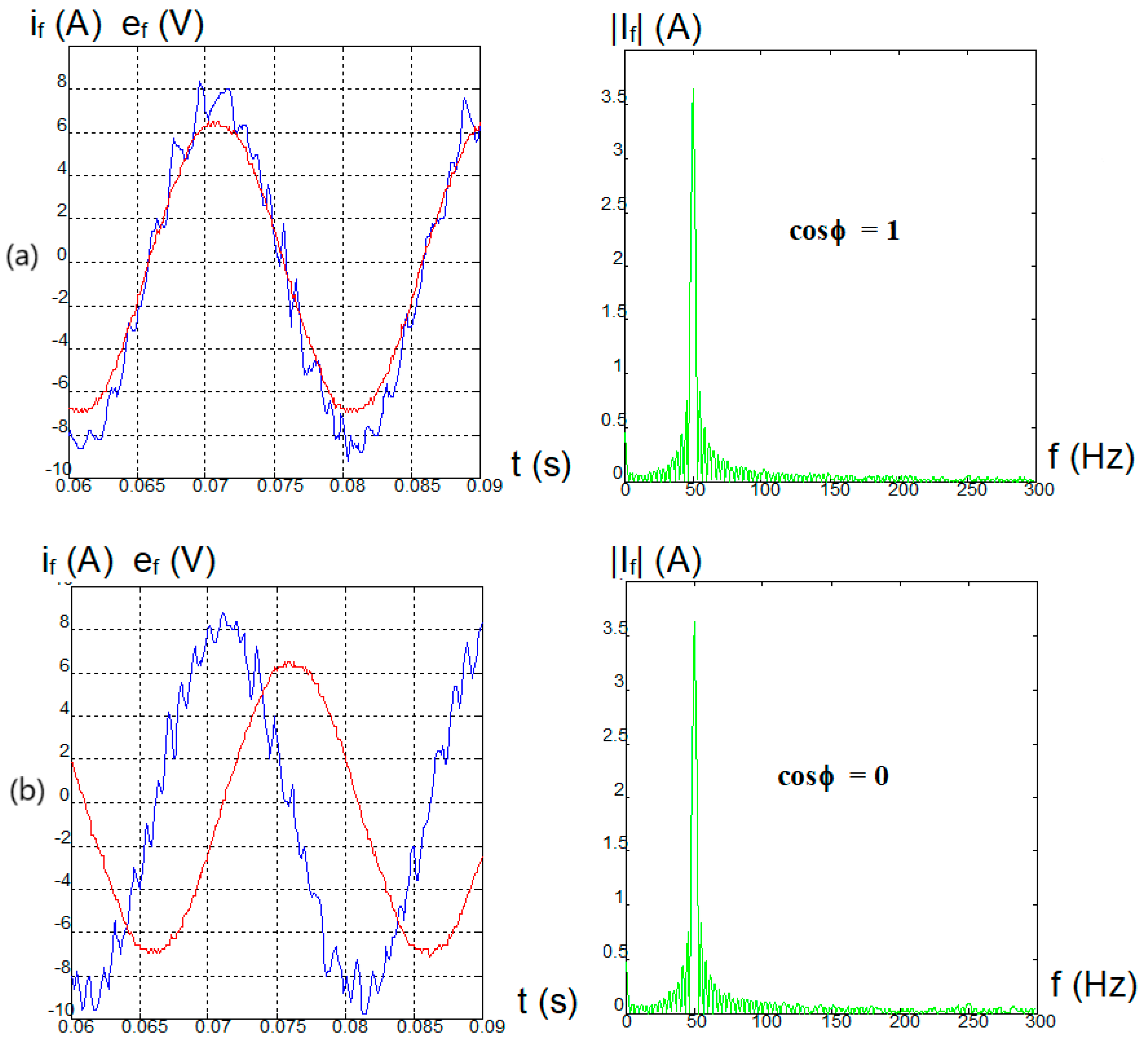
2.2.2. Results of Simulation Tests of Selected Hysteresis Algorithms
2.2.3. Evaluating Results of Simulation Tests
2.2.4. Experimental Tests of Hysteresis Algorithms
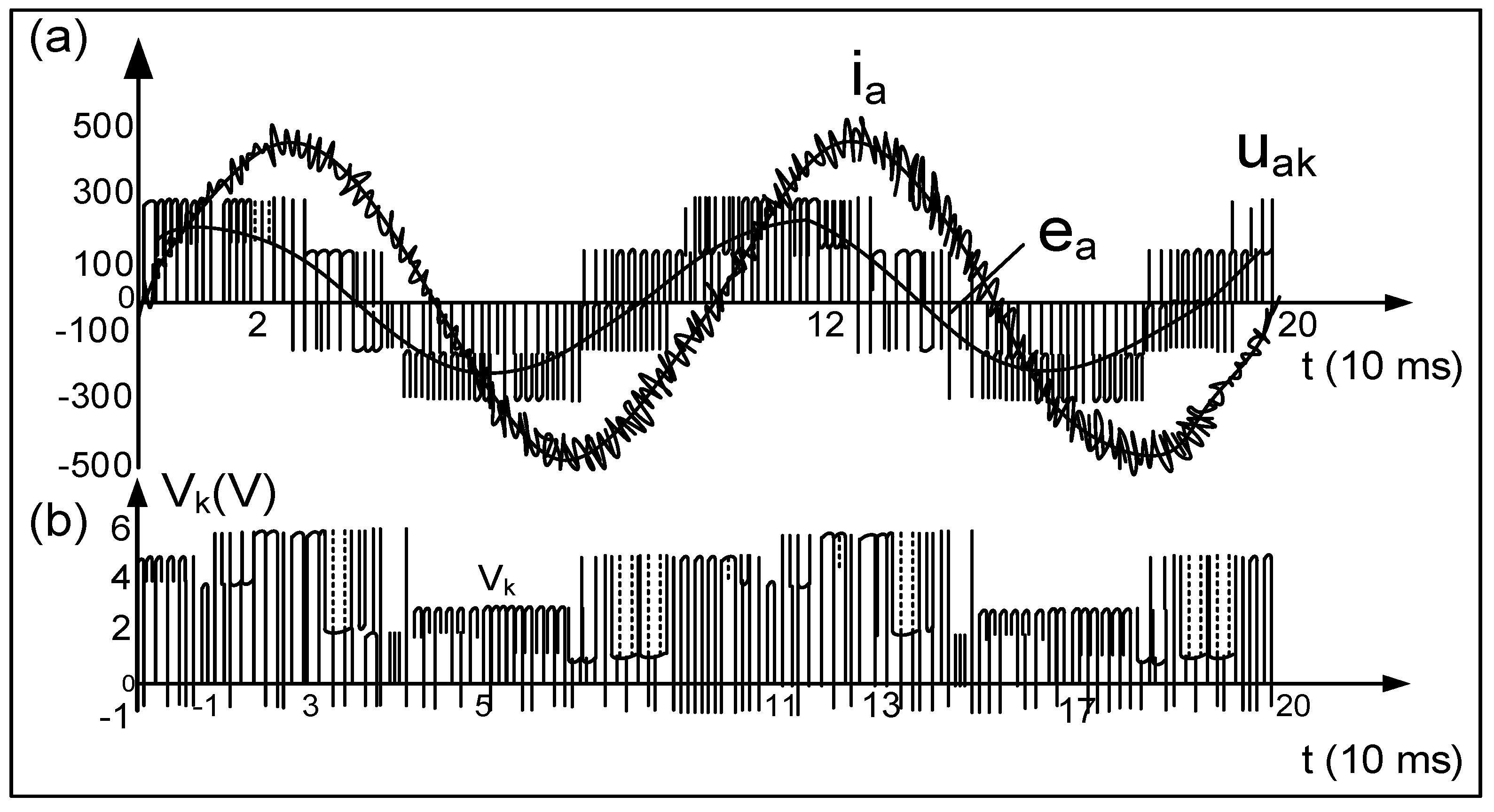
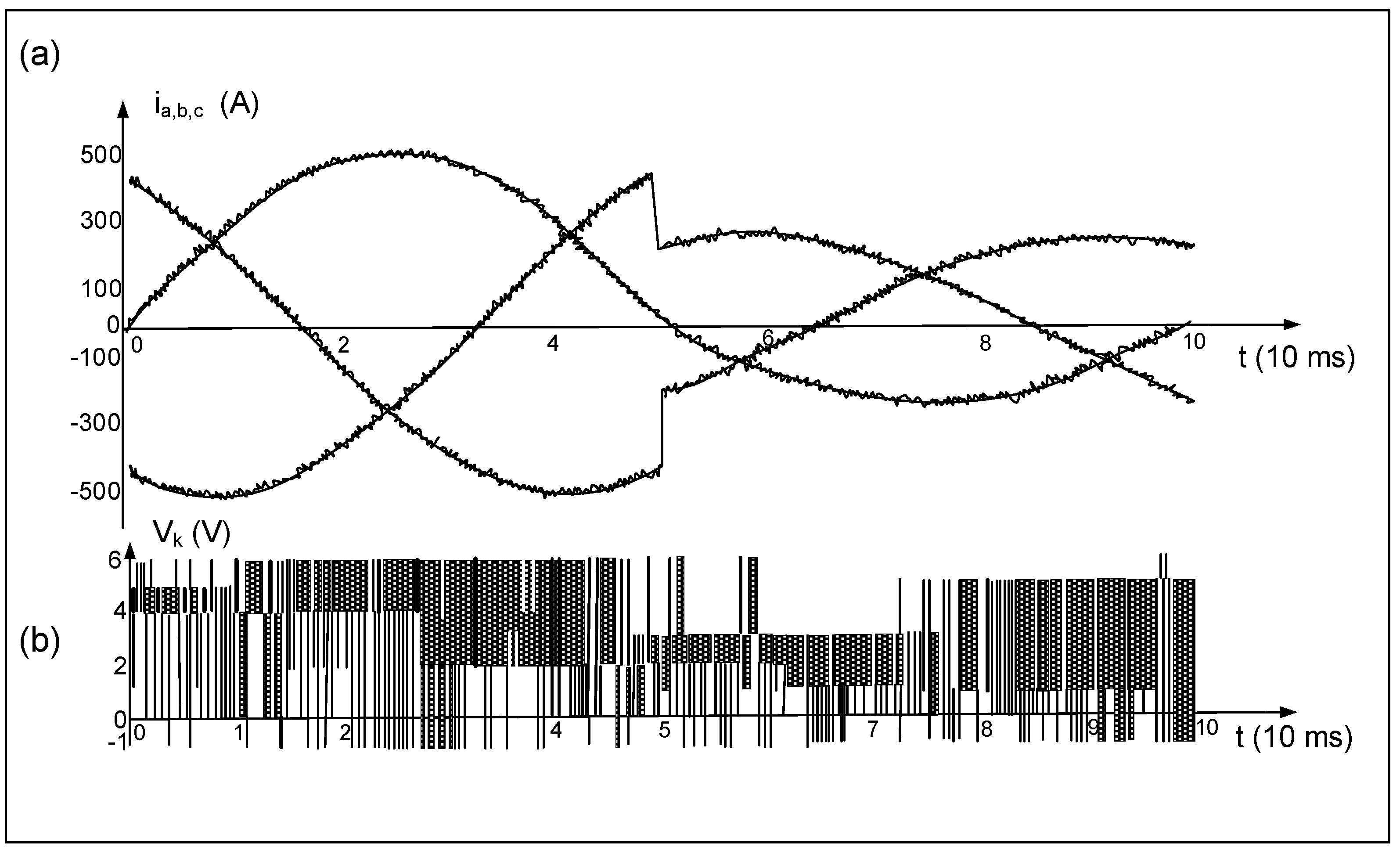
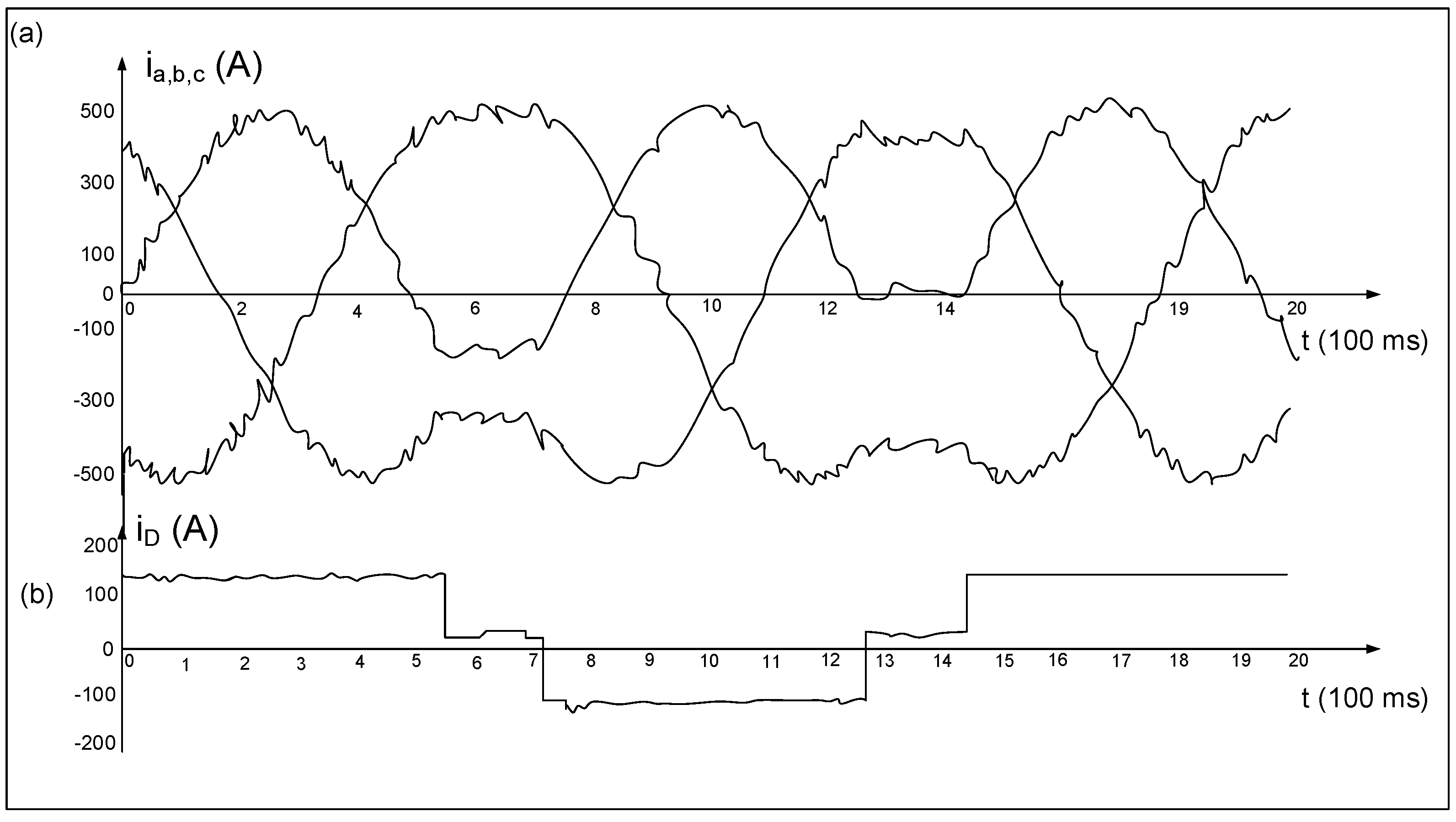
3. Rectifier and Inverter Operation of Mains Converter
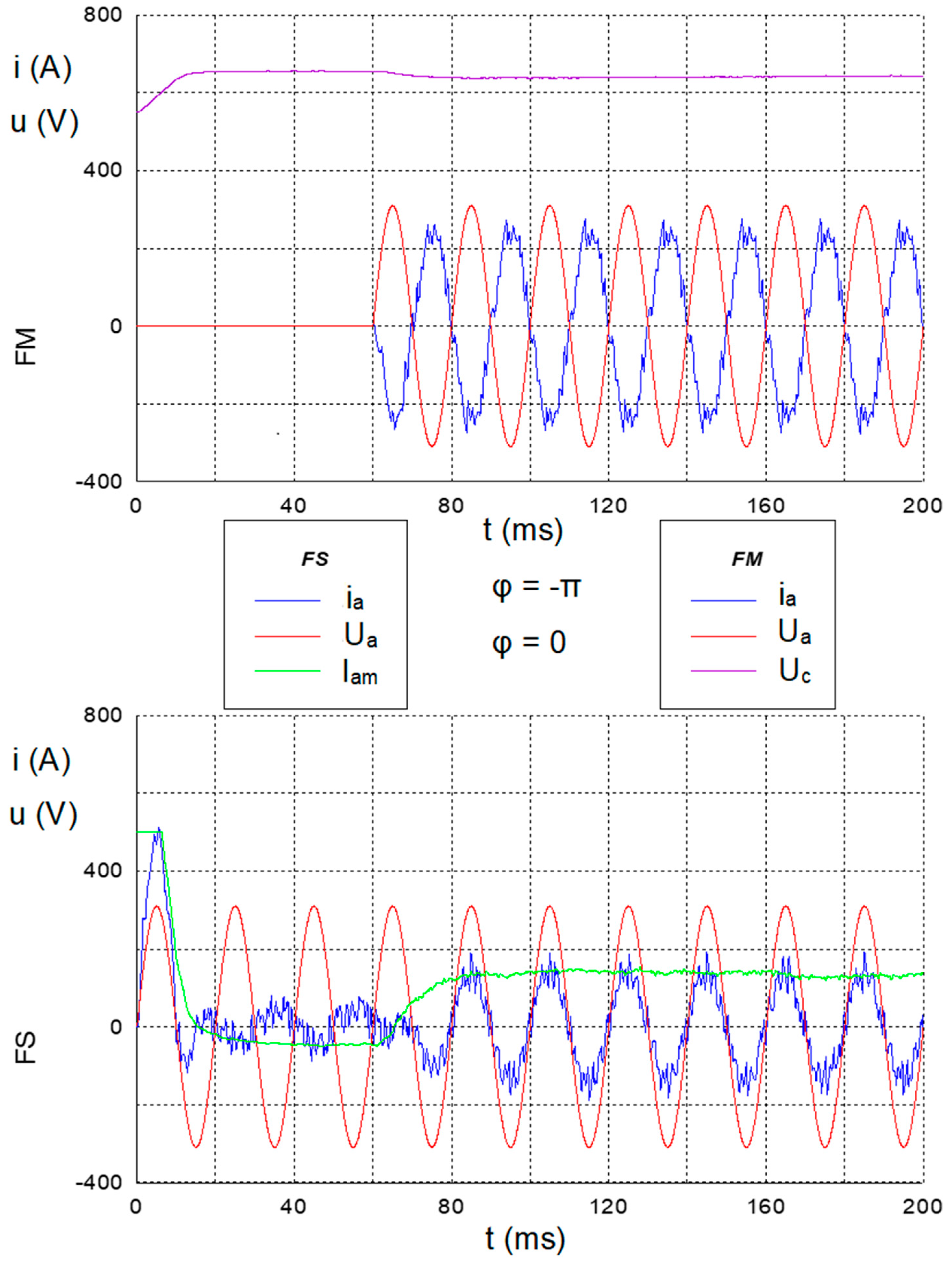
3.1. Simulation Tests of the Converter
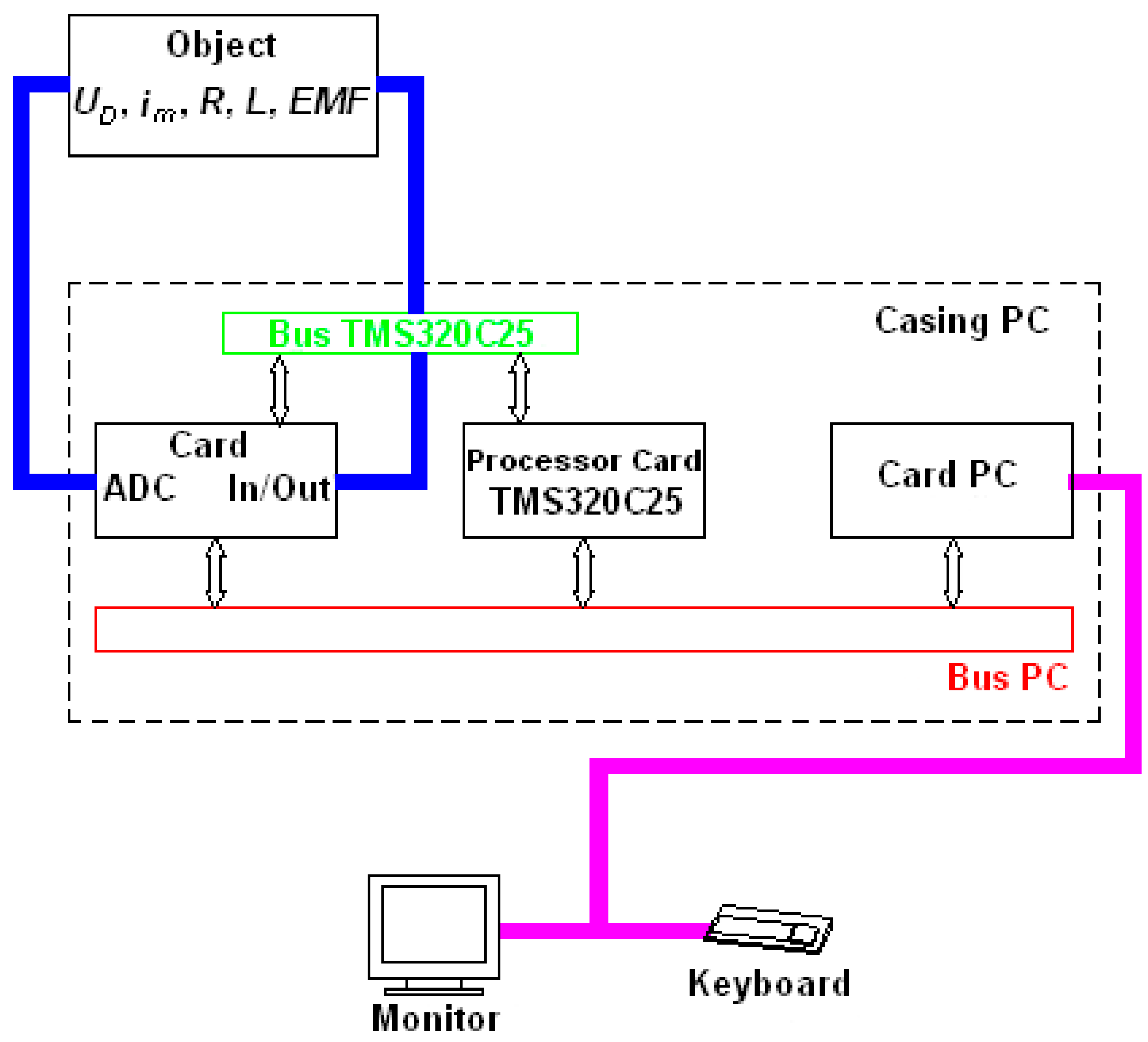
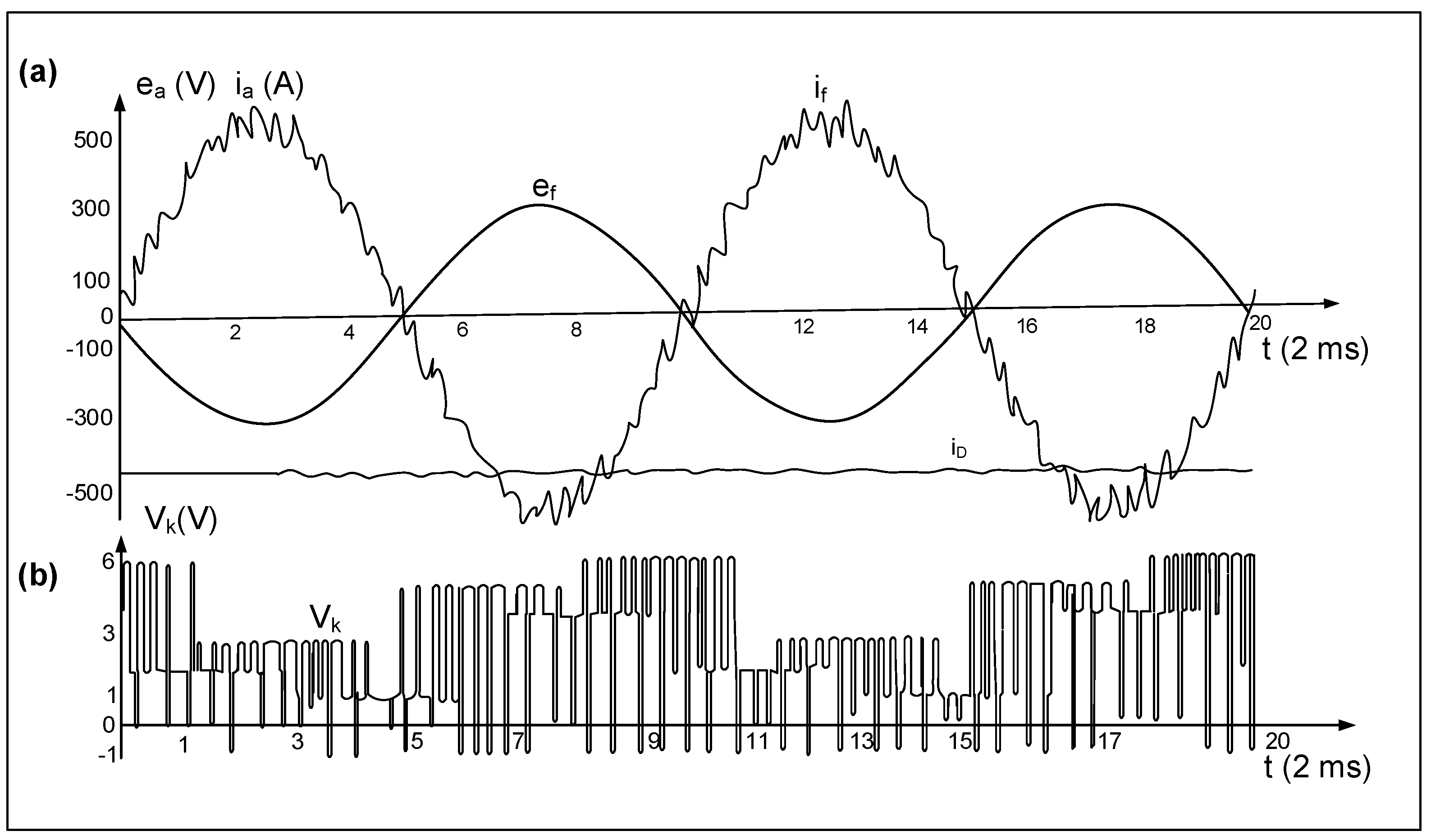
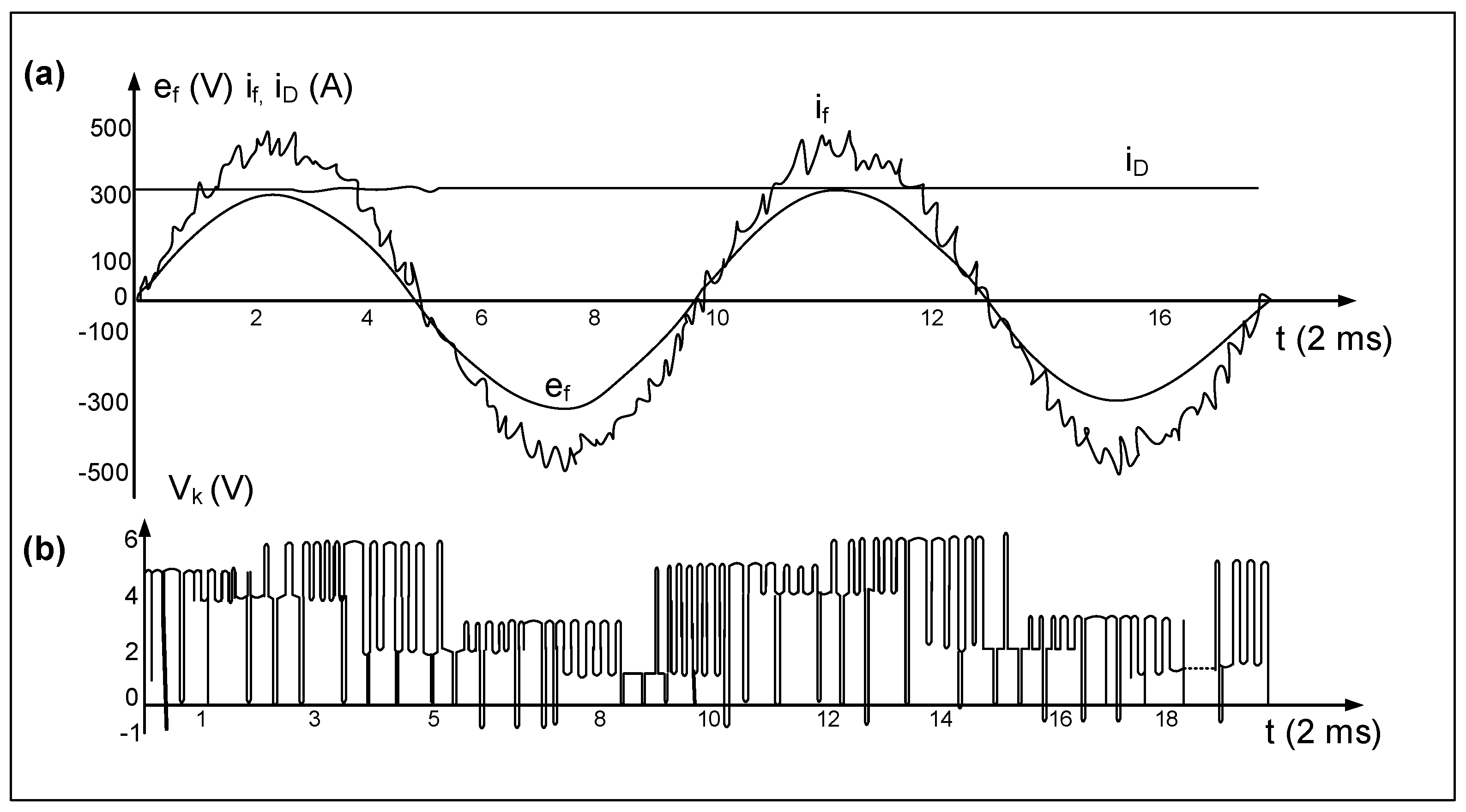
3.2. Experimental Tests of Converters
- ;
- ;
- ;
- ;
- ;
- ;
- .
- ;
- .
- .
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gopi, R.R.; Sreejith, S. Converter topologies in photovoltaic applications—A review. Renew. Sustain. Energy Rev. 2018, 94, 1–14. [Google Scholar] [CrossRef]
- Donadi, A.K.; Jahnavi, W. Review of dc-dc converters in photovoltaic systems for mppt systems. Int. J. Res. Eng. Technol. 2019, 6, 1914–1918. [Google Scholar]
- Sher, H.A.; Addoweesh, K.E. Micro-inverters promising solutions in solar photovoltaics. Energy Sustain. Develop. 2012, 16, 389–400. [Google Scholar] [CrossRef]
- Alajmi, B.N.; Ahmed, K.H.; Adam, G.P.; Williams, B.W. Single-phase single-stage transformerless grid- connected PV system. IEEE Trans. Power Electron 2013, 28, 2664–2676. [Google Scholar] [CrossRef]
- Aganah, K.; Chukwuma, J.; Ndoye, M. A Review of Off-Grid Plug-and-Play Solar Power Systems: Toward a New “I Better Pass My Neighbour” Generator. In Proceedings of the 2019 IEEE PES/IAS PowerAfrica, Abuja, Nigeria, 20–23 August 2019. [Google Scholar] [CrossRef]
- Kwon, O.; Kim, K.-S.; Kwon, B.-H. Highly efficient single-stage DAB microinverter using a novel modulation strategy to minimize reactive power. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 544–552. [Google Scholar] [CrossRef]
- Pal, A.; Basu, K. A single-stage soft-switched isolated three-phase DC–AC converter with three-phase unfolder. IEEE Trans. Power Electron. 2020, 35, 3601–3615. [Google Scholar] [CrossRef]
- Koznowski, W.; Łebkowski, A. Analysis of Hull Shape Impact on Energy Consumption in an Electric Port Tugboat. Energies 2022, 15, 339. [Google Scholar] [CrossRef]
- Szewczyk, P.; Łebkowski, A. Studies on Energy Consumption of Electric Light Commercial Vehicle Powered by In-Wheel Drive Modules. Energies 2021, 14, 7524. [Google Scholar] [CrossRef]
- Muc, A. The three-Phase Converter with Configurable DC Input and Multilevel AC Output. In Proceedings of the 2024 IEEE 18th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Gdynia, Poland, 24–26 June 2024. [Google Scholar] [CrossRef]
- Liu, K.; Sheng, W.; Wang, S.; Ding, H.; Huang, J. Stability of distribution network with large-scale PV penetration under off-grid operation. In Proceedings of the International Conference on Frontiers of Energy and Environment Engineering, CFEEE 2022, Beihai, China, 16–18 December 2022. [Google Scholar]
- Xie, B.; Zhou, L.; Zheng, C.; Zhang, Q. Stability and resonance analysis and improved design of N-paralleled grid-connected PV inverters coupled due to grid impedance. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition. (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 362–367. [Google Scholar]
- Fu, Q.; Du, W.; Wang, H.; Zheng, Z.; Xiao, X. Impact of the differences in VSC average model parameters on the DC voltage critical stability of an MTDC power system. IEEE Trans. Power Syst. 2022, 38, 2805–2819. [Google Scholar] [CrossRef]
- Fu, Q.; Du, W.; Wang, H.; Xiao, X. Effect of the dynamics of the MTDC power system on DC voltage oscillation stability. IEEE Trans. Power Syst. 2022, 37, 3482–3494. [Google Scholar] [CrossRef]
- Fu, Q.; Du, W.; Wang, H. Analysis of harmonic oscillations caused by grid-connected VSCs. IEEE Trans. Power Deliv. 2021, 36, 1202–1210. [Google Scholar] [CrossRef]
- Fu, Q.; Du, W.; Wang, H.; Ma, X.; Xiao, X. DC voltage oscillation stability analysis of DC-voltage-droop-controlled multi-terminal DC distribution system using reduced-order modal calculation. IEEE Trans. Smart Grid. 2022, 13, 4327–4339. [Google Scholar] [CrossRef]
- Oggier, G.G.; Jimenez, R.G.; Zhao, Y.; Balda, J.C. Modeling and characterization of 10-kV SiC Mosfet modules for medium-voltage distribution systems. In Proceedings of the 2020 IEEE 11th International Symposium on Power Electronics for Distributed Generation Systems (PEDG) (2020), Dubrovnik, Croatia, 28 September–1 October 2020; pp. 583–590. [Google Scholar]
- Edwin, F.F.; Xiao, W.; Khadkikar, V. Dynamic modeling and control of interleaved flyback module-integrated converter for PV power applications. IEEE Trans. Ind. Electron. 2013, 61, 1377–1388. [Google Scholar] [CrossRef]
- Komurcugil, H.; Bayhan, S.; Bagheri, F.; Kukrer, O.; Abu-Rub, H. Model-based current control for single-phase grid-tied quasi-Z-source inverters with virtual time constant. IEEE Trans. Ind. Electron. 2018, 65, 8277–8286. [Google Scholar] [CrossRef]
- Sulkowski, W. Modified Hysteresis Current Regulator for 3-Phase PWM-VSI. In Proceedings of the 6th Global Power, Energy and Communication Conference, Budapest, Hungary, 4–7 June 2024; 1990; Volume 2, pp. 474–478. [Google Scholar]
- Iwaszkiewicz, J. A predictive algorithm for current controlled voltage source inverter. In Proceedings of the ISIE ’93—Budapest: IEEE International Symposium on Industrial Electronics Conference, Budapest, Hungary, 1–3 June 1993; pp. 514–518. [Google Scholar]
- Nagy, I. Novel Adaptive Tolerane Band PWM for Field-Oriented Control of Induction Machines. IEEE Trans. Ind. Electron. 1994, 41, 406–417. [Google Scholar] [CrossRef]
- Rajeev, M.; Agarwal, V. Single phase current source inverter with multiloop control for transformerless grid–PV interface. IEEE Trans. Ind. Appl. 2018, 54, 2416–2424. [Google Scholar] [CrossRef]
- Mohomad, H.; Saleh, S.A.; Chang, L. Disturbance estimator-based predictive current controller for single-phase interconnected PV systems. IEEE Trans. Ind. Appl. 2017, 53, 4201–4209. [Google Scholar] [CrossRef]
- Dumitrescu, A.-M.; Griva, G.; Bojoi, R.; Bostan, V.; Magureanu, R. Design of current controllers for active power filters using naslin polynomial technique. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–7. [Google Scholar]
- Akbar, F.; Cha, H.; Do, D.-T. CSI7: Novel Three-Phase Current-Source Inverter With Improved Reliability. IEEE Trans. Power Electron. 2021, 36, 9170–9182. [Google Scholar] [CrossRef]
- Estévez-Bén, A.A.; Tapia, H.J.C.L.; Carrillo-Serrano, R.V.; Rodríguez-Reséndiz, J.; Nava, N.V. A New Predictive Control Strategy for Multilevel Current-Source Inverter Grid-Connected. Electronics 2019, 8, 902. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Cha, H. Five-Level Current Source Inverter with Inductor Cell Using Switching-Cell Structure. IEEE Trans. Ind. Electron. 2022, 69, 6859–6869. [Google Scholar] [CrossRef]
- Senthilnathan, K.; Annapoorani, I. Multi-Port Current Source Inverter for Smart Microgrid Applications: A Cyber Physical Paradigm. Electronics 2019, 8, 1. [Google Scholar] [CrossRef]
- Dai, H.; Torres, R.A.; Gossmann, J.; Lee, W.; Jahns, T.M.; Sarlioglu, B. A Seven-Switch Current-Source Inverter Using Wide Bandgap Dual-Gate Bidirectional Switches. IEEE Trans. Ind. Appl. 2022, 58, 3721–3737. [Google Scholar] [CrossRef]
- He, J.; Lyu, Y.; Han, J.; Wang, C. An SVM Approach for Five-Phase Current Source Converters Output Current Harmonics and Common-Mode Voltage Mitigation. IEEE Trans. Ind. Electron. 2020, 67, 5232–5245. [Google Scholar] [CrossRef]
- Aldin, M.F.; Dagan, K.J. A Novel Single-Phase Five-Level Current-Source Inverter Topology. Electronics 2024, 13, 1213. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.; Xu, P.; Li, D.; Liu, B. A Current Control Method for Grid-Connected Inverters. Energies 2023, 16, 6558. [Google Scholar] [CrossRef]
- Fu, T.; Gao, J.; Liu, H.; Xia, B. Research on the Control and Modulation Scheme for a Novel Five-Switch Current Source Inverter. Energies 2024, 17, 3640. [Google Scholar] [CrossRef]
- Roth-Stielow, J.; Zimmermann, W.; Boehringer, A.; Schwarz, B. Zwei zeitdiskrete Steuer-verfahren fur Pulsumrichter im Vergleich. Etz-Archiv. 1989, 11, 389–396. [Google Scholar]
- Holz, J. Pulsewidth modulation—A Survey. In Proceedings of the PESC ‘92 Record. 23rd Annual IEEE Power Electronics Specialists Conference, Toledo, Spain, 29 June–3 July 1992; pp. 11–18. [Google Scholar]






| 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 |
| 0 | 0 | |||||||
| 0 | 0 | |||||||
| 0 | 0 | |||||||
| 0 |
| 0 | 0 |
| 4 | 2 | 3 | 0 | 5 | 1 |
| Parameter | Algorithm | |||||
|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | ||
| vnum | 1344 | 594 | 696 | 549 | 642 | |
| s | s | s | s | s | ||
| s | s | s | s | s | ||
| 48.0 | 7.0 | 5.0 | 7.0 | 7.7 | ||
| Tśr | s | s | s | s | s | |
| ID | 294.7 A | 297.1 A | 296.3 A | 296.2 A | 294.5 A | |
| Phase a | 352.6 | 345.7 | 345.0 | 345.1 | 353.2 | |
| I | Phase b | 352.6 | 346.3 | 346.5 | 345.8 | 353.6 |
| Phase c | 352.6 | 345.8 | 345.8 | 345.2 | 353.5 | |
| THD | 0.257% | 0.597% | 0.539% | 0.539 % | 0.317% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwaszkiewicz, J.; Mysiak, P.; Muc, A. Current Controlled AC/DC Converter and Its Performance—A Mathematical Model. Energies 2025, 18, 419. https://doi.org/10.3390/en18020419
Iwaszkiewicz J, Mysiak P, Muc A. Current Controlled AC/DC Converter and Its Performance—A Mathematical Model. Energies. 2025; 18(2):419. https://doi.org/10.3390/en18020419
Chicago/Turabian StyleIwaszkiewicz, Jan, Piotr Mysiak, and Adam Muc. 2025. "Current Controlled AC/DC Converter and Its Performance—A Mathematical Model" Energies 18, no. 2: 419. https://doi.org/10.3390/en18020419
APA StyleIwaszkiewicz, J., Mysiak, P., & Muc, A. (2025). Current Controlled AC/DC Converter and Its Performance—A Mathematical Model. Energies, 18(2), 419. https://doi.org/10.3390/en18020419






