Optimizing Rural MG’s Performance: A Scenario-Based Approach Using an Improved Multi-Objective Crow Search Algorithm Considering Uncertainty
Abstract
1. Introduction
- The paper presents two renewable energy source-based RMG models: IRMG and a system of three interconnected RMGs linked to the distribution network.
- It proposes a new sophisticated scenario-based methodology incorporating correlations among load, PV, and WT uncertainties, enhancing RMG modeling fidelity.
- IMOCSA is introduced, featuring a chaotic-based initial population generation, an adaptive chaotic AP, a roulette-wheel-based position-updating method, and a new mutation strategy, enhancing multi-objective optimization efficacy for RMGs.
2. Problem Formulation
2.1. The First Model (IRMG)
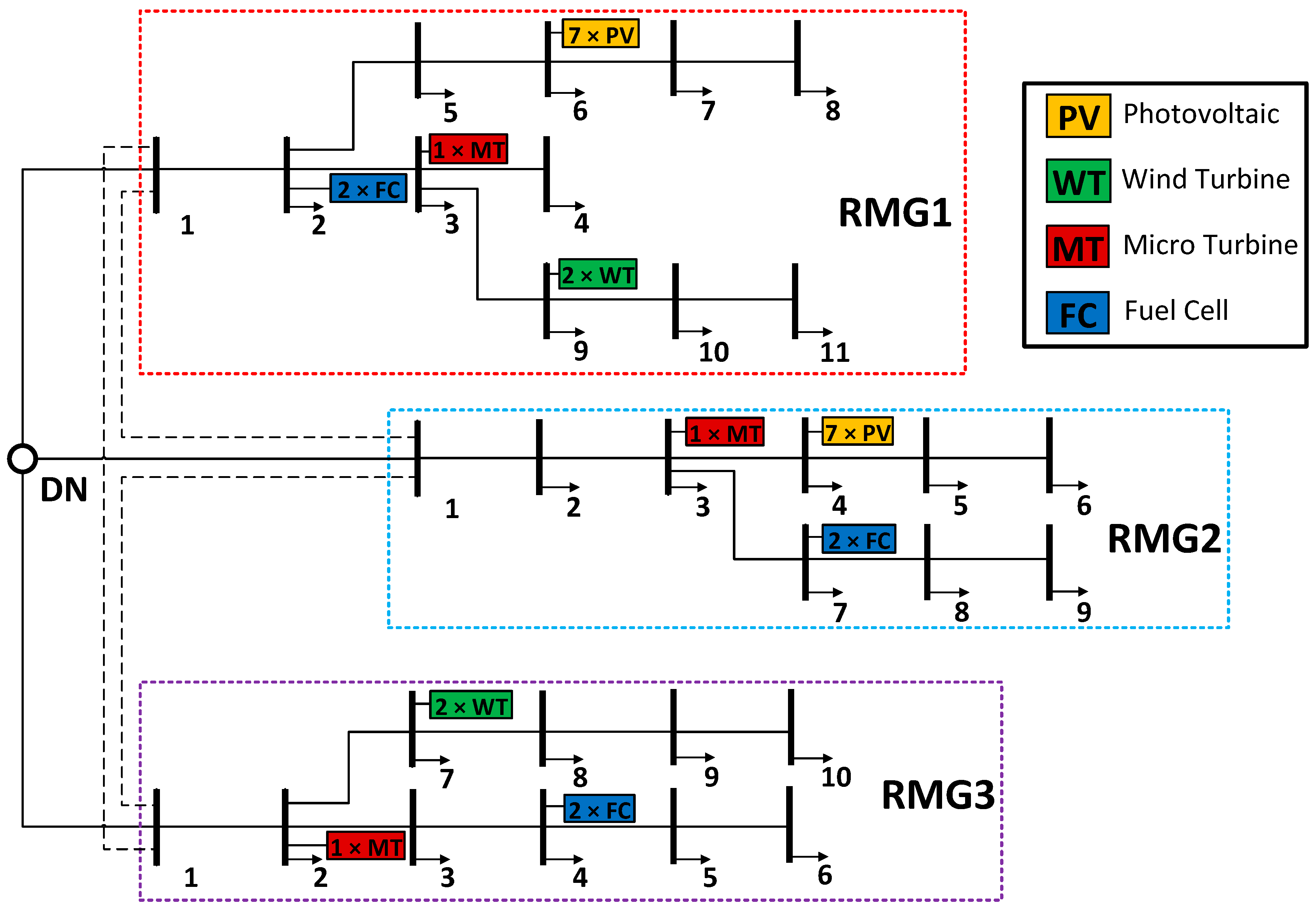
2.2. The Second Model (Three RMGs and Distribution Network)
3. Scenario Generation and Mitigation
3.1. Modeling of Load, Wind Speed, and Solar Irradiance
3.2. Proposed Scenario Generation and Reduction
- First, for each random variable, a set of independent random numbers following a standard normal distribution is generated, corresponding to the number of scenarios.
- The matrix is multiplied by the Cholesky matrix.
- CDF is calculated from the standard normal distribution .
- Then, scenarios are generated using for each variable based on the defined distribution functions while preserving their correlation.
- Finally, the generated scenarios are reduced to the desired number and WT and PV output power are calculated [30].
4. Proposed Crow Search Algorithm
4.1. CSA
- Step 1:
- Define the decision variables and CSA parameters.
- Step 2:
- Randomly place in a d-dimensional search space as the initial population. Each crow is a potential solution.
- Step 3:
- Initialize each crow’s memory, assuming they have hidden food at their initial positions because of lack of experience.
- Step 4:
- Calculate the objective function value for each crow.
- Step 5:
- In each iteration, a crow updates its position by randomly selecting another crow to chase for food . Depending on , crow either approaches or is deceived.
- Step 6:
- By meeting the constraints, the new position of the crow is accepted and the objective function value is calculated.
- Step 7:
- If the new position has a better objective function value, update the crow’s memory with the new position.
- Step 8:
- Repeat steps 5–8 until the number of iterations reaches . The best memory position is reported as the optimal solution when the termination criterion is met.
4.2. IMOCSA
| Algorithm 1. Improve the Multi-Objective Crow search algorithm. |
| Initialize the problem parameters and set the algorithm parameters. |
| Generate an initial population of crows using Equations (42)–(45). |
| Evaluate the fitness (fit()) of each crow. |
| Initialize the memory of crows and create a repository of non-dominated solutions. |
| Select the best solution from the initial population. |
| = 1:itermax |
| Calculate . |
| = 1:N |
| Randomly choose a crow j to follow (j ≠ i). |
| Calculate . |
| else |
| Select a method using roulette wheel selection. |
| If method = 1 |
| Identify the global best position (). |
| Calculate the mean of population positions (). |
| . |
| . |
| elseif method = 2 |
| Identify the global best position (). |
| elseif method = 3 |
| . |
| end If |
| end If |
| Check if the new position is feasible. |
| Evaluate the fitness of the new position for crow i. |
| Randomly select two members R_1 and R_2 from the repository. |
| Calculate . |
| If rand ≥ |
| else |
| Identify the global best position (); |
| Calculate the mean of repository positions (). |
| . |
| end If |
| Check if the mutated position is feasible. |
| Evaluate the fitness of the mutated position. |
| Update the memory of crow i and the best solution found. |
| If iter ≥ 25 and the better solution belongs to a specific method |
| Increase the selection probability of that method. |
| end If |
| end for |
| Update the repository with new non-dominated solutions. |
| Control the repository size using the k-means clustering method. |
| Randomly select a member from the repository as the current best solution. |
| end for |
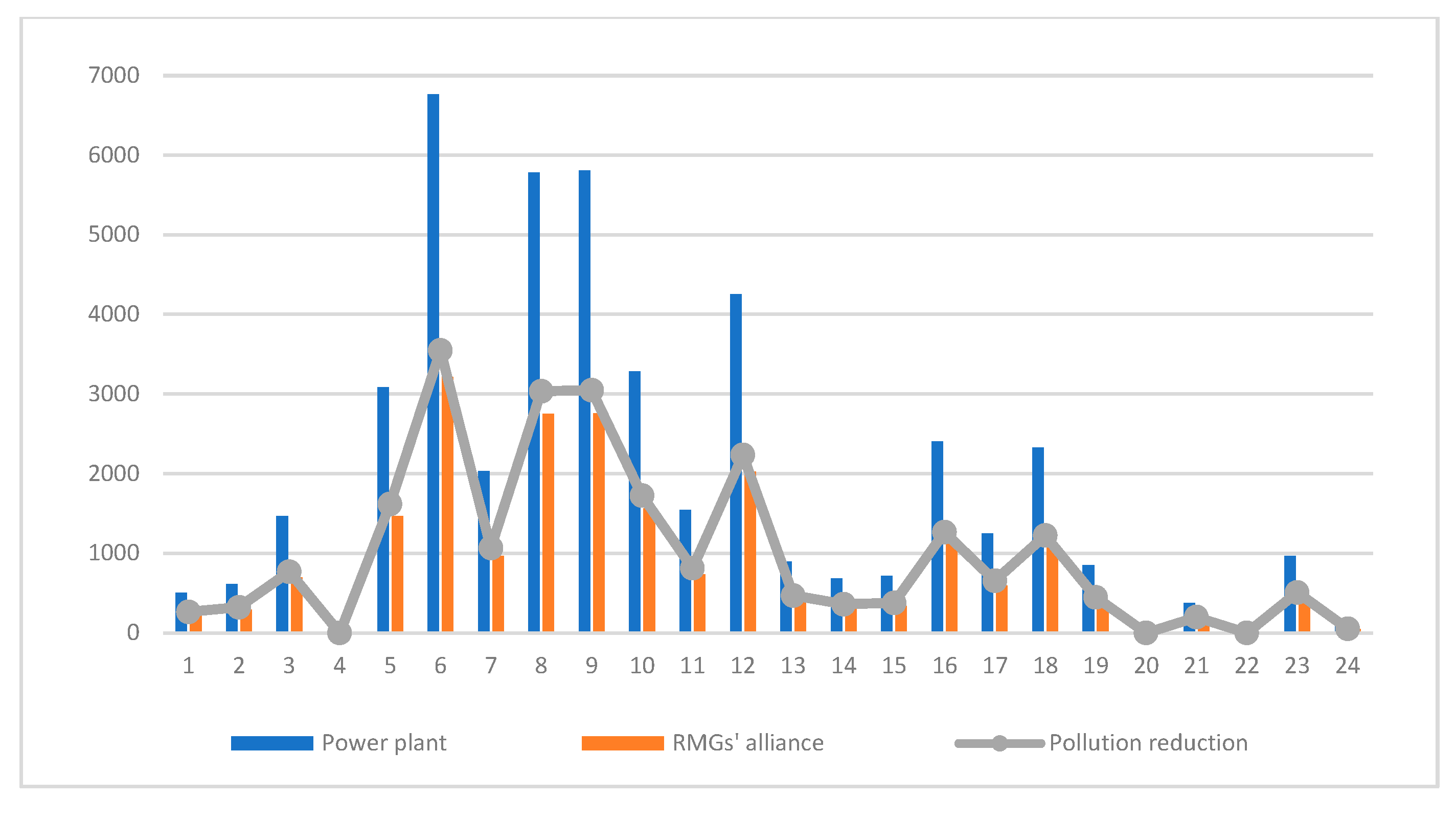
5. Simulation and Analysis Results
- IMOCSA: fl = 1.5 and α = 2.
- CSA: fl = 2 and AP = 0.1.
- PSO: Maximum inertia weight = 0.9, minimum inertia weight = 0.4, and learning factors = 2.
- TLBO and JAYA: Without setting parameters.
5.1. First Model
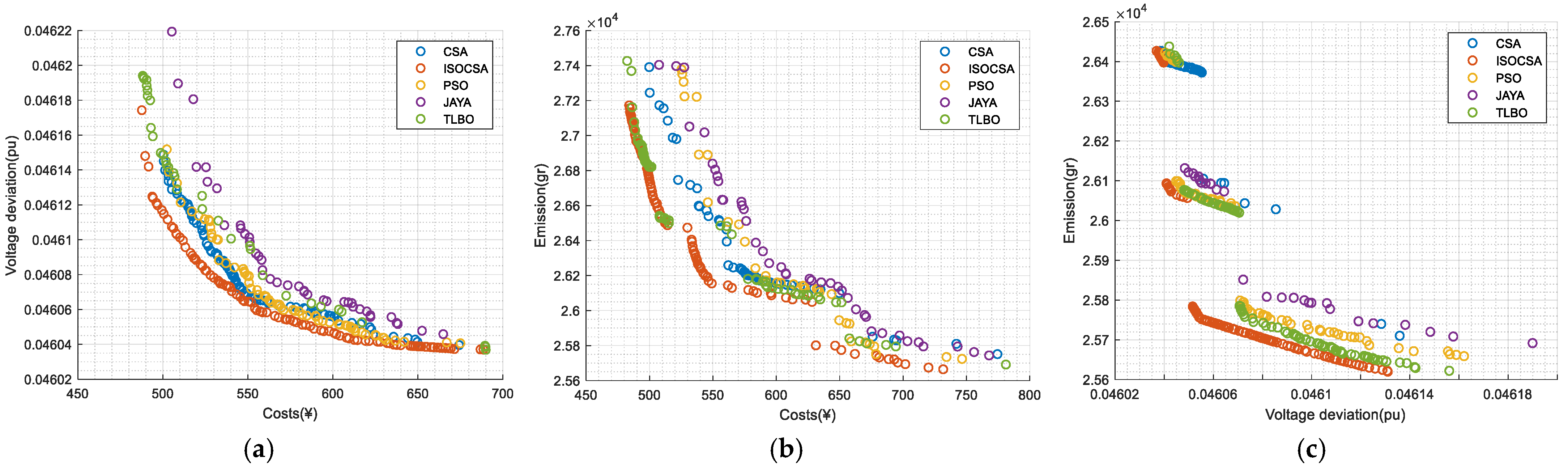
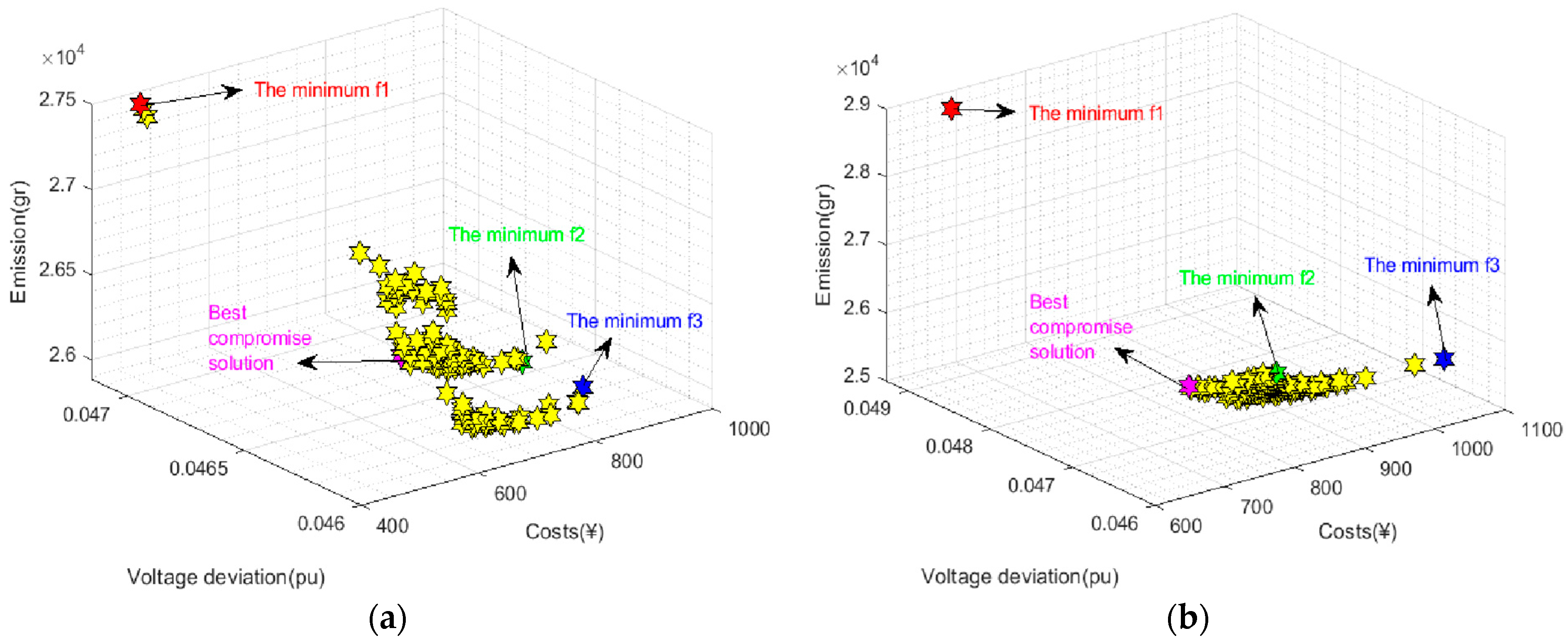
5.1.1. Evaluation of the Proposed Method
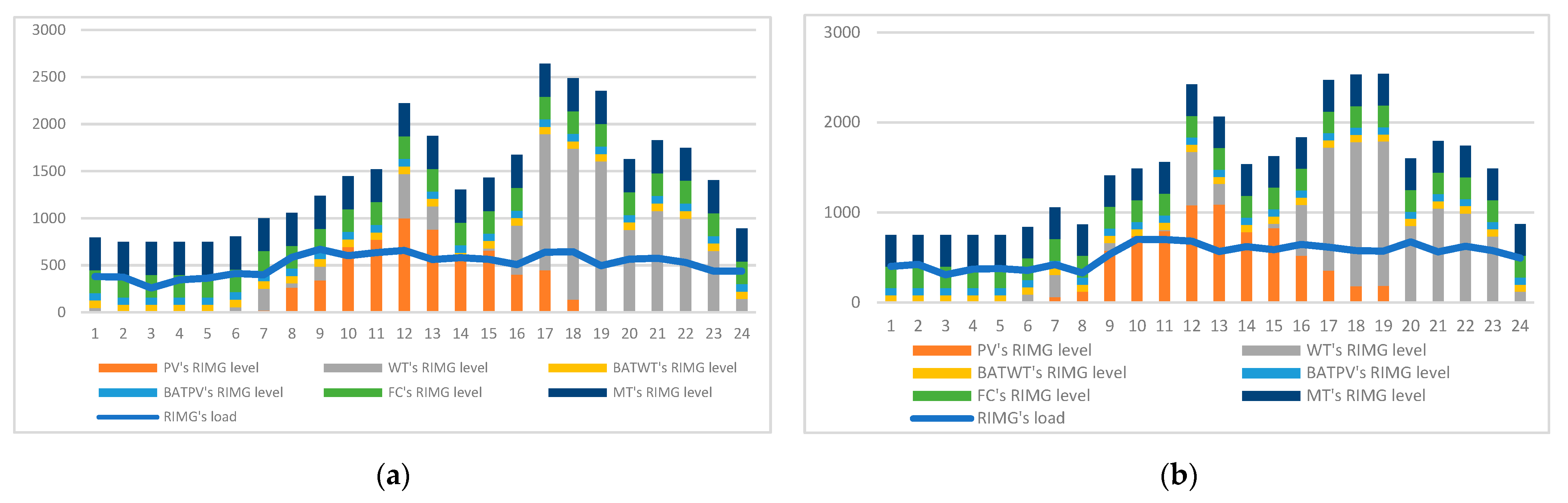
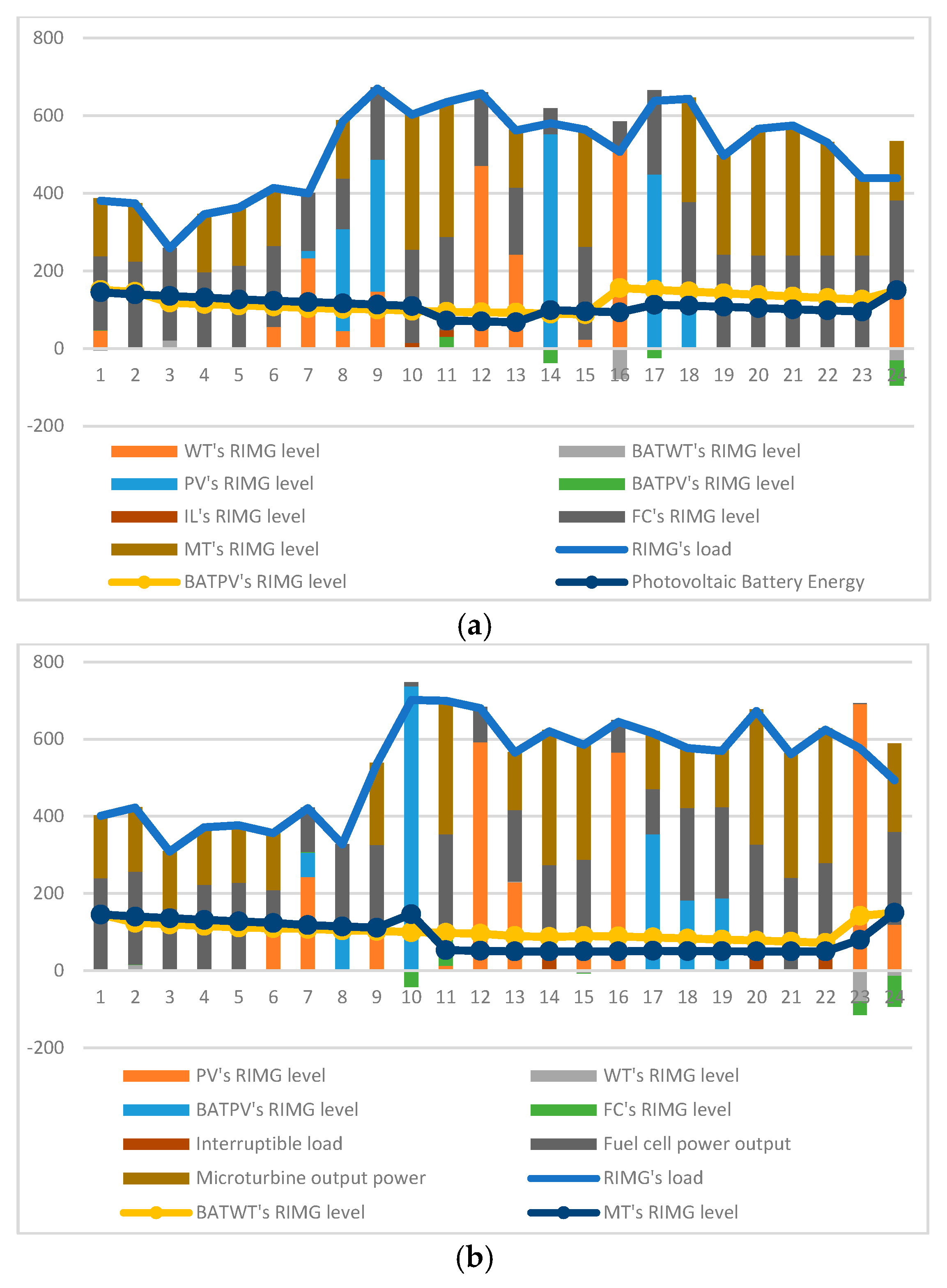
5.1.2. Results of the First Model
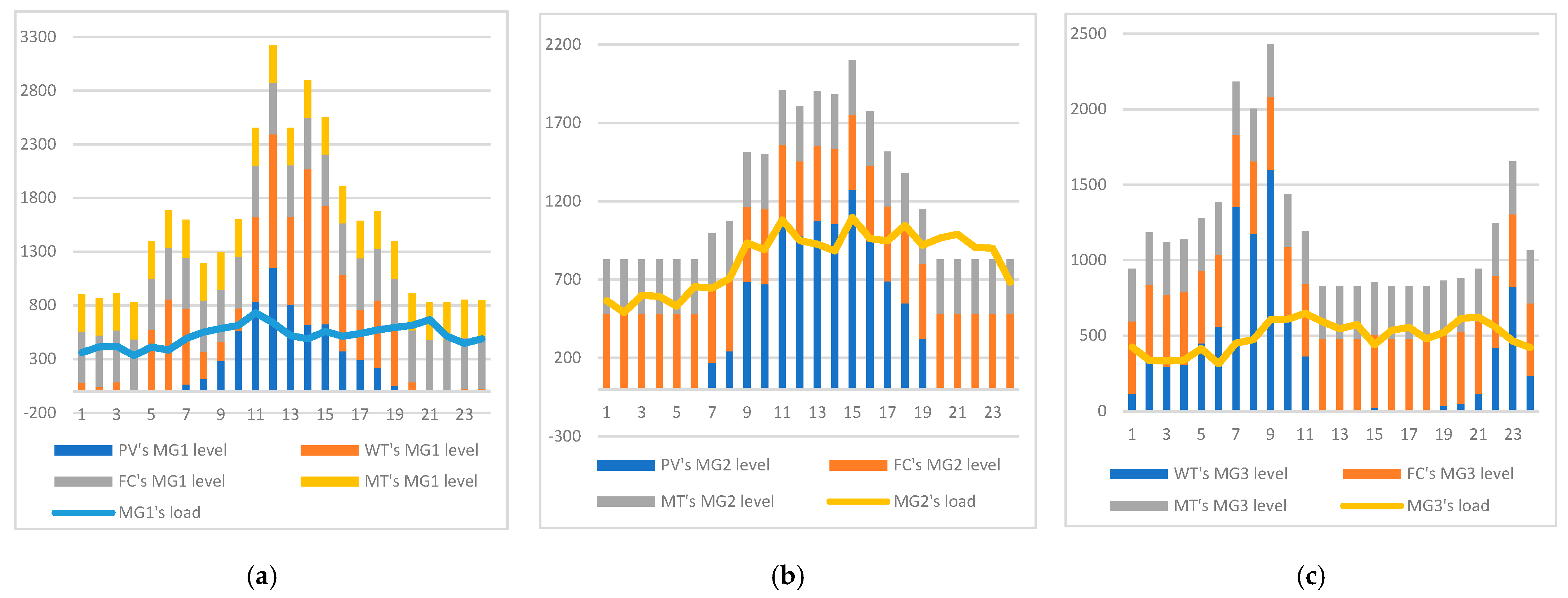
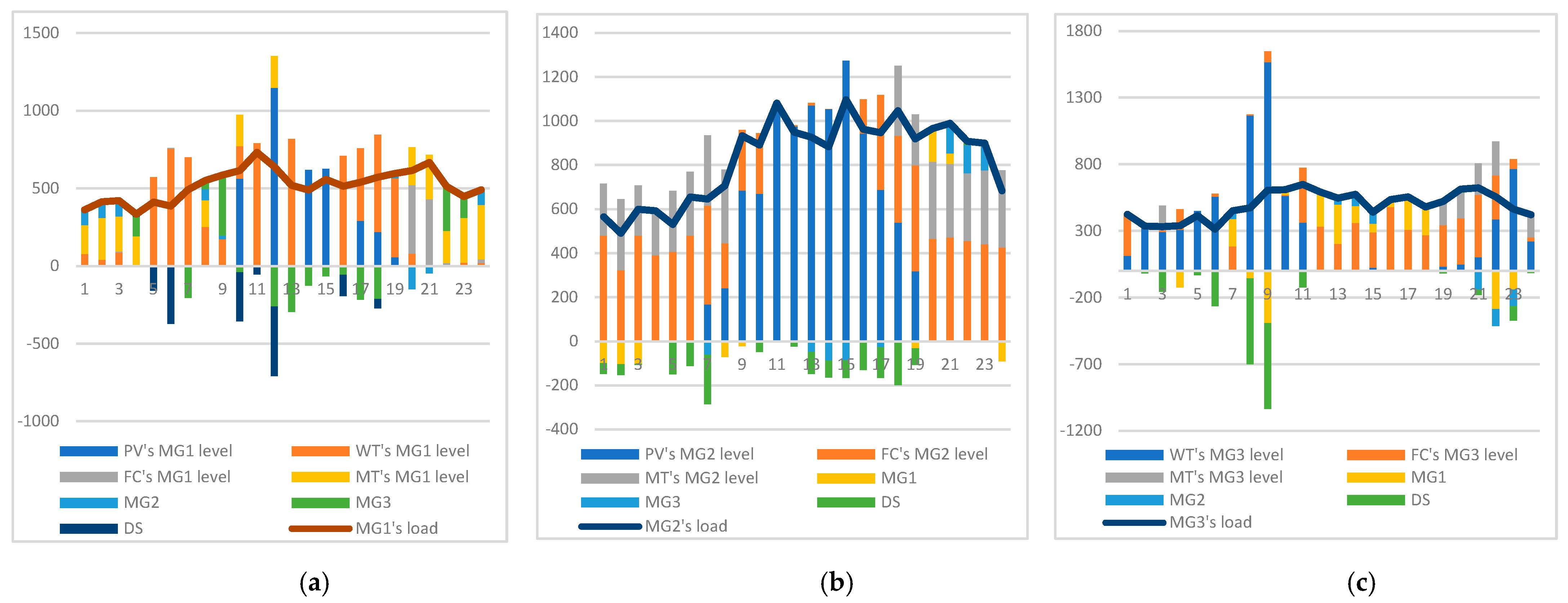
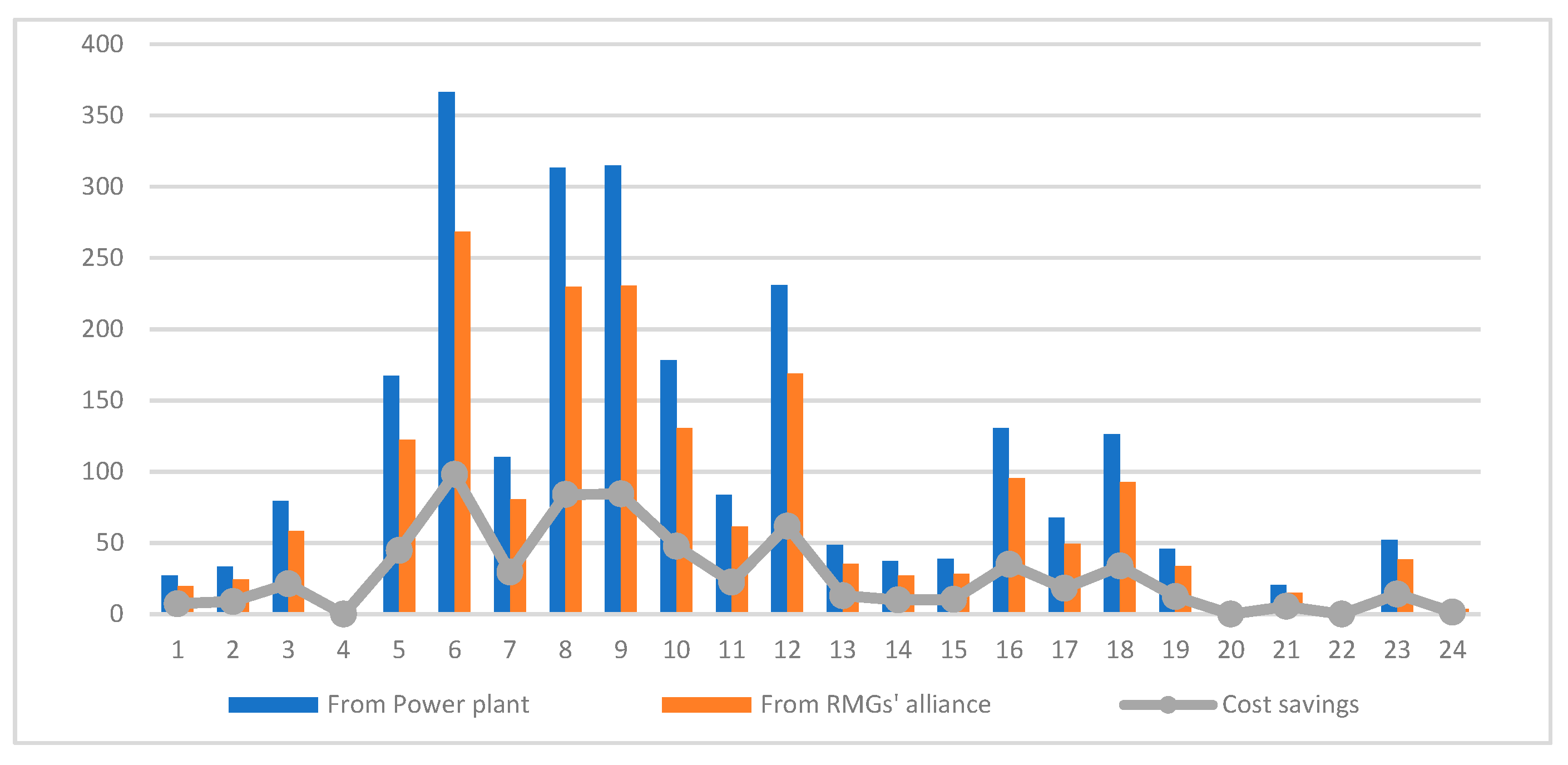
5.2. Results of the Second Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| SG | Smart grid |
| EMS | Energy management system |
| RES | Renewable energy source |
| DG | Distributed generation |
| FC | Fuel cell |
| MT | Microturbine |
| BAT | Battery |
| CSA | Crow search algorithm |
| ISOCSA | Improved single-objective CSA |
| DNN | Deep neural network |
| CNN | Convolutional neural network |
| Bi-LSTM | Bidirectional long short-term memory |
| EMM | Energy management model |
| ANN | Artificial neural network |
| SoC | State of charge |
| MPPT | Maximum power point tracking |
| PEM | Point estimate method |
| UT | Unscented transformation |
| MC | Monte Carlo |
| Probability density function | |
| CDF | Cumulative distribution function |
| IL | Interruptible load |
| C | Correlation matrix |
| Step time | |
| Output power of PV/WT/FC/MT at time in IRMG | |
| Output power of PV/WT/FC/MT at time in nth RMG | |
| Output power of the PV/WT BAT at time in IRMG | |
| The amount of IL in the IRMG in time | |
| The load value of the (IRMG/nth RMG) at time | |
| Maintenance cost of PV/WT/FC/MT units | |
| Maintenance cost of BAT units | |
| The cost of compensation for IL | |
| Number of buses in (IRMG/nth RMG) | |
| The price of purchasing/selling power from/to the distribution network for the coalition of RMGs | |
| Base nominal power/base voltage level | |
| X | Decision variables vector |
| V ref | Nominal voltage |
| The voltage level of bus in (IRMG/nth RMG) in time | |
| Highest/lowest voltage of each bus | |
| Emission coefficient of MT/FC/grid | |
| The maximum/minimum power output level of the PV in time | |
| The maximum/minimum power output level of the WT in time | |
| The maximum/minimum power output level of the FC in time | |
| The maximum/minimum power output level of the MT in time | |
| (Wind rejection/discard solar) rate | |
| Total energy of the BAT in time | |
| Self-discharge rate of BAT | |
| The state of BAT charge/discharge in time | |
| Charge/discharge efficiency of BAT | |
| BAT’s initial stored energy | |
| Upper/lower limit of BAT charging power | |
| Upper/lower limit of BAT discharging power | |
| Upper/lower limit of BAT energy | |
| rep | Repository |
| Population size of crows | |
| Current iteration | |
| Maximum number of iterations | |
| Flight length | |
| AP | Awareness probability |
| from the rep for mutation in | |
| d | Number of decision variables |
| The position of the foods hidden by crow | |
| of the position of the foods hidden by crow | |
| The position of the mutated crow in | |
| The number of objective functions | |
| Fixed coefficient | |
| Upper/lower boundary of optimization variables | |
| Best compromise solution | |
| Mean of the population positions | |
| The value of the objective function number | |
| Size of the repository | |
| positions | |
| The number of RMGs | |
| Fitness function |
References
- Islam, M.M.; Nagrial, M.; Rizk, J.; Hellany, A. General aspects, islanding detection, and energy management in Microgrids: A review. Sustainability 2021, 13, 9301. [Google Scholar] [CrossRef]
- Dashtaki, A.A.; Hakimi, S.M.; Farahani, E.S.; HassanzadehFard, H. Simultaneous optimal location and sizing of DGs in distribution system considering different types of MGs in an electricity market. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 2443–2459. [Google Scholar] [CrossRef]
- Rashwan, A.; Faragalla, A.; Abo-Zahhad, E.M.; El-Dein, A.Z.; Liu, Y.; Chen, Y.; Abdelhameed, E.H. Techno-economic Optimization of Isolated Hybrid Microgrids for Remote Areas Electrification: Aswan city as a Case Study. Smart Grids Sustain. Energy 2024, 9, 18. [Google Scholar] [CrossRef]
- Bashir, A.A.; Pourakbari-Kasmaei, M.; Contreras, J.; Lehtonen, M. A novel energy scheduling framework for reliable and economic operation of islanded and grid-connected microgrids. Electr. Power Syst. Res. 2019, 171, 85–96. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, K.; Li, H.; Coelho, E.A.A.; Guerrero, J.M. MAS-based distributed coordinated control and optimization in microgrid and microgrid clusters: A comprehensive overview. IEEE Trans. Power Electron. 2017, 33, 6488–6508. [Google Scholar] [CrossRef]
- Chen, G.; Wang, J.-M.; Yuan, X.-D.; Chen, L.; Zhao, L.-J.; He, Y.-L. Chinese national condition based power dispatching optimization in microgrids. J. Control. Sci. Eng. 2018, 2018, 8695391. [Google Scholar] [CrossRef]
- Khan, M.R.; Haider, Z.M.; Malik, F.H.; Almasoudi, F.M.; Alatawi, K.S.S.; Bhutta, M.S. A Comprehensive Review of Microgrid Energy Management Strategies Considering Electric Vehicles, Energy Storage Systems, and AI Techniques. Processes 2024, 12, 270. [Google Scholar] [CrossRef]
- Prinsloo, G.; Mammoli, A.; Dobson, R. Customer domain supply and load coordination: A case for smart villages and transactive control in rural off-grid microgrids. Energy 2017, 135, 430–441. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J. Decentralized energy management system for networked microgrids in grid-connected and islanded modes. IEEE Trans. Smart Grid 2015, 7, 1097–1105. [Google Scholar] [CrossRef]
- Espín-Sarzosa, D.; Palma-Behnke, R.; Núñez-Mata, O. Energy management systems for microgrids: Main existing trends in centralized control architectures. Energies 2020, 13, 547. [Google Scholar] [CrossRef]
- Sabzalian, M.H.; Pirouzi, S.; Aredes, M.; Franca, B.W.; Cunha, A.C. Two-Layer Coordinated Energy Management Method in the Smart Distribution Network including Multi-Microgrid Based on the Hybrid Flexible and Securable Operation Strategy. Int. Trans. Electr. Energy Syst. 2022, 2022, 3378538. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Q.; Wang, L.; Feng, W. Robust optimization for energy transactions in multi-microgrids under uncertainty. Appl. Energy 2018, 217, 346–360. [Google Scholar] [CrossRef]
- Huang, B.; Li, Y.; Zhang, H.; Sun, Q. Distributed optimal co-multi-microgrids energy management for energy internet. IEEE/CAA J. Autom. Sin. 2016, 3, 357–364. [Google Scholar] [CrossRef]
- Arefifar, S.A.; Ordonez, M.; Mohamed, Y.A.-R.I. Energy management in multi-microgrid systems—Development and assessment. IEEE Trans. Power Syst. 2016, 32, 910–922. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Z.; He, Y. A Deep Neural Network-Based Optimal Scheduling Decision-Making Method for Microgrids. Energies 2023, 16, 7635. [Google Scholar] [CrossRef]
- Du, Y.; Li, F. Intelligent multi-microgrid energy management based on deep neural network and model-free reinforcement learning. IEEE Trans. Smart Grid 2019, 11, 1066–1076. [Google Scholar] [CrossRef]
- Aguila-Leon, J.; Vargas-Salgado, C.; Chiñas-Palacios, C.; Díaz-Bello, D. Energy management model for a standalone hybrid microgrid through a particle Swarm optimization and artificial neural networks approach. Energy Convers. Manag. 2022, 267, 115920. [Google Scholar] [CrossRef]
- Roldán-Blay, C.; Escrivá-Escrivá, G.; Roldán-Porta, C.; Dasí-Crespo, D. Optimal sizing and design of renewable power plants in rural microgrids using multi-objective particle swarm optimization and branch and bound methods. Energy 2023, 284, 129318. [Google Scholar] [CrossRef]
- Zhang, X.; Son, Y.; Cheong, T.; Choi, S. Affine-arithmetic-based microgrid interval optimization considering uncertainty and battery energy storage system degradation. Energy 2022, 242, 123015. [Google Scholar] [CrossRef]
- Tan, B.; Chen, H. Multi-objective energy management of multiple microgrids under random electric vehicle charging. Energy 2020, 208, 118360. [Google Scholar] [CrossRef]
- Dev, A.; Mondal, B.; Verma, V.K.; Kumar, V. Teaching learning optimization-based sliding mode control for frequency regulation in microgrid. Electr. Eng. 2024, 106, 7009–7021. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, S.; Li, D.; Zhang, S. Improved whale optimization algorithm for solving microgrid operations planning problems. Symmetry 2022, 15, 36. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Xu, Y.; Guo, Q.; Sun, H.; Fei, Z. Distributed discrete robust secondary cooperative control for islanded microgrids. IEEE Trans. Smart Grid 2018, 10, 3620–3629. [Google Scholar] [CrossRef]
- Jia, Y.; Wen; Yan, Y.; Huo, L. Joint operation and transaction mode of rural multi microgrid and distribution network. IEEE Access 2021, 9, 14409–14421. [Google Scholar] [CrossRef]
- Roustaei, M.; Niknam, T.; Salari, S.; Chabok, H.; Sheikh, M.; Kavousi-Fard, A.; Aghaei, J. A scenario-based approach for the design of Smart Energy and Water Hub. Energy 2020, 195, 116931. [Google Scholar] [CrossRef]
- Christopher, S.B.; Mabel, M.C. A bio-inspired approach for probabilistic energy management of micro-grid incorporating uncertainty in statistical cost estimation. Energy 2020, 203, 117810. [Google Scholar] [CrossRef]
- Atwa, Y.M.; El-Saadany, E. Optimal allocation of ESS in distribution systems with a high penetration of wind energy. IEEE Trans. Power Syst. 2010, 25, 1815–1822. [Google Scholar] [CrossRef]
- Tabatabaee, S.; Mortazavi, S.S.; Niknam, T. Stochastic energy management of renewable micro-grids in the correlated environment using unscented transformation. Energy 2016, 109, 365–377. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, N.; Mallipeddi, R.; Amaratunga, G.A. Optimal reactive power dispatch with uncertainties in load demand and renewable energy sources adopting scenario-based approach. Appl. Soft Comput. 2019, 75, 616–632. [Google Scholar] [CrossRef]
- Lins, D.R.; Guedes, K.S.; Pitombeira-Neto, A.R.; Rocha, A.C.; de Andrade, C.F. Comparison of the performance of different wind speed distribution models applied to onshore and offshore wind speed data in the Northeast Brazil. Energy 2023, 278, 127787. [Google Scholar] [CrossRef]
- Elgamal, M.; Korovkin, N.; Elmitwally, A.; Menaem, A.A.; Chen, Z. A framework for profit maximization in a grid-connected microgrid with hybrid resources using a novel rule base-bat algorithm. IEEE Access 2020, 8, 71460–71474. [Google Scholar] [CrossRef]
- Shen, J.; Jiang, C.; Liu, Y.; Wang, X. A microgrid energy management system and risk management under an electricity market environment. IEEE Access 2016, 4, 2349–2356. [Google Scholar] [CrossRef]
- Talaat, M.; Elkholy, M.; Alblawi, A.; Said, T. Artificial intelligence applications for microgrids integration and management of hybrid renewable energy sources. Artif. Intell. Rev. 2023, 56, 10557–10611. [Google Scholar] [CrossRef]
- Makhdoomi, S.; Askarzadeh, A. Optimizing operation of a photovoltaic/diesel generator hybrid energy system with pumped hydro storage by a modified crow search algorithm. J. Energy Storage 2020, 27, 101040. [Google Scholar] [CrossRef]
- Gholami, J.; Mardukhi, F.; Zawbaa, H.M. An improved crow search algorithm for solving numerical optimization functions. Soft Comput. 2021, 25, 9441–9454. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Elattar, E.E.; Abd-Elrazek, A.S. A modified crow search optimizer for solving non-linear OPF problem with emissions. IEEE Access 2021, 9, 43107–43120. [Google Scholar] [CrossRef]
- Song, X.; Lin, H.; De, G.; Li, H.; Fu, X.; Tan, Z. An energy optimal dispatching model of an integrated energy system based on uncertain bilevel programming. Energies 2020, 13, 477. [Google Scholar] [CrossRef]
- Niknam, T.; Bornapour, M.; Gheisari, A.; Bahmani-Firouzi, B. Impact of heat, power and hydrogen generation on optimal placement and operation of fuel cell power plants. Int. J. Hydrogen Energy 2013, 38, 1111–1127. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, C.; Zheng, C.; Rui, T.; Shen, W.; Wang, B. Distributed peer-to-peer electricity trading considering network loss in a distribution system. Energies 2019, 12, 4318. [Google Scholar] [CrossRef]

| Power Generation Type | Unit Investment Cost (¥/kW) | Lifetime (Years) | Operation and Maintenance Cost (¥/kW) | Rated Power Capacity (kW) | Maximum Access Capacity (kW) | Minimum Access Capacity (kW) | Specific Features |
|---|---|---|---|---|---|---|---|
| PV | 20,000 | 25 | 0.0096 | 240 | 240 | 0 | - |
| WT | 50,000 | 20 | 0.0132 | 800 | 800 | 0 | Rotor Diameter: 48 m, Hub Height: 50 m, Operating Speed Range: 3–28 m/s |
| MT | 10,000 | 25 | 0.04109 | 350 | 350 | 150 | - |
| FC | 12,000 | 25 | 0.0296 | 240 | 240 | 0 | - |
| Load | Wind Speed | Solar Irradiance | |
|---|---|---|---|
| Load | 1 | 0.442767 | 0.627774 |
| Wind Speed | 0.442767 | 1 | −0.17639 |
| Solar Irradiance | 0.627774 | −0.17639 | 1 |
| Load of RMG 1 | Wind Speed of RMG 1 | Solar Irradiance of RMG 1 | Load of RMG 2 | Solar Irradiance of RMG 2 | Load of RMG 3 | Wind Speed of RMG 3 | |
|---|---|---|---|---|---|---|---|
| Load of RMG 1 | 1 | 0.338 | 0.624 | 0 | 0 | 0 | 0 |
| Wind Speed of RMG 1 | 0.338 | 1 | 0.707 | 0 | 0 | 0 | 0 |
| Solar Irradiance of RMG 1 | 0.624 | 0.707 | 1 | 0 | 0 | 0 | 0 |
| Load of RMG 2 | 0 | 0 | 0 | 1 | 0.743 | 0 | 0 |
| Solar Irradiance of RMG 2 | 0 | 0 | 0 | 0.743 | 1 | 0 | 0 |
| Load of RMG 3 | 0 | 0 | 0 | 0 | 0 | 1 | −0.095 |
| Wind Speed of RMG 3 | 0 | 0 | 0 | 0 | 0 | −0.095 | 1 |
| Function | Analysis | ISOCSA (fl = 1.5, α = 0.5) | ISOCSA (fl = 1.5, α = 1) | ISOCSA (fl = 1.5, α = 2) | ISOCSA (fl = 2, α = 0.5) | ISOCSA (fl = 2, α = 1) | ISOCSA (fl = 2, α = 2) | ISOCSA (fl = 2.5, α = 0.5) | ISOCSA (fl = 2.5, α = 1) | ISOCSA (fl = 2.5, α = 2) | CSA | PSO | JAYA | TLBO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f₁ | Best | 481.9568 | 481.9904 | 482.2295 | 482.144 | 482.4778 | 482.2312 | 483.3879 | 483.5854 | 484.3614 | 483.2319 | 487.1854 | 483.634 | 482.0054 |
| Worst | 482.4872 | 483.2655 | 490.7695 | 491.4336 | 486.027 | 489.904 | 503.5032 | 497.2385 | 497.3467 | 484.3887 | 490.2728 | 485.766 | 482.713 | |
| Median | 482.3428 | 482.6224 | 483.3581 | 483.6339 | 483.7233 | 484.2281 | 487.9092 | 487.4907 | 487.5329 | 483.718 | 487.8968 | 484.4448 | 482.4149 | |
| Std. Dev. | 0.2012 | 0.2963 | 1.5692 | 1.6709 | 0.8692 | 1.4174 | 4.3039 | 3.9132 | 3.8889 | 0.2634 | 0.8523 | 0.4865 | 0.2025 | |
| f₂ | Best | 4.5368 × 10−2 | 4.5516 × 10−2 | 4.6012 × 10−2 | 4.5993 × 10−2 | 4.6096 × 10−2 | 4.6056 × 10−2 | 4.6236 × 10−2 | 4.6332 × 10−2 | 4.6525 × 10−2 | 4.6122 × 10−2 | 4.6937 × 10−2 | 4.6037 × 10−2 | 4.5851× 10−2 |
| Worst | 4.6037 × 10−2 | 4.6070 × 10−2 | 4.7388 × 10−2 | 4.7571 × 10−2 | 4.6992 × 10−2 | 4.7232 × 10−2 | 5.1532 × 10−2 | 4.8332 × 10−2 | 4.8513 × 10−2 | 4.6598 × 10−2 | 4.7346 × 10−2 | 4.6711 × 10−2 | 4.6044 × 10−2 | |
| Median | 4.5722 × 10−2 | 4.5774 × 10−2 | 4.6623 × 10−2 | 4.6625 × 10−2 | 4.6471 × 10−2 | 4.6553 × 10−2 | 4.8978 × 10−2 | 4.7255 × 10−2 | 4.7471 × 10−2 | 4.6379 × 10−2 | 4.7152 × 10−2 | 4.6344 × 10−2 | 4.5936 × 10−2 | |
| Std. Dev. | 3.7667 × 10−8 | 2.0751 × 10−7 | 4.1080 × 10−7 | 9.1000 × 10−7 | 2.7971 × 10−7 | 2.8233 × 10−7 | 4.4051 × 10−4 | 1.8625 × 10−4 | 4.8919 × 10−5 | 1.6877 × 10−7 | 2.7962 × 10−7 | 2.7281 × 10−7 | 1.3505 × 10−7 | |
| f₃ | Best | 2.3587 × 104 | 2.3807 × 104 | 2.4325 × 104 | 2.4213 × 104 | 2.4379 × 104 | 2.4353 × 104 | 2.4728 × 104 | 2.4776 × 104 | 2.5385 × 104 | 2.4679 × 104 | 2.5786 × 104 | 2.4822 × 104 | 2.4141 × 104 |
| Worst | 2.4106 × 104 | 2.4865 × 104 | 2.6224 × 104 | 2.6347 × 104 | 2.5841 × 104 | 2.6028 × 104 | 2.7078 × 104 | 2.6649 × 104 | 2.6701 × 104 | 2.5025 × 104 | 2.6523 × 104 | 2.5385 × 104 | 2.4506 × 104 | |
| Median | 2.3715 × 104 | 2.5262 × 104 | 2.5883 × 104 | 2.5918 × 104 | 2.5998 × 104 | 2.6046 × 104 | 2.6149 × 104 | 2.6005 × 104 | 2.6122 × 104 | 2.5921 × 104 | 2.6125 × 104 | 2.6061 × 104 | 2.5738 × 104 | |
| Std. Dev. | 123.1301 | 204.4091 | 238.8368 | 240.2564 | 222.1366 | 230.0278 | 422.4928 | 389.2940 | 255.5197 | 184.0515 | 218.6731 | 215.7913 | 151.1341 |
| Scenario | With Correlation | Without Correlation | |||||
|---|---|---|---|---|---|---|---|
| f1 | f2 | f3 | f1 | f2 | f3 | ||
| 1 | f1,min | 1024.16 | 0.05089 | 29,466.86 | 1016.89 | 0.05007 | 27,629.38 |
| f2,min | 1146.52 | 0.05082 | 28,871.58 | 1198.98 | 0.04943 | 26,520.63 | |
| f3,min | 1175.08 | 0.05087 | 28,438.98 | 1212.68 | 0.04949 | 26,268.10 | |
| Best compromise solution | 1026.07 | 0.05092 | 29,211.41 | 1055.92 | 0.04954 | 26,954.56 | |
| 2 | f1,min | 548.20 | 0.04401 | 25,983.69 | 440.57 | 0.04169 | 23,911.64 |
| f2,min | 747.27 | 0.04214 | 22,693.28 | 578.66 | 0.04149 | 23,502.80 | |
| f3,min | 986.73 | 0.04227 | 22,289.29 | 772.09 | 0.04165 | 22,721.67 | |
| Best compromise solution | 563.91 | 0.04235 | 23,442.24 | 440.57 | 0.04169 | 23,911.64 | |
| 3 | f1,min | 573.26 | 0.04565 | 27,078.34 | 668.45 | 0.04701 | 28,346.14 |
| f2,min | 759.22 | 0.04554 | 26,875.41 | 801.61 | 0.04691 | 27,975.56 | |
| f3,min | 1111.22 | 0.04585 | 26,150.10 | 1065.18 | 0.04712 | 26,977.99 | |
| Best compromise solution | 573.26 | 0.04565 | 27,078.34 | 693.80 | 0.04699 | 27,963.38 | |
| 4 | f1,min | 481.99 | 0.04715 | 27,426.66 | 554.10 | 0.04793 | 29,159.79 |
| f2,min | 689.90 | 0.04537 | 26,426.47 | 804.08 | 0.04716 | 27,856.34 | |
| f3,min | 908.34 | 0.04633 | 23,587.80 | 849.94 | 0.04726 | 26,833.79 | |
| Best compromise solution | 519.15 | 0.04613 | 26,565.07 | 582.21 | 0.04727 | 27,901.27 | |
| 5 | f1,min | 702.30 | 0.04203 | 21,510.89 | 693.53 | 0.04927 | 28,744.74 |
| f2,min | 1054.19 | 0.04173 | 20,695.99 | 818.38 | 0.04638 | 26,117.71 | |
| f3,min | 1202.06 | 0.04187 | 20,128.81 | 1079.01 | 0.04657 | 25,492.73 | |
| Best compromise solution | 702.30 | 0.04203 | 21,510.89 | 703.29 | 0.04647 | 26,203.15 | |
| Scenario | Form of Alliance | With Correlation | Without Correlation | ||||
|---|---|---|---|---|---|---|---|
| f1 | f2 | f3 | f1 | f2 | f3 | ||
| 1 | {MG1,MG2} | 118.24 | −0.00025 | 6827.9 | 270.59 | 0 | 9335.2 |
| {MG1,MG3} | 65.6 | −0.00025 | 13,183.9 | 16.2 | 0 | 2305.3 | |
| {MG2,MG3} | 196.41 | 0.00017 | 4209.3 | 302.55 | −0.00023 | 7448.3 | |
| {MG1,MG2,MG3} | 197.94 | 0.00019 | 20,989.6 | 304.51 | 0.00017 | 13,993.9 | |
| 2 | {MG1,MG2} | 282.5 | 0 | 6769.1 | 320.93 | 0.00002 | 8243.5 |
| {MG1,MG3} | 78.79 | 0 | 9748.1 | 48.23 | 0.00002 | 10,616.9 | |
| {MG2,MG3} | 490.97 | 0 | 11,349.5 | 398.01 | −0.00011 | 10,559.2 | |
| {MG1,MG2,MG3} | 567.59 | 0 | 24,009.8 | 413.05 | 0.000015 | 20,017.5 | |
| 3 | {MG1,MG2} | 319.76 | 0.00024 | 8629.3 | 230.44 | 0.00044 | 9112.2 |
| {MG1,MG3} | −27.65 | 0.00024 | 12,763.8 | 22.45 | 0.00044 | 11,675.7 | |
| {MG2,MG3} | 367.79 | 0.00001 | 9430.1 | 264.79 | 0.00018 | 8665.6 | |
| {MG1,MG2,MG3} | 368.93 | 0.00025 | 22,447.8 | 266.46 | 0.00059 | 21,719.9 | |
| 4 | {MG1,MG2} | 304.55 | −0.00022 | 7932 | 147.77 | 0.00259 | 8460.04 |
| {MG1,MG3} | 18.77 | −0.00022 | 8969.3 | 50.45 | 0.00259 | 10,492.4 | |
| {MG2,MG3} | 381.4 | −0.00021 | 11,760.8 | 180.95 | 0.00273 | 8287.7 | |
| {MG1,MG2,MG3} | 382.82 | 0.0008 | 21,206.6 | 182.44 | 0.00296 | 20,622.9 | |
| 5 | {MG1,MG2} | 284.52 | −0.00002 | 9451.1 | 232.61 | 0.00004 | 9788.8 |
| {MG1,MG3} | 27.78 | −0.00002 | 13,479.2 | 41.07 | 0.00004 | 11,286.5 | |
| {MG2,MG3} | 368.95 | 0.00003 | 9932.6 | 290.38 | −0.00047 | 10,660.2 | |
| {MG1,MG2,MG3} | 370.35 | 0.00013 | 23,483.9 | 291.72 | 0.00014 | 22,838.5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taabodi, M.H.; Niknam, T.; Sharifhosseini, S.M.; Aghajari, H.A.; Bornapour, S.M.; Sheybani, E.; Javidi, G. Optimizing Rural MG’s Performance: A Scenario-Based Approach Using an Improved Multi-Objective Crow Search Algorithm Considering Uncertainty. Energies 2025, 18, 294. https://doi.org/10.3390/en18020294
Taabodi MH, Niknam T, Sharifhosseini SM, Aghajari HA, Bornapour SM, Sheybani E, Javidi G. Optimizing Rural MG’s Performance: A Scenario-Based Approach Using an Improved Multi-Objective Crow Search Algorithm Considering Uncertainty. Energies. 2025; 18(2):294. https://doi.org/10.3390/en18020294
Chicago/Turabian StyleTaabodi, Mohammad Hossein, Taher Niknam, Seyed Mohammad Sharifhosseini, Habib Asadi Aghajari, Seyyed Mohammad Bornapour, Ehsan Sheybani, and Giti Javidi. 2025. "Optimizing Rural MG’s Performance: A Scenario-Based Approach Using an Improved Multi-Objective Crow Search Algorithm Considering Uncertainty" Energies 18, no. 2: 294. https://doi.org/10.3390/en18020294
APA StyleTaabodi, M. H., Niknam, T., Sharifhosseini, S. M., Aghajari, H. A., Bornapour, S. M., Sheybani, E., & Javidi, G. (2025). Optimizing Rural MG’s Performance: A Scenario-Based Approach Using an Improved Multi-Objective Crow Search Algorithm Considering Uncertainty. Energies, 18(2), 294. https://doi.org/10.3390/en18020294








