Abstract
In recent years, the growth of utilizing rural microgrids (RMGs) has been accompanied by various challenges. These necessitate the development of appropriate models for optimal generation in RMGs and RMGs’ coordination. In this paper, two distinct models for RMGs are presented. The first model includes an islanded rural microgrid (IRMG) and the second model consists of three RMGs that are interconnected with one another and linked to the distribution network. The proposed models take into account the uncertainty in load, photovoltaics (PVs), and wind turbines (WTs) with consideration of their correlation by using a scenario-based technique. Three objective functions are defined for optimization: minimizing operational costs including maintenance and fuel expenses, reducing voltage deviation to maintain power quality, and decreasing pollution emissions from fuel cells and microturbines. A new optimization method, namely the Improved Multi-Objective Crow Search Algorithm (IMOCSA), is proposed to solve the problem models. IMOCSA enhances the standard Crow Search Algorithm through three key improvements: an adaptive chaotic awareness probability to better balance exploration and exploitation, a mutation mechanism applied to the solution repository to prevent premature convergence, and a K-means clustering method to control repository size and increase algorithmic efficiency. Since the proposed problem is a multi-objective non-linear optimization problem with conflicting objectives, the idea of the Pareto front is used to find a group of optimal solutions. To assess the effectiveness and efficiency of the proposed models, they are implemented in two different case studies and the analysis and results are illustrated.
1. Introduction
An RMG is a part of the distribution network which encompasses DGs, energy storage devices, and various loads. DGs include various technologies such as MTs, FCs, PVs, WTs, etc. Since some of these DGs are used to supply RMGs’ requirements, making coordination between these sources and determining their production levels highly important. Furthermore, when RMGs are interconnected with each other, the issue of coordination and cooperation by considering objectives such as cost and pollution emission through DGs in RMGs becomes significant. The utilization of DGs in MGs minimizes transmitted power in transmission lines, delays generation and transmission infrastructure expansion, decreases fossil fuel consumption, and improves power system efficiency [1]. Despite the mentioned benefits, MGs also pose challenges. Since each MG consists of various types of DGs, coordinating their operations and creating a suitable method for optimal MG generation are essential [2]. Two modes of operation are available for MGs: connected to grid mode and islanded mode. An “islanded MG” only operates independently of the main grid and cannot be connected to a broader power system. MGs have their own specific electricity sources which are complemented by an energy storage system. MGs are often used in locations where transmitting and distributing electricity from a centralized energy source to operate take place over a long distance and are costly [3]. Collaboration among various DGs in an islanded MG enhances energy consumption efficiency and minimizes the operational costs of MGs. Numerous studies have been conducted in this field and some of them are discussed below. An energy management framework, which merges active and reactive methods to effectively tackle uncertainties associated with generation and demand, was proposed in [4] during the operation of MGs in both islanded and interconnected modes. In [5], in order to optimize utilization of DGs within each MG and transmit the supported power to the distribution network or MGs with power shortages, methods such as the implementation of a robust EMS and appropriate power distribution in SGs have been proposed. Under normal conditions, power dispatching was carried out in a highly balanced manner which took into account both cost considerations and eco-management [6]. Strategies for energy management and utilization of RMGs have been utilized [7,8]. In [9,10], the decentralized and centralized energy management systems of multiple MGs were studied and analyzed. In [11], an approach involving double-layer coordination for energy management was proposed for MGs’ operation. A robust energy management method for MGs with uncertainties was introduced in [12]. In [13], a distributed energy management method based on data related to the exchange of energy among neighboring MGs was presented. Additionally, an optimal and coordinated energy management system for MGs along with a new index for modeling uncertainty was presented in [14]. In this paper, according to the increasing penetration of DGs and the growing demand for electricity in RMGs, two models for RMGs are proposed to solve the problems by optimizing cost, voltage deviation, and pollution emission. These problems include optimal scheduling of distributed generation in IRMGs, modeling uncertainty related to RESs and load, coordinated operation of RMG clusters, and coordination between RMGs and the distribution network.
Recent advancements in artificial intelligence have expanded the scope of optimization methods, with neural networks and machine learning approaches increasingly being adopted for microgrid optimization. DNNs have shown significant promise in addressing the limitations of traditional optimization methods, particularly in handling system uncertainties and complex operational constraints. For example, DNN-based approaches have been demonstrated to significantly reduce the solution time for intra-day rolling optimization to milliseconds while maintaining solution quality [15]. Hybrid approaches combining CNNs with Bi-LSTM networks have also been effectively employed for rapid decision making in microgrid scheduling, offering improved computational efficiency and decision-making accuracy compared to conventional methods [15].
Another notable development is the use of model-free reinforcement learning techniques for multi-microgrid energy management [16]. These approaches have demonstrated high accuracy in estimating power exchange, with studies reporting average relative errors as low as 0.96 for 2400 test samples [16]. Additionally, deep learning methods have proven valuable in maintaining user privacy while optimizing system performance, as they can effectively simulate microgrid operations without requiring access to local generation or consumption data [16].
In the domain of standalone hybrid microgrids, EMM incorporating ANNs has achieved significant improvements, including reductions in prediction errors by 59% for single-step and 56% for multiple-step energy parameter estimations [17]. However, neural network-based approaches also face certain limitations, such as challenges in predicting parameters like the SoC of energy storage systems and potential issues with input variable selection [17]. Moreover, these methods can be influenced by network topology and various uncertainties, including load variations and fluctuations in distributed renewable generation [16].
Since the abovementioned problems are non-linear, metaheuristic techniques are utilized. Many studies have been carried out focusing on the utilization of metaheuristic algorithms to optimize the operation of MGs. Some used algorithms include PSO [18], GA [19], DE [20], TLBO [21], and WOA [22]. In this paper, CSA [23] is utilized. However, to address limitations in existing CSA variants and enhance its performance for multi-objective optimization, this paper proposes IMOCSA. IMOCSA incorporates two key enhancements: (1) an adaptive chaotic AP to better balance exploration and exploitation throughout the optimization process and (2) a mutation mechanism applied to the solution repository to prevent premature convergence. Additionally, the K-means method is employed to control the size of the repository and increase algorithmic efficiency. These modifications aim to address challenges such as inconsistent awareness probabilities, limited exploration in later iterations, and insufficient diversity in Pareto front representation, ensuring more robust and efficient optimization performance. Therefore, the key contributions of this paper are as follows:
- The paper presents two renewable energy source-based RMG models: IRMG and a system of three interconnected RMGs linked to the distribution network.
- It proposes a new sophisticated scenario-based methodology incorporating correlations among load, PV, and WT uncertainties, enhancing RMG modeling fidelity.
- IMOCSA is introduced, featuring a chaotic-based initial population generation, an adaptive chaotic AP, a roulette-wheel-based position-updating method, and a new mutation strategy, enhancing multi-objective optimization efficacy for RMGs.
In the following, in Section 2, the objective functions and constraints related to both models are presented. In Section 3, modeling of input random variables and scenario selections are discussed. In Section 4, IMOCSA is introduced for optimizing the models. In Section 5, simulation results are presented and are analyzed. In Section 6, the findings of the study are concluded.
2. Problem Formulation
Before presenting the mathematical models, it is essential to understand the key DG technologies utilized in the RMG systems and their operational characteristics:
MTs are compact combustion turbines with generation capacities typically ranging from 25 to 500 kW. MTs operate on the Brayton cycle where compressed air is mixed with fuel, burned in a combustion chamber, and the resulting hot gas drives a turbine connected to a generator. They offer high operational efficiency, reaching up to 80% in combined heat and power applications. MTs feature fast startup and shutdown capabilities, along with the ability to use various fuel types, including natural gas, biogas, and diesel. Their design incorporates fewer moving parts, resulting in low maintenance requirements. The stable power output makes them particularly suitable for baseload operation in microgrid systems.
FCs are electrochemical devices that convert chemical energy directly into electrical energy through reactions between hydrogen and oxygen. In the process, hydrogen fuel is split into protons and electrons at the anode, with protons passing through a membrane while electrons travel through an external circuit. Oxygen then combines with protons and electrons at the cathode to produce water. FCs achieve high electrical efficiency of 40–60% and produce near-zero emissions when using hydrogen fuel. Their operation is notably quiet due to the absence of moving parts, and they provide reliable continuous power generation. The modular design allows for flexible capacity scaling to meet varying power requirements.
PVs convert sunlight directly into electricity using semiconductor materials exhibiting the photovoltaic effect. The system architecture includes PV modules for power generation, inverters for DC to AC conversion, maximum power point tracking (MPPT) systems for optimization, and supporting structures and wiring. PV systems produce zero operational emissions and feature high reliability due to the absence of moving parts. Their power output varies with solar irradiance and temperature, requiring significant installation area and limiting generation to daylight hours.
WTs harness wind energy through aerodynamic blades that capture kinetic energy from wind, utilizing a gearbox to increase rotational speed in most designs, and a generator to convert mechanical energy to electrical power. The power output varies cubically with wind speed, with typical cut-in wind speeds of 3–5 m/s and rated power achieved at 10–15 m/s. For safety, turbines implement cut-out mechanisms at high wind speeds. Like PV systems, WTs produce zero operational emissions during power generation.
2.1. The First Model (IRMG)
The operation of islanded MGs emphasizes power sharing and system stability [24]. The proposed model for the IRMG is developed based on assumptions regarding the load curve of power consumption and IL for residential users. Three objective functions are defined for the model. The first is the operational cost (), which minimizes the total cost of operating the IRMG, accounting for power generation, maintenance costs, and IL compensation (1). The second is voltage deviation (), which minimizes the deviation of bus voltages from a reference level, ensuring voltage stability and system reliability (2). The third is pollution emissions (), which minimizes the environmental impact by reducing emissions from power generation units such as MTs and FCs (3).
In addition to DG units, the model incorporates a BAT associated with WT and PV units. The relationship between BAT capacity and its charge/discharge power over time is governed by (11) that reflects the energy dynamics of the BAT, considering self-discharge rates, charging/discharging efficiencies, and power constraints.
The model also includes a set of constraints to ensure practical and feasible operation. The power balance constraint (12) ensures that the total power generated matches the total load demand (including IL) at every time step, maintaining energy balance. Generation limits (13)–(16) define the permissible operational ranges for each DG unit (e.g., PV, WT, MT, FC). These constraints prevent overloading and ensure that generation stays within technical and physical limits. Renewable energy curtailment constraints include the maximum wind rejection (17), which limits the amount of wind energy that can be curtailed, and the maximum discarded solar energy (18), which restricts the extent to which solar energy can be wasted, ensuring optimal utilization of renewable resources.
Battery energy constraints (19)–(23) ensure the BAT’s energy levels remain within defined bounds, maintaining operational integrity. These include capacity limits (19) and (20), which keep the BAT’s energy levels within acceptable bounds, and charging/discharging power limits (21) and (22), which specify the maximum permissible rates of charging and discharging for the BAT. The state of charge equality constraint (23) mandates that the BAT returns to its initial state of charge by the end of the operational cycle, ensuring readiness for subsequent periods. Voltage constraints (24) ensure that the bus voltages across the IRMG remain within acceptable limits, preventing operational instability and equipment damage.
The combination of these objectives and constraints provides a robust framework for optimizing the IRMG’s performance while maintaining stability, reliability, and environmental sustainability.
2.2. The Second Model (Three RMGs and Distribution Network)
In this paper, rather than only considering the cost objective function () as established based on cooperative game theory in [25], two additional objective functions are introduced: voltage deviation () and pollution emission () (25)–(27). These objective functions collectively aim to optimize the performance of three interconnected RMGs linked to a distribution network. The inclusion of voltage deviation and pollution emission objectives highlights the importance of ensuring power quality and minimizing environmental impact alongside economic considerations.
The model introduces a switch () to represent the state of electricity purchasing and selling. When equals 1, the RMG coalition operates in surplus power mode and sells electricity to the distribution network. Conversely, when equals 0, the coalition experiences a power shortage and purchases electricity from the distribution network. This mechanism enables dynamic interaction between the RMGs and the distribution network, ensuring adaptability to varying power supply and demand conditions.
Unlike the first model, the second model does not include constraints related to BAT or forced shutdown scenarios. The power balance constraint, which ensures that the total power generated and exchanged matches the total load demand at each time step, is expressed as a core equation of this model.
The remaining constraints, such as generation limits, renewable energy curtailment, and voltage stability, are consistent with those defined in the first model. These constraints collectively ensure that the operational boundaries of the RMGs and their interaction with the distribution network adhere to technical, economic, and environmental standards. This model expands the scope of optimization by incorporating the interconnected operation of multiple RMGs and their coordinated interaction with the larger power distribution network, providing a holistic approach to rural microgrid management.
3. Scenario Generation and Mitigation
Various approaches, including the scenario-based method [26], PEM [27], MC method [28], and UT [29], have been utilized to address uncertainty in load forecasting and RESs’ output. This paper utilizes a scenario-based method to model stochastic parameters of wind speed, solar irradiance, and load. Initially, a large number of scenarios are generated using an MC and then reduced to a specific number.
3.1. Modeling of Load, Wind Speed, and Solar Irradiance
The uncertainty of the load, wind speed, and solar irradiance are modeled using a normal distribution [30], Weibull distribution [31] and beta distribution [32], respectively.
3.2. Proposed Scenario Generation and Reduction
More scenarios improve accuracy but increase the calculation volume, leading to time-consuming simulations [33]. A wide range of scenarios for input variables are initially generated, after which a scenario reduction strategy is implemented to reach a pre-defined number [30]. The proposed approach considers the correlation between random variables, which was not previously considered. The steps of scenario generation and reduction are described below:
- First, for each random variable, a set of independent random numbers following a standard normal distribution is generated, corresponding to the number of scenarios.
- The matrix is multiplied by the Cholesky matrix.
- CDF is calculated from the standard normal distribution .
- Then, scenarios are generated using for each variable based on the defined distribution functions while preserving their correlation.
- Finally, the generated scenarios are reduced to the desired number and WT and PV output power are calculated [30].
4. Proposed Crow Search Algorithm
4.1. CSA
CSA [23] is a metaheuristic technique that offers optimal mathematical methods. To run CSA, the following steps need to be considered:
- Step 1:
- Define the decision variables and CSA parameters.
- Step 2:
- Randomly place in a d-dimensional search space as the initial population. Each crow is a potential solution.
- Step 3:
- Initialize each crow’s memory, assuming they have hidden food at their initial positions because of lack of experience.
- Step 4:
- Calculate the objective function value for each crow.
- Step 5:
- In each iteration, a crow updates its position by randomly selecting another crow to chase for food . Depending on , crow either approaches or is deceived.
- Step 6:
- By meeting the constraints, the new position of the crow is accepted and the objective function value is calculated.
- Step 7:
- If the new position has a better objective function value, update the crow’s memory with the new position.
- Step 8:
- Repeat steps 5–8 until the number of iterations reaches . The best memory position is reported as the optimal solution when the termination criterion is met.
4.2. IMOCSA
In this paper, several methods are employed to enhance the overall performance of CSA. Initially, in IMOCSA, the initial population is generated through the tent method, according to (42)–(45). This approach potentially leads to faster convergence and reduced sensitivity to outliers, so an appropriate balance between exploration and exploitation is struck. Furthermore, it offers improved stability across multiple runs and can be adapted to match the expected structure of the problem space.
Secondly, the balance between diversification and intensification, which is regulated by AP, significantly affects the performance of CSA [34]. It is noted that intensification is promoted by smaller AP values, while larger values enhance diversification. The initiative proposed in [35] enhances CSA by using an adaptive chaotic for single-objective problems. This paper extends this approach to multi-objective problems by introducing , thus redefining for such problems.
and are the constant coefficient chaotic sequence, respectively [35].
IMOCSA employs an adaptive strategy for position updating when the awareness probability of the jth crow falls below a random number, according to (48). This approach utilizes three distinct methods, selected via a roulette wheel mechanism. Initially, for the first 25 iterations, each method has an equal probability of selection, with the selection probability vector set to [1,1,1]. After the 25th iteration, the algorithm introduces a performance-based adaptation. If a method obtains a superior solution compared to the others, its selection probability is incrementally increased by one unit. This dynamic adjustment allows the algorithm to favor more effective methods over time, potentially enhancing its exploration and exploitation capabilities. The first method [36] improves local search ability, the second method [37] enhances convergence speed, and the third method reduces the likelihood of getting stuck in local optima. This combination of methods aims to balance the algorithm’s search efficiency and solution quality throughout the optimization process.
To prevent getting stuck in local optima, a mutation on the solution repository is proposed. The mutation is applied by randomly selecting two members, and , from the solution repository ( ≠ ). AP for the desired mutation is calculated as follows:
Then, a new position resulting from the mutation is obtained as follows:
Additionally, to control the repository size and enhance the algorithm’s speed, the K-means method is employed. This decision is because this approach clusters similar solutions, thereby preserving diversity, reducing dimensionality, and improving decision making by offering a clearer view of trade-offs. The method increases computational efficiency and scales effectively with problem complexity by focusing on representative solutions. Furthermore, it facilitates improved visualization of high-dimensional objective spaces. These benefits collectively contribute to a more streamlined and effective optimization process. The pseudocode for IMOCSA is provided as Algorithm 1.
| Algorithm 1. Improve the Multi-Objective Crow search algorithm. |
| Initialize the problem parameters and set the algorithm parameters. |
| Generate an initial population of crows using Equations (42)–(45). |
| Evaluate the fitness (fit()) of each crow. |
| Initialize the memory of crows and create a repository of non-dominated solutions. |
| Select the best solution from the initial population. |
| = 1:itermax |
| Calculate . |
| = 1:N |
| Randomly choose a crow j to follow (j ≠ i). |
| Calculate . |
| else |
| Select a method using roulette wheel selection. |
| If method = 1 |
| Identify the global best position (). |
| Calculate the mean of population positions (). |
| . |
| . |
| elseif method = 2 |
| Identify the global best position (). |
| elseif method = 3 |
| . |
| end If |
| end If |
| Check if the new position is feasible. |
| Evaluate the fitness of the new position for crow i. |
| Randomly select two members R_1 and R_2 from the repository. |
| Calculate . |
| If rand ≥ |
| else |
| Identify the global best position (); |
| Calculate the mean of repository positions (). |
| . |
| end If |
| Check if the mutated position is feasible. |
| Evaluate the fitness of the mutated position. |
| Update the memory of crow i and the best solution found. |
| If iter ≥ 25 and the better solution belongs to a specific method |
| Increase the selection probability of that method. |
| end If |
| end for |
| Update the repository with new non-dominated solutions. |
| Control the repository size using the k-means clustering method. |
| Randomly select a member from the repository as the current best solution. |
| end for |
5. Simulation and Analysis Results
The models specifically designed for RMGs and their simulation results are analyzed in this section. and are considered to be 10 MVA and 12.66 kV, respectively. The single-line diagram related to the first and second models along with the number of units is shown in Figure 1 and Figure 2, respectively. The technical and economic characteristics for PV, WT, FC, and MT units, including their maintenance costs, rated capacities, and operational parameters, are detailed in Table 1 [25,38,39]. The distribution network provides power to MGs in exchange for CNY 0.4880, whereas MGs sell power back to the distribution network at CNY 0.3573 [40].
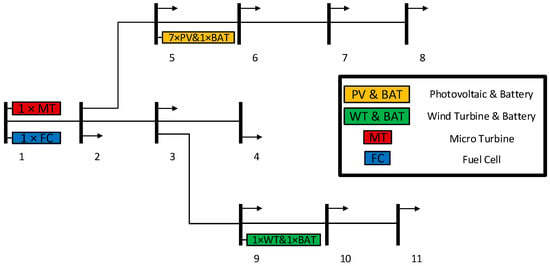
Figure 1.
Diagram of the first model.
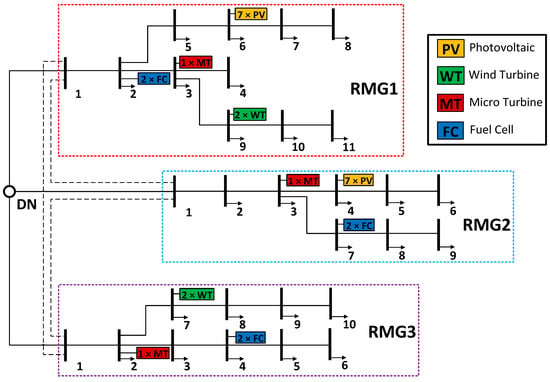
Figure 2.
Diagram of the second model.

Table 1.
Technical and Economic Characteristics of Microgrid Power Sources.
In this paper, the uncertainties of solar irradiance, wind speed, and load are modeled using scenario-based methods, characterized by beta, Weibull, and normal distribution functions, respectively. Scenarios have been generated separately in two distinct ways for each model: (1) taking into account the correlation between uncertain variables and (2) without considering correlation. The correlation matrices for the uncertain variables within the first and second models are presented in Table 2 and Table 3, respectively. Initially, 20,000 scenarios are generated for each case, then 5 scenarios are selected.

Table 2.
Correlation Matrix of the Uncertain Variables in the First Model.

Table 3.
Correlation Matrix of the Uncertain Variables in the Second Model.
Additionally, to evaluate the performance of the proposed algorithm, it is compared with algorithms including IMOCSA, CSA, JAYA, PSO, and TLBO and the related parameters for each algorithm are as follows:
- IMOCSA: fl = 1.5 and α = 2.
- CSA: fl = 2 and AP = 0.1.
- PSO: Maximum inertia weight = 0.9, minimum inertia weight = 0.4, and learning factors = 2.
- TLBO and JAYA: Without setting parameters.
5.1. First Model
5.1.1. Evaluation of the Proposed Method
Initially, to analyze the algorithm’s effectiveness, the proposed algorithm has been applied to the model for only the most probable scenario with correlation, in both single and multi-objective states. The results of a single objective function for ISOCSA, where the mutation is applied to the crow’s memories rather than the repository (47), are compared with other algorithms. Table 4 shows the values for the best, worst, mean, and standard deviation, which are derived from 30 executions of the algorithm and across various parameter settings for the proposed ISOCSA. Additionally, the maximum numbers of iterations and population size have been set to 5000 and 200, respectively. The results demonstrate that ISOCSA consistently outperforms the other algorithms in optimizing the three objective functions: cost (), voltage deviation (), and emissions ().

Table 4.
All functions’ comparison of the algorithms.
For the cost objective (), when fl and α equal 1.5 and 0.5, respectively, ISOCSA achieves the best result of 481.9568, which is lower than the best results of CSA (483.2319), PSO (487.1854), JAYA (483.634), and TLBO (482.0054). This configuration of ISOCSA also shows the smallest standard deviation of 0.2012, indicating high consistency in finding the most optimal solutions. The worst performance of ISOCSA with this configuration (482.4872) is still better than the best performance of the other algorithms, illustrating its robustness. In terms of voltage deviation () and emissions objective (), the algorithm performs similarly to the cost objective () and preserves its superiority over other algorithms.
The analysis reveals that ISOCSA’s performance is sensitive to the choice of fl and α parameters. Generally, lower values of fl and α (particularly fl = 1.5 and α = 0.5) tend to yield better results across all three objectives. As these values increase, there is a trend towards slightly worse performance and higher standard deviations, indicating reduced consistency in finding optimal solutions. However, it is important to note that ISOCSA exhibits limitations under specific conditions. For example, Table 4 indicates that for higher values of fl and α (e.g., fl = 2.5 and α = 2), ISOCSA’s performance deteriorates, with higher standard deviations and less competitive results compared to CSA and TLBO for specific objectives such as voltage deviation (f₂). This degradation is primarily attributed to reduced exploitation capabilities and premature convergence to suboptimal solutions when the algorithm’s exploration is overly emphasized.
Additionally, while ISOCSA’s multi-objective performance typically results in a dominant Pareto front (as illustrated in Figure 3), scenarios involving highly complex and non-linear interactions between objectives may cause ISOCSA to struggle in maintaining diversity on the Pareto front. In such cases, algorithms like PSO and JAYA occasionally achieve better trade-offs for specific objectives due to their inherent balance between exploration and exploitation. This underscores the importance of fine-tuning algorithm parameters and understanding the problem’s characteristics when applying ISOCSA.
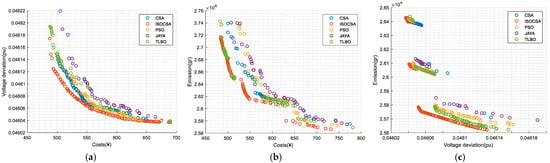
Figure 3.
Comparison of the Pareto front of the proposed algorithm and other algorithms. (a) Pareto front algorithms for costs and voltage deviation objectives. (b) Pareto front algorithms for emission and voltage deviation objectives. (c) Pareto front algorithms for costs and emission objectives.
Overall, while ISOCSA demonstrates superior robustness and effectiveness in handling multi-objective optimization problems, acknowledging its limitations provides a more nuanced understanding of its performance, enabling informed decisions on its applicability to different scenarios.
5.1.2. Results of the First Model
To address the multi-objective problem, all three objectives (, , and ) are considered. Figure 4 illustrates the Pareto front curves for the most probable scenarios both with and without correlation, using to identify the best compromise solution. The figure also presents the values for the best compromise solution and the minimum of each objective. Figure 5 shows the maximum output of each distributed power source in the RMG over a 24 h period and the maximum power discharged from electric energy storage devices under these scenarios. Additionally, Figure 6 demonstrates the DG results for the most probable scenario with and without correlation for the chosen best compromise solution on the Pareto front in Figure 4.
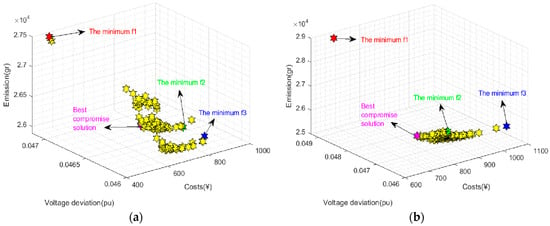
Figure 4.
Pareto front of the first model for multi-objective function. (a) Pareto front for the most probable scenario with correlation. (b) Pareto front for the most probable scenario without correlation.
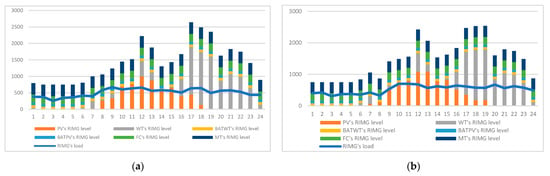
Figure 5.
Power load and generation level of the first model. (a) With correlation. (b) Without correlation.
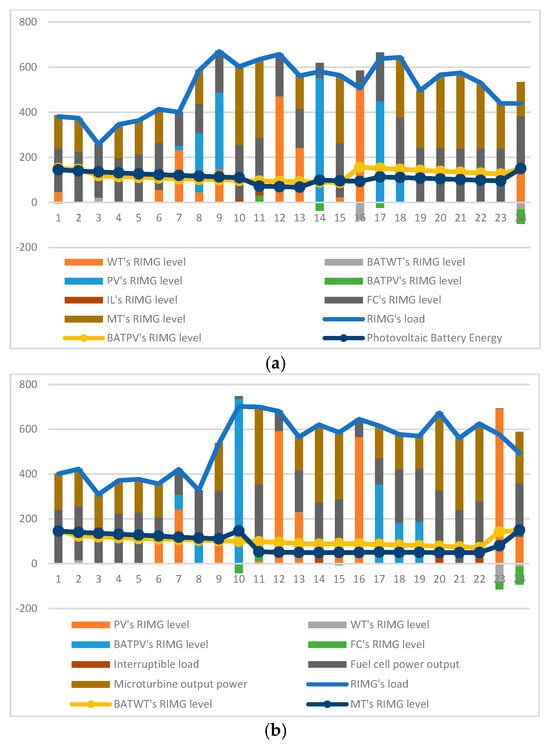
Figure 6.
Output optimization of the first model. (a) With correlation. (b) Without correlation.
The assumptions regarding power consumption and IL curves for residential users significantly influence these results. These assumptions are based on typical residential load profiles, where peak loads occur during specific hours due to household activities. Consequently, the power balance and dispatch schedules are adjusted to meet these temporal variations. In scenarios with correlation, the stochastic dependencies between load, PV, and WT outputs are considered, leading to a more realistic representation of resource availability and usage. Without correlation, the independent treatment of these variables may lead to discrepancies, such as overestimation or underestimation of resource contributions.
For instance, in Figure 6b, which corresponds to the most probable scenario without correlation, observations at hour 14 reveal that despite the presence of PV output power, the load is supplied independently of PV units. This discrepancy arises because the minimum PV power required to meet the load exceeds the calculated output after considering the discard solar rate (1.9%) as per constraint (18). Even with excess power stored in the BAT associated with PV, an unutilized surplus remains, rendering solar power ineffective during this hour. This phenomenon also occurs from hours 11–13 and 15–16. However, in Figure 6a, which accounts for correlation, similar occurrences are observed but slightly shifted due to the interdependencies among variables, affecting the allocation of resources.
Fluctuations in BAT energy are minimal across both scenarios due to the high maintenance cost of BATs. BATs are charged only with their excess energy, and maintaining the energy level at hour 24 is a key constraint. This requirement necessitates either rescheduling energy allocation in prior hours or sourcing additional energy from the network. Such conditions are most evident for the WT’s BATs at hour 24, where insufficient WT output necessitates adjustments to ensure BAT energy returns to its initial value, as shown in Figure 6.
Table 5 summarizes the outcomes for various scenarios with and without correlation. It highlights significant variations in cost () and emissions () between scenarios. For example, in the third scenario with correlation, minimizing cost results in a value of CNY 573.26, whereas minimizing emissions yields a cost of CNY 1111.22, a 93.84% difference. Similarly, the emission values differ by 16.57% when minimizing cost compared to emission optimization. These variations emphasize the need for a multi-objective solution approach, as neglecting correlation can significantly impact the optimal trade-offs among objectives.

Table 5.
Fuzzy Decision Making on the Pareto Front for the First Model.
Furthermore, voltage deviation () differences are particularly noteworthy. The second scenario with correlation exhibits a 4.44% change, while the fifth scenario without correlation shows a 5.8% change. If a decision-maker sets a maximum permissible change of 6%, voltage deviation may be deprioritized when simultaneously considering cost and pollution emissions. Overall, these findings underscore the critical role of assumptions in shaping model results and the importance of accounting for stochastic interdependencies in RMG optimization.
5.2. Results of the Second Model
RMGs, when operating conventionally, engage in power exchange solely with the distribution network. Table 6 depicts the variation between the optimized values under all feasible states of RMGs among generated alliances and their conventional operations. These differences are evaluated while the cost, emission, and voltage deviation are taken into account as the objective functions in selected scenarios.

Table 6.
Fuzzy Decision Making on all Alliances for the Second Model.
Moreover, Table 6 indicates that when the objective function is either the optimization of cost or emission pollution regardless of whether the correlation is taken into account, the most optimal form of alliance across all scenarios is a full alliance. Moreover, when the objective is voltage deviation with or without correlation considering the unit’s capacity and load, the differences compared to the conventional operation are remarkably minimal, and the alliance form does not affect the optimization. Consequently, according to the presented results, the most favorable strategy for optimizing the cost, voltage deviation, and pollution emission is the formation of a full alliance, and the consideration of correlation does not influence the outcomes.
Figure 7 presents the maximum power generation values for RMGs and their corresponding loads under the most probable scenario with correlation. Figure 8 illustrates the power generation value associated with the best compromise solution from the resulting repository with = 0.33 for the same scenario. As shown in Figure 7c, RMG3 does not generate sufficient wind output power from hours 12 to 18 to meet its load requirements, and under conventional operation, it must source this power from either the distribution network or its own MT and FC, which increases the cost and pollution.
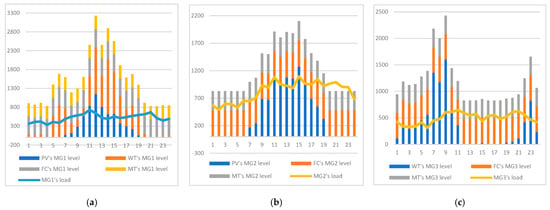
Figure 7.
Power load and generation level of the second model. (a) For MG1. (b) For MG2. (c) For MG3.
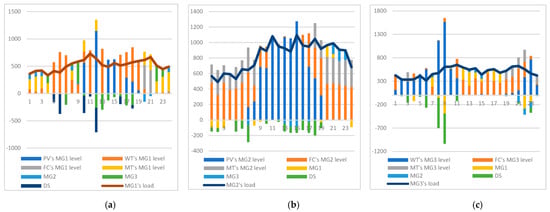
Figure 8.
Outcomes of RMGs’ alliance operation. (a) For MG1. (b) For MG2. (c) For MG3.
However, as depicted in Figure 8c, after alliance generation by utilizing the excess power of RMG1 and RMG2 generated via their wind and solar units, both emission production and cost have been simultaneously reduced. Additionally, RMG3 has excess power from its WT unit at hour 23 while both RMG1 and RMG2 lack wind and solar output power. By transferring this excess power, both cost and pollution can be reduced. Therefore, the function of all three RMGs in energy provision and load management is complementary, and the alliance generation helps efficient energy planning to reduce both the cost and emission pollution.
Figure 9 and Figure 10 illustrate that it is more cost-effective and less polluting for the distribution network to purchase the surplus power from the RMG coalition than from the power plant. The cost-saving value is quantified at CNY 663.68, and the reduction in pollution emission is measured at 23,982.88 g.
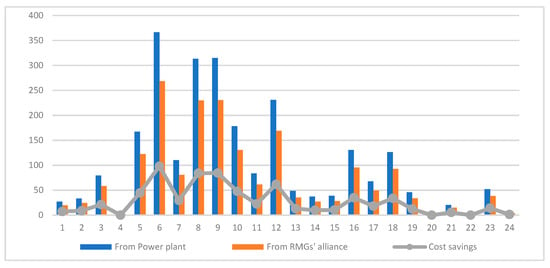
Figure 9.
Comparison of power purchasing cost for the distribution network.
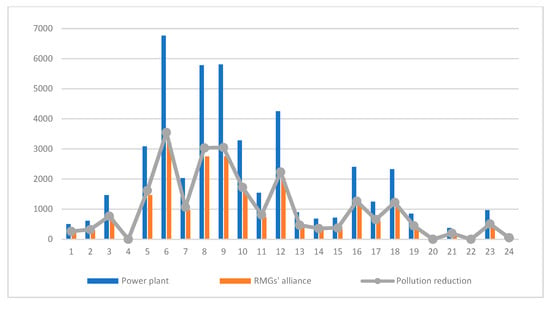
Figure 10.
Comparison of emission pollution for the distribution network.
6. Conclusions
MGs that integrate renewable power sources like PV and WT offer cost-effective and environmentally friendly energy alternatives. Hence, their utilization is particularly beneficial for rural communities. However, designing optimal scheduling for efficient generation is recognized as an important challenge. Therefore, in this paper, two distinct models, including an islanded mode and connection to the distribution network, were employed. They were utilized in rural areas in order to supply energy to consumers and optimize system performance along with reducing pollution emission, utilization of fossil fuels, and simultaneously increasing cost saving. The scientific novelty of this work lies in three key contributions: the development of IMOCSA that enhances optimization performance through adaptive chaotic awareness probability and mutation mechanisms, the introduction of a sophisticated scenario-based methodology incorporating correlations among uncertainties, and the presentation of a comprehensive two-model approach addressing both islanded and grid-connected operations. The practical significance is demonstrated through substantial reductions in operational costs and environmental impacts, with IMOCSA showing superior performance in handling multi-objective optimization, making it a valuable tool for system operators managing complex microgrid networks. Simulation results indicated that the coalition generation across all RMGs not only reduced operational costs and environmental impacts but also decreased the power purchasing cost from the power plant for the distribution network. These results have important implications for rural electrification projects, offering a practical framework for implementing cost-effective and environmentally sustainable power systems. Furthermore, we found that the correlation did not significantly influence the alliance results, which simplifies implementation for practical applications.
Author Contributions
M.H.T.: Data curation, Writing—original draft; T.N.: Project administration, Supervision, Validation; S.M.S.: Investigation, Writing—original draft; H.A.A.: Formal analysis, Writing—original draft; S.M.B.: Project administration, Supervision; E.S.: Funding acquisition, Formal analysis, Methodology, Validation; G.J.: Formal analysis, Methodology, Conceptualization. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| SG | Smart grid |
| EMS | Energy management system |
| RES | Renewable energy source |
| DG | Distributed generation |
| FC | Fuel cell |
| MT | Microturbine |
| BAT | Battery |
| CSA | Crow search algorithm |
| ISOCSA | Improved single-objective CSA |
| DNN | Deep neural network |
| CNN | Convolutional neural network |
| Bi-LSTM | Bidirectional long short-term memory |
| EMM | Energy management model |
| ANN | Artificial neural network |
| SoC | State of charge |
| MPPT | Maximum power point tracking |
| PEM | Point estimate method |
| UT | Unscented transformation |
| MC | Monte Carlo |
| Probability density function | |
| CDF | Cumulative distribution function |
| IL | Interruptible load |
| C | Correlation matrix |
| Step time | |
| Output power of PV/WT/FC/MT at time in IRMG | |
| Output power of PV/WT/FC/MT at time in nth RMG | |
| Output power of the PV/WT BAT at time in IRMG | |
| The amount of IL in the IRMG in time | |
| The load value of the (IRMG/nth RMG) at time | |
| Maintenance cost of PV/WT/FC/MT units | |
| Maintenance cost of BAT units | |
| The cost of compensation for IL | |
| Number of buses in (IRMG/nth RMG) | |
| The price of purchasing/selling power from/to the distribution network for the coalition of RMGs | |
| Base nominal power/base voltage level | |
| X | Decision variables vector |
| V ref | Nominal voltage |
| The voltage level of bus in (IRMG/nth RMG) in time | |
| Highest/lowest voltage of each bus | |
| Emission coefficient of MT/FC/grid | |
| The maximum/minimum power output level of the PV in time | |
| The maximum/minimum power output level of the WT in time | |
| The maximum/minimum power output level of the FC in time | |
| The maximum/minimum power output level of the MT in time | |
| (Wind rejection/discard solar) rate | |
| Total energy of the BAT in time | |
| Self-discharge rate of BAT | |
| The state of BAT charge/discharge in time | |
| Charge/discharge efficiency of BAT | |
| BAT’s initial stored energy | |
| Upper/lower limit of BAT charging power | |
| Upper/lower limit of BAT discharging power | |
| Upper/lower limit of BAT energy | |
| rep | Repository |
| Population size of crows | |
| Current iteration | |
| Maximum number of iterations | |
| Flight length | |
| AP | Awareness probability |
| from the rep for mutation in | |
| d | Number of decision variables |
| The position of the foods hidden by crow | |
| of the position of the foods hidden by crow | |
| The position of the mutated crow in | |
| The number of objective functions | |
| Fixed coefficient | |
| Upper/lower boundary of optimization variables | |
| Best compromise solution | |
| Mean of the population positions | |
| The value of the objective function number | |
| Size of the repository | |
| positions | |
| The number of RMGs | |
| Fitness function |
References
- Islam, M.M.; Nagrial, M.; Rizk, J.; Hellany, A. General aspects, islanding detection, and energy management in Microgrids: A review. Sustainability 2021, 13, 9301. [Google Scholar] [CrossRef]
- Dashtaki, A.A.; Hakimi, S.M.; Farahani, E.S.; HassanzadehFard, H. Simultaneous optimal location and sizing of DGs in distribution system considering different types of MGs in an electricity market. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 2443–2459. [Google Scholar] [CrossRef]
- Rashwan, A.; Faragalla, A.; Abo-Zahhad, E.M.; El-Dein, A.Z.; Liu, Y.; Chen, Y.; Abdelhameed, E.H. Techno-economic Optimization of Isolated Hybrid Microgrids for Remote Areas Electrification: Aswan city as a Case Study. Smart Grids Sustain. Energy 2024, 9, 18. [Google Scholar] [CrossRef]
- Bashir, A.A.; Pourakbari-Kasmaei, M.; Contreras, J.; Lehtonen, M. A novel energy scheduling framework for reliable and economic operation of islanded and grid-connected microgrids. Electr. Power Syst. Res. 2019, 171, 85–96. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, K.; Li, H.; Coelho, E.A.A.; Guerrero, J.M. MAS-based distributed coordinated control and optimization in microgrid and microgrid clusters: A comprehensive overview. IEEE Trans. Power Electron. 2017, 33, 6488–6508. [Google Scholar] [CrossRef]
- Chen, G.; Wang, J.-M.; Yuan, X.-D.; Chen, L.; Zhao, L.-J.; He, Y.-L. Chinese national condition based power dispatching optimization in microgrids. J. Control. Sci. Eng. 2018, 2018, 8695391. [Google Scholar] [CrossRef]
- Khan, M.R.; Haider, Z.M.; Malik, F.H.; Almasoudi, F.M.; Alatawi, K.S.S.; Bhutta, M.S. A Comprehensive Review of Microgrid Energy Management Strategies Considering Electric Vehicles, Energy Storage Systems, and AI Techniques. Processes 2024, 12, 270. [Google Scholar] [CrossRef]
- Prinsloo, G.; Mammoli, A.; Dobson, R. Customer domain supply and load coordination: A case for smart villages and transactive control in rural off-grid microgrids. Energy 2017, 135, 430–441. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J. Decentralized energy management system for networked microgrids in grid-connected and islanded modes. IEEE Trans. Smart Grid 2015, 7, 1097–1105. [Google Scholar] [CrossRef]
- Espín-Sarzosa, D.; Palma-Behnke, R.; Núñez-Mata, O. Energy management systems for microgrids: Main existing trends in centralized control architectures. Energies 2020, 13, 547. [Google Scholar] [CrossRef]
- Sabzalian, M.H.; Pirouzi, S.; Aredes, M.; Franca, B.W.; Cunha, A.C. Two-Layer Coordinated Energy Management Method in the Smart Distribution Network including Multi-Microgrid Based on the Hybrid Flexible and Securable Operation Strategy. Int. Trans. Electr. Energy Syst. 2022, 2022, 3378538. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Q.; Wang, L.; Feng, W. Robust optimization for energy transactions in multi-microgrids under uncertainty. Appl. Energy 2018, 217, 346–360. [Google Scholar] [CrossRef]
- Huang, B.; Li, Y.; Zhang, H.; Sun, Q. Distributed optimal co-multi-microgrids energy management for energy internet. IEEE/CAA J. Autom. Sin. 2016, 3, 357–364. [Google Scholar] [CrossRef]
- Arefifar, S.A.; Ordonez, M.; Mohamed, Y.A.-R.I. Energy management in multi-microgrid systems—Development and assessment. IEEE Trans. Power Syst. 2016, 32, 910–922. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Z.; He, Y. A Deep Neural Network-Based Optimal Scheduling Decision-Making Method for Microgrids. Energies 2023, 16, 7635. [Google Scholar] [CrossRef]
- Du, Y.; Li, F. Intelligent multi-microgrid energy management based on deep neural network and model-free reinforcement learning. IEEE Trans. Smart Grid 2019, 11, 1066–1076. [Google Scholar] [CrossRef]
- Aguila-Leon, J.; Vargas-Salgado, C.; Chiñas-Palacios, C.; Díaz-Bello, D. Energy management model for a standalone hybrid microgrid through a particle Swarm optimization and artificial neural networks approach. Energy Convers. Manag. 2022, 267, 115920. [Google Scholar] [CrossRef]
- Roldán-Blay, C.; Escrivá-Escrivá, G.; Roldán-Porta, C.; Dasí-Crespo, D. Optimal sizing and design of renewable power plants in rural microgrids using multi-objective particle swarm optimization and branch and bound methods. Energy 2023, 284, 129318. [Google Scholar] [CrossRef]
- Zhang, X.; Son, Y.; Cheong, T.; Choi, S. Affine-arithmetic-based microgrid interval optimization considering uncertainty and battery energy storage system degradation. Energy 2022, 242, 123015. [Google Scholar] [CrossRef]
- Tan, B.; Chen, H. Multi-objective energy management of multiple microgrids under random electric vehicle charging. Energy 2020, 208, 118360. [Google Scholar] [CrossRef]
- Dev, A.; Mondal, B.; Verma, V.K.; Kumar, V. Teaching learning optimization-based sliding mode control for frequency regulation in microgrid. Electr. Eng. 2024, 106, 7009–7021. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, S.; Li, D.; Zhang, S. Improved whale optimization algorithm for solving microgrid operations planning problems. Symmetry 2022, 15, 36. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Xu, Y.; Guo, Q.; Sun, H.; Fei, Z. Distributed discrete robust secondary cooperative control for islanded microgrids. IEEE Trans. Smart Grid 2018, 10, 3620–3629. [Google Scholar] [CrossRef]
- Jia, Y.; Wen; Yan, Y.; Huo, L. Joint operation and transaction mode of rural multi microgrid and distribution network. IEEE Access 2021, 9, 14409–14421. [Google Scholar] [CrossRef]
- Roustaei, M.; Niknam, T.; Salari, S.; Chabok, H.; Sheikh, M.; Kavousi-Fard, A.; Aghaei, J. A scenario-based approach for the design of Smart Energy and Water Hub. Energy 2020, 195, 116931. [Google Scholar] [CrossRef]
- Christopher, S.B.; Mabel, M.C. A bio-inspired approach for probabilistic energy management of micro-grid incorporating uncertainty in statistical cost estimation. Energy 2020, 203, 117810. [Google Scholar] [CrossRef]
- Atwa, Y.M.; El-Saadany, E. Optimal allocation of ESS in distribution systems with a high penetration of wind energy. IEEE Trans. Power Syst. 2010, 25, 1815–1822. [Google Scholar] [CrossRef]
- Tabatabaee, S.; Mortazavi, S.S.; Niknam, T. Stochastic energy management of renewable micro-grids in the correlated environment using unscented transformation. Energy 2016, 109, 365–377. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, N.; Mallipeddi, R.; Amaratunga, G.A. Optimal reactive power dispatch with uncertainties in load demand and renewable energy sources adopting scenario-based approach. Appl. Soft Comput. 2019, 75, 616–632. [Google Scholar] [CrossRef]
- Lins, D.R.; Guedes, K.S.; Pitombeira-Neto, A.R.; Rocha, A.C.; de Andrade, C.F. Comparison of the performance of different wind speed distribution models applied to onshore and offshore wind speed data in the Northeast Brazil. Energy 2023, 278, 127787. [Google Scholar] [CrossRef]
- Elgamal, M.; Korovkin, N.; Elmitwally, A.; Menaem, A.A.; Chen, Z. A framework for profit maximization in a grid-connected microgrid with hybrid resources using a novel rule base-bat algorithm. IEEE Access 2020, 8, 71460–71474. [Google Scholar] [CrossRef]
- Shen, J.; Jiang, C.; Liu, Y.; Wang, X. A microgrid energy management system and risk management under an electricity market environment. IEEE Access 2016, 4, 2349–2356. [Google Scholar] [CrossRef]
- Talaat, M.; Elkholy, M.; Alblawi, A.; Said, T. Artificial intelligence applications for microgrids integration and management of hybrid renewable energy sources. Artif. Intell. Rev. 2023, 56, 10557–10611. [Google Scholar] [CrossRef]
- Makhdoomi, S.; Askarzadeh, A. Optimizing operation of a photovoltaic/diesel generator hybrid energy system with pumped hydro storage by a modified crow search algorithm. J. Energy Storage 2020, 27, 101040. [Google Scholar] [CrossRef]
- Gholami, J.; Mardukhi, F.; Zawbaa, H.M. An improved crow search algorithm for solving numerical optimization functions. Soft Comput. 2021, 25, 9441–9454. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Elattar, E.E.; Abd-Elrazek, A.S. A modified crow search optimizer for solving non-linear OPF problem with emissions. IEEE Access 2021, 9, 43107–43120. [Google Scholar] [CrossRef]
- Song, X.; Lin, H.; De, G.; Li, H.; Fu, X.; Tan, Z. An energy optimal dispatching model of an integrated energy system based on uncertain bilevel programming. Energies 2020, 13, 477. [Google Scholar] [CrossRef]
- Niknam, T.; Bornapour, M.; Gheisari, A.; Bahmani-Firouzi, B. Impact of heat, power and hydrogen generation on optimal placement and operation of fuel cell power plants. Int. J. Hydrogen Energy 2013, 38, 1111–1127. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, C.; Zheng, C.; Rui, T.; Shen, W.; Wang, B. Distributed peer-to-peer electricity trading considering network loss in a distribution system. Energies 2019, 12, 4318. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).