Rate Transient Analysis for Commingled Production Wells with Multiple Channel Sand Layers in Tight Gas Reservoirs

Abstract

To address the challenges of characterizing commingled production from multiple channel sand layers with varying boundaries and shapes in tight gas reservoirs, a novel Rate Transient Analysis (RTA) model was established based on the principle of equivalent seepage volume (ESV). This model enables the determination of boundary sizes and permeabilities of individual channel sand layers within commingled tight reservoirs using modern production decline analysis theory. The production decline behavior under different channel sizes, numbers, and configurations was systematically investigated through type curve analysis. The results reveal the existence of five distinct stages in the production decline curves for unequal-width channel sands. The intermediate transient flow stage serves as a diagnostic indicator for identifying boundary disparities among layers. Furthermore, reservoirs with smaller boundary distances, fewer wide channel sand layers, and lower thickness proportions of wider channels exhibit poorer productivity and tend to experience accelerated production decline during early and middle transient flow stages. The proposed method provides an effective approach for characterizing boundary parameters of commingled tight reservoirs and offers a theoretical foundation for evaluating individual layer contributions and productivity.

1. Introduction

China’s tight gas reservoirs are mainly composed of continental channel sediments, which are characterized by a wide distribution range, multilayer interaction, and complex channel sand layer distribution patterns [1,2]. Among them, multilayer tight gas reservoirs, such as the Daniudi and Shenmu Gasfield in the Ordos Basin [3,4,5], and the Xinchang and Xujiahe Gasfield in the Sichuan Basin [6], account for a considerable proportion of the tight gas reservoir types in China. Due to the relatively thin thickness of a single-channel sand layer of the sandstone tight reservoir, and poor seepage capacity, it is difficult to obtain industrial gas flow through single-channel sand layer development. At present, this type of tight gas reservoir generally adopts the production method of multilayer commingled production. However, the production contribution rate of each channel sand layer is not directly related to the differences in the properties of each channel sand layer in the tight reservoir. Taking the Daniudi gas field in China’s Ordos Basin as an example, its multilayered wells face problems such as difficulty in splitting production and unclear utilization levels of each channel sand layer [7,8]. Therefore, it is very necessary to analyze the spatial distribution characteristics and physical properties of comingled channel sand layers through test data of tight gas reservoir production wells.

For wells producing from multiple layers simultaneously, Ehlig-Economides and Joseph [9] compiled and evaluated systems involving multilayered reservoirs. They showed that measuring both wellbore pressure and individual layer flow rates offers enough data to fully characterize the layered reservoir properties. Tariq and Ramey [10] observed that solving the analytical model becomes challenging and its practical application decreases when more than two layers are involved. Regarding composite reservoirs with multiple layers, Gomes and Ambastha [11] formulated a comprehensive analytical solution for pressure transient behavior in an n-layered composite system, accounting for pseudo-steady-state crossflow between layers. Their work also reviewed and expanded on the foundation set by Ehilg-Economides and Joseph [9], examining models published since 1960 for multilayered reservoirs with crossflow. Out of 59 models surveyed, only five addressed composite reservoir configurations. Satman et al. [12] introduced models for both pressure drawdown and buildup in commingled, multilayered composite reservoirs. Their approach allowed varying radii of discontinuity boundaries across layers, which is useful for modeling improved recovery techniques like steam flooding. In addition, some studies have been conducted in unconventional oil and gas, mainly used to determine the boundary issues of reservoirs [13,14].

Satman and Oskay [15] modeled the reservoir as a multilayered composite system without crossflow, treating the discontinuity boundary as a tilted front to represent gravity override effects. Hatzignatiou et al. [16] derived a solution for analyzing interference pressure transients in a two-layered reservoir exhibiting pseudo-steady-state crossflow, and introduced a type-curve matching method to estimate reservoir parameters. Anbarci et al. [17] developed an analytical model including wellbore storage and skin effects for a two-layered composite reservoir with pseudo-steady crossflow, applying type-curve matching to identify the flood front position in a specific layer. Nevertheless, a multilayered composite reservoir model incorporating formation crossflow specifically for carbonate reservoirs or other multi-porosity media has not yet been developed. Shi et al. [18] provided a pressure transient analysis model to calculate the pressure under different boundary length differences, but this method can only calculate an equivalent boundary value corresponding to all boundaries, and this method is suitable for the case of continuous multilayer distribution in the longitudinal direction. Sun et al. [19] provided a planar radial flow pressure analysis model for the double-layer commingled production and three-layer commingled production flow model [20]. However, this type of model is suitable for infinite horizontal plate-shaped commingled production. Most models are based on the assumption of plane radial flow or regular geometric morphology, and do not consider the band shape and boundary differences of river sand. Based on the above analysis, all comingled production flow models are not suitable for irregularly shaped channel sand sedimentation.

The existing multilayer, commingled production flow models have the following characteristics: (i) Pressure transient analysis models are often used to obtain reservoir parameters, but pressure tests generally only last for hundreds of hours, and test data over the years have changed greatly, and the results of pressure interpretation methods may be accidental. (ii) Most of those flow models are based on plane radial flow and do not consider the shape of the channel sedimentary sand layer, nor the commingled production of multiple convex mirror-shaped sand layers in the longitudinal direction. (iii) At present, multilayer commingled flow models mainly consider the characteristics of interlayer crossflow, which does not apply to the situation of multilayered commingled production of a superimposed sand layer. (iv) Lastly, the difference in boundary size of each commingled production layer is not considered, and it is difficult to clarify the pressure and production change behavior caused by boundary differences between each layer.

To fill this gap and promote the expansion and application of complex seepage models, this paper first considers the morphological characteristics of each channel sand layer encountered during drilling, and based on the modern production rate decline analysis theory, establishes a novel Rate Transient Analysis (RTA) method for determining the channel sand layer boundaries of multilayered tight reservoirs. Secondly, the production rate transient behavior under different boundary sizes, layer numbers, and sand layer locations of the channel sand layer was discussed. Finally, the established RTA method was applied to an actual tight gas reservoir, and the case analysis results confirmed the effectiveness of the correct summing method of this model. The research results can provide theoretical support for production rate decline analysis and production prediction of multilayer commingled production wells in tight oil and gas reservoirs.

2. Methodology

2.1. Physical Model

The effective sand layer of the layered tight reservoir is the fluid storage space formed by channel deposition. Production wells are arranged along the distribution direction of the channel sand layer and control the channel sand layer in sections. A production well that encounters multiple channel sand layers longitudinally is shown in Figure 1a. The spatial location and coordinates of the production wells are shown in Figure 1b. In many continental tight gas reservoirs such as the Ordos Basin, river sand bodies are usually separated by dense mudstone or siltstone partitions, and the interlayer fluid flow can be negligible. Other basic assumptions are as follows.

The channel sand layer is strip-shaped on the plane, the vertical strip direction is set to x, and the direction along the river channel is set to y and the longitudinal section of the sand body is bowl-shaped.

Moreover, the channel sand layer is approximately in the shape of a horizontal plate of equal thickness near the wellbore and is in the shape of a thin semi-lens at the boundary of the channel sand layer. It describes the geometric characteristics of the cross-section of the river sand body from an approximately equal thickness near the well to the edge of the two sides, which is a common pattern of river sedimentary geology in the Ordos Basin.

The thickness h_j, width W_j, and control length L_j of the j-th layer of channel sand layers encountered by the production well are different, and the porosity of each layer is φ_j, the permeability is k_j, and the comprehensive compression coefficient is c_tj.

Beyond this, the wellbore radius of the production well is r_w, the wellhead production is Q, the production well has a constant pressure production system, and the bottomhole pressure p_w is a constant value. The viscosity of the fluid in the channel sand layer is μ, the flow rate of each layer of the channel sand layer to the wellbore is q_j, and the fluid volume coefficient is B.

Finally, the layer of channel sand layers is not connected, there is no interlayer crossflow between channel sand layers, and the influence of temperature changes and gravity during the flow process is not considered.

2.2. Mathematical Model

In order to make this model suitable for oil and gas well production analysis, we first define the normalized pseudo-time and the normalized pseudo-pressure. For the normalized pseudo-time, we have [21] as Equation (1) and for the normalized pseudo-pressure [22,23], we have Equation (2).

$$t\ast ={\int }_{t_i}^t{\displaystyle \frac{{\mu }_g\left(t_i\right)c_g\left(t_i\right)}{{\mu }_g\left(t\right)c_g\left(t\right)}}dt$$

(1)

$$p\ast ={\displaystyle \frac{{\mu }_g\left(p_i\right)Z\left(p_i\right)}{p_i}}{\int }_{p_i}^p{\displaystyle \frac{2p}{{\mu }_g\left(p\right)Z\left(p\right)}}dp$$

(2)

where t_i is the initial production time, s; μ_g is gas viscosity, Pa·s; c_g is the gas compressibility, Pa⁻¹; p_i is the initial pressure, Pa; and Z is the gas deviation factor.

Based on the above normalized parametric form, various gas well testing models can adopt the dimensionless parameter definition formula of the oil well testing model [24]. Therefore, no distinction is made between oil and gas in the following. In the dimensionless flow equation, pressure p and time t are uniformly used to represent the normalized pseudo-pressure p* and the normalized pseudo-production n time t*. The parameters that characterize this mathematical model are defined as shown in

Table 1. Dimensionless variables and definitions.

Parameters	Definition
Dimensionless distance	$x_D={\displaystyle \frac{x}{x_w}},y_D={\displaystyle \frac{y}{y_w}},r_D={\displaystyle \frac{r}{r_w}}$
Dimensionless distance of boundary	$W_D={\displaystyle \frac{W}{x_w}},L_D={\displaystyle \frac{L}{y_w}}$
Dimensionless time	$t_D={\displaystyle \frac{k_{a}t}{\mu {(\phi c_t)}_a{r_w}^2}}$
Dimensionless thickness	$h_{Dj}={\displaystyle \frac{h_j}{{\displaystyle \sum _{j=1}^n{h}_j}}}$
Dimensionless pressure	$p_{Dj}={\displaystyle \frac{p_i-p_j}{p_i-p_w}}$
Dimensionless flow rate	$q_D={\displaystyle \frac{Q\mu B}{2\pi k_a{h}_t(p_i-p_w)}}$
Average permeability	$k_a={\displaystyle \sum _{j=1}^n\left(k_j{h}_{jD}\right)}$
Average storability	${\left(\phi c_t\right)}_a={\displaystyle \sum _{j=1}^n\left[{\left(\phi c_t\right)}_j{h}_{jD}\right]}$
Flow coefficient	${\chi }_j={\displaystyle \frac{k_j}{k_a}}{\displaystyle \frac{h_j}{{\displaystyle \sum _{j=1}^n{h}_j}}}$
Storability ratio	${\omega }_j={\displaystyle \frac{{\phi }_j{c}_{t_j}}{{\left(\phi c_t\right)}_a}}{\displaystyle \frac{ h_j}{{\displaystyle \sum _{j=1}^n{h}_j}}}$

where p_j is the pressure of the j-th layer, Pa; p_w is the bottomhole pressure, Pa; Q is the flow rate at the wellhead, m³/s; B is the volume coefficient; k is the permeability, m²; h is the thickness, m; W is the width of the sand layer, m; L is the length of the sand layer, m; φ is the porosity, %; c_t is the total compressibility, Pa⁻¹; x, y is the distance at x, y direction, m; r is the radial distance, m; and r_w is the wellbore radius, m.

.

On the physical model and assumptions, the dimensionless form of the corresponding mathematical model is

$$\left\{\begin{array}{l}{\displaystyle \frac{{\partial }^2{p}_{jD}}{\partial {x_D}^2}}+{\displaystyle \frac{{\partial }^2{p}_{jD}}{\partial {y_D}^2}}={\displaystyle \frac{{\omega }_j}{{\chi }_j}}{p}_{jD}\\ {\left.p_{jD}\right|}_{t_D=0}=0\\ {\left.p_{jD}\right|}_{r_D=1}=1\\ {\left.{\displaystyle \frac{\partial p_{jD}}{\partial x_D}}\right|}_{x_D=\pm {\displaystyle \frac{W_{Dj}^{\ast }}{2}}}={\left.{\displaystyle \frac{\partial p_{jD}}{\partial y_D}}\right|}_{y_D=\pm {\displaystyle \frac{L_{Dj}}{2}}}=0\end{array}\right.$$

(3)

In Equation (3), the subscript D represents a dimensionless parameter, and $W_j^{*}$ represents the equivalent width of the j-th layer of the channel sand, which is calculated by the following formula based on the ESV concept [18]:

$$\left\{\begin{array}{l}{W}_j^{*}={\displaystyle \frac{\frac{\pi {R_j}^2}{2}-\left[\left(R_j-h_j\right)\sqrt{2h_j{R}_j-{R_j}^2}+{R_j}^2\mathit{arcsin}\left(\frac{R_j-h_j}{R_j}\right)\right]}{h_j}}\\ R_j={\displaystyle \frac{{h_j}^2+\frac{W_j}{4}}{2h_j}}\end{array}\right.$$

(4)

where R is the radius of the curvature of the channel sand layer, m.

2.3. Solution Approach

In the Laplace domain, the pressure solution of this mathematical model is

$$\left\{\begin{array}{l}{\bar{p}}_{jD}(r_D,u)=A_j{I}_0\left(r_D\sqrt{{\displaystyle \frac{u{\omega }_j}{{\chi }_j}}}\right)+B_j{K}_0\left(r_D\sqrt{{\displaystyle \frac{u{\omega }_j}{{\chi }_j}}}\right)\\ r_D=\sqrt{x_D^2+y_D^2}\end{array}\right.$$

(5)

Substituting Equation (5) into the boundary conditions of the mathematical model, one can obtain a system of linear equations about A_j and B_j.

$$\left[\begin{array}{c}\begin{array}{cccccccc}{a}_1& b_1& & & & & & \\ & & \dots & & & & & \\ & & & a_j& b_j& & & \\ & & & & & \dots & & \\ & & & & & & a_n& b_n\end{array}\\ \begin{array}{cccccccc}{c}_1& d_1& & & & & & \\ & & \dots & & & & & \\ & & & c_j& d_j& & & \\ & & & & & \dots & & \\ & & & & & & c_n& d_n\end{array}\end{array}\right]\cdot \left[\begin{array}{c}{A}_1\\ B_1\\ \begin{array}{c}.\\ .\end{array}\\ A_j\\ B_j\\ \begin{array}{c}.\\ .\end{array}\\ A_n\\ B_n\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{1}{u}}\\ \begin{array}{c}.\\ .\end{array}\\ {\displaystyle \frac{1}{u}}\\ 0\\ \begin{array}{l}.\\ .\end{array}\\ 0\end{array}\right]$$

(6)

The elements of Equation (6) are as follows:

$$\left\{\begin{array}{c}{a}_j=I_0\left(\sqrt{{\displaystyle \frac{u{\omega }_j}{{\chi }_j}}}\right)\\ b_j=K_0\left(\sqrt{{\displaystyle \frac{u{\omega }_j}{{\chi }_j}}}\right)\\ c_j=\sqrt{{\displaystyle \frac{u{\omega }_j}{{\chi }_j}}}{I}_1\left(\sqrt{{\displaystyle \frac{u{\omega }_j}{{\chi }_j}}}\sqrt{{\displaystyle \frac{W_{Dj}^{*}{L}_{Dj}}{\pi }}}\right)\\ d_j=-\sqrt{{\displaystyle \frac{u{\omega }_j}{{\chi }_j}}}{K}_1\left(\sqrt{{\displaystyle \frac{u{\omega }_j}{{\chi }_j}}}\sqrt{{\displaystyle \frac{W_{Dj}^{*}{L}_{Dj}}{\pi }}}\right)\end{array}\right.$$

(7)

In Equations (5)~(7), u is the Laplace variable, I₀ is the 0-order modified Bessel function of the first kind [25], K₀ is the 0-order modified Bessel function of the second kind [26], I₁ is the 1-order modified Bessel function of the first kind, and K₁ is the 1-order modified Bessel function of the second kind.

After obtaining the A_j and B_j, the dimensionless pressure of j-th layer in the Laplace domain is

$${\bar{p}}_{wDj}\left(u\right)=A_j{I}_0\left(\sqrt{{\displaystyle \frac{u{\omega }_j}{{\chi }_j}}}\right)+B_j{K}_0\left(\sqrt{{\displaystyle \frac{u{\omega }_j}{{\chi }_j}}}\right)$$

(8)

Through the Duhamel superposition principle [27], the bottomhole pressure is obtained based on the mutual coupling of the wellbore position pressures of each channel sand layer, and then based on the pressure and production conversion relationship. The production well rate is obtained as

$${\bar{q}}_D(u)=\sum _{j=1}^n{\displaystyle \frac{1}{u^2{\overline{p}}_{wDj}(u)}}$$

(9)

According to the Stehfest numerical inverse transformation method [28], we can calculate dimensionless flow rate in real space. In this work, we wrote code based on the formula in Reference [29], and the parameter N in the Stehfest numerical inversion algorithm is set to 8, which has been widely verified to have sufficient accuracy and numerical stability in such seepage problems. Based on the research of Blasingame [30], the multiple solutions of yield fitting can be reduced by defining three types of function [31,32] expressed as

$$\left\{\begin{array}{l}{q}_{Dd}=q_D\cdot b_{Dpss}\\ q_{Ddi}={\displaystyle \frac{1}{t_{cDd}}}{\int }_0^{t_{cDd}}{q}_{Dd}\left(\tau \right)d\tau \\ q_{Ddid}=t_{cDd}{\displaystyle \frac{d{q}_{Ddi}}{d{t}_{Dd}}}\\ t_{cDd}={\displaystyle \frac{\alpha }{b_{Dpss}}}{t}_D\end{array}\right.$$

(10)

where q_Dd is the dimensionless decline rate, q_Ddi is the dimensionless decline rate integral, q_Ddid is the dimensionless decline rate integral derivative, and t_cDd is the dimensionless material balance pseudo-time.

In Equation (10), the coefficients involved in calculating the dimensionless balance material pseudo-time are

$$\left\{\begin{array}{c}\alpha ={\displaystyle \frac{2}{{\sum }_{j=1}^n{\omega }_j\frac{W_j^{*}{L}_j}{\pi }}}\\ b_{Dpss}={\displaystyle \frac{{\alpha }^2}{4}}{\displaystyle \sum _{j=1}^n}\left[{\left({\displaystyle \frac{W_j^{*}{L}_j}{\pi }}\right)}^2{\displaystyle \frac{{\omega }_j}{{\chi }_j}}\left(0.5\mathit{ln}{\displaystyle \frac{W_j^{*}{L}_j}{\pi }}-0.75\right)\right]\end{array}\right.$$

(11)

3. Results and Analysis

3.1. Type Curve and Flow Regime

Taking three channel sand layers as an example, equal-width channel sand layers mean that the widths of the sand layers are the same (all widths are 100 m), while unequal-width channel sand layers mean that each sand layer has different widths (from top to bottom is 100 m, 200 m, and 300 m, respectively). Comparing the characteristics of RTA type curves under equal-width and unequal-width channel sand layers (Figure 2), it can be seen that there are three stages of flow rate decline under equal-width channel sand layers (unsteady flow stage, transitional flow stage, and boundary flow stage), and the flow rate decline under unequal-width channel sand layers has five stages (I is early stage of unstable flow, II is middle stage of unstable flow, III is late stage of unstable flow, IV is transitional flow stage, and V is boundary flow stage). Among them, the middle stage of unsteady flow (II) is the transitional flow caused by unequal-width sand layers and is also a diagnostic window for judging whether the width of each channel sand layer is equal.

The physical mechanism of the occurrence of additional flow states (II) during the combined harvest of unequal-width river sand is in the superposition and interference of boundary effects. Layers with smaller widths will reach the quasi-steady state more quickly and begin to yield decreases, while layers with larger widths are still in the mid-stage of unstable flow. This asynchronous depletion of the process of depletion between different layers produces a clear transition feature (II) on the total yield curve of the combined harvest wells, which is not present in the monowide model. From the perspective of flow mechanism and output mechanism, stage I (early stage of unstable flow) mainly reflects the superposition of independent flows of each layer; stage II (mid-stable flow) is a typical feature caused by interlayer interference, that is, the small boundary layer begins to fail while the large boundary layer is still in an unstable flow, resulting in a “step-by-step” decline in the total yield curve, which is a key window to diagnose whether the boundaries of each layer are equal; and stage III (late-stable flow) marks that all layers begin to transition to the boundary.

Therefore, the decreasing rate cannot be merely based on (q_Dd) curve for diagnosis, and the decreasing rate integral should be used in combination (q_Ddi) with the decreasing rate integral derivative (q_Ddid) curve. In particular, the q_Ddid curve, which is extremely sensitive to fluid state transitions, can more clearly show the “concave” characteristics of stage II, thereby clearly distinguishing it from stages I and III.

3.2. Sensitivity Analysis

In order to discuss the impact of differences in multiple channel sand layers on commingled production rate decline, several sand layers with larger widths (hereinafter referred to as wider channel sand layers) are set up in the multiple channel sand layers, and the widths of the remaining sand layers are the same. Taking the wide channel sand layer as the research object, the influence characteristics of the thickness, quantity, and location of the wide channel sand layer on the behavior of the rate decline were analyzed.

3.2.1. Number of Wide Channel Sand Layers

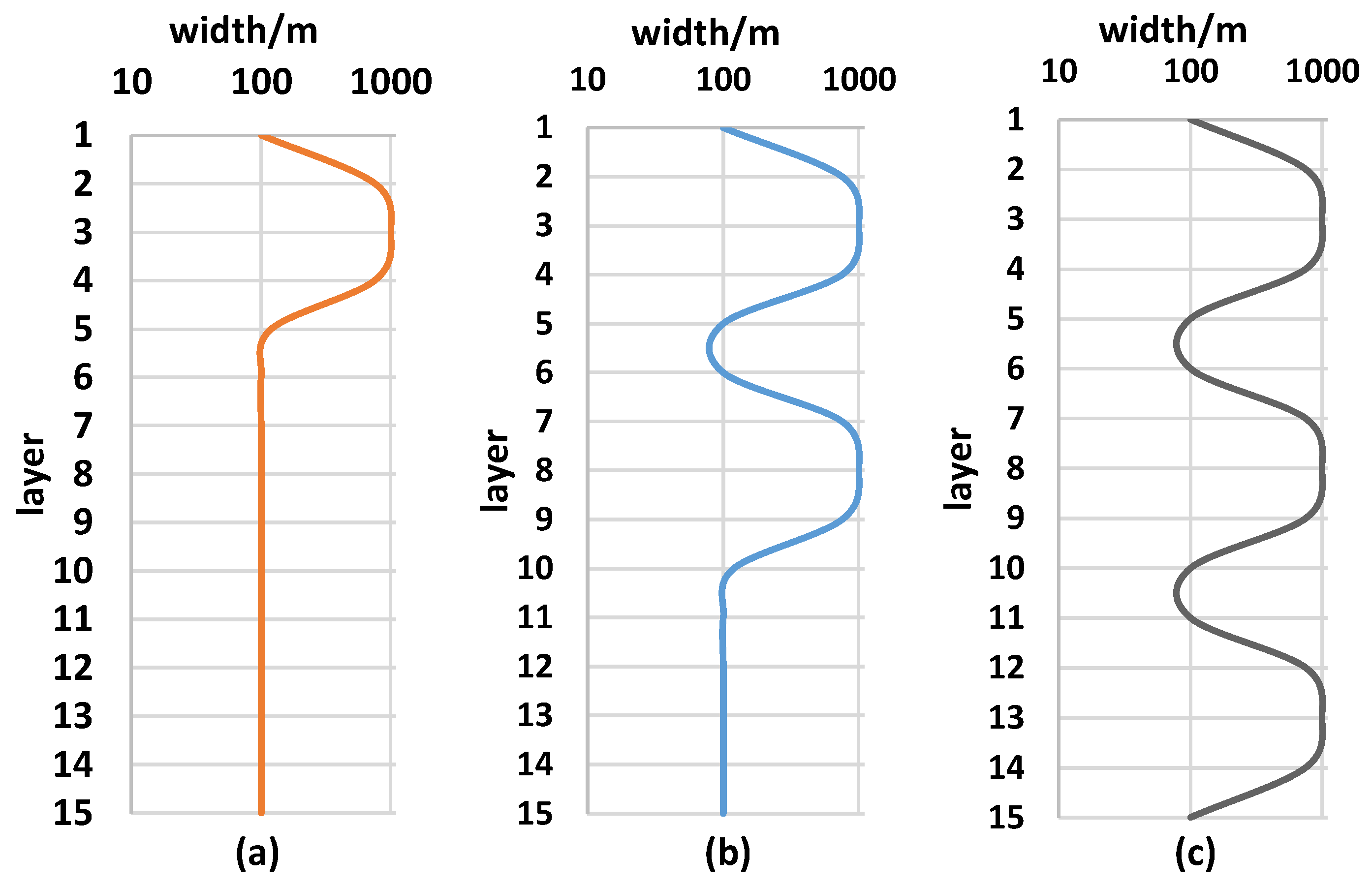
Without loss of generality, 15 channel sand layers are set for this analysis. In Figure 3, the single-wide case (Figure 3a) indicates that the 2 to 4 layers are wide channel sand, the double-wide case (Figure 3b) indicates that the 2 to 4 layers and 7 to 9 layers are wide channel sand, and the triple-wide case (Figure 3c) indicates that layers 2 to 4, 7 to 9, and 12 to 14 are wide channel sand. Among the 15 channel sand layers, the maximum width of the channel sand is 1000 m and the minimum width is 100 m. The width of the remaining channel sand is obtained by interpolation using a quadratic function.

The impact of the number of wide channel sand layers on RTA curves is shown in Figure 4. As the number of wide channel sand layers increases, the decline rate curve shifts significantly downwards in the early stage of unsteady flow (I), and the decline rate difference of dimensionless decline rate (q_Dd) in the middle stage of unsteady flow (red line) becomes smaller. The results show that the smaller the number of wide sand bodies, the worse the reservoir’s ability to stabilize production, and early production will quickly accelerate decline.

3.2.2. Position of Wide Channel Sand Layers

To discuss the impact of wide channel sand layers at different locations, a single-wide case was taken as the research object. Among the 10 commingled sand layers, the maximum width of the channel sand is 1000 m and the minimum width is 100 m. The width of the channel sand in the remaining layers is obtained by interpolation using a quadratic function. As shown in Figure 5, when layers 2 to 5 are wide channel sand, it means that the single-wide case is in the upper part. When layers 4 to 7 are wide channel sand, it means that the single-wide case is in the center part, and, when layers 6 to 9 are wide channel sand, it means that the single-wide case is in the bottom part.

The RTA curves at different positions of the wide channel sand layer are shown in Figure 6. Since the volumes of the wide channel sand layer at different locations are the same, the corresponding ESV are also the same. Therefore, there is no difference in the rate decline type curves of different positions of the wide channel sand layer under this condition, and the curves overlap.

3.2.3. Thickness of Wide Channel Sand Layers

Figure 7 shows the distribution of wide channel sand layers under different thickness proportions, where the wide channel sand thickness proportion β is the ratio of the number of wide channel sand layers to the total number of channel sand layers. β = 0.2 means that layers 5~6 are wide channel sand, β = 0.4 means layers 4~7 are wide channel sand, β = 0.6 means layers 3~8 are wide channel sand, β = 0.8 means layers 2~9 are wide channel sand, and β = 1.0 means that layers 1 to 10 are all wide channel sand. Among the 10 layers of commingled channel sand, the maximum width of channel sand is 1000 m and the minimum width is 100 m. The width of the other channel sand layers is obtained by interpolation using a quadratic function.

The RTA curves under different thickness proportions of the wide sand layers are shown in Figure 8. As the thickness proportion of wide channel sand layers increases, the dimensionless decline rate (q_Dd) (red line) and the dimensionless decline rate integral (q_Ddi) (blue line) change in the unstable flow. It moves downward in the early stage, and the slope of the curve gradually decreases in the middle stage of unsteady flow, while the dimensionless decline rate integral derivative (q_Ddid) (green line) moves downward and its volatility gradually weakens in the entire unsteady flow stage. The results show that the smaller the thickness proportion of wide channel sand layers, the weaker the stable production capacity of the tight reservoir, and it is easy to accelerate the rate decline during the unstable flow stage.

4. Field Application

The initial reservoir pressure of a gas reservoir in Sulige is 30.2 MPa, and the reservoir temperature is 101.91 °C. The main production layers drilled in Well A are H₈, S₁, and S₂. The effective thicknesses of each layer are 9.1 m, 9.2 m, and 5.1 m, respectively. The porosity of each layer is 8.11%, 8.18%, and 7.93%, respectively. The gas saturations were 46.86%, 70.89%, and 59.27%, respectively. The gas deviation factor measured in an indoor experiment under reservoir conditions is 0.921, the viscosity is 1.54 × 10⁻⁵ Pa·s, the relative density is 0.6, the volume coefficient is 1.05 × 10⁻², and the compression coefficient is 3.97 × 10⁻⁸ Pa⁻¹.

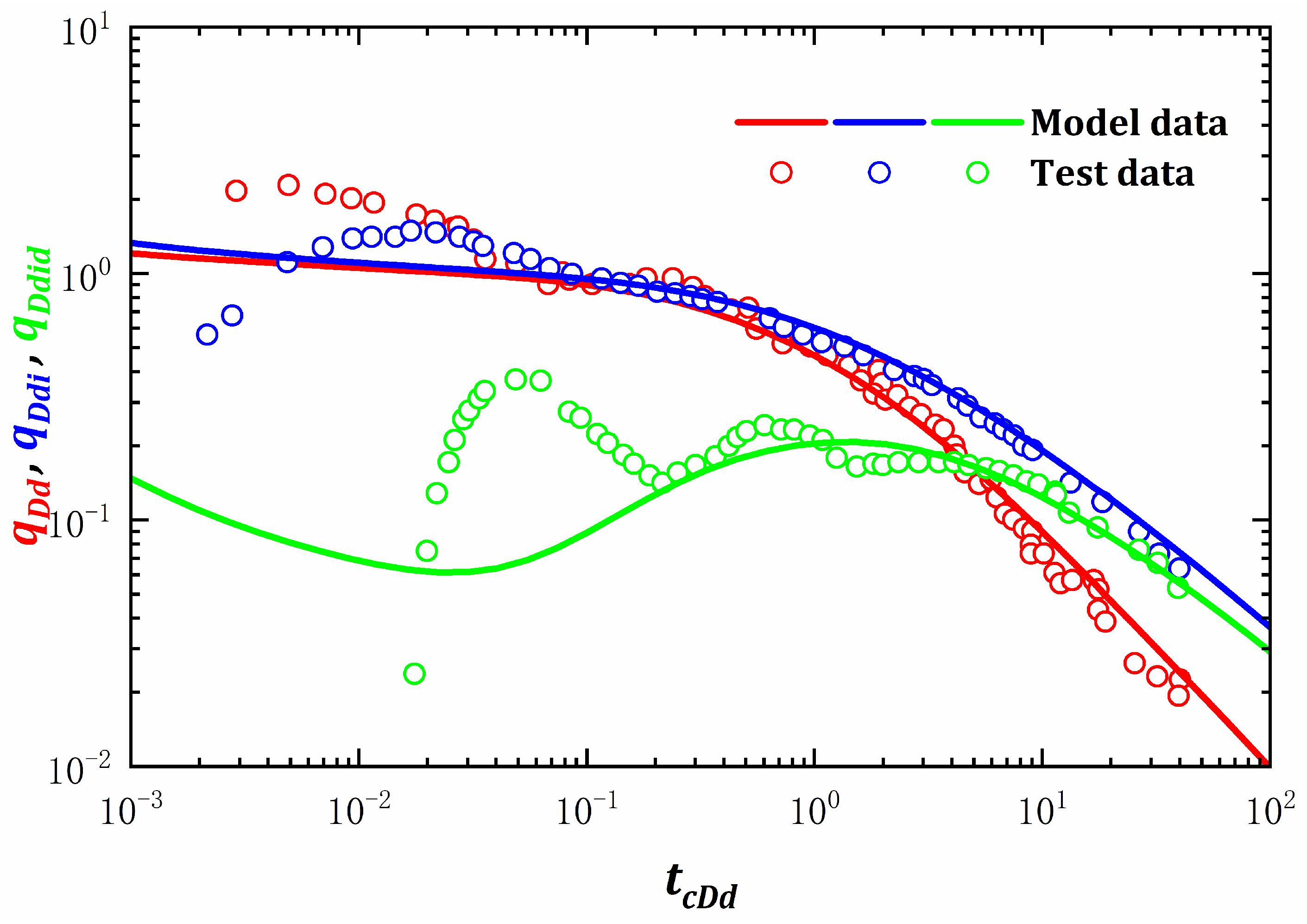
To apply this method to the decline rate analysis of this well, first, the dimensionless material balance pseudo-time and dimensionless decline rate processing are performed, and then the RTA model of the three channel sand layers is used to analyze the production data. The selection of model layers is extremely dependent on the geological data display and immediate data of the test well. The fitting curve is shown in Figure 9. According to the pressure buildup well testing data of Well A, the single layer equal-thickness homogeneous reservoir model (effective thickness value is 23.4 m) is used to explain the permeability of 0.11 × 10⁻³ μm². This RTA model explains that the permeabilities of each layer are 0.065 × 10⁻³ μm², 0.19 × 10⁻³ μm², and 0.072 × 10⁻³ μm². The equivalent permeability weighted according to thickness is 0.12 × 10⁻³ μm², which proves that the interpretation results of this RTA model are credible.

The results of this RTA model are shown in

Table 2. Case well interpretation parameter table.

Parameters	H8	S1	S2
Width (m)	280.63	428.15	312.27
Length (m)	340.16	645.46	497.68
Permeability (10−3 μm2)	0.065	0.19	0.072
Reservoir ratio	15.16%	67.72%	17.71%

. Based on the results of interpreting the width and length of the channel sand layer, the dynamically controlled reserves of Well A are calculated to be 2.75 × 10⁷ m³. S₁ is the main production layer, with the larger channel sand and higher gas saturation, and the reserve ratio is 67.72%. H₈ and S₂ are secondary production layers, with reserve ratios of 15.16% and 17.71%, respectively. As of 2023, the cumulative gas production of Well A is 1.51 × 10⁷ m³, and the recovery degree is 54.87%. Based on the interpreted permeability results, there is not much difference between H₈ and S₂, but the reserve proportion of S₂ (17.71%) is slightly larger than that of H8 (15.16%), and the thickness of S₂ (5.1 m) is significantly smaller than that of H₈ (9.1 m). Therefore, taking into account the subsequent decline in production of S₁, the main production layer, priority will be given to H₈ to carry out corresponding production stabilization measures for the secondary production layer.

Conventional well test explanations can only give the equivalent permeability of one whole wellbore. This RTA model achieves the unique solution of permeability of each single layer from the co-acquisition data for the first time. More importantly, this model inverts the boundary dimensions of each single layer, thus calculating the dynamic control reserves and their contribution rates for each layer. This information that conventional pressure recovery well tests have is completely unavailable. Although the model was developed for river sand bodies of tight gas reservoirs, its core approach (using ESV to treat irregular morphology, analyzing production dynamics) is applicable to other reservoir types with similar characteristics, such as continental tight reservoirs or separating reservoirs.

5. Conclusions and Discussion

5.1. Summary and Conclusions

Accurately characterizing the production behavior of commingled wells in tight gas reservoirs is challenging due to the complex morphology and varying boundary sizes of individual channel sand layers. This study develops a novel RTA model based on the ESV principle to address this issue. The model is specifically designed to interpret the production data from wells commingling multiple, irregularly shaped channel sands. Several conclusions and suggestions are obtained from this work.

Based on production decline theory and the principle of ESV, and taking into account the differences in the shape and boundary size of the channel sand layer in the commingled production well, a novel RTA model for commingling production well with multiple channel sand layers in tight reservoirs was established. This model and method can determine the channel sand layer boundaries of commingled production wells in tight reservoirs.

The RTA type curve shows that there are five stages of decline in the multiple channel sand commingled production wells in tight reservoirs: the early stage of unstable flow, the middle stage of unstable flow, the late stage of unstable flow, the transitional flow stage, and the boundary flow stage. Among them, the mid-stage of unsteady flow is a transitional flow pattern caused by differences in sand boundaries and is a diagnostic window for judging whether the boundaries of each channel sand layer are equal.

The number, position, and thickness of wide channel sand layers all have an impact on the flow and behavior of the rate decline of the commingled production wells in tight reservoirs. The smaller the boundary range of the channel sand layer, or the smaller the number and thickness proportion of wide channel sand layers, the worse the reservoir’s ability to stabilize production, and it is easy to accelerate the production decline rate in the early and middle stages of unstable flow.

The production decline behavior of the commingled channel sand layer is a macroscopic manifestation of microscopic flow, and the interpretation results of production decline behavior have multiple solutions. When the number and thickness of the wider channel sand layers in the commingled production well are the same, it is necessary to jointly determine the specific location of the wider channel sand layers based on comprehensive reservoir geological data.

5.2. Discussion and Prospects

Traditional models usually invert near-well parameters such as permeability, epidermal coefficient, or an equivalent comprehensive boundary. The core innovation of this model is the introduction of the concept of ESV to describe river sand of various shapes, rather than traditional circular or infinite boundaries. This allows the model to more realistically simulate the geological conditions and invert the boundary parameters of each single layer through the yield reduction curve, which cannot be achieved by traditional multilayer well test models. However, this model is mainly based on the assumptions of Section 2.1, so there are the following directions that can be studied in the future in this study.

The interlayer crossflow was not considered. The impact of interlayer crossflow can be considered in new geological models and new oil and gas seepage models to extend the application of the model in more complex, tight sandstone oil and gas reservoirs.

The boundary-specific representation of the model is not fine enough. The boundary distance values of each layer of the model are mainly represented by a simple difference value. In the future, the representation of boundary distances can be described more carefully and case analysis can be added.

The heterogeneity of thick reservoirs is not sufficiently considered. For multilayered commingled reservoirs with sedimentary rhythm, the longitudinal distribution characteristics of their permeability or flow coefficient are an important direction for future research.

There is also an insufficient number of case analyses. In the future, it is necessary to combine existing artificial intelligence analysis methods to add a large number of boundary types and boundary numbers cases. After some experience or proxy model between the stroke boundary distribution and yield characteristic values, boundary distance information can be obtained based on the yield characteristic.