Numerical Analysis of Aerodynamics and Aeroacoustics in Heterogeneous Vehicle Platoons: Impacts on Fuel Consumption and Environmental Emissions

Abstract

The systematic economic development of European Union member states has resulted in a dynamic increase in road transport, accompanied by adverse environmental impacts. Consequently, research efforts have focused on identifying technical solutions to reduce fuel and/or energy consumption. One promising approach involves the formation of homogeneous and heterogeneous vehicle platoons. This study presents the results of numerical simulations and analyses of aerodynamic and aeroacoustic phenomena generated by heterogeneous vehicle platoons composed of passenger cars, delivery vans, and trucks. A total of 54 numerical models were developed in various configurations, considering three vehicle speeds and three inter-vehicle distances. The analysis was conducted using Computational Fluid Dynamics (CFD) methods with the following two turbulence models: the k–ω Shear Stress Transport (SST) model and Large Eddy Simulation (LES), combined with the Ffowcs Williams–Hawkings acoustic analogy to determine sound pressure levels. Verification calculations were performed using methods dedicated to environmental noise analysis, supplemented by acoustic field measurements. The results conclusively demonstrate that vehicle movement in specific platoon configurations can lead to significant fuel and/or energy savings, as well as reductions in harmful emissions. This solution may be implemented in the future as an integral component of Intelligent Transportation Systems (ITSs) and Intelligent Environmental Management Systems (IEMSs).

1. Introduction

Transport has been an integral part of human civilization since its inception. Alongside communication, it constitutes a vital sector of the economy by enhancing the utility of goods through their spatial mobility. Moreover, transport plays a fundamental role in human mobility, thereby influencing personal development, health, and recreational activities. The transport sector is closely interlinked with other economic sectors; its advancement fosters overall economic growth, while underdevelopment in either domain can hinder progress in the other.

Road transport, characterized by its high flexibility, has experienced significant expansion. However, its efficiency is moderate, particularly when considering its substantial environmental impact. This inefficiency stems from the relatively low payload capacity of vehicles, the high energy consumption inherent to road transport, and the considerable capital investment required for constructing transport infrastructure, including roadways, fuel stations, and maintenance facilities. Despite these limitations, road transport remains a critical component of the global economy and plays a pivotal role in European integration, facilitating the free movement of people, goods, and services.

Statistical analyses were specifically conducted for the years 2021 [1] and 2022 [2], reflecting the transitional period following the COVID-19 pandemic and the renewed armed conflict in Ukraine commencing on 24 February 2022. Furthermore, in 2021, comprehensive road noise monitoring and acoustic mapping were performed in Poland, with subsequent assessments planned for 2026.

Transport contributes approximately 5% to the European Union’s gross domestic product (GDP) and employs over 10 million individuals across Europe. The transport system is essential for European enterprises and global supply chains. However, transport activities impose significant external costs on society, including greenhouse gas emissions, environmental pollution, noise, road traffic accidents, and congestion.

The European Union’s road transport policy aims to stimulate economic growth by supporting the development of a modern infrastructure network that facilitates safer and more efficient travel. Concurrently, the policy promotes sustainable and digital innovations. Among EU member states, the most extensive motorway networks are observed in Spain (15,860 km), Germany (13,155 km), Italy (6978 km), Portugal (3065 km), the Netherlands (2790 km), Sweden (2185 km), and Hungary (1860 km). Poland’s road network is undergoing systematic expansion; by the end of 2021, the total length of public roads reached approximately 430,000 km. Motorway length increased by 48.3 km compared to 2020, totaling 1760.5 km. This corresponds to 5.6 km of motorway per 1000 km² of national territory and 4.6 km per 100,000 inhabitants. Expressways (both single and dual carriageways) extended by 246.4 km, reaching 2794.9 km by the end of 2021. In 2022, Poland recorded the highest motorization rate within the EU, with 687 vehicles per 1000 inhabitants, surpassing Luxembourg (681) and Italy (675).

Motorways and expressways in the EU are also heavily utilized for freight transport. In 2022, the total road freight transport volume remained stable relative to 2021, at approximately 1920 billion ton-kilometers (tkm). Poland led in freight transport volume with 385,089 million tkm, followed by Germany (303,948 million tkm) and Spain (266,724 million tkm). Regarding the weight of goods transported, Germany (3,060,964 thousand tons), France (1,631,139 thousand tons), and Poland (1,599,513 thousand tons) ranked highest.

The transport system’s primary vehicle categories include freight vehicles with maximum permissible weights both up to and exceeding 3.5 tons. The largest registrations of vehicles up to 3.5 tons were reported in France (4,868,148), Spain (4,696,170), Germany (3,018,598), Italy (3,774,192), and Poland (2,905,731). For heavy-duty vehicles exceeding 3.5 tons, the highest numbers were observed in Poland (728,465), Germany (530,994), Italy (515,850), Spain (349,197), and France (307,433). Additionally, over 253 million passenger cars are registered across the EU, with the highest concentrations in Germany (48,540,878), France (39,822,723), Italy (38,738,590), Poland (25,869,804), and Spain (24,913,132), collectively accounting for 70% of the EU’s passenger car fleet.

Operational analysis for 2022 indicates a 1.0% increase in international road freight transport performance (measured in ton-kilometers) compared to 2021, representing 25.4% of total EU road freight transport. This segment has demonstrated robust growth since 2021 relative to prior years. Conversely, cabotage transport decreased by 8.9%, while national transport and cross-trade operations each declined marginally by 0.1% in the same period.

In Poland, revenue generated from road transport services across all transport units increased by 9.8% in 2021 compared to 2020, reaching PLN 201.5 billion. The private sector experienced a 10.1% revenue growth, whereas the public sector’s revenue increased by 7.3%.

In 2021, the road transport sector was predominantly powered by gas/diesel oil (66.5%) and petrol (24.0%). Liquefied petroleum gas (LPG) constituted a minor share of fuel consumption in this sector, accounting for approximately 2%, with considerable variation in its use across different countries. The uptake of alternative fuels in road transport has gradually increased, driven by key European Union policies, technological advancements, and evolving consumer preferences. In 2021, renewable energy sources and biofuels comprised 6.4% of actual fuel consumption within the EU road transport sector. Despite a gradual increase over recent years, electricity maintained a marginal role, representing only 0.2% of total consumption.

An analysis of road traffic in Poland was conducted using data from the General Traffic Measurement, the National Traffic Model for the road network, and the Central Statistical Office’s survey on freight vehicle transport activity. In 2021, the total vehicle-kilometers traveled on Poland’s public road network reached 248.6 billion, reflecting an 8.8% increase relative to 2020. Passenger cars dominated traffic, contributing 203.3 billion vehicle-kilometers—also an 8.8% increase over the previous year. Traffic volumes increased for other vehicle categories as well: trucks by 8.4% (including vehicles over 3.5 tons gross vehicle weight by 8.0%), buses by 9.0%, and motorcycles by 8.5%.

Vehicles registered in Poland accounted for 94.2% of total traffic on the national public road network (234.1 billion vehicle-kilometers), while foreign-registered vehicles comprised 5.8% (14.5 billion vehicle-kilometers). Passenger cars predominated in both groups, constituting 82.5% of Polish vehicles and 70.0% of foreign vehicles. Trucks represented the second-largest category, accounting for 15.1% of Polish vehicles and 29.8% of foreign vehicles.

Traffic increased across all road categories in 2021, with the most pronounced growth observed on voivodeship roads (10.7%). The highest traffic volume was recorded on national roads, totaling 98.6 billion vehicle-kilometers—an 8.4% increase compared to 2020.

By the end of 2021, the number of registered passenger cars in Poland reached 25.9 million, marking a 3.0% increase from the previous year. Of these, 21.4 million vehicles were up to 30 years old, representing a 1.8% increase since 2020. The proportion of passenger cars aged up to 5 years slightly decreased from 11.2% in 2020 to 11.1% in 2021, whereas the share of vehicles aged 16–30 years increased marginally from 43.2% to 43.3%, and those over 30 years increased from 16.4% to 17.4%.

The registered truck population (including light trucks) totaled 3.6 million at the end of 2021, a 3.0% increase over the previous year. Among these, 2.8 million vehicles were up to 30 years old. The age distribution of trucks remained consistent with the prior year: 11.5% were up to 5 years old, 37.5% were between 16 and 30 years old, and the proportion of trucks over 30 years increased from 21.9% to 22.6%. Slight increases were noted in trucks with payload capacities below 1.5 tons (from 79.7% in 2020 to 80.0% in 2021) and those with payloads of 10 tons or more (from 4.1% to 4.2%). Regarding engine types, 69.7% of trucks were diesel-powered (compared to 68.8% in 2020), 16.8% utilized gasoline engines (17.4% in 2020), and 4.7% were LPG-powered (4.9% in 2020).

Pollutant emissions from road transport primarily originate from fuel combustion within vehicle engines, as well as from tire and brake pad wear and the resuspension of road surface dust. The magnitude of emissions is influenced by vehicle fleet size and age, road surface conditions, and traffic management. The principal gaseous pollutants emitted by road transport include carbon dioxide (CO₂) at 61,362 thousand tons, carbon monoxide (CO) at 288.5 thousand tons, nitrogen oxides (NOₓ) at 204.1 thousand tons, non-methane volatile organic compounds (NMVOCs) at 34.8 thousand tons, and particulate matter (PM) at 20.2 thousand tons. These pollutants exert substantial adverse effects on human health and ecosystems through air quality degradation. In 2020, road transport accounted for approximately 20% of total CO₂ emissions, 13% of CO emissions, 34% of NOₓ emissions, 5% of NMVOCs, and 4% of total suspended particulates (TSPs) in Poland.

Despite the implementation of increasingly stringent emission standards for passenger cars, trucks, and buses, as well as ongoing developments in road infrastructure, emissions from road transport remain one of the most critical factors adversely affecting air quality—particularly in densely populated urban areas.

Road traffic constitutes the most significant source of noise pollution for humans, primarily due to its widespread occurrence and persistent impact during both daytime and nighttime hours. Noise monitoring, based on acoustic mapping, revealed that in 2021, road traffic noise posed a substantial threat mainly within urbanized regions and affected an increasing number of residents. Of the nearly 300 km of roads monitored in 2021, approximately 33% exhibited noise levels up to 60 dB (decibels), which corresponds to permissible daytime noise limits for residential areas adjacent to roadways. Conversely, on more than 67% of the monitored roads, noise levels exceeded these regulatory thresholds.

For several years, road traffic noise levels in urban centers have consistently remained high, typically ranging between 70 and 80 dB. In 2021, the highest proportions of streets where noise levels surpassed the maximum permissible value of 60 dB (relative to the total length of monitored streets) were recorded in cities within the voivodeships of Lubelskie, Lubuskie, Łódzkie, and Małopolskie (all at 100%), as well as Dolnośląskie and Warmińsko-Mazurskie (both at 93%). The lowest exceedance rates were observed in Mazowieckie (25%) and Pomorskie (37%).

The substantial volume of vehicles operating on the road network presents significant challenges regarding energy consumption reduction and environmental protection. The adoption of sustainable and innovative transport modes is pivotal to achieving the climate and energy objectives set by both Poland and the European Union. These initiatives primarily aim to support transport systems in addressing their principal—often conflicting—challenges, which include enhancing the competitiveness of the European transport sector vis-à-vis rapidly expanding global markets; improving infrastructure quality; developing modern vehicle technologies; alleviating traffic congestion that impairs road transport efficiency; reducing fossil fuel consumption, notably diesel and petrol; achieving a 60% reduction in emissions by 2050 relative to 1990 levels; and pursuing further emission reductions beyond that target.

The combination of a large vehicle fleet and a relatively underdeveloped network of highways and expressways poses a significant challenge in identifying and implementing technical solutions focused on improving traffic safety, minimizing energy consumption, and mitigating adverse environmental impacts. One potential approach involves the formation of homogeneous and heterogeneous vehicle platoons with optimized structural configurations, inter-vehicle spacing, and speeds, supported by advanced vehicle fleet control and management systems.

The type of platoon—homogeneous or heterogeneous—determines significant differences in driving dynamics, safety, energy efficiency, as well as aerodynamic and aeroacoustic performance. Homogeneous platoons, composed of vehicles with similar technical parameters, enable more consistent and predictable driving. Uniform acceleration, braking, and control system responses help reduce speed fluctuations and enhance string stability. Cut-in and cut-out maneuvers are executed more smoothly, and vehicles can maintain shorter, constant gaps. As a result, not only does traffic throughput improve, but so do aerodynamic and aeroacoustic conditions—airflow around the platoon becomes more orderly, reducing drag and leading to substantial fuel or energy savings.

Heterogeneous platoons, composed of vehicles with varying technical parameters such as engine power, acceleration, braking performance, or mass, exhibit non-uniform responses to speed changes, which complicates the maintenance of stable inter-vehicle gaps and increases susceptibility to string instability. Vehicle diversity also affects the execution of cut-in and cut-out maneuvers, leading to temporary slowdowns and fluctuations in traffic flow stability. The flexible spacing required in such platoons limits aerodynamic benefits, while speed variations increase fuel or electric energy consumption and elevate the risk of collisions. From an aerodynamic and aeroacoustic perspective, differences in vehicle body shapes and larger inter-vehicle gaps generate airflow disturbances and vortices, resulting in higher levels of aerodynamic noise, perceptible both inside the vehicles and in the surrounding environment.

Owing to the rapid development of science and technology, as well as proposed regulatory changes in the EU and in the world’s most advanced countries, intensive research is being conducted on homogeneous and heterogeneous platoons. A fundamental transformation is expected with the introduction of the 6G standard and the adoption of advanced methods and techniques based on artificial intelligence, modern powertrains, and control systems. Selected studies in this field will be presented in the subsequent sections of this work.

The authors focused on numerical aerodynamic and aeroacoustic analyses of heterogeneous platoons and their impact on fuel consumption and environmental effects. The main contributions of this work are summarized below. Within the scope of the study:

• Aerodynamic analyses were performed on 54 developed and implemented geometric–numerical models of heterogeneous platoons, composed of combinations of passenger cars, light commercial vehicles, and heavy trucks.
• Fuel consumption was determined for individual vehicles as well as for all 54 heterogeneous platoon combinations at three different speeds and three inter-vehicle distances.
• Aeroacoustic analyses were conducted at three speeds using the Ffowcs Williams–Hawkings analogy and geometric methods for nine selected configurations of heterogeneous platoon models and individual vehicles.
• Additionally, for speeds ranging from 50 to 140 km/h, at 10 km/h intervals, the percentage fuel consumption of selected heterogeneous platoon models was estimated in comparison with vehicles driving outside the platoon, along with their acoustic impact on the environment, using geometric methods.

2. Selected Aspects of Vehicle and Vehicle Platoon Aerodynamics and Aeroacoustics

2.1. History of Road Vehicle Aerodynamics

The history of road vehicle aerodynamics dates back to the late 19th century [3]. Early designers often drew inspiration from shapes proven in marine engineering and airship design. The earliest known vehicle designed with aerodynamic efficiency in mind was the electric car built by Camille Jenatzy, which featured a torpedo-shaped body. This vehicle was the first to exceed 100 km/h, achieving a record speed of 105.9 km/h on 29 April 1899. In 1913, at the behest of Count Marco Ricotti, a vehicle with an airship-inspired design was constructed on an Alfa Romeo chassis, incorporating a fully enclosed passenger cabin.

Significant advancements in vehicle aerodynamics occurred following World War I. Beginning in 1919, Rumpler, renowned for the “Rumpler Taube” aircraft, developed several vehicles he termed “tear-drop shaped cars.” When viewed from above, these vehicles resembled airfoils. To optimize the otherwise narrow streamlined tail section, Rumpler positioned the engine at the rear of the vehicle. In 1922, wind tunnel tests on a 1:7.5 scale model were conducted at the Aerodynamic Laboratory in Göttingen. Results indicated that the drag of the Rumpler vehicle was approximately one-third that of contemporary competitors. However, minimizing aerodynamic drag was not Rumpler’s principal design objective; promotional materials from the era emphasized that his car generated substantially less dust and mud than others. Wind tunnel testing of the original Rumpler car in 1979 yielded a drag coefficient (C_d) of 0.28 and a frontal area (A) of 2.57 m². Notably, such a low drag coefficient was not matched in production vehicles until decades later, exemplified by the 1986 Opel Omega. The aerodynamic performance of the Rumpler car is especially remarkable considering its fully exposed wheels.

Contemporaneous to Rumpler, Jaray initiated aerodynamic vehicle design research, publishing an article entitled “The Streamlined Car, a New Shape for the Automobile Body.” In 1938, wind tunnel testing of Jaray’s designs—initially started by Klemperer in 1921–1922—was resumed under Ludwig Prandtl’s supervision in Göttingen. Jaray’s vehicle body featured two horizontal profiles: a primary main profile and a secondary profile starting from the base of the windshield. Consistent with Jaray’s design principles, the secondary profile had a rounded top, resulting in the so-called “Lange car” shape. Model testing demonstrated a drag coefficient as low as 0.14, with subsequent measurements on a 1:5 scale model by the author and collaborators confirming values near 0.16. These models, however, did not include details such as chassis components, wheel arches, or window recesses.

In 1939, the French manufacturer Mauboussin adopted a similar aerodynamic approach for the “Mistral,” which was based on an airfoil-shaped outline but featured a vertical trailing edge. A prominent rear “fin” enhanced stability in crosswinds at the expense of interior space.

In the early 1930s, Lay conducted systematic aerodynamic studies at the University of Michigan, modifying front and rear vehicle geometries to isolate aerodynamic phenomena. His research revealed a strong interaction between flow fields at the vehicle’s front and rear. The low drag observed in long-tailed models was contingent upon flow adherence over the front body surface. However, Lay’s segmented model, constructed from assembled parts with parallel sidewalls and sharp corners, exhibited high drag, limiting the applicability of his findings.

Similar insights were previously reported by Dornier in 1920, based on measurements of airfoil sections with truncated trailing edges. In 1934, engineer Wunibald Kamm introduced the “Kamm-back” design, which truncated the vehicle’s long tapered tail. This approach offered increased rear interior volume while maintaining a reduced drag coefficient. The low drag was attributed to attached flow that separated at the vehicle’s rear over a significantly reduced cross-sectional area.

The first passenger car featuring a Kamm-type rear was the “Everling,” built in 1938. Wunibald Kamm subsequently developed several “K-type” vehicles, culminating in the refined K5 model, which was suitable for series production. However, plans for mass production were halted by the outbreak of World War II in 1939.

The “streamlined shapes” of automobile bodies developed in the early 20th century were infrequently employed in mass vehicle production. During that period, fuel consumption was not prioritized over aesthetic considerations and prevailing styling trends. However, the 1973 oil crisis marked a pivotal shift in design priorities. The reduction in oil supply, escalating fuel prices, and growing concerns regarding the depletion of natural resources underscored the critical importance of reducing aerodynamic drag in vehicle design. Consequently, the late 1970s and 1980s are recognized as a breakthrough era for the mass production of aerodynamic vehicles. Leading automotive manufacturers, including Audi, BMW, Volkswagen, Citroën, Opel, SAAB, and Ford, dedicated efforts to refining streamlined body geometries. Notable reductions in drag coefficients (C_d) were achieved during this period; for example, the Volkswagen Passat’s Cd decreased from 0.41 in 1978 to 0.27 in 1996, while the 1989 Opel Calibra attained a C_d of 0.26, and the 1982 Citroën GSA X3 exhibited a C_d of 0.34 [4,5,6].

2.2. State of the Art

Research aimed at drag reduction continues to advance, employing a variety of strategies. Aerodynamic resistance can be minimized through both shape optimization and the integration of auxiliary body components. Elsayed [7] investigated three methods for enhancing vehicle aerodynamics: the installation of a horizontal rear roof spoiler, the modification of the roof surface with specialized grooves, and the addition of vertical side fins at window level. These interventions yielded reductions in aerodynamic drag force of 15.87%, 19.82%, and 22.67%, respectively. Vedrtnam et al. [8] explored passive aerodynamic devices, utilizing vortex generators (VGs) and a rear spoiler to manipulate airflow around the vehicle. Twenty-six configurations were examined, with varying wing angles, VG applications, and crosswind directions. The most effective configuration produced a drag coefficient reduction of up to 68.18%.

A comprehensive discussion, along with the presentation of results concerning the potential reduction in vehicle aerodynamic drag and drag coefficients, is provided in [9]. The authors presented various solutions aimed at minimizing aerodynamic drag in heavy-duty vehicles. It was emphasized that approximately 75% of the total aerodynamic drag generated by road trains is associated with the trailer or semi-trailer, which justifies intensive research efforts to minimize this effect. The publication identifies several structural components affecting the aerodynamics of heavy-duty vehicles and presents the potential fuel savings resulting from their implementation. Among other aspects, roof deflectors and fairings, the front bumper, windshield, external mirrors, and the possibility of replacing them with camera-based systems were discussed. Attention was also drawn to the significant influence of the vehicle underbody shape, chassis and axle enclosures, as well as wheel covers and aerodynamic mudflaps.

The research results showed that a rear deflector can reduce aerodynamic drag during flat-road driving at 90 km/h by approximately 2%, side skirts by 3.4%, and their combined use can achieve a reduction of around 6.5%. In addition to passive solutions, the Plasma Stream technology was presented, based on active airflow control using plasma actuators developed at the University of Notre Dame. This system demonstrates high efficiency and enables fuel consumption reductions of 7–10% at speeds exceeding 100 km/h.

Intensive research and development efforts are ongoing to develop novel solutions employing both passive and active systems to reduce the aerodynamic drag coefficient in electric vehicles, including passenger cars and trucks. A notable example is provided by Tesla, as reported in a study on the Tesla Semi truck [10]. Simulations were carried out using computational fluid dynamics (CFD) methods, with the geometric model encompassing the cabin shape, windshield, side fairings, and trailer. Tests were conducted at typical highway speeds (80 km/h and 100 km/h) under flow conditions representative of unobstructed open environments. The results of the numerical analyses demonstrated a significant reduction in the aerodynamic drag coefficient to a value of C_d = 0.339.

Active aerodynamic systems have been described by Piechna [11], who presented intelligent technologies that adapt aerodynamic characteristics dynamically in response to vehicle speed. Additional parameters such as acceleration, yaw angle, steering angle, and brake pressure are also incorporated. These adaptive systems aim to enhance aerodynamic efficiency, contributing to decreased fuel consumption, improved safety, and greater driving comfort.

A comprehensive review of contemporary drag reduction methodologies was conducted by Szodrai [12], covering both passive and active aerodynamic enhancements. The study focused on two vehicle categories: hatchbacks and notchbacks. An alternative approach to road vehicle aerodynamics was proposed by Kurec et al. [13], who analyzed an active aerodynamic braking system. By deploying strategically positioned plates on the hood and roof of a passenger vehicle, additional aerodynamic forces were generated to increase drag and downforce. The enhanced drag serves to decelerate the vehicle, while increased downforce improves traction, thereby augmenting driving safety.

The aforementioned studies primarily address drag reduction at the level of individual vehicles, achieved via modifications to body geometry and the implementation of passive or active aerodynamic systems. A fundamentally different approach involves exploiting the aerodynamic wake generated behind vehicles to reduce drag without altering the vehicles themselves. This strategy focuses on optimizing the aerodynamics of vehicle groups, or platoons. A vehicle platoon consists of multiple road vehicles traveling consecutively in a single lane, maintaining uniform speed and prescribed inter-vehicle distances. When all vehicles in a platoon share identical body types, the platoon is classified as homogeneous; if the vehicles differ in body type, the platoon is heterogeneous.

Aerodynamic interactions between vehicles have been investigated extensively over many years. These studies vary with respect to vehicle geometries analyzed, inter-vehicle spacing, and platoon speeds. Zabat et al. [14] examined homogeneous platoons composed of two to four passenger cars. The experiments were conducted in a wind tunnel using scaled models, each vehicle measuring 0.6 m in length, with inter-vehicle distances ranging from zero to three vehicle lengths. Drag coefficients were measured at an airflow velocity of 25 m/s. Schito et al. [15] analyzed homogeneous platoons of one to six vehicles, each 4 m in length, focusing primarily on the drag coefficient. Tests were performed at three inter-vehicle spacings: 2, 3, and 4 m. The same study also investigated three heterogeneous platoons configured as truck–hatchback–sedan, van–hatchback–sedan, and sedan–hatchback–van. Each platoon consisted of three vehicles with differing body types, maintaining spacings between 0.5 and 3 m. The test velocity was set at 30 m/s. In all configurations, the greatest reduction in drag coefficient was observed for the vehicle positioned centrally within the platoon; notably, in every case, the middle vehicle was the smallest.

Le Good et al. [16] performed scaled wind tunnel tests on homogeneous platoons comprising two to five passenger vehicles. At sufficiently small inter-vehicle distances, an adverse effect was noted: an increase in aerodynamic drag induced by platoon formation. The majority of research has focused on platoons exclusively composed of heavy-duty vehicles. Browand et al. [17] conducted on-road experiments with two trucks at spacing intervals from 3 to 10 m and speeds of 88.5 km/h. Fuel consumption decreased by 5–10% for the lead vehicle and by 10–12% for the following vehicle. Lammert et al. [18] carried out similar on-road tests in 2014, examining the influence of both inter-vehicle spacing (6 to 22.5 m) and platoon speed on fuel consumption reduction. Humphreys et al. [19], in 2016, investigated a homogeneous platoon of two trucks and additionally examined the effect of lateral offset of one vehicle from the centerline on aerodynamic drag.

In 2018, several studies addressed vehicle platoons. Siemon [20] investigated a homogeneous platoon of four trucks as well as a heterogeneous platoon also composed of four trucks differing in cargo type. Vohra [21] conducted experiments with two- and three-truck platoons. Gnatowska and Sosnowski [22] studied platoons based on vehicles modeled with Ahmed body geometry.

Jaffar et al. [23] employed machine learning techniques to predict drag coefficients of vehicle platoons. Their research focused on homogeneous platoons of two, three, and four vehicles, applying five algorithms: support vector regression, polynomial regression, linear regression, and two neural network models. Experimental data from [24] served as the training dataset. Additionally, Computational Fluid Dynamics (CFD) simulations were conducted for the same platoon configurations. The study demonstrated the utility of supervised learning as a complementary approach for analyzing vehicle aerodynamic properties.

Kaluva et al. [25] analyzed drag coefficients for two types of homogeneous platoons: autonomous transport minibuses (Dynamic Autonomous Road Transit, DART) and notchback passenger cars. Aerodynamic parameters were evaluated for individual vehicles and for platoons of two to seven vehicles. CFD simulations were performed using ANSYS Fluent Academic Research with an unstructured mesh. Results showed an average drag coefficient reduction of 23% for the DART platoon and 24% for the passenger car platoon.

Robertson et al. [26] reported experimental research on homogeneous platoons using 1:20 scale truck models to simulate convoys of eight vehicles. The setup replicated vehicle motion relative to the ground. Three inter-vehicle distances—0.5, 1, and 1.5 vehicle lengths—were tested at 25 m/s. At the smallest spacing, an average drag coefficient reduction per vehicle of 48% was achieved. He et al. [27] performed similar simulations on homogeneous platoons using the Detached Eddy Simulation (DES) turbulence model to analyze flow behavior and aerodynamic coefficients. Their results aligned well with experimental data.

Despite the considerable benefits demonstrated by the aforementioned studies, it is essential to consider existing legal regulations. The provisions of the Polish Road Traffic Act [28] dated 20 June 1997, impose specific restrictions on the operation of vehicle platoons. Article 32, paragraph 1, stipulates the maximum number of vehicles permitted in a convoy: the number of passenger cars traveling in an organized platoon shall not exceed ten vehicles, whereas for trucks, the limit is five vehicles. According to the traffic code, a van may be classified into one of two categories depending on its intended use: it is categorized as a passenger car if designed to transport up to nine persons, or as a mixed-use vehicle (cargo-passenger) if structurally intended to carry cargo and between four and nine persons, including the driver. Accordingly, the maximum number of vans permitted in an organized convoy may be either ten or five vehicles, respectively.

A separate regulation defines the allowable inter-vehicle distance. Article 19, paragraph 2, section 3 of the Road Traffic Act mandates that the driver “maintain a distance sufficient to avoid collision in the event of braking or stopping of the vehicle ahead.” Section 3, applicable to non-urban areas, requires that vehicle combinations exceeding seven meters in length “maintain a distance from the preceding motor vehicle sufficient to allow other overtaking vehicles to safely enter the gap between them.” Section 3a specifies the minimum permissible distance between vehicles on motorways and expressways: this distance, expressed in meters, must be no less than half the numerical value of the vehicle’s speed in kilometers per hour.

The previously cited studies indicate that aerodynamic drag reduction is achievable only at inter-vehicle distances shorter than those permitted under the current “Road Traffic Act.” A potential solution may reside in the deployment of modern intelligent systems that facilitate vehicle control and inter-vehicle communication. One such system is the Vehicle-to-Vehicle (V2V) communication system, which enables vehicles within a convoy to maintain precisely defined spacing. This capability is primarily realized through the synchronized acceleration and braking of all vehicles. A convoy operating under such systems is commonly referred to as a “platoon”.

The principal advantages of platooning include increased fuel efficiency [29,30], reduced emissions of harmful pollutants [31,32], enhanced driving comfort and traffic flow [33], decreased road space utilization [34,35,36], and improved road safety [37,38,39]. Owing to these benefits, numerous international projects have been initiated that exploit the platooning concept. Initiatives such as Safe Road Trains for the Environment (SARTRE) [40,41] and the Grand Cooperative Driving Challenge (GCDC) [40] primarily focus on heterogeneous vehicle platoons, whereas PATH [40,42], KONVOI [43], Energy ITS [40], SCANIA [40], COMPANION [44], and the European Truck Platoon Challenge (ETPC) target homogeneous platoons predominantly composed of trucks.

Directions for future research and near-term developments in platooning have been outlined by Sivanandham et al. [45]. Beyond emphasizing the substantial advantages of organized road transport, the authors highlight current limitations impeding the widespread adoption of these technologies. Another intensively explored research area involves the implementation of advanced control and communication systems for truck platoons. The most widely utilized controller currently is the Cooperative Adaptive Cruise Control (CACC) system—an enhanced variant of Adaptive Cruise Control (ACC). Existing CACC systems employ short-range wireless communication [46]; however, ongoing research investigates alternative communication protocols, including Wi-Fi [47], LTE and 5G [48,49,50], as well as cloud computing technologies [51]. Reference [52] provides a comprehensive characterization of selected CACC controllers. In recent years, numerous novel approaches have been proposed for vehicle communication and automated control system design, including consensus-based controllers [53,54], model predictive control [55,56], sliding mode control [57,58,59,60,61,62], and adaptive controllers [63,64].

In recent years, issues related to the formation of vehicle convoys—comprising both automated and autonomous vehicles (CAVs—Connected and Automated Vehicles) and conventional human-driven vehicles (HDVs—Human-Driven Vehicles)—have attracted increasing attention from the scientific community. Control strategies for such mixed traffic platoons have been widely studied; however, most research has focused on fixed-structure formations, where the spatial arrangement of CAVs and HDVs is predetermined. Representative configurations examined in the literature include HDV-HDV-CAV [65], CAV-HDV-...-HDV-CAV [66], HDV-CAV-HDV [67], HDV-CAV-HDV-CAV-HDV [68], and CAV-CAV-...-CAV-HDV [69].

Nevertheless, the structural configuration of a convoy and the spatial positioning of CAVs within the platoon play a critical role, significantly affecting traffic safety, energy efficiency, and the overall throughput of the transportation system, as shown in studies [70,71,72]. Additionally, the dynamics of platoon formation—particularly in response to highway and urban traffic conditions—have also been addressed in recent research [73,74,75].

This topic has been further investigated in subsequent studies. Jin et al. [76] examined the influence of CAV positioning on energy efficiency and traffic throughput in mixed vehicle platoons by analyzing three scenarios: a random distribution of CAVs and HDVs, an alternating configuration, and a layout in which all CAVs are concentrated in the central segment of the platoon. In a related study, Li et al. [77] assessed the impact of platoon formation on stability, utilizing an objective function optimization framework for three CAV arrangement patterns: uniform, random, and clustered.

Both studies assumed homogeneous and predefined spatial distributions of CAVs and HDVs. However, in real-world traffic environments, vehicle fleet heterogeneity and the stochastic behavior of HDV drivers introduce complex interactions that may considerably affect the performance of mixed platoons. This issue was addressed in [78], where the authors proposed a heterogeneous platoon model comprising both CAVs and HDVs. Their findings demonstrated that platoon formation structure substantially influences both energy efficiency and traffic throughput—variations in formation configuration resulted in changes in energy consumption ranging from 1.24% to 26.27%, and in traffic throughput from 0.49% to 29.47%.

The development of efficient driving strategies for mixed vehicle platoons encompasses, among other aspects, the optimization of longitudinal and lateral trajectories for the entire vehicle ensemble. Under highway conditions, the trajectories of autonomous vehicles (CAVs—Connected and Automated Vehicles) are formulated by incorporating the heterogeneous behaviors of conventional human-driven vehicles (HDVs—Human-Driven Vehicles), including variations in driving styles [65], lane-changing maneuvers [79], and on-ramp merging processes [80].

Owing to the increased complexity of urban environments—characterized by factors such as traffic signalization and fluctuating traffic density—the management of mixed vehicle platoons in urban scenarios presents considerable challenges. In response, Wang et al. [81] and Shi et al. [66] proposed control frameworks for mixed traffic at signalized intersections, targeting the minimization of both energy consumption and travel time. It is important to note, however, that these investigations primarily focused on optimizing CAV trajectories while neglecting the influence of HDV presence within the objective function. As a result, the potential for energy consumption reduction in fully mixed platoons remains substantially underutilized.

To address this gap, Yang et al. [82], Wang et al. [67], and Li et al. [68] developed eco-driving strategies for mixed platoons that explicitly consider the effect of CAV driving behavior on the dynamics and energy consumption of trailing HDVs. These methodologies aim to improve the overall energy efficiency of the entire platoon.

In the realm of platoon control, novel strategies have been introduced based on centralized, distributed, and hybrid control architectures. A notable example is the switching control strategy termed Cooperative Adaptive Cruise Platoon Control (CACPC), which primarily focuses on maintaining stability and robustness against disturbances during dynamic controller transitions [83]. Concurrently, Quadri et al. [84] developed PLATO, a dynamic multi-platoon management system leveraging 5G communication technologies and edge computing architectures. This system synergistically integrates the benefits of centralized and distributed control paradigms, facilitating reliable real-time management of a large fleet of platoons.

Furthermore, Zhang et al. concentrated on the design of robust control methodologies, emphasizing behavioral stability and resilience to stochastic disturbances. Their management of heterogeneous platoons employed a Robust Model Predictive Control (RMPC) framework [85], ensuring system adaptability under varying operational conditions.

Recent literature reports also indicate considerable research interest in the areas of maintaining constant time gaps between vehicles in a platoon, simultaneous coordination of vehicle motion within the platoon (car-following), data transmission scheduling, precise trajectory tracking, maintaining constant curvilinear spacing, and coordinated linear velocity, as well as their impact on fuel efficiency and driving comfort. These issues are discussed in detail in the studies presented below.

Study [86] addresses the determination of the time headway necessary to ensure robust string stability in platoons of connected and autonomous vehicles in the presence of V2V communication disturbances. The influence of noise in the acceleration signal transmitted from the preceding vehicle on the effectiveness of the Constant Time Headway Policy (CTHP) was analyzed. A control model was developed, utilizing both onboard sensor measurements and data from the wireless network. Conditions for controller gains and the minimum allowable time gap were derived, ensuring system stability in the presence of signal noise.

In the study [87], a new approach for joint platoon coordination and data transmission scheduling in cooperative vehicle–infrastructure systems (CVISs) using mobile edge computing (MEC) is presented. A two-level approach was proposed, comprising a mobility optimization layer to enhance fuel efficiency and a vehicle-to-infrastructure (V2I) communication layer for reliable data transmission scheduling. The developed models enable fuel consumption minimization and improved communication reliability by considering platoon mobility, channel characteristics, and application requirements. Simulation results showed that the proposed method reduces the platoon’s fuel consumption per time slot by 16.4% while improving communication reliability by a factor of 1.31 compared to conventional approaches.

The article [88] presents a novel method for platooning connected autonomous vehicles (CAVs) on curved roads, combining a longitudinal regulator based on deep reinforcement learning (DRL) with a nonlinear lateral controller. The DRL agents learn the optimal acceleration by iteratively interacting with an effective lateral controller. The use of distributed control and vehicle-to-vehicle (V2V) communication enables efficient cooperation among multiple vehicles, rapid adaptation to environmental changes, and maintenance of optimal trajectories, constant gaps, and driving comfort. Numerical experiments demonstrated the effectiveness of the method under various scenarios, including lane changes by the platoon and left turns at roundabouts.

Promising results from research on advanced technical solutions in control systems, communication, and artificial intelligence, together with anticipated changes in traffic regulations and the implementation of 6G communication, suggest that future roads will host not only homogeneous but also heterogeneous vehicle platoons, currently being tested on research proving grounds and selected road sections. The deployment of 6G communication technology, as presented in the studies listed below, is particularly promising.

Article [89] analyzes the advantages of edge computing over traditional cloud computing in critical applications requiring ultra-low latency and high reliability, such as drone networks, autonomous vehicles, telesurgery, and Augmented Reality (AR). Edge intelligence enables local processing of large datasets and complex tasks in near real time, thereby mitigating latency and data storage challenges. A case study on 6G-based edge intelligence demonstrates a significant improvement in communication latency (10–100 μs) compared to 5G (<5 ms) and 4G (<10 ms). These solutions demonstrate the potential of 6G networks to provide efficient, secure, and mobile computing infrastructure while highlighting open research challenges in this area.

Study [90] discusses the architecture, communication, resource allocation, key features, and application examples, as well as technological and non-technological challenges. It identifies key requirements and future research directions for the development of 6G Autonomous Intelligent Transportation Systems (6G-AITSs).

Article [91] presents the concept of traffic flow optimization in autonomous vehicle networks using 6G communication technology. The proposed approach eliminates traditional traffic lights by employing vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) communication, supported by multi-agent reinforcement learning. The results of theoretical analyses indicate a 40–50% reduction in intersection waiting times, a 50–70% decrease in the probability of accidents, and a 35% reduction in the carbon footprint. The ultra-low latency and high scalability of 6G enable support for up to 10,000 vehicles per km².

Another aspect related to the environmental impact of road transport is the noise it generates. According to the research conducted by Helfer [92], aerodynamic noise becomes comparable in magnitude to tire noise at speeds of approximately 120 km/h for passenger cars and 80 km/h for delivery vehicles.

In study [93], Bergamini et al. performed simulation research using Computational AeroAcoustics (CAA). The mathematical models were based on Lighthill’s acoustic analogy. The investigated geometries featured a trapezoidal shape with a flat front and a rear end inclined at a 50-degree angle. Results from CFD simulations were incorporated into the Ffowcs Williams–Hawkings equation to determine the generated aerodynamic noise. For model validation, a CFD simulation of a two-dimensional cylindrical object was conducted and compared with existing literature data. The second stage of validation involved a wind tunnel experiment.

Tsai et al. [94] conducted an aeroacoustic analysis of a car equipped with a rear spoiler. An unstructured mesh was employed in the CFD study. Airflow simulation around the vehicle was performed in two phases: initially, steady-state calculations using the k-ε Renormalization Group (RNG) turbulence model, followed by unsteady-state computations using the steady-state results as initial conditions. The objective was to identify the optimal rear spoiler configuration regarding aerodynamic noise and forces.

To analyze the acoustic pressure level around an Ahmed body geometry, Duncan et al. [95] applied the Lattice Boltzmann Method as implemented in the PowerFLOW software. The unsteady-state simulation was conducted using the Very Large Eddy Simulation (VLES) model, with model discretization performed via the software’s integrated meshing tool.

The authors of this study have been conducting research over several years, initially focusing on simplified models and currently addressing complex vehicle platoon structures. The research began with a simplified vehicle geometry widely recognized in the scientific community as the Ahmed body. In the work presented in [96], key characteristics and parameters of the numerical mesh were defined, alongside the selection of appropriate initial and boundary conditions and computational models. For steady-state simulations, the k-ω SST turbulence model was employed. Subsequent unsteady-state analyses were performed using the Large Eddy Simulation (LES) model with a time step of 10⁻⁵ s. During the model validation process, computed quantities were compared with experimental data and numerical results from the literature. Vortex structures in the aerodynamic wake, velocity profiles in the symmetry plane, and values of drag and lift coefficients were analyzed. The unsteady-state simulations also enabled aeroacoustic analysis of the Ahmed body geometry, applying the Ffowcs Williams–Hawkings equations to determine the acoustic field at discrete points surrounding the vehicle model.

The study reported in [97] presents simulation results for a vehicle platoon consisting of three identical truck models traveling at a uniform speed of 90 km/h. The modeling employed a previously developed truck model, arranged into platoons with three distinct inter-vehicle distances. The study defined key numerical mesh parameters and applied appropriate boundary and initial conditions along with validated turbulence models. Analyses included investigation of drag and lift coefficients, as well as distribution of the overall sound pressure level. Several figures illustrate velocity, pressure, and turbulence intensity distributions around the analyzed truck platoons.

Research described in [98] focused primarily on highly detailed modeling of structured meshes used for simulations of individual vehicles and heterogeneous platoons, consisting of three distinct vehicle types: a passenger car, a van, and a truck. The study specified numerical mesh features and parameters, boundary and initial conditions, and computational models. The principal aim was to develop universal models enabling future studies of platoons with arbitrary vehicle numbers, configurations, inter-vehicle distances, and speeds. Velocity fields, streamlines, pressure distributions, and turbulence kinetic energy dissipation were graphically presented for the heterogeneous platoons. Additionally, overall sound pressure levels were calculated at selected points within the computational domain.

In study [3], a comprehensive process for modeling aerodynamic and aeroacoustic phenomena in different vehicle platoons—both homogeneous and heterogeneous—was presented. Digital models were developed, and fuel consumption was assessed for various platoon configurations, along with their environmental impacts. Studies [99,100] introduced novel Acoustic Environment Management Systems employing Geographic Information Systems (GISs), which integrate graphical information with textual data stored in databases. The system incorporated information on the effects of road, rail, industrial, municipal, and aircraft noise on urban residents. Its development involved thousands of acoustic measurements conducted in the Kraków metropolitan area, followed by the creation and validation of acoustic models. Upon completion, the system was implemented and has since been systematically updated and further enhanced. Additional improvements were achieved through studies [101,102,103], which enabled the determination of optimal travel routes across the Kraków metropolitan area, taking into account, among others, acoustic criteria. Graph-based algorithms, genetic algorithms, and neural networks were applied for this purpose. The research currently being carried out by the authors, as well as that planned for the future, is expected to significantly enrich this system with elements of an Intelligent Transportation System (ITS).

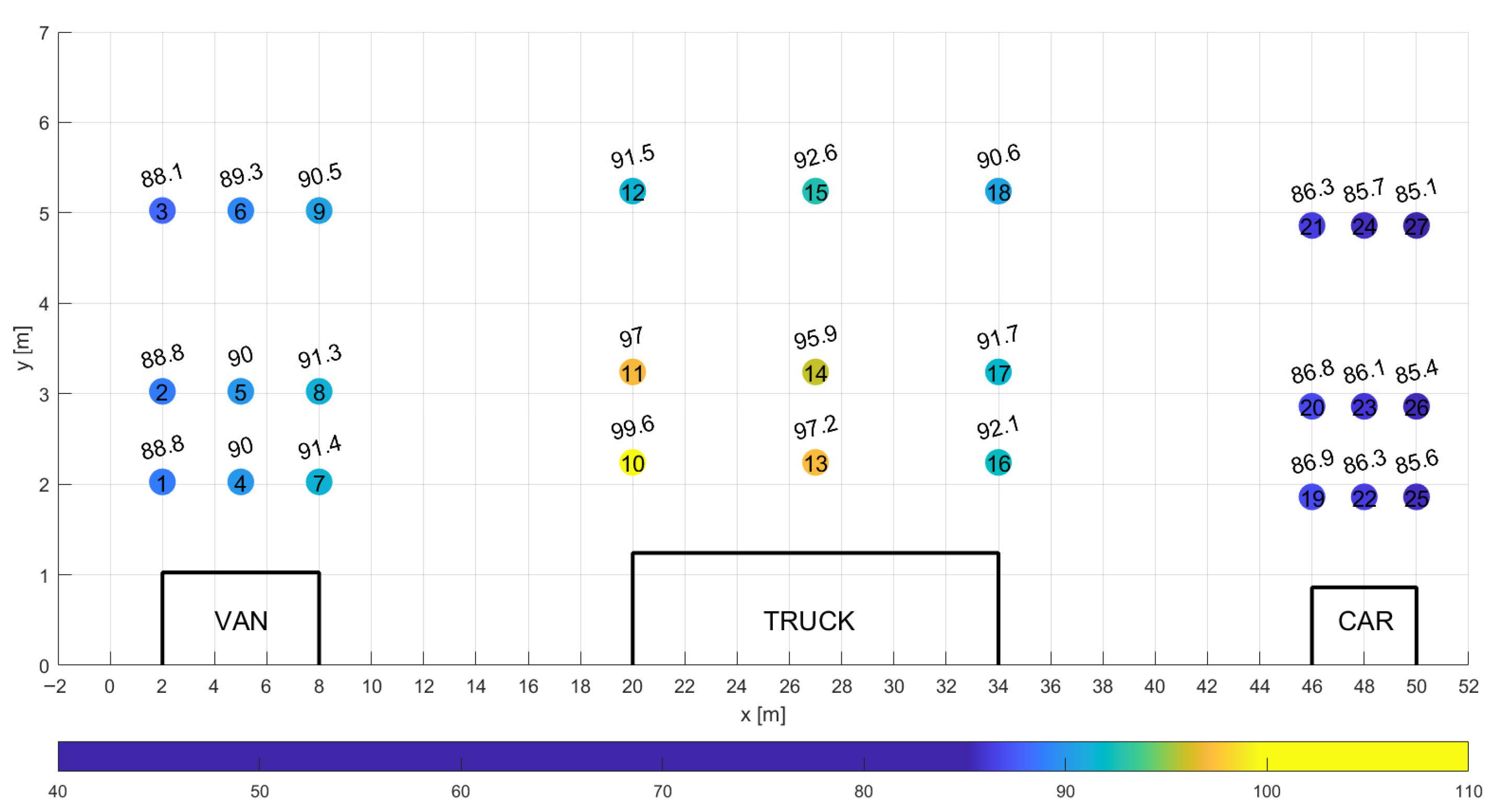
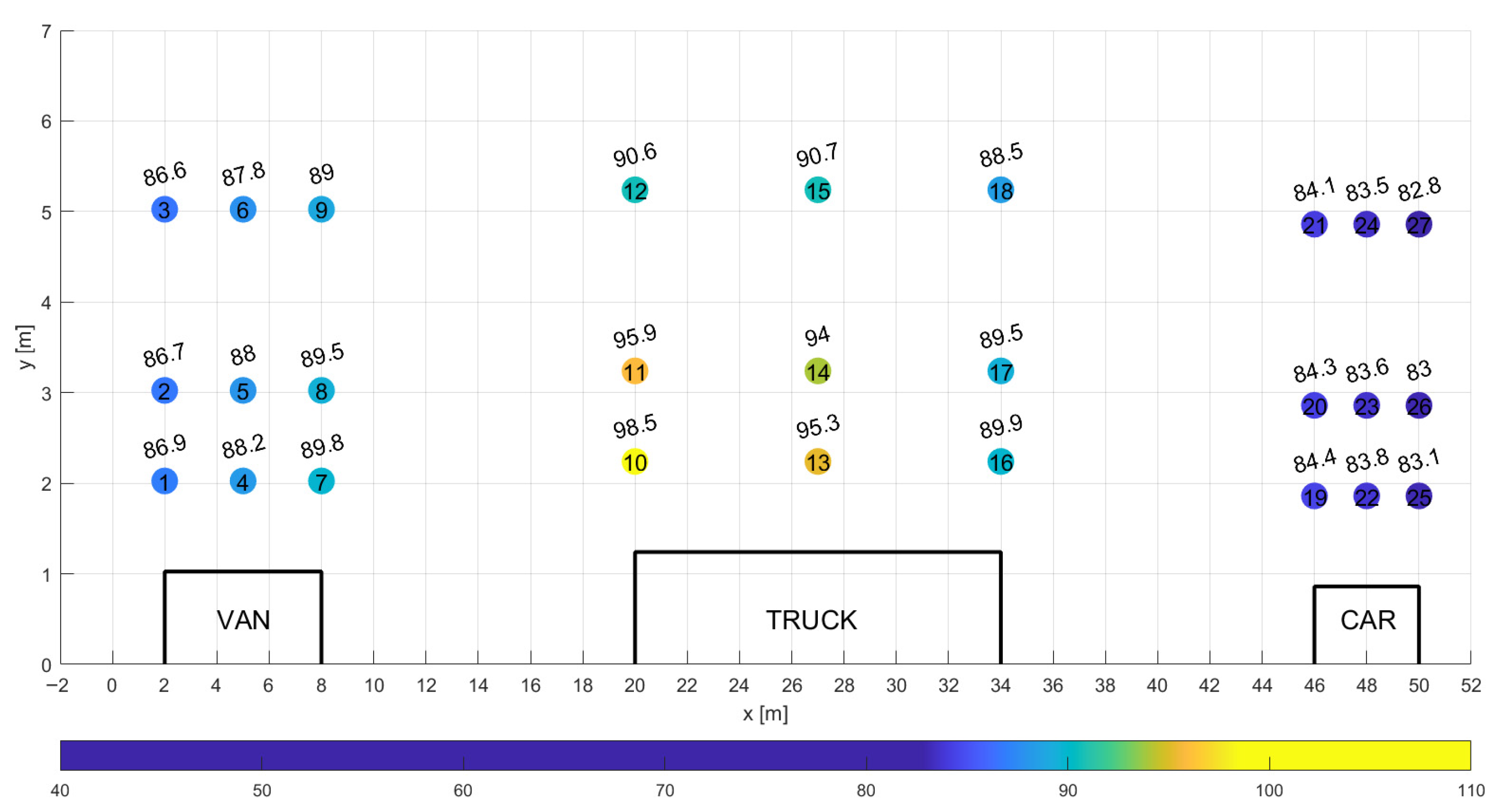
The primary objective of the study was to develop and execute 54 numerical models of heterogeneous vehicle platoons, varying in vehicle composition, traveling at three speeds: 50 km/h, 90 km/h, and 140 km/h, and at three inter-vehicle distances: 4 m, 8 m, and 12 m. Each platoon comprised three vehicles of differing body types: a small passenger car (Audi A3), a medium-sized delivery van (Fiat Ducato, model L3H2), and a large truck (Mercedes-Benz Actros F with trailer).

The study aimed to determine aerodynamic drag forces for individual vehicles and total drag for the platoons, drag coefficients and their percentage reductions, average fuel consumption and corresponding percentage reductions for individual vehicles, and total fuel consumption for heterogeneous platoons. For the most favorable platoon configurations, distributions of A-weighted sound pressure levels were also to be determined.

The simulations utilized the k-ω SST turbulence model, Large Eddy Simulation (LES), and the Ffowcs Williams–Hawkings acoustic analogy. CFD computations were performed at the Cyfronet Academic Computer Centre in Kraków using the Prometheus supercomputer and Ansys Fluent software. Additional verification was conducted using the NMPB-Routes-2008 method [104] and ISO 9613-2 standard [105,106] via SoundPlan software 8.2 and 9.1. The developed models and analysis results will support further research on acoustic and aerodynamic phenomena related to moving road vehicles, contributing to the so-called “active layer” of the Integrated Acoustic Environment Management System for the Royal Capital City of Kraków—currently under development by the authors [3,99,100,101,102,103]—as well as applications within Intelligent Transportation Systems (ITSs).

Given that this work was conducted over a period of three years, a variety of computational environments and software packages were utilized, including Ansys Academic Research, CATIA V5 Student Edition, CATIA Academic License Program, SoundPlan 8.2 and 9.1 Research & Education License, and MATLAB Academic Research. The authors have had, and continue to have, access to the latest research and educational versions of these software packages.

3. Materials and Methods

3.1. Geometrical and Numerical Model

Aerodynamic phenomena associated with vehicle motion can be effectively analyzed through simulation-based studies. Computational Fluid Dynamics (CFD) is a field that focuses on solving fluid flow problems using numerical methods. When the parameters of interest—such as fluid velocity, pressure, or density—vary over time, the simulations are categorized as unsteady-state (transient) analyses. While unsteady simulations provide a more realistic representation of fluid behavior, they are computationally expensive due to the necessity of extremely small time steps and substantial computational resources.

In scenarios where temporal variations in flow parameters are not critical, steady-state simulations are employed. These models assume time-invariant conditions and provide time-averaged values of the analyzed parameters, thereby reducing computational effort. Depending on the nature of the flow domain, numerical simulations can be divided into two categories. Internal flow analyses pertain to fluid motion within geometries enclosed by solid boundaries—for example, flows through pipelines, tanks, or HVAC systems. In contrast, external flow simulations concern fluid motion around bodies immersed in an unbounded environment, where the computational domain is defined by artificial boundaries rather than physical walls. Typical examples include aerodynamic analyses of aircraft, buildings, and road vehicles. The present study focuses on external flow phenomena, specifically airflow around road vehicles.

The study considers three vehicle types, each representing a distinct body category: a passenger car, a delivery van, and a heavy-duty truck. These vehicle geometries are employed both for individual aerodynamic simulations and for simulations of vehicle platoons consisting of three units. A platoon comprising vehicles of identical body types is referred to as homogeneous, whereas a platoon composed of different body types is referred to as heterogeneous.

In all three geometric models, the key features that influence aerodynamic performance—primarily body shape—were retained. However, to reduce mesh complexity and improve discretization quality, several simplifications were introduced. These include the omission of side mirrors, antennas, wheel arches, as well as detailed underbody structures such as cooling systems, drivetrain components, and exhaust assemblies. Figure 1 presents an isometric view of the developed vehicle models: passenger car, delivery van, and truck.

The passenger car used in the study is a 1998 Audi A3, a hatchback commonly found in Central Europe. This specific model was selected due to its availability to the authors. The vehicle dimensions are as follows: length—4.152 m, width—1.72 m, and height—1.42 m. The cataloged drag coefficient for this model is C_d = 0.31. The frontal area projected onto a plane perpendicular to the direction of airflow is A_car = 1.95 m².

The van used in the analysis is a Fiat Ducato, model L3H2. The vehicle measures 6.00 m in length, 2.05 m in width, and 2.564 m in height. For the 2014 model, the drag coefficient is C_d = 0.31. The frontal area perpendicular to the airflow is A_van = 4.57 m².

The truck configuration includes a tractor unit represented by the Mercedes-Benz Actros F, equipped with a roof fairing, and a standard trailer. The total length of the truck is 14.00 m, with a width of 2.48 m and a height of 4.00 m. Drag coefficient values for similar vehicle configurations have been reported in the literature: C_d = 0.542 in the study by Hariram et al. [107], C_d = 0.554 in Landman et al. [108], and C_d = 0.563 in Skrucany et al. [109]. The frontal area projected perpendicularly to the flow direction for the truck is A_truck = 9.30 m².

All vehicle models were developed using CATIA V5 software. Both surface and solid modeling modules were employed to accurately reproduce the vehicle geometries.

The assumptions defined in the mathematical model could only be satisfied within sufficiently small regions of the domain. Therefore, the computational domain was subdivided into finite volumes. The discretized form of the partial differential equations, expressed as a system of equations, was solved using the Finite Volume Method (FVM) implemented in the ANSYS Fluent software.

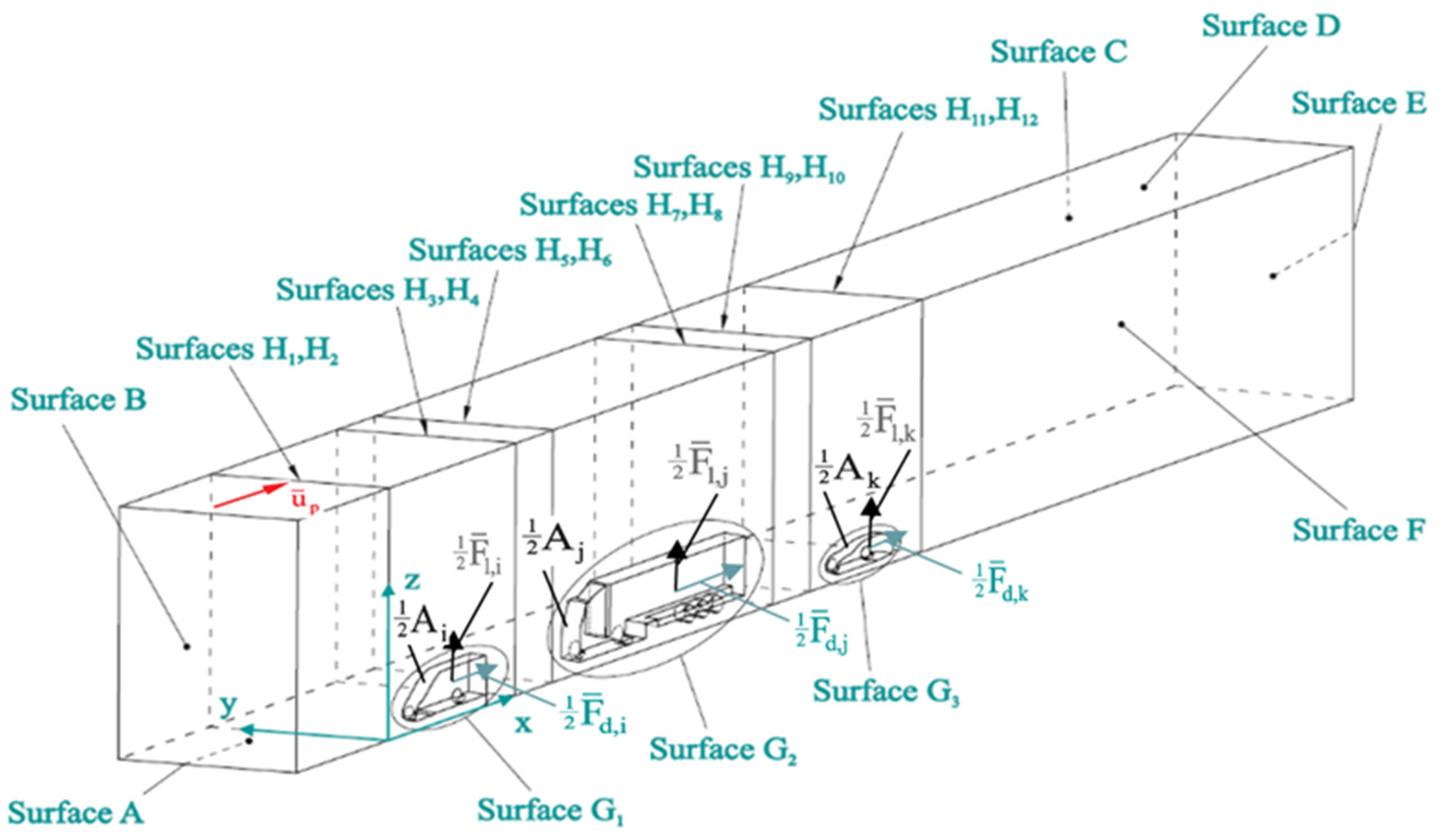
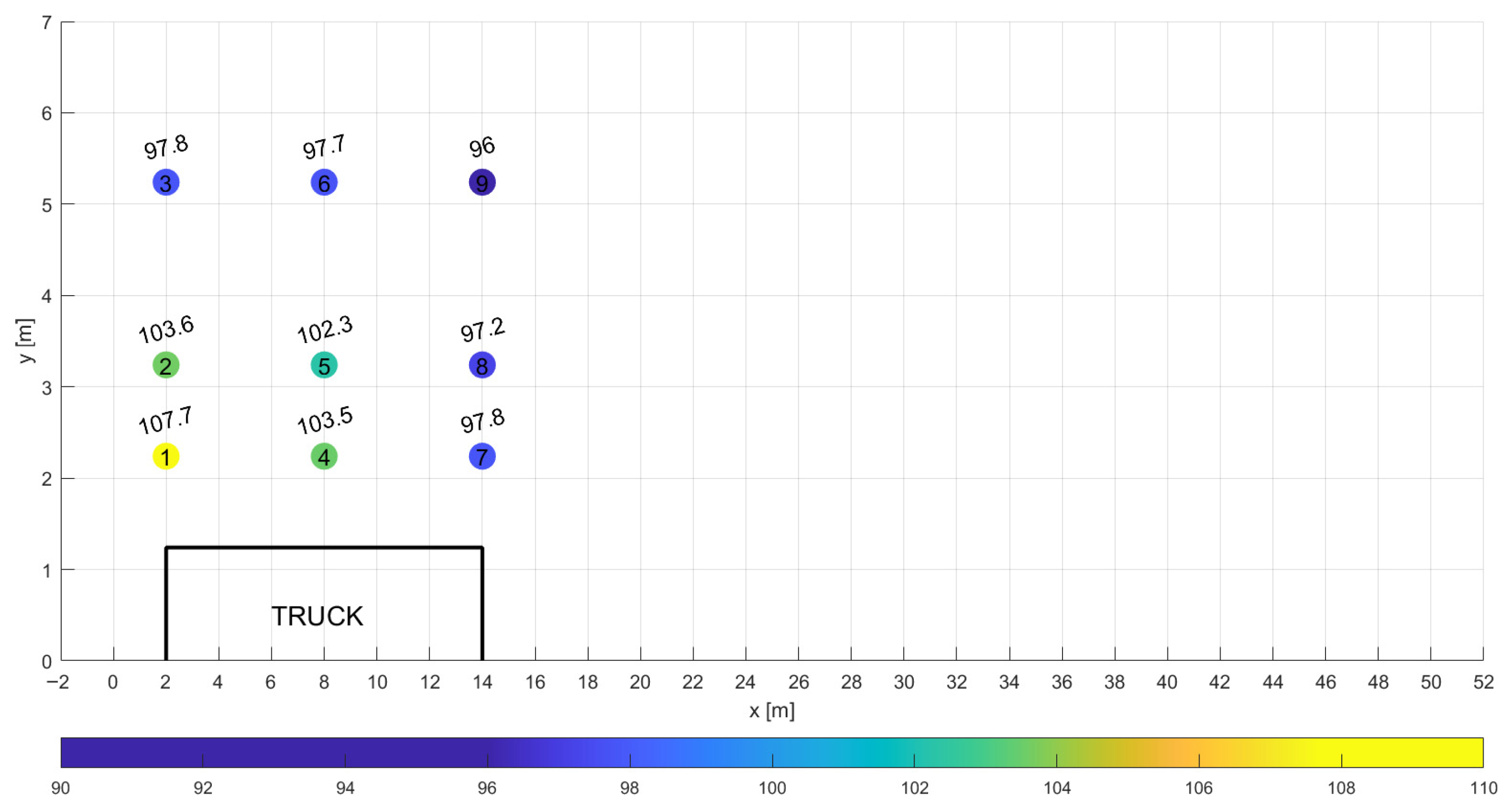
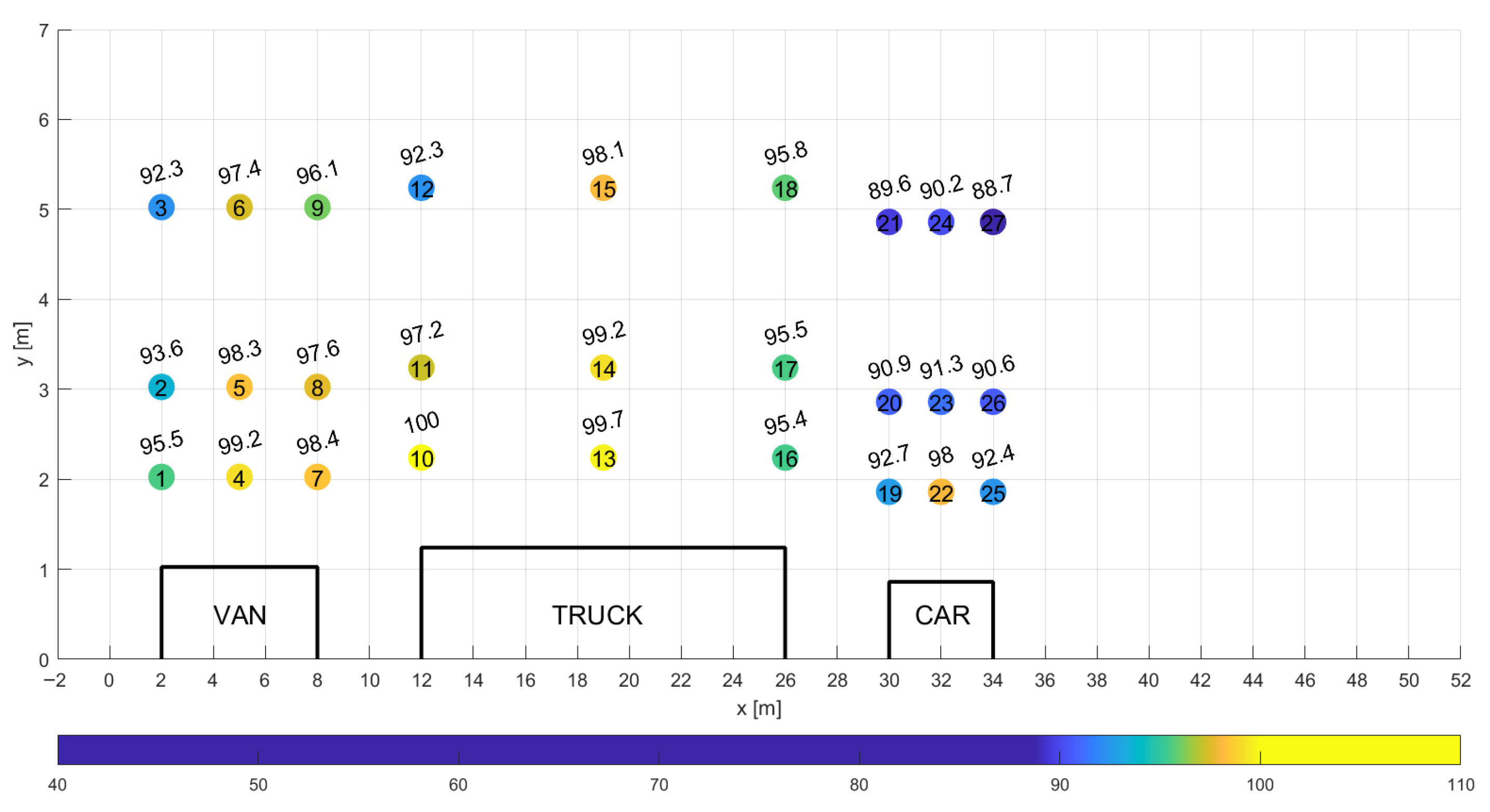
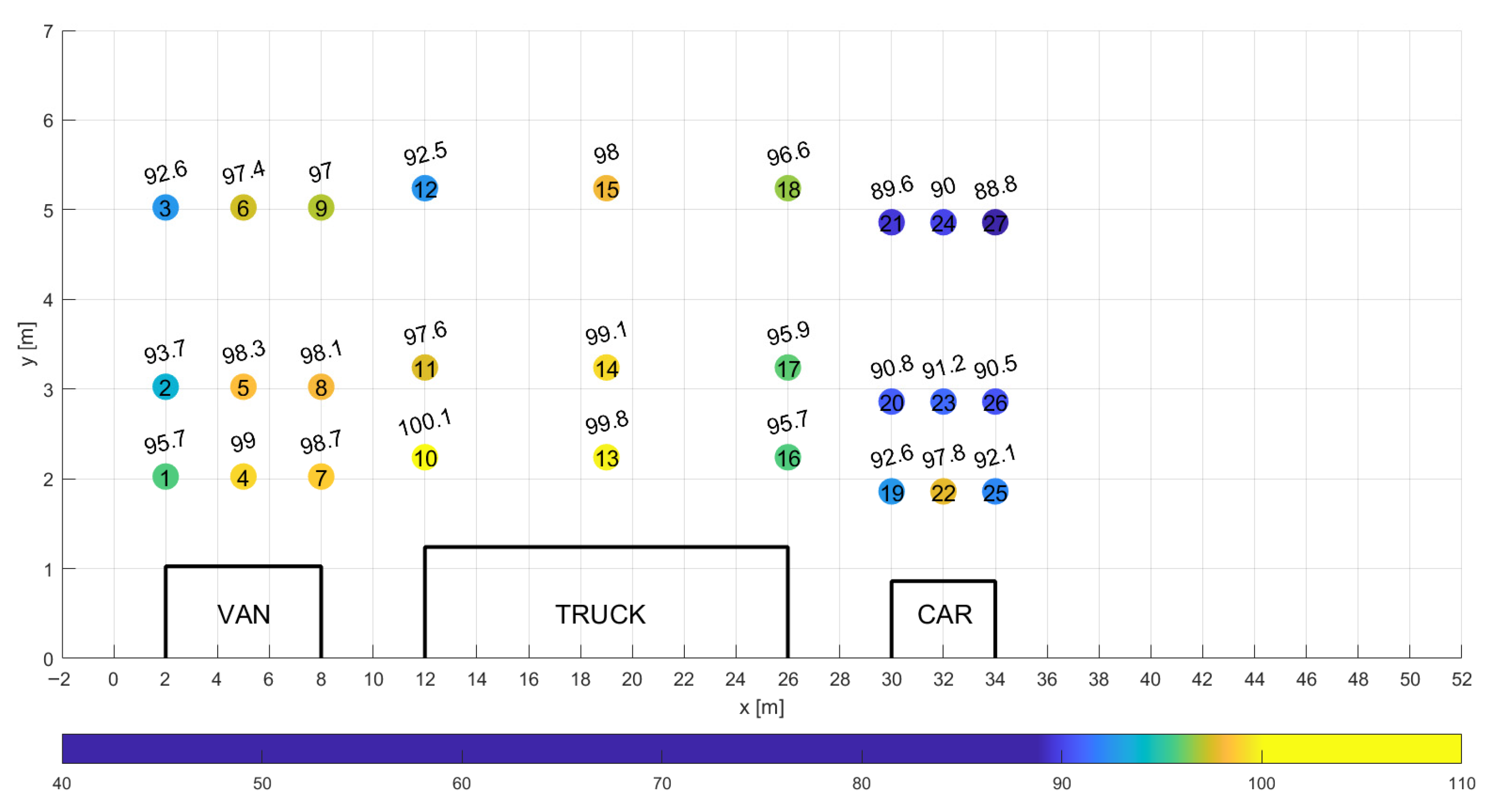
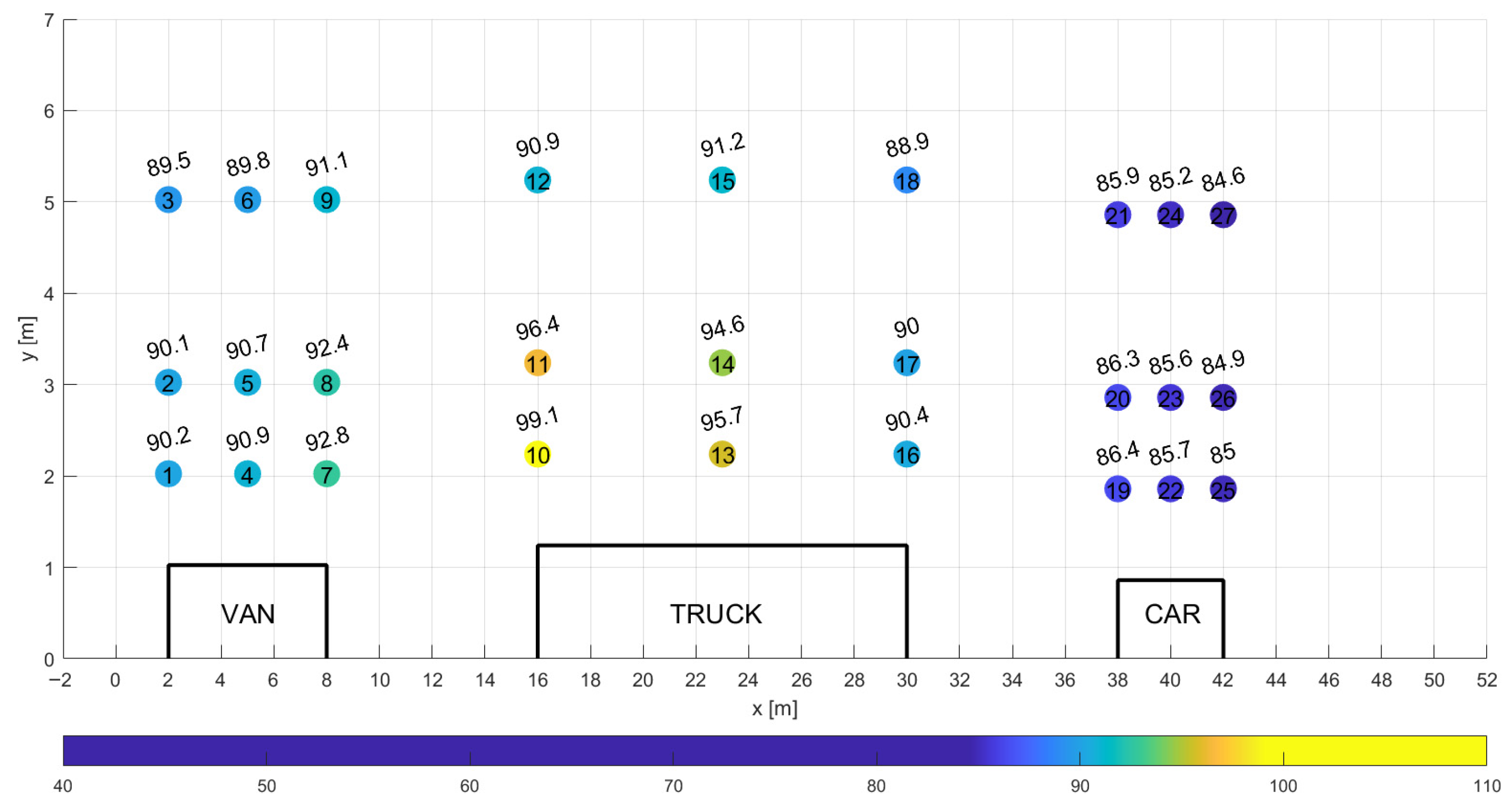
A schematic representation of the airflow model around the vehicle platoon, developed for aerodynamic analysis, is shown in Figure 2. The figure includes simplified geometries of the three vehicles and highlights the surfaces used to define the boundary conditions.

To reduce the total number of finite volumes, a symmetry plane was introduced in the model. As a result, the projected surface areas of the vehicles onto the plane perpendicular to the flow direction, as well as the aerodynamic forces, represent half of their actual values. The total side force, after accounting for the mirrored configuration, is zero.

The computational domain was constructed using modular blocks, with the number of elements (in millions) varying depending on the inter-vehicle spacing: inlet block—4.09, van block—33.3, intermediate block—from 3.29 to 9.79, truck block—63.3, second intermediate block—from 3.29 to 9.79, passenger car block—28.28, and outlet block—10.51. A structured mesh topology was applied.

For all analyzed configurations, the non-dimensional wall distance parameter y⁺ did not exceed a value of 1, indicating adequate resolution of the near-wall flow region. Furthermore, a transitional (inflation) layer was applied, consisting of 15 layers with a growth rate of 1.15 between successive layers. The mesh quality, assessed by the minimum orthogonal quality metric, remained above 0.1 in all cases, ensuring the required level of numerical accuracy for reliable simulation results.

Figure 2 presents the following designations: the bottom plane (surface A) represents the road surface. In the computational models, this surface moves in the direction opposite to the actual motion of the vehicles, with an absolute velocity u_p equal to the velocity of the vehicle platoon u_veh.

Surface B, located at the domain inlet, defines the inlet boundary condition. A constant velocity—depending on the analyzed case—of 13.89 m/s, 25 m/s, or 38.89 m/s was applied, corresponding to vehicle speeds of 50 km/h, 90 km/h, and 140 km/h, respectively. A uniform airflow was subjected to an initial disturbance described by the turbulence intensity parameter III.

Surfaces C and D correspond to the lateral boundaries of the domain, where a zero-gradient condition was applied to all considered physical variables. The rear plane (Surface E) defines the outlet boundary condition, where a reference static pressure of zero was specified.

To reduce the total number of computational elements, model symmetry was employed. A symmetry boundary condition was applied on Surface F. The surfaces of the vehicle bodies were labeled as G1 through G3 and treated as no-slip walls (flow velocity at the wall surface equal to zero).

The computational blocks were connected via interface planes labeled H1 to H12. The numerical mesh on these interfaces was matched across adjoining blocks to ensure grid continuity and maintain numerical consistency throughout the domain.

A comprehensive mathematical formulation of the boundary conditions, expressed as Equations (A1)–(A26), is provided in detail in reference [98].

3.2. Mathematical Model

In this section, a comprehensive methodology and the mathematical models employed to determine pressures, velocities, aerodynamic drag forces, as well as A-weighted sound pressure levels and fuel consumption, are presented. The study utilized the finite volume method implemented in Ansys Fluent. This software enables the numerical solution of partial differential equations governing the motion of fluid particles. The fundamental equations of fluid mechanics are the continuity Equation (1) and the momentum Equation (2) [110]. Solving these equations requires the adoption of an additional hypothesis regarding viscosity.

Years of accumulated experience, along with numerous studies reported in [3,96,97,98], demonstrate the effectiveness of the k-ω SST model, which belongs to the group of RANS (Reynolds-Averaged Navier–Stokes) models, and was employed in this work for steady-state calculations. For unsteady simulations, the Large Eddy Simulation (LES) approach [3] was applied. The simulations assumed a viscous, Newtonian, and incompressible fluid, while gravitational effects were neglected.

Using the Ffowcs Williams–Hawkings (FW-H) Equations (3)–(3D) [111], acoustic pressure was determined at selected points, and the corresponding A-weighted sound pressure levels were subsequently calculated. For the analysis of the acoustic field, unsteady numerical simulations were conducted using the Large Eddy Simulation (LES) approach. Due to the low Mach number (Ma ≤ 0.075), the acoustic calculations were carried out using Farassat’s method [112,113]. In the following part of the study, aerodynamic drag forces were evaluated for both individual vehicles and vehicle convoys. Drag coefficients, percentage reductions in drag coefficients, average fuel consumption, and percentage reductions in fuel consumption for individual vehicles were also calculated, along with the total fuel consumption for heterogeneous vehicle convoys.

Continuity equation:

$$\nabla ·\mathrm{u}=0$$

(1)

Momentum equation:

$${\rho }_0{\displaystyle \frac{\mathrm{d}\mathrm{u}}{\mathrm{d}\mathrm{t}}}=-\nabla \mathrm{p}+\nabla ·{\tau }_{\mathrm{i}\mathrm{j}}$$

(2)

where

u—air velocity vector

p—pressure

ρ₀—air density

${\tau }_{\mathrm{i}\mathrm{j}}$—stress tensor

To determine the acoustic field around vehicles and vehicle platoons, the Ffowcs Williams–Hawkings analogy (3–7) was used [111]. The physical quantity of interest is the acoustic pressure p′.

Ffowcs Williams–Hawkings equation:

$${\displaystyle \frac{1}{{\mathrm{c}}_0^2}}{\displaystyle \frac{{\partial }^2\mathrm{p}\prime }{{\partial \mathrm{t}}^2}}-{\nabla }^2{(\mathrm{p}}^{\prime })={\displaystyle \frac{{\partial }^2}{\partial {\mathrm{x}}_{\mathrm{i}}\partial {\mathrm{x}}_{\mathrm{j}}}}[{\mathrm{T}}_{\mathrm{i}\mathrm{j}}\mathrm{H}(\mathrm{f})]+{\displaystyle \frac{\partial }{\partial \mathrm{t}}}[{\mathrm{Q}}_{\mathrm{n}}\delta (\mathrm{f})]+{\displaystyle \frac{\partial }{{\partial \mathrm{x}}_{\mathrm{i}}}}[{\mathrm{L}}_{\mathrm{i}\mathrm{j}}\delta (\mathrm{f})]$$

(3)

$${\mathrm{T}}_{\mathrm{i}\mathrm{j}}={\rho }_0{\mathrm{u}}_{\mathrm{i}}{\mathrm{u}}_{\mathrm{j}}+{\mathrm{P}}_{\mathrm{i}\mathrm{j}}-{\mathrm{c}}_0^2\left({\rho -\rho }_0\right){\delta }_{\mathrm{i}\mathrm{j}}$$

(4)

$${\mathrm{P}}_{\mathrm{i}\mathrm{j}}=\mathrm{p}{\delta }_{\mathrm{i}\mathrm{j}}-{\mathsf{\mu }}_{\mathrm{p}}\left[{\displaystyle \frac{\partial {\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}}+{\displaystyle \frac{\partial {\mathrm{u}}_{\mathrm{j}}}{\partial {\mathrm{x}}_{\mathrm{i}}}}-{\displaystyle \frac{2}{3}}{\displaystyle \frac{\partial {\mathrm{u}}_{\mathrm{k}}}{\partial {\mathrm{x}}_{\mathrm{k}}}}{\delta }_{\mathrm{i}\mathrm{j}}\right]$$

(5)

$${\mathrm{Q}}_{\mathrm{n}}={\rho }_0{\mathrm{v}}_{\mathrm{n}}+\rho \left({\mathrm{u}}_{\mathrm{n}}-{\mathrm{v}}_{\mathrm{n}}\right)$$

(6)

$${\mathrm{L}}_{\mathrm{i}\mathrm{j}}={\mathrm{P}}_{\mathrm{i}\mathrm{j}}{\mathrm{n}}_{\mathrm{j}}+\rho {\mathrm{u}}_{\mathrm{i}}\left({\mathrm{u}}_{\mathrm{n}}-{\mathrm{v}}_{\mathrm{n}}\right)$$

(7)

where

u_i—fluid velocity component in the x_i direction

u_n—fluid velocity component normal to the surface f

v_i—surface velocity component in the x_i direction

v_n—surface velocity component normal to the surface f

T_ij—Lighthill turbulence stress tensor

P_ij—compressible stress tensor

H(f)—Heaviside function

δ(f)—Dirac delta function

δ_ij(f)—Kronecker delta

c₀—speed of the sound

ρ₀—density fluctuation

The obtained time-dependent pressure values were utilized to calculate the sound pressure level according to Equation (8) [114], followed by the determination of the A-weighted sound pressure level and the equivalent A-weighted sound pressure level in accordance with Equation (9) [114].

$${\mathrm{L}}_{\mathrm{p}}=20{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}{\displaystyle \frac{{\mathrm{p}}^{\prime }}{{\mathrm{p}}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}$$

(8)

where

p′—pressure fluctuation

p_ref = 2 × 10⁻⁵ [Pa]—reference acoustic pressure.

$${\mathrm{L}}_{\mathrm{A}\mathrm{e}\mathrm{q}}=10{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left[{\int }_0^{\mathrm{T}}{\displaystyle \frac{{\mathrm{p}}_{\mathrm{A}}^2}{{\mathrm{p}}_{\mathrm{r}\mathrm{e}\mathrm{f}}^2}}\mathrm{d}\mathrm{t}\right]$$

(9)

where

p_A—acoustic pressure corrected according to the A-weighted frequency response

p_ref—reference acoustic pressure,

T—the time interval for which the equivalent A-weighted sound level is determined.

The drag coefficient C_d is calculated according to Equation (10) [4,115] based on the viscous and pressure forces acting on the vehicles.

$${\mathrm{C}}_{\mathrm{d}}={\displaystyle \frac{{2\mathrm{F}}_{\mathrm{d}}}{{\rho }_{\mathrm{p}}\mathrm{A}{\mathrm{u}}^2}}$$

(10)

where

F_d—acting drag force

ρ_p—air density

A—frontal area of the vehicle,

u—relative air velocity.

Based on the drag coefficient values C_d,i for individual vehicles in the platoon obtained from simulation studies, and the drag coefficient value C_d for a single vehicle, the reduction in the drag coefficient was calculated according to Equation (11) [116].

$${∆\mathrm{C}}_{\mathrm{d},\mathrm{i}}={\displaystyle \frac{{\mathrm{C}}_{\mathrm{d}}-{\mathrm{C}}_{\mathrm{d},\mathrm{i}}}{{\mathrm{C}}_{\mathrm{d}}}}·100\mathrm{\%}$$

(11)

where

C_d—drag coefficient of a single vehicle

C_d,i—drag coefficient of the i-th vehicle in the platoon.

The amount of fuel consumed during driving is a function of numerous variables, including vehicle speed, forces acting on the vehicle, engine efficiency, drivetrain efficiency, and the type of fuel used. Assuming that the vehicles travel on a flat road at a constant velocity, the total resistance force is primarily composed of aerodynamic drag and rolling resistance [5]. To estimate the average fuel consumption K_avg Equation (12), as presented in studies [117,118], was employed.

$${\mathrm{K}}_{\mathrm{a}\mathrm{v}\mathrm{g}}={\displaystyle \frac{100·({\mathrm{P}}_{\mathrm{r}}·{\mathrm{P}}_{\mathrm{a}})}{{\mathrm{Q}}_{\mathrm{w}}·{\mathrm{u}}_{\mathrm{v}\mathrm{e}\mathrm{h}}·{\eta }_{\mathrm{e}}·{\eta }_{\mathrm{t}}·{\rho }_{\mathrm{f}}}}$$

(12)

where

P_r—power required to overcome rolling resistance

P_a—power required to overcome aerodynamic drag

${\mathrm{Q}}_{\mathrm{w}}$—calorific value of the fuel

u_veh—vehicle speed

${\eta }_{\mathrm{e}}$—engine efficiency

${\eta }_{\mathrm{t}}$—drivetrain efficiency

${\rho }_{\mathrm{f}}$—fuel density.

The power required to overcome motion resistance can be calculated using the following Formulas (13) and (14) [5]:

$${\mathrm{P}}_{\mathrm{r}}={\mathrm{F}}_{\mathrm{r}}·{\mathrm{u}}_{\mathrm{v}\mathrm{e}\mathrm{h}}$$

(13)

$${\mathrm{P}}_{\mathrm{a}}={\mathrm{F}}_{\mathrm{d}}·{\mathrm{u}}_{\mathrm{v}\mathrm{e}\mathrm{h}}$$

(14)

where

F_d—drag force,

F_r—rolling resistance force

u_veh—vehicle speed.

The aerodynamic drag coefficient primarily depends on the shape of the vehicle, and for full-size vehicles, its value changes only slightly with speed [5]. For the analyzed vehicles, the aerodynamic drag force was calculated at speeds of 50, 90, and 140 km/h.

The weight of the passenger car and the van corresponds to vehicles loaded to three-quarters of their maximum gross weight. For the truck, the calculations were based on the maximum permissible gross vehicle weight, which, for a five-axle vehicle combination (a two-axle truck and a three-axle trailer), is 40,000 kg, in accordance with the Regulation of the Minister of Infrastructure on the technical conditions of vehicles and the scope of their necessary equipment.

The rolling resistance coefficient was assumed as kr = 0.009 [3,119], and the gravitational acceleration was taken as g = 9.81 m/s². For the most commonly used radial tires, the rolling resistance coefficient remains constant for speeds up to 140 km/h [5]. Due to the low lift coefficient values for the individual vehicles, its influence on rolling resistance was neglected. The rolling resistance force for each vehicle was calculated using Equation (15) [5].

$${\mathrm{F}}_{\mathrm{r}}={\mathrm{k}}_{\mathrm{r}}·\mathrm{M}·\mathrm{g}$$

(15)

where

k_r—rolling resistance coefficient,

M—vehicle mass

g—gravitational acceleration.

The percentage reduction in fuel consumption of the i-th vehicle, ΔK_i was estimated based on the method presented in [5], and can be expressed by Equation (16). For the calculations, it was assumed that the vehicles travel at a constant speed u_veh, the drag coefficient changes to C_d,i due to aerodynamic interactions between vehicles, and the engine efficiency remains constant.

$${∆\mathrm{K}}_{\mathrm{i}}={\displaystyle \frac{\frac{{∆\mathrm{C}}_{\mathrm{d},\mathrm{i}}}{100}{\mathrm{F}}_{\mathrm{d}}}{{\mathrm{F}}_{\mathrm{d}}+{\mathrm{F}}_{\mathrm{r},\mathrm{i}}}}·100\mathrm{\%}$$

(16)

where

ΔC_d,i—percentage reduction in the drag coefficient of the i-th vehicle in the platoon

F_d—drag force of the vehicle traveling outside the convoy

F_r,i—rolling resistance force of the i-th vehicle

The total aerodynamic drag force of all vehicles in the platoon, F_d,c was calculated using Equation (17) [3].

$${\mathrm{F}}_{\mathrm{d},\mathrm{c}}=\sum _{\mathrm{i}=1}^3{\mathrm{F}}_{\mathrm{d},\mathrm{i}}$$

(17)

where F_d,i—drag force of the i-th vehicle in the platoon.

Using the average fuel consumption values of individual vehicles operating outside the platoon K_avg (

Table A3. Average fuel consumption of individual vehicles operating outside the platoon.

Vehicle	Velocity uveh [km/h]	Average Fuel Consumption Kavg [L/100 km]
Car	50 90 140	3.4 6.03 11.44
Van	50 90 140	4.05 7.39 14.25
Truck	50 90 140	26.97 35.97 54.46

), the percentage reduction in fuel consumption ΔK_i and Equation (18) [3], the average fuel consumption of each vehicle in the platoon K_avg,i was determined. Subsequently, to calculate the total fuel consumption of all vehicles in the platoon K_c per 100 km traveled, the average fuel consumption values K_avg,i were summed according to Equation (19) [3].

$${\mathrm{K}}_{\mathrm{a}\mathrm{v}\mathrm{g},\mathrm{i}}={\mathrm{K}}_{\mathrm{a}\mathrm{v}\mathrm{g}}·\left(1-{\displaystyle \frac{∆{\mathrm{K}}_{\mathrm{i}}}{100}}\right)$$

(18)

where

K_avg—average fuel consumption per 100 km of a vehicle outside the platoon

ΔK_i—percentage reduction in fuel consumption by the i-th vehicle in the platoon.

$${\mathrm{K}}_{\mathrm{c}}={\displaystyle \sum _{\mathrm{i}=1}^3}{\mathrm{K}}_{\mathrm{a}\mathrm{v}\mathrm{g},\mathrm{i}}$$

(19)

where

K_avg,i—average fuel consumption per 100 km by the i-th vehicle in the platoon.

All additional information regarding the individual vehicles used in the calculations is provided in Appendix A,

Table A1. Drag force and rolling drag force for individual vehicles.

Vehicle	Weight M [kg]	Velocity uveh [km/h]	Drag Force Fd [N]	Rolling Drag Force Fd [N]
Car	1522.5	50 90 140	71.16 230.57 557.92	134.42
Van	2977.5	50 90 140	152.97 495.62 1199.27	262.88
Truck	40000	50 90 140	618.26 2003 4847.16	3531

,

Table A2. Values of parameters and coefficients used to calculate fuel consumption.

Vehicle	Parameter	Unit	Value
Car	${\mathrm{Q}}_{\mathrm{w}}$ ${\eta }_{\mathrm{e}}$ ${\eta }_{\mathrm{t}}$ ${\rho }_{\mathrm{f}}$	[W·h/kg] [-] [-] [kg/L]	11,944.44 0.2 0.95 0.741
Van	${\mathrm{Q}}_{\mathrm{w}}$ ${\eta }_{\mathrm{e}}$ ${\eta }_{\mathrm{t}}$ ${\rho }_{\mathrm{f}}$	[W·h/kg] [-] [-] [kg/L]	11,944.44 0.3 0.95 0.837
Truck	${\mathrm{Q}}_{\mathrm{w}}$ ${\eta }_{\mathrm{e}}$ ${\eta }_{\mathrm{t}}$ ${\rho }_{\mathrm{f}}$	[W·h/kg] [-] [-] [kg/L]	11,944.44 0.45 0.95 0.837

and Table A3. Table A1 presents data on vehicle mass, calculated aerodynamic drag values at various speeds, and rolling resistance values. The parameter values utilized for calculating the average fuel consumption of the vehicles are listed in Table A2. The fuel calorific value Q_w was adopted in accordance with the Regulation of the Minister of Climate [120], while the fuel density was based on the Announcement of the Minister of Energy [121]. Engine efficiency and drivetrain efficiency were adopted following references [3,117]. Table A3 shows the calculated average fuel consumption for a passenger car, van, and truck at three different speeds. These results were subsequently used to evaluate the fuel consumption reduction for vehicles operating in heterogeneous platoons composed of a passenger car, van, and truck.

4. Analysis of Drag Force and Fuel Consumption Reduction in Heterogeneous Vehicle Platoons

A key aspect of the present study is the explicit consideration of heterogeneity within vehicle platoons. Unlike homogeneous formations, heterogeneous platoons consist of vehicles with markedly different dimensions, masses, aerodynamic characteristics, and powertrains. These differences substantially affect energy consumption and pollutant emissions, as the aerodynamic interactions, drag reduction potential, and overall dynamics vary depending on the specific vehicle composition. To account for these effects, the study includes both passenger cars and heavy-duty trucks with a total length of up to 14 m. This approach allowed for the investigation of how variations in vehicle geometry, speed, and inter-vehicle distance influence fuel consumption, environmental emissions, and acoustic performance. By integrating these heterogeneous features into the computational framework, the analysis captures realistic mixed-traffic conditions and provides insights that are directly applicable to modern road transport systems.

After developing the models and conducting simulation studies, an analysis of drag force and fuel consumption reduction was performed for various configurations of heterogeneous vehicle platoons.

Table A4. Values of drag force reduction and fuel consumption reduction for the configuration: van–truck–car.

Velocity uveh [km/h]	Spacing D [m]	Name	Fd,i [N]	Cd,i [-]	∆Cd,i [%]	∆Ki [%]	Kavg,i [L/100 km]
50	4	Van 1 Truck 2 Car 3 Sum	52.58 529.63 38.53 620.74	0.099 0.490 0.170 -	65.63 14.34 45.86 -	24.14 2.14 15.87 -	3.08 26.40 2.86 32.33
50	8	Van 1 Truck 2 Car 3 Sum	122.16 491.80 11.13 662.23	0.230 0.455 0.213 -	20.14 20.45 32.17 -	7.41 3.05 8.27 -	3.75 26.15 3.02 32.92
50	12	Van 1 Truck 2 Car 3 Sum	147.13 506.93 51.22 705.27	0.277 0.469 0.226 -	3.82 18.01 28.03 -	1.40 2.68 9.70 -	4.00 26.25 3.07 33.31
90	4	Van 1 Truck 2 Car 3 Sum	160.04 1715.99 129.97 2006.01	0.093 0.490 0.177 -	67.71 14.34 43.63 -	44.24 5.19 27.56 -	4.12 34.11 4.37 42.60
90	8	Van 1 Truck 2 Car 3 Sum	387.20 1610.93 182.84 2180.98	0.225 0.460 0.249 -	21.88 19.58 20.70 -	14.29 7.09 13.08 -	6.34 33.42 5.24 45.00
90	12	Van 1 Truck 2 Car 3 Sum	464.64 1733.50 236.44 2434.59	0.270 0.495 0.322 -	6.25 13.46 −2.55 -	4.08 4.87 −1.61 -	7.09 34.22 6.13 47.44
140	4	Van 1 Truck 2 Car 3 Sum	366.44 4186.18 351.81 4904.44	0.088 0.494 0.198 -	69.44 13.64 36.94 -	56.96 7.89 29.77 -	6.14 50.16 8.03 64.33
140	8	Van 1 Truck 2 Car 3 Sum	920.27 4067.55 463.75 5451.57	0.221 0.480 0.261 -	23.26 16.08 16.88 -	19.08 9.30 13.60 -	11.53 49.39 9.88 70.80
140	12	Van 1 Truck 2 Car 3 Sum	1120.15 4169.24 463.75 5753.14	0.269 0.492 0.261 -	6.60 13.99 16.88 -	5.41 8.09 13.60 -	13.48 50.05 9.88 73.41

,

Table A5. Values of drag force reduction and fuel consumption reduction for the configuration: van–car–truck.

Velocity uveh [m/s]	Spacing D [m]	Name	Fd,i [N]	Cd,i [-]	∆Cd,i [%]	∆Ki [%]	Kavg,i [L/100 km]
50	4	Van 1 Car 2 Truck 3 Sum	127.48 31.05 496.12 654.64	0.240 0.137 0.459 -	16.67 56.37 19.76 -	6.13 19.51 2.94 -	3.81 2.73 26.18 32.72
50	8	Van 1 Car 2 Truck 3 Sum	149.78 32.72 511.25 698.20	0.282 0.164 0.473 -	2.08 47.77 17.31 -	0.77 16.54 2.58 -	4.02 2.83 26.28 33.13
50	12	Van 1 Car 2 Truck 3 Sum	154.56 41.02 520.98 716.56	0.291 0.181 0.482 -	−1.04 42.36 15.73 -	−0.38 14.66 2.34 -	4.07 2.90 26.34 33.31
90	4	Van 1 Car 2 Truck 3 Sum	402.69 102.80 1603.93 2109.42	0.234 0.140 0.458 -	18.75 55.41 19.93 -	12.25 35.01 7.21 -	6.49 3.92 33.38 43.78
90	8	Van 1 Car 2 Truck 3 Sum	476.69 118.96 1656.46 2252.11	0.277 0.162 0.378 -	3.82 48.41 17.31 -	2.50 30.58 6.26 -	7.21 4.19 33.72 45.11
90	12	Van 1 Car 2 Truck 3 Sum	481.85 183.57 1779.03 2444.46	0.280 0.250 0.508 -	2.78 20.38 11.19 -	1.82 12.88 4.05 -	7.26 5.25 34.52 47.03
140	4	Van 1 Car 2 Truck 3 Sum	957.75 250.53 3906.54 5114.82	0.230 0.141 0.461 -	20.14 55.10 19.41 -	16.52 44.40 11.23 -	11.90 6.36 48.34 66.60
140	8	Van 1 Car 2 Truck 3 Sum	1136.81 293.17 4076.02 5506.00	0.273 0.165 0.481 -	20.14 55.10 15.91 -	4.27 38.24 9.20 -	13.65 7.06 49.44 70.15
140	12	Van 1 Car 2 Truck 3 Sum	1174.29 360.69 4287.87 5822.85	0.282 0.203 0.506 -	2.08 35.35 11.54 -	1.71 28.49 6.68 -	14.01 8.18 50.82 73.01

,

Table A6. Values of drag force reduction and fuel consumption reduction for the configuration: car–van–truck.

Velocity uveh [m/s]	Spacing D [m]	Name	Fd,i [N]	Cd,i [-]	∆Cd,i [%]	∆Ki [%]	Kavg,i [L/100 km]
50	4	Car 1 Van 2 Truck 3 Sum	52.58 61.61 540.44 654.63	0.232 0.116 0.500 -	59.72 26.11 12.59 -	9.04 21.97 1.88 -	3.09 3.16 26.47 32.72
50	8	Car 1 Van 2 Truck 3 Sum	66.63 117.38 504.77 688.78	0.294 0.221 0.467 -	6.37 23.26 18.36 -	2.20 8.56 2.73 -	3.32 3.71 26.23 33.26
50	12	Car 1 Van 2 Truck 3 Sum	68.89 135.97 506.93 711.80	0.304 0.256 0.469 -	3.18 11.11 18.01 -	1.01 4.09 2.68 -	3.36 3.89 26.25 33.49
90	4	Car 1 Van 2 Truck 3 Sum	171.83 194.46 1793.04 2159.33	0.234 0.113 0.512 -	25.48 60.76 10.49 -	16.09 39.70 3.80 -	5.06 4.46 34.61 44.12
90	8	Car 1 Van 2 Truck 3 Sum	220.29 382.04 1596.92 2199.25	0.300 0.222 0.456 -	4.46 22.92 20.28 -	2.82 14.97 7.34 -	5.86 6.29 33.33 45.48
90	12	Car 1 Van 2 Truck 3 Sum	228.37 447.43 1652.96 2328.76	0.311 0.260 0.472 -	0.96 9.72 17.48 -	0.60 6.35 6.33 -	5.99 6.92 33.70 46.61
140	4	Car 1 Van 2 Truck 3 Sum	424.66 453.89 4389.56 5268.11	0.239 0.109 0.518 -	23.89 62.15 9.44 -	19.25 50.98 5.46 -	9.23 6.99 51.48 67.71
140	8	Car 1 Van 2 Truck 3 Sum	653.87 966.08 3881.12 5501.06	0.368 0.232 0.458 -	−17.20 19.44 19.93 -	−13.86 15.95 11.53 -	13.02 11.98 48.18 73.18
140	12	Car 1 Van 2 Truck 3 Sum	675.19 1165.96 4135.34 5979.49	0.380 0.280 0.488 -	−21.02 2.78 14.69 -	−16.94 2.28 8.50 -	13.37 13.93 49.83 77.13

,

Table A7. Values of drag force reduction and fuel consumption reduction for the configuration: car–truck–van.

Velocity uveh [m/s]	Spacing D [m]	Name	Fd,i [N]	Cd,i [-]	∆Cd,i [%]	∆Ki [%]	Kavg,i [L/100 km]
50	4	Car 1 Truck 2 Van 3 Sum	31.05 573.94 158.28 763.27	0.137 0.531 0.298 -	56.37 7.17 −3.47 -	19.51 1.07 −1.28 -	2.73 26.68 4.11 33.52
50	8	Car 1 Truck 2 Van 3 Sum	61.42 570.70 133.32 765.43	0.271 0.528 0.251 -	13.69 7.69 12.85 -	4.74 1.15 4.73 -	3.23 26.66 3.86 33.76
50	12	Car 1 Truck 2 Van 3 Sum	67.53 590.16 121.63 779.32	0.298 0.546 0.229 -	5.10 4.55 20.49 -	1.76 0.68 7.54 -	3.34 26.79 3.75 33.87
90	4	Car 1 Truck 2 Van 3 Sum	102.80 1831.56 459.48 2393.84	0.140 0.523 0.267 -	55.41 8.57 7.29 -	35.01 3.10 4.76 -	3.92 34.86 7.04 45.82
90	8	Car 1 Truck 2 Van 3 Sum	202.67 1817.55 421.62 2441.84	0.276 0.519 0.245 -	12.10 9.27 14.93 -	7.64 3.35 9.76 -	5.57 34.77 6.67 47.01
90	12	Car 1 Truck 2 Van 3 Sum	223.23 1887.59 382.04 2492.86	0.304 0.539 0.222 -	3.18 5.77 22.92 -	2.01 2.09 14.97 -	5.91 35.22 6.29 47.42
140	4	Car 1 Truck 2 Van 3 Sum	250.53 4296.35 1053.53 5600.40	0.141 0.507 0.253 -	55.10 11.36 12.15 -	44.40 6.57 9.97 -	6.36 50.88 12.83 70.07
140	8	Car 1 Truck 2 Van 3 Sum	620.11 4448.88 1053.53 6122.51	0.349 0.525 0.253 -	−11.15 8.22 12.15 -	−8.98 4.75 9.97 -	12.46 51.87 12.83 77.17
140	12	Car 1 Truck 2 Van 3 Sum	660.98 4652.26 891.12 6204.36	0.372 0.549 0.214 -	−18.47 4.02 25.69 -	−14.89 2.33 21.07 -	13.14 53.19 11.25 77.58

,

Table A8. Values of drag force reduction and fuel consumption reduction for the configuration: truck–car–van.

Velocity uveh [m/s]	Spacing D [m]	Name	Fd,i [N]	Cd,i [-]	∆Cd,i [%]	∆Ki [%]	Kavg,i [L/100 km]
50	4	Truck 1 Car 2 Van 3 Sum	610.69 32.41 132.79 775.89	0.565 0.143 0.250 -	1.22 54.46 13.19 -	0.18 18.85 4.85 -	26.92 2.76 3.86 33.54
50	8	Truck 1 Car 2 Van 3 Sum	620.42 53.94 131.19 805.55	0.574 0.238 0.247 -	−0.35 24.20 14.24 -	−0.05 8.38 5.24 -	26.99 3.11 3.84 33.94
50	12	Truck 1 Car 2 Van 3 Suma	625.83 51.67 126.41 803.91	0.579 0.228 0.238 -	−1.22 27.39 17.36 -	−0.18 9.48 6.39 -	27.02 3.07 3.80 33.89
90	4	Truck 1 Car 2 Van 3 Sum	1964.64 128.50 450.88 2544.02	0.561 0.175 0.262 -	1.92 44.27 9.03 -	0.70 27.96 5.90 -	35.72 4.34 6.96 47.02
90	8	Truck 1 Car 2 Van 3 Sum	1992.65 185.04 425.06 2602.76	0.569 0.252 0.247 -	0.52 19.75 14.24 -	0.19 12.47 9.30 -	35.90 5.28 6.71 47.89
90	12	Truck 1 Car 2 Van 3 Sum	2010.16 177.70 413.02 2600.88	0.574 0.242 0.240 -	−0.35 22.93 16.67 -	−0.13 14.49 10.89 -	36.02 5.16 6.59 47.76
140	4	Truck 1 Car 2 Van 3 Sum	4711.58 339.37 1099.33 6150.28	0.556 0.191 0.264 -	2.80 39.17 8.33 -	1.62 31.57 6.84 -	53.58 7.83 13.28 74.68
140	8	Truck 1 Car 2 Van 3 Sum	4770.89 451.31 1020.21 6242.42	0.563 0.254 0.245 -	1.57 19.11 14.93 -	0.91 15.40 12.25 -	53.96 9.68 12.51 76.14
140	12	Truck 1 Car 2 Van 3 Sum	4813.26 445.98 995.23 6254.47	0.568 0.251 0.239 -	0.70 20.06 17.01 -	0.40 16.17 13.95 -	54.24 9.59 12.27 76.09

and

Table A9. Values of drag force reduction and fuel consumption reduction for the configuration: truck–van–car.

Velocity uveh [m/s]	Spacing D [m]	Name	Fd,i [N]	Cd,i [-]	∆Cd,i [%]	∆Ki [%]	Kavg,i [L/100 km]
50	4	Truck 1 Van 2 Car 3 Sum	581.51 128.01 44.42 753.93	0.538 0.241 0.196 -	5.94 16.32 37.58 -	0.89 6.00 13.01 -	26.73 3.81 2.95 33.50
50	8	Truck 1 Van 2 Car 3 Sum	607.45 129.07 36.94 773.46	0.562 0.243 0.163 -	1.75 15.63 48.09 -	0.26 5.75 16.65 -	26.90 3.82 2.83 33.50
50	12	Truck 1 Van 2 Car 3 Sum	623.66 120.04 37.17 780.87	0.577 0.226 0.164 -	−0.87 21.53 47.77 -	−0.13 7.92 16.54 -	27.01 3.73 2.83 33.57
90	4	Truck 1 Van 2 Car 3 Sum	1877.09 425.06 148.33 2450.48	0.536 0.247 0.202 -	6.29 14.24 35.67 -	2.28 9.30 22.53 -	35.15 6.71 4.67 46.53
90	8	Truck 1 Van 2 Car 3 Sum	1954.13 416.46 121.16 2491.75	0.558 0.242 0.165 -	2.45 15.97 47.45 -	0.89 10.44 29.98 -	35.65 6.62 4.22 46.50
90	12	Truck 1 Van 2 Car 3 Sum	1999.66 387.20 126.30 2513.16	0.571 0.225 0.172 -	0.17 21.88 45.22 -	0.06 14.29 28.57 -	35.95 6.34 4.31 46.59
140	4	Truck 1 Van 2 Car 3 Sum	4491.25 1028.54 355.36 5875.15	0.530 0.247 0.200 -	7.34 14.24 36.31 -	4.25 11.68 29.26 -	52.14 12.59 8.09 72.82
140	8	Truck 1 Van 2 Car 3 Sum	4686.15 1007.72 341.15 6035.02	0.553 0.242 0.192 -	3.32 15.97 38.85 -	1.92 13.10 31.31 -	53.41 12.39 7.86 73.65
140	12	Truck 1 Van 2 Car 3 Sum	4787.84 936.93 392.68 6117.45	0.565 0.225 0.221 -	1.22 21.88 29.62 -	0.71 17.94 23.87 -	54.07 11.70 8.71 74.47

in Appendix B present the results for heterogeneous platoons composed of three vehicles in each of the six possible configurations.

The first column in each table specifies the convoy speed, with analyses conducted at three speeds: 50, 90, and 140 km/h. The second column indicates the inter-vehicle spacing, ranging from 4 to 12 m. The third column details the vehicle sequence within the platoon—for instance, in Table A4, the platoon configuration consists of a van leading, followed by a truck in the middle, and a passenger car at the rear.

Columns 4 through 7 present the computed aerodynamic parameters: the drag force F_d,i acting on the i-th vehicle in the platoon, the drag coefficient C_d,i for the i-th vehicle, the calculated reduction in drag coefficient ΔC_d,i, the percentage reduction in fuel consumption ΔK_i, and the average fuel consumption per 100 km for the i-th vehicle in the platoon K_avg,i. Values of drag force reduction and fuel consumption reduction for all heterogeneous vehicle column configurations are provided in the Appendix B (Table A4, Table A5, Table A6, Table A7, Table A8 and Table A9).

Analysis of the results shown in Table A4 for the van–truck–car configuration revealed an increase in drag force ranging from 620.74 to 5753.14 N, and a corresponding increase in total fuel consumption from 32.33 to 73.41 L/100 km. The drag coefficient C_d,i ranged from 0.088 to 0.277 for the van, 0.455 to 0.495 for the truck, and 0.170 to 0.322 for the passenger car. Drag coefficient reduction ΔC_d,i varied between 3.82% and 69.44% for the van, 13.46% and 20.45% for the truck, and from −2.55% to 45.86% for the passenger car. Percentage reductions in fuel consumption ΔK_i ranged from 1.4% to 56.96% for the van, 2.14% to 9.3% for the truck, and −1.61% to 29.77% for the passenger car.

Similarly, analysis of Table A5 for the van–car–truck configuration showed drag force values between 654.64 and 5822.85 N and total fuel consumption between 32.72 and 73.01 L/100 km. The drag coefficient C_d,i ranged from 0.230 to 0.291 for the van, 0.378 to 0.508 for the truck, and 0.137 to 0.250 for the passenger car. The drag coefficient reduction ΔC_d,i ranged from −1.04% to 20.14% for the van, 11.19% to 19.93% for the truck, and 20.38% to 56.37% for the passenger car. Percentage reductions in fuel consumption ΔK_i varied between −0.38% and 16.52% for the van, 2.34% and 11.23% for the truck, and 12.88% to 44.40% for the passenger car.

The analysis of the results presented in Table A6 for the car–van–truck vehicle configuration revealed a significant increase in drag force ranging from 654.63 to 5979.49 N, along with a corresponding increase in total fuel consumption from 32.72 to 77.13 L/100 km. The drag coefficient C_d,i, ranged between 0.113 and 0.280 for the van, 0.456 and 0.518 for the truck, and 0.232 and 0.380 for the passenger car. The drag reduction ΔC_d,i varied from 2.78% to 62.15% for the van, 9.44% to 20.28% for the truck, and −21.02% to 59.72% for the passenger car. The percentage reduction in fuel consumption ΔK_i ranged from 2.28% to 50.98% for the van, 1.88% to 11.53% for the truck, and −16.94% to 19.25% for the passenger car.

The analysis of Table A7 for the car–truck–van configuration indicated an increase in drag force from 763.27 to 6204.36 N and fuel consumption from 33.52 to 77.58 L/100 km. The drag coefficient C_d,i ranged from 0.214 to 0.298 for the van, 0.507 to 0.549 for the truck, and 0.137 to 0.372 for the passenger car. The drag reduction ΔC_d,i ranged between −3.47% and 25.69% for the van, 4.02% to 11.36% for the truck, and −18.47% to 56.37% for the passenger car. Fuel consumption reduction ΔK_i varied from −1.28% to 21.07% for the van, 0.68% to 6.57% for the truck, and −14.89% to 44.40% for the passenger car.

According to Table A8, for the truck–car–van configuration, drag force increased from 775.89 to 6254.47 N, with fuel consumption rising from 33.54 to 76.09 L/100 km. Drag coefficients ranged from 0.238 to 0.264 for the van, 0.561 to 0.579 for the truck, and 0.143 to 0.254 for the passenger car. Drag reduction ΔC_d,i spanned 8.33% to 17.36% for the van, −1.22% to 2.80% for the truck, and 19.11% to 54.46% for the passenger car. Fuel consumption reduction ΔK_i ranged from 4.85% to 13.95% for the van, −0.18% to 1.62% for the truck, and 8.38% to 31.57% for the passenger car.

For the truck–van–car configuration (Table A9), drag force increased from 775.93 to 6117.45 N, with fuel consumption ranging from 33.50 to 74.47 L/100 km. Drag coefficients varied between 0.225 and 0.247 for the van, 0.530 and 0.577 for the truck, and 0.163 and 0.221 for the passenger car. Drag reduction ΔC_d,i ranged from 14.24% to 21.88% for the van, −0.87% to 7.34% for the truck, and 29.62% to 48.09% for the passenger car. The percentage reduction in fuel consumption ΔK_i ranged from 5.75% to 17.94% for the van, −0.13% to 4.25% for the truck, and 13.01% to 31.31% for the passenger car.

In 8 out of 54 cases considered (three speeds × three vehicle spacings), the lowest total aerodynamic drag force F_d,c among the six analyzed vehicle configurations was observed for the van–truck–passenger car platoon, highlighted in green in Table A4, Table A5, Table A6, Table A7, Table A8 and Table A9. At 90 km/h and 12 m spacing, the lowest total drag force occurred for the passenger car–van–truck configuration. The lowest average fuel consumption values K_avg,i were recorded for six configurations with the van–truck–car (V–T–C) sequence (Table A4), two with the van–car–truck (V–C–T) sequence (Table A5), and one with the truck–van–car (T–V–C) sequence (Table A9), marked in red in the respective tables.

Table 1. Assessment of fuel consumption reduction for the car depending on the column structure.

		Most Favorable Structure			Least Favorable Structure
Speed uveh [km/h]	Position	Structure	Spacing [m]	∆Kmax [%]	Structure	Spacing [m]	∆Kmax [%]
50	Leading Middle Rear	C–T–V V–C–T T–V–C	4 4 8	19.51 19.51 16.65	C–V–T T–C–V V–T–C	12 8 12	1.01 8.38 9.70
90	Leading Middle Rear	C–T–V V–C–T T–V–C	4 4 8	35.01 35.01 29.98	C–V–T T–C–V V–T–C	12 8 12	0.60 12.47 3.96
140	Leading Middle Rear	C–T–V V–C–T T–V–C	4 4 8	44.40 44.40 31.30	C–V–T T–C–V V–T–C	12 8 8, 12	−16.94 15.40 13.60

,

Table 2. Assessment of fuel consumption reduction for the van depending on the column structure.

		Most Favorable Structure			Least Favorable Structure
Speed uveh [km/h]	Position	Structure	Spacing [m]	∆Kmax [%]	Structure	Spacing [m]	∆Kmax [%]
50	Leading Middle Rear	V–T–C C–V–T C–T–V	4 4 12	24.14 21.97 7.54	V–C–T C–V–T C–T–V	12 12 4	−0.38 4.09 −1.28
90	Leading Middle Rear	V–T–C C–V–T C–T–V	4 4 12	44.24 39.70 14.97	V–C–T C–V–T C–T–V	12 12 4	1.82 6.35 4.73
140	Leading Middle Rear	V–T–C C–V–T C–T–V	4 4 12	56.96 50.98 21.07	V–C–T C–V–T C–T–V	12 12 4	1.71 2.28 6.84

and

Table 3. Assessment of fuel consumption reduction for the truck depending on the column structure.

		Most Favorable Structure			Least Favorable Structure
Speed uveh [km/h]	Position	Structure	Spacing [m]	∆Kmax [%]	Structure	Spacing [m]	∆Kmax [%]
50	Leading Middle Rear	T–V–C V–T–C V–C–T	4 8 4	0.89 3.05 2.94	T–C–V C–T–V C–V–T	12 12 4	−0.18 0.68 1.88
90	Leading Middle Rear	T–V–C V–T–C C–V–T	4 8 8	2.28 7.09 7.34	T–C–V C–T–V C–V–T	12 12 4	−0.13 2.09 3.80
140	Leading Middle Rear	T–V–C V–T–C C–V–T	4 8 8	4.25 9.30 11.53	T–C–V C–T–V C–V–T	12 12 4	0.40 2.33 5.46

display vehicle platoon structures based on the position occupied by each vehicle within the convoy. For each analyzed speed and vehicle position, the most and least favorable platoon structures regarding fuel consumption reduction were identified. “Position” refers to the location of the analyzed vehicle in the platoon, while “Structure” denotes the sequence of vehicles. The following abbreviations are used: C—passenger car, V—van, T—truck.

For the passenger car (Table 1), the highest percentage fuel consumption reduction was achieved with configurations C–T–V and V–C–T, both at 4-m spacing and 140 km/h, resulting in a reduction of ΔK_i = 44.40%. Conversely, the C–V–T configuration at 12 m spacing showed the least favorable outcome, with an estimated fuel consumption increase of 16.94%. For the van (Table 2), the greatest fuel savings occurred in the V–T–C configuration at 140 km/h and 4-m spacing, with ΔK_i = 56.96%. In contrast, the C–T–V arrangement at 50 km/h and 4-m spacing led to a 1.28% increase in fuel consumption.

For the truck (Table 3), the most favorable configuration was V–C–T, with the truck positioned last in the platoon at 140 km/h and 4-m spacing, yielding fuel savings of 11.53%. The least favorable was the T–C–V configuration at 50 km/h and 12-m spacing, with an estimated fuel consumption increase of approximately 0.18%.

The aerodynamic interactions within heterogeneous platoons reveal important mechanisms that directly influence fuel consumption. The leading vehicle travels in an undisturbed airflow, and its drag reduction is primarily achieved through the mitigation of the wake region formed behind it. For passenger cars and light-duty vans, this reduction is most effective when their wake zones are aligned with the high-pressure area at the front of a following heavy truck—the largest vehicle in the platoon. Data presented in Table 1 and Table 2 confirm this effect: at all investigated convoy speeds, the most favorable results for both passenger cars and vans were obtained when a heavy truck followed directly behind (configurations C–T and V–T). In contrast, for the truck itself, the dominant aerodynamic factor is the large high-pressure zone at the vehicle’s front, which remains unchanged when the truck leads the platoon compared to driving outside the formation.

However, its wake region is effectively reduced when smaller vehicles follow behind, resulting in substantial drag and fuel consumption reductions. Consequently, the greatest reduction in fuel use for the heavy truck was observed when it was positioned either in the middle (at 50 km/h) or at the end of the heterogeneous platoon (at 90 and 140 km/h)—Table 3.

Using the obtained data, an estimation was made of the fuel savings on a route extending from east to west across Poland, with a total length of 671 km—from the town of Korczowa to Jędrzychowice. The analysis was performed for a heterogeneous vehicle platoon configured as van–truck–passenger car, traveling at a speed of 90 km/h and maintaining a 4-m inter-vehicle spacing. The passenger car is powered by a gasoline engine, while both the van and the truck are equipped with diesel engines. It was assumed that the passenger car and the van were loaded to 75% of their capacity, whereas the truck operated at full load. The average fuel consumption values for the vehicles are as follows: passenger car—6.03 L/100 km; van—7.39 L/100 km; truck—35.97 L/100 km. Based on these parameters, the analyzed convoy is estimated to save approximately 44.87 liters of fuel over the 671 km route. Considering gasoline priced at €1.44 per liter and diesel at €1.78 per liter, the total fuel cost reduction is approximately €76.20. For the same vehicle configuration and route parameters applied to the Warsaw–Madrid route (2858 km), the convoy would save 191.12 liters of fuel, corresponding to a fuel cost reduction of approximately €324.60.

5. Analysis of the Acoustic Field Surrounding Individual Vehicles and Heterogeneous Vehicle Platoons

Following the completion of the simulations, an analysis of the acoustic field surrounding individual vehicles and heterogeneous vehicle platoons was performed. Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 depict the A-weighted sound pressure levels measured at various speeds adjacent to the passenger car, van, and truck. Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 present the A-weighted sound pressure levels computed alongside three-vehicle platoons at different inter-vehicle distances and speeds. The platoon configuration comprised a van, a truck, and a passenger car, arranged sequentially. This configuration was selected for several reasons. Primarily, it corresponded to the lowest aerodynamic drag forces, ranging from 620.74 to 5753.14 N, and the lowest total fuel consumption, ranging from 32.33 to 73.41 L/100 km. Additionally, the computational demands were substantial, including high disk storage, processing power, and extended simulation times at the speed of 140 km/h.

An additional consideration for the acoustic analysis was a regulatory constraint: in most EU countries, trucks are prohibited from traveling below 90 km/h. Consequently, three vehicle speeds—50 km/h, 70 km/h, and 90 km/h—were selected for further acoustic evaluation of both individual vehicles and heterogeneous platoons. A-weighted sound pressure levels were calculated according to Equation (4) at discrete receiver points located 1, 2, and 4 m from the lateral surfaces of the vehicles. The receivers were positioned at the front, midsection, and rear of each vehicle at a height of 1.7 m.

For a single passenger car traveling at 50 km/h (Figure 3), the highest A-weighted sound pressure levels were observed at points 4, 1, and 5, corresponding to the first and second cross-sections, whereas the lowest levels were recorded at points 6, 9, and 7, located 4 m and 1 m away from the vehicle. The maximum A-weighted sound pressure level was 61.8 dB at point 4 (1 m from the vehicle), and the minimum was 43.1 dB at point 6 (4 m from the vehicle). The largest difference in overall A-weighted sound levels was found in cross-section 2 between points 5 and 6, amounting to 15.5 dB, while the smallest difference of 0.4 dB occurred between points 2 and 3 in cross-section 1. The most uniform distributions of A-weighted sound levels were 1.4 dB in cross-section 1, 3.5 dB in cross-section 3, and 18.7 dB in cross-section 2. The greatest non-uniformity between individual measurement points across the analyzed area reached 18.7 dB.

For a single passenger car moving at 70 km/h (Figure 4), the highest A-weighted sound pressure levels were detected at points 4, 5, and 2, located in the first and second cross-sections, while the lowest levels were recorded at points 6, 9, and 3, all situated 4 m from the vehicle. The peak A-weighted sound pressure level was 66.1 dB at point 4 (1 m from the vehicle), with the minimum value being 48.1 dB at point 6 (4 m from the vehicle). The greatest difference in sound levels was observed in cross-section 2 between points 5 and 6, equal to 15.7 dB, whereas the smallest difference of 2.6 dB was recorded between points 8 and 9 in cross-section 3. The most uniform distributions of A-weighted sound levels were 2.6 dB in cross-section 3, 3.9 dB in cross-section 1, and 18.0 dB in cross-section 2. The maximum non-uniformity within the measurement area was 18.0 dB.

For a single passenger car traveling at 90 km/h (Figure 5), the highest A-weighted sound pressure levels occurred at points 4, 5, and 8, located in the second and third cross-sections, whereas the lowest levels were measured at points 6, 3, and 9, all 4 m from the vehicle. The maximum A-weighted sound pressure level was 67.3 dB at point 4 (1 m from the vehicle), while the minimum was 51.1 dB at point 6 (4 m from the vehicle). The largest difference in sound levels was found in cross-section 2 between points 5 and 6, amounting to 14.9 dB, and the smallest difference of 1.8 dB was observed between points 7 and 8 in cross-section 3. The most uniform distributions of A-weighted sound levels were 4.5 dB in cross-section 1, 5.1 dB in cross-section 3, and 16.2 dB in cross-section 2. The greatest non-uniformity among measurement points in the analyzed area was 16.2 dB.

For a single van moving at 50 km/h (Figure 6), the highest A-weighted sound pressure levels were recorded at points 2, 4, and 5, corresponding to the first and second cross-sections, while the lowest levels were found at points 9, 8, and 7 in the third cross-section. The maximum A-weighted sound pressure level was 62.8 dB at point 2 (2 m from the vehicle), and the minimum was 48.9 dB at point 9 (4 m from the vehicle). The largest difference in A-weighted sound pressure levels was detected in cross-section 1 between points 2 and 3, amounting to 11.7 dB, whereas the smallest difference of 0.6 dB was observed between points 7 and 8 in cross-section 3. The most uniform distributions of A-weighted sound levels were 1.3 dB in cross-section 3, 6.9 dB in cross-section 2, and 11.7 dB in cross-section 1. The greatest non-uniformity between individual measurement points in the studied area was 13.9 dB.

For a single van traveling at 70 km/h (Figure 7), the highest A-weighted sound pressure levels were observed at points 5, 4, and 6, corresponding to the second cross-section, while the lowest levels were recorded at points 9, 3, and 8, located in the third and first cross-sections. The maximum A-weighted sound level was 67.1 dB at point 5, at a distance of 2 m from the vehicle, and the minimum value was 50.2 dB at points 9 and 3, both situated 4 m from the van. The greatest difference in A-weighted sound levels was detected in cross-section 2 between points 5 and 6, amounting to 8.4 dB, whereas the smallest difference of 0.4 dB was recorded between points 8 and 9 in cross-section 3. The most uniform distributions of A-weighted sound levels were 3.8 dB in cross-section 3, 7.0 dB in cross-section 1, and 8.4 dB in cross-section 2. The highest non-uniformity of A-weighted sound levels between individual points in the analyzed area reached 16.9 dB.

For a single van traveling at 90 km/h (Figure 8), the highest A-weighted sound pressure levels were recorded at points 4, 6, and 5 in the second cross-section, while the lowest levels were measured at points 3, 9, and 2 in the first and third cross-sections. The peak A-weighted sound level was 67.3 dB at point 4, 1 m from the vehicle, while the minimum was 52.0 dB at point 3, 4 m from the van. The largest difference in A-weighted sound levels was observed in cross-section 1 between points 1 and 2, amounting to 4.1 dB, whereas the smallest difference of 0.9 dB was found between points 6 and 5 in cross-section 2. The most uniform distributions of A-weighted sound levels were 3.4 dB in cross-section 2, 6.7 dB in cross-section 3, and 7.5 dB in cross-section 1. The greatest non-uniformity in the analyzed area was 15.3 dB.

For a single truck moving at 50 km/h (Figure 9), the highest A-weighted sound pressure levels were observed at points 1, 4, and 2, within the first and second cross-sections, while the lowest levels were recorded at points 9, 3, and 8, located 4 and 2 m from the vehicle. The maximum A-weighted sound level was 107.8 dB at point 1, 1 m from the truck, and the minimum was 96.3 dB at point 9, 4 m away. The greatest difference in sound levels was detected in cross-section 1 between points 2 and 3, amounting to 5.8 dB, while the smallest difference of 0.6 dB occurred between points 7 and 8 in cross-section 3. The most uniform distributions were 1.8 dB in cross-section 3, 5.9 dB in cross-section 2, and 10.4 dB in cross-section 1. The largest non-uniformity in the analyzed area was 11.5 dB.

For a single truck moving at 70 km/h (Figure 10), the highest A-weighted sound pressure levels were observed at points 1, 4, and 2, in the first and second cross-sections, while the lowest levels were recorded at points 9, 8, and 3, located in the third and first cross-sections. The maximum sound level was 107.9 dB at point 1, 1 m from the vehicle, and the minimum was 96.2 dB at point 9, 4 m from the truck. The largest difference in sound levels was found in cross-section 1 between points 2 and 3, amounting to 5.8 dB, whereas the smallest difference of 0.5 dB was between points 7 and 8 in cross-section 3. The most uniform distributions were 1.6 dB in cross-section 3, 6.0 dB in cross-section 2, and 10.3 dB in cross-section 1. The greatest non-uniformity in the analyzed area was 11.7 dB.

For a single truck traveling at 90 km/h (Figure 11), the highest A-weighted sound pressure levels were recorded at points 1, 2, and 4, within the first and second cross-sections, while the lowest levels were observed at points 9, 8, and 6, located in the third and second cross-sections. The peak sound level was 107.7 dB at point 1, 1 m from the vehicle, and the minimum was 96.0 dB at point 9, 4 m away. The greatest difference in sound levels was detected in cross-section 1 between points 2 and 3, amounting to 5.8 dB, while the smallest difference of 0.6 dB occurred between points 7 and 8 in cross-section 3. The most uniform distributions were 1.8 dB in cross-section 3, 5.8 dB in cross-section 2, and 9.9 dB in cross-section 1. The highest non-uniformity in the analyzed area was 11.7 dB.

In the subsequent stage of the study, the distributions of A-weighted sound levels were analyzed for a vehicle platoon traveling at speeds of 50 km/h, 70 km/h, and 90 km/h, with inter-vehicle spacings of 4, 8, and 12 m.

Based on the analysis of the results (Figure 12) of A-weighted sound level distributions for a platoon moving at 50 km/h with a 4-m spacing, it was concluded that the highest sound pressure levels occurred at a distance of 1 m from the truck and the van—specifically at measurement points 10, 13, and 4. Conversely, the lowest A-weighted sound levels were recorded at a distance of 4 m from the passenger car—at points 27, 21, and 24. The maximum A-weighted sound level was 100.0 dB at point 10, located 1 m from the truck, while the minimum value was 88.7 dB at point 27, located 4 m from the passenger car. Furthermore, the greatest difference in A-weighted sound levels was observed in cross-section 8 between points 22 and 23, amounting to 6.7 dB, whereas the smallest difference—0.1 dB—was noted between points 17 and 16 in cross-section 6. The most uniform distributions of A-weighted sound level were observed as follows: 0.4 dB in section 6; 1.6 dB in section 5; 1.8 dB in section 2; 2.3 dB in section 3; 3.1 dB in section 7; 3.2 dB in section 1; 3.7 dB in section 9; 7.7 dB in section 4; and 7.8 dB in section 8. The maximum nonuniformity in A-weighted sound level between individual points within the analyzed area reached 11.3 dB.

Based on the analysis of the results (Figure 13) presenting the distributions of A-weighted sound levels for a vehicle platoon traveling at a speed of 70 km/h with an inter-vehicle spacing of 4 m, it can be concluded that the highest sound levels were recorded at distances of 1 m and 2 m from the truck, specifically at points 10, 13, and 14. The lowest A-weighted sound levels were observed at a distance of 4 m from the passenger car, namely at points 27, 21, and 24. The maximum A-weighted sound level reached 100.1 dB at point 10 (1 m from the truck), while the minimum was 88.8 dB at point 27 (4 m from the passenger car). Furthermore, the greatest difference in A-weighted sound levels was found in cross-section 8 between points 22 and 23, amounting to 6.6 dB, whereas the smallest difference, 0.2 dB, was observed between points 17 and 16 in cross-section 6. The most uniform A-weighted sound level distributions were identified in the following cross-sections: 0.9 dB in section 6; 1.6 dB in section 2; 1.7 dB in section 3; 1.8 dB in section 5; 3.0 dB in section 7; 3.1 dB in section 1; 3.3 dB in section 9; 7.6 dB in section 4; and 7.8 dB in section 8. The maximum variation in A-weighted sound level across the entire analyzed domain was 11.3 dB.

According to the analysis of the results (Figure 14) showing the A-weighted sound level distributions for a platoon traveling at 90 km/h with a 4-m spacing, the highest levels occurred at distances of 1 m and 2 m from the truck and van—specifically at points 10, 13, and 4. The lowest levels were again recorded at a distance of 4 m from the passenger car, at points 27, 21, and 24. The maximum A-weighted sound level was 100.1 dB at point 10 (1 m from the truck), while the minimum was 88.3 dB at point 27 (4 m from the passenger car). The greatest difference in A-weighted levels was observed in cross-section 8 between points 22 and 23 (6.2 dB), whereas the smallest difference, 0.4 dB, was observed between points 7 and 8 in cross-section 3. The most uniform distributions were found in the following sections: 1.2 dB (section 6), 1.4 dB (section 3), 1.8 dB (section 2), 1.9 dB (section 5), 2.8 dB (section 7), 3.0 dB (section 1), 3.4 dB (section 9), 7.2 dB (section 8), and 7.6 dB (section 4). The maximum variation in A-weighted sound levels across the entire analyzed area was 11.8 dB.

Based on the analysis of the results (Figure 15) for a platoon traveling at a speed of 50 km/h with an 8-m inter-vehicle distance, the highest sound levels were recorded at 1 m and 2 m from the truck (points 10, 13, and 11), whereas the lowest were observed 4 m from the passenger car (points 27, 26, and 24). The maximum A-weighted sound level was 100.0 dB at point 10, and the minimum was 86.3 dB at point 27. The largest difference in A-weighted levels occurred in cross-section 4 between points 11 and 12 (5.7 dB), while the smallest difference (0.2 dB) appeared in four cross-sections: points 1–2 (section 1), 19–20 (section 7), 22–23 (section 8), and 25–26 (section 9). The most uniform distributions were recorded as follows: 0.6 dB (section 9), 0.7 dB (section 8), 0.8 dB (section 7), 1.0 dB (section 1), 1.2 dB (section 2), 1.5 dB (section 6), 1.8 dB (section 3), 4.5 dB (section 5), and 8.4 dB (section 4). The maximum nonuniformity in A-weighted sound level across the analyzed domain was 13.7 dB.

Based on the analysis of the results (Figure 16) illustrating the distribution of A-weighted sound pressure levels for a vehicle platoon traveling at a speed of 70 km/h with an 8-m inter-vehicle spacing, it can be concluded that the highest sound levels were observed at distances of 1 m and 2 m from the truck, specifically at points 10, 11, and 16. The lowest A-weighted sound levels were recorded at a distance of 4 m from the passenger car and the van, namely at points 27, 24, and 3. The maximum A-weighted sound level reached 96.9 dB at point 10 (1 m from the truck), while the minimum value was 80.9 dB at point 15 (4 m from the passenger car). Furthermore, the largest difference in A-weighted sound levels was found in cross-section 5 between points 14 and 15, amounting to 8.1 dB, while the smallest difference was 0.1 dB between points 1 and 2 in cross-section 1. The most uniform distributions of A-weighted sound levels were recorded as follows: 0.9 dB (section 1), 1.0 dB (section 9), 1.1 dB (section 2), 1.2 dB (section 8), 1.3 dB (section 7), 1.7 dB (section 3), 2.9 dB (section 6), 3.4 dB (section 4), and 12.8 dB (section 5). The maximum variability in A-weighted sound levels across the analyzed domain was 16.0 dB.

Based on the analysis of the results (Figure 17) showing the A-weighted sound level distribution for a convoy moving at 90 km/h with an 8-m spacing between vehicles, the highest sound levels were recorded at 1 m and 2 m from the truck, specifically at points 10, 11, and 13. The lowest A-weighted sound levels were observed 4 m from the passenger car, namely at points 27, 26, and 25. The maximum A-weighted sound level was 99.1 dB at point 10 (1 m from the truck), while the minimum was 84.6 dB at point 27 (4 m from the passenger car). The greatest difference in A-weighted sound levels was recorded in cross-section 8 between points 11 and 12 (5.5 dB), whereas the smallest difference of 0.1 dB was observed in four cross-sections: points 1–2 (section 1), 19–20 (section 7), 22–23 (section 7), and 25–26 (section 9). The most uniform distributions were recorded as follows: 0.4 dB (section 9), 0.5 dB (sections 8 and 7), 0.7 dB (section 1), 1.1 dB (section 2), 1.5 dB (section 6), 1.7 dB (section 3), 4.5 dB (section 5), and 8.2 dB (section 4). The maximum variation in A-weighted sound levels within the analyzed area was 14.5 dB.

From the analysis of the results (Figure 18) presenting the A-weighted sound level distribution for a convoy moving at 50 km/h with a 12-m spacing between vehicles, it can be inferred that the highest sound levels occurred at distances of 1 m and 2 m from the truck—specifically at points 10, 13, and 11. The lowest sound levels were recorded at 4 m from the passenger car (points 27, 26, and 25). The maximum A-weighted sound level was 99.6 dB at point 10 (1 m from the truck), and the minimum was 85.1 dB at point 27 (4 m from the passenger car). The greatest difference in A-weighted sound levels was recorded in cross-section 4 between points 11 and 12 (5.5 dB), while the smallest difference, 0.0 dB, occurred between points 1–2 (section 1) and 4–5 (section 2). The most uniform sound level distributions were as follows: 0.5 dB (section 9), 0.6 dB (sections 8 and 7), 0.7 dB (sections 1 and 2), 0.9 dB (section 3), 1.5 dB (section 6), 4.6 dB (section 5), and 8.1 dB (section 4). The maximum nonuniformity of A-weighted sound levels within the measurement domain was 14.5 dB.

According to the analysis of the results (Figure 19) showing A-weighted sound level distributions for a convoy traveling at 70 km/h with a 12-m spacing between vehicles, the highest sound levels were observed at 1 m and 2 m from the truck, namely at points 10, 11, and 14. The lowest sound levels were recorded at 4 m from the passenger car—points 27, 26, and 25. The maximum A-weighted sound level was 99.1 dB at point 10 (1 m from the truck), while the minimum was 84.7 dB at point 27 (4 m from the passenger car). The largest difference in A-weighted levels was observed in cross-section 4 between points 11 and 12 (5.4 dB), and the smallest difference of 0.1 dB occurred between points 1–2 (section 1), 4–5 (section 2), and 7–8 (section 3). Uniform distributions of A-weighted sound levels were recorded as follows: 0.5 dB (section 9), 0.6 dB (sections 1, 7, and 8), 0.8 dB (section 2), 1.0 dB (section 3), 1.5 dB (section 6), 3.8 dB (section 5), and 8.1 dB (section 4). The greatest nonuniformity in A-weighted sound levels across the analyzed area was 14.4 dB.

The analysis of the results (Figure 20) of A-weighted sound level distributions for a convoy moving at 90 km/h with 12-m vehicle spacing indicates that the highest sound levels occurred at 1 m and 2 m from the truck (points 10, 11, and 13). The lowest levels were observed 4 m from the passenger car, at points 27, 26, and 25.

The maximum A-weighted sound level reached 98.5 dB at point 10 (1 m from the truck), and the minimum was 82.8 dB at point 27 (4 m from the passenger car). The largest difference in A-weighted sound levels occurred in cross-section 4 between points 11 and 12 (5.3 dB), while the smallest difference of 0.1 dB was recorded between points 19–20 (section 7) and 25–26 (section 9). The most uniform distributions of A-weighted sound levels were recorded as follows: 0.3 dB (sections 1, 7, 8, and 9), 0.4 dB (section 2), 0.8 dB (section 3), 1.4 dB (section 6), 4.6 dB (section 5), and 7.9 dB (section 4). The greatest nonuniformity in A-weighted sound levels within the study area was 15.7 dB.

A comparative analysis of the compiled A-weighted sound pressure levels for both individual vehicles and vehicle platoons demonstrated that the truck constitutes the dominant source of noise. Among the individual vehicles, the van exhibited the lowest A-weighted sound pressure levels. Due to the substantial differences in A-weighted sound levels at locations situated in close proximity to both individual vehicles and platoons, additional calculations were conducted at a horizontal distance of 15 m and a height of 4 m. The equivalent continuous A-weighted sound pressure levels (L_Aeq) were determined in accordance with Equation (5). For individual vehicles traveling at a speed of 50 km/h, the calculated L_Aeq values were as follows: passenger car—35.1 dB, van—35.6 dB, and truck—81.1 dB. At 70 km/h: passenger car—38.0 dB, van—37.6 dB, and truck—81.1 dB. At 90 km/h: passenger car—40.6 dB, van—39.3 dB, and truck—81.5 dB.

Subsequently, the equivalent continuous A-weighted sound pressure level (L_Aeq) was determined for a heterogeneous vehicle platoon. At a driving speed of 50 km/h, the L_Aeq was calculated to be 86.6 dB for an inter-vehicle spacing of 4 m, 81.7 dB for 8 m, and 81.5 dB for 12 m. For a speed of 70 km/h, the corresponding L_Aeq values were 86.4 dB, 81.0 dB, and 81.4 dB, respectively. At 90 km/h, the L_Aeq decreased slightly, reaching 85.6 dB for 4-m spacing, 80.4 dB for 8 m, and 80.0 dB for 12 m.

In order to validate the obtained results, supplementary computational methods recommended for evaluating the environmental impact of road traffic noise were employed [104,105,106]. The simulations were conducted using the SoundPlan 8.2 and 9.1 software. At this stage of the research, 18 numerical models were developed in accordance with the NMPB-Routes-2008 methodology and the ISO 9613-2 standard. The models encompassed both individual vehicles and heterogeneous vehicle platoons, configured with three different inter-vehicle spacings. The analysis was based on input parameters derived from the dimensions of the vehicles and their spacing, which were subsequently converted into traffic flow rates expressed in vehicles per hour. Three driving speed scenarios were considered in the analyzed variants: 50, 70, and 90 km/h. For a platoon consisting of a delivery van, a truck, and a passenger car, the calculated traffic flow rates were as follows: 7500 vehicles/h for an inter-vehicle distance of 4 m, 5625 vehicles/h for 8 m, and 4500 vehicles/h for 12 m. Trucks represented one-third of the total traffic volume, while passenger cars and delivery vans accounted for the remaining two-thirds.

After data input, equivalent continuous A-weighted sound pressure levels (L_Aeq) were calculated. For a single truck traveling at 90 km/h, L_Aeq was found to be 81.6 dB, whereas for a passenger car and a van, L_Aeq was 72.7 dB.

The subsequent phase of the study involved the determination of L_Aeq values for heterogeneous vehicle platoons traveling at various speeds and inter-vehicle distances. For a platoon moving at 90 km/h, the resulting LAeq values were: 84.0 dB for a 4-m gap, 82.8 dB for 8 m, and 81.8 dB for 12 m. At a speed of 70 km/h, the L_Aeq values were: 81.9 dB (4 m), 80.6 dB (8 m), and 79.7 dB (12 m). At 50 km/h, the measured values were: 81.4 dB (4 m), 80.2 dB (8 m), and 79.2 dB (12 m).

Analyzing the results presented above for heterogeneous vehicle platoons, it can be stated that in 7 out of 9 cases, the differences between the values obtained using computational methods—namely the NMPB-Routes-2008 method and the finite volume method—fall within the range of −2.3 dB to 2.4 dB. In two cases, specifically for an inter-vehicle distance of 4 m and speeds of 50 km/h and 70 km/h, the discrepancies are higher, amounting to −5.2 dB and −4.5 dB, respectively.

The differences observed in the CFD-based results primarily stem from simplifications in the geometry, particularly of the truck model—such as the presence of sharp edges and the omission of dynamic tire–road interaction. This is indirectly confirmed by CFD results obtained for individual vehicles.

Therefore, future research should focus on improving the geometric fidelity of the truck model. However, such enhancements will inevitably lead to a significant increase in the number of finite volume elements in the models and, consequently, a longer computational time.

As part of the research, in situ measurements of the equivalent continuous A-weighted sound pressure level (L_Aeq) were conducted in the Kraków metropolitan area. The measurements were carried out using a Svan 945A sound level meter, manufactured by the Polish company Svantek. Data acquisition was performed during nighttime hours, after 11:00 p.m., under calm wind conditions and at an ambient temperature between 12 °C and 14 °C.

The noise measurements were conducted during the pass-by of individual vehicles traveling at a constant speed of 90 km/h, with the engine running but under no load (i.e., not transmitting torque). Sound pressure levels were recorded at a distance of 15 m from the vehicle path and at a height of 4 m.

The following equivalent continuous A-weighted sound pressure levels (L_Aeq) were recorded: truck—81.5 dB, car—75.3 dB and van—72.9 dB. For comparison, L_Aeq values calculated using the NMPB-Routes-2008 method were: car and van—72.7 dB and truck—81.6 dB.

The differences between the measured and NMPB-Routes-2008-calculated values were: −0.1 dB for the truck, 2.6 dB for the passenger car, and 0.2 dB for the van. These discrepancies are considered acceptable and within the expected range of measurement and modeling uncertainty.

The largest deviation, observed for the passenger car, is primarily attributed to the technical condition of its tires.

Due to the lack of dedicated access to delivery vans and heavy-duty trucks, it was not possible to freely configure vehicle combinations into heterogeneous platoons. As a result, the cumulative equivalent continuous A-weighted sound pressure levels (L_Aeq) for such platoons were determined analytically, based on measurement data obtained from individual vehicle pass-by events.

For a heterogeneous platoon composed of the aforementioned vehicle types, traveling at a speed of 90 km/h and evaluated at a distance of 15 m, the analytically estimated L_Aeq values were: 4-m inter-vehicle spacing—82.0 dB, 8-m spacing—81.6 dB and 12-m spacing—81.3 dB.

These values were calculated without accounting for acoustic interactions or potential sound wave interference that may occur within a real-world vehicle platoon. Nevertheless, in the absence of empirical data for actual heterogeneous platoons, the analytically derived values were adopted as reference levels.

Based on this comparison, the differences between the analytical approach and the NMPB-Routes-2008 method were: −2.0 dB, −1.2 dB, and −0.5 dB for 4 m, 8 m, and 12 m spacing, respectively. For comparison, the corresponding discrepancies relative to the Computational Fluid Dynamics (CFD) model were: +3.6 dB, −1.2 dB, and −1.3 dB, respectively.

6. Discussion and Conclusions

The study presents the results of numerical simulations and analyses of aerodynamic and aeroacoustic phenomena generated by heterogeneous vehicle platoons, together with an assessment of their impact on fuel consumption and environmental effects. The research was structured into several stages.

In the initial stage, a comprehensive literature review was conducted concerning transportation within the European Union, with a particular emphasis on Poland, the authors’ country of origin. A comparative analysis of the road network and the volume of goods transported via road infrastructure was performed. Special attention was given to Poland due to the dynamic expansion of its truck fleet, which plays a significant role in European transport but also exerts a considerable negative environmental impact. Emissions from road transport primarily arise from fuel combustion in vehicle engines, tire and brake pad wear, secondary resuspension of road dust, and noise emissions causing environmental emission. Noise monitoring data derived from acoustic maps, updated every five years, indicated that in 2021, road traffic noise posed a substantial threat mainly in urbanized areas, increasingly affecting a growing number of residents.

The second stage comprised a focused literature review on selected aspects of vehicle and vehicle platoon aerodynamics and aeroacoustics. The review emphasized drag coefficients and vehicle geometries influencing the aerodynamics of single vehicles and platoons. Selected national and international studies were evaluated, particularly those developing scientific and technical solutions for the formation, control, and communication within both homogeneous and heterogeneous platoons. Research involving autonomous vehicles and their cooperative interactions with conventional vehicles in platoon formation was also highlighted.

In the primary stage of the research, numerical models of heterogeneous vehicle platoons with various configurations were developed and refined. These platoons consisted of a passenger car (Audi A3), a delivery van (Fiat Ducato L3H2), and a heavy-duty truck (Mercedes-Benz Actros F with trailer). A total of 54 heterogeneous platoon models were generated, traveling at three speeds—50 km/h, 90 km/h, and 140 km/h—and with three inter-vehicle distances: 4 m, 8 m, and 12 m.

Aerodynamic drag forces were determined for individual vehicles and aggregated for entire platoons. Drag coefficients and their percentage reductions were calculated alongside average fuel consumption and fuel savings for single vehicles, as well as total fuel consumption for all platoons. A comprehensive analysis was conducted to assess the effects of vehicle dimensions, platoon ordering, inter-vehicle spacing, and convoy speed on aerodynamic and aeroacoustic behavior. The most aerodynamically favorable platoon configurations were identified, and corresponding fuel consumption reduction potentials were estimated. Additionally, A-weighted sound pressure levels and equivalent sound levels were computed around the vehicles and for a selected heterogeneous platoon configuration (van–truck–car). Acoustic simulations were performed for three inter-vehicle distances and speeds of 50 km/h, 70 km/h, and 90 km/h.

The simulation framework employed the k-ω SST turbulence model and Large Eddy Simulation (LES), coupled with the Ffowcs Williams–Hawkings acoustic analogy. CFD computations were carried out on the Prometheus supercomputer at the Cyfronet Academic Computer Centre in Kraków, using Ansys Fluent software. In total, 54 steady-state and 18 unsteady-state simulations were conducted. The total computational time for the research exceeded 4,500,000 CPU hours. For parallel computations on Prometheus, an additional GPU queue was employed. Due to the model size, the required RAM for post-processing exceeded 600 GB. Verification analyses utilized the NMPB-Routes-2008 and ISO 9613-2 methodologies implemented in the SoundPlan software, yielding 18 validation studies.

Analysis of all 54 platoon configurations across 8 scenarios (3 speeds × 3 inter-vehicle distances) showed that the lowest total aerodynamic drag force, F_d,c, among six vehicle arrangements occurred for the van–truck–car configuration. The only exception was at 25 m/s and a 12 m inter-vehicle gap, where the car–van–truck configuration exhibited the lowest drag.

Specific drag force values for the van–truck–car configuration were as follows: at 50 km/h with 4 m, 8 m, and 12 m spacing: 620.74 N, 662.23 N, and 705.27 N, respectively; at 90 km/h for 4 m and 8 m: 2006.01 N and 2180.98 N; and at 140 km/h for 4 m, 8 m, and 12 m: 4904.44 N, 5451.57 N, and 5753.14 N. For the car–van–truck configuration at 90 km/h and 12 m spacing, the drag force was 2328.76 N.

Lowest average fuel consumption values (K_avg,i) were found in six configurations with the van–truck–car structure, two with van–car–truck, and one with truck–van–car. For the van–truck–car platoon, average fuel consumption [L/100 km] was: at 50 km/h with 4 m, 8 m, and 12 m gaps: 32.33, 32.92, and 33.31; at 90 km/h for 4 m and 8 m: 42.60 and 45.00; and at 140 km/h for 4 m: 64.33. For the truck–van–car at 90 km/h and 12 m spacing, consumption was 46.59 L/100 km; and for van–car–truck at 140 km/h with 8 m and 12 m, 70.15 and 73.01 L/100 km, respectively.

The acoustic study, detailed in the preceding chapter, included CFD-based determination of equivalent A-weighted sound pressure levels (L_Aeq) for heterogeneous platoons. At 50 km/h with 4 m spacing, L_Aeq was 86.6 dB; at 8 m and 12 m, 81.7 dB and 81.5 dB, respectively. At 70 km/h and 4 m, L_Aeq was 86.4 dB; at 8 m and 12 m, 81.0 dB and 81.4 dB. At 90 km/h and 4 m, L_Aeq was 85.6 dB; at 8 m and 12 m, 80.4 dB and 80.0 dB.

Verification using NMPB-Routes-2008 and ISO 9613-2 methods—recommended for environmental noise assessment—was performed using geometric approaches in SoundPlan software. Resulting L_Aeq values for the platoon at 90 km/h were 84.0 dB, 82.8 dB, and 81.8 dB for 4 m, 8 m, and 12 m spacings; at 70 km/h, 81.9 dB, 80.6 dB, and 79.7 dB; and at 50 km/h, 81.4 dB, 80.2 dB, and 79.2 dB.

In conclusion, the optimal platoon configuration is van–truck–car with 4 m inter-vehicle distances. For urban traffic and built-up areas with 50 km/h limits, 8 m spacing is preferred due to minimal (1.8%) increase in fuel consumption (32.92 L/100 km) and advantages in driving safety, driver/autonomous system response, traffic flow stability, and reduced noise emissions (L_Aeq 81.7 dB). For highway speeds of 90 km/h, 4 m spacing is optimal, corresponding to L_Aeq 85.6 dB. At 140 km/h with 4 m spacing (hypothetical no speed limits), fuel consumption increased by 51% (64.33 L/100 km) compared to 90 km/h, with noise levels reaching L_Aeq 87.9 dB per NMPB-Routes-2008 and ISO 9613-2.

At the current stage, it was not possible to further enhance the study, as anticipated by the scientific community, or to extend the aerodynamic and aeroacoustic simulations using CFD and the Ffowcs Williams–Hawkings analogy within a reasonable timeframe. The results obtained so far required an extremely high computational effort. Transient-state simulations, necessary for determining equivalent A-weighted sound levels, were particularly time-consuming. The actual time required to perform these calculations amounted to approximately one and a half years, considering limited access to the computational queue. Simulations were performed on the Prometheus supercomputer at the Academic Computer Centre Cyfronet AGH. Each steady-state numerical simulation was executed using 8 nodes and 192 cores, while transient-state simulations utilized 10 nodes and 240 cores. The total computational time for the research exceeded 4,500,000 CPU hours. For parallel computations on Prometheus, an additional GPU queue was employed. Due to the model size, the required RAM for post-processing exceeded 600 GB. A total of 54 convoy structure models were developed for steady-state calculations and 18 for transient-state simulations.

Therefore, for the speed range between 50 and 140 km/h, an estimation of the percentage reduction in fuel consumption for the selected van–truck–car platoon was performed in comparison with vehicles driving outside the platoon. To account for the nature of the phenomenon and ensure numerical stability, a polynomial interpolation method [122] was applied. A second-order polynomial was used, and the system of equations was solved using the Gaussian elimination method. For computations at 10 km/h intervals, Horner’s algorithm was employed. The values of the polynomial interpolation coefficients are presented in

Table A10. A second-degree interpolating polynomial and its coefficients, describing the reduction in fuel consumption for a selected heterogeneous platoon of vehicles (van–truck–car) compared to the operation of these vehicles individually, for three different inter-vehicle distances.

Inter-Vehicle Distances in a Platoon: Van–Truck–Car D	A Second-Degree Interpolating Polynomial Fuel Consumption Reduction Fcr(uveh) = a∙uveh2 + b∙uveh + c and Its Coefficients
[m]	a	b	c
4	−0.00080222	0.30431111	−7.14
8	−0.00064277	0.20323888	−4.195
12	0.00078833	−0.09211666	5.855

for three inter-vehicle distances within the heterogeneous platoon.

Equivalent A-weighted sound levels L_Aeq were determined at a distance of 15 m from the heterogeneous platoon for each speed individually, using the NMPB-Routes-2008 and ISO 9613-2 methods. The results of the polynomial interpolation concerning the percentage reduction in fuel consumption and the equivalent A-weighted sound levels are summarized in

Table A11. Percentage reductions in fuel consumption and noise levels—expressed as equivalent A-weighted sound level (L_Aeq)—for the selected heterogeneous vehicle platoon (van–truck–car), compared with the operation of these vehicles outside the platoon.

Speed of the Vehicle Platoon uveh [km/h]	Inter-Vehicle Distance: 4 m		Inter-Vehicle Distance: 8 m		Inter-Vehicle Distance: 12 m
	Fuel Consump. Reduction [%]	LAeq at 15 m [dB]	Fuel Consump. Reduction [%]	LAeq at 15 m [dB]	Fuel Consump. Reduction [%]	LAeq at 15 m [dB]
50	6.07	81.4	4.36	80.2	3.22	79.2
60	8.23	81.6	5.68	80.3	3.17	79.3
70	10.23	81.9	6.88	80.6	3.27	79.6
80	12.07	83.0	7.95	81.8	3.53	80.8
90	13.75	84.0	8.89	82.8	3.95	81.8
100	15.27	84.9	9.70	83.7	4.53	82.7
110	16.63	85.8	10.38	84.5	5.26	83.5
120	17.82	86.5	10.94	85.3	6.15	84.3
130	18.86	87.2	11.36	86.0	7.20	85.0
140	19.74	87.8	11.66	86.6	8.41	85.6

in Appendix B. In the future, the interpolation results should be verified using the developed methodology, as was performed for the speeds of 50, 90, and 140 km/h, and further validated at a dedicated field testing ground.

The research contributes mathematical, geometrical, and numerical models relevant to contemporary transport challenges. Results demonstrate the benefits of platooning in reducing aerodynamic drag, fuel consumption, and pollutant emissions. Findings are documented in nine tables and twenty figures.

While results are satisfactory, future work will refine models—especially the truck—to enhance accuracy. Planned research includes sensitivity analyses of geometric features, particularly real truck dimensions, and the integration of artificial intelligence techniques to optimize aerodynamic drag and fuel/energy consumption reductions, thereby mitigating environmental impact.

In conclusion, it should be noted that driving in a convoy and maintaining precisely defined inter-vehicle distances directly affect the aerodynamic efficiency of the entire platoon. When vehicles travel closely in a coordinated formation, the trailing vehicles operate within the reduced-pressure wake generated by the lead vehicle, resulting in lower aerodynamic drag. This reduction in drag not only decreases fuel consumption but also contributes to a significant lowering of emissions, making platooning an effective strategy for sustainable transport. Additionally, the choice of inter-vehicle spacing is critical: too large a distance diminishes the aerodynamic benefit, while too small a distance requires advanced control systems to ensure safety and synchronization. By emphasizing these factors, the study clearly demonstrates how platooning can optimize energy efficiency in real-world traffic conditions while maintaining operational safety.

For this reason, studies on both heterogeneous and homogeneous vehicle platoons should be preceded by comprehensive aerodynamic and aeroacoustic analyses to assess their impact on fuel and/or energy consumption, as well as their environmental implications. The authors have successfully undertaken this task and plan to carry out extensive analytical, numerical, and field investigations of heterogeneous and homogeneous vehicle platoons in the future.

Promising results reported by the scientific community regarding the development and implementation of advanced technical solutions in the field of intelligent transportation systems include powertrain systems, control systems, 6G communication, and novel artificial intelligence techniques. These factors, combined with anticipated changes in traffic regulations, suggest that both homogeneous and heterogeneous vehicle platoons will soon operate on public roads. Currently, primarily the former are being tested on research proving grounds and selected road sections; however, this is expected to change in the near future.

6.1. Conclusions

The study presents a comprehensive numerical analysis of aerodynamic and aeroacoustic phenomena in heterogeneous vehicle platoons and evaluates their impact on fuel consumption and environmental emissions. The results demonstrate the practical applicability of the proposed models, showing that platoon formation—particularly the van–truck–car configuration with designated inter-vehicle distances—can significantly reduce aerodynamic drag, fuel consumption, and pollutant emissions. Data on the acoustic effects of heterogeneous platoons may inform the implementation of active and passive measures, such as traffic management of vehicle platoons in urban areas, construction of noise barriers along selected roads and highways, and the use of low-noise pavement surfaces.

The conducted research and analyses show that:

• The best configuration of a heterogeneous platoon among the 54 analyzed is the van–truck–car arrangement.
• Outside built-up areas, on highways, heterogeneous platoons should be formed with inter-vehicle distances of 4 m.
• In cities and urban agglomerations, heterogeneous platoons should be formed with inter-vehicle distances of 4 m, or alternatively 8 m, between vehicles.
• Each kilometer traveled under steady-state conditions by the selected heterogeneous platoon configuration results in a reduction in fuel consumption.
• In cities and urban agglomerations, operating a heterogeneous platoon with 4-m inter-vehicle distances may lead to the perception of impulsive noise, whereas 8-m distances may lead to the perception of stationary noise.

6.2. Future Research Directions

In the future, the authors plan to carry out further studies according to the following schedule:

▪

Perform numerical aerodynamic and aeroacoustic simulations using CFD and the Ffowcs Williams–Hawkings analogy for individual vehicles and heterogeneous platoons at speeds ranging from 30 to 135 km/h, with 5 km/h intervals,

▪

Conduct numerical aerodynamic and aeroacoustic simulations of heterogeneous platoons including a heavy-duty truck with a drag coefficient C_d < 0.35,

▪

Develop and perform nonlinear and transient models of powertrain systems for various vehicles powered by conventional fuels, hydrogen, and electric energy,

▪

Carry out aerodynamic and acoustic investigations as well as analyses of fuel and/or energy consumption at a dedicated field testing ground.

The study has universal applicability, aiding transport operators and national/international economies in efficient fuel and energy resource management. This may contribute to reducing CO₂ and other pollutant emissions and noise pollution. Strategically organized vehicle platoons will become integral components of future Intelligent Transportation Systems (ITSs) and Intelligent Environmental Management Systems (IEMSs). The forthcoming publication will focus on an intelligent environmental management system that incorporates road transport, exemplified by the Royal Capital City of Krakow.