Development of a Novel Weighted Maximum Likelihood-Based Parameter Estimation Technique for Improved Annual Energy Production Estimation of Wind Turbines
Abstract
1. Introduction
2. Materials and Methods
2.1. Reference Wind Turbine Model
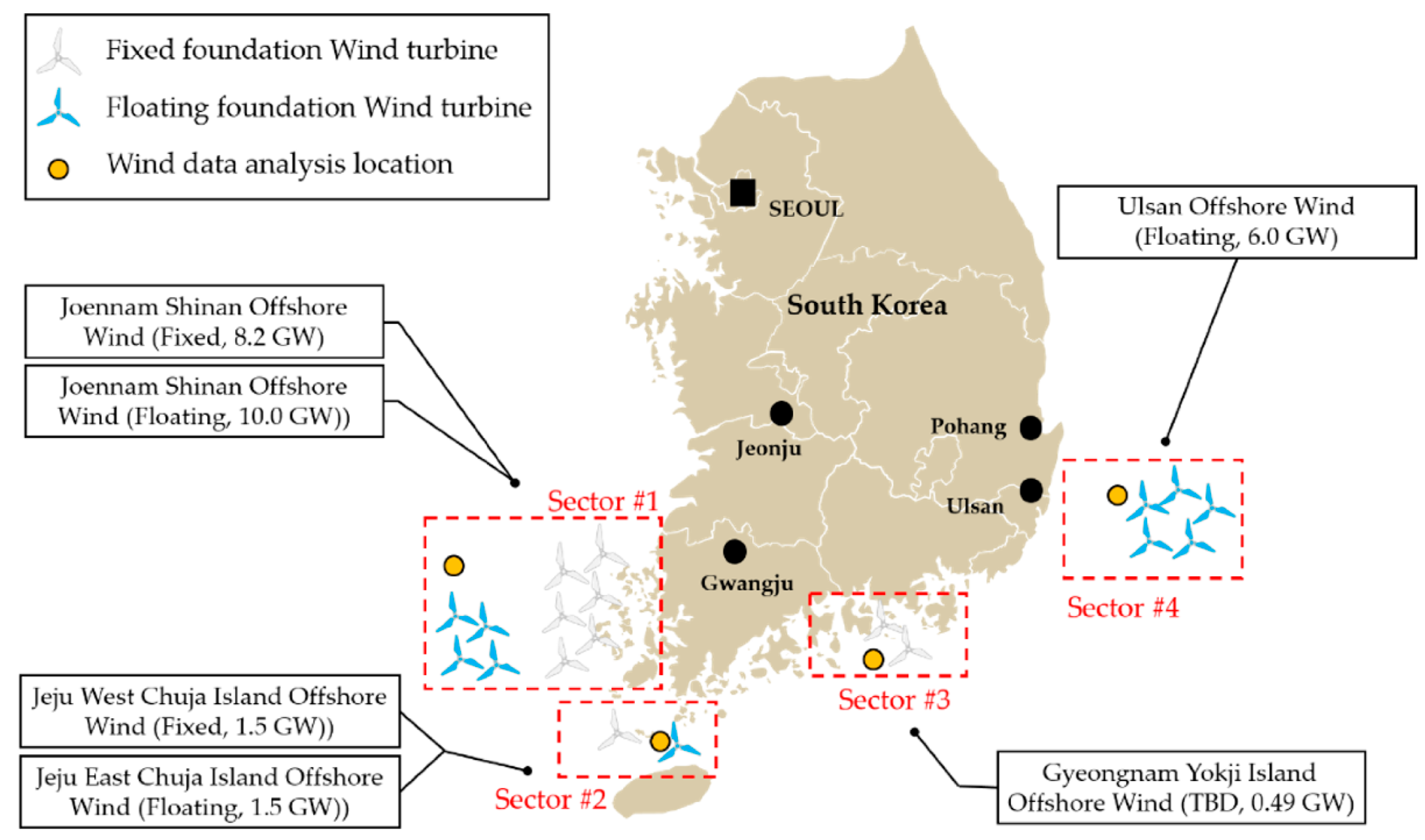
2.2. Wind Resource Data
2.3. Wind Shear Exponent
2.4. Weibull Distribution
2.5. Parameter Estimation
2.5.1. Least Squares Method
2.5.2. Method of Moments
2.5.3. Probability Weighted Moment
2.5.4. Empirical Method
2.5.5. Energy Pattern Factor Method
2.5.6. Power Density Method
2.5.7. Maximum Likelihood Estimation
2.6. Annual Energy Production-Based Goodness-of-Fit
3. Proposed Methodology
Weighted Maximum Likelihood Estimation
4. Results and Discussion
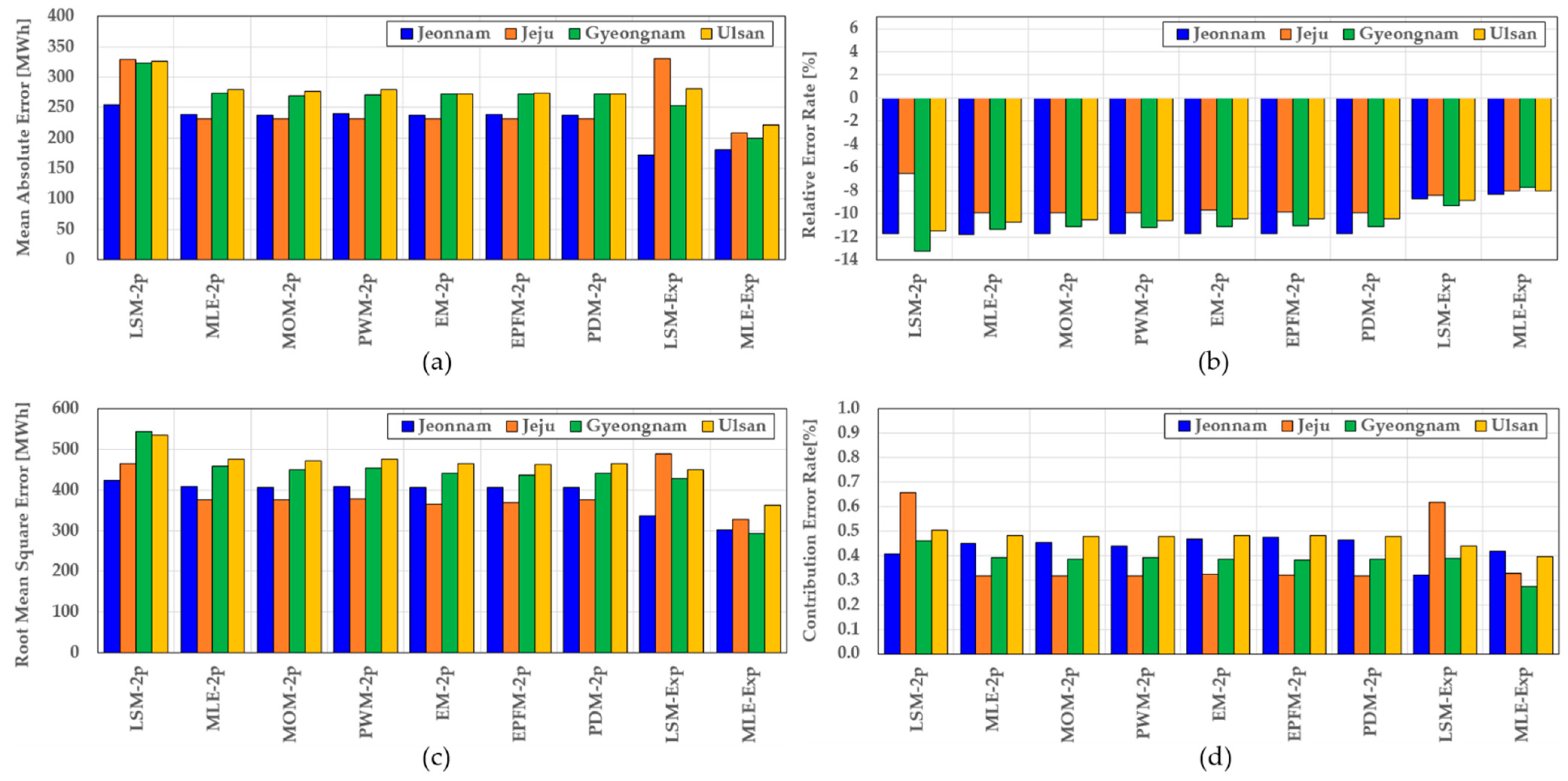
4.1. Evaluating the Accuracy of Annual Energy Production Predictions in Conventional Wind Statistical Models
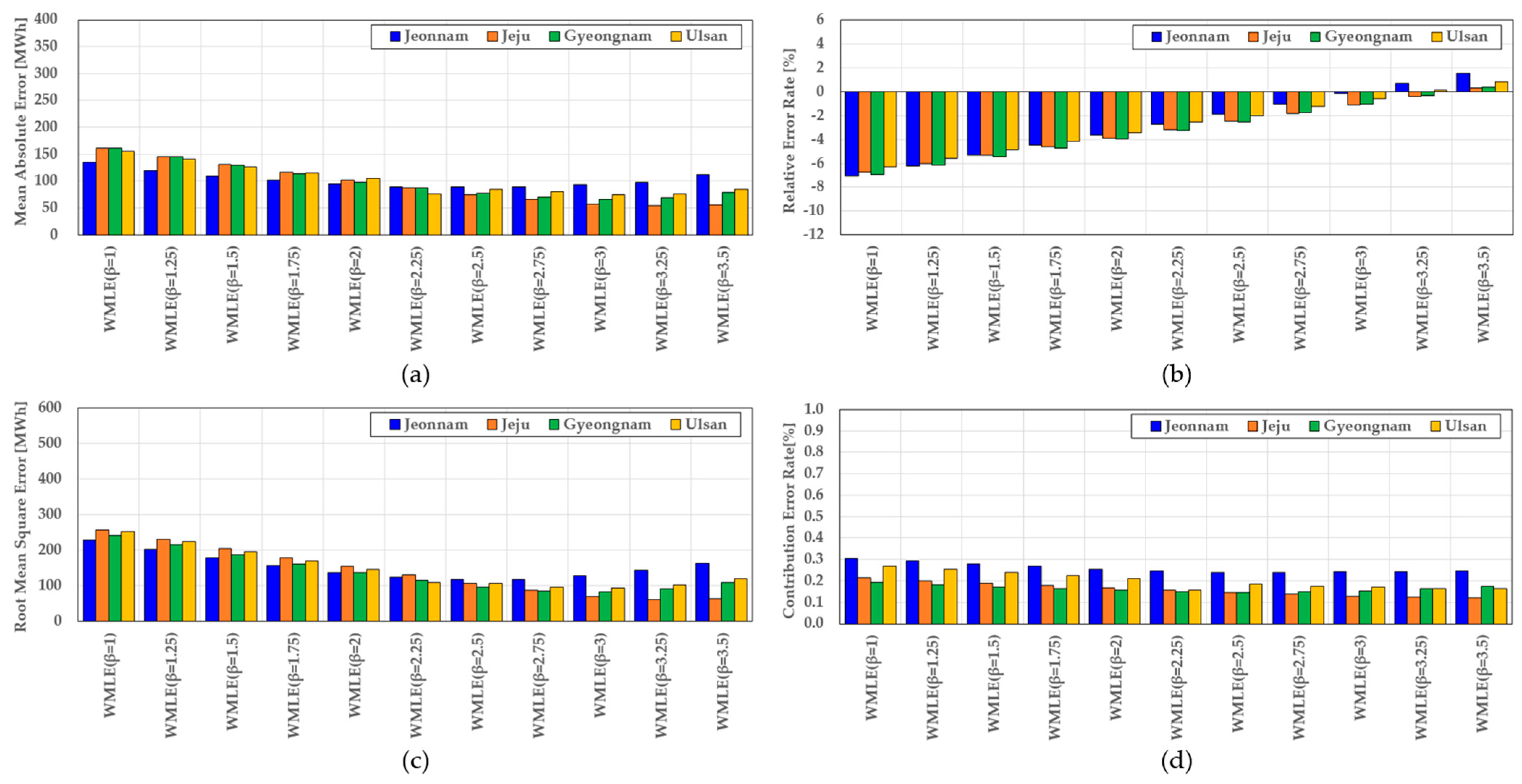
4.2. Determination of the Optimal Weight Exponent (β)
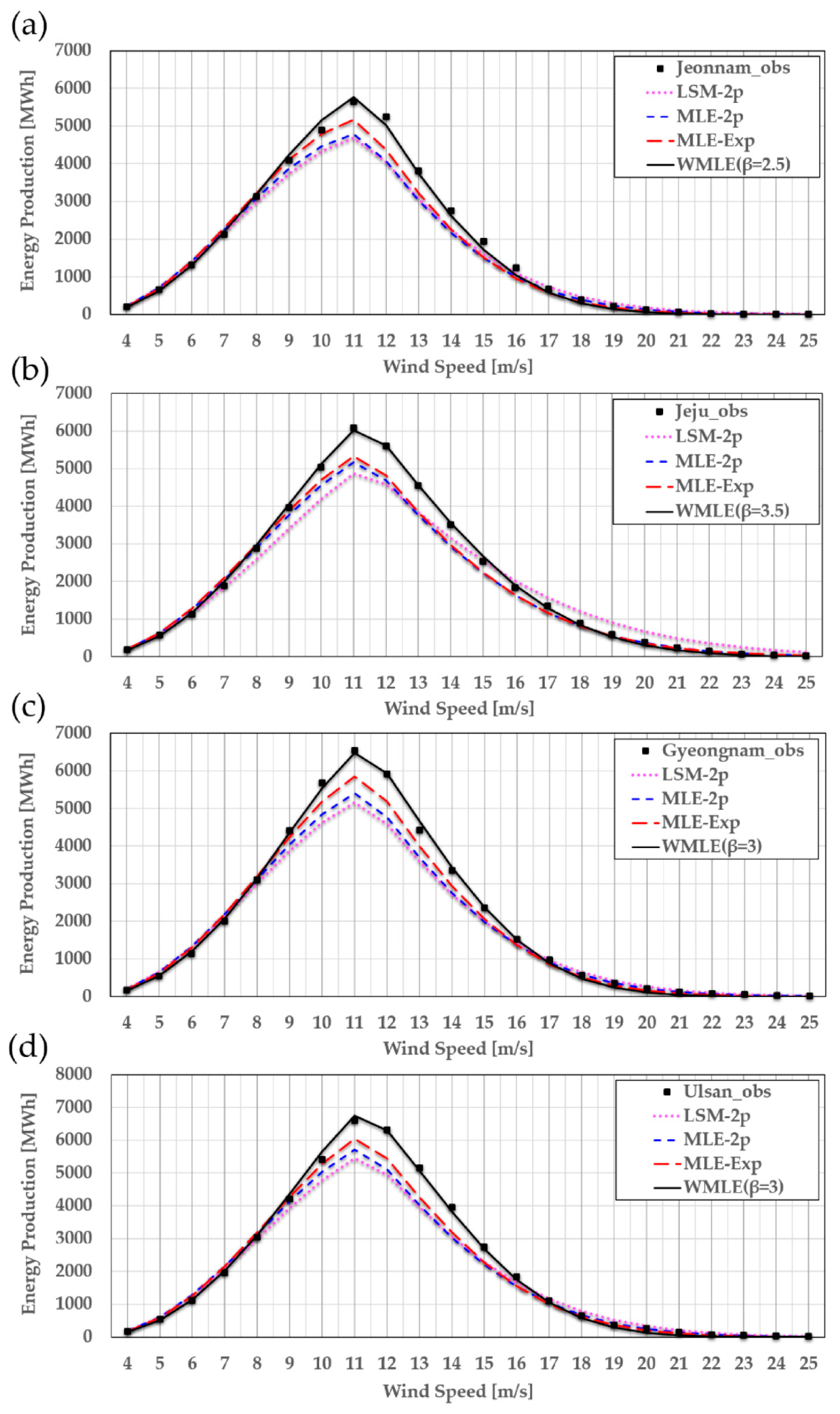
4.3. Evaluation of Wind Statistical Models for Annual Energy Production Estimation and the Effectiveness of Weighted Maximum Likelihood Estimation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WMLE | Weighted Maximum Likelihood Estimation |
| AEP | Annual energy production |
| GOF | Goodness-of-fit |
| NEPFM | Novel Energy Pattern Factor Method |
| SSA | Simplex Search Algorithm |
| WRF | Weather Research and Forecasting |
| MLE | Maximum Likelihood Estimation |
| MOM | Method of Moments |
| EM | Empirical Method |
| PDM | Power Density Method |
| LSM | Least Squares Method |
| WLSM | Weighted Least Squares Method |
| EPFM | Energy Pattern Factor Method |
| DTU | Technical University of Denmark |
| Probability density function | |
| CDF | Cumulative distribution function |
| PWM | Probability Weighted Moment |
| EPF | Energy Pattern Factor |
| MAE | Mean absolute error |
| RER | Relative error rate |
| RMSE | Root mean square error |
| CER | Contribution error rate |
Appendix A
| Bin [m/s] | [MWh] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Below 4 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 204 | 0.005 | 1.005 | 1.007 | 1.008 | 1.009 | 1.011 | 1.012 | 1.013 | 1.015 | 1.016 | 1.017 | 1.019 |
| 5 | 659 | 0.017 | 1.017 | 1.021 | 1.026 | 1.030 | 1.034 | 1.039 | 1.043 | 1.048 | 1.052 | 1.057 | 1.061 |
| 6 | 1321 | 0.034 | 1.034 | 1.043 | 1.052 | 1.061 | 1.070 | 1.079 | 1.088 | 1.097 | 1.106 | 1.115 | 1.125 |
| 7 | 2122 | 0.055 | 1.055 | 1.069 | 1.083 | 1.098 | 1.113 | 1.128 | 1.143 | 1.158 | 1.174 | 1.190 | 1.206 |
| 8 | 3134 | 0.081 | 1.081 | 1.102 | 1.124 | 1.146 | 1.169 | 1.192 | 1.215 | 1.239 | 1.263 | 1.288 | 1.314 |
| 9 | 4116 | 0.106 | 1.106 | 1.135 | 1.164 | 1.194 | 1.224 | 1.256 | 1.288 | 1.321 | 1.355 | 1.389 | 1.425 |
| 10 | 4907 | 0.127 | 1.127 | 1.161 | 1.196 | 1.233 | 1.270 | 1.308 | 1.348 | 1.389 | 1.431 | 1.475 | 1.519 |
| 11 | 5666 | 0.147 | 1.147 | 1.186 | 1.228 | 1.270 | 1.315 | 1.360 | 1.408 | 1.457 | 1.507 | 1.560 | 1.614 |
| 12 | 5266 | 0.136 | 1.136 | 1.173 | 1.211 | 1.250 | 1.291 | 1.333 | 1.376 | 1.421 | 1.467 | 1.514 | 1.564 |
| 13 | 3822 | 0.099 | 1.099 | 1.125 | 1.152 | 1.179 | 1.208 | 1.236 | 1.266 | 1.296 | 1.327 | 1.359 | 1.391 |
| 14 | 2747 | 0.071 | 1.071 | 1.090 | 1.108 | 1.128 | 1.147 | 1.167 | 1.187 | 1.208 | 1.229 | 1.250 | 1.272 |
| 15 | 1937 | 0.050 | 1.050 | 1.063 | 1.076 | 1.089 | 1.103 | 1.116 | 1.130 | 1.144 | 1.158 | 1.172 | 1.187 |
| 16 | 1234 | 0.032 | 1.032 | 1.040 | 1.048 | 1.057 | 1.065 | 1.073 | 1.082 | 1.090 | 1.099 | 1.108 | 1.116 |
| 17 | 682 | 0.018 | 1.018 | 1.022 | 1.027 | 1.031 | 1.036 | 1.040 | 1.045 | 1.049 | 1.054 | 1.058 | 1.063 |
| 18 | 394 | 0.010 | 1.010 | 1.013 | 1.015 | 1.018 | 1.021 | 1.023 | 1.026 | 1.028 | 1.031 | 1.034 | 1.036 |
| 19 | 214 | 0.006 | 1.006 | 1.007 | 1.008 | 1.010 | 1.011 | 1.013 | 1.014 | 1.015 | 1.017 | 1.018 | 1.020 |
| 20 | 121 | 0.003 | 1.003 | 1.004 | 1.005 | 1.006 | 1.006 | 1.007 | 1.008 | 1.009 | 1.009 | 1.010 | 1.011 |
| 21 | 60 | 0.002 | 1.002 | 1.002 | 1.002 | 1.003 | 1.003 | 1.004 | 1.004 | 1.004 | 1.005 | 1.005 | 1.005 |
| 22 | 23 | 0.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.002 | 1.002 | 1.002 | 1.002 | 1.002 |
| 23 | 9 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 |
| 24 | 10 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 |
| 25 | 7 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.001 | 1.001 | 1.001 | 1.001 |
| Above 25 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Bin [m/s] | [MWh] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Below 4 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 185 | 0.004 | 1.004 | 1.005 | 1.006 | 1.007 | 1.009 | 1.010 | 1.011 | 1.012 | 1.013 | 1.014 | 1.015 |
| 5 | 572 | 0.013 | 1.013 | 1.016 | 1.020 | 1.023 | 1.026 | 1.030 | 1.033 | 1.037 | 1.040 | 1.043 | 1.047 |
| 6 | 1132 | 0.026 | 1.026 | 1.033 | 1.039 | 1.046 | 1.053 | 1.059 | 1.066 | 1.073 | 1.080 | 1.087 | 1.094 |
| 7 | 1885 | 0.043 | 1.043 | 1.054 | 1.066 | 1.077 | 1.088 | 1.100 | 1.112 | 1.124 | 1.136 | 1.148 | 1.160 |
| 8 | 2880 | 0.066 | 1.066 | 1.083 | 1.101 | 1.119 | 1.137 | 1.155 | 1.174 | 1.193 | 1.212 | 1.231 | 1.251 |
| 9 | 3962 | 0.091 | 1.091 | 1.115 | 1.140 | 1.165 | 1.190 | 1.216 | 1.243 | 1.271 | 1.299 | 1.327 | 1.356 |
| 10 | 5044 | 0.116 | 1.116 | 1.147 | 1.179 | 1.211 | 1.245 | 1.280 | 1.315 | 1.352 | 1.389 | 1.428 | 1.468 |
| 11 | 6084 | 0.140 | 1.140 | 1.178 | 1.217 | 1.257 | 1.299 | 1.342 | 1.387 | 1.433 | 1.480 | 1.530 | 1.581 |
| 12 | 5602 | 0.129 | 1.129 | 1.163 | 1.199 | 1.236 | 1.274 | 1.313 | 1.353 | 1.395 | 1.438 | 1.482 | 1.527 |
| 13 | 4555 | 0.105 | 1.105 | 1.132 | 1.161 | 1.190 | 1.220 | 1.251 | 1.282 | 1.315 | 1.348 | 1.382 | 1.417 |
| 14 | 3509 | 0.081 | 1.081 | 1.102 | 1.123 | 1.145 | 1.168 | 1.191 | 1.214 | 1.238 | 1.262 | 1.286 | 1.312 |
| 15 | 2543 | 0.058 | 1.058 | 1.074 | 1.089 | 1.104 | 1.120 | 1.136 | 1.152 | 1.169 | 1.186 | 1.203 | 1.220 |
| 16 | 1836 | 0.042 | 1.042 | 1.053 | 1.064 | 1.075 | 1.086 | 1.097 | 1.109 | 1.120 | 1.132 | 1.144 | 1.156 |
| 17 | 1348 | 0.031 | 1.031 | 1.039 | 1.047 | 1.055 | 1.063 | 1.071 | 1.079 | 1.087 | 1.096 | 1.104 | 1.113 |
| 18 | 898 | 0.021 | 1.021 | 1.026 | 1.031 | 1.036 | 1.042 | 1.047 | 1.052 | 1.058 | 1.063 | 1.069 | 1.074 |
| 19 | 586 | 0.013 | 1.013 | 1.017 | 1.020 | 1.024 | 1.027 | 1.031 | 1.034 | 1.037 | 1.041 | 1.044 | 1.048 |
| 20 | 381 | 0.009 | 1.009 | 1.011 | 1.013 | 1.015 | 1.018 | 1.020 | 1.022 | 1.024 | 1.026 | 1.029 | 1.031 |
| 21 | 241 | 0.006 | 1.006 | 1.007 | 1.008 | 1.010 | 1.011 | 1.013 | 1.014 | 1.015 | 1.017 | 1.018 | 1.020 |
| 22 | 149 | 0.003 | 1.003 | 1.004 | 1.005 | 1.006 | 1.007 | 1.008 | 1.009 | 1.009 | 1.010 | 1.011 | 1.012 |
| 23 | 72 | 0.002 | 1.002 | 1.002 | 1.002 | 1.003 | 1.003 | 1.004 | 1.004 | 1.005 | 1.005 | 1.005 | 1.006 |
| 24 | 42 | 0.001 | 1.001 | 1.001 | 1.001 | 1.002 | 1.002 | 1.002 | 1.002 | 1.003 | 1.003 | 1.003 | 1.003 |
| 25 | 33 | 0.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.002 | 1.002 | 1.002 | 1.002 | 1.002 | 1.002 | 1.003 |
| Above 25 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Bin [m/s] | [MWh] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Below 4 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 174 | 0.004 | 1.004 | 1.005 | 1.006 | 1.007 | 1.008 | 1.009 | 1.010 | 1.011 | 1.012 | 1.013 | 1.014 |
| 5 | 546 | 0.013 | 1.013 | 1.016 | 1.019 | 1.022 | 1.025 | 1.028 | 1.032 | 1.035 | 1.038 | 1.041 | 1.045 |
| 6 | 1136 | 0.026 | 1.026 | 1.033 | 1.039 | 1.046 | 1.053 | 1.060 | 1.066 | 1.073 | 1.080 | 1.087 | 1.094 |
| 7 | 2002 | 0.046 | 1.046 | 1.058 | 1.070 | 1.082 | 1.094 | 1.106 | 1.119 | 1.131 | 1.144 | 1.157 | 1.170 |
| 8 | 3107 | 0.071 | 1.071 | 1.090 | 1.109 | 1.128 | 1.148 | 1.168 | 1.188 | 1.208 | 1.229 | 1.251 | 1.272 |
| 9 | 4409 | 0.101 | 1.101 | 1.128 | 1.155 | 1.184 | 1.212 | 1.242 | 1.272 | 1.303 | 1.335 | 1.368 | 1.401 |
| 10 | 5684 | 0.130 | 1.130 | 1.166 | 1.202 | 1.239 | 1.278 | 1.317 | 1.358 | 1.401 | 1.444 | 1.489 | 1.536 |
| 11 | 6550 | 0.150 | 1.150 | 1.191 | 1.234 | 1.278 | 1.323 | 1.370 | 1.419 | 1.470 | 1.522 | 1.576 | 1.632 |
| 12 | 5921 | 0.136 | 1.136 | 1.173 | 1.210 | 1.250 | 1.290 | 1.332 | 1.375 | 1.419 | 1.465 | 1.513 | 1.562 |
| 13 | 4424 | 0.101 | 1.101 | 1.128 | 1.156 | 1.184 | 1.213 | 1.243 | 1.273 | 1.304 | 1.336 | 1.369 | 1.403 |
| 14 | 3351 | 0.077 | 1.077 | 1.097 | 1.117 | 1.138 | 1.160 | 1.181 | 1.203 | 1.226 | 1.249 | 1.272 | 1.296 |
| 15 | 2364 | 0.054 | 1.054 | 1.068 | 1.082 | 1.097 | 1.111 | 1.126 | 1.141 | 1.156 | 1.172 | 1.187 | 1.203 |
| 16 | 1526 | 0.035 | 1.035 | 1.044 | 1.053 | 1.062 | 1.071 | 1.080 | 1.090 | 1.099 | 1.109 | 1.118 | 1.128 |
| 17 | 966 | 0.022 | 1.022 | 1.028 | 1.033 | 1.039 | 1.045 | 1.051 | 1.056 | 1.062 | 1.068 | 1.074 | 1.080 |
| 18 | 566 | 0.013 | 1.013 | 1.016 | 1.020 | 1.023 | 1.026 | 1.029 | 1.033 | 1.036 | 1.039 | 1.043 | 1.046 |
| 19 | 361 | 0.008 | 1.008 | 1.010 | 1.012 | 1.015 | 1.017 | 1.019 | 1.021 | 1.023 | 1.025 | 1.027 | 1.029 |
| 20 | 206 | 0.005 | 1.005 | 1.006 | 1.007 | 1.008 | 1.009 | 1.011 | 1.012 | 1.013 | 1.014 | 1.015 | 1.017 |
| 21 | 119 | 0.003 | 1.003 | 1.003 | 1.004 | 1.005 | 1.005 | 1.006 | 1.007 | 1.008 | 1.008 | 1.009 | 1.010 |
| 22 | 82 | 0.002 | 1.002 | 1.002 | 1.003 | 1.003 | 1.004 | 1.004 | 1.005 | 1.005 | 1.006 | 1.006 | 1.007 |
| 23 | 56 | 0.001 | 1.001 | 1.002 | 1.002 | 1.002 | 1.003 | 1.003 | 1.003 | 1.004 | 1.004 | 1.004 | 1.005 |
| 24 | 27 | 0.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.002 | 1.002 | 1.002 | 1.002 | 1.002 |
| 25 | 20 | 0.000 | 1.000 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.002 | 1.002 |
| Above 25 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Bin [m/s] | [MWh] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Below 4 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 166 | 0.004 | 1.004 | 1.005 | 1.005 | 1.006 | 1.007 | 1.008 | 1.009 | 1.010 | 1.011 | 1.012 | 1.013 |
| 5 | 548 | 0.012 | 1.012 | 1.015 | 1.018 | 1.021 | 1.024 | 1.027 | 1.030 | 1.033 | 1.036 | 1.039 | 1.043 |
| 6 | 1125 | 0.025 | 1.025 | 1.031 | 1.037 | 1.043 | 1.050 | 1.056 | 1.063 | 1.069 | 1.076 | 1.082 | 1.089 |
| 7 | 1954 | 0.043 | 1.043 | 1.054 | 1.065 | 1.076 | 1.087 | 1.099 | 1.110 | 1.122 | 1.134 | 1.146 | 1.158 |
| 8 | 3036 | 0.066 | 1.066 | 1.084 | 1.101 | 1.119 | 1.137 | 1.156 | 1.174 | 1.193 | 1.213 | 1.232 | 1.252 |
| 9 | 4208 | 0.092 | 1.092 | 1.116 | 1.141 | 1.167 | 1.193 | 1.219 | 1.246 | 1.274 | 1.302 | 1.331 | 1.361 |
| 10 | 5404 | 0.118 | 1.118 | 1.150 | 1.182 | 1.216 | 1.250 | 1.286 | 1.322 | 1.360 | 1.398 | 1.438 | 1.479 |
| 11 | 6599 | 0.144 | 1.144 | 1.184 | 1.224 | 1.266 | 1.310 | 1.354 | 1.401 | 1.449 | 1.499 | 1.550 | 1.603 |
| 12 | 6309 | 0.138 | 1.138 | 1.175 | 1.214 | 1.254 | 1.295 | 1.338 | 1.381 | 1.427 | 1.474 | 1.522 | 1.572 |
| 13 | 5150 | 0.113 | 1.113 | 1.143 | 1.174 | 1.205 | 1.238 | 1.271 | 1.306 | 1.341 | 1.377 | 1.415 | 1.453 |
| 14 | 3956 | 0.087 | 1.087 | 1.109 | 1.133 | 1.156 | 1.181 | 1.205 | 1.231 | 1.256 | 1.283 | 1.310 | 1.337 |
| 15 | 2743 | 0.060 | 1.060 | 1.076 | 1.091 | 1.107 | 1.124 | 1.140 | 1.157 | 1.174 | 1.191 | 1.208 | 1.226 |
| 16 | 1837 | 0.040 | 1.040 | 1.050 | 1.061 | 1.071 | 1.082 | 1.093 | 1.103 | 1.114 | 1.125 | 1.137 | 1.148 |
| 17 | 1102 | 0.024 | 1.024 | 1.030 | 1.036 | 1.043 | 1.049 | 1.055 | 1.061 | 1.068 | 1.074 | 1.080 | 1.087 |
| 18 | 650 | 0.014 | 1.014 | 1.018 | 1.021 | 1.025 | 1.029 | 1.032 | 1.036 | 1.040 | 1.043 | 1.047 | 1.051 |
| 19 | 372 | 0.008 | 1.008 | 1.010 | 1.012 | 1.014 | 1.016 | 1.018 | 1.020 | 1.023 | 1.025 | 1.027 | 1.029 |
| 20 | 256 | 0.006 | 1.006 | 1.007 | 1.008 | 1.010 | 1.011 | 1.013 | 1.014 | 1.015 | 1.017 | 1.018 | 1.020 |
| 21 | 136 | 0.003 | 1.003 | 1.004 | 1.004 | 1.005 | 1.006 | 1.007 | 1.007 | 1.008 | 1.009 | 1.010 | 1.010 |
| 22 | 75 | 0.002 | 1.002 | 1.002 | 1.002 | 1.003 | 1.003 | 1.004 | 1.004 | 1.004 | 1.005 | 1.005 | 1.006 |
| 23 | 48 | 0.001 | 1.001 | 1.001 | 1.002 | 1.002 | 1.002 | 1.002 | 1.003 | 1.003 | 1.003 | 1.003 | 1.004 |
| 24 | 31 | 0.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.002 | 1.002 | 1.002 | 1.002 | 1.002 | 1.002 |
| 25 | 15 | 0.000 | 1.000 | 1.000 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 |
| Above 25 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Method | MAE | RMSE | RER | CER |
|---|---|---|---|---|
| LSM-2p | 254.3 | 423 | −11.7 | 0.407 |
| MLE-2p | 239.2 | 409 | −11.8 | 0.451 |
| MOM-2p | 237.9 | 407 | −11.7 | 0.451 |
| PWM-2p | 239.6 | 409 | −11.7 | 0.440 |
| EM-2p | 237.4 | 407 | −11.7 | 0.467 |
| EPFM-2p | 238.3 | 407 | −11.7 | 0.473 |
| PDM-2p | 237.3 | 407 | −11.7 | 0.463 |
| LSM-Exp | 171.5 | 337 | −8.7 | 0.319 |
| MLE-Exp | 180.1 | 301 | −8.3 | 0.416 |
| WMLE (β = 1) | 134.8 | 229 | −7.07 | 0.304 |
| WMLE (β = 1.25) | 119.5 | 203 | −6.21 | 0.292 |
| WMLE (β = 1.5) | 108.9 | 179 | −5.34 | 0.280 |
| WMLE (β = 1.75) | 101.3 | 156 | −4.47 | 0.267 |
| WMLE (β = 2) | 94.1 | 138 | −3.60 | 0.255 |
| WMLE (β = 2.25) | 89.2 | 124 | −2.74 | 0.247 |
| WMLE (β = 2.5) | 88.9 | 117 | −1.87 | 0.238 |
| WMLE (β = 2.75) | 88.5 | 119 | −1.00 | 0.239 |
| WMLE (β = 3) | 92.7 | 128 | −0.14 | 0.242 |
| WMLE (β = 3.25) | 97.8 | 144 | 0.72 | 0.244 |
| WMLE (β = 3.5) | 112.3 | 164 | 1.58 | 0.246 |
| Method | MAE | RMSE | RER | CER |
|---|---|---|---|---|
| LSM-2p | 329.0 | 466 | −6.5 | 0.656 |
| MLE-2p | 231.0 | 376 | −9.9 | 0.316 |
| MOM-2p | 231.0 | 376 | −9.9 | 0.316 |
| PWM-2p | 231.0 | 377 | −9.9 | 0.316 |
| EM-2p | 232.0 | 365 | −9.7 | 0.323 |
| EPFM-2p | 232.0 | 370 | −9.8 | 0.319 |
| PDM-2p | 231.0 | 375 | −9.9 | 0.316 |
| LSM-Exp | 331.0 | 489 | −8.4 | 0.617 |
| MLE-Exp | 209.0 | 327 | −8 | 0.327 |
| WMLE (β = 1) | 160.6 | 256 | −6.73 | 0.213 |
| WMLE (β = 1.25) | 145.7 | 230 | −6.02 | 0.200 |
| WMLE (β = 1.5) | 131.0 | 205 | −5.31 | 0.189 |
| WMLE (β = 1.75) | 116.4 | 180 | −4.61 | 0.178 |
| WMLE (β = 2) | 101.7 | 155 | −3.90 | 0.167 |
| WMLE (β = 2.25) | 87.1 | 131 | −3.19 | 0.157 |
| WMLE (β = 2.5) | 74.5 | 108 | −2.49 | 0.147 |
| WMLE (β = 2.75) | 65.7 | 87 | −1.79 | 0.138 |
| WMLE (β = 3) | 57.7 | 71 | −1.09 | 0.129 |
| WMLE (β = 3.25) | 54.1 | 62 | −0.40 | 0.126 |
| WMLE (β = 3.5) | 55.5 | 64 | 0.30 | 0.122 |
| Method | MAE | RMSE | RER | CER |
|---|---|---|---|---|
| LSM-2p | 323.0 | 543 | −13.2 | 0.460 |
| MLE-2p | 274.0 | 459 | −11.3 | 0.394 |
| MOM-2p | 270.0 | 449 | −11.1 | 0.386 |
| PWM-2p | 271.0 | 454 | −11.2 | 0.391 |
| EM-2p | 272.0 | 440 | −11.1 | 0.384 |
| EPFM-2p | 273.0 | 437 | −11 | 0.383 |
| PDM-2p | 272.0 | 441 | −11.1 | 0.384 |
| LSM-Exp | 254.0 | 427 | −9.3 | 0.388 |
| MLE-Exp | 199.0 | 293 | −7.7 | 0.275 |
| WMLE (β = 1) | 160.9 | 242 | −6.91 | 0.193 |
| WMLE (β = 1.25) | 145.0 | 215 | −6.18 | 0.181 |
| WMLE (β = 1.5) | 129.3 | 188 | −5.44 | 0.170 |
| WMLE (β = 1.75) | 113.8 | 162 | −4.70 | 0.162 |
| WMLE (β = 2) | 98.2 | 137 | −3.96 | 0.155 |
| WMLE (β = 2.25) | 86.9 | 115 | −3.23 | 0.149 |
| WMLE (β = 2.5) | 77.2 | 97 | −2.50 | 0.146 |
| WMLE (β = 2.75) | 70.3 | 86 | −1.77 | 0.149 |
| WMLE (β = 3) | 65.2 | 84 | −1.04 | 0.153 |
| WMLE (β = 3.25) | 68.7 | 93 | −0.32 | 0.163 |
| WMLE (β = 3.5) | 78.8 | 109 | 0.39 | 0.174 |
| Method | MAE | RMSE | RER | CER |
|---|---|---|---|---|
| LSM-2p | 326.0 | 534 | −11.5 | 0.503 |
| MLE-2p | 279.0 | 476 | −10.7 | 0.481 |
| MOM-2p | 276.0 | 471 | −10.5 | 0.478 |
| PWM-2p | 279.0 | 476 | −10.6 | 0.477 |
| EM-2p | 273.0 | 465 | −10.4 | 0.480 |
| EPFM-2p | 274.0 | 463 | −10.4 | 0.481 |
| PDM-2p | 273.0 | 465 | −10.4 | 0.480 |
| LSM-Exp | 281.0 | 449 | −8.8 | 0.439 |
| MLE-Exp | 221.0 | 362 | −8 | 0.397 |
| WMLE (β = 1) | 155.5 | 252 | −6.31 | 0.267 |
| WMLE (β = 1.25) | 140.4 | 224 | −5.58 | 0.253 |
| WMLE (β = 1.5) | 125.9 | 197 | −4.85 | 0.239 |
| WMLE (β = 1.75) | 114.8 | 170 | −4.13 | 0.225 |
| WMLE (β = 2) | 104.1 | 146 | −3.41 | 0.211 |
| WMLE (β = 2.25) | 76.5 | 109 | −2.51 | 0.155 |
| WMLE (β = 2.5) | 84.4 | 106 | −1.98 | 0.186 |
| WMLE (β = 2.75) | 79.7 | 96 | −1.26 | 0.175 |
| WMLE (β = 3) | 75.0 | 95 | −0.55 | 0.170 |
| WMLE (β = 3.25) | 76.7 | 103 | 0.16 | 0.166 |
| WMLE (β = 3.5) | 85.2 | 119 | 0.86 | 0.165 |
| Location | Jeonnam | Jeju | Gyeongnam | Ulsan | |
|---|---|---|---|---|---|
| LSM (2P) | k | 1.985 | 1.794 | 2.038 | 2.067 |
| c | 8.332 | 9.391 | 8.848 | 9.223 | |
| MLE (2P) | k | 2.064 | 1.979 | 2.129 | 2.179 |
| c | 8.331 | 9.067 | 8.947 | 9.243 | |
| MOM (2P) | k | 2.067 | 1.980 | 2.140 | 2.185 |
| c | 8.335 | 9.067 | 8.959 | 9.251 | |
| PWM (2P) | k | 2.049 | 1.977 | 2.128 | 2.169 |
| c | 8.334 | 9.067 | 8.959 | 9.251 | |
| EM (2P) | k | 2.089 | 2.003 | 2.161 | 2.205 |
| c | 8.335 | 9.069 | 8.959 | 9.251 | |
| EPFM (2P) | k | 2.096 | 1.992 | 2.169 | 2.214 |
| c | 8.336 | 9.068 | 8.959 | 9.251 | |
| PDM (2P) | k | 2.084 | 1.981 | 2.159 | 2.205 |
| c | 8.335 | 9.067 | 8.959 | 9.251 | |
| LSM (Exp) | k | 2.117 | 1.717 | 2.254 | 2.210 |
| c | 8.892 | 8.892 | 9.712 | 9.824 | |
| 0.890 | 1.090 | 0.840 | 0.890 | ||
| MEL (Exp) | k | 2.294 | 1.948 | 2.445 | 2.409 |
| c | 8.837 | 8.831 | 9.672 | 9.764 | |
| 0.903 | 1.096 | 0.851 | 0.893 | ||
| WMLE (Exp) | k | 2.537 | 2.175 | 2.689 | 2.756 |
| c | 9.542 | 9.700 | 10.326 | 10.638 | |
| 0.738 | 0.885 | 0.708 | 0.708 | ||
| WMLE (Exp) | k | 2.587 | 2.211 | 2.733 | 2.803 |
| c | 9.649 | 9.802 | 10.410 | 10.726 | |
| 0.722 | 0.870 | 0.698 | 0.696 | ||
| WMLE (Exp) | k | 2.638 | 2.246 | 2.778 | 2.851 |
| c | 9.754 | 9.902 | 10.491 | 10.812 | |
| 0.707 | 0.856 | 0.688 | 0.685 | ||
| WMLE (Exp) | k | 2.689 | 2.282 | 2.822 | 2.898 |
| c | 9.856 | 9.999 | 10.570 | 10.895 | |
| 0.693 | 0.842 | 0.678 | 0.675 | ||
| WMLE (Exp) | 2.740 | 2.318 | 2.866 | 2.946 | |
| 9.955 | 10.093 | 10.645 | 10.975 | ||
| 0.680 | 0.829 | 0.670 | 0.666 | ||
| WMLE (Exp) | k | 2.792 | 2.354 | 2.910 | 2.993 |
| c | 10.051 | 10.184 | 10.718 | 11.051 | |
| 0.667 | 0.817 | 0.661 | 0.656 | ||
| WMLE (Exp) | k | 2.844 | 2.389 | 2.954 | 3.040 |
| c | 10.144 | 10.271 | 10.789 | 11.125 | |
| 0.655 | 0.806 | 0.653 | 0.648 | ||
| WMLE (Exp) | k | 2.896 | 2.425 | 2.998 | 3.087 |
| c | 10.235 | 10.356 | 10.856 | 11.196 | |
| 0.643 | 0.795 | 0.645 | 0.640 | ||
| WMLE (Exp) | k | 2.949 | 2.461 | 3.042 | 3.134 |
| c | 10.322 | 10.439 | 10.921 | 11.264 | |
| 0.632 | 0.784 | 0.638 | 0.632 | ||
| WMLE (Exp) | k | 3.002 | 2.496 | 3.086 | 3.181 |
| c | 10.407 | 10.518 | 10.983 | 11.330 | |
| 0.622 | 0.774 | 0.632 | 0.625 | ||
| WMLE (Exp) | k | 3.054 | 2.532 | 3.129 | 3.227 |
| c | 10.488 | 10.594 | 11.042 | 11.392 | |
| 0.612 | 0.765 | 0.626 | 0.618 | ||
References
- Rabbi, M.F.; Popp, J.; Máté, D.; Kovács, S. Energy security and energy transition to achieve carbon neutrality. Energies 2022, 15, 8126. [Google Scholar] [CrossRef]
- World Wind Energy Association (WWEA). Global Wind Report. 2024. Available online: http://www.wwindea.org (accessed on 15 January 2025).
- Pobočíková, I.; Sedliačková, Z.; Michalková, M.; George, F. Monte Carlo comparison of the methods for estimating the Weibull distribution parameters—Wind speed application. Commun. Sci. Lett. Univ. Zilina 2017, 19, 79–86. Available online: https://komunikacie.uniza.sk/artkey/csl-201711-0013_monte-carlo-comparison-of-the-methods-for-estimating-the-weibull-distribution-parameters-wind-speed-applicati.php?back=/magno/csl/2017/mn11.php?secid=1 (accessed on 15 January 2025).
- Kaoga, D.K.; Serge, D.Y.; Raidan, D.; Djongyang, N. Performance assessment of two-parameter Weibull distribution methods for wind energy applications in the District of Maroua in Cameroon. Int. J. Sci. Basic Appl. Res. 2014, 17, 39–59. Available online: https://www.gssrr.org/JournalOfBasicAndApplied/article/view/2450 (accessed on 15 January 2025).
- Onay, A.E.; Dokur, E.; Kurban, M. Performance comparison of new generation parameter estimation methods for Weibull distribution to compute wind energy density. Elektron. Elektrotech. 2021, 27, 41–48. [Google Scholar] [CrossRef]
- Pobočíková, I.; Michalková, M.; Sedliačková, Z.; Jurášová, D. Modelling the wind speed using exponentiated Weibull distribution: Case study of Poprad-Tatry, Slovakia. Appl. Sci. 2023, 13, 4031. [Google Scholar] [CrossRef]
- Abbas, G.; Ali, A.; Rashid, F.; Ashraf, N.; Mushtaq, Z.; Zubair, M. An optimal approach for assessing Weibull parameters and wind power potential for six coastal cities in Pakistan. IEEE Access 2025, 13, 2503–2518. [Google Scholar] [CrossRef]
- Carvalho, R.M.F. Time Series vs. Statistical Approaches in Estimating Wind Turbines Energy Yield. Master’s Thesis, University of Porto, Porto, Portugal, 2023. Available online: https://hdl.handle.net/10216/152093 (accessed on 16 September 2025).
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine. In Proceedings of the Danish Wind Power Research 2013, Fredericia, Denmark, 27–28 May 2013; Technical University of Denmark: Roskilde, Denmark, 2013. Available online: https://orbit.dtu.dk/en/publications/bc5f61cd-4c51-442f-89eb-02df89ab0aa4 (accessed on 15 January 2025).
- Lemmer, F.; Amann, F.; Raach, S.; Schlipf, D.; Faerron, G.R. Definition of the SWE-TripleSpar Floating Platform for the DTU 10 MW Reference Wind Turbine. Stuttgart Wind Energy (SWE); University of Stuttgart: Stuttgart, Germany, 2016. Available online: https://nwtc.nrel.gov/OpenFAST (accessed on 15 January 2025).
- Konagaya, M.; Ohsawa, T.; Itoshima, Y.; Kambayashi, M.; Leonard, E.; Tromeur, E.; Misaki, T.; Shintaku, E.; Araki, R.; Hamada, K. Estimation of Wind Conditions in the Offshore Direction Using Multiple Numerical Models and In Situ Observations. Energies 2025, 18, 3000. [Google Scholar] [CrossRef]
- Yang, P.; Zou, S.; Chen, N.; Xu, Z. Offshore wind resource assessment based on WRF model. In Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference(APPEEC), Hong Kong, China, 8–11 December 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Murthy, D.N.P.; Xie, M.; Jiang, R. Weibull Models; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 978-0-471-36092-9. [Google Scholar]
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramírez, P.; Velázquez, S. A review of wind speed probability distributions used in wind energy analysis: Case studies in the Canary Islands. Renew. Sustain. Energy Rev. 2009, 13, 933–955. [Google Scholar] [CrossRef]
- Fyrippis, I.; Axaopoulos, P.J.; Panayiotou, G. Wind energy potential assessment in Naxos Island, Greece. Appl. Energy 2010, 87, 577–586. [Google Scholar] [CrossRef]
- Rinne, H. The Weibull Distribution: A Handbook; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability weighted moments: Definition and relation to parameters of several distributions expressable in inverse form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Rocha, P.A.C.; Sousa, R.C.; Andrade, C.F.; da Silva, V.M.E. Comparison of seven numerical methods for determining Weibull parameters for wind energy generation in the northeast region of Brazil. Appl. Energy 2012, 89, 395–400. [Google Scholar] [CrossRef]
- Mohammadi, K.; Mostafaeipour, A. Using different methods for comprehensive study of wind turbine utilization in Zarrineh, Iran. Energy Convers. Manag. 2013, 65, 463–470. [Google Scholar] [CrossRef]
- Carrillo, C.; Cidrás, J.; Díaz-Dorado, E.; Obando-Montaño, A.F. An Approach to Determine the Weibull Parameters for Wind Energy Analysis: The Case of Galicia (Spain). Energies 2014, 7, 2676–2700. [Google Scholar] [CrossRef]
- Pobočíková, I.; Sedliačková, Z. Comparison of four methods for estimating the Weibull distribution parameters. Appl. Math. Sci. 2014, 8, 4137–4149. [Google Scholar] [CrossRef]
- Draxl, C.; Hodge, B.-M.; Clifton, A. Overview and Meteorological Validation of the Wind Integration National Dataset Toolkit; Technical Report for National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2015. Available online: https://www.nrel.gov/docs/fy15osti/61740.pdf (accessed on 15 January 2025).


| Parameter | Unit | Description |
|---|---|---|
| Rating | MW | 10 |
| Rotor Orientation, Configuration | - | Upwind, 3 blades |
| Control | - | Variable Speed, Collective Pitch |
| Rotor Diameter, Hub height | m | 178.3, 119 |
| Cut-in, Rated, Cut-out Wind Speeds | m/s | 4, 11.4, 25 |
| Location | Coordinates | Period | Variables |
|---|---|---|---|
| Jeonnam | 35.032° N 124.207° E | 1 January 1994–31 August 2019 | Wind Speed, Wind Direction, Turbulence Intensity (at 75 m, 100 m, and 150 m above sea level) |
| Jeju | 33.921° N 126.48° E | 1 January 1994–2 August 2019 | |
| Gyeongnam | 34.384° N 128.23° E | 1 January 1994–31 August 2019 | |
| Ulsan | 35.356° N 129.85° E | 1 January 1994–31 August 2019 |
| Location | |
|---|---|
| Jeonnam | 0.0989 |
| Jeju | 0.0636 |
| Gyeongnam | 0.0690 |
| Ulsan | 0.0667 |
| Site | MAE | RMSE | RER | CER | Optimal β |
|---|---|---|---|---|---|
| Jeonnam | 2.75 | 2.50 | 3.00 | 2.50 | 2.50 |
| Jeju | 3.25 | 3.25 | 3.50 | 3.50 | 3.50 |
| Gyeongnam | 3.00 | 3.00 | 3.25 | 2.50 | 3.00 |
| Ulsan | 3.00 | 3.00 | 3.25 | 3.50 | 3.00 |
| Performance | Representative Method | Description |
|---|---|---|
| Bad | LSM (Two) | Fundamental method for initializing parameter estimates |
| Fair | MLE (Two) | Most widely used conventional method in wind resource assessments |
| Good | MLE (Exponentiated) | Improved accuracy demonstrated in recent studies |
| Excellent | WMLE (Exponentiated, ) | Proposed method incorporating AEP contribution as a weighting function |
| Site | Method | MAE (MWh) | RMSE (MWh) | RER (%) | CER (%) |
|---|---|---|---|---|---|
| Jeonnam | LSM-2p | 254 | 423 | −11.7 | 0.41 |
| MLE-2p | 239 | 409 | −11.8 | 0.45 | |
| MEL-Exp | 180 | 301 | −8.3 | 0.42 | |
| WMLE | 89 | 117 | −1.9 | 0.24 | |
| Jeju | LSM-2p | 329 | 466 | −6.5 | 0.65 |
| MLE-2p | 231 | 376 | −9.9 | 0.32 | |
| MEL–Exp | 209 | 327 | −8 | 0.33 | |
| WMLE | 55 | 64 | 0.3 | 0.12 | |
| Gyeongnam | LSM-2p | 323 | 543 | −13.2 | 0.46 |
| MLE-2p | 274 | 459 | −11.3 | 0.39 | |
| MEL–Exp | 199 | 293 | −7.7 | 0.28 | |
| WMLE | 65 | 84 | −1.0 | 0.15 | |
| Ulsan | LSM-2p | 326 | 534 | −11.5 | 0.50 |
| MLE-2p | 279 | 476 | −10.7 | 0.48 | |
| MEL–Exp | 221 | 362 | −8 | 0.40 | |
| WMLE | 75 | 95 | −0.55 | 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, W.; Lee, K.; Kim, J.; Lee, S. Development of a Novel Weighted Maximum Likelihood-Based Parameter Estimation Technique for Improved Annual Energy Production Estimation of Wind Turbines. Energies 2025, 18, 5265. https://doi.org/10.3390/en18195265
Han W, Lee K, Kim J, Lee S. Development of a Novel Weighted Maximum Likelihood-Based Parameter Estimation Technique for Improved Annual Energy Production Estimation of Wind Turbines. Energies. 2025; 18(19):5265. https://doi.org/10.3390/en18195265
Chicago/Turabian StyleHan, Woobeom, Kanghee Lee, Jonghwa Kim, and Seungjae Lee. 2025. "Development of a Novel Weighted Maximum Likelihood-Based Parameter Estimation Technique for Improved Annual Energy Production Estimation of Wind Turbines" Energies 18, no. 19: 5265. https://doi.org/10.3390/en18195265
APA StyleHan, W., Lee, K., Kim, J., & Lee, S. (2025). Development of a Novel Weighted Maximum Likelihood-Based Parameter Estimation Technique for Improved Annual Energy Production Estimation of Wind Turbines. Energies, 18(19), 5265. https://doi.org/10.3390/en18195265








