Numerical Modeling of Photovoltaic Cells with the Meshless Global Radial Basis Function Collocation Method
Abstract
1. Introduction
- (1)
- A side-by-side comparison of GA and GMQ bases across wide shape parameter and node density ranges;
- (2)
- Stability windows and near-optimal plateaus that practitioners can use to select basis/parameter pairs that preserve accuracy in the P- and N-region QNRs without incurring ill-conditioning;
- (3)
- A multi-objective optimization framework that balances error against central processing unit (CPU) time and yields practical node-count guidelines;
- (4)
- Actionable best-practice recommendations (basis selection, shape-parameter tuning, and conditioning strategies) that translate directly to PV modeling workflows.
2. Current Continuity Equations for a PV Cell
3. Radial Basis Function Collocation Method
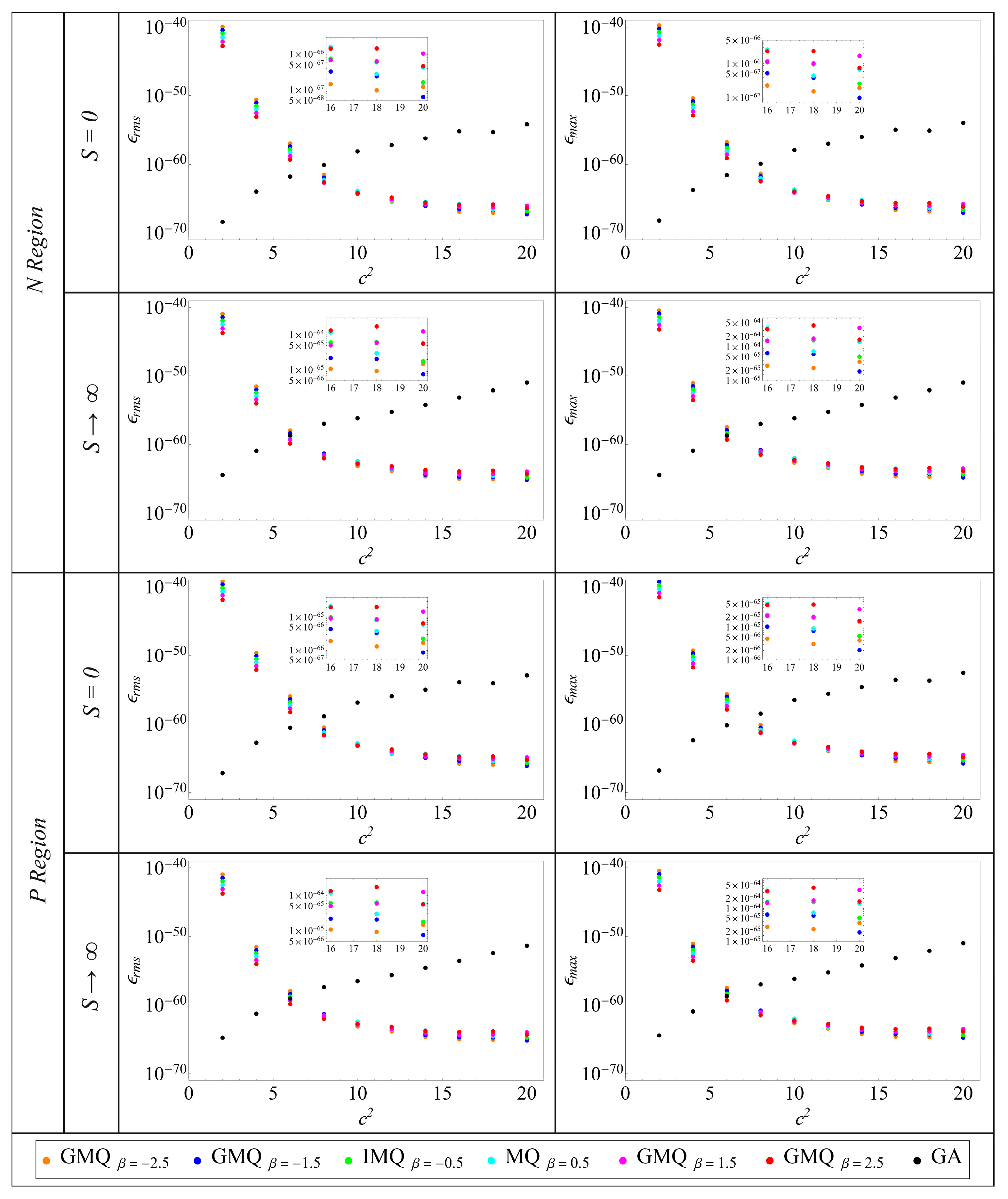
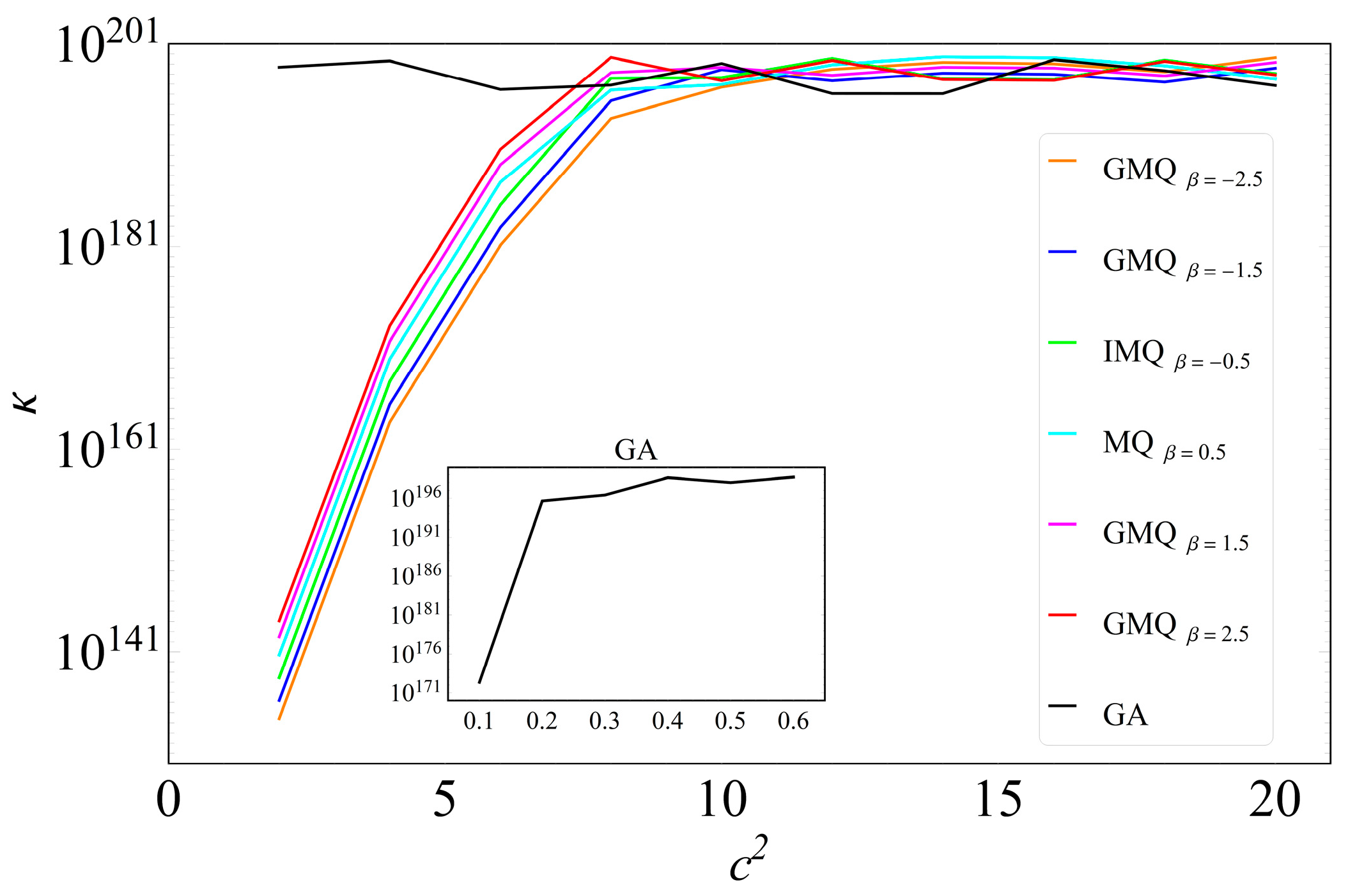
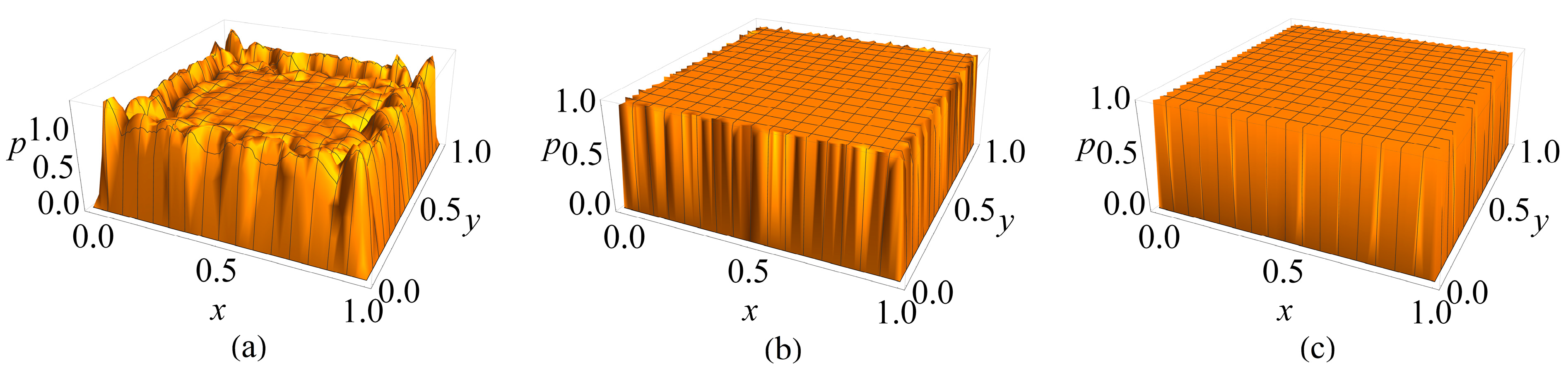
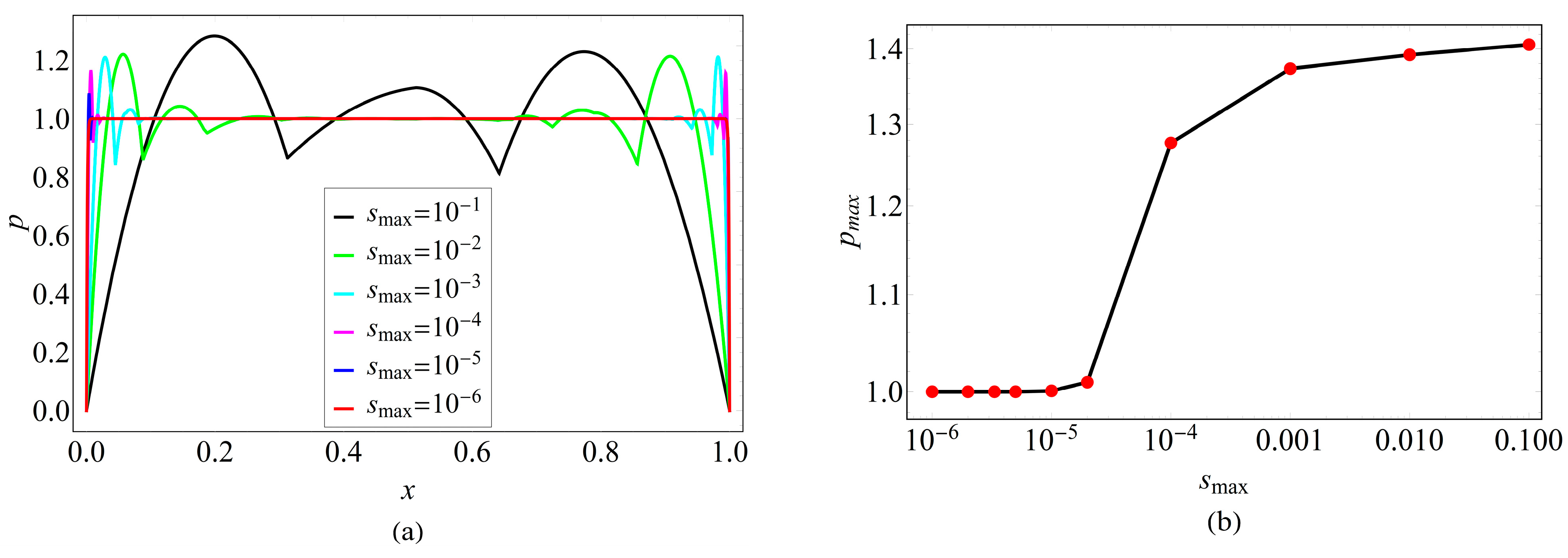
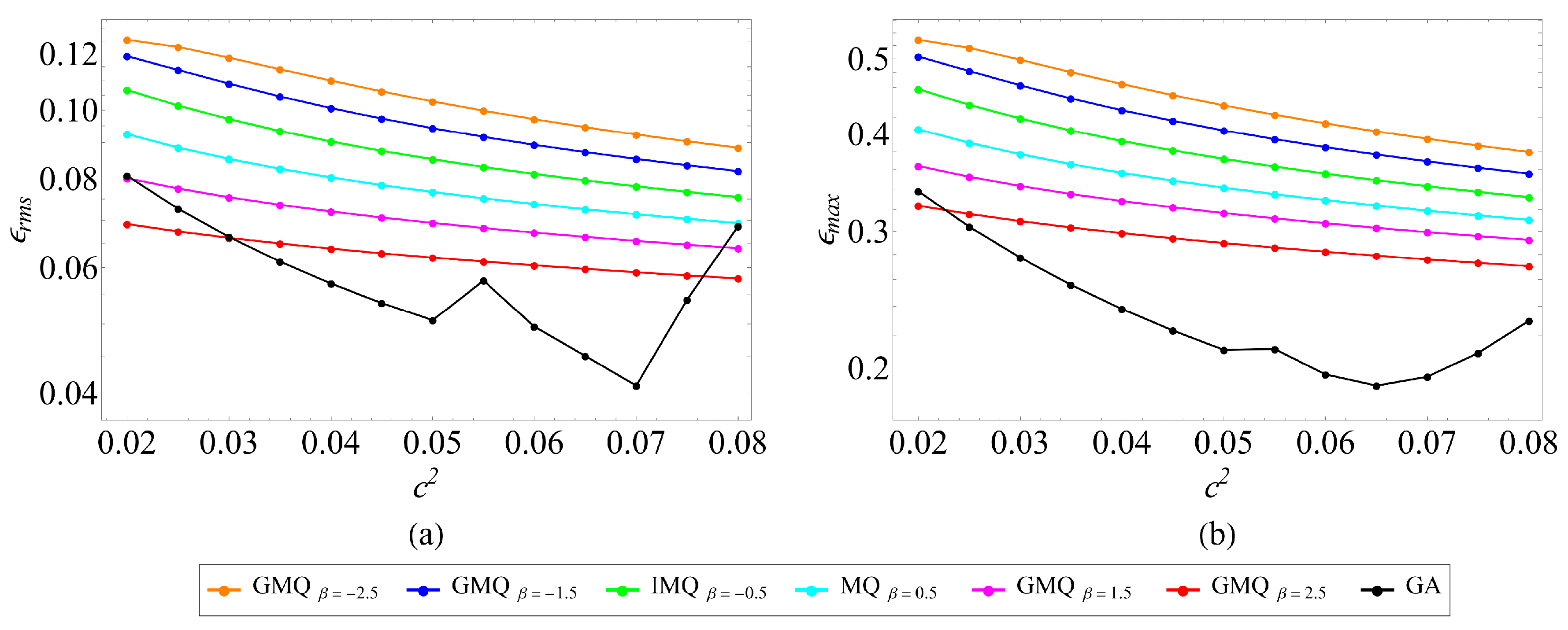
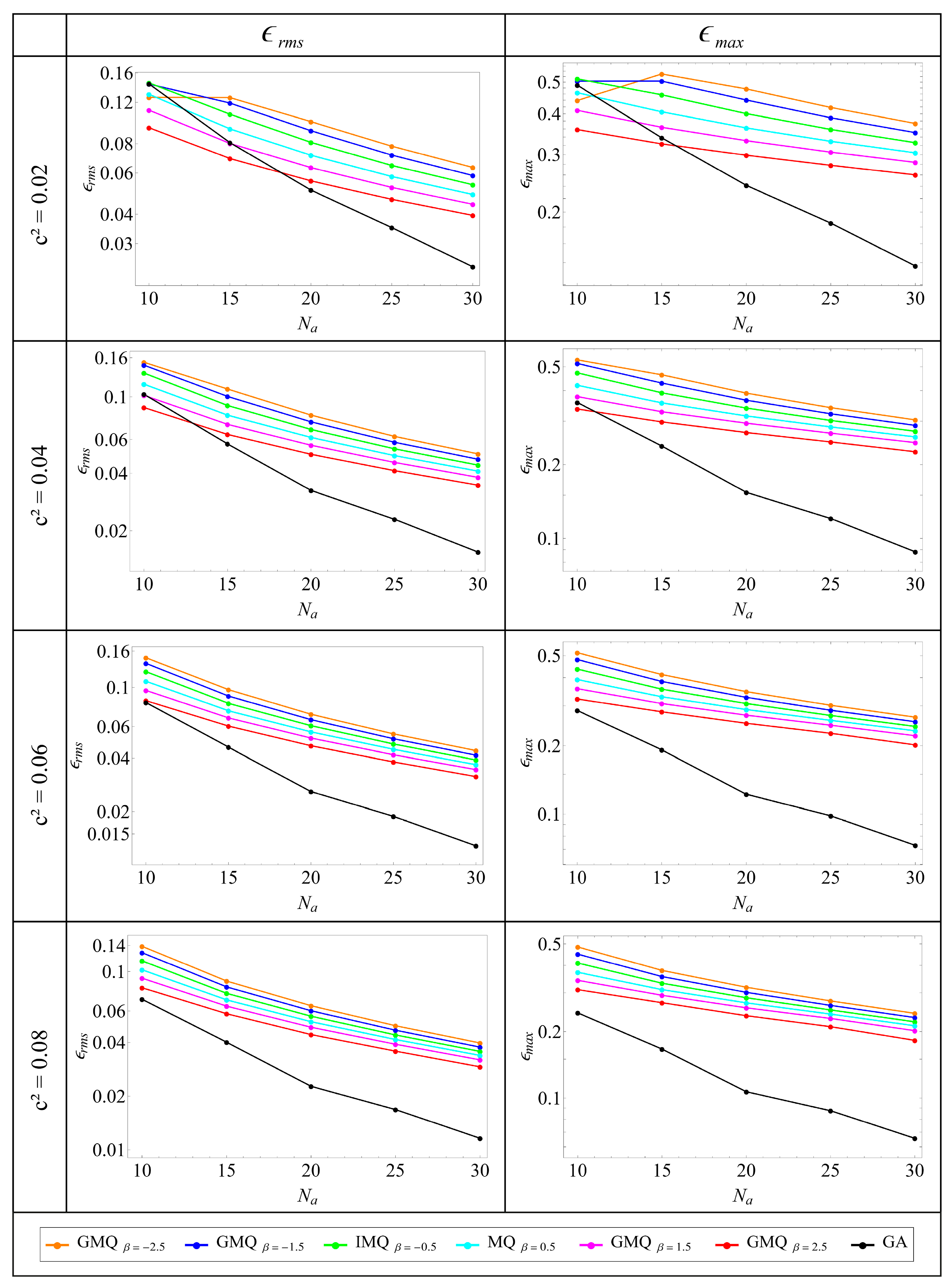
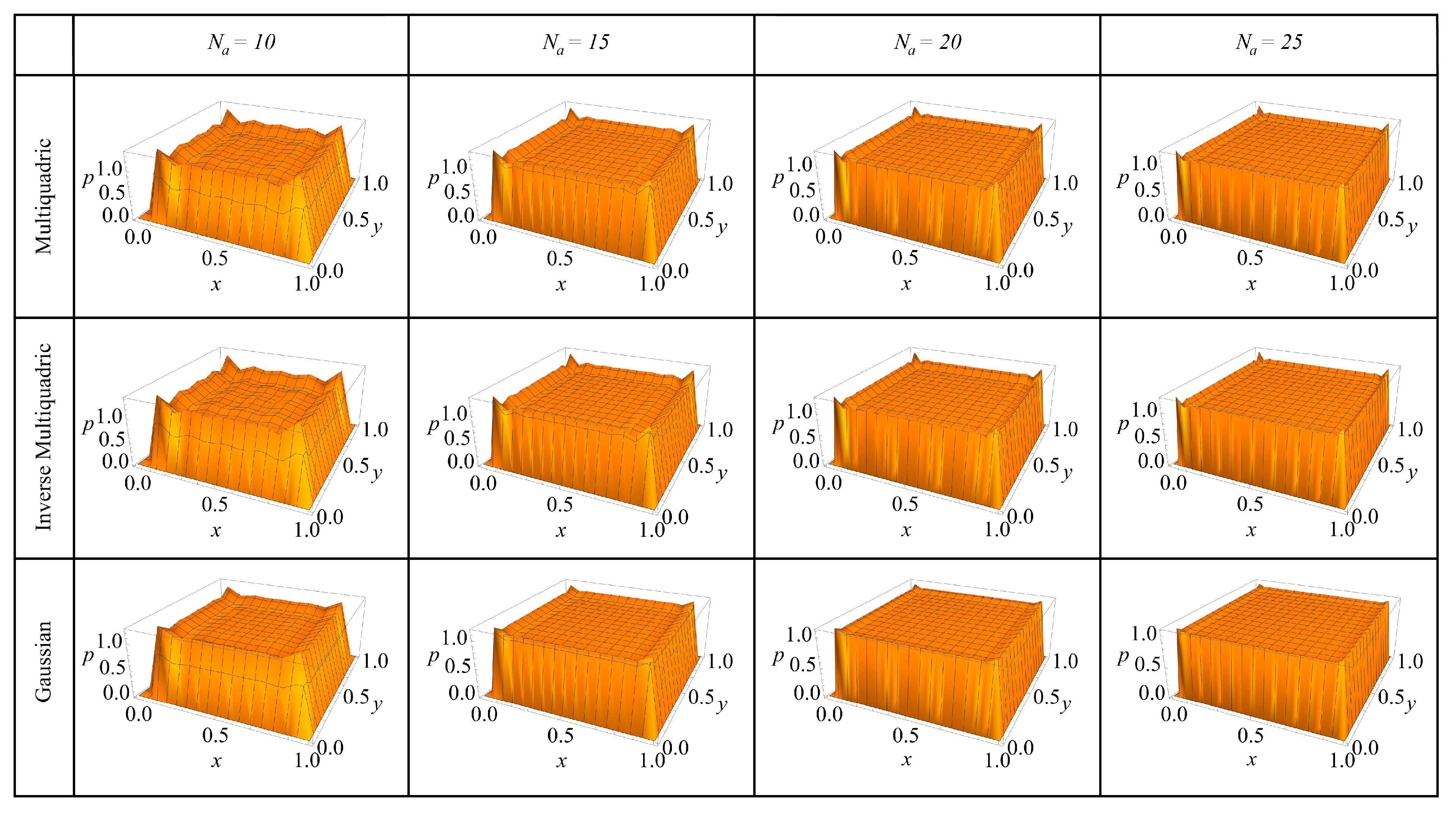
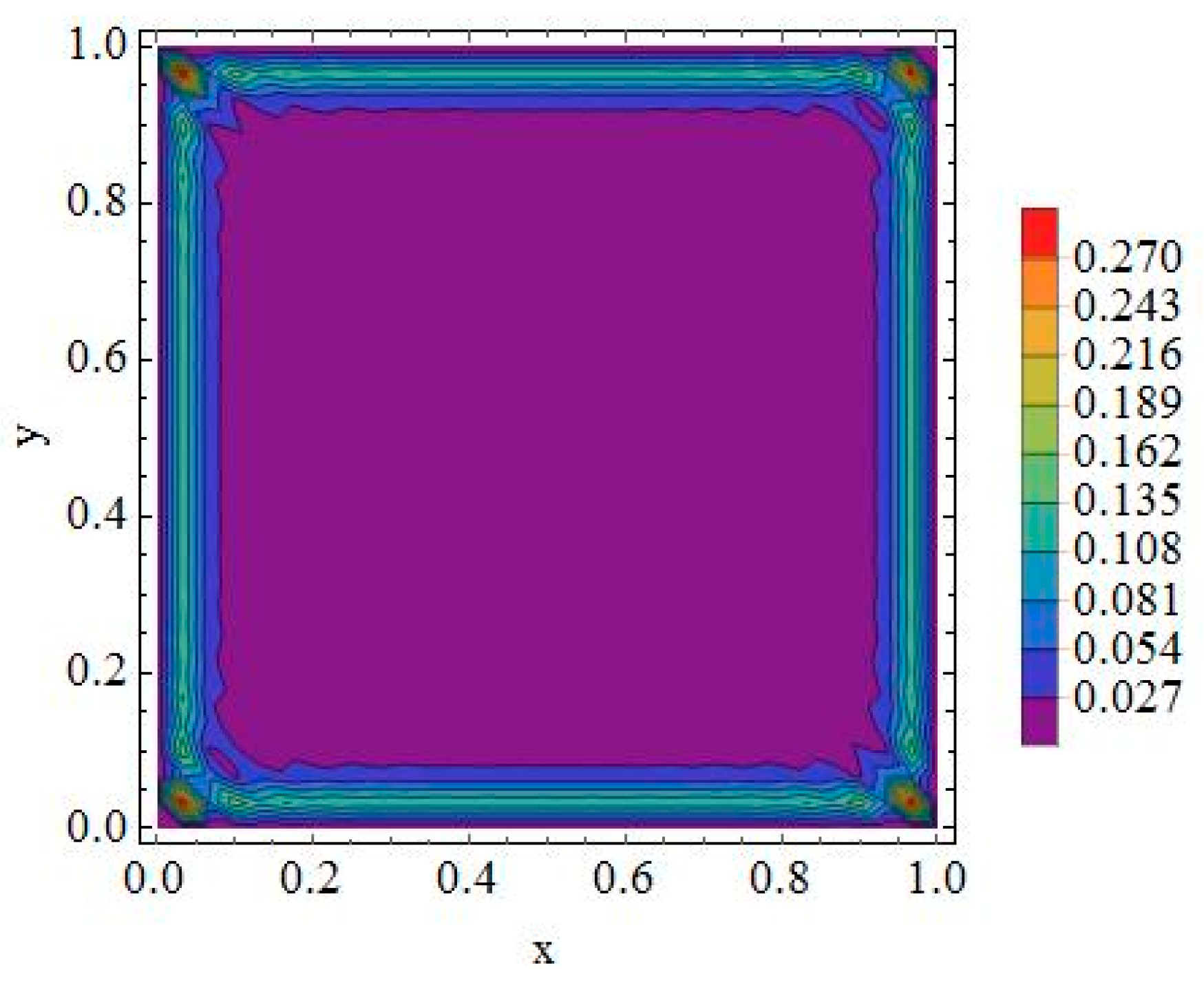
4. Results and Discussion
4.1. One-Dimensional Two-Region Problem
4.2. Two-Dimensional Single Region Problem
5. Conclusions
- The global RBF collocation method accurately reproduces carrier distributions in one-dimensional P-N junctions and two-dimensional domains, confirming its suitability for semiconductor device modeling.
- Basis selection matters: GA basis typically exhibits faster convergence and lower errors at comparable node counts but over a narrower stability window; GMQ variants are more robust to shape-parameter variation, albeit with slightly slower convergence.
- Shape parameter critically affects both error and conditioning; stable plateaus exist where accuracy is near-optimal without severe ill-conditioning, while an overly large shape parameter can destabilize GA in particular.
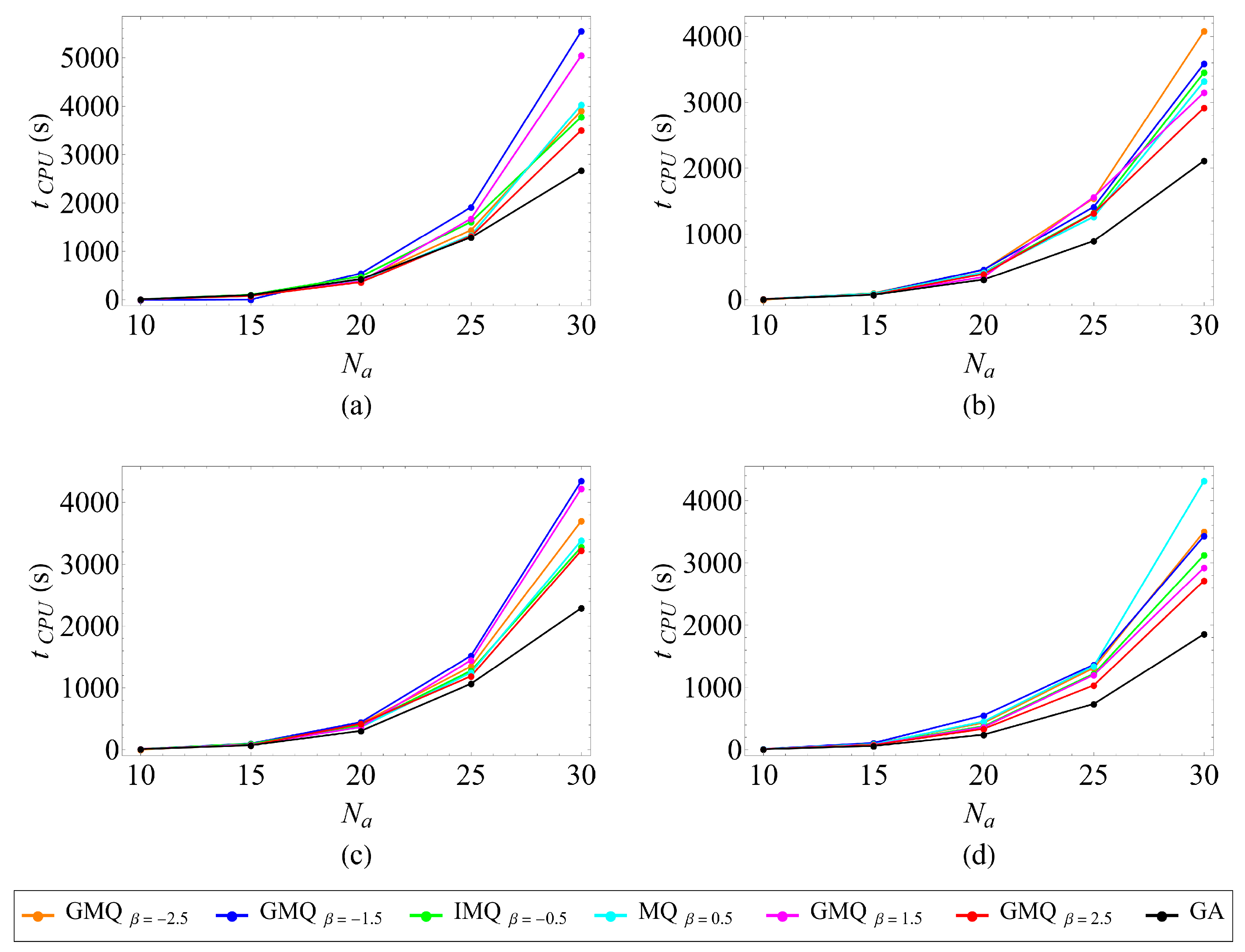
- Because the collocation matrix is dense, CPU time rises rapidly with node count. A utopia-point multi-objective optimization that balances error and runtime yields practical design guidance: for the 2D problem considered, an optimum of 19 intervals per side (equal weights on accuracy and CPU time) gives a near-Pareto solution, largely insensitive to the specific RBF choice.
- Physically, the meshless solver captures the expected sensitivities of carrier densities to surface recombination velocity, diffusion length, and absorption coefficient, aligning with analytical trends and reinforcing the model’s predictive value.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CPU | Central processing unit |
| FEM | Finite element method |
| GA | Gaussian |
| GMQ | Generalized multiquadric |
| IMQ | Inverse multiquadric |
| MQ | Multiquadric |
| PV | Photovoltaic |
| QNR | Quasi-neutral region |
| RBF | Radial basis function |
References
- Sze, S.M.; Ng, K.K. Physics of Semidoncuctor Devices, 3rd ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Nelson, J. The Physics of Solar Cells; Imperial College Press: Singapore, 2003. [Google Scholar]
- Velazquez-Perez, J.E.; Gurevich, Y.G. Charge-carrier transport in thin film solar cells: New formulation. Int. J. Photoenergy 2011, 2011, 976063. [Google Scholar] [CrossRef]
- Biswas, S.; Sinha, A. An analytical study of the minority carrier distribution and photocurrent of a p–i–n quantum dot solar cell based on the InAs/GaAs system. Indian J. Phys. 2017, 91, 1197–1203. [Google Scholar] [CrossRef]
- Sahin, G.; Kerimli, G. Effect of the depth base along the vertical on the electrical parameters of a vertical parallel silicon solar cell in open and short circuit. Results Phys. 2018, 8, 257–261. [Google Scholar] [CrossRef]
- Guo, M.; Li, Y.; Qin, G.; Zhao, M. Nonlinear solutions of PN junctions of piezoelectric semiconductors. Acta Mech. 2019, 230, 1825–1841. [Google Scholar] [CrossRef]
- Nihako, J.N.; Simo, E.; Essouma, D.D.A.; Leutchouang, M.N.; Tsakem, C.R.A.; Tchienou, C.Y.T.; Watia, J.S.K.; Logerais, P.O.; Djouda, J.M. Realistic modeling of photovoltaic solar cell: A simple and accurate two-diode model. Appl. Res. 2025, 4, e70010. [Google Scholar] [CrossRef]
- Snowden, C.M.; Miles, R.E. Compound Semiconductor Device Modelling; Springer: London, UK, 1993. [Google Scholar]
- Sugiura, T.; Nakano, N. Review: Numerical simulation approaches of crystalline-Si photovoltaics. Energy Sci. Eng. 2023, 11, 3888–3906. [Google Scholar] [CrossRef]
- Haddout, A.; Raidou, A.; Fahoume, M. A review on the numerical modeling of CdS/CZTS-based solar cells. Appl. Phys. A 2019, 125, 124. [Google Scholar] [CrossRef]
- Nkele, A.C.; Ike, I.S.; Ezugwu, S.; Maaza, M.; Ezema, F.I. An overview of the mathematical modelling of perovskite solar cells towards achieving highly efficient perovskite devices. Int. J. Energy Res. 2021, 45, 1496–1516. [Google Scholar] [CrossRef]
- Groves, C. Simulating charge transport in organic semiconductors and devices: A review. Rep. Prog. Phys. 2017, 80, 026502. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Kansa, E.J. Application of Hardy’s Multiquadric Interpolation to Hydrodynamics. In Proceedings of the 1986 Summer Computer Simulation Conference, San Diego, CA, USA, 23–25 January 1986; Crosbie, R., Luker, P., Eds.; Society for Computer Simulation: San Diego, CA, USA, 1986; Volume 4, pp. 111–117. [Google Scholar]
- Jamil, M.; Ng, E.Y.K. Evaluation of meshless radial basis collocation method (RBCM) for heterogeneous conduction and simulation of temperature inside biological tissues. Int. J. Therm. Sci. 2013, 68, 42–52. [Google Scholar] [CrossRef]
- Waters, J.; Pepper, D.W. Global versus localized RBF meshless methods for solving incompressible fluid flow with heat transfer. Numer. Heat Transf. B 2015, 68, 185–203. [Google Scholar] [CrossRef]
- Karabaş, N.İ.; Korkut, S.Ö.; Tanoğlu, G.; Aziz, I.; Islam, S. An efficient approach for solving nonlinear multidimensional Schrödinger equations. Eng. Anal. Bound. Elem. 2021, 132, 263–270. [Google Scholar] [CrossRef]
- Tanbay, T.; Ozgener, B. Fully meshless solution of the one-dimensional multigroup neutron transport equation with the radial basis function collocation method. Comput. Math. Appl. 2020, 79, 1266–1286. [Google Scholar] [CrossRef]
- Duan, Y. A note on the meshless method using radial basis functions. Comput. Math. Appl. 2008, 55, 66–75. [Google Scholar] [CrossRef]
- Wordelman, C.J.; Aluru, N.R.; Ravaioli, U. A meshless method for the numerical solution of the 2- and 3-D semiconductor Poisson equation. CMES Comput. Model. Eng. Sci. 2000, 1, 121–126. [Google Scholar] [CrossRef]
- Kosec, G.; Trobec, R. Simulation of semiconductor devices with a local numerical approach. Eng. Anal. Bound. Elem. 2015, 50, 69–75. [Google Scholar] [CrossRef]
- Kinani, M.; Amine, A.; Mir, Y.; Zazoui, M. A numerical study of InGaAs/GaAsP multiple quantum well solar cells using radial basis functions. In Proceedings of the 2nd International Conference on Electronic Engineering and Renewable Energy Systems, Saidia, Morocco, 2–4 April 2020; Hajji, B., Mellit, A., Tina, G.M., Rabhi, A., Launay, J., Naimi, S.E., Eds.; Springer: Singapore, 2021; Volume 681, pp. 231–238. [Google Scholar]
- Riganti, R.; Alasio, M.G.C.; Bellotti, E.; Dal Negro, L. DDNet: A unified physics-ınformed deep learning framework for semiconductor device modeling. arXiv 2025. [Google Scholar] [CrossRef]
- Tian, X.; Zhou, H.; Hu, Y.; Deng, Q.; Xu, M.; Sladek, J.; Sladek, V.; Shen, S. Nonlinear interaction studies of flexoelectricity and electron transport around nano-cracks in semiconductors via the collocation mixed finite element method. J. Appl. Phys. 2025, 137, 194103. [Google Scholar] [CrossRef]
- Brezzi, F.; Marini, L.D.; Micheletti, S.; Pietra, P.; Sacco, R.; Wang, S. Discretization of semiconductor device problems (I). Handb. Numer. Anal. 2005, 13, 317–441. [Google Scholar] [CrossRef]
- Archer, M.D.; Bolton, J.R.; Siklos, S.T.C. A review of analytic solutions for a model p–n junction cell under low-injection conditions. Sol. Energy Mater. Sol. Cells 1996, 40, 133–176. [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial Basis Functions: Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Schaback, R. Error estimates and condition numbers for radial basis function interpolation. Adv. Comput. Math. 1995, 3, 251–264. [Google Scholar] [CrossRef]
- Tanbay, T.; Ozgener, B. A comparison of the meshless RBF collocation method with finite element and boundary element methods in neutron diffusion calculations. Eng. Anal. Bound. Elem. 2014, 46, 30–40. [Google Scholar] [CrossRef]
- Huang, C.-S.; Lee, C.-F.; Cheng, A.H.-D. Error estimate, optimal shape factor, and high precision computation of multiquadric collocation method. Eng. Anal. Bound. Elem. 2007, 31, 614–623. [Google Scholar] [CrossRef]
- Luh, L.T. The choice of the shape parameter—A friendly approach. Eng. Anal. Bound. Elem. 2019, 98, 103–109. [Google Scholar] [CrossRef]
- Kansa, E.J.; Hon, Y.C. Circumventing the ill-conditioning problem with multiquadric radial basis functions: Applications to elliptic partial differential equations. Comput. Math. Appl. 2000, 39, 123–137. [Google Scholar] [CrossRef]
- Cheng, A.H.-D. Multiquadric and its shape parameter-A numerical investigation of error estimate, condition number, and round-off error by arbitrary precision computation. Eng. Anal. Bound. Elem. 2012, 36, 220–239. [Google Scholar] [CrossRef]
- Fahrenbruch, A.; Bube, R. Fundamentals of Solar Cells: Photovoltaic Solar Energy Conversion; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Cheng, A.H.-D.; Golberg, M.A.; Kansa, E.J.; Zammito, G. Exponential convergence and h-c multiquadric collocation method for partial differential equations. Numer. Methods Partial Differ. Equ. 2003, 19, 571–594. [Google Scholar] [CrossRef]








| RBF | Limit | |||||
|---|---|---|---|---|---|---|
| 18 | ||||||
| 18 | ||||||
| 18 | ||||||
| 18 | ||||||
| 17 | ||||||
| 11 | ||||||
| 0.6 |
| RBF | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| MQ | 0.1 | 11 | 0.1136 | 9 | 0.1154 | 10 | 0.1155 | 11 | 0.1152 |
| 0.3 | 15 | 0.2599 | 14 | 0.2707 | 15 | 0.2635 | 15 | 0.2555 | |
| 0.5 | 19 | 0.3981 | 19 | 0.4000 | 19 | 0.3931 | 19 | 0.3852 | |
| 0.7 | 25 | 0.5021 | 25 | 0.4926 | 25 | 0.4859 | 25 | 0.4799 | |
| 0.9 | 33 | 0.5551 | 33 | 0.5419 | 33 | 0.5328 | 33 | 0.5254 | |
| IMQ | 0.1 | 8 | 0.1054 | 10 | 0.1142 | 9 | 0.1154 | 9 | 0.1147 |
| 0.3 | 14 | 0.2783 | 14 | 0.2680 | 14 | 0.2675 | 14 | 0.2669 | |
| 0.5 | 18 | 0.4151 | 19 | 0.3940 | 19 | 0.3904 | 19 | 0.3886 | |
| 0.7 | 26 | 0.5074 | 25 | 0.4817 | 25 | 0.4749 | 25 | 0.4713 | |
| 0.9 | 36 | 0.5370 | 33 | 0.5265 | 32 | 0.5184 | 32 | 0.5121 | |
| GA | 0.1 | 6 | 0.0848 | 8 | 0.1103 | 8 | 0.1025 | 9 | 0.1182 |
| 0.3 | 14 | 0.2731 | 15 | 0.2633 | 14 | 0.2622 | 15 | 0.2581 | |
| 0.5 | 19 | 0.3631 | 19 | 0.3449 | 19 | 0.3481 | 20 | 0.3448 | |
| 0.7 | 26 | 0.3950 | 25 | 0.3763 | 25 | 0.3812 | 25 | 0.3851 | |
| 0.9 | 32 | 0.3824 | 31 | 0.3685 | 31 | 0.376 | 31 | 0.3855 | |
| GMQ | 0.1 | 10 | 0.1049 | 9 | 0.1033 | 10 | 0.1058 | 10 | 0.1151 |
| 0.3 | 14 | 0.2666 | 14 | 0.2678 | 15 | 0.2617 | 15 | 0.2635 | |
| 0.5 | 19 | 0.4054 | 19 | 0.4010 | 19 | 0.3833 | 19 | 0.3799 | |
| 0.7 | 26 | 0.5031 | 26 | 0.4889 | 25 | 0.4650 | 25 | 0.4570 | |
| 0.9 | 37 | 0.5290 | 36 | 0.5063 | 33 | 0.5013 | 32 | 0.4942 | |
| GMQ | 0.1 | 11 | 0.0868 | 9 | 0.1112 | 11 | 0.1134 | 7 | 0.1024 |
| 0.3 | 15 | 0.2509 | 14 | 0.2666 | 15 | 0.2514 | 14 | 0.2755 | |
| 0.5 | 19 | 0.3885 | 19 | 0.3850 | 19 | 0.3673 | 19 | 0.3905 | |
| 0.7 | 25 | 0.4852 | 25 | 0.4644 | 25 | 0.4483 | 25 | 0.4637 | |
| 0.9 | 33 | 0.5273 | 31 | 0.5085 | 30 | 0.4961 | 32 | 0.5011 | |
| GMQ | 0.1 | 12 | 0.1071 | 8 | 0.0985 | 11 | 0.1112 | 9 | 0.1104 |
| 0.3 | 15 | 0.2543 | 14 | 0.2753 | 15 | 0.2562 | 14 | 0.2730 | |
| 0.5 | 19 | 0.3996 | 18 | 0.4133 | 19 | 0.3936 | 19 | 0.4038 | |
| 0.7 | 25 | 0.5119 | 25 | 0.5074 | 25 | 0.4953 | 26 | 0.4940 | |
| 0.9 | 33 | 0.5724 | 33 | 0.556 | 33 | 0.5447 | 34 | 0.5355 | |
| GMQ | 0.1 | 10 | 0.1139 | 8 | 0.1024 | 9 | 0.1112 | 9 | 0.1150 |
| 0.3 | 14 | 0.2700 | 13 | 0.2806 | 14 | 0.2724 | 14 | 0.2728 | |
| 0.5 | 18 | 0.4147 | 18 | 0.4197 | 19 | 0.4084 | 19 | 0.4064 | |
| 0.7 | 25 | 0.5267 | 25 | 0.5176 | 26 | 0.5068 | 26 | 0.5009 | |
| 0.9 | 34 | 0.5886 | 34 | 0.5669 | 34 | 0.5515 | 35 | 0.5393 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ispir, M.; Tanbay, T. Numerical Modeling of Photovoltaic Cells with the Meshless Global Radial Basis Function Collocation Method. Energies 2025, 18, 5267. https://doi.org/10.3390/en18195267
Ispir M, Tanbay T. Numerical Modeling of Photovoltaic Cells with the Meshless Global Radial Basis Function Collocation Method. Energies. 2025; 18(19):5267. https://doi.org/10.3390/en18195267
Chicago/Turabian StyleIspir, Murat, and Tayfun Tanbay. 2025. "Numerical Modeling of Photovoltaic Cells with the Meshless Global Radial Basis Function Collocation Method" Energies 18, no. 19: 5267. https://doi.org/10.3390/en18195267
APA StyleIspir, M., & Tanbay, T. (2025). Numerical Modeling of Photovoltaic Cells with the Meshless Global Radial Basis Function Collocation Method. Energies, 18(19), 5267. https://doi.org/10.3390/en18195267







