Solar Resource Mapping of the Tigray Region, Ethiopia, Based on Satellite and Meteorological Data

Abstract

The availability of properly analyzed energy resource potential data is a prerequisite in energy planning and development. However, this was sparsely applied in Ethiopia’s renewable energy turnkey project development strategies. This study focuses on developing a solar energy resource map of Tigray to accelerate the expansion of solar energy to improve electricity access through on-grid and off-grid development schemes. This study uses monthly sunshine hour data from sixteen meteorological stations, measured at a 2 m height, and average yearly solar radiation data from twenty-two satellite stations, validated by solar radiation data and measured at three sites at 10 and 30 m heights. The solar energy potential was analyzed by taking relevant atmospheric and meteorological factors to produce solar radiation components. Accordingly, the average annual solar radiation of Tigray was found to be 6.1 kWh/m²/day and 5.3 kWh/m²/day based on meteorological and satellite data, respectively. The meteorological result gave a closer estimate to Ethiopia’s ESMAP Global Solar result of 5.83 kWh/m²/day. Finally, monthly and annual average solar radiation maps of the region were developed using ArcGIS10.5. The study’s results could contribute to assisting various solar energy developers in preparing better solar energy development plans to alleviate the chronic energy poverty of the region.

1. Introduction

Solar energy is an abundant, free, and clean form of energy that can be utilized to produce reliable energy for household and industrial consumption. The amount of solar energy that reaches the earth’s surface is influenced by several factors, such as temperature, evaporation, humidity, longitude, latitude, and sun angle [1]. Generally, the surface temperature of the sun is equivalent to a blackbody temperature of 5760 K and produces ${1.5\times 10}^{18}$ kWh of energy every year, which is about 10,000 times greater than the world’s current yearly energy usage. The sun emits this energy almost constantly for 24 h daily and 365 days annually. However, the earth’s surface is exposed to solar energy for about 12 h, and the amount of solar energy reaching the surface can be reduced by atmospheric conditions such as clouds and dust [2,3,4].

Globally, renewable energy sources are expected to provide about 60–70% of total primary energy and nearly 90% of electricity generation by 2050 [5]. In this perspective, solar energy plays a key role in energy transition and building long-term sustainability [6]. For example, the development of solar-powered cars indicates the sector’s role in decarbonizing the transportation sector [7]. Accordingly, studies have contributed to greatly reducing the cost of solar photovoltaic (PV) modules and have increased their installed capacity.

On the other hand, Ethiopia’s energy sector faces significant challenges in utilizing its renewable energy resources, such as solar energy [8,9,10], due to the unavailability of well-developed resource data that can support planning, development, and policy. The variability of solar radiation impacts the power generation efficiency of photovoltaics, and in return, this affects the planning and development of solar power generation [11,12]. It is therefore imperative to employ different techniques and methods to map solar resource potential and to develop energy planning accordingly. ArcGIS10.5 is a decision-support tool that is used to develop maps for proposing suitable sites for planning and development. GIS mapping can create synergies and trade-offs between energy and sustainable development goals [13,14].

Solar resource maps can be developed by using shortwave solar radiation data retrieved from the satellite application facility on climate monitoring and global circulation models [15], by measuring real-time surface irradiance, and by formulating a solar irradiance forecasting model to attempt to map the relationship between sky images and solar irradiance. For example, a GIS-based model was developed to assess solar PV potential by analyzing the geographical suitability for solar power projects in China [16].

The operational efficiency of photovoltaic cells is contingent on local meteorological conditions, which can vary considerably over wide geographic areas. An essential consideration in the analysis of solar energy potential is the effect of temperature on efficiency losses of photovoltaics, as standard maps of solar potential only show solar resources. Solar resources can be utilized by installing solar PVs on rooftops. Rooftop solar arrays can substitute for or reduce the amount of electricity required in buildings, as shown in the European energy transition [17,18,19,20,21,22].

The purpose of this study was to develop the solar resource potential of the Tigray region by using meteorological and satellite (NASA) data. By validating these data sources, GIS-based solar radiation maps were generated to provide spatial solar energy potential across the region. The high-resolution solar resource maps generated in this study provide the essential foundational data layer for future land-use suitability analyses. Such analyses integrate comprehensive exclusion criteria, including protected areas, topography, land cover, and infrastructure proximity, with the solar potential data presented here to identify optimal sites for solar energy development [23,24,25,26]. The results of this study will support strategic planning and informed investment decisions by spotting areas with high solar energy potential. Ultimately, the findings will contribute to promoting sustainable electrification and the development of renewable energy in the region.

Study Area and Data Settings

Ethiopia is located in a solar belt that spans between latitudes 3° N and 15° N and longitudes 33° E and 48° E. The geographical location of the study area lies between 4°57′ and 14°55′ N latitude and 36°27′ and 39°59′ E longitude, covering about 1.13 million square kilometers, as shown in Figure 1. The monthly global solar radiation in Ethiopia ranges from 5000 to 7500 MW/m², with regional variations from 4.25 kWh/m²/day in its western lowlands to 6.25 kWh/m²/day in its northeastern parts [8,9].

2. Materials and Methods

This study analyzed solar energy resource data and developed a solar energy atlas for the Tigray region. The methodologies followed to carry out this study include data collection, data and error analysis, conceptual model development, resource mapping, and resource classification. The overall methodologies and data flow are presented in Figure 2.

2.1. Data Collection and Analysis

The primary data for this study includes solar radiation and sunshine duration data measured at a height of 2 m by the National Meteorological Agency (NMA) at sixteen meteorological stations (minimum of one year and maximum of seventeen years of data), as shown in

Table 1. Latitude, longitude, and altitude of meteorological sites.

No.	Site Name	Location		Altitude (m)	Measurement Period
		Latitude (°)	Longitude (°)
1	Adigrat	14.48	39.46	2457	2004–2018
2	Axum	14.11	38.73	2132	2009–2018
3	Mekelle airport	13.47	39.53	2033	2002–2018
4	Mekelle obs	13.53	39.47	2052	2004–2019
5	Adwa	14.17	38.88	1907	2002–2016
6	Atsbi	13.88	39.74	2630	2009–2016
7	Shire	12.88	38.28	1963	2004–2019
8	Sheraro	14.41	37.77	1246	2007–2016
9	Mychew	13.55	39.55	1535	2004–2015
10	Senkata	14.07	39.57	2480	2003–2017
11	Chercher	13.21	39.77	1780	2007–2011
12	Tekeze	13.34	38.75	1256	2010
13	Setit Humora	14.27	36.61	602	2008–2012
14	Nebelet	14.10	39.27	2016	2009–2016
15	Samre	13.22	39.22	2033	2018
16	Humora airport	14.25	36.58	786.1	2011–2012

; thirty-eight years of solar radiation data from twenty-two sites, obtained from the National Aeronautics and Space Administration (NASA), as shown in

Table 2. Latitude, longitude, and altitude of NASA’s satellite sites.

No.	Site Name	Location		Data Period
		Latitude (°)	Longitude (°)
1	Adi Remets	13.75	37.32	1981–2018
2	Adwa	14.17	38.92	1981–2018
3	Agulae	13.69	39.58	1981–2018
4	Aksum	14.11	38.73	1981–2018
5	Alamata	14.43	39.58	1981–2018
6	Alitena	14.53	39.57	1981–2018
7	Ambalage	12.94	39.52	1981–2018
8	Atsbi	13.88	39.72	1981–2018
9	Entcho	14.40	39.17	1981–2018
10	Freweyni	14.07	39.57	1981–2018
11	Gijet	13.33	39.17	1981–2018
12	Hagereselam	13.65	39.17	1981–2018
13	Hawzen	14.02	39.39	1981–2018
14	Korem	12.72	39.54	1981–2018
15	Maichew	13.55	39.54	1981–2018
16	Mekelle	13.53	39.48	1981–2018
17	Sero	13.89	39.60	1981–2018
18	Rama	14.41	38.79	1981–2018
19	Samre	13.22	39.22	1981–2018
20	Sheraro	14.41	38.24	1981–2018
21	Shire	14.11	38.29	1981–2018
22	Wukro	13.79	39.60	1981–2018

; and two years of global solar radiation data from three sites, measured at heights of 10 and 30 m and used for validation, as shown in Table 1.

A critical aspect of resource assessment is the quality and provenance of the input data. The sunshine duration data was measured using Campbell–Stokes sunshine recorders, administered by the NMA following standard World Meteorological Organization (WMO) procedures. The satellite-derived solar radiation data was obtained from the NASA Prediction of Worldwide Energy Resources (POWER) project, specifically the ALLSKY_SFC_SW_DWN parameter, which provides surface shortwave radiation under all-sky conditions at a spatial resolution of 0.5° × 0.5°.

Empirical models were used to estimate solar radiation components, and Geographic Information System (GIS) was used to process and visualize the spatial distribution of the solar resources across the region based on these data from the sites shown in Figure 3. In addition, necessary secondary data from the literature were used. The meteorological and satellite data were filtered and qualified for five years of microscale and mesoscale data. Later, validation procedures were applied to ensure the reliability of the dataset.

To ensure the reliability and robustness of the datasets, a systematic validation procedure was undertaken prior to their integration into the analytical framework. The validation process involved a comparative analysis between the data obtained from the NMA and the corresponding NASA data. Statistical performance indicators, including Root Mean Square Error (RMSE), Mean Bias Error (MBE), Mean Percentage Error (MPE), mean absolute percentage error (MAPE), and coefficient of determination $\left(R^2\right)$, were employed to evaluate the degree of agreement between the datasets. The ground-based observations served as the reference standard, while the satellite-derived datasets were assessed against these observations for all available temporal and spatial points. Any anomalous or outlier values exceeding predefined quality thresholds were excluded from further analysis. The validation ensured that only datasets meeting acceptable accuracy levels were retained, thereby guaranteeing the integrity of subsequent empirical modeling and GIS-based spatial analysis.

2.2. Development of Site-Adapted Solar Radiation Estimating Model

After reviewing various established methods applied in resource estimation, a modified Angstrom relation, enhanced by studies [27,28,29], was considered for this study’s application. This approach provided a solid foundation for developing a new topography-dependent model and served as the initial input formula. However, the final geography-dependent formula was derived from actual measurements taken at meteorological stations. This formula was tested to estimate solar radiation based on three-mast data before estimation based on meteorological and satellite station data was performed. The approach was primarily based on the well-known Angstrom linear relation and is given in Equation $\left(1\right)$.

$$\mathrm{H}=H_0[\mathrm{a}+\mathrm{b}]{\displaystyle \frac{N}{N_0}}$$

(1)

Every data point was averaged daily and processed to obtain a monthly average. The data were filtered, and monthly data for more than sixteen days and yearly data for more than six months without either sunlight hour or global solar radiation records were eliminated to avoid wrong interpretation and mapping. The regression coefficients a and b were determined using Equations $\left(2\right)\mathrm{a}\mathrm{n}\mathrm{d}\left(3\right)$.

$$\mathrm{a}=-0.309+0.539\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\phi }-0.0693\mathrm{h}+0.29\left({\displaystyle \frac{N}{N_0}}\right)$$

(2)

$$\mathrm{b}=1.529-1.027\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\phi }+0.0926\mathrm{h}-0.359\left({\displaystyle \frac{N}{N_0}}\right)$$

(3)

The conceptual model was developed to estimate the monthly average day length $\left(N_0\right)$, sunset hour angle, and declination angle. Equations (4)–(6) were used to determine the average day duration on a monthly basis.

$$N_0={\displaystyle \frac{24}{\pi }}{\times \omega }_s\to {\displaystyle \frac{2}{15}}\times {cos}^{-1}\left[-tan\left(\varnothing \right)tan\left(\delta \right)\right]$$

(4)

$${\omega }_s={cos}^{-1}\left[-tan\left(\varnothing \right)tan\left(\delta \right)\right]$$

(5)

$$\delta =23.49sin\left[3600\left({\displaystyle \frac{284+nd}{365}}\right)\right]$$

(6)

Similarly, the extra-terrestrial solar radiation $\left(H_0\right)$ was estimated using Equation $\left(7\right).$

$$H_0={\displaystyle \frac{\left(24\times 360\times G_{sc}\right)}{\pi }}\left[1+0.033cos\left({\displaystyle \frac{\left(360\times nd\right)}{365}}\right)\right]\left[cos\left(\phi \right)cos\left(\delta \right)sin\left({\omega }_s\right)+{\displaystyle \frac{\left(\pi \times {\omega }_s\right)}{180}}sin\left(\phi \right)sin\left(\delta \right)\right]$$

(7)

The measurement history of the three validation sites is presented in

Table 3. Global solar radiation data used for regression analysis [28].

No.	Station	Period	Years	Altitude (m)	Latitude (°)	Longitude (°)
1	Dera	2011–2012	2	2870	13.59	39.43
2	Hagereselam	2011–2012	2	2632	13.39	39.11
3	Myderhu	2011–2012	2	2512	13.17	39.23

[28]. These data were used for the formulation of the new correlation model. These data were recorded on a daily average basis and processed to obtain monthly average values. Equation $\left(8\right)$ is the new estimation model used to estimate the resource and originated from regression analysis using measured solar radiation data from the three validation sites. This regression provided the site-specific coefficients that underpin the proposed model.

$${\displaystyle \frac{H}{H_0}}=D_1+D_2\Phi +D_{3}h+D_4{\displaystyle \frac{N}{N_0}}$$

(8)

Table 4. Average days of each month and declination angle [30].

No.	nd for ith Day		Average Day of the Month
Month		Date	Day of Year	Declination δ (°)
Jan.	I	17	17	−20.9
Feb.	31+i	16	47	−13
Mar.	59+i	16	75	−2.42
Apr.	90+i	15	105	9.4
May.	120+i	15	135	18.8
Jun.	151+i	11	162	23.1
Jul.	181+i	17	198	21.2
Aug.	212+i	16	228	13.5
Sep.	243+i	15	258	2.2
Oct.	273+i	15	288	−9.6
Nov.	304+i	14	318	−18.9
Dec.	334+i	10	344	−23

presents the average days of each month, along with their corresponding day of the year and solar declination angle $\left(\delta \right)$. The declination values range from about –23° in December to +23° in June, reflecting the seasonal tilt of the earth’s axis. These average values are commonly used in solar radiation calculations to approximate the position of the sun for each month.

2.3. Statistical Error Test Analysis

Several statistical test techniques are available for evaluating the performance of solar radiation estimation models. The most prevalent ones were reviewed and identified based on existing studies [28,29]. To conduct a comprehensive statistical evaluation of the model’s estimated values, a range of performance metrics were employed, including MBE, RMSE, MPE, and t-test. These metrics collectively assess various aspects of the model’s performance. MBE measured the average deviation and indicated systematic bias, RMSE evaluated the overall accuracy by quantifying the magnitude of prediction errors, MPE expressed the error in percentage terms to highlight proportional inaccuracies, and the t-test assessed the statistical significance of differences between predicted and observed values. By examining these indicators, the statistical tests offered a detailed and reliable assessment of the models’ accuracy and consistency in replicating actual solar radiation data. The mathematical expressions used to perform this statistical analysis are summarized in

Table 5. Summary of statistical analysis for the evaluation of model performance [30,31].

No.	Statistical Tools	Mathematical Expression in Terms of Measured $\left(\mathit{M}\mathit{i}\right)$ and Calculated $\left(\mathit{C}\mathit{i}\right)$ Value	Preferable Value	Equation
1	Relative Percentage Error (e%)	e$\%=\left({\displaystyle \frac{{\mathrm{M}}_{\mathrm{i}}-{\mathrm{C}}_{\mathrm{i}}}{{\mathrm{M}}_{\mathrm{i}}}}\right)\times$ 100	-	$\left(9\right)$
2	Coefficient of Determination (R2)	$R^2={\displaystyle \frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{C}}_{\mathrm{i}}-{\mathrm{C}}_{\mathrm{a}}\right)\times \left({\mathrm{M}}_{\mathrm{i}}-{\mathrm{M}}_{\mathrm{a}}\right)}{\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{C}}_{\mathrm{i}}-{\mathrm{C}}_{\mathrm{a}}\right)}^2\times \sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{M}}_{\mathrm{i}}-{\mathrm{M}}_{\mathrm{a}}\right)}^2}}}$	Ranges between 0 and 1 (0 < R2 < 1)	$\left(10\right)$
3	Mean Percentage Error (MPE)	$\mathrm{M}\mathrm{P}\mathrm{E}={\displaystyle \frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{{\mathrm{M}}_{\mathrm{i}}-{\mathrm{C}}_{\mathrm{i}}}{{\mathrm{M}}_{\mathrm{i}}}\right)}{\mathrm{n}}}$ $\times \mathrm{ 100}$	Between −10% and +10%.	$\left(11\right)$
4	Mean Absolute Percentage Error	$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{\frac{1}{\mathrm{N}}\sum _{\mathrm{i}=1}^{\mathrm{n}}\left|{\mathrm{M}}_{\mathrm{i}}-{\mathrm{C}}_{\mathrm{i}}\right|}{\frac{1}{\mathrm{n}}\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{C}}_{\mathrm{I}}}}$ $\times \mathrm{ 100}$	-	$\left(12\right)$
5	Mean Bias Error (MBE)	$\mathrm{M}\mathrm{B}\mathrm{E}={\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}({\mathrm{M}}_{\mathrm{i}}-{\mathrm{C}}_{\mathrm{i}})$	Close to zero	$\left(13\right)$
6	Root Mean Square Error (RMSE)	$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{\left({\mathrm{C}}_{\mathrm{i}}-{\mathrm{M}}_{\mathrm{i}}\right)}^2}$	Close to zero	$\left(14\right)$
7	t−stat Method	$\mathrm{t}-\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}=\sqrt{{\displaystyle \frac{\left(\mathrm{n}-1\right){{\mathrm{M}\mathrm{B}\mathrm{E}}^2}_{\mathrm{t}}}{{{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}^2}_{\mathrm{t}}-{{\mathrm{M}\mathrm{B}\mathrm{E}}^2}_{\mathrm{t}}}}}$	–	$\left(15\right)$

.

2.4. Mapping of Solar Potential

The solar radiation output of the conceptual estimation model, analyzed using GIS, used a monthly mean format from January through December. ArcGIS 10.5 was used in this work for mapping global solar radiation and solar energy distribution. The solar radiation map depicted the spatial distribution of global solar radiation (kWh/m²/day) across the region, representing the average amount of incident solar energy on a horizontal surface. This map provided insights into the raw solar resources available at different locations. In contrast, the solar energy map illustrated the spatial variation in total solar energy potential, representing the cumulative energy yield over a given period and derived directly from the radiation data. This distinction would allow for targeted evaluation of the resource availability and its potential for conversion into usable energy. To develop a map, there are various techniques, such as ozone concentration [32,33] and the IDW method [33]. While ozone has limited aerosol impacts, water vapor and cloud cover exerted greater influence on the attenuation and variability of solar irradiance to generate a solar radiation surface plot [34,35,36]. In this context, incorporating these parameters into solar resource assessments is essential for producing accurate and meaningful characterizations of solar radiation patterns [37,38]. However, in this study, a 3D surface plot was generated using a scattered Z-value with an X–Y coordinate. Solar radiation and solar energy were taken as Z-values, and geographical coordinates (latitude and longitude) were considered as X–Y coordinates. The surface plot was then analyzed using a spatial analysis to form a contoured plot of solar radiation. The steps used to develop the map are summarized in Figure 4.

2.5. Resource Classification

To support strategic planning and investment prioritization, the spatial distribution of solar resources was classified into three distinct potential categories, high, medium, and low, based on the global solar radiation (GSR) values obtained from the topography-dependent model, which is presented in

Table 6. Solar resource potential classifications.

No.	Potential Category	Radiation Range (kWh/m2/day)	Suitable Applications
1	High	>6.0	Utility-scale PV plants, concentrated solar power (CSP) facilities, industrial solar farms, large-scale grid-connected projects
2	Medium	4.5–6.0	Community solar projects, medium-sized PV systems, hybrid systems (solar–diesel, solar–wind), agricultural applications (irrigation, water pumping)
3	Low	<4.5	Small off-grid solar systems for lighting, mobile charging, small appliances; hybrid systems with other renewable sources

. It is imperative to note that this classification was a preliminary assessment of the technical solar resource. Actual project feasibility and technology selection for any specific application are contingent upon a comprehensive evaluation of numerous other critical factors, including land availability and suitability, proximity to transmission infrastructure, environmental constraints, and socioeconomic considerations. The classification thresholds were determined by analyzing the statistical distribution of the modeled radiation data and referencing established benchmarks from similar regional solar resource studies.

This classification framework would enable stakeholders to prioritize development in the region with greater economic and technical feasibility, while still recognizing the potential for decentralized or hybrid solutions in lower-resource areas. By linking resource levels directly to suitable applications, the framework would ensure that solar energy development aligns with local energy needs and long-term sustainability goals.

3. Results and Discussion

3.1. Solar Energy Assessment Results

The three sites selected for model validation have sufficient geographical information (latitude, longitude, and elevation) and climate data to allow for model evaluation for differing seasons. In addition, the sixteen meteorological sites’ latitude, longitude, elevation, and climate indicated that Tigray is located in the tropical zone.

3.2. Conceptual Model Estimation

Based on the adapted conceptual model, the regression analysis results for the validation site dataset presented in Table 3 are summarized in

Table 7. Regression summary of Dera, Hagereselam, and Myderhu sites.

Regression Statistics	Value
Multiple R	0.992898
R Square	0.985847
Adjusted R Square	0.98452
Standard Error	0.015792
Observations	36
	Df	SS	MS	F		Significance F
Regression	3	0.555894	0.185298	743.0031		1.19 × 10−29
Residual	32	0.007981	0.000249
Total	35	0.563875
	Coefficients	Standard Error	t Stat	p-value	Lower 95%	Upper 95%	Lower 95.0%	Upper 95.0%
Intercept	−0.03002	0.638122	−0.04704	0.96277	−1.32983	1.269791	−1.32983	1.269791
N/No	0.586132	0.012572	46.62043	5.44 × 10−31	0.560523	0.611741	0.560523	0.611741
Latitude	1.256942	3.456504	0.363645	0.718514	−5.78373	8.297611	−5.78373	8.297611
Altitude	−0.03222	0.066882	−0.48181	0.633218	−0.16846	0.10401	−0.16846	0.10401

.

Equation (16) was developed to estimate global solar radiation based on the conceptual model given in Equation $\left(8\right).$

$${\displaystyle \frac{H}{H_o}}=-0.03002+0.586132{\displaystyle \frac{N}{N_0}}+1.256942\mathsf{\Phi }-0.03222\mathrm{h}$$

(16)

The correlation coefficients of Equation (16) indicated that solar radiation is more related to relative sunshine hours than the latitude and altitude of any site. The negative sign of coefficients indicates a converse relation between radiation and the ratio of sunshine hours and/or altitude, i.e., in line with the theory that classifies countries near the equator as having first-class solar resource potential. The common precision measurement in regression analysis is the determination coefficient $R^2$ and the standard error. These values were found to be 0.985847 and 0.015792, respectively, indicating acceptable accuracy of the model’s estimations.

3.3. Model Validation Using Statistical Error Tests

To ensure the robustness of the evaluation of the dataset and model performance, appropriate statistical indicators must be selected to capture the accuracy, bias, and correlation between measured and estimated values. Various statistical measures can be applied for this purpose; however, the choice of metrics should reflect both the nature of the data and the objectives of the analysis. Accordingly, RMSE, MBE, MPE, and $R^2$ are more appropriate to determine the statistical findings.

The regression analysis of all stations, such as relative error percentage (e%), determination coefficient ($R^2$), MPE%, mean absolute percentage error (MAPE%), MBE, and RMSE values, were calculated, and their values are given in

Table 8. Statical regression analysis results for all sites.

No.	Site	R2	R	MPE	MAPE	MBE	RMSE
1	Mekelle a. p	0.996	0.998	0.490	0.089	2.801	1.166
2	Shire	0.952	0.976	0.099	0.037	1.341	0.659
3	Aksum	0.941	0.970	0.889	0.170	5.583	2.309
4	Atsbi	0.963	0.982	0.277	0.045	1.591	0.929
5	Adwa	0.990	0.995	0.368	0.059	1.947	0.895
6	Mekelle obs	0.941	0.970	0.128	0.021	0.663	0.340
7	Adigrat	0.967	0.983	0.898	0.174	6.002	2.566
8	Mychew	0.965	0.982	0.744	0.140	4.681	1.973
9	Sheraro	0.948	0.973	0.123	0.032	1.126	0.543
10	Senkata	0.980	0.990	0.538	0.097	3.402	1.448
11	Samre	0.946	0.972	0.094	0.016	0.525	0.315
12	Nebelet	0.943	0.971	0.897	0.169	5.235	2.554
13	Humora	0.954	0.977	0.291	0.065	2.349	1.139
14	Tekeze	0.946	0.973	0.234	0.040	1.312	0.640
15	Chercher	0.953	0.976	0.040	0.012	0.403	0.179
16	Setit Humora	0.960	0.980	0.440	0.082	2.922	1.370
	Avg.	0.959	0.979	0.41	0.078	2.618	1.183

. The values of $R^2$ for all sites exceeded 0.9407, with the lowest values being found at Mekelle obs Station. The average values of $R^2$, MPE%, MAPE, MBE, and RMSE were calculated by applying Equation (9) to Equation (15) and were found to be 0.9589, 0.4095, 0.0779, 2.618, and 1.1828, respectively.

The model’s estimated monthly mean global solar radiation of all stations matched the measured values of the validation stations shown in Table 8, except for Adigrat station (MBE = 6.002), which was an outlier with a significantly higher MBE. This indicated that the model gave higher values of RMSE, MBE, MPE, and MAPE, which was expected for a model with a higher correlation (Avg.$R$= 0.979). The model’s Mean Percentage Error, MPE, was found to be in an acceptable range of 0.040% to 0.898%, with the lowest RMSE values being 0.179 to 2.554. Likewise, the MBE values of the stations were very close to zero, with the exception of Adigrat, Aksum, Mychew, and Nebelet. Table 8 shows that all stations achieved good results (above 0.941), indicating compatibility with the measured data given in Table 8.

3.4. Solar Radiation Estimate Based on Meteorological Data

The adapted conceptual model was used to estimate the global solar radiation at the sixteen meteorological stations by validating it with measured global solar radiation data from the validation sites. Figure 5 depicts the monthly average global solar radiation in the region as 6.1 kWh/m², with the lowest value being found at Mekelle Obs station (5.3 kWh/m²/day) and maximum value at Adigrat station (6.7 kWh/m²/day). When comparing these results to study [27], which was based on measurements of four sites, the average daily global horizontal radiation is close to the catchment’s result of 5.59 kWh/m²/day. Similarly, the estimated radiation of the Adigrat site was near to this study’s result for the Dera site, which is a nearby station. However, the measured values at the Mekelle site in this study were higher than the model’s estimate for the Mekelle Observatory site, indicating that the meteorological data was affected by shading effects. This indicated that the model provided better estimations based on meteorological data with lower values in sites where vegetation or buildings might affect sunshine measurements at lower heights.

3.5. Solar Radiation Estimate Based on Satellite Data

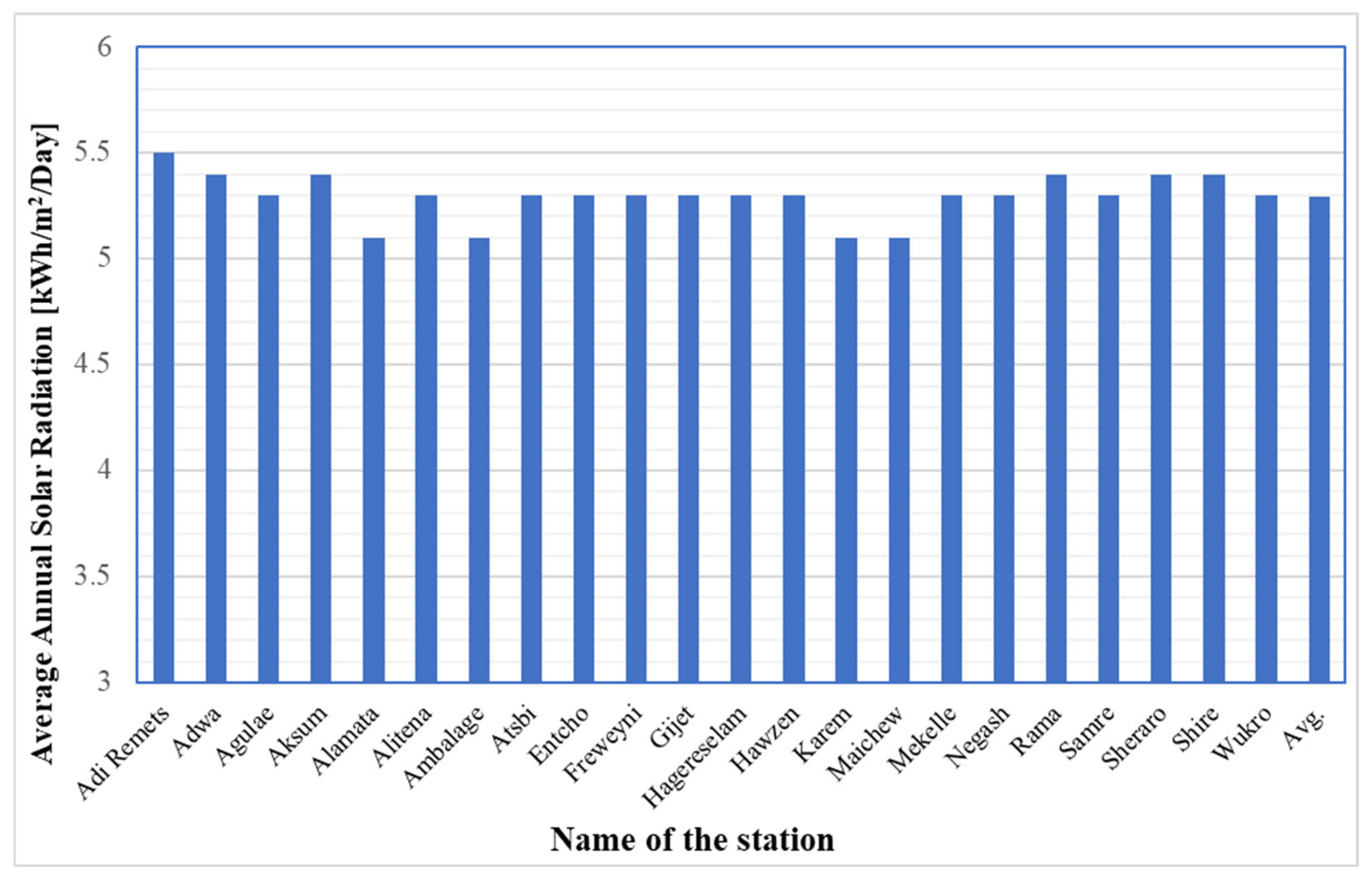
Figure 6 presents the average annual solar radiation over thirty-eight years (1981–2018). Based on these data estimations, a maximum average annual solar radiation of 5.5 kWh/m²/day was found for the Adi Remets site. This differs from previous findings reported by the Energy Sector Management Assistance Program (ESMAP) [5] and the meteorological estimation of Sheraro, a nearby site with 6.1kWh/m²/day. This indicated a possible shift in the resource belt in the region that might highlight the limitations of relying on satellite-based estimates for site selection or planning.

3.6. Meteorological vs. Satellite Solar Radiation Estimates

The solar radiation estimates based on the two datasets revealed notable differences in the average annual solar radiation value across several stations. Although the long-duration satellite-based estimate indicated lower average global solar radiation, it demonstrated similar trends to the meteorological estimates for Aksum, Mychew, Senkata, and Humora in the rankings of their relative solar potential. This pattern consistently suggested that both data sources gave reliable solar radiation estimates, despite their different estimation values. However, the substantial discrepancies observed at specific stations, such as Adigrat, Aksum, and Nebelet, were likely attributable to fundamental differences in data collection methodology: the ground-based meteorological data represents a point measurement that is susceptible to local microclimatic effects (e.g., topographic shading, vegetation, or instrumental drift at the 2m height), while the satellite-derived data provided an area average over a 0.5° × 0.5° grid cell, which may smooth over critical local topographic variations that are inherent to Tigray’s complex terrain. Consequently, for precise local feasibility studies, the meteorological estimate will give optimal energy estimates and better development planning in the region. According to this study, Tigray is categorized as a region with higher and medium resource potential according to the meteorological and satellite data, respectively.

3.7. Mapping of Solar Potential Using Meteorological and Satellite Data

In this study, the map developed by using meteorological data provided better visualization of the available solar potential in the region at all stations. This map depicted the maximum and minimum solar radiation given by ESMAP [5], with 6.7 kWh/m²/day and 5.3 kWh/m²/day values, respectively. The solar radiation was found to be stable in January, with the lowest standard deviation of 0.32, and unstable in July, with a higher standard deviation of 0.76, as shown in the average daily solar radiation contour maps of Figure 7. This pronounced seasonal variability was directly linked to regional climatic patterns. January falls within the dry season, characterized by minimal cloud cover and stable atmospheric conditions, whereas July occurs during the main rainy season, featuring frequent convective cloud formation, higher aerosol loads, and increased atmospheric moisture, all contributing to greater variability in the daily irradiation. For comparison purposes, the average daily solar radiation maps for the sixteen meteorological stations and twenty-two satellite stations are given in Figure 8 and Figure 9, respectively. In addition, the monthly average solar radiation map of the region was developed based on meteorological data, as shown in Figure 10.

3.8. Estimates of Exploitable Solar Resource Potential

Generally, Tigray exhibited a strong solar resource base, with annual average solar radiation ranging from 5.30 to 6.70 kWh/m²/day, which is suitable for power generation. The areas with the highest potential, with values exceeding 5.4 kWh/m²/day, are suitable for large-scale solar projects and located in the western zone of the region. However, this resource potential needs further consideration of parameters such as temperature to give advice on development priorities.

4. Conclusion and Future Work

This study assessed the solar resource potential of Tigray through comprehensive analyses of meteorological and satellite data. The study developed and adapted a conceptual solar insolation estimation model based on the classical Angström relation but enhanced it through the integration of geographical parameters, specifically latitude and altitude, to improve the spatial accuracy. The model’s accuracy gave a coefficient of determination of 0.99 and a standard error of 0.016, which were within acceptable ranges. Accordingly, the average annual solar radiation distribution of the study area was found to be 6.1 kWh/m²/day and 5.3 kWh/m²/day based on meteorological and satellite data, respectively. These results were close to Ethiopia’s mean average of 5.83 kWh/m²/day. In this study, it was observed that the prediction-based meteorological data gave relatively better prediction than the satellite data. In this view, the results of this study would help to prepare realistic solar energy development planning. The study can also act as a base for advanced modeling using machine learning or hybrid approaches to incorporate cloud cover, humidity, and aerosol optical depth to improve irradiance predictions and expand the temporal scope to include long-term seasonal and interannual variability to gain deeper insights into long-term solar energy planning.