A Classification Algorithm for Revenue Range Estimation in Ancillary Service Markets

Abstract

In the last decades, the introduction of intermittent renewable energy sources has transformed the operation of power systems. In this framework, ancillary service markets (ASMs) play an important role, due to their contribution in supporting system operators to balance demand and supply and managing real-time contingencies. Usually, ASMs require that energy is committed before actual participation, hence scheduling systems of plants and microgrids are required to compute the dispatching program and bidding strategy before needs of the market are revealed. Since possible ASM requirements are given as input to scheduling systems, the chance of accessing accurate estimates may be helpful to define reliable dispatching programs and effective bidding strategies. Within this context, this paper proposes a methodology to estimate the revenue range of energy exchange proposals in the ASM. To this end, the possible revenues are discretized into ranges and a classification pattern recognition algorithm is implemented. Modeling is performed using extreme gradient boosting. Input data to be fed to the algorithm are selected because of relationships with the production unit making the proposal, with the location and temporal indication, with the grid power dispatch and with the market regulations. Different tests are set up using historical data referred to the Italian ASM. Results show that the model can appropriately estimate rejection and the revenue range of awarded bids and offers, respectively, in more than 82% and 70% of cases.

1. Introduction

The rapid expansion of renewable energy sources (RES) of the last decades has transformed the operation and management of power systems [1]. Indeed, unlike conventional power plants, the intermittency caused by power generation from RES may lead to challenges in maintaining grid stability and safe working conditions [2,3,4,5]. Additionally, as fossil fuel-based power plants—which traditionally supplied services like, such as, providing balancing powers or procuring reserve capacity—are gradually dismissed, alternative ways are required to guarantee reliable power system operations while ensuring RES integration [6,7,8,9,10,11]. Within this context, the relevance of ancillary service markets (ASMs) is rapidly increasing since their importance in supporting system operators to maintain the demand-supply balance and to manage the real-time contingencies [12,13,14,15,16,17]. Specifically, units participating in the ASM may propose energy quantities to be traded and, when needed, the transmission system operator (TSO) establishes if the proposal is rejected or awarded (totally or partially) [18]. However, most electricity markets require that the amount of energy exchanged is committed ahead of actual participation, typically, one day before the real energy exchange. Nevertheless, at the time of decision making, information about network needs is uncertain and producers are subject to monetary penalties if they deviate from the committed schedules. Hence, producers should be able to schedule the dispatching program of the units composing the production plant and the bidding strategy before the real-time requirements are revealed, thus relying on forecasts of possible requests from the TSO [19,20,21]. For this reason, the chance of producing accurate estimates of the revenues from participation in the electricity market is an important research line in the field of the implementation of scheduling systems that integrate market participation into dispatching programs. Typically, scheduling problems are solved by energy management systems (EMSs) aimed at optimally dispatching programmable units, while minimizing (maximizing) given functions, such as operation costs (revenues) [22,23]. In recent years, some algorithms have been proposed to compute estimates of the possible revenues deriving from participation in electricity markets and to forecast the energy quantities to be traded. Two widely used approaches in this field are time series methods and pattern recognition (PR) algorithms [24].

Popular techniques for exploiting time series analysis are autoregressive integrated moving average (ARIMA) models [25,26,27], multivariate transfer function models, [28], dynamic models [26], and generalized autoregressive conditional heteroskedasticity models [29]. Although these models demonstrated strong predictive performance, in many cases the computational burden and the requirement to identify pre-defined ranges of the involved variables to obtain feasible solutions were recognized as significant limitations [24].

Concerning PR algorithms, some approaches have been developed in recent years. For instance, researchers of [30] proposed a neural network (NN) to estimate the trading quantity in day-ahead and the real-time markets, a priori defining two values of the possible quantities to be proposed in the market. Authors of [31] used an NN to forecast system marginal prices, considering differences in prices during weekdays, weekends and public holidays. The possible incomes were computed by considering the traded quantity and the related prices, this latter supposed to be an average price allocated to the whole scheduled period in proportion to the output in that period. In [32] an NN aimed at predicting market-clearing prices and the related revenues from participation to the market sessions was proposed. However, the methodology implemented did not address network contingencies and possible variations in the energy quantity to be proposed. Although the NNs in [30,31,32] exhibited good predictive performance, the process of tuning the network parameters turned out to be a limitation, since this process demands a large number of samples and involves a significant computational effort [24]. A transformer-based time-series forecasting model was proposed in [33]. Also in this case, the need to access a huge amount of training data and the computational burden were identified as possible limitations. In [34] different PR algorithms were compared for predicting market clearing prices. The results showed that ensemble learning techniques improved average prediction accuracy by approximately 25% compared to support vector machines and NNs. Moreover, the lower computational requirements of ensemble learning techniques compared to NNs were highlighted as an additional advantage of the method. In [35] a comparison of different PR algorithms to forecast energy prices and the related possible revenues in the day ahead market was performed. Outcomes revealed that the model based on gradient boosting technique reached higher performance than NNs. The model in [35] included the temporal indication amongst the features while, as far as RES production is concerned, only the power produced by wind plants was considered. Moreover, no inputs associated with the location of the supply point were included. From this perspective, it is worth noting that recent studies [36,37] have highlighted the importance of incorporating such information, as energy exchanges may take place in areas with high load demand variability or significant fluctuations of renewable generation. Therefore, including locational data can enhance the model’s ability to characterize the relationship between inputs and targets. Furthermore, the timeliness with which input data are retrieved was not addressed in [35], hence limiting the practical applicability of the model. Researchers of [38] utilized an efficient and widely used implementation of gradient boosted trees, i.e., a technique that adds a few more improvements beyond traditional ensemble tree methods, referred to as extreme gradient boosting (XGBoost) [39], for locational marginal price forecasting. XGB was used to incorporate the stochastic changes in electricity prices. Outcomes indicated that the XGB model achieves higher accuracy while requiring less computational time compared to commonly used NN-based models. Nevertheless, the algorithm in [39] did not consider the influence of actual network contingencies, which were found in [8] and [30] to have a significant impact on the market prices.

In this framework, the work proposed in this paper is part of a project developed thanks to the cooperation between the researchers of the University of Genoa and Nadara Italy S.p.A. The project is related to the creation of an EMS, presented in [40,41,42], able to account for many short- and long-term technical details of units composing power plants, and allowing to perform an estimate of the revenues obtained thanks to electricity markets. In [42] the implementation of the EMS enabling the participation in the day ahead market (DAM) and ASM was presented. To account for the strong dependence of the solution on the TSO acceptance/rejection in the ASM, a statistical approach was proposed. Precisely, the optimization process was split in two steps so that the first one optimally dispatches the energy units and proposed DAM and ASM offers. Then, a Monte Carlo method is launched. At each extraction, the TSO decisions in ASM are extracted from a uniform probability density function (PDF), and, subsequently, a second step of optimization is launched to optimally re-dispatch the units after the TSO decisions. The validation of the EMS on a real grid-connected MG revealed that the main limitations of the approach were linked with the assumption of uniform PDF used to characterize the TSO requests, which was assumed as a reliable guess of the TSO behavior. Hence, the work presented here is focused on the implementation of a methodology to compute reliable estimates of the revenues resulting from the TSO’s acceptance or rejection of bids and offers in the ASM. To this end, leveraging the computational efficiency of PR algorithms, this paper presents the implementation of a classification algorithm based on gradient boosting techniques to estimate revenues corresponding to energy exchange proposals in the ASM, discretized into a finite set of ranges. Input data to be fed to the algorithm are selected because of relationships with the grid power dispatch and with the electricity market regulation. Additionally, inputs are chosen considering the possibility to be retrieved in time intervals consistent with the trading temporal limitations of the ASM or to be forecasted with an appropriate degree of reliability. Precisely, the input data to be fed to the algorithm refer to the quantity of energy proposed for the exchange, the related price, technical information related to the production unit (such as the rated power and the ratio between the proposed quantity and the rated power), the total load request and the total production from RES in the market area, and a reference number identifying the location of the connection node between the production unit and the transmission system. Information associated with the temporal indication is also included amongst the inputs, since it can be linked with both the load demand and the RES production, and hence could help the algorithm in characterizing the relation between the inputs and the target. The algorithm employed is XGB, due to its demonstrated ability to handle stochastic variations in electricity markets [34,38], its superior resistance to overfitting compared to other ensemble learning techniques, and its faster training time with lower computational requirements relative to other PR algorithms, such as NNs and transformers [35].

The algorithm outputs an estimate of the revenue range corresponding to the energy exchange proposed. Estimates computed by the model are intended to be given as input to scheduling systems aimed at optimizing the power dispatching program of microgrids and production plants that join the ASM.

Operatively, the algorithm is trained and tested using historical data referred to the Italian electricity market.

The novelty of the proposed methodology is as follows:

(i)

The development of an algorithm to accurately estimate the revenue range of energy exchange proposals in the ASM, based on information associated with the temporal indication, to the location of the supply point and on actual network contingencies;

(ii)

The creation of a model that requires as inputs data available with a timeliness consistent with temporal limitations of the ASM.

The outline of the paper follows. Section 2 provides an insight in the regulation of the Italian ASM, Section 3 illustrates the methodology implemented, Section 4 details the case study, and Section 5 shows the related results. Finally, Section 6 concludes the contribution.

2. Italian Ancillary Service Market Regulation

The Italian electricity market (IEM) [43] is organized in three spot markets where the electrical energy is commercialized in the form of different products with distinct types of transactions and stakeholders. Specifically, the three IEM spot markets are the DAM, the intraday market (IM), and the ASM (in Italian “mercato per il servizio di dispacciamento”, MSD) [44]. Additionally, to optimize the dispatch, a zonal market model is adopted. Precisely, since January 2021 the market zones in which the IEM is split are as follows: North (NORD), Center-North (CNOR), Center-South (CSUD), South (SUD), Calabria (CALA), Sicily (SICI), and Sardinia (SARD). Since the analyses proposed here are focused on the ASM, a brief insight into the Italian ASM structure is presented.

Specifically, ASM is the venue used by the Italian TSO, namely, Terna S.p.A., for the trading of offers and bids in respect of ancillary services. The difference between ASM bids and offers is related to the fact that offers are proposals to reduce demand or increase generation, while bids are proposals to increase demand or reduce generation. Terna uses the ASM to acquire resources for relieving intrazonal congestion, procuring reserve capacity, and balancing injections and withdrawals in real time. In this context, the role of Terna is to anticipate every possible imbalance that may happen in the system, and this is realized by securing the right amount of power reserves. In the ASM, bids and offers are remunerated at the offered price (pay-as-bid mechanism). In detail, the acceptance of selling offers corresponds to an expense for the TSO, while the acceptance of purchase bids corresponds to a revenue for the TSO. Hence, in this latter case, production plants propose to the TSO the availability to produce less than initially scheduled, at a price generally lower than the selling price in the DAM and IM. If the TSO accepts, the plant must buy back the energy previously sold on the DAM/IM and no longer produced, thereby generating a profit linked to the difference between the selling price in the DAM/IM and the repurchase price in the ASM. The scheduling stage of the Italian ASM consists of a scheduling substage (ex-ante MSD) and a balancing market (MB). Each production unit participating in the ex-ante MSD can propose a minimum of one block to a maximum of three blocks. The price of each block must not be lower than the price of the preceding block. After the ex-ante MSD session closes, a bidding program (BP) is assigned to the production unit, and any possible imbalance due to the non-fulfillment of the BP will be evaluated a posteriori, based on the procured difference, according to a mechanism designed to be explicitly disadvantageous for the production unit. This makes the ex-ante MSD substage the last market in which the unit can adjust its production program, stressing its strategic importance. For this reason, the focus of the work proposed here is on the ex-ante MSD stage. In the following, to lighten the notation, ASM will refer to the ex-ante MSD substage.

3. Methodology

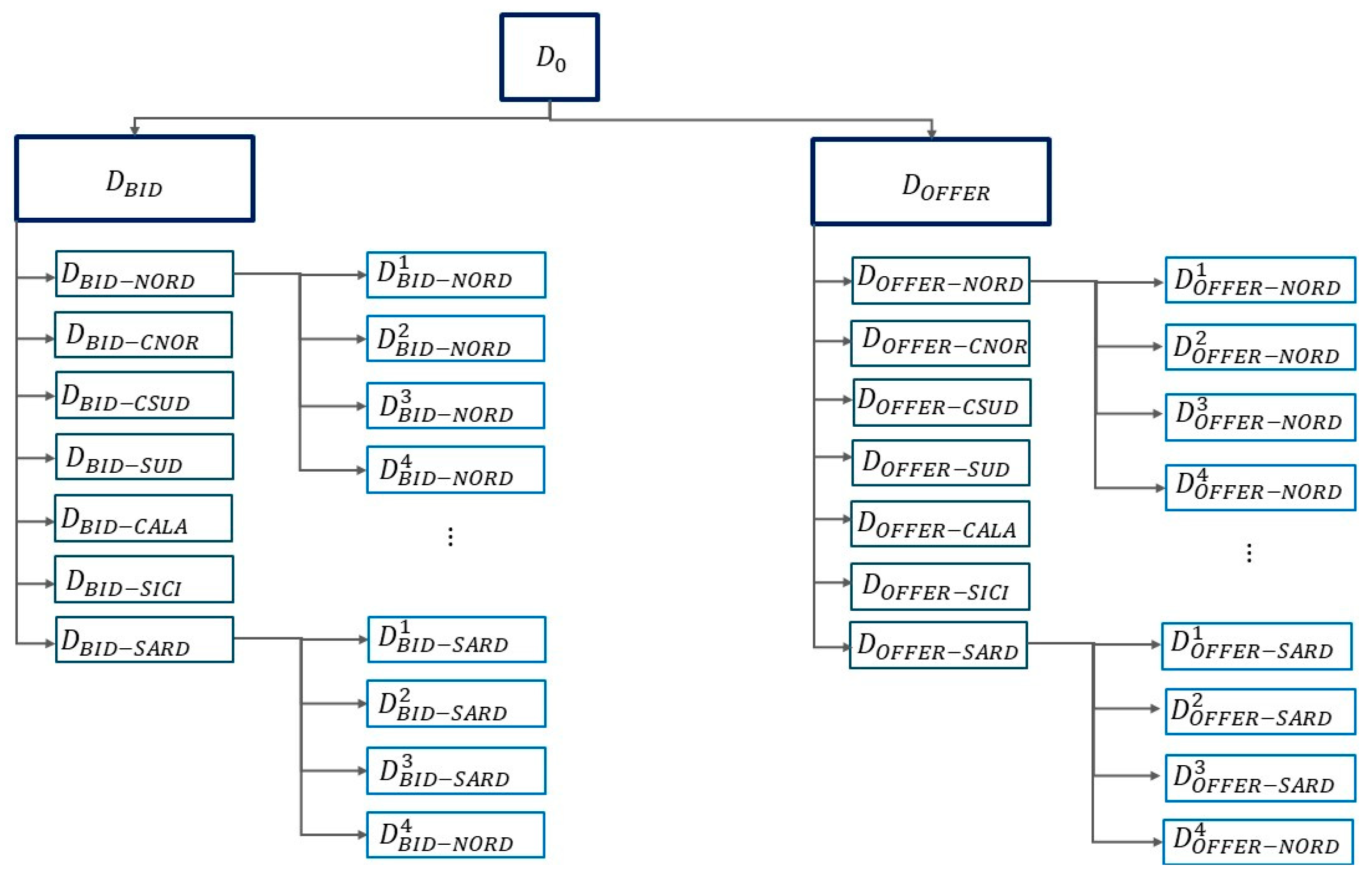
3.1. Algorithm

The created model is based on PR techniques. Precisely, considering the demonstrated abilities in various engineering fields [30,35,38,45,46,47,48], the flexibility and the faster training time required with respect to traditional NNs used for the specific application [35], the selected algorithm is the XGB. The XGB is used as a classification algorithm to estimate the revenue range associated with a given energy exchange proposal in the ASM. The possible revenues are discretized into a finite set of ranges. Accordingly, the problem is addressed as a multiclass classification task. To be consistent with the terminology of PR algorithms, from now on the ranges in which the possible revenues are split will be referred to as “classes”.

In what follows, the basic principles of XGB algorithms are recalled.

XGB is an efficient and widely used implementation of gradient boosted trees, i.e., a category of algorithms based on decision trees [35]. More precisely, decision trees are defined by recursively partitioning the input space and defining a local model in each resulting region of input space (referred to as “class”). The overall model can be represented by a tree, with one leaf per region. For classification problems, the leaves contain a distribution over the class labels, and the output space is a set of $N_C$ mutually exclusive labels, referred to as classes. To reduce the intrinsic variance of decision trees, a procedure referred to as ensemble learning allows building the prediction model by combining simpler base models [33]. Precisely, for a given dataset $D=\left\{\left({\mathit{x}}_1,y_1\right),\dots , \left({\mathit{x}}_{\mathcal{l}},y_{\mathcal{l}}\right)\right\}$ composed of $\mathcal{l}$ samples, let ${\mathit{x}}_i$ be the feature vector referred to the $i$-th sample, i.e., the set of inputs used to characterize the $i$-th target, and $y_i$ the real value assumed by the target. A decision tree ensemble model uses $M$ trees to predict the output of the $i$-th sample, referred to as ${\widehat{y}}_i$:

$$\stackrel{\wedge }{y_i}={\displaystyle \frac{1}{\left|M\right|}}\sum _{m=1}^M{f}_m\left(y|x_i\right), f_m\in \Theta$$

(1)

where $\Theta$ is the function space of the trees and $f_m\left({\mathit{x}}_i\right)$ represents the $m$-th tree, named as base model [39]. Among decision tree ensemble models, XGB is a peculiar type of boosting algorithm, i.e., algorithms enabling sequentially fitting additive models where each $m$-th tree is a binary classifier. XGB utilizes decision trees as base models and employs regularization techniques to enhance generalization abilities. Hence, the objective function of an XGB model includes the loss function and the regularization term, and is defined as:

$$obj=\mathrm{m}\mathrm{i}\mathrm{n}\left(\sum _{i=1}^{\mathcal{l}}l(y_i,\stackrel{\wedge }{y_i})+\sum _{m=1}^M\Omega \left(f_m\right)\right)$$

(2)

$$\Omega (f_m)=\alpha J+{\displaystyle \frac{1}{2}}\beta \sum _{j=1}^J{\omega }_j^2$$

(3)

where l denotes a generic differentiable loss function, which measures the difference between the actual target $y_i$ and the predicted value ${\widehat{y}}_i$, ${\Omega (f}_m)$ represents the regularization term used to control the model complexity and avoid overfitting, $j$ is the number of leaves in the tree, ${\omega }_j$ is the weight of the $j$-th leaf, and $\alpha$ and $\beta$ are the parameters to control the complexity of the tree. For the specific application, the selected loss function is the categorical cross entropy since its demonstrated good performances in many engineering fields [45]. Precisely, cross entropy is calculated on a SoftMax output, hence the output of the model is converted into a probability vector and, by selecting the objective function as in (2), the model is trained to optimize the parameters defining its structure in such a way that higher probabilities are assigned to the correct class [39]. Consequently, for each sample, the model outputs the class reaching the highest probability among all the possibilities. Specifically, being $p_{c,i,t}$ the estimated probability that the $i$-th sample belongs to the class $C_{i,t}$, the model outputs the class reaching the highest probability among all the classes, indicated with ${\widehat{C}}_{i,t}$. Besides, since several parameters related to the tree structure need to be optimized, grid search strategy is applied. These parameters are chosen on the basis of the results obtained in previous works in the field [38,48]. Precisely, the maximum depth of decision trees, the features by tree, the number of estimators, and the learning rate are optimized since outcomes of [38,48] revealed their influence in the estimation skills of the model. Details on the influence of the parameters on the architecture of the model can be found in [39]. In addition, to avoid overfitting, k-fold cross-validation (CV) is implemented [39].

3.2. Input Data

Generally, the performance of a PR algorithm heavily depends on the representativeness of the input data, also referred to as features [39]. However, for many tasks, it is difficult to a priori define which inputs should be selected to obtain a good representation of the phenomenon analyzed. Under this assumption, in this work input data to be fed to the algorithm are selected because of

• the availability,
• the ease with which they can be retrieved and the timeliness compared to the timings of the market sessions,
• the relationship with the power dispatch.

Furthermore, since the outcomes of the algorithm proposed here are intended to be used to define an effective bidding strategy before real-time requirements by the TSO are revealed, the non-deterministic features included are selected considering the possibility of being forecasted with an acceptable degree of reliability.

Specifically, since, as mentioned above, ASM is the market through which the TSO aims to ensure power system security and service quality, the need to accept offers in the ASM arises from variations in load demand or generation [30]. For instance, in the event of a generation unit disconnection from the grid (or a sudden increase in the load request), it becomes necessary to compensate for the resulting production shortfall—which would otherwise lead to a frequency drop below the nominal value—by activating a dedicated reserve capacity. This reserve consists of either increasing power injections or reducing withdrawals. In such cases, the TSO relies on the availability of offers in the ASM to counteract imbalances and maintain system stability. It should be noted that, in this case, the generation shortfall may result either from a technical issue affecting conventional generation units or from the variability of RES, whose production is intrinsically subject to fluctuations [8]. Accordingly, the total load demand and the RES generation in the market area are included among the inputs of the model. In addition, it is important to consider that both load demand and RES generation typically exhibit time-dependent patterns throughout the day. For instance, photovoltaic production is highly influenced by the season and time of day, while load demand generally varies between daytime and nighttime hours [36,37]. Therefore, the model should consider a variable associated with a temporal indication. To this end, in the developed algorithm, the temporal indication is split into information on the time slot within the day, the month, and whether the day is a weekday or a holiday. Furthermore, recalling the reasons why the TSO makes use of ASM services, it is clear that both the proposed quantity and the associated price are key variables to be considered for the potential acceptance of bids and offers. Consequently, both values are provided as input data to the model. Finally, it should be noted that previous research works in the field highlighted that the likelihood of deficiencies for a grid supply point (GSP)—i.e., the point at which energy is taken from the transmission system into the distribution system—is higher for GSPs connected with a substantial share of RES or subject to significant load variability. In contrast, GSPs not connected to RES generation or rarely experiencing load fluctuations present a lower likelihood of deficiencies [49]. Hence, input data fed to the algorithm also include a reference identifier indicating the location of the GSP.

For the training phase, target data, i.e., the awarded and rejected bids and offers in the ASM associated with the related energy quantities and prices, are obtained from historical data. Since the target of the model is the estimate of the revenue range of each proposed bid and offer, initially the income ($E_{i,t}$) of each proposal is calculated multiplying the awarded quantity $P_{awarded,i,t}$ by the related awarded price $P_{price,i,t}$

$$E_{i,t}=P_{awarded,i,t}{P}_{price,i,t}\left[€\right].$$

(4)

Subsequently, the values assumed by all $E_{i,t}$ are utilized to group the bids (offers) into ranges, referred to as “classes”. Two classes splits are created to test the effects on the model’s performance. In both cases, classes are divided to ensure an equal number of samples in each. To maintain consistency with the PR terminology, the vector collecting input data and the related ranges (classes) will be from now on referred to as feature vector. It should be emphasized that offers generate revenue for the production unit, whereas bids require the unit to repurchase from the TSO the energy previously sold but no longer requested for production. In the latter case, the potential profit for the plant arises from the difference between the selling price in the DAM/IM and the repurchase price in the ASM. Accordingly, the adopted sign convention for the awarded quantity ($P_{awarded,i,t}$) in (4) is to define it as always positive. The algorithm is therefore trained to estimate the revenue range associated with proposals of energy quantity-price combinations. The production unit can then evaluate the related profit, which for offers corresponds directly to the estimated revenue range, while for bids it is calculated a posteriori as the difference between the unit selling price in the DAM/IM multiplied by the awarded quantity and the estimated revenue range.

Moreover, it should be noted that many electricity markets are nowadays divided into market zones (corresponding to different geographical areas) that may differ significantly in terms of RES share (e.g., plains areas typically do not have hydroelectric plants) and load demand (that may vary with population and/or industrial plant density) [50]. Since these characteristics may influence the number of plants joining electricity markets, the proposed methodology includes the implementation of a dedicated model for each market zone. Accordingly, input data referring to different market zones are collected in different datasets that are subsequently used to train distinct algorithms.

4. Case Study

4.1. Algorithm

Recalling the implementation addressed in Section 3.1, as far as the choice of the parameters defining the models is concerned, the sets in which the optimal values are sought are defined considering outcomes of previous research in the field [27,28,29,30,31,32]. Precisely, the maximum depth values looped are $md\in S_{md}=\{6,8,10,12,14\}$, the analysed features by tree values are $cs\in S_{cs}=\left\{\mathrm{0.4,0.6,0.8,1}\right\}$, and the possible number of estimators are $ne\in S_{ne}=\{400,500,600,700,800,900\}$. Finally, the learning rate is sought in the set $lr\in S_{lr}=\left\{\mathrm{0.1,0.01}\right\}$.

Recalling that production units participating in the ASM can propose up to three proposals with different energy quantities and prices, this aspect is taken into account by considering these blocks as independent samples. This means that bids (offers) characterized by different quantities (prices) are treated as separate samples, i.e., having different values of $P_{proposed,i,t}\left(P_{price,i,t}\right)$.

To train and test the algorithms, the dataset is split into the following two subsets: 75% of data is used to train the algorithm and is referred to as training set, while the remaining data are used for the test phase and are referred to as test set. Additionally, in this work, the number of folds to implement the CV is selected because of its extensive use in previous works related to the topic [35], and is thus set to five.

In addition, the robustness of the proposed algorithm to variations on non-deterministic data, such as RES production, is assessed. Specifically, based on the widely applied procedure when dealing with stochastic processes to randomly sample the value used to perturb stochastic variables [51], inputs (features) that can experience stochastic variations have been perturbed of random values uniformly distributed over predefined intervals. Specifically, following the procedure implemented in [51], a ±5% interval is considered to perturb variables referred to the power produced by RES and to the load request.

Furthermore, to compare the reliability of the results obtained using the proposed method, an NN based on the methodology presented in [30] is implemented. Accordingly, the architecture of the NN consists of an input layer, two hidden layers, and an output layer. The output layer uses the softmax activation function to produce a probability distribution over the multiple output classes. The selection of hyperparameters is performed through a grid search strategy. Specifically, the learning rate is sought in the set $l{r}_N\in S_{l{r}_N}=\left\{\mathrm{0.1,0.01}\right\}$, the batch size is sought in the set ${bs}_N\in S_{{bs}_N}=\left\{\mathrm{5,10,20,50,100}\right\}$, and the network is trained for 100 epochs. Dropout regularization is applied after each hidden layer to improve generalization and reduce the risk of overfitting. The model is trained using the categorical cross-entropy loss function, appropriate for multiclass classification tasks [39]. Optimization is carried out using the Adam optimizer, which provides adaptive learning rates and robust performance across a variety of settings. It should be noted that, in this case, a shallow NN architecture is adopted. This choice is motivated by the fact that NNs typically require large amounts of data to effectively train and optimize all network parameters [39]. Consequently, the number of parameters to be learnt should not exceed the number of available training samples. Recalling that, for certain market zones, the number of awarded ASM bids and offers can be limited (possibly due to a lack of production units adequate to join the ASM), the samples referring to awarded proposals to be fed to the algorithm during the training phase may be extremely limited. Hence, a shallow NN architecture is implemented to ensure model stability for all market zones.

4.2. Input Data and Pre-Processing

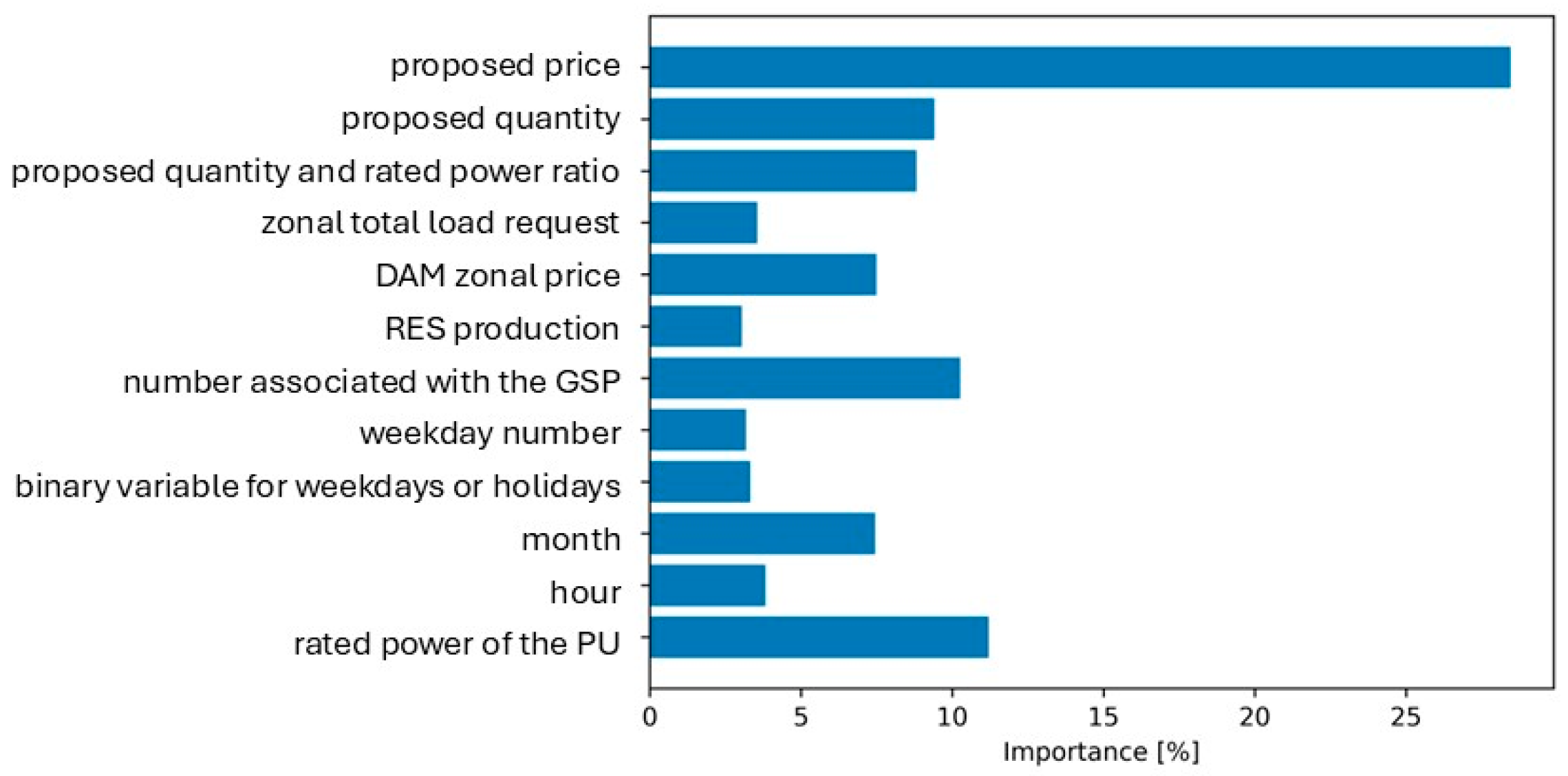
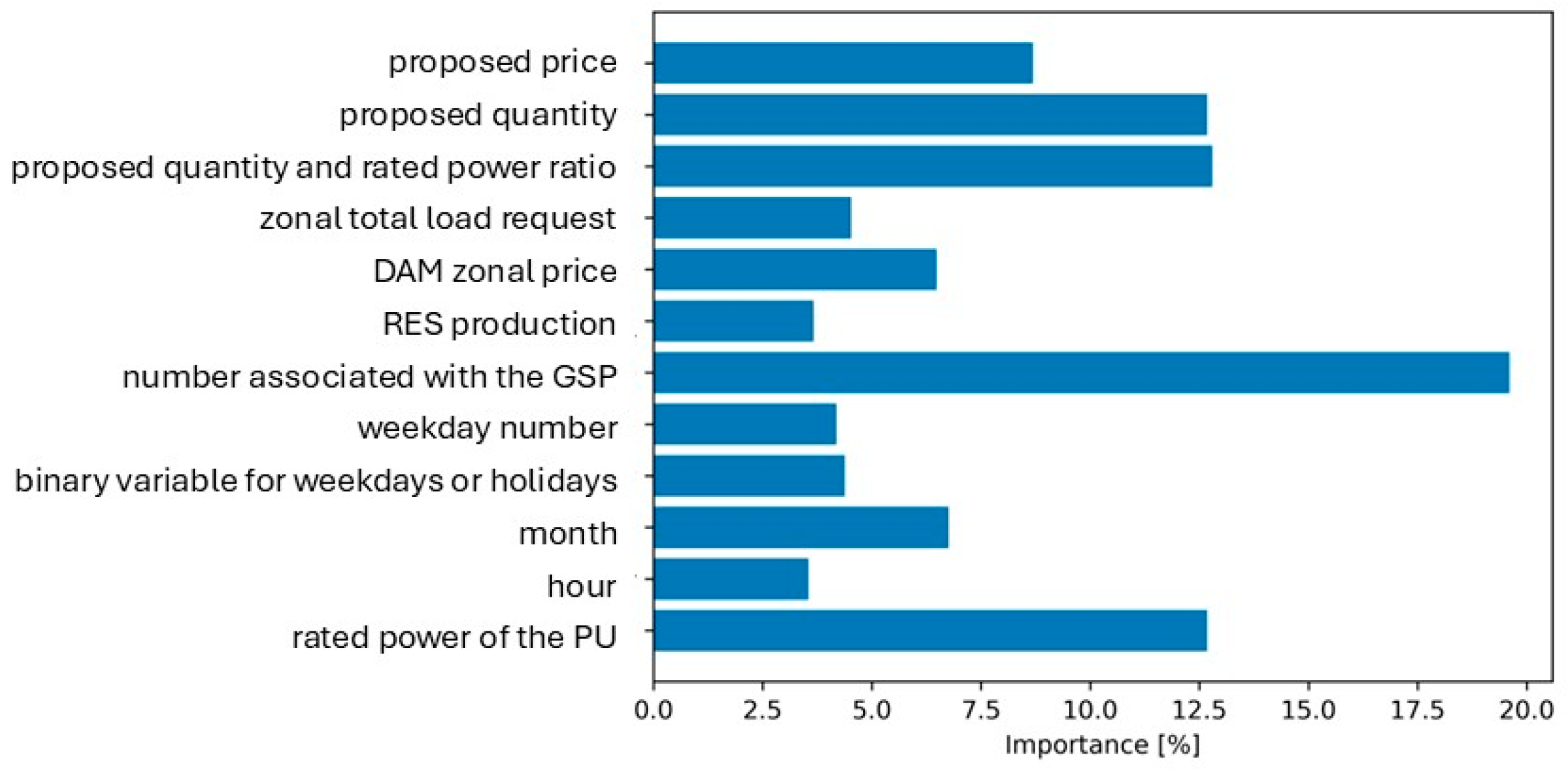
4.2.1. Input Data

Data to be fed to the algorithm for the training and test phase refer to historical data related to the Italian ASM. Precisely, data refer to the years 2022 and 2023 and are available on the GME website [52,53]. A flowchart of the procedure used to organize data is shown in Figure 1. More precisely, the dataset $D_0$ is initially created by collecting all data referring to ASM bids and offers during the period of interest for all market zones. These data refer to the temporal indication of the proposed bid/offer, reference information of the proponent production unit (PU), information on the load request and RES generation of each market area, as well as the proposed and awarded quantity and the related price. Each bid (offer) proposed by a PU represents a sample. Thereafter, since preliminary analyses of data in $D_0$ (supported by [37] and not reported for compactness) demonstrated that these values are extremely different for bids and offers, one dedicated dataset is created by extracting samples referring to bids from $D_0$ and one by extracting samples referring to offers, referred to as $D_{BID}$ and $D_{OFFER}$, respectively (Figure 1). Moreover, the preliminary analyses demonstrated that the number of PUs participating in the ASM is different for each market zone (MZ), and, consequently, the tradable energy quantities significantly vary among them. Hence, for each MZ, one dedicated dataset is extracted from $D_{BID}$ and $D_{OFFER}$ so that specific models can be trained for each of them. Under a PR perspective, the creation of separate models enables us to homogenize the feature vector fed to the algorithm, reducing misleading imbalances among the samples. Thus, $D_{BID-mz}$ is created for each market zone, being this latter identified with $mz\in \left\{NORD, CNOD, CSUD, SUD, CALA, SICI, SARD\right\}$, as detailed in Figure 1. The same splitting procedure is performed on $D_{OFFER}$, generating seven additional datasets $D_{OFFER-mz}$.

To define the set of input variables used for target estimation, preliminary analyses were conducted. In particular, a feature importance analysis was implemented to evaluate and quantify the relative contribution of each input variable to the model’s predictive performance [39]. The results are shown in Figure 2 and Figure 3, in which the average performance on all MZs is shown for bids and offers, respectively. Figure 2 and Figure 3 highlight distinct patterns when dealing with bids and offers. In detail, for bids, across the different MZs, the variable representing the proposed price exhibited the highest importance. Comparable importance was observed for the reference number associated with the GSP, the proposed quantity, the PU rated power, and the ratio between the proposed quantity and the rated power of the unit. Slightly lower importance was attributed to the DAM price, the load request and the zonal RES production. Among the temporal variables, the month was found to be more influential than the hour, the weekday number, and the binary variable distinguishing weekdays from holidays. Conversely, as far as offers are concerned, the reference number associated with the GSP reached the highest importance. Similar levels of importance were observed for the proposed quantity, the rated power of the proposing unit and the ratio between the proposed quantity and the PU rated power. Slightly lower importance was assigned to the proposed price, the DAM zonal price, the load request, and RES production. Again, within the temporal variables, the month was identified as more influential than the hour, weekday number, and the weekday/holiday binary variable.

To compare the effects on the performance of the model of the variables included in the feature vector, for each MZ and for each type of energy exchange, four different datasets are created. Precisely, $D_{BID-mz}^1$ and $D_{OFFER-mz}^1$ are generated to train and test the first model created. Similarly, the second, the third, and the fourth datasets are created and referred to as $D_{BID-mz}^2$, $D_{OFFER-mz}^2, D_{BID-mz}^3$, $D_{OFFER-mz}^3$, $D_{BID-mz}^4$, $D_{OFFER-mz}^4$, respectively (as shown in Figure 1).

Details on the variables included in each dataset follow and are summarized in

Table 1. Feature vector composition.

	${\mathit{D}}_{\mathit{B}\mathit{I}\mathit{D}-\mathit{m}\mathit{z}}^1$ ${\mathit{D}}_{\mathit{O}\mathit{F}\mathit{F}\mathit{E}\mathit{R}-\mathit{m}\mathit{z}}^1$	${\mathit{D}}_{\mathit{B}\mathit{I}\mathit{D}-\mathit{m}\mathit{z}}^2$ ${\mathit{D}}_{\mathit{O}\mathit{F}\mathit{F}\mathit{E}\mathit{R}-\mathit{m}\mathit{z}}^2$	${\mathit{D}}_{\mathit{B}\mathit{I}\mathit{D}-\mathit{m}\mathit{z}}^3$ ${\mathit{D}}_{\mathit{O}\mathit{F}\mathit{F}\mathit{E}\mathit{R}-\mathit{m}\mathit{z}}^3$	${\mathit{D}}_{\mathit{B}\mathit{I}\mathit{D}-\mathit{m}\mathit{z}}^4$ ${\mathit{D}}_{\mathit{O}\mathit{F}\mathit{F}\mathit{E}\mathit{R}-\mathit{m}\mathit{z}}^4$
${hour}_{i,t}$	•	•	•	•
${month}_{i,t}$	•	•	•	•
${wd}_{i,t}$	•	•	•	•
${hw}_{i,t}$	•	•	•	•
$P_{max,nom,i}$	•	•	•	•
$R_{,i,t}$	•	•	•	•
$P_{DAM,t}$	•	•	•	•
$L_t$	•	•	•	•
$S_i$	•	•	•	•
$P_{RES,t}$	•	•
$P_{RES-thermal,t}$			•	•
$P_{RES-PV,t}$			•	•
$P_{RES-hydro,t}$			•	•
$P_{RES-wind,t}$			•	•
${ty}_{,i}$		•	•	•
$P_{proposed,i,t}$	•	•	•	•
$P_{price,i,t}$	•	•	•	•
$N_c$	3	3	3	6

. For each sample $i$ referring to a temporal indication $t$, in $D_{BID-mz}^1$ and $D_{OFFER-mz}^1$ the feature vector includes the following variables:

i.

the hour referred to the temporal indication, identified with the variable ${hour}_{i,t}$. Actually, since national reports [36,37] show peculiar trends for specific hours’ slots, it is reasonable to group the hours of the day within these slots. Precisely, in [36,37] it can be noticed that in the slot 07 a.m.–23 p.m. the average load request is higher than the demand related to other hours of the day. Consequently, following the procedure proposed in [35], in this work, two time slots are considered: the first one is referred to 07 a.m.–23 p.m. (${hour}_{i,t}$ = 1), and the second is referred to the remaining hours of the day (${hour}_{i,t}$ = 2);

ii.

the month referred to the temporal indication, indicated with the variable ${month}_{i,t}$

iii.

the weekday number referred to the temporal indication, namely ${wd}_{i,t}$; e.g., Monday is represented by the value ${wd}_{i,t}$ = 0 and Sunday by the value ${wd}_{i,t}$ = 6;

iv.

a binary variable distinguishing between weekdays or holidays, identified by ${hw}_{i,t}$ = 0 for weekdays and ${hw}_{i,t}$ = 1 for holidays, respectively. This distinctions is performed to separate days in which the load request may be extremely different, as suggested by [31];

v.

the rated power of the PU proposing the bid (offer), namely $P_{max,nom,i}$;

vi.

the ratio between the proposed quantity and the rated power of the PU, referred using the variable $R_{i,t}$;

vii.

the DAM zonal price, referred to as $P_{DAM,t}$;

viii.

the zonal total load request, referred to as $L_t$;

ix.

the reference number associated with the GSP, namely $S_i$;

x.

the total production in the MZ from RES, referred to as $P_{RES,t}$, accounting for photovoltaic (PV), wind, geothermal and biomass, and hydroelectric power production;

xi.

the variable representing the proposed quantity, i.e., $P_{proposed,i,t}$ [MW];

xii.

the variable representing the proposed price, i.e., $P_{price,i,t}$ [€/MWh].

Datasets $D_{BID-mz}^2$ and $D_{OFFER-mz}^2$ are composed of all the variables included in $D_{BID-mz}^1$ and $D_{OFFER-mz}^1$, but in $D_{BID-mz}^2$ and $D_{OFFER-mz}^2$ the type of plant is added amongst the features. The related variable is ${ty}_i$. Precisely, based on the analyses in [8], traditional thermal based (${ty}_i$ = 0) or hydroelectric-based (${ty}_i$ = 1) production plants are distinguished. Differently, datasets $D_{BID-mz}^3$, $D_{OFFER-mz}^3$, $D_{BID-mz}^4$ and $D_{OFFER-mz}^4$ are composed of the variables included in $D_{BID-mz}^2$ and $D_{OFFER-mz}^2$, but in $D_{BID-mz}^3$, $D_{OFFER-mz}^3$, $D_{BID-mz}^4$ and $D_{OFFER-mz}^4$ the RES production is split by technology, following the procedure detailed in [8]. Thus, these datasets are composed of all the variables detailed in 4.2.i-xii but 4.2.x. The variable in 4.2.x is substituted with four variables, namely the production from PV plants, i.e., $P_{RES-PV,t}$; the production from wind-based plants, i.e., $P_{RES-wind,t}$; and the production from geothermal and biomass plants, i.e., $P_{RES-thermal,t}$; the production from hydroelectric plants, i.e., $P_{RES-hydro,t}$.

Furthermore, to define the discretization ranges (classes) of revenues, the value corresponding to the revenue related to each bid (offer) is initially computed as in (4). Then, two different values of discretization ranges are compared to assess how the model performance changes because of the number of classes in which the target is split. The number of classes in which the target is split is selected because of outcomes of preliminary analyses (as detailed in [36,37] and not reported for brevity) on historical data. Precisely, being $N_C$ the number of classes considered, $N_C$ = 3 and $N_C$ = 6 are considered. Hence, $D_{BID-mz}^1, D_{OFFER-mz}^1, D_{BID-mz}^2$, $D_{OFFER-mz}^2$, $D_{BID-mz}^3, D_{OFFER-mz}^3$ are merged with the vector dividing the target into three classes ($N_C$ = 3). Conversely, $D_{BID-mz}^4$ and $D_{OFFER-mz}^4$ are merged with the vector dividing the target in six classes ($N_C$ = 6). A summary of the features included in each dataset and the class split is shown in Table 1. An example of the resulting discretization ranges for MZ $NORD$ is detailed in

Table 2. Income ranges for $D_{BID-NORD}^1$, $D_{OFFER-NORD}^1$, $D_{BID-NORD}^2$, $D_{OFFER-NORD}^2, D_{BID-NORD}^3$, $D_{OFFER-NORD}^3 (N_C=3)$ and $D_{BID-NORD}^4$, $D_{OFF-NORD}^4 (N_C=6)$. The last row indicates the number of samples in each range.

	BID		OFFER
	$${\mathit{N}}_{\mathit{C}}=3$$	$${\mathit{N}}_{\mathit{C}}=6$$	$${\mathit{N}}_{\mathit{C}}=3$$	$${\mathit{N}}_{\mathit{C}}=6$$
$$C_{i,t}=2$$	(0–6032]€	(0–3145]€	(0–11,310]€	(0–4700]€
$$C_{i,t}=3$$	(6032–103,985]€	(3145–5016]€	(11,310–228,380]€	(4700–9399]€
$$C_{i,t}=4$$		(5016–7281]€		(9399–13,455]€
$$C_{i,t}=5$$		(7281–10,944]€		(13,455–20,615]€
$$C_{i,t}=6$$		(10,944–103,985]€		(20,615–228,380]€
samples	~38,200	~15,300	~13,800	~5500

.

For each dataset, a dedicated algorithm is trained, and the resulting performance on the test set is compared with the outcomes of the other ones. Recalling that separated datasets are created for all the seven IEM MZs and for the two the types of energy exchange, 56 datasets are created to train and test 56 different algorithms.

4.2.2. Balancing Procedure

Preliminary analyses of the available datasets (supported by national reports [36,37] but not reported for compactness) showed that more than 90% of the proposed bids and offers are typically rejected by the TSO. Besides, amongst the awarded ones, the distributions of the data are gathered at the lower values. This fact would cause an extreme imbalance in the datasets and could drive to a misleading modeling [39], especially for the classification of the accepted bids (offers). Under this perspective, several research works [54,55] showed that imbalanced class distributions often lead to the majority class being well-learned while the minority class may be inadequately represented, negatively affecting classification performance.

Consequently, a pre-processing methodology to balance the samples in each dataset is performed as follows:

• The number of awarded bids (offers) in the dataset is counted, i.e., samples for which $P_{awarded,i,t}>0$;
• Being $n_{aw}$ the total number of awarded bids (offers), an equal number $n_{rej}$ = $n_{aw}$ of bids (offers) is randomly selected among the rejected ones, i.e., bids (offers) for which $P_{awarded,i,t}=0$;
• The value $C_{i,t}$=1 is always assigned to samples for which $P_{awarded,i,t}=0$;
• Among the samples for which $P_{awarded,i,t}>0$, the same number of samples for each class is sought, i.e., for the target split $N_C$ = 3 the split is performed so that the samples for which $C_{i,t}$ = 2 is the same as the samples for which $C_{i,t}$ = 3. Similarly, for the target split $N_C$ = 6 the split is performed so that the number of samples in each of the classes is the same.

It is stressed that exploratory investigations (not reported for brevity) revealed that the use of widely applied data balancing methods, i.e., synthetic minority oversampling technique (SMOTE) and adaptive synthetic sampling (ADASYN), do not significantly increase the performance of the algorithm. Hence, to avoid generating synthetic data that do not correspond to real occurrences and to adhere strictly to the original dataset, the aforementioned methodology is preferred for implementation.

4.3. Evaluation Metrics

For all the created models, the performances are compared analyzing the related confusion matrix (CM), i.e., the matrix where the element $e_{wz}$ is the number of times an item with true class label $w$ is (mis)classified as having label $z$ [33]. Precisely, among the elements of the CM, the following quantities are extracted:

• $V_Y$ representing the percentage of the samples in the test set for which the model correctly estimates the related class of the awarded bid (offer), i.e., ${\widehat{C}}_{i,t}=C_{i,t}>1$;

• $V_A$ representing the percentage of the samples in the test set for which the model correctly forecasts that the bid (offer) is awarded but the related class is wrongly labelled, i.e., ${\widehat{C}}_{i,t}\ne C_{i,t}\bigwedge C_{i,t}>1\bigwedge {\widehat{C}}_{i,t}>1$;

• $V_R$ representing the percentage of the samples in the test set for which the model correctly forecasts that the bid (offer) is rejected, i.e., ${\widehat{C}}_{i,t}=C_{i,t}=1$.

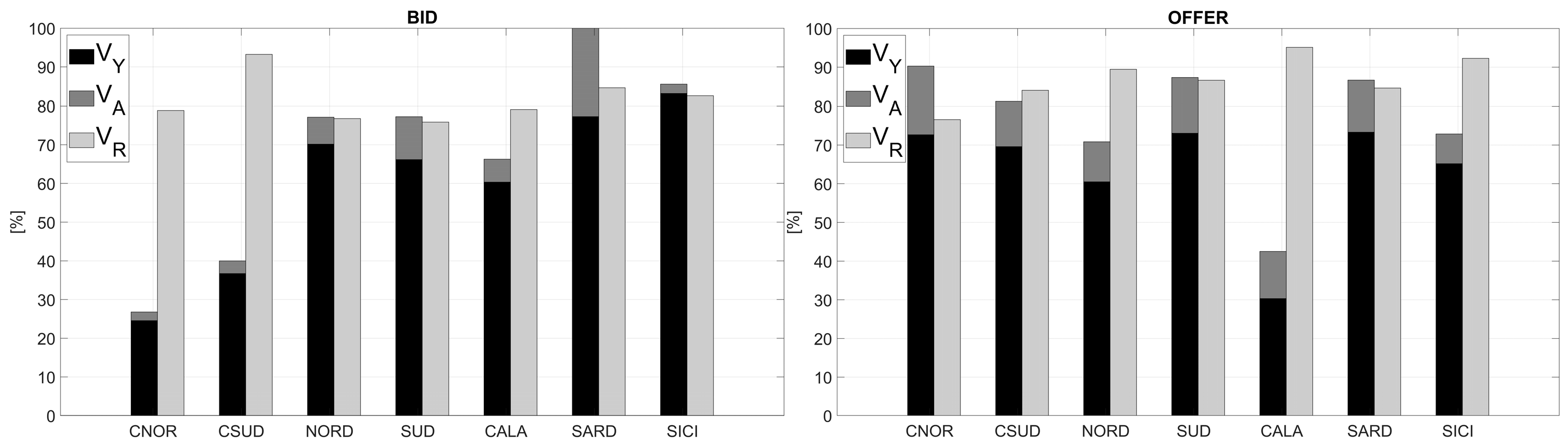
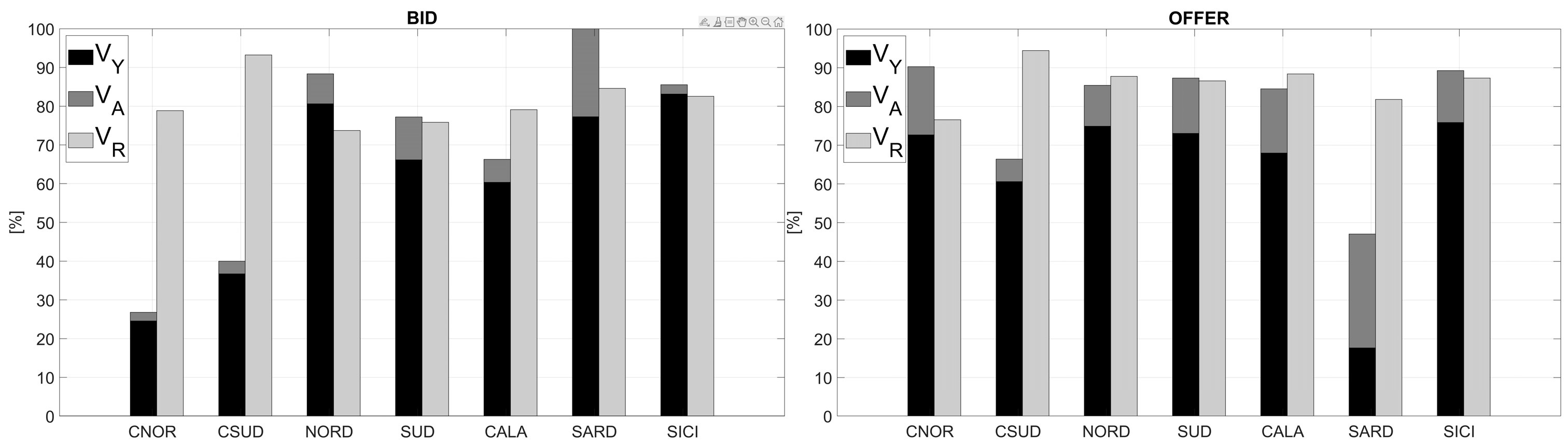
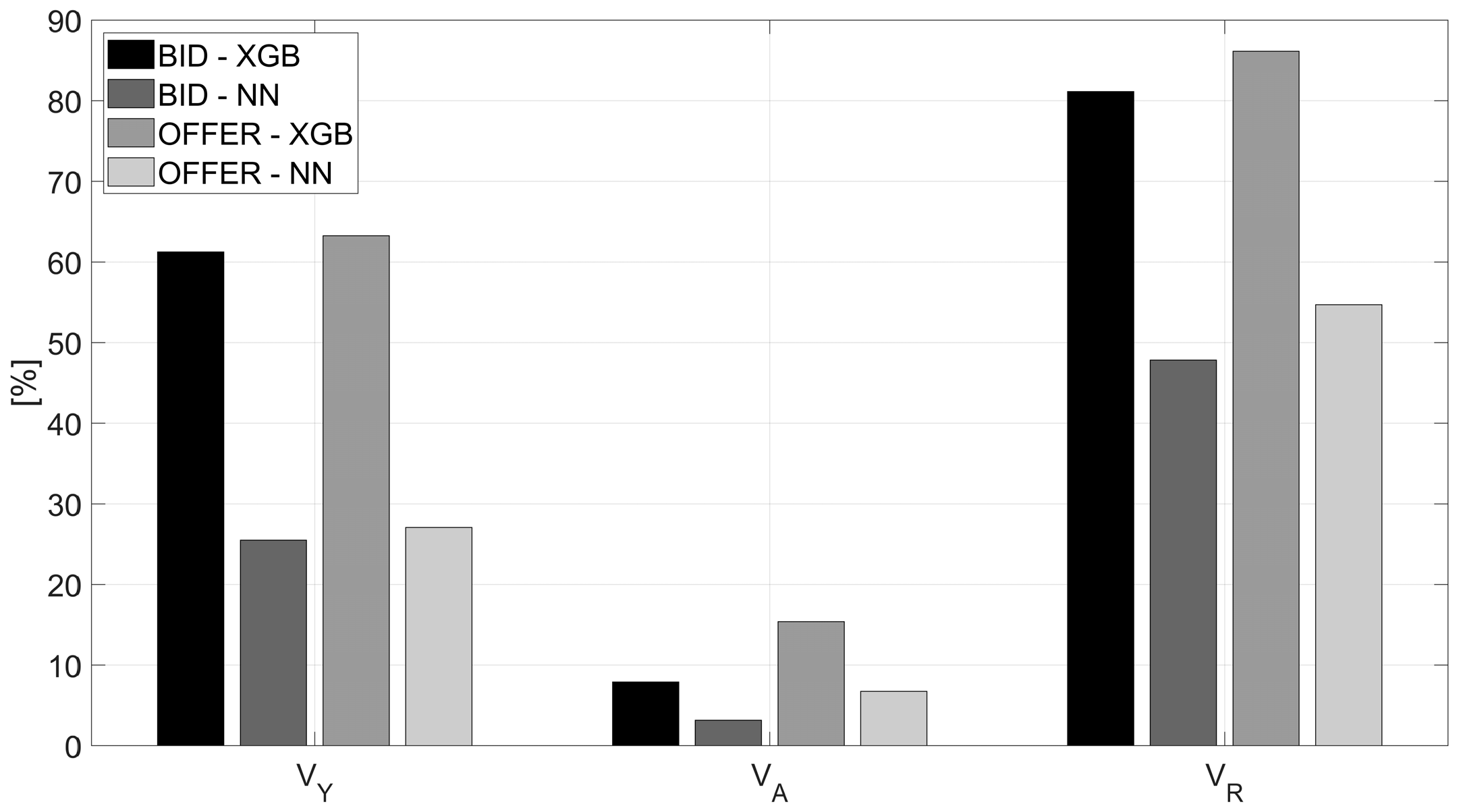
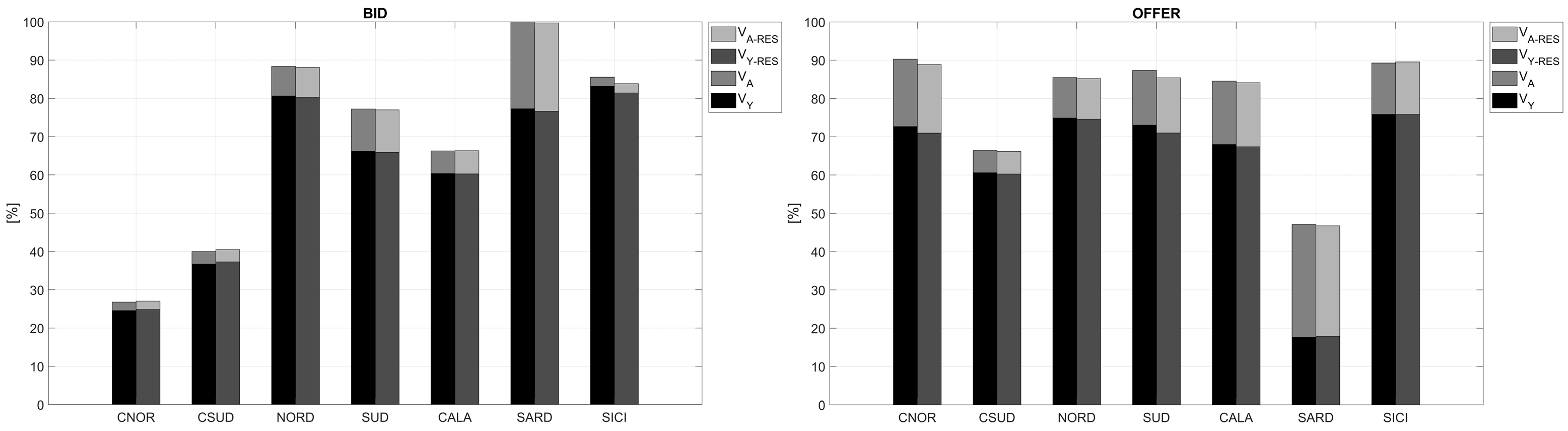
5. Results

This section shows the outcomes on the case study, discussing the performance on the test sets created for each MZ and for each type of energy exchange.

Figure 4 summarizes the results obtained using the best performing parameters configuaration for $D_{BID-mz}^1$ and $D_{OFFER-mz}^1$. Figure 4 shows the percentage of bids and offers correctly labelled as awarded, i.e., ${(V}_Y+V_A)$, (black and dark gray bars) and rejected, i.e., ${(V}_R)$, (light gray bars). Similarly, Figure 5 summarizes the results for $D_{BID-mz}^2$ and $D_{OFFER-mz}^2$. Generally lower performance is observed for bids than for offers. Precisely, for $D_{BID-mz}^1$ the average value of ${(V}_Y+V_A)$ is approximately 68% and $V_R$ reaches 82%. When $D_{BID-mz}^2$ is utilized, the average value of ${(V}_Y+V_A)$ is 70% and $V_R$ is 82%. Concerning offers, for $D_{OFFER-mz}^1$ the average value of ${(V}_Y+V_A)$ is approximately 75% and $V_R$ reaches 87%. When $D_{OFFER-mz}^2$ is used ${(V}_Y+V_A)$ is 78% and $V_R$ 87%. The obtained results suggest that, on average, datasets $D_{BID-mz}^2$ and $D_{OFFER-mz}^2$ allows to reach higher performance than datasets $D_{BID-mz}^1$ and $D_{OFFER-mz}^1$.

From a broad perspective, the fact that different performance is obtained for the MZs indicates that the choice of training disticnt models for each of them is appropriate.

More precisely, as far as offers are concerned, the algorithms trained and tested with $D_{OFFER-mz}^2$ performs better than the ones trained and tested with ${\mathrm{D}}_{\mathrm{O}\mathrm{F}\mathrm{F}\mathrm{E}\mathrm{R}-\mathrm{m}\mathrm{z}}^1$ for MZ $NORD$, $CALA$ and $SICI$; indeed, the percentage of offers correctly labelled as accepted is above 80% (details in Figure 4 and Figure 5). Differently, for MZ $SARD$, the reduction of the performances on the test set of $D_{OFFER-mz}^2$ with respect to the test set of $D_{OFFER-mz}^1$ is linked with the fact that only a small portion of the available samples is referred to hydroelectric plants, consequently the introduction of the variable referred to the PU technology amongst the feature vector causes an insufficient ability of the model in characterizing the features behavior. Besides, for MZ $CSUD$, the reason for the reduction in the performance on the test set extracted from $D_{OFFER-mz}^2$ with respect to the test set extracted from $D_{OFFER-mz}^1$ may lie in the fact that, since PUs joining the ASM are a few, an extremely small variability is available among the features, and this may drive to difficulties in finding the relationships that link them. Under this perspective, the inclusion of the type of PU among the features in the datasets $D_{OFFER-mz}^2$ may result to not be useful for all MZs. In this sense, future enhancements of the tool proposed will deal with the research of additional features to be included in the models related to MZs in which a small number of PUs participate to the ASM.

When considering bids, similar performance is obtained when the algorithm is trained with $D_{BID-mz}^1$ and $D_{BID-mz}^2$ for all MZs but for $NORD$ (details in Figure 4 and Figure 5). This finding suggests that, in this latter market area, the type of plant is a relevant feature for the model to estimate the revenue range. This result could be linked to the high variability of PUs in the zone. Differently, for others MZs, this feature seems not to influence the model’s performance.

Furthermore, the outcomes of the algorithms trained and tested using $D_{BID-mz}^3$, $D_{OFFER-mz}^3{, D}_{BID-mz}^4$, and $D_{OFFER-mz}^4$ are analyzed and compared with the previous results. On average, lower performances are reached for all MZs for both bids and offers with respect to the results obtained extracting the test set from $D_{BID-mz}^1$, $D_{OFFER-mz}^1$, $D_{BID-mz}^2$, and $D_{OFFER-mz}^2$. For compactness, only results referred to the MZ $NORD$ are reported in

Table 3. Performance on the test sets extracted from $D_{BID-NORD}^3$, $D_{OFFER-NORD}^3$, $D_{BID-NORD}^4$, and $D_{OFFER-NORD}^4$. Percentage values of $V_Y,V_A,$ and $V_R$.

	$${\mathit{D}}_{\mathit{B}\mathit{I}\mathit{D}-\mathit{N}\mathit{O}\mathit{R}\mathit{D}}^3$$	$${\mathit{D}}_{\mathit{B}\mathit{I}\mathit{D}-\mathit{N}\mathit{O}\mathit{R}\mathit{D}}^4$$	$${\mathit{D}}_{\mathit{O}\mathit{F}\mathit{F}\mathit{E}\mathit{R}-\mathit{N}\mathit{O}\mathit{R}\mathit{D}}^3$$	$${\mathit{D}}_{\mathit{O}\mathit{F}\mathit{F}\mathit{E}\mathit{R}-\mathit{N}\mathit{O}\mathit{R}\mathit{D}}^4$$
$$V_Y$$	52.30	47.91	76.12	74.97
$$V_A$$	0.06	12.00	5.14	10.57
$$V_R$$	89.15	82.67	88.12	87.79

, since the results referring to the other MZs reach lower values. This outcome can be attributed to the split of the RES production within the feature vector that could lead to an increase in the complexity of the model. Specifically, the different seasonal and daily trends characterizing PV, wind, and hydroelectric plants hinder the model’s ability to uncover the relation between the features and the target. The average performance of the models trained with $D_{BID-mz}^3$, $D_{OFFER-mz}^3{, D}_{BID-mz}^4$, and $D_{OFFER-mz}^4$ is summarized in

Table 4. Performance on the test sets extracted from $D_{BID-mz}^3$, $D_{OFFER-mz}^3$, $D_{BID-mz}^4$, and $D_{OFFER-mz}^4$. Average value of $V_Y,V_A,$ and $V_R$.

	$${\mathit{D}}_{\mathit{B}\mathit{I}\mathit{D}-\mathit{N}\mathit{O}\mathit{R}\mathit{D}}^3$$	$${\mathit{D}}_{\mathit{B}\mathit{I}\mathit{D}-\mathit{N}\mathit{O}\mathit{R}\mathit{D}}^4$$	$${\mathit{D}}_{\mathit{O}\mathit{F}\mathit{F}\mathit{E}\mathit{R}-\mathit{N}\mathit{O}\mathit{R}\mathit{D}}^3$$	$${\mathit{D}}_{\mathit{O}\mathit{F}\mathit{F}\mathit{E}\mathit{R}-\mathit{N}\mathit{O}\mathit{R}\mathit{D}}^4$$
$$V_Y$$	42.46	35.72	68.20	61.53
$$V_A$$	0.03	8.87	4.50	7.73
$$V_R$$	75.83	64.91	78.34	74.65

. As it can be seen, lower performance is again obtained for bids than for offers. Additionally, for both bids and offers, better results are achieved for $N_C=3$ compared to those obtained with $N_C=6$. This could be linked with the fact that the splitting of the target in six classes reduces the number of samples available for class. Consequently, the limited sample size in the algorithms trained with $D_{BID-mz}^4$ and $D_{OFFER-mz}^4$ can lead to suboptimal parameter settings, resulting in poor performance in capturing the relationship between the features and the target. Therefore, from the obtained outcomes it can be assumed that the split of the possible income range into six classes is not suitable for the intended objective.

Moreover, the findings concerning the comparison of the performance of the proposed models and with that of the method presented in [30] are reported in Figure 6. In Figure 6 results refers to the percentage values ${\mathrm{V}}_{\mathrm{Y}},{\mathrm{V}}_{\mathrm{A}},$ and ${\mathrm{V}}_{\mathrm{R}}$ when $D_{BID-mz}^2$ and $D_{OFFER-mz}^2$ are utilized. The choice of the datasets is due to the superior performance reached with respect to the results obtained with the other datasets. In Figure 6 it can be observed that, for both bids and offers, the NN generally exhibits lower performance compared to the XGB algorithm. This outcome may be attributed to the extremely limited number of training samples available for certain MZs, which can hinder the effective optimization of the NN’s parameters. This limitation could lead to lower performance, as illustrated in Figure 6. Consequently, it can be concluded that the XGB methodology is well-suited for this application, since its formulation enables the model to adapt to various MZs characterized by highly diverse parameters, such as markedly different revenues and proposed/awarded energy quantities.

In addition, the analysis of the effect of uncertainties is peroformed on $D_{BID-mz}^2$ and $D_{OFFER-mz}^2$, since the superior performance is demonstrated by these datasets in the abovementioned analyses. Specifically, outcomes obtained applying the random variations to the test set extracted from $D_{BID-mz}^2$ and $D_{OFFER-mz}^2$ are shown in Figure 7. The resulting sets are referred to as $D_{BID-mz}^5$ and $D_{OFFER-mz}^5$. In Figure 7, the metrics referring to the samples of $D_{BID-mz}^5$ and $D_{OFFER-mz}^5$ are indicated with $V_{Y-RES}$ and $V_{A-RES}$, respectively referring to the percentage of samples correctly labelled and to the percentage of samples correctly identified as awarded but wrongly labelled. As can be seen, the application of random fluctuations causes small variations in the performance of the algorithm for both bids and offers. Precisely, as far as bids are concerned, for MZ $CNOR, CSUD$, and $CALA$, $V_Y$ and $V_{Y-RES}$ assume similar values. When considering the MZ $NORD, SUD, SARD$, and $SICI$ $V_{Y-RES}$ and $V_{A-RES}$ slightly decrease with respect to $V_Y$ and $V_A$. The decrease is always lower than 3%. For offers, variations applied to the test set samples lead to comparable outcomes for the $NORD, CALA, SARD$, and $SICI$ MZ. A small decrease in $V_{Y-RES}$ and $V_{A-RES}$ is visible for the remaining market zones with respect to the values assumed by the metric when the test set is extracted from $D_{OFFER-mz}^2$. In this latter case, the decrease is lower than 4%. Consequently, the findings indicate that the algorithm can reliably predict the revenue range of samples despite fluctuations in RES generation and load request, emphasizing its robustness to uncertainty.

6. Conclusions and Practical Implications of the Proposed Methodology

6.1. Conclusions

In this paper, an algorithm to estimate the revenue range associated with energy exchange proposals in the ancillary service market was developed. Precisely, a pattern recognition model able to compute the revenue range of bids and offers based on the relationships with variables involved in the power dispatch and with the proposed energy quantity and price was created. The extreme gradient boosting algorithm was utilized to perform the modeling. The features of the model were selected because of the relationships with the grid power dispatch and with the electricity markets regulation. Differentiated tests were set up using historical data referred to the Italian electricity market. The results were analyzed to identify the optimal combination of features and revenue discretization ranges that yield the highest performance. The analysis of the outcomes suggested that the algorithm enabled us to appropriately estimate the revenue ranges of both bids and offers when three classes are considered. Precisely, the created models, in most of the market zones, correctly estimated awarded bids and offers in more than 70% and 78% of cases, respectively. Moreover, on average, rejection was correctly predicted in 82% and 87% of samples, referring to bids and offers, respectively. However, in market zones in which most of the proposals were performed by a small subset of plants, the model turned out to reach lower performances with respect to average values. The observed behavior may stem from the limited number of samples used for training, which can hinder optimal tuning of the parameters. From this perspective, future enhancements of the model will probably deal with the research of features that help characterize the acceptance/rejection trends related to market zones presenting a small variability of the production units joining the markets.

6.2. Practical Implications

The work reported in this paper is part of a project in which the researchers of the University of Genoa and Nadara Italy S.p.A cooperated. Specifically, the methodology proposed here is intended to overcome the assumption of uniform PDF to extract awarded bids and offers to be given as input to the EMS discussed in [40,41,42]. The chance to accurately estimate the revenue range associated with proposed bids and offers enables the EMS to formulate effective power dispatching strategies, hence optimizing operational costs.