Investigation of the Optimum Solar Insolation for PV Systems Considering the Effect of Tilt Angle and Ambient Temperature
Abstract
1. Introduction
2. Analysis of Solar Angles and Insolation
2.1. Solar Angles
2.2. Solar Insolation
- Direct Normal Irradiance (DNI)
- Diffuse Horizintal irradiance (DHI)
- Reflected Solar Irradiance
- Global Horizontal Irradiance (GHI)
- Extraterrestrial Irradiance
3. PV Power Generation
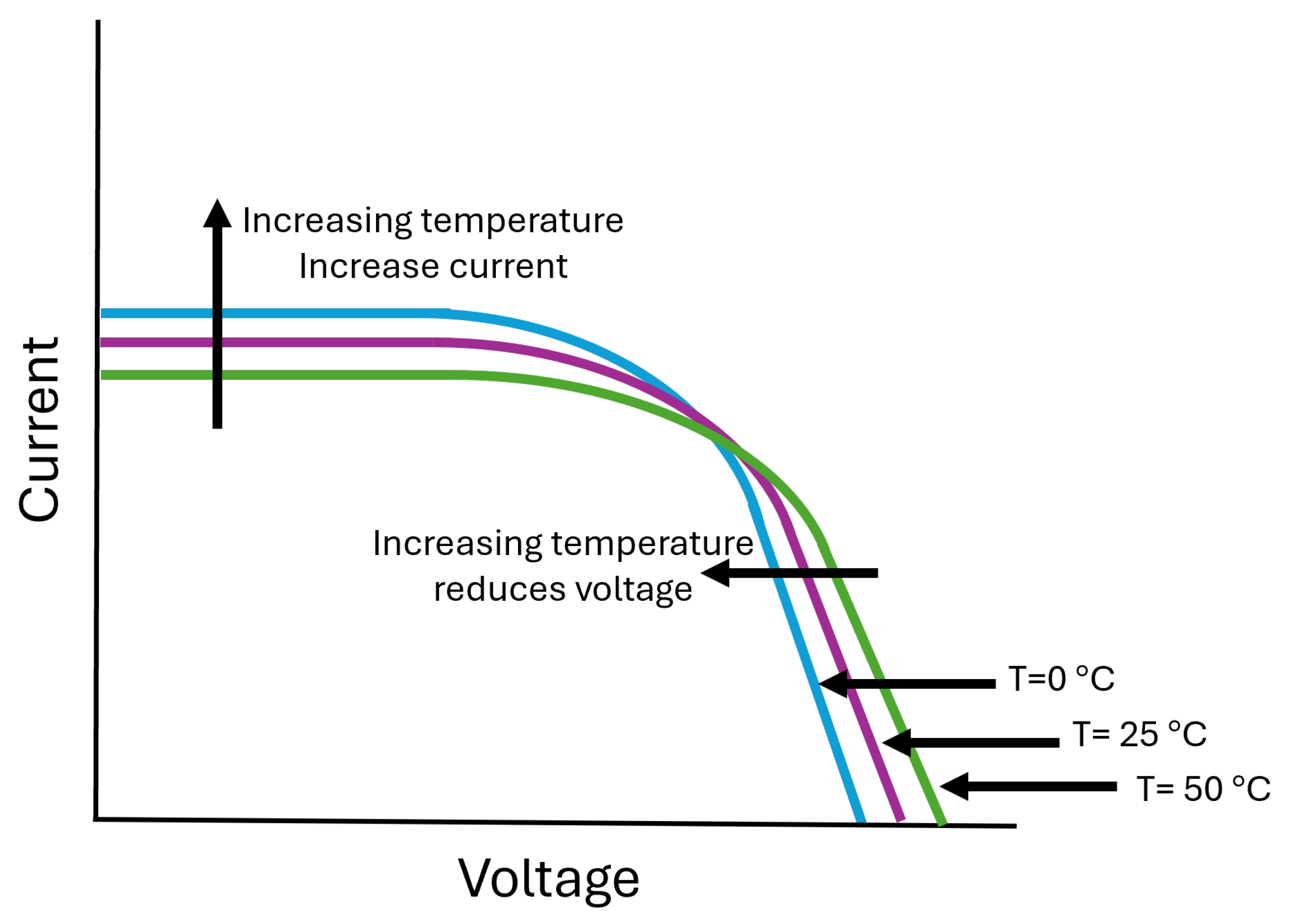
3.1. PV Cell Temperature
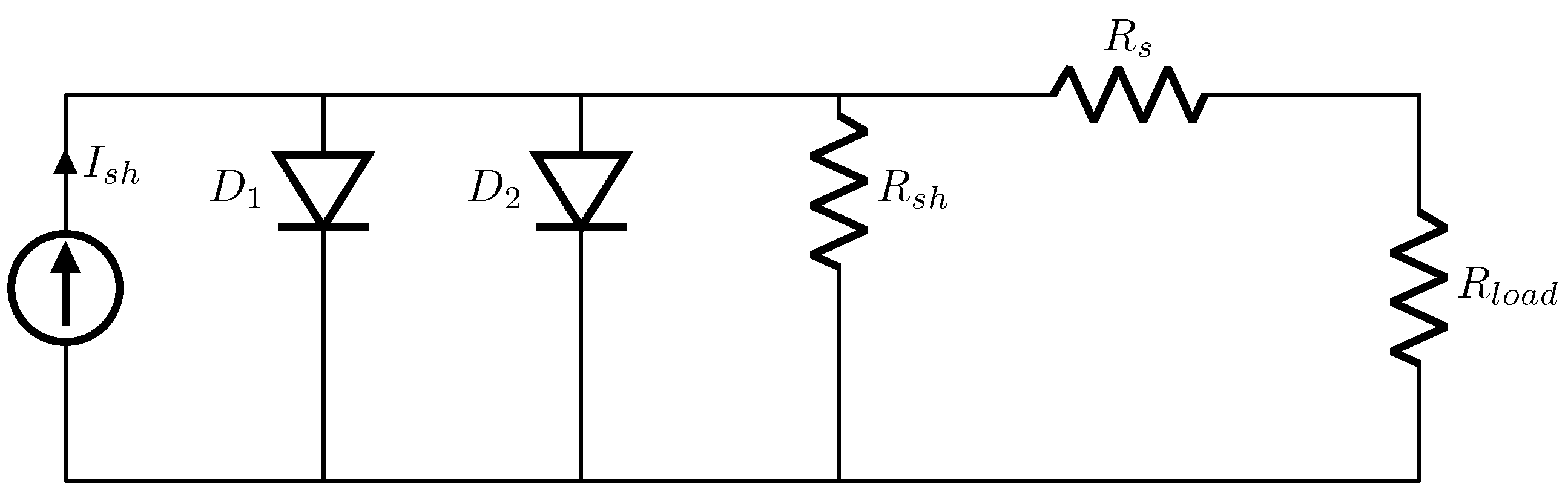
3.2. PV Module Power Output for a Double-Diode Model
- I: Current through the PV cell.
- : Photo-generated current, or the current generated by the absorption of light in the PV cell.
- : Reverse saturation current of the first diode in the model.
- q: Elementary charge (1.602 × 10−19 Coulombs).
- V: Voltage across the PV cell.
- : Series resistance of the PV cell.
- : Ideality factor of the first diode.
- k: Boltzmann constant (1.381 × 10−23 J/K).
- T: Temperature in Kelvin.
- : Reverse saturation current of the second diode in the model.
- : Ideality factor of the second diode.
- : Shunt resistance of the PV cell.
- I is the output current from the solar panel.
- is the short-circuit current, which is the current produced by the solar panel under standard test conditions (STC).
- G is the actual irradiance level incident on the solar panel (in watts per square meter, W/m2).
- is the irradiance under standard test conditions, usually defined as 1000 W/m2.
- Open-Circuit Voltage (Voc):
- 2.
- Short-Circuit Current ():
- 3.
- Maximum Power Point (MPP):
4. Methodology
5. Results and Discussion
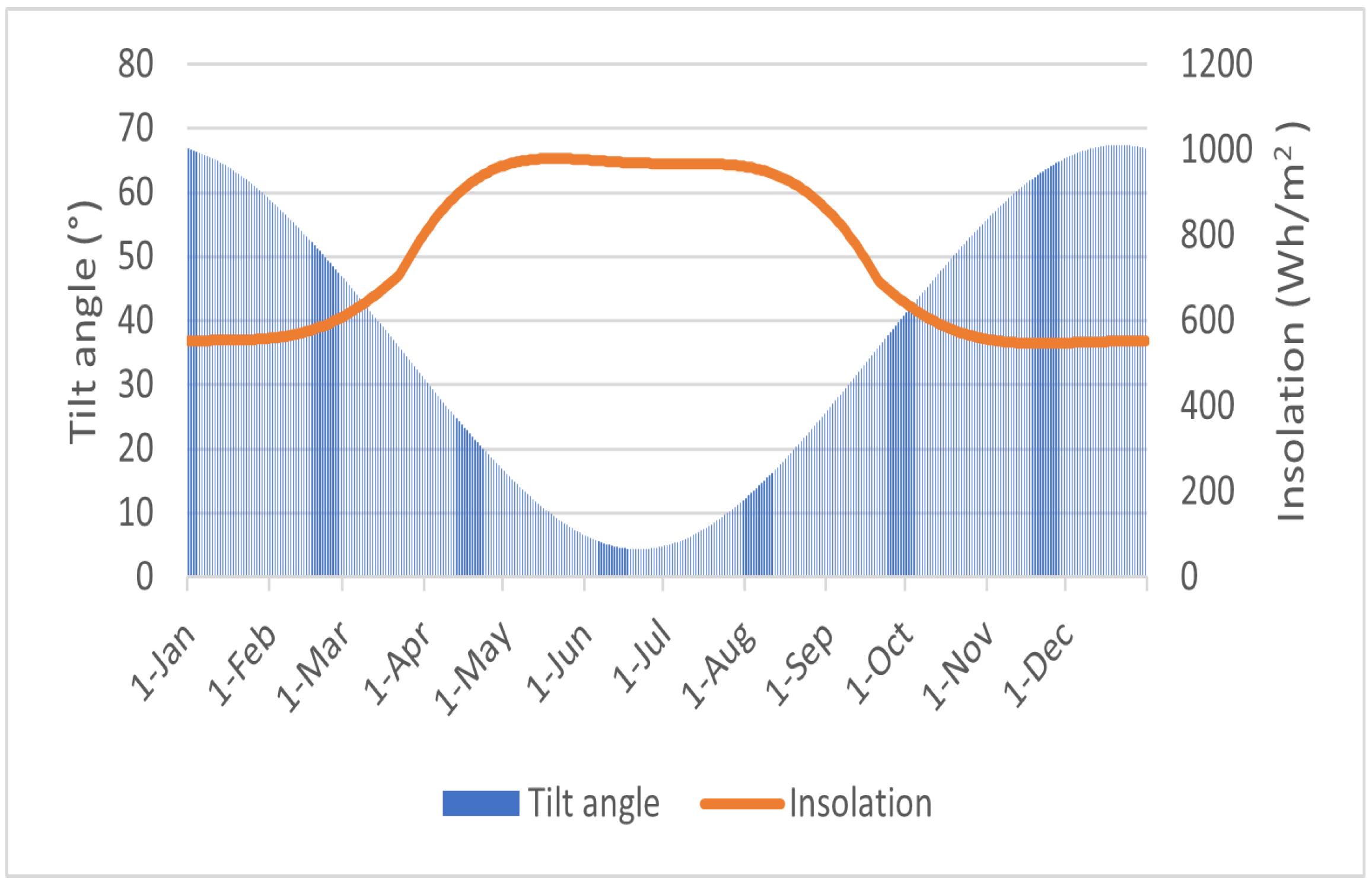
5.1. Fujairah City
5.2. Other Locations
- A.
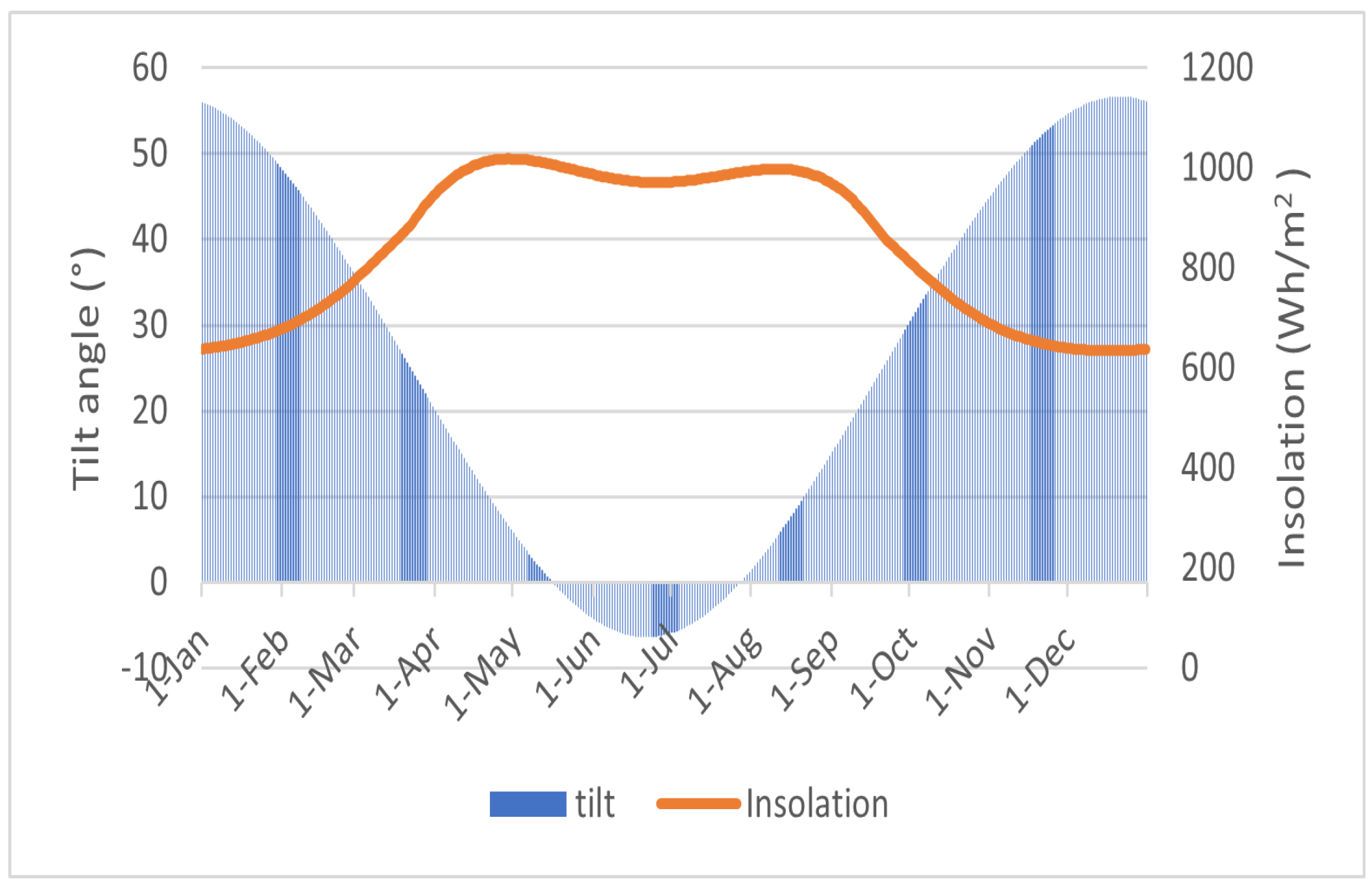
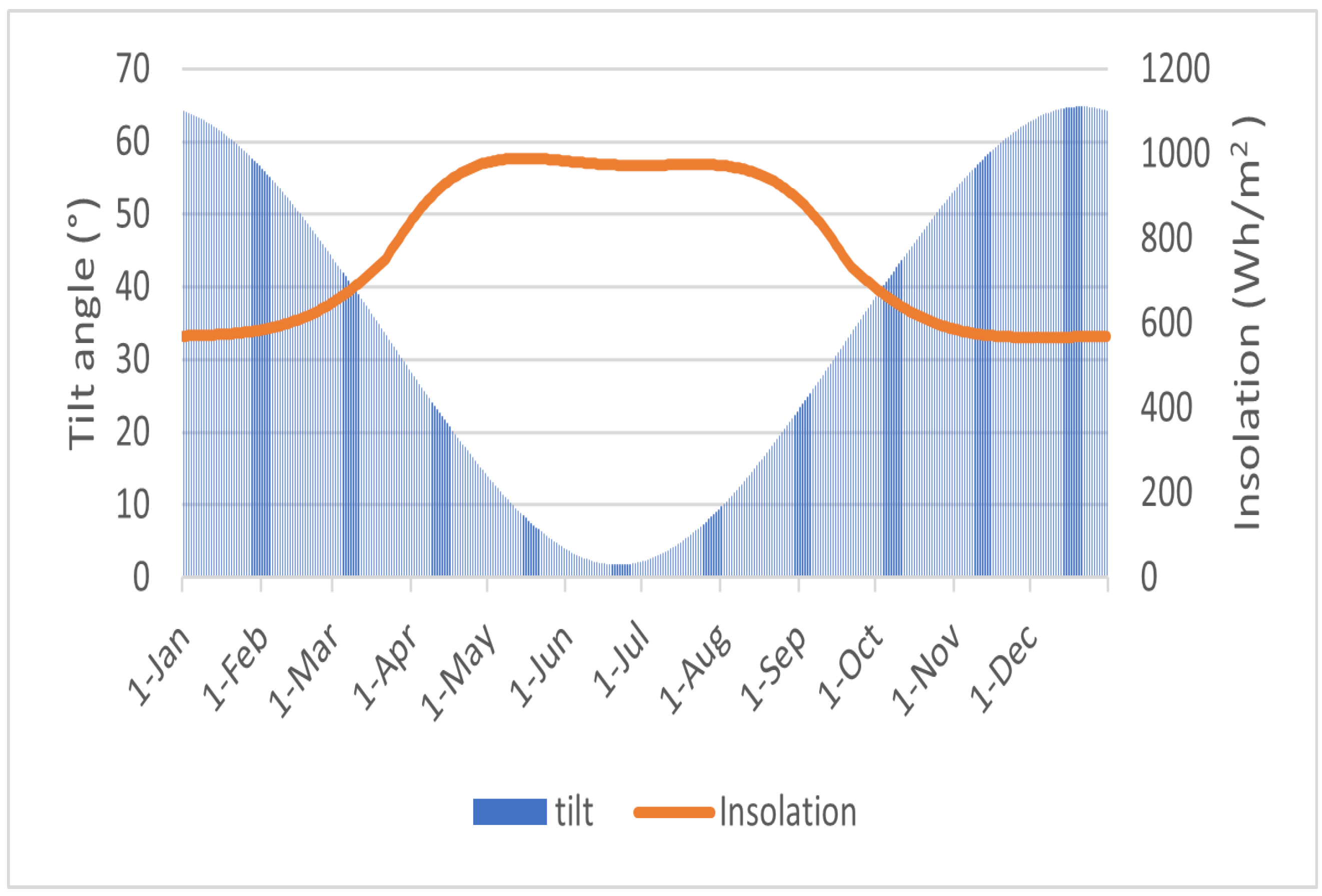
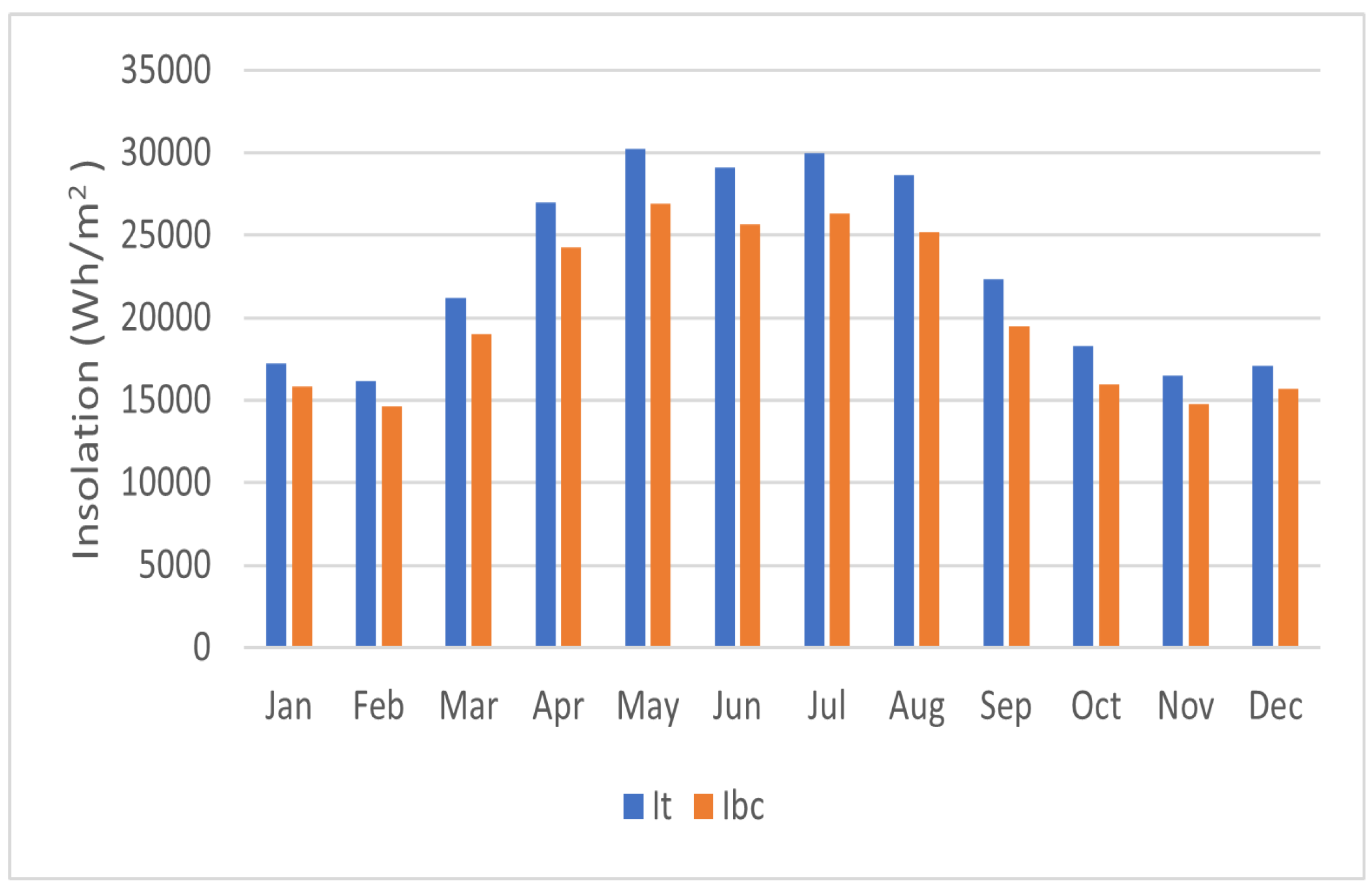
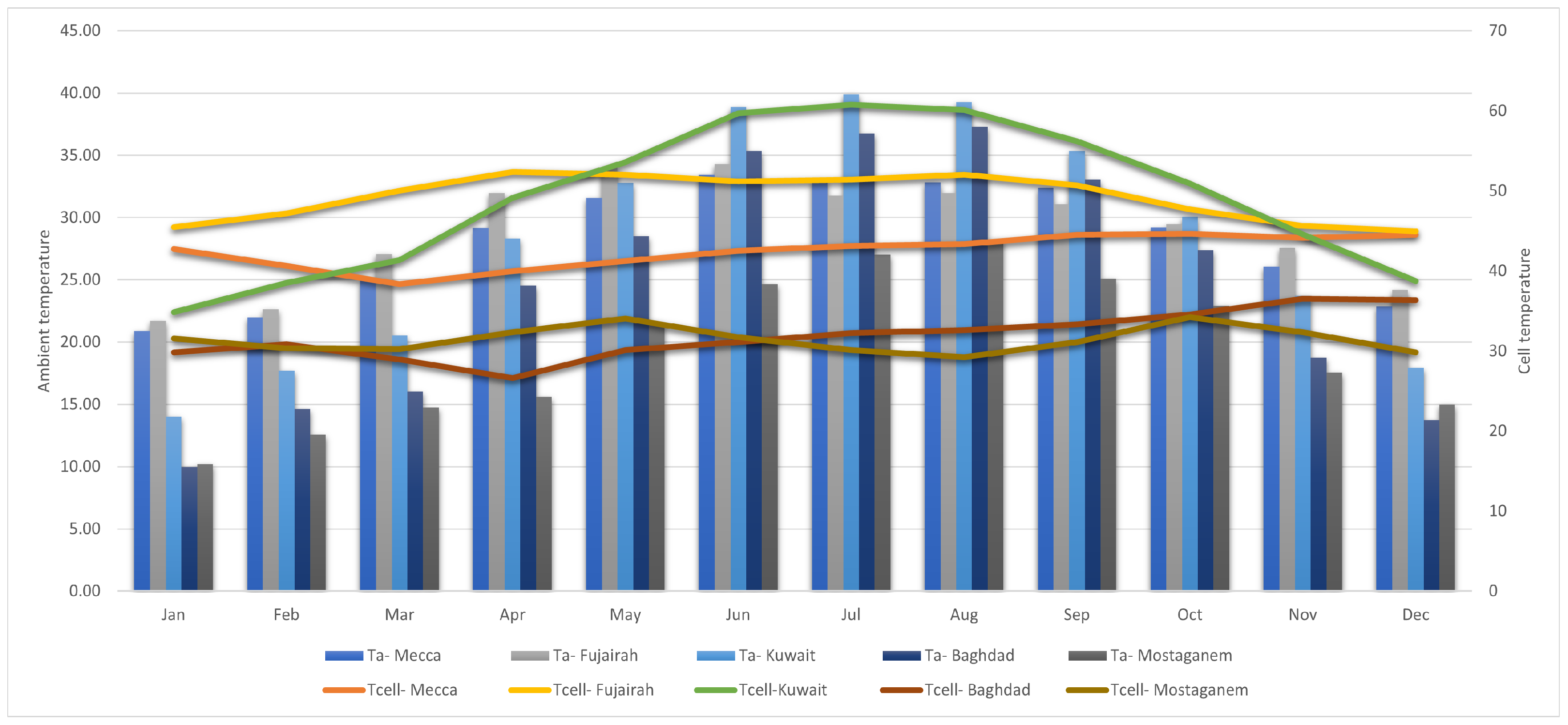
- Mecca City: In this section, we present a case study focusing on estimating the maximum power generation of a PV array in Mecca, a city situated in the eastern region of Saudi Arabia. The weather station used for data collection was positioned at the city center, precisely at 21.4° N and 39.8579° E. Figure 8 showcases the monthly average daily solar radiation () for Mecca, along with the corresponding tilt angle. Throughout the year, Mecca experiences a range of solar radiation levels, with an insolation varying from 21.5 to 31.14 kWh/m2/month. Notably, the month of May registers the highest recorded radiation. Furthermore, the maximum ambient temperature is observed in June, reaching 33.43 °C, while the minimum temperature occurs in January, measuring 20.79 °C. On average, the annual ambient temperature in Mecca is approximately 28.19 °C. Table 2 provides valuable information regarding the monthly average daily global horizontal radiation, ambient temperature, and monthly optimum tilt angle for Mecca. Additionally, the table includes the temperature cell data for the PV system. In general, the models used to calculate the total solar radiation on tilted surfaces represent an improvement over the solar radiation received on horizontal surfaces. Figure 9 visually demonstrates this enhancement, highlighting the increased solar radiation captured by the tilted surface compared to the horizontal surface.
- B.
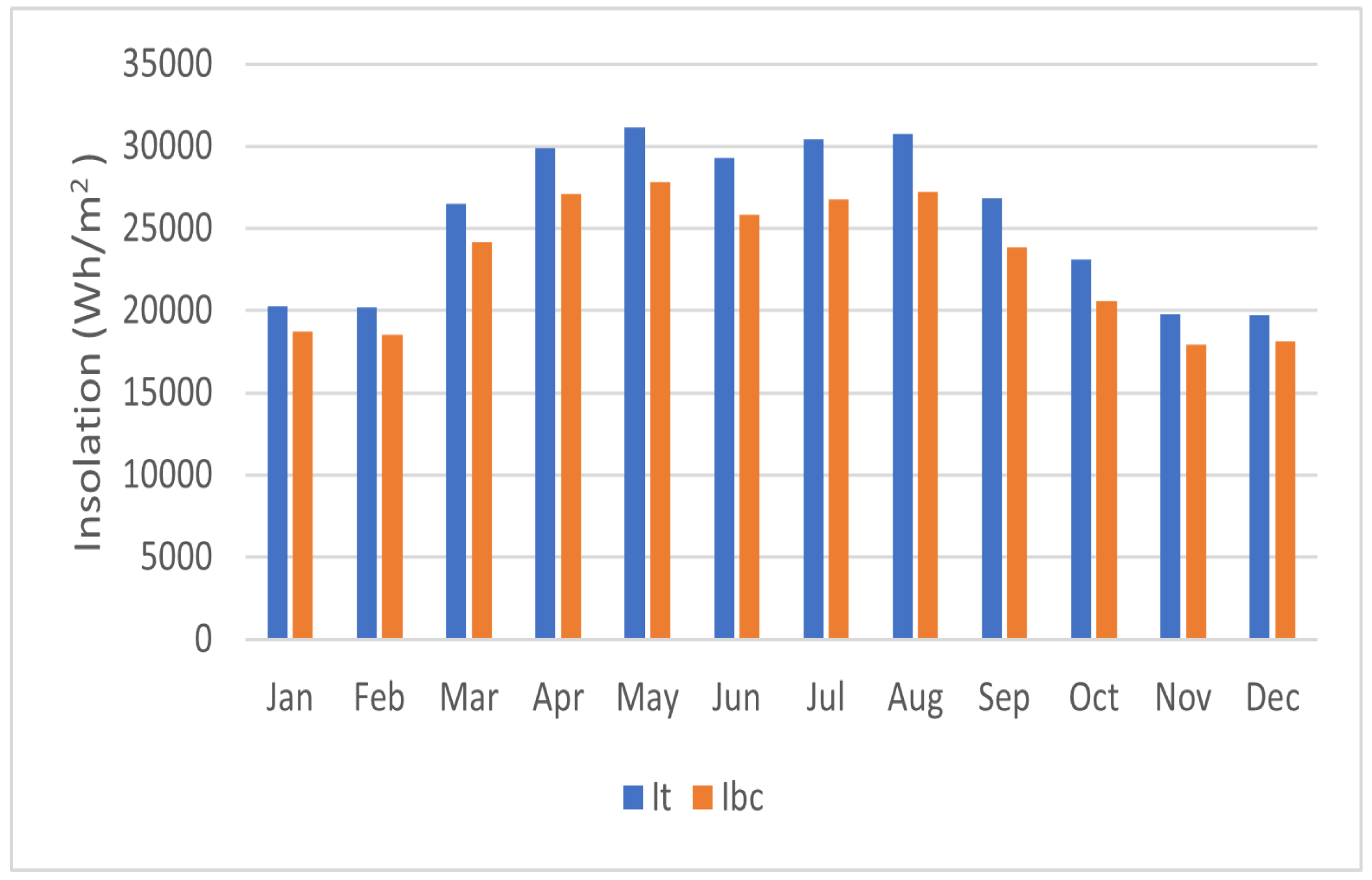
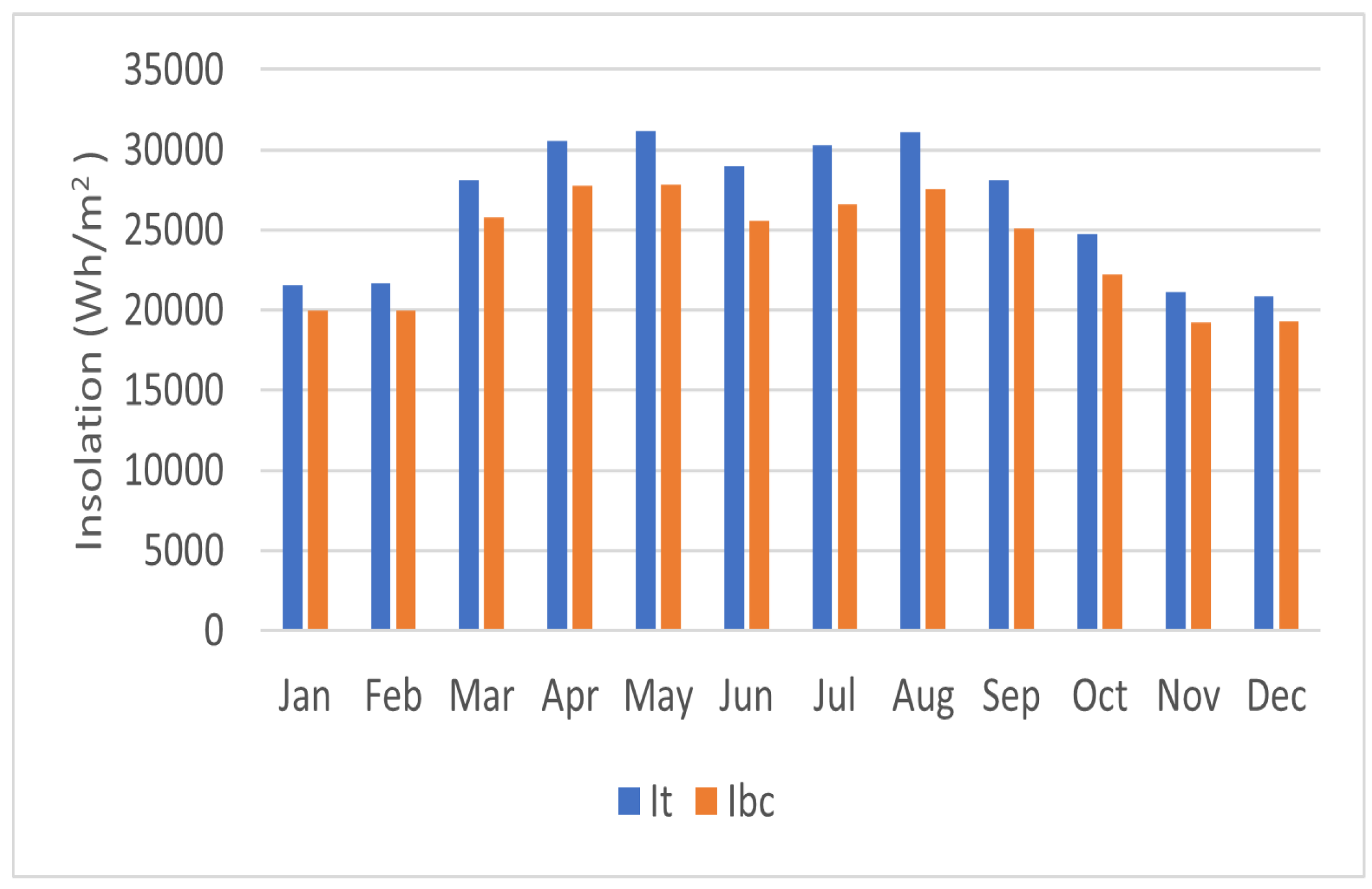
- Kuwait City: Located at approximately 29.31° N and 47.48° E, Kuwait experiences over 300 sunny days annually, with an average of 10 h of sunshine per day. This highlights Kuwait’s significant potential for solar energy generation. To optimize PV system performance, the tilt angle of the panels should be designed according to the site’s latitude. For Kuwait (29.31° N), tilting PV modules with the optimal solar angles maximizes irradiance capture and enhances power output. Table 3 summarizes the tilt angle, insolation, and associated ambient and cell temperatures, while Figure 10 and Figure 11 illustrate the monthly change of insolation and beam irradiance at different tilt angles.
- C.
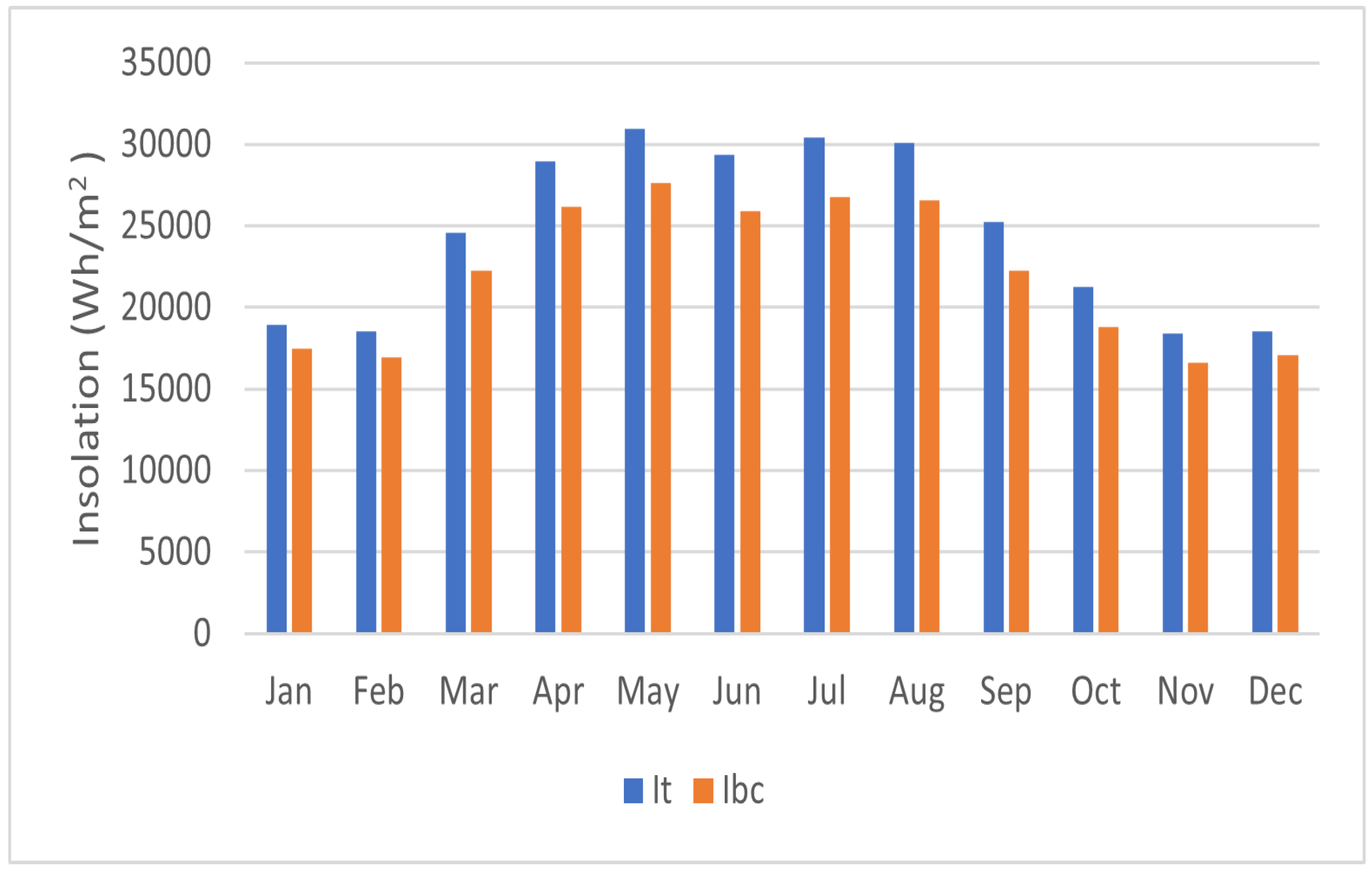
- Baghdad City: Baghdad, the capital of Iraq, is located in the Middle East region of Asia. Situated at a latitude of approximately 33.3°, the city experiences a diverse range of ambient temperatures throughout the year. In January, the minimum recorded temperature drops to 9.98°, while the maximum temperature peaks at 37.28° in August. Similarly, the cell temperature, which refers to the temperature of PV cells, reaches its minimum of 30.7° in January and its maximum of 58.11° in August. The tilt angle, which determines the angle at which the solar panels are positioned, exhibits its lowest value of 2.32° in June and its highest value of 64.31° in December. Further information regarding these findings can be found in Table 4. Additionally, the table indicates that insolation values vary throughout the year. The highest insolation value of 30.1 kWh/m2/month is recorded in July, while the lowest value of 17.6 kWh/m2/month is observed in November. For a visual representation, Figure 12 displays the daily tilt angle in conjunction with the irradiance for Baghdad. Furthermore, Figure 13 illustrates the monthly radiation values and the horizontal position of PVs without any tilt.
- D.
- Mostaganem city–Algeria: Mostaganem is a city located in Algeria, situated in the North African region. As the city is positioned at a latitude of approximately 35.93°, it experiences distinct ambient temperature variations throughout the year. In January, the minimum recorded temperature in Mostaganem is 10.18°, while the maximum temperature peaks at 28.2° in August. In terms of cell temperature, the lowest value of 31.02° occurs in January, whereas the highest value of 49.03° is recorded in August. The tilt angle, which determines the inclination of the solar panels, shows a minimum value of 4.92° in June and a maximum value of 66.91° in December. Table 5 provides further details on these outcomes. Moreover, insolation values vary over the course of the year in Mostaganem. The highest insolation value of 30.25 kWh/m2/month is observed in May, while the lowest value of 16.4 kWh/m2/month occurs in November. For visual representations, Figure 14 illustrates the daily tilt angle alongside the irradiance for Mostaganem. Furthermore, Figure 15 illustrates the monthly radiation values and the horizontal position of PVs without any tilt.
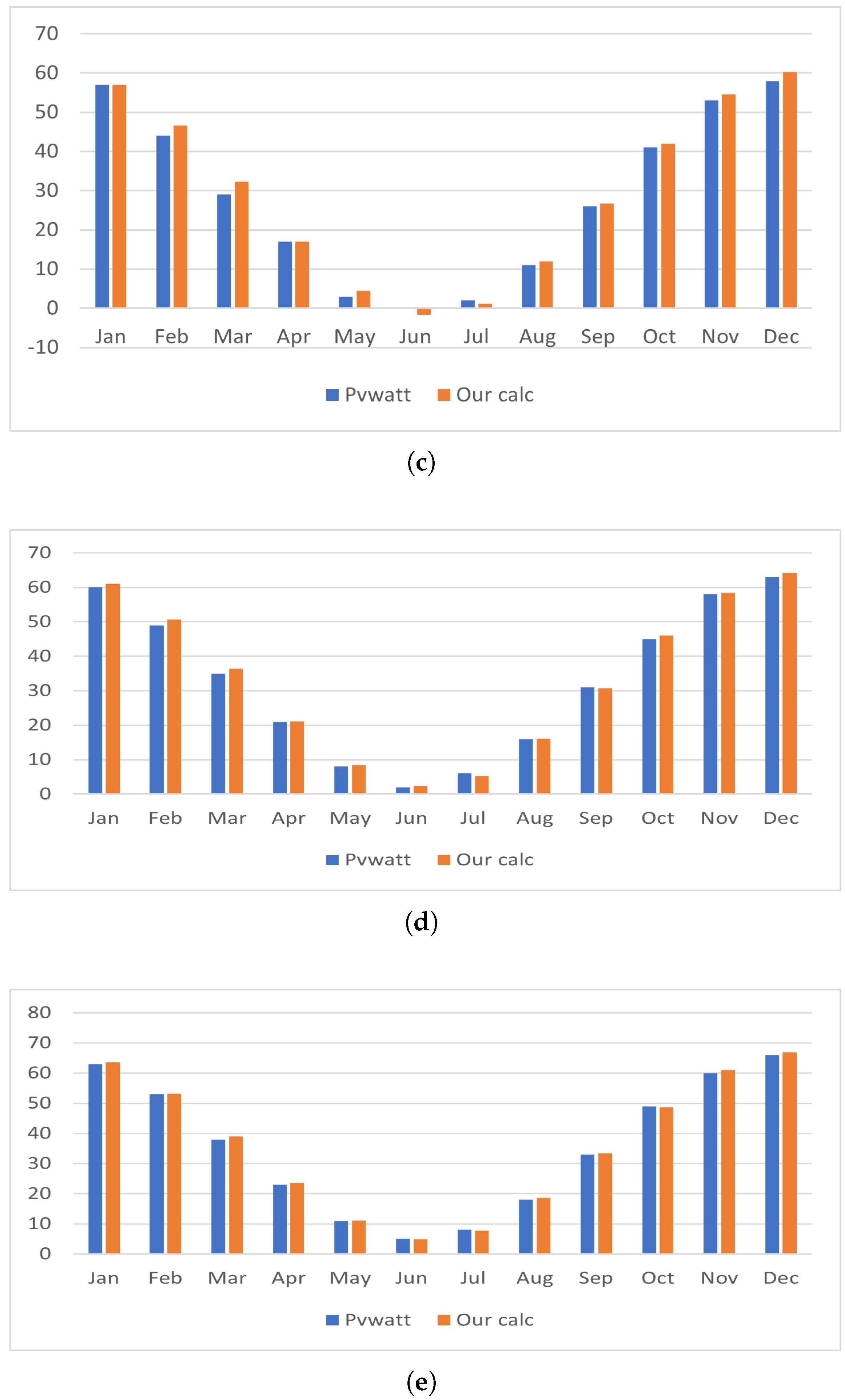
5.3. PVWatt Tilt Angle
5.4. Power Output of the PV Solar System
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tagliapietra, S. The impact of the global energy transition on MENA oil and gas producers. Energy Strategy Rev. 2019, 26, 100397. [Google Scholar] [CrossRef]
- Tazikeh, S.; Mohammadzadeh, O.; Zendehboudi, S.; Saady, N.M.C.; Albayati, T.M.; Chatzis, I. Energy development and management in the Middle East: A holistic analysis. Energy Convers. Manag. 2025, 323, 119124. [Google Scholar] [CrossRef]
- Islam, M.T.; Ali, A. Sustainable green energy transition in Saudi Arabia: Characterizing policy framework, interrelations and future research directions. Next Energy 2024, 5, 100161. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Alnaqbi, S.; Alami, A. Sustainability and Renewable Energy in the UAE: A Case Study of Sharjah. Energies 2023, 16, 7034. [Google Scholar] [CrossRef]
- Tamimi. Greening the Energy Mix: Saudi Arabia, the United Arab Emirates, and Qatar. 2023. Available online: https://www.tamimi.com/law-update-articles/greening-the-energy-mix-saudi-arabia-the-united-arab-emirates-and-qatar/ (accessed on 20 September 2025).
- Tok, E. The Gulf Cooperation Council states: Crystallization of the regional cooperation and alliances amid dwindling resources. Dig. Middle East Stud. 2021, 30, 53–69. [Google Scholar] [CrossRef]
- Saif, A.G.H.; Alquaity, A.B.; Mokheimer, E.M. Techno-economic analysis of green hydrogen production in Saudi Arabia: A comparative study of solar PV and CSP technologies. Int. J. Hydrogen Energy 2025, 105, 1361–1374. [Google Scholar] [CrossRef]
- Alnaser, W.; Alnaser, N. The impact of the rise of using solar energy in GCC countries. In Renewable Energy and Sustainable Buildings: Selected Papers from the World Renewable Energy Congress WREC 2018; Springer: Berlin/Heidelberg, Germany, 2019; pp. 167–183. [Google Scholar]
- deve Venkatachalam, S.; Al Nadabi, A.; Al Shukaili, A.A.; Al Hinai, A.S.; Al Shuaili, A.S.; said Al Shukaili, I. Performance and suitability analysis of rooftop solar PV in Oman: A case study of university branches. Heliyon 2025, 11, e42578. [Google Scholar] [CrossRef]
- Mamun, M.; Islam, M.; Hasanuzzaman, M.; Selvaraj, J. Effect of tilt angle on the performance and electrical parameters of a PV module: Comparative indoor and outdoor experimental investigation. Energy Built Environ. 2022, 3, 278–290. [Google Scholar] [CrossRef]
- Teyabeen, A.A.; Mohamed, F. Estimation of the Optimum Tilt Angle of Solar PV Panels to Maximize Incident Solar Radiation in Libya. Energies 2024, 17, 5891. [Google Scholar] [CrossRef]
- Shaik, F.; Lingala, S.S.; Veeraboina, P. Effect of various parameters on the performance of solar PV power plant: A review and the experimental study. Sustain. Energy Res. 2023, 10, 6. [Google Scholar] [CrossRef]
- Dubey, S.; Sarvaiya, J.N.; Seshadri, B. Temperature dependent photovoltaic (PV) efficiency and its effect on PV production in the world—A review. Energy Procedia 2013, 33, 311–321. [Google Scholar] [CrossRef]
- Dhanalakshmi, S.; Chakravartula, V.; Narayanamoorthi, R.; Kumar, R.; Dooly, G.; Duraibabu, D.B.; Senthil, R. Thermal management of solar photovoltaic panels using a fibre Bragg grating sensor-based temperature monitoring. Case Stud. Therm. Eng. 2022, 31, 101834. [Google Scholar] [CrossRef]
- Shaker, L.M.; Al-Amiery, A.A.; Hanoon, M.M.; Al-Azzawi, W.K.; Kadhum, A.A.H. Examining the influence of thermal effects on solar cells: A comprehensive review. Sustain. Energy Res. 2024, 11, 6. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Chin, V.J.; Salam, Z.; Ishaque, K. An accurate two diode model computation for CIS thin film PV module using the hybrid approach. In Proceedings of the 2015 4th International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 24–26 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Mansour, R.B.; Khan, M.A.M.; Alsulaiman, F.A.; Mansour, R.B. Optimizing the solar PV tilt angle to maximize the power output: A case study for Saudi Arabia. IEEE Access 2021, 9, 15914–15928. [Google Scholar] [CrossRef]
- Melhem, R.; Shaker, Y. Estimating the Optimum Tilt Angle of Solar Panels in Fujairah. In Proceedings of the 2023 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 20–23 February 2023; pp. 1–5. [Google Scholar]
- Melhem, R.; Shaker, Y. Optimum tilt angle and solar radiation of photovoltaic modules for gulf collaboration council countries. Int. J. Energy Res. 2023, 2023, 8381696. [Google Scholar] [CrossRef]
- Kaddoura, T.O.; Ramli, M.A.; Al-Turki, Y.A. On the estimation of the optimum tilt angle of PV panel in Saudi Arabia. Renew. Sustain. Energy Rev. 2016, 65, 626–634. [Google Scholar] [CrossRef]
- Liu, H.; Xu, X.; Meng, Y.; Yu, D.; Shi, K. A research for the influence of tilt angles of the solar panel on photovoltaic power generation. In Proceedings of the 2018 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Kajang, Malaysia, 29 May–1 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 95–100. [Google Scholar]
- Selvi, S.; Mohanraj, M.; Duraipandy, P.; Kaliappan, S.; Natrayan, L.; Vinayagam, N. Optimization of solar panel orientation for maximum energy efficiency. In Proceedings of the 2023 4th International Conference on Smart Electronics and Communication (ICOSEC), Trichy, India, 20–22 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 159–162. [Google Scholar]
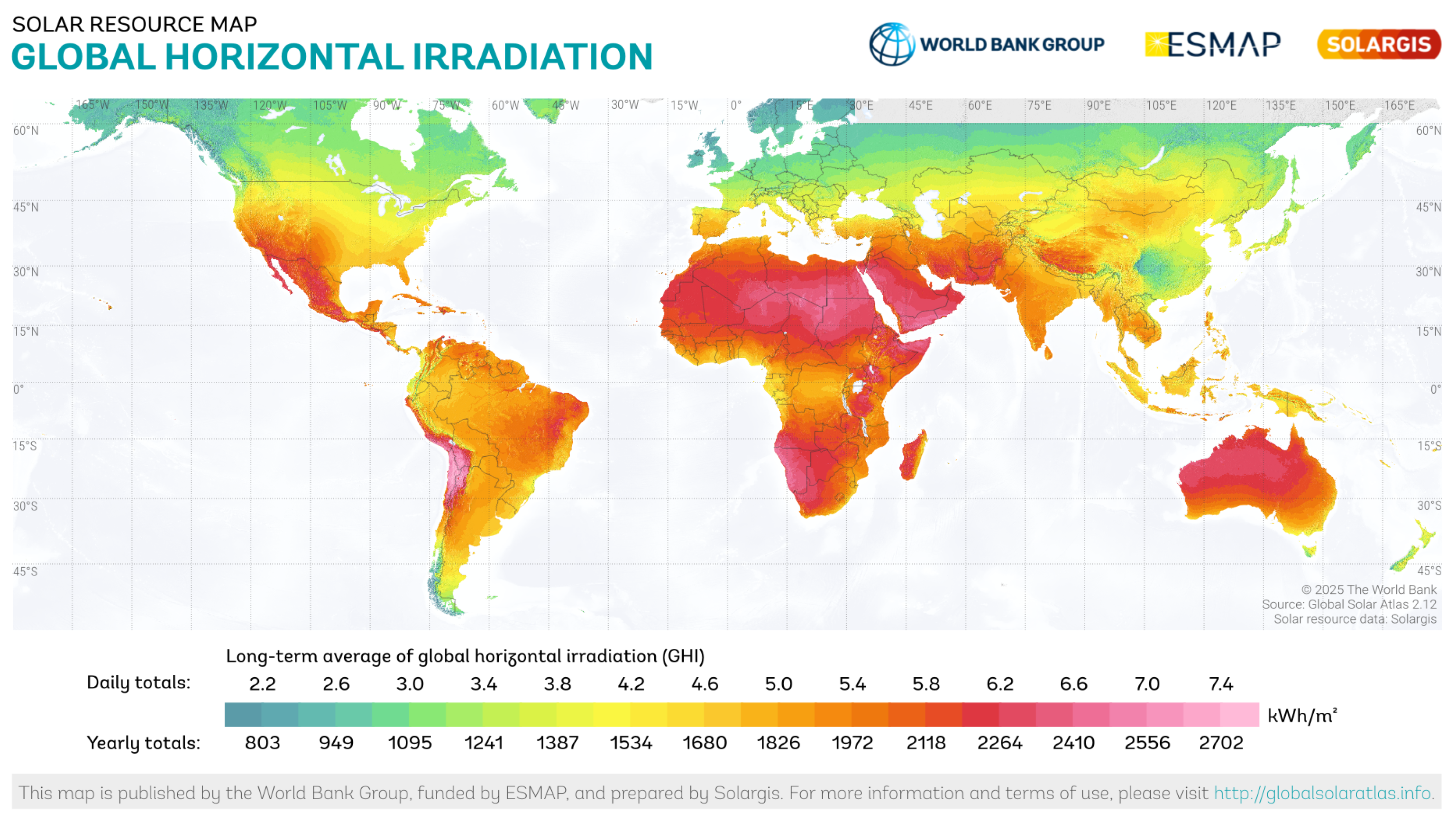
- Solargis. Global Solar Atlas 2.0, Solar Resource Data. 2021. Available online: https://solargis.com (accessed on 20 September 2025).
- Khan, M.S.; Ramli, M.A.; Sindi, H.F.; Hidayat, T.; Bouchekara, H.R. Estimation of solar radiation on a PV panel surface with an optimal tilt angle using electric charged particles optimization. Electronics 2022, 11, 2056. [Google Scholar] [CrossRef]
- Abdallah, R.; Juaidi, A.; Abdel-Fattah, S.; Manzano-Agugliaro, F. Estimating the optimum tilt angles for south-facing surfaces in Palestine. Energies 2020, 13, 623. [Google Scholar] [CrossRef]
- Wang, H.; Sun, Y.; Dong, F. Bismuth metal and semiconductor-based photocatalysts: structure tuning, activity enhancement, and reaction mechanism. In Interface Science and Technology; Elsevier: Amsterdam, The Netherlands, 2020; Volume 31, pp. 349–377. [Google Scholar]
- Oliveira, M.; Silva Lopes, H.; Mendonça, P.; Tenpierik, M.; Silva, L.T. Solar radiation measurement tools and their impact on in situ testing—A Portuguese case study. Buildings 2024, 14, 2117. [Google Scholar] [CrossRef]
- Li, H.; Lian, Y.; Wang, X.; Ma, W.; Zhao, L. Solar constant values for estimating solar radiation. Energy 2011, 36, 1785–1789. [Google Scholar] [CrossRef]
- Jatskevich, J.; Spagnuolo, G.; Xiao, W.; Edwin, F.F. Efficient Approaches for Modeling and Simulating Photovoltaic Power Systems. IEEE J. Photovoltaics 2013, 3, 500–508. [Google Scholar]
- Yahya-Khotbehsara, A.; Shahhoseini, A. A fast modeling of the double-diode model for PV modules using combined analytical and numerical approach. Sol. Energy 2018, 162, 403–409. [Google Scholar] [CrossRef]
- Sarniak, M.T.; Wernik, J.; Wołosz, K.J. Application of the double diode model of photovoltaic cells for simulation studies on the impact of partial shading of silicon photovoltaic modules on the waveforms of their current-voltage characteristic. Energies 2019, 12, 2421. [Google Scholar] [CrossRef]
- Markvart, T.; Castañer, L. Principles of solar cell operation. In McEvoy’s Handbook of Photovoltaics; Elsevier: Amsterdam, The Netherlands, 2018; pp. 3–28. [Google Scholar]









| Cell Temperature (°C) | Ambient Temperature (°C) | Tilt Angle (°) | Insolation (kWh/m2/month) | |
|---|---|---|---|---|
| Jan | 45.45 | 21.70 | 52.86 | 20.26 |
| Feb | 47.16 | 22.63 | 42.43 | 20.17 |
| Mar | 50.03 | 27.06 | 28.18 | 26.50 |
| Apr | 52.37 | 31.98 | 12.90 | 29.91 |
| May | 52.02 | 34.09 | 0.30 | 31.16 |
| Jun | 51.21 | 34.27 | −5.85 | 29.27 |
| Jul | 51.43 | 31.75 | −2.97 | 30.43 |
| Aug | 52.01 | 31.95 | 7.86 | 30.73 |
| Sep | 50.67 | 31.06 | 22.58 | 26.85 |
| Oct | 47.71 | 29.46 | 37.83 | 23.11 |
| Nov | 45.64 | 27.55 | 50.30 | 19.78 |
| Dec | 44.96 | 24.20 | 56.14 | 19.71 |
| Average | 49.22 | 28.97 | 25.21 | 30.79 |
| Cell Temperature (°C) | Ambient Temperature (°C) | Tilt Angle (°) | Insolation (kWh/m2/month) | |
|---|---|---|---|---|
| Jan | 41.72 | 20.79 | 49.13 | 21.56 |
| Feb | 42.82 | 21.99 | 38.70 | 21.64 |
| Mar | 45.77 | 24.93 | 24.45 | 28.11 |
| Apr | 50.00 | 29.17 | 9.17 | 30.58 |
| May | 52.42 | 31.59 | −3.43 | 31.14 |
| Jun | 54.26 | 33.43 | −9.58 | 29.00 |
| Jul | 53.85 | 33.01 | −6.70 | 30.27 |
| Aug | 53.65 | 32.82 | 4.13 | 31.10 |
| Sep | 53.21 | 32.38 | 18.85 | 28.13 |
| Oct | 50.05 | 29.22 | 34.10 | 24.76 |
| Nov | 46.88 | 26.05 | 46.57 | 21.12 |
| Dec | 43.70 | 22.87 | 52.41 | 20.89 |
| Average | 49.03 | 28.19 | 21.48 | 26.53 |
| Cell Temperature (°C) | Ambient Temperature (°C) | Tilt Angle (°) | Insolation (kWh/m2/month) | |
|---|---|---|---|---|
| Jan | 35.43 | 14.01 | 57.03 | 18.93 |
| Feb | 34.93 | 17.69 | 46.60 | 18.55 |
| Mar | 34.93 | 20.53 | 32.35 | 24.54 |
| Apr | 33.13 | 28.31 | 17.07 | 28.93 |
| May | 32.63 | 32.77 | 4.47 | 30.97 |
| Jun | 33.73 | 38.85 | −1.68 | 29.37 |
| Jul | 34.13 | 39.91 | 1.20 | 30.41 |
| Aug | 33.93 | 39.24 | 12.03 | 30.09 |
| Sep | 34.73 | 35.34 | 26.75 | 25.23 |
| Oct | 36.23 | 30.06 | 42.00 | 21.22 |
| Nov | 38.53 | 23.71 | 54.47 | 18.38 |
| Dec | 37.83 | 17.90 | 60.31 | 18.55 |
| Average | 38.63 | 28.19 | 29.38 | 24.60 |
| Cell Temperature (°C) | Ambient Temperature (°C) | Tilt Angle (°) | Insolation (kWh/m2/month) | |
|---|---|---|---|---|
| Jan | 30.71 | 9.98 | 61.03 | 17.82 |
| Feb | 35.45 | 14.61 | 50.60 | 17.07 |
| Mar | 36.84 | 16.00 | 36.35 | 22.55 |
| Apr | 45.37 | 24.54 | 21.07 | 27.80 |
| May | 49.31 | 28.48 | 8.47 | 30.59 |
| Jun | 56.17 | 35.34 | 2.32 | 29.28 |
| Jul | 57.59 | 36.76 | 5.20 | 30.19 |
| Aug | 58.11 | 37.28 | 16.03 | 29.28 |
| Sep | 53.87 | 33.04 | 30.75 | 23.52 |
| Oct | 48.22 | 27.38 | 46.00 | 19.43 |
| Nov | 39.58 | 18.75 | 58.47 | 17.17 |
| Dec | 34.56 | 13.73 | 64.31 | 17.60 |
| Average | 45.49 | 24.66 | 33.38 | 23.53 |
| Cell Temperature (°C) | Ambient Temperature (°C) | Tilt Angle (°) | Insolation (kWh/m2/month) | |
|---|---|---|---|---|
| Jan | 31.02 | 10.18 | 63.63 | 17.19 |
| Feb | 33.38 | 12.55 | 53.20 | 16.16 |
| Mar | 35.58 | 14.75 | 38.95 | 21.21 |
| Apr | 36.43 | 15.60 | 23.67 | 26.97 |
| May | 42.34 | 21.51 | 11.07 | 30.25 |
| Jun | 45.51 | 24.68 | 4.92 | 29.13 |
| Jul | 47.88 | 27.05 | 7.80 | 29.96 |
| Aug | 49.03 | 28.20 | 18.63 | 28.66 |
| Sep | 45.93 | 25.10 | 33.35 | 22.34 |
| Oct | 43.76 | 22.92 | 48.60 | 18.29 |
| Nov | 38.38 | 17.55 | 61.07 | 16.47 |
| Dec | 35.83 | 14.99 | 66.91 | 17.07 |
| Average | 40.42 | 19.59 | 35.98 | 22.81 |
| City | Annual Tilt Angle (°) () | Energy (kWh) at | Energy (kWh) at Horizon Surface |
|---|---|---|---|
| Fujairah | 25.21 | 7057 | 6565 |
| Mecca | 21.48 | 7071 | 6608 |
| Kuwait | 29.38 | 6210 | 5879 |
| Baghdad | 33.38 | 5818 | 5167 |
| Mostaganem | 35.98 | 5800 | 5223 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melhem, R.; Shaker, Y.; Mazen, F.M.A.; Abou-Elnour, A. Investigation of the Optimum Solar Insolation for PV Systems Considering the Effect of Tilt Angle and Ambient Temperature. Energies 2025, 18, 5257. https://doi.org/10.3390/en18195257
Melhem R, Shaker Y, Mazen FMA, Abou-Elnour A. Investigation of the Optimum Solar Insolation for PV Systems Considering the Effect of Tilt Angle and Ambient Temperature. Energies. 2025; 18(19):5257. https://doi.org/10.3390/en18195257
Chicago/Turabian StyleMelhem, Raghed, Yomna Shaker, Fatma Mazen Ali Mazen, and Ali Abou-Elnour. 2025. "Investigation of the Optimum Solar Insolation for PV Systems Considering the Effect of Tilt Angle and Ambient Temperature" Energies 18, no. 19: 5257. https://doi.org/10.3390/en18195257
APA StyleMelhem, R., Shaker, Y., Mazen, F. M. A., & Abou-Elnour, A. (2025). Investigation of the Optimum Solar Insolation for PV Systems Considering the Effect of Tilt Angle and Ambient Temperature. Energies, 18(19), 5257. https://doi.org/10.3390/en18195257







