A Risk-Averse Data-Driven Distributionally Robust Optimization Method for Transmission Power Systems Under Uncertainty
Abstract
1. Introduction
1.1. Problem Definition
1.2. Literature Review
1.3. Highlights and Contributions
- Data-driven uncertainty modeling from machine learning forecasts. We develop a forecasting framework using XGBoost with cyclical encodings and multi-scale lag features to predict wind, photovoltaic, and multi-bus demand profiles. Hourly residual distributions are then used to construct quantile-based bounds, providing realistic, data-driven representations of renewable and load uncertainty.
- Integration of distributionally robust optimization with full network constraints. To the best of our knowledge, this work is among the first to embed a DRO framework directly into a UC and optimal power flow (OPF) formulation on a 24-bus transmission system. The Wasserstein-based ambiguity set, coupled with dual reformulation, ensures tractable yet rigorous handling of uncertainty.
- Co-optimization of BESS with realistic dynamics and incentives. A utility-scale BESS is explicitly modeled with state-of-charge dynamics, efficiency losses, and charge/discharge exclusivity. Time-varying incentives for charging and discharging are incorporated, demonstrating how policy signals can be integrated into a risk-averse operational strategy.
- System-wide reliability assessment. The proposed framework explicitly balances economic cost against reliability by quantifying worst-case demand–generation mismatches, renewable shortfalls, and demand surges. Case studies on representative daily horizons illustrate that the DDRO model significantly reduces load shedding and reliability violations, albeit at modest additional operating cost.
- Practical validation through real-world data and scenario testing. The model is validated using multi-year renewable and demand datasets, tested across twelve representative operating days. Comparative analysis against baseline forecasts and actual realizations highlights the robustness of the proposed approach to uncertainty exceedance and its scalability to realistic network sizes.
2. Mathematical Modeling
2.1. Objective Functions
2.2. Unit-Commitment Constraints
2.3. Battery Energy Storage Constraints
2.4. Power-Flow and Network Constraints
2.5. Renewable Generation Modeling
2.6. Demand Response Modeling
3. Uncertainty Quantification and Distributionally Robust Formulation
3.1. Forecasting of Renewable Generation and Demand
3.2. Quantile-Based Uncertainty Bounds
3.3. Wasserstein Ambiguity Set Construction
3.4. Distributionally Robust Optimization Model
4. Case Study and Numerical Experiments
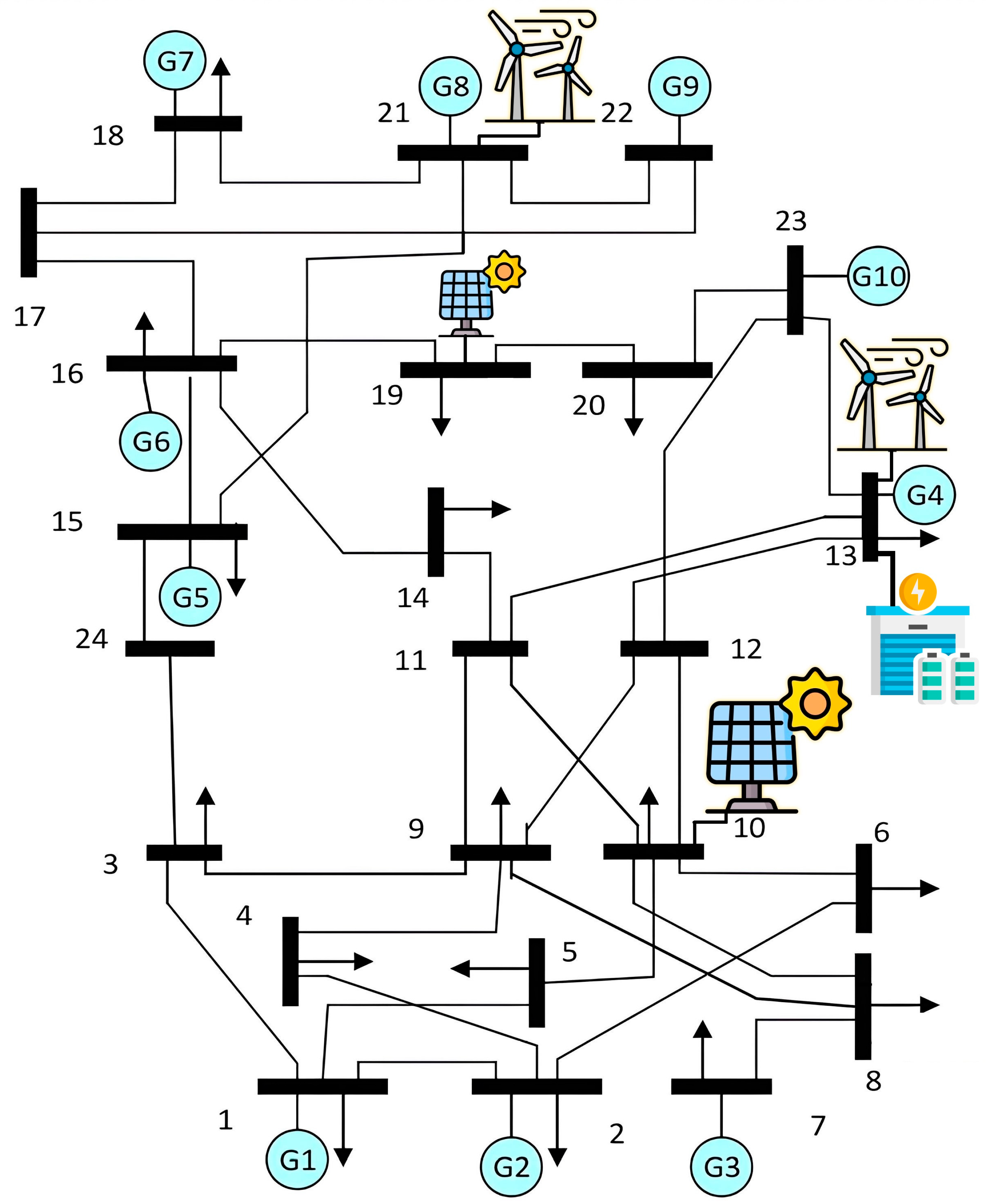
4.1. Test System Data and Parameterization
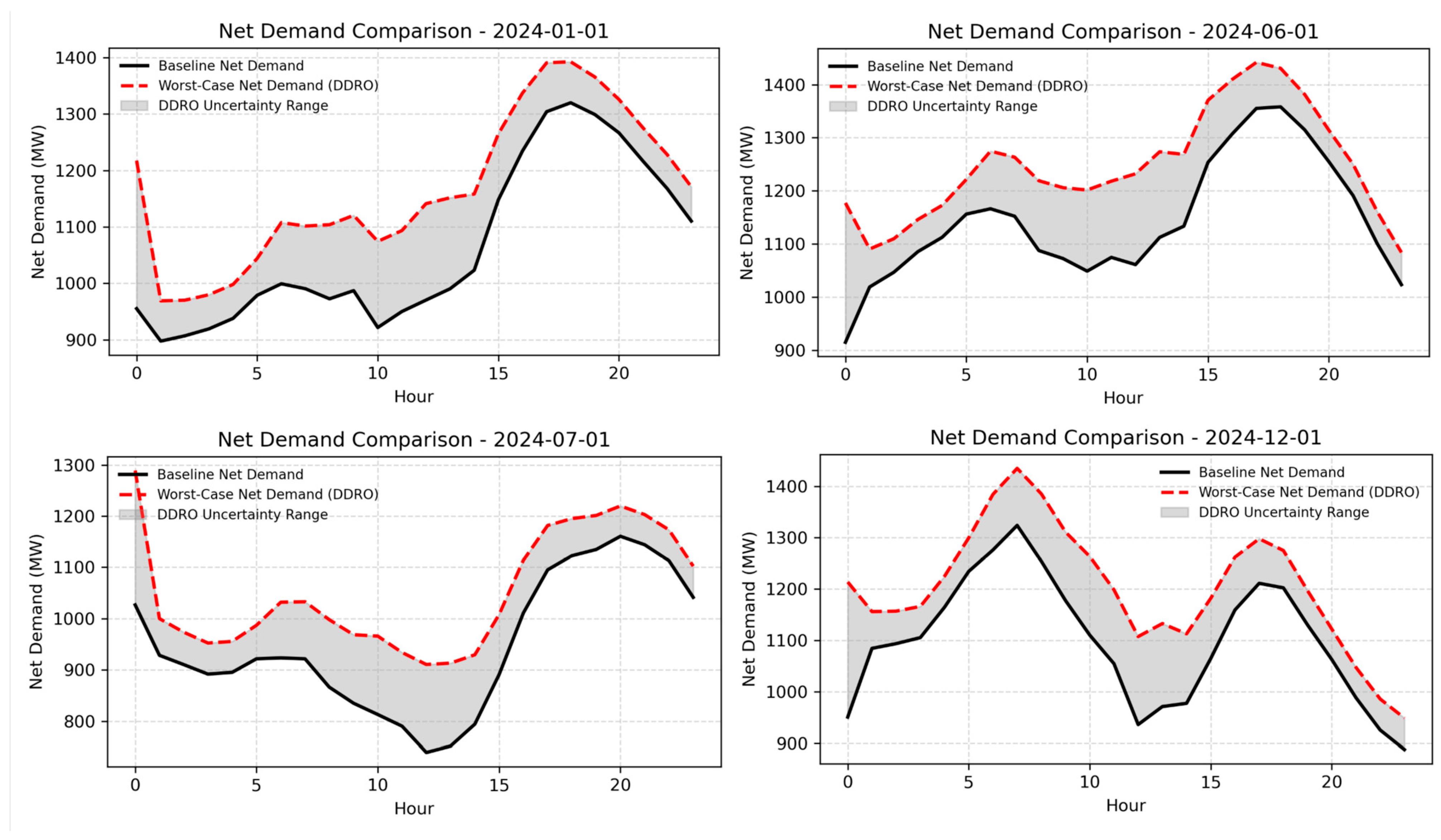
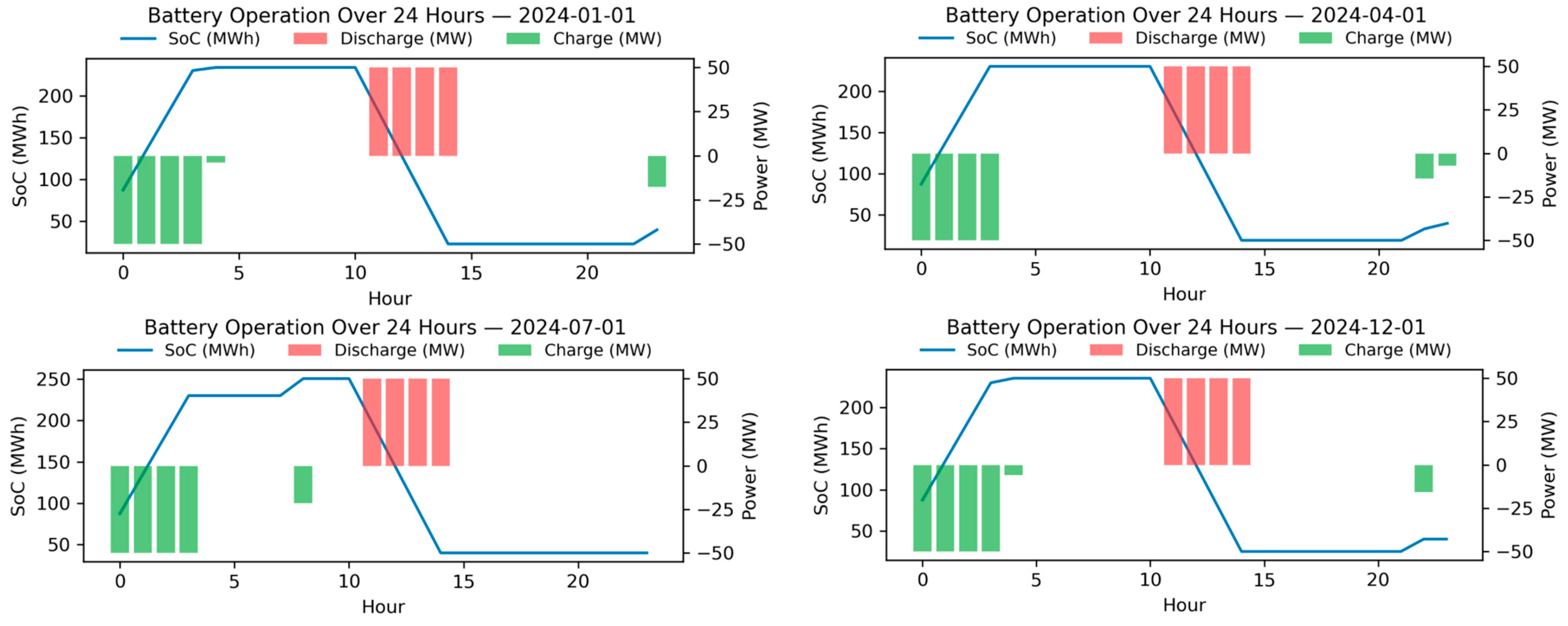
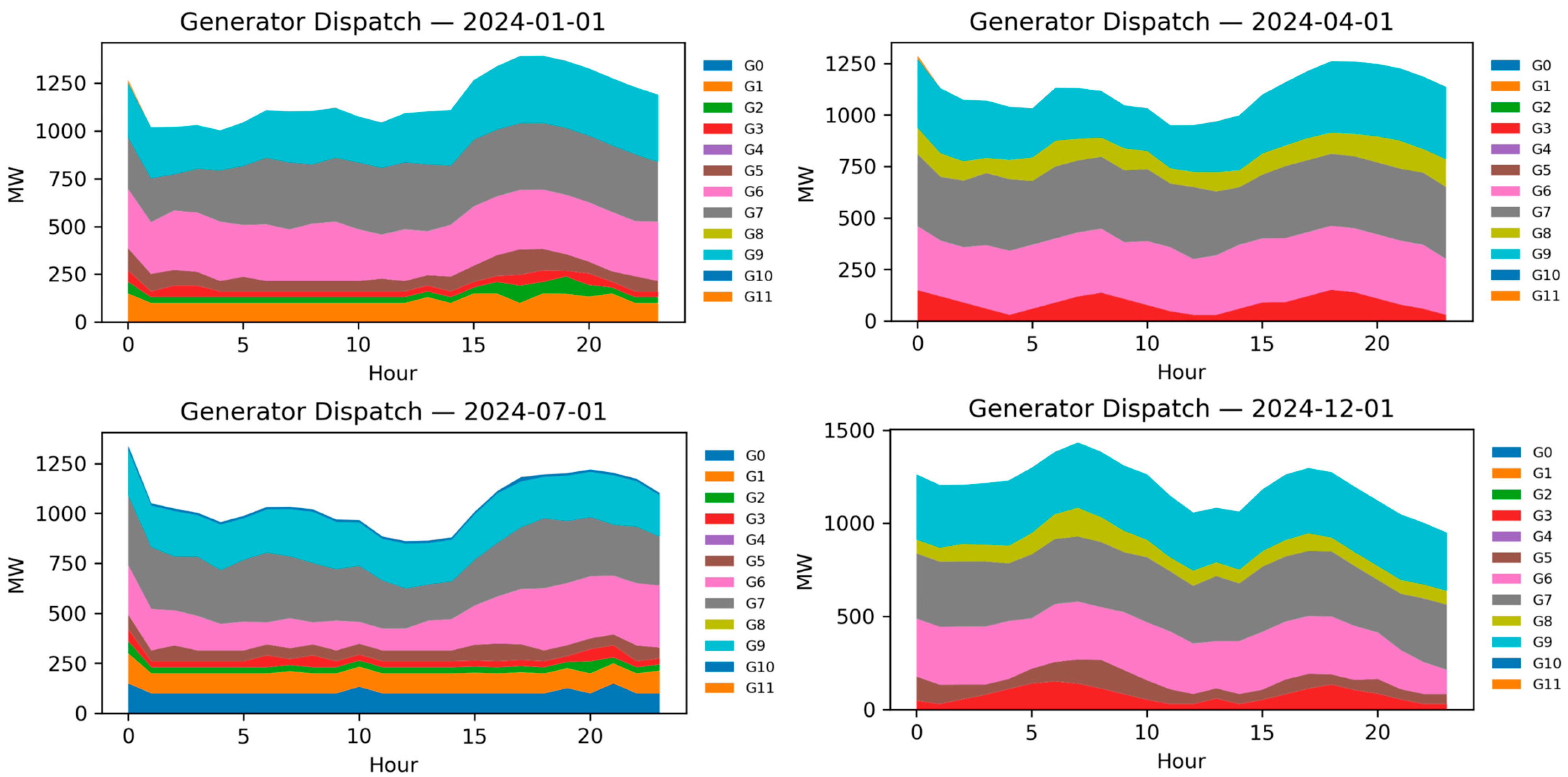
4.2. Results and Outputs
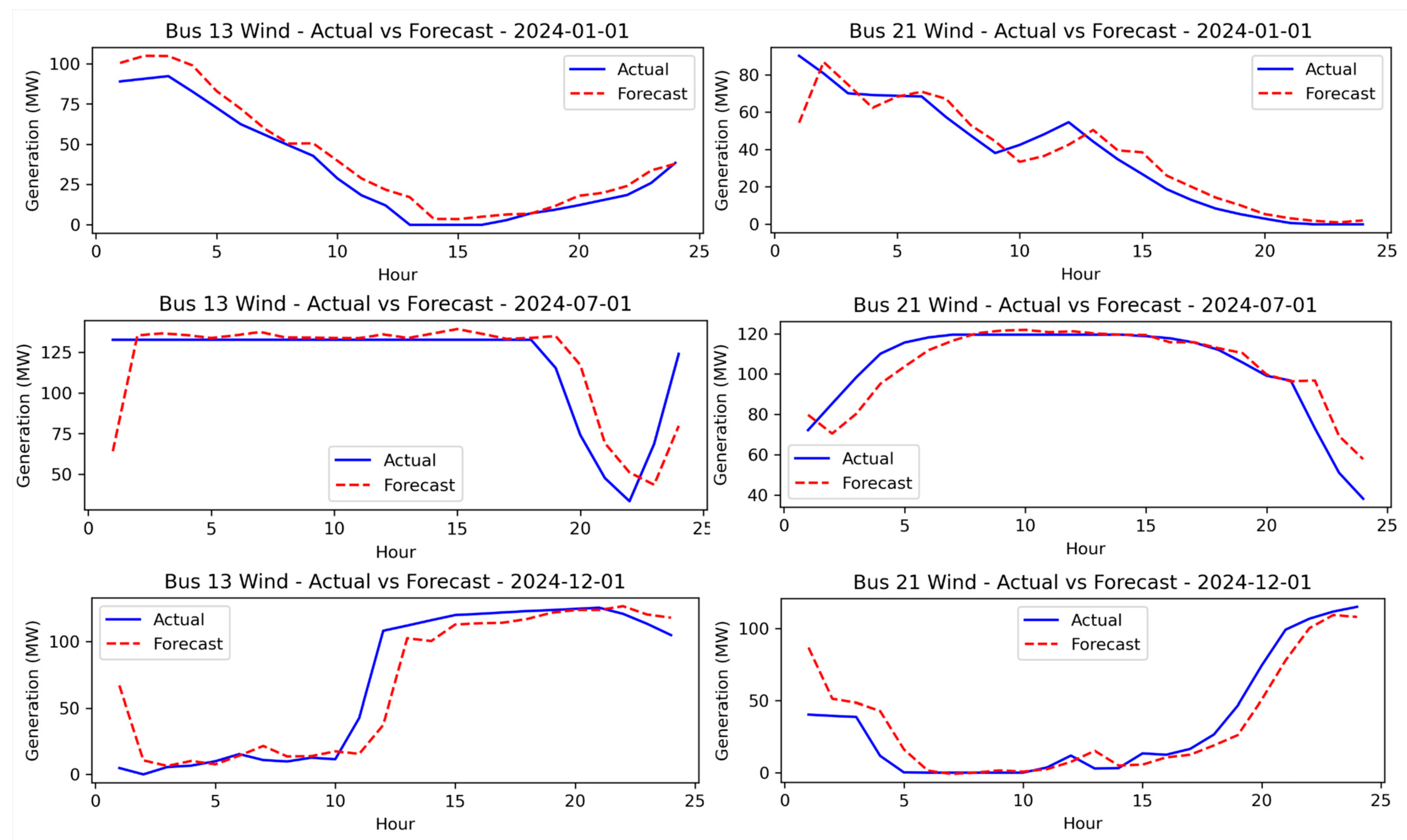
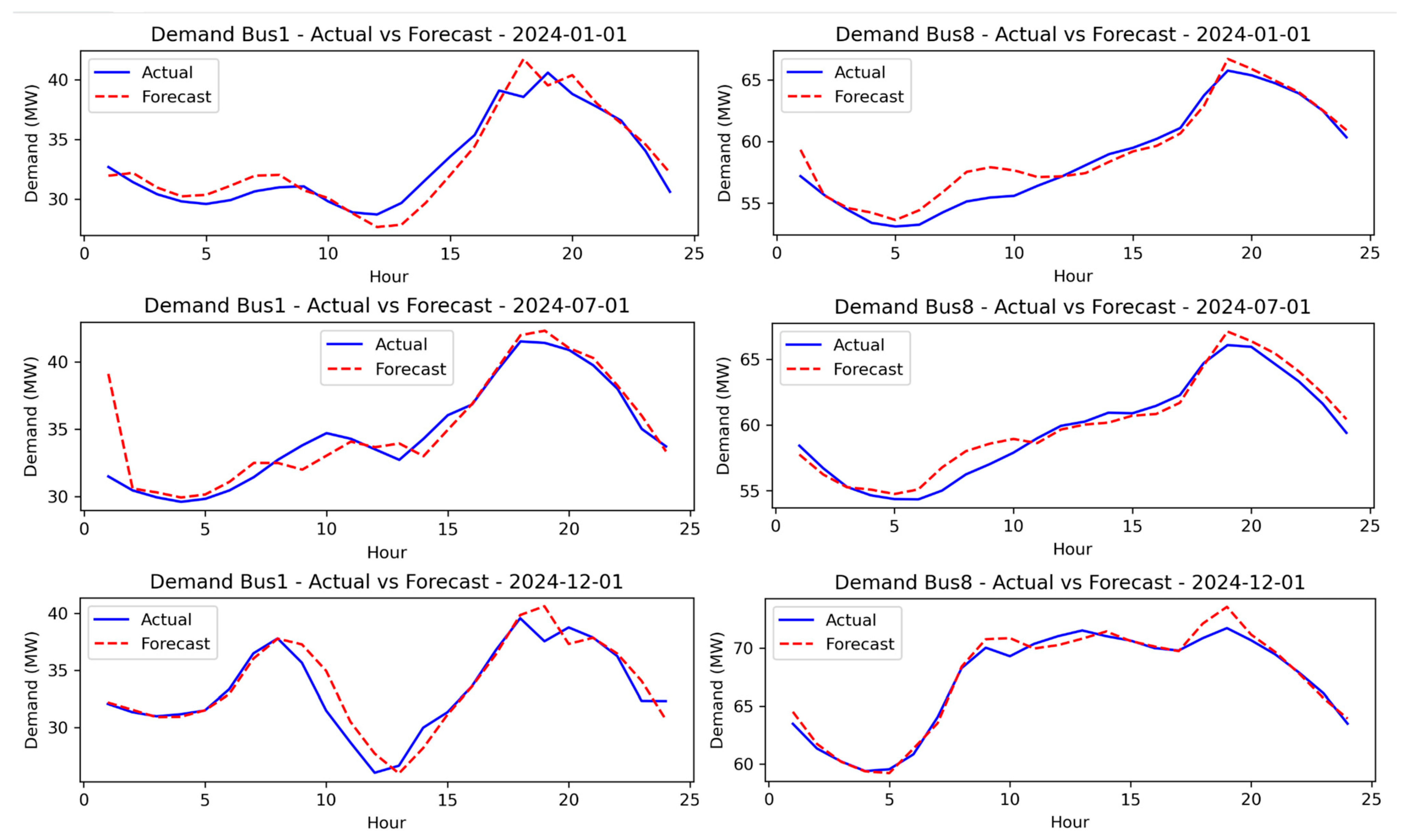
4.2.1. Forecasting Performance
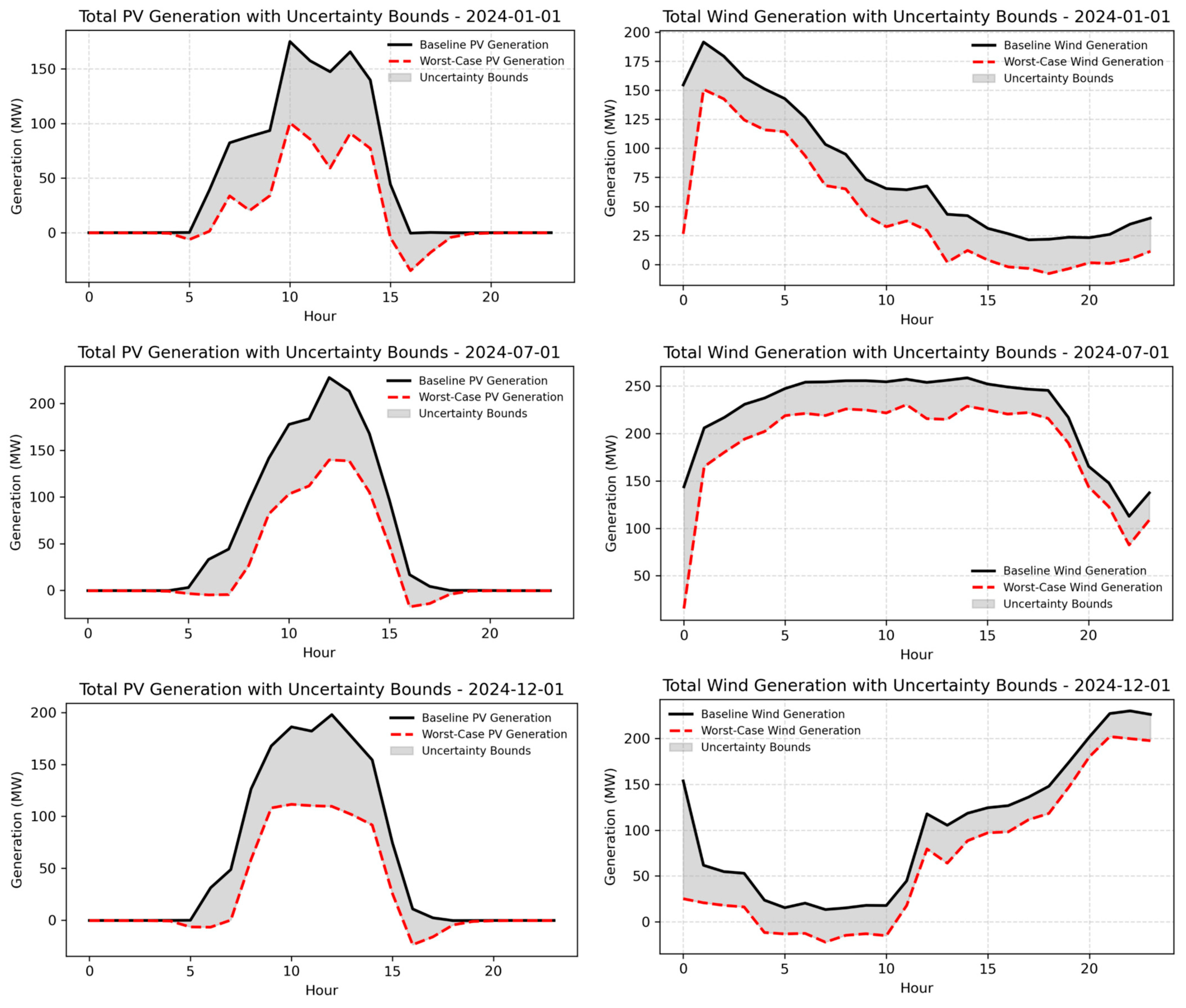
4.2.2. Uncertainty Characterization
4.2.3. Optimization Results
4.2.4. Benchmark Comparison with Stochastic and Robust Models
4.2.5. Sensitivity to Wasserstein Radius, Cost-Scaling Parameter, and Percentile Bounds
4.2.6. Computational Performance and Scalability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | Symbol | Description |
| Set of time periods (hours) | Battery state-of-charge at end of hour (%) | ||
| Set of thermal generators | Battery charging power at hour (MW) | ||
| Set of buses | Battery discharging power at hour (MW) | ||
| Set of directed network lines | Marginal cost of generator (MWh) | ||
| Set of preferred battery charging hours | Load-shedding penalty cost (USD/MWh) | ||
| Set of preferred battery discharging hours | Demand-response cost coefficient at bus () | ||
| Set of renewable resources (wind and PV) | BESS charging/discharging incentives () | ||
| Set of demand resources | Maximum/minimum capacity of generator (MW) | ||
| Set of all uncertain resources () | Ramp-up/down limits of generator (MW/h) | ||
| Power output of generator at hour (MW) | Minimum up-time/down-time of generator | ||
| Binary on/off status of generator at hour | Battery round-trip efficiency | ||
| Binary startup indicator for generator at hour | Maximum BESS charge/discharge rates (MW) | ||
| Binary shutdown indicator for generator at hour | Reactance of line (pu) | ||
| Load shedding at bus , hour (MW) | Susceptance of line () (pu) | ||
| collector area at bus | Thermal limit of line (i,j) (MW) | ||
| Binary battery mode at hour ( charge, discharge) | Cut-in/rated/cut-out wind speeds at bus (m/s) | ||
| Power flow on line () at hour (MW) | Rated wind capacity at bus (MW) | ||
| Voltage-phase angle at bus , hour (rad) | PV module efficiency | ||
| Demand deviation recourse at bus hour (MW) | Nameplate PV capacity at bus (MW) | ||
| Renewable deviation recourse at bus , hour (MW) | DR adjustment Min and Max bounds at bus (MW) | ||
| Dual multiplier for Wasserstein-ball radius | Minimum uncertainty margin (MW) | ||
| Auxiliary dual variable for DRO at hour | Wasserstein-ball radius (MW) | ||
| Demand-response adjustment at bus and hour t (MW) | Ground-metric (transport) scale in the chosen cost used for the Wasserstein distance | ||
| Number of validation residual samples | Forecast residual of resource at hour (MW) | ||
| Wasserstein ambiguity set | Empirical -quantile operator | ||
| Empirical distribution of residuals | Forecast demand at bus hour (MW) |
Appendix A
Appendix A.1. Derivation of the Surrogate Dual Reformulation
Appendix A.2. Choice of Recourse Loss and Ground Metric
Appendix A.3. Surrogate Reformulation
Appendix A.4. Interpretation
- is the dual variable associated with the Wasserstein radius, penalizing the distance from the empirical distribution.
- controls the size of the ambiguity set: larger values increase conservatism.
- is the transport-cost scale in the ground metric: larger values enforce stricter penalties on deviations, also increasing conservatism.
- are auxiliary variables bounding the worst-case deviation cost at each time t.
References
- Cavus, M. Advancing Power Systems with Renewable Energy and Intelligent Technologies: A Comprehensive Review on Grid Transformation and Integration. Electronics 2025, 14, 1159. [Google Scholar] [CrossRef]
- Ghahramani, M.; Habibi, D.; Ghamari, S.; Aziz, A. Optimal Operation of an Islanded Hybrid Energy System Integrating Power and Gas Systems. IEEE Access 2024, 12, 196591–196608. [Google Scholar] [CrossRef]
- Soleimani, H.; Habibi, D.; Ghahramani, M.; Aziz, A. Strengthening power systems for net zero: A review of the role of synchronous condensers and emerging challenges. Energies 2024, 17, 3291. [Google Scholar] [CrossRef]
- Ghahramani, M.; Sadat-Mohammadi, M.; Nazari-Heris, M.; Asadi, S.; Mohammadi-Ivatloo, B. Introduction and literature review of the operation of multi-carrier energy networks. In Planning and Operation of Multi-Carrier Energy Networks; Springer: Berlin/Heidelberg, Germany, 2021; pp. 39–57. [Google Scholar]
- Ghahramani, M.; Habibi, D.; Ghamari, S.; Soleimani, H.; Aziz, A. Renewable-Based Isolated Power Systems: A Review of Scalability, Reliability, and Uncertainty Modeling. Clean Technol. 2025, 7, 80. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, Y.; Zhang, S.; Guo, Y.; Sun, H. Multi-objective robust optimization of integrated energy system with hydrogen energy storage. Energies 2024, 17, 1132. [Google Scholar] [CrossRef]
- Liang, J.; Miao, J.; Sun, L.; Zhao, L.; Wu, J.; Du, P.; Cao, G.; Zhao, W. Supply–Demand Dynamics Quantification and Distributionally Robust Scheduling for Renewable-Integrated Power Systems with Flexibility Constraints. Energies 2025, 18, 1181. [Google Scholar] [CrossRef]
- Lu, G.; Yuan, B.; Nie, B.; Xia, P.; Wu, C.; Sun, G. Enhanced dynamic expansion planning model incorporating Q-Learning and distributionally robust optimization for resilient and Cost-Efficient distribution networks. Energies 2025, 18, 1020. [Google Scholar] [CrossRef]
- Cai, P.; Wen, C.; Cao, B.; Qiao, J. A Wasserstein metric distributionally robust chance-constrained peer aggregation energy sharing mechanism for hydrogen-based microgrids considering low-carbon drivers. Energy 2025, 325, 136178. [Google Scholar] [CrossRef]
- Hao, J.; Guo, X.; Li, Y.; Wu, T. Uncertain scheduling of the power system based on wasserstein distributionally robust optimization and improved differential evolution algorithm. Energies 2024, 17, 3846. [Google Scholar] [CrossRef]
- Yin, C.; Dong, J.; Zhang, Y. Distributionally Robust Bilevel Optimization Model for Distribution Network with Demand Response under Uncertain Renewables Using Wasserstein Metrics. IEEE Trans. Sustain. Energy 2024, 16, 1165–1176. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, H.; Zhang, S.; Cheng, H.; Chen, F.; Wang, Z.; Zhang, X. A multi-scenario distributionally robust model for resilience-oriented offshore wind farms and transmission network integrated planning considering typhoon disasters. Appl. Energy 2025, 392, 125937. [Google Scholar] [CrossRef]
- Singh, U.; Rizwan, M.; Alaraj, M.; Alsaidan, I. A machine learning-based gradient boosting regression approach for wind power production forecasting: A step towards smart grid environments. Energies 2021, 14, 5196. [Google Scholar] [CrossRef]
- Ghahramani, M.; Nazari-Heris, M.; Zare, K.; Mohammadi-ivatloo, B. Robust short-term scheduling of smart distribution systems considering renewable sources and demand response programs. In Robust Optimal Planning and Operation of Electrical Energy Systems; Springer: Berlin/Heidelberg, Germany, 2019; pp. 253–270. [Google Scholar]
- Ghahramani, M.; Nazari-Heris, M.; Zare, K.; Mohammadi-Ivatloo, B. Energy and reserve management of a smart distribution system by incorporating responsive-loads/battery/wind turbines considering uncertain parameters. Energy 2019, 183, 205–219. [Google Scholar] [CrossRef]
- Ghahramani, M.; Habibi, D.; Ghamari, S.; Aziz, A.; Ghahramani, M.; Habibi, D.; Ghamari, S.; Aziz, A. Addressing Uncertainty in Renewable Energy Integration for Western Australia’s Mining Sector: A Robust Optimization Approach. Energies 2024, 17, 5679. [Google Scholar] [CrossRef]
- Khaloie, H.; Dolanyi, M.; Toubeau, J.-F.; Vallée, F. Review of machine learning techniques for optimal power flow. Appl. Energy 2025, 388, 125637. [Google Scholar] [CrossRef]
- Jamal, R.; Khan, N.H.; Ebeed, M.; Zeinoddini-Meymand, H.; Shahnia, F. An improved pelican optimization algorithm for solving stochastic optimal power flow problem of power systems considering uncertainty of renewable energy resources. Results Eng. 2025, 26, 104553. [Google Scholar] [CrossRef]
- Ghahramani, M.; Heris, M.N.; Zare, K.; Ivatloo, B.M. Robust Optimization of Renewable Energy Based Distribution Networks Considering Electrical Energy Storage and Fuel Cell. In Proceedings of the Electrical Engineering (ICEE), Iranian Conference on, Mashhad, Iran, 8–10 May 2018; pp. 1343–1349. [Google Scholar]
- Shui, Y.; Gao, H.; Wang, L.; Wei, Z.; Liu, J. A data-driven distributionally robust coordinated dispatch model for integrated power and heating systems considering wind power uncertainties. Int. J. Electr. Power Energy Syst. 2019, 104, 255–258. [Google Scholar] [CrossRef]
- Zhang, S.; Qiu, G.; Liu, Y.; Ding, L.; Shui, Y.; Zhang, S.; Qiu, G.; Liu, Y.; Ding, L.; Shui, Y. Data-Driven Distributionally Robust Optimization-Based Coordinated Dispatching for Cascaded Hydro-PV-PSH Combined System. Electronics 2024, 13, 667. [Google Scholar] [CrossRef]
- Zhou, Y.; Hou, H.; Yan, H.; Wang, X.; Zhou, R. Data-driven distributionally robust stochastic optimal dispatching method of integrated energy system considering multiple uncertainties. Energy 2025, 325, 136104. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Shahidehpour, M.; Li, J.; Long, C. Data-driven distributionally robust scheduling of community integrated energy systems with uncertain renewable generations considering integrated demand response. Appl. Energy 2023, 335, 120749. [Google Scholar] [CrossRef]
- Liu, H.; Qiu, J.; Zhao, J. A data-driven scheduling model of virtual power plant using Wasserstein distributionally robust optimization. Int. J. Electr. Power Energy Syst. 2022, 137, 107801. [Google Scholar] [CrossRef]
- Saberi, H.; Zhang, C.; Dong, Z.Y. Data-driven distributionally robust hierarchical coordination for home energy management. IEEE Trans. Smart Grid 2021, 12, 4090–4101. [Google Scholar] [CrossRef]
- Parvar, S.S.; Nazaripouya, H. Optimal Operation of Battery Energy Storage Under Uncertainty Using Data-Driven Distributionally Robust Optimization. Electr. Power Syst. Res. 2022, 211, 108180. [Google Scholar] [CrossRef]
- Li, H.; Lu, X.; Zhou, K.; Shao, Z. Distributionally robust optimal dispatching method for integrated energy system with concentrating solar power plant. Renew. Energy 2024, 229, 120792. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Z.; Chen, S. Optimal low-carbon operation of regional integrated energy systems: A data-driven hybrid stochastic-distributionally robust optimization approach. Sustain. Energy Grids Netw. 2023, 34, 101013. [Google Scholar] [CrossRef]
- Han, J.; Han, K.; Han, T.; Wang, Y.; Han, Y.; Lin, J. Data-driven distributionally robust optimization of low-carbon data center energy systems considering multi-task response and renewable energy uncertainty. J. Build. Eng. 2025, 102, 111937. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, T.; Liu, Y.; Feng, Y.; Wang, R.; Huang, S. Energy management of multi-microgrid system with renewable energy using data-driven distributionally robust optimization. Int. J. Green Energy 2024, 21, 2699–2711. [Google Scholar] [CrossRef]
- Zhang, X.; Ge, S.; Liu, H.; Zhou, Y.; He, X.; Xu, Z. Distributionally robust optimization for peer-to-peer energy trading considering data-driven ambiguity sets. Appl. Energy 2023, 331, 120436. [Google Scholar] [CrossRef]
- Li, J.; Khodayar, M.E.; Wang, J.; Zhou, B. Data-driven distributionally robust co-optimization of P2P energy trading and network operation for interconnected microgrids. IEEE Trans. Smart Grid 2021, 12, 5172–5184. [Google Scholar] [CrossRef]
- Duan, C.; Jiang, L.; Fang, W.; Liu, J.; Liu, S. Data-driven distributionally robust energy-reserve-storage dispatch. IEEE Trans. Ind. Inform. 2017, 14, 2826–2836. [Google Scholar] [CrossRef]
- Wang, H.; Yi, Z.; Xu, Y.; Cai, Q.; Li, Z.; Wang, H.; Bai, X. Data-driven distributionally robust optimization approach for the coordinated dispatching of the power system considering the correlation of wind power. Electr. Power Syst. Res. 2024, 230, 110224. [Google Scholar] [CrossRef]
- Gurumoorthi, G.; Senthilkumar, S.; Karthikeyan, G.; Alsaif, F.; Gurumoorthi, G.; Senthilkumar, S.; Karthikeyan, G.; Alsaif, F. A hybrid deep learning approach to solve optimal power flow problem in hybrid renewable energy systems. Sci. Rep. 2024, 14, 19377. [Google Scholar] [CrossRef] [PubMed]
- Hasanien, H.M.; Alsaleh, I.; Ullah, Z.; Alassaf, A. Probabilistic optimal power flow in power systems with Renewable energy integration using Enhanced walrus optimization algorithm. Ain Shams Eng. J. 2024, 15, 102663. [Google Scholar] [CrossRef]
- Mouassa, S.; Alateeq, A.; Alassaf, A.; Bayindir, R.; Alsaleh, I.; Jurado, F. Optimal power flow analysis with renewable energy resource uncertainty using dwarf mongoose optimizer: Case of ADRAR isolated electrical network. IEEE Access 2024, 12, 10202–10218. [Google Scholar] [CrossRef]
- Mahmoodi, M.; RA, S.M.N.; Blackhall, L.; Scott, P. A comparison on power flow models for optimal power flow studies in integrated medium-low voltage unbalanced distribution systems. Sustain. Energy Grids Netw. 2024, 38, 101339. [Google Scholar] [CrossRef]
- Dai, X.; Zhai, J.; Jiang, Y.; Guo, Y.; Jones, C.N.; Hagenmeyer, V. Advancing distributed AC optimal power flow for integrated transmission-distribution systems. IEEE Trans. Netw. Sci. Eng. 2025, 12, 1210–1223. [Google Scholar] [CrossRef]
- Tiwari, D.; Zideh, M.J.; Talreja, V.; Verma, V.; Solanki, S.K.; Solanki, J. Power flow analysis using deep neural networks in three-phase unbalanced smart distribution grids. IEEE Access 2024, 12, 29959–29970. [Google Scholar] [CrossRef]
- Hussan, U.; Wang, H.; Ayub, M.A.; Rasheed, H.; Majeed, M.A.; Peng, J.; Jiang, H. Decentralized stochastic recursive gradient method for fully decentralized OPF in multi-area power systems. Mathematics 2024, 12, 3064. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, C.; Xu, Y.; Zhang, Y.; Sun, H. Statistical machine learning for power flow analysis considering the influence of weather factors on photovoltaic power generation. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 5348–5362. [Google Scholar] [CrossRef]
- Zhao, Y.; Gan, W.; Yan, M.; Wen, J.; Zhou, Y. A scalable stochastic scheme for identifying critical substations considering the epistemic uncertainty of contingency in power systems. Appl. Energy 2025, 381, 125119. [Google Scholar] [CrossRef]
- Guo, Y.; Baker, K.; Dall’Anese, E.; Hu, Z.; Summers, T.H. Data-based distributionally robust stochastic optimal power flow—Part I: Methodologies. IEEE Trans. Power Syst. 2018, 34, 1483–1492. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Ma, J.; Li, D.; Zhang, W. Distributionally robust optimal dispatching method of integrated electricity and heating system based on improved Wasserstein metric. Int. J. Electr. Power Energy Syst. 2023, 151, 109120. [Google Scholar] [CrossRef]
- Zhai, J.; Wang, S.; Guo, L.; Jiang, Y.; Kang, Z.; Jones, C.N. Data-driven distributionally robust joint chance-constrained energy management for multi-energy microgrid. Appl. Energy 2022, 326, 119939. [Google Scholar] [CrossRef]
- Wang, H.; Bie, Z. Data-Driven Distributionally Robust Energy and Reserve Scheduling Considering RES Flexibility. IEEE Trans. Power Syst. 2024, 40, 2438–2450. [Google Scholar] [CrossRef]
- Liu, L.; Hu, Z.; Duan, X.; Pathak, N. Data-driven distributionally robust optimization for real-time economic dispatch considering secondary frequency regulation cost. IEEE Trans. Power Syst. 2021, 36, 4172–4184. [Google Scholar] [CrossRef]
- Zishan, F.; Akbari, E.; Montoya, O.D. Analysis of probabilistic optimal power flow in the power system with the presence of microgrid correlation coefficients. Cogent Eng. 2024, 11, 2292325. [Google Scholar] [CrossRef]
- ALAhmad, A.K.; Verayiah, R.; Ramasamy, A.; Shareef, H. Enhancing optimization accuracy in power systems: Investigating correlation effects on objective function values. Results Eng. 2024, 22, 102351. [Google Scholar] [CrossRef]
- Shah, A.A.; Wang, S.C.; Liu, G.; Hassan, R.U.; Nawaz, A. Scenario Based Optimal Power Flow Evaluation for Wind Power Allocation Capacity in Modern Power Systems. IEEE Access 2025, 13, 38443–38453. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, S. Stochastic two-stage multi-objective unit commitment of distributed resource energy systems considering uncertainties and unit failures. Reliab. Eng. Syst. Saf. 2025, 253, 110520. [Google Scholar] [CrossRef]
- Jain, T.; Verma, K. Reliability enhancement with coordinated operation of wind power and battery energy storage using machine learning based unit commitment decision. J. Energy Storage 2025, 111, 115455. [Google Scholar] [CrossRef]
- Taheri, B.; Molzahn, D.K. Optimizing parameters of the DC power flow. Electr. Power Syst. Res. 2024, 235, 110719. [Google Scholar] [CrossRef]
- Subcommittee, P.M. IEEE reliability test system. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 2047–2054. [Google Scholar] [CrossRef]
- Bracken, C.; Underwood, S.; Campbell, A.; Thurber, T.B.; Voisin, N. Hourly Wind and Solar Generation Profiles for Every EIA 2020 Plant in the CONUS; Zenodo: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Interconnection, P. Hourly Load: Metered. Available online: https://dataminer2.pjm.com/feed/hrl_load_metered (accessed on 10 July 2025).
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Hart, W.E.; Laird, C.D.; Watson, J.-P.; Woodruff, D.L.; Hackebeil, G.A.; Nicholson, B.L.; Siirola, J.D. Pyomo-Optimization Modeling in Python; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Gurobi Optimization LLC. Gurobi Optimizer Reference Manual; Gurobi Optimization LLC: Beaverton, OR, USA, 2023. [Google Scholar]

| Ref. | Methodology | Uncertainty Model | System/Application | Constraints & Focus | Approach |
|---|---|---|---|---|---|
| [44] | Multi-stage DRO | Wasserstein Ambiguity Set | Transmission & Distribution Systems | Risk (CVaR), Reserve Policies, OPF Control Policies | Modeling of historical forecast errors |
| [33] | DRO | Data-driven Ambiguity Set | Transmission System (IEEE 118) | Energy-Reserve-Storage Co-dispatch | Based on historical data |
| [47] | DDRO-Chance constraint | Data-driven Uncertainty Model | General Power System | Economic Dispatch, Reliability | Modeling variation ranges and distributions |
| [34] | DDRO | Scenario Clustering | Transmission System (IEEE 30, 118) | UC, Spatial Correlations | Data-driven scenario clustering |
| [48] | DDRO | Wasserstein Metric | Real-Time Economic Dispatch | Automatic Generation Control, Frequency Regulation Constraints | Copula-based modeling of correlated signals |
| [45] | DRO | Improved Wasserstein Metric | Transmission System (IEEE 118) | Optimal Dispatch, Electric vehicles Uncertainty | Based on extreme scenarios for efficiency |
| [35] | Metaheuristic | N/A | Transmission System (IEEE 30) | OPF (Fuel cost, loss, voltage deviation) | Deep Reinforcement Learning Algorithm |
| [49] | Probabilistic Analysis | Probabilistic Distributions | Transmission System (IEEE 30) | Probabilistic OPF | N/A |
| [36] | Metaheuristic | N/A | Transmission System (IEEE 30, 118) | Probabilistic OPF | Evolutionary Whale Optimization Algorithm |
| [37] | Metaheuristic | Stochastic OPF | Transmission System (IEEE 30) | Stochastic OPF, Reserve/Penalty Costs | Discrete Multi-Objective Algorithm |
| [50] | Stochastic Simulation | Monte Carlo | Transmission System (30, 57, 118) | OPF, Modeling variable correlations | N/A |
| [51] | Stochastic OPF | Scenario-based | Transmission Grid | OPF, Reserve Management, Curtailment Minimization | Gaussian Distribution Forecasting Model for advanced forecasting |
| [43] | Stochastic Tri-level | Epistemic Uncertainty (Failures) | Transmission System (IEEE 24, 118) | Reliability, Cascading Failures, Criticality Analysis | N/A |
| [39] | Distributed Optimization | Deterministic | Integrated Trans.-Dist. System | AC OPF, Scalability | ‘aladin’ Algorithm |
| From Bus | To Bus | r (p.u.) | x (p.u.) | b (p.u.) | Limit (MW) |
|---|---|---|---|---|---|
| 1 | 2 | 0.0026 | 0.0139 | 0.4611 | 175 |
| 1 | 3 | 0.0546 | 0.2112 | 0.0572 | 175 |
| 1 | 5 | 0.0218 | 0.0845 | 0.0229 | 175 |
| 2 | 4 | 0.0328 | 0.1267 | 0.0343 | 175 |
| 2 | 6 | 0.0497 | 0.192 | 0.052 | 175 |
| 3 | 9 | 0.0308 | 0.119 | 0.0322 | 175 |
| 3 | 24 | 0.0023 | 0.0839 | 0.0 | 400 |
| 4 | 9 | 0.0268 | 0.1037 | 0.0281 | 175 |
| 5 | 10 | 0.0228 | 0.0883 | 0.0239 | 175 |
| 6 | 10 | 0.0139 | 0.0605 | 2.459 | 175 |
| 7 | 8 | 0.0159 | 0.0614 | 0.0166 | 175 |
| 8 | 9 | 0.0427 | 0.1651 | 0.0447 | 175 |
| 8 | 10 | 0.0427 | 0.1651 | 0.0447 | 175 |
| 9 | 11 | 0.0023 | 0.0839 | 0.0 | 400 |
| 9 | 12 | 0.0023 | 0.0839 | 0.0 | 400 |
| 10 | 11 | 0.0023 | 0.0839 | 0.0 | 400 |
| 10 | 12 | 0.0023 | 0.0839 | 0.0 | 400 |
| 11 | 13 | 0.0061 | 0.0476 | 0.0999 | 500 |
| 11 | 14 | 0.0054 | 0.0418 | 0.0879 | 500 |
| 12 | 13 | 0.0061 | 0.0476 | 0.0999 | 500 |
| 12 | 23 | 0.0124 | 0.0966 | 0.203 | 500 |
| 13 | 23 | 0.0111 | 0.0865 | 0.1818 | 500 |
| 14 | 16 | 0.0050 | 0.0389 | 0.0818 | 500 |
| 15 | 16 | 0.0022 | 0.0173 | 0.0364 | 500 |
| 15 | 21 | 0.00315 | 0.0245 | 0.206 | 1000 |
| 15 | 24 | 0.0067 | 0.0519 | 0.1091 | 500 |
| 16 | 17 | 0.0033 | 0.0259 | 0.0545 | 500 |
| 16 | 19 | 0.0030 | 0.0231 | 0.0485 | 500 |
| 17 | 18 | 0.0018 | 0.0144 | 0.0303 | 500 |
| 17 | 22 | 0.0135 | 0.1053 | 0.2212 | 500 |
| 18 | 21 | 0.00165 | 0.01295 | 0.109 | 1000 |
| 19 | 20 | 0.00255 | 0.0198 | 0.1666 | 1000 |
| 20 | 23 | 0.0014 | 0.0108 | 0.091 | 1000 |
| 21 | 22 | 0.0087 | 0.0678 | 0.1424 | 500 |
| Gen | Pmax (MW) | Pmin (MW) | RampUp (MW/h) | RampDown (MW/h) | MinUp (h) | MinDown (h) | b ($/MWh) | c ($) | CostsD ($) | Costst ($) | cp (Bus) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| g1 | 400 | 100 | 50 | 50 | 3 | 2 | 5.47 | 54.7 | 0 | 0 | 18 |
| g2 | 400 | 100 | 50 | 50 | 3 | 2 | 5.47 | 54.7 | 0 | 0 | 21 |
| g3 | 152 | 30.4 | 30 | 30 | 3 | 2 | 13.32 | 133.2 | 1430.4 | 1430.4 | 1 |
| g4 | 152 | 30.4 | 30 | 30 | 3 | 2 | 13.32 | 133.2 | 1430.4 | 1430.4 | 2 |
| g5 | 155 | 54.25 | 25 | 25 | 3 | 2 | 16 | 16 | 0 | 0 | 15 |
| g6 | 155 | 54.25 | 25 | 25 | 3 | 2 | 10.52 | 105.2 | 312 | 312 | 16 |
| g7 | 310 | 108.5 | 40 | 40 | 3 | 2 | 10.52 | 105.2 | 624 | 624 | 23 |
| g8 | 350 | 140 | 40 | 40 | 3 | 2 | 10.89 | 108.9 | 2298 | 2298 | 23 |
| g9 | 350 | 75 | 20 | 20 | 3 | 2 | 20.7 | 207 | 1725 | 1725 | 7 |
| g10 | 350 | 206.85 | 20 | 20 | 3 | 2 | 20.93 | 209.3 | 3056.7 | 3056.7 | 13 |
| g11 | 60 | 12 | 10 | 10 | 3 | 2 | 26.11 | 261.1 | 437 | 437 | 15 |
| g12 | 300 | 0 | 15 | 15 | 3 | 2 | 0 | 0 | 0 | 0 | 22 |
| Resource/Demand | Validation MAE (MW) | Validation RMSE (MW) | Test MAE (MW) | Test RMSE (MW) |
|---|---|---|---|---|
| Bus 13 Wind | 7.838 | 12.975 | 7.998 | 13.315 |
| Bus 21 Wind | 7.364 | 11.946 | 7.688 | 12.714 |
| Bus 10 PV | 6.381 | 14.911 | 6.002 | 14.098 |
| Bus 19 PV | 4.097 | 9.554 | 3.970 | 9.411 |
| Demand Bus 1 | 0.879 | 1.365 | 0.840 | 1.258 |
| Demand Bus 2 | 0.544 | 0.890 | 0.585 | 1.030 |
| Demand Bus 3 | 1.334 | 1.842 | 1.354 | 1.935 |
| Demand Bus 4 | 0.442 | 0.709 | 0.470 | 0.814 |
| Demand Bus 5 | 0.405 | 0.600 | 0.493 | 0.795 |
| Demand Bus 6 | 0.805 | 1.302 | 0.840 | 1.370 |
| Demand Bus 7 | 0.836 | 1.333 | 0.870 | 1.374 |
| Demand Bus 8 | 0.760 | 1.337 | 0.795 | 1.353 |
| Demand Bus 9 | 0.996 | 1.517 | 1.105 | 1.847 |
| Demand Bus 10 | 1.135 | 1.731 | 1.226 | 1.972 |
| Demand Bus 13 | 1.672 | 2.746 | 2.251 | 4.092 |
| Demand Bus 14 | 1.436 | 2.424 | 1.444 | 2.342 |
| Demand Bus 15 | 1.712 | 2.624 | 1.850 | 2.987 |
| Demand Bus 16 | 0.832 | 1.356 | 0.844 | 1.292 |
| Demand Bus 18 | 3.363 | 4.640 | 3.794 | 6.252 |
| Demand Bus 19 | 1.147 | 1.761 | 1.159 | 1.750 |
| Demand Bus 20 | 0.778 | 1.243 | 0.832 | 1.307 |
| Resource/Demand | Capacity/Mean (MW) | MAE (MW) | MAE % | RMSE (MW) | RMSE % |
|---|---|---|---|---|---|
| Bus 13 Wind | 150 | 8.0 | 5.3 | 13.3 | 8.9 |
| Bus 21 Wind | 150 | 7.7 | 5.1 | 12.7 | 8.5 |
| Bus 10 PV | 200 | 6.0 | 3.0 | 14.1 | 7.1 |
| Bus 19 PV | 100 | 4.0 | 4.0 | 9.4 | 9.4 |
| Demand Bus 1 | 75 | 0.8 | 1.1 | 1.3 | 1.7 |
| Demand Bus 2 | 97 | 0.6 | 0.6 | 1.0 | 1.0 |
| Demand Bus 3 | 180 | 1.4 | 0.8 | 1.9 | 1.1 |
| Demand Bus 4 | 74 | 0.5 | 0.7 | 0.8 | 1.1 |
| Demand Bus 5 | 71 | 0.5 | 0.7 | 0.8 | 1.1 |
| Demand Bus 6 | 136 | 0.8 | 0.6 | 1.4 | 1.0 |
| Demand Bus 7 | 125 | 0.9 | 0.7 | 1.4 | 1.1 |
| Demand Bus 8 | 171 | 0.8 | 0.5 | 1.4 | 0.8 |
| Demand Bus 9 | 175 | 1.1 | 0.6 | 1.8 | 1.0 |
| Demand Bus 10 | 195 | 1.2 | 0.6 | 2.0 | 1.0 |
| Demand Bus 13 | 265 | 2.3 | 0.9 | 4.1 | 1.5 |
| Demand Bus 14 | 194 | 1.4 | 0.7 | 2.3 | 1.2 |
| Demand Bus 15 | 317 | 1.9 | 0.6 | 3.0 | 0.9 |
| Demand Bus 16 | 100 | 0.8 | 0.8 | 1.3 | 1.3 |
| Demand Bus 18 | 160 | 3.8 | 2.4 | 6.3 | 3.9 |
| Demand Bus 19 | 181 | 1.2 | 0.7 | 1.8 | 1.0 |
| Demand Bus 20 | 128 | 0.8 | 0.6 | 1.3 | 1.0 |
| Resource | Min Delta | Max Delta | Avg. Delta | Std. Dev. |
|---|---|---|---|---|
| Bus 13 Wind | 12.06 | 70.57 | 17.89 | 13.45 |
| Bus 21 Wind | 9.90 | 65.30 | 16.20 | 12.10 |
| Bus 10 PV | 0.05 | 45.20 | 10.30 | 9.80 |
| Bus 19 PV | 0.05 | 22.10 | 5.60 | 4.90 |
| Demands (Avg.) | 0.74 | 4.70 | 1.82 | 0.62 |
| Date 2024 | Total Cost ($) | DG Generation (MW) | Renewable Actual (MW) | Renewable Forecast (MW) | Renewable Diff. (MW) | Demand Actual (MW) | Demand Forecast (MW) | Demand Diff. (MW) | Renew. Exceedance (%) | Demand Exceedance (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 January | 280,551 | 28,004 | 2828 | 3042 | −214 | 28,442 | 28,509 | −66 | 2.0 | 20.5 |
| 1 February | 284,436 | 28,392 | 4798 | 4813 | −15 | 30,857 | 30,669 | 188 | 17.7 | 7.6 |
| 1 March | 292,834 | 29,232 | 5025 | 4851 | 174 | 31,643 | 31,546 | 97 | 10.4 | 11.7 |
| 1 April | 267,908 | 26,739 | 7315 | 7187 | 128 | 31,658 | 31,389 | 268 | 9.3 | 11.0 |
| 1 May | 279,506 | 27,899 | 7465 | 7232 | 233 | 32,840 | 32,595 | 246 | 10.4 | 22.3 |
| 1 June | 299,927 | 29,941 | 3418 | 3491 | −73 | 30,908 | 30,895 | 13 | 13.5 | 23.7 |
| 1 July | 253,129 | 25,261 | 6739 | 6758 | −19 | 29,319 | 29,483 | −164 | 25.0 | 19.1 |
| 1 August | 273,628 | 27,311 | 5849 | 6115 | −267 | 30,878 | 30,890 | −12 | 14.5 | 13.2 |
| 1 September | 300,514 | 30,000 | 3318 | 3463 | −146 | 30,906 | 30,927 | −21 | 21.8 | 14.9 |
| 1 October | 272,327 | 27,181 | 5893 | 5768 | 125 | 30,489 | 30,412 | 77 | 18.7 | 12.9 |
| 1 November | 274,825 | 27,431 | 5473 | 5506 | −33 | 30,505 | 30,401 | 104 | 20.8 | 16.4 |
| 1 December | 289,354 | 28,884 | 3926 | 3783 | 143 | 30,102 | 30,130 | −29 | 15.6 | 22.3 |
| Method | Avg. Daily Cost (USD) | Avg. Renewable Exceedance (%) | Avg. Demand Exceedance (%) | Remarks |
|---|---|---|---|---|
| Deterministic | 265,000 | 22.0 | 20.5 | Lowest cost, poor reliability |
| Stochastic | 278,000 | 17.0 | 16.8 | Moderate improvement |
| Γ-Robust | 305,000 | 11.5 | 11.0 | Reliable but costly |
| Proposed DDRO | 289,000 | 14.8 | 15.9 | Balanced trade-off |
| ε | Avg. Daily Cost (USD) | Renew. Exceedance (%) | Demand Exceedance (%) | Avg. Runtime (min) | Remarks | |
|---|---|---|---|---|---|---|
| 0.5 | 0.05 | 276,000 | 19.8 | 20.2 | 3.1 | Optimistic, low cost, low reliability |
| 1.0 | 0.05 | 289,000 | 14.8 | 15.9 | 3.4 | Balanced |
| 2.0 | 0.05 | 304,000 | 11.6 | 12.2 | 3.7 | Very conservative, costly |
| 1.0 | 0.02 | 285,000 | 17.9 | 18.2 | 3.2 | Smaller weakens robustness |
| 1.0 | 0.10 | 295,000 | 13.2 | 13.7 | 3.8 | Larger enforces stricter protection |
| Percentile Bounds | Avg. Daily Cost (USD) | Renew. Exceedance (%) | Demand Exceedance (%) | Remarks |
|---|---|---|---|---|
| 10th–90th | 277,000 | 19.6 | 19.2 | Narrow bounds: lower cost, weaker protection |
| 5th–95th | 289,000 | 14.8 | 15.9 | Balanced trade-off |
| 2.5th–97.5th | 296,000 | 13.4 | 13.7 | Wide bounds: higher cost, stronger protection |
| Date (2024) | Solution Time (s) | Date (2024) | Solution Time (s) |
|---|---|---|---|
| 1 January | 87 | 1 July | 126 |
| 1 February | 91 | 1 August | 96 |
| 1 March | 103 | 1 September | 118 |
| 1 April | 85 | 1 October | 92 |
| 1 May | 112 | 1 November | 101 |
| 1 June | 129 | 1 December | 108 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghahramani, M.; Habibi, D.; Aziz, A. A Risk-Averse Data-Driven Distributionally Robust Optimization Method for Transmission Power Systems Under Uncertainty. Energies 2025, 18, 5245. https://doi.org/10.3390/en18195245
Ghahramani M, Habibi D, Aziz A. A Risk-Averse Data-Driven Distributionally Robust Optimization Method for Transmission Power Systems Under Uncertainty. Energies. 2025; 18(19):5245. https://doi.org/10.3390/en18195245
Chicago/Turabian StyleGhahramani, Mehrdad, Daryoush Habibi, and Asma Aziz. 2025. "A Risk-Averse Data-Driven Distributionally Robust Optimization Method for Transmission Power Systems Under Uncertainty" Energies 18, no. 19: 5245. https://doi.org/10.3390/en18195245
APA StyleGhahramani, M., Habibi, D., & Aziz, A. (2025). A Risk-Averse Data-Driven Distributionally Robust Optimization Method for Transmission Power Systems Under Uncertainty. Energies, 18(19), 5245. https://doi.org/10.3390/en18195245










