PV Cell Temperature Prediction Under Various Atmospheric Conditions †
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model
- -
- Tempered glass cover;
- -
- Ethylene-vinyl acetate (EVA);
- -
- Solar cells and bus-bars;
- -
- Tedlar film.
2.2. Model Validation
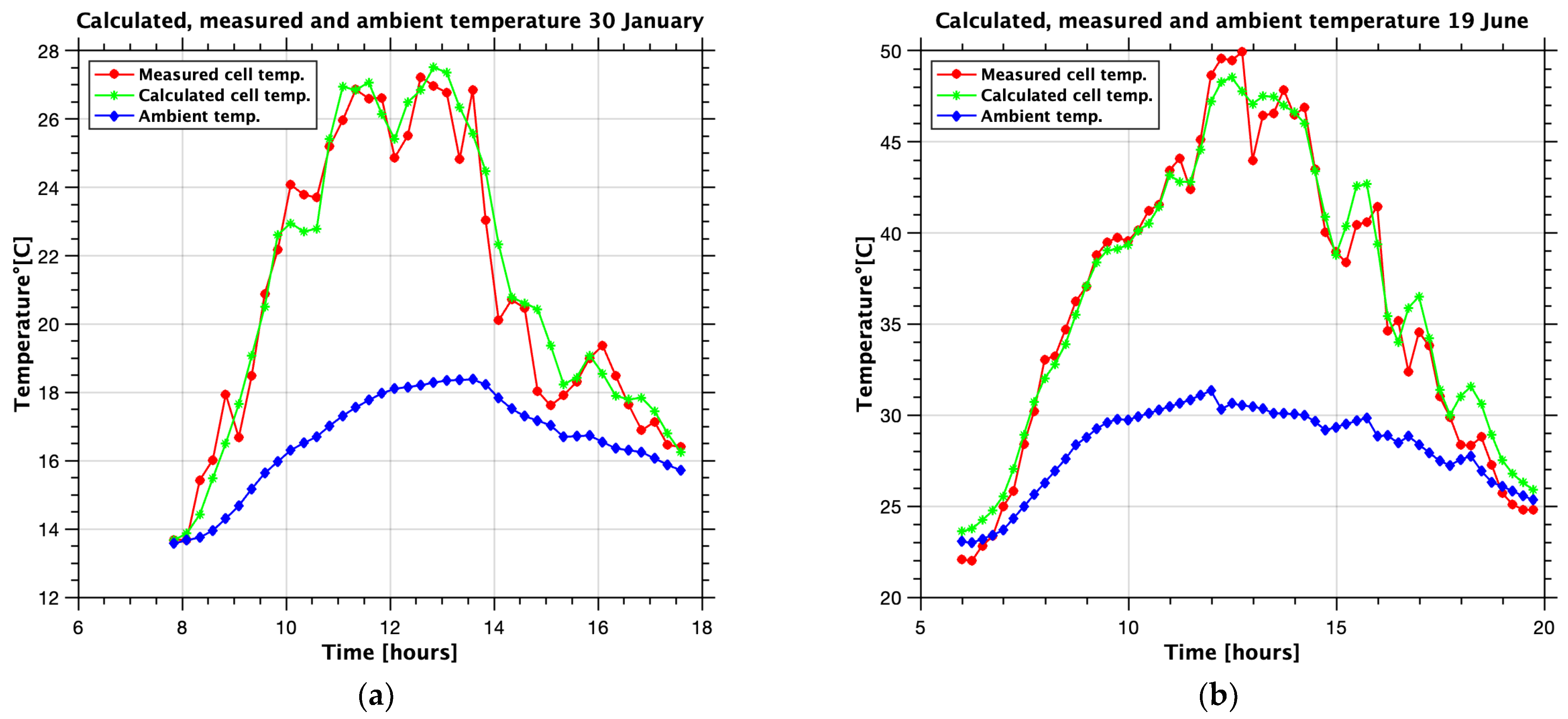
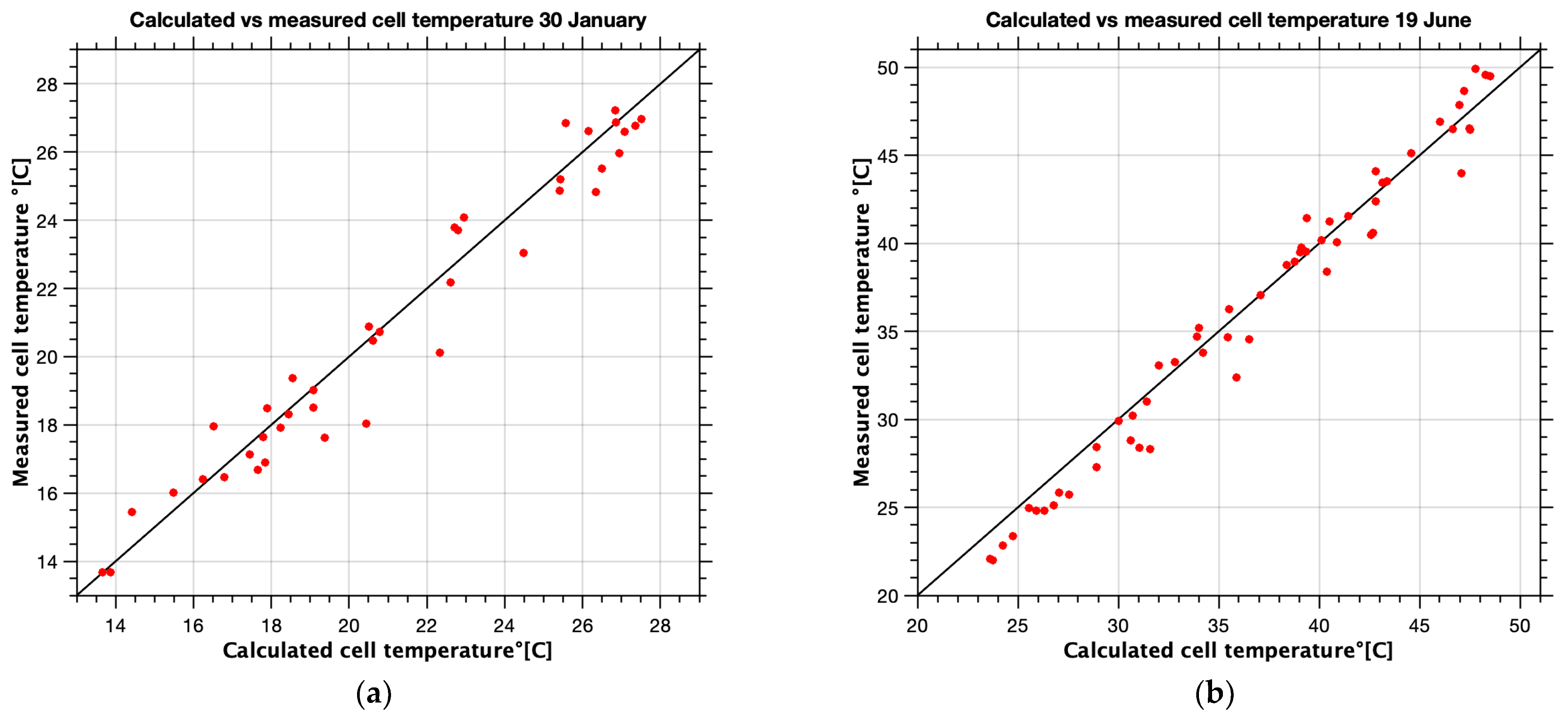
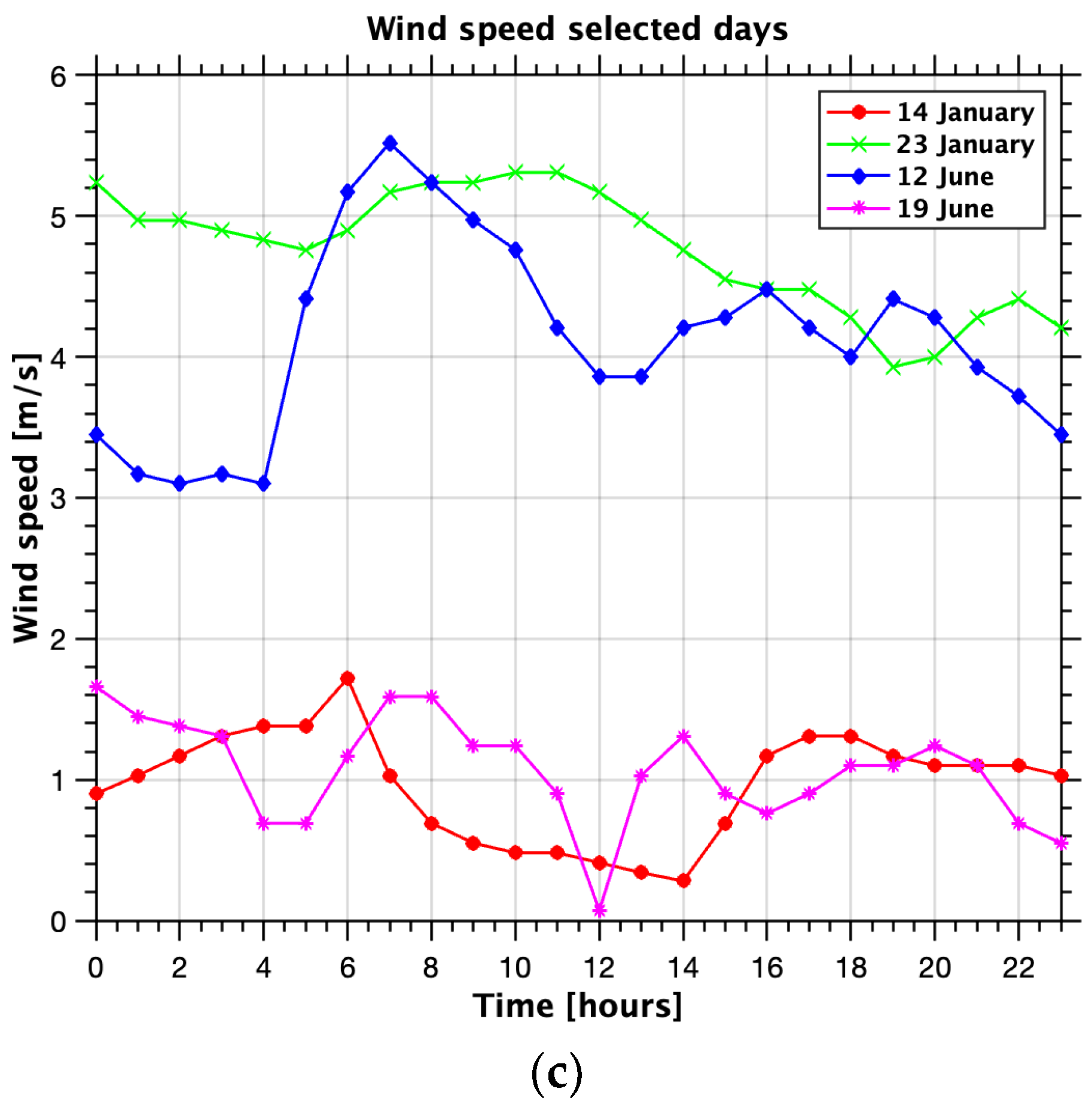
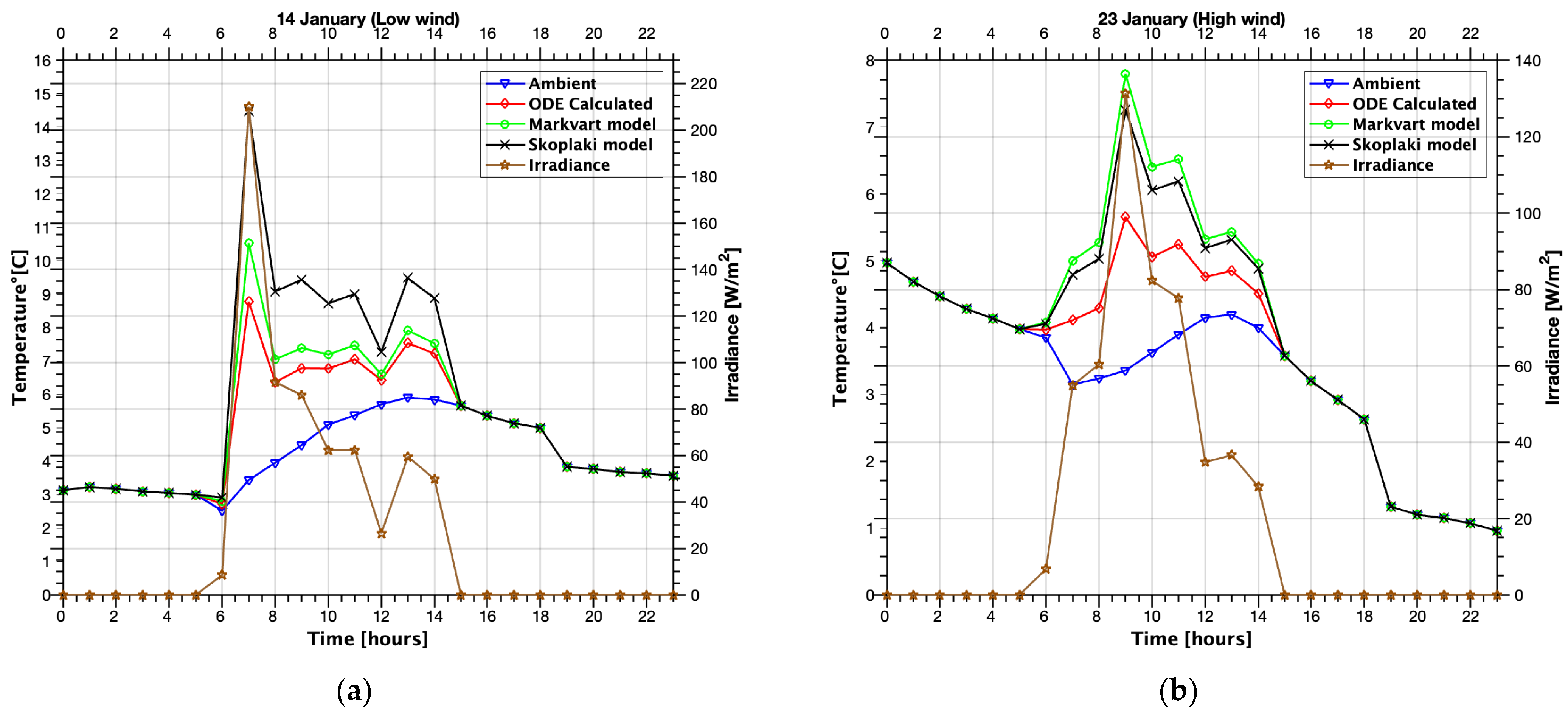
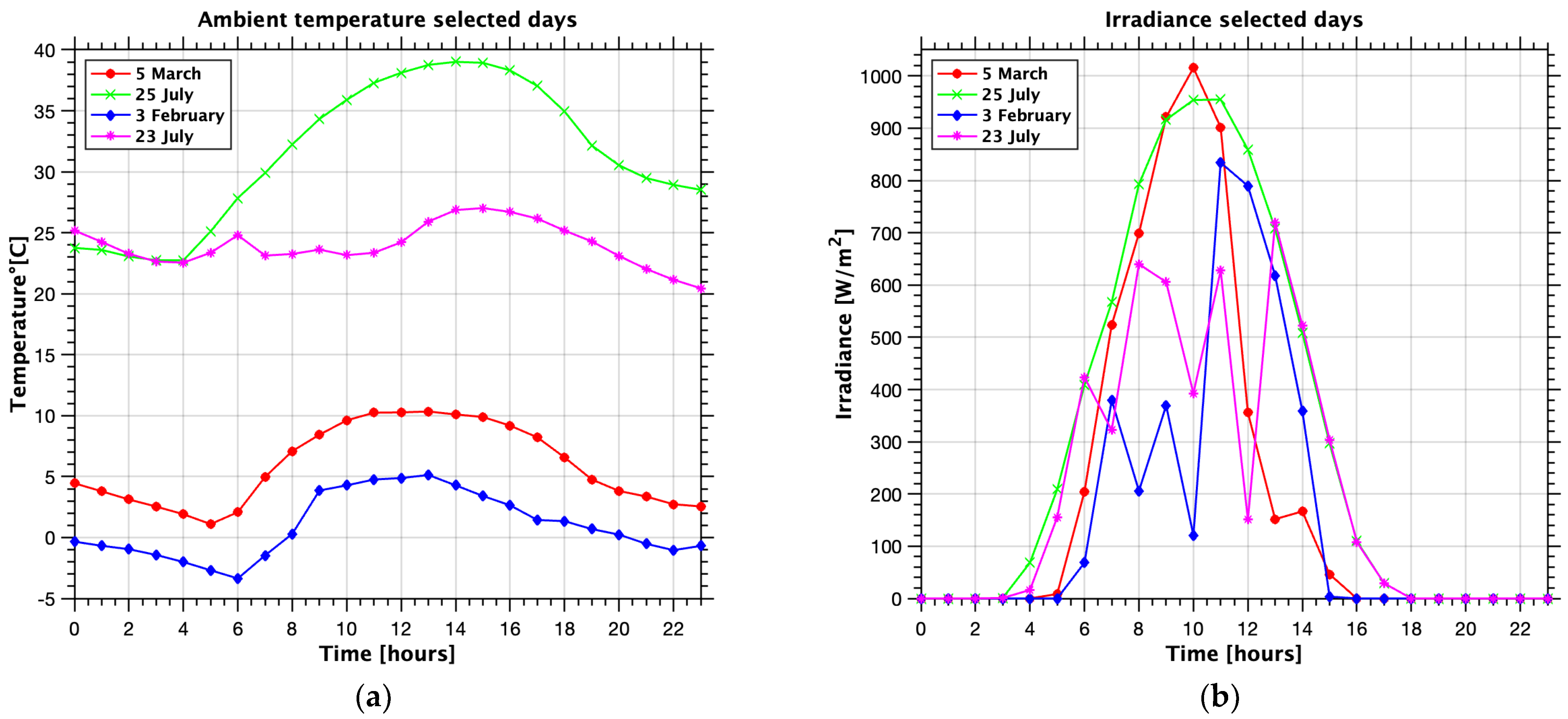
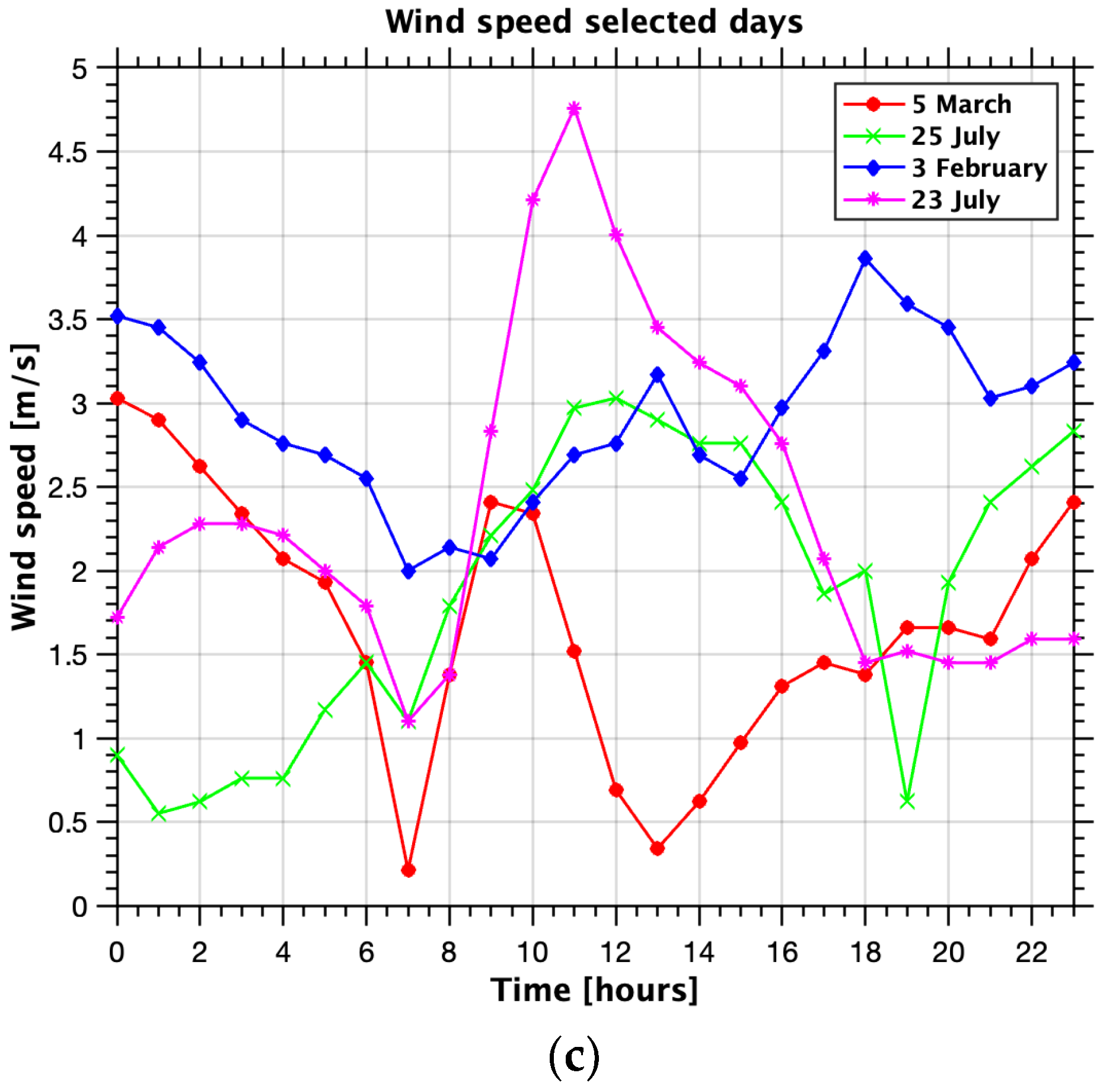
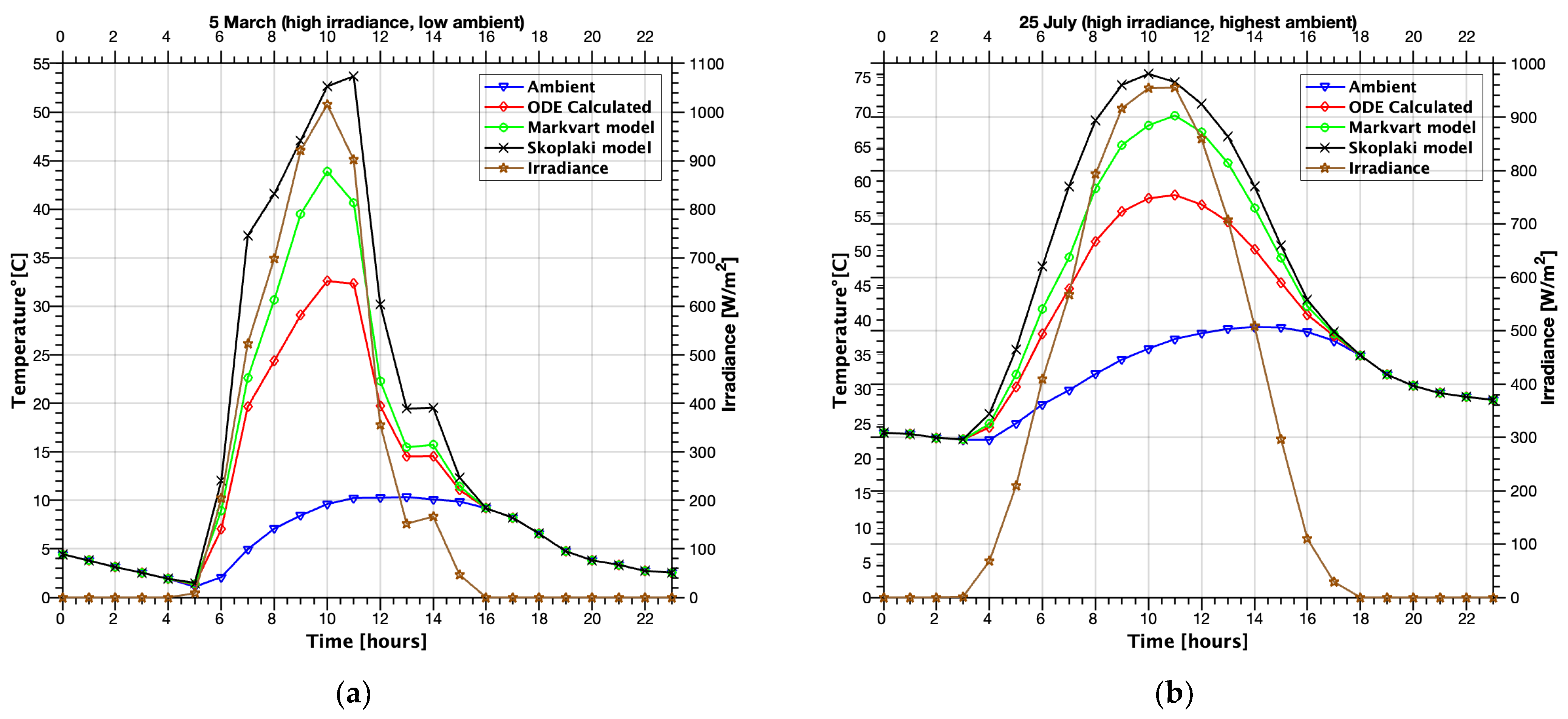
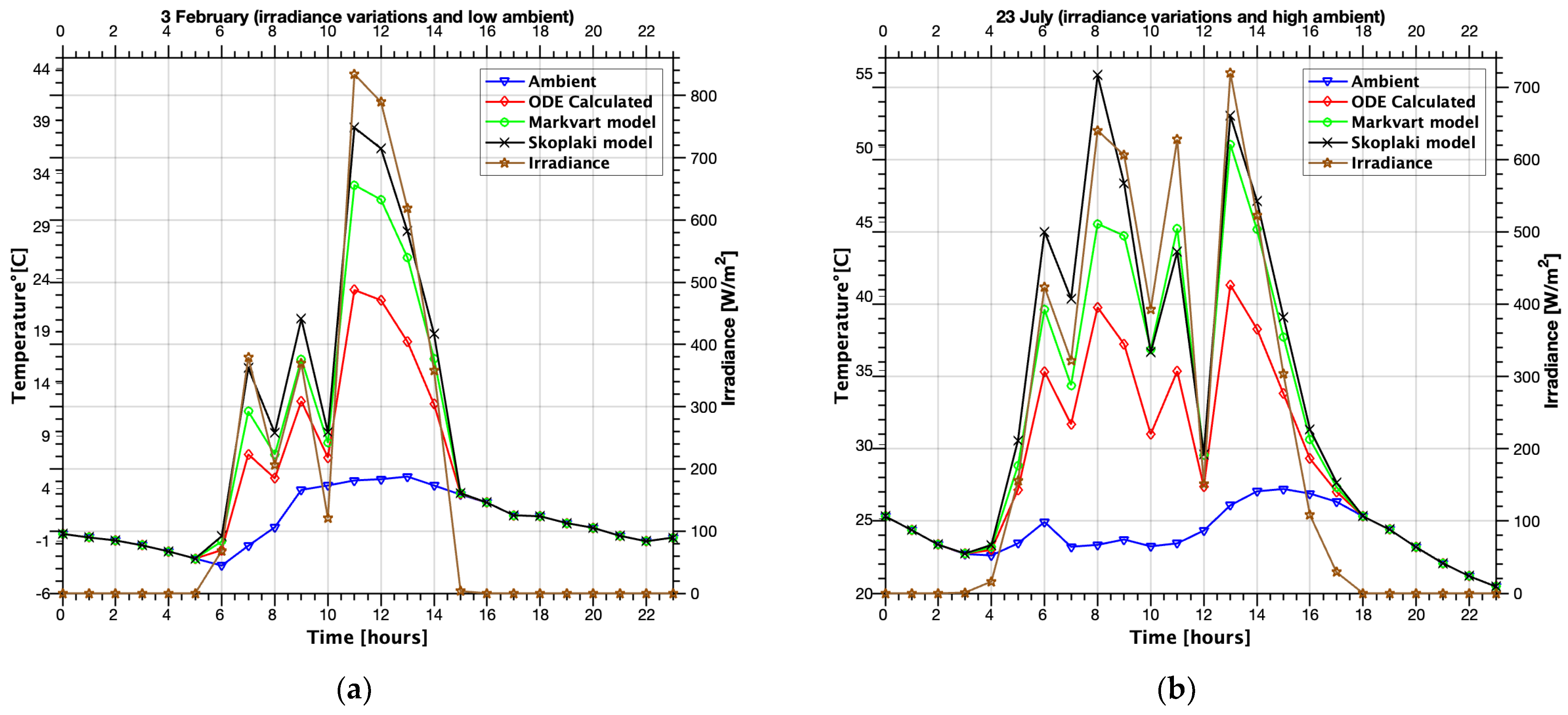
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PV | Photovoltaic module |
| BIPV | Building-integrated photovoltaic panels |
| NOCT | Normal operating cell temperature |
| SNL | Sandia National Laboratory |
References
- Bayrak, F. Prediction of photovoltaic panel cell temperatures: Application of empirical and machine learning models. Energy 2025, 323, 135764. [Google Scholar] [CrossRef]
- Chouder, A.; Silvestre, S.; Taghezouit, B.; Karatepe, E. Monitoring, modelling and simulation of PV systems using LabVIEW. Sol. Energy 2013, 91, 337–349. [Google Scholar] [CrossRef]
- Markvart, T. Solar Electricity, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2000. [Google Scholar]
- Nicoletti, F.; Cucumo, M.A.; Ferraro, V.; Kaliakatsos, D.; Gigliotti, A. A Thermal Model to Estimate PV Electrical Power and Temperature Profile along Panel Thickness. Energies 2022, 15, 7577. [Google Scholar] [CrossRef]
- Boudjelthia, E.A.K.; Abbas, M.L.; Semaoui, S.; Kerkouche, K.; Zeraïa, H.; Yaïche, R. Role of the wind speed in the evolution of the temperature of the PV module: Comparison of prediction models. Rev. Energ. Renouvelables 2016, 19, 119–126. [Google Scholar] [CrossRef]
- Lamaamara, I.; Tiliouaa, A.; Zaida, Z.B.; Babaouia, A.; Ettaknib, M.; Alaoui, M.A.H. Evaluation of different models for validating of photovoltaic cell temperature under semi-arid conditions. Heliyon 2021, 7, e08534. [Google Scholar] [CrossRef] [PubMed]
- Yaman, K.; Arslan, G. A detailed mathematical model and experimental validation for coupled thermal and electrical performance of a photovoltaic (PV) module. Appl. Therm. Eng. 2021, 195, 117224. [Google Scholar] [CrossRef]
- Santos, L.O.; Carvalho, P.C.M.; Filho, C.O.C. Photovoltaic Cell Operating Temperature Models: A Review of Correlations and Parameters. IEEE J. Photovolt. 2022, 12, 179–190. [Google Scholar] [CrossRef]
- Mattei, M.; Notton, G.; Cristofari, C.; Muselli, M.; Poggi, P. Calculation of the polycrystalline PV module temperature using a simple method of energy balance. Renew. Energy 2006, 31, 553–567. [Google Scholar] [CrossRef]
- Trinuruk, P.; Sorapipatana, S.; Chenvidhya, D. Estimating operating cell temperature of BIPV modules in Thailand. Renew. Energy 2009, 34, 2515–2523. [Google Scholar] [CrossRef]
- Nicola, M.; Berwind, M. Improving Module Temperature Prediction Models for Floating Photovoltaic Systems: Analytical Insights from Operational Data. Energies 2024, 17, 4289. [Google Scholar] [CrossRef]
- Filho, J.F.B.D.F.; Neves, W.L.A.; Costa, F.B. Photovoltaic Module Temperature Prediction Model Incorporating Wind Direction and Precipitation Effects. IEEE J. Photovolt. 2025, 15, 701–711. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Meng, Q.; Yang, C.; Lin, Y.; Zhu, J.; Zhao, Z.; Zhou, C.; Zheng, C.; Gao, X. Accurate photovoltaic power prediction via temperature correction with physics-informed neural networks. Energy 2025, 328, 136546. [Google Scholar] [CrossRef]
- Kim, Y.M.; Lee, H.L.; Park, J.; Moon, S.J. Predicting module temperature and photovoltaic electricity generation using meteorological data. J. Mech. Sci. Technol. 2024, 38, 5123–5133. [Google Scholar] [CrossRef]
- Skoplaki, E.; Boudouvis, A.G.; Palyvos, J.A. A simple correlation for the operating temperature of photovoltaic modules of arbitrary mounting. Sol. Energy Mater. Sol. Cells 2008, 92, 1393–1402. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar Energy Engineering Processes and Systems, 3rd ed.; Academic Press: London, UK; Elsevier: London, UK, 2024. [Google Scholar]
- Tuncel, B.; Ozden, T.; Balog, R.S.; Akinoglu, B.G. Dynamic thermal modelling of PV performance and effect of heat capacity on the module temperature. Case Stud. Therm. Eng. 2020, 22, 100754. [Google Scholar] [CrossRef]
- Bostan, I.; Dulgheru, V.; Sobor, I.; Bostan, V.; Sochirean, A. Sisteme de Conversie a Energiilor Regenerabile; Tehnica-Info: Chișinău, Moldova, 2007. [Google Scholar]
- Photovoltaic Geographical Information System (PVGIS). An Official Website of the European Union. Available online: http://re.jrc.ec.europa.eu/pvgis/apps4/pvest.php (accessed on 10 December 2024).
- Șișu, P.; Goga, E.I.; Stanciu, C.; Stanciu, D.; Constantin, A.; Șoriga, I. Optimum Tilt For Maximum Yearly Electric Energy Of a Photovoltaic Module Operating In Bucharest. In Proceedings of the 16th International Conference on Thermal Engineering ICTEA, Bucharest, Romania, 18–20 June 2025. [Google Scholar]




| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Maximum Power | 270 | W | |
| Open Circuit Voltage | 38 | V | |
| Short Circuit Current | Isc,st | 9.2 | A |
| Maximum Power Voltage | 31 | V | |
| Maximum Power Current | 8.7 | A | |
| Module Efficiency | 16.45 | % | |
| Length | 1648 | mm | |
| Width | 995 | mm | |
| Active Area | 1.64 | m2 | |
| Voltage Temperature Coefficient | −0.34 | %/°C | |
| Current Temperature Coefficient | 0.06 | %/°C | |
| Nominal Operating Cell Temperature | 47 | °C | |
| Standard Test Conditions Temperature | 25 | °C | |
| Solar Absorptance-Transmittance Product | 0.9 | [-] |
| Indicator | Unit | Summer | Winter |
|---|---|---|---|
| rRMSE | % | 3.851180905 | 4.396517861 |
| rMBE | % | 1.248191368 | 0.974324998 |
| RMSE | °C | 1.398635819 | 0.921622656 |
| Mmed | °C | 36.3170636 | 20.96255912 |
| MBE | °C | 0.453306453 | 0.204243454 |
| R2 | - | 0.9708 | 0.9511 |
| Indicator | Unit | Annual Markvart vs. ODE | Annual Skoplaki vs. ODE |
|---|---|---|---|
| rRMSE | % | 22.7956 | 39.1309 |
| rMBE | % | 12.0552 | 20.59 |
| RMSE | °C | 4.2522 | 7.2993 |
| MBE | °C | 2.2487 | 3.8408 |
| R2 | - | 0.9038 | 0.7166 |
| Day | Model | rRMSE [%] | rMBE [%] | RMSE [°C] | MBE °C | Mmed °C | R2 [-] |
|---|---|---|---|---|---|---|---|
| 5 March | Markvart | 35.6578 | 17.6394 | 3.9112 | 1.9348 | 10.9687 | 0.8434 |
| Skoplaki | 82.7135 | 46.0188 | 9.0726 | 5.0477 | 0.1574 | ||
| 25 July | Markvart | 13.6312 | 8.6142 | 5.2417 | 3.3125 | 38.4541 | 0.8161 |
| Skoplaki | 24.0261 | 15.8024 | 9.239 | 6.0767 | 0.4286 | ||
| 3 Febr. | Markvart | 83.7058 | 42.8939 | 3.6257 | 1.8579 | 4.3314 | 0.7655 |
| Skoplaki | 129.7739 | 68.5759 | 5.6211 | 2.9703 | 0.4365 | ||
| 23 July | Markvart | 14.168 | 8.8502 | 4.0405 | 2.524 | 28.5188 | 0.5587 |
| Skoplaki | 21.0605 | 13.3552 | 6.0062 | 3.8087 | 0.025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şoriga, I.; Stanciu, C.; Şişu, P.; Goga, I. PV Cell Temperature Prediction Under Various Atmospheric Conditions. Energies 2025, 18, 5239. https://doi.org/10.3390/en18195239
Şoriga I, Stanciu C, Şişu P, Goga I. PV Cell Temperature Prediction Under Various Atmospheric Conditions. Energies. 2025; 18(19):5239. https://doi.org/10.3390/en18195239
Chicago/Turabian StyleŞoriga, Iuliana, Camelia Stanciu, Patricia Şişu, and Iuliana Goga. 2025. "PV Cell Temperature Prediction Under Various Atmospheric Conditions" Energies 18, no. 19: 5239. https://doi.org/10.3390/en18195239
APA StyleŞoriga, I., Stanciu, C., Şişu, P., & Goga, I. (2025). PV Cell Temperature Prediction Under Various Atmospheric Conditions. Energies, 18(19), 5239. https://doi.org/10.3390/en18195239








