Machine Learning-Assisted Reconstruction of In-Cylinder Pressure in Internal Combustion Engines Under Unmeasured Operating Conditions

Abstract

In-cylinder pressure provides critical insights for analyzing and optimizing combustion in internal combustion engines, yet its acquisition across the full operating space requires extensive testing, while physics-based models are computationally demanding. Machine learning (ML) offers an alternative, but its application to direct reconstruction of full pressure traces remains limited. This study evaluates three strategies for reconstructing cylinder pressure under unmeasured operating conditions, establishing a machine learning-assisted framework that generates the complete pressure–crank angle (P–CA) trace. The framework treats crank angle and operating conditions as inputs and predicts either pressure directly or apparent heat release rate (HRR) as an intermediate variable, which is then integrated to reconstruct pressure. In all approaches, discrete pointwise predictions are combined to form the full P–CA curve. Direct pressure prediction achieves high accuracy for overall traces but underestimates HRR-related combustion features. Training on HRR improves combustion representation but introduces baseline shifts in reconstructed pressure. A hybrid approach, combining non-combustion pressure prediction with combustion-phase HRR-based reconstruction delivers the most robust and physically consistent results. These findings demonstrate that ML can efficiently reconstruct in-cylinder pressure at unmeasured conditions, reducing experimental requirements while supporting combustion diagnostics, calibration, and digital twin applications.

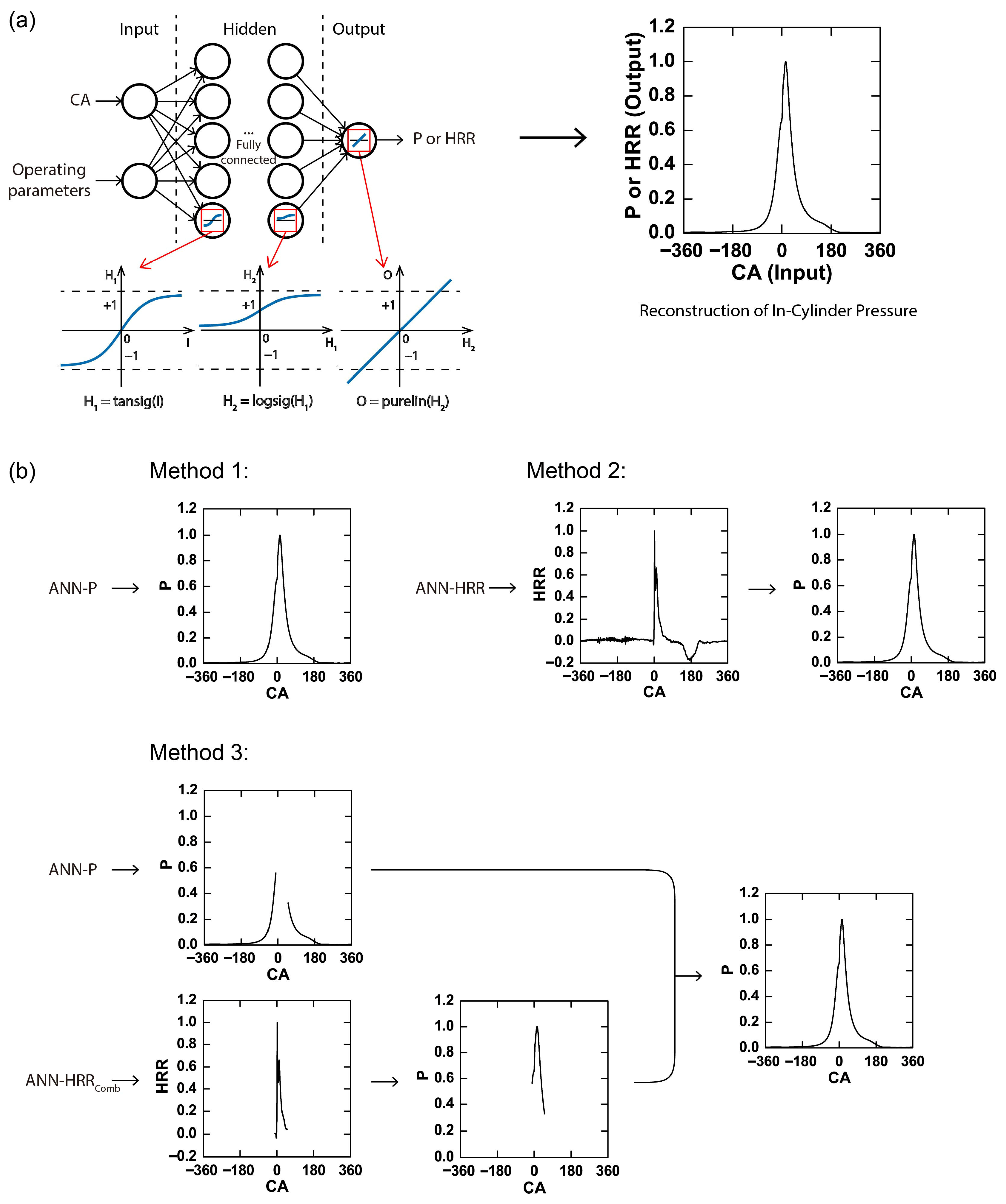
1. Introduction

Internal combustion engines (ICEs) remain among the most widely used prime movers in transportation and power generation, despite the rapid advancement of electrification technologies [1]. Their high power density, established manufacturing base, and fuel flexibility ensure continued relevance in both on-road and off-road applications [2]. With growing demands for higher efficiency and lower emissions, a detailed understanding of in-cylinder combustion has become essential [3]. Among available diagnostic signals, the in-cylinder pressure trace provides the most direct and comprehensive insight into combustion [4]. From this signal, key indicators such as indicated mean effective pressure, heat release rate, and combustion phasing can be derived, offering critical information on thermal efficiency and reliability, particularly when analyzed in conjunction with engine-out emissions [5]. Pressure-based analysis is also central to detecting abnormal combustion phenomena such as knock, pre-ignition, and misfire, which strongly affect durability and emissions compliance [6]. For these reasons, in-cylinder pressure measurement is regarded as the “gold standard” for engine diagnostics and calibration [7]. However, obtaining such data across a wide range of operating conditions is challenging [8]. Dedicated pressure transducers are costly, susceptible to drift, and unsuitable for long-term vehicle use, limiting their application primarily to laboratory settings [9]. Moreover, modern engines operate over diverse speeds, loads, and control strategies, making exhaustive experimental coverage impractical [10]. Consequently, efficient and accurate reconstruction or prediction of in-cylinder pressure under varied operating conditions has become a critical topic in engine research and development [11]. This demand is driven by both practical and technical considerations. From a practical standpoint, reconstruction can substantially reduce experimental costs by combining a limited number of measured points with predictive models, thereby enabling pressure estimation at untested conditions [12]. It also enhances data coverage, as the multidimensional operating space of modern engines, which involves variations in speed, load, ambient environment, and fuel properties, cannot be exhaustively mapped through conventional testing [13]. From a technical perspective, reconstruction provides virtual pressure data to support calibration and optimization, enables real-time monitoring and control where direct measurement is impractical, and underpins digital twin frameworks for predictive maintenance and state assessment [14]. Despite these advantages, existing approaches remain inadequate. Physics-based models, including zero-dimensional formulations and multi-dimensional computational fluid dynamics (CFD), require extensive calibration and detailed chemical kinetic mechanisms, involve considerable computational expense, and lack flexibility for rapid interpolation or prediction [15]. In particular, three-dimensional CFD simulations are often constrained by immature reaction mechanisms, limiting their predictive accuracy [16]. Therefore, the development of a low-cost, efficient, and robust method for reconstructing in-cylinder pressure under unmeasured conditions is highly desirable [17]. In this context, data-driven approaches, particularly machine learning (ML), have emerged as powerful tools for addressing complex and nonlinear problems in combustion and engine research [18]. Numerous studies have demonstrated the capability of ML models to predict combustion characteristics, estimate pollutant emissions, and model overall engine performance, often achieving accuracy comparable to or surpassing that of traditional physics-based methods [19]. Unlike conventional models that depend on detailed chemical kinetics or extensive calibration of physical sub-models, ML directly learns input–output relationships from data, making it particularly suitable for extrapolating from limited experimental datasets to untested operating conditions [20]. This capability is especially valuable in engine applications, where the multidimensional operating space cannot be experimentally covered in its entirety and rapid predictions are frequently required [21]. Despite these advantages, most prior studies have focused on predicting aggregate performance metrics (e.g., brake-specific fuel consumption, thermal efficiency, indicated mean effective pressure) or emissions (e.g., nitrogen oxides, soot) [22], while relatively few have addressed the reconstruction of complete in-cylinder pressure traces [23]. Previous attempts to reconstruct pressure traces have typically relied on simplified physical models such as the Wiebe function, where coefficients vary irregularly with operating conditions and limit predictive accuracy. Yet, accurate pressure reconstruction is critical, as it underpins combustion analysis, real-time monitoring, and control. Consequently, applying ML to in-cylinder pressure reconstruction under unmeasured operating conditions represents a promising but underexplored direction that warrants systematic investigation.

The objective of this study is to assess the feasibility of machine learning (ML)-based modeling for reconstructing in-cylinder pressure at untested conditions. An artificial neural network (ANN) is employed owing to its strong capability in nonlinear function approximation and its demonstrated effectiveness in capturing complex, multivariable relationships in combustion-related problems [24]. These properties make ANN particularly well suited to represent the nonlinear and coupled interactions between operating parameters and cylinder pressure evolution. The proposed framework utilizes experimental data collected at discrete operating points to train the ANN, which is then used to predict pressure traces at intermediate or unmeasured conditions. To our knowledge, this study represents the first attempt to reconstruct the full pressure–crank angle trace directly from input–output mapping in the internal combustion engine field. As a representative case study, pressure reconstruction at different altitude levels is conducted based on training data obtained at other altitudes, thereby demonstrating both feasibility and potential. Beyond this specific application, the proposed framework establishes a new paradigm for pressure reconstruction in engine research, providing a data-driven alternative to conventional indicator-based or physics-model-based approaches. The remainder of this paper introduces the data acquisition process and the machine learning framework, presents and discusses the modeling results with emphasis on predictive performance and physical implications, and concludes with a summary of the main findings along with perspectives for future work.

2. Data Collection and Machine Learning Modeling

To evaluate the feasibility of ML-based modeling for reconstructing in-cylinder pressure under untested operating conditions, this study considers altitude variation as a representative case. In this framework, pressure traces measured at several discrete altitude levels are used to train the ML model, which is then applied to predict pressure traces at intermediate, unmeasured altitudes. The experimental data were obtained from a turbocharged and intercooled four-stroke direct-injection diesel engine operating under steady-state conditions. The test campaign covered altitudes from sea level to 5000 m in 1000 m increments, with the injected fuel quantity and engine speed kept constant. As altitude increased, the reduced intake pressure lowered the air charge, thereby deteriorating combustion and altering the in-cylinder pressure evolution. Detailed specifications of the research engine, operating conditions, and measurement procedures are provided in Ref. [25]. Cylinder pressure at each altitude was measured using a piezoelectric transducer with a crank-angle resolution of 0.1° CA. For each operating point, more than 100 consecutive steady-state cycles were recorded, and ensemble-averaged traces were used in the analysis since the coefficient of variation of indicated mean effective pressure was below 2%, indicating stable operation across all altitudes. The raw averaged pressure signals were further processed using a fourth-order Butterworth low-pass digital filter to suppress high-frequency noise while preserving the main combustion characteristics. These processed signals served as the dataset for this study.

In terms of ML algorithm, artificial neural networks (ANNs) are selected in this study as the modeling framework for cylinder pressure reconstruction because of their universal function approximation capability and proven performance in handling highly nonlinear and coupled systems. In comparison with traditional regression techniques or physics-based reduced-order models, ANNs can flexibly capture complex input–output relationships without requiring explicit prior knowledge of the underlying combustion chemistry or thermodynamics. This makes them particularly well suited for problems such as in-cylinder pressure prediction, where the interactions among engine operating parameters and pressure evolution are strongly nonlinear. In essence, an ANN is composed of an input layer, one or more hidden layers, and an output layer. Each neuron in a layer processes the weighted sum of inputs from the previous layer, adds a bias term, and applies a nonlinear activation function to generate its output. By propagating information through successive layers and iteratively adjusting the weights and biases during training, the network learns to approximate the mapping between input variables and target outputs. Once trained, the ANN can generalize to unseen operating conditions, making it an effective tool for reconstructing in-cylinder pressure at unmeasured altitudes.

Figure 1 illustrates the fully connected feedforward ANN employed in this study. The network consists of an input layer representing crank angle and operating parameters, and an output layer predicting in-cylinder pressure. This forward-only structure enables the ANN to approximate complex nonlinear mappings between engine operating conditions and combustion-related outputs. In the present application, the inputs are crank angle (CA) and altitude (H), and the output is cylinder pressure (P). A cylinder pressure trace is defined as the pressure profile versus crank angle, where the predicted pressure corresponds to a specific crank angle at a given altitude. To obtain a complete pressure trace at a particular altitude, both the output pressure data and the corresponding crank angle input are required. Among the operating parameters, only altitude is included as an input, since intake pressure varies directly with altitude. Fuel injection quantity and engine speed are excluded because they are kept constant throughout the experiments. The primary objective of the ANN is to reconstruct the cylinder pressure trace, which can also be derived from the apparent heat release rate (HRR). Accordingly, either cylinder pressure or HRR at a given crank angle and altitude is selected as the model output. To evaluate this, three modeling strategies are compared. Method 1 directly uses cylinder pressure as the output, enabling straightforward pressure prediction. Methods 2 and 3 adopt a different strategy by predicting HRR instead of pressure. The cylinder pressure is then reconstructed from the predicted HRR using a single-zone heat release model, subject to several simplifying assumptions: a spatially uniform in-cylinder mixture, ideal-gas behavior, a constant specific heat ratio, and negligible heat transfer and crevice losses [26]. Although restrictive, these assumptions establish a direct link between HRR and cylinder pressure, allowing pressure reconstruction from the energy release history. The distinction between Methods 2 and 3 lies in the HRR range considered. In Method 2, the neural network is trained to predict the full-cycle HRR, covering both combustion and non-combustion periods. With the initial pressure (defined by the intake pressure at a given altitude) as the starting condition, the entire cylinder pressure trace, comprising compression, combustion, expansion, and exhaust, can be reconstructed by integrating HRR over the full cycle. In contrast, Method 3 restricts the prediction to the combustion-phase HRR only, while HRR outside the combustion period is approximated as zero. Because this assumption provides insufficient information to recover pressure evolution during intake, compression, expansion, and exhaust, Method 3 necessarily combines two predictive models: (i) a pressure-prediction ANN to reconstruct cylinder pressure during non-combustion phases, and (ii) a combustion-HRR ANN to predict HRR during combustion and reconstruct pressure for that portion of the cycle. The final pressure trace is then obtained by splicing together the non-combustion pressure prediction with the combustion-phase HRR-based reconstruction.

In terms of dataset construction, each fired cycle covers 720° crank angle (four strokes) with a sampling resolution of 0.1° CA, yielding 7200 data points per operating condition. Five operating conditions (0, 1000, 2000, 4000, and 5000 m) were grouped as the training dataset, while the 3000 m case (7200 points) was withheld as an independent test set. Within the training dataset, a standard resampling strategy was applied, with 70% of the data used for weight updates, 15% for internal validation to monitor overfitting and apply early stopping, and 15% for internal testing. Accordingly, Method 1 involves 36,000 pressure data points for training and 7200 points for testing. Method 2 follows the same structure but uses HRR as the output, yielding 36,000 HRR points for training and 7200 for testing. Method 3 focuses only on the combustion window between −10° and 50° CA ATDC, corresponding to 600 data points per cycle. In this case, the HRR dataset comprises 3000 training points and 600 test points, while the complementary pressure dataset covers 6600 points per condition (33,000 training and 6600 testing). This two-level strategy, which combines internal resampling for robust training and an external unseen altitude for independent testing, ensures that both model generalization and physical consistency are rigorously evaluated.

The network is trained using the backpropagation algorithm under a supervised learning framework, where the model adjusts internal weights and biases to minimize the mean squared error (MSE) between predicted and measured values. Prior to training, input and output variables are normalized to the range [0, 1] using min–max scaling. This normalization ensures that all variables contribute comparably during optimization and prevents bias toward variables with larger magnitudes. The maximum number of training epochs is set to 500, the target MSE to 1 × 10⁻⁵, and the learning rate to 0.01, balancing model accuracy and computational efficiency. After training, predicted outputs are rescaled to physical units using the inverse transformation. Hyperparameter tuning shows that the network achieves the most favorable performance with two hidden layers, each containing five neurons, and this configuration is robust across all three modeling strategies, regardless of whether pressure or HRR is used as the output. This architecture represents the best compromise between predictive accuracy, training stability, and computational efficiency. The nonlinear transfer functions applied in the hidden layers are a hyperbolic tangent sigmoid (tansig) in the first layer and a logistic sigmoid (logsig) in the second, while a linear activation function (purelin) is employed in the output layer to accurately represent continuous regression outputs. It should be noted that the overarching goal of this study is not to perform exhaustive hyperparameter optimization, but rather to demonstrate the feasibility of directly reconstructing the full pressure–crank angle trace as a new paradigm in engine research.

The predictive performance of the ANN models is evaluated using the root mean square error (RMSE) and the coefficient of determination (R²). RMSE provides a direct measure of the average deviation between predicted and measured signals, while R² quantifies the proportion of variance in the measured data explained by the model. Lower RMSE values indicate higher prediction accuracy, with RMSE approaching zero representing near-perfect agreement between predicted and measured signals. R² values closer to unity indicate better model fit, with R² = 1 corresponding to a perfect prediction. In addition to these quantitative metrics, the model-predicted pressure traces and HRR profiles are compared with experimental data. Such comparisons provide complementary insight into the accuracy of pressure reconstruction and, more importantly, the fidelity of derived combustion characteristics. Since the practical value of in-cylinder pressure reconstruction lies not only in minimizing numerical error but also in preserving physically meaningful profiles for combustion analysis, direct profile comparison is essential. This approach also enables systematic evaluation of the relative merits of the three reconstruction methods proposed in this study.

3. Results and Discussion

This section presents and discusses the results of machine learning-assisted reconstruction of in-cylinder pressure under unmeasured operating conditions. The primary objective is to evaluate whether the proposed ML framework can accurately reproduce pressure traces at untested altitudes, thereby demonstrating its feasibility for combustion analysis. Three modeling strategies are examined: Method 1, direct prediction of in-cylinder pressure (ANN-P); Method 2, indirect prediction via full-cycle HRR modeling (ANN-HRR); and Method 3, a hybrid approach that combines pressure prediction outside combustion (ANN-P) with combustion-phase HRR modeling (ANN-HRR_Comb). All results are obtained using ANN models after parameter tuning to ensure fair and meaningful comparison. For each method, results are presented in two steps: first, by reporting statistical performance indicators, and second, by directly comparing the reconstructed pressure and HRR profiles with experimental measurements. This combined analysis enables both a quantitative assessment of prediction accuracy and a qualitative evaluation of combustion characteristics, providing a comprehensive basis for comparing the three reconstruction strategies. The comparative analysis highlights the relative strengths and limitations of the three approaches and offers insights into their suitability for practical engine applications.

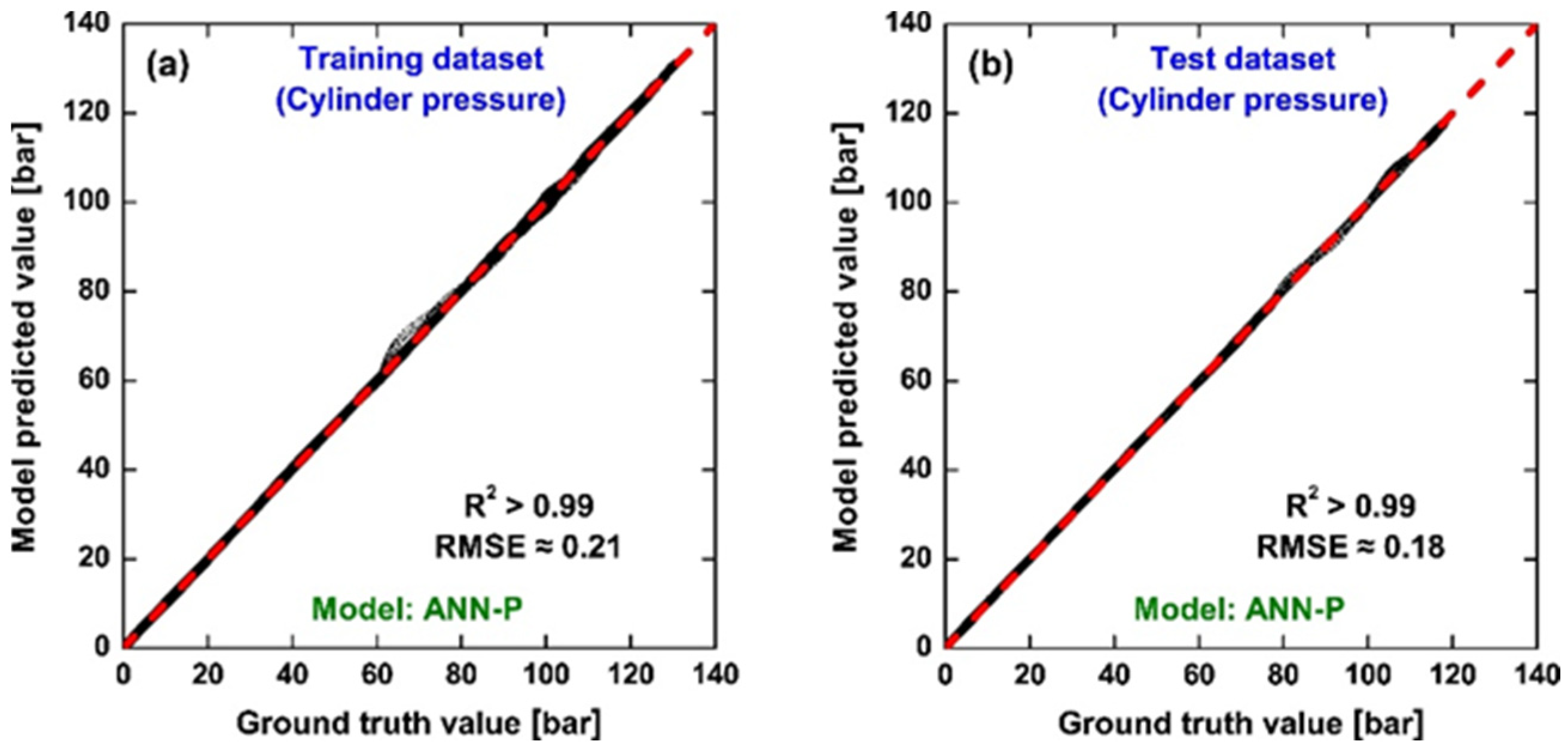
Figure 2, Figure 3 and Figure 4 collectively demonstrate the effectiveness of Method 1 (ML-based direct pressure prediction) in reconstructing in-cylinder pressure under both measured and unmeasured operating conditions. Figure 2 illustrates the performance of the ANN-P model in directly predicting in-cylinder pressure traces, with predicted values plotted against the corresponding experimental measurements. The 45° dashed line represents perfect agreement, and the close clustering of most data points along this line indicates excellent predictive accuracy. Both the training dataset (Figure 2a) and the independent test dataset at 3000 m (Figure 2b) show high consistency, with R² values above 0.99 and RMSE values below 0.25 bar. These results confirm that the network successfully learns the nonlinear relationship between crank angle, altitude, and in-cylinder pressure, and generalizes well to unmeasured operating conditions. Nevertheless, small deviations can be observed, particularly in the pressure range between approximately 60 and 80 bar, where the predicted values tend to slightly depart from the 45° line. This region coincides with the onset of combustion, where pressure rises rapidly, making accurate prediction more challenging. At later crank angles with higher cylinder pressures, small discrepancies can also be identified, which are associated with the main combustion event. These aspects will be further examined in Figure 3 and Figure 4, where the reconstructed pressure traces are directly compared with experimental data in the crank-angle domain, and the implications for combustion analysis are discussed.

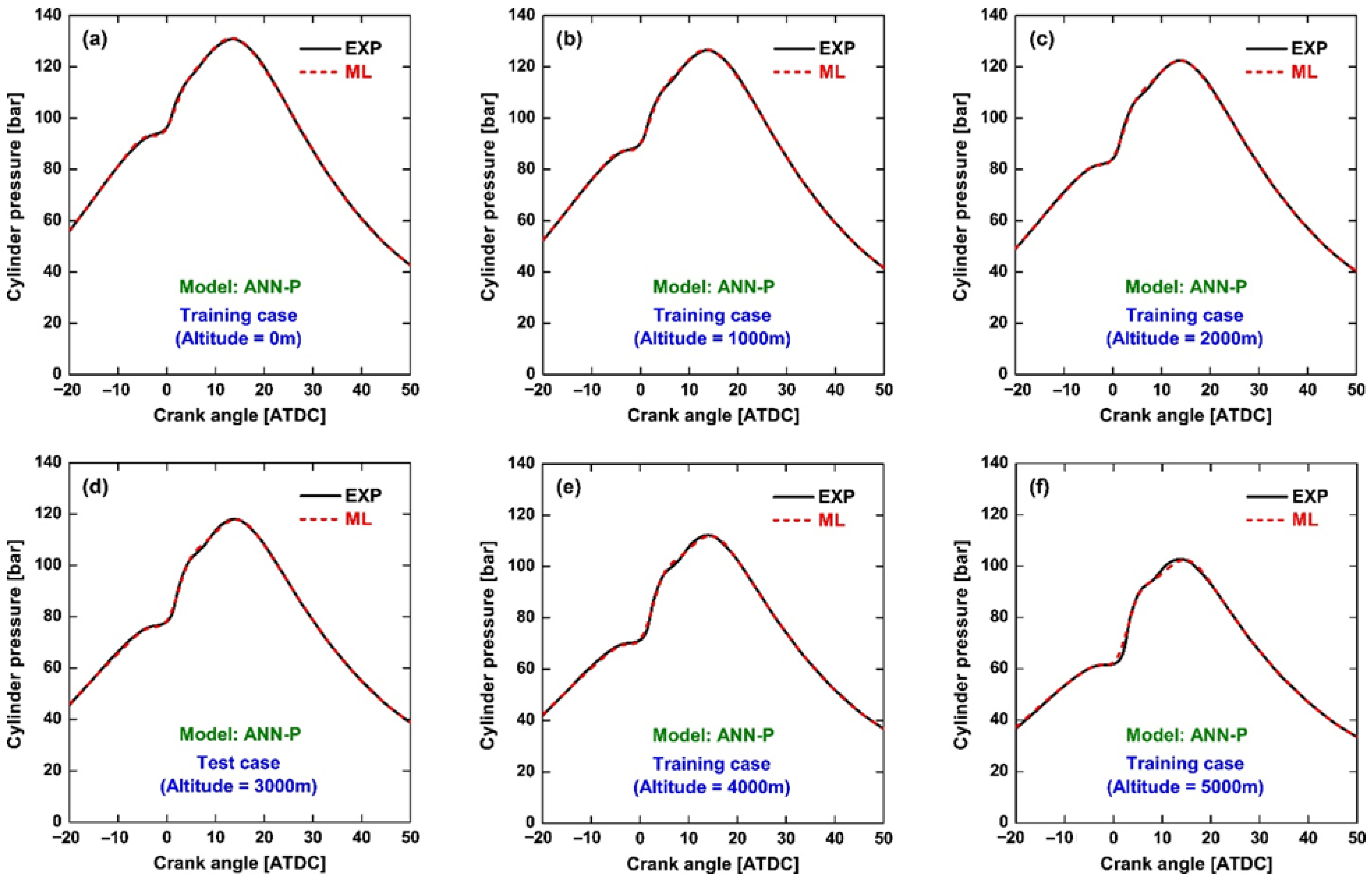
Figure 3 further substantiates the findings from Figure 2 by directly comparing the predicted and experimental in-cylinder pressure traces across all operating points. The agreement between reconstructed and measured curves is nearly perfect for both the training altitudes (0–5000 m) and the unseen test altitude (3000 m), demonstrating that the network generalizes well to unmeasured conditions. The overall pressure evolution, including compression, the main combustion event, and the subsequent expansion, is accurately reproduced. Only minor discrepancies are observed during the rapid pressure rise following combustion, where the model slightly underpredicts or overpredicts the pressure slope. This deviation is consistent with the scatter observed in the 60–80 bar range in Figure 2 and reflects the difficulty of fully capturing the highly transient combustion onset. At higher crank angles, the peak pressure magnitude and its phasing are reproduced with high fidelity, underscoring the robustness of the direct prediction method. In addition, the altitude effect on cylinder pressure is clearly reflected in both the experimental and predicted traces. As altitude increases, the compression pressure and the peak cylinder pressure decrease systematically due to reduced intake density and deteriorated combustion. The fact that the model captures this monotonic trend indicates not only its predictive accuracy but also its capability to reproduce physically meaningful variations. This feature provides confidence that the reconstructed traces can be used not only for accurate prediction but also for preliminary combustion analysis under different ambient conditions. These aspects are further illustrated in Figure 4, where the apparent HRR profiles are examined.

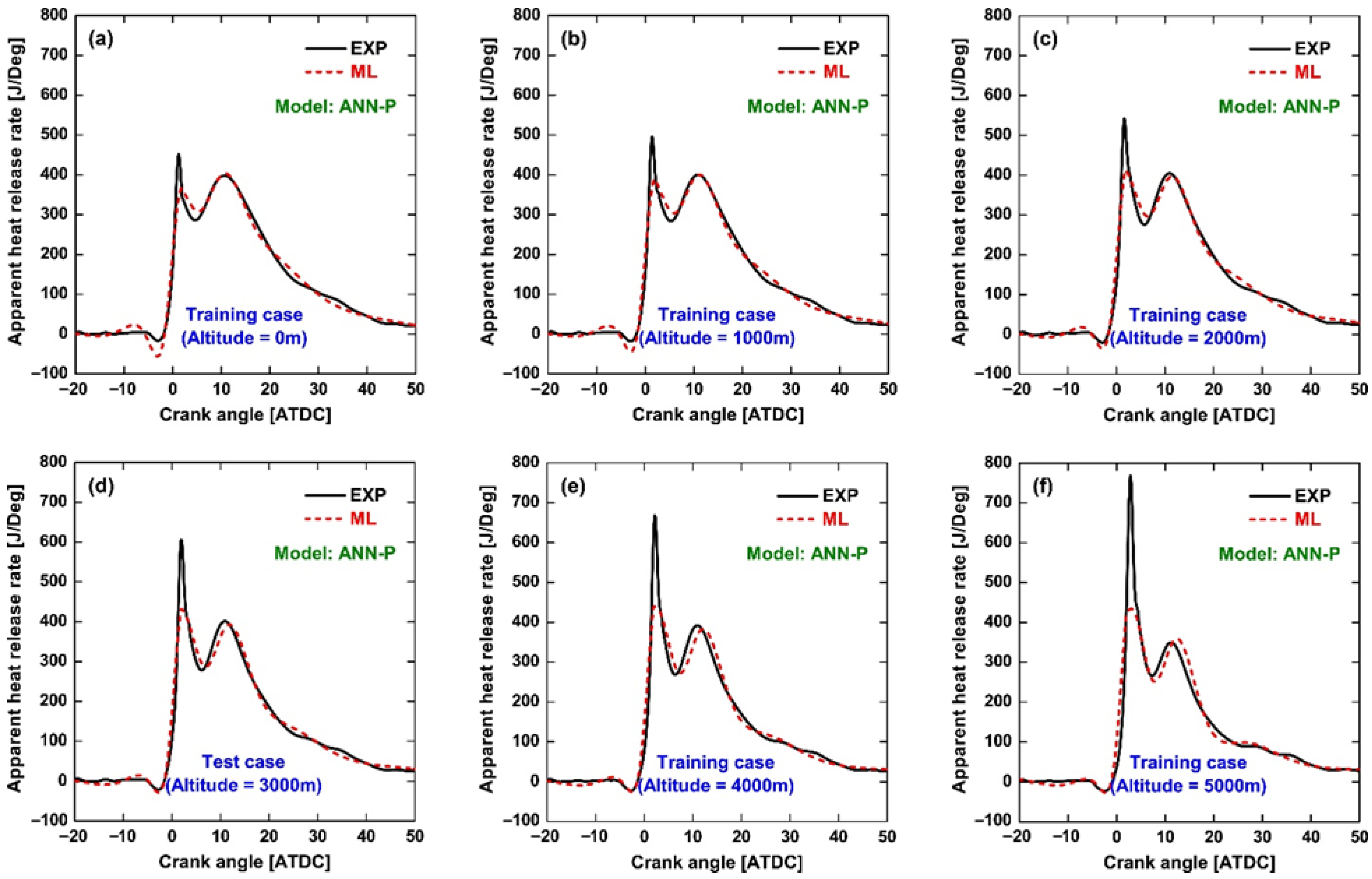
Figure 4 illustrates the comparison between predicted and experimental HRR profiles, providing further insight into the combustion characteristics reconstructed by Method 1. For clarity, the diesel HRR curve can generally be divided into three stages [27]. The first stage corresponds to premixed combustion, characterized by a very rapid pressure rise and a sharp HRR peak lasting only a few crank angle degrees. The second stage is the diffusion-controlled combustion phase, which typically extends over ~40° CA and accounts for the majority of fuel energy release. Finally, the third stage represents the late combustion tail, where a smaller but distinct rate of heat release persists during the expansion stroke. Within this framework, the model reproduces the overall HRR evolution reasonably well, including the transition from premixed to diffusion combustion and the subsequent late-burning phase. However, consistent with the pressure prediction discrepancies noted in Figure 2 and Figure 3, the premixed combustion peak is underestimated due to slight inaccuracies in capturing the steep pressure rise immediately after ignition. Since HRR is derived from the crank-angle derivative of the in-cylinder pressure trace [28], even minor pressure errors in this region are amplified, resulting in noticeable discrepancies in the predicted premixed peak. In the diffusion combustion phase, both the magnitude and phasing of the HRR peak are predicted with acceptable accuracy, which is expected since the pressure phasing is well captured. At higher crank angles, the late combustion tail is also reproduced with only minor deviations. An additional observation is the altitude dependence of HRR. As altitude increases, the premixed combustion peak becomes progressively higher, reflecting the influence of reduced intake density and longer ignition delay. This trend is clearly observed in the experimental data and is also captured by Method 1, suggesting that the model can reproduce physically meaningful variations in combustion behavior. Overall, Method 1 is acceptable for reconstructing cylinder pressure and can, after careful fine tuning, capture the general trends of HRR, such as the altitude-induced increase of the premixed peak. Nevertheless, an inherent limitation of Method 1 is that, although direct pressure prediction achieves excellent agreement with measured pressure traces and is adequate for global performance evaluation, it is less reliable for detailed combustion diagnostics where HRR-derived metrics such as ignition delay, combustion phasing, and premixed burn intensity are of primary importance. In the present altitude variation case, ignition delay and combustion phasing are well reproduced, while the premixed burn intensity is somewhat underestimated. However, under other operating conditions, discrepancies could manifest in all three metrics, underscoring the sensitivity of HRR-based analysis to small errors in pressure prediction.

The discussion of Method 1 has shown that, despite its excellent performance in reproducing in-cylinder pressure traces, the quantitative accuracy of HRR analysis remains limited. This limitation arises because HRR is obtained as the derivative of the pressure signal, making it highly sensitive to even small prediction errors. To address this issue, Method 2 reverses the modeling strategy by directly using HRR as the output of the neural network. Since HRR inherently reflects the fundamental combustion process, predicting it directly provides a more robust way to capture combustion phasing and intensity. The reconstructed pressure trace can then be obtained by integrating the predicted HRR profiles through the first law of thermodynamics. This approach not only has the potential to avoid error amplification from pressure differentiation but also to provide a more combustion-centered representation of the process. 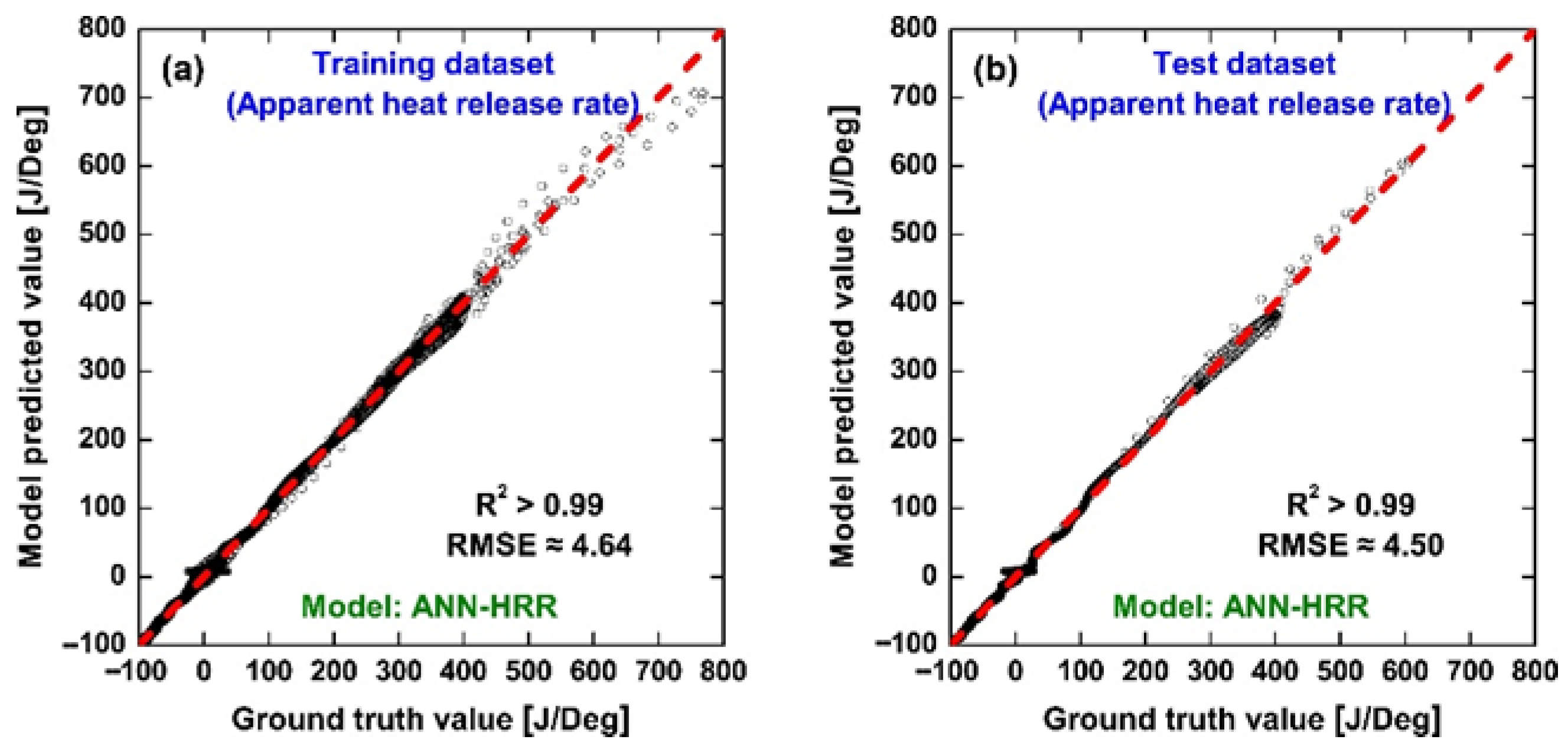Figure 5, Figure 6 and Figure 7 present the performance of Method 2, in which the neural network is trained to predict apparent HRR directly, and the pressure trace is subsequently reconstructed by integrating the predicted HRR. The parity plots in Figure 5 illustrate the predictive performance of the ANN-HRR model for both training and test datasets. Most of the scattered points closely follow the 45° diagonal line, confirming excellent agreement between predicted and measured HRR values. The statistical metrics, with R² values above 0.99 and RMSE around 4.5 J/deg, further corroborate the high predictive accuracy. It is noteworthy that a large cluster of points is located near HRR ≈ 0, corresponding to the non-combustion regions of the cycle (intake, compression, and exhaust). In these regions, the HRR signal is inherently very small and often dominated by measurement noise, which explains the slightly larger deviations from the diagonal line. By contrast, during the combustion phases where HRR is substantial, the predicted values align almost perfectly with the measured ones, which demonstrates the capability of the model to capture the key combustion dynamics with high fidelity.

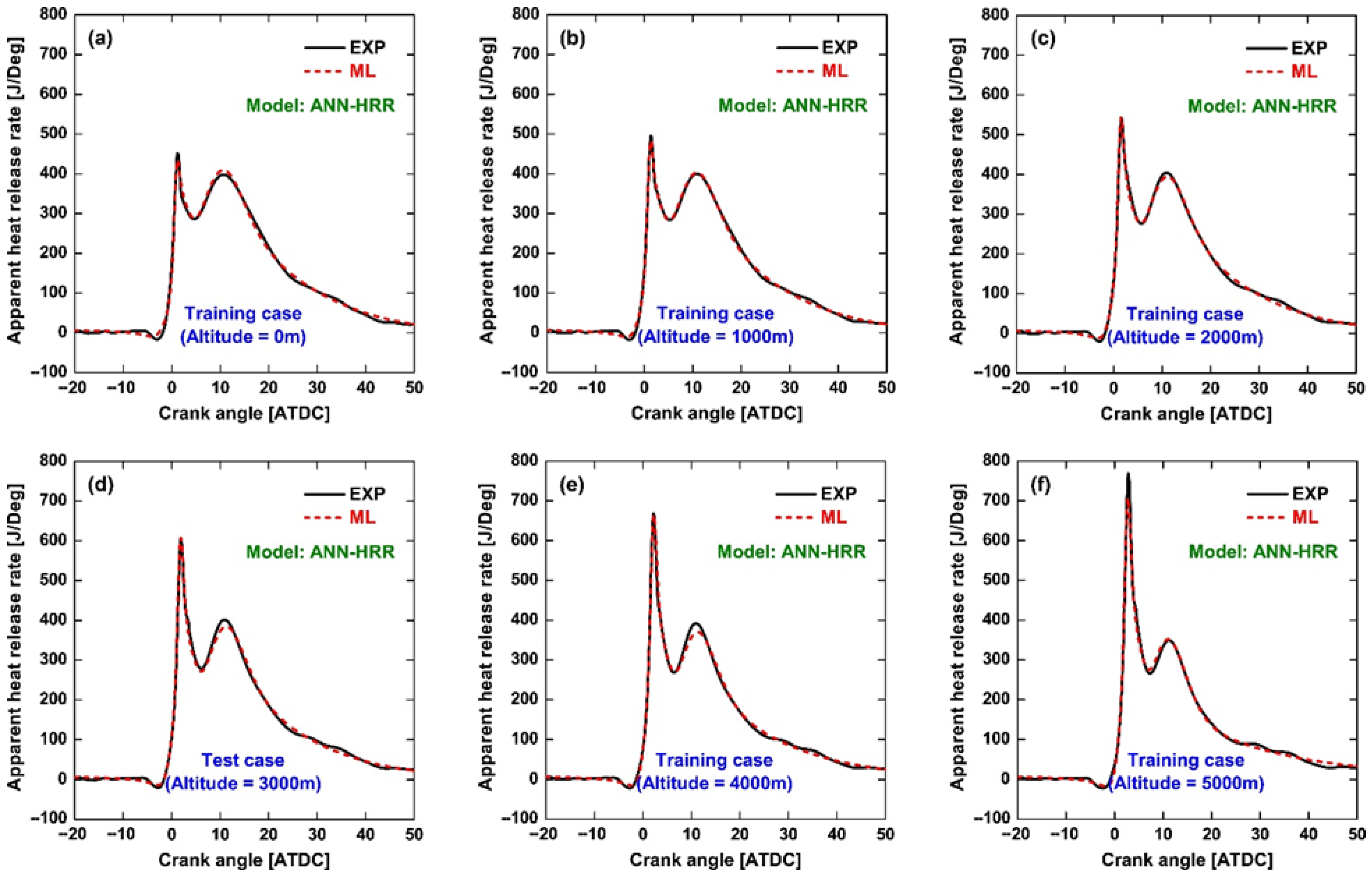
As shown in Figure 6, the ANN-HRR model reproduces the experimental HRR profiles with remarkable fidelity across all operating conditions, including both the training cases (0–5000 m) and the unseen test case at 3000 m. The three major phases of diesel combustion are well captured: the sharp premixed combustion peak immediately after ignition, the diffusion-controlled heat release that dominates the main combustion phase, and the long tail of late burning extending into the expansion stroke. This agreement highlights the capability of the model to learn and reproduce the essential features of the combustion process. At the same time, certain systematic patterns can be identified. The regions of HRR ≈ 0, corresponding to the non-combustion periods, exhibit larger deviations between prediction and measurement. This observation is consistent with the parity plots in Figure 5, where points clustered near HRR ≈ 0 showed greater scatter because the HRR signal in these regions is inherently very small and strongly influenced by experimental noise. In addition, a short period of negative HRR appears between the start of injection and the start of combustion, reflecting the ignition delay stage where fuel vaporization absorbs heat. The ANN-HRR model does not capture this feature as accurately as the main combustion phases, partly because the negative HRR magnitude is small and easily masked by noise, and partly because its short duration provides relatively few representative samples for training. Nevertheless, this limitation would have little impact on the overall combustion reconstruction, as the premixed and diffusion peaks dominate the heat release process. Compared to Method 1, Method 2 provides a much more accurate representation of the HRR profile, especially in reproducing the premixed combustion peak. Moreover, both the magnitude and phasing of the diffusion-controlled heat release are captured with higher accuracy across all altitude conditions. These improvements indicate that shifting the model output from pressure to HRR is advantageous for combustion-centered diagnostics and lays the foundation for more reliable pressure reconstruction in the subsequent analysis.

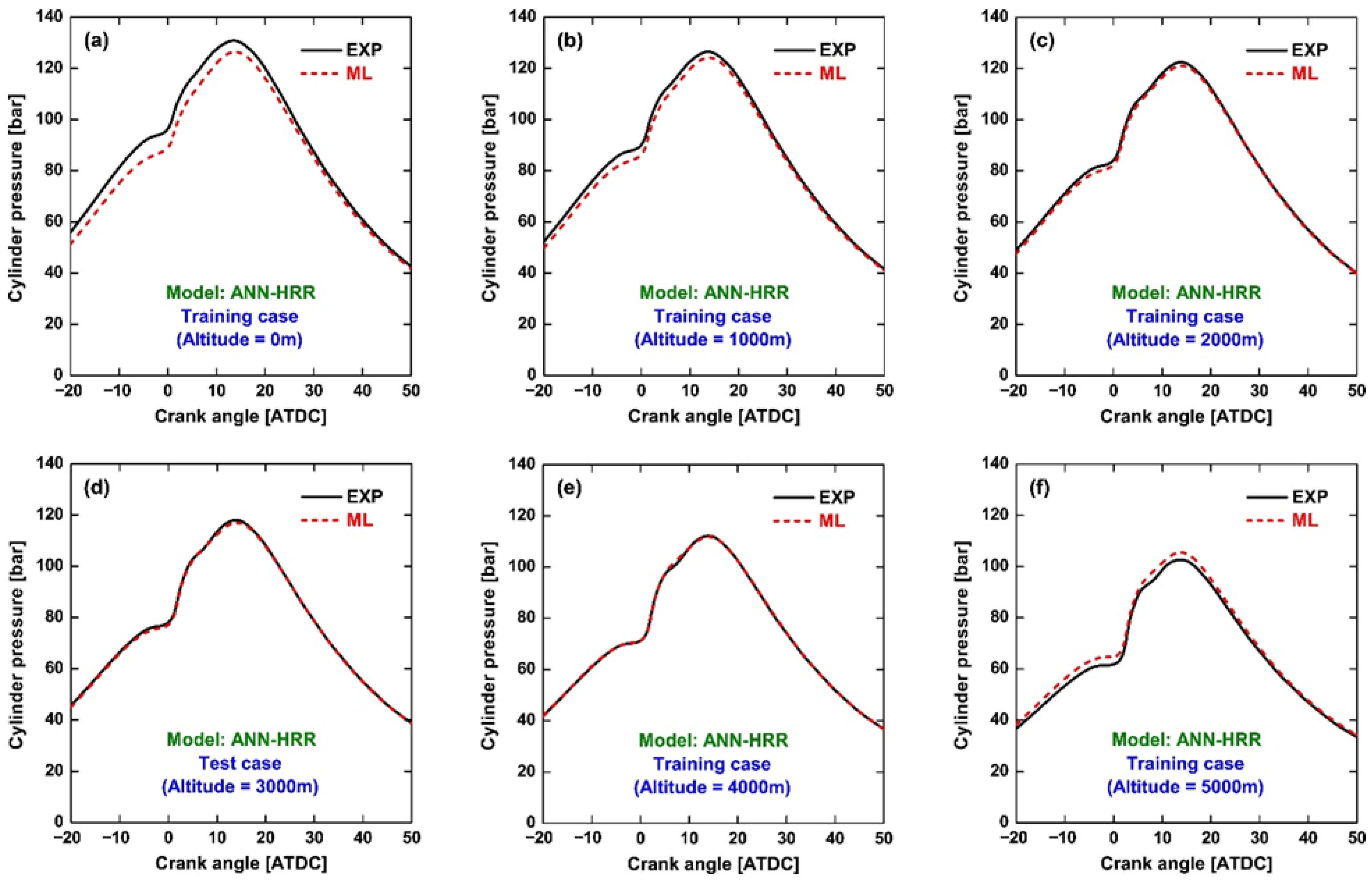
Figure 7 presents the reconstructed cylinder pressure traces obtained by integrating the ANN-HRR predictions. Overall, the model reproduces the pressure evolution across all altitudes with reasonable accuracy, particularly during the combustion phase where the predicted and experimental curves overlap closely. This consistency is expected, since the HRR predictions in Figure 6 captured the premixed and diffusion combustion peaks with high fidelity, which dominate the rapid pressure rise after ignition. Nevertheless, systematic discrepancies emerge in the non-combustion regions, most notably during the intake and compression strokes where the true HRR approaches zero. In these intervals, the experimental HRR signal is inherently weak and often dominated by noise, leaving the network with limited physical information to learn from. As a result, the ANN predictions in these regions contain spurious fluctuations that, although small in magnitude, accumulate when integrated over crank angle. This accumulation manifests as baseline offsets in the reconstructed pressure prior to ignition. For example, at lower altitudes (0, 1000, and 2000 m), the predicted pressure at the onset of combustion is slightly lower than the measured values, whereas at 5000 m the opposite trend is observed, with the predicted pressure being slightly higher. By contrast, at intermediate altitudes such as 3000 and 4000 m, the predicted baseline aligns more closely with the experimental traces, leading to better overall agreement.

These observations imply that Method 2 performs more robustly when combustion signals are strong relative to non-combustion contributions, but its ability to reconstruct the compression pressure baseline remains limited. In this sense, Method 2 is better suited for applications focused on combustion diagnostics, such as analyzing heat release characteristics and combustion phasing, rather than for tasks requiring precise cylinder pressure reconstruction over the entire engine cycle. Consequently, while Method 2 provides meaningful improvements over Method 1 in capturing combustion-induced pressure dynamics, the persistent baseline shift underscores the need for a hybrid strategy (Method 3) that combines the strengths of both direct pressure prediction and HRR-based reconstruction. Building on these insights, Method 3 is developed as a hybrid approach to address the limitations of Method 2. As described earlier, this strategy employs two complementary networks: an ANN-P model to predict cylinder pressure during the non-combustion phases, and an ANN-HRR_Comb model to predict HRR during combustion, from which pressure is reconstructed. By splicing these two components, a complete pressure trace over the full engine cycle can be obtained. Figure 8, Figure 9 and Figure 10 present the results of this hybrid method, illustrating its performance in both training and test cases.

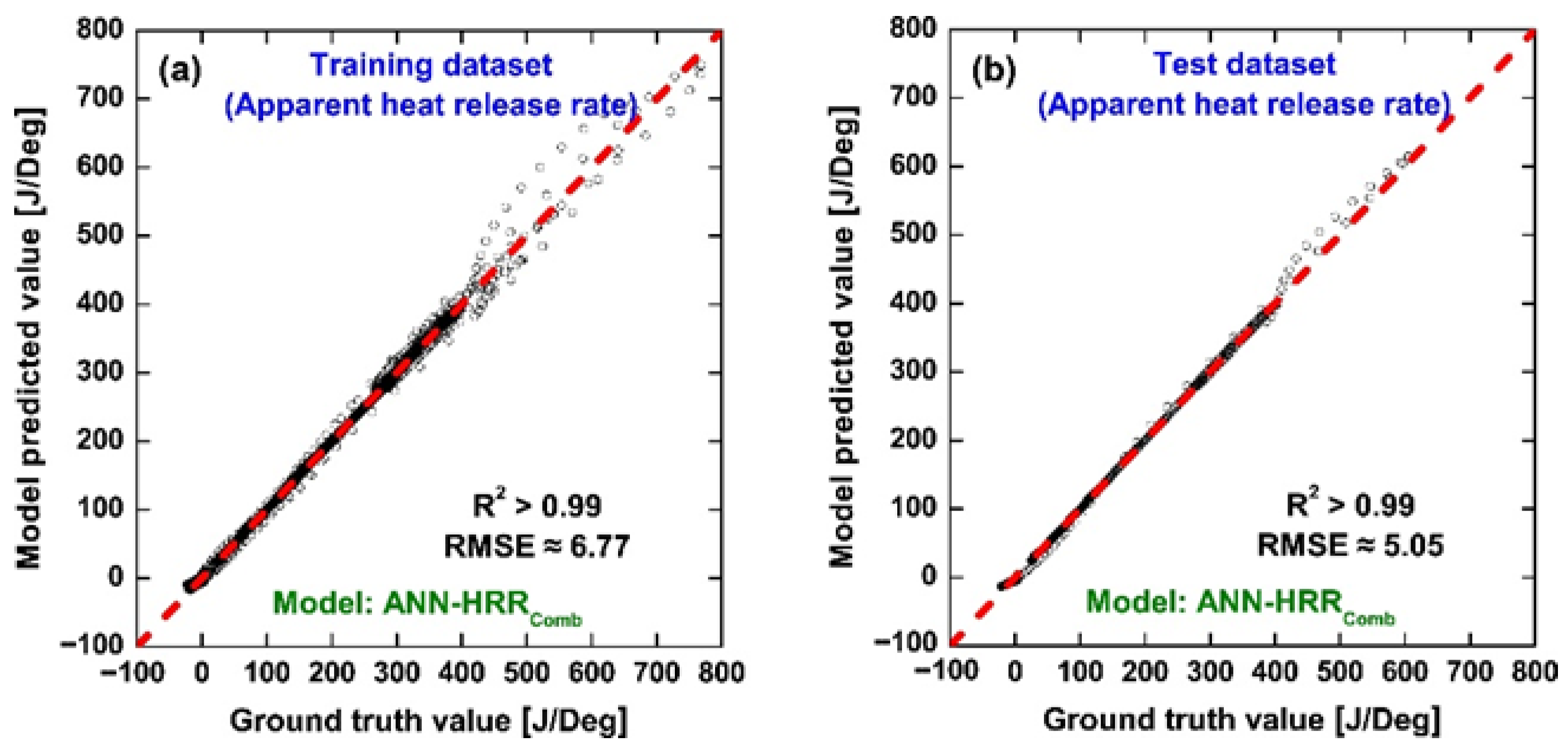
Figure 8 illustrates the parity plots of the ANN-HRR_Comb model for both the training and test datasets. Most of the predicted values align very closely with the 45° diagonal line, indicating excellent agreement with the measured HRR values. The statistical metrics confirm this observation, with R² values exceeding 0.99 and RMSE remaining within 5–7 J/deg. Compared with Method 2, a key improvement is evident around HRR ≈ 0. Because the ANN-HRR_Comb model only considers the combustion period and approximates HRR outside this phase as zero, the number of near-zero points is greatly reduced, and the corresponding scatter is minimized. This design effectively eliminates the influence of measurement noise in the non-combustion regions, which is a major source of error in Method 2. Another improvement is the absence of unrealistically large negative HRR values, which in Method 2 occasionally reach magnitudes of about −100 J/deg. In Method 3, these spurious negative values are suppressed since non-combustion HRR is directly treated as zero. Together, these results confirm that Method 3 provides a more robust and physically meaningful prediction of HRR during the combustion process.

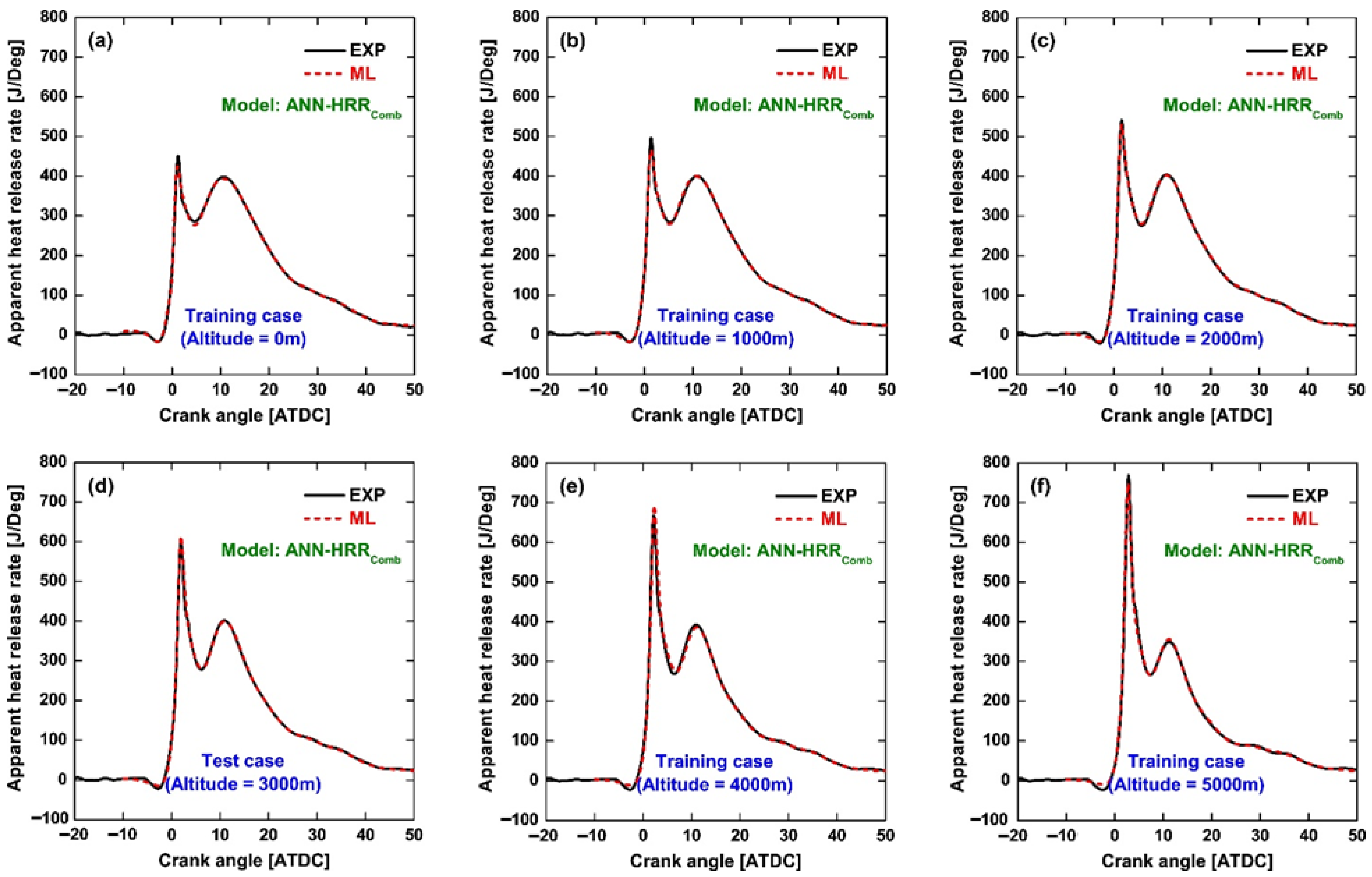
Figure 9 compares the combustion-phase HRR profiles predicted by the ANN-HRR_Comb model with experimental data. Across all operating conditions, including the unseen test case at 3000 m, the agreement is nearly perfect, with the premixed peak, diffusion-controlled phase, and late-burning tail all well reproduced. Compared to Method 2, the improvement is evident: by excluding the non-combustion regions dominated by measurement noise, the model concentrates on the physically meaningful combustion signals, leading to more accurate learning and prediction. As a result, the spurious oscillations and unrealistically large negative HRR values observed in Method 2 are no longer present. The ignition-delay-related negative HRR is still underpredicted, but its magnitude is closer to realistic levels. Moreover, the altitude-induced trend of increasing premixed peak with decreasing intake density is faithfully captured, further demonstrating the robustness of Method 3. Overall, this method yields a clearer and more reliable representation of HRR evolution, providing a solid foundation for subsequent pressure reconstruction.

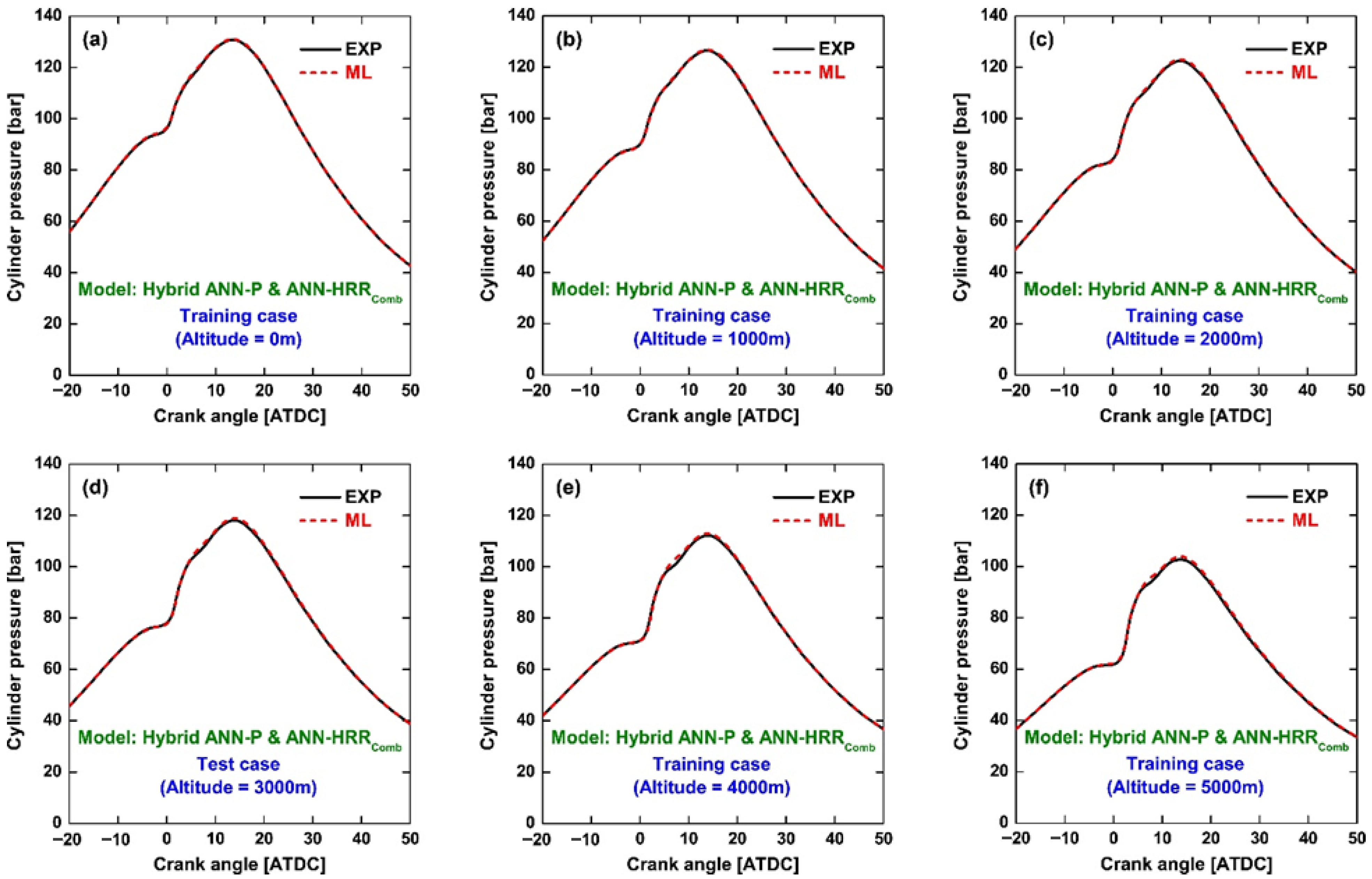
Figure 10 presents the reconstructed cylinder pressure traces obtained using the hybrid ANN-P & ANN-HRR_Comb model. Across all altitudes, the predicted pressure profiles show excellent agreement with the experimental data, with both the magnitude and phasing of peak pressure captured with high accuracy. The hybrid strategy effectively corrects the local discrepancies observed in Method 1 during the rapid pressure rise at combustion onset, while also mitigating the baseline shifts associated with Method 2. Furthermore, the altitude-induced trends, including reduced compression pressure and lower peak pressure at higher altitudes, are consistently reproduced, confirming the robustness of the hybrid model in capturing both global and local combustion features.

To complement these qualitative observations,

Table 1. Quantitative performance comparison of Methods 1–3 under different altitude conditions, evaluated by R² and RMSE for in-cylinder pressure and apparent heat release rate.

	Method	0 m	1000 m	2000 m	3000 m	4000 m	5000 m
R2 (Pressure)	1	1.0000	1.0000	1.0000	1.0000	0.9999	0.9998
	2	0.9986	0.9988	0.9985	0.9985	0.9996	0.9953
	3	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
RMSE (Pressure)	1	0.2334	0.1681	0.1501	0.1758	0.2126	0.2825
	2	1.7650	1.2164	1.1064	1.0293	0.4581	1.6576
	3	0.0744	0.0674	0.1201	0.1529	0.1677	0.1999
R2 (HRR)	1	0.9853	0.9859	0.9854	0.9814	0.9722	0.9467
	2	0.9944	0.9951	0.9953	0.9951	0.9945	0.9939
	3	0.9987	0.9991	0.9994	0.9990	0.9944	0.9977
RMSE (HRR)	1	7.8317	7.6586	7.7799	8.7860	10.5856	14.2358
	2	4.8327	4.5072	4.3913	4.4963	4.6740	4.8001
	3	5.0700	4.0423	3.7726	5.0530	11.0452	7.1181

summarizes the quantitative prediction performance of the three strategies across different altitude conditions. For Methods 1 and 2, both pressure and HRR predictions are evaluated over the full cycle (7200 points per condition), whereas in Method 3, HRR prediction is restricted to the combustion window (–10° to 50° CA ATDC, 600 points), while pressure is still assessed over the entire cycle (7200 points). For pressure reconstruction, Method 3 consistently delivers the highest accuracy, as reflected by both R² and RMSE, owing to its hybrid design that mitigates the baseline drift observed in Method 2 and the HRR-related underestimation in Method 1. Method 1 also outperforms Method 2, since the latter suffers from cumulative integration errors when reconstructing pressure from HRR across non-combustion regions. For HRR prediction, Method 3 achieves performance comparable to or slightly better than Method 2, whereas Method 1 shows markedly inferior results. This is evident from both the lower R² and the substantially higher RMSE values of Method 1, indicating its limited ability to capture detailed combustion features. The slightly higher RMSE of Method 3 compared with Method 2 can be attributed to the difference in the number of data points considered (600 points for Method 3 vs. 7200 for Method 2). Taken together, these results demonstrate that the hybrid strategy provides the most reliable and physically consistent reconstruction of both pressure and HRR, striking a favorable balance between global trace accuracy and combustion feature fidelity, albeit at the cost of coordinating two separate networks.

4. Summary and Conclusions

This study presents a machine learning-assisted framework for reconstructing in-cylinder pressure under unmeasured operating conditions, using experimental data from a turbocharged diesel engine across altitudes ranging from sea level to 5000 m. Three ANN-based strategies are compared, and the work represents a new paradigm in engine research by constructing the full pressure–crank angle trace directly from input–output mapping. This approach goes beyond conventional ML applications that mainly predict scalar indicators or rely on simplified physical models, and it demonstrates the feasibility of generating complete cylinder pressure traces purely from data. The key conclusions are as follows:

(1)

Method 1 directly predicts in-cylinder pressure. This approach achieves excellent predictive accuracy and reliably reproduces the overall pressure evolution across both training and unseen test conditions. However, small discrepancies in the steep pressure rise region are amplified when deriving apparent heat release rate, leading to underestimation of the premixed combustion peak. Consequently, Method 1 is well suited for global pressure-based evaluations but remains limited in detailed HRR-oriented diagnostics.

(2)

Method 2 indirectly reconstructs cylinder pressure by first predicting the full-cycle HRR and then integrating it using a single-zone heat release model. This strategy improves the fidelity of HRR predictions, especially the premixed and diffusion peaks, and therefore better captures combustion phasing. Nevertheless, inaccuracies in the non-combustion regions, where HRR is dominated by noise and lacks clear physical patterns, accumulate into baseline shifts in the reconstructed pressure. As a result, Method 2 is more suitable for combustion diagnostics than for cycle-resolved pressure reconstruction.

(3)

Method 3 integrates the advantages of the two preceding methods in a hybrid configuration, applying an ANN to predict pressure in the non-combustion phases and another ANN to predict HRR during combustion for reconstructing pressure in the combustion phase. This design significantly improves pressure reconstruction, correcting both the baseline shift of Method 2 and the premixed HRR underestimation of Method 1. The hybrid model consistently reproduces altitude-induced variations in cylinder pressure and HRR, demonstrating the most robust and physically consistent performance among the three strategies. This improvement comes at the cost of added complexity in coordinating two networks.

Overall, the results highlight that machine learning serves as an efficient and accurate tool for reconstructing in-cylinder pressure at unmeasured conditions, reducing experimental burden while enabling combustion analysis across a wide range of operating points. The direct pressure prediction (Method 1) is appropriate for rapid pressure reconstruction; the full-cycle HRR approach (Method 2) is advantageous for combustion diagnostics; and the hybrid framework (Method 3) offers the most balanced performance for applications requiring both reliable pressure traces and detailed combustion metrics.

The present study is limited to varying a single operating parameter due to the availability of experimental data. Nonetheless, it establishes an important first step toward a new paradigm, directly reconstructing the full pressure–crank angle trace from data rather than relying solely on scalar indicators or simplified physical models. Future studies will extend the framework beyond one-dimensional variation by incorporating additional engine and boundary parameters, such as intake pressure and temperature, injection pressure, injection quantity, injection timing, engine speed, and even fuel properties. As collecting such comprehensive datasets experimentally is often impractical, forthcoming work will leverage CFD-generated data to augment limited measurements and enable large-scale training across multidimensional operating spaces. Expanding the input space in this way will allow the model to generalize more effectively and predict pressure traces for arbitrary combinations of parameters. The ultimate goal is to establish a versatile machine-learning-based framework capable of providing reliable cylinder pressure reconstruction across the entire engine map, thereby supporting efficient calibration, digital twin applications, and real-time combustion diagnostics.