Multi-Objective Collaborative Optimization of Distribution Networks with Energy Storage and Electric Vehicles Using an Improved NSGA-II Algorithm
Abstract
1. Introduction
2. Basic Equipment Models
2.1. Distributed Generation Output Models
2.2. Non-Dispatchable Electric Vehicles Load Model
- (1)
- SOC limits (SOCmin ≤ SOC(t) ≤ SOCmax);
- (2)
- Maximum charging/discharging power limits (Pc,max, Pd,max);
- (3)
- Availability windows aligned with typical residential/workplace charging behavior.
2.3. Energy Storage and Schedulable Electric Vehicles Charging–Discharging Model
3. Coordinated Response Model and Algorithm for Energy Storage and Electric Vehicles
3.1. Objective Function
- (1)
- Investment cost Fm
- (2)
- Expected Grid Energy Shortage Em
- (3)
- Network Loss Floss
- (4)
- Operation and Maintenance Cost Fom
3.2. Constraints
- (1)
- Equality constraints:
- (2)
- Inequality constraints
4. Solution Procedure for the Configuration Scheme Based on the NSGA-II Algorithm
4.1. Planning Model and Control-Variable Encoding Strategy
4.2. Multi-Objective Handling and Optimal-Solution Selection
5. Case Study Analysis
5.1. Case Parameters
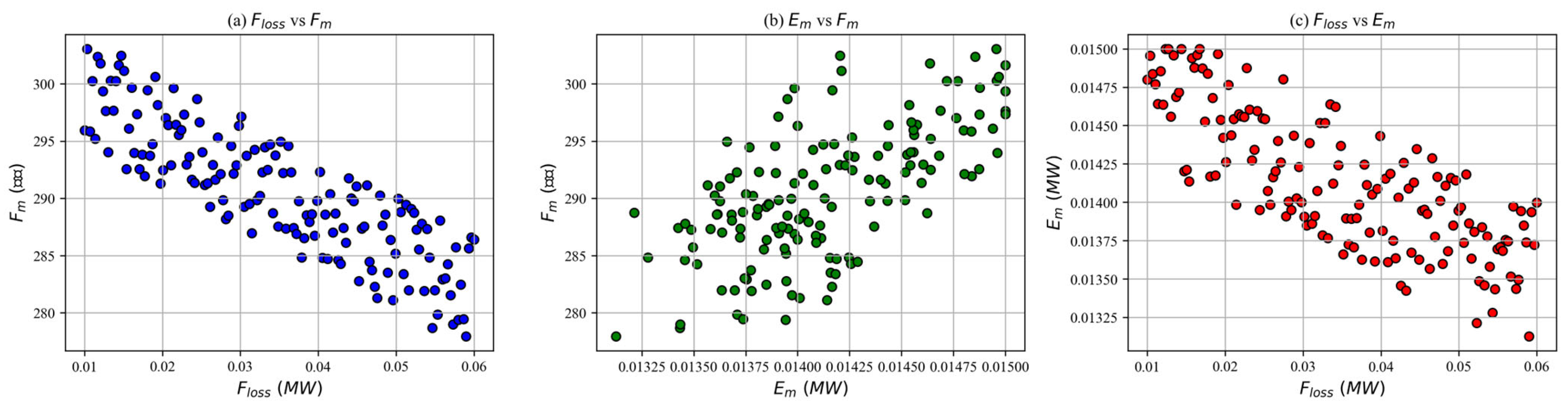
5.2. Comparison and Analysis of Computational Results
- (1)
- Optimization Results and Discussion
- (2)
- Comparison of Power-Supply Schemes
5.3. Sensitivity Analysis
- (i)
- Post-evaluation sensitivity: The optimal configuration in Table 2 is fixed (the capacity and nodes of PV, WT, and ES remain unchanged), and only the operating point (daytime/nighttime, irradiation intensity, wind speed, and ES operation strategy) is changed, and the operability indicators are recalculated.
- (ii)
- Re-optimization sensitivity: When the ES access location (trunk/terminal) is changed, it is re-optimized as a planning variable, and the migration of the compromise solution and the change in indicators are compared.
6. Conclusions
- (1)
- Scalability verification: Applying the method to larger-scale distribution networks to assess its scalability and computational performance in more complex scenarios.
- (2)
- Algorithmic enhancement: Integrating the framework with hybrid optimization algorithms or advanced approaches (e.g., deep reinforcement learning) to improve convergence speed and global search capability.
- (3)
- Demand–response integration: Incorporating demand–response mechanisms and real-time scheduling strategies to enhance adaptability and robustness under fluctuating loads and renewable-generation variations.
- (4)
- Engineering validation: Implementing the proposed approach in real-world distribution-network projects for field demonstration and operational verification. In practice, the method can use standard grid operation data such as load profiles and renewable output, and its computational complexity remains manageable. The algorithm can also be extended to larger grids through parallel evaluation, which supports scalability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, P.; Wang, J.; Sun, L.; Li, Y.; Xia, H.; He, W. Optimal electrode configuration and system design of compactly-assembled industrial alkaline water electrolyzer. Energy Convers. Manag. 2023, 299, 117875. [Google Scholar] [CrossRef]
- Cheng, Z.; Yan, Y.; Zhou, E.; Gao, B.; Qin, G.; Zhang, K.; Chen, T.; Ma, G.; Huang, X. Synergistic Optimization of Pore and Conductive Network of Short-Cut Graphene Porous Fibers for Lightweight Broadband Electromagnetic Wave Absorption. Small 2025, 21, e05866. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Tian, X.; Chen, H.; Zhu, H.; Qiao, R. Edge collaborative caching solution based on improved NSGA II algorithm in Internet of Vehicles. Comput. Netw. 2024, 244, 110307. [Google Scholar] [CrossRef]
- Liu, Z.; Su, J.; Du, S.; Wang, J.; Zhang, W. A Novel Cooperative Dynamic Optimization Method of Network Reconfiguration and DG Scheduling in Active Distribution Network. J. Electr. Eng. Technol. 2025, 1–14. [Google Scholar] [CrossRef]
- Jiang, T.; Guan, Z.; Li, H.; Zhang, M.; Mu, S.; Wu, C.; Jin, M. Collaborative optimization method of cleaning operational performance and multiparameter online control system for combine harvesters. Comput. Electron. Agric. 2025, 235, 110389. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Y.; Sun, H.; Tai, N. Frequency-constrained microgrid-distribution network coordinated load restoration: A distributed carbon-aware optimization approach. Appl. Energy 2025, 395, 126221. [Google Scholar] [CrossRef]
- Chen, Y.; Bao, Z.; Tan, Y.; Wang, J.; Liu, Y.; Sang, H.; Yuan, X. Hierarchical Charging Scheduling Strategy for Electric Vehicles Based on NSGA-II. Energies 2025, 18, 3269. [Google Scholar] [CrossRef]
- Sun, S.; Yu, P.; Xing, J.; Wang, Y.; Yang, S. Multi-objective collaborative optimization of active distribution network operation based on improved particle swarm optimization algorithm. Sci. Rep. 2025, 15, 8999. [Google Scholar] [CrossRef]
- Li, Y.; Li, K.; Fan, R.; Chen, J.; Zhao, Y. Multi-objective planning of distribution network based on distributionally robust model predictive control. Front. Energy Res. 2024, 12, 1478040. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Y.; Zhuo, R.; Jia, H. Energy storage capacity optimization for autonomy microgrid considering CHP and EV scheduling. Appl. Energy 2018, 210, 1113–1125. [Google Scholar] [CrossRef]
- Tong, X.; Ma, Q.; Tang, K.; Liu, H.; Li, C. Influence of electric vehicle access mode on the static voltage stability margin and accommodated capacity of the distribution network. J. Eng. 2019, 2019, 2658–2662. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A.; Soomro, A.M.; Baloch, M.; Chaudhary, S.T.; Shaikh, M.A. A Comprehensive Review of Optimizing Multi-Energy Multi-Objective Distribution Systems with Electric Vehicle Charging Stations. World Electr. Veh. J. 2024, 15, 523. [Google Scholar] [CrossRef]
- Su, R.; He, G.; Su, S.; Duan, Y.; Cheng, J.; Chen, H.; Wang, K.; Zhang, C. Optimal placement and capacity sizing of energy storage systems via NSGA-II in active distribution network. Front. Energy Res. 2023, 10, 1073194. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, Q.; Shi, L.; Weng, Y.; Li, J. A Safe energy policy optimization method for multienergy microgrid control. IEEE Trans. Power Syst. 2025, 40, 1686–1698. [Google Scholar] [CrossRef]
- Li, J.; Shi, L.; Fu, H. Multi-objective short-term optimal dispatching of cascade hydro–wind–solar–thermal hybrid generation system with pumped storage hydropower. Energies 2025, 17, 98. [Google Scholar] [CrossRef]
- Jensen, M. Reducing the run-time complexity of multiobjective EAs: The NSGA-II and other algorithms. IEEE Trans. Evol. Comput. 2003, 7, 503–515. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, T.; Liao, Z.; Tang, Z.; Pei, Y.; Cui, Q.; Shu, J.; Zheng, W. Optimal operation strategy for distribution network with high-penetration distributed PV based on soft open point and multi-device collaboration. Energy 2025, 325, 136191. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Jie, G.; Qirui, R.; Yu, H.; Yuxiao, Z.; Zhang, H. A Cooperative Operation Optimization Method for Medium-and Low-Voltage Distribution Networks Considering Flexible Interconnected Distribution Substation Areas. Processes 2025, 13, 1123. [Google Scholar] [CrossRef]
- Boubaker, S.; Kraiem, H.; Ghazouani, N.; Kamel, S.; Mellit, A.; Alsubaei, F.S.; Bourennani, F.; Meskine, W.; Alqubaysi, T. Multi-objective optimization framework for electric vehicle charging and discharging scheduling in distribution networks using the red deer algorithm. Sci. Rep. 2025, 15, 13343. [Google Scholar] [CrossRef]
- Baptista, J.E.R.; Rodrigues, A.B.; Silva, M.D.G. Probabilistic Analysis of PV generation impacts on voltage sags in LV distribution networks considering failure rates dependent on feeder loading. IEEE Trans. Sustain. Energy 2018, 10, 1342–1350. [Google Scholar] [CrossRef]
- Li, S.; Shao, J.; Zhang, S.; Chen, H. Distribution network reconfiguration incorporating thermostatic loads after multiple line contingency. Energy Rep. 2025, 13, 813–823. [Google Scholar] [CrossRef]
- Heris, S.M.K.; Khaloozadeh, H. Open- and closed-loop multiobjective optimal strategies for HIV therapy using NSGA-II. IEEE Trans. Biomed. Eng. 2011, 58, 1678–1685. [Google Scholar] [CrossRef] [PubMed]
- Nie, S.; Cai, J.; Ji, H.; Zhang, J.; Hong, R. Multi-objective optimization integrating weighted average surrogate model and NSGA-II intelligent algorithm applied to a self-excited oscillation mixer used in mixed flow descaling. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 7444–7462. [Google Scholar] [CrossRef]
- Yang, X.; Long, J.; Liu, P.; Zhang, X.; Liu, X. Optimal scheduling of microgrid with distributed power based on water cycle algorithm. Energies 2018, 11, 2381. [Google Scholar] [CrossRef]
- Gbadega, P.A.; Sun, Y.; Balogun, O.A. A Unified Optimization Framework for Cost-Effective and Voltage-Stable Operation of Renewable Energy-Based Microgrids Using Mixed-Integer Nonlinear Programming. e-Prime 2025, 12, 101010. [Google Scholar] [CrossRef]
- Xie, H.; Lin, G.; Wu, H.; Tong, Z.; He, Y.; Chen, L.; Liu, C.; Jiang, T. Sensing Performance of Crn (n = 1–3) Clusters Doped WSe2 and WTe2 for Gases in Power Transformer Winding Deformation Fault by DFT Calculation. Langmuir 2025, 41, 8781–8803. [Google Scholar] [CrossRef]
- Pang, H.; Wang, J.; Hu, X. Understanding the potential influence of wechat engagement on bonding capital, bridging capital, and electronic word-of-mouth intention. Sustainability 2021, 13, 8489. [Google Scholar] [CrossRef]





| Parameter Name | Retrieve a Value | Parameter Name | Retrieve a Value |
|---|---|---|---|
| CES | ¥130 million/MW | 0 | |
| CPV | ¥100 million/MW | 0.25 | |
| Cwind | ¥100 million/MW | ′ | 0.33 |
| a | ¥46.5 million/MW | Nl,max | 3 |
| b | ¥5 million | Npv,max, Nwind,max | 3 |
| pin | 0.0013 | pout | 0.01 |
| Typology | Access Point Location | Quantitative/MW |
|---|---|---|
| Wind power | 9 | 0.0159 |
| Wind power | 16 | 0.2299 |
| Photovoltaic | 6 | 0.4201 |
| Photovoltaic | 16 | 0.1496 |
| Load | 6 | 0.4121 |
| Load | 11 | 0.2201 |
| Load | 16 | 0.3610 |
| Energy storage | 10 | 0.1998 |
| Method | Convergence Generations | Fm (10−4 Yuan) | Em (10−4 Yuan) | Floss (10−4 Yuan) |
|---|---|---|---|---|
| Improved NSGA-II | 40 | 167 | 51 | 2.5 |
| PSO | 75 | 190 | 65 | 3.1 |
| Program | Distribution Network Capacity /MW | Fm/ (10−4 Million Yuan) | Em/ (10−4 Million Yuan) | Floss/ (10−4 Million Yuan) |
|---|---|---|---|---|
| 1 | — | 80 | 100 | 2.7 |
| 2 | 1.8000 | 215 | 27 | 27 |
| 3 | 1.6613 | 196 | 33 | 12 |
| 4 | 1.1501 | 167 | 51 | 2.5 |
| Energy Storage/(Million Yuan/MW) | Energy Storage Configuration | On-Net Load and DG | Off-Net Loads and DG | |||
|---|---|---|---|---|---|---|
| Placement | Quantitative/MW | Load/MW | DG/MW | Load/MW | DG/MW | |
| 110 | 9 | 0.2468 | 0.7901 | 0.5702 | 0.2097 | 0.2339 |
| 120 | 13 | 0.2311 | 0.7184 | 0.4811 | 0.2796 | 0.3236 |
| 130 | 10 | 0.1998 | 0.5812 | 0.3698 | 0.4197 | 0.4323 |
| Scenario | Operating Setting | Finv (104 CNY) | Em (104 CNY) | Floss (104 CNY) | Rationale |
|---|---|---|---|---|---|
| S0 Baseline | PV: Rc = Rr, Tc = 25 °C; WT: v ≈ 0.8vr; ES: real-time | 1175 | 51.0 | 2.50 | Optimal configuration at typical daily operating point |
| S1 PV-cloudy | PV: Rc = 0.6Rr (cloudy sky), other parameters are the same as S0 | 1175 | 58.5 | 2.85 | PV output decreases → grid-side compensation is required → power outages and grid losses increase |
| S2 PV-winter | PV: Rc = 0.75Rr, Tc = 5 °C, other parameters are the same as S0 | 1175 | 54.0 | 2.65 | The radiation is weakened but the temperature is reduced to suppress the temperature rise loss, and the impact is moderate |
| S3 WT-high | WT: v = 0.9vr (high wind), other parameters are the same as S0 | 1175 | 48.0 | 2.30 | Increased wind power → Enhanced local supply → Reduced power outages and grid losses |
| S4 WT-low | WT: v = 0.6vr (low wind), other parameters are the same as S0 | 1175 | 61.0 | 3.20 | Wind power weakens → tidal backflow increases → network losses rise significantly |
| S5 ES-ND | ES strategy: night charge (0–6 h)/day discharge (10–16 h), other similarities to S0 | 1175 | 52.5 | 2.55 | Fixed-period strategies are slightly weaker than real-time strategies, and peak-valley alignment is insufficient. |
| S6 ES-RT | ES real-time (voltage/marginal loss trigger), others are the same as S0 | 1175 | 49.5 | 2.35 | On-demand scheduling → better voltage and loss characteristics |
| ES Bus | ES Size/MW | PV Size/MW | WT Size/MW | Finv (104 CNY) | Em (104 CNY) | Floss (104 CNY) | Note |
|---|---|---|---|---|---|---|---|
| 10 (main) | 0.200 | 0.570 | 0.370 | 1175 | 51.0 | 2.50 | Baseline compromise solution (trunk injection) |
| 16 (end) | 0.240 | 0.540 | 0.360 | 1190 | 53.0 | 2.90 | The terminal connection requires a larger ES to suppress the voltage drop/loss |
| 6 (mid) | 0.215 | 0.560 | 0.365 | 1182 | 51.8 | 2.62 | The mid-section layout is a compromise between performance and cost |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, R.; Hao, J.; Zhou, H.; Chen, F. Multi-Objective Collaborative Optimization of Distribution Networks with Energy Storage and Electric Vehicles Using an Improved NSGA-II Algorithm. Energies 2025, 18, 5232. https://doi.org/10.3390/en18195232
He R, Hao J, Zhou H, Chen F. Multi-Objective Collaborative Optimization of Distribution Networks with Energy Storage and Electric Vehicles Using an Improved NSGA-II Algorithm. Energies. 2025; 18(19):5232. https://doi.org/10.3390/en18195232
Chicago/Turabian StyleHe, Runquan, Jiayin Hao, Heng Zhou, and Fei Chen. 2025. "Multi-Objective Collaborative Optimization of Distribution Networks with Energy Storage and Electric Vehicles Using an Improved NSGA-II Algorithm" Energies 18, no. 19: 5232. https://doi.org/10.3390/en18195232
APA StyleHe, R., Hao, J., Zhou, H., & Chen, F. (2025). Multi-Objective Collaborative Optimization of Distribution Networks with Energy Storage and Electric Vehicles Using an Improved NSGA-II Algorithm. Energies, 18(19), 5232. https://doi.org/10.3390/en18195232





