Research on Green Distribution Problems of Mixed Fleets Considering Multiple Charging Methods
Abstract
1. Introduction
- We propose the MFGVRPTW-C model, which integrates mixed fleet route planning, time windows, multi-mode charging, and carbon cost accounting, achieving unified optimization under a single objective.
- We design an IALNS framework tailored to the problem, incorporating problem-specific construction methods, operators, and local improvement strategies, jointly addressing charging mode selection.
- Through benchmark tests and a real-world case study, we provide managerial insights into how fleet composition and charging methods influence cost and emission outcomes.
2. Literature Review
3. Problem Description and Mathematical Formulations
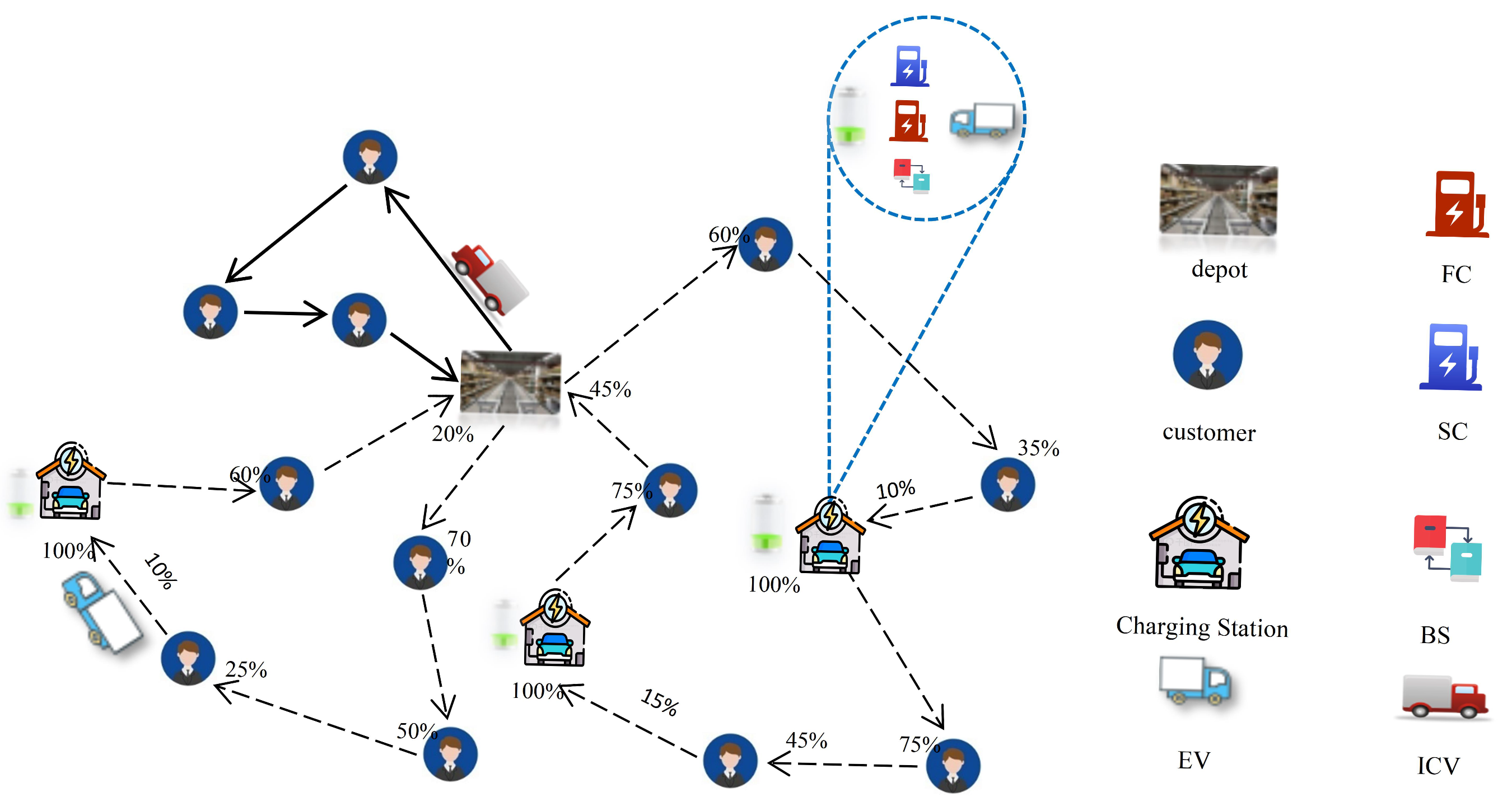
3.1. Problem Description
- (1)
- Each customer is exclusively served once by one vehicle (either fuel-powered or electric), with customer demand non-splittable.
- (2)
- When a vehicle arrives at a customer node or charging station, its engine is turned off, resulting in no energy consumption or carbon emissions.
- (3)
- Each charging station has no capacity limit, allowing multiple vehicles to receive charging or battery-swapping services simultaneously. Only one charging method can be selected per vehicle, the charging amount is linearly proportional to the charging time, and each vehicle is limited to a single charging event.
- (4)
- The two types of delivery vehicles (fuel and electric) are homogeneous within their respective types and have the same travel speed.
- (5)
- During the delivery process, a sufficient number of EVs and FVs are available for selection; that is to say, there is no restriction on the number of fuel-powered vehicles and electric vehicles.
3.2. Mathematical Formulations
3.2.1. Objective Function
3.2.2. Model Formulation
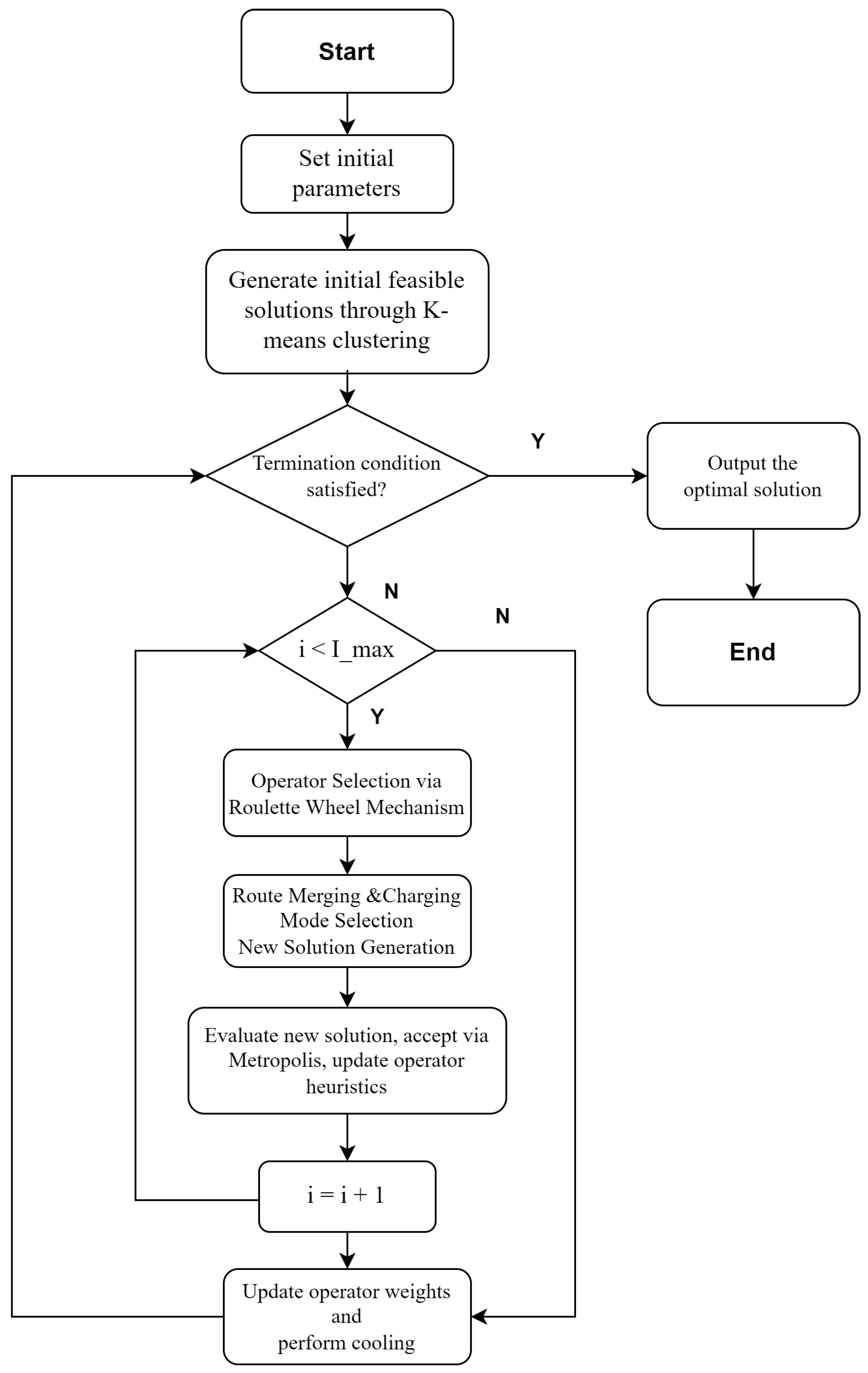
4. IALNS Algorithm
- Employing the K-means clustering method to generate an initial feasible solution.
- Designing distinct removal and repair operators for customer nodes and charging stations, tailored to the transportation process of a mixed fleet.
- Developing two local optimization operators to accelerate convergence.
4.1. Encoding Scheme
4.2. Construction of Initial Solutions
4.3. Removal Operators
4.3.1. Customer Node Removal
4.3.2. Charging Station Removal
4.4. Insertion Operators
4.4.1. Customer Node Insertion
4.4.2. Charging Station Insertion
4.5. Local Optimization Operators
| Algorithm 1: Route merging strategy. |
 |
| Algorithm 2: Select charging methods. |
 |
4.6. Operator Selection Strategy and Adaptive Adjustment Mechanism
- When operator i generates a solution that improves the best-known solution, its score is increased by .
- When operator i generates a solution that improves the current solution, its score is increased by .
- When operator i generates a solution worse than the current solution but the solution is accepted, its score is increased by .
4.7. Solution Acceptance Criterion and Algorithm Termination Conditions
5. Computational Results
5.1. Experiment Preparation
5.2. Performance of the Algorithm
5.2.1. Small-Scale Numerical Example Experiment
5.2.2. Medium- and Large-Scale Numerical Example Analysis
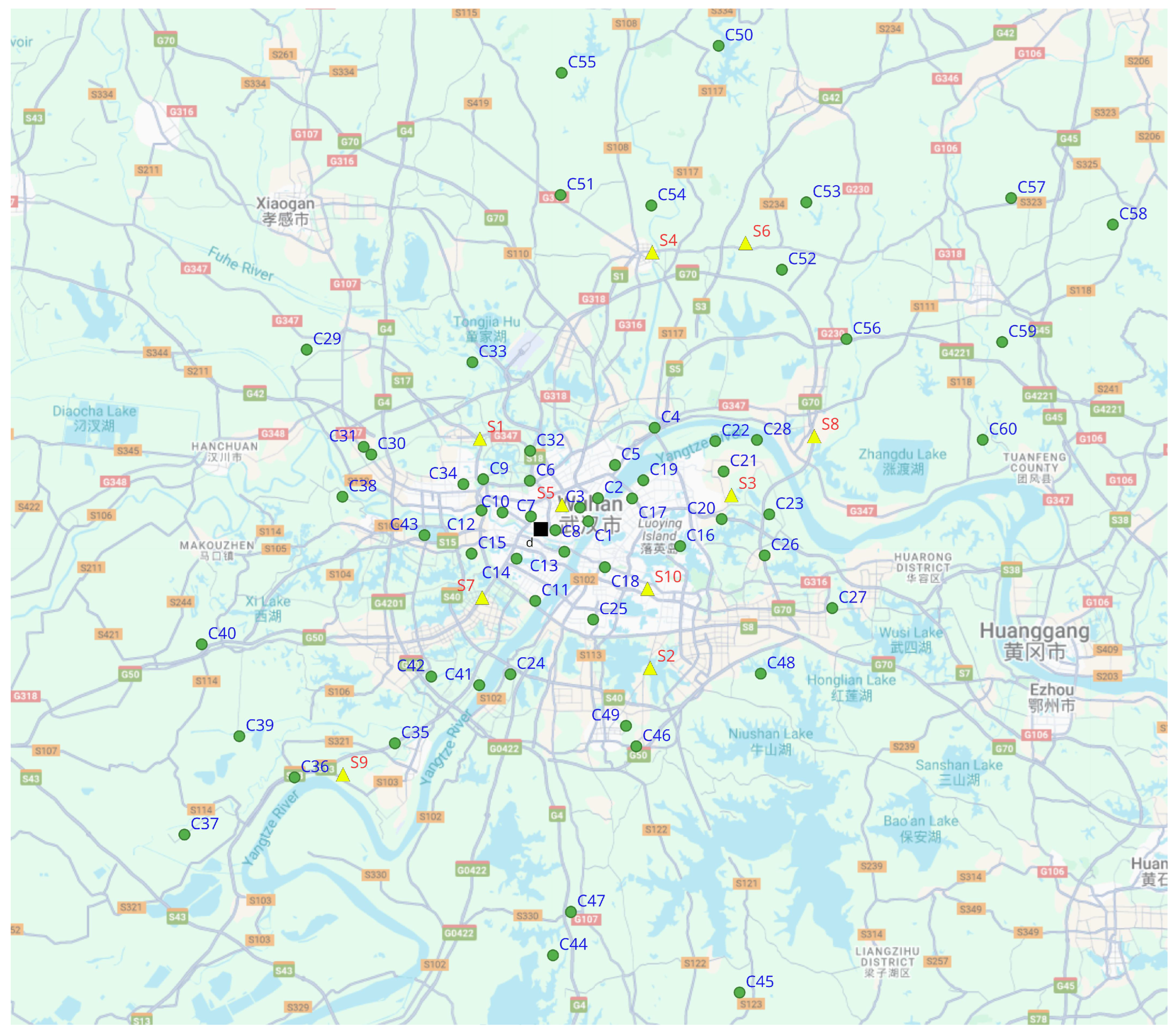
5.2.3. Simulation Case Study Experiment
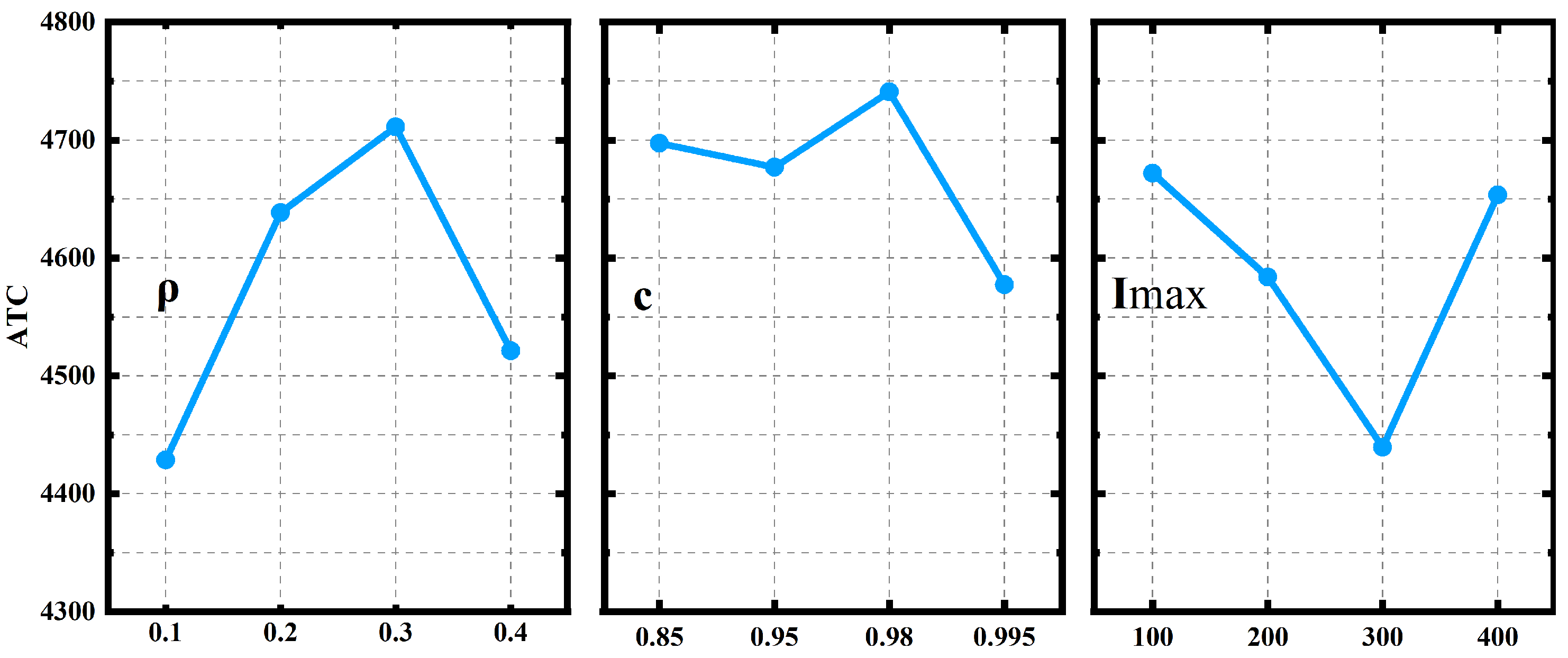
5.3. Sensitivity Analysis
5.3.1. Fleet Configuration
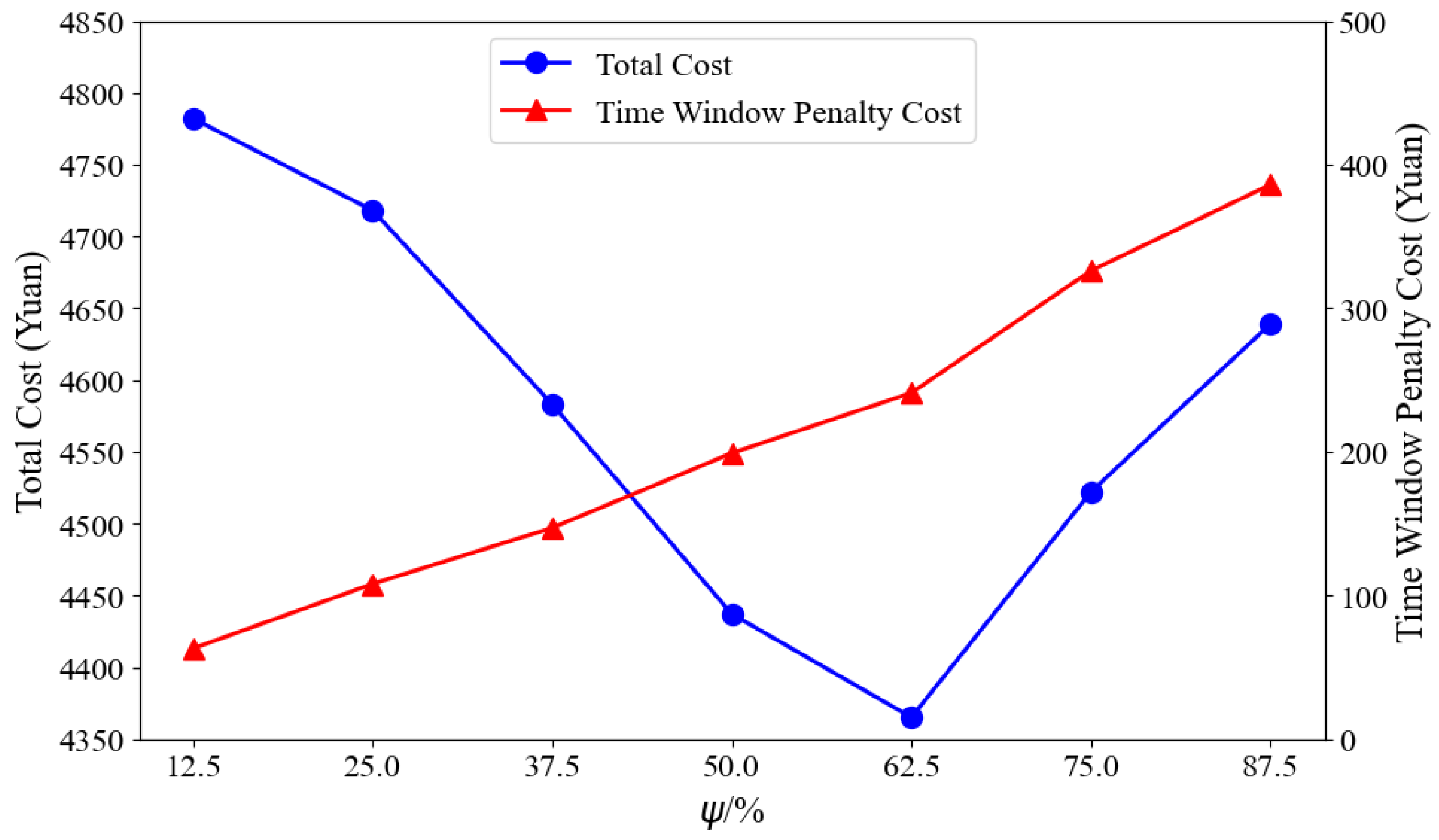
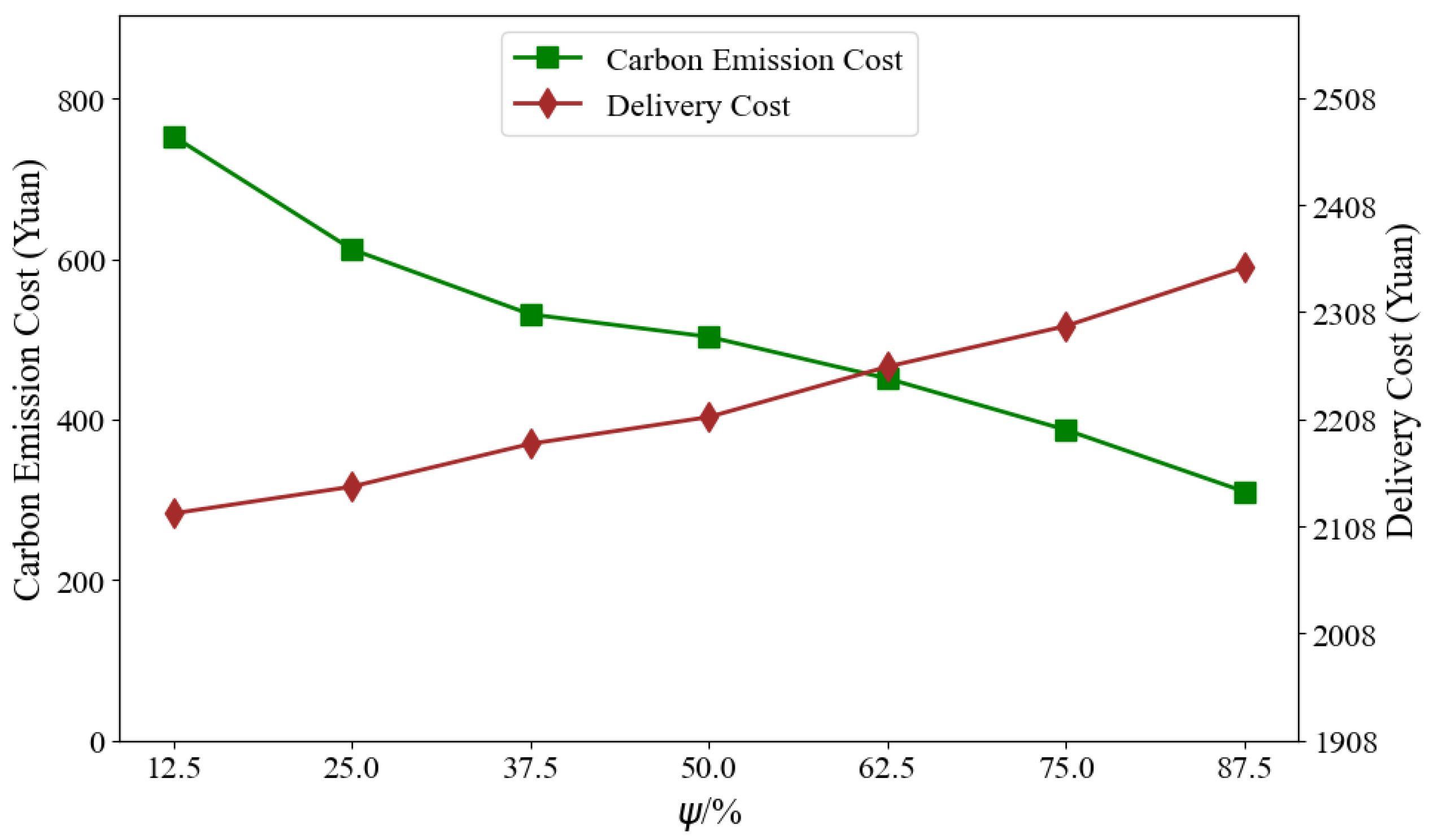
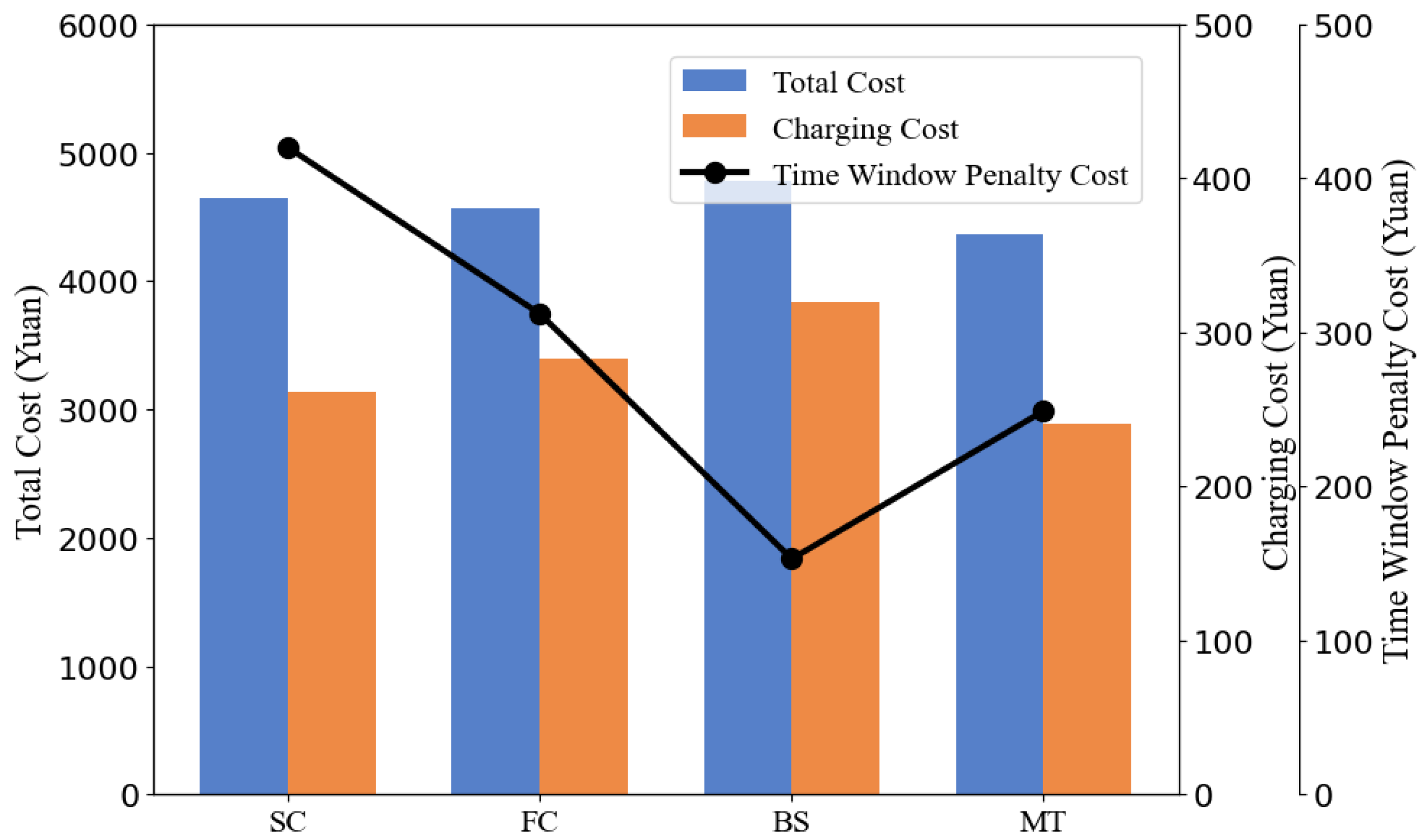
5.3.2. Different Charging Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| The starting and ending depot nodes. | |
| C | Set of customer nodes. |
| R | Set of charging station nodes. |
| Set of all customer and charging station nodes. | |
| Set of origin nodes, including the depot, customers, and charging | |
| stations. | |
| Set of destination nodes, including customers, charging stations, | |
| and the end depot. | |
| Set of all vehicles available at the depot. | |
| Sets of electric and fuel vehicles, respectively. | |
| Demand of customer node . | |
| Load carried by vehicle on arc . | |
| Distance of arc . | |
| Travel time from node i to node j. | |
| Arrival time of vehicle at node i. | |
| Departure time of vehicle from node i. | |
| Charging time of vehicle at node . | |
| Waiting time of vehicle at node i. | |
| Service time at node for vehicle . | |
| Service time window for customer node . | |
| Maximum load capacity of electric and fuel vehicles, respectively. | |
| Battery capacity of electric vehicles. | |
| Energy consumption rate of electric vehicles (in kWh/km). | |
| Battery level of vehicle upon arrival at/departure from node i. | |
| Amount of energy recharged by vehicle at node . | |
| Binary variable, equal to 1 if vehicle traverses arc , | |
| and 0 otherwise. | |
| Binary variable, equal to 1 if vehicle uses slow charging at node | |
| , and 0 otherwise. | |
| Binary variable, equal to 1 if vehicle uses fast charging at node | |
| , and 0 otherwise. | |
| Binary variable, equal to 1 if vehicle uses battery swapping at | |
| node , and 0 otherwise. | |
| M | A large positive constant used for constraint enforcement. |
References
- CO2 Emissions in 2023–Analysis—IEA. 2025. Available online: https://www.iea.org/reports/co2-emissions-in-2023 (accessed on 1 August 2025).
- Pamidimukkala, A.; Kermanshachi, S.; Rosenberger, J.; Hladik, G. Barriers and Motivators to the Adoption of Electric Vehicles: A Global Review. Green Energy Intell. Transp. 2024, 3, 100153. [Google Scholar] [CrossRef]
- Alanazi, F. Electric Vehicles: Benefits, Challenges, and Potential Solutions for Widespread Adaptation. Appl. Sci. 2023, 13, 6016. [Google Scholar] [CrossRef]
- Bunkar, A.; Gupta, S.; Sharma, D. Electrifying the Future: The Rise of Electric Vehicles. Int. J. Sci. Res. Eng. Manag. 2024, 8, 1–5. [Google Scholar] [CrossRef]
- Barman, P.; Dutta, L.; Bordoloi, S.; Kalita, A.; Buragohain, P.; Bharali, S.; Azzopardi, B. Renewable energy integration with electric vehicle technology: A review of the existing smart charging approaches. Renew. Sustain. Energy Rev. 2023, 183, 113518. [Google Scholar] [CrossRef]
- Koniak, M.; Jaskowski, P.; Tomczuk, K. Review of Economic, Technical and Environmental Aspects of Electric Vehicles. Sustainability 2024, 16, 9849. [Google Scholar] [CrossRef]
- Li, D.; Lau, A.D.; Gong, Y. Electric Vehicles Empowering the Construction of Green Sustainable Transportation Networks in Chinese Cities: Dynamic Evolution, Frontier Trends, and Construction Pathways. Energies 2025, 18, 1943. [Google Scholar] [CrossRef]
- Mohammed, A.; Saif, O.; Abo-Adma, M.; Fahmy, A.; Elazab, R. Strategies and sustainability in fast charging station deployment for electric vehicles. Sci. Rep. 2024, 14, 283. [Google Scholar] [CrossRef]
- Kumar, M.; Panda, K.; Naayagi, R.T.; Thakur, R.; Panda, G. Comprehensive Review of Electric Vehicle Technology and Its Impacts: Detailed Investigation of Charging Infrastructure, Power Management, and Control Techniques. Appl. Sci. 2023, 13, 8919. [Google Scholar] [CrossRef]
- Adamashvili, N.; Thrassou, A. Towards Sustainable Decarbonization: Addressing Challenges in Electric Vehicle Adoption and Infrastructure Development. Energies 2024, 17, 5443. [Google Scholar] [CrossRef]
- Jeong, J.; Ghaddar, B.; Zufferey, N.; Nathwani, J. Adaptive robust electric vehicle routing under energy consumption uncertainty. Transp. Res. Part C Emerg. Technol. 2024, 160, 104529. [Google Scholar] [CrossRef]
- Apata, O.; Bokoro, P.; Sharma, G. The Risks and Challenges of Electric Vehicle Integration into Smart Cities. Energies 2023, 16, 5274. [Google Scholar] [CrossRef]
- Liu, B.; Ni, W.; Liu, R.; Guo, Y.J.; Zhu, H. Optimal Electric Vehicle Charging Strategies for Long-Distance Driving. IEEE Trans. Veh. Technol. 2024, 73, 4949–4960. [Google Scholar] [CrossRef]
- Bruj, O.; Calborean, A. Lifecycle Evaluation of Lithium-Ion Batteries Under Fast Charging and Discharging Conditions. Batteries 2025, 11, 65. [Google Scholar] [CrossRef]
- Jiang, Y.; Ke, Y.; Yang, F.; Ji, J.; Peng, W. State of Health Estimation for Second-Life Lithium-Ion Batteries in Energy Storage System with Partial Charging-Discharging Workloads. IEEE Trans. Ind. Electron. 2024, 71, 13178–13188. [Google Scholar] [CrossRef]
- Leijon, J.; Boström, C. Charging Electric Vehicles Today and in the Future. World Electr. Veh. J. 2022, 13, 139. [Google Scholar] [CrossRef]
- Li, Y.; Li, F.; Li, Q.; Zhang, P. Battery swapping station location routing problem: A Cooperative Business Model. Comput. Ind. Eng. 2024, 200, 110775. [Google Scholar] [CrossRef]
- Qi, W.; Zhang, Y.; Zhang, N. Scaling Up Electric-Vehicle Battery Swapping Services in Cities: A Joint Location and Repairable-Inventory Model. Manag. Sci. 2023, 69, 6855–6875. [Google Scholar] [CrossRef]
- Ferro, G.; Paolucci, M.; Robba, M. Optimal Charging and Routing of Electric Vehicles with Power Constraints and Time-of-Use Energy Prices. IEEE Trans. Veh. Technol. 2020, 69, 14436–14447. [Google Scholar] [CrossRef]
- Xie, D.-F.; Yu, Y.; Zhou, G.; Zhao, X.; Chen, Y. Collaborative optimization of electric bus line scheduling with multiple charging modes. Transp. Res. Part D Transp. Environ. 2023, 114, 103551. [Google Scholar] [CrossRef]
- Wang, W.; Adulyasak, Y.; Cordeau, J.F.; He, G. The Heterogeneous-Fleet Electric Vehicle Routing Problem with Nonlinear Charging Functions. Transp. Res. Part C Emerg. Technol. 2025, 170, 104932. [Google Scholar] [CrossRef]
- Ma, H.; Yang, R.; Li, X. Delivery routing for a mixed fleet of conventional and electric vehicles with road restrictions. Int. J. Prod. Res. 2024. [Google Scholar] [CrossRef]
- Li, Y.; Liao, W.; Huang, Y. Mixed fleet-based two-echelon vehicle routing optimization for cold chain logistics with diverse recharging strategies. PLoS ONE 2025, 20, e0318765. [Google Scholar] [CrossRef] [PubMed]
- Dantzig, G.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Demir, E.; Bektaş, T.; Laporte, G. The bi-objective Pollution-Routing Problem. Eur. J. Oper. Res. 2014, 232, 464–478. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Y.; Qin, J. The pollution-routing problem with one general period of congestion. J. Model. Manag. 2022, 18, 1529–1560. [Google Scholar] [CrossRef]
- Erdoğan, S.; Miller-Hooks, E. A Green Vehicle Routing Problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Çatay, B.; Keskin, M. The impact of quick charging stations on the route planning of Electric Vehicles. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; pp. 152–157. [Google Scholar] [CrossRef]
- Felipe, Á.; Ortuño, M.T.; Righini, G.; Tirado, G. A heuristic approach for the green vehicle routing problem with multiple technologies and partial recharges. Transp. Res. Part E-Logist. Transp. Rev. 2014, 71, 111–128. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B. Partial recharge strategies for the electric vehicle routing problem with time windows. Transp. Res. Part C-Emerg. Technol. 2016, 65, 111–127. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, M.; Lee, C. Capacity Planning for an Electric Vehicle Charging Station Considering Fuzzy Quality of Service and Multiple Charging Options. IEEE Trans. Veh. Technol. 2021, 70, 12529–12541. [Google Scholar] [CrossRef]
- Aljabri, B.S.; Fararah, E.S. Electric vehicle routing problem with time windows, battery swapping van, and energy consumption (EVRPTW-BSV-EC). World J. Adv. Res. Rev. 2024, 22, 1914–1926. [Google Scholar] [CrossRef]
- Kancharla, S.R.; Ramadurai, G. Electric vehicle routing problem with non-linear charging and load-dependent discharging. Expert Syst. Appl. 2020, 160, 113714. [Google Scholar] [CrossRef]
- Ren, X.; Huang, H.; Feng, S.; Liang, G. An improved variable neighborhood search for bi-objective mixed-energy fleet vehicle routing problem. J. Clean. Prod. 2020, 275, 124155. [Google Scholar] [CrossRef]
- Ding, N.; Li, M.; Hao, J. A Two-Phase Approach to Routing a Mixed Fleet with Intermediate Depots. Mathematics 2023, 11, 1924. [Google Scholar] [CrossRef]
- Dönmez, S.; Koç, Ç.; Altiparmak, F. The mixed fleet vehicle routing problem with partial recharging by multiple chargers. Transp. Res. Part E Logist. Transp. Rev. 2022, 167, 102917. [Google Scholar] [CrossRef]
- Røpke, S.; Pisinger, D. An Adaptive Large Neighborhood Search Heuristic for the Pickup and Delivery Problem with Time Windows. Transp. Sci. 2006, 40, 455–472. [Google Scholar] [CrossRef]
- Naccache, S.; Côté, J.F.; Coelho, L.C. The multi-pickup and delivery problem with time windows. Eur. J. Oper. Res. 2018, 269, 353–362. [Google Scholar] [CrossRef]
- Pereira, V.G.; Alves-Junior, O.C.; Baldo, F. An Approach to Solve the Heterogeneous Fixed Fleet Vehicle Routing Problem with Time Window Based on Adaptive Large Neighborhood Search Meta-Heuristic. IEEE Trans. Intell. Transp. Syst. 2024, 25, 8148–8157. [Google Scholar] [CrossRef]
- Amiri, A.; Zolfagharinia, H.; Amin, S.H. Routing a mixed fleet of conventional and electric vehicles for urban delivery problems: Considering different charging technologies and battery swapping. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2191804. [Google Scholar] [CrossRef]
- Xue, S.; Song, R.; He, S.; An, J.; Wang, Y. An Improved Adaptive Large Neighborhood Search Algorithm for the Heterogeneous Customized Bus Service with Multiple Pickup and Delivery Candidate Locations. J. Adv. Transp. 2022, 2022, 1679469. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, F.; Ding, L.; Jiang, J.; Han, Z. A Novel Approach for Optimizing Mixed Hazardous Material Fleet Vehicle Routing Problem Method Through Intermediate Bulk Container Sharing with Adaptive Intuitionistic Fuzzy Large Neighborhood Search. Int. J. Fuzzy Syst. 2024, 27, 1827–1845. [Google Scholar] [CrossRef]
- Mo, Y.; Yang, K.; Han, S.; Gupta, S. Multi-period heterogeneous fleet vehicle routing problem with self-pickup point selection: A last-mile delivery scenario in urban and rural areas. Ann. Oper. Res. 2024. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Aydınalp, Z.; Özgen, D. Solving vehicle routing problem with time windows using metaheuristic approaches. Int. J. Intell. Comput. Cybern. 2022, 16, 121–138. [Google Scholar] [CrossRef]
- Liu, Y.; Roberto, B.; Zhou, J.; Yu, Y.; Sun, W. Efficient feasibility checks and an adaptive large neighborhood search algorithm for the time-dependent green vehicle routing problem with time windows. Eur. J. Oper. Res. 2023, 310, 133–155. [Google Scholar] [CrossRef]
- Meng, F.; Zhou, X.; Piao, X.; Chu, D. Variable neighbourhood search based on Metropolis criterion for crowdsourced delivery scheduling problem in dispatch model. Comput. Oper. Res. 2024, 167, 106662. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Goeke, D. The Electric Vehicle-Routing Problem with Time Windows and Recharging Stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, J.; Sun, Y.; Fan, J.; Wang, Z.; Wang, H. Collaborative multidepot electric vehicle routing problem with time windows and shared charging stations. Expert Syst. Appl. 2023, 219, 119654. [Google Scholar] [CrossRef]
| Instance | Gurobi | IALNS Algorithm | %GAP | ||
|---|---|---|---|---|---|
| T | TC | T | TC | ||
| c101C10F5 | 1013.24 | 3686.34 | 31.34 | 3686.34 | 0.00% |
| c104C10F5 | 1800.00 | 1861.47 | 20.57 | 1861.47 | 0.00% |
| c201C10F5 | 1054.28 | 1709.61 | 48.12 | 1709.61 | 0.00% |
| c205C10F5 | 34.92 | 1592.25 | 19.89 | 1592.25 | 0.00% |
| r102C10F5 | 16.25 | 1833.37 | 21.45 | 1833.37 | 0.00% |
| r103C10F5 | 1800 | 1319.26 | 16.73 | 1319.26 | 0.00% |
| r201C10F5 | 76.45 | 1631.39 | 35.19 | 1631.39 | 0.00% |
| r203C10F5 | 1800 | 1087.26 | 55.68 | 1087.26 | 0.00% |
| rc102C10F5 | 19.63 | 2670.25 | 21.02 | 2638.86 | −1.18% |
| rc108C10F5 | 1247.90 | 1733.88 | 22.91 | 1733.88 | 0.00% |
| rc201C10F5 | 180.14 | 1797.89 | 37.47 | 1797.89 | 0.00% |
| rc205C10F5 | 83.72 | 2175.70 | 28.83 | 2175.70 | 0.00% |
| c103C15F5 | 1800 | 3644.41 | 90.25 | 3644.41 | 0.00% |
| c106C15F5 | 23.19 | 2848.19 | 54.96 | 2848.19 | 0.00% |
| c202C15F5 | 1800 | 2279.88 | 99.14 | 2279.88 | 0.00% |
| c208C15F5 | 430.61 | 1778.02 | 76.60 | 1778.02 | 0.00% |
| r102C15F5 | 1800 | 3006.59 | 59.39 | 3020.79 | 0.47% |
| r105C15F5 | 1800 | 2676.02 | 51.71 | 2676.02 | 0.00% |
| r202C15F5 | 1800 | 1984.58 | 135.05 | 1984.58 | 0.00% |
| r209C15F5 | 1800 | 1855.30 | 138.28 | 1855.30 | 0.00% |
| rc103C15F5 | 1800 | 2764.30 | 48.84 | 2741.91 | −0.82% |
| rc108C15F5 | 1800 | 2351.23 | 61.67 | 2351.23 | 0.00% |
| rc202C15F5 | 1800 | 2921.81 | 123.93 | 2867.18 | −1.86% |
| rc204C15F5 | 1800 | 1914.40 | 256.50 | 1914.40 | 0.00% |
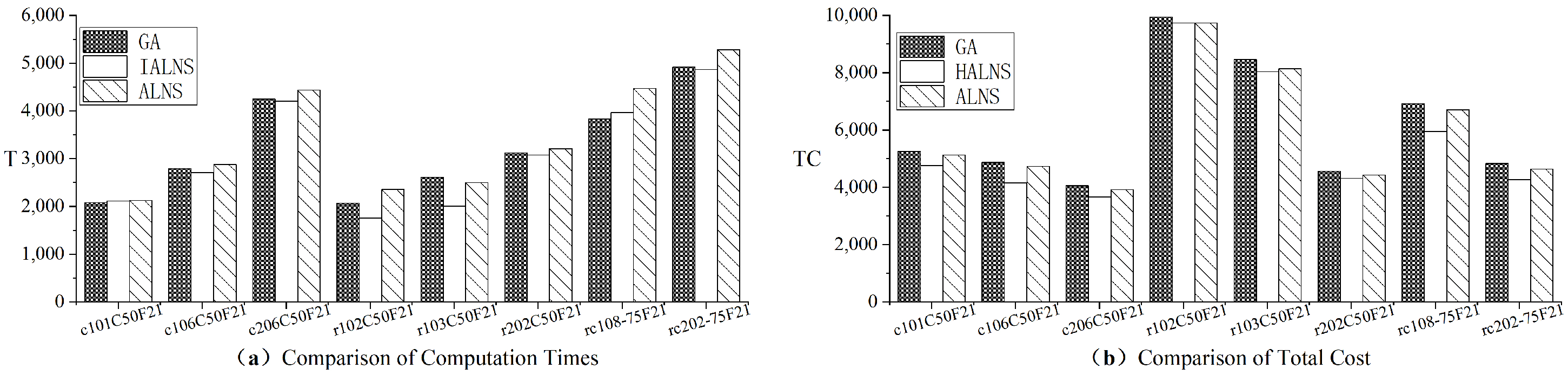
| Instance | GA | IALNS | ALNS | %GAP | |||
|---|---|---|---|---|---|---|---|
| TC | T | TC | T | TC | T | ||
| c101C5OF21 | 5259.05 | 2083.72 | 4769.55 | 2117.96 | 5130.78 | 2127.35 | 7.57 |
| c106C5OF21 | 4874.84 | 2796.98 | 4162.45 | 2712.98 | 4733.41 | 2881.83 | 13.72 |
| c206C50F21 | 4057.38 | 4253.67 | 3661.08 | 4208.18 | 3920.17 | 4436.93 | 7.08 |
| r102C50F21 | 9938.52 | 2073.62 | 9738.76 | 1755.99 | 9743.65 | 2361.12 | 0.05 |
| r103C50F21 | 8470.51 | 2613.79 | 8036.42 | 2007.97 | 8144.72 | 2504.2 | 1.35 |
| rc206C50F21 | 4564.76 | 3121.76 | 4509.05 | 3078.52 | 4439.28 | 3152.24 | 2.79 |
| rc108C75F21 | 6925.46 | 3836.63 | 5955.41 | 3968.49 | 6710.72 | 4409.67 | 12.68 |
| rc202C75F21 | 4841.49 | 4918.75 | 4278.13 | 4870.41 | 4636.31 | 5287.53 | 8.37 |
| Parameters | Valve | Parameters | Valve |
|---|---|---|---|
| 100, 150 yuan/per vehicle | 90 kwh | ||
| 1.5, 1.2 yuan/km | 0.88 kwh/km | ||
| 5, 10 yuan/h | 4.9, 4.5 t | ||
| 0.5 yuan/kg | V | 50 km/h | |
| 0.24, 0.08 L/km | 30, 10 kw | ||
| 2.65 kg/L | 0.68, 1.46 yuan/kwh | ||
| 0.72 | 80 yuan | ||
| 0.94 kg/kwh | p | 8 min |
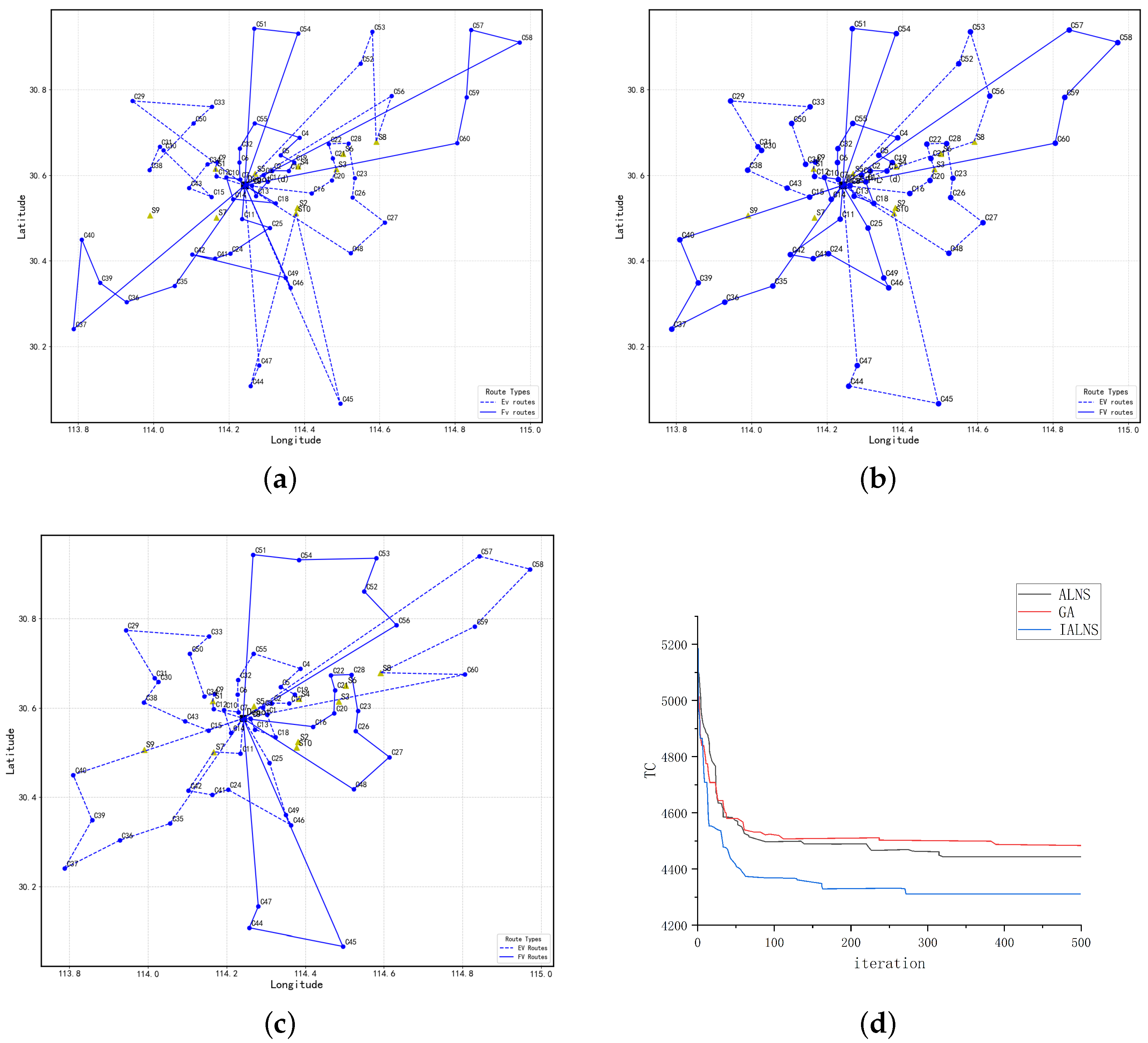
| Algorithm | Vehicle EV_FV | Total Distance (km) | Total Time (min) | Charging Cost (Yuan) | Total Cost (Yuan) |
|---|---|---|---|---|---|
| GA | 4_5 | 1155.74 | 2119.40 | 253.88 | 4578.32 |
| ALNS | 4_5 | 1107.90 | 2087.54 | 241.79 | 4497.39 |
| IALNS | 5_3 | 976.73 | 1873.92 | 228.98 | 4365.02 |
| IALNS vs. GA Reduction (%) | 11.1% | 15.5% | 13.1% | 9.8% | 4.6% |
| IALNS vs. ALNS Reduction (%) | 11.1% | 11.7% | 11.4% | 5.3% | 2.9% |
| Configuration Method | Total Cost (Yuan) | Transportation Cost (Yuan) | Carbon Cost (Yuan) | Time Window Cost (Yuan) | Charging Time (min) |
|---|---|---|---|---|---|
| Pure Fuel | 4972.86 | 2234.18 | 872.25 | 0 | 0 |
| Mixed Fleet | 4365.02 | 2257.51 | 451.41 | 241.59 | 351.92 |
| Pure Electric | 4738.52 | 2720.56 | 264.91 | 418.36 | 634.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, L.; Zhu, R.; Jian, D. Research on Green Distribution Problems of Mixed Fleets Considering Multiple Charging Methods. Energies 2025, 18, 5220. https://doi.org/10.3390/en18195220
Yin L, Zhu R, Jian D. Research on Green Distribution Problems of Mixed Fleets Considering Multiple Charging Methods. Energies. 2025; 18(19):5220. https://doi.org/10.3390/en18195220
Chicago/Turabian StyleYin, Lvjiang, Ruixue Zhu, and Dandan Jian. 2025. "Research on Green Distribution Problems of Mixed Fleets Considering Multiple Charging Methods" Energies 18, no. 19: 5220. https://doi.org/10.3390/en18195220
APA StyleYin, L., Zhu, R., & Jian, D. (2025). Research on Green Distribution Problems of Mixed Fleets Considering Multiple Charging Methods. Energies, 18(19), 5220. https://doi.org/10.3390/en18195220






