Comparative Performance Analysis of Machine Learning-Based Annual and Seasonal Approaches for Power Output Prediction in Combined Cycle Power Plants
Abstract
1. Introduction
- Context of Energy Transition: The global increase in energy demand shows that fossil fuels continue to dominate the energy system, despite the growing share of renewables. In this context, CCPPs play a strategic role with their high efficiency and low emissions.
- Critical Role of EPO: EPO is the most direct indicator of plant efficiency and economic performance. Accurate EPO prediction is essential for meeting market commitments and reducing operational costs.
- Limitations of Traditional Methods: Classical thermodynamic and deterministic mathematical models fall short in real-time applications due to the need to solve numerous nonlinear equations, leading to high computational costs.
- ML Approach: The study utilizes data-driven ML-based methods to predict EPO, incorporating ambient variables such as AT, V, AP, and RH.
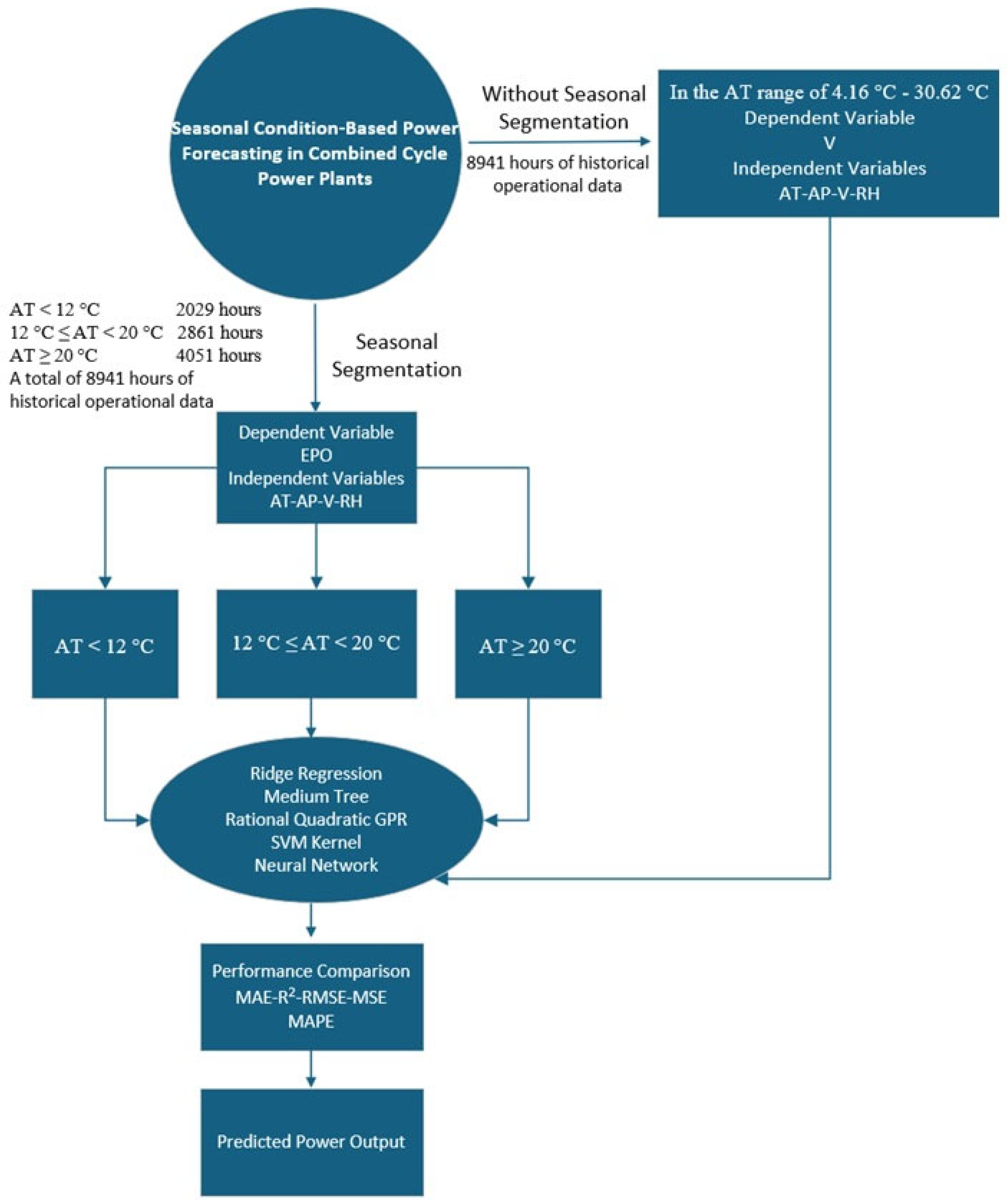
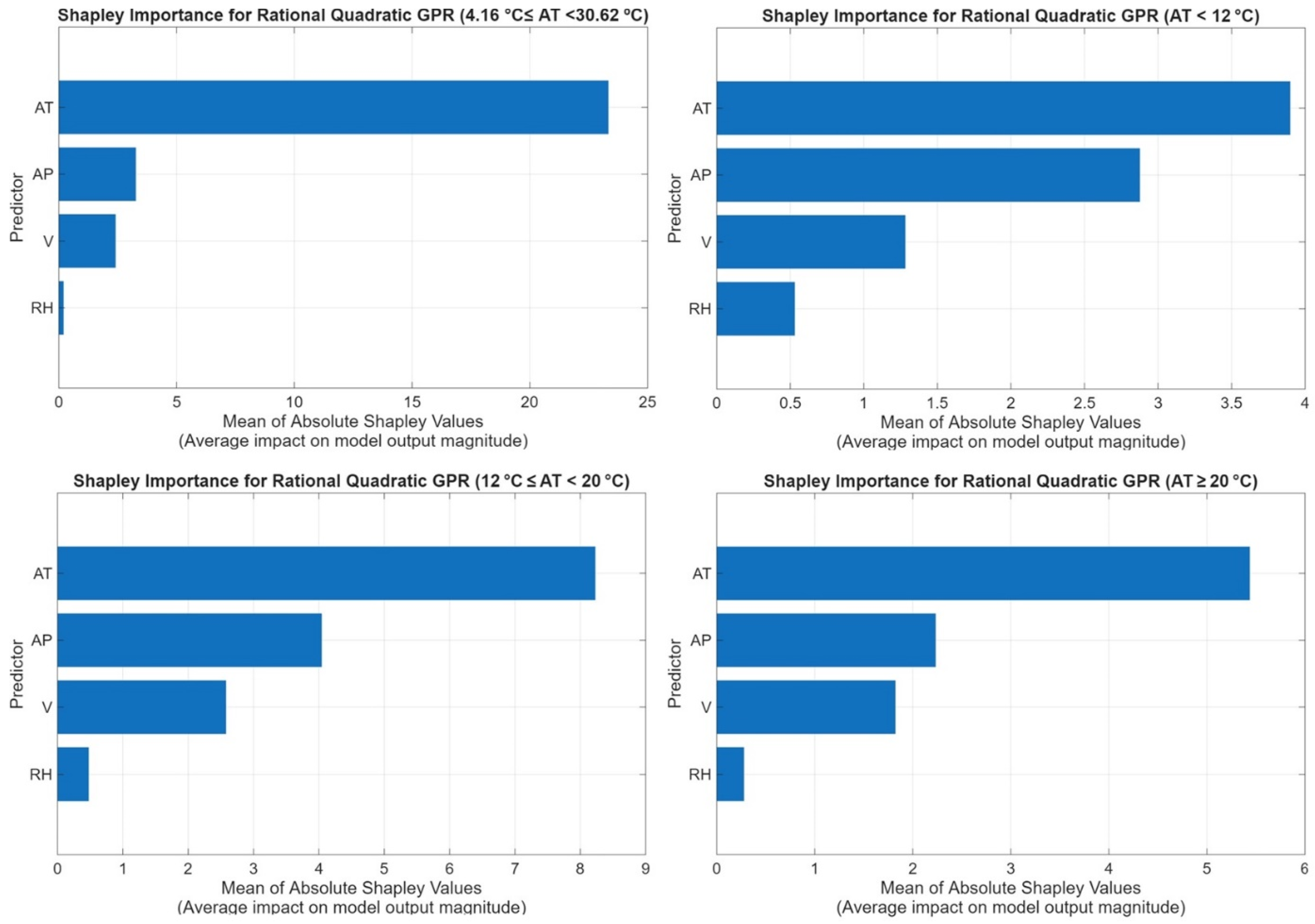
- Addressing a Gap in the Literature: While previous studies generally used a single comprehensive model across the entire year, this study considers seasonal effects by developing separate models for three temperature ranges based on AT (AT < 12 °C, 12 °C ≤ AT < 20 °C, and AT ≥ 20 °C).
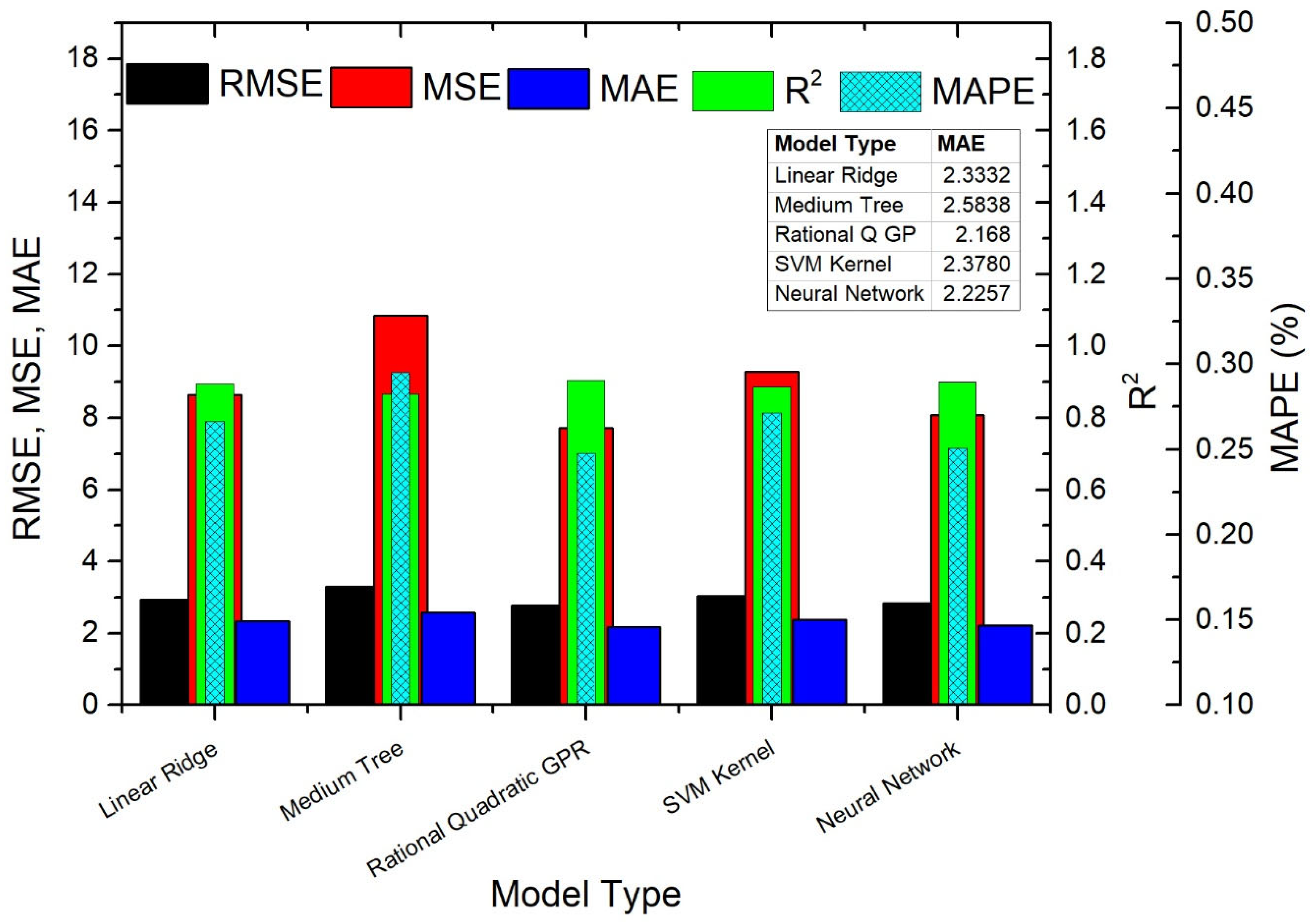
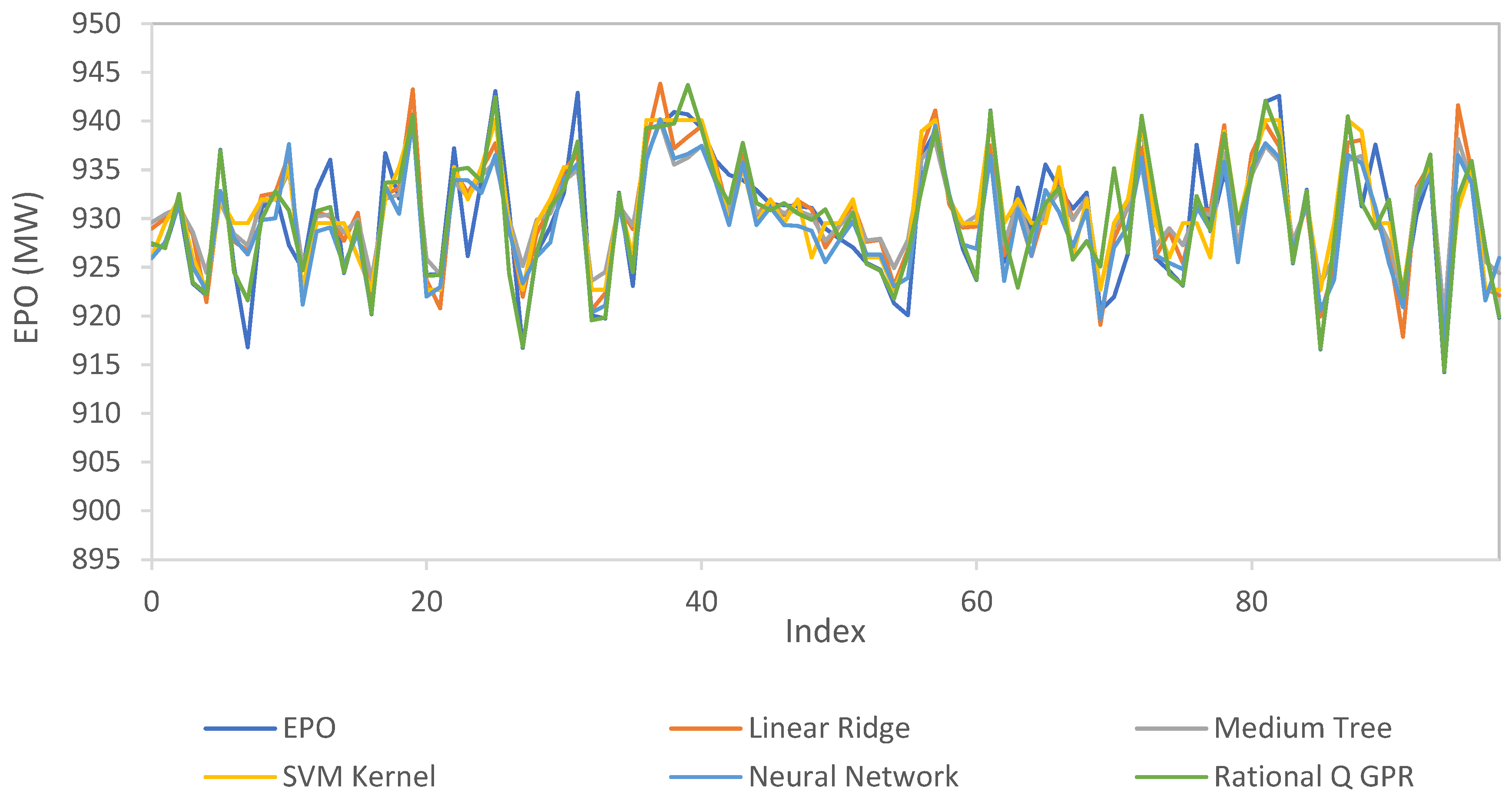
- Comprehensive Model Comparison: Five different methods (Linear Ridge, Medium Tree, Rational Quadratic GPR, SVM Kernel, and Neural Network) were tested on both the full dataset and the segmented temperature ranges to compare their performance.
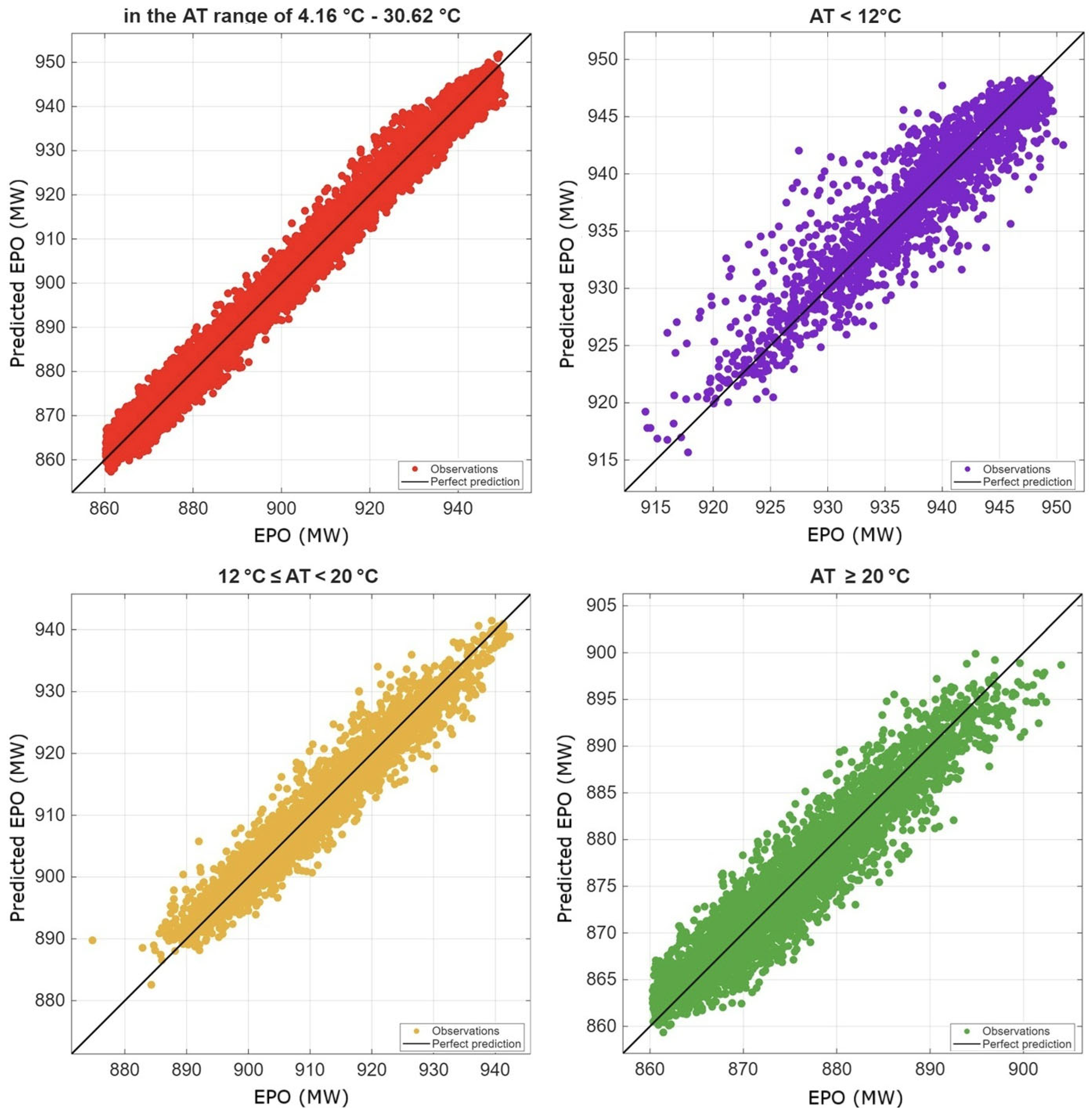
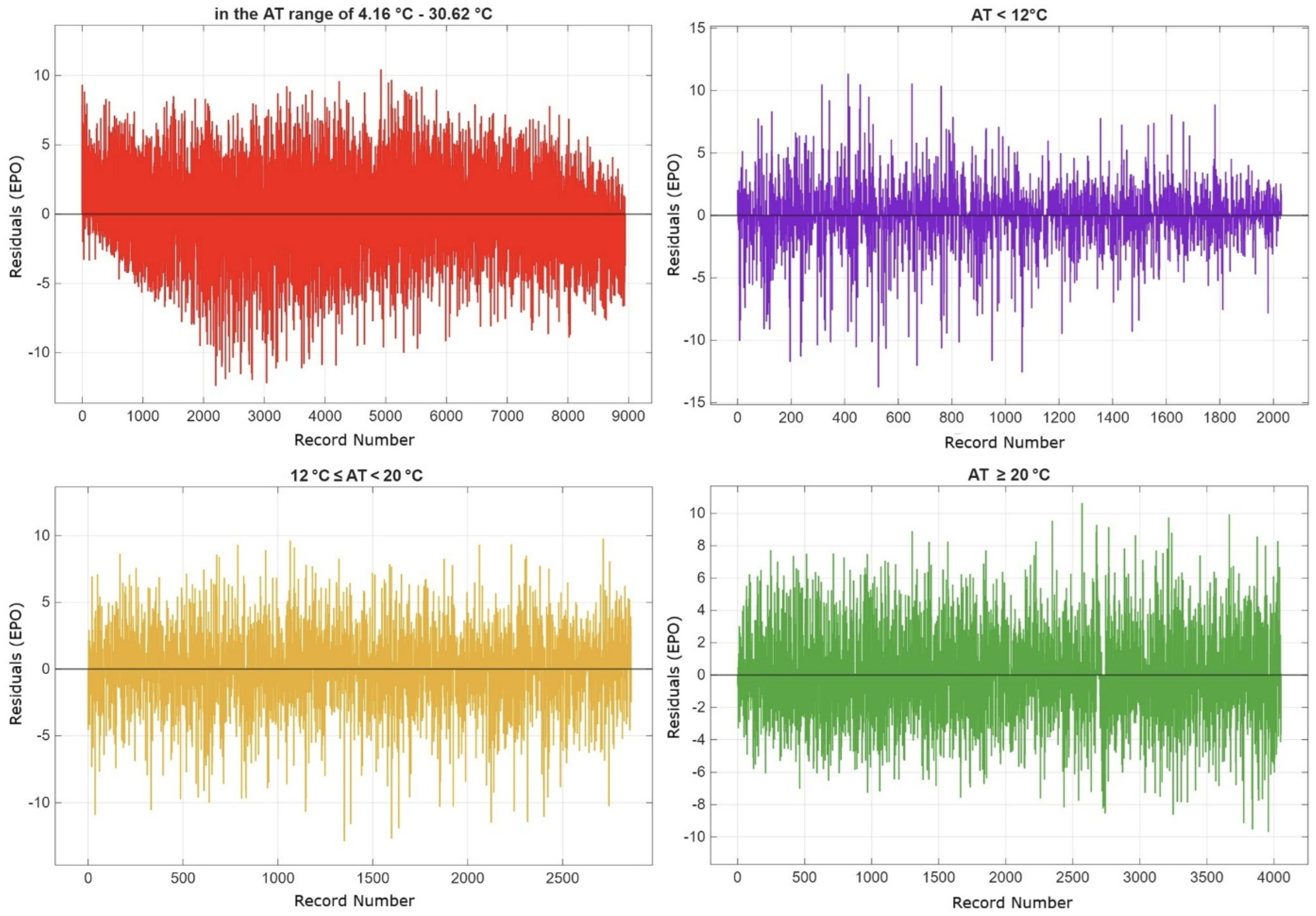
- Impact of Segmentation: The findings show that modeling based on temperature segmentation significantly improves prediction accuracy and reliability.
- Contribution to the Literature: By presenting a segmentation-based modeling approach and a comprehensive comparison of different ML methods, the study offers a novel contribution to the literature on CCPP performance prediction.
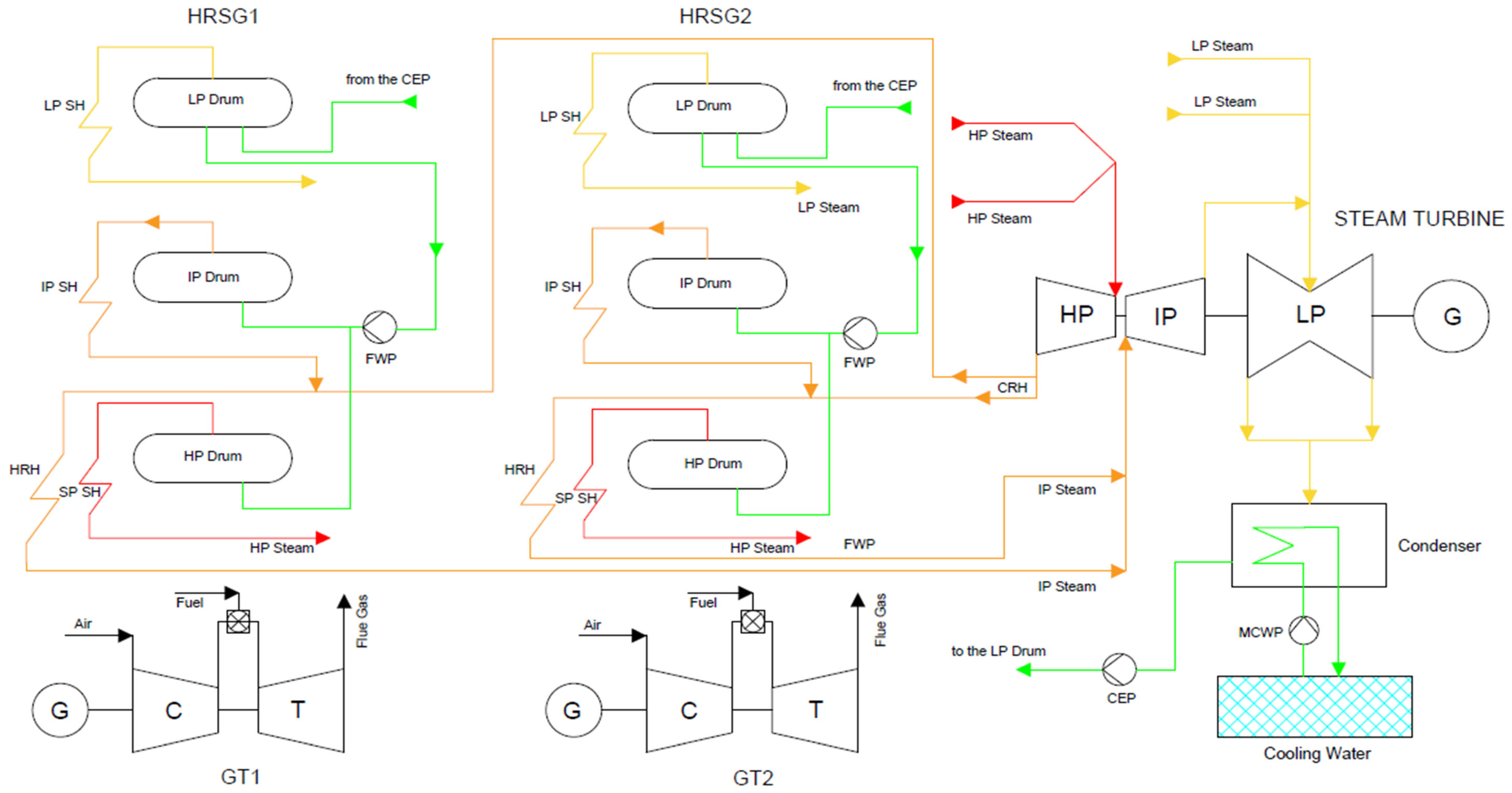
2. System Description
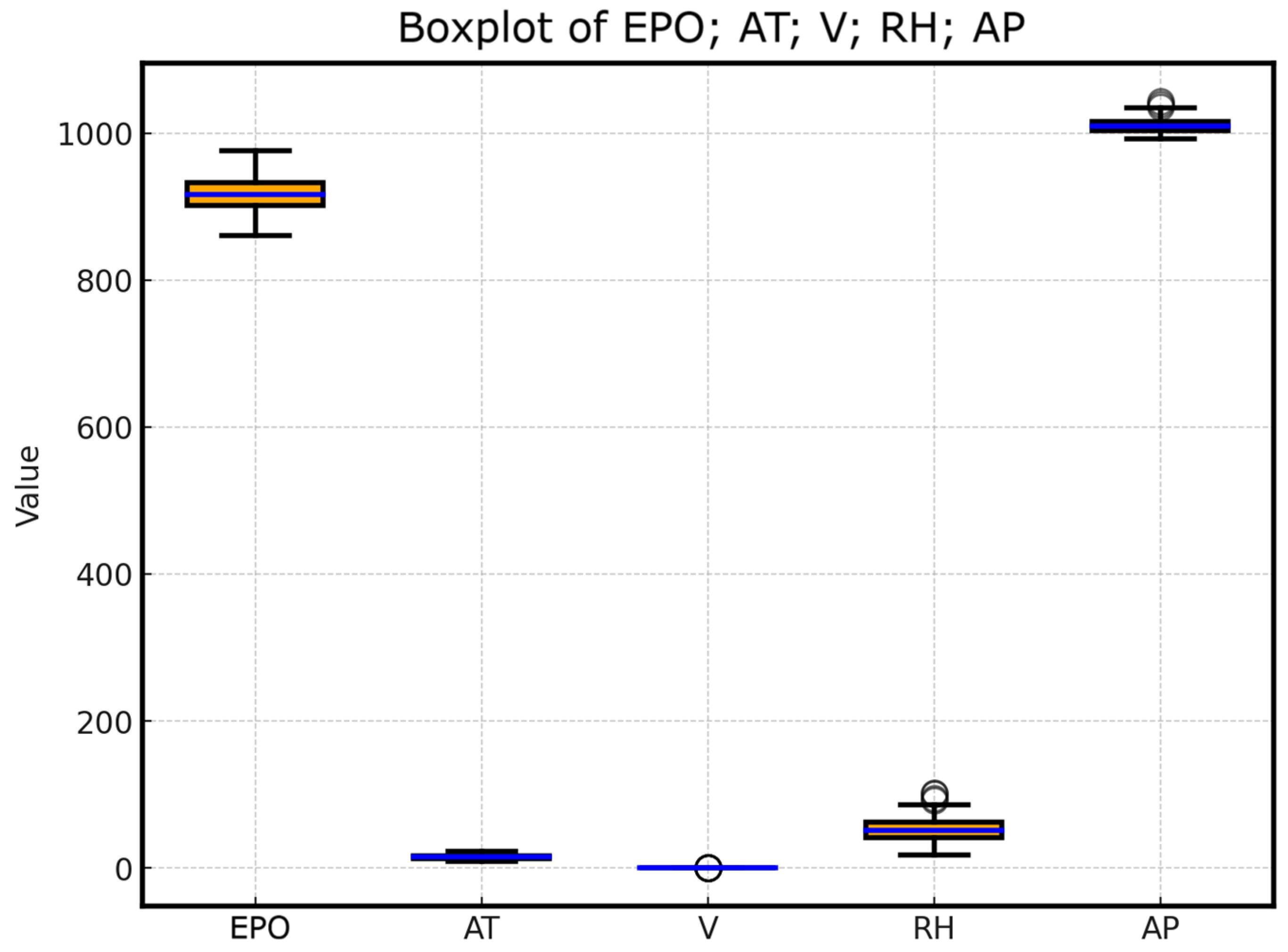
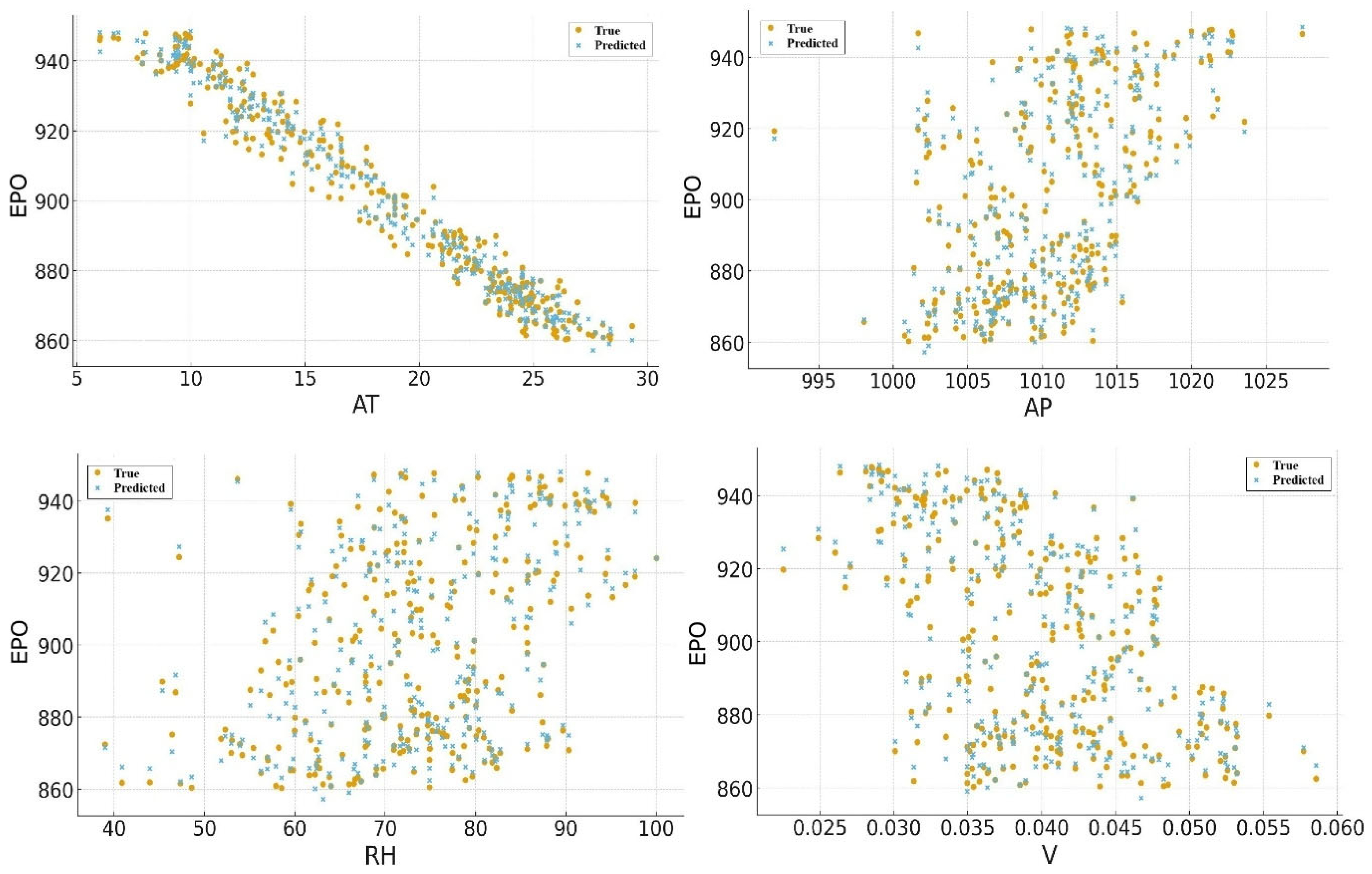
- AT is an input variable with values ranging from 4.16 °C to 30.62 °C.
- AP is an input variable with values ranging from 982.54 mbar to 1027.78 mbar.
- RH is an input variable with values ranging from 24.61% to 100.00%.
- V is an input variable with values ranging from 0.022 bara to 0.059 bara.
- EPO is the target variable with values ranging from 860.30 MW to 950.56 MW.
3. Regression Methods
3.1. Ridge Regression
3.2. Regression Trees
3.3. Rational Quadratic GPR
3.4. SVM Kernel
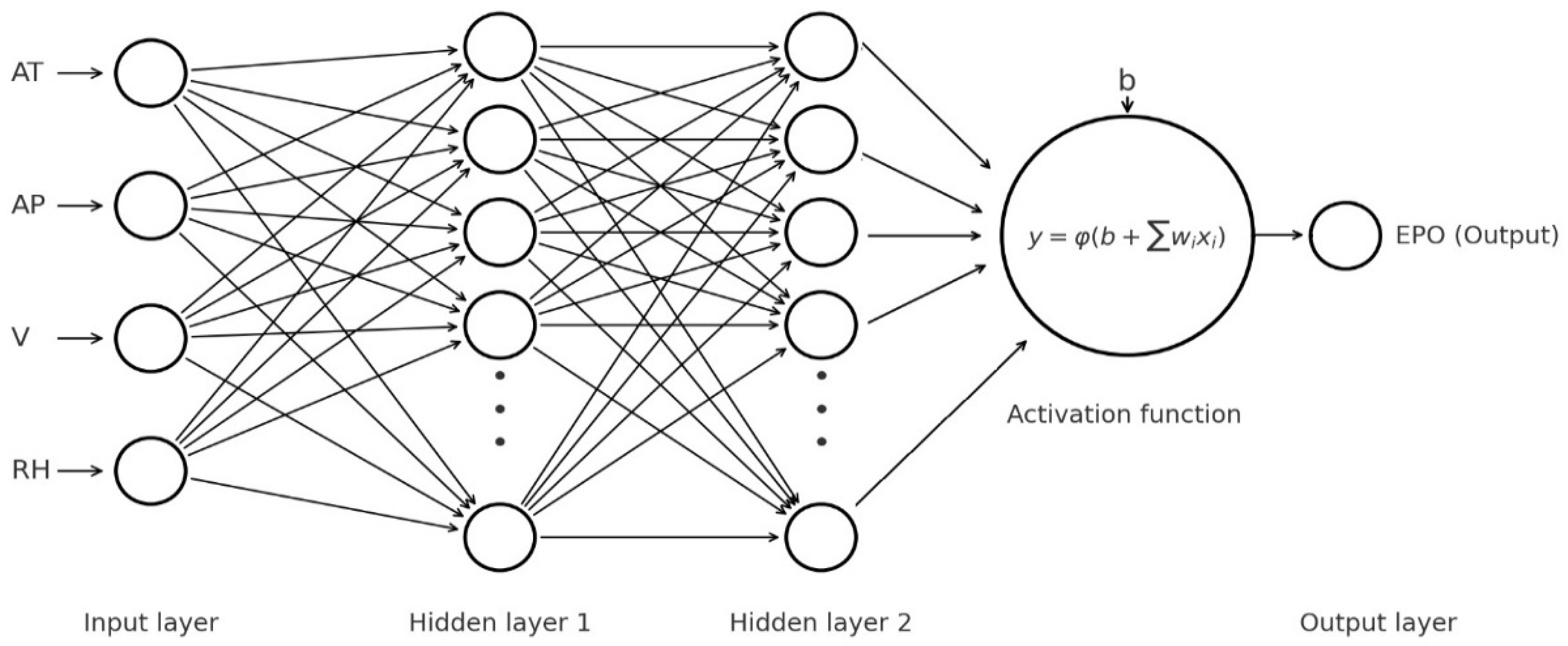
3.5. Artificial Neural Network
4. Performance Assessment
4.1. Coefficient of Determination (R2)
4.2. Mean Absolute Error (MAE)
4.3. Mean Square Error (MSE)
4.4. Root Mean-Squared Error (RMSE)
4.5. Mean Absolute Percentage Error (MAPE)
4.6. Average Convergence Rate
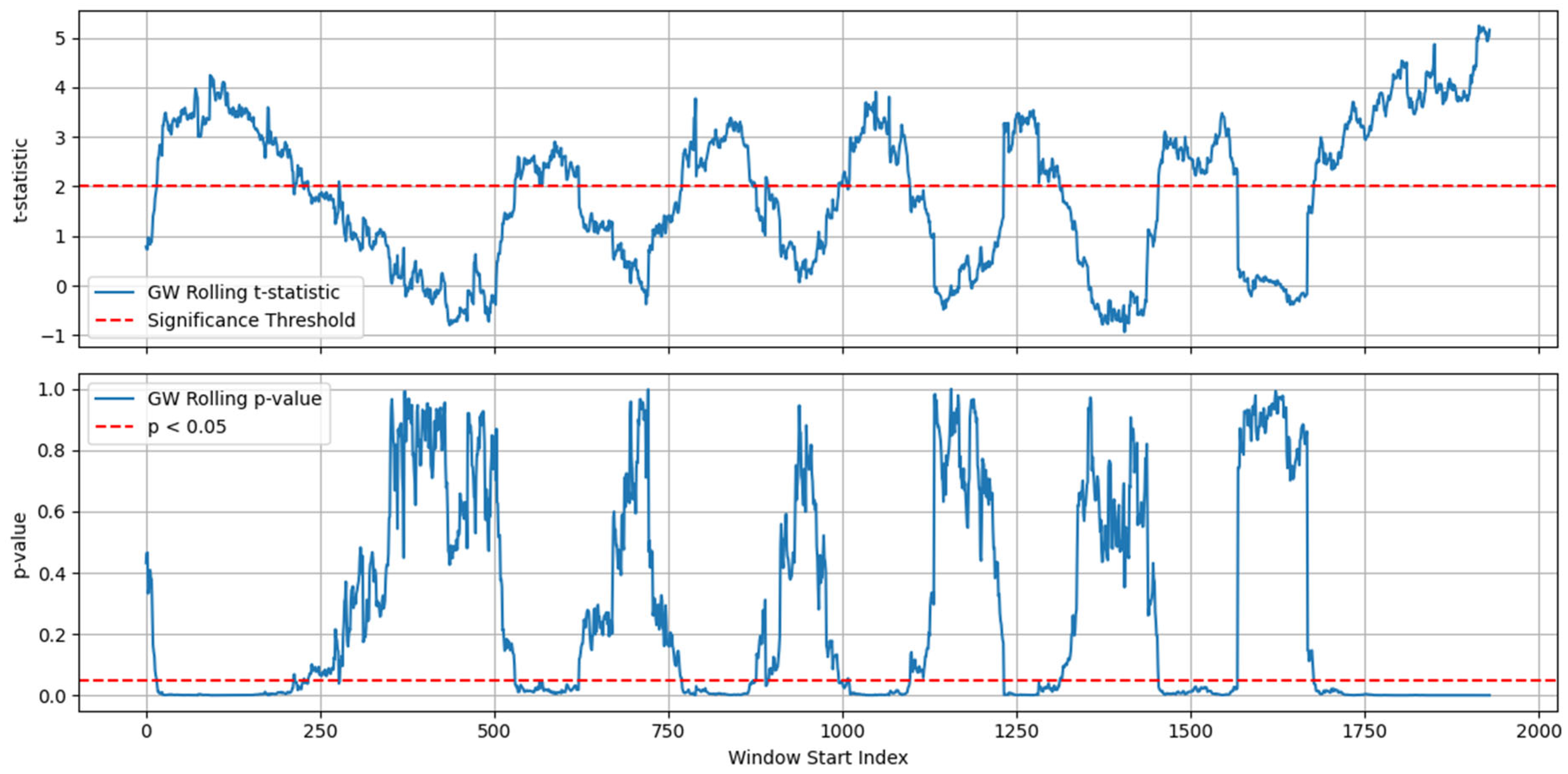
4.7. Forecast Evaluation Using Diebold–Mariano and Giacomini–White Tests
4.8. Bootstrap Method
5. Results
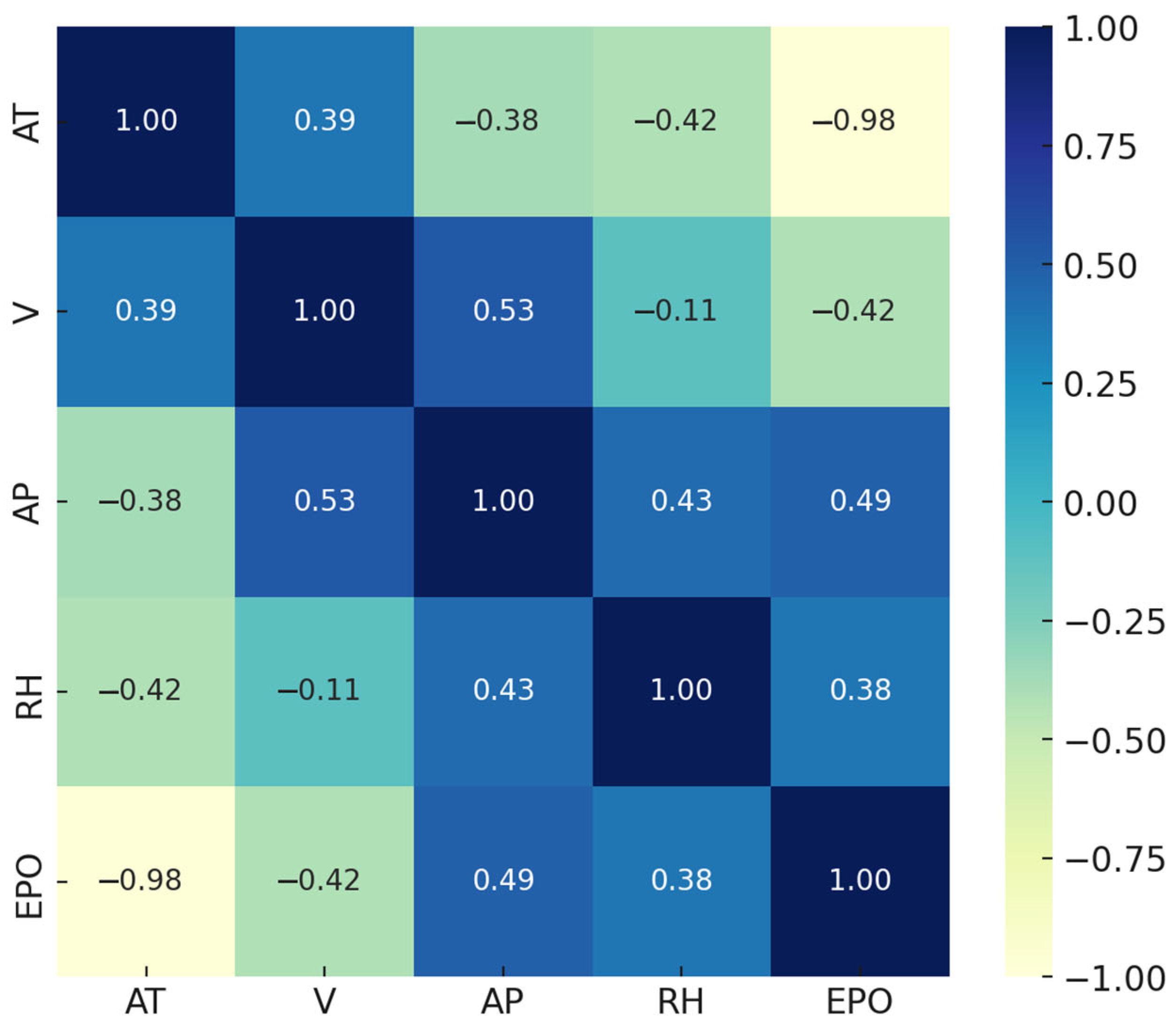
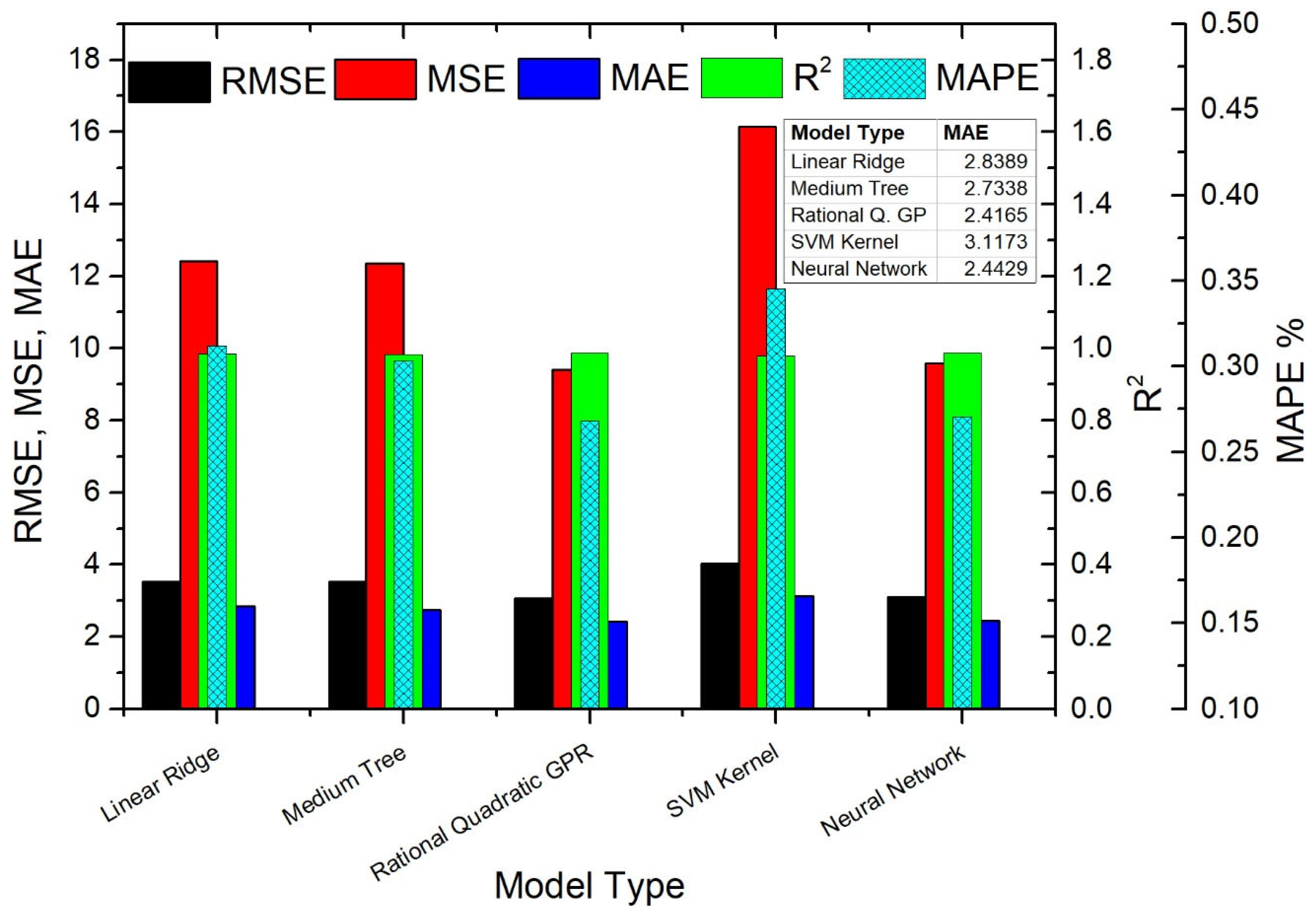
5.1. Findings of Regression Analysis on the Entire Dataset
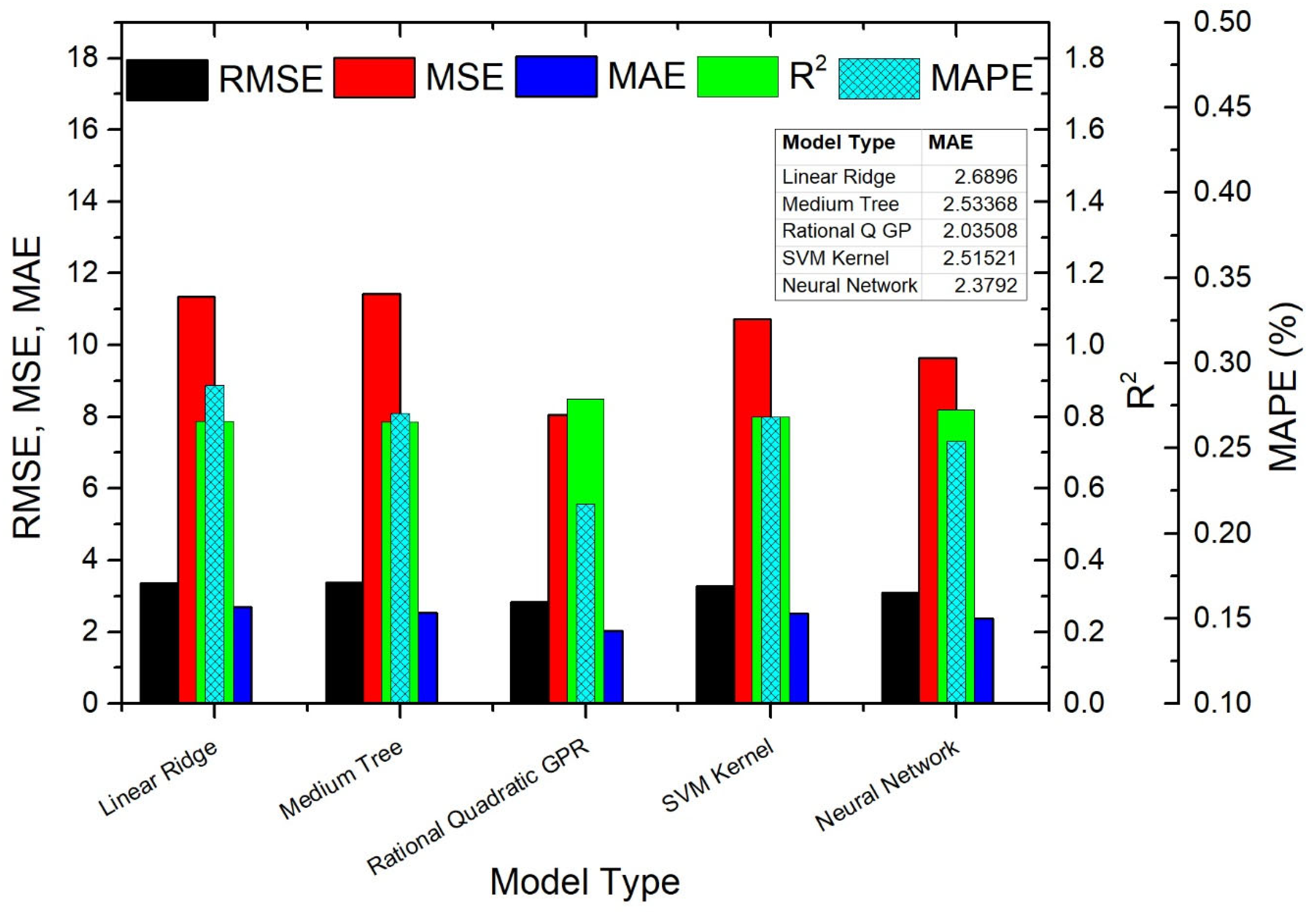
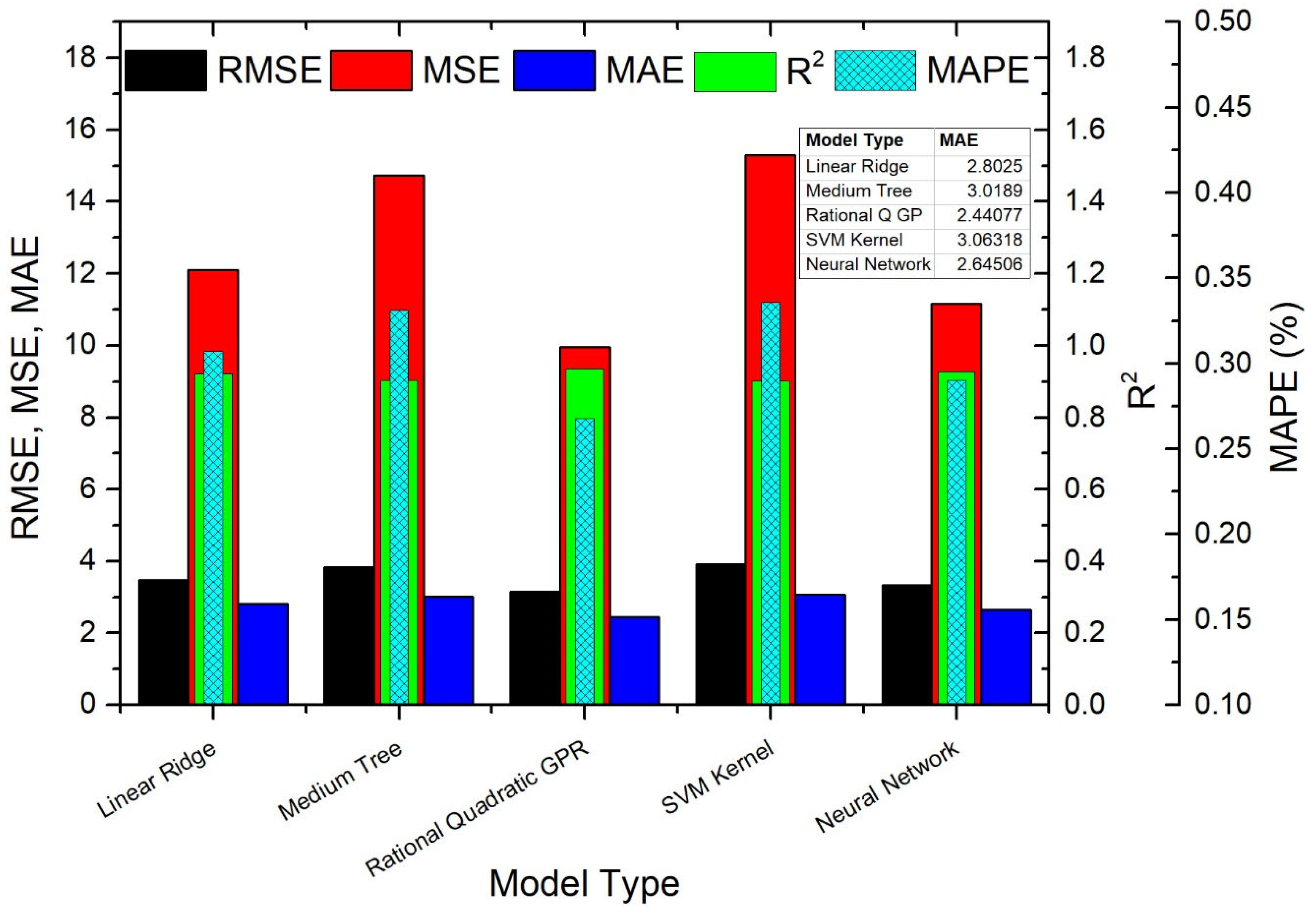
5.2. Findings of Regression Analysis Based on Seasonal Temperature Ranges (AT < 12 °C, 12 °C ≤ AT < 20 °C, and AT ≥ 20 °C)
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Abbreviations
| ANN | Artificial Neural Network |
| AP | Atmospheric Pressure |
| AT | Ambient Temperature |
| CCPP | Combined Cycle Power Plant |
| DCS | Distributed Control System |
| DM | Diebold–Mariano |
| DNN | Deep Neural Network |
| DT | Decision Tree |
| EPO | Electrical Power Output |
| GPR | Gaussian Process Regression |
| GT | Gas Turbine |
| GW | Giacomini–White |
| HRSG | Heat Recovery Steam Generator |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| MSE | Mean Square Error |
| R2 | Coefficient of Determination |
| RH | Relative Humidity |
| RMSE | Root Mean Square Error |
| ST | Steam Turbine |
| SVM | Support Vector Machine |
| V | Condenser Vacuum |
References
- International Energy Agency (IEA). 2025. Available online: www.iea.org (accessed on 1 August 2025).
- López Hernández, O.; Romero Romero, D.; Badaoui, M. Economic Dispatch of Combined Cycle Power Plant: A Mixed-Integer Programming Approach. Processes 2024, 12, 1199. [Google Scholar] [CrossRef]
- Yi, Q.; Xiong, H.; Wang, D. Predicting power generation from a combined cycle power plant using transformer encoders with DNN. Electronics 2023, 12, 2431. [Google Scholar] [CrossRef]
- Kotowicz, J.; Brzęczek, M. Analysis of increasing efficiency of modern combined cycle power plant: A case study. Energy 2018, 153, 90–99. [Google Scholar] [CrossRef]
- Surase, R.S.; Konijeti, R.; Chopade, R.P. Thermal performance analysis of gas turbine power plant using soft computing techniques: A review. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2374317. [Google Scholar] [CrossRef]
- Mattos, H.A.D.S.; Bringhenti, C.; Cavalca, D.F.; Silva, O.F.R.; Campos, G.B.D.; Tomita, J.T. Combined cycle performance evaluation and dynamic response simulation. J. Aerosp. Technol. Manag. 2016, 8, 491–497. [Google Scholar] [CrossRef]
- Arferiandi, Y.D.; Caesarendra, W.; Nugraha, H. Heat rate prediction of combined cycle power plant using an artificial neural network (ANN) method. Sensors 2021, 21, 1022. [Google Scholar] [CrossRef] [PubMed]
- Siddiqui, R.; Anwar, H.; Ullah, F.; Ullah, R.; Rehman, M.A.; Jan, N.; Zaman, F. Power prediction of combined cycle power plant (CCPP) using machine learning algorithm-based paradigm. Wirel. Commun. Mob. Comput. 2021, 2021, 9966395. [Google Scholar] [CrossRef]
- Lobo, J.L.; Ballesteros, I.; Oregi, I.; Del Ser, J.; Salcedo-Sanz, S. Stream learning in energy IoT systems: A case study in combined cycle power plants. Energies 2020, 13, 740. [Google Scholar] [CrossRef]
- Castillo, A. Risk analysis and management in power outage and restoration: A literature survey. Electr. Power Syst. Res. 2014, 107, 9–15. [Google Scholar] [CrossRef]
- Kesgin, U.; Heperkan, H. Simulation of thermodynamic systems using soft computing techniques. Int. J. Energy Res. 2005, 29, 581–611. [Google Scholar] [CrossRef]
- Pachauri, N.; Ahn, C.W. Electrical energy prediction of combined cycle power plant using gradient boosted generalized additive model. IEEE Access 2022, 10, 24566–24577. [Google Scholar] [CrossRef]
- Afzal, A.; Alshahrani, S.; Alrobaian, A.; Buradi, A.; Khan, S.A. Power plant energy predictions based on thermal factors using ridge and support vector regressor algorithms. Energies 2021, 14, 7254. [Google Scholar] [CrossRef]
- Qu, Z.; Xu, J.; Wang, Z.; Chi, R.; Liu, H. Prediction of electricity generation from a combined cycle power plant based on a stacking ensemble and its hyperparameter optimization with a grid-search method. Energy 2021, 227, 120309. [Google Scholar] [CrossRef]
- Sun, L.; Liu, T.; Xie, Y.; Zhang, D.; Xia, X. Real-time power prediction approach for turbine using deep learning techniques. Energy 2021, 233, 121130. [Google Scholar] [CrossRef]
- Song, Y.; Park, J.; Suh, M.S.; Kim, C. Prediction of Full-Load Electrical Power Output of Combined Cycle Power Plant Using a Super Learner Ensemble. Appl. Sci. 2024, 14, 11638. [Google Scholar] [CrossRef]
- Fakir, K.; Ennawaoui, C.; El Mouden, M. Deep learning algorithms to predict output electrical power of an industrial steam turbine. Appl. Syst. Innov. 2022, 5, 123. [Google Scholar] [CrossRef]
- Wood, D.A. Combined cycle gas turbine power output prediction and data mining with optimized data matching algorithm. SN Appl. Sci. 2020, 2, 441. [Google Scholar] [CrossRef]
- Miller, J. The combined cycle and variations that use HRSGs. In Heat Recovery Steam Generator Technology; Woodhead Publishing: Sawston, UK, 2017; pp. 17–43. [Google Scholar]
- Huda, A.N.; Živanović, R. Large-scale integration of distributed generation into distribution networks: Study objectives, review of models and computational tools. Renew. Sustain. Energy Rev. 2017, 76, 974–988. [Google Scholar] [CrossRef]
- Thelwall, M.; Wilson, P. Regression for citation data: An evaluation of different methods. J. Informetr. 2014, 8, 963–971. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Månsson, K.; Shukur, G. A Poisson ridge regression estimator. Econ. Model. 2011, 28, 1475–1481. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An İntroduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013; Volume 103. [Google Scholar]
- Bocci, L.; D’Urso, P.; Vicari, D.; Vitale, V. A regression tree-based analysis of the European regional competitiveness. Soc. Indic. Res. 2024, 173, 137–167. [Google Scholar] [CrossRef]
- Argüello-Prada, E.J.; Villota Ojeda, A.V.; Villota Ojeda, M.Y. Non-invasive prediction of cholesterol levels from photoplethysmogram (PPG)-based features using machine learning techniques: A proof-of-concept study. Cogent Eng. 2025, 12, 2467153. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Quinonero-Candela, J.; Rasmussen, C.E. A unifying view of sparse approximate Gaussian process regression. J. Mach. Learn. Res. 2005, 6, 1939–1959. [Google Scholar]
- Wang, B.; Alruyemi, I. Comprehensive modeling in predicting biodiesel density using Gaussian process regression approach. BioMed Res. Int. 2021, 2021, 6069010. [Google Scholar] [CrossRef]
- Pande, C.B.; Kushwaha, N.L.; Orimoloye, I.R.; Kumar, R.; Abdo, H.G.; Tolche, A.D.; Elbeltagi, A. Comparative assessment of improved SVM method under different kernel functions for predicting multi-scale drought index. Water Resour. Manag. 2023, 37, 1367–1399. [Google Scholar] [CrossRef]
- Patle, A.; Chouhan, D.S. SVM kernel functions for classification. In Proceedings of the 2013 International Conference on Advances in Technology and Engineering (ICATE), Mumbai, India, 23–25 January 2013; IEEE: New York, NY, USA, 2013; pp. 1–9. [Google Scholar]
- Almaiah, M.A.; Almomani, O.; Alsaaidah, A.; Al-Otaibi, S.; Bani-Hani, N.; Hwaitat, A.K.A.; Al-Zahrani, A.; Lutfi, A.; Awad, A.B.; Aldhyani, T.H. Performance investigation of principal component analysis for intrusion detection system using different support vector machine kernels. Electronics 2022, 11, 3571. [Google Scholar] [CrossRef]
- Kurucan, M.; Özbaltan, M.; Yetgin, Z.; Alkaya, A. Applications of artificial neural network based battery management systems: A literature review. Renew. Sustain. Energy Rev. 2024, 192, 114262. [Google Scholar] [CrossRef]
- Piepho, H.P. An adjusted coefficient of determination (R2) for generalized linear mixed models in one go. Biom. J. 2023, 65, 2200290. [Google Scholar] [CrossRef]
- Guo, B.; Yang, B.; Shi, W.; Yang, F.; Wang, D.; Wang, S. CCPP Power Prediction Using CatBoost with Domain Knowledge and Recursive Feature Elimination. Energies 2025, 18, 4272. [Google Scholar] [CrossRef]
- Robeson, S.M.; Willmott, C.J. Decomposition of the mean absolute error (MAE) into systematic and unsystematic components. PLoS ONE 2023, 18, e0279774. [Google Scholar] [CrossRef] [PubMed]
- Rasheed, A.A. Improving prediction efficiency by revolutionary machine learning models. Mater. Today Proc. 2023, 81, 577–583. [Google Scholar] [CrossRef]
- Hodson, T.O.; Over, T.M.; Foks, S.S. Mean squared error, deconstructed. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002681. [Google Scholar] [CrossRef]
- Santarisi, N.S.; Faouri, S.S. Prediction of combined cycle power plant electrical output power using machine learning regression algorithms. East.-Eur. J. Enterp. Technol. 2021, 6, 114. [Google Scholar] [CrossRef]
- Rajarao, P.B.V.; Ushanag, S.; Rao, T.P.; Moses, G.J.; Lakshmanarao, A. Power Prediction in CCPP Through ML-Based Probabilistic Regression Models and Ensemble Techniques. In Proceedings of the International Conference on Sustainable Power and Energy Research, Warangal, India, 29 February–2 March 2024; Springer Nature: Singapore, 2024; pp. 223–232. [Google Scholar]
- Hodson, T.O. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. Discuss. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Mutavhatsindi, T.; Sigauke, C.; Mbuvha, R. Forecasting hourly global horizontal solar irradiance in South Africa using machine learning models. IEEE Access 2020, 8, 198872–198885. [Google Scholar] [CrossRef]
- Buturac, G. Measurement of economic forecast accuracy: A systematic overview of the empirical literature. J. Risk Financ. Manag. 2021, 15, 1. [Google Scholar] [CrossRef]
- Wasserman, L. All of Statistics: A Concise Course in Statistical İnference; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
| Min | Max | Mean | Std. Deviation | |
|---|---|---|---|---|
| EPO | 860.30 | 950.56 | 901.54 | 27.46 |
| AT | 4.16 | 30.62 | 18.14 | 6.13 |
| RH | 24.61 | 100.00 | 74.61 | 11.91 |
| V | 0.022 | 0.059 | 0.039 | 0.006 |
| AP | 982.54 | 1027.78 | 1010.20 | 5.13 |
| Bootstrap (B = 2000) | Confidence | q_low (residual) | q_high (residual) | Average Width (MW) | Empirical Coverage | Mean Winkler Score | Mean Interval Score |
| 95% | −6.3925 | 5.3422 | 11.7347 | 0.9497 | 15.7437 | 15.7437 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aslan, A.; Büyükköse, A.O. Comparative Performance Analysis of Machine Learning-Based Annual and Seasonal Approaches for Power Output Prediction in Combined Cycle Power Plants. Energies 2025, 18, 5110. https://doi.org/10.3390/en18195110
Aslan A, Büyükköse AO. Comparative Performance Analysis of Machine Learning-Based Annual and Seasonal Approaches for Power Output Prediction in Combined Cycle Power Plants. Energies. 2025; 18(19):5110. https://doi.org/10.3390/en18195110
Chicago/Turabian StyleAslan, Asiye, and Ali Osman Büyükköse. 2025. "Comparative Performance Analysis of Machine Learning-Based Annual and Seasonal Approaches for Power Output Prediction in Combined Cycle Power Plants" Energies 18, no. 19: 5110. https://doi.org/10.3390/en18195110
APA StyleAslan, A., & Büyükköse, A. O. (2025). Comparative Performance Analysis of Machine Learning-Based Annual and Seasonal Approaches for Power Output Prediction in Combined Cycle Power Plants. Energies, 18(19), 5110. https://doi.org/10.3390/en18195110







