A Method for Energy Storage Capacity Configuration in the Power Grid Along Mountainous Railway Based on Chance-Constrained Optimization

Abstract

To address the challenges of weak power-grid infrastructure, insufficient power supply capacity along mountainous railways, and severe three-phase imbalance caused by imbalanced traction loads at the point of common coupling (PCC), this paper proposes an energy storage configuration method for mountainous railway power grids considering renewable energy integration. First, a distributionally robust chance-constrained energy storage system configuration model is established, with the capacity and rated power of the energy storage system as decision variables, and the investment costs, operational costs, and grid operation costs as the objective function. Subsequently, by linearizing the three-phase AC power flow equations and transforming the model into a directly solvable linear form using conditional value-at-risk (CVaR) theory, the original configuration problem is converted into a mixed-integer linear programming (MILP) formulation. Finally, simulations based on an actual high-altitude mountainous railway power grid validate the economic efficiency and effectiveness of the proposed model. Results demonstrate that energy storage deployment reduces overall system voltage deviation by 40.7% and improves three-phase voltage magnitude imbalance by 16%.

1. Introduction

In recent years, with the ongoing advancement of mountainous railway projects, higher demands have been placed on the power supply capacity of railway corridor grids. On the one hand, the inherently weak structure of mountainous power networks makes them prone to insufficient power supply capacity under traction load integration. On the other hand, unevenly distributed loads along railway corridors, coupled with significant fluctuations in traction loads, lead to substantial voltage deviations and three-phase imbalances during power system operations. These issues not only directly compromise train operational safety but also present challenges to power supply system stability [1,2,3,4].

Energy storage systems have become an effective means to address insufficient power supply capacity in power systems due to their advantages in energy time-shifting, voltage support, and load balancing [5,6]. In recent years, academia has studied energy storage system capacity allocation from various perspectives. Reference [7] proposed a bi-level optimization method for composite energy storage capacity configuration to increase renewable energy penetration in regional power systems. Reference [8] established an optimal capacity configuration model incorporating pumped hydro and battery storage, considering operational characteristics, minimizing costs and carbon emissions using the Non-dominated Sorting Genetic Algorithm [9]. Ammonia-based energy storage systems are increasingly adopted as storage media owing to high energy density, explosion resistance, and low cost [10,11]. Reference [12] developed a hydrogen–ammonia hybrid storage optimization model for microgrids with high renewable penetration, minimizing operational costs while maximizing wind power utilization. These studies employ deterministic approaches assuming known renewable generation to obtain optimal configurations. However, mountainous railway power grids exhibit severe load fluctuations and renewable uncertainties, which limit the applicability of traditional deterministic optimization methods and make it difficult to address uncertainty risks in actual operation.

Building upon this foundation, to enhance the adaptability of configuration methods under uncertain scenarios, existing research has incorporated uncertainty modeling approaches into energy storage configuration. Reference [13] used a stochastic optimization method to optimize a hybrid energy scheduling model that integrates multiple energy storage systems, which can effectively reduce economic costs and carbon emissions. Reference [14] proposed a bi-level robust optimization (RO) method to address shared energy storage allocation considering wind farm cluster leasing in electricity markets, based on RO’s capability to handle source-load uncertainties [15]. While robust optimization constructs uncertainty boundaries and optimizes for worst-case performance to ensure system conservativeness, it may lead to resource overallocation [16,17]. In recent years, distributionally robust optimization (DRO) has been widely applied to power system uncertainty management [18,19]. This method establishes probability distribution ambiguity sets from historical data to quantify uncertainties. Reference [20] adopted DRO to model wind–solar output uncertainty, co-optimizing transmission corridors with energy storage, while Reference [21] developed a DRO-based reactive power optimization model for multi-region offshore wind farms while preserving privacy. However, these studies simplified their analysis using single-phase grid models, neglecting load asymmetry and the probabilistic satisfaction of uncertain constraints. In contrast, the distributionally robust chance-constrained (DRCC) optimization method relaxes constraints within acceptable risk levels [22], achieving economic and flexible resource allocation while controlling risk, and has been extensively applied in distribution networks and microgrid storage planning. Reference [23] investigated a chance-constrained energy storage configuration model considering time-of-use pricing and PV uncertainty under multi-station integration scenarios, validating its effectiveness and economy. Nevertheless, most existing research focuses on balanced-load distribution networks or islanded microgrids using single-phase models, overlooking the complexity introduced by high-power imbalanced traction loads in mountainous railway grids [24,25]. Therefore, there is an urgent need for tailored modeling methods and optimization strategies for railway-integrated power systems.

In summary, existing energy storage configuration models are primarily based on a single-phase grid model and mainly accommodate three-phase symmetric loads, making them ineffective in handling scenarios involving three-phase imbalanced traction loads. By simplifying the grid to a single-phase equivalent model, these approaches fail to account for the three-phase voltage characteristics of nodes. Although they consider the uncertainty of renewable energy generation, the utilization rate of uncertain renewable energy output is not incorporated into the optimization objectives. The main contributions of this work are as follows:

(1)

This paper adopts a three-phase linear power flow model to develop a linearized calculation method for node voltages, integrating three-phase voltage deviation and imbalance into the optimization objectives.

(2)

Chance constraints are introduced to characterize the randomness of renewable energy generation, and the utilization rate of uncertain renewable energy output is included in the optimization framework. The model is transformed into a solvable mixed-integer linear programming (MILP) formulation based on conditional value-at-risk (CVaR) theory.

(3)

A novel energy storage configuration method is proposed, which optimizes both three-phase imbalance mitigation and renewable energy utilization. The effectiveness of the proposed method is demonstrated through simulations on a case study of a power grid along a railway in the mountainous region of Southwest China.

2. Energy Storage System Configuration Model for Mountainous Railway Power Grids

When high-power imbalanced traction loads are connected to the grid’s point of common coupling (PCC), significant three-phase voltage imbalance and deviation occur due to unequal load distribution across phases. To mitigate these impacts, this paper introduces an energy storage system at the PCC node, suppressing voltage imbalance through coordinated dispatch of three-phase charging/discharging power. Additionally, considering the limited power supply capacity of mountainous power grids, renewable energy sources such as wind and photovoltaic systems are widely integrated along railway corridors. Proper utilization of renewables not only enhances system power supply capability but also reduces operational costs. However, the inherent uncertainty in renewable generation makes it difficult to strictly satisfy operational constraints. Therefore, this paper establishes a chance-constrained energy storage capacity configuration model that comprehensively considers initial investment costs and long-term operational expenses to achieve economic objectives.

2.1. Objective Function

The capacity configuration of energy storage systems for mountainous railway power grids primarily considers investment costs and operational costs, as shown in Equation (1):

$$\min C_{\mathrm{TDC}}=C_{\mathrm{INV}}+C_{\mathrm{OP}}$$

(1)

where C_TDC denotes the objective function for energy storage system configuration, which consists of two components: the daily investment cost (C_INV) and the daily operational cost (C_OP).

The investment cost C_INV of the energy storage system comprises two components: initial construction cost and long-term maintenance cost, calculated by Equation (2):

$$\begin{array}{l}{C}_{\mathrm{INV}}={\displaystyle \sum _{i\in E}[\xi (Y_{\mathrm{ESS}})+m_{\mathrm{ESS}}]\cdot (c_{\mathrm{ESS}}^{\mathrm{p}}{P}_{\mathrm{ESS},i}^{\mathrm{norm}}+c_{\mathrm{ESS}}^{\mathrm{e}}{E}_{\mathrm{ESS},i}^{\mathrm{norm}})/365}\\ \xi (Y_{\mathrm{ESS}})=r\cdot {[1-{(1+r)}^{-Y_{\mathrm{ESS}}}]}^{-1}\end{array}$$

(2)

where E is the set of energy storage systems, Y_ESS is the service lifespan (in years) of energy storage systems, m_ESS is the maintenance cost coefficient of energy storage systems, $c_{\mathrm{E}\mathrm{S}\mathrm{S}}^{\mathrm{p}}$$c_{\mathrm{E}\mathrm{S}\mathrm{S}}^{\mathrm{e}}$ is the unit cost of the internal power conversion subsystem in energy storage systems, c is to the unit cost of energy storage units, r stands for the discount rate for investments, $P_{\mathrm{ESS},i}^{\mathrm{norm}}$ and $E_{\mathrm{ESS},i}^{\mathrm{norm}}$ are the required capacity (in MW) and rated power (in MW) to be constructed for energy storage system i, respectively.

The operational costs of mountainous power grids are shown in Equation (3), primarily comprising power generation costs (C_gen), energy storage operation costs (C_ess), renewable energy utilization penalty costs (C_new), PCC node voltage imbalance penalty costs (C_unb), and voltage deviation penalty costs (C_dev).

$$C_{\mathrm{op}}=C_{\mathrm{gen}}+C_{\mathrm{ess}}+C_{\mathrm{new}}+C_{\mathrm{unb}}+C_{\mathrm{dev}}$$

(3)

The power generation cost C_gen and energy storage operation cost C_ess are calculated by Equation (4):

$$\begin{array}{l}{C}_{\mathrm{gen}}={\displaystyle \sum _{t\in T}{\displaystyle \sum _{i\in G}{c}_{\mathrm{gen},i}{p}_{i,t}^{\mathrm{gen}}\Delta t}}\\ C_{\mathrm{ess}}={\displaystyle \sum _{t\in T}{\displaystyle \sum _{i\in E}(c_{\mathrm{ch},i}{p}_{\mathrm{ch},i}^t+c_{\mathrm{dis},i}{p}_{\mathrm{dis},i}^t)\Delta t}}\end{array}$$

(4)

where T is the set of operation periods; G is the set of thermal power units; Δt is the dispatch time interval; c_gen,i is the generation cost coefficient for thermal unit i; $p_{i,t}^{\mathrm{gen}}$ stands for the active power output of thermal unit i during period t; c_ch,i and c_dis,i are the charging/discharging cost coefficients of energy storage system i, respectively; the specific values are from the Reference [26]. According to the study in [27], the impact of charging and discharging operations on the lifespan of the energy storage system is neglected, as the ratio of charging/discharging power to capacity in this paper is less than 1. $p_{\mathrm{ch},i}^t$ and $p_{\mathrm{dis},i}^t$ are the charging/discharging active power of energy storage system i during period t, respectively.

To enhance the renewable energy accommodation capacity of mountainous railway power grids, the optimization objective incorporates multiple renewable energy utilization factors as shown in Equation (5):

$$C_{\mathrm{new}}=c_{\mathrm{new}}{\displaystyle \sum _{m\in S_{\mathrm{new}}}(1-{\alpha }_m)}$$

(5)

where c_new is the penalty coefficient for insufficient renewable energy utilization, S_new is the set of renewable energy power stations, and α_m indicates the generation utilization rate of the m-th renewable energy station. This paper constructs a three-phase voltage imbalance objective function by taking the maximum value of the voltage magnitude difference between any two phases, as shown in Equation (6):

$$\begin{array}{ll}{C}_{\mathrm{unb}}=& {\displaystyle \sum _{t\in T}{\displaystyle \sum _{i\in C}{c}_{\mathrm{unb}}{U}_{i,\mathrm{unb}}}}\\ \mathrm{s}.\mathrm{t}.& \left|U_{ia}-U_{ib}\right|\le U_{i,\mathrm{unb}}\\ & \left|U_{ia}-U_{ic}\right|\le U_{i,\mathrm{unb}}\\ & \left|U_{ib}-U_{ic}\right|\le U_{i,\mathrm{unb}}\end{array}$$

(6)

where c_unb is the three-phase imbalance penalty coefficient; U_i,unb is the three-phase imbalance degree at node i; and U_ia, U_ib, and U_ic are the voltage magnitudes of phases a, b, and c, respectively. C is the set of PCC nodes.

The objective function for three-phase voltage deviation is constructed using Equation (7):

$$C_{\mathrm{dev}}={\displaystyle \sum _{t\in T}{\displaystyle \sum _{i\in C}{c}_{\mathrm{dev}}{\displaystyle \sum _{p=\mathrm{a},\mathrm{b},\mathrm{c}}\left|U_{ip}-1\right|}}}$$

(7)

where c_dev is the penalty coefficient for three-phase voltage deviation.

To calculate the voltage imbalance degree and voltage deviation at PCC nodes, it is necessary to perform power flow calculations for mountainous railway power grids. Taking phase a as an example, the original three-phase power flow equations are shown in Equation (8):

$$\begin{array}{l}{P}_{i\mathrm{a}}=U_{i\mathrm{a}}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{m\in \left\{\mathrm{a},\mathrm{b},\mathrm{c}\right\}}(G_{ij\mathrm{a}m}\cos {\theta }_{i\mathrm{a}jm}+B_{ij\mathrm{a}m}\sin {\theta }_{i\mathrm{a}jm})U_{jm}}}\\ Q_{i\mathrm{a}}=U_{i\mathrm{a}}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{m\in \left\{\mathrm{a},\mathrm{b},\mathrm{c}\right\}}(G_{ij\mathrm{a}m}\sin {\theta }_{i\mathrm{a}jm}-B_{ij\mathrm{a}m}\cos {\theta }_{i\mathrm{a}jm})U_{jm}}}\end{array}$$

(8)

where P_ia and Q_ia are the active and reactive power injections at phase a of node i, respectively, U_ia is the voltage magnitude at phase a of node i, N is the set of all grid nodes, G_ijam and B_ijam are the real and imaginary parts of the three-phase admittance matrix between phase a of node i and phase m of node j, θ_ijam represents the phase angle difference between phase a of node i and phase m of node j, calculated as θ_ijam = θ_ia − θ_jm. Since Equation (8) constitutes a set of non-convex nonlinear equations, conventional computation employs the Newton–Raphson method for iterative solving, while this paper applies linearization processing. Through the variable substitution shown in Equation (9):

$$\begin{array}{l}{G}_{ij\mathrm{ab},\Gamma }=-{\displaystyle \frac{1}{2}}{G}_{ij\mathrm{ab}}+{\displaystyle \frac{\sqrt{3}}{2}}{B}_{ij\mathrm{ab}},B_{ij\mathrm{ab},\Gamma }=-{\displaystyle \frac{\sqrt{3}}{2}}{G}_{ij\mathrm{ab}}-{\displaystyle \frac{1}{2}}{B}_{ij\mathrm{ab}}\\ G_{ij\mathrm{ac},\Gamma }=-{\displaystyle \frac{1}{2}}{G}_{ij\mathrm{ac}}-{\displaystyle \frac{\sqrt{3}}{2}}{B}_{ij\mathrm{ac}},B_{ij\mathrm{ac},\Gamma }={\displaystyle \frac{\sqrt{3}}{2}}{G}_{ij\mathrm{ac}}-{\displaystyle \frac{1}{2}}{B}_{ij\mathrm{ac}}\end{array}$$

(9)

The power flow equation for active power P_ia can be transformed into the form shown in Equation (10):

$$\begin{array}{c}{P}_{i\mathrm{a}}\approx U_{i\mathrm{a}}{\displaystyle \sum _{j\in N}[(G_{ij\mathrm{aa}}\cos {\theta }_{i\mathrm{a}j\mathrm{a}}+B_{ij\mathrm{aa}}\sin {\theta }_{i\mathrm{a}j\mathrm{a}})U_{j\mathrm{a}}}\\ +(G_{ij\mathrm{ab},T}\cos {\theta }_{i\mathrm{b}j\mathrm{b}}+B_{ij\mathrm{ab},\mathrm{T}}\sin {\theta }_{i\mathrm{b}j\mathrm{b}})U_{j\mathrm{b}}\\ +(G_{ij\mathrm{ac},\mathrm{T}}\cos {\theta }_{i\mathrm{c}j\mathrm{c}}+B_{ij\mathrm{ac},\mathrm{T}}\sin {\theta }_{i\mathrm{c}j\mathrm{c}})U_{j\mathrm{c}}\end{array}$$

(10)

Based on the linearized formulation g_ijU_j(U_i − U_jcosθ_ij) ≈ g_ij(U_i − U_j) derived from single-phase power flow calculation, the linearized power flow equation for active power P_ia can be obtained as shown in Equation (11):

$$\begin{array}{ll}{P}_{i\mathrm{a}}& \approx g_{ii\mathrm{aa}}{U}_{i\mathrm{a}}+{\displaystyle \sum _{j\in N,j\ne i}{g}_{ij\mathrm{aa}}(U_{i\mathrm{a}}-U_{j\mathrm{a}})}-{\displaystyle \sum _{j\in N,j\ne i}{b}_{ij\mathrm{aa}}({\theta }_{i\mathrm{a}}-{\theta }_{j\mathrm{a}})}\\ & +g_{ii\mathrm{ab},\Gamma }{U}_{i\mathrm{b}}+{\displaystyle \sum _{j\in N,j\ne i}{g}_{ij\mathrm{ab},\Gamma }(U_{i\mathrm{b}}-U_{j\mathrm{b}})}-{\displaystyle \sum _{j\in N,j\ne i}{b}_{ij\mathrm{ab},\Gamma }({\theta }_{i\mathrm{b}}-{\theta }_{j\mathrm{b}})}\\ & +g_{ii\mathrm{ac},\Gamma }{U}_{i\mathrm{c}}+{\displaystyle \sum _{j\in N,j\ne i}{g}_{ij\mathrm{ac},\Gamma }(U_{i\mathrm{c}}-U_{j\mathrm{c}})}-{\displaystyle \sum _{j\in N,j\ne i}{b}_{ij\mathrm{ac},\Gamma }({\theta }_{i\mathrm{c}}-{\theta }_{j\mathrm{c}})}\end{array}$$

(11)

The linearized power flow equation for reactive power Q_ia can be similarly derived, which will not be elaborated here. According to the research results of references [28,29], for most scenarios in real power systems, the absolute value of phase angle differences across lines is mostly within 10°. In the power grid studied in this paper, the error calculated between the linearization method used and the Newton–Raphson method is within 1%. The linearized power flow equations can be directly embedded into the optimization model for node voltage calculations.

2.2. Constraint Conditions

Due to equipment installation environments and technical limitations, the planned capacity and rated power of energy storage systems should be constrained within reasonable ranges. Equation (12) presents the constraints for energy storage system capacity and power ratings:

$$\begin{array}{l}{E}_{\mathrm{ess},i}^{\mathrm{l}}\le E_{\mathrm{ess},i}^{\mathrm{norm}}\le E_{\mathrm{ess},i}^{\mathrm{u}},\forall i\in E\\ c^{\mathrm{l}}{E}_{\mathrm{ess},i}^{\mathrm{norm}}\le P_{\mathrm{ess},i}^{\mathrm{norm}}\le c^{\mathrm{u}}{E}_{\mathrm{ess},i}^{\mathrm{norm}},\forall i\in E\end{array}$$

(12)

where $E_{\mathrm{ess},i}^{\mathrm{l}}$ and $E_{\mathrm{ess},i}^{\mathrm{u}}$ are the lower and upper capacity limits for energy storage system i, respectively; c^l and c^u are the lower and upper ratios of rated power to capacity for energy storage systems, respectively.

$$\begin{array}{l}{s}_{\mathrm{g},i}^t{P}_{\mathrm{g},i}^{\min }\le p_{\mathrm{g},i}^t\le P_{\mathrm{g},i}^{t,\max }\\ 0\le P_{\mathrm{g},i}^{t,\max }\le P_{\mathrm{g},i}^{\max }{s}_{\mathrm{g},i}^t\\ P_{\mathrm{g},i}^{t,\max }\le p_{\mathrm{g},i}^{t-\Delta t}+R_{\mathrm{g},i}^{\mathrm{up}}{s}_{g,i}^{t-1}+S_{\mathrm{g},i}^{\mathrm{up}}(s_{\mathrm{g},i}^t-s_{\mathrm{g},i}^{t-\Delta t})+P_{\mathrm{g},i}^{\max }(1-s_{\mathrm{g},i}^t)\\ P_{\mathrm{g},i}^{t,\max }\le P_{\mathrm{g},i}^{\max }{s}_{\mathrm{g},i}^{t+\Delta t}+S_{\mathrm{g},i}^{\mathrm{down}}(s_{\mathrm{g},i}^t-s_{\mathrm{g},i}^{t+\Delta t})\\ p_{\mathrm{g},i}^{t-\Delta t}-p_{\mathrm{g},i}^t\le R_{\mathrm{g},i}^{\mathrm{down}}{s}_{\mathrm{g},i}^t+S_{\mathrm{g},i}^{\mathrm{down}}(s_{\mathrm{g},i}^{t-\Delta t}-s_{\mathrm{g},i}^t)+P_{\mathrm{g},i}^{\max }(1-s_{\mathrm{g},i}^{t-\Delta t})\end{array}$$

(13)

where $s_{\mathrm{g},i}^t$ is the operating state of generator i during period t (0—shut down, 1—start up); $P_{\mathrm{g},i}^{\min }$ and $P_{\mathrm{g},i}^{\max }$ are the minimum and maximum active power output of generator i, respectively; $R_{\mathrm{g},i}^{\mathrm{down}}$ and $R_{\mathrm{g},i}^{\mathrm{up}}$ are the downward and upward ramp rates of generator i; $S_{\mathrm{g},i}^{\mathrm{down}}$ and $S_{\mathrm{g},i}^{\mathrm{up}}$ are the maximum allowable power change for shutdown and startup of generator i.

The operational constraints of the energy storage system are shown in Equation (14):

$$\begin{array}{l}{s}_{\mathrm{ch},i}^t+s_{\mathrm{dis},i}^t\le 1\\ E_{\mathrm{ess},i}^{\min }\le E_{\mathrm{ess},i}^t\le E_{\mathrm{ess},i}^{\max }\\ E_{\mathrm{ess},i}^t=E_{\mathrm{ess},i}^{t-\Delta t}+{\eta }_{\mathrm{ch},i}{p}_{\mathrm{ch},i}^t-{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\eta }_{\mathrm{dis},i}$}\right.}{p}_{\mathrm{dis},i}^t\\ E_{\mathrm{ess},i}^{\Delta t}=E_{\mathrm{ess},i}^0+{\eta }_{\mathrm{ch},i}{p}_{\mathrm{ch},i}^{\Delta t}-{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\eta }_{\mathrm{dis},i}$}\right.}{p}_{\mathrm{dis},i}^{\Delta t}\\ 0\le {\eta }_{\mathrm{ch},i}{p}_{\mathrm{ch},i}^t\le s_{\mathrm{ch},i}^t{P}_{\mathrm{ess},i}^{\mathrm{norm}}\\ 0\le {\displaystyle \raisebox{1ex}{$p_{\mathrm{dis},i}^t$}\!\left/ \!\raisebox{-1ex}{${\eta }_{\mathrm{dis},i}$}\right.}\le s_{\mathrm{dis},i}^t{P}_{\mathrm{ess},i}^{\mathrm{norm}}\\ E_{\mathrm{ess},i}^0=E_{\mathrm{ess},i}^{T-\Delta t}+{\eta }_{\mathrm{ch},i}{p}_{\mathrm{ch},i}^T-{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\eta }_{\mathrm{dis},i}$}\right.}{p}_{\mathrm{dis},i}^T\end{array}$$

(14)

where $s_{\mathrm{ch},i}^t$ and $s_{\mathrm{dis},i}^t$ are the charging and discharging states of energy storage system i during period t, respectively; $E_{\mathrm{ess},i}^{\min }$ and $E_{\mathrm{ess},i}^{\max }$ are the minimum and maximum safe capacity limits of the i-th energy storage system, respectively; η_ch,i and η_dis,i are the charging and discharging efficiency coefficients of energy storage system i, respectively; $p_{\mathrm{ch},i}^t$ and $p_{\mathrm{dis},i}^t$ are the charging/discharging power of energy storage system i during period t, respectively; $E_{\mathrm{ess},i}^t$ is the remaining capacity of energy storage system i at period t.

At time t, the power balance constraint during system operation is given by Equation (15):

$${\displaystyle \sum _{i\in G}{p}_{\mathrm{g},i}^t}+{\displaystyle \sum _{i\in E}(p_{\mathrm{dis},i}^t-p_{\mathrm{ch},i}^t)}+{\displaystyle \sum _{m\in S_{\mathrm{new}}}{p}_m^t}=p_{\mathrm{Load}}^t$$

(15)

where $p_{\mathrm{Load}}^t$ is the active power load of the system during time period t.

To increase the utilization rate of wind–solar renewable energy generation along railway corridors, in addition to flexible dispatch based on their output, it is also necessary to ensure that the daily generation utilization rates of multiple renewable energy stations exceed a predefined threshold, as specified in Equation (16):

$${\displaystyle \sum _{t\in T}{p}_m^t\ge {\alpha }_m{\displaystyle \sum _{t\in T}{\tilde{p}}_m^t}},\hspace{1em}\hspace{1em}\forall m\in S_{\mathrm{new}}$$

(16)

where $p_m^t$ and ${\tilde{p}}_m^t$ are the dispatched power and actual generation power of the m-th renewable energy station during period t, respectively; α_m is the generation utilization threshold for the m-th renewable energy station.

Furthermore, the dispatched output of renewable energy must not exceed its actual generation output at any time period, as constrained by Equation (17):

$$p_m^t\le {\tilde{p}}_m^t,\hspace{1em}\hspace{1em}\forall m\in S_{\mathrm{new}}$$

(17)

3. DRCC-Based Energy Storage System Configuration Model Transformation

In the previously described deterministic optimization model, the renewable energy output constraints (as shown in Equations (16) and (17)) treat predicted renewable generation as precise values while ignoring their inherent uncertainty. In reality, renewable power stations along mountainous railway lines exhibit significant output uncertainty. Employing deterministic methods to solve renewable-integrated configuration models would lead to deviations between configuration/operation results and actual conditions. For optimization models incorporating uncertainty, robust optimization and stochastic optimization are commonly used solution approaches. Stochastic optimization requires probability distributions of random variables, which are often difficult to obtain accurately in practice [30]. Robust optimization transforms the model into a solvable form by constructing fluctuation intervals for random variables, but tends to yield overly conservative results. To address these limitations, this paper develops a data-driven distributionally robust chance-constrained (DRCC) model for energy storage configuration in mountainous railway power grids. The proposed method has the following features:

• Leverages historical renewable generation data without requiring exact probability distributions or fluctuation ranges;
• Incorporates adjustable confidence parameters to control solution conservativeness;
• Enhances configuration/operation flexibility through data-driven uncertainty characterization

3.1. Chance-Constrained Modeling for Uncertain Renewable Energy

The renewable energy utilization rate is defined as the ratio of consumed renewable generation to available generation capacity. For computational convenience, it is formulated in discrete form as shown in Equation (18):

$${\alpha }_m={\displaystyle \frac{{\displaystyle \sum _{t\in T}{p}_m^t}}{{\displaystyle \sum _{t\in T}{\tilde{p}}_m^t}}},\forall m\in S_{\mathrm{new}}$$

(18)

To enhance renewable energy utilization efficiency, the conventional approach involves setting a lower-bound threshold for the renewable energy utilization rate in the model. However, this threshold is often difficult to determine reasonably, and under renewable generation uncertainty, a fixed threshold may render the model infeasible in certain scenarios. To address this, this paper incorporates the renewable energy utilization rate into the objective function for optimization, while formulating the chance constraint shown in Equation (19). This ensures that, under uncertain conditions, the renewable energy utilization rate achieves the desired level with a confidence probability of at least 1 − ε.

$$\mathrm{Pr}\left\{{\displaystyle \sum _{t\in T}{p}_m^t}\ge {\alpha }_m{\displaystyle \sum _{t\in T}{\tilde{p}}_m^t}\right\}\ge 1-\epsilon ,\hspace{1em}\hspace{1em}\forall m\in S_{\mathrm{new}}$$

(19)

Furthermore, to ensure that the scheduled renewable power does not exceed its actual generation capacity under output uncertainty, this condition must hold with a confidence level of at least 1 − ε. Accordingly, this paper establishes the chance-constrained condition for renewable energy output as formulated in Equation (20).

$$Pr\left\{p_m^t\le {\tilde{P}}_m^t\right\}\ge 1-\epsilon ,\hspace{1em}\hspace{1em}\forall m\in S_{\mathrm{new}}$$

(20)

3.2. Wasserstein Distance-Based Distributionally Robust Chance-Constrained (DRCC) Model

Based on N historical sample data vectors $\widehat{\mathit{\xi }}$, we can derive their empirical distribution $\widehat{P}={\displaystyle \sum _{i=1}^N{\delta }_{{\widehat{\mathit{\xi }}}_i}}$, where δ is the Dirac distribution. However, in practice, there is often a certain discrepancy between the true distribution P of the random vector ξ and the empirical distribution $\widehat{P}$. Therefore, it is necessary to construct an ambiguity set of the random variables based on the empirical distribution. Currently, there are two main approaches for constructing ambiguity sets of probability distributions: moment-based methods and probability distance-based methods. Moment-based methods utilize only low-order moment information (e.g., restricting the fluctuation ranges of mean and variance) but fail to effectively capture the distributional characteristics of historical data. Probability distance-based methods, in contrast, can fully exploit historical data information. The Wasserstein distance is a widely used metric for measuring the discrepancy between two distributions.

Let the probability density of the empirical distribution $\widehat{P}$ be denoted as $\widehat{p}$, and that of the true distribution P as p. Accordingly, we construct an ambiguity set M for the random variable’s probability distribution using the Wasserstein distance as defined in Equation (21).

$$\begin{array}{l}M=\{P:d_w(P,\widehat{P})\le \theta \}\\ \begin{array}{ll}{d}_w(P,\widehat{P})& =\inf {\displaystyle {\int }_{{\Xi }^2}‖\mathsf{\xi }- \hat{\mathsf{\xi }}‖\mathit{\Pi }(d\mathsf{\xi },d \hat{\mathsf{\xi }})}\\ & =\inf {\displaystyle {\int }_{{\Xi }^2}‖\mathsf{\xi }- \hat{\mathsf{\xi }}‖\pi (\mathsf{\xi }, \hat{\mathsf{\xi }})d\mathsf{\xi }d \hat{\mathsf{\xi }}}\end{array}\end{array}$$

(21)

where Ξ is the support set of the random variable, typically defined as the range of historical data across all dimensions; Π is the joint distribution function of the random variables ξ and $\widehat{\mathit{\xi }}$; with marginal distributions corresponding to P (true distribution) and $\widehat{P}$ (empirical distribution), respectively; π is the probability density function of Π; θ is the radius of the ambiguity set based on the Wasserstein distance. The ambiguity set M contains all probability distributions P whose Wasserstein distance from the empirical distribution $\widehat{P}$ is less than θ, d_w(P,$\widehat{P}$) computes the Wasserstein distance between any distribution P and the empirical distribution $\widehat{P}$. θ can control the conservativeness of the model; a larger θ implies greater uncertainty and a more conservative solution. The value of θ can be adjusted flexibly during model optimization to balance robustness and performance. The term ||*|| denotes the vector norm. For computational tractability, this paper adopts the 1-norm (L1 norm) in subsequent calculations.

Reference [31] first established the ambiguity set of chance constraints over the Wasserstein distance, and it then proposed a Wasserstein distance-based distributionally robust optimization model with chance constraints. Based on the above analysis, the chance constraints (19) and (20) can be reformulated as Equations (22) and (23) below.

$$\underset{P\in M}{\inf }Pr\left\{{\displaystyle \sum _{t\in T}{p}_m^t}\ge {\alpha }_m{\displaystyle \sum _{t\in T}{\tilde{p}}_m^t}\right\}\ge 1-\epsilon ,\forall m\in S_{\mathrm{new}}$$

(22)

$$\underset{P\in M}{\inf }Pr\left\{p_m^t\le {\tilde{p}}_m^t\right\}\ge 1-\epsilon ,\forall m\in S_{\mathrm{new}}$$

(23)

3.3. Chance-Constrained Model Reformulation

An optimization model containing probabilistic expressions in the form of Equation (22) is said to incorporate chance constraints. Since chance-constrained models cannot be solved directly, these probabilistic constraints must first be converted into deterministic linear constraints. To facilitate the derivation, we first perform the following transformation:

$$\begin{array}{l}{\xi }_m={\displaystyle \sum _{t\in T}{\tilde{p}}_m^t}\\ b_m={\displaystyle \sum _{t\in T}{p}_m^t}\end{array}$$

(24)

where ξ_m and b_m are newly introduced variables used to represent the summation expressions concerning P and $\widehat{P}$. Let ${\xi }_m^j$ denote the j-th historical sample data point of the uncertain variable ξ_m. Then, Equation (22) can be transformed into the following form:

$$\underset{P\in M}{\inf }Pr\{{\alpha }_m{\xi }_m\le b_m\}\ge 1-\epsilon$$

(25)

According to the findings in Reference [32], the conditional value at risk (CVaR) theory can be employed to approximate the feasible region characterized by chance constraints. The constrained domain described by constraint condition (25) can be equivalently represented as the set shown in Equation (26).

$$Z_{\mathrm{CVaR}}=\left\{{\mathit{p}}_m\in {ℝ}^{\left|T\right|}:\underset{P\in M}{\sup }\underset{\beta }{\inf }\left[-\epsilon \beta +E_P\left[{\left(\max ({\alpha }_m{\xi }_m-b_m)+\beta \right)}_{+}\right]\right]\le 0\right\}$$

(26)

where the set Z_CVaR is a convex approximation of the feasible region defined by the chance constraint (25), p_m is the power output vector of renewable energy station m across all time periods, and β is a newly introduced real-valued slack variable. The notation (*)₊ denotes the positive part operation on the enclosed expression, which takes the original value when the expression is positive and zero otherwise. E_P[*] represents the expectation operation over the expression containing uncertain variables, where the distribution of these variables follows P. |T| indicates the cardinality of the operation time set T. According to Reference [33], the convex approximation shown in Equation (26) can be further transformed into a set of linear constraints as presented in Equation (27).

$$\left\{\begin{array}{l}\theta v-\epsilon \gamma \le {\displaystyle \frac{1}{N_{\mathrm{sample}}}}{\displaystyle \sum _{j=1}^N{z}_j}\\ z_j+\gamma \le b_m-{\alpha }_m{\xi }_m^j,\forall j\in [N_{\mathrm{sample}}]\\ {‖{\alpha }_m‖}_{*}\le v\\ z_j\le 0,\forall j\in [N_{\mathrm{sample}}]\\ 0\le v,0\le \gamma \end{array}\right.$$

(27)

where v and γ are intermediate dual variables generated during the transformation, z is an introduced slack variable, N_sample is the number of samples, with [N_sample] representing the index set {1, 2, …, N_sample}, and ${\xi }_m^j$ is the j-th historical sample data point of the uncertain variable ξ_m. Similarly, the chance constraint in Equation (23) can be converted into a set of linear constraints using this method, which will not be elaborated further.

At this stage, within the ambiguity set of random variable distributions constructed via the Wasserstein distance, the non-convex and nonlinear chance constraints in the model have been transformed into a set of tractable linear constraints through the CVaR approximation method. Consequently, the original optimization problem is reformulated as a mixed-integer linear programming (MILP) problem, which can be directly solved using mathematical programming solvers.

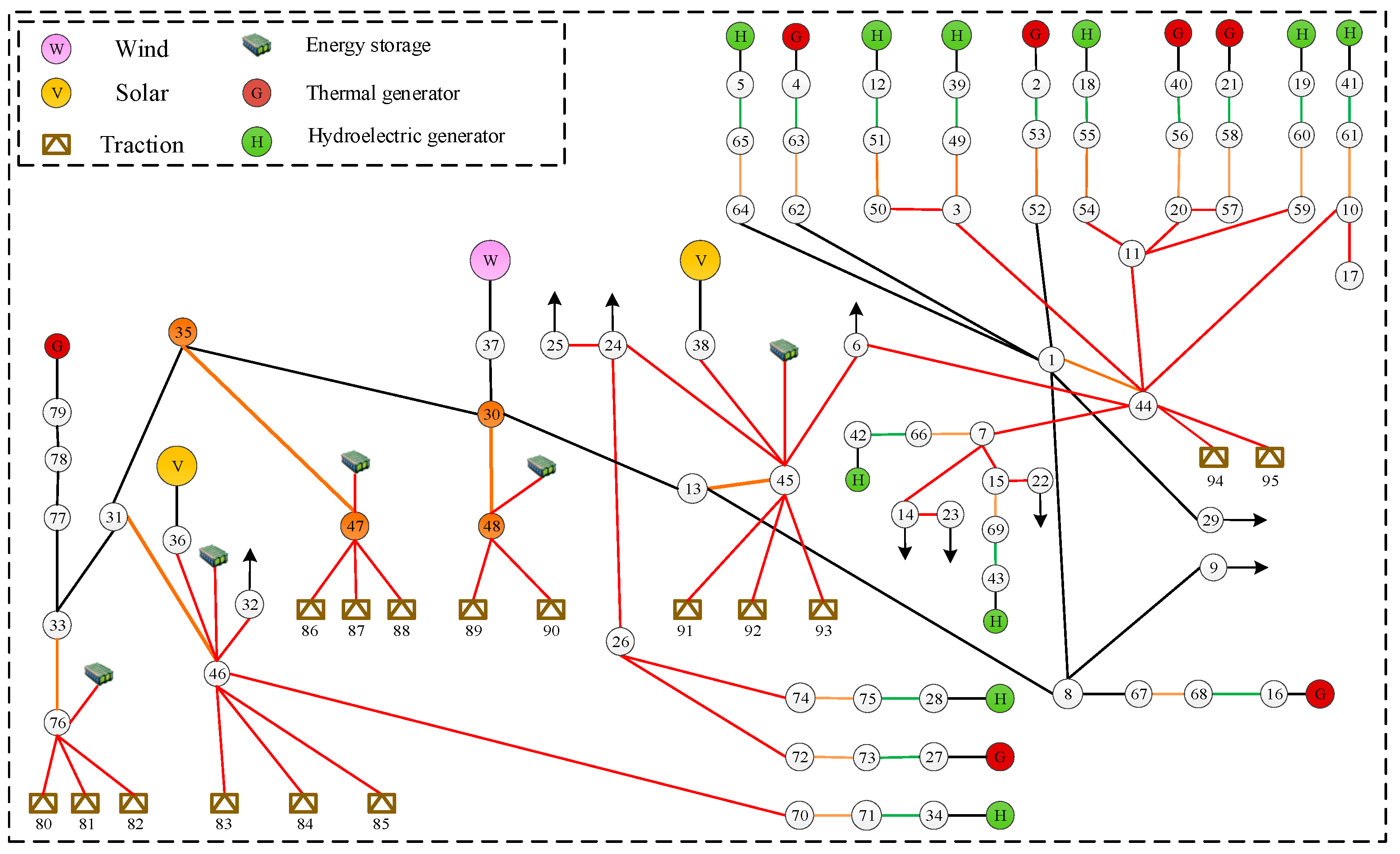
4. Case Study

4.1. Case Study Description

This paper establishes a chance-constrained optimization model considering three-phase imbalance, based on a power grid along a railway in Southwest China. As shown in Figure 1, the grid system consists of 95 nodes, including 6 PCC nodes connecting traction substations along the railway. Since Node 44 has fewer connected traction substations, PCC Nodes 45, 46, 47, 48, and 76 are selected as energy storage allocation nodes. For renewable energy integration, Nodes 36 and 38 are each connected to 200 MW photovoltaic farms, while Node 37 is connected to a 1200 MW wind farm.

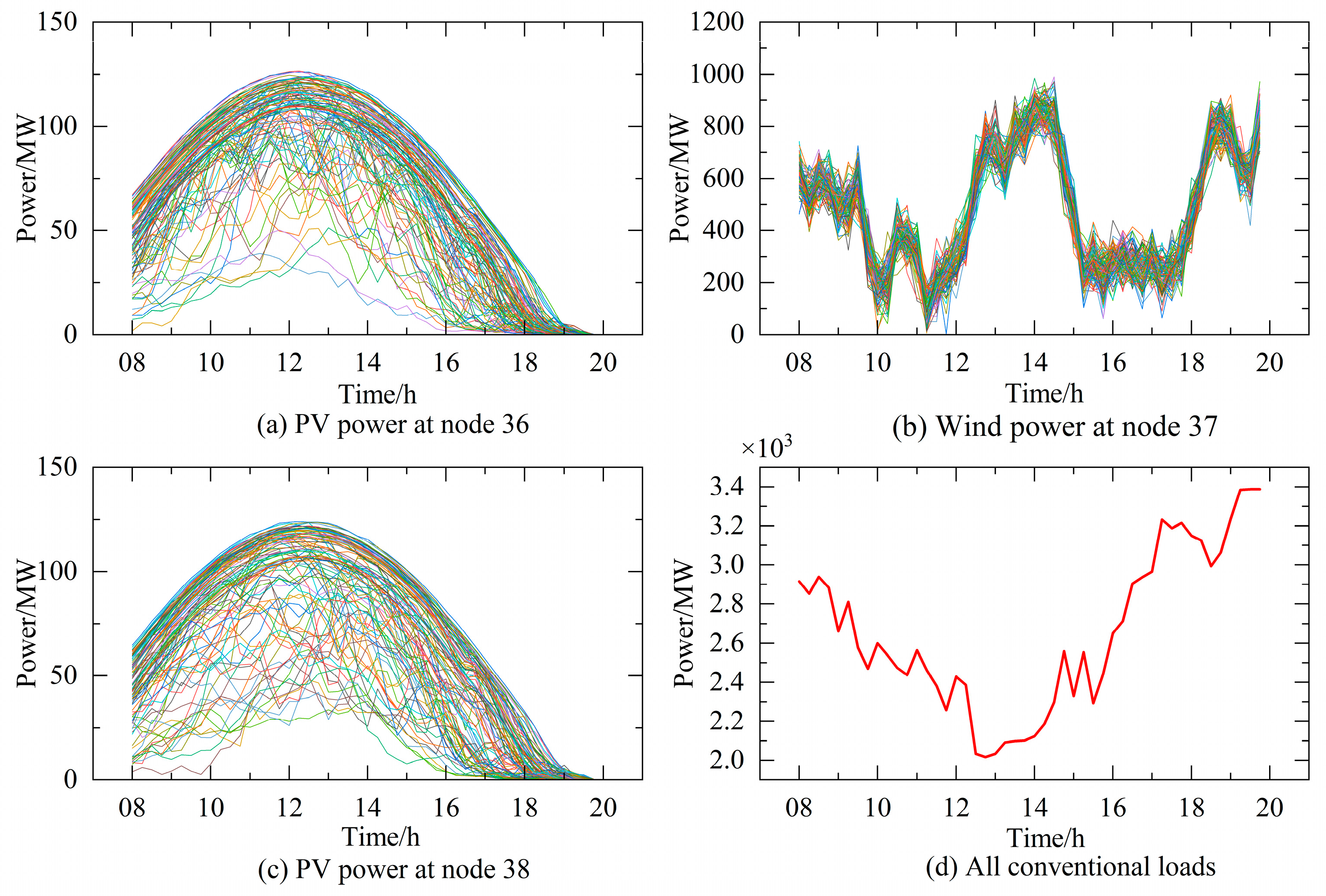
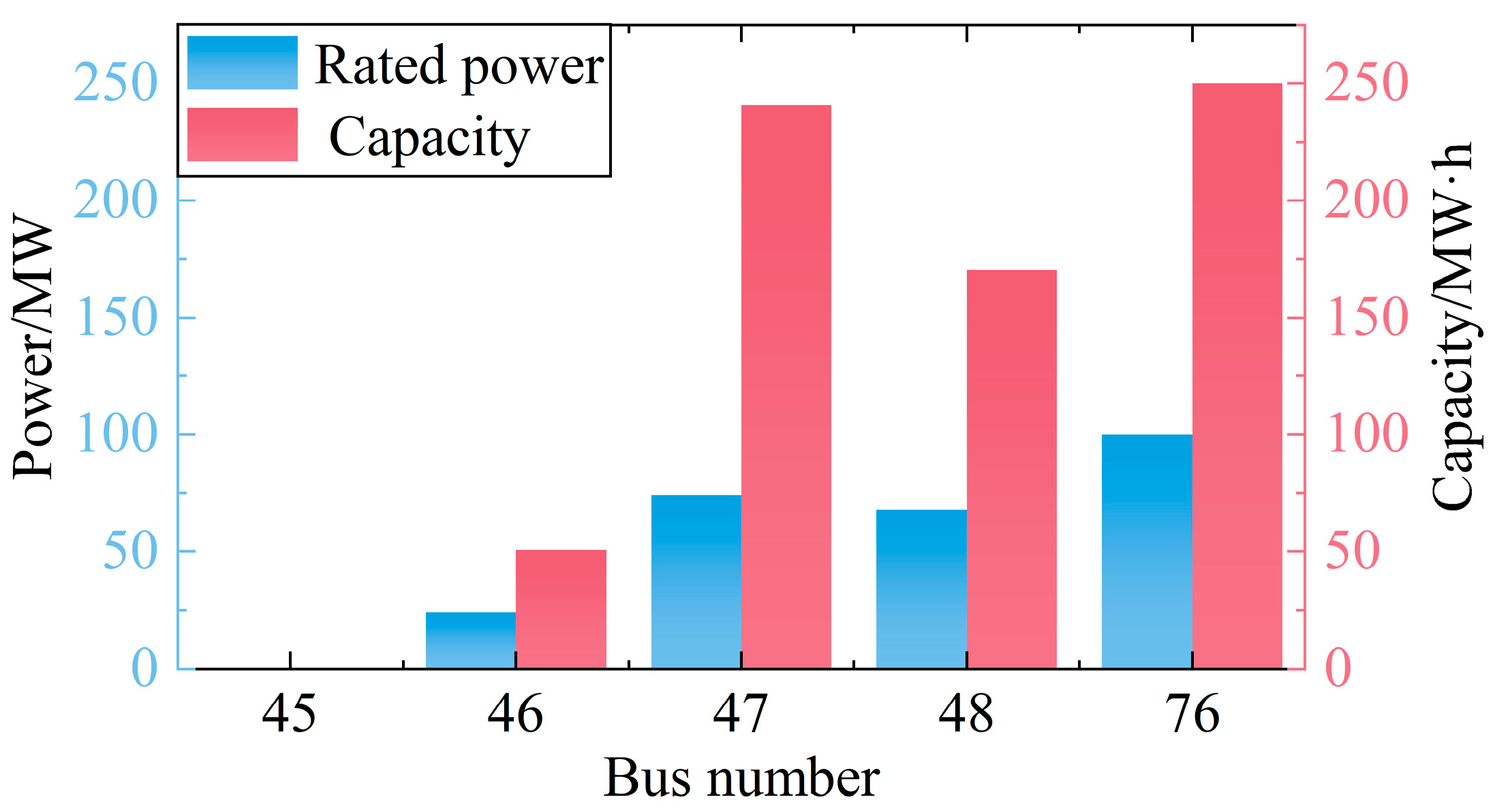
4.2. Case Data

The power generation curves for renewable energy sources and conventional loads (excluding traction loads) are shown in Figure 2. To account for the uncertainty in wind and solar farm output, we selected 365 days of historical generation data as the basis for constructing the uncertainty set of renewable energy output distributions. Given that the mountainous railway under study primarily operates trains during daytime hours, data from 8:00 to 20:00 were extracted for analysis. The load data represents the expected values for each time period across a typical day, with a scheduling time interval Δt of 15 min. The relevant parameters of the energy storage system are shown in

Table 1. Parameters of the energy storage system.

Parameters	Value	Parameters	Value
$c_{\mathrm{E}\mathrm{S}\mathrm{S}}^{\mathrm{p}}$ (¥/MW)	1.51 × 106	cl	0.2
$c_{\mathrm{E}\mathrm{S}\mathrm{S}}^{\mathrm{e}}$ (¥/MWh)	1.35 × 106	cu	0.6
r (year)	10	$E_{\mathrm{e}\mathrm{s}\mathrm{s}}^{\mathrm{l}}$ (MWh)	0
cch/cdis (¥/MWh)	50	$E_{\mathrm{e}\mathrm{s}\mathrm{s}}^{\mathrm{u}}$ (MWh)	250

below.

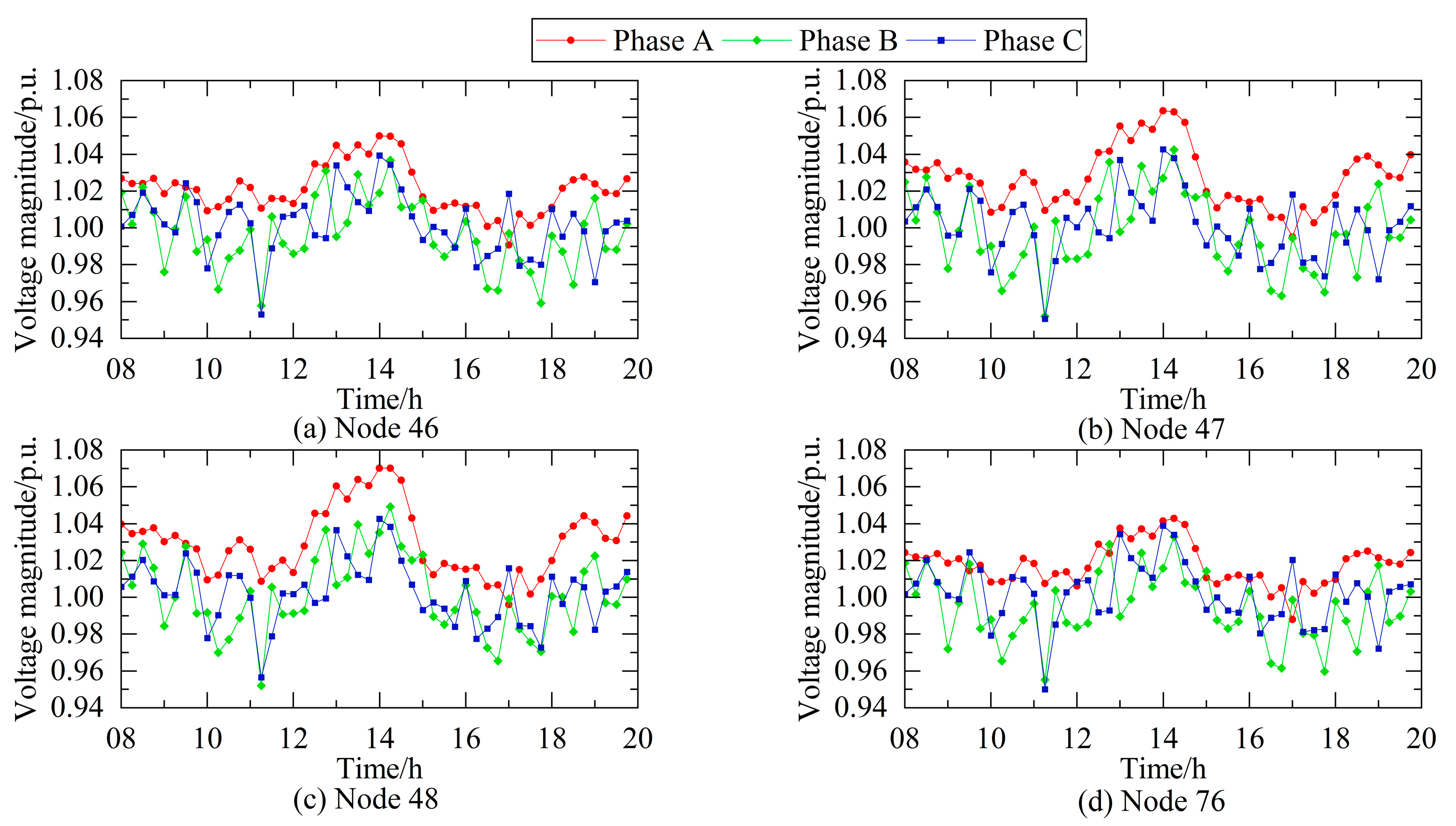
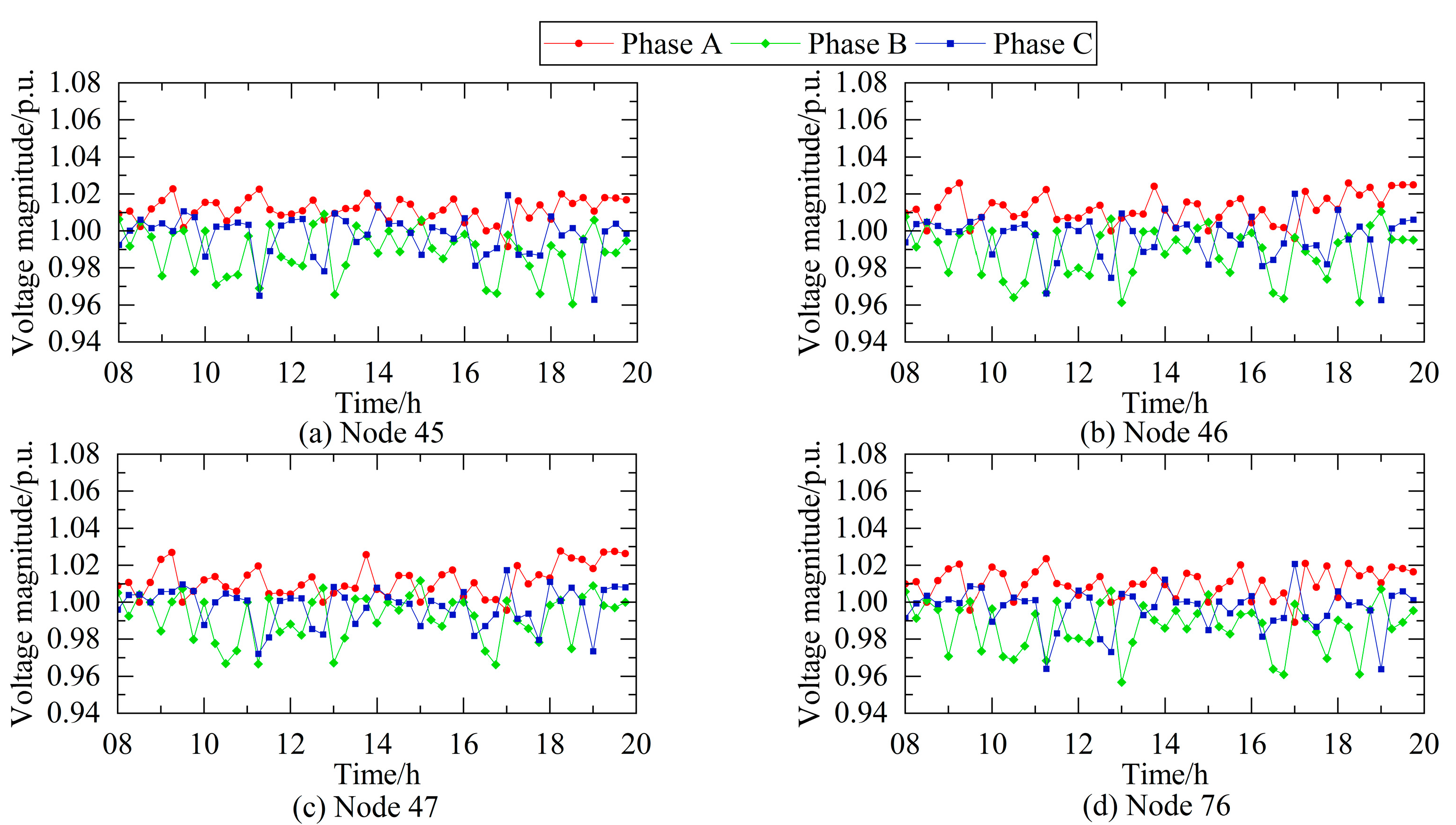
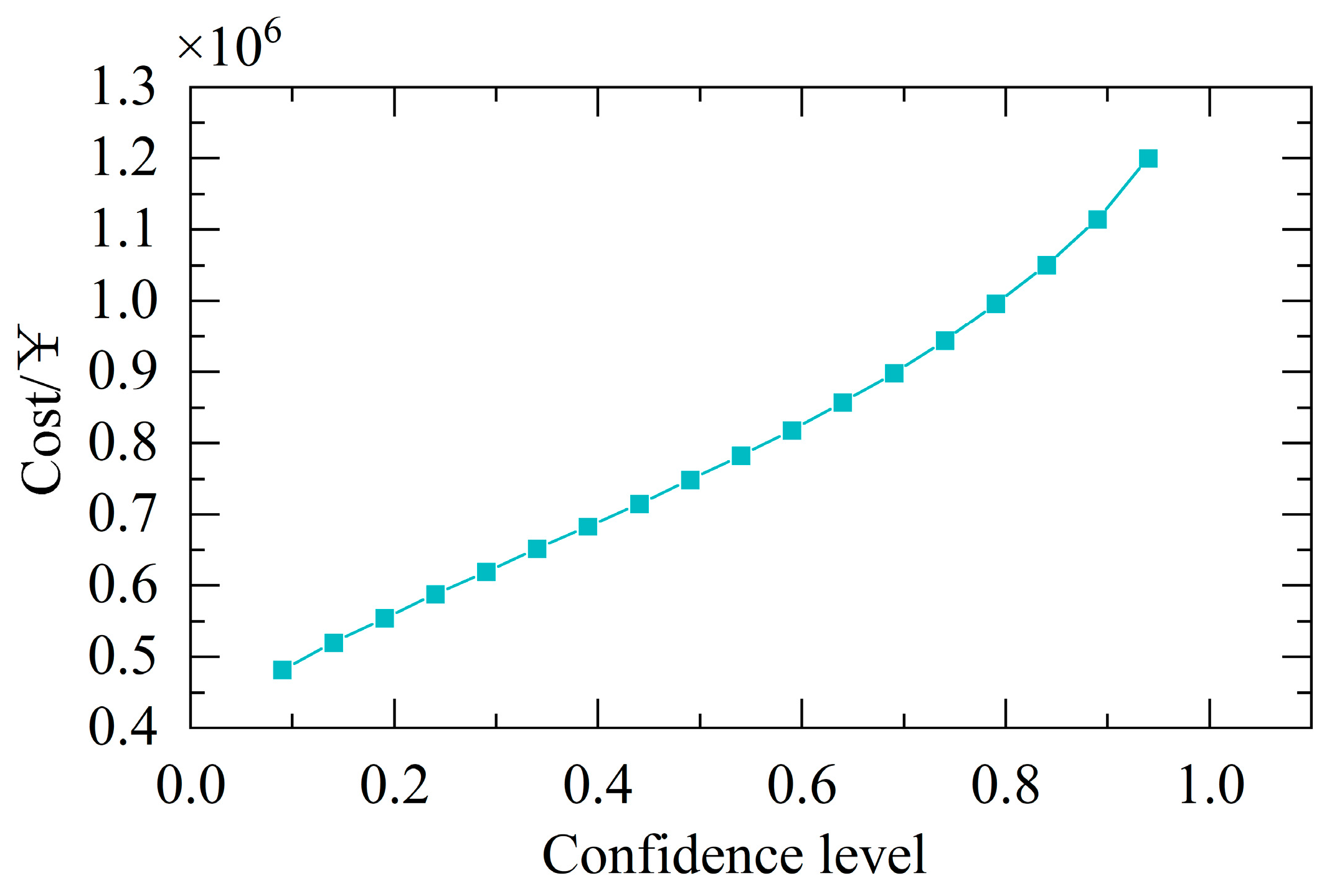
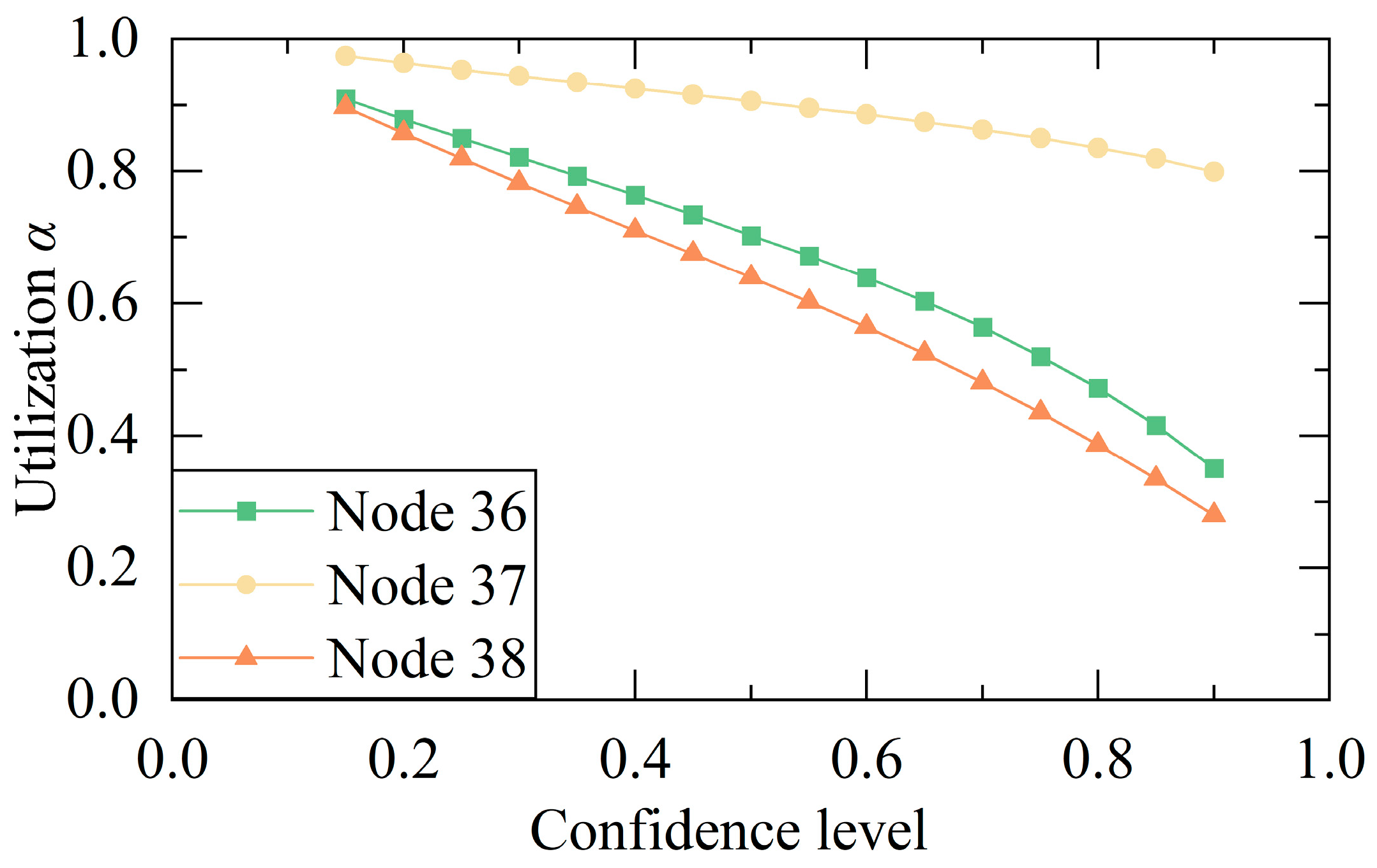
4.3. Analysis of Simulation Results

This paper establishes a mixed-integer linear programming (MILP) model for energy storage configuration by linearizing the three-phase AC power flow equations and transforming the non-convex nonlinear chance constraints using the CVaR method. The model is implemented in MATLAB R2024b with YALMIP and solved using Gurobi 12.1.

Under the system constraints and power balance conditions, the energy storage configuration results at a 90% confidence level (1 − ε) are obtained, as shown in Figure 3. The model was solved in 18.85 s. The results indicate that no energy storage system is required at Node 45 (planned capacity = 0). This is because, according to the system configuration illustrated in Figure 1, PCC Nodes 44 and 45 are surrounded by numerous conventional generation units with strong output regulation capability. These existing units are already sufficient to maintain regional voltage stability without relying on additional energy storage devices for voltage support.

By deploying energy storage systems at Nodes 46, 47, 48, and 76, the three-phase voltage magnitudes at these four PCC nodes during the scheduling period are shown in Figure 4, while the voltage quality optimization results are presented in Figure 5. After optimization, the cumulative system voltage deviation decreases from the original 10.4527 p.u. to 6.1983 p.u., representing a 40.7% overall reduction. Additionally, the cumulative three-phase voltage imbalance is reduced from 6.31 p.u. to 5.30 p.u., achieving a 16% improvement. These results demonstrate that the proposed energy storage configuration effectively mitigates voltage fluctuations and three-phase imbalances caused by traction loads.

This paper establishes an energy storage configuration model based on the distributionally robust chance-constrained (DRCC) method, aiming to fully exploit the uncertainty of renewable energy output and enhance its utilization rate. Compared with the deterministic approach using the predicted renewable energy output values (as shown in

Table 2. Comparison of results between DRCC model and deterministic model.

Model	Utilization Rates			Cost/¥
	Node 36	Node 37	Node 38
DRCC	67.22%	89.57%	60.20%	7.76 × 105
Deterministic	50.35%	72.95%	47.10%	9.62 × 105

), since the predicted values used the expected historical values, the confidence parameter (1 − ε) of the DRCC model was set to 0.5. It can be observed that the DRCC-based optimization model effectively improves the utilization of renewable energy. The utilization rates at nodes 36, 37, and 38 increase by 16.87%, 16.62%, and 13.10%, respectively, while the configuration cost of the energy storage system is reduced by 19.33%. This is because the deterministic model only utilizes predicted renewable energy output values, ignoring the possibility of actual output exceeding predictions, leading to conservative results. In contrast, the DRCC-based model allows decision-makers to flexibly adjust uncertainty parameters based on historical data, enabling more rational decision-making.

This paper comprehensively considers the uncertainty of wind and solar power generation in the configuration model by employing chance-constrained programming to formulate renewable energy output constraints, where ε represents the failure probability and (1 − ε) denotes the confidence level. Through multiple simulation experiments, we analyzed the impact of the confidence parameter on model outcomes. As shown in Figure 6, the total optimization cost exhibits an increasing trend with higher confidence levels—as the failure probability of renewable energy constraints decreases, the system adopts more conservative wind–solar power dispatch strategies to ensure operational security, consequently raising overall system costs. Figure 7 demonstrates the variation in utilization rates for the three renewable energy farms across different confidence levels. At lower confidence levels, all three renewable plants maintain utilization rates above 90%, while at higher confidence levels, their utilization must decrease to satisfy threshold constraints.

5. Conclusions

For the optimal configuration and operation of energy storage systems in mountainous railway power grids, this paper comprehensively considers the uncertainty of wind and solar power generation as well as the voltage deviation and imbalance issues caused by traction load integration. A novel energy storage configuration method is proposed for mountainous railway power grids incorporating renewable energy integration. The simulation results lead to the following conclusions:

• Energy storage configuration can effectively mitigate voltage fluctuations and three-phase imbalance induced by traction loads. Simulation results demonstrate that compared to systems without energy storage, the implemented energy storage solution reduces overall voltage deviation by 40.7% and improves three-phase voltage imbalance by 16%.
• As the confidence level increases, the system adopts more conservative scheduling strategies for renewable energy output to prevent power shortages. However, this approach reduces renewable energy utilization rates, leading to increased generation costs from conventional power units and higher wind–solar curtailment costs, ultimately resulting in elevated overall operational costs.