Predicting Methane Dry Reforming Performance via Multi-Output Machine Learning: A Comparative Study of Regression Models
Abstract
1. Introduction
1.1. Contributions to SDG 7 (Affordable and Clean Energy)
1.2. Scope and Research Objectives
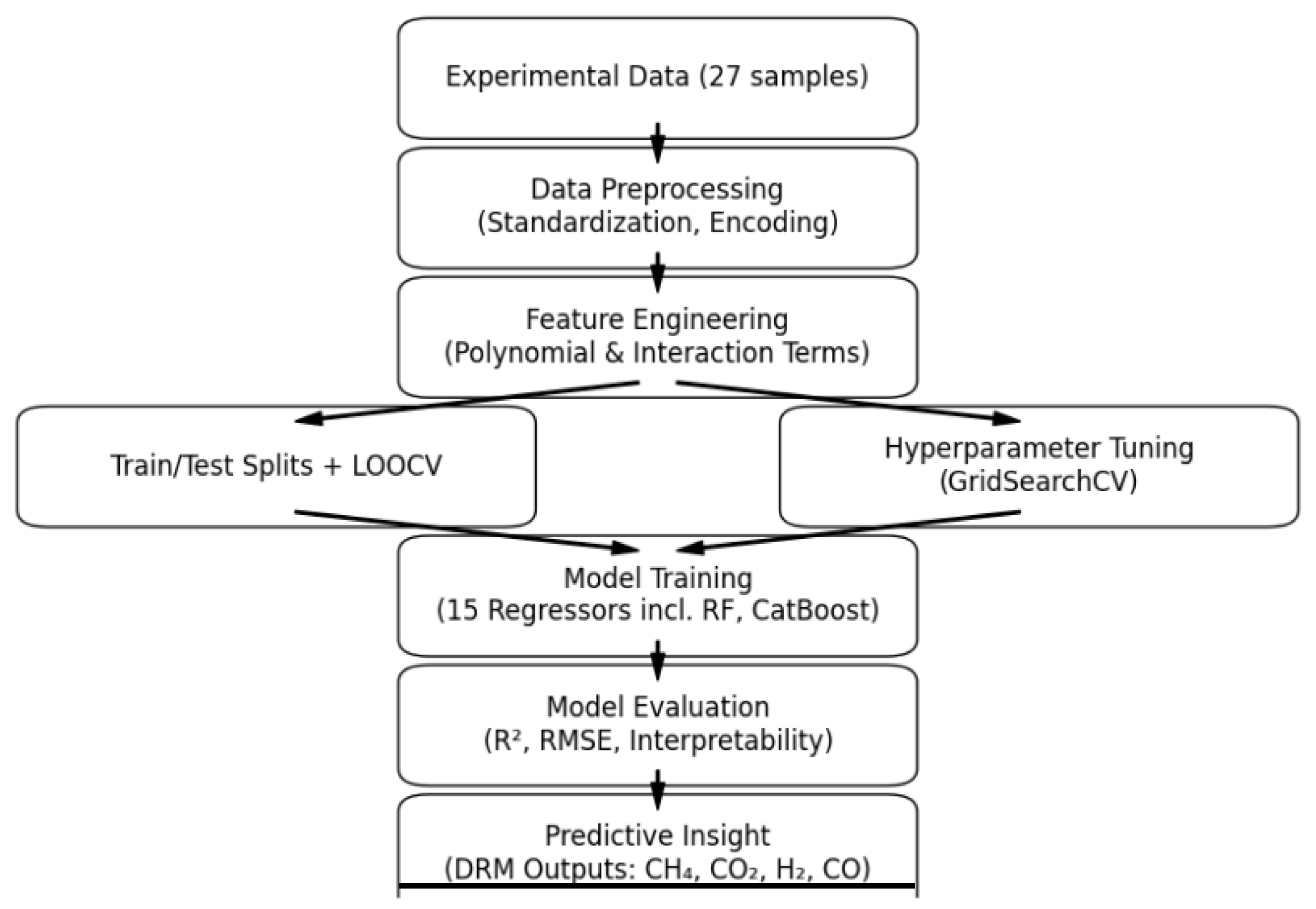
2. Materials and Methods
2.1. Feature Set
2.2. Feature Engineering
2.3. Machine Learning Regression Models for DRM
2.4. Model Training and Validation
2.5. Performance Metrics
2.6. Preprocessing the Data
2.7. Descriptive Statistics Summarizing the Main Characteristics of the Data
2.8. Outlier Detection
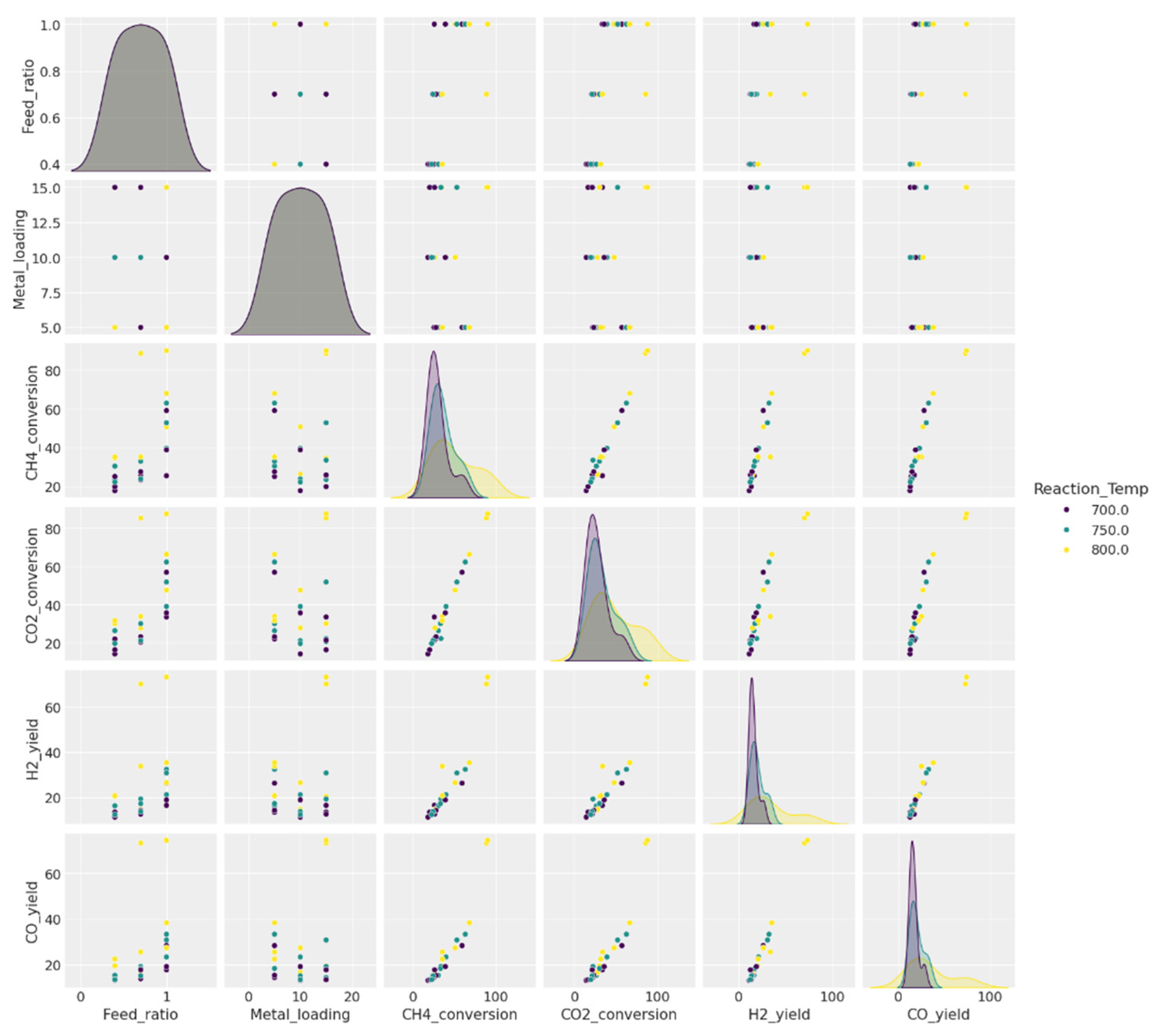
2.9. Visualizing the Data
3. Results and Discussion
3.1. Model Evaluation
- Ensemble methods and neural networks captured complex patterns via multiple learners or layers.
- Kernel methods (SVR, NuSVR) effectively modelled non-linearities via feature space transformations.
- Regularized models (Ridge, Lasso, ElasticNet) addressed multicollinearity by penalizing large coefficients.
- Bayesian Ridge introduced probabilistic regularization via priors.
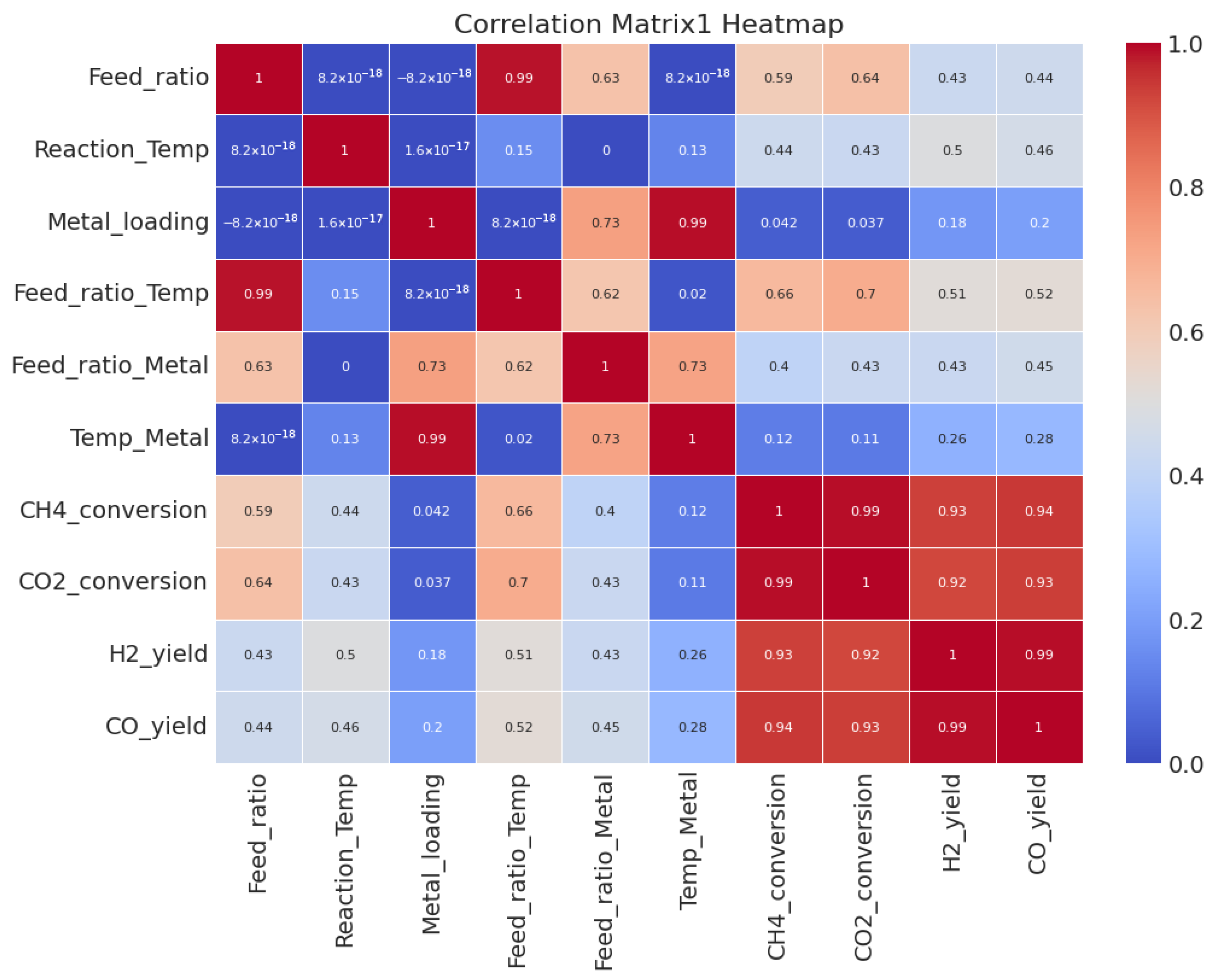
3.2. Correlation Analysis
3.3. Prediction Models and Hyperparameter Tuning
3.3.1. GridSearchCV Results
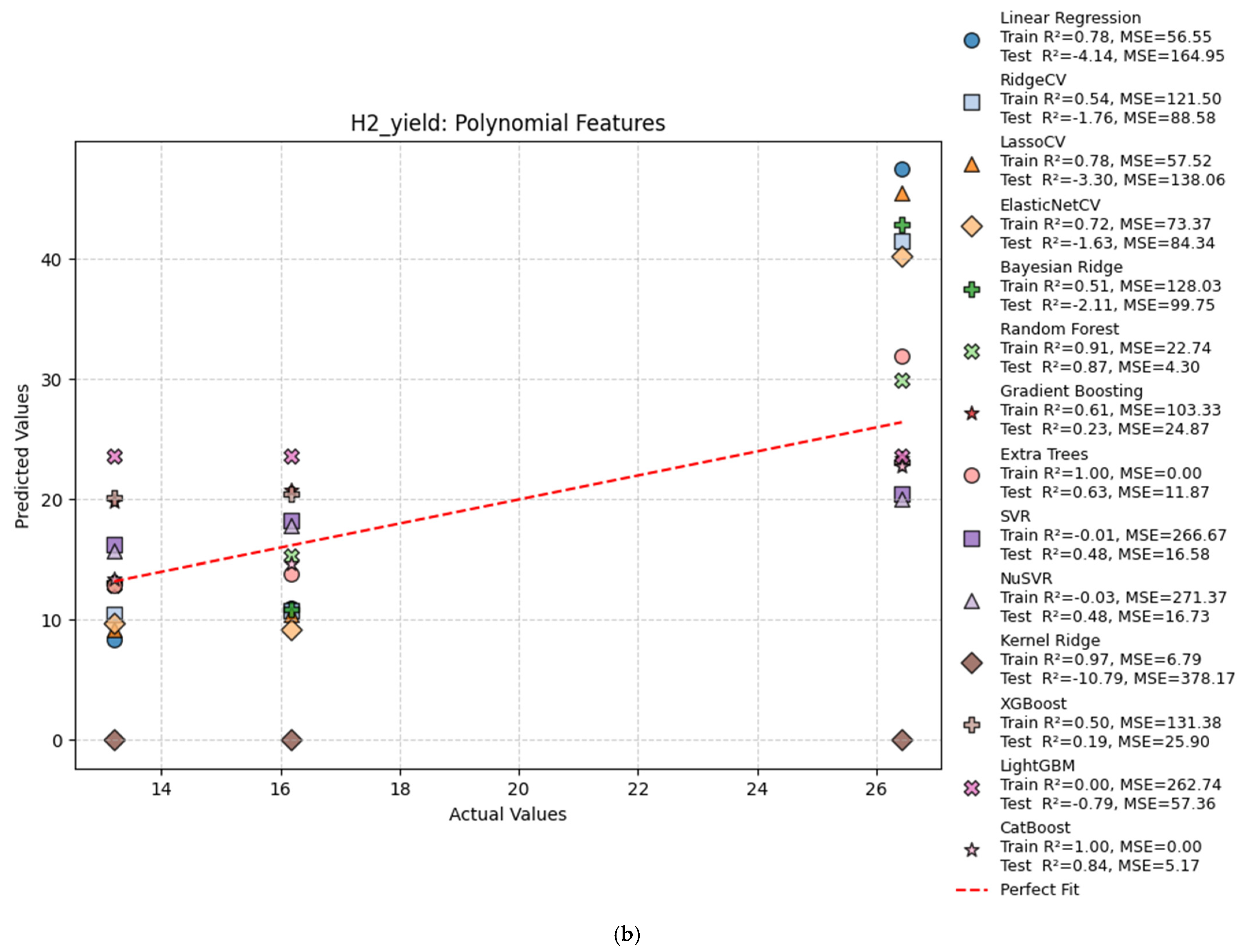
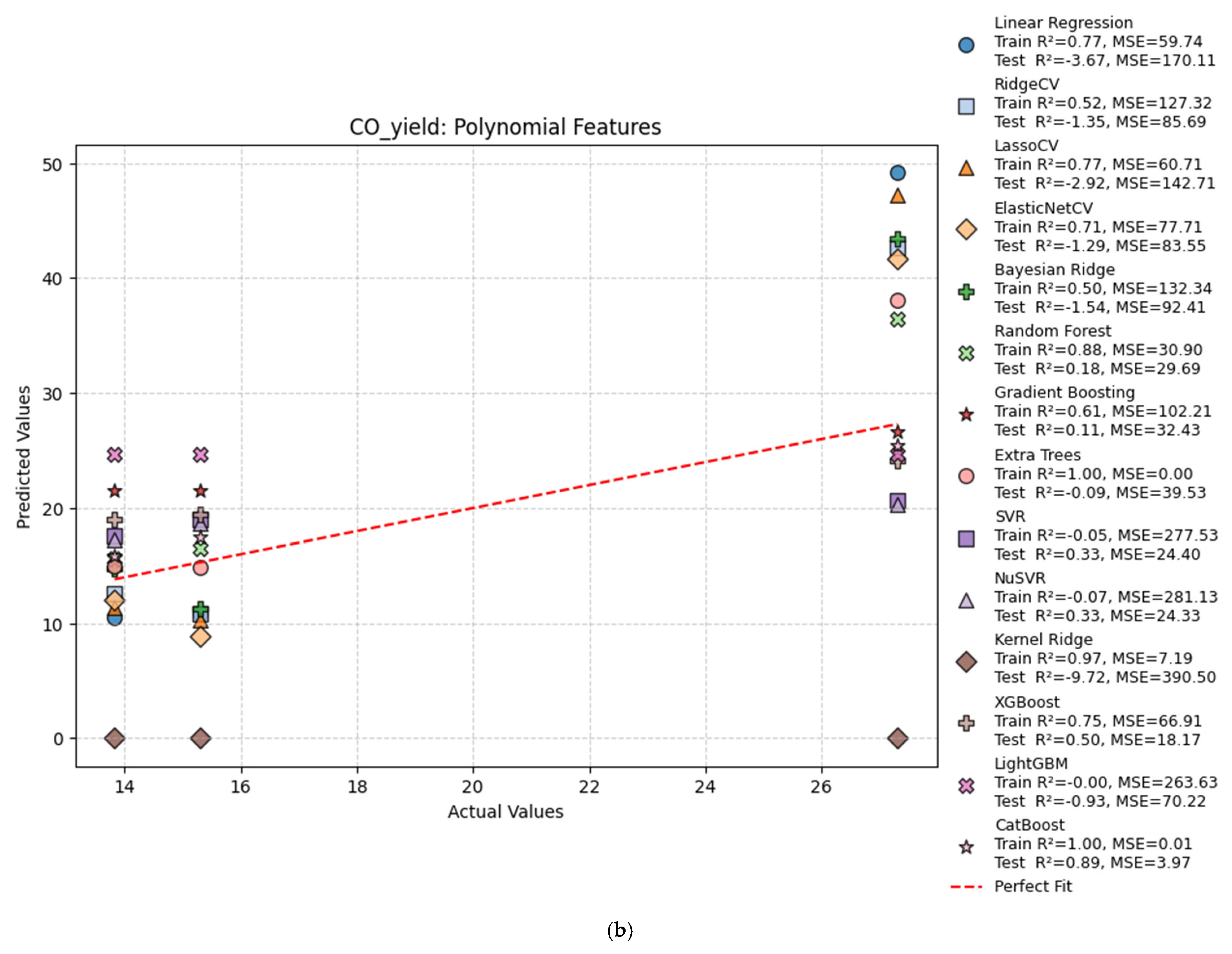
3.3.2. Prediction Results
3.3.3. Cross-Validation Comparison (CV = 3 vs. CV = 5)
3.3.4. Best Hyperparameters
3.3.5. Model Performance and Evaluation Metrics
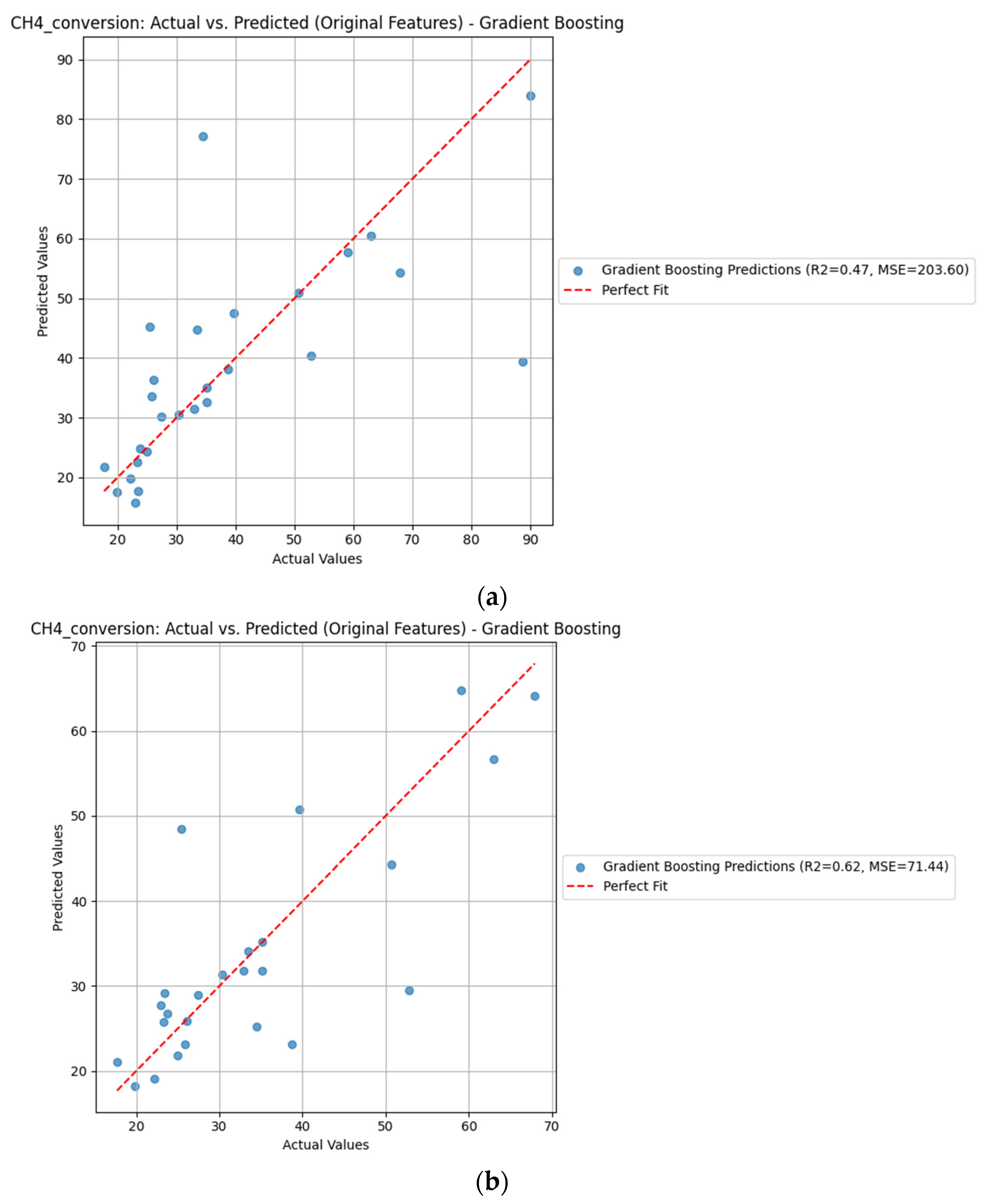
3.3.6. Leave-One-Out Cross-Validation (LOOCV) Results
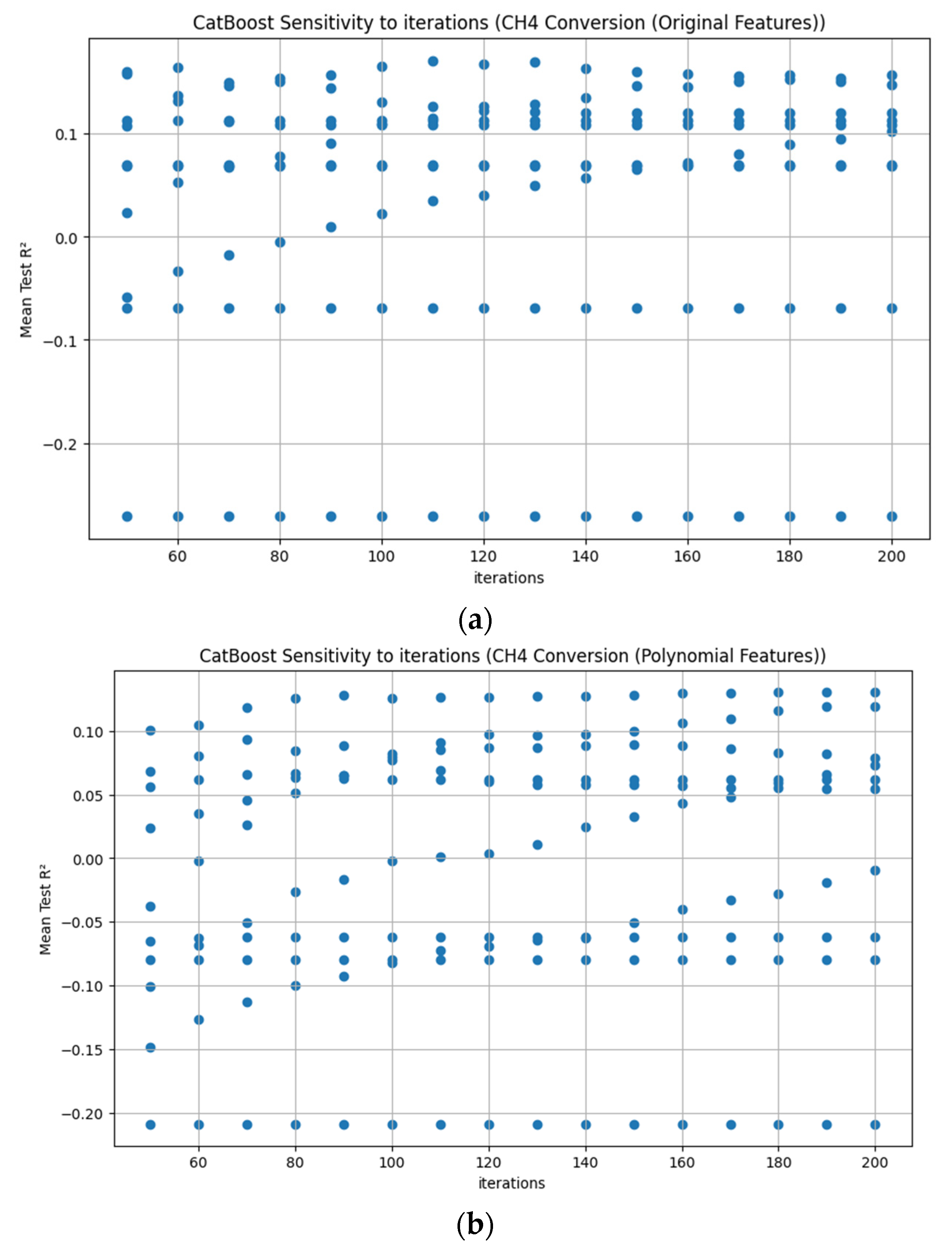
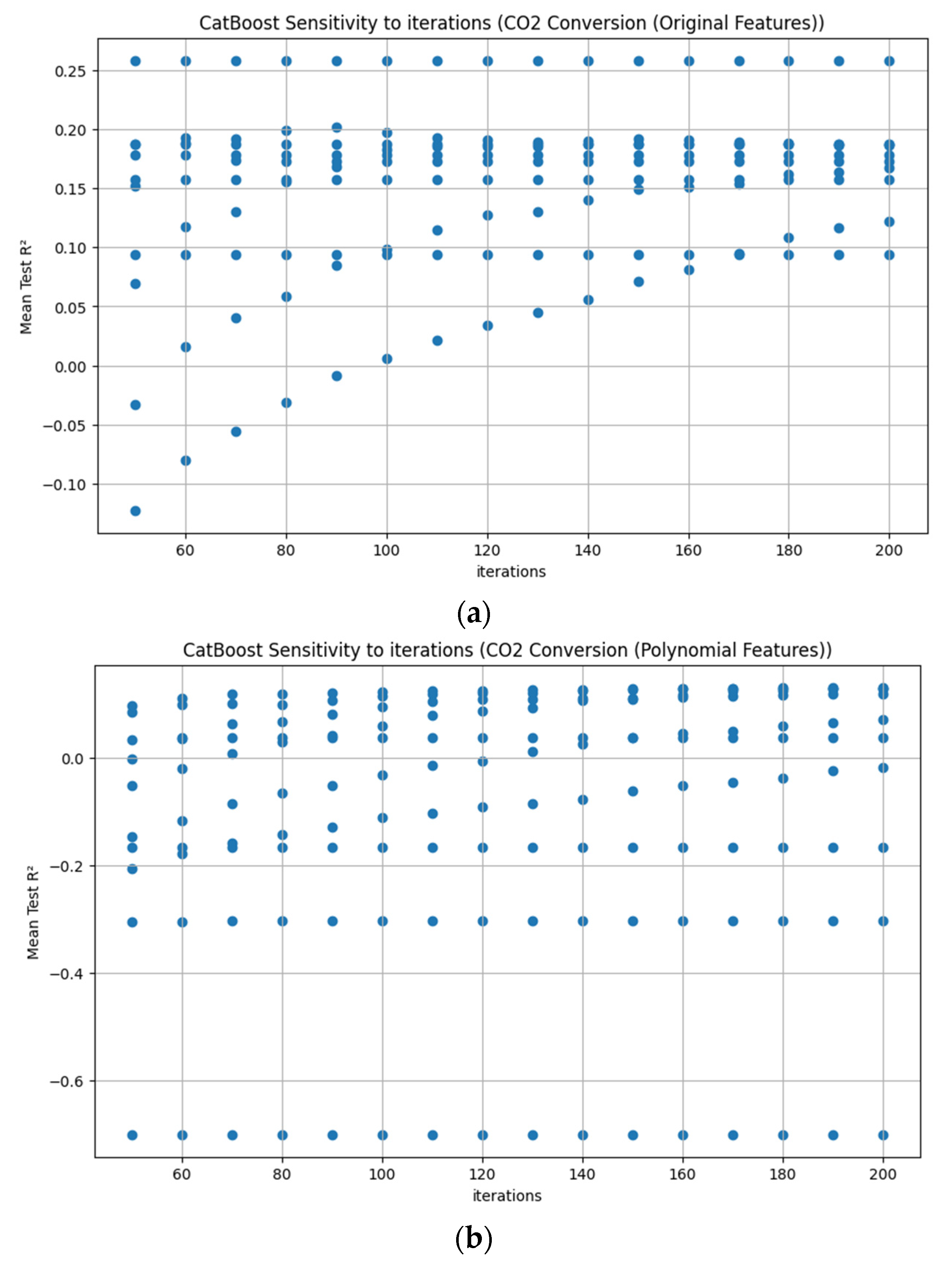
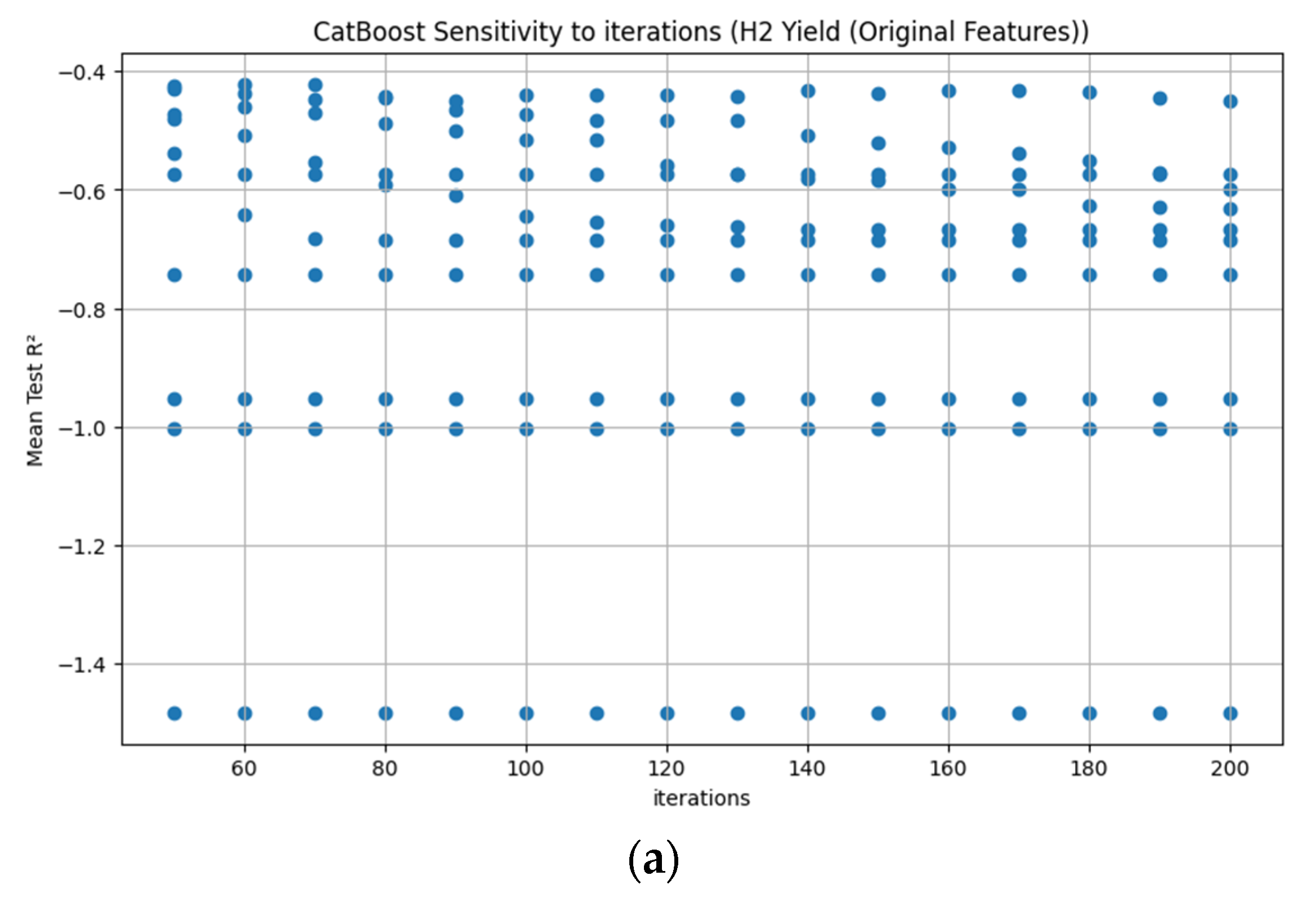
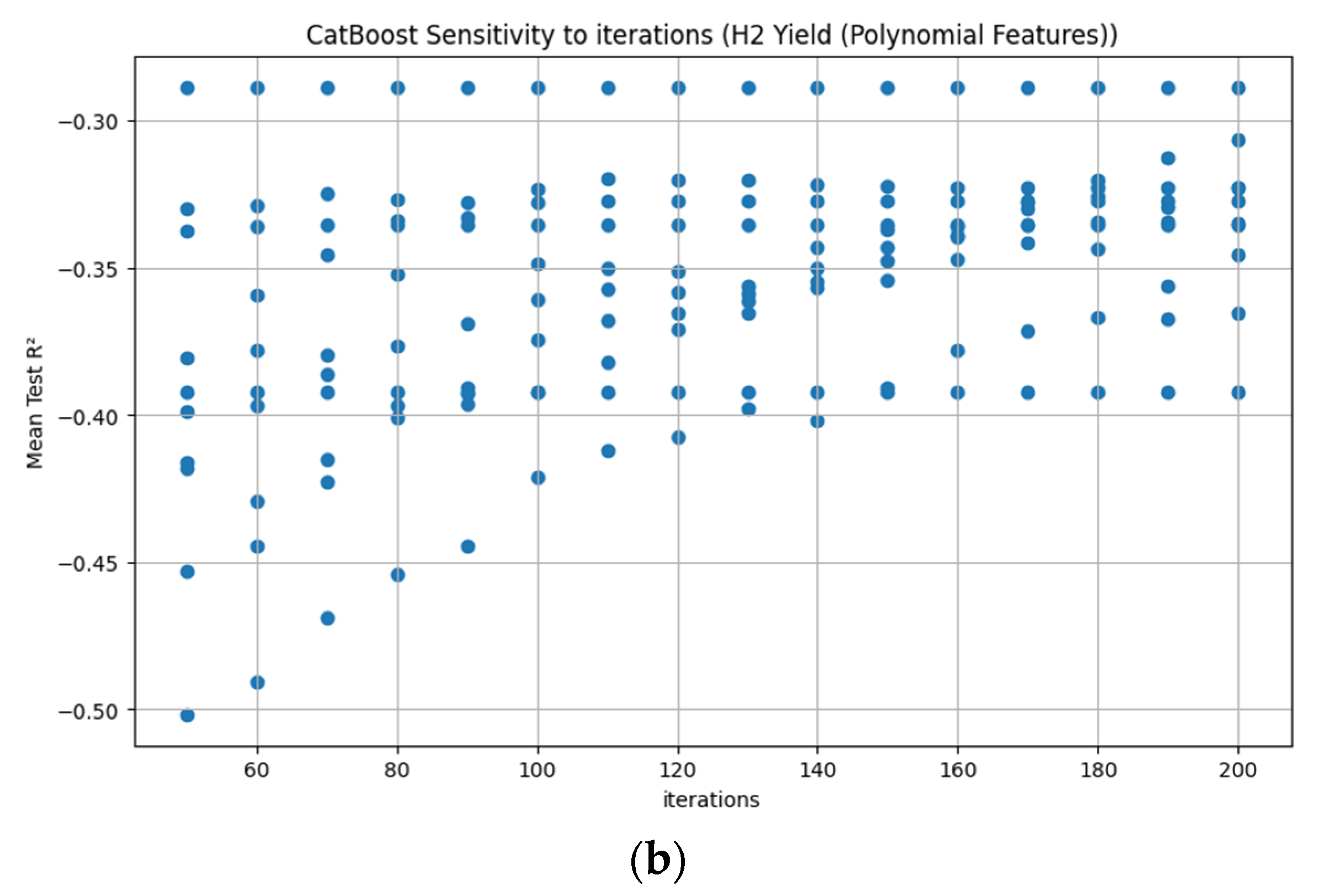
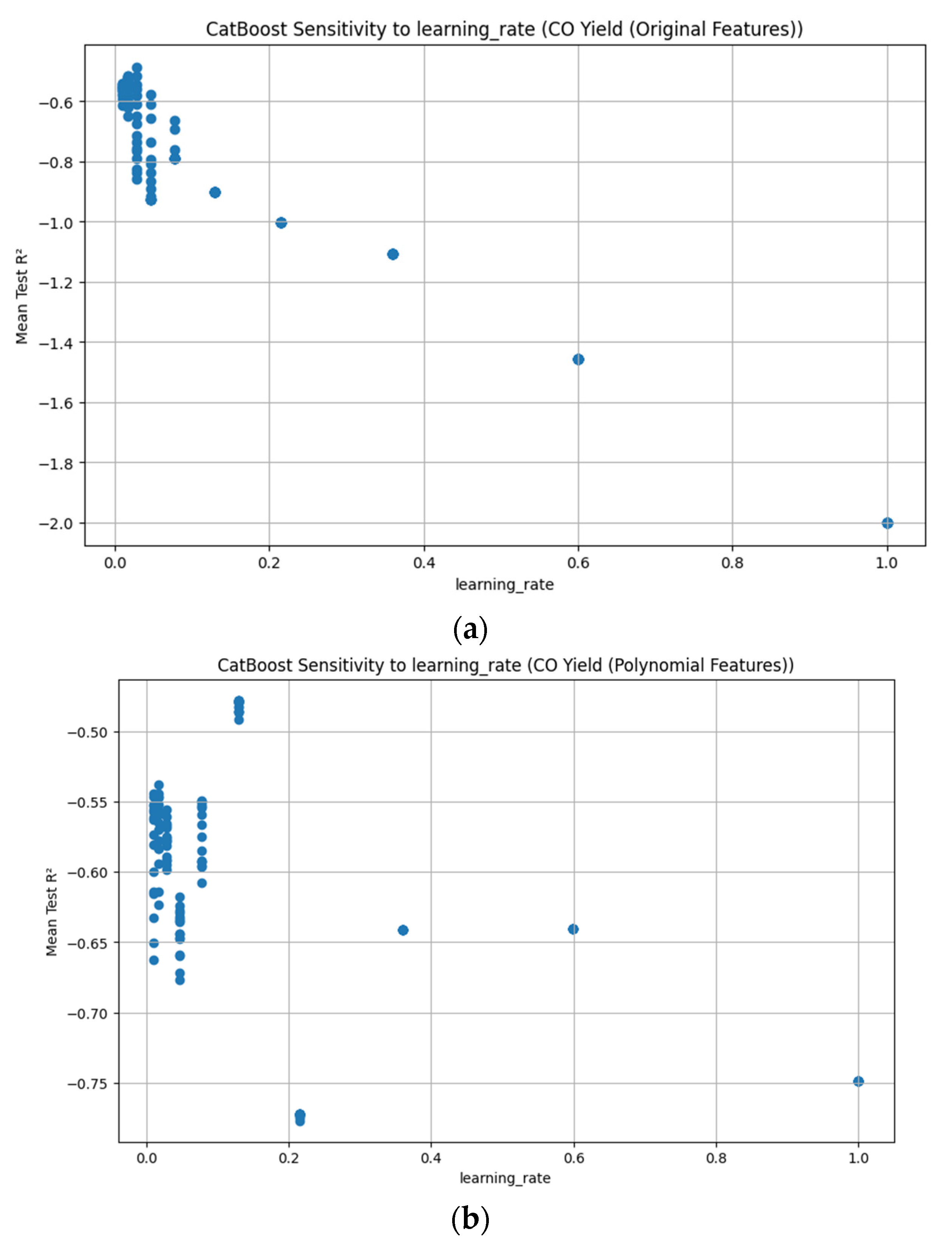
3.3.7. CatBoost Hyperparameter R2 Analysis
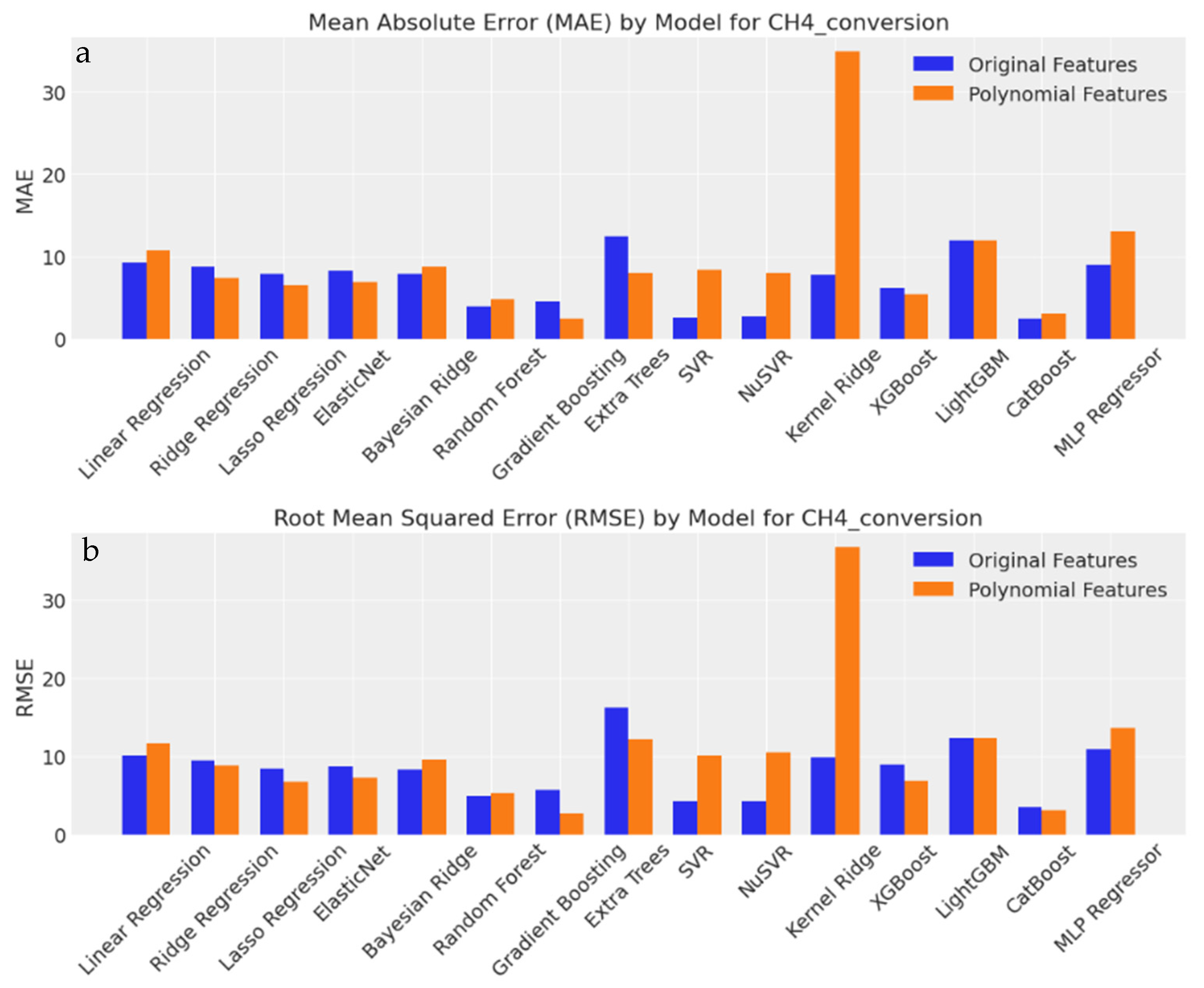
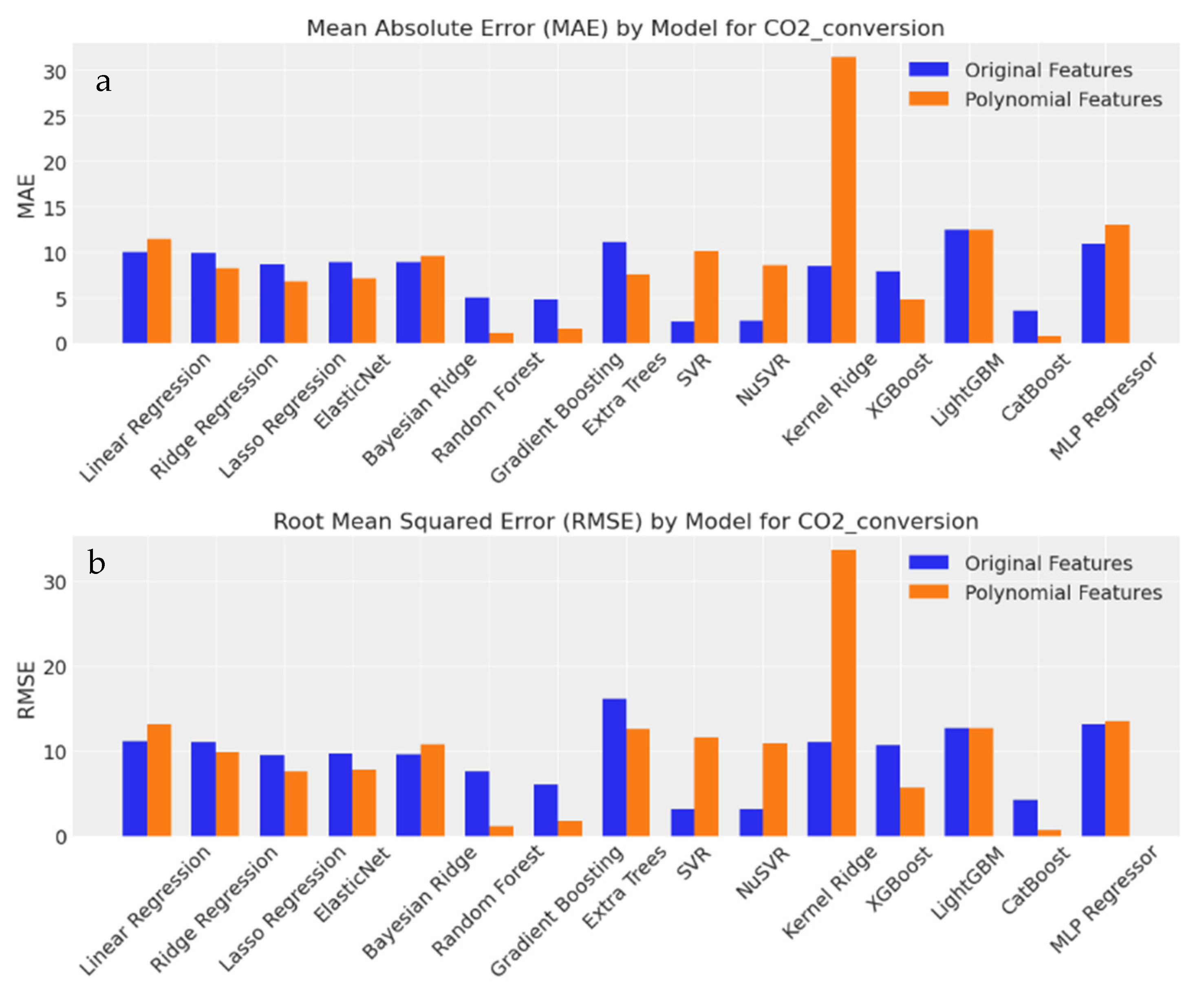
3.3.8. Evaluation of Output Predictions Based on MAE and RMSE
4. Model Performance Metrics in DRM: Comparing CH4 and CO2 Conversions with H2 and CO Yields
5. Parametric Influence, Interactions, and Predictive Insight
6. Novelty and Impact
7. Limitations and Future Work
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Expt. Runs | Inputs | Outputs | |||||
|---|---|---|---|---|---|---|---|
| Feed Ratio | Reaction Temp (°C) | Metal Loading (%) | CH4 Conversion (%) | CO2 Conversion (%) | H2 Yield (%) | CO Yield (%) | |
| 1 | 0.40 | 800.00 | 10.00 | 22.99 | 20.84 | 13.24 | 14.56 |
| 2 | 0.70 | 800.00 | 15.00 | 88.63 | 85.41 | 70.31 | 73.21 |
| 3 | 0.40 | 750.00 | 15.00 | 23.43 | 20.68 | 13.54 | 14.37 |
| 4 | 1.00 | 700.00 | 5.00 | 59.08 | 56.97 | 26.22 | 28.32 |
| 5 | 1.00 | 700.00 | 15.00 | 25.38 | 33.52 | 16.35 | 17.70 |
| 6 | 1.00 | 750.00 | 10.00 | 39.60 | 38.98 | 21.11 | 23.32 |
| 7 | 0.40 | 700.00 | 5.00 | 25.01 | 21.96 | 13.26 | 14.31 |
| 8 | 0.40 | 800.00 | 15.00 | 34.48 | 30.02 | 20.32 | 19.44 |
| 9 | 1.00 | 800.00 | 10.00 | 50.70 | 47.60 | 26.43 | 27.31 |
| 10 | 0.40 | 750.00 | 5.00 | 30.34 | 26.32 | 16.17 | 15.31 |
| 11 | 0.70 | 750.00 | 15.00 | 33.45 | 22.22 | 19.15 | 19.15 |
| 12 | 0.70 | 800.00 | 10.00 | 26.11 | 27.77 | 14.54 | 16.59 |
| 13 | 0.40 | 700.00 | 10.00 | 17.69 | 14.15 | 11.12 | 13.09 |
| 14 | 0.70 | 700.00 | 10.00 | 23.27 | 20.35 | 13.21 | 13.83 |
| 15 | 0.40 | 700.00 | 15.00 | 19.78 | 16.31 | 13.37 | 13.37 |
| 16 | 0.70 | 750.00 | 5.00 | 32.89 | 30.02 | 17.15 | 18.32 |
| 17 | 1.00 | 750.00 | 5.00 | 62.93 | 62.34 | 32.36 | 33.31 |
| 18 | 1.00 | 750.00 | 15.00 | 52.76 | 51.85 | 30.77 | 30.77 |
| 19 | 0.70 | 700.00 | 15.00 | 25.82 | 21.34 | 12.45 | 17.70 |
| 20 | 0.70 | 800.00 | 5.00 | 35.09 | 33.77 | 33.77 | 25.54 |
| 21 | 1.00 | 700.00 | 10.00 | 38.75 | 35.68 | 18.78 | 19.11 |
| 22 | 0.70 | 700.00 | 5.00 | 27.46 | 23.15 | 14.14 | 15.32 |
| 23 | 0.70 | 750.00 | 10.00 | 23.78 | 21.13 | 13.56 | 15.06 |
| 24 | 1.00 | 800.00 | 15.00 | 90.04 | 87.60 | 73.42 | 74.43 |
| 25 | 0.40 | 800.00 | 5.00 | 35.10 | 31.62 | 20.64 | 22.41 |
| 26 | 0.40 | 750.00 | 10.00 | 22.16 | 19.60 | 12.21 | 13.39 |
| 27 | 1.00 | 800.00 | 5.00 | 67.93 | 66.39 | 35.36 | 38.31 |
Appendix B
Appendix C
| Model | Metric | CV = 3, Original | CV = 5, Original |
|---|---|---|---|
| Linear | CH4_conversion | Train R2 = 0.55, Test R2 = 0.24 | Train R2 = 0.55, Test R2 = 0.24 |
| CO2_conversion | Train R2 = 0.60, Test R2 = 0.09 | Train R2 = 0.60, Test R2 = 0.09 | |
| H2_yield | Train R2 = 0.49, Test R2 = −2.28 | Train R2 = 0.49, Test R2 = −2.28 | |
| CO_yield | Train R2 = 0.48, Test R2 = −1.68 | Train R2 = 0.48, Test R2 = −1.68 | |
| Ridge | CH4_conversion | Train R2 = 0.55, Test R2 = 0.34 | Train R2 = 0.55, Test R2 = 0.34 |
| CO2_conversion | Train R2 = 0.60, Test R2 = 0.21 | Train R2 = 0.60, Test R2 = 0.11 | |
| H2_yield | Train R2 = 0.49, Test R2 = −2.28 | Train R2 = 0.49, Test R2 = −2.24 | |
| CO_yield | Train R2 = 0.48, Test R2 = −1.65 | Train R2 = 0.48, Test R2 = −1.65 | |
| Lasso | CH4_conversion | Train R2 = 0.54, Test R2 = 0.48 | Train R2 = 0.54, Test R2 = 0.48 |
| CO2_conversion | Train R2 = 0.60, Test R2 = 0.34 | Train R2 = 0.60, Test R2 = 0.34 | |
| H2_yield | Train R2 = 0.49, Test R2 = −2.16 | Train R2 = 0.49, Test R2 = −2.16 | |
| CO_yield | Train R2 = 0.48, Test R2 = −1.59 | Train R2 = 0.48, Test R2 = −1.59 | |
| ElasticNet | CH4_conversion | Train R2 = 0.55, Test R2 = 0.44 | Train R2 = 0.55, Test R2 = 0.44 |
| CO2_conversion | Train R2 = 0.60, Test R2 = 0.24 | Train R2 = 0.60, Test R2 = 0.31 | |
| H2_yield | Train R2 = 0.49, Test R2 = −1.81 | Train R2 = 0.49, Test R2 = −1.81 | |
| CO_yield | Train R2 = 0.47, Test R2 = −1.31 | Train R2 = 0.47, Test R2 = −1.31 | |
| Bayesian Ridge | CH4_conversion | Train R2 = 0.54, Test R2 = 0.49 | Train R2 = 0.54, Test R2 = 0.49 |
| CO2_conversion | Train R2 = 0.60, Test R2 = 0.33 | Train R2 = 0.60, Test R2 = 0.33 | |
| H2_yield | Train R2 = 0.48, Test R2 = −1.16 | Train R2 = 0.48, Test R2 = −1.16 | |
| CO_yield | Train R2 = 0.46, Test R2 = −0.75 | Train R2 = 0.46, Test R2 = −0.75 | |
| Random Forest | CH4_conversion | Train R2 = 0.93, Test R2 = 0.79 | Train R2 = 0.91, Test R2 = 0.76 |
| CO2_conversion | Train R2 = 0.93, Test R2 = 0.77 | Train R2 = 0.94, Test R2 = 0.72 | |
| H2_yield | Train R2 = 0.91, Test R2 = 0.69 | Train R2 = 0.93, Test R2 = 0.72 | |
| CO_yield | Train R2 = 0.91, Test R2 = −0.22 | Train R2 = 0.92, Test R2 = 0.46 | |
| Gradient Boosting | CH4_conversion | Train R2 = 0.50, Test R2 = 0.66 | Train R2 = 0.74, Test R2 = 0.76 |
| CO2_conversion | Train R2 = 0.52, Test R2 = 0.70 | Train R2 = 0.91, Test R2 = 0.73 | |
| H2_yield | Train R2 = 1.00, Test R2 = 0.61 | Train R2 = 0.61, Test R2 = −0.05 | |
| CO_yield | Train R2 = 0.62, Test R2 = 0.21 | Train R2 = 0.62, Test R2 = 0.21 | |
| Extra Trees | CH4_conversion | Train R2 = 1.00, Test R2 = −0.66 | Train R2 = 1.00, Test R2 = −0.87 |
| CO2_conversion | Train R2 = 1.00, Test R2 = −1.04 | Train R2 = 1.00, Test R2 = −1.02 | |
| H2_yield | Train R2 = 1.00, Test R2 = 0.44 | Train R2 = 1.00, Test R2 = 0.86 | |
| CO_yield | Train R2 = 1.00, Test R2 = −0.03 | Train R2 = 1.00, Test R2 = 0.10 | |
| SVR | CH4_conversion | Train R2 = 0.52, Test R2 = 0.87 | Train R2 = 0.52, Test R2 = 0.87 |
| CO2_conversion | Train R2 = 0.49, Test R2 = 0.93 | Train R2 = 0.49, Test R2 = 0.93 | |
| H2_yield | Train R2 = 0.50, Test R2 = 0.55 | Train R2 = 0.50, Test R2 = 0.55 | |
| CO_yield | Train R2 = 0.43, Test R2 = 0.82 | Train R2 = 0.43, Test R2 = 0.82 | |
| NuSVR | CH4_conversion | Train R2 = 0.57, Test R2 = 0.98 | Train R2 = 0.51, Test R2 = 0.87 |
| CO2_conversion | Train R2 = 0.48, Test R2 = 0.92 | Train R2 = 0.48, Test R2 = 0.92 | |
| H2_yield | Train R2 = 0.51, Test R2 = 0.68 | Train R2 = 0.51, Test R2 = 0.68 | |
| CO_yield | Train R2 = 0.46, Test R2 = 0.76 | Train R2 = 0.46, Test R2 = 0.76 | |
| Kernel Ridge | CH4_conversion | Train R2 = 0.83, Test R2 = 0.29 | Train R2 = 0.83, Test R2 = 0.29 |
| CO2_conversion | Train R2 = 0.84, Test R2 = 0.10 | Train R2 = 0.84, Test R2 = 0.10 | |
| H2_yield | Train R2 = 0.81, Test R2 = −2.81 | Train R2 = 0.81, Test R2 = −2.81 | |
| CO_yield | Train R2 = 0.80, Test R2 = −2.49 | Train R2 = 0.80, Test R2 = −2.49 | |
| XGBoost | CH4_conversion | Train R2 = 0.69, Test R2 = 0.65 | Train R2 = 1.00, Test R2 = 0.42 |
| CO2_conversion | Train R2 = 1.00, Test R2 = 0.16 | Train R2 = 1.00, Test R2 = 0.16 | |
| H2_yield | Train R2 = 1.00, Test R2 = 0.33 | Train R2 = 0.50, Test R2 = 0.02 | |
| CO_yield | Train R2 = 1.00, Test R2 = 0.07 | Train R2 = 0.49, Test R2 = 0.17 | |
| LightGBM | CH4_conversion | Train R2 = 0.00, Test R2 = −0.12 | Train R2 = 0.00, Test R2 = −0.12 |
| CO2_conversion | Train R2 = 0.00, Test R2 = −0.18 | Train R2 = 0.00, Test R2 = −0.18 | |
| H2_yield | Train R2 = 0.00, Test R2 = −0.79 | Train R2 = 0.00, Test R2 = −0.79 | |
| CO_yield | Train R2 = −0.00, Test R2 = −0.93 | Train R2 = −0.00, Test R2 = −0.93 | |
| CatBoost | CH4_conversion | Train R2 = 0.99, Test R2 = 0.91 | Train R2 = 0.91, Test R2 = 0.91 |
| CO2_conversion | Train R2 = 0.92, Test R2 = 0.87 | Train R2 = 0.92, Test R2 = 0.87 | |
| H2_yield | Train R2 = 1.00, Test R2 = 0.67 | Train R2 = 0.93, Test R2 = 0.85 | |
| CO_yield | Train R2 = 1.00, Test R2 = 0.77 | Train R2 = 0.93, Test R2 = 0.79 | |
| MLP Regressor | CH4_conversion | Train R2 = 0.98, Test R2 = 0.39 | Train R2 = 0.80, Test R2 = −0.12 |
| CO2_conversion | Train R2 = 0.82, Test R2 = −0.16 | Train R2 = 0.82, Test R2 = −0.44 | |
| H2_yield | Train R2 = 0.76, Test R2 = −4.79 | Train R2 = 0.76, Test R2 = −4.84 | |
| CO_yield | Train R2 = 0.75, Test R2 = −4.03 | Train R2 = 0.75, Test R2 = −4.10 |
| CH4 Conversion | ||
|---|---|---|
| Feature Type | Model | Parameters |
| Original | Linear Regression | {} |
| Original | Ridge Regression | {‘alphas’: 1.0} |
| Original | Lasso Regression | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103]} |
| Original | ElasticNet | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103], ‘l1_ratio’: 0.1} |
| Original | Bayesian Ridge | {‘alpha_1’: 0.001, ‘alpha_2’: 1 × 10−6, ‘lambda_1’: 1 × 10−6, ‘lambda_2’: 0.001} |
| Original | Random Forest | {‘max_depth’: None, ‘n_estimators’: 100} |
| Original | Gradient Boosting | {‘learning_rate’: 0.01, ‘n_estimators’: 100} |
| Original | Extra Trees | {‘max_depth’: None, ‘n_estimators’: 100} |
| Original | SVR | {‘C’: 10, ‘gamma’: ‘scale’} |
| Original | NuSVR | {‘C’: 10, ‘nu’: 0.9} |
| Original | Kernel Ridge | {‘alpha’: 0.1, ‘gamma’: 0.1} |
| Original | XGBoost | {‘learning_rate’: 1, ‘n_estimators’: 50} |
| Original | LightGBM | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Original | CatBoost | {‘iterations’: 50, ‘learning_rate’: 0.1} |
| Original | MLP Regressor | {‘activation’: ‘relu’, ‘alpha’: 0.01, ‘batch_size’: 32, ‘hidden_layer_sizes’: (100,), ‘solver’: ‘adam’} |
| Poly | Linear Regression | {} |
| Poly | Ridge Regression | {‘alphas’: 1000.0} |
| Poly | Lasso Regression | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103]} |
| Poly | ElasticNet | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103], ‘l1_ratio’: 0.1} |
| Poly | Bayesian Ridge | {‘alpha_1’: 0.001, ‘alpha_2’: 1 × 10−6, ‘lambda_1’: 1 × 10−6, ‘lambda_2’: 0.001} |
| Poly | Random Forest | {‘max_depth’: 20, ‘n_estimators’: 100} |
| Poly | Gradient Boosting | {‘learning_rate’: 0.01, ‘n_estimators’: 200} |
| Poly | Extra Trees | {‘max_depth’: None, ‘n_estimators’: 50} |
| Poly | SVR | {‘C’: 10, ‘gamma’: ‘scale’} |
| Poly | NuSVR | {‘C’: 10, ‘nu’: 0.9} |
| Poly | Kernel Ridge | {‘alpha’: 0.1, ‘gamma’: 0.1} |
| Poly | XGBoost | {‘learning_rate’: 0.01, ‘n_estimators’: 200} |
| Poly | LightGBM | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Poly | CatBoost | {‘iterations’: 200, ‘learning_rate’: 1} |
| Poly | MLP Regressor | {‘activation’: ‘logistic’, ‘alpha’: 0.01, ‘batch_size’: 128, ‘hidden_layer_sizes’: (100, 50), ‘solver’: ‘adam’} |
| CO2 Conversion | ||
| Original | Linear Regression | {} |
| Original | Ridge Regression | {‘alphas’: 0.1} |
| Original | Lasso Regression | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103]} |
| Original | ElasticNet | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103], ‘l1_ratio’: 0.1} |
| Original | Bayesian Ridge | {‘alpha_1’: 0.001, ‘alpha_2’: 1 × 10−6, ‘lambda_1’: 1 × 10−6, ‘lambda_2’: 0.001} |
| Original | Random Forest | {‘max_depth’: 20, ‘n_estimators’: 100} |
| Original | Gradient Boosting | {‘learning_rate’: 0.01, ‘n_estimators’: 200} |
| Original | Extra Trees | {‘max_depth’: None, ‘n_estimators’: 50} |
| Original | SVR | {‘C’: 10, ‘gamma’: ‘scale’} |
| Original | NuSVR | {‘C’: 10, ‘nu’: 0.9} |
| Original | Kernel Ridge | {‘alpha’: 0.1, ‘gamma’: 0.1} |
| Original | XGBoost | {‘learning_rate’: 1, ‘n_estimators’: 50} |
| Original | LightGBM | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Original | CatBoost | {‘iterations’: 50, ‘learning_rate’: 0.1} |
| Original | MLP Regressor | {‘activation’: ‘relu’, ‘alpha’: 0.001, ‘batch_size’: 64, ‘hidden_layer_sizes’: (100,), ‘solver’: ‘adam’} |
| Poly | Linear Regression | {} |
| Poly | Ridge Regression | {‘alphas’: 1000.0} |
| Poly | Lasso Regression | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103]} |
| Poly | ElasticNet | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103], ‘l1_ratio’: 0.5} |
| Poly | Bayesian Ridge | {‘alpha_1’: 0.001, ‘alpha_2’: 1 × 10−6, ‘lambda_1’: 1 × 10−6, ‘lambda_2’: 0.001} |
| Poly | Random Forest | {‘max_depth’: 10, ‘n_estimators’: 50} |
| Poly | Gradient Boosting | {‘learning_rate’: 0.1, ‘n_estimators’: 100} |
| Poly | Extra Trees | {‘max_depth’: 20, ‘n_estimators’: 50} |
| Poly | SVR | {‘C’: 1, ‘gamma’: ‘scale’} |
| Poly | NuSVR | {‘C’: 10, ‘nu’: 0.9} |
| Poly | Kernel Ridge | {‘alpha’: 0.1, ‘gamma’: 0.1} |
| Poly | XGBoost | {‘learning_rate’: 0.01, ‘n_estimators’: 200} |
| Poly | LightGBM | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Poly | CatBoost | {‘iterations’: 200, ‘learning_rate’: 0.1} |
| Poly | MLP Regressor | {‘activation’: ‘logistic’, ‘alpha’: 0.001, ‘batch_size’: 64, ‘hidden_layer_sizes’: (100, 50), ‘solver’: ‘adam’} |
| H2 Yield | ||
| Original | Linear Regression | {} |
| Original | Ridge Regression | {‘alphas’: 0.1} |
| Original | Lasso Regression | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103]} |
| Original | ElasticNet | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103], ‘l1_ratio’: 0.5} |
| Original | Bayesian Ridge | {‘alpha_1’: 0.001, ‘alpha_2’: 1 × 10−6, ‘lambda_1’: 1 × 10−6, ‘lambda_2’: 0.001} |
| Original | Random Forest | {‘max_depth’: 20, ‘n_estimators’: 50} |
| Original | Gradient Boosting | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Original | Extra Trees | {‘max_depth’: 10, ‘n_estimators’: 50} |
| Original | SVR | {‘C’: 10, ‘gamma’: ‘scale’} |
| Original | NuSVR | {‘C’: 10, ‘nu’: 0.5} |
| Original | Kernel Ridge | {‘alpha’: 0.1, ‘gamma’: 0.1} |
| Original | XGBoost | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Original | LightGBM | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Original | CatBoost | {‘iterations’: 50, ‘learning_rate’: 0.1} |
| Original | MLP Regressor | {‘activation’: ‘relu’, ‘alpha’: 0.001, ‘batch_size’: 64, ‘hidden_layer_sizes’: (100,), ‘solver’: ‘adam’} |
| Poly | Linear Regression | {} |
| Poly | Ridge Regression | {‘alphas’: 1000.0} |
| Poly | Lasso Regression | {‘alphas’: [0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0]} |
| Poly | ElasticNet | {‘alphas’: [0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0], ‘l1_ratio’: 0.1} |
| Poly | Bayesian Ridge | {‘alpha_1’: 0.001, ‘alpha_2’: 1 × 10−6, ‘lambda_1’: 1 × 10−6, ‘lambda_2’: 0.001} |
| Poly | Random Forest | {‘max_depth’: 10, ‘n_estimators’: 50} |
| Poly | Gradient Boosting | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Poly | Extra Trees | {‘max_depth’: 20, ‘n_estimators’: 50} |
| Poly | SVR | {‘C’: 10, ‘gamma’: ‘scale’} |
| Poly | NuSVR | {‘C’: 10, ‘nu’: 0.9} |
| Poly | Kernel Ridge | {‘alpha’: 0.1, ‘gamma’: 0.1} |
| Poly | XGBoost | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Poly | LightGBM | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Poly | CatBoost | {‘iterations’: 200, ‘learning_rate’: 0.1} |
| Poly | MLP Regressor | {‘activation’: ‘logistic’, ‘alpha’: 0.001, ‘batch_size’: 128, ‘hidden_layer_sizes’: (100, 100, 50), ‘solver’: ‘adam’} |
| CO Yield | ||
| Original | Linear Regression | {} |
| Original | Ridge Regression | {‘alphas’: 0.1} |
| Original | Lasso Regression | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103]} |
| Original | ElasticNet | {‘alphas’: [1.0 × 10−3, 1.0 × 10−2, 1.0 × 10−1, 1.0 × 100, 1.0 × 101, 1.0 × 102, 1.0 × 103], ‘l1_ratio’: 0.5} |
| Original | Bayesian Ridge | {‘alpha_1’: 0.001, ‘alpha_2’: 1 × 10−6, ‘lambda_1’: 1 × 10−6, ‘lambda_2’: 0.001} |
| Original | Random Forest | {‘max_depth’: None, ‘n_estimators’: 50} |
| Original | Gradient Boosting | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Original | Extra Trees | {‘max_depth’: 10, ‘n_estimators’: 200} |
| Original | SVR | {‘C’: 10, ‘gamma’: ‘scale’} |
| Original | NuSVR | {‘C’: 10, ‘nu’: 0.5} |
| Original | Kernel Ridge | {‘alpha’: 0.1, ‘gamma’: 0.1} |
| Original | XGBoost | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Original | LightGBM | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Original | CatBoost | {‘iterations’: 50, ‘learning_rate’: 0.1} |
| Original | MLP Regressor | {‘activation’: ‘relu’, ‘alpha’: 0.001, ‘batch_size’: 64, ‘hidden_layer_sizes’: (100,), ‘solver’: ‘adam’} |
| Poly | Linear Regression | {} |
| Poly | Ridge Regression | {‘alphas’: 1000.0} |
| Poly | Lasso Regression | {‘alphas’: [0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0]} |
| Poly | ElasticNet | {‘alphas’: [0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0], ‘l1_ratio’: 0.5} |
| Poly | Bayesian Ridge | {‘alpha_1’: 0.001, ‘alpha_2’: 1 × 10−6, ‘lambda_1’: 1 × 10−6, ‘lambda_2’: 0.001} |
| Poly | Random Forest | {‘max_depth’: 20, ‘n_estimators’: 50} |
| Poly | Gradient Boosting | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Poly | Extra Trees | {‘max_depth’: None, ‘n_estimators’: 100} |
| Poly | SVR | {‘C’: 10, ‘gamma’: ‘scale’} |
| Poly | NuSVR | {‘C’: 10, ‘nu’: 0.9} |
| Poly | Kernel Ridge | {‘alpha’: 0.1, ‘gamma’: 0.1} |
| Poly | XGBoost | {‘learning_rate’: 0.01, ‘n_estimators’: 100} |
| Poly | LightGBM | {‘learning_rate’: 0.01, ‘n_estimators’: 50} |
| Poly | CatBoost | {‘iterations’: 200, ‘learning_rate’: 0.1} |
| Poly | MLP Regressor | {‘activation’: ‘logistic’, ‘alpha’: 0.0001, ‘batch_size’: 32, ‘hidden_layer_sizes’: (100, 100, 50), ‘solver’: ‘adam’} |
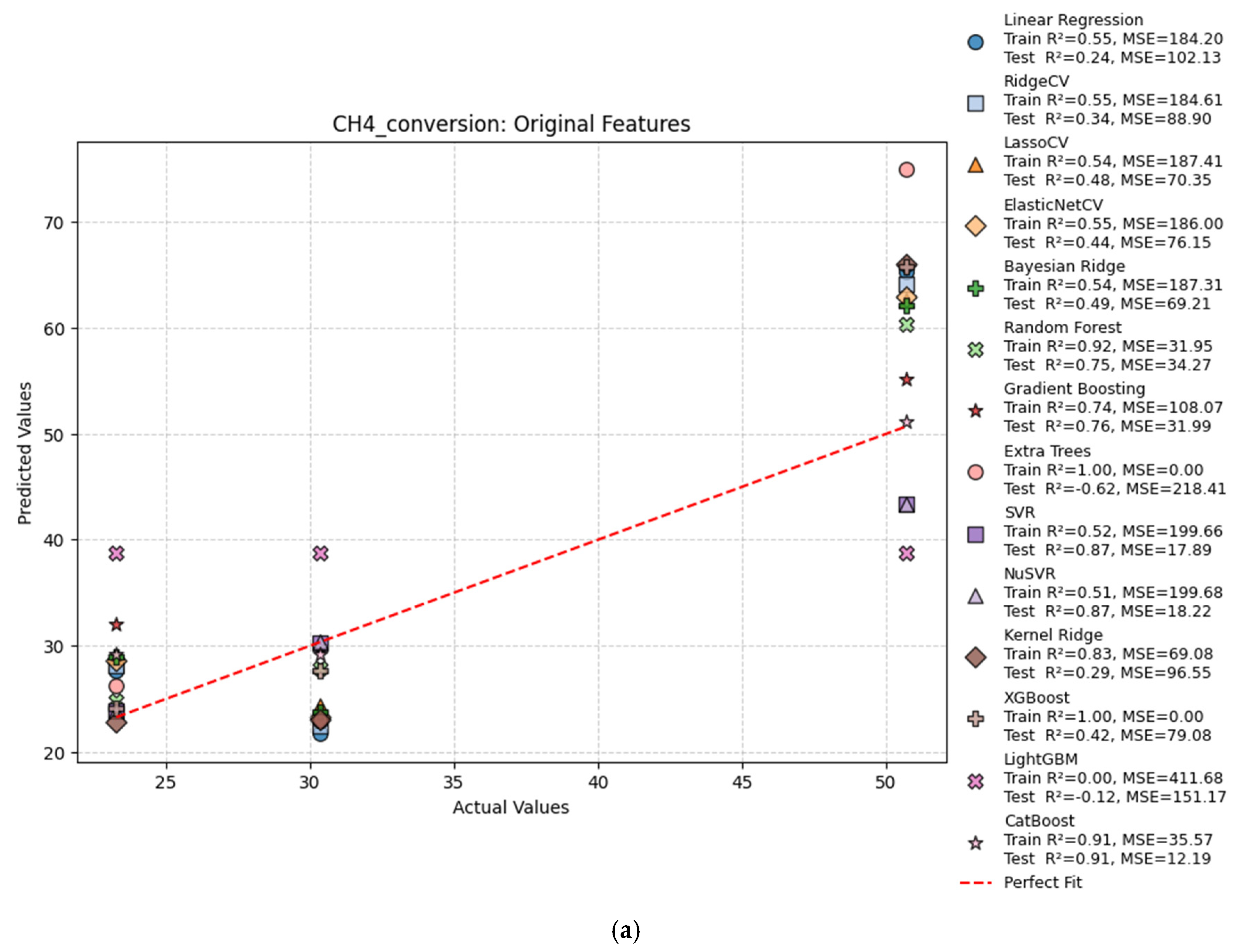
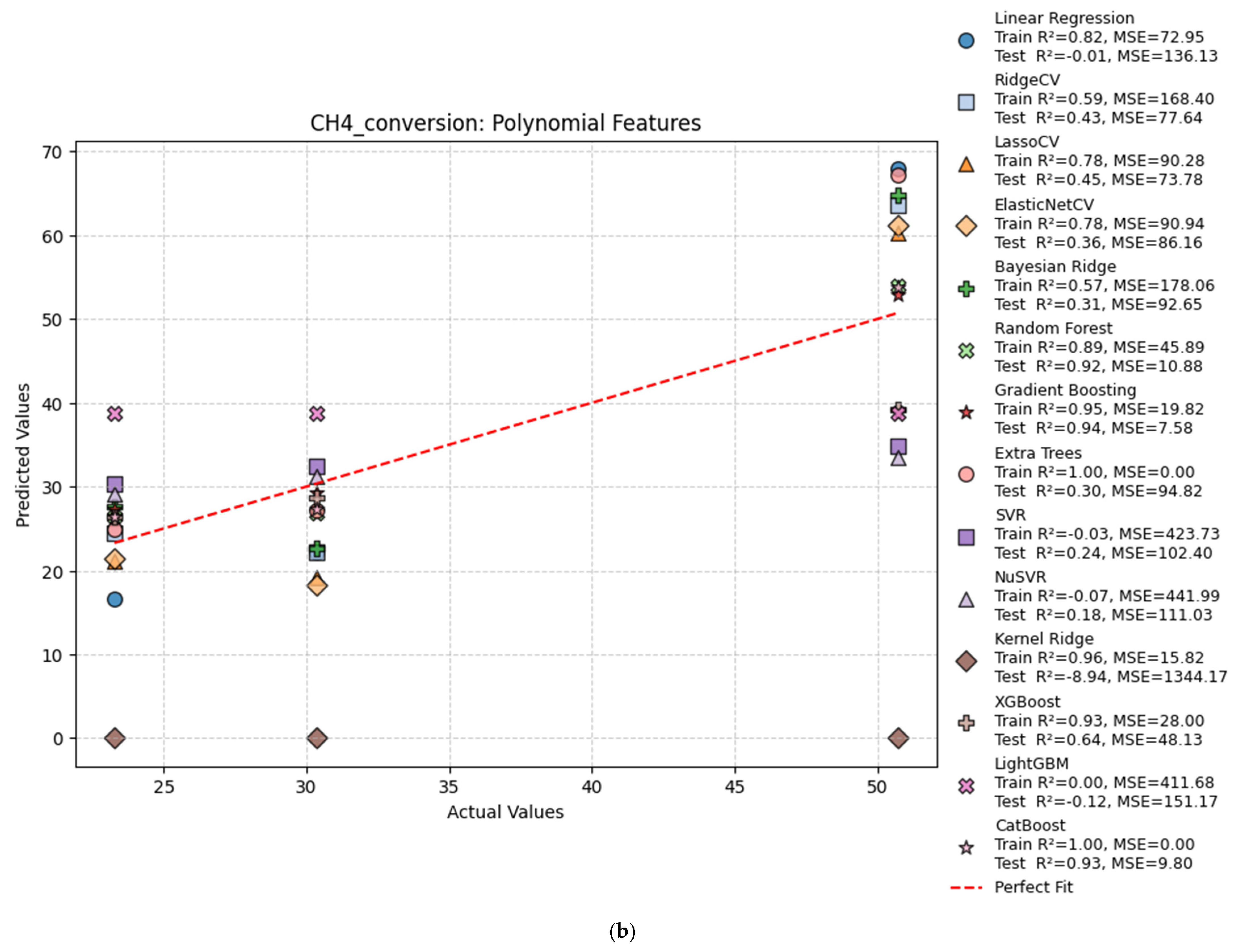
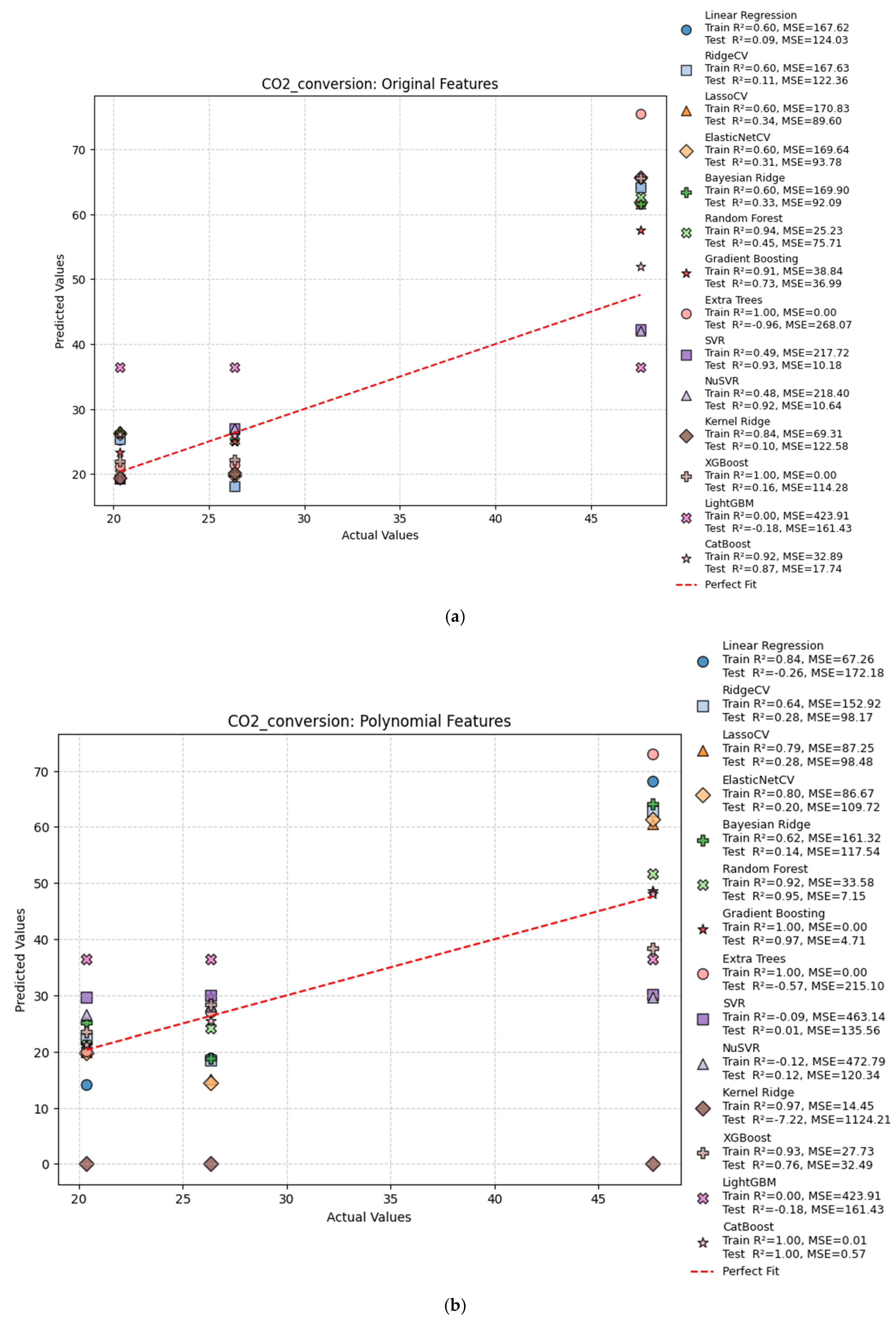
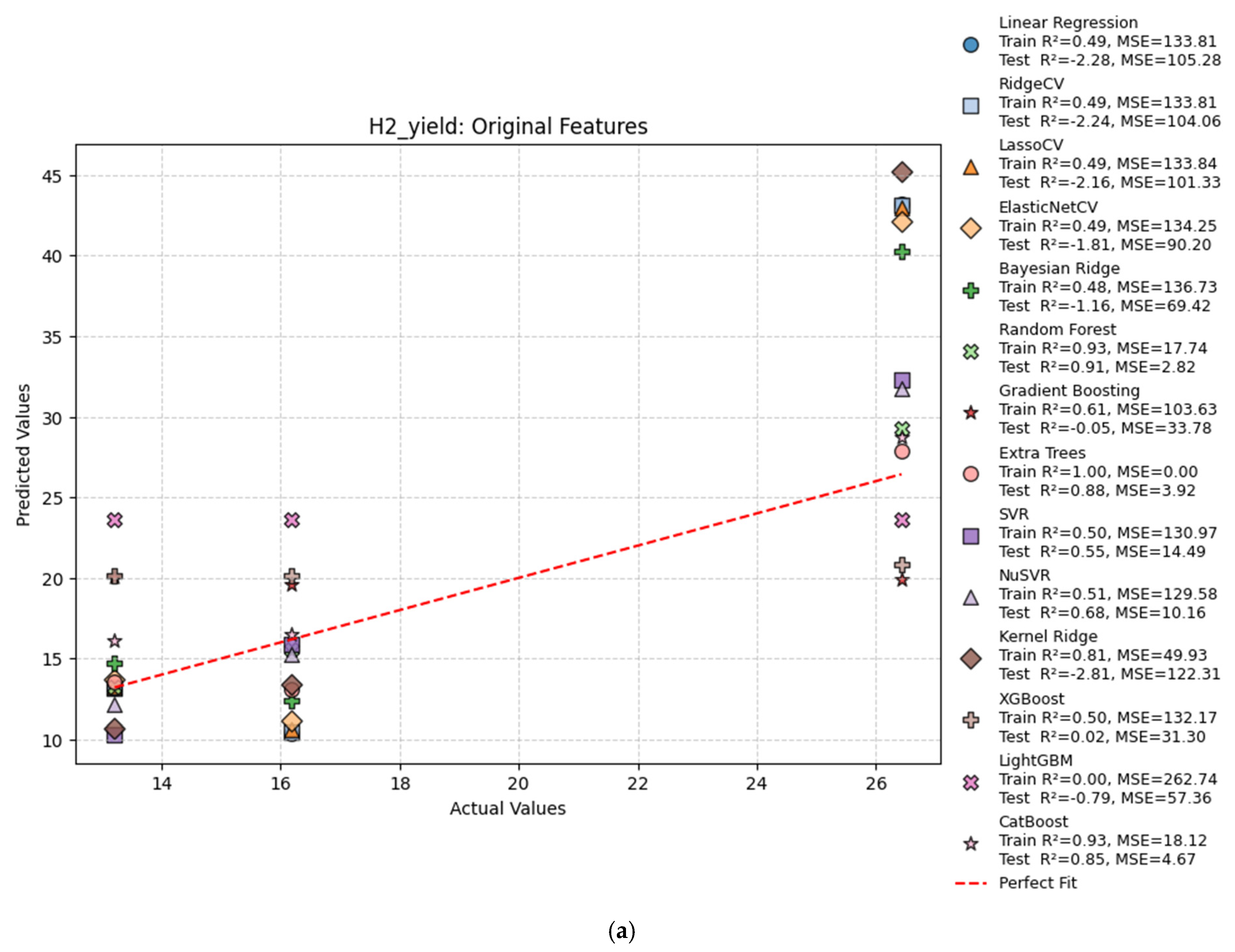
Appendix D. Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7 and Figure A8
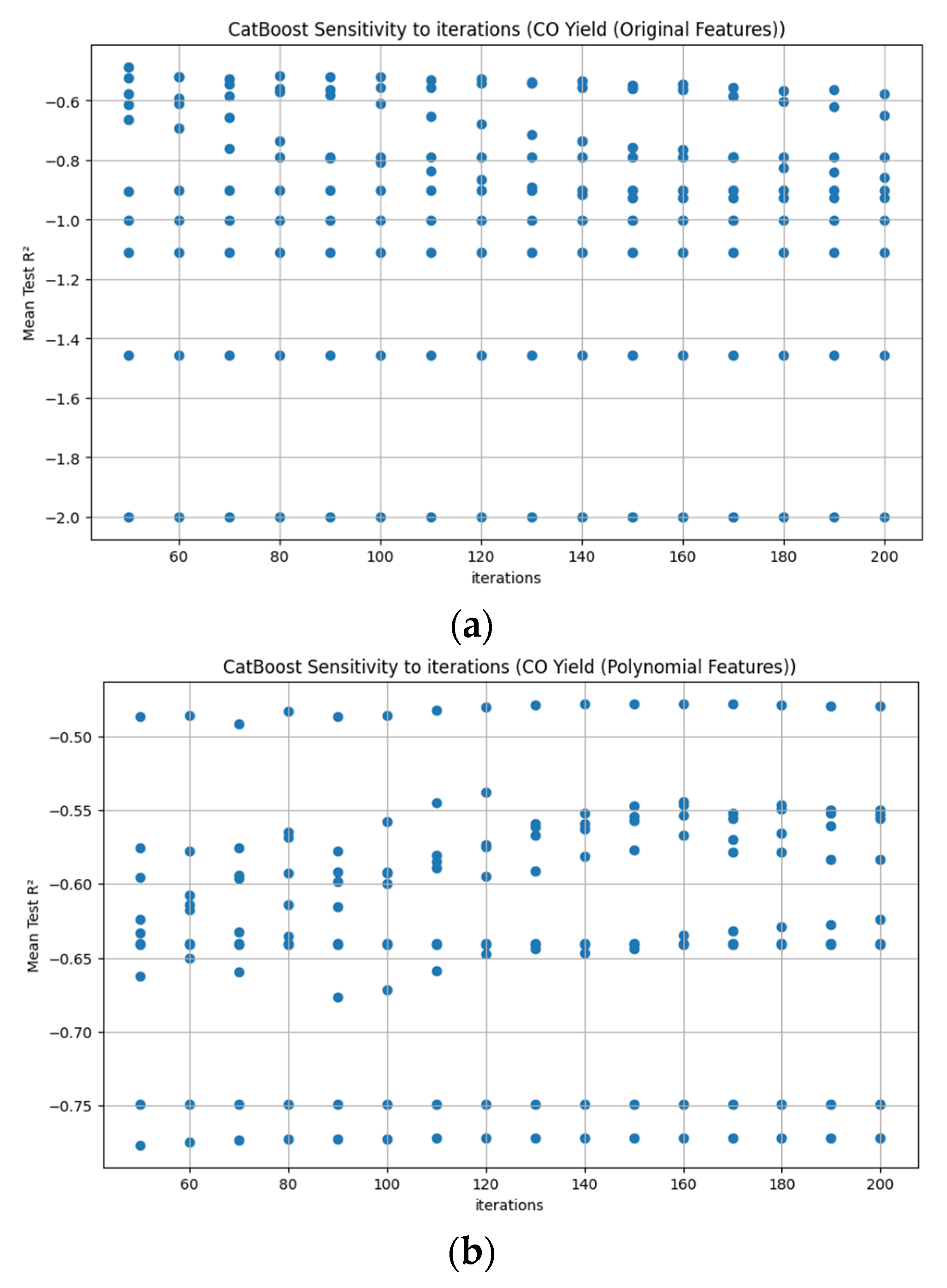
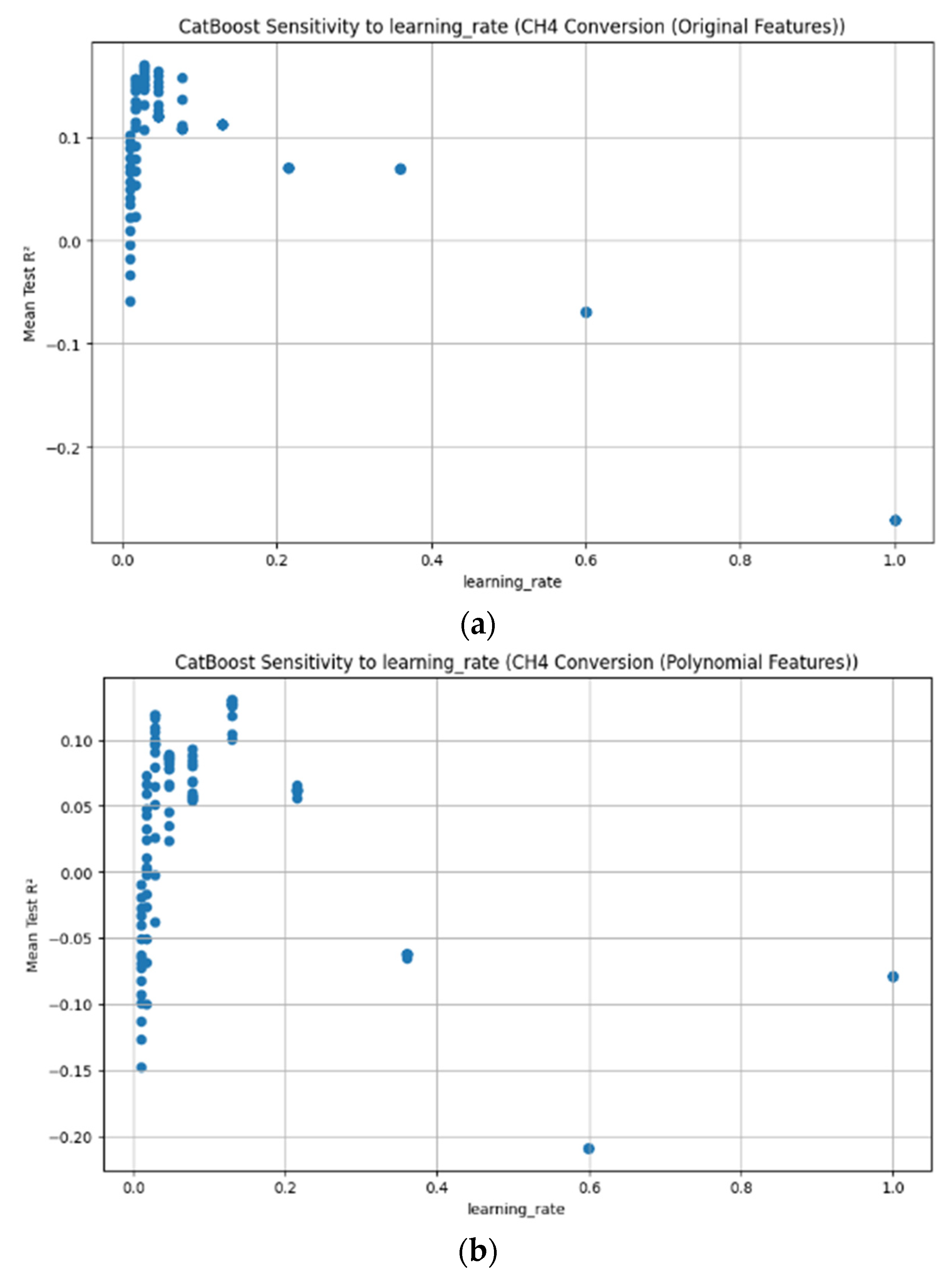
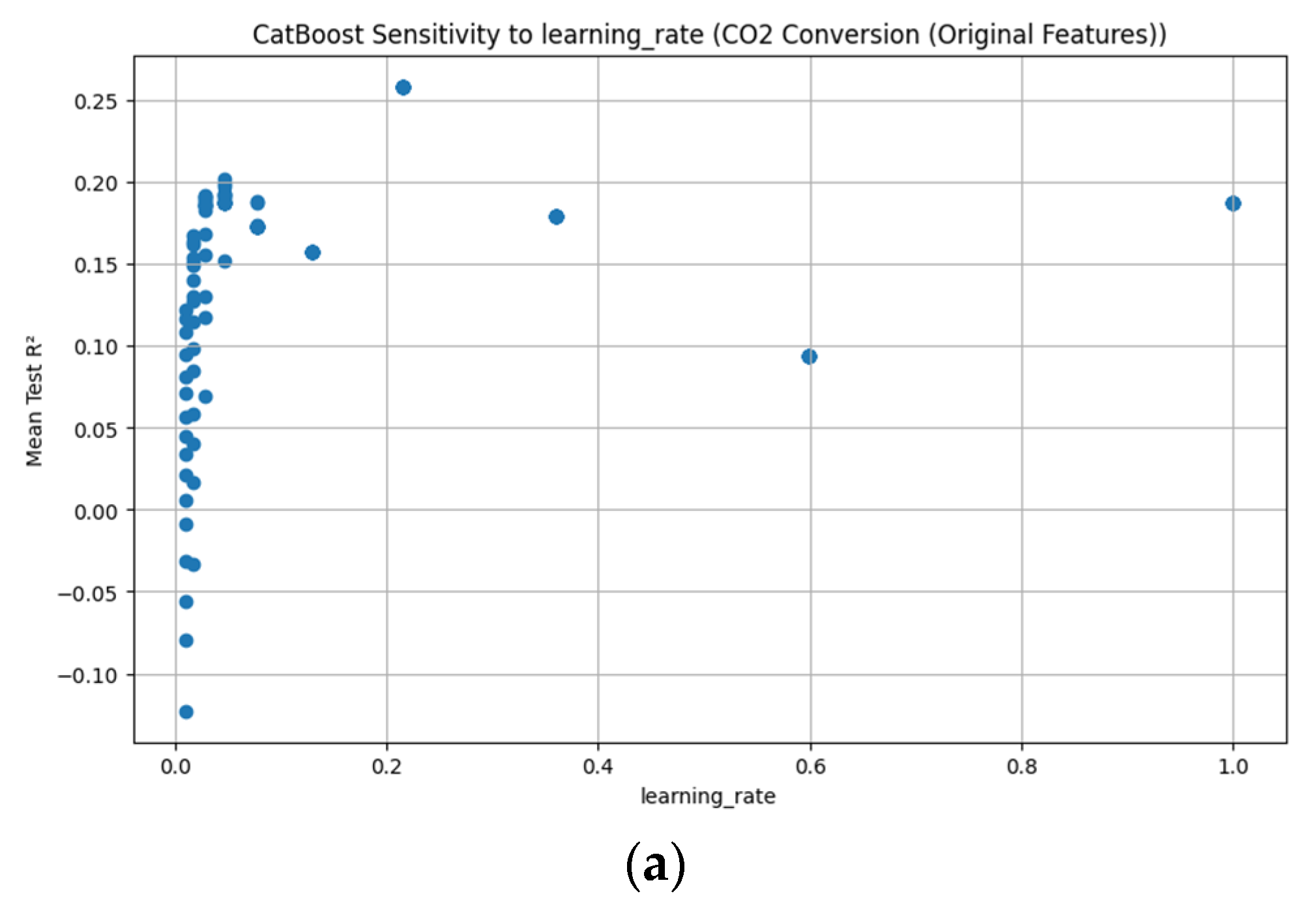

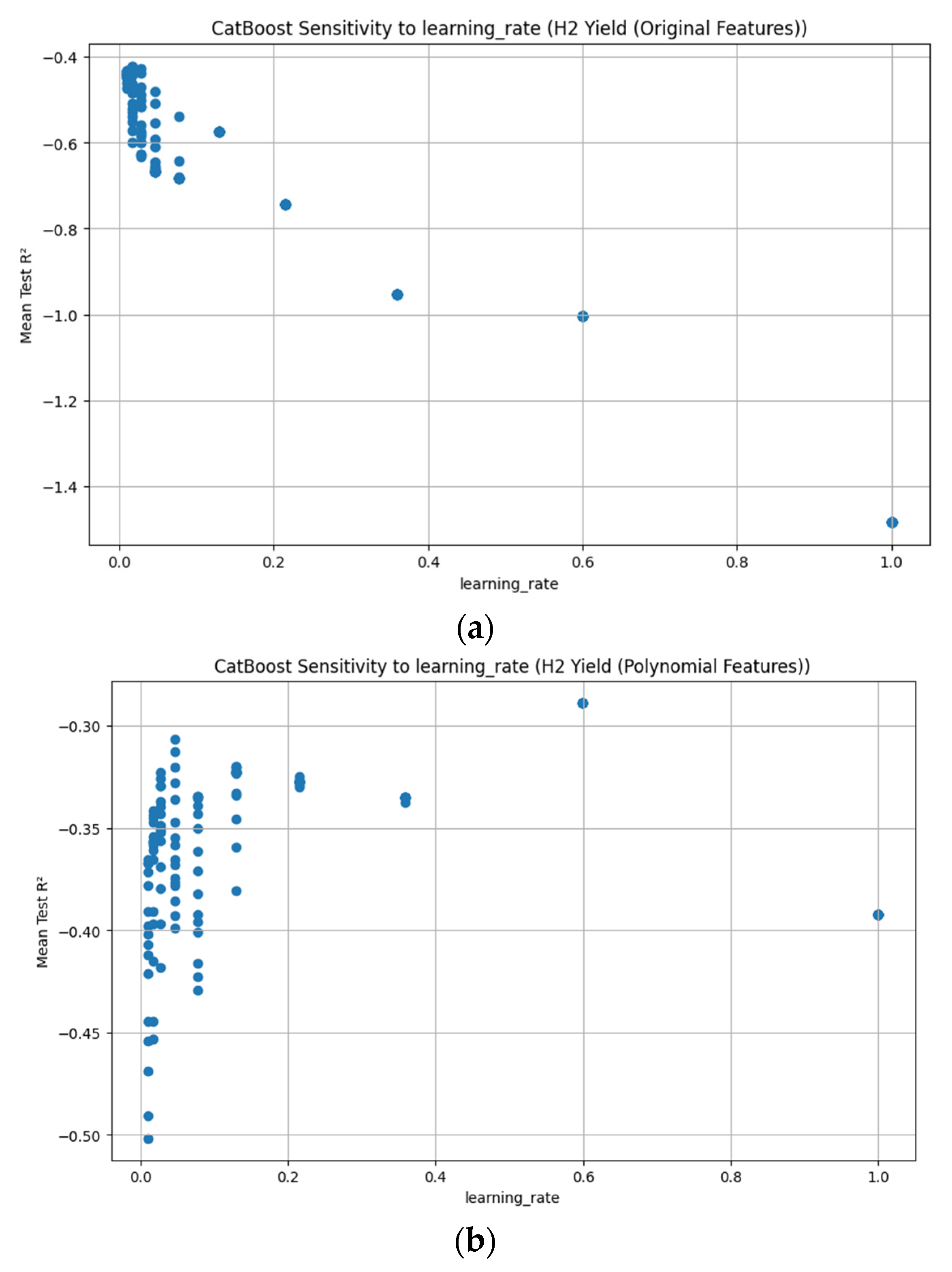
References
- Ayodele, B.V.; Khan, M.R.; Cheng, C.K. Syngas production from CO2 reforming of methane over ceria supported cobalt catalyst: Effects of reactants partial pressure. J. Nat. Gas Sci. Eng. 2015, 27, 1016–1023. [Google Scholar] [CrossRef]
- Alenazey, F.S. Utilizing carbon dioxide as a regenerative agent in methane dry reforming to improve hydrogen production and catalyst activity and longevity. Int. J. Hydrogen Energy 2014, 39, 18632–18641. [Google Scholar] [CrossRef]
- Augusto, B.; Marco, P.; Cesare, S. Solar steam reforming of natural gas integrated with a gas turbine power plant. Sol. Energy 2013, 96, 46–55. [Google Scholar] [CrossRef]
- Dean, J.A. Lange’s Handbook of Chemistry, 12th ed.; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Alper, E.; Orhan, O.Y. CO2 utilization: Developments in conversion processes. Petroleum 2017, 3, 109–126. [Google Scholar] [CrossRef]
- Braga, T.P.; Santos, R.C.; Sales, B.M.; da Silva, B.R.; Pinheiro, A.N.; Leite, E.R.; Valentini, A. CO2 mitigation by carbon nanotube formation during dry reforming of methane analyzed by factorial design combined with response surface methodology. Chin. J. Catal. 2014, 35, 514–523. [Google Scholar] [CrossRef]
- Hossain, M.A.; Ayodele, B.V.; Cheng, C.K.; Khan, M.R. Artificial neural network modeling of hydrogen-rich syngas production from methane dry reforming over novel Ni/CaFe2O4 catalysts. Int. J. Hydrogen Energy 2016, 41, 11119–11130. [Google Scholar] [CrossRef]
- Lavoie, J.-M. Review on dry reforming of methane, a potentially more environmentally-friendly approach to the increasing natural gas exploitation. Front. Chem. 2014, 2, 81. [Google Scholar] [CrossRef]
- Nikoo, M.K.; Amin, N. Thermodynamic analysis of carbon dioxide reforming of methane in view of solid carbon formation. Fuel Process. Technol. 2011, 92, 678–691. [Google Scholar] [CrossRef]
- Sodesawa, T.; Dobashi, A.; Nozaki, F. Catalytic reaction of methane with carbon dioxide. React. Kinet. Catal. Lett. 1979, 12, 107–111. [Google Scholar] [CrossRef]
- Mohamad, H.A. A Mini-Review on CO2 Reforming of Methane. Prog. Petrochem. Sci. 2018, 2, 532. [Google Scholar] [CrossRef]
- Rostrup-Nielsen, J.R. Catal. Today 1993, 18, 305–324. [Google Scholar] [CrossRef]
- Fan, M.; Abdullah, A.Z.; Bhatia, S. Catalytic technology for carbon dioxide reforming of methane to synthesis gas. ChemCatChem 2009, 1, 192–208. [Google Scholar] [CrossRef]
- García-Vargas, J.M.; Valverde, J.L.; Dorado, F.; Sánchez, P. Influence of the support on the catalytic behaviour of Ni catalysts for the dry reforming reaction and the tri-reforming process. J. Mol. Catal. A Chem. 2014, 395, 108–116. [Google Scholar] [CrossRef]
- Devasahayam, S. Catalytic actions of MgCO3/MgO system for efficient carbon reforming processes. Sustain. Mater. Technol. 2019, 22, e00122. [Google Scholar] [CrossRef]
- Devasahayam, S. Review: Opportunities for simultaneous energy/materials conversion of carbon dioxide and plastics in metallurgical processes. Sustain. Mater. Technol. 2019, 22, 119883. [Google Scholar] [CrossRef]
- Devasahayam, S.; Strezov, V. Thermal decomposition of magnesium carbonate with biomass and plastic wastes for simultaneous production of hydrogen and carbon avoidance. J. Clean. Prod. 2018, 174, 1089–1095. [Google Scholar] [CrossRef]
- Devasahayam, S. Decarbonising the Portland and Other Cements—Via Simultaneous Feedstock Recycling and Carbon Conversions Sans External Catalysts. Polymers 2021, 13, 2462. [Google Scholar] [CrossRef]
- IRENA. Breakthrough Agenda Report 2023—Hydrogen; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Hydrogen Council and McKinsey and Company. Hydrogen Insights 2024; Hydrogen Council: Rotterdam, The Netherlands, 2024. [Google Scholar]
- Cozzolino, R.; Bella, G. A review of electrolyzer-based systems providing grid ancillary services: Current status, market, challenges and future directions. Front. Energy Res. 2024, 12, 1358333. [Google Scholar] [CrossRef]
- Fu, H.; Wang, Z.; Nichani, E.; Lee, J.D. Learning Hierarchical Polynomials of Multiple Nonlinear Features with Three-Layer Networks. arXiv 2024, arXiv:2411.17201. [Google Scholar] [CrossRef]
- Devasahayam, S. Deep learning models in Python for predicting hydrogen production: A comparative study. Energy 2023, 280, 128088. [Google Scholar] [CrossRef]
- Devasahayam, S.; Albijanic, B. Predicting hydrogen production from co-gasification of biomass and plastics using tree based machine learning algorithms. Renew. Energy 2023, 222, 119883. [Google Scholar] [CrossRef]
- Breiman, L.; Cutler, A. Random Forests. J. Mach. Learn. Res. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rocca, J. Ensemble Methods: Bagging, Boosting and Stacking 2019. Available online: https://towardsdatascience.com/ensemble-methods-bagging-boosting-and-stacking-c9214a10a205 (accessed on 5 May 2022).
- Lasso and Ridge Regression in Python Tutorial. Available online: https://www.datacamp.com/tutorial/tutorial-lasso-ridge-regression (accessed on 5 May 2022).
- Chinda, A.; Derevlev, N. Support Vector Machines: An Overview of Optimization Techniques and Model Selection; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Choudhury, A. AdaBoost vs. Gradient Boosting: A Comparison of Leading Boosting Algorithms, 18 January 2021. Available online: https://analyticsindiamag.com/adaboost-vs-gradient-boosting-a-comparison-of-leading-boosting-algorithms/#:~:text=AdaBoost%20is%20the%20first%20designed,Boosting%20more%20flexible%20than%20AdaBoost (accessed on 13 December 2022).
- Scikit-learn. Gradient Boosting Regression, 2010–2016. Available online: https://scikit-learn.org/0.18/auto_examples/ensemble/plot_gradient_boosting_regression.html#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-regression-py (accessed on 16 December 2022).
- Scikit-learn. Gradient Boosting Regression, 2007–2022. Available online: https://scikit-learn.org/stable/auto_examples/ensemble/plot_gradient_boosting_regression.html#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-regression-py (accessed on 16 December 2022).
- Devasahayam, S. Advancing Flotation Process Modeling: Bayesian vs. Sklearn Approaches for Gold Grade Prediction. Minerals 2025, 15, 591. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python: Cross-validation: Evaluating estimator performance. J. Mach. Learn. Res 2011, 12, 2825–2830. [Google Scholar]
- Brownlee, J. Ensemble Learning: Gradient Boosting with Scikit-Learn, XGBoost, LightGBM, and CatBoost, 27 April 2021. Available online: https://machinelearningmastery.com/gradient-boosting-with-scikit-learn-xgboost-lightgbm-and-catboost/ (accessed on 7 December 2022).
- Clyde, M.; Çetinkaya-Rundel, M.; Rundel, C.; Banks, D.; Chai, C.; Huang, L. An Introduction to Bayesian Thinking A Companion to the Statistics with R Course; 2022. Available online: https://bookdown.org (accessed on 23 August 2025).
- Brownlee, J. How to Develop Elastic Net Regression Models in Python, 12 June 2020. Available online: https://machinelearningmastery.com/elastic-net-regression-in-python/ (accessed on 23 August 2025).
- Hastie, T.; Tibshirani, R.; Friedman, J. Elements of Statistical Learning, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Yorkinov. Regression Accuracy Check in Python (MAE, MSE, RMSE, R-Squared), 10 October 2019. Available online: https://www.datatechnotes.com/2019/10/accuracy-check-in-python-mae-mse-rmse-r.html (accessed on 23 August 2025).
- Alawi, N.; Barifcani, A.; Abid, H. Optimisation of CH4 and CO2 conversion and selectivity of H2 and CO for the dry re-forming of methane by a microwave plasma technique using a Box-Behnken design. Asia Pac. J. Chem. Eng. 2018, 13, e2254. [Google Scholar] [CrossRef]
- Jiayin, L.; Jing, X.; Evgeny, R.; Annemie, B. Machine learning-based prediction and optimization of plasma-catalytic dry reforming of methane in a dielectric barrier discharge reactor. Chem. Eng. J. 2025, 507, 159897. [Google Scholar]
- Jiayin, L.; Jing, X.; Evgeny, R.; Bart, W.; Annemie, B. Machine learning-based prediction and optimization of plasma-based conversion of CO2 and CH4 in an atmospheric pressure glow discharge plasma. Green Chem. 2025, 27, 3916–3931. [Google Scholar]
- Alotaibi, F.N.; Berrouk, A.S.; Salim, I.M. Scaling up dry methane reforming: Integrating computational fluid dynamics and machine learning for enhanced hydrogen production in industrial-scale fluidized bed reactors. Fuel 2024, 376, 132673. [Google Scholar] [CrossRef]





| Hydrogen Production Method | Reaction | Feedstocks | Typical H2/CO Ratio | CO2 Emissions (kg CO2/kg H2) | Energy Efficiency | Fuel Relevance |
|---|---|---|---|---|---|---|
| Steam Methane Reforming (SMR) [19,20] | CH4 + H2O → CO + 3H2 | CH4, H2O (steam) | ~3.0 | ~9–11 | ~65–75% | Dominant method; high emissions |
| Dry Reforming of Methane (DRM) [8,9] | CH4 + CO2 → 2CO + 2H2 | CH4, CO2 | ~1.0 | ~5–7 | ~55–65% | Syngas for Fischer–Tropsch, methanol, SNG |
| Electrolysis (Renewable) [21] | H2O → H2 + ½O2 (via electricity) | Water + Renewable Power | ∞ (pure H2) | 0 (if fully renewable) | ~60–70% | Green hydrogen; no carbon-based fuel generated |
| Feed Ratio | Reaction Temp | Metal Loading | CH4 Conversion | CO2 Conversion | H2 Yield | CO Yield | |
|---|---|---|---|---|---|---|---|
| count | 27.00 | 27.00 | 27.00 | 27.00 | 27.00 | 27.00 | 27.00 |
| mean | 0.70 | 750.00 | 10.00 | 38.32 | 35.84 | 23.07 | 23.98 |
| std | 0.25 | 41.60 | 4.16 | 19.93 | 20.24 | 15.77 | 15.84 |
| min | 0.40 | 700.00 | 5.00 | 17.69 | 14.15 | 11.12 | 13.09 |
| 25% | 0.40 | 700.00 | 5.00 | 24.39 | 21.24 | 13.46 | 14.81 |
| 50% | 0.70 | 750.00 | 10.00 | 32.89 | 30.02 | 17.15 | 18.32 |
| 75% | 1.00 | 800.00 | 15.00 | 45.15 | 43.29 | 26.33 | 26.43 |
| max | 1.00 | 800.00 | 15.00 | 90.04 | 87.60 | 73.42 | 74.43 |
| Variable | Q1 | Q3 | IQR | Lower Bound | Upper Bound | Potential Outliers |
|---|---|---|---|---|---|---|
| Feed_ratio | 0.40 | 1.00 | 0.60 | −0.50 | 1.90 | None |
| Reaction_Temp | 700.00 | 800.00 | 100.00 | 550.00 | 950.00 | None |
| Metal_loading | 5.00 | 15.00 | 10.00 | −10.00 | 30.00 | None |
| CH4_conversion | 24.39 | 45.15 | 20.76 | −6.75 | 76.29 | <−6.75; >76.29 |
| CO2_conversion | 21.24 | 43.29 | 22.05 | −11.83 | 76.36 | <−11.83; >76.36 |
| H2_yield | 13.46 | 26.33 | 12.87 | −6.85 | 46.64 | <−6.85; >46.64 |
| CO_yield | 14.81 | 26.43 | 11.62 | −2.62 | 43.86 | <−2.62; >43.86 |
| Feature | CH4 Conversion | CO2 Conversion | H2 Yield | CO Yield |
|---|---|---|---|---|
| Feed Ratio | 0.59 | 0.64 | 0.43 | 0.44 |
| Reaction Temperature | 0.43 | 0.50 | 0.46 | 0.42 |
| Metal Loading | 0.31 | 0.29 | 0.33 | 0.37 |
| Feed Ratio × Temperature | 0.66 | 0.70 | 0.58 | 0.61 |
| CH4 Conversion | |||||
|---|---|---|---|---|---|
| Features | Model | Train R2 | Test R2 | Train MSE | Test MSE |
| Original | Linear Regression | 0.55 | 0.24 | 184.20 | 102.13 |
| Original | Ridge Regression | 0.55 | 0.34 | 184.61 | 88.90 |
| Original | Lasso Regression | 0.54 | 0.48 | 187.41 | 70.35 |
| Original | ElasticNet | 0.55 | 0.44 | 186.00 | 76.15 |
| Original | Bayesian Ridge | 0.54 | 0.49 | 187.31 | 69.21 |
| Original | Random Forest | 0.93 | 0.84 | 27.17 | 21.54 |
| Original | Gradient Boosting | 0.74 | 0.76 | 108.07 | 31.99 |
| Original | Extra Trees | 1.00 | −1.00 | 0.00 | 270.33 |
| Original | SVR | 0.52 | 0.87 | 199.66 | 17.89 |
| Original | NuSVR | 0.51 | 0.87 | 199.68 | 18.22 |
| Original | Kernel Ridge | 0.83 | 0.29 | 69.08 | 96.55 |
| Original | XGBoost | 1.00 | 0.42 | 0.00 | 79.08 |
| Original | LightGBM | 0.00 | −0.12 | 411.68 | 151.17 |
| Original | CatBoost | 0.91 | 0.91 | 35.57 | 12.19 |
| Original | MLP Regressor | 0.81 | −0.03 | 76.24 | 139.37 |
| Poly | Linear Regression | 0.82 | −0.01 | 72.95 | 136.13 |
| Poly | Ridge Regression | 0.59 | 0.43 | 168.40 | 77.64 |
| Poly | Lasso Regression | 0.77 | 0.66 | 94.02 | 46.37 |
| Poly | ElasticNet | 0.77 | 0.61 | 94.60 | 52.83 |
| Poly | Bayesian Ridge | 0.57 | 0.31 | 178.06 | 92.65 |
| Poly | Random Forest | 0.92 | 0.93 | 33.16 | 9.29 |
| Poly | Gradient Boosting | 0.95 | 0.94 | 19.82 | 7.58 |
| Poly | Extra Trees | 1.00 | −0.27 | 0.00 | 171.21 |
| Poly | SVR | −0.03 | 0.24 | 423.73 | 102.40 |
| Poly | NuSVR | −0.07 | 0.18 | 441.99 | 111.03 |
| Poly | Kernel Ridge | 0.96 | −8.94 | 15.82 | 1344.17 |
| Poly | XGBoost | 0.93 | 0.64 | 28.00 | 48.13 |
| Poly | LightGBM | 0.00 | −0.12 | 411.68 | 151.17 |
| Poly | CatBoost | 1.00 | 0.93 | 0.00 | 9.80 |
| Poly | MLP Regressor | −0.23 | −0.24 | 505.51 | 167.62 |
| CO2 Conversion | |||||
| Original | Linear Regression | 0.60 | 0.09 | 167.62 | 124.03 |
| Original | Ridge Regression | 0.60 | 0.11 | 167.63 | 122.36 |
| Original | Lasso Regression | 0.60 | 0.34 | 170.83 | 89.60 |
| Original | ElasticNet | 0.60 | 0.31 | 169.64 | 93.78 |
| Original | Bayesian Ridge | 0.60 | 0.33 | 169.90 | 92.09 |
| Original | Random Forest | 0.91 | 0.80 | 38.10 | 27.30 |
| Original | Gradient Boosting | 0.91 | 0.73 | 38.84 | 36.99 |
| Original | Extra Trees | 1.00 | −0.79 | 0.00 | 244.22 |
| Original | SVR | 0.49 | 0.93 | 217.72 | 10.18 |
| Original | NuSVR | 0.48 | 0.92 | 218.40 | 10.64 |
| Original | Kernel Ridge | 0.84 | 0.10 | 69.31 | 122.58 |
| Original | XGBoost | 1.00 | 0.16 | 0.00 | 114.28 |
| Original | LightGBM | 0.00 | −0.18 | 423.91 | 161.43 |
| Original | CatBoost | 0.92 | 0.87 | 32.89 | 17.74 |
| Original | MLP Regressor | 0.81 | −0.23 | 80.68 | 167.99 |
| Poly | Linear Regression | 0.84 | −0.26 | 67.26 | 172.18 |
| Poly | Ridge Regression | 0.64 | 0.28 | 152.92 | 98.17 |
| Poly | Lasso Regression | 0.78 | 0.58 | 92.40 | 58.05 |
| Poly | ElasticNet | 0.79 | 0.55 | 89.94 | 61.13 |
| Poly | Bayesian Ridge | 0.62 | 0.14 | 161.32 | 117.54 |
| Poly | Random Forest | 0.93 | 0.96 | 31.62 | 5.74 |
| Poly | Gradient Boosting | 1.00 | 0.99 | 1.00 | 1.99 |
| Poly | Extra Trees | 1.00 | −0.42 | 0.00 | 194.76 |
| Poly | SVR | −0.09 | 0.01 | 463.14 | 135.56 |
| Poly | NuSVR | −0.12 | 0.12 | 472.79 | 120.34 |
| Poly | Kernel Ridge | 0.97 | −7.22 | 14.45 | 1124.21 |
| Poly | XGBoost | 0.93 | 0.76 | 27.73 | 32.49 |
| Poly | LightGBM | 0.00 | −0.18 | 423.91 | 161.43 |
| Poly | CatBoost | 1.00 | 1.00 | 0.01 | 0.57 |
| Poly | MLP Regressor | −0.10 | −0.01 | 464.30 | 138.71 |
| H2 Yield | |||||
| Original | Linear Regression | 0.49 | −2.28 | 133.81 | 105.28 |
| Original | Ridge Regression | 0.49 | −2.24 | 133.81 | 104.06 |
| Original | Lasso Regression | 0.49 | −2.16 | 133.84 | 101.33 |
| Original | ElasticNet | 0.49 | −1.81 | 134.25 | 90.20 |
| Original | Bayesian Ridge | 0.48 | −1.16 | 136.73 | 69.42 |
| Original | Random Forest | 0.91 | 0.88 | 23.73 | 3.72 |
| Original | Gradient Boosting | 0.61 | −0.05 | 103.63 | 33.78 |
| Original | Extra Trees | 1.00 | 0.81 | 0.00 | 6.24 |
| Original | SVR | 0.50 | 0.55 | 130.97 | 14.49 |
| Original | NuSVR | 0.51 | 0.68 | 129.58 | 10.16 |
| Original | Kernel Ridge | 0.81 | −2.81 | 49.93 | 122.31 |
| Original | XGBoost | 0.50 | 0.02 | 132.17 | 31.30 |
| Original | LightGBM | 0.00 | −0.79 | 262.74 | 57.36 |
| Original | CatBoost | 0.93 | 0.85 | 18.12 | 4.67 |
| Original | MLP Regressor | 0.76 | −4.82 | 62.78 | 186.81 |
| Poly | Linear Regression | 0.78 | −4.14 | 56.55 | 164.95 |
| Poly | Ridge Regression | 0.54 | −1.76 | 121.50 | 88.58 |
| Poly | Lasso Regression | 0.76 | −2.14 | 63.15 | 100.70 |
| Poly | ElasticNet | 0.70 | −0.79 | 78.14 | 57.43 |
| Poly | Bayesian Ridge | 0.51 | −2.11 | 128.03 | 99.75 |
| Poly | Random Forest | 0.91 | 0.66 | 22.37 | 10.80 |
| Poly | Gradient Boosting | 0.61 | 0.23 | 103.33 | 24.87 |
| Poly | Extra Trees | 1.00 | 0.31 | 0.00 | 22.13 |
| Poly | SVR | −0.01 | 0.48 | 266.67 | 16.58 |
| Poly | NuSVR | −0.03 | 0.48 | 271.37 | 16.73 |
| Poly | Kernel Ridge | 0.97 | −10.79 | 6.79 | 378.17 |
| Poly | XGBoost | 0.50 | 0.19 | 131.38 | 25.90 |
| Poly | LightGBM | 0.00 | −0.79 | 262.74 | 57.36 |
| Poly | CatBoost | 1.00 | 0.84 | 0.00 | 5.17 |
| Poly | MLP Regressor | −0.00 | −0.55 | 263.42 | 49.74 |
| CO Yield | |||||
| Original | Linear Regression | 0.48 | −1.68 | 138.31 | 97.79 |
| Original | Ridge Regression | 0.48 | −1.65 | 138.31 | 96.69 |
| Original | Lasso Regression | 0.48 | −1.59 | 138.34 | 94.21 |
| Original | ElasticNet | 0.47 | −1.31 | 138.74 | 84.13 |
| Original | Bayesian Ridge | 0.46 | −0.75 | 141.53 | 63.83 |
| Original | Random Forest | 0.89 | −0.00 | 29.68 | 36.56 |
| Original | Gradient Boosting | 0.62 | 0.21 | 101.32 | 28.90 |
| Original | Extra Trees | 1.00 | −0.34 | 0.00 | 48.71 |
| Original | SVR | 0.43 | 0.82 | 151.50 | 6.67 |
| Original | NuSVR | 0.46 | 0.76 | 141.57 | 8.64 |
| Original | Kernel Ridge | 0.80 | −2.49 | 51.58 | 127.00 |
| Original | XGBoost | 0.49 | 0.17 | 133.45 | 30.14 |
| Original | LightGBM | −0.00 | −0.93 | 263.63 | 70.22 |
| Original | CatBoost | 0.93 | 0.79 | 17.65 | 7.64 |
| Original | MLP Regressor | 0.74 | −3.86 | 68.31 | 177.14 |
| Poly | Linear Regression | 0.77 | −3.67 | 59.74 | 170.11 |
| Poly | Ridge Regression | 0.52 | −1.35 | 127.32 | 85.69 |
| Poly | Lasso Regression | 0.68 | −0.43 | 83.09 | 52.07 |
| Poly | ElasticNet | 0.69 | −0.46 | 81.68 | 53.16 |
| Poly | Bayesian Ridge | 0.50 | −1.54 | 132.34 | 92.41 |
| Poly | Random Forest | 0.89 | 0.13 | 27.96 | 31.82 |
| Poly | Gradient Boosting | 0.61 | 0.11 | 102.21 | 32.43 |
| Poly | Extra Trees | 1.00 | −0.92 | 0.00 | 70.13 |
| Poly | SVR | −0.05 | 0.33 | 277.53 | 24.40 |
| Poly | NuSVR | −0.07 | 0.33 | 281.13 | 24.33 |
| Poly | Kernel Ridge | 0.97 | −9.72 | 7.19 | 390.50 |
| Poly | XGBoost | 0.75 | 0.50 | 66.91 | 18.17 |
| Poly | LightGBM | −0.00 | −0.93 | 263.63 | 70.22 |
| Poly | CatBoost | 1.00 | 0.89 | 0.01 | 3.97 |
| Poly | MLP Regressor | −0.00 | −0.63 | 264.70 | 59.26 |
| Model | Target | Feature Type | R2 After Removal of Outliers | MSE After Removal of Outliers | R2 Without Removal of Outliers | MSE Without Removal of Outliers |
|---|---|---|---|---|---|---|
| Random Forest | CH4_conversion | Original | 0.68 | 60.79 | 0.39 | 232.70 |
| Gradient Boosting | CH4_conversion | Original | 0.62 | 71.44 | 0.47 | 203.60 |
| SVR | CH4_conversion | Original | −0.07 | 201.26 | −0.00 | 383.03 |
| CatBoost | CH4_conversion | Original | 0.55 | 85.05 | 0.22 | 296.99 |
| Random Forest | CH4_conversion | Polynomial | 0.59 | 77.48 | 0.33 | 256.60 |
| Gradient Boosting | CH4_conversion | Polynomial | 0.59 | 76.47 | 0.17 | 317.54 |
| SVR | CH4_conversion | Polynomial | −0.17 | 221.06 | −0.09 | 415.53 |
| CatBoost | CH4_conversion | Polynomial | 0.42 | 108.88 | 0.18 | 314.33 |
| Random Forest | CO2_conversion | Original | 0.86 | 29.20 | 0.45 | 216.55 |
| Gradient Boosting | CO2_conversion | Original | 0.82 | 36.19 | 0.44 | 222.20 |
| SVR | CO2_conversion | Original | 0.01 | 201.30 | −0.04 | 408.69 |
| CatBoost | CO2_conversion | Original | 0.68 | 65.26 | 0.26 | 292.33 |
| Random Forest | CO2_conversion | Polynomial | 0.77 | 46.09 | 0.40 | 235.11 |
| Gradient Boosting | CO2_conversion | Polynomial | 0.82 | 36.06 | 0.16 | 329.38 |
| SVR | CO2_conversion | Polynomial | −0.06 | 216.97 | −0.10 | 432.73 |
| CatBoost | CO2_conversion | Polynomial | 0.60 | 81.57 | 0.25 | 295.61 |
| Random Forest | H2_yield | Original | 0.41 | 31.20 | 0.30 | 168.51 |
| Gradient Boosting | H2_yield | Original | 0.31 | 36.29 | 0.29 | 169.16 |
| SVR | H2_yield | Original | 0.06 | 49.88 | −0.04 | 250.12 |
| CatBoost | H2_yield | Original | 0.32 | 35.80 | 0.21 | 188.09 |
| Random Forest | H2_yield | Polynomial | 0.20 | 42.47 | 0.08 | 220.01 |
| Gradient Boosting | H2_yield | Polynomial | 0.15 | 44.97 | 0.19 | 192.93 |
| SVR | H2_yield | Polynomial | −0.09 | 57.82 | −0.12 | 267.80 |
| CatBoost | H2_yield | Polynomial | 0.25 | 39.93 | 0.23 | 183.36 |
| Random Forest | CO_yield | Original | 0.69 | 14.25 | 0.27 | 176.98 |
| Gradient Boosting | CO_yield | Original | 0.72 | 12.82 | 0.27 | 175.99 |
| SVR | CO_yield | Original | 0.10 | 41.98 | −0.02 | 246.21 |
| CatBoost | CO_yield | Original | 0.50 | 23.03 | 0.18 | 197.30 |
| Random Forest | CO_yield | Polynomial | 0.45 | 25.41 | 0.06 | 226.24 |
| Gradient Boosting | CO_yield | Polynomial | 0.56 | 20.20 | 0.09 | 220.04 |
| SVR | CO_yield | Polynomial | −0.06 | 49.14 | −0.08 | 261.20 |
| CatBoost | CO_yield | Polynomial | 0.41 | 27.44 | 0.17 | 200.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devasahayam, S.; Thella, J.S.; Mohanty, M.K. Predicting Methane Dry Reforming Performance via Multi-Output Machine Learning: A Comparative Study of Regression Models. Energies 2025, 18, 4807. https://doi.org/10.3390/en18184807
Devasahayam S, Thella JS, Mohanty MK. Predicting Methane Dry Reforming Performance via Multi-Output Machine Learning: A Comparative Study of Regression Models. Energies. 2025; 18(18):4807. https://doi.org/10.3390/en18184807
Chicago/Turabian StyleDevasahayam, Sheila, John Samuel Thella, and Manoj K. Mohanty. 2025. "Predicting Methane Dry Reforming Performance via Multi-Output Machine Learning: A Comparative Study of Regression Models" Energies 18, no. 18: 4807. https://doi.org/10.3390/en18184807
APA StyleDevasahayam, S., Thella, J. S., & Mohanty, M. K. (2025). Predicting Methane Dry Reforming Performance via Multi-Output Machine Learning: A Comparative Study of Regression Models. Energies, 18(18), 4807. https://doi.org/10.3390/en18184807







