Experimental Energy and Exergy Performance Evaluation of a Novel Pumpless Rankine Cycle (PRC) Unit Employing Low-Temperature Heat Sources
Abstract
1. Introduction
2. Materials and Methods
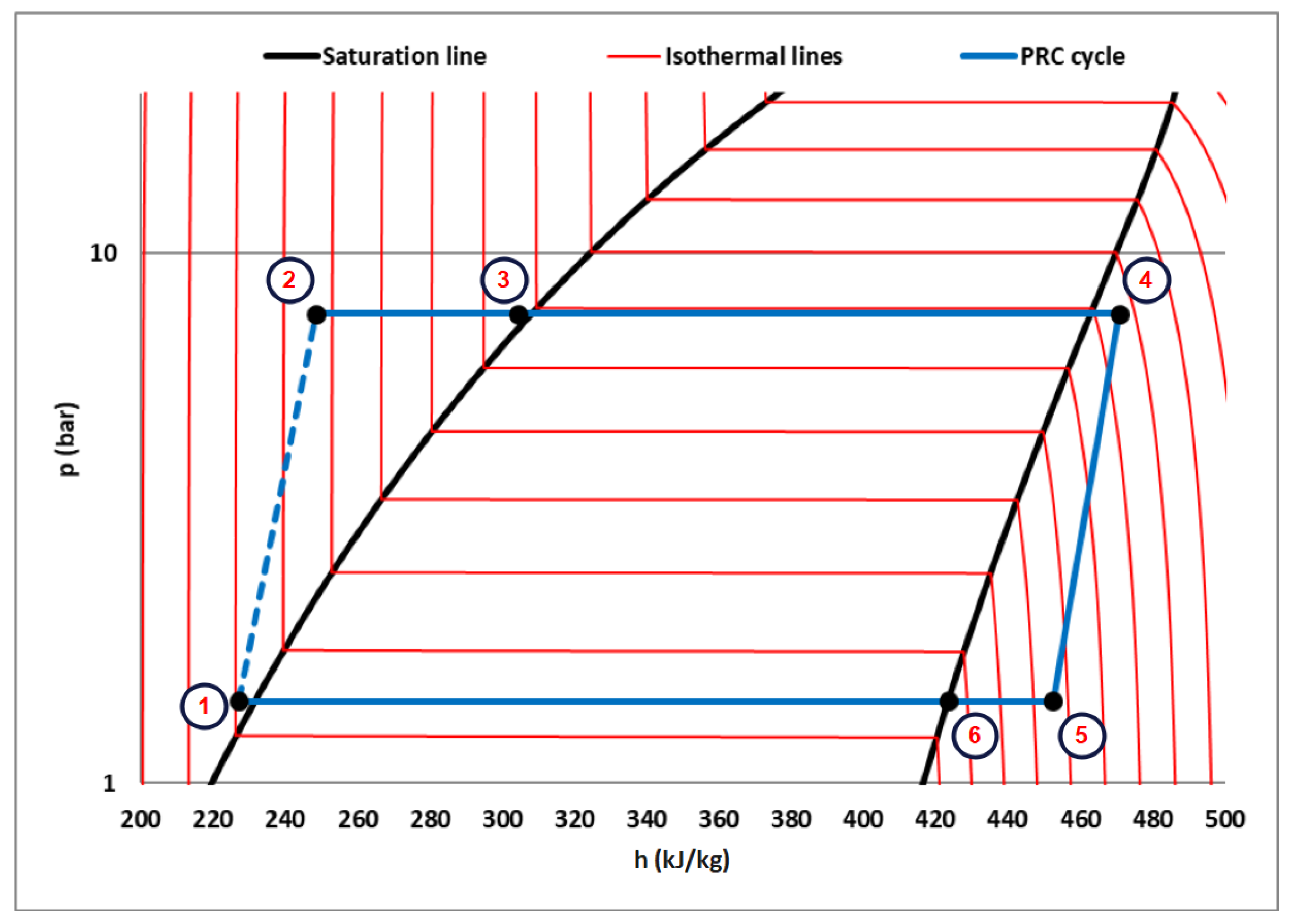
2.1. The Examined PRC Configuration
2.2. The Experimental Test Setup
2.3. The Experimental Procedure
- Four different heat source temperature levels (thwin): 60.0, 70.0, 80.0 and 90.0 °C, with a maximum deviation of ±1.0 K. The heat source temperature level was configured by setting the temperature of the secondary fluid (water) at the inlet of the evaporator heat exchanger and fixing the water flow rate to ~8 lpm.
- Four different heat sink temperature levels (tcwin): 10.0, 20.0, 30.0 and 40.0 °C, with a maximum deviation of ±0.5 K. The heat sink temperature level was configured by setting the temperature of the secondary fluid (water) at the inlet of the condenser heat exchanger and fixing the water flow rate to ~8 lpm.
- The test runs carried out included 16 different test runs for each pair of the heat source and heat sink temperature levels mentioned above.
2.4. Thermodynamic Formulation
2.5. Followed Methodology
- The heat transfer between the different devices and their surroundings is negligible;
- The pressure differences in the gaseous phases of the cycle are considered negligible;
- The energy analysis was performed under quasi-steady state conditions for each timestep.
3. Results and Discussion
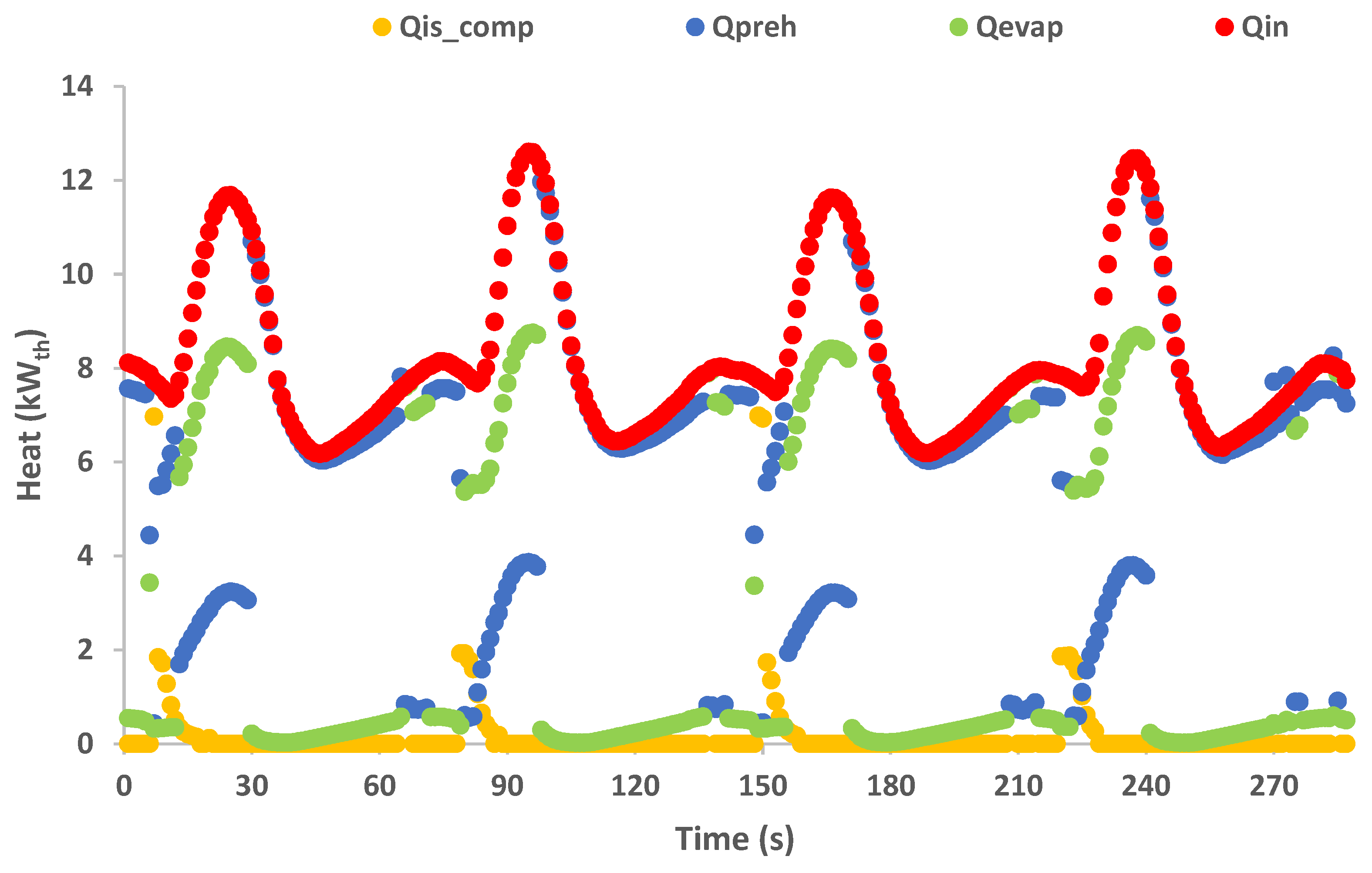
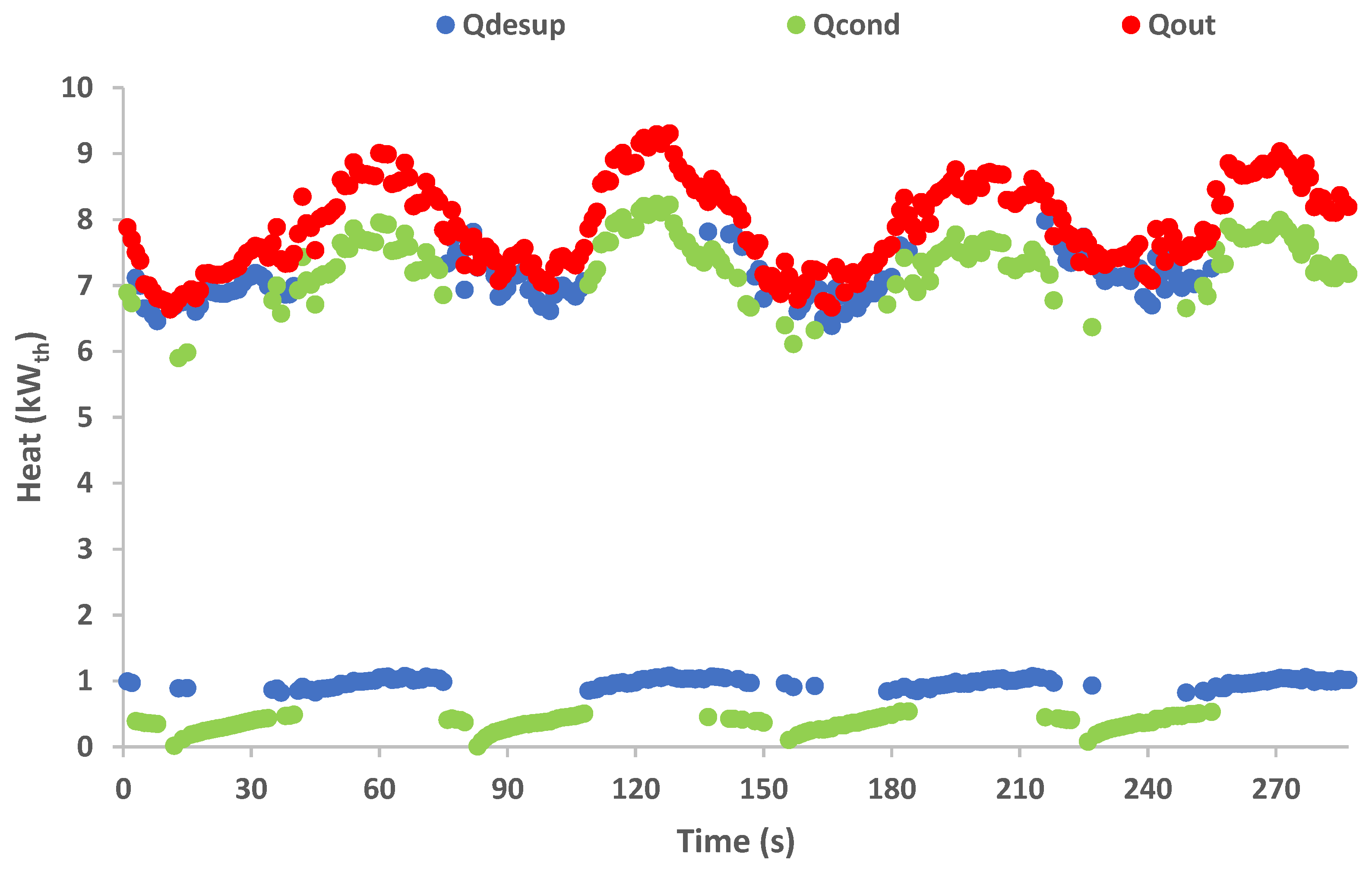
3.1. Preliminary Experimental Results Analysis
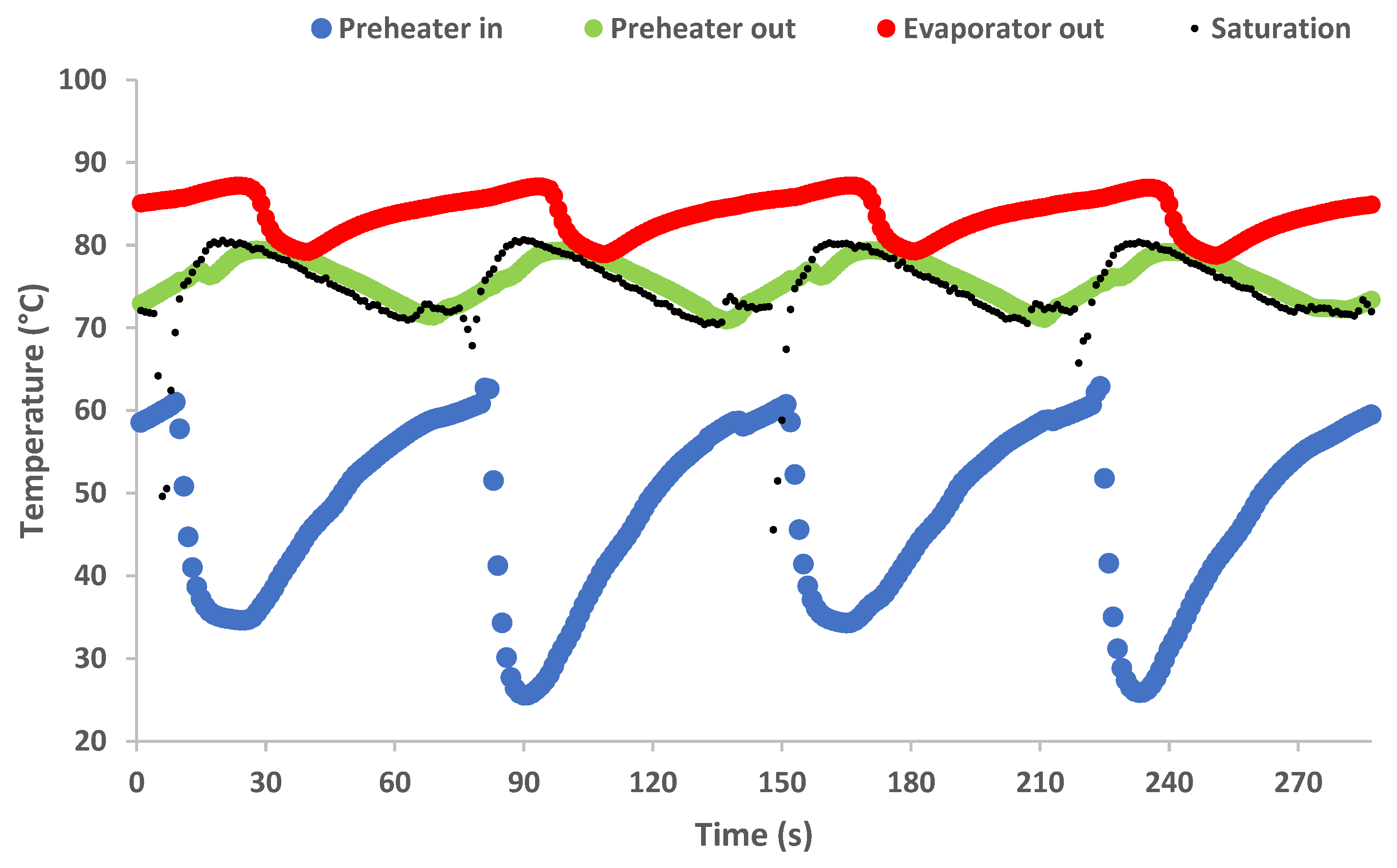
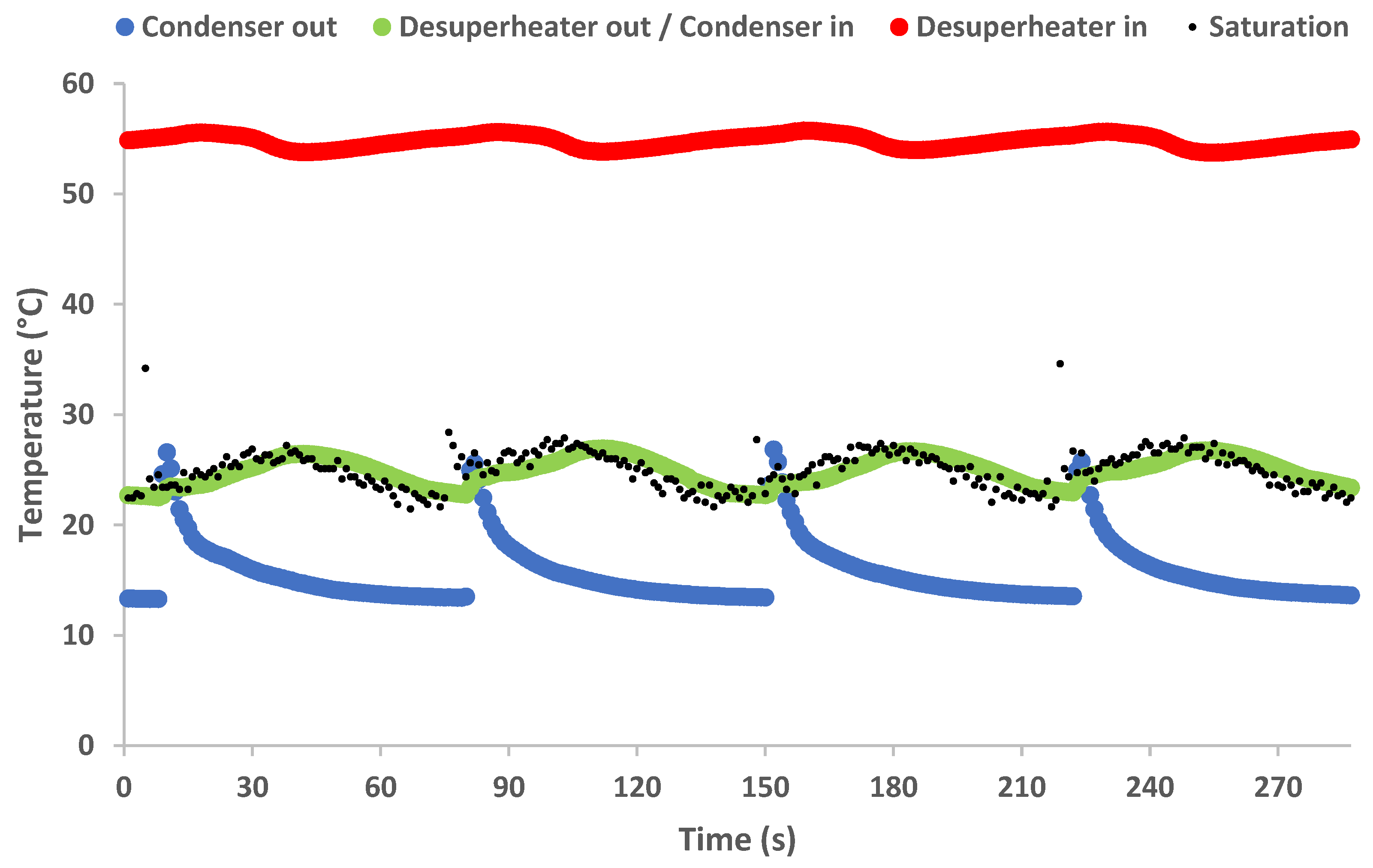
3.2. Thermal Energy Analysis
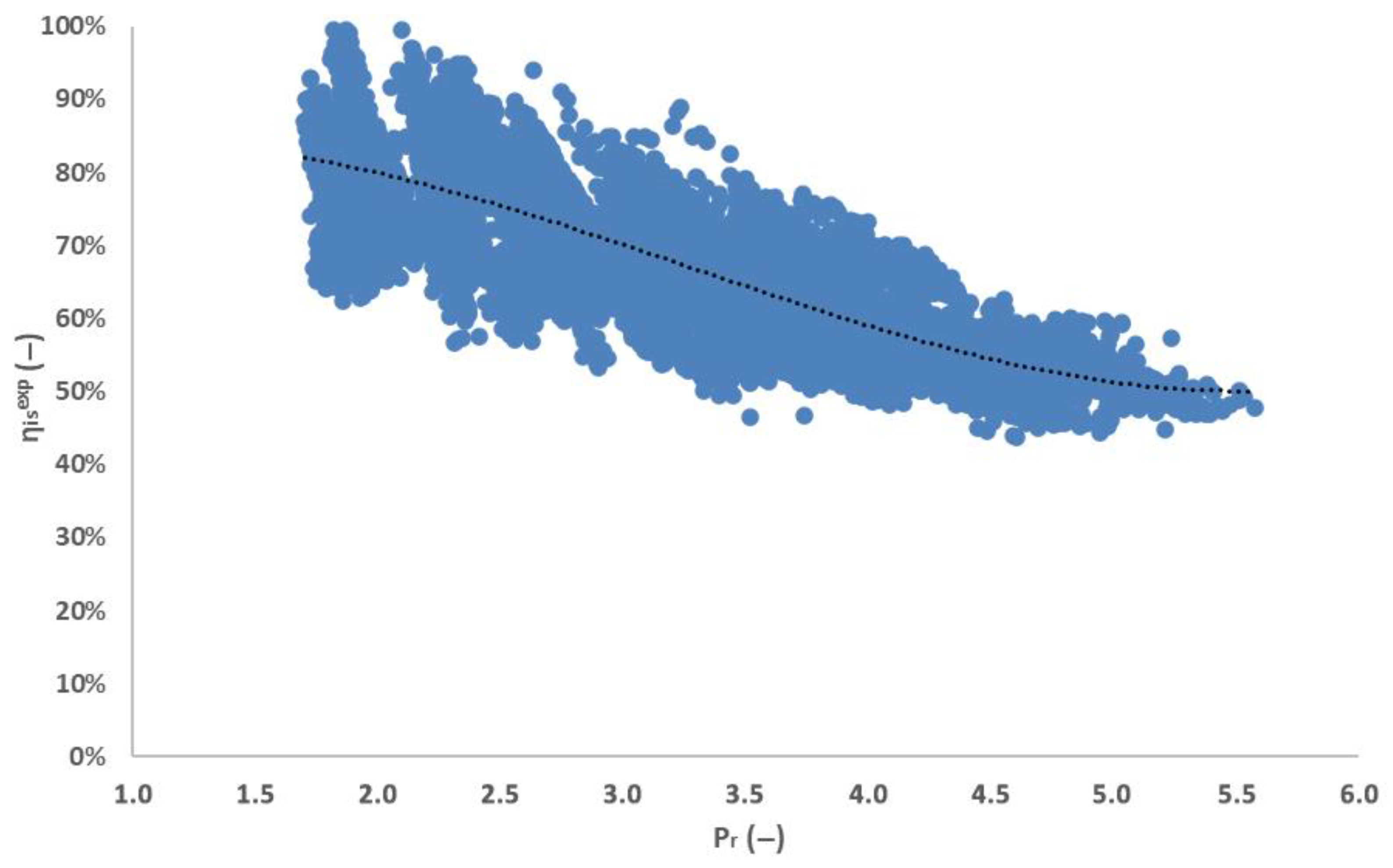
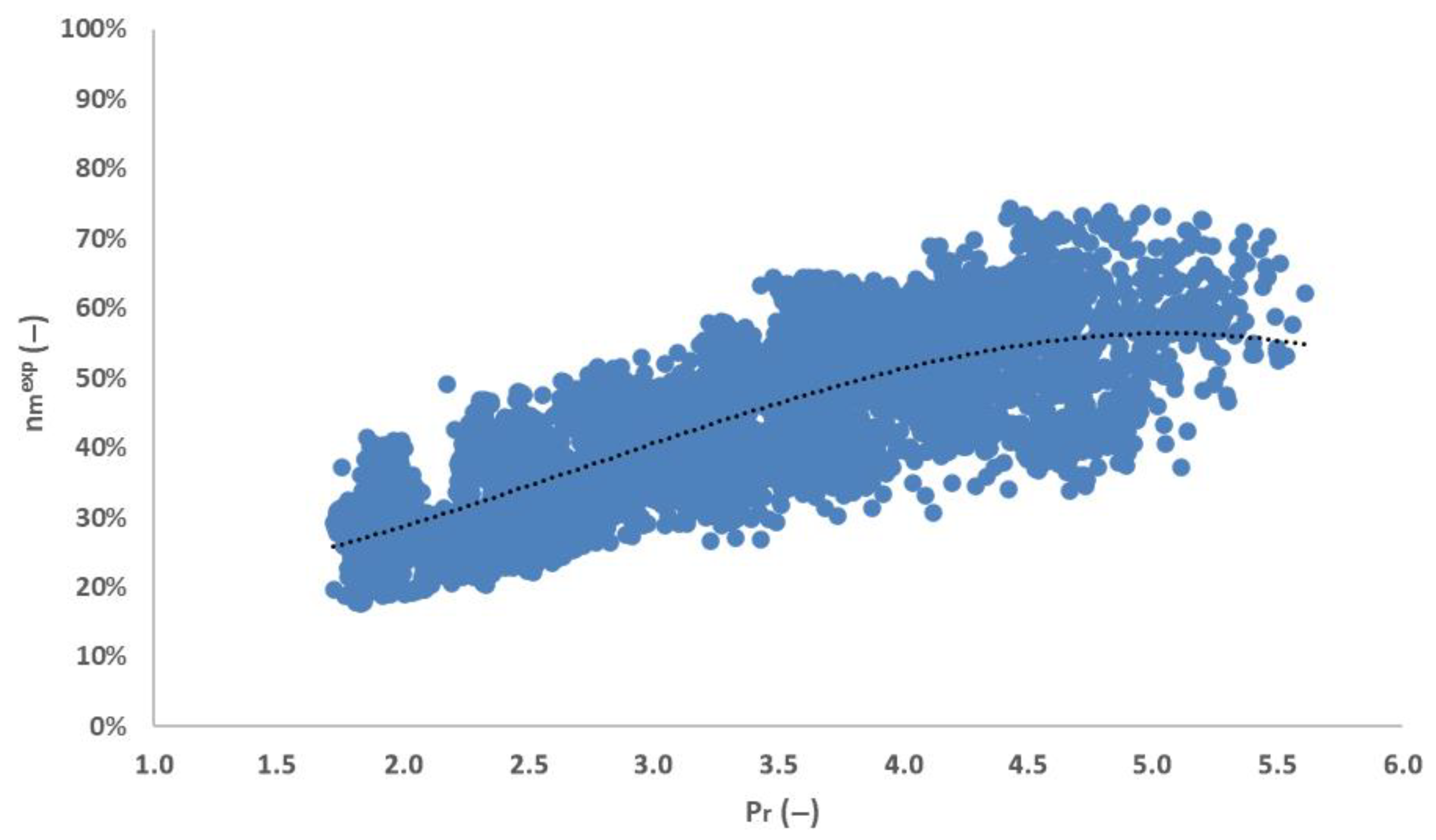
3.3. Expander Analysis
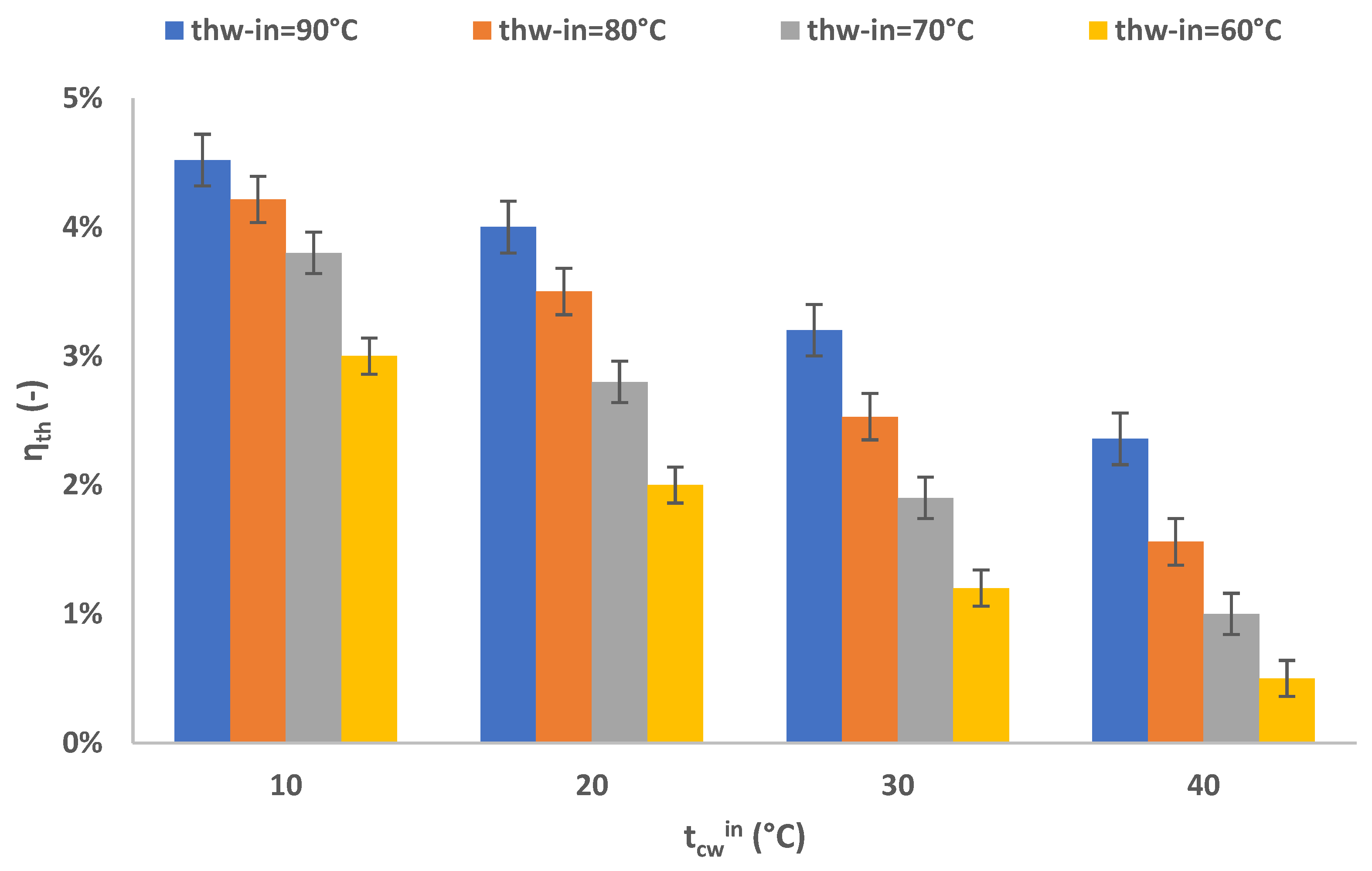
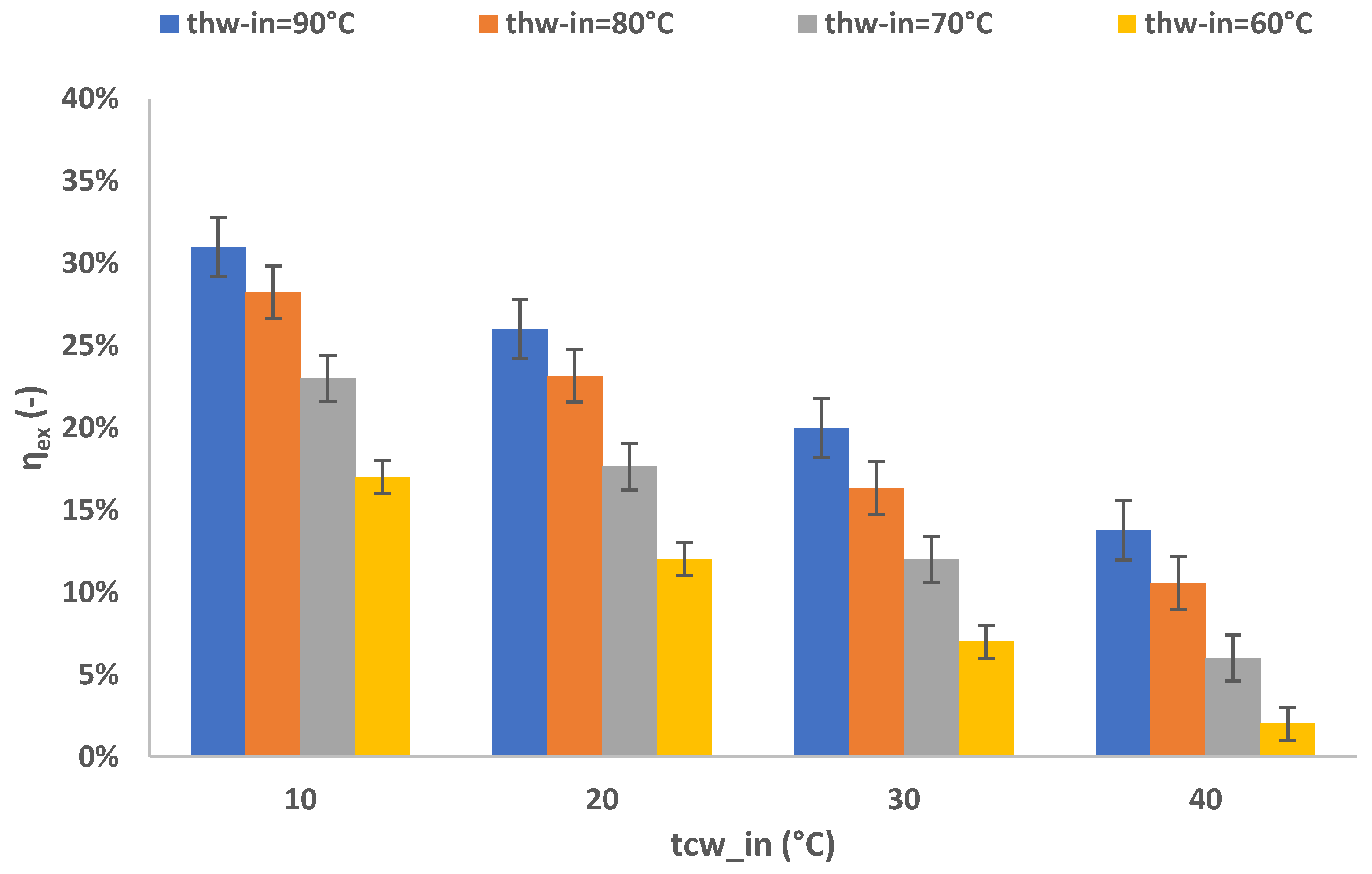
3.4. Energy and Exergy Performance Analysis
3.5. Simulation Models Validation
3.5.1. Verification of the PRC Simulation Model
3.5.2. Verification of the ORC Simulation Model Used as the Baseline
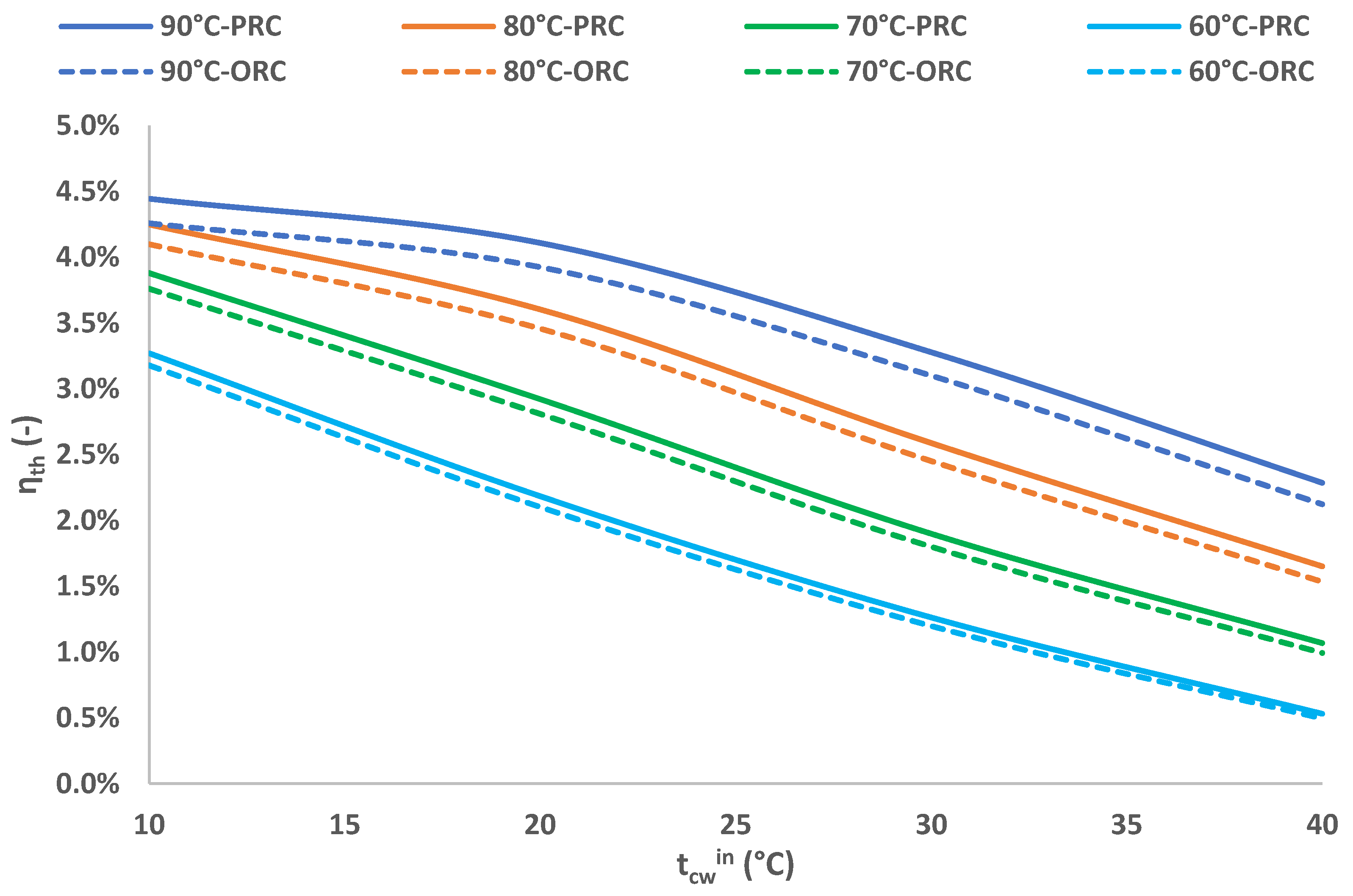
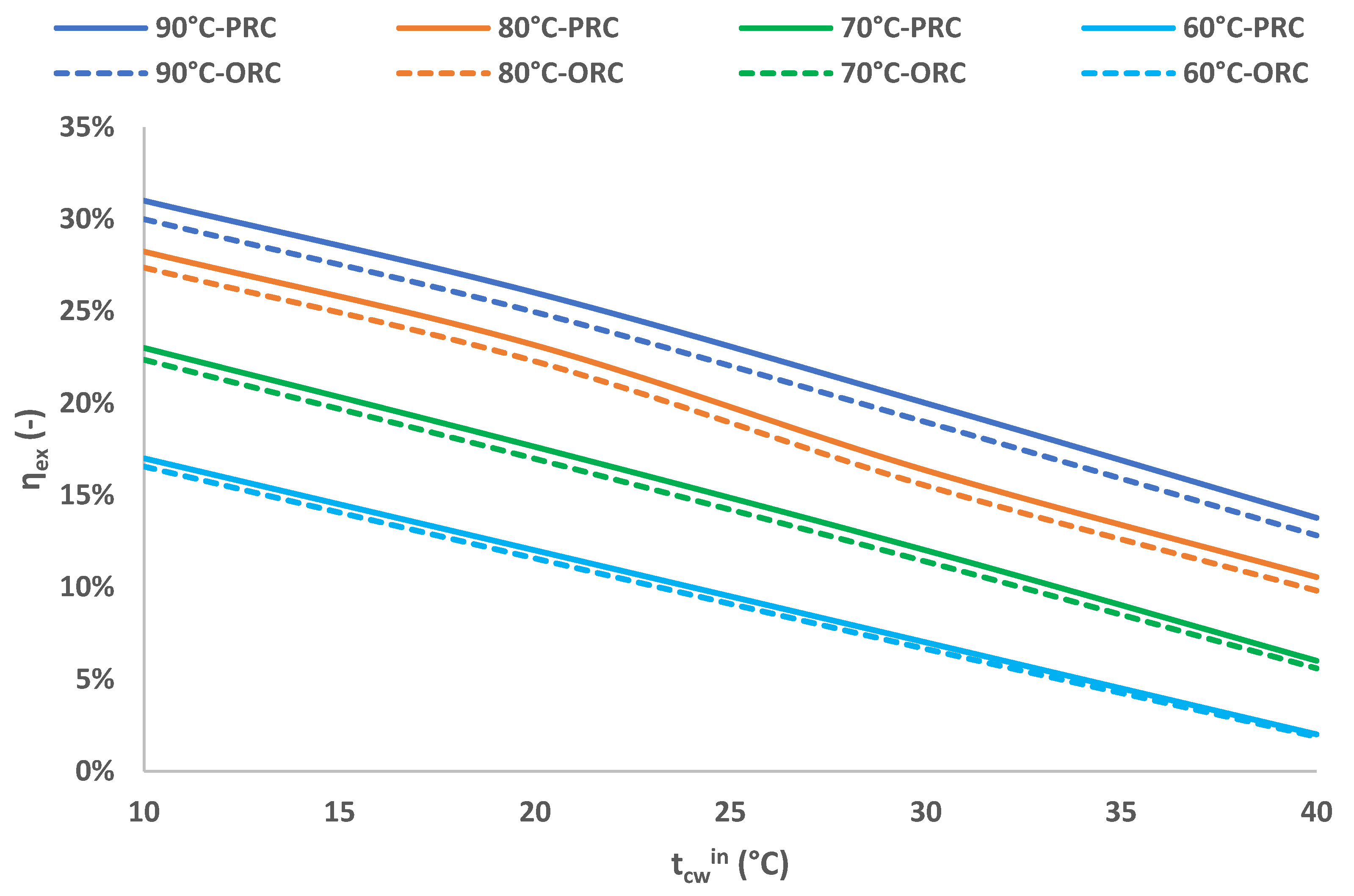
3.6. Performance Comparison to the Conventional System
4. Conclusions
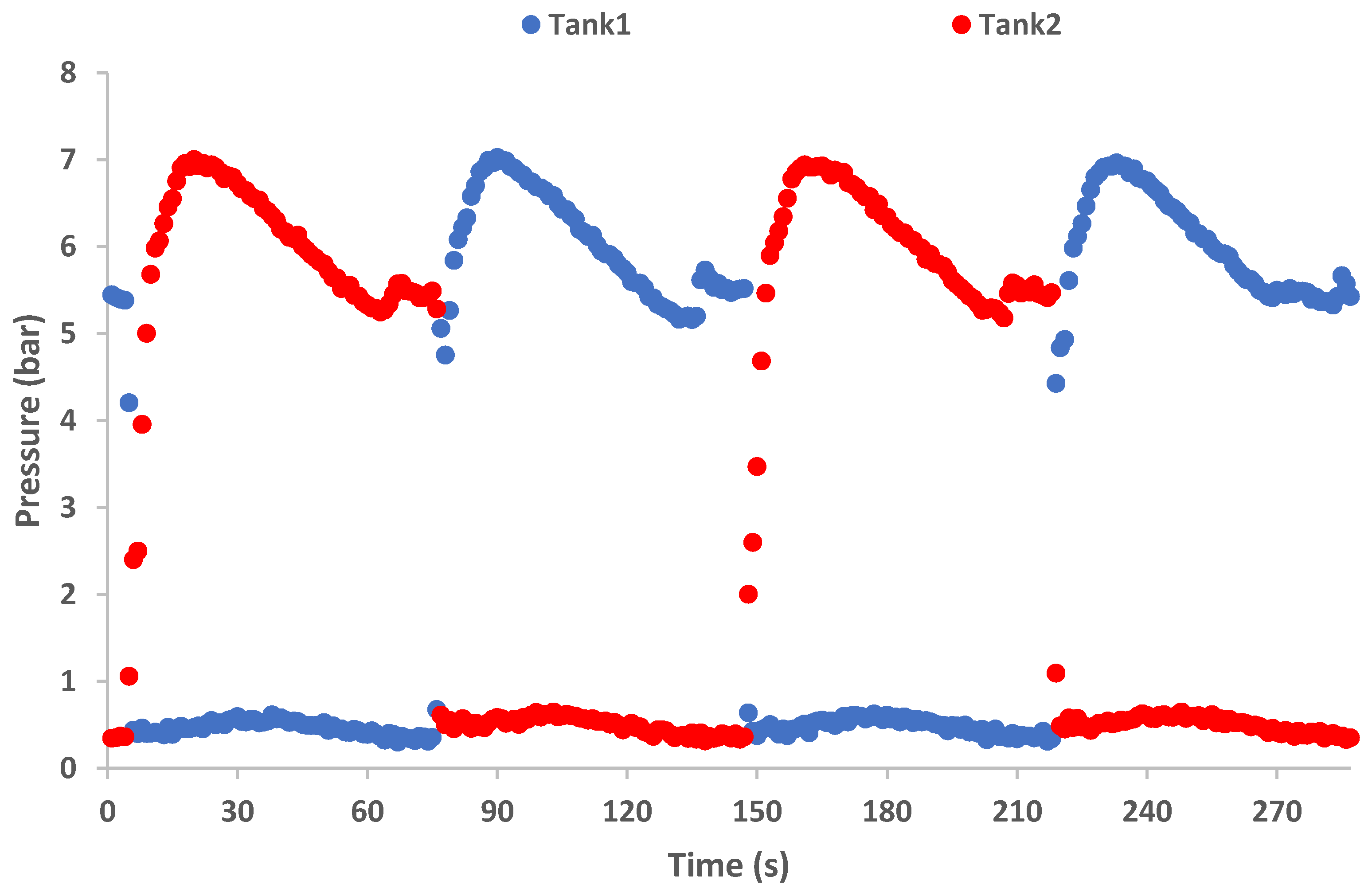
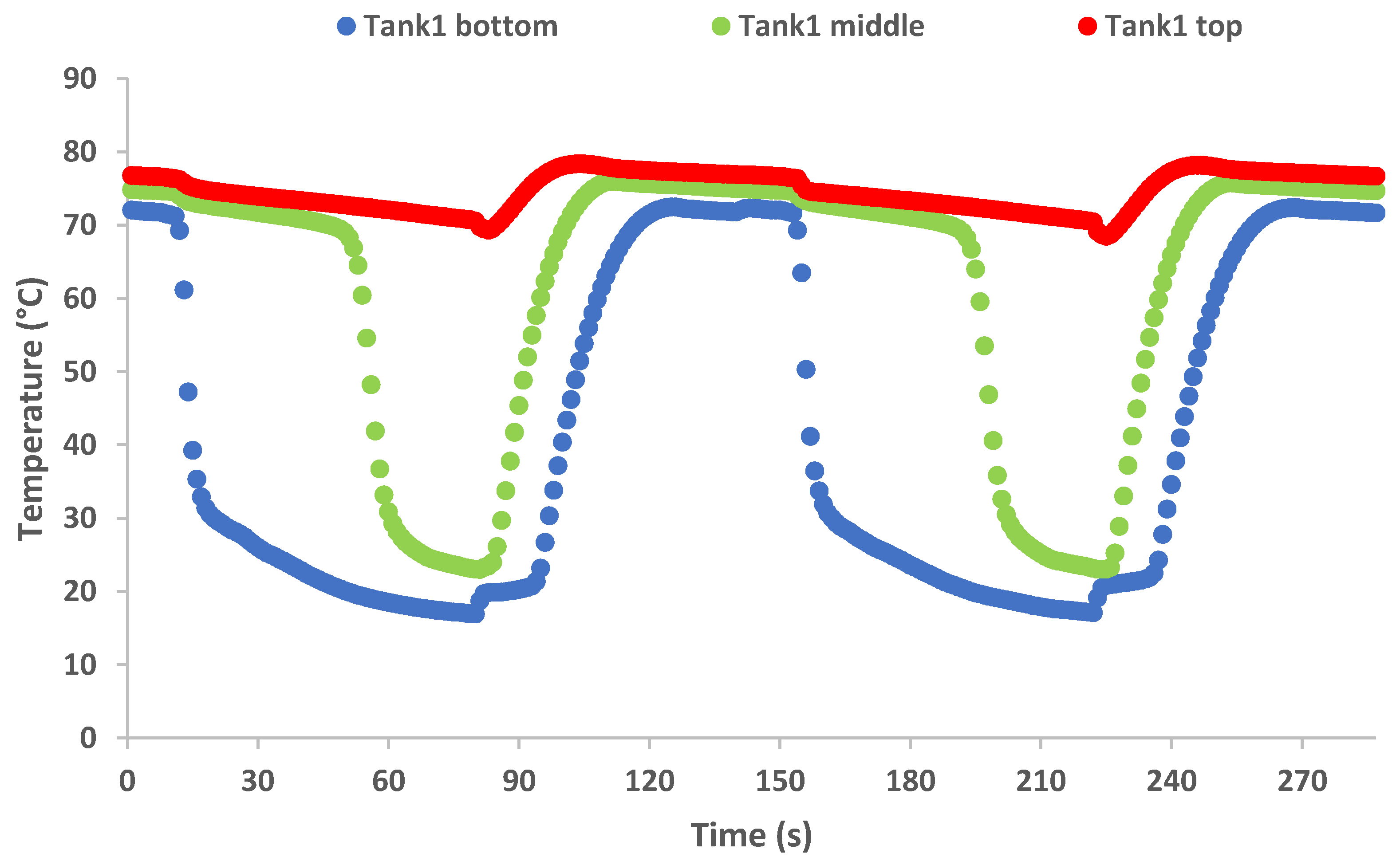
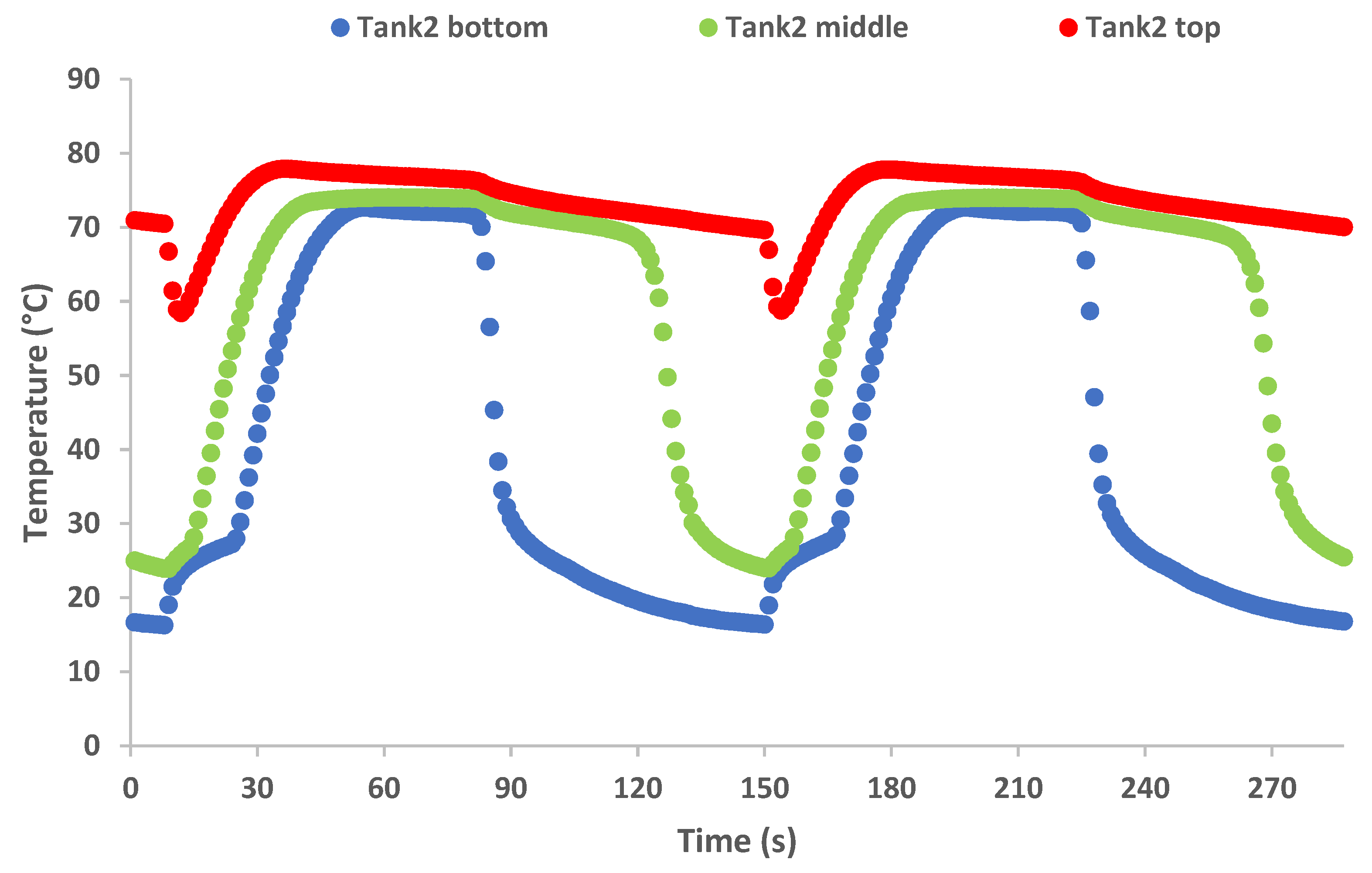
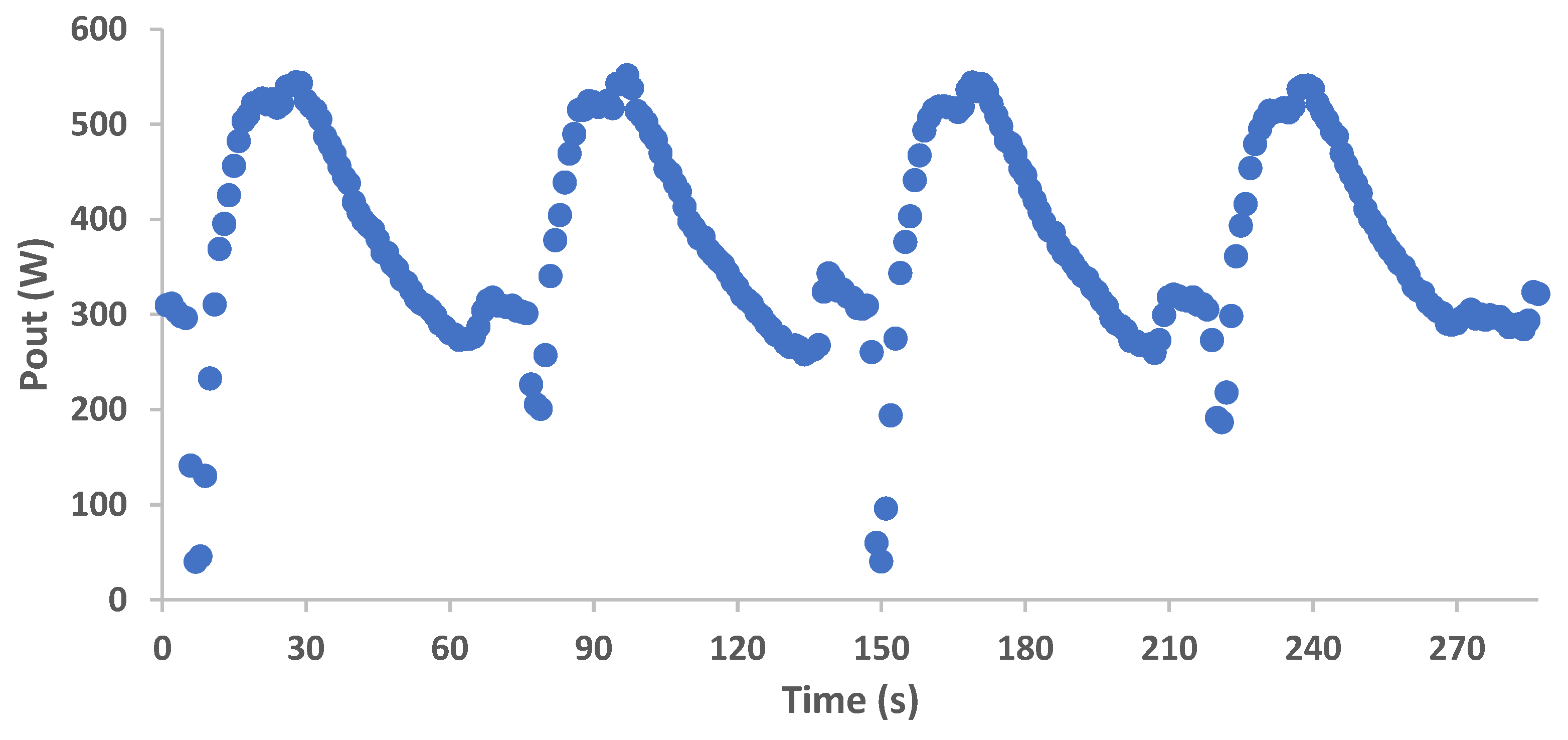
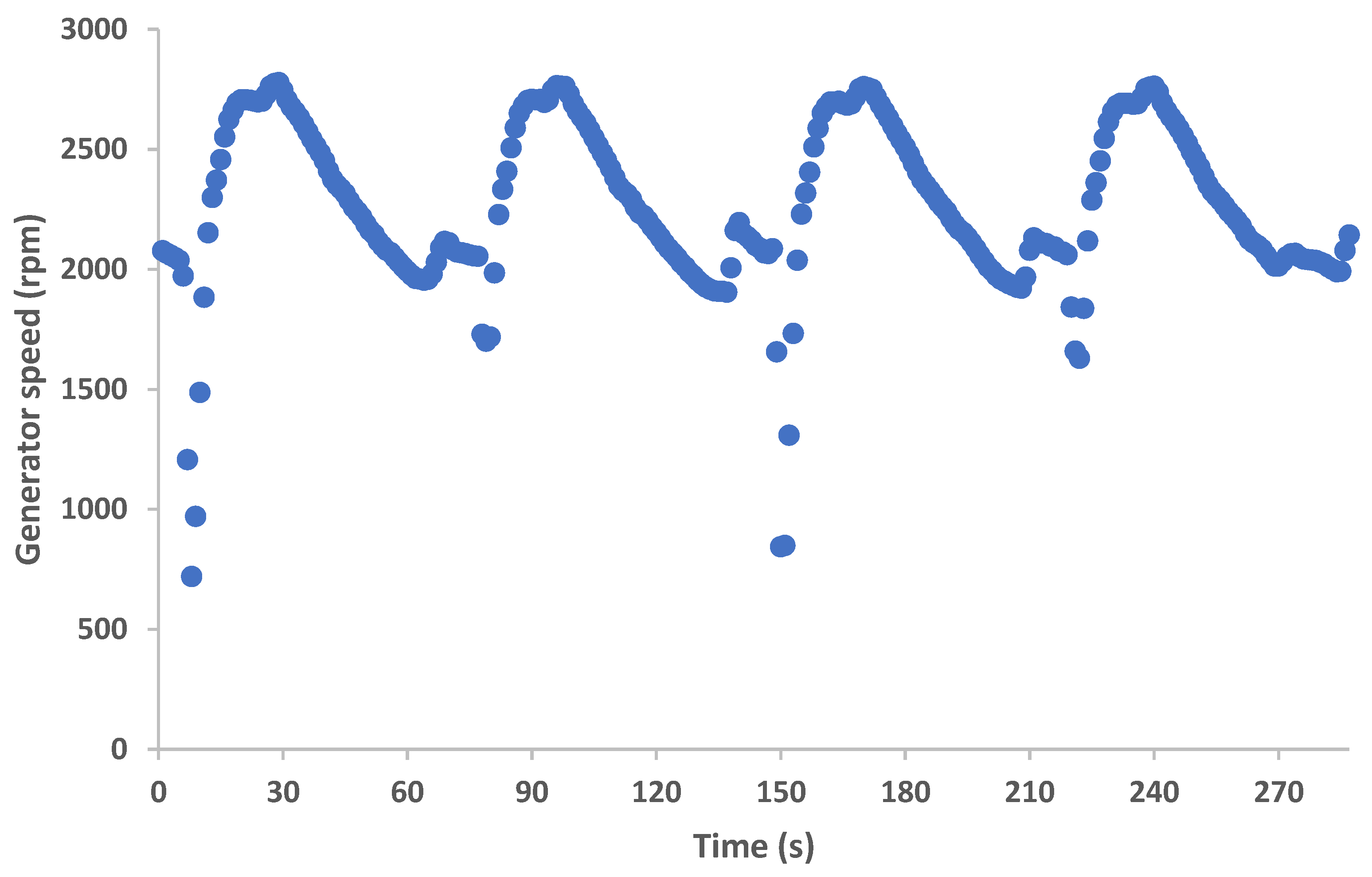
- The experimental results of the pressure in the buffer tanks, the temperatures in the different points of the PRC cycle and the output power and generation speed show approximately the same variation patterns on every thermal cycle.
- The examined configuration shows a relatively stable operation, with continuous power generation despite the switching phase, which inherently disrupts the constant refrigerant flow throughout the cycle.
- Efficiency figures increase along with the temperature difference between the heat source and heat sink. For the thwin = 90 °C and tcwin = 10 °C working conditions, the maximum time-averaged thermal efficiency is 4.5%, while the time-averaged exergy efficiency was calculated at 31%, respectively.
- Even for cases with low temperature difference between the heat source and heat sink, the tested prototype was able to operate and generate power, even with relatively low performance values, since for the working pair of thwin = 60 °C and tcwin = 40 °C, thermal efficiency was nearly 0.5%, and the corresponding exergy efficiency was at 2%.
- For all the examined cases, the PRC system results in higher efficiency figures compared to the conventional ORC solution. The deviation between the two cases shows increased values along with the increment of both tcwin and thwin. More precisely, for the case of tcwin = 40 °C and thwin = 90 °C, the ηth and the ηex calculated for the PRC are 7.7% and 7.5% higher, respectively, than the case of the ORC.
- PRC technology efficiency enhancement could be obtained by optimizing its design in future research, focusing on architectures providing continuous liquid refrigerant flow in the evaporator heat exchanger by increasing the buffer tank volume to prolong the continuous power generation of the configuration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Subscripts and superscripts | ||
| cp | specific heat, kW∙kg−1K−1 | avg | average |
| Ex | exergy, kW | cond | condenser |
| h | specific enthalpy, kj∙kg−1K−1 | cw | cold water |
| m | mass flow rate, kg∙s−1 | desup | desuperheater |
| P | pressure, bar | hw | hot water |
| Pout | output power, kW | evap | evaporation |
| Pr | expander pressure ratio, - | ex | exergy |
| Q | heat load, kW | exp | expander |
| t | temperature, °C | is.comp | isochoric compression |
| W | work load, kW | o | dead state |
| preh | preheater | ||
| r | refrigerant | ||
| Abbreviation | th | thermal | |
| CHP | Combined heat and power | Greek Symbols | |
| HFCs | Hydrofluorocarbons refrigerants | δ | uncertainty, - |
| ORC | Organic Rankine cycle | ηex | exergy efficiency, - |
| PCFs | Perfluorocarbons refrigerants | ηm | mechanical efficiency, - |
| PRC | Pumpless Rankine cycle | ηis | isentropic efficiency, - |
| ηth | thermal efficiency, - | ||
Appendix A

| Experimental Set (thwin–tcwin) | ηth (−) | ηex (−) | δηth (−) | δηth/ηth (−) | δηex (−) | δηex/ηex (−) |
|---|---|---|---|---|---|---|
| 90–10 | 4.5% | 31.0% | 0.0004 | 0.96% | 0.0034 | 1.11% |
| 90–20 | 4.0% | 26.0% | 0.0004 | 0.97% | 0.0029 | 1.12% |
| 90–30 | 3.2% | 20.0% | 0.0003 | 0.97% | 0.0021 | 1.12% |
| 90–40 | 2.4% | 13.8% | 0.0002 | 0.98% | 0.0015 | 1.13% |
| 80–10 | 4.2% | 28.2% | 0.0004 | 1.04% | 0.0035 | 1.21% |
| 80–20 | 3.5% | 23.1% | 0.0004 | 1.05% | 0.0028 | 1.22% |
| 80–30 | 2.5% | 16.3% | 0.0003 | 1.09% | 0.0020 | 1.25% |
| 80–40 | 1.6% | 10.5% | 0.0002 | 1.57% | 0.0018 | 1.69% |
| 70–10 | 3.8% | 23.0% | 0.0004 | 1.25% | 0.0032 | 1.44% |
| 70–20 | 2.8% | 17.6% | 0.0003 | 1.25% | 0.0025 | 1.44% |
| 70–30 | 1.9% | 12.0% | 0.0002 | 1.53% | 0.0018 | 1.68% |
| 70–40 | 1.0% | 6.0% | 0.0002 | 2.67% | 0.0015 | 2.77% |
| 60–10 | 3.0% | 17.0% | 0.0002 | 1.95% | 0.0025 | 2.12% |
| 60–20 | 2.0% | 12.0% | 0.0002 | 2.57% | 0.0022 | 2.70% |
| 60–30 | 1.2% | 7.0% | 0.0001 | 2.64% | 0.0013 | 2.77% |
| 60–40 | 0.5% | 2.0% | 0.0001 | 2.68% | 0.0004 | 2.81% |
References
- IEA. Global Energy Review 2025. 2025. Available online: https://www.iea.org/reports/global-energy-review-2025 (accessed on 26 June 2025).
- Feng, X.; Shi, F.; Qiao, G.; Li, Y.; Liu, C. Integrating organic Rankine cycle with thermoelectric generator in various applications utilizing low-grade energy: A review. Sustain. Energy Technol. Assess. 2024, 68, 103882. [Google Scholar] [CrossRef]
- Huo, D.; Tian, H.; Wang, W.; Shu, G. Na/K mixed electrolyte for high power density and heat-to-electricity conversion efficiency low-grade heat harvesting system. Mater. Today Nano 2022, 18, 100206. [Google Scholar] [CrossRef]
- Lykas, P.; Atsonios, K.; Gkountas, A.; Bakalis, P.; Manolakos, D.; Grammelis, P.; Itskos, G.; Nikolopoulos, N. Energy, exergy, and economic comparison of ORC with quasi-isothermal expansion with other ORC designs for low-grade waste heat recovery. Therm. Sci. Eng. Prog. 2024, 55, 103010. [Google Scholar] [CrossRef]
- Liang, Y.; Wu, J.; Sun, Z.; Zhu, Y.; Ye, K.; Dong, M.; Lu, J. Thermodynamic and economic analysis of refrigerant mixture R290/R1234ze used in an ORC-EERC system for low temperature heat sources. Appl. Therm. Eng. 2023, 229, 120635. [Google Scholar] [CrossRef]
- Wang, X.; Liu, D.; Gao, G.; Li, J.; Yang, Z.; Lin, R. Thermal performance study of a solar-coupled phase changes thermal energy storage system for ORC power generation. J. Energy Storage 2024, 78, 110126. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Parametric analysis and optimization of a solar driven trigeneration system based on ORC and absorption heat pump. J. Clean. Prod. 2017, 161, 493–509. [Google Scholar] [CrossRef]
- Chitgar, N.; Hemmati, A.; Sadrzadeh, M. A comparative performance analysis, working fluid selection, and machine learning optimization of ORC systems driven by geothermal energy. Energy Convers. Manag. 2023, 286, 117072. [Google Scholar] [CrossRef]
- Akbari, S.; Faghiri, S.; Zinjanabi, A.M.; Bijarchi, M.A.; Shafii, M.B.; Hosseinzadeh, K. Thermo-economic investigation and comparative multi-objective optimization of dual-pressure evaporation ORC using binary zeotropic mixtures as working fluids for geothermal energy application. Int. J. Thermofluids 2024, 24, 100899. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, Y.-Q.; Xu, K.-J.; Liang, H.-J.; Liu, Z.-N.; Zhao, C.-Y.; Wang, Y.-Z.; Sapin, P.; Markides, C.N. Dynamic behaviour and performance evaluation of a biomass-fired organic Rankine cycle combined heat and power (ORC-CHP) system under different control strategies. Appl. Therm. Eng. 2024, 248, 123236. [Google Scholar] [CrossRef]
- Nguyen, T.; Lin, L. Potentials and effects of electricity cogeneration via ORC integration in small-scale biomass district heating system. Green Energy Resour. 2025, 3, 100113. [Google Scholar] [CrossRef]
- Kosmadakis, G.; Neofytou, P. Reversible high-temperature heat pump/ORC for waste heat recovery in various ships: A techno-economic assessment. Energy 2022, 256, 124634. [Google Scholar] [CrossRef]
- Asim, M.; Khan, S.; Khan, S.A.; Baig, T.; Imran, M.; Zia, A.W.; Riaz, F.; Leung, M.K. Thermal analysis and optimal fluid selection for the novel integrated vapor compression cycle and ORC system for ultra-low grade waste heat recovery using the desuperheating method. Energy Nexus 2025, 17, 100357. [Google Scholar] [CrossRef]
- Bianchi, M.; Branchini, L.; De Pascale, A.; Melino, F.; Ottaviano, S.; Peretto, A.; Torricelli, N.; Zampieri, G. Performance and operation of micro-ORC energy system using geothermal heat source. Energy Procedia 2018, 148, 384–391. [Google Scholar] [CrossRef]
- Algieri, A.; Morrone, P. Energetic analysis of biomass-fired ORC systems for micro-scale combined heat and power (CHP) generation. A possible application to the Italian residential sector. Appl. Therm. Eng. 2014, 71, 751–759. [Google Scholar] [CrossRef]
- Mateu-Royo, C.; Mota-Babiloni, A.; Navarro-Esbrí, J.; Peris, B.; Molés, F.; Amat-Albuixech, M. Multi-objective optimization of a novel reversible High-Temperature Heat Pump-Organic Rankine Cycle (HTHP-ORC) for industrial low-grade waste heat recovery. Energy Convers. Manag. 2019, 197, 111908. [Google Scholar] [CrossRef]
- Mana, A.A.; Kaitouni, S.I.; Kousksou, T.; Jamil, A. Enhancing sustainable energy conversion: Comparative study of superheated and recuperative ORC systems for waste heat recovery and geothermal applications, with focus on 4E performance. Energy 2023, 284, 128654. [Google Scholar] [CrossRef]
- Aliahmadi, M.; Moosavi, A.; Sadrhosseini, H. Multi-objective optimization of regenerative ORC system integrated with thermoelectric generators for low-temperature waste heat recovery. Energy Rep. 2021, 7, 300–313. [Google Scholar] [CrossRef]
- Yamada, N.; Minami, T.; Mohamad, M.N.A. Fundamental experiment of pumpless Rankine-type cycle for low-temperature heat recovery. Energy 2011, 36, 1010–1017. [Google Scholar] [CrossRef]
- Safarian, S.; Aramoun, F. Energy and exergy assessments of modified Organic Rankine Cycles (ORCs). Energy Rep. 2015, 1, 1–7. [Google Scholar] [CrossRef]
- Li, J.; Pei, G.; Li, Y.; Ji, J. Analysis of a novel gravity driven organic Rankine cycle for small-scale cogeneration applications. Appl. Energy 2013, 108, 34–44. [Google Scholar] [CrossRef]
- Bao, H.; Wang, Y.; Roskilly, A.P. Modelling of a chemisorption refrigeration and power cogeneration system. Appl. Energy 2014, 119, 351–362. [Google Scholar] [CrossRef]
- Yamada, N.; Watanabe, M.; Hoshi, A. Experiment on pumpless Rankine-type cycle with scroll expander. Energy 2013, 49, 137–145. [Google Scholar] [CrossRef]
- Gao, P.; Wang, L.W.; Wang, R.Z.; Jiang, L.; Zhou, Z.S. Experimental investigation on a small pumpless ORC (organic rankine cycle) system driven by the low temperature heat source. Energy 2015, 91, 324–333. [Google Scholar] [CrossRef]
- Jiang, L.; Lu, H.T.; Wang, L.W.; Gao, P.; Zhu, F.Q.; Wang, R.Z.; Roskilly, A.P. Investigation on a small-scale pumpless Organic Rankine Cycle (ORC) system driven by the low temperature heat source. Appl. Energy 2017, 195, 478–486. [Google Scholar] [CrossRef]
- Gao, P.; Wang, Z.X.; Wang, L.W.; Lu, H.T. Technical feasibility of a gravity-type pumpless ORC system with one evaporator and two condensers. Appl. Therm. Eng. 2018, 145, 569–575. [Google Scholar] [CrossRef]
- Gkimisis, L.; Arapkoules, N.; Vasileiou, G.; Soldatos, A.; Spitas, V. Modelling and numerical simulation of a novel Pumpless Rankine Cycle (PRC). Appl. Therm. Eng. 2020, 178, 115523. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Zhu, H. Investigation on a novel pumpless module driven by thermal energy and gravity and its application in an ORC system. Renew. Energy 2022, 195, 476–487. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, X.; Gao, Z.; Wang, L.; Wang, Z. Thermodynamic analysis and experimental study of two-stage thermal-gravitational pumping ORC under low evaporation temperatures. Sustain. Energy Technol. Assess. 2024, 66, 103820. [Google Scholar] [CrossRef]
- Świerzewski, M.; Kalina, J.; Musiał, A. Techno-economic optimization of ORC system structure, size and working fluid within biomass-fired municipal cogeneration plant retrofitting project. Renew. Energy 2021, 180, 281–296. [Google Scholar] [CrossRef]
- Kajurek, J.; Rusowicz, A.; Grzebielec, A.; Bujalski, W.; Futyma, K.; Rudowicz, Z. Selection of refrigerants for a modified organic Rankine cycle. Energy 2019, 168, 1–8. [Google Scholar] [CrossRef]
- E2ReLab. Available online: https://e2relab.core.uoa.gr/ (accessed on 30 June 2025).
- Moffat, R.J. Using Uncertainty Analysis in the Planning of an Experiment. 1985. Available online: https://fluidsengineering.asmedigitalcollection.asme.org (accessed on 10 August 2025).
- Eyerer, S.; Dawo, F.; Kaindl, J.; Wieland, C.; Spliethoff, H. Experimental investigation of modern ORC working fluids R1224yd(Z) and R1233zd(E) as replacements for R245fa. Appl. Energy 2019, 240, 946–963. [Google Scholar] [CrossRef]







| Measured Variable | Measurement Device | Range | Calibrated Accuracy |
|---|---|---|---|
| Temperature probes | |||
| Hot water in | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Hot water out | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Cold water in | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Cold water out | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Main liquid line | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Preheater out | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Expander in | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Expander out | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Desuperheater out | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Condenser out | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Tank 1 liquid line | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Tank 1 bottom | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Tank 1 middle | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Tank 1 top | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Tank 1 vapor line | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Tank 2 liquid line | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Tank 2 bottom | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Tank 2 middle | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Tank 2 top | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Tank 2 vapor line | T-type thermocouple | 0.0 to 140.0 °C | ±0.5 K |
| Flow meters | |||
| Hot-water flow | Magnetic flow meter | 0.0 to 10.0 lpm | ±0.03% of the rate |
| Hot-water flow | Magnetic flow meter | 0.0 to 10.0 lpm | ±0.03% of the rate |
| Pressure transmitters | |||
| Tank 1 pressure | Pressure gauge | 0.0 to 10.0 bar | ±0.6% of the span |
| Tank 2 pressure | Pressure gauge | 0.0 to 10.0 bar | ±0.6% of the span |
| Generator measurements | |||
| Generator power output | Digital watt meter | 0.0 to 1000.0 W | ±0.5% of the reading |
| Generator speed | Digital tachometer | 0 to 2500 rpm | ±0.5% of the reading |
| thwin (°C) | tcwin (°C) | ηth | Deviation | |
|---|---|---|---|---|
| Experiment | Simulation | |||
| 90 | 10 | 0.045 | 0.044 | −1.7% |
| 90 | 20 | 0.04 | 0.041 | 2.7% |
| 90 | 30 | 0.032 | 0.033 | 2.4% |
| 90 | 40 | 0.024 | 0.023 | −3.0% |
| 80 | 10 | 0.042 | 0.042 | 0.8% |
| 80 | 20 | 0.035 | 0.036 | 2.9% |
| 80 | 30 | 0.025 | 0.026 | 2.3% |
| 80 | 40 | 0.016 | 0.017 | 5.9% |
| 70 | 10 | 0.038 | 0.039 | 2.1% |
| 70 | 20 | 0.028 | 0.029 | 4.3% |
| 70 | 30 | 0.019 | 0.019 | −0.1% |
| 70 | 40 | 0.01 | 0.011 | 6.8% |
| 60 | 10 | 0.03 | 0.033 | 9.0% |
| 60 | 20 | 0.02 | 0.022 | 9.2% |
| 60 | 30 | 0.012 | 0.013 | 5.3% |
| 60 | 40 | 0.005 | 0.005 | 6.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syngounas, E.; Konstantaras, J.; Arapkoules, N.; Tsimpoukis, D.; Koukou, M.K.; Vrachopoulos, M.G. Experimental Energy and Exergy Performance Evaluation of a Novel Pumpless Rankine Cycle (PRC) Unit Employing Low-Temperature Heat Sources. Energies 2025, 18, 4766. https://doi.org/10.3390/en18174766
Syngounas E, Konstantaras J, Arapkoules N, Tsimpoukis D, Koukou MK, Vrachopoulos MG. Experimental Energy and Exergy Performance Evaluation of a Novel Pumpless Rankine Cycle (PRC) Unit Employing Low-Temperature Heat Sources. Energies. 2025; 18(17):4766. https://doi.org/10.3390/en18174766
Chicago/Turabian StyleSyngounas, Evangelos, John Konstantaras, Nikolaos Arapkoules, Dimitrios Tsimpoukis, Maria K. Koukou, and Michail Gr. Vrachopoulos. 2025. "Experimental Energy and Exergy Performance Evaluation of a Novel Pumpless Rankine Cycle (PRC) Unit Employing Low-Temperature Heat Sources" Energies 18, no. 17: 4766. https://doi.org/10.3390/en18174766
APA StyleSyngounas, E., Konstantaras, J., Arapkoules, N., Tsimpoukis, D., Koukou, M. K., & Vrachopoulos, M. G. (2025). Experimental Energy and Exergy Performance Evaluation of a Novel Pumpless Rankine Cycle (PRC) Unit Employing Low-Temperature Heat Sources. Energies, 18(17), 4766. https://doi.org/10.3390/en18174766







