A Coordinated Neuro-Fuzzy Control System for Hybrid Energy Storage Integration: Virtual Inertia and Frequency Support in Low-Inertia Power Systems
Abstract
1. Introduction
- -
- The design of a neuro-fuzzy controller applied to the HESS for providing virtual inertia and virtual droop control, considering the state of charge of the supercapacitors.
- -
- A control strategy for power transition based on SOC, which coordinates energy exchange between the HESS and the conventional generation unit (CGU), ensuring reliable and efficient energy dispatch.
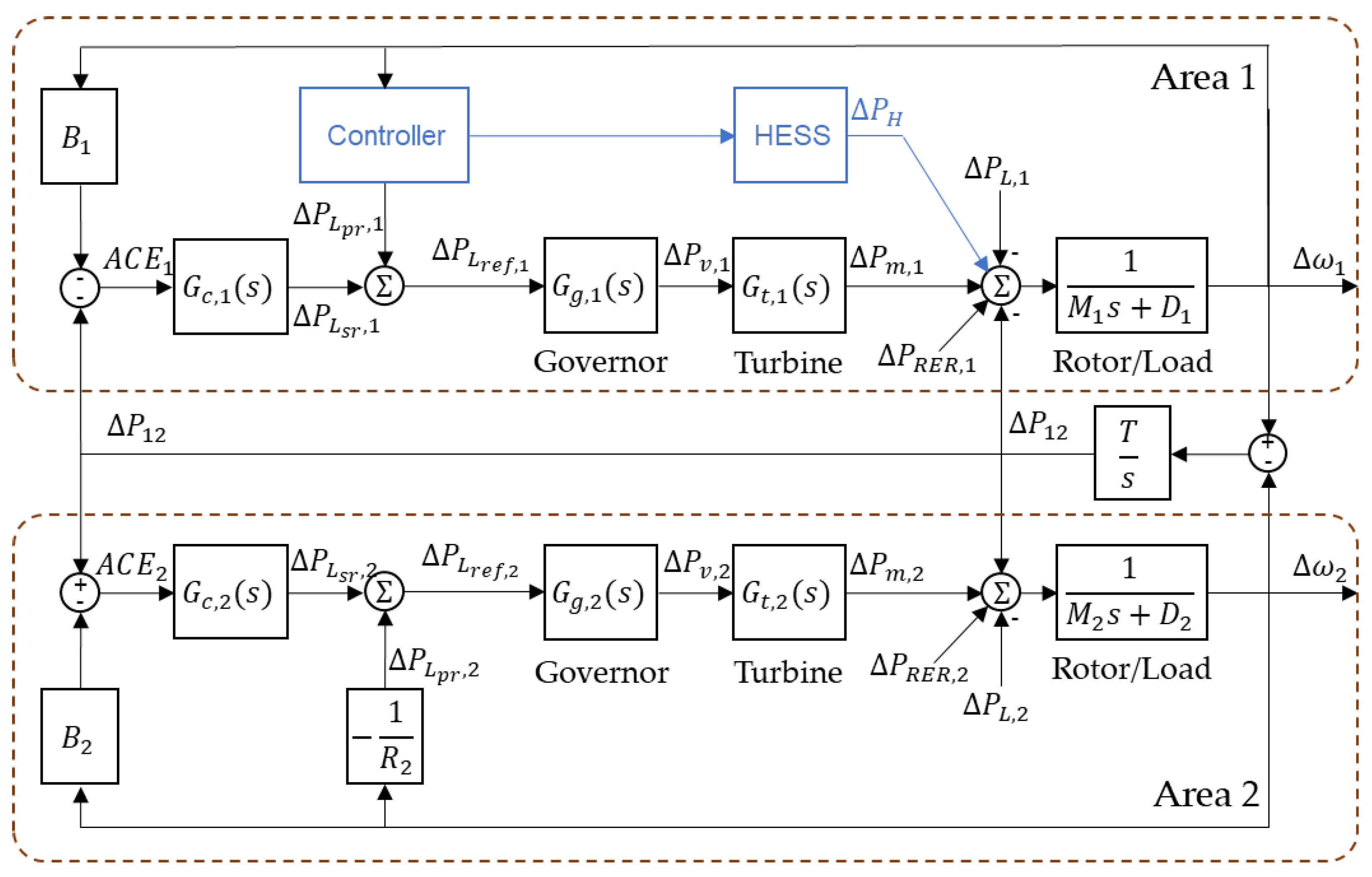
2. System Modeling
3. Control Strategies
3.1. Inertial Response and Primary Regulation
3.1.1. Strategy 1: Inertial Response and Primary Regulation with BESS
3.1.2. Strategy 2: Inertial Response with Supercapacitors and Primary Regulation with Batteries (HESS)
3.2. SOC Control
3.2.1. Strategy 1: Sigmoid Function
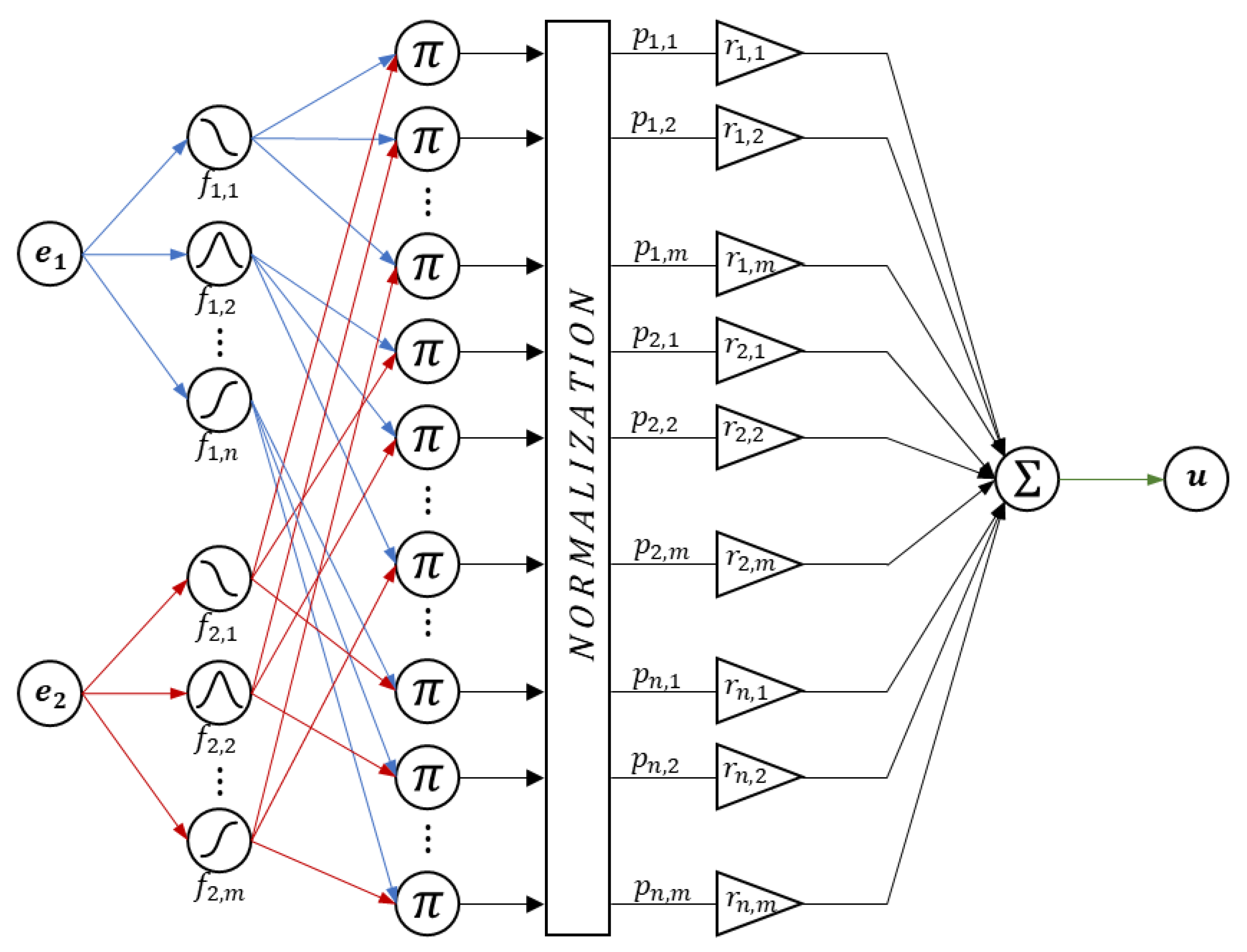
3.2.2. Strategy 1: Fuzzy-Logic Controller
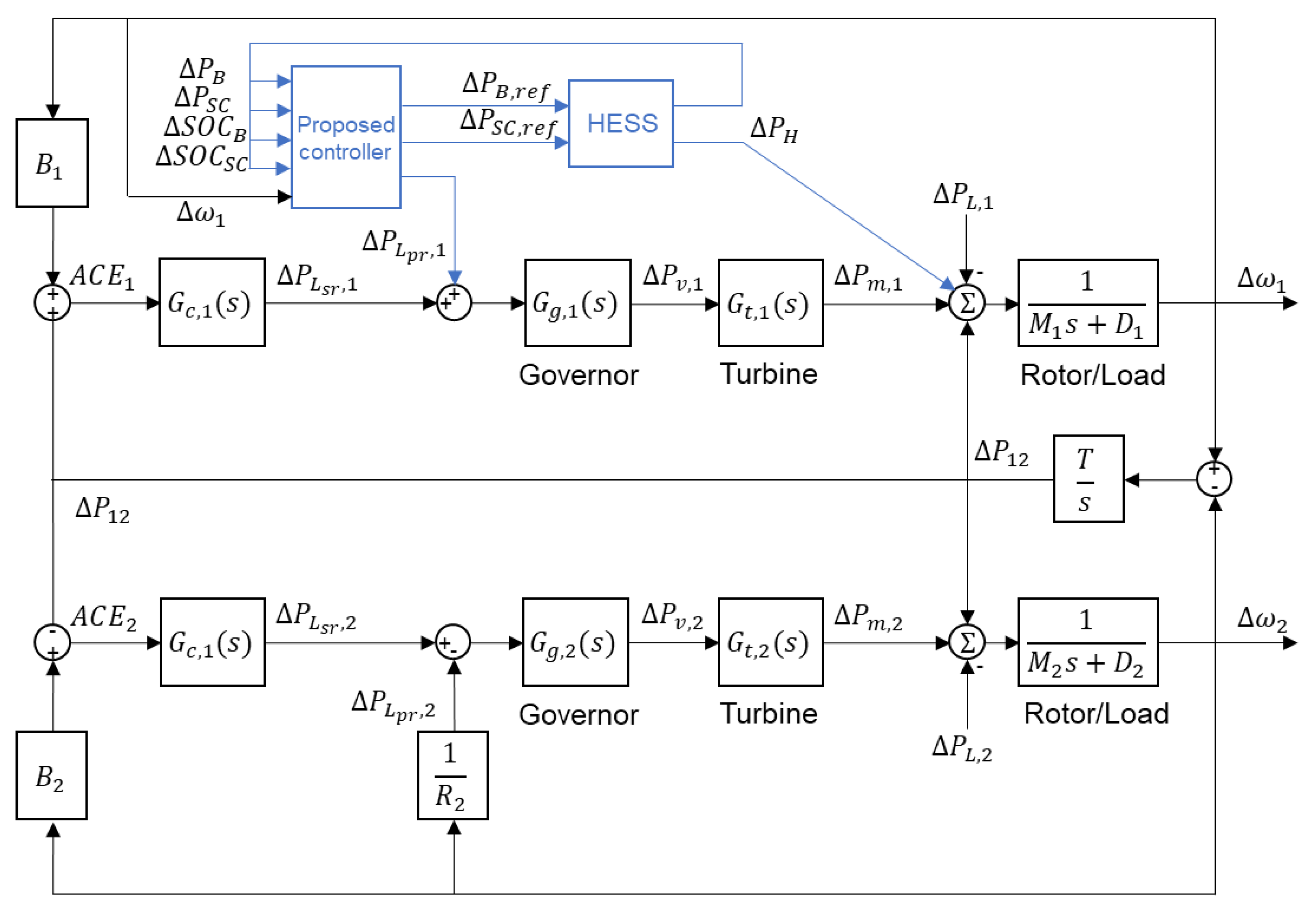
3.3. Proposed Strategy
- -
- Inertial response and the initial stage of primary regulation unfold over short time windows (hundreds of milliseconds to a few seconds). Introducing online adaptation during these transients may yield time-varying closed loop dynamics and nonmonotonic actions, which can jeopardize frequency recovery [38]. A fixed parameter zero-order Takagi–Sugeno design guarantees deterministic behavior and repeatability [37].
- -
- Grid support controllers often face stringent requirements for verification, validation, and fail-safe operation according to IEEE 1547-2018 [9] and IEEE 1547.1-2020 [39]. In practice, product certification, such as UL-1741 Supplement SB [40], follows prescribed test procedures with specified parameter ranges and response times. Controllers with deterministic, bounded settings therefore align naturally with these test matrices and facilitate verification and repeatability, whereas online adaptation can complicate repeatable testing under fixed test conditions.
- -
- Online adaptation can be sensitive to measurement noise (frequency estimation, ROCOF, SOC observers). Prior reviews have noted that measurement noise and modeling uncertainties can undermine the robustness of online or adaptive SOC estimators, particularly for Kalman filter-based and observer-based approaches [41].
- -
- Recent reviews indicate that machine-learning models in power systems face risks of overfitting and limited generalization under nonstationary and heterogeneous data, which motivates scenario-based design with explicit rule structures rather than purely data-driven tuning [42].
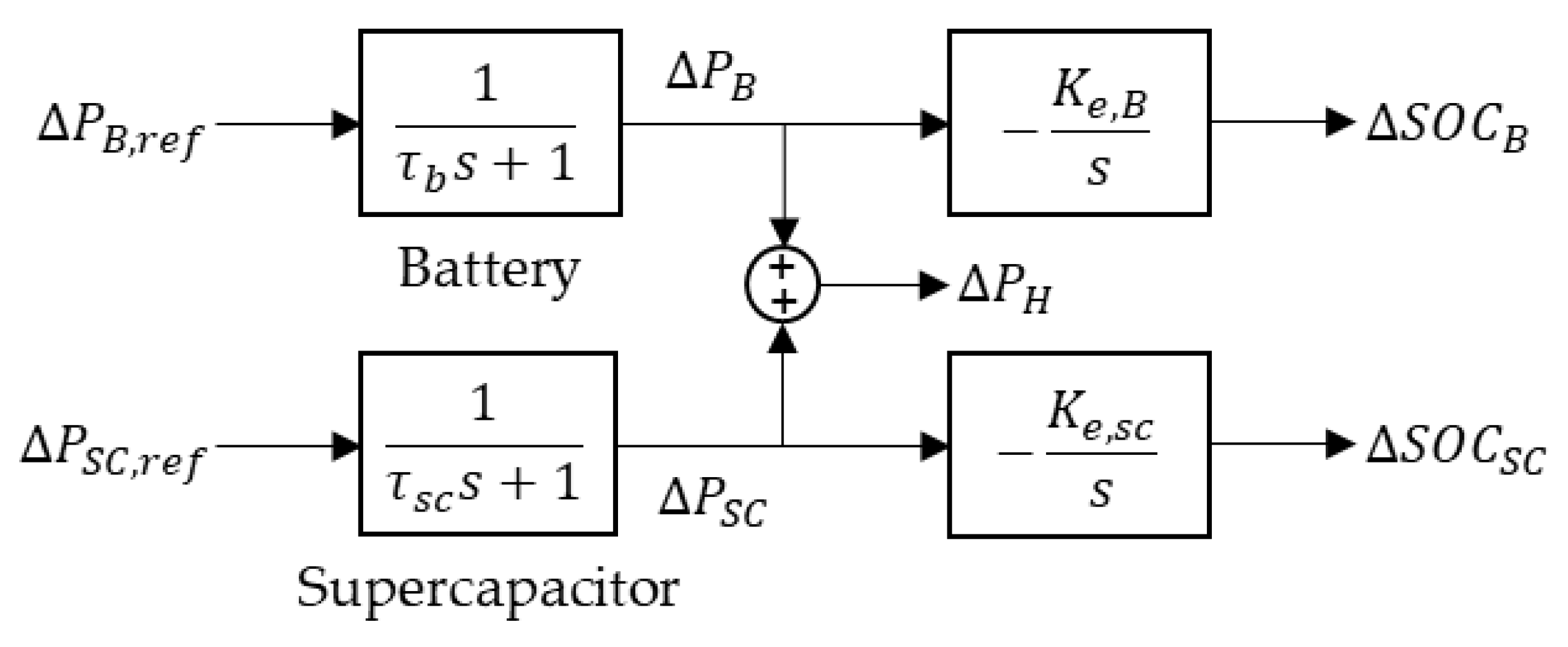
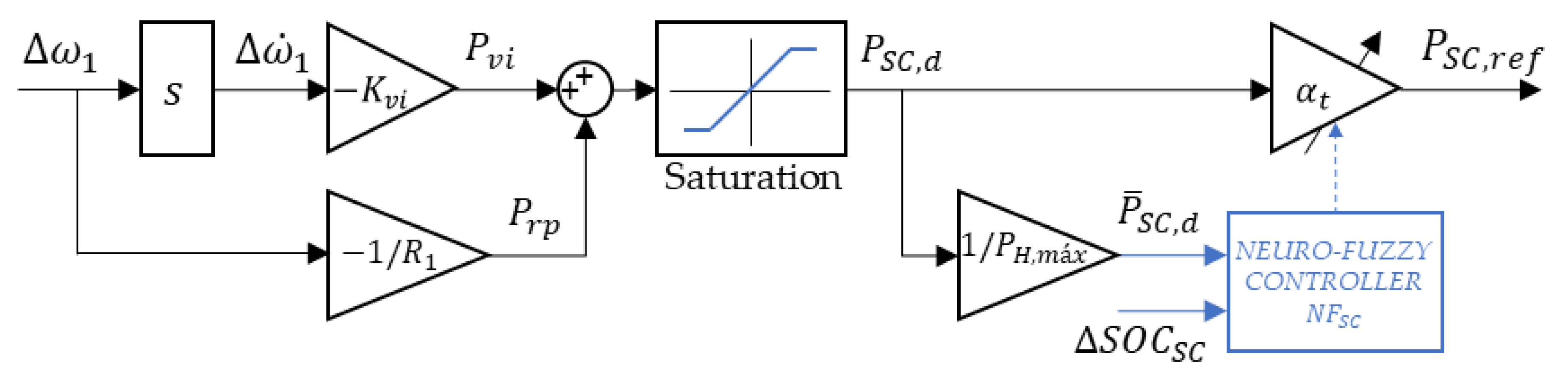
3.3.1. Supercapacitor Control System
3.3.2. Battery Control System
3.3.3. Conventional Generation Unit
3.4. Implementation Considerations for Real-World Deployment
4. Results
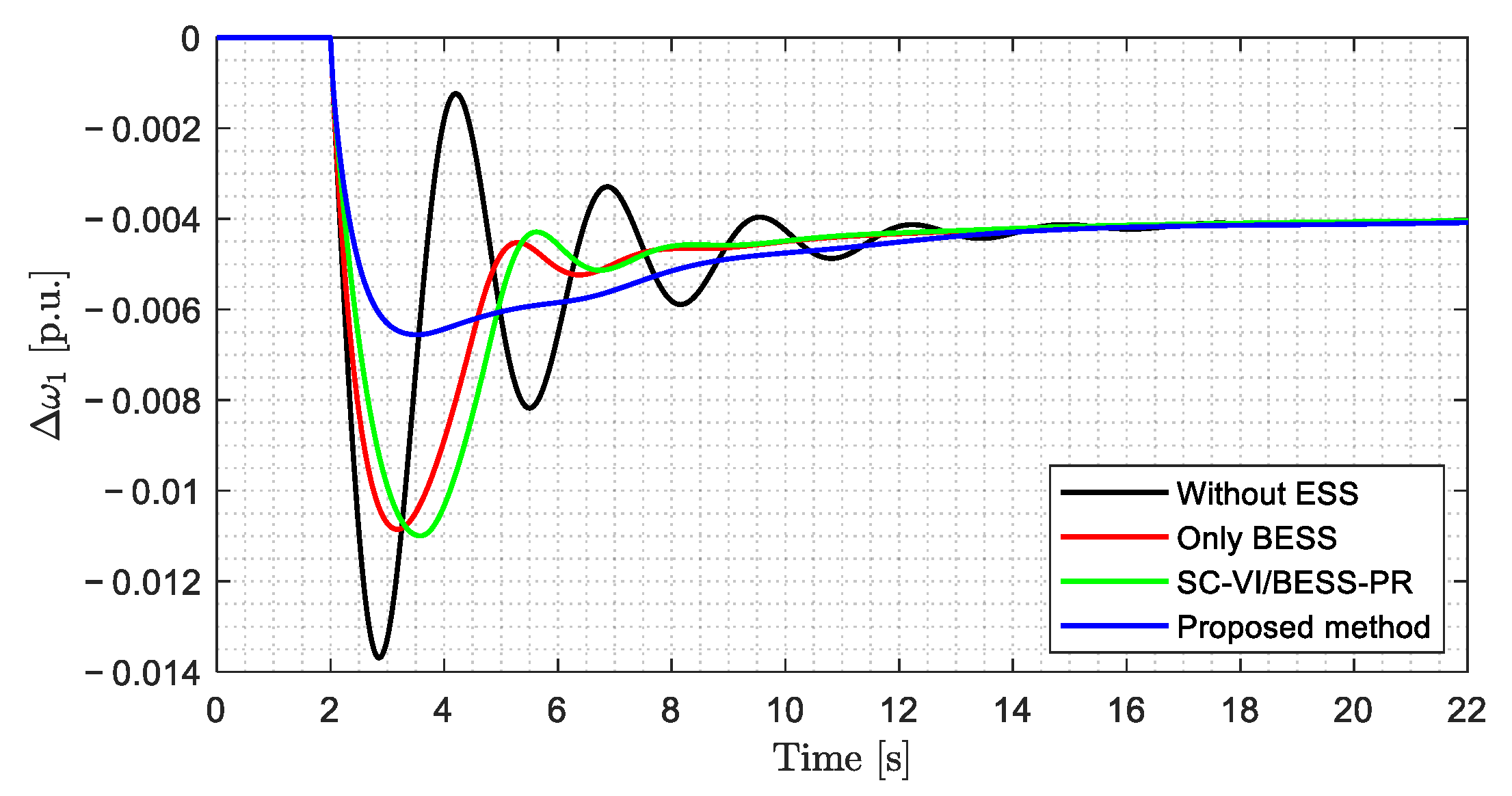
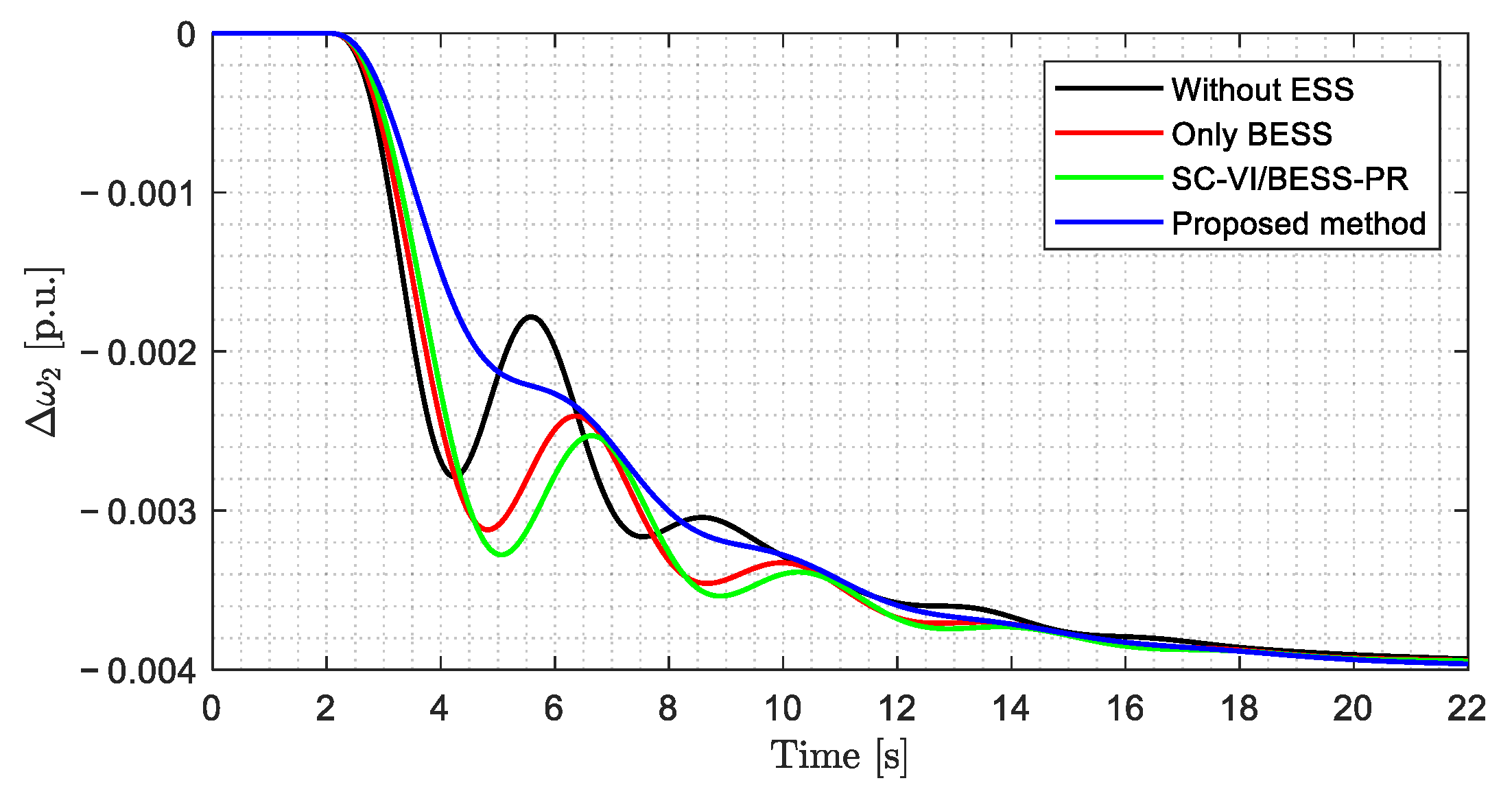
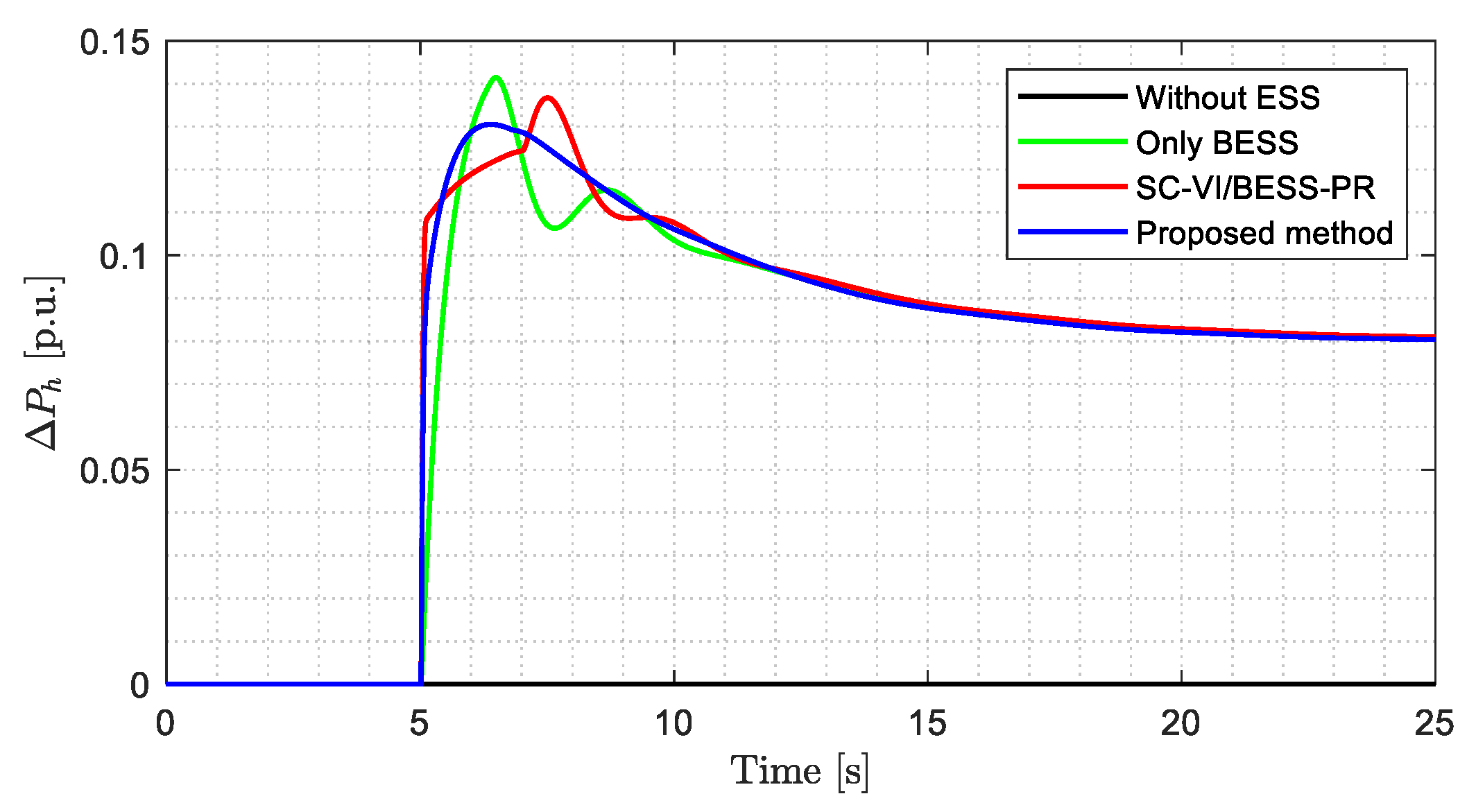
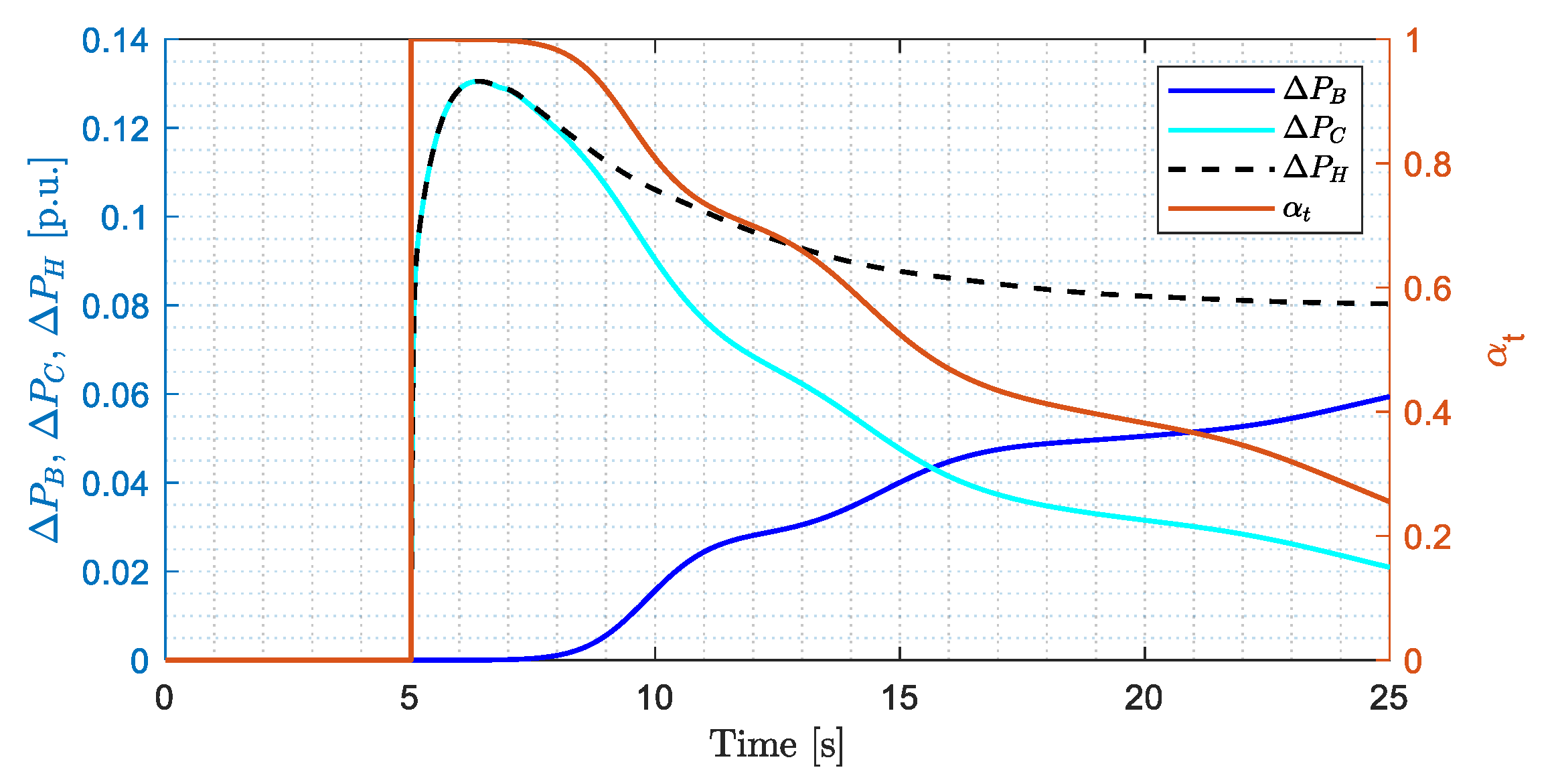
4.1. Inertial Response and Primary Frequency Regulation
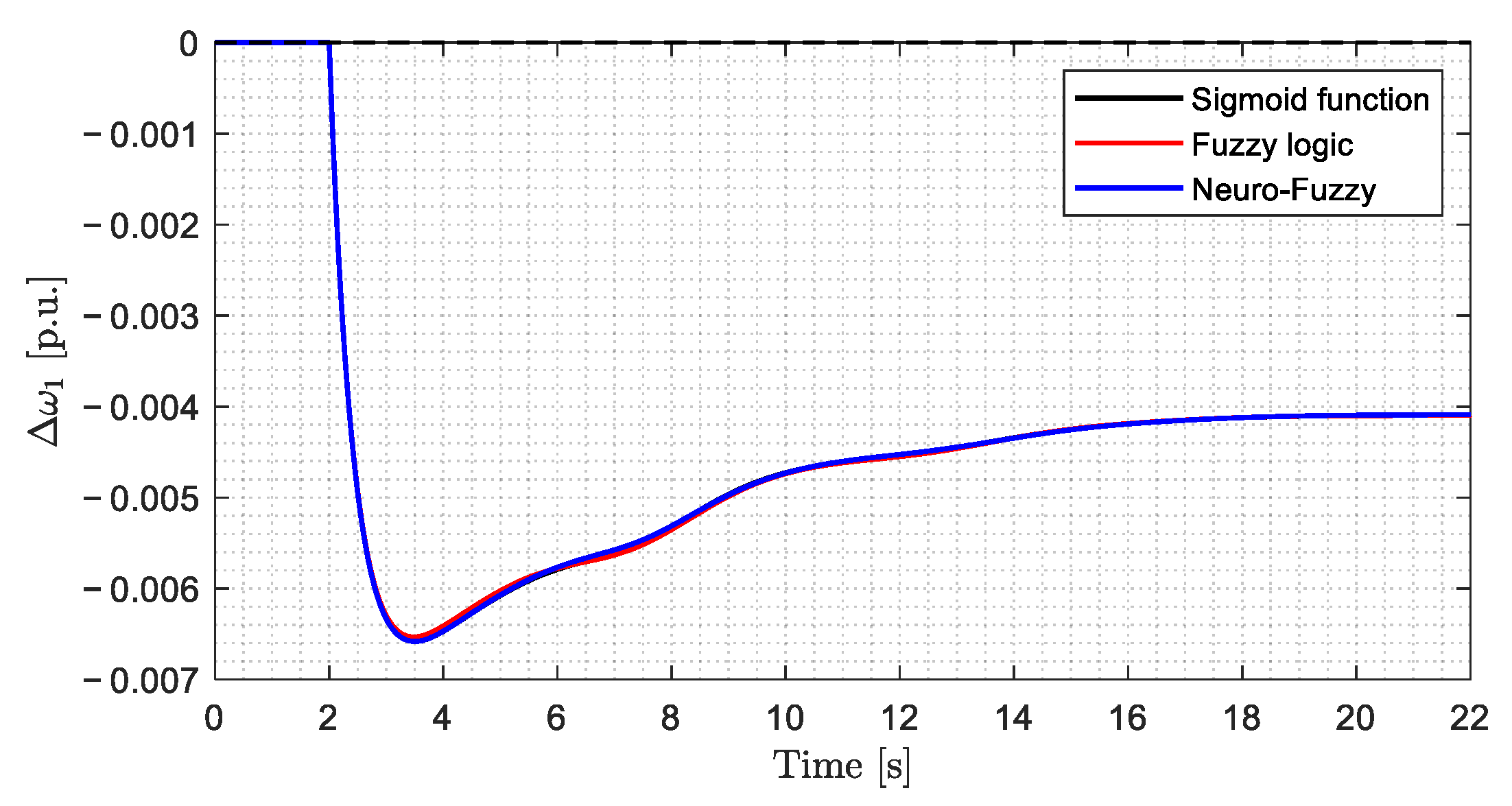
4.2. SOC Control
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| BESS | Battery Energy Storage System |
| CGU | Conventional Generation Unit |
| ESS | Energy Storage System |
| HESS | Hybrid Energy Storage System |
| IAE | Integral of Absolute Error |
| ISE | Integral of Squared Error |
| ITAE | Integral of Time-Weighted Absolute Error |
| ITSE | Integral of Time-Weighted Squared Error |
| PID | Proportional–Integral–Derivative |
| PRER | Percentage of Renewable Energy Replacement |
| ROCOF | Rate of Change of Frequency |
| SC | Supercapacitor |
| SOC | State of Charge |
Appendix A
References
- Zhao, T.; Parisio, A.; Milanovic, J.V. Distributed Control of Battery Energy Storage Systems for Improved Frequency Regulation. IEEE Trans. Power Syst. 2020, 35, 3729–3738. [Google Scholar] [CrossRef]
- Shim, J.W.; Verbic, G.; Zhang, N.; Hur, K. Harmonious Integration of Faster-Acting Energy Storage Systems into Frequency Control Reserves in Power Grid with High Renewable Generation. IEEE Trans. Power Syst. 2018, 33, 6193–6205. [Google Scholar] [CrossRef]
- Cheng, Y.; Azizipanah-Abarghooee, R.; Azizi, S.; Ding, L.; Terzija, V. Smart Frequency Control in Low Inertia Energy Systems Based on Frequency Response Techniques: A Review. Appl. Energy 2020, 279, 115798. [Google Scholar] [CrossRef]
- Ulbig, A.; Borsche, T.S.; Andersson, G. Impact of Low Rotational Inertia on Power System Stability and Operation. IFAC Proc. Vol. 2014, 47, 7290–7297. [Google Scholar] [CrossRef]
- Kebede, A.A.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. A Comprehensive Review of Stationary Energy Storage Devices for Large Scale Renewable Energy Sources Grid Integration. Renew. Sustain. Energy Rev. 2022, 159, 112213. [Google Scholar] [CrossRef]
- Xing, W.; Wang, H.; Lu, L.; Han, X.; Sun, K.; Ouyang, M. An Adaptive Virtual Inertia Control Strategy for Distributed Battery Energy Storage System in Microgrids. Energy 2021, 233, 121155. [Google Scholar] [CrossRef]
- Jufri, F.H.; Jung, J.; Sudiarto, B.; Garniwa, I. Development of Virtual Inertia Control with State-of-Charge Recovery Strategy Using Coordinated Secondary Frequency Control for Optimized Battery Capacity in Isolated Low Inertia Grid. Energies 2023, 16, 5463. [Google Scholar] [CrossRef]
- Varhegyi, G.; Nour, M. Advancing Fast Frequency Response Ancillary Services in Renewable-Heavy Grids: A Global Review of Energy Storage-Based Solutions and Market Dynamics. Energies 2024, 17, 3737. [Google Scholar] [CrossRef]
- IEEE Std 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: New York, NY, USA, 2018.
- European Commission. Commission Regulation (EU) 2016/631 of 14 April 2016 Establishing a Network Code on Requirements for Grid Connection of Generators; Official Journal of the European Union: Brussels, Belgium, 2016. [Google Scholar]
- North American Electric Reliability Corporation. BAL-003-2—Frequency Response and Frequency Bias Setting; North American Electric Reliability Corporation: Atlanta, GA, USA, 2020. [Google Scholar]
- Chatzigeorgiou, N.G.; Theocharides, S.; Makrides, G.; Georghiou, G.E. A Review on Battery Energy Storage Systems: Applications, Developments, and Research Trends of Hybrid Installations in the End-User Sector. J. Energy Storage 2024, 86, 111192. [Google Scholar] [CrossRef]
- Margaris, I.D.; Papathanassiou, S.A.; Hatziargyriou, N.D.; Hansen, A.D.; Sorensen, P. Frequency Control in Autonomous Power Systems with High Wind Power Penetration. IEEE Trans. Sustain. Energy 2012, 3, 189–199. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, W.; Gao, T.; Yan, W.; Zhang, H.; Yan, S.; Wang, X. State-of-the-Art Review on Frequency Response of Wind Power Plants in Power Systems. J. Mod. Power Syst. Clean. Energy 2018, 6, 1–16. [Google Scholar] [CrossRef]
- Tan, Y.; Muttaqi, K.M.; Ciufo, P.; Meegahapola, L.; Guo, X.; Chen, B.; Chen, H. Enhanced Frequency Regulation Using Multilevel Energy Storage in Remote Area Power Supply Systems. IEEE Trans. Power Syst. 2019, 34, 163–170. [Google Scholar] [CrossRef]
- Qian, Y.; Wang, H.; Zhou, M.; Lv, H.; Liu, Y. Frequency Trajectory Planning-Based Frequency Regulation Strategy for Wind Turbines Equipped with Energy Storage System. Chin. J. Electr. Eng. 2022, 8, 52–61. [Google Scholar] [CrossRef]
- Dhundhara, S.; Verma, Y.P. Grid Frequency Enhancement Using Coordinated Action of Wind Unit with Redox Flow Battery in a Deregulated Electricity Market. Int. Trans. Electr. Energy Syst. 2020, 30, 12189. [Google Scholar] [CrossRef]
- Rakhshani, E.; Remon, D.; Mir Cantarellas, A.; Rodriguez, P. Analysis of Derivative Control Based Virtual Inertia in Multi-Area High-Voltage Direct Current Interconnected Power Systems. IET Gener. Transm. Distrib. 2016, 10, 1458–1469. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y. Virtual Inertia Control Application to Enhance Frequency Stability of Interconnected Power Systems with High Renewable Energy Penetration. Energies 2018, 11, 981. [Google Scholar] [CrossRef]
- Turk, A.; Sandelic, M.; Noto, G.; Pillai, J.R.; Chaudhary, S.K. Primary Frequency Regulation Supported by Battery Storage Systems in Power System Dominated by Renewable Energy Sources. J. Eng. 2019, 2019, 4986–4990. [Google Scholar] [CrossRef]
- Fang, J.; Tang, Y.; Li, H.; Li, X. A Battery/Ultracapacitor Hybrid Energy Storage System for Implementing the Power Management of Virtual Synchronous Generators. IEEE Trans. Power Electron. 2018, 33, 2820–2824. [Google Scholar] [CrossRef]
- Akram, U.; Shah, R.; Mithulananthan, N. Hybrid Energy Stoarage System for Frequency Regulation in Microgrids with Source and Load Uncertainties. IET Gener. Transm. Distrib. 2019, 13, 5048–5057. [Google Scholar] [CrossRef]
- Nguyen-Huu, T.A.; Van Nguyen, T.; Hur, K.; Shim, J.W. Coordinated Control of a Hybrid Energy Storage System for Improving the Capability of Frequency Regulation and State-of-Charge Management. Energies 2020, 13, 6304. [Google Scholar] [CrossRef]
- Choi, W.Y.; Kook, K.S.; Yu, G.R. Control Strategy of BESS for Providing Both Virtual Inertia and Primary Frequency Response in the Korean Power System. Energies 2019, 12, 4060. [Google Scholar] [CrossRef]
- Amin, M.R.; Negnevitsky, M.; Franklin, E.; Alam, K.S.; Naderi, S.B. Application of Battery Energy Storage Systems for Primary Frequency Control in Power Systems with High Renewable Energy Penetration. Energies 2021, 14, 1379. [Google Scholar] [CrossRef]
- Wei, N.; Yan, X.; Han, X.; Ma, X.; Cui, J.; Sun, W. Research on Control Strategy of Hybrid Energy Storage System Participating in Primary Frequency Regulation of Power Grid. J. Phys. Conf. Ser. 2023, 2592, 012061. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, Y. Coordinated Control Strategy of a Battery Energy Storage System to Support a Wind Power Plant Providing Multi-Timescale Frequency Ancillary Services. IEEE Trans. Sustain. Energy 2017, 8, 1140–1153. [Google Scholar] [CrossRef]
- Chen, W.; Sun, N.; Ma, Z.; Liu, W.; Dong, H. A Two-Layer Optimization Strategy for Battery Energy Storage Systems to Achieve Primary Frequency Regulation of Power Grid. Energies 2023, 16, 2811. [Google Scholar] [CrossRef]
- Fang, Z.; Shek, J.K.H.; Sun, W. A Review of Grid-Connected Hybrid Energy Storage Systems: Sizing Configurations, Control Strategies, and Future Directions. J. Energy Storage 2025, 118, 116226. [Google Scholar] [CrossRef]
- Kundur, P.S.; Malik, O.P. Power System Stability and Control, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2022; ISBN 9781260473544. [Google Scholar]
- Akram, U.; Khalid, M.; Shafiq, S. An Innovative Hybrid Wind-Solar and Battery-Supercapacitor Microgrid System—Development and Optimization. IEEE Access 2017, 5, 25897–25912. [Google Scholar] [CrossRef]
- Massaro, F.; Musca, R.; Vasile, A.; Zizzo, G. A Simulation Study for Assessing the Impact of Energy Storage Systems for Fast Reserve with Additional Synthetic Inertia Control on the Continental Europe Synchronous Area. Sustain. Energy Technol. Assess. 2022, 53, 102763. [Google Scholar] [CrossRef]
- Tan, Z.; Li, X.; He, L.; Li, Y.; Huang, J. Primary Frequency Control with BESS Considering Adaptive SoC Recovery. Int. J. Electr. Power Energy Syst. 2020, 117, 105588. [Google Scholar] [CrossRef]
- Li, P.; Tan, Z.; Zhou, Y.; Li, C.; Li, R.; Qi, X. Secondary Frequency Regulation Strategy with Fuzzy Logic Method and Self-Adaptive Modification of State of Charge. IEEE Access 2018, 6, 43575–43585. [Google Scholar] [CrossRef]
- Meng, Y.; Li, X.; Liu, X.; Cui, X.; Xu, P.; Li, S. A Control Strategy for Battery Energy Storage Systems Participating in Primary Frequency Control Considering the Disturbance Type. IEEE Access 2021, 9, 102004–102018. [Google Scholar] [CrossRef]
- Roger Jang, J.-S. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Chen, H.; Sha, C.; Jiao, M.; Shao, C.; Gao, S.; Yu, H.; Qin, B. DIA-TSK: A Dynamic Incremental Adaptive Takagi–Sugeno–Kang Fuzzy Classifier. Mathematics 2025, 13, 1054. [Google Scholar] [CrossRef]
- Meng, L.; Zafar, J.; Khadem, S.K.; Collinson, A.; Murchie, K.C.; Coffele, F.; Burt, G.M. Fast Frequency Response from Energy Storage Systems—A Review of Grid Standards, Projects and Technical Issues. IEEE Trans. Smart Grid 2020, 11, 1566–1581. [Google Scholar] [CrossRef]
- IEEE Std 1547.1-2020; IEEE Standard Conformance Test Procedures for Equipment Interconnecting Distributed Energy Resources with Electric Power Systems and Associated Interfaces. IEEE: New York, NY, USA, 2020; pp. 1–282.
- Underwriters Laboratories. Standard for Inverters, Converters, Controllers and Interconnection System Equipment for Use with Distributed Energy Resources (Including Supplement SB). In UL 1741, 3rd ed.; UL LLC: Northbrook, IL, USA, 2021. [Google Scholar]
- Ghaeminezhad, N.; Ouyang, Q.; Wei, J.; Xue, Y.; Wang, Z. Review on State of Charge Estimation Techniques of Lithium-Ion Batteries: A Control-Oriented Approach. J. Energy Storage 2023, 72, 108707. [Google Scholar] [CrossRef]
- Strielkowski, W.; Vlasov, A.; Selivanov, K.; Muraviev, K.; Shakhnov, V. Prospects and Challenges of the Machine Learning and Data-Driven Methods for the Predictive Analysis of Power Systems: A Review. Energies 2023, 16, 4025. [Google Scholar] [CrossRef]
- Naseri, F.; Karimi, S.; Farjah, E.; Schaltz, E. Supercapacitor Management System: A Comprehensive Review of Modeling, Estimation, Balancing, and Protection Techniques. Renew. Sustain. Energy Rev. 2022, 155, 111913. [Google Scholar] [CrossRef]
- El Brouji, E.H.; Briat, O.; Vinassa, J.M.; Bertrand, N.; Woirgard, E. Impact of Calendar Life and Cycling Ageing on Supercapacitor Performance. IEEE Trans. Veh. Technol. 2009, 58, 3917–3929. [Google Scholar] [CrossRef]
- Meng, G.; Chang, Q.; Sun, Y.; Rao, Y.; Zhang, F.; Wu, Y.; Su, L. Energy Storage Auxiliary Frequency Modulation Control Strategy Considering ACE and SOC of Energy Storage. IEEE Access 2021, 9, 26271–26277. [Google Scholar] [CrossRef]
- Deng, X.; Mo, R.; Wang, P.; Chen, J.; Nan, D.; Liu, M. Review of RoCoF Estimation Techniques for Low-Inertia Power Systems. Energies 2023, 16, 3708. [Google Scholar] [CrossRef]
- IEEE Std C37.118.1-2011; IEEE Standard for Synchrophasor Measurements for Power Systems. IEEE: New York, NY, USA, 2011; pp. 1–61.
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; Wiley-IEEE Press: Hoboken, NJ, USA, 2010; ISBN 978-0-470-55156-1. [Google Scholar]
- Hespanha, J.P.; Naghshtabrizi, P.; Xu, Y. A Survey of Recent Results in Networked Control Systems. Proc. IEEE 2007, 95, 138–172. [Google Scholar] [CrossRef]
- Oshnoei, A.; Kheradmandi, M.; Muyeen, S.M. Robust Control Scheme for Distributed Battery Energy Storage Systems in Load Frequency Control. IEEE Trans. Power Syst. 2020, 35, 4781–4791. [Google Scholar] [CrossRef]
- Sharma, M.; Dhundhara, S.; Singh Sran, R. Impact of Hybrid Electrical Energy Storage System on Realistic Deregulated Power System Having Large-Scale Renewable Generation. Sustain. Energy Technol. Assess. 2023, 56, 103025. [Google Scholar] [CrossRef]
- COES-SINAC. Procedimiento Técnico COES-SINAC PR-21: Reserva Rotante para Regulación Primaria de Frecuencia; COES-SINAC: Lima, Perú, 2020. [Google Scholar]
- PHC Servicios Integrados Group S.A.S. Informe 2: Revisión Propuesta Simulación y Conceptualización SSCC; Comisión de Regulación de Energía y Gas (CREG): Bogotá, Colombia, 2022. [Google Scholar]
- Secretaría Nacional de Energía. Resolución de 13 de Julio de 2006, de la Secretaría General de Energía, por la Que se Aprueba el Procedimiento de Operación 1.5 «Establecimiento de la Reserva para la Regulación Frecuencia-Potencia»; Boletín Oficial del Estado: Madrid, España, 2006. [Google Scholar]
- Khan, I.A.; Mokhlis, H.; Mansor, N.N.; Illias, H.A.; Jamilatul Awalin, L.; Wang, L. New Trends and Future Directions in Load Frequency Control and Flexible Power System: A Comprehensive Review. Alex. Eng. J. 2023, 71, 263–308. [Google Scholar] [CrossRef]
- Izci, D.; Ekinci, S.; Çelik, E.; Bajaj, M.; Blazek, V.; Prokop, L. Dynamic Load Frequency Control in Power Systems Using a Hybrid Simulated Annealing Based Quadratic Interpolation Optimizer. Sci. Rep. 2024, 14, 26011. [Google Scholar] [CrossRef]
- Alahakoon, S.; Roy, R.B.; Arachchillage, S.J. Optimizing Load Frequency Control in Standalone Marine Microgrids Using Meta-Heuristic Techniques. Energies 2023, 16, 4846. [Google Scholar] [CrossRef]
- Aghmadi, A.; Mohammed, O.A. Energy Storage Systems: Technologies and High-Power Applications. Batteries 2024, 10, 141. [Google Scholar] [CrossRef]
- Xu, C.; Qiu, W.; Si, L.; Zhang, T.; Li, J.; Chen, G.; Yu, H.; Lu, J.; Lin, Z. Economic Analysis of Li-Ion Battery–Supercapacitor Hybrid Energy Storage System Considering Multitype Frequency Response Benefits in Power Systems. Energies 2023, 16, 6621. [Google Scholar] [CrossRef]
- Diaz, V.S.; Cantane, D.A.; Santos, A.Q.O.; Ando Junior, O.H. Comparative Analysis of Degradation Assessment of Battery Energy Storage Systems in PV Smoothing Application. Energies 2021, 14, 3600. [Google Scholar] [CrossRef]
- Shan, W.; Schwalm, M.; Shan, M. A Design Tool for Battery/Supercapacitor Hybrid Energy Storage Systems Based on the Physical–Electrochemical Degradation Battery Model BaSiS. Energies 2024, 17, 3481. [Google Scholar] [CrossRef]
- Sirimanne, D.C.U.; Kularatna, N.; Arawwawala, N. Electrical Performance of Current Commercial Supercapacitors and Their Future Applications. Electronics 2023, 12, 2465. [Google Scholar] [CrossRef]

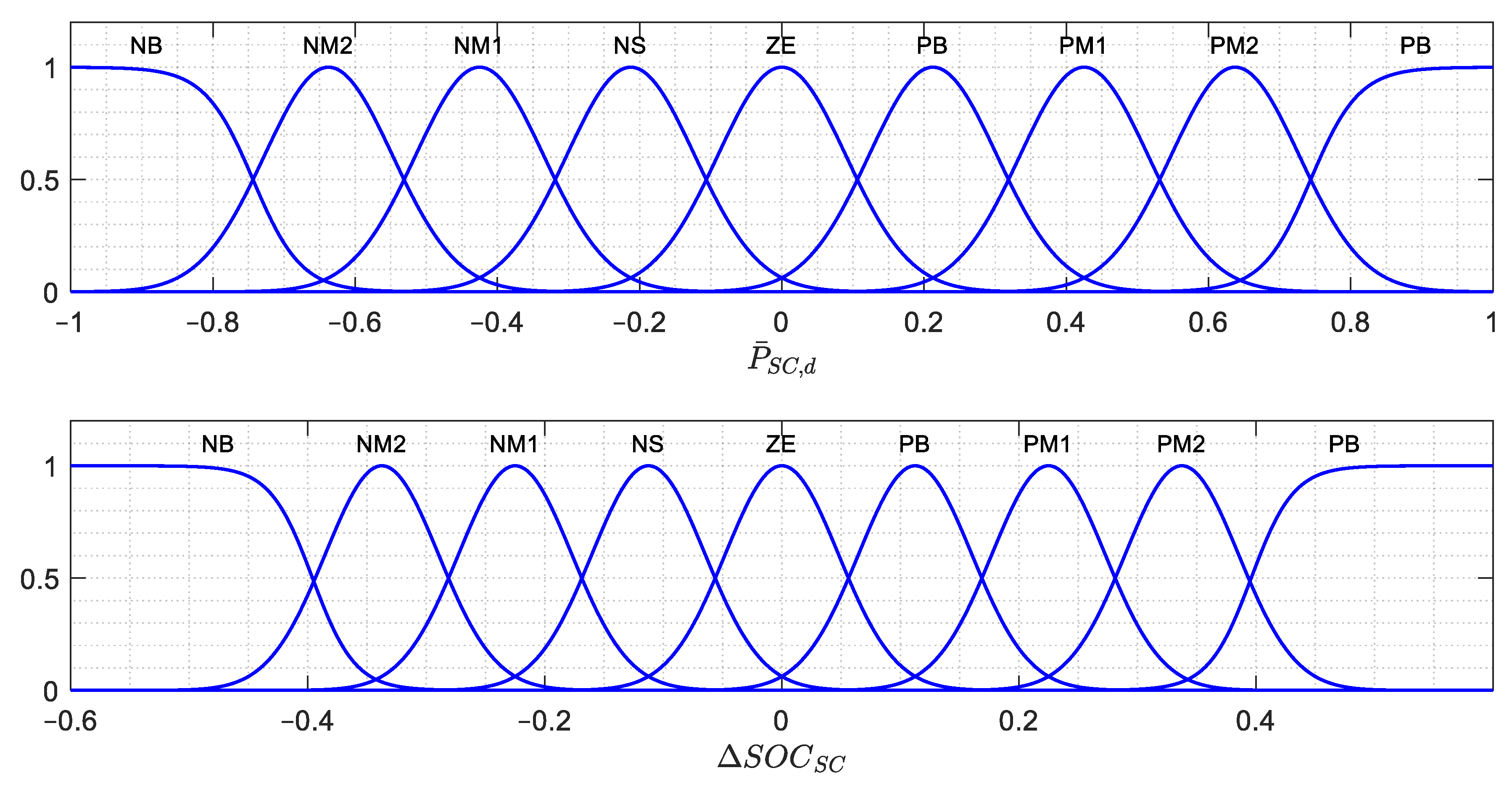








| NB | NM2 | NM1 | NS | ZE | PS | PM1 | PM2 | PB | ||
| PB | NB | NM2 | NM1 | NS | ZE | ZE | ZE | ZE | ZE | |
| PM | NB | NM2 | NM1 | NS | ZE | PS | PM1 | PM2 | PB | |
| PS | NB | NM2 | NM1 | NS | ZE | PS | PM1 | PM2 | PB | |
| ZE | NB | NM2 | NM1 | NS | ZE | PS | PM1 | PM2 | PB | |
| NS | NB | NM2 | NM1 | NS | ZE | PS | PM1 | PM2 | PB | |
| NM | NB | NM2 | NM1 | NS | ZE | PS | PM1 | PM2 | PB | |
| NB | ZE | ZE | ZE | ZE | ZE | PS | PM1 | PM2 | PB | |
| NB | NM2 | NM1 | NS | ZE | PS | PM1 | PM2 | PB | ||
| PB | 0 | 0 | 0 | 0 | 0 | 1.00 | 1.00 | 1.00 | 1.00 | |
| PM2 | 0.25 | 0.33 | 0.50 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| PM1 | 0.50 | 0.67 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| PS | 0.75 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| ZE | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| NS | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.75 | |
| NM1 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.67 | 0.50 | |
| NM2 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.50 | 0.33 | 0.25 | |
| NB | 1.00 | 1.00 | 1.00 | 1.00 | 0 | 0 | 0 | 0 | 0 | |
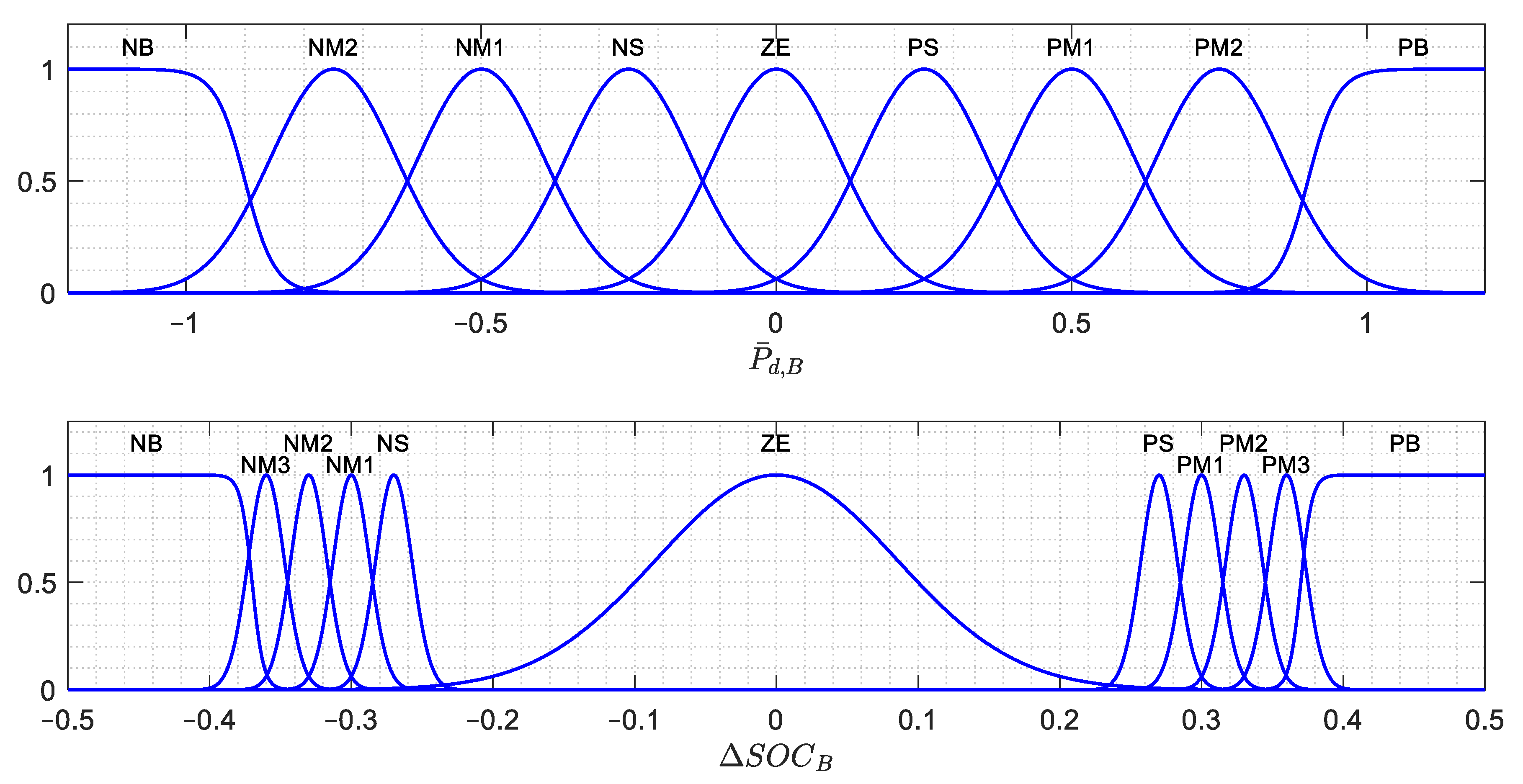
| NB | NM2 | NM1 | NS | ZE | PS | PM1 | PM2 | PB | ||
| PB | 0 | 0 | 0 | 0 | 0 | 1.00 | 1.00 | 1.00 | 1.00 | |
| PM3 | 0.25 | 0.33 | 0.50 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| PM2 | 0.50 | 0.67 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| PM1 | 0.75 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| PS | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| ZE | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| NS | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| NM1 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.75 | |
| NM2 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.67 | 0.50 | |
| NM3 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.50 | 0.33 | 0.25 | |
| NB | 1.00 | 1.00 | 1.00 | 1.00 | 0 | 0 | 0 | 0 | 0 | |
| Parameter | Value (p.u.) | Parameter | Value (p.u.) |
|---|---|---|---|
| 0.5 | 0.3 | ||
| 0.2 | 0.6 | ||
| 0.6 | 0.9 | ||
| 5.0 | 4.0 | ||
| 0.05 | 0.0625 | ||
| 20.6 | 16.9 | ||
| 0.1 | 0.3 | ||
| 0.5 | 0.05 | ||
| 5.0 | 2.0 | ||
| 0.15 | 0.496 | ||
| 0.04 | 12 × 0.0008 |
| Scenario | (p.u.) | PRER (%) |
|---|---|---|
| 1 | 0.5 | 10 |
| 2 | 0.5 | 20 |
| 3 | 0.5 | 40 |
| 4 | 1.0 | 10 |
| 5 | 1.0 | 20 |
| 6 | 1.0 | 40 |
| 7 | 1.5 | 10 |
| 8 | 1.5 | 20 |
| 9 | 1.5 | 40 |
| Scenario | Strategy | ITSE | ISE | ITAE | IAE | Nadir |
|---|---|---|---|---|---|---|
| 1 | Without ESS | 0.00054 | 0.00006 | 0.35336 | 0.03206 | −0.00374 |
| Only BESS | 0.00053 | 0.00005 | 0.35419 | 0.03186 | −0.00299 | |
| SC-VI/BESS-PR | 0.00053 | 0.00005 | 0.35422 | 0.03186 | −0.00299 | |
| Proposed method | 0.00054 | 0.00005 | 0.35595 | 0.03157 | −0.00219 | |
| 2 | Without ESS | 0.00054 | 0.00006 | 0.35314 | 0.03209 | −0.00396 |
| Only BESS | 0.00053 | 0.00005 | 0.35403 | 0.03183 | −0.00298 | |
| SC-VI/BESS-PR | 0.00053 | 0.00005 | 0.35408 | 0.03183 | −0.00298 | |
| Proposed method | 0.00054 | 0.00005 | 0.35578 | 0.03155 | −0.00219 | |
| 3 | Without ESS | 0.00055 | 0.00006 | 0.35269 | 0.03217 | −0.00456 |
| Only BESS | 0.00053 | 0.00005 | 0.35371 | 0.03177 | −0.00296 | |
| SC-VI/BESS-PR | 0.00053 | 0.00005 | 0.35381 | 0.03177 | −0.00296 | |
| Proposed method | 0.00053 | 0.00005 | 0.35546 | 0.03153 | −0.00219 | |
| 4 | Without ESS | 0.00216 | 0.00023 | 0.70673 | 0.06412 | −0.00748 |
| Only BESS | 0.00214 | 0.00021 | 0.70842 | 0.06369 | −0.00594 | |
| SC-VI/BESS-PR | 0.00214 | 0.00021 | 0.70849 | 0.06369 | −0.00595 | |
| Proposed method | 0.00218 | 0.00021 | 0.71759 | 0.06347 | −0.00439 | |
| 5 | Without ESS | 0.00217 | 0.00023 | 0.70628 | 0.06419 | −0.00792 |
| Only BESS | 0.00213 | 0.00021 | 0.70809 | 0.06362 | −0.00590 | |
| SC-VI/BESS-PR | 0.00213 | 0.00021 | 0.70822 | 0.06362 | −0.00593 | |
| Proposed method | 0.00218 | 0.00021 | 0.71725 | 0.06343 | −0.00438 | |
| 6 | Without ESS | 0.00221 | 0.00024 | 0.70538 | 0.06433 | −0.00913 |
| Only BESS | 0.00212 | 0.00021 | 0.70748 | 0.06348 | −0.00581 | |
| SC-VI/BESS-PR | 0.00213 | 0.00021 | 0.70771 | 0.06347 | −0.00587 | |
| Proposed method | 0.00217 | 0.00021 | 0.71658 | 0.06337 | −0.00437 | |
| 7 | Without ESS | 0.00486 | 0.00051 | 1.06009 | 0.09618 | −0.01122 |
| Only BESS | 0.0049 | 0.00052 | 1.06381 | 0.09774 | −0.00977 | |
| SC-VI/BESS-PR | 0.00492 | 0.00053 | 1.06416 | 0.09788 | −0.00986 | |
| Proposed method | 0.0049 | 0.00047 | 1.07488 | 0.09542 | −0.00658 | |
| 8 | Without ESS | 0.00488 | 0.00052 | 1.05941 | 0.09628 | −0.01187 |
| Only BESS | 0.0049 | 0.00052 | 1.06309 | 0.09775 | −0.00993 | |
| SC-VI/BESS-PR | 0.00493 | 0.00053 | 1.06383 | 0.09804 | −0.01011 | |
| Proposed method | 0.00489 | 0.00047 | 1.07441 | 0.09537 | −0.00657 | |
| 9 | Without ESS | 0.00497 | 0.00055 | 1.05807 | 0.0965 | −0.01369 |
| Only BESS | 0.00491 | 0.00054 | 1.06168 | 0.09835 | −0.01085 | |
| SC-VI/BESS-PR | 0.00497 | 0.00055 | 1.06333 | 0.09873 | −0.01100 | |
| Proposed method | 0.00488 | 0.00047 | 1.07348 | 0.09526 | −0.00656 |
| Scenario | Strategy | Only Primary Regulation | Primary and Secondary Regulation | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Without ESS | 0 | 0 | 0 | 0.000173 | 0 | 0.061509 | 0 | 0 | 0.003699 |
| Only BESS | 0.000174 | 0 | 0.000174 | 0 | 0.052071 | 0 | 0.000856 | 0 | 0.002844 | |
| SC-VI/BESS-PR | 0.000173 | 0.000001 | 0.000174 | 0 | 0.051917 | 0 | 0.000856 | 0.000001 | 0.002844 | |
| Proposed method | 0 | 0.000175 | 0.000175 | 0 | 0.043893 | 0 | 0.000484 | 0.000371 | 0.002847 | |
| 2 | Without ESS | 0 | 0 | 0 | 0.000173 | 0 | 0.063515 | 0 | 0 | 0.003699 |
| Only BESS | 0.000174 | 0 | 0.000174 | 0 | 0.05184 | 0 | 0.000857 | 0 | 0.002844 | |
| SC-VI/BESS-PR | 0.000173 | 0.000001 | 0.000174 | 0 | 0.051524 | 0 | 0.000855 | 0.000001 | 0.002844 | |
| Proposed method | 0 | 0.000176 | 0.000176 | 0 | 0.043882 | 0 | 0.000484 | 0.000371 | 0.002847 | |
| 3 | Without ESS | 0 | 0 | 0 | 0.000173 | 0 | 0.068575 | 0 | 0 | 0.003699 |
| Only BESS | 0.000175 | 0 | 0.000175 | 0 | 0.051343 | 0 | 0.000858 | 0 | 0.002843 | |
| SC-VI/BESS-PR | 0.000173 | 0.000003 | 0.000175 | 0 | 0.050657 | 0 | 0.000855 | 0.000003 | 0.002843 | |
| Proposed method | 0 | 0.000177 | 0.000177 | 0 | 0.043976 | 0 | 0.000485 | 0.000371 | 0.002847 | |
| 4 | Without ESS | 0 | 0 | 0 | 0.000346 | 0 | 0.123019 | 0 | 0 | 0.007400 |
| Only BESS | 0.000348 | 0 | 0.000348 | 0 | 0.103678 | 0 | 0.001712 | 0 | 0.005689 | |
| SC-VI/BESS-PR | 0.000346 | 0.000002 | 0.000348 | 0 | 0.103521 | 0 | 0.001711 | 0.000002 | 0.005689 | |
| Proposed method | 0.000041 | 0.000309 | 0.00035 | 0 | 0.087752 | 0 | 0.001327 | 0.000383 | 0.005692 | |
| 5 | Without ESS | 0 | 0 | 0 | 0.000346 | 0 | 0.127031 | 0 | 0 | 0.007399 |
| Only BESS | 0.000349 | 0 | 0.000349 | 0 | 0.103039 | 0 | 0.001713 | 0 | 0.005689 | |
| SC-VI/BESS-PR | 0.000346 | 0.000003 | 0.000349 | 0 | 0.102715 | 0 | 0.001710 | 0.000003 | 0.005689 | |
| Proposed method | 0.000041 | 0.000309 | 0.000351 | 0 | 0.087718 | 0 | 0.001328 | 0.000383 | 0.005692 | |
| 6 | Without ESS | 0 | 0 | 0 | 0.000347 | 0 | 0.137151 | 0 | 0 | 0.007399 |
| Only BESS | 0.000351 | 0 | 0.000351 | 0 | 0.101672 | 0 | 0.001715 | 0 | 0.005688 | |
| SC-VI/BESS-PR | 0.000345 | 0.000006 | 0.000351 | 0 | 0.100955 | 0 | 0.001709 | 0.000006 | 0.005688 | |
| Proposed method | 0.000042 | 0.000310 | 0.000353 | 0 | 0.087883 | 0 | 0.001329 | 0.000384 | 0.005691 | |
| 7 | Without ESS | 0 | 0 | 0 | 0.000519 | 0 | 0.184528 | 0 | 0 | 0.011100 |
| Only BESS | 0.000511 | 0 | 0.000511 | 0 | 0.139059 | 0 | 0.002558 | 0 | 0.008534 | |
| SC-VI/BESS-PR | 0.000508 | 0.000003 | 0.000511 | 0 | 0.13895 | 0 | 0.002554 | 0.000003 | 0.008534 | |
| Proposed method | 0.000188 | 0.000335 | 0.000523 | 0 | 0.131609 | 0 | 0.002082 | 0.000387 | 0.008720 | |
| 8 | Without ESS | 0 | 0 | 0 | 0.000519 | 0 | 0.190546 | 0 | 0 | 0.011099 |
| Only BESS | 0.000513 | 0 | 0.000513 | 0 | 0.138983 | 0 | 0.002558 | 0 | 0.008534 | |
| SC-VI/BESS-PR | 0.000506 | 0.000005 | 0.000511 | 0 | 0.138724 | 0 | 0.002552 | 0.000005 | 0.008534 | |
| Proposed method | 0.000189 | 0.000336 | 0.000525 | 0 | 0.131554 | 0 | 0.002083 | 0.000387 | 0.008719 | |
| 9 | Without ESS | 0 | 0 | 0 | 0.000520 | 0 | 0.205726 | 0 | 0 | 0.011099 |
| Only BESS | 0.000512 | 0 | 0.000512 | 0 | 0.138829 | 0 | 0.002558 | 0 | 0.008532 | |
| SC-VI/BESS-PR | 0.000499 | 0.000012 | 0.00051 | 0 | 0.138038 | 0 | 0.002544 | 0.000012 | 0.008532 | |
| Proposed method | 0.000191 | 0.000336 | 0.000527 | 0 | 0.131798 | 0 | 0.002085 | 0.000387 | 0.008718 | |
| Scenario | Strategy | () | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | Only BESS | 0.191484 | 0.259649 | 1.041423 | 0.017127 | 0.008564 | 0.057213 | 0.046195 |
| SC-VI/BESS-PR | 0.191329 | 0.259329 | 1.038347 | 0.017113 | 0.008557 | 0.053859 | 0.046142 | |
| Proposed method | 0.108202 | 0.138577 | 0.283576 | 0.009678 | 0.004839 | 0.001291 | 0.020387 | |
| 2 | Only BESS | 0.19158 | 0.259738 | 1.036807 | 0.017136 | 0.008568 | 0.06238 | 0.046229 |
| SC-VI/BESS-PR | 0.191272 | 0.259093 | 1.030478 | 0.017108 | 0.008554 | 0.053817 | 0.046122 | |
| Proposed method | 0.108272 | 0.138653 | 0.283712 | 0.009684 | 0.004842 | 0.001292 | 0.020406 | |
| 3 | Only BESS | 0.191769 | 0.259948 | 1.026863 | 0.017153 | 0.008576 | 0.087328 | 0.046294 |
| SC-VI/BESS-PR | 0.191158 | 0.258631 | 1.013137 | 0.017098 | 0.008549 | 0.053703 | 0.046083 | |
| Proposed method | 0.108414 | 0.138805 | 0.28398 | 0.009697 | 0.004849 | 0.001292 | 0.020445 | |
| 4 | Only BESS | 0.382859 | 0.519121 | 2.073568 | 0.034245 | 0.017122 | 0.110901 | 0.12468 |
| SC-VI/BESS-PR | 0.382521 | 0.518463 | 2.070418 | 0.034214 | 0.017107 | 0.105567 | 0.124522 | |
| Proposed method | 0.296698 | 0.376365 | 0.790042 | 0.026538 | 0.013269 | 0.004989 | 0.086522 | |
| 5 | Only BESS | 0.383076 | 0.519319 | 2.060772 | 0.034264 | 0.017132 | 0.119098 | 0.124781 |
| SC-VI/BESS-PR | 0.382404 | 0.517985 | 2.054305 | 0.034204 | 0.017102 | 0.105306 | 0.124468 | |
| Proposed method | 0.296873 | 0.376546 | 0.790402 | 0.026554 | 0.013277 | 0.00499 | 0.086596 | |
| 6 | Only BESS | 0.383502 | 0.519791 | 2.033438 | 0.034302 | 0.017151 | 0.160126 | 0.12498 |
| SC-VI/BESS-PR | 0.382174 | 0.517052 | 2.019091 | 0.034183 | 0.017092 | 0.104729 | 0.124361 | |
| Proposed method | 0.297223 | 0.376906 | 0.79112 | 0.026585 | 0.013293 | 0.004984 | 0.086742 | |
| 7 | Only BESS | 0.57188 | 0.772081 | 2.781172 | 0.051152 | 0.025576 | 0.16507 | 0.221575 |
| SC-VI/BESS-PR | 0.571154 | 0.770576 | 2.778993 | 0.051087 | 0.025543 | 0.156337 | 0.221172 | |
| Proposed method | 0.465532 | 0.599735 | 1.338839 | 0.041639 | 0.02082 | 0.014209 | 0.164996 | |
| 8 | Only BESS | 0.572081 | 0.772095 | 2.77966 | 0.05117 | 0.025585 | 0.176244 | 0.221686 |
| SC-VI/BESS-PR | 0.570581 | 0.76893 | 2.774477 | 0.051035 | 0.025518 | 0.151769 | 0.220854 | |
| Proposed method | 0.465789 | 0.600016 | 1.33894 | 0.041662 | 0.020831 | 0.014254 | 0.165127 | |
| 9 | Only BESS | 0.571862 | 0.770748 | 2.776583 | 0.05115 | 0.025575 | 0.233615 | 0.221565 |
| SC-VI/BESS-PR | 0.568863 | 0.764276 | 2.76076 | 0.050882 | 0.025441 | 0.131557 | 0.219901 | |
| Proposed method | 0.466309 | 0.600586 | 1.339854 | 0.041709 | 0.020854 | 0.014341 | 0.165391 |
| Scenario | Strategy | |||||
|---|---|---|---|---|---|---|
| 2 | Without ESS | 1.5023 | 1.4783 | 1.0000 | 1.0002 | 1.0000 |
| Only BESS | 1.5023 | 1.5238 | 1.0000 | 0.9994 | 0.9898 | |
| SC-VI/BESS-PR | 1.5023 | 1.5238 | 1.0001 | 0.9994 | 0.9949 | |
| Proposed method | 1.5046 | 1.5238 | 1.0079 | 1.0052 | 1.0000 | |
| 8 | Without ESS | 2.4977 | 2.5217 | 1.0000 | 0.9998 | 0.9975 |
| Only BESS | 2.6009 | 2.9524 | 1.0027 | 1.0729 | 1.3661 | |
| SC-VI/BESS-PR | 2.6291 | 3.0476 | 1.0042 | 1.0820 | 1.4098 | |
| Proposed method | 2.4862 | 2.4762 | 0.9959 | 1.0071 | 1.0000 |
| Scenario | Strategy | |||||
|---|---|---|---|---|---|---|
| 4 | Without ESS | 0.0092 | 0.0000 | −0.0013 | 0.0022 | 0.1111 |
| Only BESS | −0.0094 | 0.0000 | −0.0009 | −0.0022 | −0.0136 | |
| SC-VI/BESS-PR | −0.0094 | 0.0000 | −0.0008 | −0.0022 | −0.0067 | |
| Proposed method | 0.0000 | 0.0000 | −0.0009 | −0.0013 | −0.0046 | |
| 6 | Without ESS | 0.0369 | 0.0870 | −0.0025 | 0.0044 | 0.3056 |
| Only BESS | −0.0094 | 0.0000 | −0.0017 | −0.0044 | −0.0305 | |
| SC-VI/BESS-PR | 0.0000 | 0.0000 | −0.0014 | −0.0047 | −0.0202 | |
| Proposed method | −0.0092 | 0.0000 | −0.0019 | −0.0019 | −0.0046 |
| Scenario | (p.u.) | Spinning Reserve for Primary Regulation | |
|---|---|---|---|
| 10 | 0.10 | −0.275 | Yes |
| 11 | 0.10 | −0.275 | No |
| 12 | 0.15 | −0.325 | Yes |
| 13 | 0.15 | −0.325 | No |
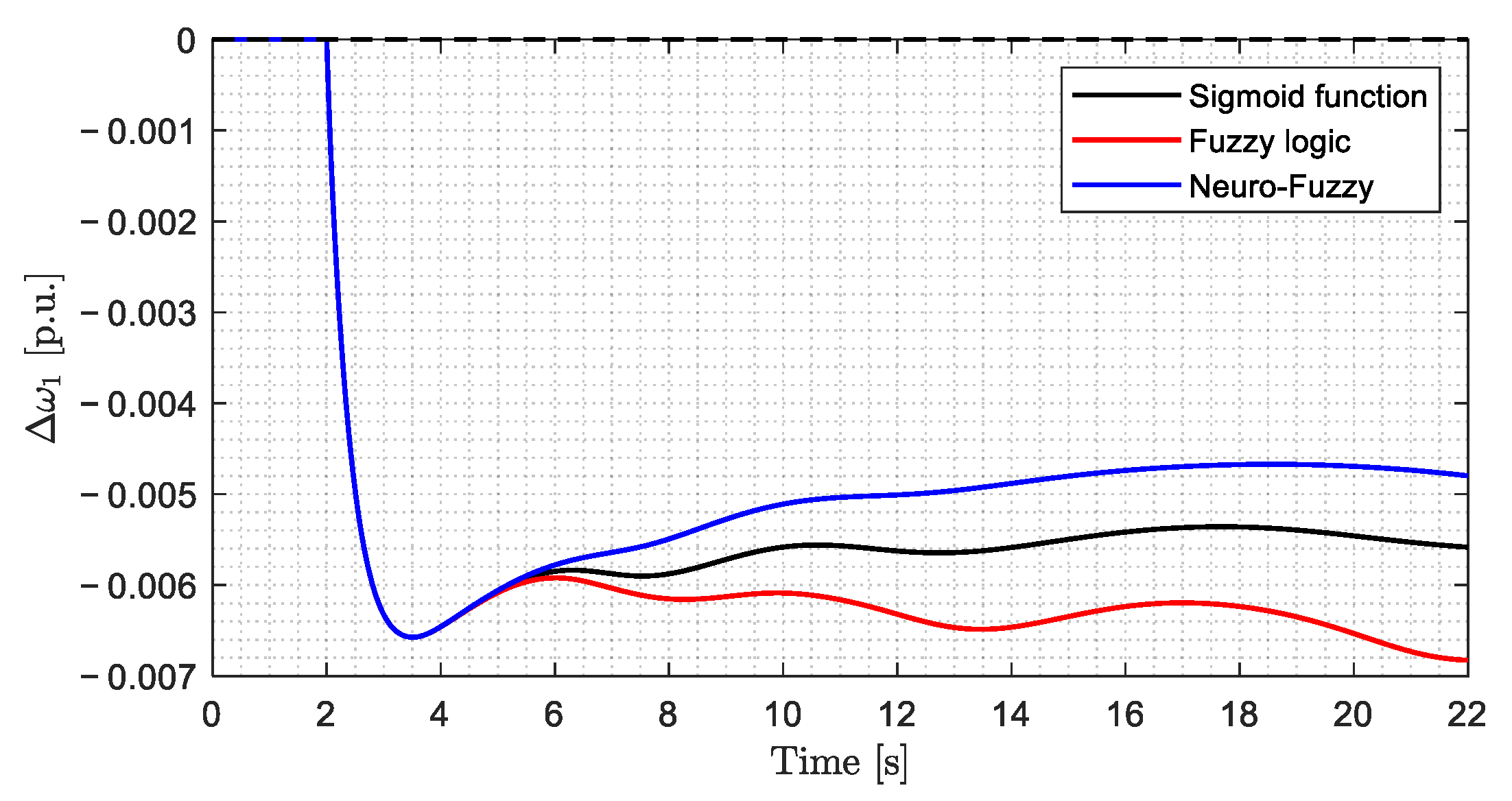
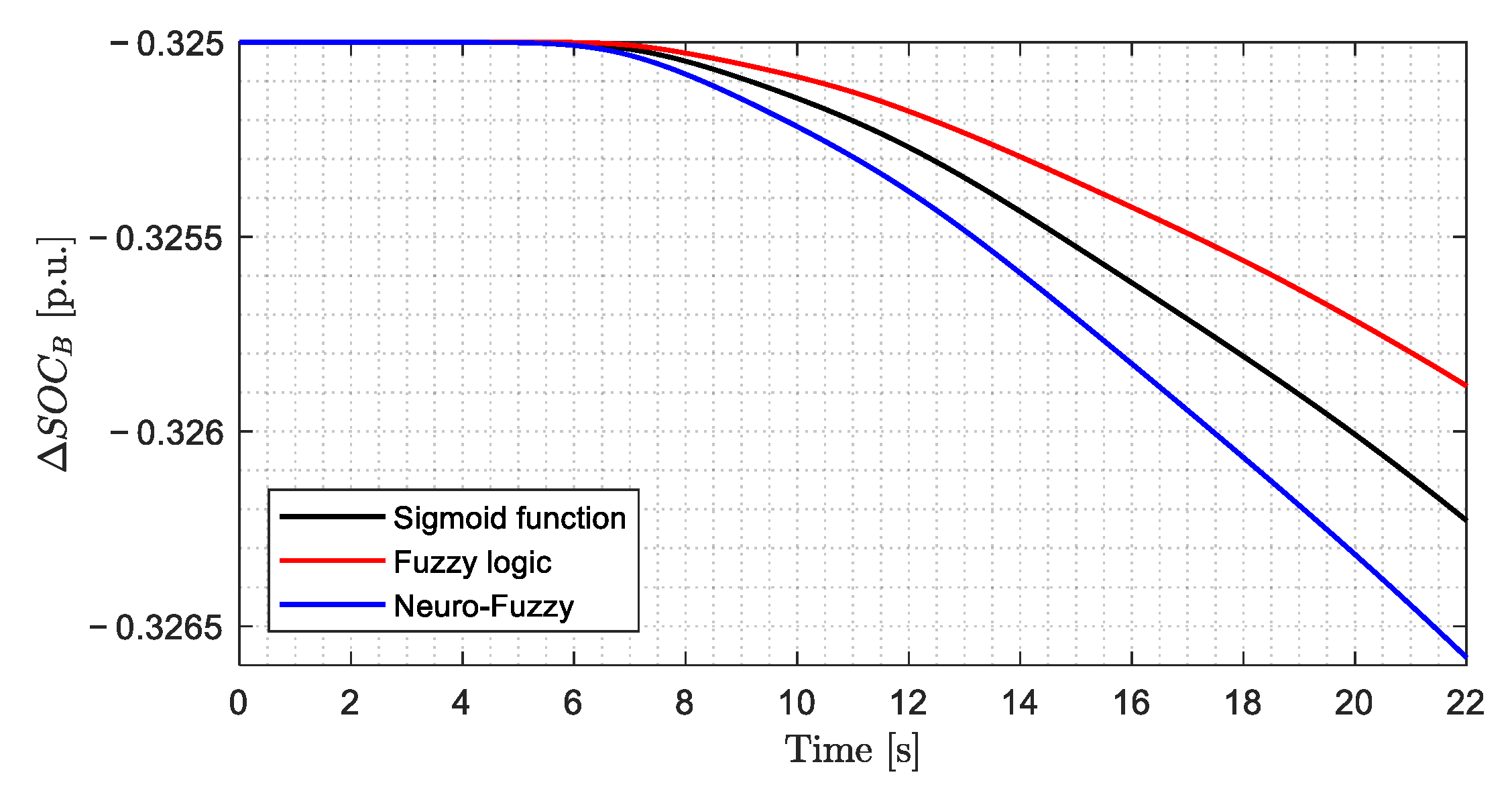
| Scenario | SOC Control Strategy | ITSE | ISE | ITAE | IAE | |
|---|---|---|---|---|---|---|
| 10 | Sigmoid Function | 0.0022 | 0.0002 | 0.7167 | 0.0634 | −0.27539 |
| Fuzzy Logic | 0.0022 | 0.0002 | 0.7163 | 0.0633 | −0.27538 | |
| Neuro-Fuzzy | 0.0022 | 0.0002 | 0.7166 | 0.0634 | −0.27540 | |
| 11 | Sigmoid Function | 0.0022 | 0.0002 | 0.7204 | 0.0636 | −0.27540 |
| Fuzzy Logic | 0.0022 | 0.0002 | 0.7184 | 0.0636 | −0.27538 | |
| Neuro-Fuzzy | 0.0022 | 0.0002 | 0.7166 | 0.0634 | −0.27540 | |
| 12 | Sigmoid Function | 0.0049 | 0.0005 | 1.0752 | 0.0954 | −0.3259 |
| Fuzzy Logic | 0.0049 | 0.0005 | 1.0755 | 0.0954 | −0.32555 | |
| Neuro-Fuzzy | 0.0049 | 0.0005 | 1.0745 | 0.0954 | −0.32636 | |
| 13 | Sigmoid Function | 0.0075 | 0.0006 | 1.3369 | 0.1125 | −0.32625 |
| Fuzzy Logic | 0.0096 | 0.0008 | 1.5138 | 0.1238 | −0.3259 | |
| Neuro-Fuzzy | 0.0059 | 0.0005 | 1.1883 | 0.1027 | −0.32658 |
| Strategy | (MWh) | (MWh) | (kUSD) | (kUSD) | (kUSD) |
|---|---|---|---|---|---|
| Only BESS | 0.992 | 0 | 130.944 | 0 | 130.944 |
| SC-VI/BESS-PR | 0.988 | 0.04 | 130.416 | 105.12 | 235.536 |
| Proposed method | 0.8 | 0.192 | 105.6 | 504.576 | 610.176 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inga Espinoza, C.H.; Palma, M.T. A Coordinated Neuro-Fuzzy Control System for Hybrid Energy Storage Integration: Virtual Inertia and Frequency Support in Low-Inertia Power Systems. Energies 2025, 18, 4728. https://doi.org/10.3390/en18174728
Inga Espinoza CH, Palma MT. A Coordinated Neuro-Fuzzy Control System for Hybrid Energy Storage Integration: Virtual Inertia and Frequency Support in Low-Inertia Power Systems. Energies. 2025; 18(17):4728. https://doi.org/10.3390/en18174728
Chicago/Turabian StyleInga Espinoza, Carlos H., and Modesto T. Palma. 2025. "A Coordinated Neuro-Fuzzy Control System for Hybrid Energy Storage Integration: Virtual Inertia and Frequency Support in Low-Inertia Power Systems" Energies 18, no. 17: 4728. https://doi.org/10.3390/en18174728
APA StyleInga Espinoza, C. H., & Palma, M. T. (2025). A Coordinated Neuro-Fuzzy Control System for Hybrid Energy Storage Integration: Virtual Inertia and Frequency Support in Low-Inertia Power Systems. Energies, 18(17), 4728. https://doi.org/10.3390/en18174728






