Modern Optimization Technologies in Hybrid Renewable Energy Systems: A Systematic Review of Research Gaps and Prospects for Decisions
Abstract
1. Introduction
1.1. The Imperative and Challenge of the Energy Transition
1.2. Risks and Obstacles in High-Penetration HRES
1.3. Geopolitical Dimensions of the HRES Transition
1.4. Motivation and Structure of the Review
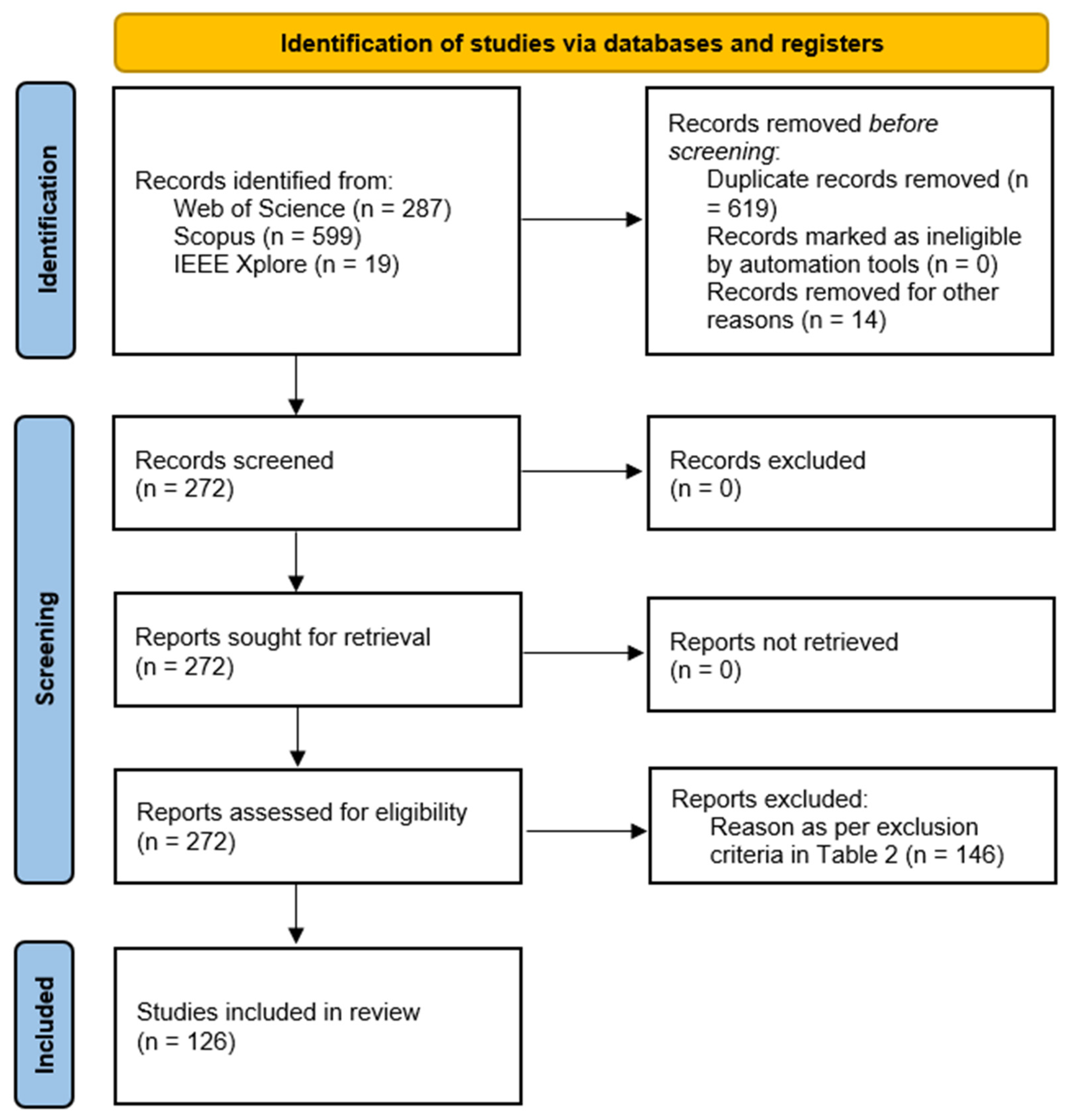
2. Materials and Methods
2.1. Development of the Systematic Search Strategy
- Scopus;
- IEEE Xplore;
- Web of Science.
2.2. Application of Inclusion and Exclusion Criteria
- Title and Abstract Screening: Titles and abstracts of all retrieved records were reviewed to identify potentially relevant studies.
- Full-Text Screening: The full texts of studies deemed potentially relevant after the initial screening were retrieved and assessed against the eligibility criteria.
| Criterion | Inclusion Criteria | Exclusion Criteria |
|---|---|---|
| Study Focus | Studies explicitly addressing “Hybrid Renewable Energy Systems (HRESs) “ or “hybrid energy system” configurations. | Studies that do not address hybrid systems (e.g., only single-energy systems) or do not address electrical energy engineering. |
| Optimization | Must involve the optimization (e.g., sizing, design, energy management, or control strategy) of an HRES. | Studies that describe HRESs but do not involve any optimization process or analysis. |
| Objectives | Must explicitly discuss or analyze optimization objectives (e.g., economic, technical, environmental, social) or performance metrics. | Studies where optimization objectives are not clearly stated or derivable. |
| Methodology | Incorporates an optimization component (e.g., system optimization, performance enhancement, techno-economic analysis related to optimization). | Studies that mention hybrid systems or renewable energy without a clear emphasis on optimization. |
| Energy Source Scope | Must include renewable energy sources (e.g., renewable energy in general, solar, wind, hydro, biomass, hydrogen). | Studies that do not include renewable energy sources as part of the system configuration. |
| Publication Type | Peer-reviewed journal articles and full conference papers presenting substantial original research and methodology. | Editorials, opinions, book reviews, abstracts only, dissertations, theses, patents, non-peer-reviewed reports, or the grey literature (unless specifically part of a supplementary search for context, which was not the primary focus here). Duplicate publications of the same study (the most comprehensive or earliest version was retained). |
| Access | Full text of the study is obtainable. | Full text of the study is unobtainable after reasonable effort. |
| Language | Written in English. | Published in languages other than English. |
| Publication Date | Published between 1 January 2015, and 26 June 2025 (inclusive). | Published before 2015 or after 2025. |
3. Results
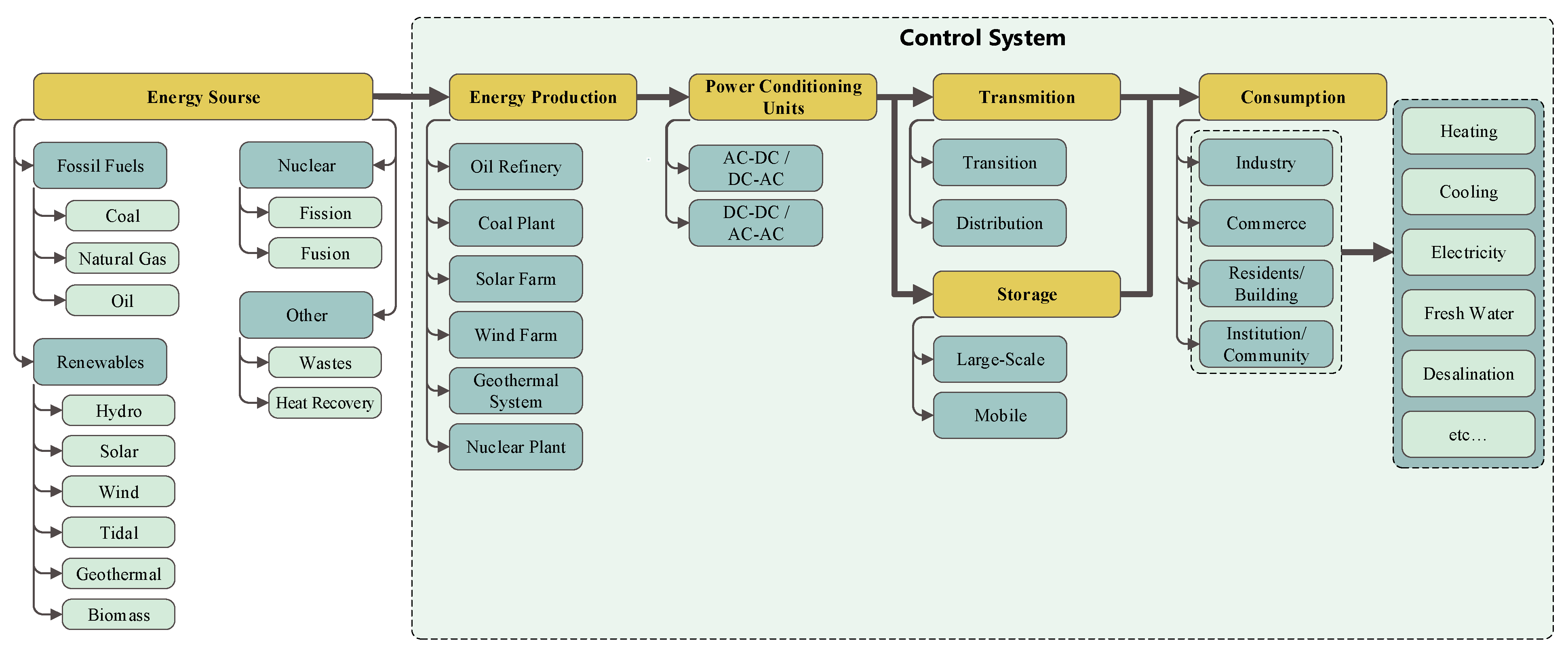
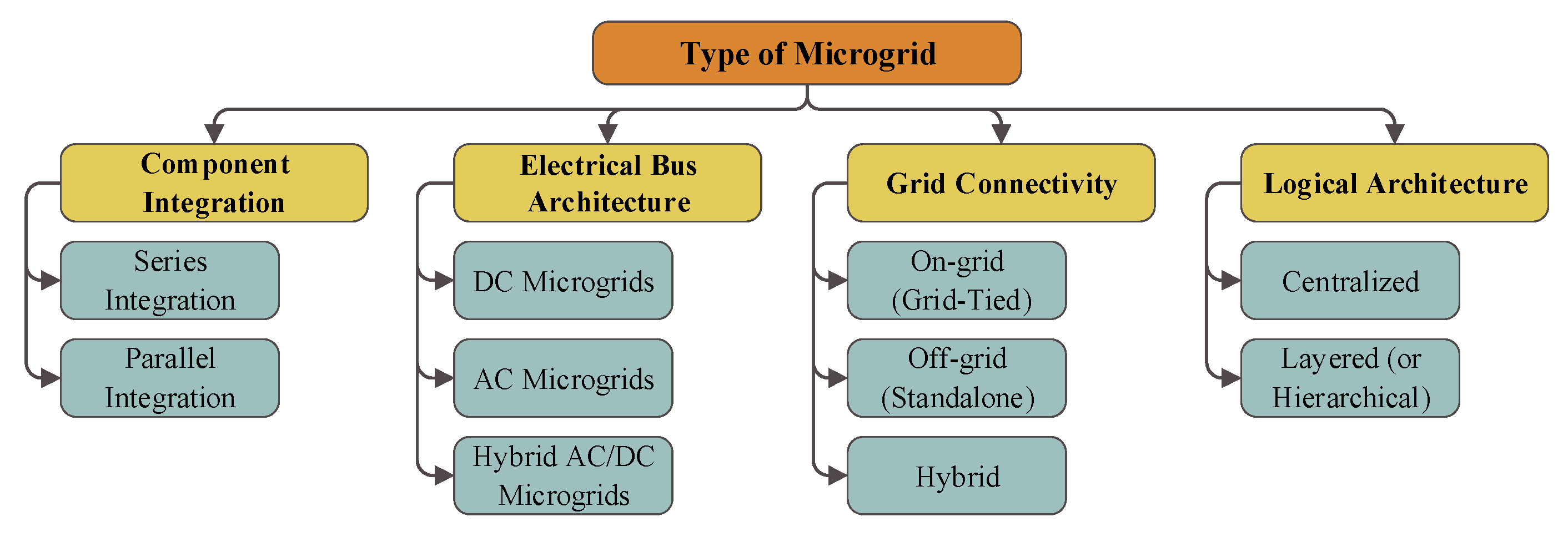
3.1. System Architectures and Topologies
- Energy sources are the primary energy generation units and include renewable energy converters like Solar Photovoltaic (PV) panels, Wind Turbine Generators (WTGs), hydropower turbines, biomass gasifiers, etc., as much as conventional generators. Often, coal, oil, or gas generators are incorporated as reliable power sources or to meet peak load demands when renewable generation and storage are insufficient [20].
- Energy storage systems (ESSs) are crucial for mitigating the effects of renewable resource intermittency and improving system reliability. Batteries, particularly lead-acid and lithium-ion, are the most prevalent form of storage, though fuel cells, hydrogen storage systems, and pumped hydro storage are also utilized or explored [21].
- Power conditioning units (PCUs) include inverters (DC to AC), rectifiers (AC to DC), and converters (DC to DC) that ensure the power output is of suitable quality (voltage and frequency) and is compatible with the load and other system components [22].
- Sophisticated control systems are essential for managing power flow between sources, storage, and loads, optimizing the overall system performance, and ensuring stability and safety [23].
- In a DC-coupled system, sources like PV panels and batteries, which are inherently DC, are connected to a common DC bus. This configuration minimizes conversion stages, potentially increasing efficiency.
- In an AC-coupled system, all sources connect to a common AC bus. This requires each DC source to have its own inverter [34], which may involve more conversion losses but simplifies integration with conventional AC loads and the grid.
- Hybrid AC/DC microgrids combine the benefits of both, featuring parallel AC and DC buses linked by a bidirectional converter [35]. This allows AC and DC sources and loads to connect to their native bus types, optimizing efficiency. While this architecture offers superior flexibility, it introduces significant planning and control challenges, such as managing the non-convex efficiency of the bidirectional converter (BdC) and handling renewable energy uncertainty [31]. Research developing advanced planning frameworks, such as the tri-level BdC-based planning model, is critical to address these complexities and unlock the full potential of this superior topology [36].
3.2. Mathematical Problem Formulation
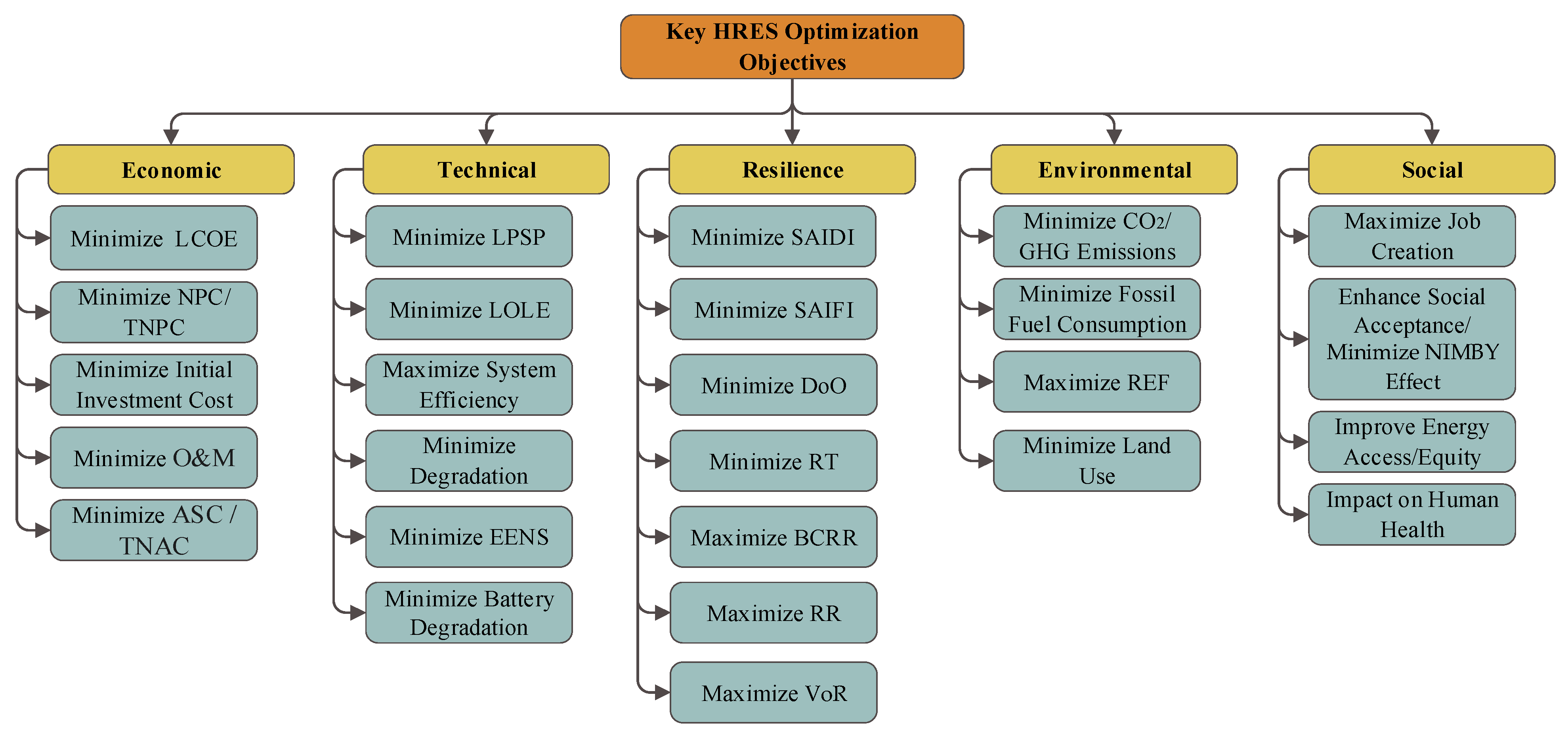
3.3. The Objective Space: A Taxonomy of Performance Criteria
| Specific Objective | Typical Mathematical Formulation | Variable Definitions | Definition/ Calculation Basis | Interpretation | Data Requirements | Common Metrics Used | Influencing Factors | Example References |
|---|---|---|---|---|---|---|---|---|
| Economic | ||||||||
| Minimize Levelized Cost of Energy (LCOE) | It: Investment expenditures in year t; Mt: Operations and maintenance expenditures in year t; Ft: Fuel expenditures in year t; Et: Energy generation in year t; r: Discount rate; T: Project lifetime in years. | Discounted sum of lifecycle costs (capital, O&M, fuel) divided by the discounted sum of energy produced over the system’s lifetime. It represents the minimum price at which energy must be sold for a project to break even (NPV = 0). | A lower LCOE indicates a more cost-effective generation technology. It is a standard metric for comparing different power generation options on a consistent per-unit-of-energy basis. However, it does not capture the economic value of a technology to the system (e.g., dispatchability, flexibility). | Annual capital expenditures, O&M costs, fuel costs, annual energy output, discount rate, and technology lifetime. | USD/kWh, EUR/kWh | Geopolitical Supply Chain Risk: Volatility in critical mineral prices (Li, Co, etc.) due to trade policy or conflict directly impacts component CAPEX. Social Acceptance Costs: Project delays, legal challenges, or required design modifications due to local opposition (NIMBY) increase overall project costs. | [58] | |
| Minimize Net Present Cost (NPC/TNPC) | Ct: Total costs in year t (capital, replacement, O&M, fuel, etc.); Rt: Total revenues in year t (salvage, grid sales); r: Real discount rate; T: Project lifetime in years. | The present value of all costs a system incurs over its lifetime, minus the present value of all revenues it earns over its lifetime. It is the primary economic output in models like HOMER for ranking system configurations. | A lower NPC indicates a more economically favorable project over its entire lifecycle. Unlike LCOE, it provides an absolute monetary value rather than a per-unit-energy cost, making it useful for comparing projects with different outputs or revenue streams. | Detailed annual cash flows for all costs (capital, replacement, O&M, fuel, grid purchases) and revenues (salvage, grid sales), discount rate, and project lifetime. | USD, EUR | Assumed future energy prices and revenues; replacement schedules and salvage values; discount rate and inflation; operation profiles and fuel use; regulatory/policy risk; project scale and modularity; contract structures (PPA). | [59] | |
| Minimize Initial Investment Cost | CAPEX: Capital expenditures. Components include civil/structural works, mechanical/electrical equipment, engineering, permitting, and owner’s costs. | The total “overnight” cost to construct a power plant, excluding financing costs. It encompasses all direct and indirect costs required to bring a project to commercial operation. | A direct measure of the upfront capital barrier for a project. Projects with high initial costs may face financing challenges, even if their lifecycle costs (LCOE) are low. It is a critical input for financial modeling and risk assessment. | Detailed cost breakdown for all equipment, materials, labor, engineering, legal fees, land acquisition, and site preparation. | USD, EUR | Economies of Scale/Learning Curves: Costs for emerging technologies like SMRs or green hydrogen are expected to decrease with wider deployment. Supply Chain Diversity: Sourcing components from multiple regions may increase upfront costs but reduces long-term risk of price shocks. | [60] | |
| Minimize Operation and Maintenance (O&M) | O&MFixed,i: Annual fixed costs for component i (USD/kW-yr); O&MVariable,i: Variable costs for component i (USD/kWh). | The sum of all costs associated with operating and maintaining system components. This includes fixed costs (e.g., staff salaries) and variable costs (e.g., consumables, hourly maintenance for generators). | Lower O&M costs reduce the ongoing financial burden of a project and improve its long-term profitability. O&M can represent 20–30% of a project’s LCOE, making its accurate estimation crucial. | Component-specific fixed O&M costs (USD/kW-yr), variable O&M costs (USD/kWh), generator operating hours, and scheduled maintenance plans. | USD/year, EUR/year | Technology maturity and reliability; remoteness and logistics; maintenance strategy (preventive/CBM); local skill base and vendor network; operating regime (cycling intensity, V2G); warranty terms and spare-part lead times. | [61] | |
| Minimize Annual System Cost (ASC)/Total Net Annual Cost (TNAC) | CNPC,tot: Total Net Present Cost; CRF: Capital Recovery Factor; i: Real discount rate; Rproj: Project lifetime in years. | The annualized value of the Total Net Present Cost (NPC). It converts the total lifecycle cost into an equivalent uniform annual cost, facilitating budgeting and comparison with annual revenues or savings. | The annualized value of the Total Net Present Cost (NPC). It converts the total lifecycle cost into an equivalent uniform annual cost, facilitating budgeting and comparison with annual revenues or savings. | Total Net Present Cost (NPC), real discount rate, and project lifetime. | USD/year, EUR/year | Discount rate and financial structure; lifetime and escalation assumptions; capacity factor and utilization; large one-off replacements timing; inflation and currency stability. | [62] | |
| Technical | ||||||||
| Minimize Loss of Power Supply Probability (LPSP) | LPS(t) = PL(t)− PGen,avail(t) if PL > PGen,avail, else 0; PL(t): Load power at time t; PGen,avail(t): Available generation at time t; Δt: Duration of time step (e.g., 1 h); T: Total time period. | The probability that the system’s power supply will be unable to meet the load demand. It is the ratio of the total energy deficit over a period to the total energy demanded in that period, measuring the frequency of failure. | A lower LPSP indicates higher system reliability. It quantifies the risk of supply shortfalls but does not describe their duration or magnitude. A system can have a high LPSP from many small, brief failures. | Time-series load and generation data. | % | Firm, Low-Carbon Generation: Integration of dispatchable sources like SMRs or geothermal provides inertia and firm capacity, directly improving reliability and reducing reliance on intermittent VREs. Advanced Storage: Deployment of long-duration storage (e.g., hydrogen) is critical for managing seasonal VRE variability. | [63] | |
| Minimize Loss of Load Expectation (LOLE) | I: Indicator function (1 if true, 0 otherwise); PL(t): Load power at time t; PGen,avail(t): Available generation at time t; Δt: Duration of time step (e.g., 1 h); T: Total time period. | The expected number of hours or days per year that the available generation capacity is insufficient to meet the electricity demand. A common reliability target is the “1 day in 10 years” criterion (LOLE of 2.4 h/year). | LOLE measures the expected duration of supply inadequacy, providing more information than LPSP. It is a primary metric used by system operators to assess generation adequacy but does not capture the magnitude of the shortfall. | Probabilistic data on generator outages (forced outage rates), installed capacity of all units, and a time-series load duration curve. | hours/year, days/year | Reserve margin and redundancy; forced outage rates; maintenance planning; extreme-event tails (multi-day low-resource events); geographic diversification of resources; interconnector reliability. | [64] | |
| Minimize Expected Energy Not Supplied (EENS) | PL(t): Load power at time t; PGen,avail(t): Available generation at time t; Δt: Duration of time step (e.g., 1 h); T: Total time period. The sum is over all time steps t where load exceeds available generation. | The total amount of energy (e.g., MWh) that is expected to be unserved over a given period due to insufficient generation capacity. It measures the magnitude of supply failures. | EENS quantifies the severity of reliability failures. A low LOLE with a high EENS indicates rare but catastrophic events. It is a key metric in European resource adequacy assessments and is crucial for understanding the societal impact of outages. | Time-series load and available generation data, including outage probabilities. | Wh/year, MWh/year, GWh/year | Duration and magnitude of shortages; correlation of renewable deficits; storage energy duration and dispatch policy; repair and recovery speed; interconnection import limits. | [65] | |
| Minimize Battery Degradation | CapAvailable: Currently available battery capacity; CapNominal: Initial nominal capacity. Degradation is modeled via functions of DOD, throughput, temperature, etc. | The irreversible loss of battery performance (capacity and power) over time and with use. It is modeled using cycle counting, depth-of-discharge (DOD) analysis, or complex electrochemical functions to estimate the cost of wear. | Quantifies the physical wear on the battery, which directly impacts its lifetime and replacement costs. Optimizing battery operation to minimize degradation is crucial for the long-term economic viability of energy storage projects. | Battery charge/discharge profile (current, SOC), depth-of-discharge per cycle, operating temperature, and manufacturer degradation data/curves. | % SOC loss/year, cost (USD) | Cycle depth and frequency (DoD, cycles/day); charge/discharge C-rates; thermal management and ambient temperature; SOC operating window; BMS algorithm sophistication; cell chemistry and manufacturing variance; regularity of deep cycles (V2G). | [66] | |
| Maximize System Efficiency | Eout: Useful energy output (e.g., kWh); Ein: Total energy input (e.g., kWh of fuel energy). | The ratio of useful energy or power output from a system to the total energy or power input. Losses are primarily due to heat, friction, and electrical resistance. | A fundamental measure of performance. Higher efficiency means less wasted energy, which translates directly to lower fuel consumption (for fossil plants) and better utilization of the resource (for renewables), ultimately reducing operating costs and environmental impact. | Measured input power/energy and output power/energy under consistent operating conditions. For thermal plants, this requires fuel input data (e.g., in Btu) and electricity output (in kWh). | % | Number/conversion stages (DC–AC–DC losses); component partial-load performance; power-electronics efficiency curves; auxiliary/parasitic loads; heat recovery opportunities; maintenance and fouling. | [67] | |
| Environmental | ||||||||
| Minimize CO2/GHG Emissions | Fuel Consumption: Amount of fuel combusted (e.g., 103 tons); NCV: Net Calorific Value of fuel (e.g., TJ/103 tons); EFCO2: Default CO2/GHG emission factor (e.g., kg CO2,GHG/TJ) | Based on IPCC guidelines, emissions are calculated by multiplying fuel consumption data by fuel-specific emission factors. Tiers 2 and 3 use more detailed, country- or technology-specific factors. | Quantifies the climate change impact of the energy system. Minimizing emissions is a primary goal of the energy transition and is often enforced through policy constraints (e.g., emissions caps or carbon taxes). Measures “greenness”. | Fuel consumption data by type, Net Calorific Values (NCVs) for each fuel, and IPCC or country-specific emission factors. | kg/year, tons/year, kg CO2eq/kWh | Lifecycle Emissions: Moving beyond operational emissions to include the carbon footprint of manufacturing and transporting components (e.g., from geopolitically distant supply chains). | [68] | |
| Minimize Fossil Fuel Consumption | Egen,i: Electricity generated by fossil plant i; ηi: Net efficiency of fossil plant i. | The total amount of primary fossil energy (e.g., coal, natural gas, oil) consumed to produce electricity and/or heat. It can be calculated from the energy output and the conversion efficiency of the power plants. | A direct measure of reliance on finite, carbon-emitting resources. This objective is closely linked to minimizing CO2 emissions and maximizing the renewable fraction. It is a key input for energy security and supply chain analyses. | Annual electricity generation from each fossil fuel plant and the corresponding plant efficiencies (or heat rates). Alternatively, direct fuel purchase and consumption data from utilities. | L/year, kWh/year, tons/year, MMBtu/year | Dispatch priorities and EMS rules; availability of low-carbon alternatives (hydrogen, biomass); storage and demand flexibility; fuel supply reliability and price; peaker vs. baseload operation. | [69] | |
| Maximize Renewable Fraction (REF) | ERen,i: Renewable energy delivered to the load in interval i; ELoad,i: Total energy consumed by the load in interval i; τ: The total period of analysis (e.g., one year) | Percentage of load met by renewable sources. It is the ratio of total renewable energy supplied to the total energy consumed by the load over a specific period. | A primary measure of a system’s “greenness” or progress toward decarbonization goals. A higher REF indicates greater reliance on renewables and is often a central policy target. | Annual renewable energy generation and load demand. | % | Curtailment Limits: High REF is practically limited by grid stability and the need to curtail excess generation; this can only be overcome with massive storage or flexible demand. | [62] | |
| Minimize Land Use | LUIE | LUIE: Land Use Intensity of Energy Ai: Area per unit of component i enclosed by the project boundary (direct + indirect) (e.g., m2, hectares); Ei: Annual energy generation of component i (e.g., GWh/y). | Quantifies the spatial footprint of an energy technology. Can be measured as total area (the entire site boundary) or direct area (land physically occupied by infrastructure). The metric is typically normalized by annual energy generation. | A critical sustainability metric, especially for land-intensive renewables like solar and biomass. High land use can lead to conflicts with agriculture, conservation, and other land uses. Minimizing land use is important for social acceptance and ecological preservation. | Project boundary data (total area) from site plans or satellite imagery; specifications of land occupied by all infrastructure (direct area); and annual energy generation data. | (m2, hectares)/GWh | Technology Choice: Land-use intensity varies dramatically between technologies (e.g., compact SMRs vs. sprawling solar farms), creating a key trade-off. | [60] |
| Social | ||||||||
| Maximize Job Creation | 1. Calculated via Input-Output models like JEDI; 2. | Jobsdirect: On-site jobs for construction and O&M; Jobsindirect: Jobs in the supply chain (e.g., manufacturing); Jobsinduced: Jobs created by the spending of direct and indirect workers. | Estimated using economic input-output models, such as the Jobs and Economic Development Impacts (JEDI) model, which uses economic multipliers to quantify the ripple effect of project spending throughout the local and state economy. | Measures the positive economic impact of an energy project on employment. It is a key metric for policymakers seeking to justify public support for energy investments and ensure a “just transition” by creating local economic opportunities. | Project cost data (CAPEX, O&M), local content share (percentage of spending within the region), and regional economic multipliers from a model like IMPLAN or REMI. | Number of jobs (direct, indirect, induced, FTE, Full-Time Equivalent) | Local Content Requirements: Policies favoring local manufacturing and labor can be an explicit objective, potentially trading off against pure economic efficiency. | [60] |
| Enhance Social Acceptance/ Minimize not-in-my-backyard (NIMBY) Effect | Not typically formulated mathematically. Measured via qualitative and survey-based methods. | N/A | Assessed through stakeholder engagement, public surveys, analysis of media coverage, and tracking of project support or opposition. Key determinants include perceived fairness of the process, distribution of costs and benefits, and trust in developers and decision-makers. | A critical, often decisive, factor for project success. Low social acceptance can lead to significant project delays, increased costs, or outright cancellation. Enhancing acceptance requires transparent communication, community engagement, and addressing local concerns. | Survey data on public attitudes, records of public meetings, analysis of local media, case study analysis of similar projects, and stakeholder interviews. | Qualitative scales, survey data, adoption rates | Procedural and Distributive Justice: Acceptance is driven by fair, transparent planning processes and equitable distribution of benefits (e.g., community benefit funds) and burdens (e.g., visual/noise impact). Quantification: Can be modeled as a constraint (e.g., setback distances) or a cost function representing economic impact of delays or reduced property values. | [70] |
| Improve Energy Access/Equity | 1. Access: % of population with electricity access. → max 2. Affordability: | Population with access: Number of people with a new or improved electricity connection. Energy Burden: A measure of affordability | Measured using national statistics and household surveys. The World Bank tracks access rates globally. Equity frameworks also assess the distribution of benefits and burdens (e.g., pollution, costs, jobs) across different demographic groups, particularly low-income and marginalized communities. | Measures progress towards universal, affordable, and just energy services (UN SDG7). High energy burden indicates affordability challenges for low-income households. Equity analysis ensures the benefits of the energy transition are shared fairly and historical injustices are not perpetuated. | National census data, household income and expenditure surveys, utility connection data, and demographic data for distributional analysis. | % population with access, reliability for communities | Tariff design and subsidies; connection cost and financing options; population density and remoteness; targeted programs for vulnerable groups; grid extension vs. distributed solutions trade-offs. | [71,72] |
| Minimize Negative Impact on Human Health | DALY: Disability-Adjusted Life Years; YLL: Years of Life Lost (due to premature mortality); YLD: Years Lived with Disability; ΔPM2.5: Change in ambient concentration of fine particulate matter (PM2.5), measured in micrograms per cubic meter (µg/m3); βDALY: Health impact coefficient linking PM2.5 exposure to disease burden. DALYs per person per year per µg/m3 | Quantified by estimating population exposure to pollutants (e.g., PM2.5 from power plants) and applying dose-response functions to calculate the resulting health burden. This burden is measured in Disability-Adjusted Life Years (DALYs), a metric developed by the WHO that combines mortality and morbidity into a single value. The DALY scale is between 0 and 1, where 0 implies perfect health while 1 equals death. | Translates environmental pollution into a standardized measure of human suffering and lost life. It allows for the comparison of health impacts across different diseases and risk factors, providing a powerful tool for cost–benefit analysis of pollution control measures and clean energy deployment. | Power plant emissions data (e.g., tons of PM2.5/year), atmospheric dispersion models, population density data, and epidemiological models linking pollutant exposure to specific diseases and their corresponding DALY weights. | Reduction in health issues, DALYs | Proximity to population centers; emissions control tech; atmospheric dispersion and topography; baseline health vulnerability; cumulative exposures and socio-economic factors. | [73] | |
| Resilience | ||||||||
| Minimize System Average Interruption Duration Index (SAIDI) | ri: Restoration time, minutes; Ni: Total number of customers interrupted; NT: Total number of customers served. | An IEEE standard reliability index that measures the average outage duration (in minutes or hours) experienced by a customer over a year. It is a backward-looking metric of distribution system performance. | SAIDI indicates the average time a customer is without power. A lower SAIDI signifies better reliability and faster restoration times. It is used by utilities and regulators to track performance and motivate investments in grid reliability. | Utility outage management system data, including the start time, end time, and number of customers affected for every sustained interruption. | minutes/customer/year, hours/customer/year | Network topology and redundancy; asset condition and predictive maintenance; vegetation/right-of-way management; automation and remote switching; mutual aid and spare parts staging; weather/climate severity and trends. | [3] | |
| Minimize System Average Interruption Frequency Index (SAIFI) | Ni: Total number of customers interrupted; NT: Total number of customers served. | An IEEE standard reliability index that measures the average number of sustained interruptions experienced by a customer over a year. It is a backward-looking metric of distribution system performance. | SAIFI indicates how often the average customer experiences an outage. A lower SAIFI signifies a more reliable system with fewer failures. Paired with SAIDI, it provides a comprehensive view of historical reliability. | Utility outage management system data, including the number of customers affected for every sustained interruption. | interruptions/customer/year | Protection coordination and settings; equipment aging and failure rates; external exposure (overhead systems); vegetation and wildlife interactions; grid automation and sectionalizing. | [3] | |
| Minimize Duration of Outage (DoO) | Trestoration: Time when power is fully or mostly restored; Tdisruption_start t: Time when the outage-causing event begins | The total time from the start of a disruptive event until power is restored to affected customers. The duration can vary significantly from minutes to weeks depending on the cause and scale of the damage (e.g., equipment failure vs. major hurricane). | A direct measure of the time customers are without power. It is a primary indicator of system resilience from the public’s perspective. Shorter durations indicate a more resilient system capable of rapid recovery. | Historical outage data from utilities (e.g., start time, end time, cause, number of customers affected) for specific events. | minutes, hours, days | Emergency spare availability and logistics chains; prepositioned crews and materials; interagency permits and coordination in disasters; redundancy and islanding (microgrids); access constraints (infrastructure damage). | [74] | |
| Minimize Recovery Time (RT) | Trestore_level: Time when a predefined service level is restored; Tdisruption_start: Time when the disruption begins. | Time from start of disruption until restoration of predefined service level. This is a more formal version of DoO, where recovery is tied to a specific, measurable service target (e.g., 95% of customers restored). | Measures agility and speed of recovery. It provides a quantifiable target for restoration efforts and allows for performance tracking against resilience goals. | Simulation of system response post-event, requiring models of damage assessment, crew dispatch, and repair processes. | hours, days | Decentralization: Systems with islandable microgrids can restore power to critical loads much faster than waiting for centralized grid repair after a major event (e.g., natural disaster, cyberattack). | ||
| Maximize Value of Resilience (VoR) | Cdamage, no res, Cdamage, res): outage costs—Monetized damages from an outage (e.g., using Value of Lost Load, VoLL); pe: event probability. | Monetized benefit = Difference in outage costs with vs. without resilient system. It quantifies the economic benefit of a resilience investment by calculating the avoided damages during an outage. | Translates resilience into financial terms for cost–benefit analysis. This allows for the comparison of resilience investments with other projects on a financial basis, helping to justify expenditures on hardening or recovery capabilities. | Customer damage functions, outage probabilities. Value of Lost Load (VoLL) data for different customer types and outage durations, and event probability data. | USD, EUR (avoided damages) | Accuracy of VoLL and damage function estimation; spatial distribution of high-value customers; frequency and severity assumptions of extreme events; interdependencies (telecom, transport). | [75,76] | |
| Maximize Benefit-Cost Ratio of Resilience (BCRR) | VoR: Value of Resilience (avoided outage costs); Costres: Upfront cost of the resilience measure | Cost–benefit metric. The ratio of the discounted total benefits of a resilience project (i.e., the VOR) to its discounted total costs. A project is considered cost-effective if the BCRR is greater than 1.0 | A standardized metric for evaluating the cost-effectiveness of a resilience investment. It allows policymakers and utilities to prioritize projects that deliver the greatest resilience benefit per dollar spent. | The calculated VoR, the total cost of the resilience project, and the discount rate. | Unitless ratio | Discount rate and time horizon; capital cost and lifespan of resilience measures; correct estimation of avoided damages; correlation of events and benefits; co-benefit (secondary benefit) inclusion. | [76] | |
| Maximize Restoration Rate (RR) | Amount of load (kW or # of customers) that has been restored at time t. | The rate at which load or customers are brought back online following an outage. It is the slope of the restoration curve. | A dynamic measure of recovery speed. A higher initial restoration rate indicates that crews are able to quickly restore service to large blocks of customers, demonstrating resourcefulness and operational agility. | Time-series data of load (or customer count) restored during a recovery period. | kW/h, MW/h | Crew dispatch optimization; automation and remote restoration capability; prepositioning of spares and contractors; priority schema for critical loads; interagency coordination. | [77] | |
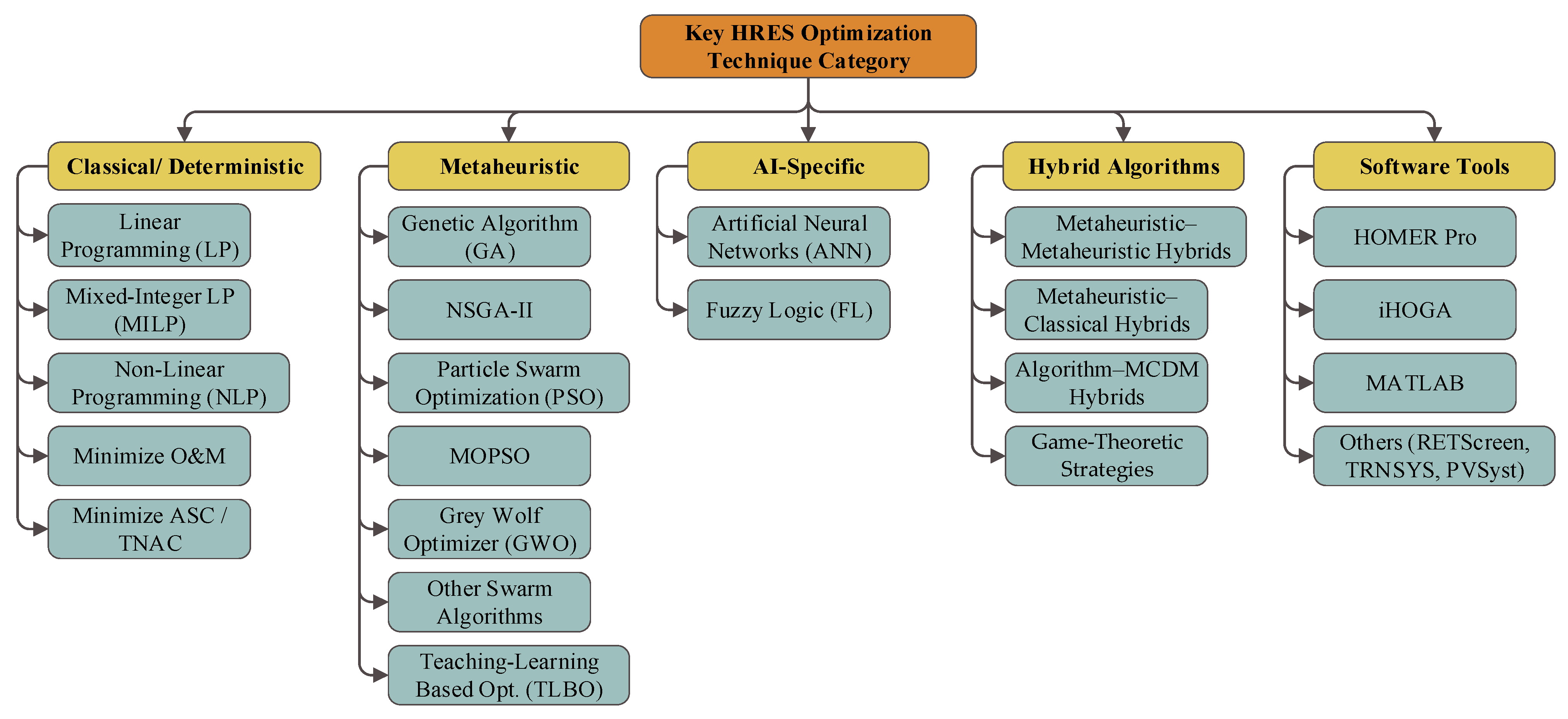
3.4. The Algorithmic and Technological Landscape
3.4.1. Classical and Mathematical Programming Methods
3.4.2. Metaheuristic Algorithms
3.4.3. AI Techniques
3.4.4. Hybrid Optimization Strategies
3.4.5. Commercial and Academic Software Tools
3.5. Advanced Modeling Paradigms and System Integration
3.5.1. Modeling Under Uncertainty
3.5.2. Advanced Energy Management Systems (EMS)
3.5.3. Integration of Emerging Technologies (Multi-Vector Energy Systems)
- Production (Electrolysis): Surplus electricity from renewable sources powers an electrolyzer, which splits water into hydrogen and oxygen. If the electricity is from renewables, the output is called “green hydrogen”.
- Storage: The produced hydrogen is typically compressed and stored in high-pressure tanks.
- Reconversion: When energy demand exceeds renewable generation, the stored hydrogen is converted back into electricity using technologies such as fuel cells (FCs), gas turbines (GTs), or hydrogen internal combustion engines (HICEs).
4. Discussion
4.1. Analysis of Trends and Evolution of Research Focus
4.2. Analysis of Trade-Offs Between Conflicting Objectives
| Conflicting Objective Pair | Description of Trade-off | Typical Impact on System Design |
|---|---|---|
| Cost (Minimize) vs. Reliability (Maximize/LPSP Minimize) | Improving reliability often requires more or larger components (e.g., batteries, generators), increasing overall costs. | Higher reliability targets lead to increased investment in generation and storage capacity. |
| Cost (Minimize) vs. Environmental Impact (Minimize Emissions) | Lower-cost systems might rely more on fossil fuels (if cheaper initially), increasing emissions. Minimizing emissions often requires higher investment in renewables and storage. | Stricter emission targets drive up the share of renewable components and storage, potentially increasing costs. |
| Renewable Fraction (Maximize) vs. System Stability/Cost (Minimize) | High renewable penetration can lead to instability and require costly solutions (storage, grid upgrades) to manage intermittency. | Higher renewable fraction targets necessitate larger storage capacities and more sophisticated control systems, impacting cost. |
| Technical Optimality vs. Social Acceptance (Maximize) | A technically optimal design (e.g., largest wind turbines for maximum yield) might face community opposition due to aesthetic, noise, or land use concerns. | Designs may need to be modified (e.g., smaller/fewer turbines, different siting) to gain social acceptance, potentially reducing technical/economic performance. |
| Economic Efficiency (Maximize) vs. Job Creation (Maximize) | More automated and economically efficient systems may create fewer local jobs compared to more labor-intensive alternatives. | Choice of technology and operational strategy can influence local employment; less automated systems might be preferred for social job creation goals despite higher operational costs. |
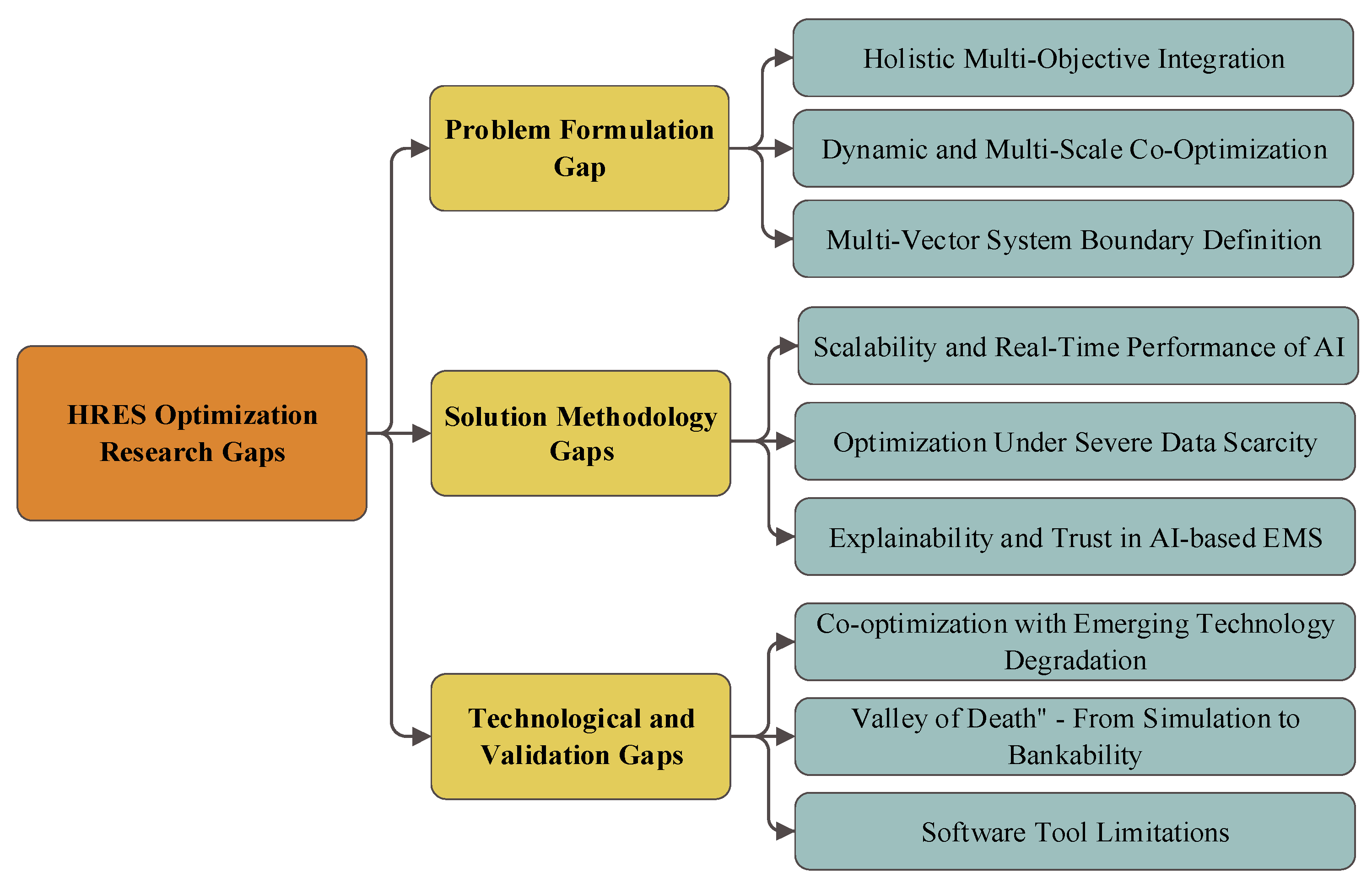
4.3. A Systematic Framework for HRES Optimization Research Gaps
4.3.1. Problem Formulation Gaps
4.3.2. Solution Methodology Gaps
4.3.3. Technological and Validation Gaps
4.4. HRES Integration High-Penetration Risks and Synergistic Solutions
4.4.1. Technological Synergy by Transforming VREs into Grid Stabilizers
4.4.2. Market and Policy Synergy by Creating Incentives for Stability
5. Conclusions
5.1. Summary of Main Findings
5.2. Limitations of the Current Work
5.3. Future Research Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| AHP | Analytic Hierarchy Process |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| ASC | Annual System Cost |
| BCRR | Benefit–Cost Ratio of Resilience |
| BdC | Bidirectional Converter |
| CAPEX | Capital Expenditures |
| CRF | Capital Recovery Factor |
| CSA | Crow Search Algorithm |
| DALYs | Disability-Adjusted Life Years |
| DC | Direct Current |
| DG | Diesel Generator |
| DoO | Duration of Outage |
| DoD | Depth of Discharge |
| DP | Dynamic Programming |
| DR | Demand Response |
| DRL | Deep Reinforcement Learning |
| EA | Evolutionary Algorithm |
| EENS | Expected Energy Not Supplied |
| EF | Emission Factor |
| EMS | Energy Management System |
| ESS | Energy Storage System |
| FC | Fuel Cell |
| FL | Fuzzy Logic |
| FTE | Full-Time Equivalent |
| GA | Genetic Algorithm |
| GHG | Greenhouse Gas |
| G2V | Grid-to-Vehicle |
| GT | Gas Turbine |
| GWO | Grey Wolf Optimizer |
| HDI | Human Development Index |
| HICE | Hydrogen Internal Combustion Engine |
| HOMER | Hybrid Optimization of Multiple Energy Resources |
| HRES | Hybrid Renewable Energy System |
| iHOGA | Improved Hybrid Optimization by Genetic Algorithms |
| IPCC | Intergovernmental Panel on Climate Change |
| JEDI | Jobs and Economic Development Impacts |
| LCC | Lifecycle Cost |
| LCLS | Loss of Critical Load Served |
| LCOE | Levelized Cost of Energy |
| LCOH | Levelized Cost of Hydrogen |
| LOLE | Loss of Load Expectation |
| LOLP | Loss of Load Probability |
| LP | Linear Programming |
| LPSP | Loss of Power Supply Probability |
| LUIE | Land Use Intensity of Energy |
| MCDM | Multi-Criteria Decision Making |
| MILP | Mixed-Integer Linear Programming |
| MOO | Multi-Objective Optimization |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| MOP | Multi-Objective Problem |
| MRFOA | Manta Ray Foraging Optimization Algorithm |
| NCV | Net Calorific Value |
| NIMBY | Not-in-my-Backyard |
| NLP | Non-Linear Programming |
| NPC | Net Present Cost |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm-II |
| N-R-HES | Nuclear-Renewable Hybrid Energy Systems |
| O&M | Operation and Maintenance |
| P2G | Power-to-Gas |
| P2H2P | Power-to-Hydrogen-to-Power |
| PCU | Power Conditioning Unit |
| PM2.5 | Fine Particulate Matter |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analyses |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| REF | Renewable Energy Fraction |
| RoCoF | Rate of Change of Frequency |
| RT | Recovery Time |
| RR | Restoration Rate |
| SAIDI | System Average Interruption Duration Index |
| SAIFI | System Average Interruption Frequency Index |
| SAO | Smell Agent Optimizer |
| SDGs | Sustainable Development Goals |
| SMR | Small Modular Reactor |
| SOC | State of Charge |
| SOH | State of Health |
| SOO | Single-Objective Optimization |
| SSA | Salp Swarm Algorithm |
| TLBO | Teaching–Learning-Based Optimization |
| TNAC | Total Net Annual Cost |
| TNPC | Total Net Present Cost |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| UMLH | Unmet Load Hours |
| V2G | Vehicle-to-Grid |
| VoLL | Value of Lost Load |
| VoR | Value of Resilience |
| VRE | Various Renewable Energy |
| WTG | Wind Turbine Generator |
| XAI | Explainable Artificial Intelligence |
| YLD | Years Lived with Disability |
| YLL | Years of Life Lost |
References
- Giedraityte, A.; Rimkevicius, S.; Marciukaitis, M.; Radziukynas, V.; Bakas, R. Hybrid Renewable Energy Systems—A Review of Optimization Approaches and Future Challenges. Appl. Sci. 2025, 15, 1744. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Sawle, Y. A Comparative Study of the Optimal Sizing and Management of Off-Grid Solar/Wind/Diesel and Battery Energy Systems for Remote Areas. Front. Energy Res. 2021, 9, 752043. [Google Scholar] [CrossRef]
- Bamisile, O.; Cai, D.; Adun, H.; Dagbasi, M.; Ukwuoma, C.C.; Huang, Q.; Johnson, N.; Bamisile, O. Towards Renewables Development: Review of Optimization Techniques for Energy Storage and Hybrid Renewable Energy Systems. Heliyon 2024, 10, e37482. [Google Scholar] [CrossRef] [PubMed]
- Ajiboye, O.K.; Ochiegbu, C.V.; Ofosu, E.A.; Gyamfi, S. A Review of Hybrid Renewable Energies Optimisation: Design, Methodologies, and Criteria. Int. J. Sustain. Energy 2023, 42, 648–684. [Google Scholar] [CrossRef]
- Mehigan, L.; Al Kez, D.; Collins, S.; Foley, A.; Ó’Gallachóir, B.; Deane, P. Renewables in the European Power System and the Impact on System Rotational Inertia. Energy 2020, 203, 117776. [Google Scholar] [CrossRef]
- Ali, J.S.; Qiblawey, Y.; Alassi, A.; Massoud, A.M.; Muyeen, S.M.; Abu-Rub, H. Power System Stability with High Penetration of Renewable Energy Sources: Challenges, Assessment, and Mitigation Strategies. IEEE Access 2025, 13, 39912–39934. [Google Scholar] [CrossRef]
- Fotis, G.; Maris, T.I.; Mladenov, V. Risks, Obstacles and Challenges of the Electrical Energy Transition in Europe: Greece as a Case Study. Sustainability 2025, 17, 5325. [Google Scholar] [CrossRef]
- Zaheb, H.; Ahmadi, M.; Rahmany, N.A.; Danish, M.S.S.; Fedayi, H.; Yona, A. Optimal Grid Flexibility Assessment for Integration of Variable Renewable-Based Electricity Generation. Sustainability 2023, 15, 15032. [Google Scholar] [CrossRef]
- Hinrichs-Rahlwes, R. Renewable Energy for Climate Protection and Energy Security: Lessons Learned from the European Green Deal and REPowerEU. In Transition Towards a Carbon Free Future; Springer: Cham, Switzerland, 2024; pp. 245–257. [Google Scholar]
- The Geopolitics of the Global Energy Transition; Hafner, M., Tagliapietra, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 73, ISBN 978-3-030-39065-5. [Google Scholar]
- Gulley, A.L. One Hundred Years of Cobalt Production in the Democratic Republic of the Congo. Resour. Policy 2022, 79, 103007. [Google Scholar] [CrossRef]
- Islam, M.M.; Mariev, O.; Sohag, K. International Mineral Trade-Cleaner Energy Transformation Nexus: How Decomposed Mineral Prices and Geopolitical Events Act? Energy Strategy Rev. 2025, 59, 101699. [Google Scholar] [CrossRef]
- Bettarelli, L.; Furceri, D.; Pisano, L.; Pizzuto, P. Greenflation: Empirical Evidence Using Macro, Regional and Sectoral Data. Eur. Econ. Rev. 2025, 174, 104983. [Google Scholar] [CrossRef]
- Chen, J.; Yan, J.; Kemmeugne, A.; Kassouf, M.; Debbabi, M. Cybersecurity of Distributed Energy Resource Systems in the Smart Grid: A Survey. Appl. Energy 2025, 383, 125364. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 Statement: An Updated Guideline for Reporting Systematic Reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef] [PubMed]
- Rezk, H.; Mukhametzyanov, I.Z.; Al-Dhaifallah, M.; Ziedan, H.A. Optimal Selection of Hybrid Renewable Energy System Using Multi-Criteria Decision-Making Algorithms. CMC-Comput. Mater. Contin. 2021, 68, 2001–2027. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, I.; Jamil, F.; Kim, D. Toward the Optimal Operation of Hybrid Renewable Energy Resources in Microgrids. Energies 2020, 13, 5482. [Google Scholar] [CrossRef]
- Singh, R.; Bansal, R.C. Review of HRESs Based on Storage Options, System Architecture and Optimisation Criteria and Methodologies. IET Renew. Power Gener. 2018, 12, 747–760. [Google Scholar] [CrossRef]
- Basnet, S.; Deschinkel, K.; Moyne, L.L.; Péra, M.C. Optimal Integration of Hybrid Renewable Energy Systems for Decarbonized Urban Electrification and Hydrogen Mobility. Int. J. Hydrogen Energy 2024, 83, 1448–1462. [Google Scholar] [CrossRef]
- Kumar, S.; Chinnamuthan, P.; Krishnasamy, V. Study on Renewable Distributed Generation, Power Controller and Islanding Management in Hybrid Microgrid System. J. Green Eng. 2018, 8, 37–70. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Yang, H.X.; Shan, K. Hybrid Renewable Energy Applications in Zero-Energy Buildings and Communities Integrating Battery and Hydrogen Vehicle Storage*. Appl. Energy 2021, 290, 116733. [Google Scholar] [CrossRef]
- Khosravi, N.; Abdolvand, A.; Oubelaid, A.; Khan, Y.A.; Bajaj, M.; Govender, S. Improvement of Power Quality Parameters Using Modulated-Unified Power Quality Conditioner and Switched-Inductor Boost Converter by the Optimization Techniques for a Hybrid AC/DC Microgrid. Sci. Rep. 2022, 12, 21675. [Google Scholar] [CrossRef]
- Sahoo, B.; Routray, S.K.; Rout, P.K. A Novel Centralized Energy Management Approach for Power Quality Improvement. Int. Trans. Electr. Energy Syst. 2021, 31, e12582. [Google Scholar] [CrossRef]
- Kumar, J.S.; Raja, S.C.; Srinivasan, D.; Venkatesh, P. Hybrid Renewable Energy-Based Distribution System for Seasonal Load Variations. Int. J. Energy Res. 2018, 42, 1066–1087. [Google Scholar] [CrossRef]
- Duan, F.D.; Eslami, M.; Khajehzadeh, M.; Basem, A.; Jasim, D.J.; Palani, S. Optimization of a Photovoltaic/Wind/Battery Energy-Based Microgrid in Distribution Network Using Machine Learning and Fuzzy Multi-Objective Improved Kepler Optimizer Algorithms. Sci. Rep. 2024, 14, 13354. [Google Scholar] [CrossRef] [PubMed]
- Ammari, C.; Belatrache, D.; Touhami, B.; Makhloufi, S. Sizing, Optimization, Control and Energy Management of Hybrid Renewable Energy System—A Review. Energy Built Environ. 2022, 3, 399–411. [Google Scholar] [CrossRef]
- Billah, M.; Yousif, M.; Numan, M.; Salam, I.U.; Kazmi, S.A.A.; Alghamdi, T.A.H. Decentralized Smart Energy Management in Hybrid Microgrids: Evaluating Operational Modes, Resources Optimization, and Environmental Impacts. IEEE Access 2023, 11, 143530–143548. [Google Scholar] [CrossRef]
- Martín-Crespo, A.; Hernández-Serrano, A.; Izquierdo-Monge, O.; Peña-Carro, P.; Hernández-Jiménez, A.; Frechoso-Escudero, F.; Baeyens, E. AC/DC Optimal Power Flow and Techno-Economic Assessment for Hybrid Microgrids: TIGON CEDER Demonstrator. Front. Energy Res. 2024, 12, 1399114. [Google Scholar] [CrossRef]
- Shirzadi, N.; Nasiri, F.; Eicker, U. Optimal Configuration and Sizing of an Integrated Renewable Energy System for Isolated and Grid-Connected Microgrids: The Case of an Urban University Campus. Energies 2020, 13, 3527. [Google Scholar] [CrossRef]
- Hamidieh, M.; Ghassemi, M. Microgrids and Resilience: A Review. IEEE Access 2022, 10, 106059–106080. [Google Scholar] [CrossRef]
- Azeem, O.; Ali, M.; Abbas, G.; Uzair, M.; Qahmash, A.; Algarni, A.; Hussain, M.R. A Comprehensive Review on Integration Challenges, Optimization Techniques and Control Strategies of Hybrid Ac/Dc Microgrid. Appl. Sci. 2021, 11, 6242. [Google Scholar] [CrossRef]
- Eriksson, E.L.V.; Gray, E.M. Optimisation and Integration of Hybrid Renewable Energy Storage Systems. In Proceedings of the IOP Conference Series Earth and Environmental Science, Perth, Australia, 12–14 June 2017; Volume 73. [Google Scholar]
- Reyasudin Basir Khan, M.; Pasupuleti, J.; Al-Fattah, J.; Tahmasebi, M. Optimal Grid-Connected PV System for a Campus Microgrid. Indones. J. Electr. Eng. Comput. Sci. 2018, 12, 899–906. [Google Scholar] [CrossRef]
- Bubalo, M.; Bašić, M.; Vukadinović, D.; Grgić, I. Hybrid Wind-Solar Power System with a Battery-Assisted Quasi-Z-Source Inverter: Optimal Power Generation by Deploying Minimum Sensors. Energies 2023, 16, 1488. [Google Scholar] [CrossRef]
- Jayaram, J.; Srinivasan, M.; Prabaharan, N.; Senjyu, T. Design of Decentralized Hybrid Microgrid Integrating Multiple Renewable Energy Sources with Power Quality Improvement. Sustainability 2022, 14, 7777. [Google Scholar] [CrossRef]
- Liang, Z.; Chung, C.Y.; Wang, Q.; Chen, H.; Yang, H.; Wu, C. Fortifying Renewable-Dominant Hybrid Microgrids: A Bi-Directional Converter Based Interconnection Planning Approach. Engineering, 2025; in press. [Google Scholar] [CrossRef]
- Pavankumar, Y.; Kollu, R.; Debnath, S. Multi-Objective Optimization of Photovoltaic/Wind/Biomass/Battery-Based Grid-Integrated Hybrid Renewable Energy System. IET Renew. Power Gener. 2021, 15, 1528–1541. [Google Scholar] [CrossRef]
- Abdullah, H.M.; Park, S.; Seong, K.; Lee, S. Hybrid Renewable Energy System Design: A Machine Learning Approach for Optimal Sizing with Net-Metering Costs. Sustainability 2023, 15, 8538. [Google Scholar] [CrossRef]
- Sharma, A.; Singh, H.P.; Viral, R.; Anwer, N. Techno-Economical Planning of an Off-Grid Integrated Renewable Energy System. U. Porto J. Eng. 2022, 8, 210–229. [Google Scholar] [CrossRef]
- Marocco, P.; Ferrero, D.; Lanzini, A.; Santarelli, M. The Role of Hydrogen in the Optimal Design of Off-Grid Hybrid Renewable Energy Systems. J. Energy Storage 2022, 46, 103893. [Google Scholar] [CrossRef]
- Treado, S. The Effect of Electric Load Profiles on the Performance of Off-Grid Residential Hybrid Renewable Energy Systems. Energies 2015, 8, 11120–11138. [Google Scholar] [CrossRef]
- Maaruf, M.; Khan, K.; Khalid, M. Robust Control for Optimized Islanded and Grid-Connected Operation of Solar/Wind/Battery Hybrid Energy. Sustainability 2022, 14, 5673. [Google Scholar] [CrossRef]
- Toularoud, M.S.; Rudposhti, M.K.; Bagheri, S.; Salemi, A.H. A Hierarchical Control Approach to Improve the Voltage and Frequency Stability for Hybrid Microgrids-Based Distributed Energy Resources. Energy Rep. 2023, 10, 2693–2709. [Google Scholar] [CrossRef]
- Shan, Y.H.; Ma, L.Q.; Yu, X.K. Hierarchical Control and Economic Optimization of Microgrids Considering the Randomness of Power Generation and Load Demand. Energies 2023, 16, 5503. [Google Scholar] [CrossRef]
- Shah, K.K.; George, D.; Swan, L.; Pearce, J.M. Performance and Analysis of Retail Store-Centered Microgrids with Solar Photovoltaic Parking Lot, Cogeneration, and Battery-Based Hybrid Systems. Eng. Rep. 2021, 3, e12418. [Google Scholar] [CrossRef]
- Khan, A.A.; Minai, A.F.; Pachauri, R.K.; Malik, H. Optimal Sizing, Control, and Management Strategies for Hybrid Renewable Energy Systems: A Comprehensive Review. Energies 2022, 15, 6249. [Google Scholar] [CrossRef]
- Rathod, A.A.; Subramanian, B. Scrutiny of Hybrid Renewable Energy Systems for Control, Power Management, Optimization and Sizing: Challenges and Future Possibilities. Sustainability 2022, 14, 16814. [Google Scholar] [CrossRef]
- Maheri, A.; Unsal, I.; Mahian, O. Multiobjective Optimisation of Hybrid Wind-PV-Battery-Fuel Cell-Electrolyser-Diesel Systems: An Integrated Configuration-Size Formulation Approach. Energy 2022, 241, 122825. [Google Scholar] [CrossRef]
- Sari, A.; Majdi, A.; Opulencia, M.J.C.; Timoshin, A.; Huy, D.T.N.; Trung, N.D.; Alsaikhan, F.; Hammid, A.T.; Akhmedov, A. New Optimized Configuration for a Hybrid PV/Diesel/Battery System Based on Coyote Optimization Algorithm: A Case Study for Hotan County. Energy Rep. 2022, 8, 15480–15492. [Google Scholar] [CrossRef]
- Agajie, T.F.; Fopah-Lele, A.; Amoussou, I.; Ali, A.; Khan, B.; Tanyi, E. Optimal Design and Mathematical Modeling of Hybrid Solar PV-Biogas Generator with Energy Storage Power Generation System in Multi-Objective Function Cases. Sustainability 2023, 15, 8264. [Google Scholar] [CrossRef]
- Li, K.W.; Song, Y.M.; Wang, R. Multi-Objective Optimal Sizing of HRES under Multiple Scenarios with Undetermined Probability. Mathematics 2022, 10, 1508. [Google Scholar] [CrossRef]
- Ganthia, B.P.; Praveen, B.M.; Kabat, S.R.; Mohapatra, B.K.; Sethi, R.; Buradi, A. Energy Management in Hybrid PV-Wind-Battery Storage-Based Microgrid Using Droop Control Technique. J. Mech. Contin. Math. Sci. 2024, 19, 44–66. [Google Scholar] [CrossRef]
- Tyass, I.; Bellat, A.; Raihani, A.; Mansouri, K. Multi-Objective Algorithm for Hybrid Microgrid Energy Management Based on Multi-Agent System. Int. J. Power Electron. Drive Syst. 2024, 15, 1235–1246. [Google Scholar] [CrossRef]
- Nallolla, C.A.; Vijayapriya, P.; Chittathuru, D.; Padmanaban, S. Multi-Objective Optimization Algorithms for a Hybrid AC/DC Microgrid Using RES: A Comprehensive Review. Electronics 2023, 12, 1062. [Google Scholar] [CrossRef]
- Zhou, Y.; Narsilio, G.A.; Soga, K.; Aye, L. Achieving Pareto Optimum for Hybrid Geothermal-Solar (PV)-Gas Heating Systems: Minimising Lifecycle Cost and Greenhouse Gas Emissions. Sustainability 2024, 16, 6595. [Google Scholar] [CrossRef]
- Ukoima, K.N.; Okoro, O.I.; Obi, P.I.; Akuru, U.B.; Davidson, I.E. Optimal Sizing, Energy Balance, Load Management and Performance Analysis of a Hybrid Renewable Energy System. Energies 2024, 17, 5275. [Google Scholar] [CrossRef]
- Huang, Y.D.; Wang, Q.; Xu, J.P. A Stackelberg-Based Biomass Power Trading Game Framework in Hybrid-Wind/Solar/Biomass System: From Technological, Economic, Environmental and Social Perspectives. J. Clean. Prod. 2023, 403, 136806. [Google Scholar] [CrossRef]
- Agajie, T.F.; Ali, A.; Fopah-Lele, A.; Amoussou, I.; Khan, B.; Velasco, C.L.R.; Tanyi, E. A Comprehensive Review on Techno-Economic Analysis and Optimal Sizing of Hybrid Renewable Energy Sources with Energy Storage Systems. Energies 2023, 16, 642. [Google Scholar] [CrossRef]
- Al Abri, A.; Al Kaaf, A.; Allouyahi, M.; Al Wahaibi, A.; Ahshan, R.; Al Abri, R.S.; Al Abri, A. Techno-Economic and Environmental Analysis of Renewable Mix Hybrid Energy System for Sustainable Electrification of Al-Dhafrat Rural Area in Oman. Energies 2023, 16, 288. [Google Scholar] [CrossRef]
- Bade, S.O.; Tomomewo, O.S. Optimizing a Hybrid Wind-Solar-Biomass System with Battery and Hydrogen Storage Using Generic Algorithm-Particle Swarm Optimization for Performance Assessment. Clean. Energy Syst. 2024, 9, 100157. [Google Scholar] [CrossRef]
- Zhang, M.; Lyu, H.; Bian, H.; Ghadimi, N. Improved Chaos Grasshopper Optimizer and Its Application to HRES Techno-Economic Evaluation. Heliyon 2024, 10, e24315. [Google Scholar] [CrossRef]
- Shah Irshad, A.; Naseer Zakir, M.; Shah Rashad, S.; Elsayed Lotfy, M.; Mikhaylov, A.; Elkholy, M.H.; Pinter, G.; Senjyu, T. Comparative Analyses and Optimizations of Hybrid Biomass and Solar Energy Systems Based upon a Variety of Biomass Technologies. Energy Convers. Manag. X 2024, 23, 100640. [Google Scholar] [CrossRef]
- Wu, E.Y.L. Multi-Neighborhood Enhanced Harris Hawks Optimization for Efficient Allocation of Hybrid Renewable Energy System with Cost and Emission Reduction. CMES-Comput. Model. Eng. Sci. 2025, 143, 1185–1214. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, Z.; Gong, Z.; Chen, P.; Razmjooy, S. The Improved Aquila Optimization Approach for Cost-Effective Design of Hybrid Renewable Energy Systems. Heliyon 2024, 10, e27281. [Google Scholar] [CrossRef]
- Sadeghitabar, E.; Ghasempour, R.; Vaziri Rad, M.A.; Toopshekan, A. Optimization and Shannon Entropy Multi-Criteria Decision-Making Method for Implementing Modern Renewable Energies in Stand-Alone Greenhouses. Energy Convers. Manag. X 2025, 27, 101139. [Google Scholar] [CrossRef]
- Hasan, S.; Meem, A.I.; Islam, M.S.; Proma, S.S.; Mitra, S.K. Comparative Techno-Economic Analyses and Optimization of Standalone and Grid-Tied Renewable Energy Systems for South Asia and Sub-Saharan Africa. Results Eng. 2024, 21, 101964. [Google Scholar] [CrossRef]
- Huang, G.; Gan, J.; Huang, Y.; Ebrahimian, H. Optimization of Off-Grid Renewable Energy Systems Using a Hybrid Version of Golden Search Algorithm. Heliyon 2024, 10, e30990. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, M.; Lubitz, W.D.; Tasnim, S.H.; Mahmud, S. Optimization of Hybrid Renewable Energy Systems for Remote Communities in Northern Canada. Renew. Energy 2025, 244, 122729. [Google Scholar] [CrossRef]
- Bilal, M.; Bokoro, P.N.; Sharma, G. Hybrid Optimization for Sustainable Design and Sizing of Standalone Microgrids Integrating Renewable Energy, Diesel Generators, and Battery Storage with Environmental Considerations. Results Eng. 2025, 25, 103764. [Google Scholar] [CrossRef]
- Mohtasim, M.S.; Das, B.K.; Paul, U.K.; Kibria, M.G.; Hossain, M.S. Hybrid Renewable Multi-Generation System Optimization: Attaining Sustainable Development Goals. Renew. Sustain. Energy Rev. 2025, 212, 115415. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Khan, A. Synergistic Nexus among Energy Security, Energy Equity and Net Electricity Regions: Optimizing Renewable Energy Integration and Demand Response for Electrical Supply Systems. Energy Strategy Rev. 2025, 57, 101611. [Google Scholar] [CrossRef]
- Emezirinwune, M.U.; Adejumobi, I.A.; Adebisi, O.I.; Akinboro, F.G. Synergizing Hybrid Renewable Energy Systems and Sustainable Agriculture for Rural Development in Nigeria. e-Prime—Adv. Electr. Eng. Electron. Energy 2024, 7, 100492. [Google Scholar] [CrossRef]
- Jaman, A.; Al Mahmud, R.; Das, B.K.; Tushar, M.S.H.K. Optimizing an Integrated Hybrid Energy System with Hydrogen-Based Storage to Develop an off-Grid Green Community for Sustainable Development in Bangladesh. Int. J. Hydrogen Energy 2025, 97, 766–786. [Google Scholar] [CrossRef]
- Sankarananth, S.; Karthiga, M.; Suganya, E.; Sountharrajan, S.; Bavirisetti, D.P. AI-Enabled Metaheuristic Optimization for Predictive Management of Renewable Energy Production in Smart Grids. Energy Rep. 2023, 10, 1299–1312. [Google Scholar] [CrossRef]
- Irshad, A.S.; Kargar, N.; Elkholy, M.H.; Ludin, G.A.; Elias, S.; Hilali, A.; Senjyu, T.; Gamil, M.M.; Pinter, G. Techno-Economic Evaluation and Comparison of the Optimal PV/Wind and Grid Hybrid System with Horizontal and Vertical Axis Wind Turbines. Energy Convers. Manag. X 2024, 23, 100638. [Google Scholar] [CrossRef]
- Cai, S.; Xie, Y.; Wu, Q.; Xiang, Z. Robust MPC-Based Microgrid Scheduling for Resilience Enhancement of Distribution System. Int. J. Electr. Power Energy Syst. 2020, 121, 106068. [Google Scholar] [CrossRef]
- Jamborsalamati, P.; Hossain, M.J.; Taghizadeh, S.; Konstantinou, G.; Manbachi, M.; Dehghanian, P. Enhancing Power Grid Resilience Through an IEC61850-Based EV-Assisted Load Restoration. IEEE Trans. Ind. Inform. 2020, 16, 1799–1810. [Google Scholar] [CrossRef]
- Li, L.; You, S.; Wang, X. Optimal Design of Standalone Hybrid Renewable Energy Systems with Biochar Production in Remote Rural Areas: A Case Study. Energy Procedia 2019, 158, 688–693. [Google Scholar] [CrossRef]
- Shadoul, M.; Al Abri, R.; Yousef, H.; Al Shereiqi, A. Designing a Dispatch Engine for Hybrid Renewable Power Stations Using a Mixed-Integer Linear Programming Technique. Energies 2024, 17, 3281. [Google Scholar] [CrossRef]
- Ehrgott, M.; Köksalan, M.; Kadziński, M.; Deb, K. Fifty Years of Multi-Objective Optimization and Decision-Making: From Mathematical Programming to Evolutionary Computation. Eur. J. Oper. Res. 2025; in press. [Google Scholar] [CrossRef]
- Hlal, I.M.; Ramachandaramurthy, V.K.; Hafiz Nagi, F.; Bin Tuan Abdullah, T.A.R. Optimal Techno-Economic Design of Standalone Hybrid Renewable Energy System Using Genetic Algorithm. In Proceedings of the IOP Conference Series Earth and Environmental Science, Kuala Lumpur, Malaysia, 11–14 December 2019; Volume 268. [Google Scholar]
- Kamjoo, A.; Maheri, A.; Dizqah, A.M.; Putrus, G.A. Multi-Objective Design under Uncertainties of Hybrid Renewable Energy System Using NSGA-II and Chance Constrained Programming. Int. J. Electr. Power Energy Syst. 2016, 74, 187–194. [Google Scholar] [CrossRef]
- Bismark, K.M.K.C.; Caballa, L.G.C.; Yap, C.M.F.; Peña, R.A.S.; Parocha, R.C.; Macabebe, E.Q.B. Optimization of a Hybrid Renewable Energy System for a Rural Community Using PSO. In Proceedings of the Iop Conference Series Earth and Environmental Science, Phnom Penh, Cambodia, 14–15 September 2022; Volume 1199. [Google Scholar]
- Sharafi, M.; Elmekkawy, T.Y. A Dynamic MOPSO Algorithm for Multiobjective Optimal Design of Hybrid Renewable Energy Systems. Int. J. Energy Res. 2014, 38, 1949–1963. [Google Scholar] [CrossRef]
- Wahab, N.I.B.A.; Mailah, N.F.B.; Tukkee, A.S. Optimal Sizing of Autonomous Hybrid Microgrids with Economic Analysis Using Grey Wolf Optimizer Technique. e-Prime Adv. Electr. Eng. Electron. Energy 2023, 3, 100123. [Google Scholar] [CrossRef]
- Devaraj, V.; Kumaresan, M. Isolated and Grid-Connected Hybrid Microgrid Model Frequency Stabilization by Novel Salp-Swarm Optimization Algorithm. SSRG Int. J. Electr. Electron. Eng. 2023, 10, 58–69. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Liu, Y.X.; Wu, Z.H.; Zhang, S.M.; Zhang, L. Improving Sparrow Search Algorithm for Optimal Operation Planning of Hydrogen-Electric Hybrid Microgrids Considering Demand Response. Symmetry 2023, 15, 919. [Google Scholar] [CrossRef]
- Mahmoudi, S.M.; Maleki, A.; Ochbelagh, D.R. Multi-Objective Optimization of Hybrid Energy Systems Using Gravitational Search Algorithm. Sci. Rep. 2025, 15, 2550. [Google Scholar] [CrossRef] [PubMed]
- Krishna, R.; Hemamalini, S. Improved TLBO Algorithm for Optimal Energy Management in a Hybrid Microgrid with Support Vector Machine-Based Forecasting of Uncertain Parameters. Results Eng. 2024, 24, 102992. [Google Scholar] [CrossRef]
- Boichenko, S.; Dubovyk, V.; Shkilniuk, I.; Korovushkin, V.; Khotian, A. Research on Photovoltaic Power Prediction Using an LSTM Recurrent Neural Network. In Systems, Decision and Control in Energy VI; Springer: Cham, Switzerland, 2024; pp. 421–443. [Google Scholar]
- Kaushal, J.; Basak, P. Frequency Control of Islanded Microgrid Using Fuzzy-PI and Autotuned Controllers. Int. J. Adv. Appl. Sci. 2019, 8, 64–72. [Google Scholar] [CrossRef]
- Güven, A.F.; Yörükeren, N. A Comparative Study on Hybrid GA-PSO Performance for Stand-Alone Hybrid Energy Systems Optimization. Sigma J. Eng. Nat. Sci. 2024, 42, 1410–1438. [Google Scholar] [CrossRef]
- Charadi, S.; Chakir, H.E.; Redouane, A.; El Hasnaoui, A.; Et-taoussi, M. Bi-Objective Optimal Active and Reactive Power Flow Management in Grid-Connected AC/DC Hybrid Microgrids Using Metaheuristic-PSO. Clean Energy 2023, 7, 1356–1380. [Google Scholar] [CrossRef]
- Ahmadi, A.; Hajinezhad, A.; Fattahi, R.; Moosavian, S.F. Techno-Economic Comparison of Battery-Flywheel With Battery-Hydrogen Storage System in the Vicinity of Off-Grid HRES for Four Climates: MCDM Method. Energy Sci. Eng. 2025, 13, 2512–2529. [Google Scholar] [CrossRef]
- Lee, J.-W.; Kim, M.-K.; Kim, H.-J. A Multi-Agent Based Optimization Model for Microgrid Operation with Hybrid Method Using Game Theory Strategy. Energies 2021, 14, 603. [Google Scholar] [CrossRef]
- Mbasso, W.F.; Dzonde Naoussi, S.R.; Jacques Molu, R.J.; Saatong, K.T.; Kamel, S. Technical Assessment of a Stand-Alone Hybrid Renewable System for Energy and Oxygen Optimal Production for Fishes Farming in a Residential Building Using HOMER Pro. Clean. Eng. Technol. 2023, 17, 100688. [Google Scholar] [CrossRef]
- Silinto, B.F.; Yamu, C.V.; Zuidema, C.; Faaij, A.P.C. Hybrid Renewable Energy Systems for Rural Electrification in Developing Countries: A Review on Energy System Models and Spatial Explicit Modelling Tools. Renew. Sustain. Energy Rev. 2025, 207, 114916. [Google Scholar] [CrossRef]
- Mohammed, B.; Amine, E.F.; Nabil, E.A. Investigation of Technoeconomic Optimization for Sizing Renewable Energy Systems Using Metaheuristic and Hybrid Algorithms. Sci. Afr. 2025, 28, e02712. [Google Scholar] [CrossRef]
- Pan, X.; Yang, F.; Ma, P.; Xing, Y.; Zhang, J.; Cao, L. A Game-Theoretic Approach of Optimized Operation of AC/DC Hybrid Microgrid Clusters. Energies 2022, 15, 5537. [Google Scholar] [CrossRef]
- Karavas, C.-S.; Arvanitis, K.; Papadakis, G. A Game Theory Approach to Multi-Agent Decentralized Energy Management of Autonomous Polygeneration Microgrids. Energies 2017, 10, 1756. [Google Scholar] [CrossRef]
- Ceran, B.; Mielcarek, A.; Hassan, Q.; Teneta, J.; Jaszczur, M. Aging Effects on Modelling and Operation of a Photovoltaic System with Hydrogen Storage. Appl. Energy 2021, 297, 117161. [Google Scholar] [CrossRef]
- Benzzine, H.; Labrim, H.; Aouni, I.; Achour, Y.; Bajit, A.; Saad, A.; Ettahri, H.; Balli, M.; Zejli, D.; El Bouayadi, R. MATLAB-TRNSYS Simulation Framework for MPC-Based Optimization of Hybrid Renewable Energy Systems. Sci. Afr. 2025, 28, e02751. [Google Scholar] [CrossRef]
- Bouaouda, A.; Sayouti, Y. Hybrid Meta-Heuristic Algorithms for Optimal Sizing of Hybrid Renewable Energy System: A Review of the State-of-the-Art. Arch. Comput. Methods Eng. 2022, 29, 4049–4083. [Google Scholar] [CrossRef]
- Park, S.-H.; Hussain, A.; Kim, H.-M. Impact Analysis of Survivability-Oriented Demand Response on Islanded Operation of Networked Microgrids with High Penetration of Renewables. Energies 2019, 12, 452. [Google Scholar] [CrossRef]
- Memon, Z.A.; Akbari, M.A. Optimizing Hybrid Photovoltaic/Battery/Diesel Microgrids in Distribution Networks Considering Uncertainty and Reliability. Sustainability 2023, 15, 13499. [Google Scholar] [CrossRef]
- Zhao, G.; Cao, T.; Wang, Y.; Zhou, H.; Zhang, C.; Wan, C. Optimal Sizing of Isolated Microgrid Containing Photovoltaic/Photothermal/Wind/Diesel/Battery. Int. J. Photoenergy 2021, 2021, 5566597. [Google Scholar] [CrossRef]
- Ayub, M.A.; Khan, H.; Peng, J.C.; Liu, Y.T. Consumer-Driven Demand-Side Management Using K-Mean Clustering and Integer Programming in Standalone Renewable Grid. Energies 2022, 15, 1006. [Google Scholar] [CrossRef]
- Perrelli, A.; Sodré, E.; Silva, V.; Santos, A. Maximizing Returns and Minimizing Risks in Hybrid Renewable Energy Systems: A Stochastic Discounted Cash Flow Analysis of Wind and Photovoltaic Systems in Brazil. Energies 2023, 16, 6833. [Google Scholar] [CrossRef]
- Alhasnawi, B.N.; Jasim, B.H.; Esteban, M.D. A New Robust Energy Management and Control Strategy for a Hybrid Microgrid System Based on Green Energy. Sustainability 2020, 12, 5724. [Google Scholar] [CrossRef]
- Núñez-Rodríguez, R.A.; Unsihuay-Vila, C.; Posada, J.; Pinzón-Ardila, O. Data-Driven Distributionally Robust Optimization for Day-Ahead Operation Planning of a Smart Transformer-Based Meshed Hybrid AC/DC Microgrid Considering the Optimal Reactive Power Dispatch. Energies 2024, 17, 4036. [Google Scholar] [CrossRef]
- Rangel, N.; Li, H.; Aristidou, P. An Optimisation Tool for Minimising Fuel Consumption, Costs and Emissions from Diesel-PV-Battery Hybrid Microgrids. Appl. Energy 2023, 335, 120748. [Google Scholar] [CrossRef]
- Wang, Z.C.; Zheng, Y.Y. Optimal Scheduling of Biomass-Hybrid Microgrids with Energy Storage: An LSTM-PMOEVO Framework for Uncertain Environments. Appl. Sci. 2025, 15, 2702. [Google Scholar] [CrossRef]
- Yu, G.Q.; Meng, Z.Y.; Ma, H.T.; Liu, L. An Adaptive Marine Predators Algorithm for Optimizing a Hybrid PV/DG/Battery System for a Remote Area in China. Energy Rep. 2021, 7, 398–412. [Google Scholar] [CrossRef]
- Phan, B.C.; Lee, M.-T.; Lai, Y.-C. Intelligent Deep-Q-Network-Based Energy Management for an Isolated Microgrid. Appl. Sci. 2022, 12, 8721. [Google Scholar] [CrossRef]
- Schleifer, A.H.; Murphy, C.A.; Cole, W.J.; Denholm, P. Exploring the Design Space of PV-plus-Battery System Configurations under Evolving Grid Conditions. Appl. Energy 2022, 308, 118339. [Google Scholar] [CrossRef]
- Paisiripas, D.; Cho, K.; Park, S. Integration of Small Modular Reactors with Renewable Energy for Carbon Neutrality: A Case Study of Phuket, Thailand. Energies 2024, 17, 5565. [Google Scholar] [CrossRef]
- Zhang, T. Techno-Economic Analysis of a Nuclear-Wind Hybrid System with Hydrogen Storage. J. Energy Storage 2022, 46, 103807. [Google Scholar] [CrossRef]
- Haghghi, M.A.; Feili, M.; Ghaebi, H.; Athari, H. Multi-Criteria Study and Machine Learning Optimization of a Novel Heat Integration for Combined Electricity, Heat, and Hydrogen Production: Application of Biogas-Fueled S-Graz Plant and Biogas Steam Reforming. Case Stud. Therm. Eng. 2024, 63, 105323. [Google Scholar] [CrossRef]
- Roy, T.K.; Saha, S.; Oo, A.M.T. Techno-Economic and Environmental Optimization of Hydrogen-Based Hybrid Energy Systems for Remote off-Grid Australian Communities. Energy Convers. Manag. X 2025, 27, 101083. [Google Scholar] [CrossRef]
- Adedoja, O.S.; Sadiku, E.R.; Hamam, Y. A Techno-Economic Assessment of the Viability of a Photovoltaic-Wind-Battery Storage-Hydrogen Energy System for Electrifying Primary Healthcare Centre in Sub-Saharan Africa. Energy Convers. Manag. X 2024, 23, 100643. [Google Scholar] [CrossRef]
- Khan, A.; Bressel, M.; Davigny, A.; Abbes, D.; Ould Bouamama, B. Comprehensive Review of Hybrid Energy Systems: Challenges, Applications, and Optimization Strategies. Energies 2025, 18, 2612. [Google Scholar] [CrossRef]
- Whiteman, Z.S.; Bubna, P.; Prasad, A.K.; Ogunnaike, B.A. Design, Operation, Control, and Economics of a Photovoltaic/Fuel Cell/Battery Hybrid Renewable Energy System for Automotive Applications. Processes 2015, 3, 452–470. [Google Scholar] [CrossRef]
- Bui, V.G.; Tu Bui, T.M.; Ong, H.C.; Nižetić, S.; Bui, V.H.; Xuan Nguyen, T.T.; Atabani, A.E.; Štěpanec, L.; Phu Pham, L.H.; Hoang, A.T. Optimizing Operation Parameters of a Spark-Ignition Engine Fueled with Biogas-Hydrogen Blend Integrated into Biomass-Solar Hybrid Renewable Energy System. Energy 2022, 252, 124052. [Google Scholar] [CrossRef]
- Goh, Q.H.; Zhang, L.; Ho, Y.K.; Chew, I.M.L. Modelling and Multi-Objective Optimisation of Sustainable Solar-Biomass-Based Hydrogen and Electricity Co-Supply Hub Using Metaheuristic-TOPSIS Approach. Energy Convers. Manag. 2023, 293, 117484. [Google Scholar] [CrossRef]
- Abdel-Hakim, A.E.; Abo-Elyousr, F.K. Heuristic Greedy Scheduling of Electric Vehicles in Vehicle-to-Grid Microgrid Owned Aggregators. Sensors 2022, 22, 2408. [Google Scholar] [CrossRef]
- Andrenacci, N.; Karagulian, F.; Genovese, A. Modelling Charge Profiles of Electric Vehicles Based on Charges Data. Open Res. Eur. 2022, 1, 156. [Google Scholar] [CrossRef]
- Sruthi, S.; Karthikumar, K.; Chandrasekar, P. Advanced Energy Management System for Hybrid AC/DC Microgrids with Electric Vehicles Using Hybridized Solution. Int. J. Electr. Electron. Res. 2024, 12, 740–745. [Google Scholar] [CrossRef]
- Subramaniam, U.; Ganesan, S.; Bhaskar, M.S.; Padmanaban, S.; Blaabjerg, F.; Almakhles, D.J. Investigations of AC Microgrid Energy Management Systems Using Distributed Energy Resources and Plug-in Electric Vehicles. Energies 2019, 12, 2834. [Google Scholar] [CrossRef]
- Babaei, M.; Abazari, A.; Muyeen, S.M. Coordination between Demand Response Programming and Learning-Based FOPID Controller for Alleviation of Frequency Excursion of Hybrid Microgrid. Energies 2020, 13, 442. [Google Scholar] [CrossRef]
- Khlifi, M.A.; Alkassem, A.; Draou, A. Performance Analysis of a Hybrid Microgrid with Energy Management. Eng. Technol. Appl. Sci. Res. 2022, 12, 8634–8639. [Google Scholar] [CrossRef]
- Vaičys, J.; Gudžius, S.; Jonaitis, A.; Račkienė, R.; Blinov, A.; Peftitsis, D. A Case Study of Optimising Energy Storage Dispatch: Convex Optimisation Approach with Degradation Considerations. J. Energy Storage 2024, 97, 112941. [Google Scholar] [CrossRef]
- Gong, X.; Dong, F.; Mohamed, M.A.; Abdalla, O.M.; Ali, Z.M. A Secured Energy Management Architecture for Smart Hybrid Microgrids Considering PEM-Fuel Cell and Electric Vehicles. IEEE Access 2020, 8, 47807–47823. [Google Scholar] [CrossRef]
- Manamperi, I.; Ahmad, I.; Habibi, D.; Aziz, A. Optimising Grid-Forming Inverters to Prevent under-Frequency Load Shedding with Minimal Energy Storage. J. Energy Storage 2024, 98, 112842. [Google Scholar] [CrossRef]
- Teske, F.; Schubert, J.; Fehrle, A.; Funk, F.; Franke, J. Techno-Economic Analysis of Battery Storage Systems and Hydrogen-Based Storage Systems as an Alternative to Grid Expansion in the Medium Voltage Grid in Germany. AIMS Energy 2023, 11, 358–401. [Google Scholar] [CrossRef]
- Geng, J.; Hao, H.; Hao, X.; Liu, M.; Dou, H.; Liu, Z.; Zhao, F. Techno-Economic Comparison of Vehicle-To-Grid and Commercial-Scale Battery Energy Storage System: Insights for the Technology Roadmap of Electric Vehicle Batteries. World Electr. Veh. J. 2025, 16, 200. [Google Scholar] [CrossRef]
- Song, M.; Xu, H.; Shen, Z.; Pan, X. Energy Market Integration and Renewable Energy Development: Evidence from the European Union Countries. J. Environ. Manag. 2022, 317, 115464. [Google Scholar] [CrossRef]
- Lu, K.-H.; Hong, C.-M.; Lian, J.; Cheng, F.-S. A Review of Synergies Between Advanced Grid Integration Strategies and Carbon Market for Wind Energy Development. Energies 2025, 18, 590. [Google Scholar] [CrossRef]
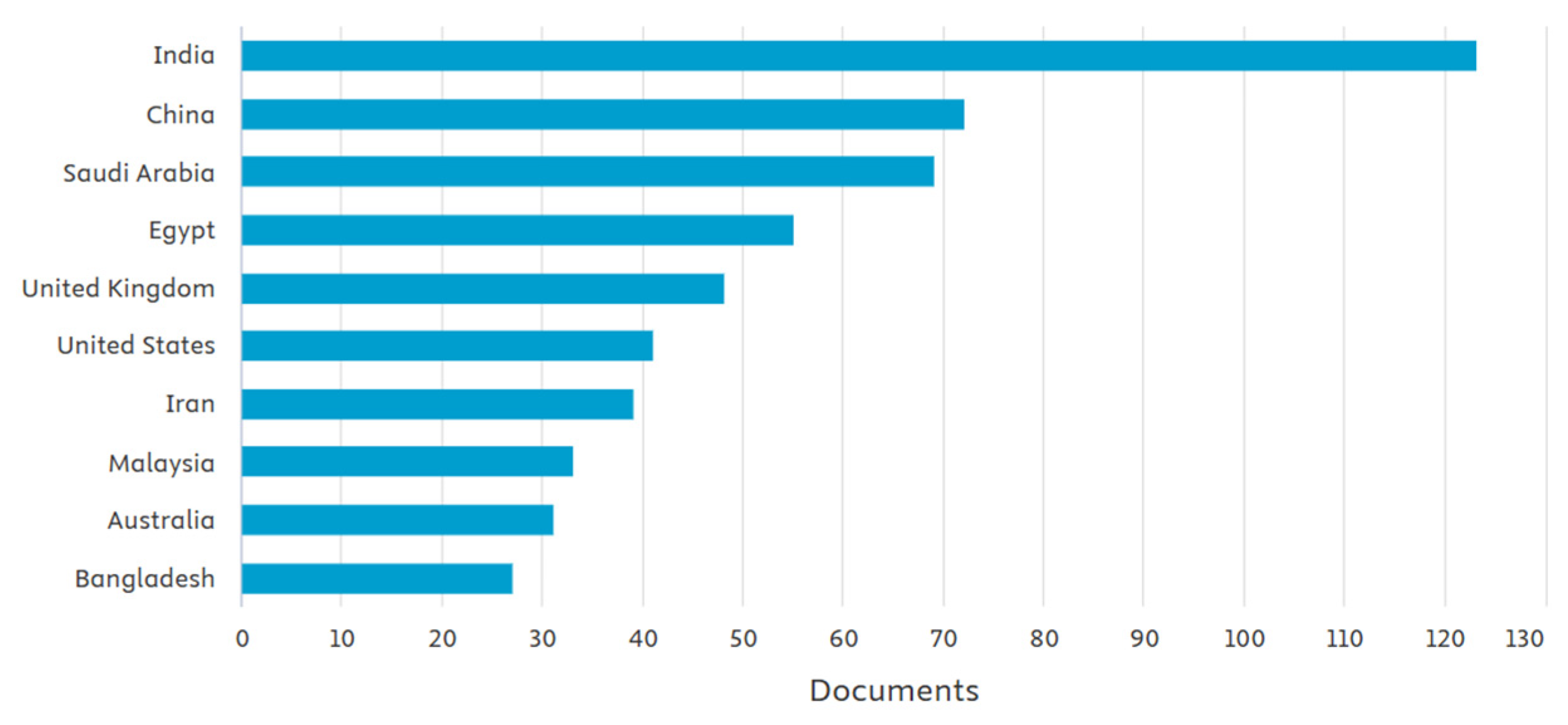
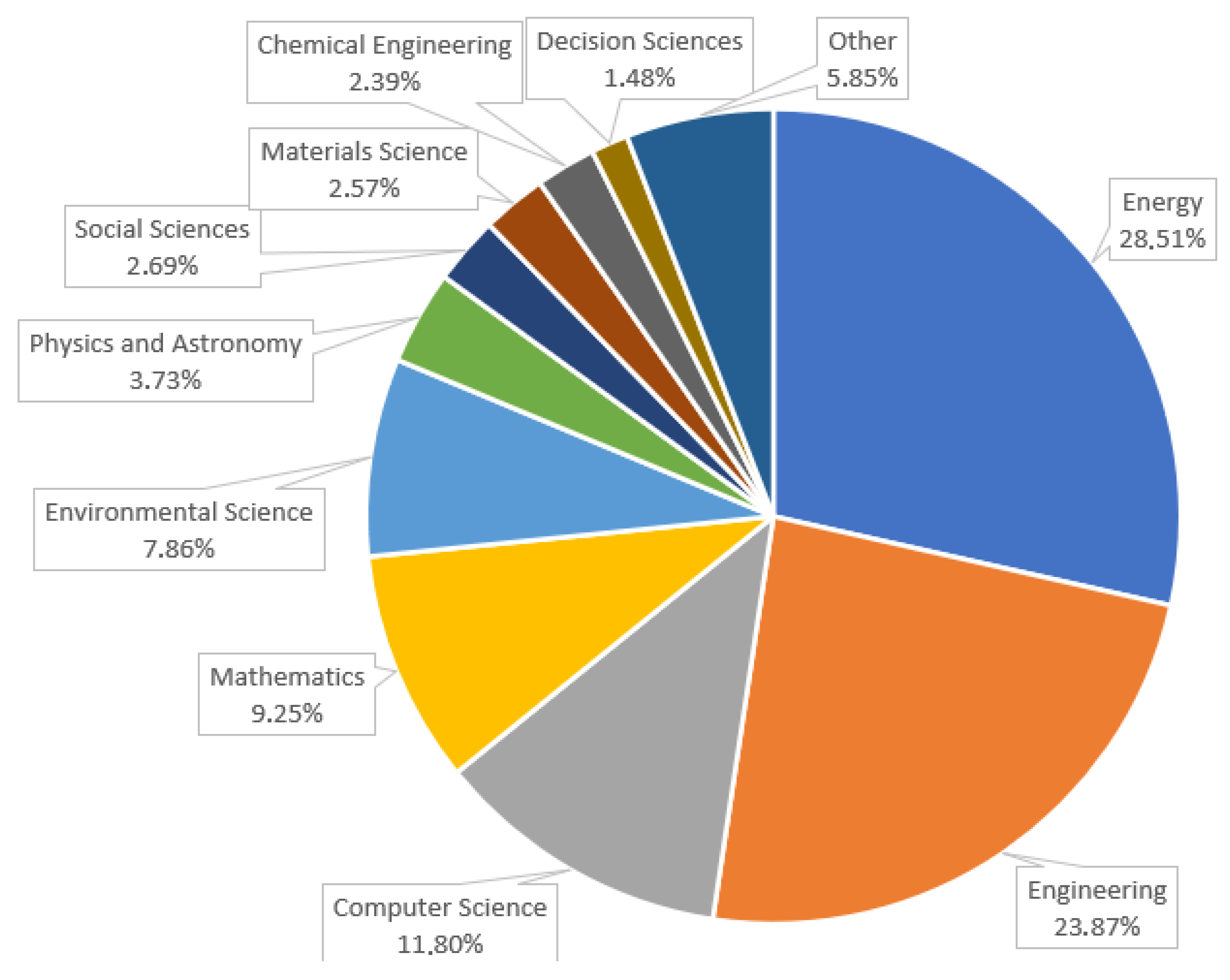

| Database Searched | Date of Last Search | Example Search String (Illustrative for Scopus) | Filters/Limits Applied |
|---|---|---|---|
| Scopus | 26 June 2025 | (TITLE-ABS-KEY (“Hybrid Renewable Energy System*” OR “HRES” OR “Hybrid Microgrid*” OR “Integrated Renewable Energy System*”) AND TITLE-ABS-KEY (“optimi*” OR “sizing” OR “design” OR “management” OR “control”) AND TITLE-ABS-KEY (“objective*” OR “goal*” OR “criteria” OR “metric*” OR “performance” OR “indicator*”) AND TITLE-ABS-KEY (“economic*” OR “cost” OR “LCOE” OR “NPC” OR “technical*” OR “reliab*” OR “LPSP” OR “efficien*” OR “environmental*” OR “emission*” OR “GHG” OR “social*” OR “job*” OR “acceptance”)) | Publication Years: 2014–2025; Language: English; Document Type: Article, Conference Paper, Review. |
| IEEE Xplore | 26 June 2025 | (((“Abstract”: “Hybrid Renewable Energy System*” OR “Abstract”: “HRES” OR “Abstract”: “Hybrid Microgrid*”) AND (“Abstract”: “optimi*” OR “Abstract”: “sizing” OR “Abstract”: “design”) AND (“Abstract”: “objective*” OR “Abstract”: “criteria” OR “Abstract”: “metric*”))) | Publication Years: 2014–2025; Content Type: Journals, Conferences |
| Web of Science (Core Collection) | 26 June 2025 | TS=(“Hybrid Renewable Energy System*” OR “HRES” OR “Hybrid Microgrid*”) AND TS=(“optimi*” OR “sizing” OR “design”) AND TS=(“objective*” OR “criteria” OR “metric*”) AND TS=(“economic*” OR “cost” OR “LCOE” OR “NPC” OR “technical*” OR “reliab*” OR “LPSP” OR “efficien*” OR “environmental*” OR “emission*” OR “GHG” OR “social*” OR “job*” OR “acceptance”) | Publication Years: 2014–2025; Language: English; Document Types: Article, Proceedings Paper |
| Decision Variable Category Example | Variable Symbol Example | Time Dependent? | Description | |
|---|---|---|---|---|
| Sizing (Design) | NPV | No | Number of PV panels | |
| NWT | No | Number of wind turbines | ||
| CBESS (kWh) | No | Rated capacity of battery energy storage | ||
| PBESS,inv (kW) | No | Rated power of battery inverter | ||
| PDG (kW) | No | Rated power of diesel generator | ||
| θ (°) | No | Orientation angle of PV modules | ||
| h (m) | No | Hub height of wind turbines | ||
| Operational (Dispatch) | Power dispatched from each generation unit at time t | PPV(t) | Yes | Power dispatched from PV at time t |
| PWT(t) | Yes | Power dispatched from wind turbines at time t | ||
| PDG(t) | Yes | Power dispatched from diesel generator at time t | ||
| Power flow to/from the battery at time t | PBESS,ch(t) | Yes | Charging power to battery at time t | |
| PBESS,dis(t) | Yes | Discharging power from battery at time t | ||
| Power exchanged with the utility grid at time t | Pgrid,buy(t) | Yes | Power imported from grid at time t | |
| Pgrid,sell(t) | Yes | Power exported to grid at time t | ||
| Power curtailed from renewable sources at time t | Pcurtail(t) | Yes | Renewable power curtailed at time t | |
| Constraint Type | Mathematical Form Example | Description |
|---|---|---|
| Equality (H(X) = 0) | ∀t: Pgen(t) + PBESS,dis(t) + Pgrid,buy(t) = Pload(t) + PBESS,ch(t) + Pgrid,sell(t) + Pcurtail(t) | Power balance at every time step: generation + imports + discharge = load + storage charge + exports + curtailment |
| Inequality (G(X) ≤ 0) | 0 ≤ PPV(t) ≤ PPV,available(t) | Generation cannot exceed resource availability |
| SOCmin ≤ SOC(t) ≤ SOCmax | Battery state-of-charge and charge/discharge rates limited by C-rate and inverter rating | |
| Pgrid,buy(t) ≤ Pgrid,max_import | Grid exchange limited by point-of-connection capacity | |
| LPSP(X) ≤ LPSPmax | Reliability requirement: Loss of power supply probability below a threshold |
| Specific Algorithm Example(s) | Brief Principle/Inspiration | Common HRES Applications | Reported Strengths | Reported Limitations/Challenges | Example References (Illustrative) |
|---|---|---|---|---|---|
| Classical/Deterministic | |||||
| Linear Programming (LP) | Solves problems with linear objective function and constraints. | Optimal dispatch, simple sizing if linearized. | Guarantees global optimum for linear problems, computationally efficient. | Limited to linear models, may oversimplify HRES component behavior. | [78] |
| Mixed-Integer LP (MILP) | LP with some integer variables. | Unit commitment, sizing with discrete component choices. | Handles discrete decisions, global optimum. | Computationally intensive for large problems. | [79] |
| Non-Linear Programming (NLP) | Solves problems with non-linear objective/constraints. | More realistic component modeling. | Can find global optimum if convex, handles non-linearities. | May get stuck in local optima for non-convex problems, complex to solve. | [80] |
| Metaheuristic | |||||
| Genetic Algorithm (GA) | Mimics natural selection and genetics. | Sizing, energy management, MOO. | Robust, good for global search, handles complex problems, widely used for MOO. | Computationally expensive, premature convergence, parameter tuning. | [81] |
| NSGA-II | Multi-objective GA producing a Pareto front of trade-off solutions. | Determining minimum energy cost, lifecycle emissions, maximizing job creation, optimal system configuration. | Efficient Pareto-front discovery; supports visualization of cost vs. reliability, etc. | Computationally expensive for many objectives; may require post-processing for decision. | [82] |
| Particle Swarm Optimization (PSO) | Simulates social behavior of bird flocking or fish schooling. | Sizing, energy management, MOO. | Simple concept, few parameters, fast convergence for some problems. | Can prematurely converge to local optima, parameter sensitivity. | [83] |
| MOPSO | Multi-objective extension of PSO. | Sizing of components, energy management, minimizing cost (LCOE, NPC), maximizing reliability, minimizing emissions. Often paired with economic criteria. | Provides Pareto front for conflicting objectives. | Shares PSO’s premature convergence issues; balancing objectives can be tricky. | [84] |
| Grey Wolf Optimizer (GWO) | Mimics leadership hierarchy and hunting behavior of grey wolves. | Sizing, parameter estimation. | Good balance of exploration/exploitation, fewer parameters. | Performance can vary with problem type, potential for local optima. | [85] |
| Other Swarm Algorithms | Sparrow search, salp swarm, gravitational search, etc. | Non-linear, multi-modal optimization problems in HRES. | Often claim improved exploration–exploitation balance. | Novelty claims not always rigorously proven; proliferation of similar variants. | [67,86,87,88] |
| Teaching–Learning-Based Opt. (TLBO) | Simulates teaching and learning process in a classroom. | Sizing, economic dispatch. | No algorithm-specific parameters to tune, often good convergence. | Can be slower than some other metaheuristics for certain problems. | [89] |
| AI-Specific (non-metaheuristic focus) | |||||
| Artificial Neural Networks (ANNs) | Inspired by biological neural networks. | Forecasting (solar, wind, load), component modeling. | Learns complex patterns from data, good for prediction. | Requires large datasets for training, “black box” nature. | [90] |
| Fuzzy Logic (FL) | Uses linguistic variables and fuzzy sets for reasoning. | Control strategies, decision making under uncertainty. | Handles imprecise/uncertain information well, human-like reasoning. | Rule base design can be complex and subjective. | [91] |
| Hybrid Algorithms | |||||
| Metaheuristic–Metaheuristic Hybrids | e.g., GA–PSO hybrids combining exploration and exploitation strengths. | Optimal sizing and configuration, operational scheduling and dispatch, multi-vector system co-optimization. | Balances global and local search, faster and more robust than single methods. | Increased algorithmic complexity; tuning two methods at once. | [92] |
| Metaheuristic–Classical Hybrids | Use metaheuristic for global region identification, then classical solver for local refinement. | Techno-economic sizing with exact bounds, robust scheduling under uncertainty. | Best of both worlds: global coverage plus precise local optimum. | Requires seamless integration; risk of inconsistency between models. | [93] |
| Algorithm–MCDM Hybrids | Generate Pareto front (e.g., NSGA II), then apply TOPSIS/AHP to pick final solution. | Pareto front exploration and selection, stakeholder-driven configuration. | Provides clear decision support among trade-offs. | Adds an extra decision analysis layer; decision-maker still needed. | [94] |
| Game-Theoretic Strategies | Models interactions between independent, rational agents (e.g., microgrids). | Cooperative/non-cooperative operation of multi-microgrid systems. | Captures strategic behavior in decentralized systems, finds stable equilibria. | Can be complex to formulate; assumes rational actors. | [95] |
| Software Tools | |||||
| HOMER Pro | Simulation and optimization software. | Microgrid design, component sizing, economic feasibility assessment, sensitivity analysis. | User-friendly, widely adopted, good for initial assessments. | Can be a “black box” for optimization algorithm, may have limitations for complex control. | [96] |
| iHOGA | GA-based HRES optimizer with detailed battery lifetime modeling. | Off-grid microgrid and standalone system sizing, multi-objective techno-economic optimization (cost, reliability, emissions), Pareto-front generation for different component mixes (PV, wind, battery, hydrogen). | More accurate battery lifetime predictions. | Less widely adopted; fewer community resources. | [97] |
| MATLAB | Flexible environment to code custom models, controls, and optimizers (including NSGA II, MOPSO, hybrids). | Implementing diverse optimization algorithms (MOPSO, NSGA-II, etc.), simulation-based scenario analysis, robust optimization, control system design. | Unlimited modeling possibilities, vast toolbox ecosystem. | Steep learning curve; high development time; license required. | [98] |
| Others (RETScreen, TRNSYS, PVSyst) | Specialized tools for energy project feasibility (RETScreen), detailed thermal/building modeling (TRNSYS), PV system analysis (PVSyst). | Preliminary feasibility screening, cash-flow modeling, and sensitivity/uncertainty studies for solar, wind, hydro, biomass and cogeneration systems. Researchers embed HRES controls and optimization loops (e.g., via external MATLAB or Python drivers) to study time-series performance, thermal–electric interactions, and component dynamics over hourly or sub-hourly steps. | Domain specific strengths: feasibility analysis, thermal dynamics, PV details. | Often single purpose; limited optimization flexibility; may require coupling with external solvers. | [101,102] |
| Strategy Type | Description | Example HRES Application |
|---|---|---|
| High-Level Relay | Algorithms are run sequentially, where the output of one algorithm serves as the input for the next. | A GA is used to find a promising region of the search space, and then a PSO is initiated in that region to quickly find a refined local optimum. |
| High-Level Co-Evolutionary | Multiple algorithms (or subpopulations) run in parallel and exchange information periodically. | A GA subpopulation and a PSO subpopulation evolve independently for several generations, after which the best individuals are exchanged between them. |
| Low-Level Relay | A component of one algorithm is replaced by another algorithm, which is then run sequentially. | An algorithm uses a standard evolutionary framework, but instead of a simple mutation operator, it calls a complete SA algorithm to explore the neighborhood of a solution. |
| Low-Level Co-Evolutionary | A component of one algorithm is replaced by a component from another algorithm. | A GA incorporates the velocity update rule from PSO as one of its mutation operators to guide the search more effectively. |
| Aspect | Early Focus (e.g., Pre-2015–Mid-2010s) | Recent Trends (e.g., Mid-2010s–Present) | Driving Factors for Change |
|---|---|---|---|
| Optimization Approach | Predominantly single-objective optimization (SOO). | Strong shift towards multi-objective optimization (MOO). | Recognition of multiple conflicting criteria in real-world projects; desire for holistic solutions. |
| Primary Objective Categories | Dominated by economic (cost) and technical (reliability) objectives. | Continued importance of economic and technical, with significant increase in environmental objectives. Emerging focus on social objectives. | Growing climate change concerns; sustainability goals; increased awareness of social impacts and equity. |
| Specific Environmental Focus | Less emphasis, often limited to fuel consumption. | Strong focus on minimizing greenhouse gas (CO2) emissions. | Global climate agreements; national emission reduction targets; increased environmental awareness. |
| Social Considerations | Rarely explicitly included in quantitative optimization. | Increasing inclusion of metrics like job creation, social acceptance, energy access. | Focus on sustainable development goals (SDGs); community engagement; energy justice. |
| Algorithm Preference | Classical methods, early metaheuristics. | Dominance of advanced metaheuristics (NSGA-II, MOPSO, etc.), hybrid algorithms, AI/ML integration. | Need for efficient handling of complex MOO problems, non-linearities, and uncertainties. |
| Gap | Sub-Gap ID | Research Gap Description | Impact/Significance | Key Research Questions |
|---|---|---|---|---|
| 1. Problem Formulation | 1.1 | Holistic Multi-Objective Integration: Lack of mathematically tractable models for co-optimizing techno-economic, environmental, social, and resilience objectives. | Neglect of social benefits or system fragility to extreme events leads to suboptimal or non-resilient solutions. | How can social metrics (e.g., job creation, HDI) be functionally linked to engineering variables? What resilience metrics are both quantifiable and optimizable? |
| 1.2 | Dynamic and Multi-Scale Co-Optimization: Disconnect between long-term sizing and short-term dispatch models. | Causes designs that perform poorly in real-world operation, increasing cost or unreliability. | How can we formulate and solve bi-level/multi-level models that bridge planning and operation? | |
| 1.3 | Multi-Vector System Boundary Definition: Ambiguity when modeling integration with transport (V2G) and gas (H2) sectors. | Prevents optimization of cross-sector synergies and can introduce systemic instability. | What frameworks best model coupled energy systems? How can we resolve multi-sector constraint conflicts? | |
| 2. Solution Methodology | 2.1 | Scalability and Real-Time Performance of AI: Metaheuristics/AI are computationally intensive and impractical for real-time or large-scale deployment. | Hinders adoption of advanced optimization in practical settings. | How can faster, scalable algorithms be designed? Can surrogate models (e.g., ANNs) approximate simulations effectively? |
| 2.2 | Optimization Under Severe Data Scarcity: Most uncertainty models rely on rich historical datasets. | Excludes deployment in remote or developing regions with minimal data. | Can transfer learning or few-shot learning improve model reliability? What robust optimization approaches suit data-poor contexts? | |
| 2.3 | Explainability and Trust in AI-based EMS: Black-box controllers (e.g., DRL) lack interpretability and auditability. | Slows real-world adoption due to low transparency and regulatory hesitancy. | How can XAI methods clarify DRL controller decisions? What constitutes “trustworthy” control from an operator’s view? | |
| 3. Tech and Validation | 3.1 | Co-Optimization with Emerging Tech Degradation: Missing accurate degradation models for V2G batteries, electrolyzers, fuel cells. | Underestimated lifecycle costs distort system design and investment strategies. | What degradation models are valid for emerging tech? How can we include them in optimization without causing intractability? |
| 3.2 | The “Valley of Death” from Simulation to Bankability: Disconnect between simulations and financeable, real-world deployment. | Limits HRES commercialization; academic outputs misaligned with investor metrics. | What validation frameworks are needed? How can we align academic performance indicators with investor risk metrics? | |
| 3.3 | Software Tool Limitations: Commercial software lacks adaptability to advanced objectives and models. | Forces researchers to create ad hoc tools, hampering collaboration and comparability. | What features should an open-source HRES tool have? How can we design for extensibility and community growth? |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korovushkin, V.; Boichenko, S.; Artyukhov, A.; Ćwik, K.; Wróblewska, D.; Jankowski, G. Modern Optimization Technologies in Hybrid Renewable Energy Systems: A Systematic Review of Research Gaps and Prospects for Decisions. Energies 2025, 18, 4727. https://doi.org/10.3390/en18174727
Korovushkin V, Boichenko S, Artyukhov A, Ćwik K, Wróblewska D, Jankowski G. Modern Optimization Technologies in Hybrid Renewable Energy Systems: A Systematic Review of Research Gaps and Prospects for Decisions. Energies. 2025; 18(17):4727. https://doi.org/10.3390/en18174727
Chicago/Turabian StyleKorovushkin, Vitalii, Sergii Boichenko, Artem Artyukhov, Kamila Ćwik, Diana Wróblewska, and Grzegorz Jankowski. 2025. "Modern Optimization Technologies in Hybrid Renewable Energy Systems: A Systematic Review of Research Gaps and Prospects for Decisions" Energies 18, no. 17: 4727. https://doi.org/10.3390/en18174727
APA StyleKorovushkin, V., Boichenko, S., Artyukhov, A., Ćwik, K., Wróblewska, D., & Jankowski, G. (2025). Modern Optimization Technologies in Hybrid Renewable Energy Systems: A Systematic Review of Research Gaps and Prospects for Decisions. Energies, 18(17), 4727. https://doi.org/10.3390/en18174727