Novel Adaptive Super-Twisting Sliding Mode Observer for the Control of the PMSM in the Centrifugal Compressors of Hydrogen Fuel Cells
Abstract
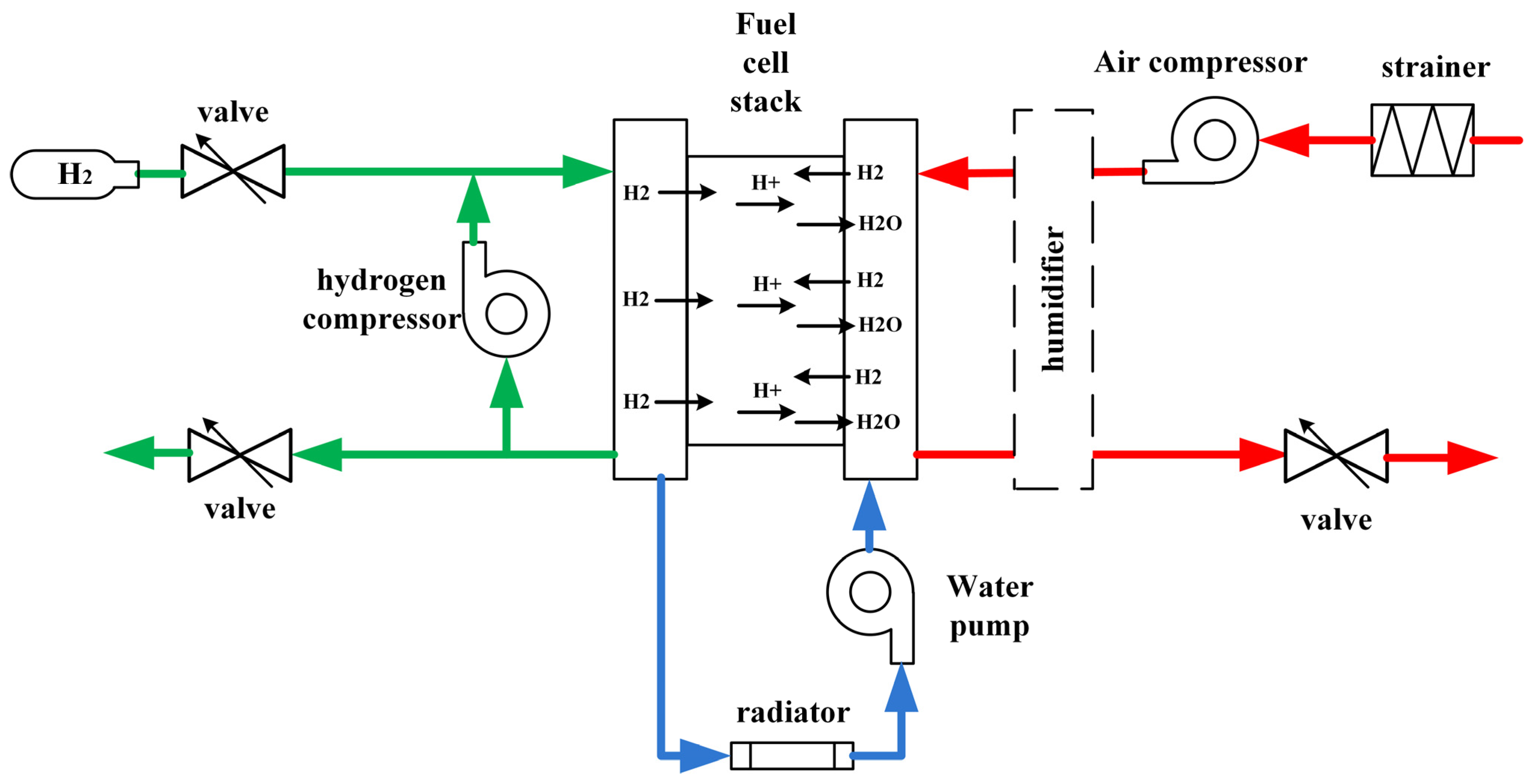
1. Introduction
- This paper proposes an improved STSMO model, which can increase the convergence speed of the SMO against sudden current change.
- This paper prosses a novel adaptive law of the STSMO. This adaptive law considers the influences of motor parameters, speed, and current change. Therefore, the STSMO using this adaptive law can suppress chattering and maintain high accuracy on complex operating conditions over a wide range of speed variations or current fluctuations.
2. Conventional ASTSMO for PMSM Control
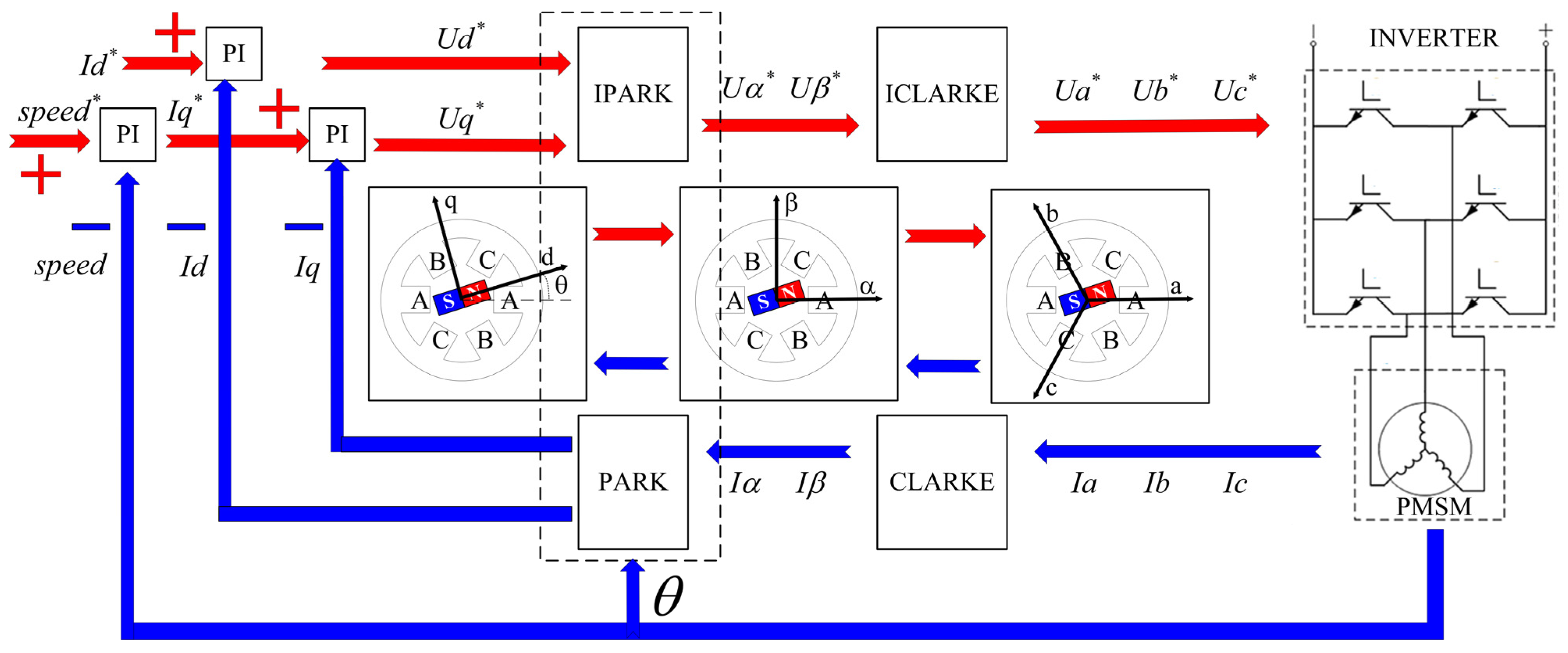
2.1. Basic Theory of FOC Strategy
2.2. Model of SMO in PMSM Control Systems
- The inductance of the d-axis is approximately equivalent to that of the q-axis.
- The magnetic field is sinusoidally distributed in space.
- The effect of magnetic cross-saturation is neglected.
2.3. Super-Twisting Algorithm
2.4. Conventional Adaptive STSMO
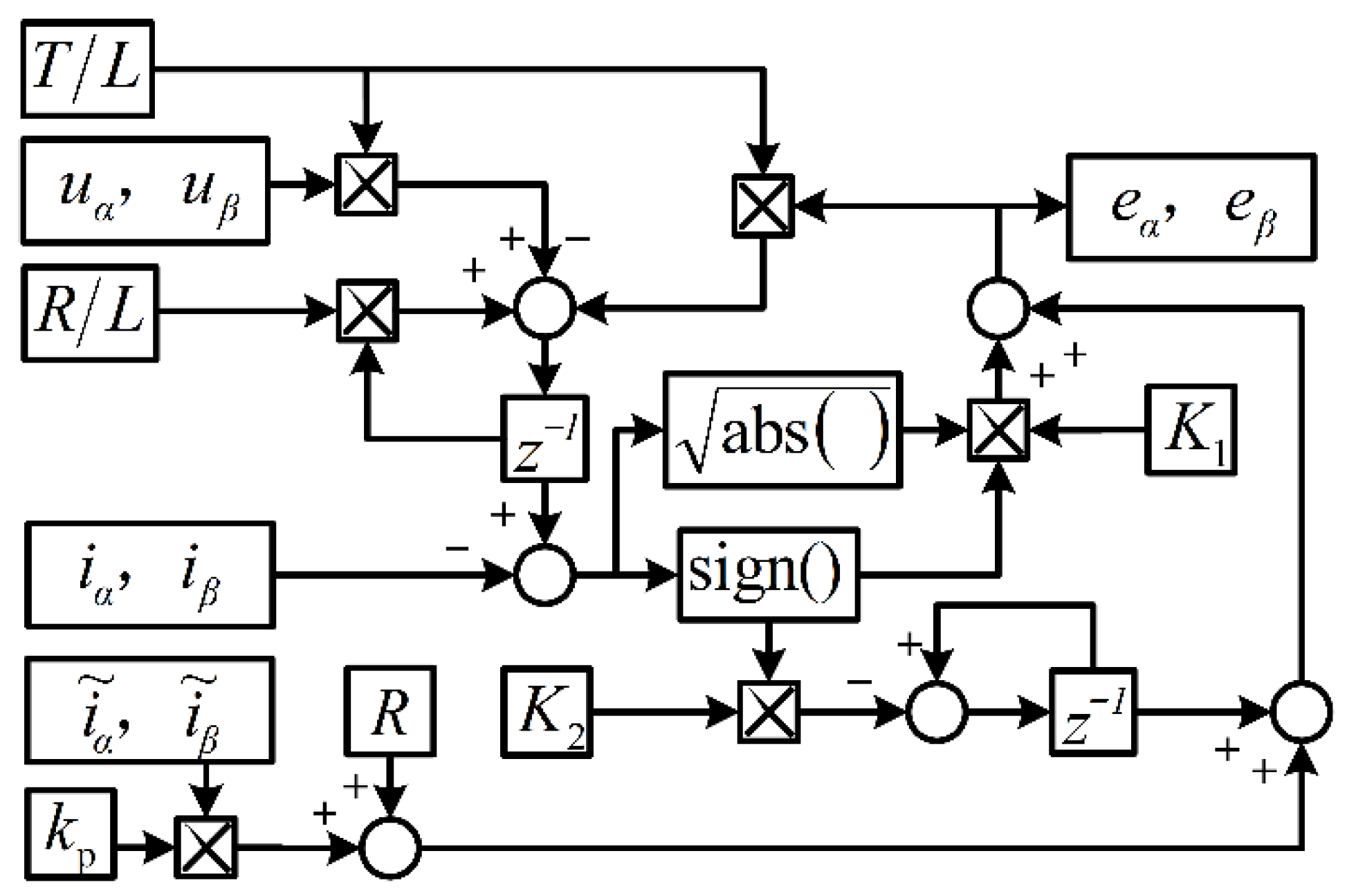
3. The Proposed Method of Novel ASTSMO
3.1. STSMO with Linear Term
3.2. Stability Analysis
3.3. Design of Adaptive Law
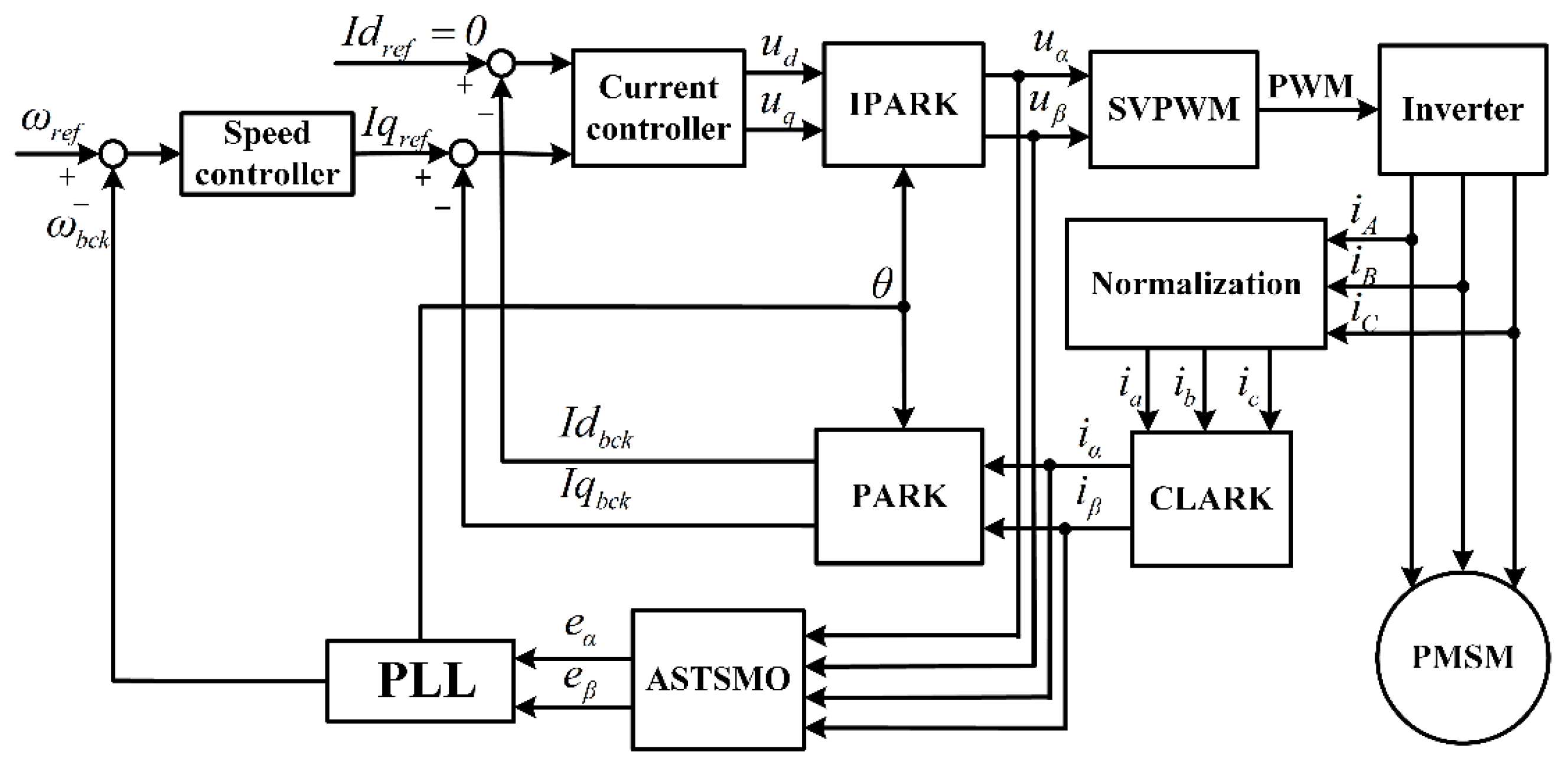
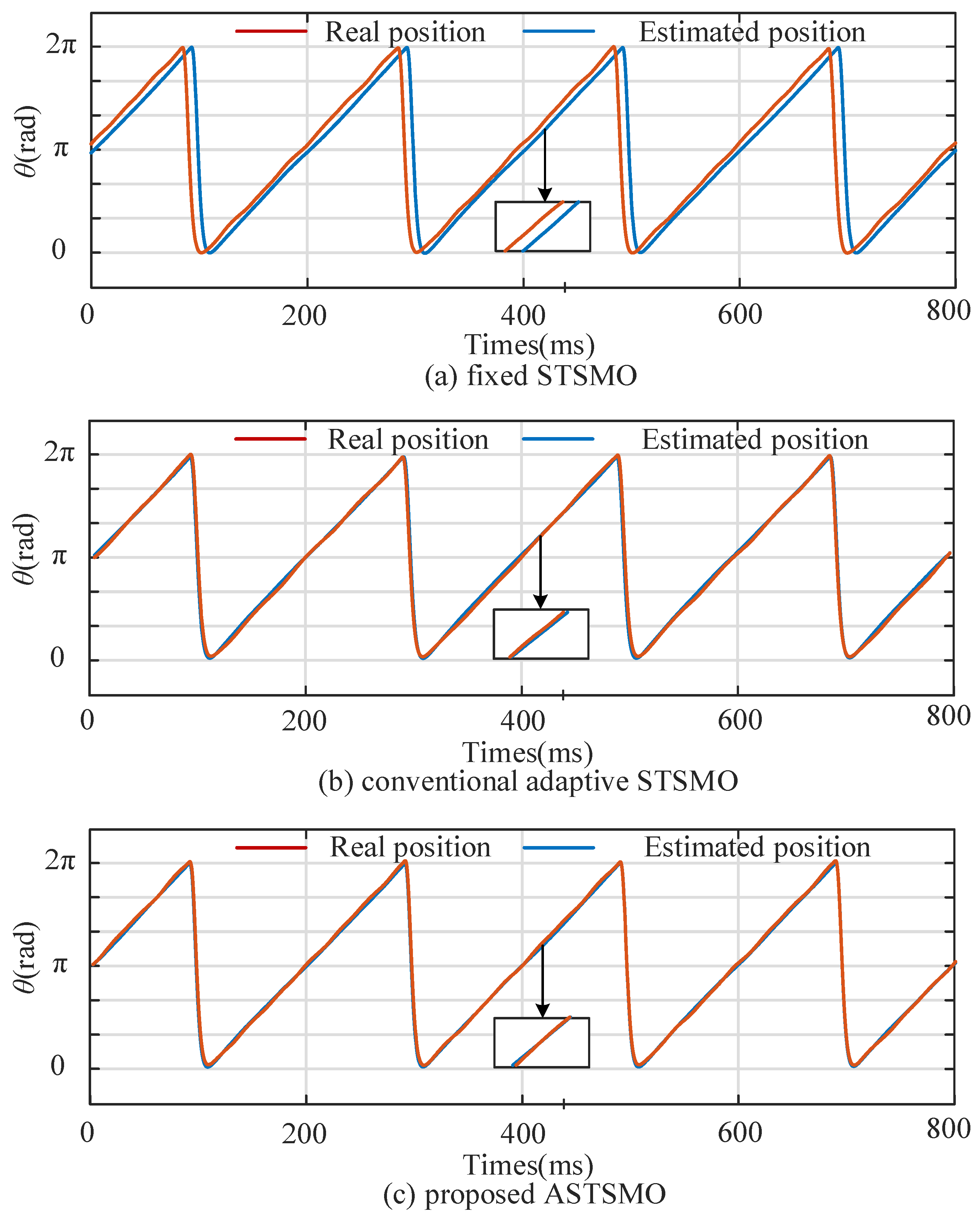
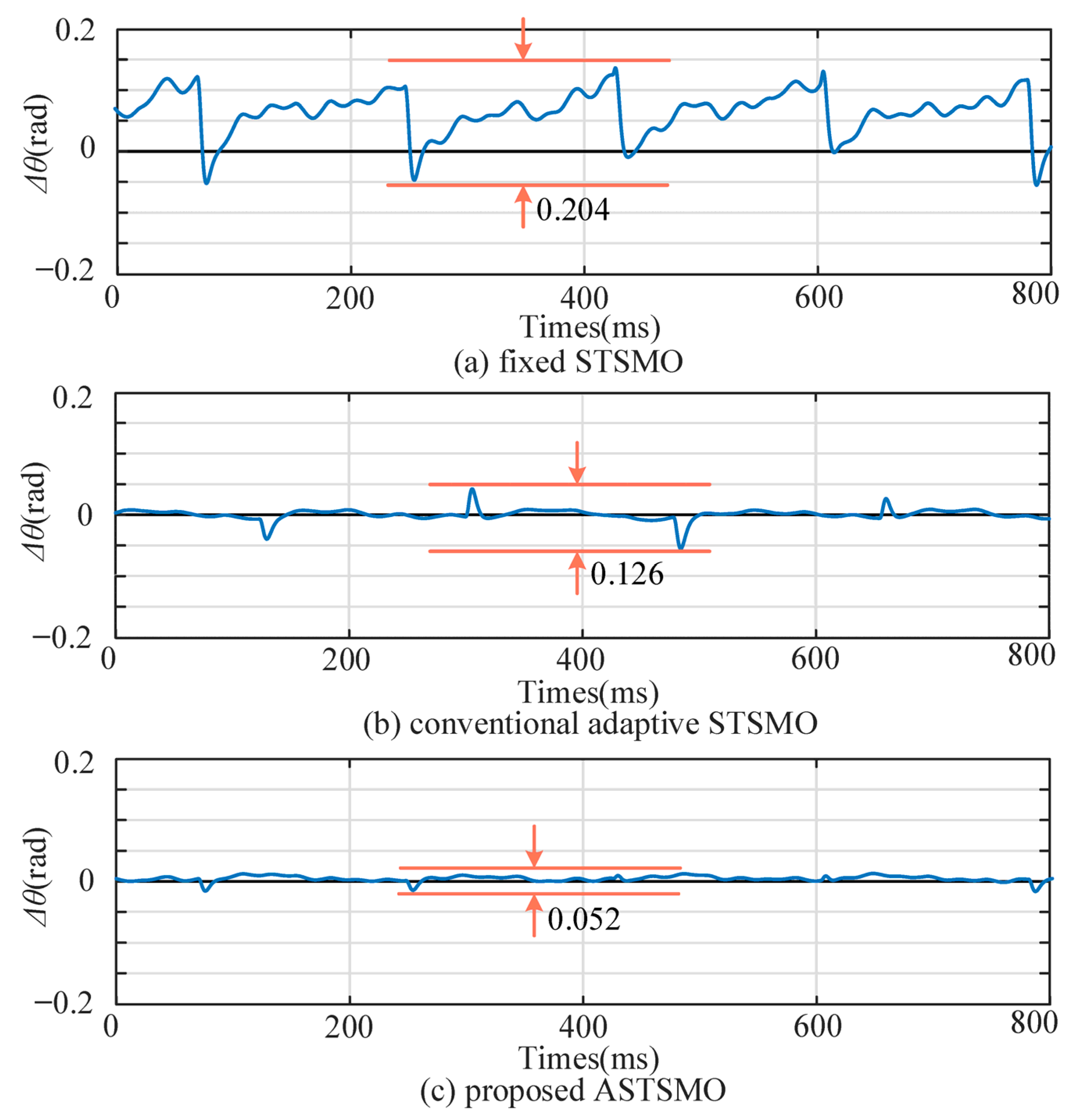
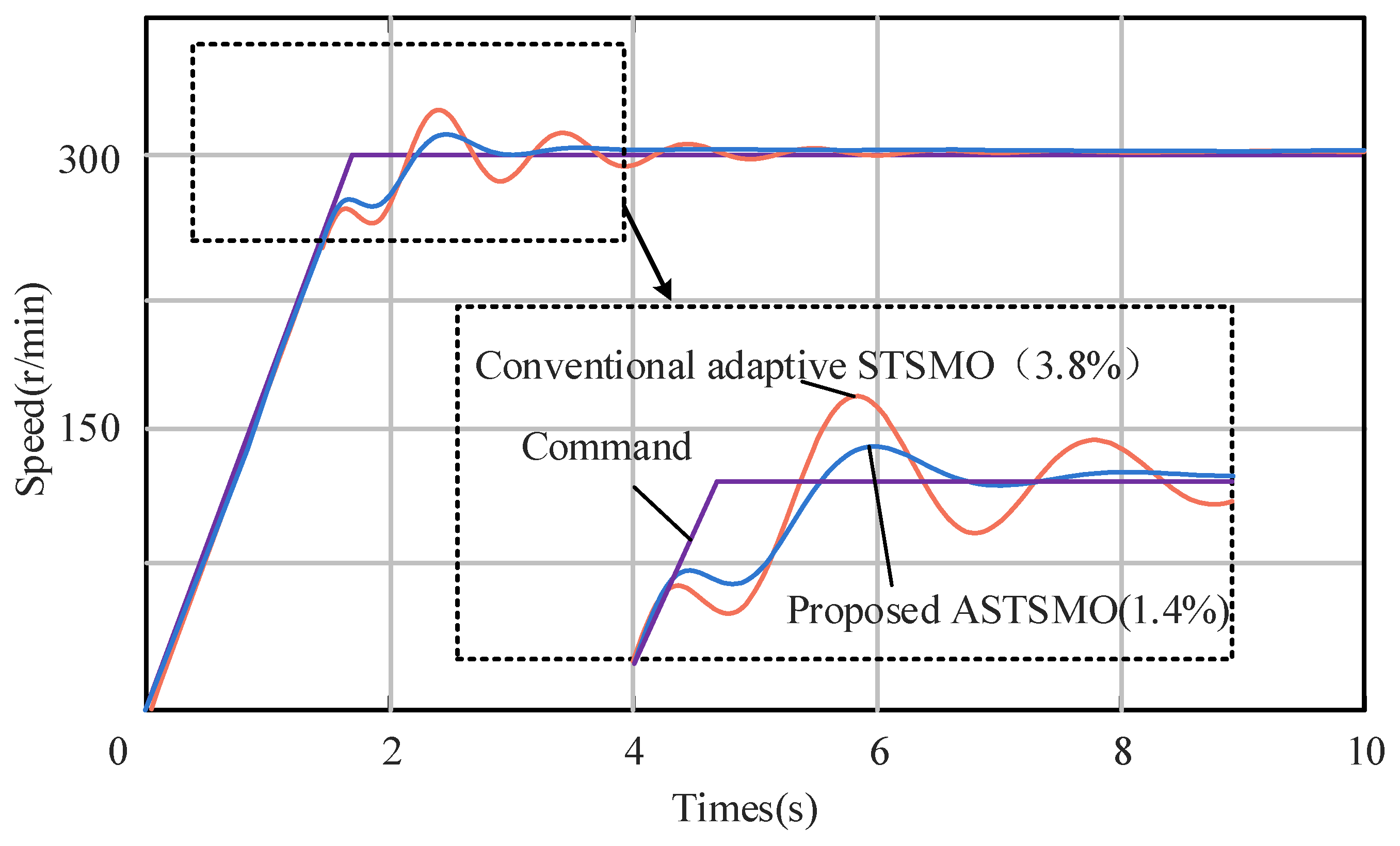
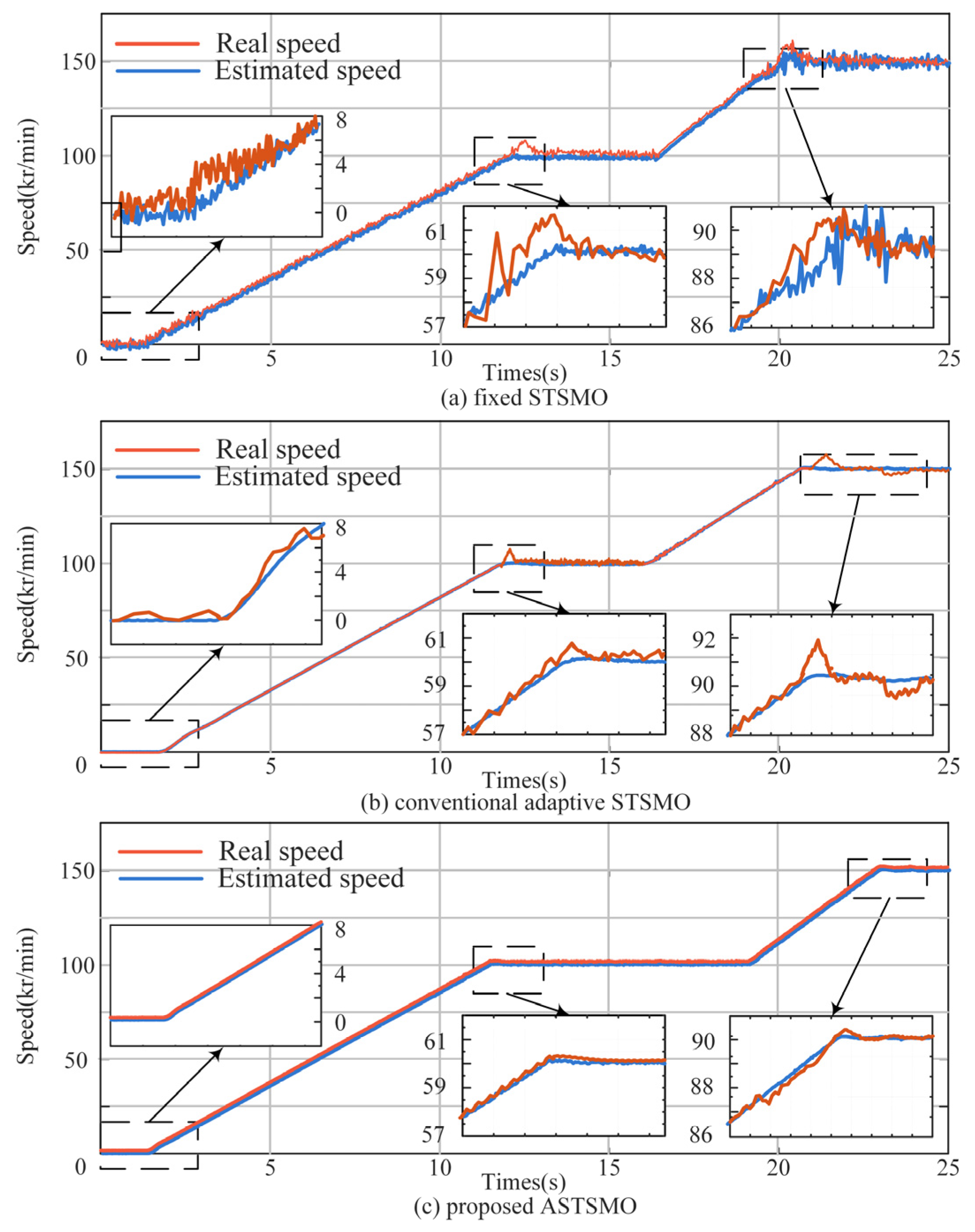
4. Experiments and Discussions
4.1. Simulation Results
4.2. Steady State Performance Experiment
4.3. Experiment with Motor Parameters Variation
4.4. Experiment with Motor Speed Variation
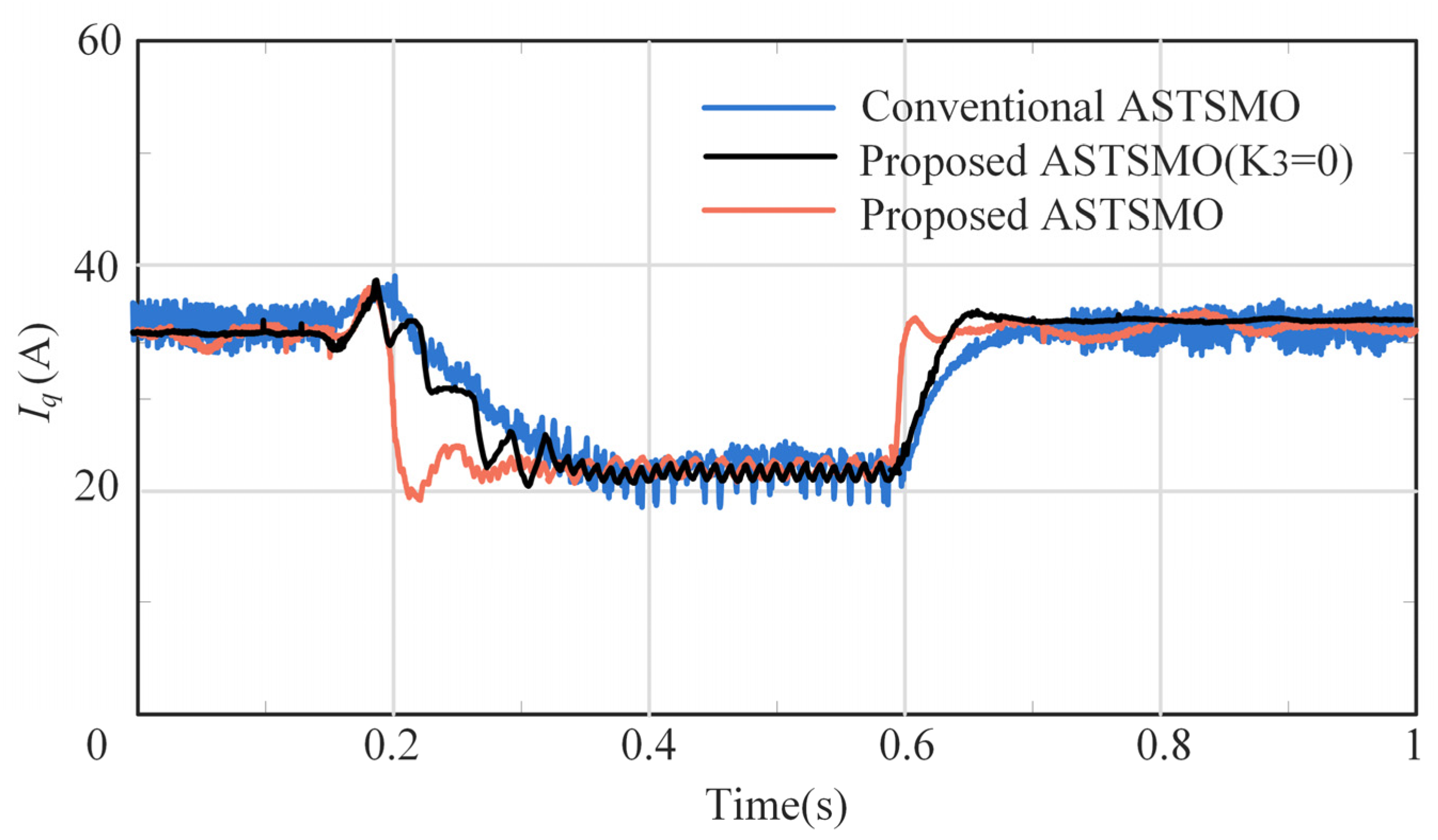
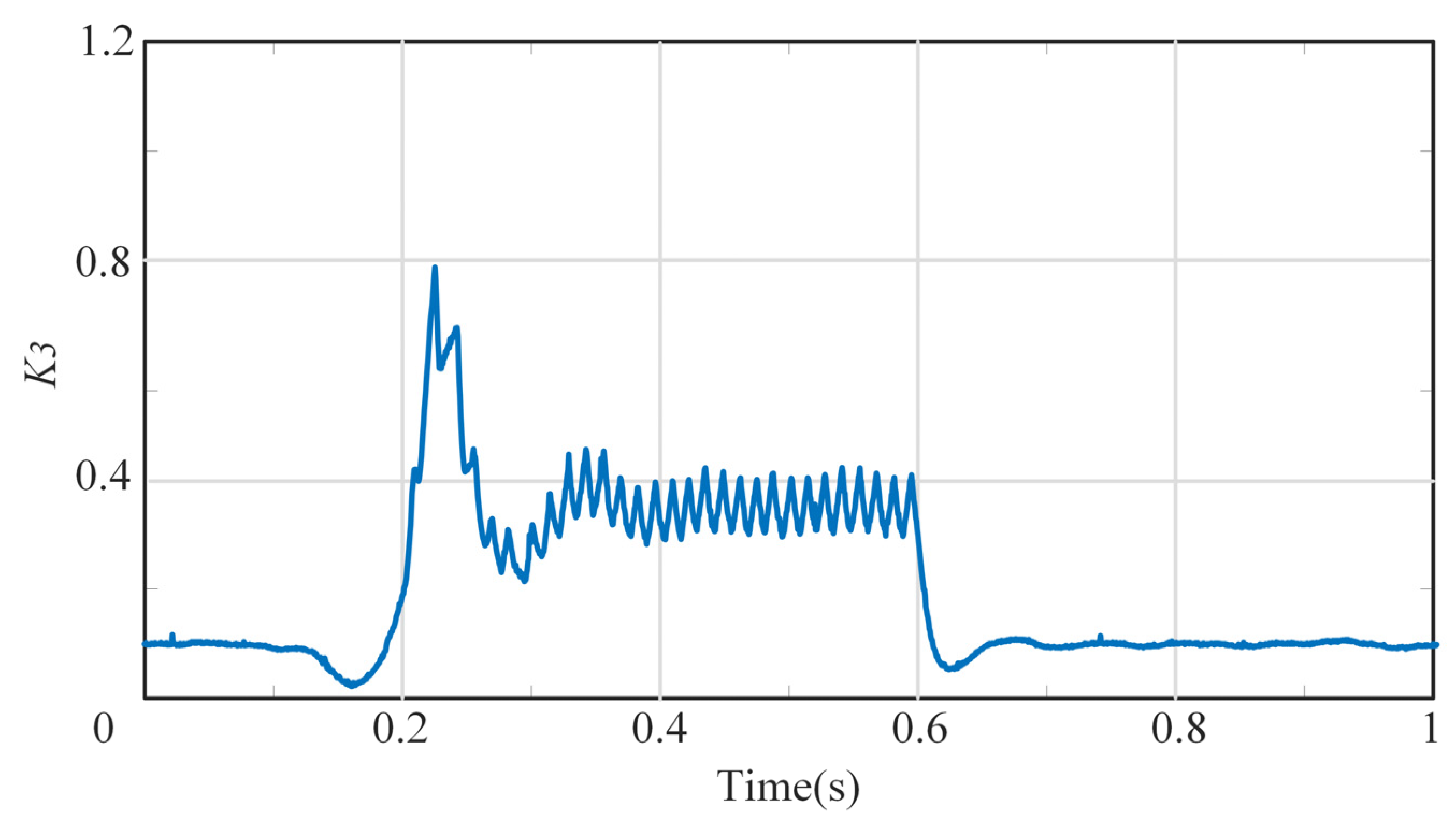
4.5. Experiment with Torque Current Variation
4.6. Test of CHC
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PMSM | Permanent magnetic synchronous motor |
| CHC | Centrifugal hydrogen compressor |
| ASTSMO | Adaptive super-twisting sliding mode observer |
| STA | Super-twisting algorithm |
| SMO | Sliding mode observer |
| FOC | Field orient control |
| PLL | Phase-lock loop |
| STSMO | Super-twisting sliding mode observer |
References
- Peng, Q.; Bao, R.; Li, J.; Ren, J.; Tang, J.; Li, J.; Pan, Z.; Ma, G.; Gao, Y.; Kang, T.; et al. Centrifugal compressor performance prediction and dynamic simulation of natural gas hydrogen blended. Int. J. Hydrogen Energy 2024, 52, 872–893. [Google Scholar] [CrossRef]
- Singh, U.R.; Bhogilla, S. A self-sustaining renewable energy driven hydrogen refuelling system utilising a metal hydride-based compressor. Int. J. Hydrogen Energy 2024, 52, 1419–1433. [Google Scholar] [CrossRef]
- Ye, J.; He, Y.; Du, Z.; Ji, R.; Xie, J.; Liu, J. The transient flow and heat transfer characteristics in reciprocated conditions of hydraulic-driven piston hydrogen compressor in hydrogen storage system. J. Energy Storage 2024, 89, 111662. [Google Scholar] [CrossRef]
- Khan, A.; Irfan, M.; Niazi, U.M.; Shah, I.; Legutko, S.; Rahman, S.; Alwadie, A.S.; Jalalah, M.; Glowacz, A.; Khan, M.K.A. Centrifugal Compressor Stall Control by the Application of Engineered Surface Roughness on Diffuser Shroud Using Numerical Simulations. Materials 2021, 14, 2033. [Google Scholar] [CrossRef]
- Dong, L.; Jiang, P. Improved super-twisting sliding mode control strategy in permanent magnet synchronous motors for hydrogen fuel cell centrifugal compressor. Heliyon 2024, 10, e24181. [Google Scholar] [CrossRef]
- Yu, Y.; Tu, Z.; Zhang, H.; Zhan, Z.; Pan, M. Comparison of degradation behaviors for open-ended and closed proton exchange membrane fuel cells during startup and shutdown cycles. J. Power Sources 2011, 196, 5077–5083. [Google Scholar] [CrossRef]
- Bacak, A.; Pınarbaşı, A.; Dalkılıç, A.S. A 3-D FSI simulation for the performance prediction and valve dynamic analysis of a hermetic reciprocating compressor. Int. J. Refrig. 2023, 150, 135–148. [Google Scholar] [CrossRef]
- Guo, X.; Hu, X.; Zhang, S. Application status of variable-frequency drive in hydrogen fuel cell air compressors from an industrial viewpoint: A review. Sustain. Energy Technol. Assess. 2024, 64, 103716. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, Y.; Tang, B.; Li, L. Dynamic performance of suction valve in stepless capacity regulation system for large-scale reciprocating compressor. Appl. Therm. Eng. 2016, 96, 167–177. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, H.; Fu, J.; Wang, X.; Liu, J. Review of recent developments in fuel cell centrifugal air compressor: Comprehensive performance and testing techniques. Int. J. Hydrogen Energy 2023, 48, 32039–32055. [Google Scholar] [CrossRef]
- Hou, J.; Yang, M.; Ke, C.; Zhang, J. Control logics and strategies for air supply in PEM fuel cell engines. Appl. Energy 2020, 269, 115059. [Google Scholar] [CrossRef]
- Gao, D.; Jin, Z.; Zhang, J.; Li, J.; Ouyang, M. Development and performance analysis of a hybrid fuel cell/battery bus with an axle integrated electric motor drive system. Int. J. Hydrogen Energy 2016, 41, 1161–1169. [Google Scholar] [CrossRef]
- Wang, K.; Yan, Y.; Mao, K.; Zheng, S.; Hao, M.; Zhang, Y. Adaptive current decoupling control scheme based on online multi-parameter identification for high-speed permanent magnet synchronous motor in fuel cell. Int. J. Hydrogen Energy 2024, 86, 542–553. [Google Scholar] [CrossRef]
- Jiang, Y.; Cheng, M. An improved initial rotor position estimation method using high-frequency pulsating voltage injection for PMSM. Def. Technol. 2024, 33, 19–29. [Google Scholar] [CrossRef]
- Chi, X.; Wang, C.; Wu, Q.; Yang, J.; Lin, W.; Zeng, P.; Li, H.; Shao, M. A ripple suppression of sensorless FOC of PMSM electrical drive system based on MRAS. Results Eng. 2023, 20, 101427. [Google Scholar] [CrossRef]
- Dan, L. EKF-based fault detection and isolation for PMSM inverter. Sustain. Energy Technol. Assess. 2022, 52, 101846. [Google Scholar] [CrossRef]
- Li, Y.; Wang, D.; Zhou, S. Moment of inertia identification for PMSM based on extended SMO and improved RBFNN. Energy Rep. 2023, 9, 521–528. [Google Scholar] [CrossRef]
- Zuo, Y.; Lai, C.; Iyer, K.L.V. A Review of Sliding Mode Observer Based Sensorless Control Methods for PMSM Drive. IEEE Trans. Power Electron. 2023, 38, 11352–11367. [Google Scholar] [CrossRef]
- Hou, Q.; Ding, S. Finite-Time Extended State Observer-Based Super-Twisting Sliding Mode Controller for PMSM Drives with Inertia Identification. IEEE Trans. Transp. Electrif. 2022, 8, 1918–1929. [Google Scholar] [CrossRef]
- Xu, W.; Cheng, S.; Ge, J.; Zhou, M.; Liao, K.; Wang, A.; Qu, G. Improved Adaptive Terminal Sliding-Mode Reaching Law for Speed Control of TPMLSM with Disturbance Observer. IEEE Trans. Ind. Appl. 2023, 59, 3210–3219. [Google Scholar] [CrossRef]
- Gong, C.; Hu, Y.; Gao, J.; Wang, Y.; Yan, L. An Improved Delay-Suppressed Sliding-Mode Observer for Sensorless Vector-Controlled PMSM. IEEE Trans. Ind. Electron. 2020, 67, 5913–5923. [Google Scholar] [CrossRef]
- An, Q.; Zhang, J.; An, Q.; Liu, X.; Shamekov, A.; Bi, K. Frequency-Adaptive Complex-Coefficient Filter-Based Enhanced Sliding Mode Observer for Sensorless Control of Permanent Magnet Synchronous Motor Drives. IEEE Trans. Ind. Appl. 2020, 56, 335–343. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, H.; Song, X. Position-Estimation Deviation-Suppression Technology of PMSM Combining Phase Self-Compensation SMO and Feed-Forward PLL. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 335–344. [Google Scholar] [CrossRef]
- Song, X.; Fang, J.; Han, B.; Zheng, S. Adaptive Compensation Method for High-Speed Surface PMSM Sensorless Drives of EMF-Based Position Estimation Error. IEEE Trans. Power Electron. 2016, 31, 1438–1449. [Google Scholar] [CrossRef]
- Li, S.; Xu, Y.; Zhang, W.; Zou, J. Robust Deadbeat Predictive Direct Speed Control for PMSM with Dual Second-Order Sliding-Mode Disturbance Observers and Sensitivity Analysis. IEEE Trans. Power Electron. 2023, 38, 8310–8326. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; Djerdir, A.; Cirrincione, M. Disturbance-Observer-Based Complementary Sliding-Mode Speed Control for PMSM Drives: A Super-Twisting Sliding-Mode Observer-Based Approach. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5416–5428. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, M.; Wang, B.; Chen, Y.; Xu, D. Precise Position Control Based on Resonant Controller and Second-Order Sliding Mode Observer for PMSM-Driven Feed Servo System. IEEE Trans. Transp. Electrif. 2023, 9, 196–209. [Google Scholar] [CrossRef]
- Lian, C.; Xiao, F.; Gao, S.; Liu, J. Load Torque and Moment of Inertia Identification for Permanent Magnet Synchronous Motor Drives Based on Sliding Mode Observer. IEEE Trans. Power Electron. 2019, 34, 5675–5683. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Zou, J. Sliding-Mode Sensorless Control of PMSM with Inverter Nonlinearity Compensation. IEEE Trans. Power Electron. 2019, 34, 10206–10220. [Google Scholar] [CrossRef]
- Morales, D.B.; Delpoux, R.; Lechappe, V.; Morales, J.D.L. Single-Gain Super-Twisting Algorithm Application to PMSM. IEEE J. Emerg. Sel. Top. Ind. Electron. 2021, 2, 237–246. [Google Scholar] [CrossRef]
- Sreejith, R.; Singh, B. Sensorless Predictive Control of SPMSM-Driven Light EV Drive Using Modified Speed Adaptive Super Twisting Sliding Mode Observer with MAF-PLL. IEEE J. Emerg. Sel. Top. Ind. Electron. 2021, 2, 42–52. [Google Scholar] [CrossRef]
- Liang, D.; Li, J.; Qu, R. Sensorless Control of Permanent Magnet Synchronous Machine Based on Second-Order Sliding-Mode Observer with Online Resistance Estimation. IEEE Trans. Ind. Appl. 2017, 53, 3672–3682. [Google Scholar] [CrossRef]
- Liang, D.; Li, J.; Qu, R.; Kong, W. Adaptive Second-Order Sliding-Mode Observer for PMSM Sensorless Control Considering VSI Nonlinearity. IEEE Trans. Power Electron. 2018, 33, 8994–9004. [Google Scholar] [CrossRef]
- Ding, L.; Li, Y.W.; Zargari, N.R. Discrete-Time SMO Sensorless Control of Current Source Converter-Fed PMSM Drives with Low Switching Frequency. IEEE Trans. Ind. Electron. 2021, 68, 2120–2129. [Google Scholar] [CrossRef]
- An, Q.; Zhang, J.; An, Q.; Shamekov, A. Quasi-Proportional-Resonant Controller Based Adaptive Position Observer for Sensorless Control of PMSM Drives Under Low Carrier Ratio. IEEE Trans. Ind. Electron. 2020, 67, 2564–2573. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2856–2861. [Google Scholar]
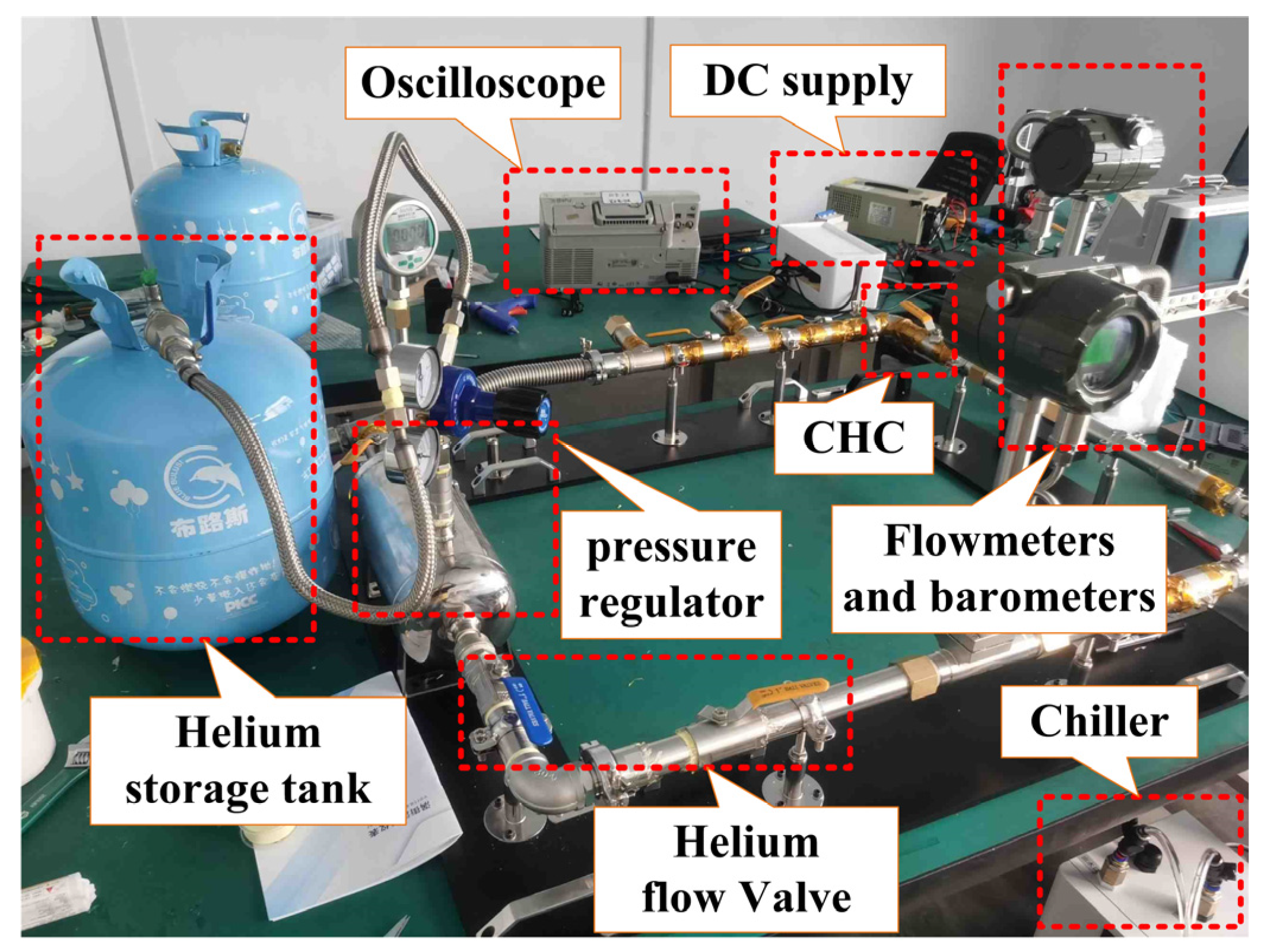
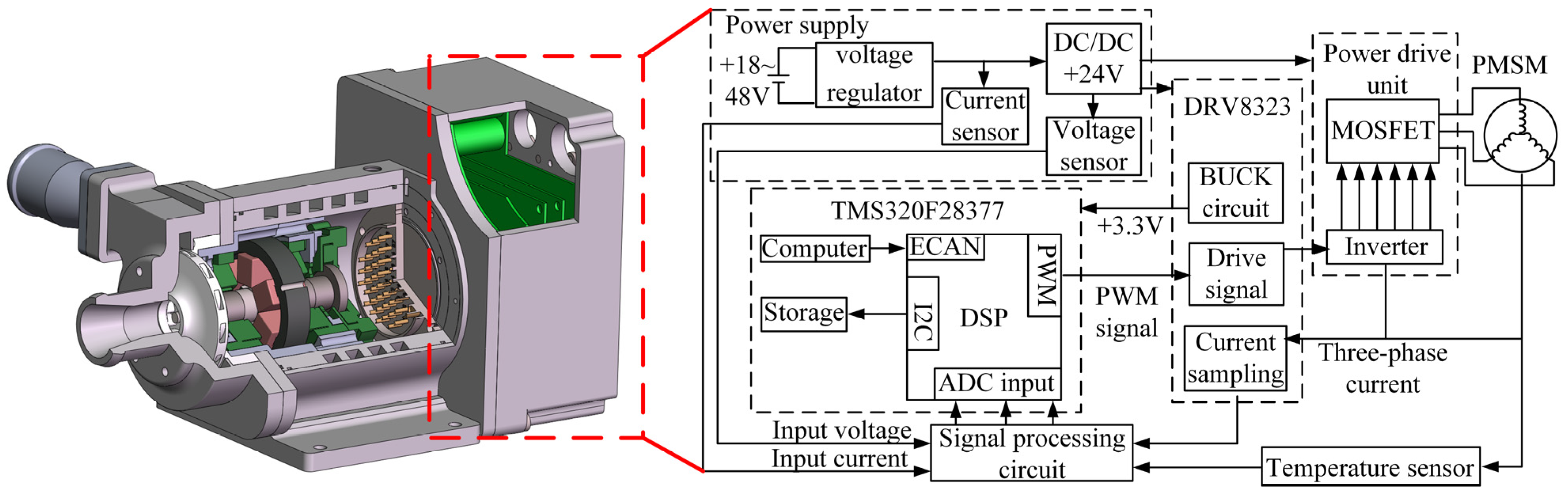
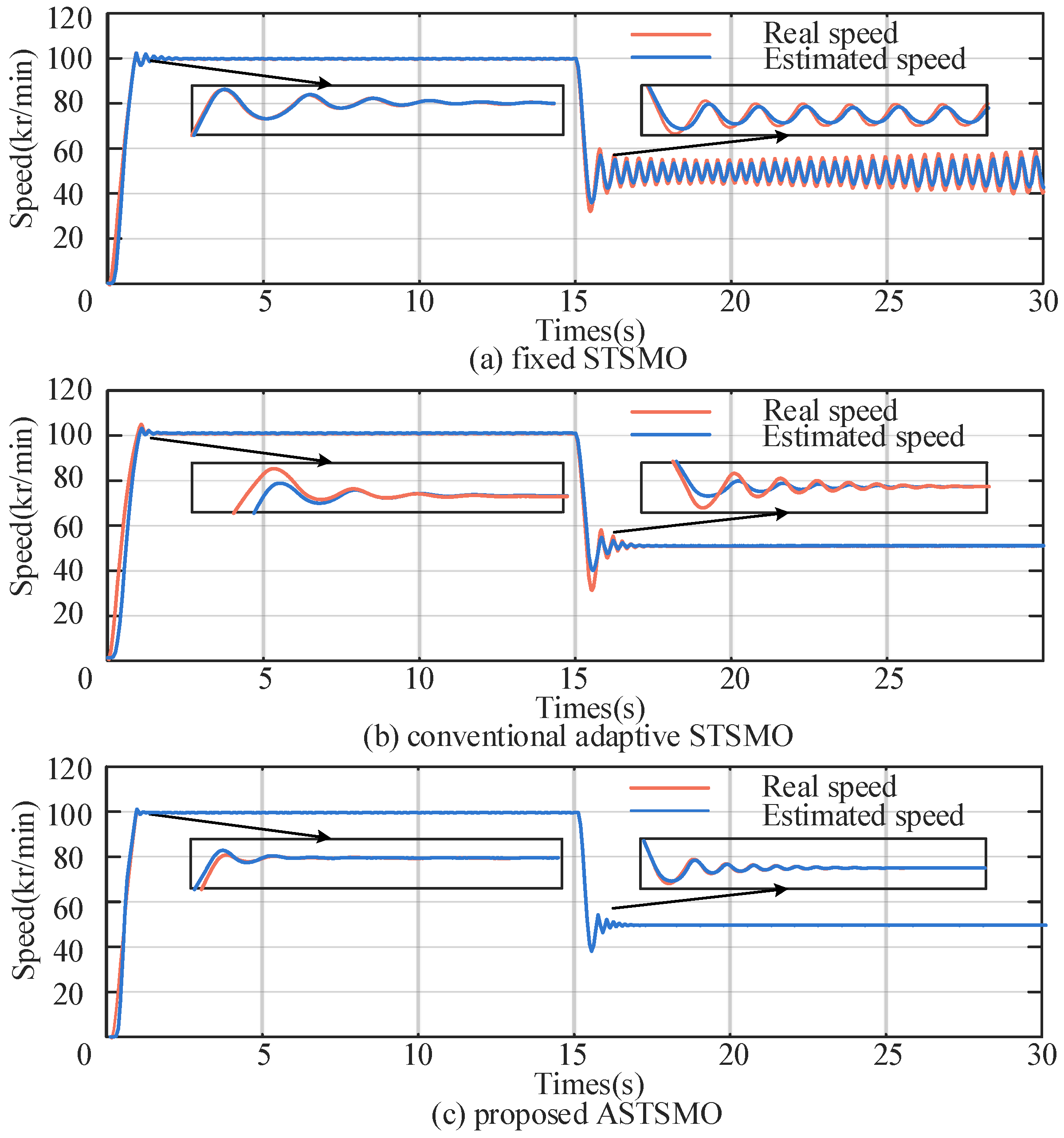
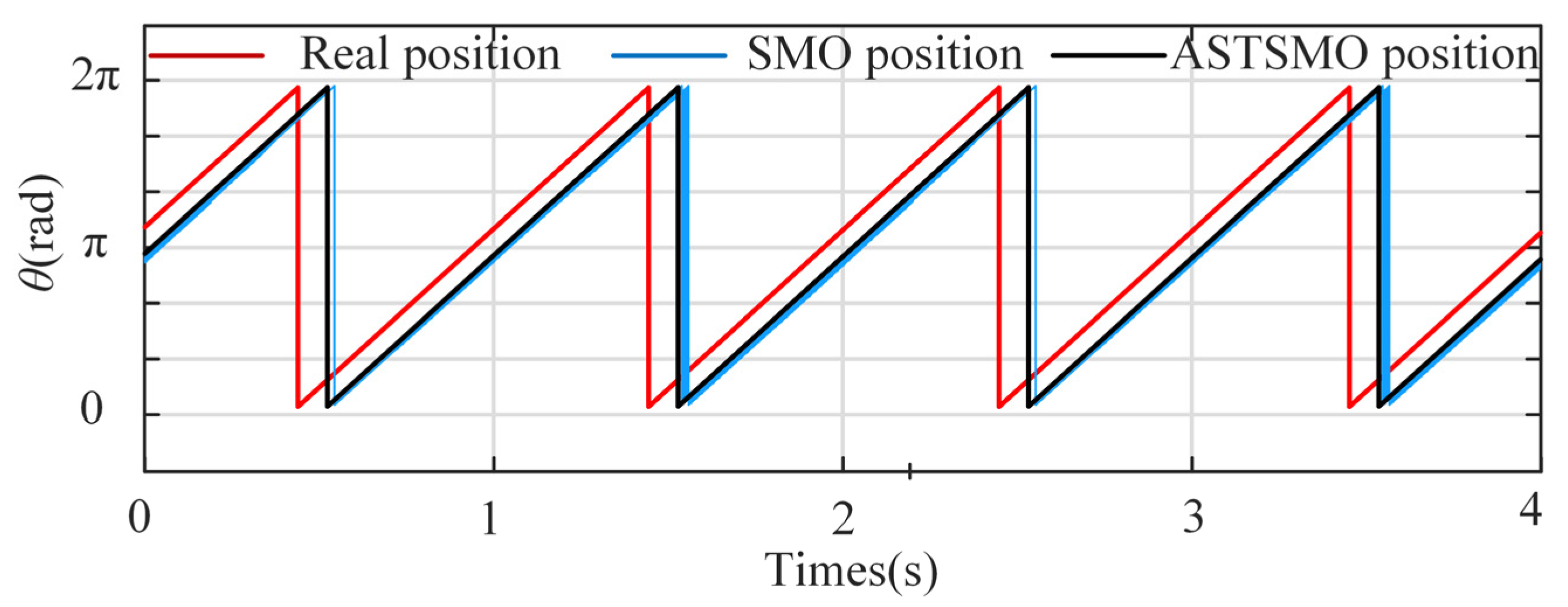
| Coefficient | Value | Unit |
|---|---|---|
| Stator resistance Rs | 17 | mΩ |
| Stator inductance Ls | 12 | μH |
| Pole pairs P | 1 | |
| Rated speed ω0 | 150 | kr/min |
| Flux linkage ψf | 0.175 | Wb |
| Inertia J | 0.001 | kg·m2 |
| Inductance (μH) | 9 | 12 | 15 |
|---|---|---|---|
| Conventional ASTSMO | 0.183 rad | 0.126 rad | 0.178 rad |
| Proposed ASTSMO | 0.057 rad | 0.052 rad | 0.055 rad |
| K1 | 1.125 | 1.5 | 1.875 |
| K2 | 150 | 200 | 250 |
| Resistance (mΩ) | 12 | 17 | 22 |
|---|---|---|---|
| Conventional ASTSMO | 0.183 rad | 0.126 rad | 0.178 rad |
| Proposed ASTSMO | 0.057 rad | 0.052 rad | 0.055 rad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, S.; Zhou, C.; Mao, K. Novel Adaptive Super-Twisting Sliding Mode Observer for the Control of the PMSM in the Centrifugal Compressors of Hydrogen Fuel Cells. Energies 2025, 18, 4675. https://doi.org/10.3390/en18174675
Zheng S, Zhou C, Mao K. Novel Adaptive Super-Twisting Sliding Mode Observer for the Control of the PMSM in the Centrifugal Compressors of Hydrogen Fuel Cells. Energies. 2025; 18(17):4675. https://doi.org/10.3390/en18174675
Chicago/Turabian StyleZheng, Shiqiang, Chong Zhou, and Kun Mao. 2025. "Novel Adaptive Super-Twisting Sliding Mode Observer for the Control of the PMSM in the Centrifugal Compressors of Hydrogen Fuel Cells" Energies 18, no. 17: 4675. https://doi.org/10.3390/en18174675
APA StyleZheng, S., Zhou, C., & Mao, K. (2025). Novel Adaptive Super-Twisting Sliding Mode Observer for the Control of the PMSM in the Centrifugal Compressors of Hydrogen Fuel Cells. Energies, 18(17), 4675. https://doi.org/10.3390/en18174675







