Distributed Multi-Agent Energy Management for Microgrids in a Co-Simulation Framework
Abstract
1. Introduction
1.1. Problem Statement and Literature Overview
1.2. Research Gaps, Contributions, and Organization
- -
- Model cost functions for energy resources by category, including dispatchable and variable sources, energy storage, and DR, as well as the objective function of the problem;
- -
- Utilize a multi-agent system and a centralized and distributed metaheuristic optimization algorithm in a co-simulation environment;
- -
- Calculate very short-term resource dispatch every five minutes to manage uncertainties related to energy sources and loads;
- -
- Implement a plug-and-play feature in the dispatch system, allowing energy resources to enter or exit spontaneously or on demand;
- -
- Develop quasi-dynamic simulation input states with five-minute intervals;
- -
- Evaluate the functionality of centralized and distributed dispatch methods;
- -
- Define test case scenarios for validating the energy resource management model.
- (a)
- Development of a plug-and-play system for integrating energy resources into an agent-based environment for very short-term optimization.
- (b)
- Analysis and parameterization of objective functions for key energy resources using the per unit (pu) representation.
- (c)
- The distribution of metaheuristics among agents, which contributes to increasing the fault tolerance of the system.
- (d)
- Using different metaheuristics in parallel at the algorithm level, incorporating competition and cooperation steps to leverage distributed hardware through MASs.
2. Methods and Computational Tools for Microgrid Resource Management
2.1. Co-Simulation
2.1.1. MAS
- (a)
- FIPA-Request: manages the sending of simple requests and responses.
- (b)
- FIPA-Subscribe: enables broadcast messaging to multiple agents subscribed to a “publisher” agent.
- (c)
- FIPA-Contract-Net: supports negotiation between agents.
2.1.2. Time Settings in Co-Simulation
2.1.3. Communication Protocols and Plug-and-Play Function
- (1)
- FIPA-Subscribe: used to identify and announce which agents are available and ready to participate in the optimization process.
- (2)
- FIPA-Request: used during the execution of the distributed optimization.
2.2. Distributed Parallelism of Metaheuristics in Intelligent Agent Environments
2.3. Modeling of the DERs
3. Results and Discussion
3.1. Parameterization of Resources
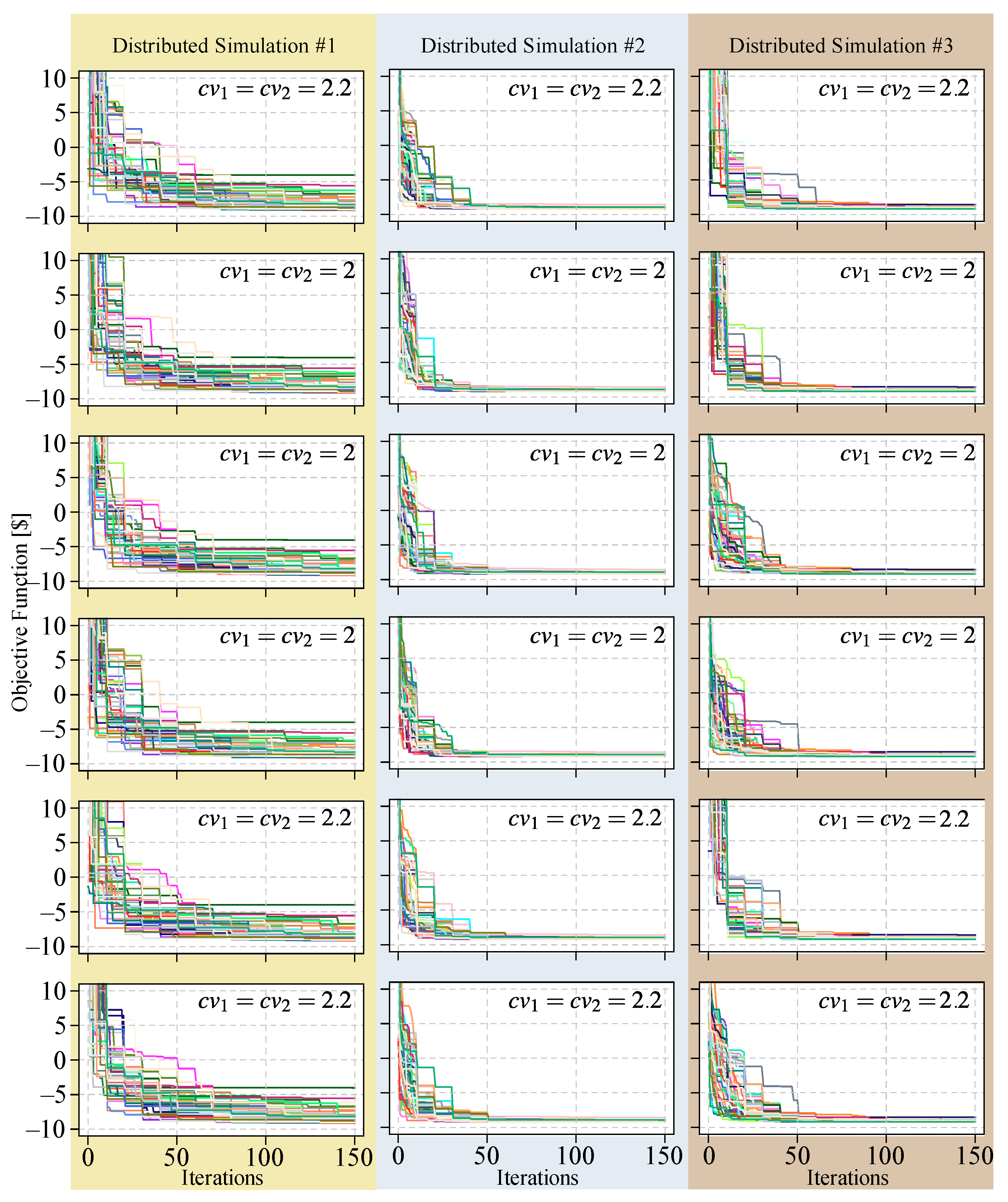
3.2. Convergence of Variables in Distributed Metaheuristics
3.3. Load Shedding
3.4. Probabilistic Analysis
3.4.1. Case #1: Evaluation of the Exponential Load Model
3.4.2. Case #2: Adjustment of Parameters in the Exponential Load Model
3.4.3. Case #3: Modification of Battery Model Parameters and Initial SoC
3.4.4. Execution Time Evaluation
3.4.5. Convergence Analysis with Adjusted Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Simulation Parameters and Initialization Settings
Appendix A.1. Parameters for Simulations in Section 3.2
Appendix A.1.1. Cost Function Coefficients
| Resource | ai [USD/MW] | bi [USD/MW] | ci [USD] |
|---|---|---|---|
| Priority load | 0.07813 | −3.12500 | 0 |
| Flexible load | 0.02315 | −1.38889 | 0 |
| Gas thermal source | 0.01667 | 0.33334 | 2.08334 |
| Biomass thermal source | 0.00240 | 0.38334 | 0.95834 |
| BESS | 0.02292 | 0.06875 | 0.22917 |
| Parameter | Value |
|---|---|
| Number of particles | 25 |
| Number of iterations | 500 |
| Exploration and exploitation coefficients (PSO/MAPSO) (cv1, cv2) | 2.0 |
| Penalty multiplier | 500 |
| Base cost (Cbase) | 1000 USD |
| Base power (Pbase) | 100 MW |
| Initial state of charge (SoC0) | 20% |
Appendix A.1.2. Generation and Load Profiles
Appendix A.2. Parameters for Disconnection and Fault Simulations in Section 3.4
Appendix A.2.1. General Settings
- For agents AgPL, AgPV, and AgBT, the cognitive and social coefficients () were set to 2.2. All other agents used a value of 2.0.
- Initial Conditions:
- ○
- PV Generation: 18.51 MW
- ○
- Flexible Load: 28.14 MW
- ○
- Priority Load: 15.2 MW
- ○
- Initial State of Charge (SoC): 50%
- Algorithm Execution:
- ○
- Centralized method: 156 particles
- ○
- Distributed method: 25 particles per agent
- ○
- Distributed method message frequency: The algorithm performs 10 iterations per message exchange.
Appendix A.2.2. Case Study #1
| Type | Ki.pu | βi.pu | Costi.base | Pi.base | Ki | βi |
|---|---|---|---|---|---|---|
| Priority load | 1 | 1 | USD 31.25 | 20 MW | USD 31.25 | 0.05 MW−1 |
| Flexible load | 1 | 0.3 | USD 20.83 | 30 MW | USD 20.83 | 0.01 MW−1 |
Appendix A.2.3. Case Study #2
Appendix A.2.4. Case Study #3
| Resource | ai [USD/MW] | bi [USD/MW] | ci [USD] |
|---|---|---|---|
| BESS | 0.02084 | 0.06250 | 0.20834 |
References
- Gulzar, M.M.; Sibtain, D.; Alqahtani, M.; Alismail, F.; Khalid, M. Load frequency control progress: A comprehensive review on recent development and challenges of modern power systems. Energy Strategy Rev. 2025, 57, 101604. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhang, Z.; Wang, Y.; Zhang, L. A review of distributed energy systems: Technologies, classification, and applications. Sustainability 2025, 17, 1346. [Google Scholar] [CrossRef]
- Zidane, T.E.K.; Muis, Z.A.; Ho, W.S.; Zahraoui, Y.; Aziz, A.S.; Su, C.-L.; Mekhilef, S.; Elia Campana, P. Power systems and microgrids resilience enhancement strategies: A review. Renew. Sustain. Energy Rev. 2025, 207, 114953. [Google Scholar] [CrossRef]
- Correia, A.F.M.; Neves, M.A.G.; Reis, A.I.C.D.; Coimbra, A.P.; Almeida, T.R.d.O.d.; Moura, P.; de Almeida, A.T. Architecture and operational control for resilient microgrids—A university case study. IEEE Access 2025, 13, 51373–51387. [Google Scholar] [CrossRef]
- Horrillo-Quintero, P.; García-Triviño, P.; Ugalde-Loo, C.E.; Hosseini, E.; García-Vázquez, C.A.; Tostado, M.; Jurado, F.; Fernández-Ramírez, L.M. Efficient energy dispatch in multi-energy microgrids with a hybrid control approach for energy management system. Energy 2025, 317, 134599. [Google Scholar] [CrossRef]
- Li, L.-L.; Ji, B.-X.; Li, Z.-T.; Lim, M.K.; Sethanan, K.; Tseng, M.-L. Microgrid energy management system with degradation cost and carbon trading mechanism: A multi-objective artificial hummingbird algorithm. Appl. Energy 2025, 378, 124853. [Google Scholar] [CrossRef]
- Imtiaz, S.; Yang, L.; Munir, H.M.; Memon, Z.A.; Kilic, H.; Naz, M.N. DC-link voltage stability enhancement in intermittent microgrids using coordinated reserve energy management strategy. IET Renew. Power Gener. 2025, 19, e13197. [Google Scholar] [CrossRef]
- Yang, T.; Xu, Z.; Ji, S.; Liu, G.; Li, X.; Kong, H. Cooperative optimal dispatch of multi-microgrids for low carbon economy based on personalized federated reinforcement learning. Appl. Energy 2025, 378, 124641. [Google Scholar] [CrossRef]
- Salman, M.; Li, Y.; Xiang, J. A distributed consensus-based optimal dispatch control strategy for hybrid ac/dc microgrids. IEEE Access 2024, 12, 90997–91010. [Google Scholar] [CrossRef]
- Kumar, S.S.; Srinivasan, C.; Balavignesh, S. Enhancing grid integration of renewable energy sources for micro grid stability using forecasting and optimal dispatch strategies. Energy 2025, 322, 135572. [Google Scholar] [CrossRef]
- Zhao, G.; Luo, J.; Song, N.; Shu, J. Multi-objective optimal dispatch of island microgrid considering a novel scheduling resource. Electr. Power Syst. Res. 2025, 241, 111378. [Google Scholar] [CrossRef]
- Li, T.; Li, Y.; Wang, F.; Gong, C.; Zhang, J.; Ma, H. Improved parallel differential evolution algorithm with small population for multi-period optimal dispatch problem of microgrids. Energies 2025, 18, 3852. [Google Scholar] [CrossRef]
- Akter, A.; Zafir, E.I.; Dana, N.H.; Joysoyal, R.; Sarker, S.K.; Li, L.; Muyeen, S.M.; Das, S.K.; Kamwa, I. A review on microgrid optimization with meta-heuristic techniques: Scopes, trends and recommendation. Energy Strategy Rev. 2024, 51, 101298. [Google Scholar] [CrossRef]
- Rajwar, K.; Deep, K.; Das, S. An exhaustive review of the metaheuristic algorithms for search and optimization: Taxonomy, applications, and open challenges. Artif. Intell. Rev. 2023, 56, 13187–13257. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, W.; Dai, C.; Cai, W. Dynamic multi-group self-adaptive differential evolution algorithm for reactive power optimization. Int. J. Electr. Power Energy Syst. 2010, 32, 351–357. [Google Scholar] [CrossRef]
- Shafik, M.B.; Chen, H.; Rashed, G.I.; El-Sehiemy, R.A. Adaptive multi objective parallel seeker optimization algorithm for incorporating TCSC devices into optimal power flow framework. IEEE Access 2019, 7, 36934–36947. [Google Scholar] [CrossRef]
- Zhang, H.; Hui, Q. Parallel multiagent coordination optimization algorithm: Implementation, evaluation, and applications. IEEE Trans. Autom. Sci. Eng. 2017, 14, 984–995. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Montoya, O.D.; Ramos-Paja, C.A. An energy management system for optimal operation of BSS in DC distributed generation environments based on a parallel PSO algorithm. J. Energy Storage 2020, 29, 101488. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Ocampo-Toro, J.A.; Montoya-Giraldo, O.D.; Montano, J.; Hernandéz, J.C. Optimal operation of battery storage systems in standalone and grid-connected DC microgrids using parallel metaheuristic optimization algorithms. J. Energy Storage 2023, 65, 107240. [Google Scholar] [CrossRef]
- Behbahani, F.M.; Ahmadi, B.; Caglar, R. Multi-objective multiverse optimization for optimal allocation of distributed energy resources: The optimal parallel processing schemes. Electr. Power Syst. Res. 2024, 231, 110298. [Google Scholar] [CrossRef]
- Montano, J.; Guzmán, J.P.; Garzón, O.D.; Barrera, A.M.R. Techno-economic approach for energy management system: Multi-objective optimization algorithms for energy storage in standalone and grid-connected DC microgrids. J. Energy Storage 2024, 102, 114069. [Google Scholar] [CrossRef]
- Chen, J.; Liu, X.; Karam, I. Short-term economic dispatch incorporating renewable power generations with plug-in electric vehicles considering emissions reduction. Environ. Dev. Sustain. 2024; early view. [Google Scholar] [CrossRef]
- Nadermahmoudi, E.; Amraee, T.; Oskouee, S.S. Stochastic very short-term economic dispatch for wind power operation using flexible ramp reserve. Int. Trans. Electr. Energy Syst. 2020, 30, e12454. [Google Scholar] [CrossRef]
- Garrido-Arévalo, V.M.; Gil-González, W.; Montoya, O.D.; Grisales-Noreña, L.F.; Hernández, J.C. Optimal dispatch of DERs and battery-based ESS in distribution grids while considering reactive power capabilities and uncertainties: A second-order cone programming formulation. IEEE Access 2024, 12, 48497–48510. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Cortés-Caicedo, B.; Montoya, O.D.; Sanin-Villa, D.; Gil-González, W. Integration of BESS in grid connected networks for reducing the power losses and CO2 emissions: A parallel master-stage methodology based on PDVSA and PSO. J. Energy Storage 2024, 87, 111355. [Google Scholar] [CrossRef]
- Cortés-Caicedo, B.; Ocampo-Toro, J.; Bolaños, R.I.; Montoya, O.D.; Grisales-Noreña, L.F. A multi-objective PSO for DC microgrids: Efficient battery management to minimize energy losses and operating costs. J. Energy Storage 2024, 96, 112550. [Google Scholar] [CrossRef]
- Cortés-Caicedo, B.; Grisales-Noreña, L.F.; Montoya, O.D.; Bolaños, R.I.; Muñoz, J. A multi-objective optimization approach based on the non-dominated sorting genetic algorithm II for power coordination in battery energy storage systems for DC distribution network applications. J. Energy Storage 2025, 113, 115430. [Google Scholar] [CrossRef]
- Yin, L.; Li, S. Hybrid metaheuristic multi-layer reinforcement learning approach for two-level energy management strategy framework of multi-microgrid systems. Eng. Appl. Artif. Intell. 2021, 104, 104326. [Google Scholar] [CrossRef]
- Fernandes, D.L.; Leopoldino, A.L.M.; de Santiago, J.; Verginis, C.; Ferreira, A.A.; de Oliveira, J.G. Distributed control on a multi-agent environment co-simulation for DC bus voltage control. Electr. Power Syst. Res. 2024, 232, 110408. [Google Scholar] [CrossRef]
- Huo, Y.; Bouffard, F.; Joós, G. Integrating learning and explicit model predictive control for unit commitment in microgrids. Appl. Energy 2022, 306, 118026. [Google Scholar] [CrossRef]
- Premkumar, M.; Sowmya, R.; Ramakrishnan, C.; Jangir, P.; Houssein, E.H.; Deb, S.; Manoj Kumar, N. An efficient and reliable scheduling algorithm for unit commitment scheme in microgrid systems using enhanced mixed integer particle swarm optimizer considering uncertainties. Energy Rep. 2023, 9, 1029–1053. [Google Scholar] [CrossRef]
- OFFIS. Scheduling and Simulation Execution. 2025. Available online: http://mosaik.readthedocs.io/en/latest/scheduler.html#time-paradigms (accessed on 29 September 2024).
- Melo, L.S.; Sampaio, R.F.; Leão, R.P.S.; Barroso, G.C.; Bezerra, J.R. Python-based multi-agent platform for application on power grids. Int. Trans. Electr. Energy Syst. 2019, 29, e12012. [Google Scholar] [CrossRef]
- Wu, H.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Thermal generation flexibility with ramping costs and hourly demand response in stochastic security-constrained scheduling of variable energy sources. IEEE Trans. Power Syst. 2015, 30, 2955–2964. [Google Scholar] [CrossRef]
- Niromandfam, A.; Yazdankhah, A.S.; Kazemzadeh, R. Modeling demand response based on utility function considering wind profit maximization in the day-ahead market. J. Clean. Prod. 2020, 251, 119317. [Google Scholar] [CrossRef]
- Azevedo, R.d.; Cintuglu, M.H.; Ma, T.; Mohammed, O.A. Multiagent-based optimal microgrid control using fully distributed diffusion strategy. IEEE Trans. Smart Grid 2017, 8, 1997–2008. [Google Scholar] [CrossRef]
















| Ref. | Method | Main Focus | Limitations/Gaps |
|---|---|---|---|
| [5] | Fuzzy logic—model predictive control (MPC)/quadratic programming | Efficient dispatch in multi-energy microgrids |
|
| [6] | Metaheuristic/artificial hummingbird algorithm | Multi-objective optimization: total degradation cost and carbon trading |
|
| [7] | Scheme flowchart for coordinated reserve energy management | Coordinated reserve energy management and dc microgrid voltage stability |
|
| [8] | Heterogeneous multi-agent twin delayed deep deterministic (HMATD3) + neural network | Optimal low-carbon economic dispatch |
|
| [9] | Consensus-based distributed secondary control strategy | Global economic operation (GOP) and optimal active/reactive power dispatch for all participating ac/dc DG units |
|
| [10] | Forecasting + optimal dispatch | Stability with renewable integration |
|
| [11] | Multi-objective optimal dispatch | Isolated microgrids with new resources |
|
| [12] | Parallel differential evolution (DE) with reduced population | Multi-period dispatch |
|
| [13] | Review of metaheuristics | Optimization in microgrids |
|
| [19] | Parallel metaheuristic optimization | Optimal BESS operation in dc microgrids |
|
| [20] | Multiverse optimization | Optimal DER allocation |
|
| [21] | Multi-objective optimization | EMS for BESSs in dc and grid-connected systems |
|
| [22] | Economic dispatch with plug-in electric vehicles | Renewable integration with emission reduction |
|
| [24] | Second-order cone programming (SOCP) for dispatch | DERs with uncertainties and reactive power |
|
| [25] | PSO combined with PDVSA | BESS integration and reduction in greenhouse gas emissions |
|
| [26] | Multi-objective PSO | Battery management in dc microgrids |
|
| [27] | NSGA-II | BESS coordination in dc microgrids |
|
| [28] | Hybrid metaheuristic + reinforcement learning (RL) | Two-level EMS in multi-microgrids |
|
| [29] | Distributed control in co-simulation | DC bus voltage control |
|
| [30] | Learning + MPC | Unit commitment in microgrids |
|
| [31] | Optimized multi-objective particle swarm optimization (MIPSO) | Reliable scheduling considering uncertainties |
|
| Present Study | Distributed MAPSO utilizing an MAS | Economic dispatch of energy resources, enabling distributed optimization to promote redundancy and scalability among agents for ultra-short-term dispatch |
|
| DER | Cost Function Principle and Rationale | Reference |
|---|---|---|
| Dispatchable generators | A standard quadratic cost function is used to model fuel consumption and operational costs. | Equation (5) |
| Renewable energy sources | Modeled with a zero marginal cost to prioritize their dispatch whenever available. | N/A |
| Controllable loads | The objective function relies on maximizing social welfare for consumers. | Equation (9) |
| ESSs | A dynamic cost function is associated with the SoC, penalizing discharging at low energy levels. | Equation (11) |
| Resource | Pnom [MW] | Pmin [MW] | Pmax [MW] | ai [pu] | bi [pu] | ci [pu] | Energy Cost [USD/MWh] | Capacity Cost [USD/MW] |
|---|---|---|---|---|---|---|---|---|
| Priority load | 20 | 0 | PPL | 1 | −2 | 0 | 375 | 31.25 |
| Flexible load | 30 | 0 | PCF | 1 | −2 | 0 | 250 | 20.83 |
| Gas thermal source | 25 | 0 | 25 | 0.5 | 0.4 | 0.1 | 250 | 20.83 |
| Biomass thermal source | 20 | 2 | 20 | 0.1 | 0.8 | 0.1 | 115 | 9.58 |
| BESS | 60 h | −12 | 30 | 0.9 | 0.09 | 0.01 | 275 | 22.92 |
| PV system | 30 | 0 | PPV | 0 | 0 | 0 | 0 | 0 |
| Resource | ai [USD/MW] | bi [USD/MW] | ci [USD] |
|---|---|---|---|
| Priority load | 0.07813 | –3.12500 | 0 |
| Flexible load | 0.02315 | –1.38889 | 0 |
| Gas thermal source | 0.01667 | 0.33334 | 2.08334 |
| Biomass thermal source | 0.00240 | 0.38334 | 0.95834 |
| BESS | 0.02292 | 0.06875 | 0.22917 |
| Agent | Distributed Simulation #1 | Distributed Simulation #2 | Distributed Simulation #3 |
|---|---|---|---|
| AgPL | PSO | MAPSO | PSO |
| AgFL | PSO | MAPSO | PSO |
| AgTG | PSO | MAPSO | MAPSO |
| AgTB | PSO | MAPSO | MAPSO |
| AgBT | PSO | MAPSO | PSO |
| AgPV | PSO | MAPSO | MAPSO |
| Variable | AgPL | AgFL | AgTG | AgTB | AgBT | AgPV | ∆max |
|---|---|---|---|---|---|---|---|
| PPL [MW] | 17.01 | 17.01 | 16.95 | 17.01 | 16.95 | 16.95 | 0.06 |
| PFL [MW] | 19.70 | 19.70 | 19.70 | 19.70 | 19.70 | 19.70 | 0.00 |
| PTG [MW] | 3.79 | 3.79 | 3.83 | 3.79 | 3.83 | 3.83 | 0.04 |
| PTB [MW] | 16.27 | 16.27 | 16.22 | 16.27 | 16.22 | 16.22 | 0.05 |
| PBT [MW] | 0.52 | 0.52 | 0.48 | 0.52 | 0.48 | 0.48 | 0.04 |
| PPV [MW] | 17.75 | 17.75 | 17.75 | 17.75 | 17.75 | 17.75 | 0.00 |
| fobj [USD] | −34.976 | −34.976 | −34.976 | −34.976 | −34.976 | −34.976 | 0.00 |
| Variable | AgPL | AgFL | AgTG | AgTB | AgBT | AgPV | ∆max |
|---|---|---|---|---|---|---|---|
| PPL [MW] | 17.07 | 17.07 | 17.07 | 17.07 | 17.07 | 17.07 | 0.00 |
| PFL [MW] | 20.12 | 20.12 | 20.12 | 20.12 | 20.12 | 20.12 | 0.00 |
| PTG [MW] | 3.88 | 3.88 | 3.88 | 3.88 | 3.88 | 3.80 | 0.00 |
| PTB [MW] | 16.78 | 16.78 | 16.78 | 16.78 | 16.78 | 16.78 | 0.00 |
| PBT [MW] | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 | 0.00 |
| PPV [MW] | 17.75 | 17.75 | 17.75 | 17.75 | 17.75 | 17.75 | 0.00 |
| fobj [USD] | −34.904 | −34.904 | −34.904 | −34.904 | −34.904 | −34.904 | 0.00 |
| Variable | AgPL | AgFL | AgTG | AgTB | AgBT | AgPV | ∆max |
|---|---|---|---|---|---|---|---|
| PPL [MW] | 16.92 | 16.94 | 16.95 | 16.94 | 16.94 | 16.94 | 0.03 |
| PFL [MW] | 19.89 | 19.91 | 19.91 | 19.91 | 19.91 | 19.91 | 0.02 |
| PTG [MW] | 4.13 | 4.13 | 4.13 | 4.13 | 4.13 | 4.13 | 0.00 |
| PTB [MW] | 16.59 | 16.68 | 16.68 | 16.68 | 16.68 | 16.68 | 0.07 |
| PBT [MW] | 0.35 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.04 |
| PPV [MW] | 17.75 | 17.75 | 17.75 | 17.75 | 17.75 | 17.75 | 0.00 |
| fobj [USD] | −34.971 | −34.970 | −34.970 | −34.970 | −34.970 | −34.970 | 0.001 |
| Number of Iterations | Distributed Simulation #1 | Distributed Simulation #2 | Distributed Simulation #3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| var | fobj | ∆max | var | fobj | ∆max | var | fobj | ∆max | |
| 1 | 280 | 286 | 0.04 MW | 276 | 284 | 0.90 MW | 275 | 287 | 0.04 MW |
| 5 | 238 | 284 | 0.24 MW | 237 | 277 | 0.87 MW | 244 | 284 | 0.19 MW |
| 10 | 199 | 280 | 0.46 MW | 215 | 259 | 1.42 MW | 201 | 286 | 0.22 MW |
| 25 | 119 | 267 | 0.89 MW | 167 | 225 | 1.52 MW | 148 | 276 | 0.53 MW |
| 50 | 88 | 230 | 0.89 MW | 135 | 201 | 1.30 MW | 107 | 245 | 2.08 MW |
| 100 | 65 | 154 | 2.34 MW | 103 | 144 | 2.06 MW | 80 | 164 | 2.50 MW |
| Type | Ki.pu | βi.pu | Costi.base | Pi.base | Ki | βi |
|---|---|---|---|---|---|---|
| Priority load | 1 | 1 | USD 31.25 | 20 MW | USD 31.25 | 0.05 MW−1 |
| Flexible load | 1 | 0.3 | USD 20.83 | 30 MW | USD 20.83 | 0.01 MW−1 |
| Variable | Value |
|---|---|
| Priority load | 15.20 MW |
| Flexible Load | 0 |
| Gas thermal source | 1.97 MW |
| Biomass thermal source | 3.24 MW |
| BESS | −7.5 MW |
| PV generation | 18.51 MW |
| Variable | Value |
|---|---|
| Priority load | 15.20 MW |
| Flexible Load | 12.91 MW |
| Gas thermal source | 3.68 MW |
| Biomass thermal source | 14.82 MW |
| BESS | −7.5 MW |
| PV generation | 18.51 MW |
| Variable | Value |
|---|---|
| Priority load | 15.20 MW |
| Flexible Load | 12.73 MW |
| Gas thermal source | 3.78 MW |
| Biomass thermal source | 2 MW |
| BESS | 4.93 MW |
| PV generation | 18.51 MW |
| Algorithm | Case #1 | Case #2 | Case #3 | |||
|---|---|---|---|---|---|---|
| Total (min) | Average (s) | Total (min) | Average (s) | Total (min) | Average (s) | |
| Centralized PSO | 02:07 | 2.54 s | 02:15 | 2.70 | 02:25 | 2.90 |
| Centralized MAPSO | 02:34 | 3.08 s | 02:50 | 3.40 | 02:38 | 3.16 |
| Distributed PSO | 04:07 | 5.56 s | 04:16 | 5.12 | 04:15 | 5.10 |
| Distributed MAPSO | 06:59 | 8.38 s | 07:13 | 8.66 | 06:58 | 8.36 |
| Distributed MAPSO+PSO | 05:42 | 6.84 s | 06:13 | 7.46 | 05:56 | 7.12 |
| Number of Iterations | Distributed Simulation #1 | Distributed Simulation #2 | Distributed Simulation #3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| var | fobj | ∆max | var | fobj | ∆max | var | fobj | ∆max | |
| 1 | 274 | 283 | 2.32 MW | 283 | 288 | 0.42 MW | 280 | 288 | 0.45 MW |
| 10 | 188 | 248 | 9.98 MW | 239 | 286 | 1.68 MW | 226 | 281 | 3.44 MW |
| 100 | 10 | 29 | 15.54 MW | 63 | 236 | 8.42 MW | 30 | 164 | 10.35 MW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almada, J.B.; Tofoli, F.L.; Gregory, R.C.F.; Sampaio, R.F.; Melo, L.S.; Leão, R.P.S. Distributed Multi-Agent Energy Management for Microgrids in a Co-Simulation Framework. Energies 2025, 18, 4620. https://doi.org/10.3390/en18174620
Almada JB, Tofoli FL, Gregory RCF, Sampaio RF, Melo LS, Leão RPS. Distributed Multi-Agent Energy Management for Microgrids in a Co-Simulation Framework. Energies. 2025; 18(17):4620. https://doi.org/10.3390/en18174620
Chicago/Turabian StyleAlmada, Janaína Barbosa, Fernando Lessa Tofoli, Raquel Cristina Filiagi Gregory, Raimundo Furtado Sampaio, Lucas Sampaio Melo, and Ruth Pastôra Saraiva Leão. 2025. "Distributed Multi-Agent Energy Management for Microgrids in a Co-Simulation Framework" Energies 18, no. 17: 4620. https://doi.org/10.3390/en18174620
APA StyleAlmada, J. B., Tofoli, F. L., Gregory, R. C. F., Sampaio, R. F., Melo, L. S., & Leão, R. P. S. (2025). Distributed Multi-Agent Energy Management for Microgrids in a Co-Simulation Framework. Energies, 18(17), 4620. https://doi.org/10.3390/en18174620






