Application of Machine Learning in Vibration Energy Harvesting from Rotating Machinery Using Jeffcott Rotor Model

Abstract

This study presents a machine learning-based framework for predicting the electrical output of a vibration energy harvesting system (VEHS) integrated with a Jeffcott rotor model. Vibration induced by rotor imbalance is converted into electrical energy via piezoelectric elements, and the system’s dynamic response is simulated using the fourth-order Runge–Kutta method across varying mass ratios, rotational speeds, and eccentricities. The resulting dataset is validated experimentally with a root-mean-square error below 5%. Three predictive models—Deep Neural Network (DNN), Long Short-Term Memory (LSTM), and eXtreme Gradient Boosting (XGBoost)—are trained and evaluated. While DNN and LSTM yield a high predictive accuracy (R² > 0.9999), XGBoost achieves comparable accuracy (R² = 0.9994) with significantly lower computational overhead. The results demonstrate that among the tested models, XGBoost provides the best trade-off between speed and accuracy, achieving R² > 0.999 while requiring the least training time. These results demonstrate that XGBoost might be particularly suitable for real-time evaluation and edge deployment in rotor-based VEHS, offering a practical balance between speed and precision.

1. Introduction

In factory workstations, rotating machinery is a common component of these machines, but it is also one of the main causes of machine vibrations. One major reason for vibrations in rotating machinery is rotor imbalance. Even though various methods can be used to reduce vibrations, the centrifugal force generated by rotating mechanical components inevitably leads to eccentric motion over time. In addition to rotor imbalance, improper installation or alignment of machinery can lead to excessive vibrations, as demonstrated by Karpenko et al. [1], who identified installation errors as the primary cause of abnormal vibration behavior in centrifugal loop dryer machines. If a vibration energy harvesting system (VEHS) can be used to collect and convert this vibrational energy into electrical energy, it would not only reduce energy waste but also provide power for factory operations, contributing to sustainability. The application of rotating machinery is not limited to factory processing equipment; for example, the drive shafts of ships can also experience vibrations due to rotor imbalance. In such cases, this system can be used to convert vibrational energy into electrical power for onboard use—such as general lighting or navigation instruments—without affecting the operation or lifespan of the equipment. However, factors that influence vibration include the mass of the rotating machine’s shaft, rotational speed, and eccentric distance. These factors directly impact the efficiency of vibration energy conversion. Therefore, determining the optimal combination for maximizing energy conversion in real time remains a challenge. With the rise of artificial intelligence (AI) and its increasing applications across various fields, this study employs machine learning to predict the overall power generation of VEH systems installed on different factory machines. By collecting data on eccentric shaft vibrations under various conditions and training deep learning models with different learning approaches, the study aims to evaluate the effectiveness of various energy conversion combinations. The goal is to identify the most suitable machine learning method for industrial applications.

The Jeffcott rotor model is a classic model in the field of rotating machinery dynamics, proposed by Jeffcott in 1919 [2]. This model assumes that the rotor consists of an elastic shaft and a concentrated mass disk, with both ends of the shaft fixed by supports. The study analyzes the frequency response and system stability of the rotor under unbalanced conditions. When the rotor is unbalanced, centrifugal forces cause the vibration amplitude to increase proportionally with rotational speed. As the speed approaches the critical speed, intense resonance can occur. The study also explores how mass distribution adjustments can mitigate these effects. Saeed et al. [3] investigated the vibration characteristics of an eccentric rotor system under friction and impact forces between the rotor and stator. Ishida [4] studied the vibration characteristics of cracked rotors, noting that rotors often experience periodic stress in the horizontal direction, making them susceptible to fatigue-induced cracks. Therefore, timely diagnosis of mechanical equipment is essential. Weng et al. [5] used numerical methods to analyze the effects of crack depth and initial bending deformation on the vibration response of the rotor system. Their findings indicate that rotors with initial bending deformation exhibit a broader chaotic region at critical speed compared to those without deformation. Hassenpflug et al. [6] explored the impact of angular acceleration on the Jeffcott rotor. They predicted the rotor’s response to imbalance under various acceleration and damping conditions and studied changes in vibration amplitude and phase. Piramoon et al. [7] proposed a SINDy-based approach to reconstruct nonlinear dynamics and suppress vibrations in vertical-shaft rotary machines. A TSMC controller is designed to reduce lateral vibrations, with experiments confirming its stability and effectiveness. Zhang et al. [8] presented a piezoelectric energy harvester for rotating machinery that captures kinetic energy and enables rotor fault detection. Experimental validation confirms its high efficiency, long lifespan, and minimal interference, making it ideal for self-powered condition monitoring. Han et al. [9] developed a 1D-CNN deep learning model to identify rotor unbalance positions based on vibration response data. The method achieves high accuracy (99.5% at subcritical and critical speeds, 99.0% at supercritical speeds), demonstrating its effectiveness in intelligent unbalance detection for aeroengine rotors. This article inspires the use of machine learning to predict the impact of rotor imbalance during rotation.

Regarding the application of machine learning, LeCun et al. [10] stated that machine learning technology is widely used in modern society. Traditional machine learning techniques are limited by the input of raw data, requiring predefined features and labels for the system to recognize and utilize the data effectively. In contrast, deep learning excels at discovering complex structures in high-dimensional data, making it suitable for various fields, including science and business. Janiesch et al. [11] analyzed machine learning and deep learning, explaining that machine learning identifies patterns from large datasets to make predictions. Baek and Chung [12] proposed a Context-DNN model based on multiple regression, where contextual information related to depression is used as input, and the probability of depression is the output. By utilizing regression analysis, this model predicts environmental factors that may influence depression risk. This method serves as a reference for multi-factor parameter estimation in this study. Avci et al. [13] applied machine learning and deep learning to extend the lifespan of civil structures, analyzing which damage conditions should be used as machine learning features and which should be avoided.

The Long Short-Term Memory (LSTM) neural network was proposed by Hochreiter in 1997 [14]. It explains how the LSTM cell architecture ensures a stable error flow, addressing the challenge of learning over long time intervals. Akhtar et al. [15] applied LSTM in power systems, including load forecasting, fault detection and diagnosis, power security, and stability assessment. Sundermeyer et al. [16] utilized LSTM for language modeling tasks, comparing it to Recurrent Neural Networks (RNNs). While RNNs can consider all previous words in a time series, they suffer from training difficulties, limiting their performance. LSTM overcomes these challenges by accurately modeling the probability distribution of word sequences, making it highly suitable for language modeling. Thus, LSTM is also one of the methods referenced in this study.

Karsoliya [17] discussed how to determine the number of hidden layers and neurons in a backpropagation neural network. If too many neurons are used, it can lead to overfitting, while too few can result in underfitting. They suggested using a trial-and-error approach to find the optimal number of hidden layers and neurons. However, increasing the number of hidden layers also increases training time, so a balance must be struck between overfitting and underfitting. Jabbar and Khan [18] explored overfitting and underfitting in artificial neural networks (ANNs) and evaluated the effectiveness of the penalty method and early stopping method in addressing these issues. Buber and Banu [19] used graphics processing units (GPUs) for deep learning computations. Since core mathematical operations in deep learning are well-suited for parallel processing, GPUs—with their multi-core architecture—offer significantly better parallel processing capabilities than central processing units (CPUs). Smith [20] discussed hyperparameter tuning in deep learning to reduce training time and improve performance. They proposed adjusting parameters based on the training and validation loss functions to assess the model’s current fit. Wilson and Martinez [21] explained how learning rate adjustments affect training speed and generalization accuracy. They found that when dealing with large and complex problems, a smaller learning rate tends to result in better generalization accuracy compared to the fastest learning rates. Lau and Lim [22] examined three types of activation functions in deep neural networks (DNNs): saturated, non-saturated, and adaptive activation functions, analyzing their impact on model performance. Saturated activation functions often suffer from gradient vanishing due to their saturation characteristics, requiring pre-training during training to mitigate this issue. Non-saturated activation functions, such as ReLU, were introduced to address the gradient vanishing problem.

This study analyzes the Jeffcott rotor under varying mass, rotational speed, and eccentric distance, examining the conversion of vibration energy into electrical power using a vibration energy harvesting device. We employ the fourth-order Runge–Kutta method (RK-4 method) to solve the Jeffcott equation, incrementally increasing mass, rotational speed, and eccentric distance at fixed intervals to generate a large dataset of voltage outputs under different conditions. These data points are then processed using supervised learning in machine learning for prediction. The data are first labeled to enable the machine to recognize patterns, ensuring accurate training. During the prediction process, the dataset is split into three categories: training, validation, and testing. By adjusting parameters and comparing prediction results, we aim to identify the deep learning model best suited for this study. Three machine learning methods are considered for predicting rotor system energy conversion efficiency: (1) Deep Neural Network (DNN)—Chosen for its simple structure and ease of use. (2) Long Short-Term Memory (LSTM)—Capable of retaining past information and selectively keeping or discarding data based on relevance. This makes LSTM particularly suited for time-series data and helps mitigate the gradient vanishing or explosion issues encountered in Recurrent Neural Networks (RNNs) when handling long-term dependencies. (3) XGBoost, or eXtreme Gradient Boosting, is a high-performance ensemble learning method based on gradient boosting. It handles nonlinear problems well, prevents overfitting, and is widely used for regression and classification tasks. Its efficiency and strong interpretability make it suitable for model comparison in this study. This study will compare these machine learning methods to determine the most effective deep learning model for our research objectives.

2. Fundamental Theoretical Analysis

2.1. Establishment of the Jeffcott System Equation

This study considers the effects of eccentric rotation in the Jeffcott rotor system, as shown in Figure 1. Referring to the Jeffcott system equation proposed by Herisanu and Marinca [23], the equations governing the eccentric rotation of the shaft, along with the bearings at both ends and the eccentric disk, can be reformulated as follows:

• Bearing

$$M_1{\overline{x}}_1^{**}+c_1{\overline{x}}_1^{*}+K_1({\overline{x}}_1-{\overline{x}}_2)+K_3{({\overline{x}}_1-{\overline{x}}_2)}^3=M_2{\overline{x}}_2^{**}$$

(1)

$$M_1{\overline{y}}_1^{**}+c_1{\overline{y}}_1^{*}+K_1({\overline{y}}_1-{\overline{y}}_2)+K_3{({\overline{y}}_1-{\overline{y}}_2)}^3=M_2{\overline{y}}_2^{**}$$

(2)

• Disk

$$M_2{\overline{x}}_2^{**}+c_2{\overline{x}}_2^{*}+K_2({\overline{x}}_2-{\overline{x}}_1)=M_2\overline{e}{\overline{\omega }}^2\cos \overline{\omega }t$$

(3)

$$M_2{\overline{y}}_2^{**}+c_2{\overline{y}}_2^{*}+K_2({\overline{y}}_2-{\overline{y}}_1)=M_2\overline{e}{\overline{\omega }}^2\sin \overline{\omega }t$$

(4)

In these equations: M₁ represents the mass of the rotor shaft, M₂ represents the mass of the disk, ( )^* denotes differentiation with respect to dimensional time (t), $\overline{e}$ represents the eccentric distance from the disk’s center of mass to its geometric center. The displacement at the bearing is denoted as $\left({\overline{x}}_1,{\overline{y}}_1\right)$, while the displacement at the disk is $\left({\overline{x}}_2,{\overline{y}}_2\right)$. $\overline{\omega }$ represents the rotational speed of the shaft. K₁ is the linear stiffness coefficient of the rotor shaft. K₂ is the linear stiffness coefficient of the disk. K₃ is the nonlinear stiffness coefficient of the bearing. c₁ and c₂ denote the damping coefficients of the bearing and disk, respectively. Considering the rotational symmetry of the rotor shaft, Equations (1)–(4) have been decoupled into separate x- and y-direction equations. This study focuses solely on the x-directional effects.

2.2. Establishment of the Piezoelectric Equation Theoretical Model

According to the design of this study, a piezoelectric patch (PZT) is installed in the $\overline{x}$ direction of the bearings at both ends of the rotor shaft (as shown in Figure 2). The PZT vibration is shown in Figure 3. The purpose of this installation is to harvest electrical energy from the vibrations induced by eccentric rotation, facilitating subsequent power generation or energy storage. The electrical energy conversion equation for the PZT installed on the bearing, influenced by the vibrations of the eccentric rotor, can be modeled as a single-degree-of-freedom system subjected to base excitation. Based on the study by Harne and Wang [24], we assume a single-degree-of-freedom system under base excitation, where the displacement of the PZT due to vibration can be expressed as:

$$M{\overline{x}}^{**}+c{\overline{x}}^{*}+{\displaystyle \frac{dU(\overline{x})}{d\overline{x}}}+\theta \overline{V}=F_B$$

(5)

In the equation: $\overline{x}$ is the strain variable of the PZT, $\theta$ is the linear piezoelectric coupling coefficient, M is the mass of the base bearing, c is the damping constant of the bearing, ${\displaystyle \frac{dU(\overline{x})}{d\overline{x}}}$ is the generic electromechanical oscillator with restoring force, F_B represents the external force applied to the bearing due to the eccentric rotor. The potential energy (U) of the system can be expressed as:

$$U(\overline{x})={\displaystyle \frac{1}{2}}{k}_1(1-r){\overline{x}}^2+{\displaystyle \frac{1}{4}}{k}_3{\overline{x}}^4$$

(6)

Here k₁ is the linear elastic coefficient of the bearing, k₃ is the nonlinear elastic coefficient of the bearing, r is a tuning parameter that adjusts the system’s response. The piezoelectric equation, representing the electrical output as a function of the load resistance, can be expressed as follows (according to Rajora et al. [25]):

$$C_P{\overline{V}}^{*}+{\displaystyle \frac{1}{{\overline{R}}_P}}\overline{V}-\theta {\overline{x}}^{*}=0$$

(7)

${\overline{R}}_P$ is the resistance, $\overline{V}$ is the voltage across the piezoelectric patch, C_p is the capacitance of the piezoelectric patch.

2.3. Non-Dimensionalized Model of the Rotor System Equations

From the previous theoretical analysis, it is known that the Jeffcott rotor system with piezoelectric energy conversion involves not only the equations for the bearings and the disk (Equations (1)–(4)) but also the piezoelectric equation for the PZT installed at the bearing (Equations (5) and (7)). To facilitate a more effective analysis and to reduce the complexity of the system, the equations can be non-dimensionalized. This step will allow for easier comparison of the system’s behavior under various conditions by scaling the system’s parameters in terms of dimensionless variables. The non-dimensionalization process typically involves defining the following: L = shaft length, x = $\overline{x}/L$, x_1,2 = ${\overline{x}}_{1,2}/L$, e = $\overline{e}/L$, ${\varsigma }_1={\displaystyle \frac{c_1}{2M_1{\omega }_1}}$, ${\varsigma }_2={\displaystyle \frac{c_2}{2M_2{\omega }_2}}$, ${\varsigma }_c=c_2/c_1$, $\tilde{\varsigma }={\displaystyle \frac{{\varsigma }_1{\varsigma }_c}{m}}$, $\tilde{K}=K_2/K_1$, m = M₂/M₁, $\overline{m}$ = M/M₁, ${\omega }_1=\sqrt{{\displaystyle \frac{K_1}{M_1}}}$, ${\omega }_2=\sqrt{{\displaystyle \frac{K_2}{M_2}}}$, $\tilde{\omega }={\omega }_2/{\omega }_1$, $\widehat{\omega }=\overline{\omega }/{\omega }_1$, F_1x = $M_2{\ddot{\overline{x}}}_2/M_{1}L{\omega }_1^2$ = $m{\tilde{\omega }}^2{\ddot{x}}_2$, where ( )^. represents derivative with respect to non-dimensional time. In addition, K₁ is the linear spring constant, K₃ is the nonlinear spring constant. Let v = C_PV/$\theta$, K² = ${\displaystyle \frac{{\theta }^2}{\overline{m}{K}_1{C}_P}}$, ${\delta }_1$ = k₁/(K₁$\overline{m}$), ${\delta }_3$= k₃/(K₁$\overline{m}$L²), $\varsigma ={\displaystyle \frac{c}{2M_1{\omega }_1\overline{m}}}$, a = ${\displaystyle \frac{1}{{\overline{R}}_P{C}_P{\omega }_1}}$. In this study, we only consider the piezoelectric energy conversion efficiency in the x-direction. Equations (1) and (3) are divided by $M_1{\omega }_1^{2}L$, and we obtain:

$${\ddot{x}}_1+2{\varsigma }_1{\dot{x}}_1+(x_1-x_2)+\delta {(x_1-x_2)}^3=m{\tilde{\omega }}^2{\ddot{x}}_2$$

(8)

$${\ddot{x}}_2+2\tilde{\varsigma }{\dot{x}}_2+{\tilde{\omega }}^2(x_2-x_1)=e{\widehat{\omega }}^2\cos \widehat{\omega }t$$

(9)

Next, we assume that the bearing external excitation force F_B in Equation (5) can be expressed as $-M_1{\overline{x}}_1^{**}$. After non-dimensionalizing Equations (5) and (7), we get:

$$\ddot{x}+2\varsigma \dot{x}+{\delta }_1(1-\gamma )x+{\delta }_3{x}^3+K^{2}v=-(1/\overline{m}){\ddot{x}}_1$$

(10)

$$\dot{v}+av-\dot{x}=0$$

(11)

The system’s governing equations are transformed by substituting these dimensionless variables and re-arranging terms accordingly. The result will be a set of non-dimensional equations that are more general and easier to analyze, enabling more efficient simulations and comparisons.

2.4. Database Construction Using the Fourth-Order Runge–Kutta Method

In this study, the fourth-order Runge–Kutta method (RK-4) is used to numerically analyze the Jeffcott system equations and piezoelectric equations to obtain voltage values. A dataset for machine learning is created by varying four key parameters: the mass ratio between the disk and shaft, the mass ratio between the bearing and shaft, the speed ratio, and the eccentric distance ratio of the disk. The ranges of these parameters are listed in

Table 1. The ranges of features.

Disk-Shaft Mass Ratio, m	Bearing-Shaft Mass Ratio, $\overline{\mathit{m}}$	Rotational Speed Ratio, $\widehat{\mathit{\omega }}$	Eccentricity Ratio, e
[0.8–1.1]	[0.02–0.2]	[0.1–6.05]	[0.01–0.059]

, resulting in a total of 0.27 million data points. An example with a disk-to-shaft mass ratio of 0.99 and the corresponding dimensionless voltage distribution is shown in Figure 4.

Figure 4 shows the dimensionless voltage distribution at the bearing when the disk-to-shaft mass ratio is fixed at 0.99, while the rotational speed and eccentric distance vary. As seen in the figure, the voltage output from the bearing PZT increases with higher rotational speeds and larger eccentric distances within this specific range.

3. Experimental Design and Theoretical Validation

3.1. Experimental Setup Design

To verify the accuracy of the theoretical voltage calculated using the fourth-order Runge–Kutta method in Section 2, a simplified experimental setup was constructed based on the theoretical model, as shown in Figure 5. The setup consists of a Jeffcott rotor, a fixed base with a bearing, a motor, an elastic steel sheet, and a piezoelectric patch. The energy harvesting system in this study is designed to convert the vibration energy generated by the high-speed rotation of an eccentric rotor into electrical energy. The vibrations drive the elastic steel mounted on the fixed base, enabling the piezoelectric patch to convert the mechanical vibrations into electrical power. The complete setup is illustrated in Figure 6.

In this experimental setup, the eccentric distance and mass of the disk are first adjusted using screws. Then, the rotational speed of the motor is controlled via Arduino, which drives the Jeffcott rotor through a gear mechanism. During rotation, the rotor generates vibrations that cause the elastic steel sheet fixed to the base to vibrate. These vibrations are captured by the piezoelectric patch, which converts the mechanical energy into electrical energy, forming a complete energy harvesting system. To confirm whether the data produced by this setup aligns with the theoretical results, voltage outputs under three different conditions are compared to validate the accuracy of the theoretical model.

3.2. Experimental Voltage Measurement and Theoretical Validation

After constructing the experimental model, the rotor speed is controlled at 1500 RPM using Arduino. Voltage outputs under various mass ratios and eccentric distances are measured using the imc voltage and power measurement system (imc^© system (CS-5008-1), TÜV Rheinland, Kölle, Germany). The theoretical dimensionless voltage values are then converted back to dimensional values based on the nondimensionalization definitions in the model and compared with the measured voltages to validate the theoretical results. In this study, three different sets of conditions are tested and compared with theoretical predictions:

Case 1: The shaft length is 200 mm. Three screws, each with one nut, are attached to the disk (see Figure 7), resulting in a mass ratio of 0.87 and an eccentric distance of 8.522 mm (eccentricity ratio e = 0.0426). The comparison between theoretical and measured voltages is shown in Figure 8.

Case 2: The shaft length is 200 mm. Three screws with two nuts each are attached to the disk (see Figure 9). The mass ratio is 0.92 and the eccentric distance is 9.577 mm (e = 0.0479). The voltage comparison is shown in Figure 10.

Case 3: The shaft length is 200 mm. Four screws with two nuts each are attached to the disk (see Figure 11). This setup yields a mass ratio of 1.03 and an eccentric distance of 10.07 mm (e = 0.0503). The voltage comparison is shown in Figure 12.

To further validate the dynamic response of the VEH system, amplitude-frequency spectra were extracted from the time-domain voltage signals using fast Fourier transform (FFT). The spectra corresponding to Figure 8, Figure 10, and Figure 12 are presented in Figure 13a–c, respectively. In all cases, the dominant frequency observed in both the theoretical and experimental signals closely matches the shaft rotation speed, confirming that the model accurately captures the primary vibration frequency. Additionally, with increasing mass ratio and eccentricity, subtle variations in harmonic content and amplitude distribution were observed, indicating the model’s sensitivity to changes in system parameters. The agreement between experimental and simulated spectra not only supports the accuracy of the proposed theoretical model but also reinforces its robustness in both the time and frequency domains.

According to

Table 2. Comparison of experimental and theoretical voltages.

	3Screw 1Nut	3Screw 2Nut	4Screw 2Nut
Mass Ratio	0.87	0.92	1.0
Eccentric Distance Ratio (mm)	8.522	9.577	10.07
Theo. (V)	0.579	0.708	0.901
Exp. (V)	0.6	0.678	0.888
RMS Error (%)	3.626	4.237	1.442

, the root mean square (RMS) errors between the theoretical and experimental voltages are all within 5%. Additionally, as the mass ratio and eccentric distance increase, the output voltage shows an upward trend. Therefore, these results are considered consistent with the expected trend and support the validity of the theoretical model proposed in this study. Figure 8, Figure 10, Figure 12 and Figure 13 compare the theoretical predictions with experimental results across different mass ratios. The root mean square (RMS) error between the two remains within 5% for all tested conditions, indicating good agreement. Although slight variations in error magnitude are observed (Table 2), there is no consistent trend suggesting that the discrepancy increases with increasing mass ratio. This result demonstrates that the proposed theoretical model retains robust predictive accuracy across a practical range of mass ratios relevant to rotor-based vibration energy harvesting systems.

4. Deep Learning

4.1. Introduction to Machine Learning

In this study, machine learning is used to predict the power generation efficiency of a vibration energy harvesting device installed on the Jeffcott system under different parameter combinations. Machine learning is an optimization method that allows computers to find optimal solutions through algorithms, helping humans process complex problems more efficiently while reducing errors when analyzing large datasets. Machine learning provides various algorithms tailored for different scenarios, such as clustering and regression models, to help users find the best model or solution. Machine learning is generally classified into four different learning modes: reinforcement learning, supervised learning, unsupervised learning, and semi-supervised learning. Reinforcement Learning (RL) learns decision-making strategies through interactions with the environment. Using a trial-and-error approach, the computer completes a series of decisions without human intervention or explicitly written instructions. Supervised learning trains models using labeled data, learning the relationships or patterns between the data and labels to perform classification or prediction. By comparing errors during training, the model can refine itself for higher accuracy. Supervised learning generally achieves higher precision compared to other learning methods. Unsupervised learning allows machines to identify internal relationships, distributions, or clusters within the data without requiring pre-labeled data. Since there are no labels, the machine categorizes similar features without predefined classifications. Semi-supervised learning is a hybrid approach between supervised and unsupervised learning, using a small amount of labeled data along with a large amount of unlabeled data. This method balances the ability to handle large-scale unlabeled data while still obtaining meaningful labeled results.

4.2. Introduction to Deep Learning

Deep learning is a data representation learning algorithm based on artificial neural networks. Its architecture consists of an input layer, an output layer, and multiple hidden layers. By utilizing multi-layer structures, deep learning autonomously learns patterns within the data, extracting different levels of features to enhance model performance. Today, deep learning includes various subfields, such as: Multi-layer Perceptron (MLP), Deep Neural Network (DNN), Convolutional Neural Network (CNN), and Recurrent Neural Network (RNN). Before constructing a deep learning model, the collected data must undergo labeling and normalization. Labeling helps the machine better recognize data, allowing it to compare errors and refine itself during training. Normalization ensures that all feature scales are standardized, preventing differences in feature scales from affecting the model’s accuracy. After preprocessing the data, it is divided into three sets: training set, validation set, and test set (as shown in Figure 14). The training set is first fed into the deep learning architecture, where the neurons in hidden layers iteratively process the data and validate the correct features. The training continues until the loss function reaches an appropriate value, completing the model development. Finally, the test set is introduced to the model to make predictions and obtain the final results.

4.3. Database Establishment

In this study, the learning method used is supervised learning, which requires data to be labeled. First, the Jeffcott system equations and piezoelectric equations are combined. Using the RK-4 method, numerical solutions are obtained to determine the voltage, which is then designated as the data labels. The mass ratio, rotational speed ratio, and eccentricity ratio are defined as the data features.

4.4. Deep Neural Network Architecture

Artificial neural networks are composed of interconnected processing units called neurons. Each neuron consists of three key components: weight (w), bias (b), and an activation function (δ), as shown in Figure 15 and Equation (12). These elements allow the neuron to mathematically approximate the functioning of the human brain. A neuron processes multiple inputs into a single output by applying weighted summation, bias adjustment, and nonlinear transformation via the activation function.

$$\mathrm{y}=\delta ({\displaystyle \sum _i^n{x}_i{w}_i+b)}$$

(12)

When neurons are connected together in layers, a Multi-Layer Perceptron (MLP) is formed. An MLP with only one hidden layer is typically referred to as a shallow neural network, while adding multiple hidden layers results in a Deep Neural Network (DNN). The depth of the network (i.e., the number of hidden layers) is what distinguishes DNNs from shallow MLPs. In this study, two different levels of network depth were considered for different purposes:

• Baseline hardware comparison (Section 5.1): A simplified MLP with one hidden layer (10 neurons) was used solely to compare training times between CPU and GPU platforms across DNN, LSTM, and XGBoost models. This shallow architecture was chosen to keep the hardware benchmarking fair and computationally light.
• Final analysis (Section 5.2): For predictive modeling, the network depth was systematically increased, and the optimal structure was found to be five hidden layers with 40 neurons each, which qualifies as a Deep Neural Network (DNN). This configuration achieved the highest accuracy with R² = 0.9999779 and the lowest MSE (1.26 × 10⁻⁷).

The overall structure of the DNN includes an input layer, multiple hidden layers, and an output layer (Figure 16). The input layer receives features, hidden layers perform nonlinear transformations, and the output layer produces predictions.

The Mean Squared Error (MSE) was selected as the loss function for regression, and weight optimization was performed using the backpropagation algorithm with gradient descent. The formula for MSE is as follows:

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n(y_i-{\widehat{y}}_i)}$$

(13)

In the above approach, y_i is the actual value, and ${\widehat{y}}_i$ is the predicted value. The model primarily utilizes Forward Propagation, meaning that data flows from the input layer through weighted sums and bias values, followed by an activation function transformation before producing an output. However, this study adopts the Backpropagation Algorithm. This algorithm propagates errors backward through the network, allowing the model to use these errors to update weights via gradient descent. By iteratively adjusting the weights, the training error is progressively reduced.

4.5. Long Short-Term Memory (LSTM) Model Architecture

Long Short-Term Memory (LSTM) is a type of Recurrent Neural Network (RNN) designed to address the long-term dependency problem that arises when processing long sequences of data. In a standard RNN, when using backpropagation to process long sequences, the hidden state at each time step is influenced by the previous hidden state and the current input. However, as the number of time step increases, the gradients can either vanish (gradually diminish to near zero) or explode (grow uncontrollably). This issue prevents the model from effectively learning long-term dependencies. The problem occurs because an RNN consists of repeating neural network modules connected in a chain-like structure. The activation function inside these modules is tanh, whose derivative lies between 0 and 1. As time steps increase, continuous multiplication in backpropagation causes the gradient to shrink exponentially, leading to the vanishing gradient problem. Conversely, if any value in the computation is extremely large, continuous multiplication may cause a gradient explosion. A schematic diagram of the RNN model is shown in Figure 17.

LSTM modifies the structure of the repeating module in an RNN by replacing a single neural network layer with four interacting layers to process information. This structural change helps address the long-term dependency problem by allowing the model to retain important information over extended sequences. A schematic diagram of the LSTM model is shown in Figure 18.

The structure of an LSTM cell primarily consists of three gates: the Forget Gate, Input Gate, and Output Gate (Figure 19). These gates control the flow of information within the memory cell. Forget Gate: The forget gate is used to determine whether the information in the cell should be retained or discarded. It calculates f_t using the previous state h_t−1 and the current input x_t, with the resulting value ranging between 0 and 1. A value of 1 indicates full retention, while 0 indicates complete discarding. The mathematical expression is given in Equation (14).

$$f_t=\sigma \left(W_f\left[h_{t-1},x_t\right]+b_f\right)$$

(14)

where W_f is the forget gate weight, which controls how much of the previous memory to forget, b_f is the forget gate bias, used to adjust the forgetting level. The input gate determines how much new information should be written into the memory cell and consists of two parts: the input gate activation i_t and the candidate value ${\tilde{C}}_t$. Their mathematical expressions are given in Equations (15) and (16), respectively.

$$i_t=\sigma \left(W_i\left[h_{t-1},x_t\right]+b_i\right)$$

(15)

$${\tilde{C}}_t=\tanh \left(W_c\left[h_{t-1},x_t\right]+b_C\right)$$

(16)

where b_i is the input gate bias, used to adjust the degree of new information written into the cell, b_c is the cell gate bias, used to adjust the candidate value of the new cell memory. The new memory cell C_t is then updated using Equation (17).

$$C_t=f_t\cdot C_{t-1}+i_t\cdot {\tilde{C}}_t$$

(17)

The output gate determines how much information is output as the current hidden state h_t and passed to the next time step. Its mathematical expressions are given in Equations (18) and (19).

$$o_t=\sigma \left(W_0\left[h_{t-1},x_t\right]+b_o\right)$$

(18)

$$h_t=o_t\ast \tanh \left(C_t\right)$$

(19)

In Equation (18), b_o is the output gate bias, which adjusts how much of the memory will be output.

4.6. XGBoost Model Architecture

Extreme Gradient Boosting (XGBoost) is a machine learning algorithm based on gradient boosting. It constructs a strong predictive model by combining multiple weak learners and iteratively reducing prediction errors to achieve improved accuracy. The basic structure consists of an ensemble of decision trees. Each tree is built to correct the residual errors from the previous iteration by optimizing an objective function, thereby enhancing predictive performance. A regularization mechanism is also incorporated to prevent overfitting and improve the model’s generalization ability. In the XGBoost architecture, each subsequent tree is generated based on the prediction errors of the previous tree. The model can be expressed as Equation (20):

$${\widehat{y}}_i^{(t)}={\widehat{y}}_i^{(t-1)}+f_t(x_i)$$

(20)

where y_i denotes the predicted value for the i-th sample, and f_t(x_i) represents the output of the t-th tree.

The objective function of the model is given in Equation (21):

$$Obj={\displaystyle \sum _{i=1}^{n}l(y_i,{\widehat{y}}_i)+{\displaystyle \sum _{i=1}^t\mathsf{\Omega }(f_t)}}$$

(21)

where l is the loss function, and Ω(f_t) is the regularization term, defined in Equation (22):

$$\Omega (f_t)=\gamma T+{\displaystyle \frac{1}{2}}\lambda {\displaystyle \sum _{j=1}^T{\omega }_j^2}$$

(22)

Here, T represents the number of leaf nodes in the decision tree, and ω_j is the weight of the j-th leaf. The regularization term is controlled by hyperparameters γ and λ, which help reduce overfitting and enhance the model’s generalization capability.

5. Deep Learning Training Analysis and Results

5.1. Comparison of Hardware Impact on Model Training Time

Before conducting model training, we first examined the impact of hardware on training time. The hardware used in this study includes an Intel Core i7-13700F CPU and an NVIDIA GeForce RTX 4070 GPU. We investigated the influence of CPU and GPU performance on the training speed of three algorithms. Each of the three algorithms was trained using identical model structures on both CPU and GPU platforms, and the training times were compared. The DNN model was configured with one hidden layer containing 10 neurons; the LSTM model also had one hidden layer with 10 neurons. Both models used a batch size of 512 and were trained for 1000 epochs. The XGBoost model was trained with a maximum tree depth of 6. The training times for the three models are shown in

Table 3. Total training time for different hardware configurations.

	DNN	LSTM	XGBoost
CPU(i7-13700F)	5397	16,479	171
GPU(RTX4070)	3734	13,875	7

Unit—seconds (s).

.

As shown in Table 3, GPU-based training demonstrates a clear advantage over CPU-based training across all three models. The difference in training time is significant, mainly because the training process involves numerous matrix multiplications and vector operations. The GPU, with its highly parallel architecture and large number of processing cores, is better suited for these computationally intensive tasks.

5.2. DNN Model Establishment and Analysis

In this study, the Jeffcott equations and piezoelectric equation were solved using the fourth-order Runge–Kutta method, resulting in 0.27 million data points. These data were split into 75% training set, 20% validation set, and 5% prediction set to build the deep neural network model. The model architecture consisted of a basic structure: one input layer, one hidden layer, and one output layer. The ReLU (Rectified Linear Unit) function was used as the activation function for the hidden layer. Since the goal was regression, the linear function was chosen as the activation function for the output layer. For the loss function, the Mean Squared Error (MSE), commonly used in regression, was selected. The Coefficient of Determination (R²) was used as the evaluation metric. The neural network had 20 neurons in the hidden layer, a batch size of 128, and was trained for 1000 epochs. The resulting R² value was 0.9919897, as shown in Figure 20.

After confirming that the model structure functions correctly, the number of neurons, batch size, and epochs are fixed while varying the number of hidden layers to determine the optimal depth for best performance. The results are shown in Figure 21 and

Table 4. Coefficient of determination (R²) for DNN with different numbers of hidden layers.

Hidden Layer	1	2	3
Coefficient of determination	0.9919897	0.9997161	0.9999345
Hidden Layer	4	5
Coefficient of determination	0.9999450	0.9999664

. From Table 4 and Figure 21, it can be observed that the optimal number of hidden layers is five. With the number of hidden layers fixed at five, different numbers of neurons are then tested to identify the best model parameters. The results are shown in Figure 22 and

Table 5. Coefficient of determination (R²) for DNN with different numbers of neurons in hidden layers.

Neurons	20	30	40
Coefficient of determination	0.9999664	0.9999532	0.9999779
Neurons	50	60
Coefficient of determination	0.9999621	0.9999626

.

From the comparison of models trained with different parameters, it can be concluded that with five hidden layers, the optimal number of neurons is 40. Under this configuration, the model achieves the highest coefficient of determination (0.9999779) and the lowest MSE (1.26 × 10⁻⁷). Therefore, the DNN model with five hidden layers and 40 neurons is adopted as the optimal training configuration for this study. The results are shown in Figure 23 and Figure 24. In Figure 23, the horizontal axis represents the actual voltage values, and the vertical axis represents the predicted voltage values. The dashed line indicates the reference line where predicted values equal actual values. In Figure 24, the horizontal axis represents the actual voltage values, and the vertical axis shows the difference between the predicted and actual values.

5.3. LSTM Model Development and Analysis

Following the same method as in the previous section, the data was split into training, validation, and prediction sets in the same proportions. Initially, a model with one input layer, one hidden layer, and one output layer was created, setting the number of neurons to 20, batch size to 128, and epoch number to 1000. The Long Short-Term Memory (LSTM) model was built, and the resulting performance yielded an R-squared value of 0.9999974. The results are shown in Figure 25.

By fixing the number of neurons, batch size, and epoch count, the hidden layer count was varied to identify the optimal number of hidden layers for this study. The results are shown in Figure 26 and

Table 6. Coefficient of determination (R²) for LSTM with different numbers of hidden layers.

Hidden Layer	1	2	3
Coefficient of determination	0.9999974	0.9999964	0.9999958
Hidden Layer	4	5
Coefficient of determination	0.9999960	0.9999937

.

From the comparison chart above, it is observed that the best performance is achieved with 2 hidden layers, resulting in an R-square value of 0.9999974. With the number of hidden layers fixed at 2, the number of neurons was varied to find the optimal parameters. The results are shown in Figure 27 and

Table 7. Coefficient of determination (R²) for LSTM with different numbers of neurons in hidden layers.

Neurons	20	30	40
Coefficient of determination	0.9999974	0.9999971	0.9999965
Neurons	50	60	70
Coefficient of determination	0.9999968	0.9999972	0.9999965

.

From the comparison chart, it is observed that the best performance in terms of R-squared value occurs when the number of neurons is 20, with an R-squared value of 0.9999974 and an MSE value of 1.46 × 10⁻⁸. Therefore, the optimal parameters for the LSTM model are set to 1 hidden layer and 20 neurons. Figure 28 and Figure 29 show the best training results for the LSTM model.

5.4. XGBoost Model Development and Analysis

In this study, the XGBoost model was constructed with the following hyperparameter settings: learning rate set to 0.03, maximum tree depth set to 1, and number of iterations set to 3000. The resulting XGBoost training model achieved an R² value of 0.6907, as shown in Figure 30.

After fixing the learning rate and the number of iterations, the maximum tree depth was varied to determine the most suitable depth for the model. The R² values for each depth are shown in

Table 8. R² values for different tree depths in XGBoost.

Max Depth	1	2	3	4
Coefficient of determination	0.593933	0.934467	0.998015	0.999677
Max Depth	5	6	7	8
Coefficient of determination	0.999793	0.999867	0.999885	0.999898
Max Depth	9	10	11	12
Coefficient of determination	0.999918	0.999927	0.999936	0.999940

and Figure 31.

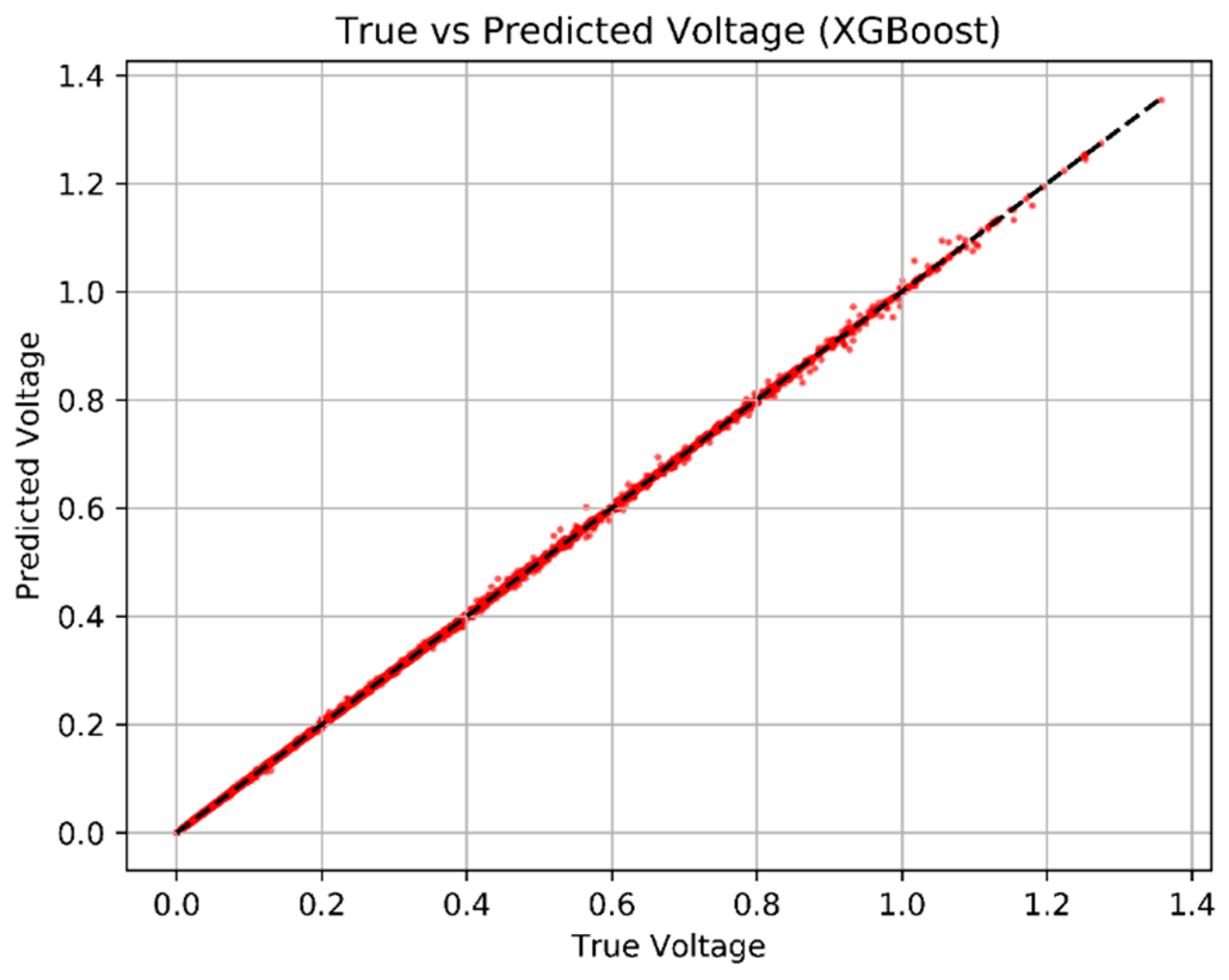
Based on Table 8 and Figure 31, the maximum tree depth is set to be 12. At this depth, the model achieves an R² value of 0.99940 and an MSE of 6.31 × 10⁻⁷. The best results are illustrated in Figure 32 and Figure 33. In Figure 32, the horizontal axis represents the actual voltage values, the vertical axis represents the predicted voltage values, and the dashed line indicates the reference line where predicted values equal actual values. 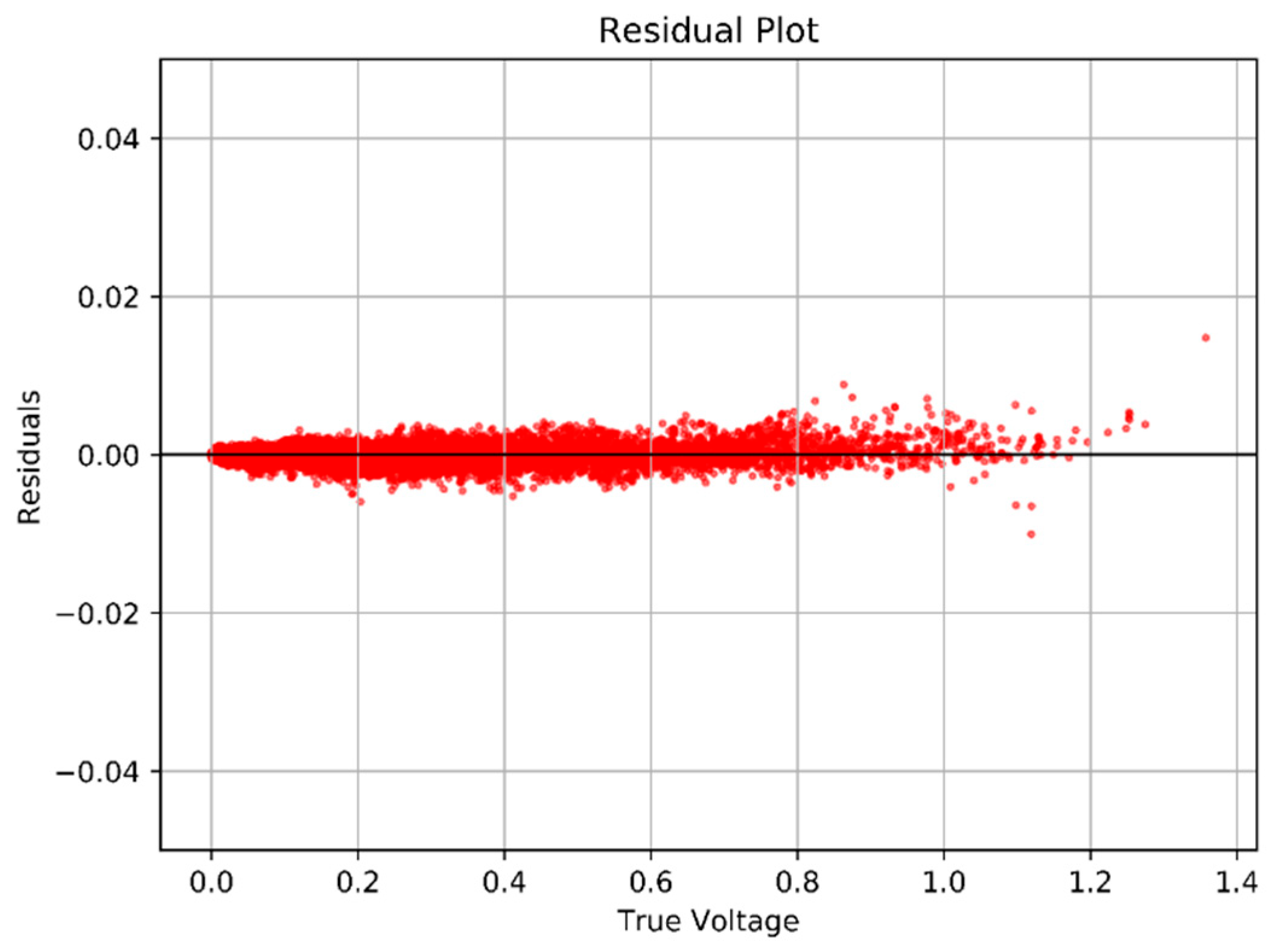In Figure 33, the horizontal axis represents the actual voltage values, while the vertical axis shows the difference between the predicted and actual values.

5.5. Training Configuration and Hyperparameters

The training hyperparameters for the DNN and LSTM models, along with the format of the training samples, are provided below: (a) Optimizer and Learning Rate: The Adam optimizer was used for both the DNN and LSTM models. A learning rate of 0.003 was applied for the DNN, while a lower learning rate of 0.003 was selected for the LSTM after tuning, to improve convergence stability. (b) Training Samples and Input Format: The DNN model was trained on discrete, tabular data points. Each input sample consisted of three features—mass ratio, rotational speed, and eccentric distance—with the corresponding output voltage as the prediction target. For the LSTM model, although the original dataset was not inherently sequential, the data was reshaped into fixed-length sequences of size 3. This preprocessing step allowed the LSTM to model temporal dependencies and enabled fair comparison with the DNN and XGBoost models under consistent feature conditions. (c) Epochs and Batch Size: The DNN model was trained for 700 epochs with a batch size of 128, while the LSTM model was trained for 1000 epochs with the same batch size.

5.6. Model Comparison, Analysis, and Discussion

In this study, three machine learning algorithms—Deep Neural Network (DNN), Long Short-Term Memory (LSTM), and eXtreme Gradient Boosting (XGBoost)—were trained and evaluated using over 0.27 million simulation data points obtained from numerical solutions of the Jeffcott rotor and piezoelectric equations. Each model was trained under various configurations, and the best-performing setup for each was selected for a comparative analysis. The evaluation was based on three primary metrics: training time, mean squared error (MSE), and coefficient of determination (R²). All three models demonstrated excellent predictive accuracy, with R² values above 0.9999 for DNN and LSTM, and above 0.999 for the optimized XGBoost model. This high degree of accuracy confirms that the vibration-to-voltage relationship in the Jeffcott rotor system is highly learnable using both deep learning and ensemble learning methods.

Table 9. Comparison of Optimal Results for Each Algorithm.

	DNN	LSTM	XGBoost
	40 Neurons	20 Neurons	12 Depth
Training Time (s)	3437	4115	48
MSE	1.26 × 10−7	1.46 × 10−8	6.31 × 10−7
R-squared	0.9999779	0.9999974	0.99940

presents the comparison of the three algorithms under their optimal configurations.

To verify the consistency of the machine learning results, each model was trained five times using different random seeds. The resulting R² values showed negligible variation, indicating that the predictions are not significantly affected by initialization randomness.

• The DNN model achieved the best overall performance in terms of R² (0.9999779) and lowest MSE (1.26 × 10⁻⁷), indicating near-perfect alignment between predicted and actual voltage values. This result highlights the capability of multilayer perceptrons in handling nonlinear regression problems when properly tuned.
• The LSTM model also performed admirably, with an R² value of 0.9999974 and MSE of 1.46 × 10⁻⁸. Although LSTM is primarily designed for temporal sequence prediction, its strong generalization ability allows it to effectively capture complex patterns in static datasets as well.
• The XGBoost model, while slightly trailing in R² (0.99940) and MSE (6.31 × 10⁻⁷), still exhibited excellent prediction performance—especially considering it is not a deep learning model but a gradient-boosted decision tree ensemble.

These results demonstrate that both neural networks and ensemble tree methods are capable of accurately modeling the VEH system, provided sufficient data and feature engineering.

While accuracy is essential, training efficiency and computational cost are critical factors for practical deployment in industrial settings.

• The XGBoost model had the shortest training time among all three, completing training in significantly less time than either DNN or LSTM. This efficiency is due to its tree-based architecture and the absence of backpropagation and large-scale matrix computations.

The DNN and LSTM models required longer training times, particularly when using CPU resources. The advantage of GPU acceleration was evident in both cases, dramatically reducing training time due to parallel processing of matrix operations.

The trade-off between training time and accuracy positions XGBoost as an ideal candidate for real-time or near-real-time prediction tasks where retraining needs to be performed frequently or where computing resources are limited. The DNN and LSTM models demonstrated strong fitting capabilities across the large dataset and showed good generalization on the test set. However, DNNs may require careful hyperparameter tuning (e.g., number of layers, neurons, learning rate) to avoid overfitting or underfitting. LSTM, while robust, is typically more sensitive to the batch size and sequence length, even when used on static input data. XGBoost, in contrast, is inherently more robust to overfitting due to its regularization mechanisms and decision-tree ensemble structure. The interpretability of XGBoost also makes it easier to analyze feature importance and system sensitivity to different parameters (e.g., speed ratio, eccentric distance, mass ratios), which is a valuable advantage in engineering applications.

Regarding the application’s suitability, for high-precision offline modeling and simulation analysis, the DNN model is most appropriate due to its superior accuracy and flexibility. The LSTM model could be more advantageous in scenarios where sequential or time-dependent behavior of vibrations is to be modeled—such as real-time health monitoring over time. The XGBoost model is particularly suitable for real-time deployment or in edge computing scenarios, such as factory workstations or shipboard systems, where fast predictions with limited computational power are necessary.

This study confirms that VEHS performance can be accurately predicted using machine learning techniques without the need for repeated physical experimentation. This approach not only reduces time and cost but also opens the possibility for real-time optimization of VEHS parameters—such as mass ratio, rotational speed, and eccentric distance—across different machinery types. Moreover, with experimental validation supporting the simulation results, the trained models can serve as digital twins, offering predictive capabilities for both energy harvesting planning and condition-based maintenance. While the Jeffcott rotor model used in this work represents a simplified system, it serves as a well-established benchmark in rotor dynamics. The model provides a clear and analytically tractable framework for isolating key mechanical and electrical parameters affecting VEH performance. This deliberate simplification enables efficient data generation and reliable integration with machine learning techniques.

6. Conclusions

This study investigates the use of machine learning techniques to predict the power generation efficiency of a vibration energy harvesting system (VEHS) installed on a Jeffcott rotor model. The rotor’s imbalance-induced vibrations are utilized to generate electrical energy through a piezoelectric device. Key findings and conclusions are as follows:

1.

Theoretical and Experimental Validation

The Jeffcott rotor and piezoelectric system were modeled and solved using the fourth-order Runge–Kutta method, generating a large dataset of voltage outputs under various operating conditions (rotational speed, mass ratio, and eccentric distance). Experimental results under different physical configurations were found to closely match the theoretical model, with RMS errors under 5%, validating the model’s accuracy.

2.

Machine Learning for Voltage Prediction

Three machine learning models—Deep Neural Network (DNN), Long Short-Term Memory (LSTM), and XGBoost—were trained using labeled simulation data to predict voltage output based on input parameters. All models demonstrated high prediction accuracy:

• DNN: R² = 0.9999779, MSE = 1.26 × 10⁻⁷;
• LSTM: R² = 0.9999974, MSE = 1.46 × 10⁻⁸;
• XGBoost: R² = 0.99940, MSE = 6.31 × 10⁻⁷.

3.

Model Comparison and Practical Considerations

While DNN and LSTM slightly outperformed XGBoost in prediction accuracy, XGBoost had a clear advantage in training speed, making it a favorable choice for real-time industrial applications. Its strong performance and low computational overhead suggest that XGBoost can be effectively deployed for online monitoring and prediction of VEHS output in factory or marine environments.

4.

Application Potential

The proposed approach offers a dual benefit: it enables the conversion of otherwise wasted vibrational energy into usable electrical power and provides a predictive framework for optimizing energy harvesting in real-world rotating machinery systems. This can enhance energy efficiency and support sustainable practices in both factory and maritime applications.

Future Work

Although this study demonstrates the predictive accuracy and computational efficiency of XGBoost for evaluating VEHS performance under various rotor conditions, it is important to note that the model has been validated only through simulation data and limited experimental testing. The Jeffcott rotor-based VEH system remains at the conceptual and proof-of-concept stage, and no real-time hardware-in-the-loop (HIL) implementation or embedded deployment has yet been conducted. Therefore, while the results suggest that XGBoost might be suitable for real-time evaluation and edge deployment, further work is needed to implement and verify the approach under actual operational conditions. Future studies should also consider incorporating additional machine parameters (e.g., damping effects, temperature influences) and exploring more advanced hybrid learning models or real-time adaptive systems to enhance prediction robustness and deployment feasibility in complex environments.