Impedance Spectroscopy for Interface Trap Effects Evaluation in Dopant-Free Silicon Solar Cells
Abstract
1. Introduction
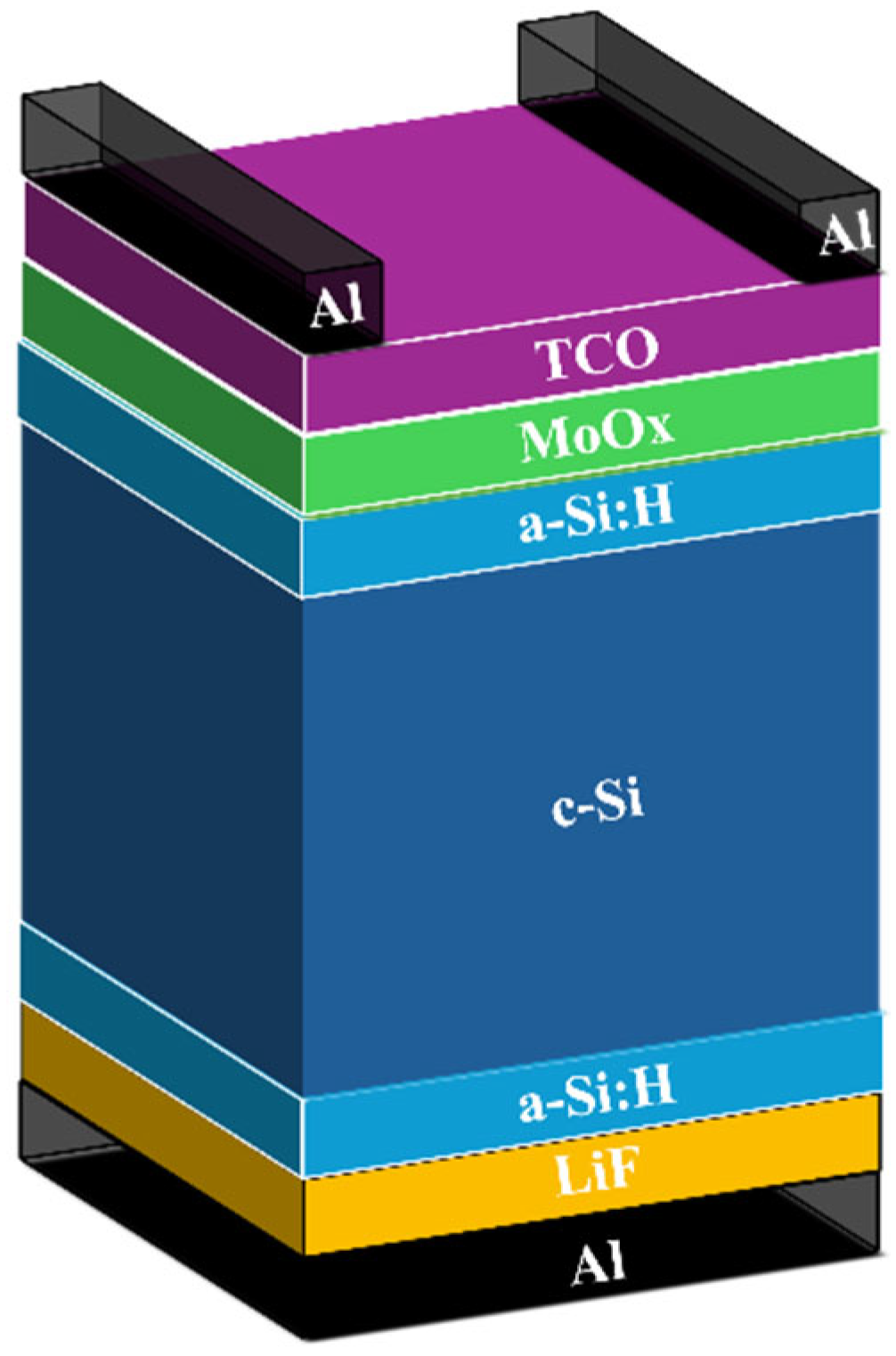
2. Solar Cells Fabrication
3. Experimental Results
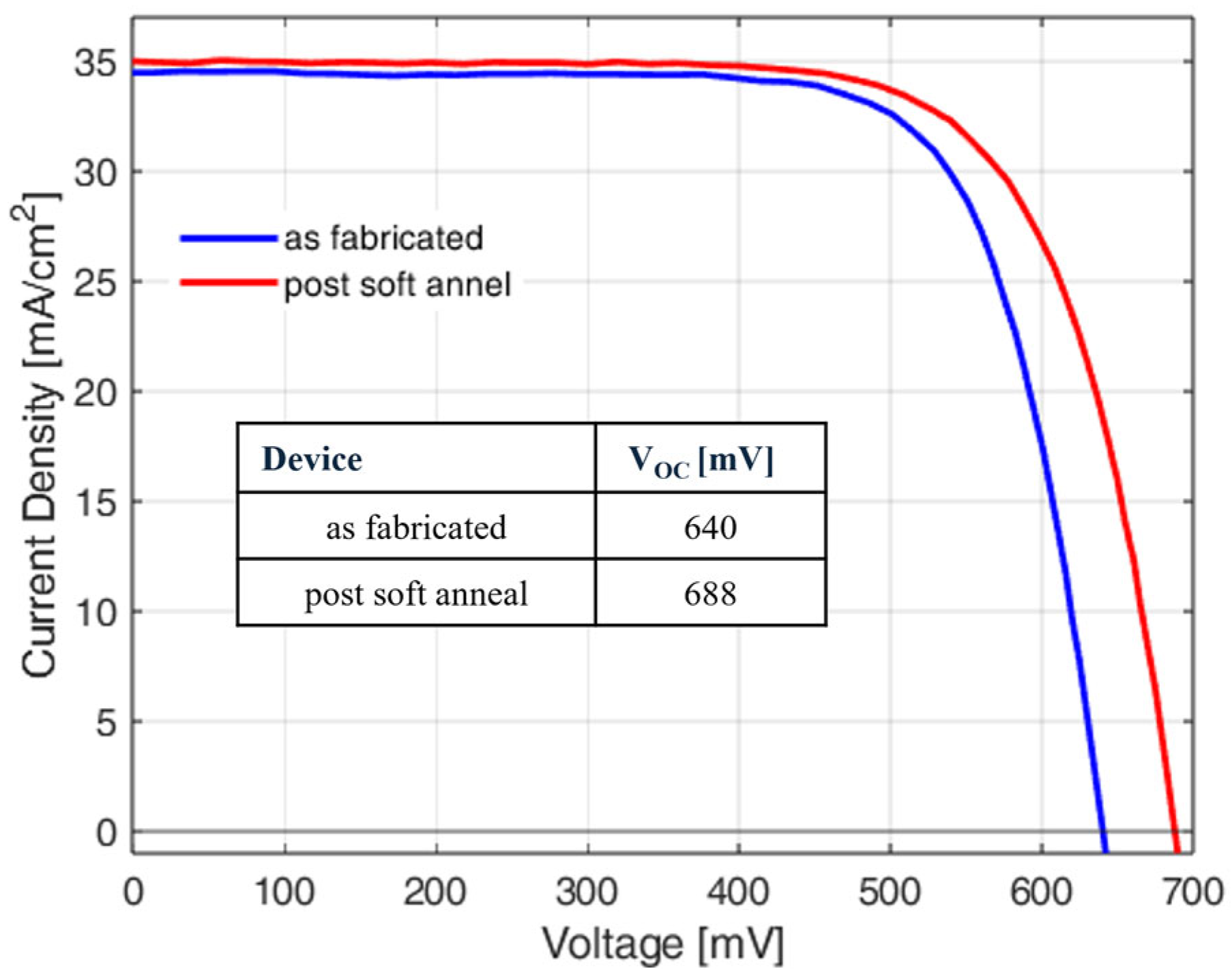
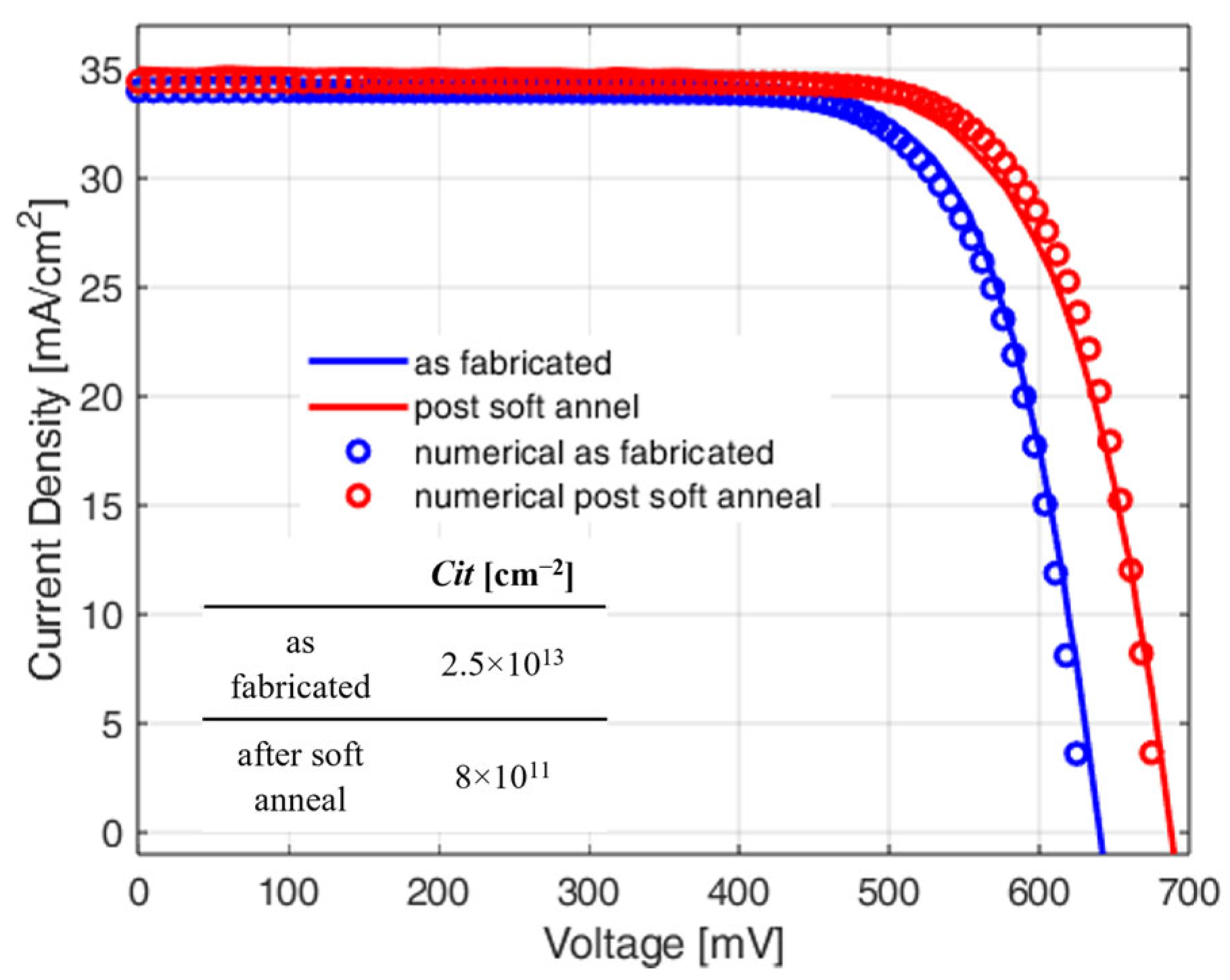
3.1. Current–Voltage Characteristics
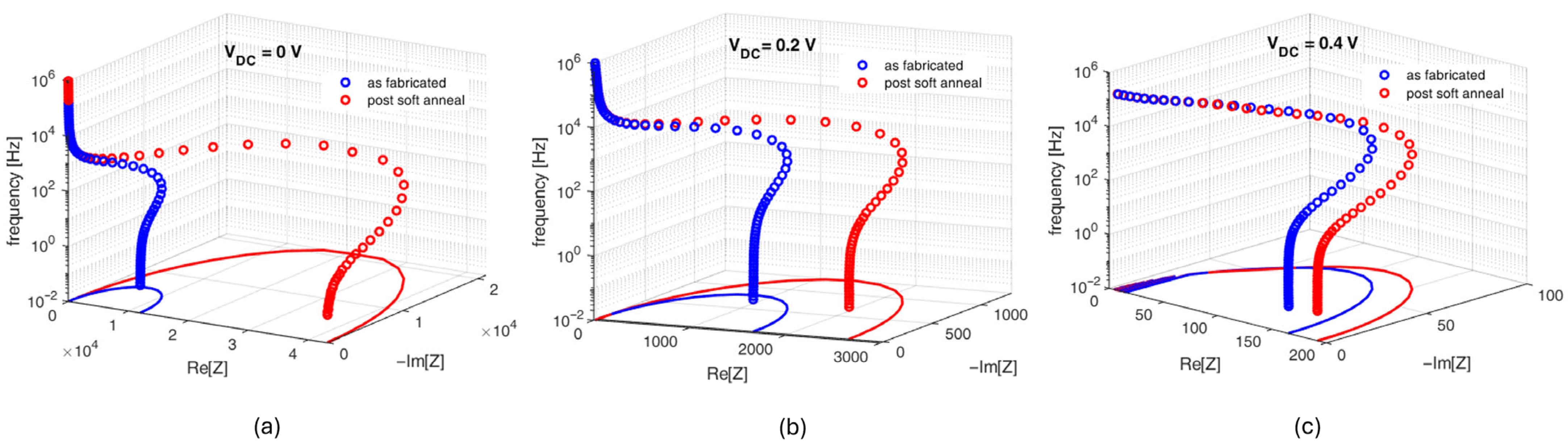
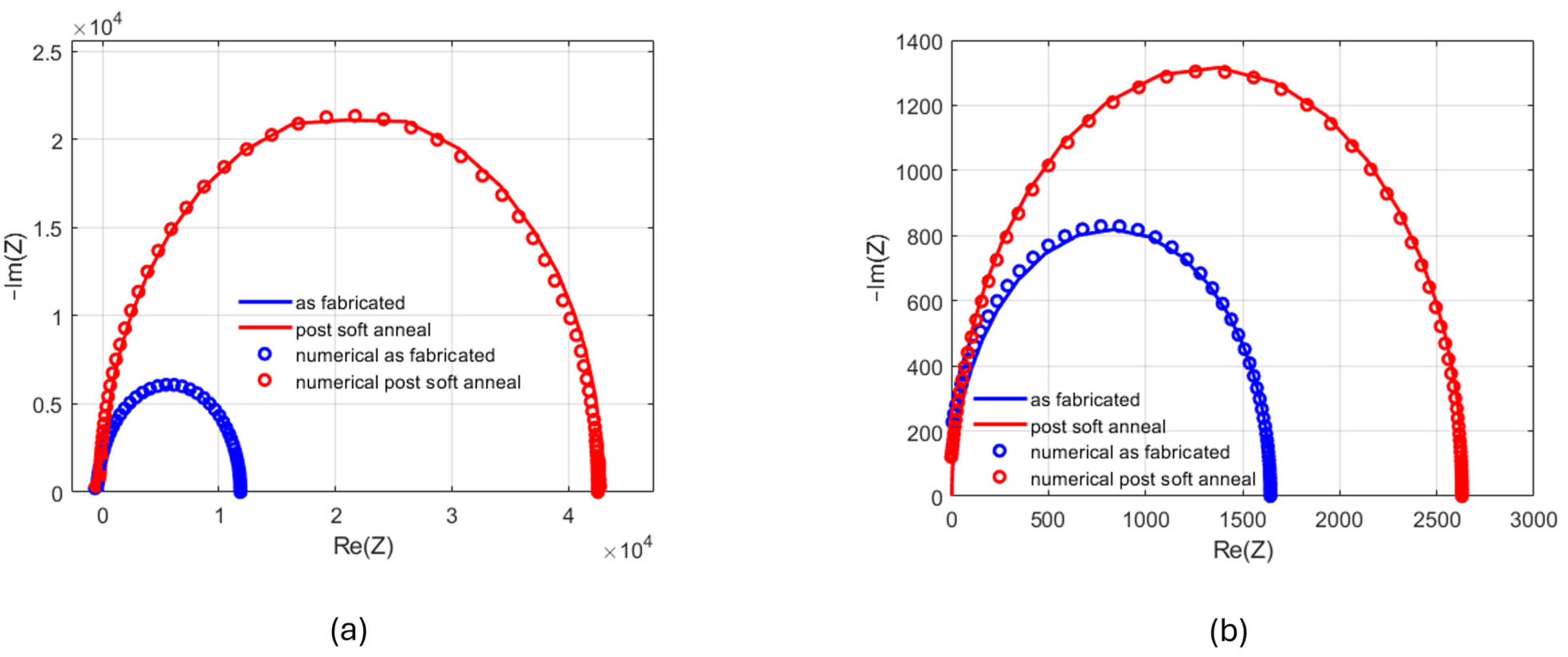
3.2. Impedance Spectroscopy
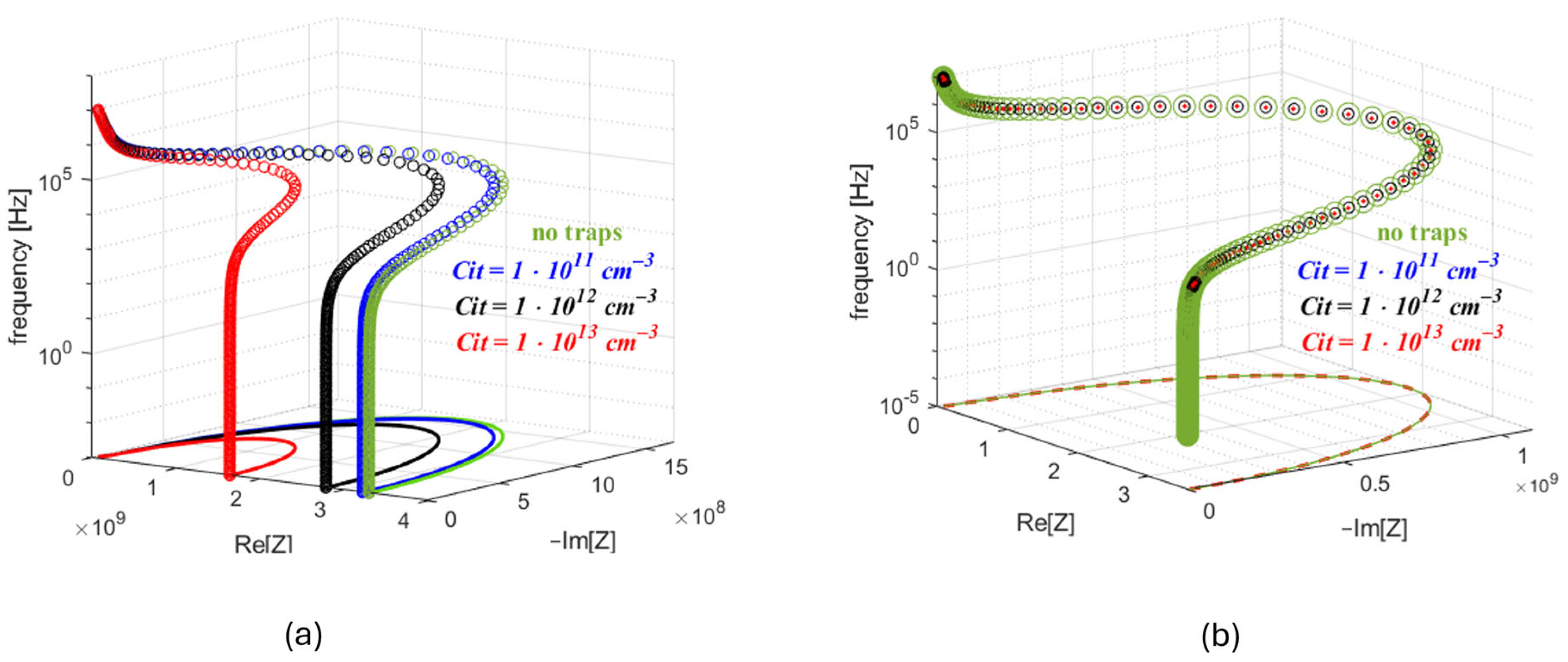
4. Numerical Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternate current |
| Al | Aluminum |
| a-Si:H | Amorphous silicon |
| c-Si | Crystalline silicon |
| DC | Direct current |
| DLTS | Deep-level transient spectroscopy |
| DUT | Device under test |
| ETL | Electron transport layer |
| HTL | Hole transport layer |
| IS | Impedance spectroscopy |
| ITO | Indium tin oxide |
| LiF | Lithium fluoride |
| MoOx | Molybdenum oxide |
| PECVD | Plasma-enhanced chemical vapor deposition |
| PERC | Passivated emitter and rear cell |
| SHJ | Silicon heterojunction |
| Si | Silicon |
| TCO | Transparent conductive oxide |
References
- Matacena, I.; Lancellotti, L.; Daliento, S.; Alfano, B.; De Maria, A.; La Ferrara, V.; Mercaldo, L.V.; Miglietta, M.L.; Polichetti, T.; Rametta, G.; et al. Impedance Spectroscopy of Perovskite Solar Cells with SnO2 Embedding Graphene Nanoplatelets. IEEE J. Photovolt. 2023, 13, 866–872. [Google Scholar] [CrossRef]
- Yadav, P.; Pandey, K.; Bhatt, V.; Kumar, M.; Kim, J. Critical aspects of impedance spectroscopy in silicon solar cell characterization: A review. Renew. Sustain. Energy Rev. 2017, 76, 1562–1578. [Google Scholar] [CrossRef]
- Sacco, A. Electrochemical impedance spectroscopy: Fundamentals and application in dye-sensitized solar cells. Renew. Sustain. Energy Rev. 2017, 79, 814–829. [Google Scholar] [CrossRef]
- Von Hauff, E.; Klotz, D. Impedance spectroscopy for perovskite solar cells: Characterisation, analysis, and diagnosis. J. Mater. Chem. C 2022, 10, 742–761. [Google Scholar] [CrossRef]
- Fabregat-Santiago, F.; Garcia-Belmonte, G.; Mora-Seró, I.; Bisquert, J. Characterization of nanostructured hybrid and organic solar cells by impedance spectroscopy. Phys. Chem. Chem. Phys. 2011, 13, 9083–9118. [Google Scholar] [CrossRef]
- Lancellotti, L.; Bobeico, E.; Della Noce, M.; Delli Veneri, P.; Matacena, I. Work Function Determination of Transparent Contact for a:Si/c-Si Heterojunction Solar Cells. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe, EEEIC/I and CPS Europe2018, Palermo, Italy, 12–15 June 2018; pp. 1–5. [Google Scholar]
- Lancellotti, L.; Lisi, N.; Veneri, P.D.; Bobeico, E.; Matacena, I.; Guerriero, P. Graphene-on-Silicon solar cells with graphite contacts. In Proceedings of the 2019 International Conference on Clean Electrical Power (ICCEP), Otranto, Italy, 2–4 July 2019; pp. 199–203. [Google Scholar]
- Blakers, A. Development of the PERC solar cell. IEEE J. Photovolt. 2019, 9, 629–635. [Google Scholar] [CrossRef]
- De Wolf, S.; Descoeudres, A.; Holman, Z.C.; Ballif, C. High-efficiency Silicon Heterojunction Solar Cells: A Review. Green 2012, 2, 7–24. [Google Scholar] [CrossRef]
- Green, M.A.; Dunlop, E.D.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Siefer, G.; Hao, X.; Jiang, J.Y. Solar Cell Efficiency Tables (Version 65). Prog. Photovolt. Res. Appl. 2025, 33, 3–15. [Google Scholar] [CrossRef]
- Holman, Z.C.; Descoeudres, A.; Barraud, L.; Fernandez, F.Z.; Seif, J.P.; De Wolf, S.; Ballif, C. Current losses at the front of silicon heterojunction solar cells. IEEE J. Photovolt. 2012, 2, 715. [Google Scholar] [CrossRef]
- Fujiwara, H.; Kondo, M. Eects of a-Si:H layer thicknesses on the performance of a-Si:H/c-Si heterojunction solar cells. J. Appl. Phys. 2007, 101, 054516. [Google Scholar] [CrossRef]
- de Nicolás, S.M.; Muñoz, D.; Ozanne, A.S.; Nguyen, N.; Ribeyron, P.J. Optimisation of doped amorphous silicon layers applied to heterojunction solar cells. In Proceedings of the SiliconPV 2011 Conference (1st International Conference on Crystalline Silicon Photovoltaics), Freiburg, Germany, 7–20 April 2011; Volume 8, p. 226231. [Google Scholar]
- Battaglia, C.; Yin, X.; Zheng, M.; Sharp, I.D.; Chen, T.; McDonnell, S.; Aztacl, A.; Carraro, C.; Ma, B.; Maboudian, R.; et al. Hole selective MoOx contact for silicon solar cells. Nano Lett. 2014, 14, 967–971. [Google Scholar] [CrossRef] [PubMed]
- Gerling, L.G.; Mahato, S.; Morales-Vilches, A.; Masmitja, G.; Ortega, P.; Voz, C.; Alcubilla, R.; Puigdollers, J. Transition metal oxides as hole-selective contacts in silicon heterojunctions solar cells. Sol. Energy Mater. Sol. Cells 2016, 145, 109–115. [Google Scholar] [CrossRef]
- Bullock, J.; Hettick, M.; Geissbühler, J.; Ong, A.J.; Allen, T.; Sutter-Fella, C.M.; Chen, T.; Ota, H.; Schaler, E.W.; De Wolf, S.; et al. Efficient silicon solar cells with dopant-free asymmetric heterocontacts. Nat. Energy 2016, 1, 15031. [Google Scholar] [CrossRef]
- Wan, Y.; Samundsett, C.; Bullock, J.; Allen, T.; Hettick, M.; Yan, D.; Zheng, P.; Zhang, X.; Cui, J.; Mckeon, J.; et al. Magnesium fluoride electron-selective contacts for crystalline silicon solar cells. ACS Appl. Mater. Interfaces 2016, 8, 14671–14677. [Google Scholar] [CrossRef]
- Xu, X.; Bullock, J.; Schelhas, L.T.; Stutz, E.Z.; Fonseca, J.J.; Hettick, M.; Pool, V.L.; Tai, K.F.; Toney, M.F.; Fang, X.; et al. Chemical bath deposition of p-type transparent, highly conducting (CuS)x:(ZnS)1–x nanocomposite thin films and fabrication of Si heterojunction solar cells. Nano Lett. 2016, 16, 1925–1932. [Google Scholar] [CrossRef]
- Zielke, D.; Pazidis, A.; Werner, F.; Schmidt, J. Organic-silicon heterojunction solar cells on n-type silicon wafers: The BackPEDOT concept. Sol. Energy Mater. Sol. Cells 2014, 131, 110–116. [Google Scholar] [CrossRef]
- Nagamatsu, K.A.; Avasthi, S.; Sahasrabudhe, G.; Man, G.; Jhaveri, J.; Berg, A.H.; Schwartz, J.; Kahn, A.; Wagner, S.; Sturm, J.C. Titanium dioxide/silicon hole-blocking selective contact to enable double-heterojunction crystalline silicon-based solar cell. Appl. Phys. Lett. 2015, 106, 123906. [Google Scholar] [CrossRef]
- Cao, L.; Procel, P.; Alcañiz, A.; Yan, J.; Tichelaar, F.; Özkol, E.; Zhao, Y.; Han, C.; Yang, G.; Yao, Z.; et al. Achieving 23.83% conversion efficiency in silicon heterojunction solar cell with ultra-thin MoOx hole collector layer via tailoring (i) a-Si: H/MoOx interface. Prog. Photovolt. Res. Appl. 2023, 31, 1245–1254. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, T.; Duan, L.; Hoex, B.; Tang, Z. Progress in passivating selective contacts for heterojunction silicon solar cells. Nano Energy 2024, 131, 110282. [Google Scholar] [CrossRef]
- Demaurex, B.; Seif, J.P.; Smit, S.; Macco, B.; Kessels, W.M.M.; Geissbühler, J.; De Wolf, S.; Ballif, C. Atomic-layer-deposited transparent electrodes for silicon heterojunction solar cells. IEEE J. Photovolt. 2014, 4, 1387–1396. [Google Scholar] [CrossRef]
- Mercaldo, L.V.; Bobeico, E.; Usatii, I.; Noce, M.D.; Lancellotti, L.; Serenelli, L.; Izzi, M.; Tuzzi, M.; Veneri, P.D. Potentials of mixed-phase doped layers in p-type Si heterojunction solar cells with ZnO:Al. Sol. Energy Mater. Sol. Cells 2017, 169, 113–121. [Google Scholar] [CrossRef]
- Essig, S.; Dréon, J.; Rucavado, E.; Mews, M.; Koida, T.; Boccard, M.; Werner, J.; Geissbühler, J.; Löper, P.; Morales-Masis, M.; et al. Toward Annealing-Stable Molybdenum-Oxide-Based Hole-Selective Contacts For Silicon Photovoltaics. Sol. RRL 2018, 2, 1700227. [Google Scholar] [CrossRef]
- Synopsys. Sentaurus Device User Manual; Synopsys: Mountain View, CA, USA, 2022. [Google Scholar]
- Andreas, F.; McIntosh, K.R.; Altermatt, P.P.; Janssen, G.J.M.; Stangl, R.; Ho-Baillie, A.; Steinkemper, H.; Greulich, J.; Muller, M.; Min, B.; et al. Input parameters for the simulation of silicon solar cells in 2014. IEEE J. Photovolt. 2015, 5, 1250–1263. [Google Scholar]
- Mehmood, H.; Nasser, H.; Tauqeer, T.; Turan, R. Simulation of silicon heterostructure solar cell featuring dopant-free carrier-selective molybdenum oxide and titanium oxide contacts. Renew. Energy 2019, 143, 359–367. [Google Scholar] [CrossRef]
- Vijayan, R.A.; Masilamani, S.; Kailasam, S.; Shivam, K.; Deenadhayalan, B.; Varadharajaperumal, M. Study of surface passivation and charge transport barriers in DASH solar cell. IEEE J. Photovolt. 2019, 9, 1208–1216. [Google Scholar] [CrossRef]
- Khokhar, M.Q.; Hussain, S.Q.; Pham, D.P.; Lee, S.; Park, H.; Kim, Y.; Cho, E.-C.; Yi, J. Simulation of silicon heterojunction solar cells for high efficiency with lithium fluoride electron carrier selective layer. Energies 2020, 13, 1635. [Google Scholar] [CrossRef]
- Liu, J.; Chen, W.; Feng, X. Numerical simulation of ultra-thin CdTe solar cells with a buffer layer of MoOx in the backwall configuration. Chin. J. Phys. 2018, 56, 1826–1833. [Google Scholar] [CrossRef]
- Khokhar, M.Q.; Hussain, S.Q.; Pham, D.P.; Alzaid, M.; Razaq, A.; Sultana, I.; Kim, Y.; Cho, Y.H.; Cho, E.-C.; Yi, J. Role of electron carrier selective contact layer of lithium fluoride films with wide bandgap and low work function for silicon heterojunction solar cells. Mater. Sci. Semicond. Process. 2021, 134, 105982. [Google Scholar] [CrossRef]

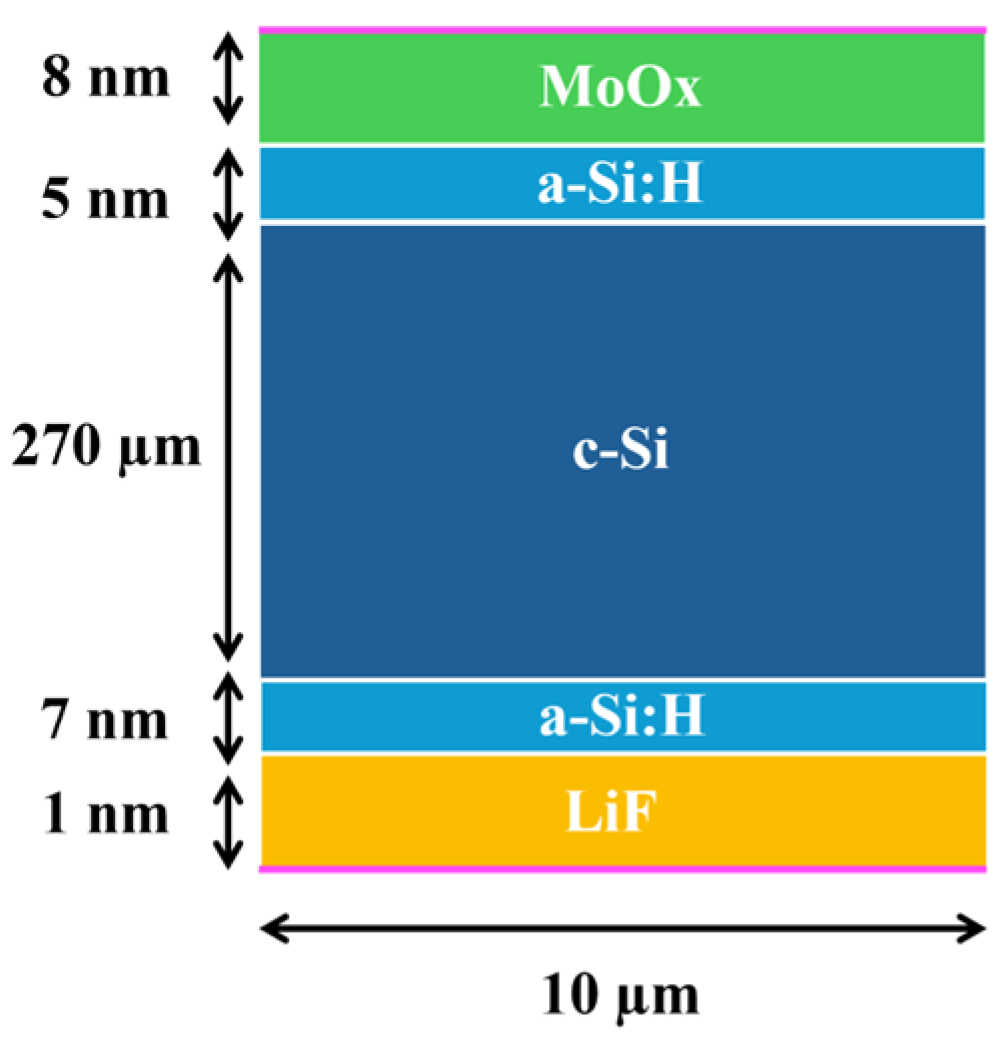
| Acceptors | Donors | |
|---|---|---|
| ETC [eV] | 0.3 | - |
| ETV [eV] | - | 0.3 |
| ETW [eV] | 0.2 | 0.2 |
| Parameters | MoOx | i—a—Si:H | c—Si | LiF |
|---|---|---|---|---|
| Electron affinity [eV] | 2.3 | 3.9 | 4.17 | 3.9 |
| Energy bandgap [eV] | 3.2 | 1.72 | 1.12 | 11 |
| Doping concentration [cm−3] | 1.0 × 1017 | − | 1 × 1015 | 1.0 × 1018 |
| Electron mobility [cm2/V × s] | 30 | 10 | 1450 | 2.5 |
| Hole mobility [cm2/V × s] | 25 | 1 | 450 | 1 |
| Effective DOS in conduction band [cm−3] | 3.2 × 1016 | 2.5 × 1020 | 2.8 × 1019 | 1.0 × 1020 |
| Effective DOS in valence band [cm−3] | 2.5 × 1016 | 2.5 × 1020 | 1.0 × 1019 | 1.0 × 1020 |
| τn [s] | 10−8 | 10−7 | 10−3 | 10−12 |
| τp [s] | 10−9 | 10−8 | 10−4 | 10−12 |
| Extracted Traps Concentration [cm−2] | |
|---|---|
| as fabricated | 2.5 × 1013 |
| after soft anneal | 8 × 1011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matacena, I.; Lancellotti, L.; Bobeico, E.; Usatii, I.; della Noce, M.; Santoro, E.; Scognamiglio, P.; Mercaldo, L.V.; Delli Veneri, P.; Daliento, S. Impedance Spectroscopy for Interface Trap Effects Evaluation in Dopant-Free Silicon Solar Cells. Energies 2025, 18, 4558. https://doi.org/10.3390/en18174558
Matacena I, Lancellotti L, Bobeico E, Usatii I, della Noce M, Santoro E, Scognamiglio P, Mercaldo LV, Delli Veneri P, Daliento S. Impedance Spectroscopy for Interface Trap Effects Evaluation in Dopant-Free Silicon Solar Cells. Energies. 2025; 18(17):4558. https://doi.org/10.3390/en18174558
Chicago/Turabian StyleMatacena, Ilaria, Laura Lancellotti, Eugenia Bobeico, Iurie Usatii, Marco della Noce, Elena Santoro, Pietro Scognamiglio, Lucia V. Mercaldo, Paola Delli Veneri, and Santolo Daliento. 2025. "Impedance Spectroscopy for Interface Trap Effects Evaluation in Dopant-Free Silicon Solar Cells" Energies 18, no. 17: 4558. https://doi.org/10.3390/en18174558
APA StyleMatacena, I., Lancellotti, L., Bobeico, E., Usatii, I., della Noce, M., Santoro, E., Scognamiglio, P., Mercaldo, L. V., Delli Veneri, P., & Daliento, S. (2025). Impedance Spectroscopy for Interface Trap Effects Evaluation in Dopant-Free Silicon Solar Cells. Energies, 18(17), 4558. https://doi.org/10.3390/en18174558








