Coupled CFD-DEM Numerical Simulation of Hydrothermal Liquefaction (HTL) of Sludge Flocs to Biocrude Oil in a Continuous Stirred Tank Reactor (CSTR) in a Scale-Up Study
Abstract
1. Introduction
2. Materials and Methods
2.1. CFD Multicomponent Modelling
2.2. Kinetics Model of Sludge Hydrothermal Liquefaction
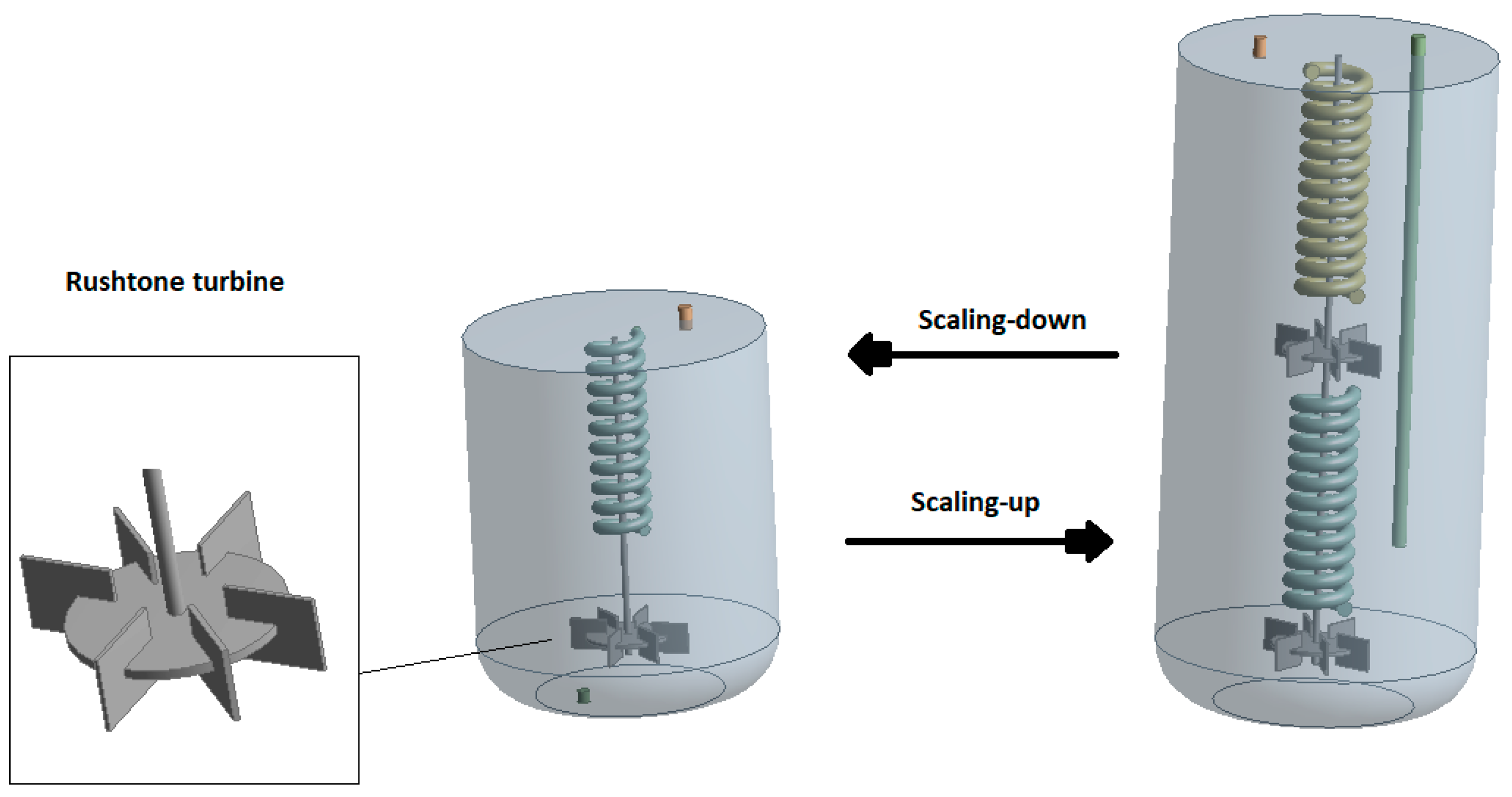
2.3. Scale-Up
2.4. Geometry and Meshing
2.5. Numerical Procedure
2.6. Thermodynamics Model of Non-Ideal Gases
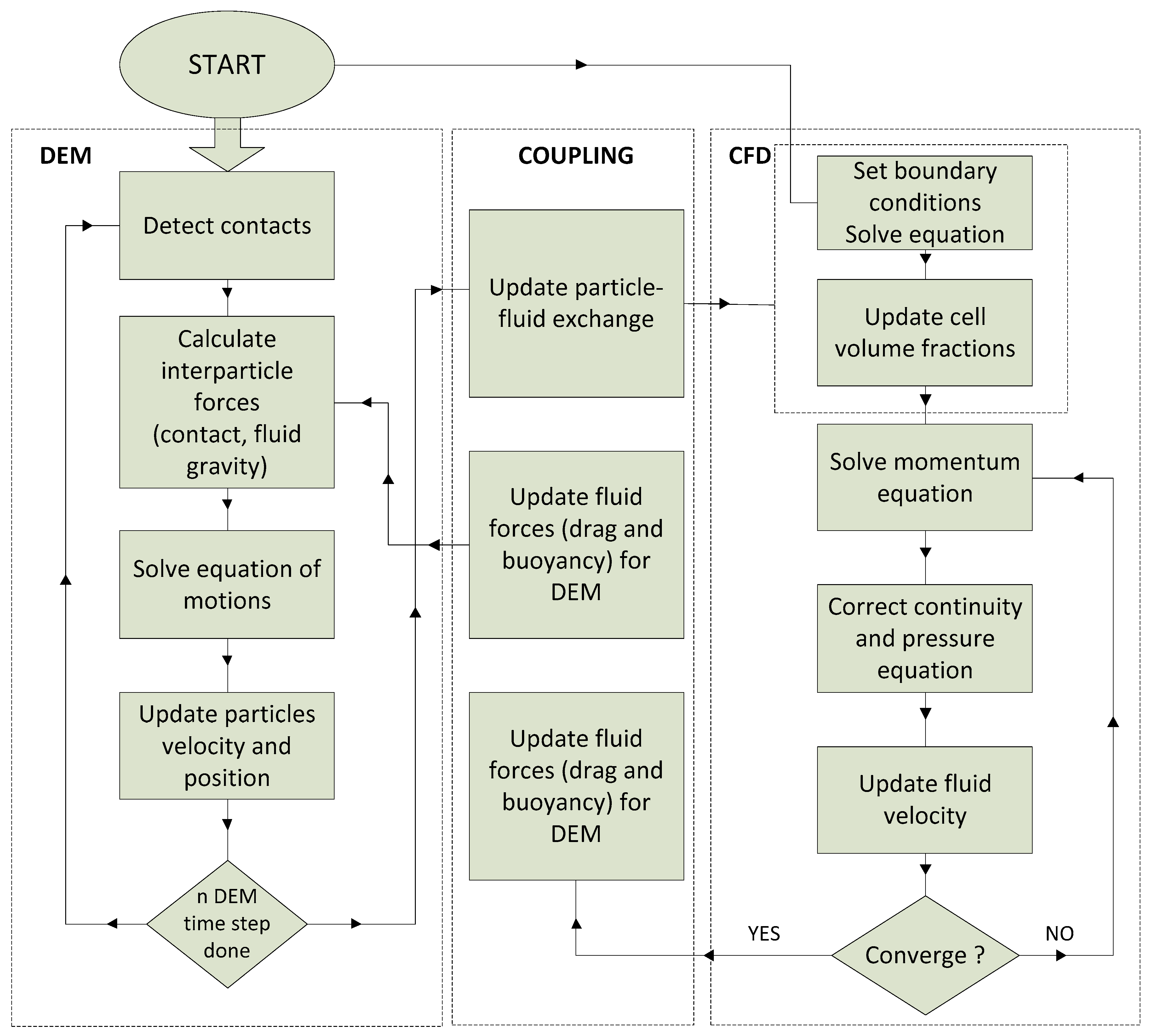
2.7. Coupling CFD-DEM Metod
2.8. CFD Multiphysics Model Experimental Setup
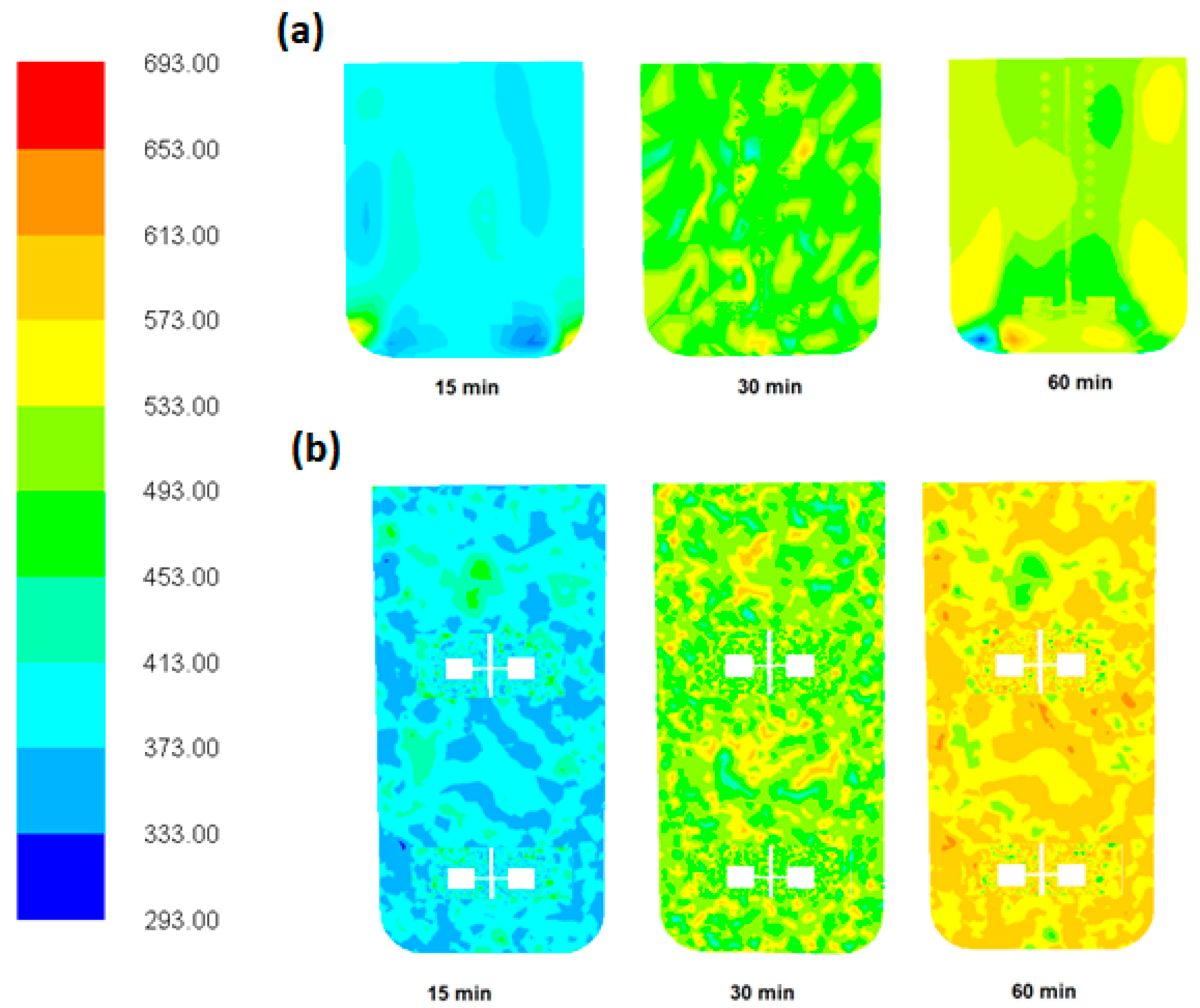
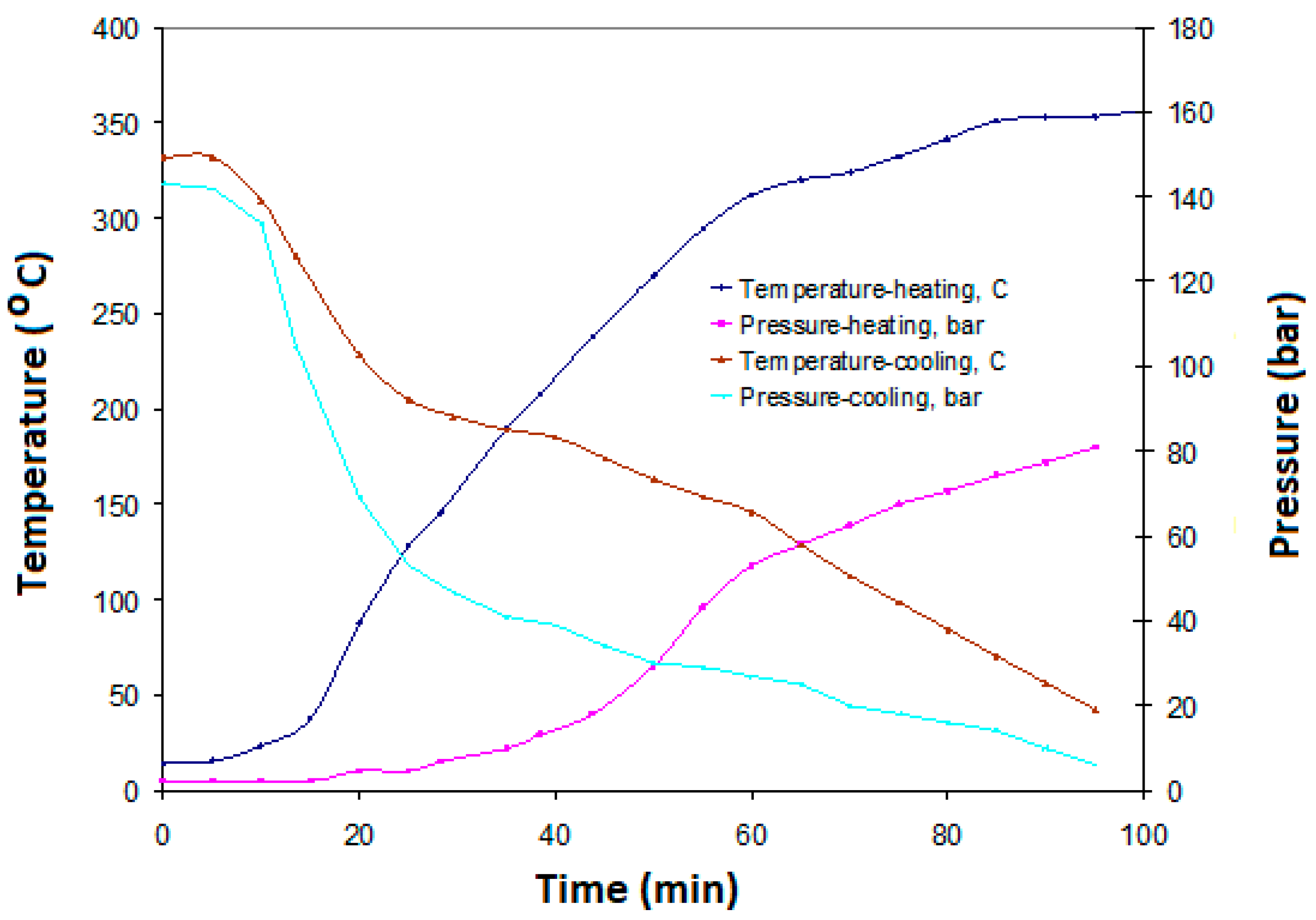
3. Results and Discussions
Hydrodynamics Flow Field of Biomass Slurry
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| flow velocity (m/s) | |
| density of fluid phase (kg/m3) | |
| liquid velocity (m/s) | |
| static pressure (Pa) | |
| stress tensor (N/m2) | |
| gravitational body force (m/s2) | |
| external force (N) | |
| gas density (kg/m3) | |
| gas velocity (m/s) | |
| interphase mass transfer terms for the gas-solid interface reactions | |
| second-order stress tensor of the gas | |
| interaction force representing momentum transfer between gas and solid phase | |
| effective mass diffusion coefficient (cm2·s−1) | |
| Reynolds number of particles | |
| specific heat of biomass particle (J/kg⋅K) | |
| k | thermal conductivity coefficient (W/mK) |
| particle temperature (K) | |
| interphase mass transfer terms for the gas–solid interface reactions | |
| h | heat transfer coefficient (W/m2K). |
| surface area of biomass particles (m2) | |
| Yi | mass fraction of gas species I |
| species source term from particle | |
| species source term from reactions | |
| T | temperature (K) |
| Sh | Sherwood number |
| emissivity | |
| incident radiation (Wh/m2) | |
| Stefan–Boltzmann constant | |
| energy source term | |
| void fraction of fluid phase | |
| velocity of fluid phase, (m/s) | |
| momentum viscous tensor | |
| Reynolds tensor | |
| momentum of source term | |
| mass of biomass particles (kg) | |
| particle temperature (K) | |
| Rq | impeller power number (depends on impeller type and dimensions) |
| velocity of fluid phase | |
| momentum viscous tensor | |
| second-order stress tensor of the gas | |
| interaction force representing momentum transfer between gas and solid phase | |
| effective mass diffusion coefficient | |
| Y | mass fraction of gas species I |
| species source term from particle | |
| species source term from reactions | |
| mass of biomass particles | |
| velocity of biomass particles | |
| kt | heat conductivity due to turbulent transport |
| specific heat of biomass particle | |
| particle temperature heat transfer coefficient | |
| surface area of biomass particles | |
| emissivity | |
| incident radiation | |
| Stefan–Boltzmann constant | |
| energy source term | |
| Greek letters | |
| gas volume fraction | |
| void fraction of fluid phase | |
| turbulence dissipation rate (m2·s−3) | |
| viscosity (Pa·s) | |
| σ | surface tension (N/m) |
| turbulent Prandtl number | |
| Subscript | |
| l | liquid phase |
| m | mixture |
| s | solid phase |
| t | turbulence |
| j | phase j |
| i | phase i |
References
- Gai, C.; Zhang, Y.; Chen, W.-T.; Zhang, P.; Dong, Y. An investigation of reaction pathways of hydrothermal liquefaction using chlorella pyrenoidosa and Spirulina platensis. Energy Convers. Manag. 2015, 96, 330–339. [Google Scholar] [CrossRef]
- Gollakota, A.R.K.; Kishore, N.; Gu, S. A review on hydrothermal liquefaction of biomass. Renew. Sustain. Energy Rev. 2018, 81, 1378–1392. [Google Scholar] [CrossRef]
- Jensen, C.U.; Rosendahl, L.A.; Olofsson, G. Impact of nitrogenous alkaline agent on continuous HTL of lignocellulosic biomass and crude bio-oil upgrading. Fuel Process Technol. 2017, 159, 376–385. [Google Scholar] [CrossRef]
- Zhang, Y.; Minaret, J.; Yuan, Z.; Dutta, A.; Xu, C. Mild hydrothermal liquefaction of high water content agricultural residue for bio-crude oil production: A parametric study. Energies 2018, 11, 3129–3142. [Google Scholar] [CrossRef]
- Dote, Y.; Sawayama, S.; Inoue, S.; Minowa, T.; Yokoyama, S. Recovery of liquid fuel from hydrocarbon- rich microalgae by thermochemical liquefaction. Fuel 1994, 73, 1855–1857. [Google Scholar] [CrossRef]
- Ginzburg, B.Z. Liquid fuel (oil) from halophilic algae: A renewable source of nonpolluting energy. Renew. Energy 1993, 3, 249–252. [Google Scholar] [CrossRef]
- Miao, X.; Wu, Q. Biodiesel production from heterotrophic microalgal oil. Bioresour. Technol. 2006, 97, 841–846. [Google Scholar] [CrossRef] [PubMed]
- Minowa, T.; Yokoyama, S.Y.; Kishimoto, M.; Okakurat, T. Oil production from algal cells of Dunaliellatertiolecta by direct thermochemical liquefaction. Fuel 1995, 74, 1735–1738. [Google Scholar] [CrossRef]
- Panahi, H.K.S.; Tabatabaei, M.; Aghbashlo, M.; Dehhaghi, M.; Rehan, M.; Nizami, A.S. Recent updates on the production and upgrading of bio-crude oil from microalgae. Bioresour. Technol. Rep. 2019, 7, 100216. [Google Scholar] [CrossRef]
- Elliott, D.C.; Biller, P.; Ross, A.B.; Schmidt, A.J.; Jones, S.B. Hydrothermal liquefaction of biomass: Developments from batch to continuous process. Bioresour. Technol. 2015, 178, 147–156. [Google Scholar] [CrossRef]
- Joshi, T.; Parkash, O.; Krishan, G. CFD modeling for slurry flow through a horizontal pipe bend at different Prandtl number. Int. J. Hydrogen Energy 2022, 47, 23731–23750. [Google Scholar] [CrossRef]
- Joshi, T.; Parkash, O.; Krishan, G. Numerical Investigation of Slurry Pressure Drop at Different Pipe Roughness in a Straight Pipe Using CFD. Arab. J. Sci. Eng. 2022, 47, 15391–15414. [Google Scholar] [CrossRef]
- Biller, P.; Ross, A. Potential yields and properties of oil from the hydrothermal liquefaction of microalgae with different biochemical content. Bioresour. Technol. 2011, 102, 215–225. [Google Scholar] [CrossRef]
- Vardon, D.R.; Sharma, B.K.; Blazina, G.V.; Rajagopalan, K.; Strathmann, T.J. Thermochemical conversion of raw and defatted algal biomass via hydrothermal liquefaction and slow pyrolysis. Bioresour. Technol. 2012, 109, 178–187. [Google Scholar] [CrossRef]
- Ranganathan, P.; Savithri, S. Computational fluid dynamics simulation of hydrothermal liquefaction of microalgae in a continuous plug-flow reactor. Bioresour. Technol. 2018, 258, 151–157. [Google Scholar] [CrossRef]
- Qian, L.; Ni, J.; Xu, Z.; Yu, B.; Wang, S.; Gu, H.; Xiang, D. Biocrude production from hydrothermal liquefaction of Chlorella: Thermodynamic modelling and reactor design. Energies 2021, 14, 6602. [Google Scholar] [CrossRef]
- Chu, W.-X.; Tsai, C.-A.; Lee, B.-H.; Cheng, K.-Y.; Wang, C.-C. Experimental investigation on heat transfer enhancement with twisted tape having various V-cut configurations. Appl. Therm. Eng. 2020, 172, 115148. [Google Scholar] [CrossRef]
- Campolo, M.; Paglianti, A.; Soldati, A. Fluid dynamic efficiency and scale-up of a retreated blade impeller CSTR. Ind. Eng. Chem. Res. 2002, 41, 164–172. [Google Scholar] [CrossRef]
- Campolo, M.; Soldati, A. Appraisal of fluid dynamic efficiency of retreated-blade and turbofoil impellers in industrial-size CSTRs. Ind. Eng. Chem. Res. 2002, 41, 1370–1377. [Google Scholar] [CrossRef]
- Wodołażski, A.; Skiba, J.; Zarębska, K.; Polański, J.; Smoliński, A. CFD modeling of the catalyst oil slurry hydrodynamics in a high pressure and temperature as potential for biomass liquefaction. Energies 2020, 13, 5694. [Google Scholar] [CrossRef]
- Wodołażski, A. Multiphase numerical CFD simulation of the hydrothermal liquefaction process (HTL) of sewage sludge in a tubular reactor. Appl. Sci. 2024, 14, 4513. [Google Scholar] [CrossRef]
- Ross, A.; Biller, P.; Kubacki, M.; Li, H.; Lea-Langton, A.; Jones, J. Hydrothermal processing of microalgae using alkali and organic acids. Fuel 2010, 89, 2234–2243. [Google Scholar] [CrossRef]
- Madsen, R.B.; Bernberg, R.Z.K.; Biller, P.; Becker, J.; Iversen, B.B.; Glasius, M. Hydrothermal co-liquefaction of biomasses quantitative analysis of bio-crude and aqueous phase composition. Sustain. Energy Fuels 2017, 1, 789–805. [Google Scholar] [CrossRef]
- Biller, P.; Ross, A.B. Hydrothermal processing of algal biomass for the production of biofuels and chemicals. Biofuels 2012, 3, 603–623. [Google Scholar] [CrossRef]
- Demirbas, A. Competitive liquid biofuels from biomass. Appl. Energy 2011, 88, 17–28. [Google Scholar] [CrossRef]
- Yu, J.; Biller, P.; Mamahkel, A.; Klemmer, M.; Becker, J.; Glasius, M.; Iversen, B.B. Catalytic hydrotreatment of bio-crude produced from the hydrothermal liquefaction of aspen wood: A catalyst screening and parameter optimization study. Sustain. Energy Fuels 2017, 1, 832–841. [Google Scholar] [CrossRef]
- Davis, H. Chemistry and stoichiometry of wood liquefaction. Biotechnol. Bioenergy Symp. 1981, 11, 151–170. [Google Scholar]
- Jarvis, J.M.; Albrecht, K.O.; Billing, J.M.; Schmidt, A.J.; Hallen, R.T.; Schaub, T.M. Assessment of hydrotreatment for hydrothermal liquefaction biocrudes from sewage sludge, microalgae, and pine feedstocks. Energy Fuels 2018, 32, 8483–8493. [Google Scholar] [CrossRef]
- Shi, W.; Liu, C.; Shu, Y.; Feng, C.; Lei, Z.; Zhang, Z. Synergistic effect of rice husk addition on hydrothermal treatment of sewage sludge: Fate and environmental risk of heavy metals. Bioresour. Technol. 2013, 149, 496–502. [Google Scholar] [CrossRef]
- Xu, D.; Lin, G.; Liu, L.; Wang, Y.; Jing, Z.; Wang, S. Comprehensive evaluation on product characteristics of fast hydrothermal liquefaction of sewage sludge at different temperatures. Energy 2018, 159, 686–695. [Google Scholar] [CrossRef]
- Huang, H.J.; Yuan, X.Z. The migration and transformation behaviors of heavy metals during the hydrothermal treatment of sewage sludge. Bioresour. Technol. 2016, 200, 991–998. [Google Scholar] [CrossRef]
- Mathew, M. Scaling up of a Continuous Stirred Tank Reactor for Hydrothermal Liquefaction of Biomass: A Concept Study on Local Mass Transfer Coefficients. 2016. Available online: https://www.researchgate.net/publication/307430186_Scaling_up_of_a_continuous_stirred_tank_reactor_for_hydrothermal_liquefaction_of_biomass_A_concept_study_on_local_mass_transfer_coefficients?channel=doi&linkId=57c5747508ae6db2cc769677&showFulltext=true (accessed on 11 July 2025).
- Alba, L.G.; Torri, C.; Fabbri, D.; Kersten, S.R.; Brilman, D.W. Microalgae growth on the aqueous phase from Hydrothermal Liquefaction of the same microalgae. Chem. Eng. J. 2013, 228, 214–223. [Google Scholar] [CrossRef]
- Di Lauro, F.; Balsamo, M.; Solimene, R.; Alfieri, M.L.; Manini, P.; Migliaccio, R.; Salatino, P.; Montagnaro, F. Characterization of Biocrude Produced by Hydrothermal Liquefaction of Municipal Sewage Sludge in a 500 mL Batch Reactor. Ind. Eng. Chem. Res. 2024, 63, 955–967. [Google Scholar] [CrossRef]
- Balsamo, M.; Di Lauro, F.; Alfieri, M.L.; Manini, P.; Salatino, P.; Montagnaro, F.; Solimene, R. Unravelling the role of biochemical compounds within the hydrothermal liquefaction process of real sludge mixtures. Sustainability 2024, 16, 1770. [Google Scholar] [CrossRef]
- Liu, H.; Basar, I.A.; Eskicioglu, C. Hydrothermal liquefaction for sludge-to-energy conversion: An evaluation of biocrude production and management of waste streams. Energy 2023, 281, 128268. [Google Scholar] [CrossRef]
- Balsamo, M.; Hejazi, B.; Di Lauro, F.; Marotta, G.; Solimene, R.; Salatino, P.; Montagnaro, F. Kinetic modelling and elemental balances applied to the hydrothermal liquefaction of sewage sludge. Chem. Eng. J. 2025, 505, 158767. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, D.; Wang, J.; Zeng, M.; Wang, Q.; Ma, T. Thermal-hydraulic performance and optimization of printed circuit heat exchangers for supercritical fluids: A review. Renew. Sustain. Energy Rev. 2025, 208, 115051. [Google Scholar] [CrossRef]
- Sun, Z.; Yao, Q.; Jin, H.; Xu, Y.; Hang, W.; Chen, H.; Li, K.; Shi, L.; Gu, J.; Zhang, Q.; et al. A novel in-situ sensor calibration method for building thermal systems based on virtual samples and autoencoder. Energy 2024, 297, 131314. [Google Scholar] [CrossRef]
- Wodołazski, A. Co-simulation of CFD-multiphase population balance coupled model aeration of sludge flocs in stirrer tank bioreactor. Int. J. Multiph. Flow 2020, 123, 103162. [Google Scholar] [CrossRef]
- Zhang, L.; Feng, Y.; Guan, H.; Wu, S.; Jia, H. A general drag coefficient model for a spherical particle incorporating rarefaction and particle-to-gas temperature ratio effects. Chem. Eng. Sci. 2024, 298, 120442. [Google Scholar] [CrossRef]
- ANSYS. Fluent Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]


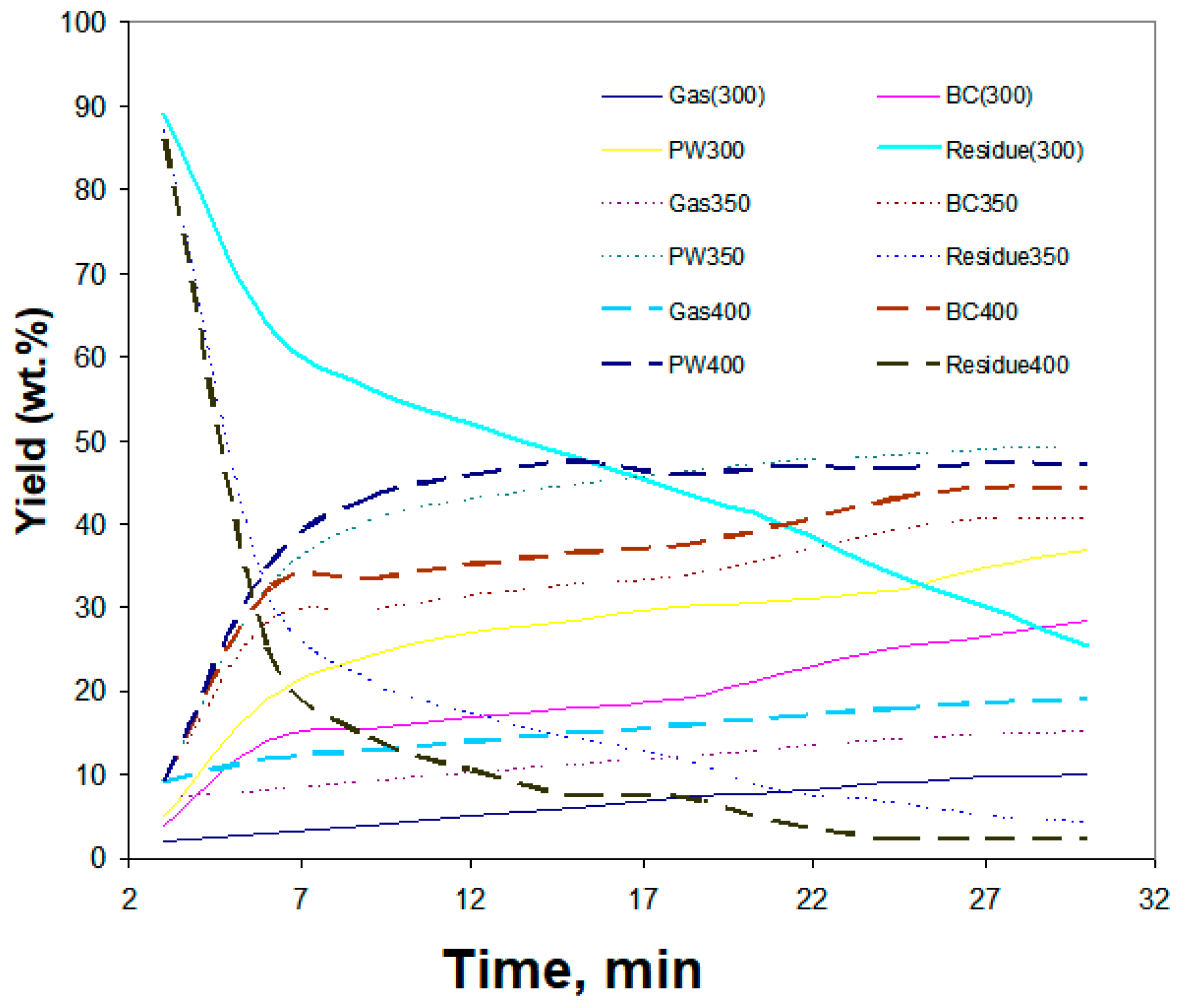

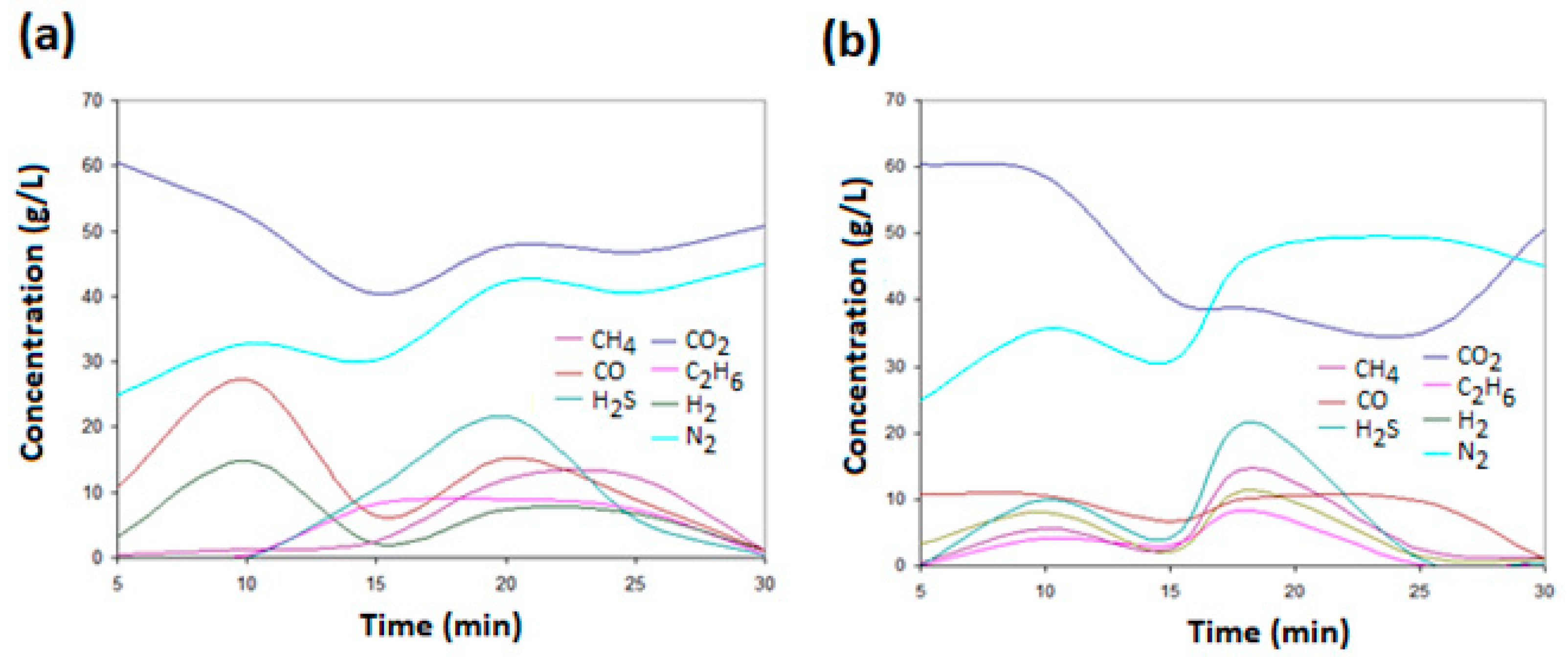

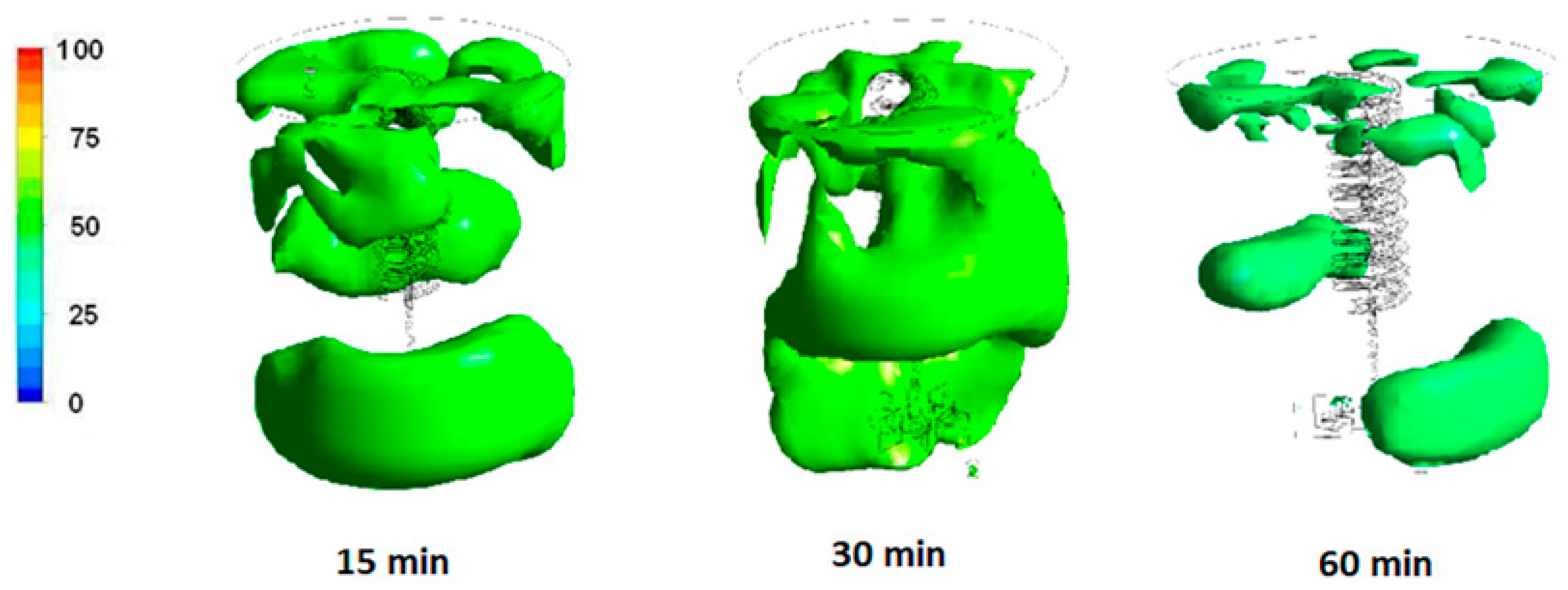

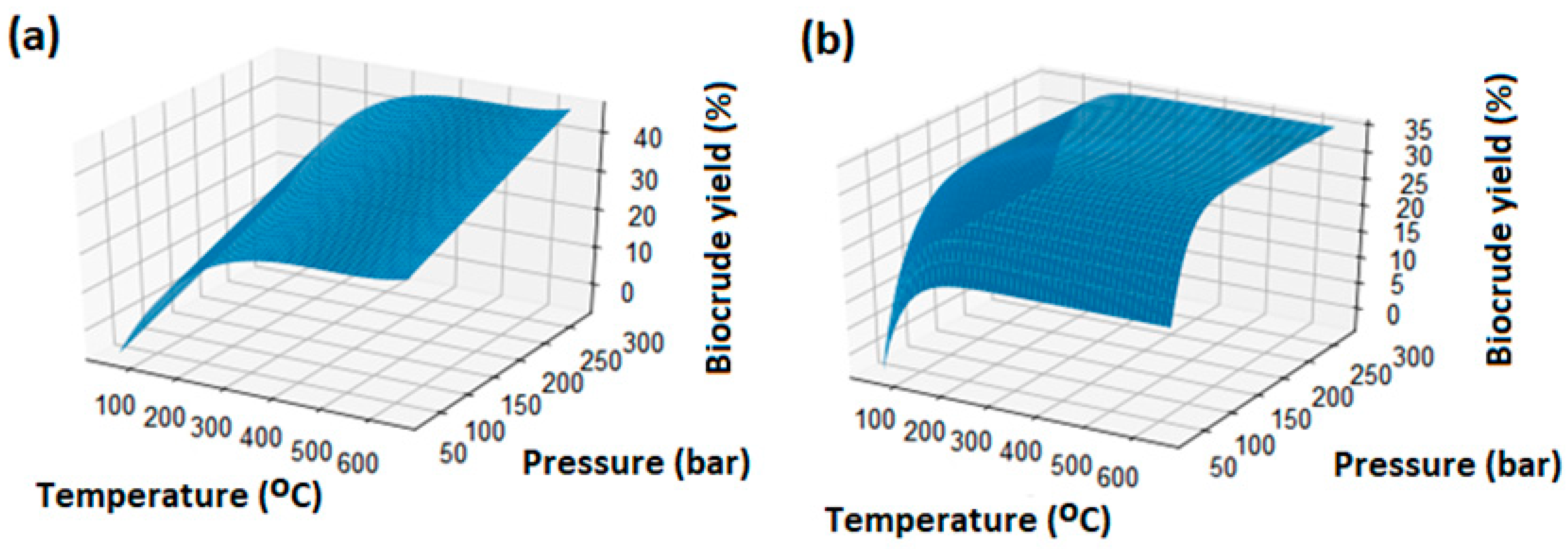
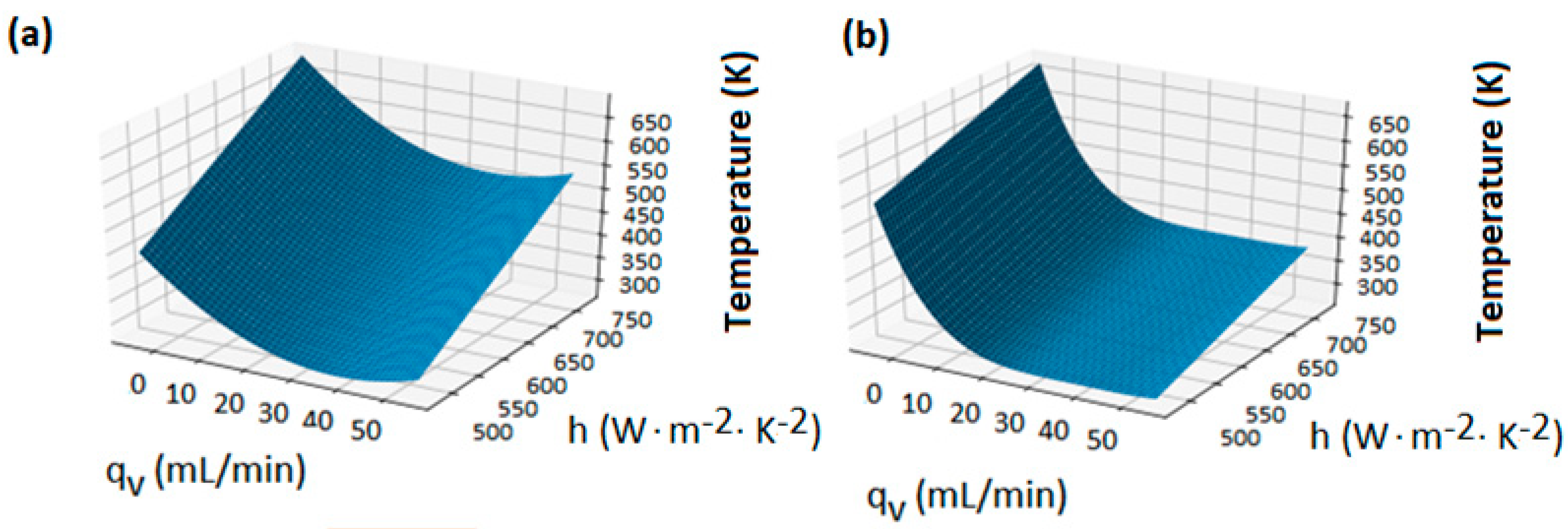
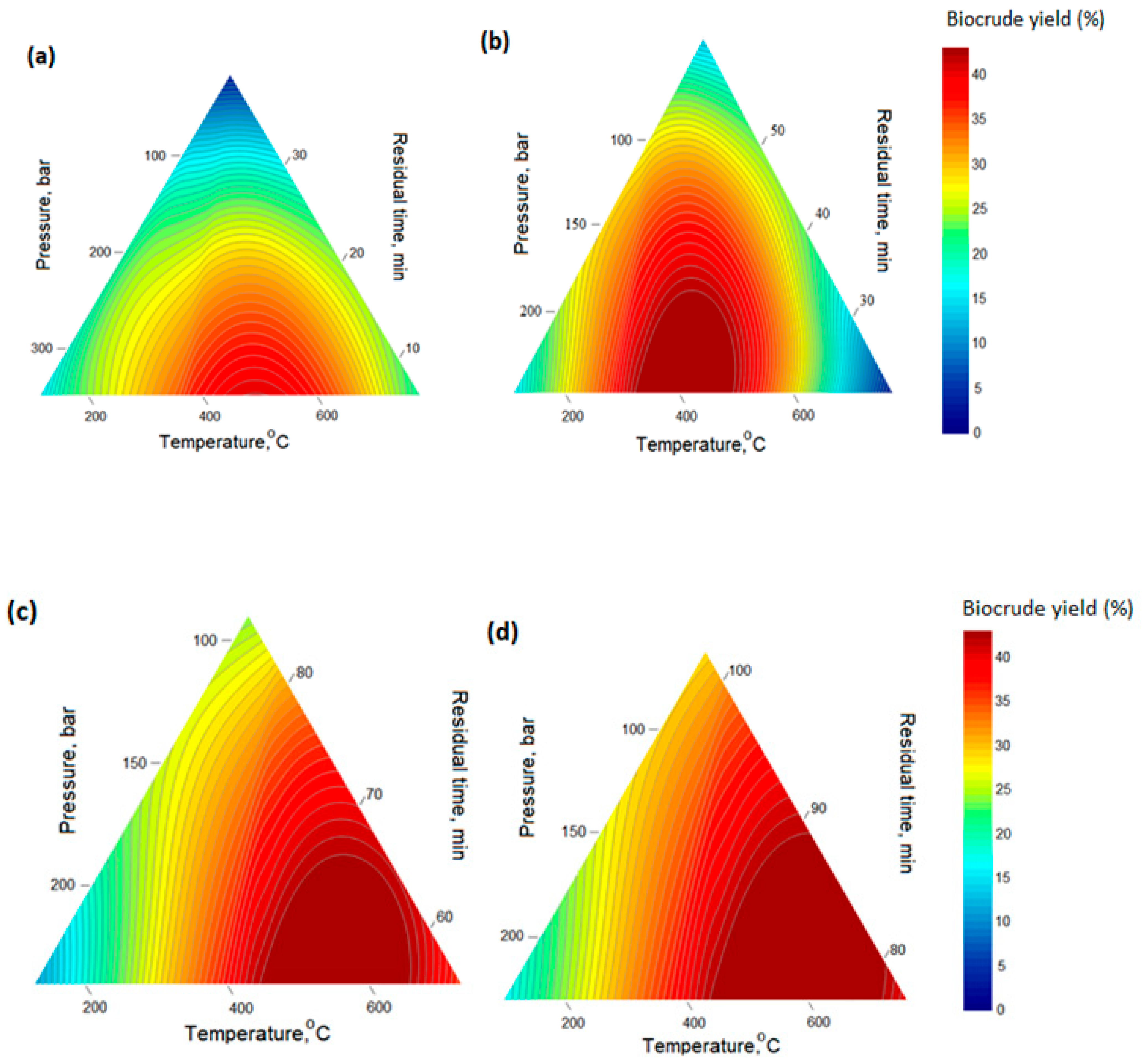
| Scale (Reactor Volume), L | Total Nodes (mln) | Total Elements (mln) |
|---|---|---|
| 3 | 0.00052863 | 0.00015233 |
| 6 | 0.00628456 | 0.00245768 |
| 9 | 0.02487536 | 0.00981112 |
| 12 | 0.58643548 | 0.08258419 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wodołażski, A. Coupled CFD-DEM Numerical Simulation of Hydrothermal Liquefaction (HTL) of Sludge Flocs to Biocrude Oil in a Continuous Stirred Tank Reactor (CSTR) in a Scale-Up Study. Energies 2025, 18, 4557. https://doi.org/10.3390/en18174557
Wodołażski A. Coupled CFD-DEM Numerical Simulation of Hydrothermal Liquefaction (HTL) of Sludge Flocs to Biocrude Oil in a Continuous Stirred Tank Reactor (CSTR) in a Scale-Up Study. Energies. 2025; 18(17):4557. https://doi.org/10.3390/en18174557
Chicago/Turabian StyleWodołażski, Artur. 2025. "Coupled CFD-DEM Numerical Simulation of Hydrothermal Liquefaction (HTL) of Sludge Flocs to Biocrude Oil in a Continuous Stirred Tank Reactor (CSTR) in a Scale-Up Study" Energies 18, no. 17: 4557. https://doi.org/10.3390/en18174557
APA StyleWodołażski, A. (2025). Coupled CFD-DEM Numerical Simulation of Hydrothermal Liquefaction (HTL) of Sludge Flocs to Biocrude Oil in a Continuous Stirred Tank Reactor (CSTR) in a Scale-Up Study. Energies, 18(17), 4557. https://doi.org/10.3390/en18174557







