Optimizing Solar-Powered EV Charging: A Techno-Economic Assessment Using Horse Herd Optimization
Abstract
1. Introduction
- Develop an optimization framework that determines the best locations for residential, commercial, and industrial EV charging infrastructure based on power loss minimization in the distribution systems.
- Develop an optimization framework to determine the optimal size of rooftop solar PV systems for integration into residential and commercial parking lots.
- In the literature, many algorithms such as PSO and GA have been applied to solve the above optimization problems. In this paper, HHO has been explored to solve the optimization problem.
- Carry out a thorough cost–benefit analysis of the commercial EV parking lot in order to maximize the profit of the parking lot owner.
2. Problem Overview and Formulation
- Proposed a framework to determine optimal locations where I-FCS, CPL, and RPL should be placed to minimize losses;
- Developed HHO to solve the proposed optimization problem;
- Provided the energy, economic, and environmental benefits of integrating PV with EVs in the distribution system.
2.1. Objective Function
2.2. Constraints
2.3. Solar Rooftop Photovoltaic System
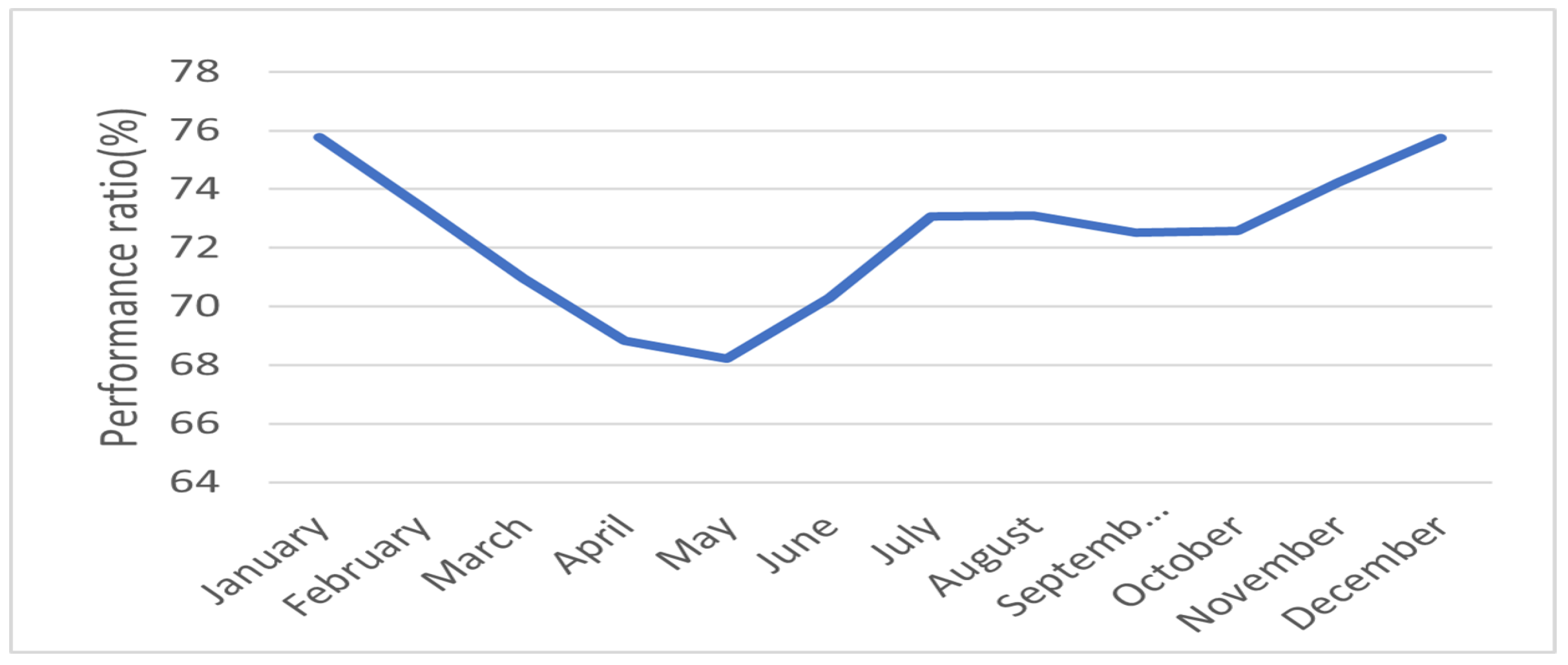
2.3.1. Energy Performance
- (i)
- Performance ratio (PR)
- (ii)
- Energy density ()
- (iii)
- Energy payback time (EPBT)
- (iv)
- Energy return on energy invested (EROI)
2.3.2. Economic Performance
- (i)
- Cost of electricity (COE)
- (ii)
- Payback period (PBP)
2.3.3. Environmental Performance
- (i)
- Carbon footprint emission ()
- (ii)
- Carbon footprint mitigation ()
2.4. Mathematical Modeling of Cost–Benefit Analysis
2.4.1. EV Charging
2.4.2. Cost–Benefit Analysis
2.5. Scheduling of Vehicles
- : indicator for high RTP at time t;
- : electricity price at time t;
- : peak electricity price over the scheduling horizon;
- : indicates a high RTP zone;
- : indicates a low RTP zone.
Constraints
- Charging or discharging of an EV should be in between arrival and departure time of that vehicle.
- The SOC of an EV at any instant neither goes below the minimum SOC nor exceeds the required SOC value.
- The charging rate of a battery at any instant should not exceed the charger rating.
- The utilized solar power at any instant should not exceed the solar generation at that instant.
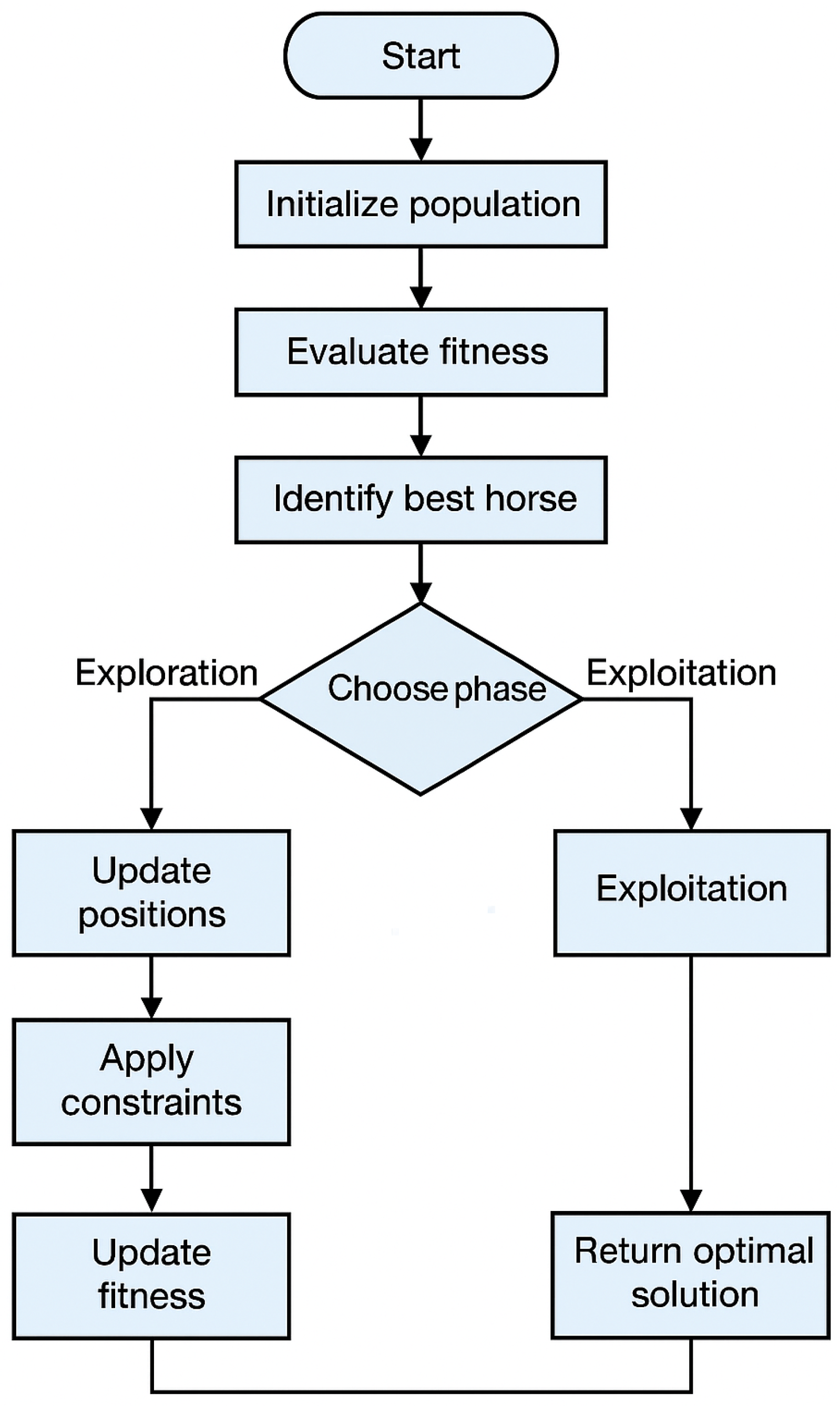
3. Methodology
- Horse Herd Optimization (HHO)
- Algorithm Summary
- Initialize the positions of horses randomly.
- Evaluate fitness for all horses.
- Repeat until termination:
- Apply exploration or exploitation based on iteration progress.
- Update positions using herd dynamics.
- Evaluate fitness and update .
- Return as the optimal solution.
3.1. Initialization
3.2. Fitness Evaluation
3.3. Exploration Phase
- and are random positions of other horses in the herd;
- and are random variables between .
3.4. Exploitation Phase
- s is a scaling factor that decreases over iterations;
- is a small random value to avoid local optima.
3.5. Herd Dynamics
- are weight factors
- is a perturbation caused by neighboring horses.
3.6. Boundary Handling
3.7. Termination Criteria
- A predefined maximum number of iterations is reached;
- The fitness reaches an acceptable error threshold.
4. Case Study and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| Index | Definition |
| PV system’s annual energy generation (kWh) | |
| Total area of array (m2) | |
| Embodied energy (kWh) | |
| C | Capital cost (Rs.) |
| Maintenance and repair cost (Rs.) | |
| Replacement cost (Rs.) | |
| Salvage cost (Rs.) | |
| M | The SPV system’s average yearly maintenance and repair costs |
| Replacement cost of PCU at 15 years’ interval | |
| Capital cost | |
| Cost of grid electricity (INR/kWh) | |
| Energy required to charge the battery to desired SOC | |
| Battery capacity of the vehicle | |
| Required SOC of EV battery | |
| Current SOC of EV battery | |
| Total energy required for charging all the vehicles | |
| Energy available for discharging scenario | |
| Minimum SOC limit that the battery can discharge | |
| Charging time | |
| Charging power | |
| Loading by the vehicle | |
| Battery capacity of the vehicle | |
| Cost of charging before implying solar (USD/day) | |
| Energy extracted from grid before implying solar (kWh/day) | |
| Real-time price at hour (USD/kWh) | |
| Cost of charging after implying solar (USD/day) | |
| Energy extracted from grid after implying solar (kWh/day) | |
| Cost of generating solar power (USD/day) | |
| Arrival time of the vehicle | |
| Charging duration of the vehicle | |
| Departure time of the vehicle | |
| SOC of the vehicle at any t instant | |
| Charging rate of the battery at any t instant | |
| Maximum charging rate of the charger at any t instant | |
| Solar energy utilization at any t instant | |
| Maximum solar energy available at any t instant |
List of Acronyms
| Acronym | Definition |
| RPL | Residential Parking Lot |
| CPL | Commercial Parking Lot |
| I-FCS | Industrial Fast Charging Station |
| SPV | Solar Photovoltaic |
| EV | Electric Vehicle |
| PL | Parking Lot |
| PV | Photovoltaic |
| HHO | Horse Herd Optimization |
| SOC | State of Charge |
| RTP | Real-Time Pricing |
| PR | Performance Ratio |
| EPBT | Energy Payback Time |
| COE | Cost of Electricity |
| LCC | Life-Cycle Cost |
| PCU | Power Conditioning Unit |
| CFe | Carbon Footprint Emission |
| CFm | Carbon Footprint Mitigation |
Appendix A. Sensitivity of HHO Parameter
| Population Size | Max Iterations | Best Fitness (MW) | Mean Fitness (MW) | Std. Dev. (MW) | CPU Time (s) |
|---|---|---|---|---|---|
| 20 | 100 | 2.6554 | 2.6618 | 0.0072 | 15.42 |
| 30 (baseline) | 100 | 2.6518 | 2.6545 | 0.0048 | 20.76 |
| 40 | 100 | 2.6515 | 2.6539 | 0.0045 | 26.94 |
| 30 | 80 | 2.6521 | 2.6553 | 0.0051 | 17.10 |
| 30 | 120 | 2.6517 | 2.6543 | 0.0048 | 24.92 |
| 30 | 150 | 2.6517 | 2.6542 | 0.0047 | 30.31 |
References
- Oruganti, K.S.P.; Vaithilingam, C.A.; Rajendran, G.; Ramasamy, A. Cost-benefit analysis of sustainable solar-powered workplace electric vehicle charging station. In Theoretical, Modelling and Numerical Simulations Toward Industry 4.0; Springer: Singapore, 2020; pp. 71–86. [Google Scholar]
- Deshmukh, S.S.; Pearce, J.M. Electric vehicle charging potential from retail parking lot solar photovoltaic awnings. Renew. Energy 2021, 169, 608–617. [Google Scholar] [CrossRef]
- Li, Y.; Pei, W.; Zhang, Q.; Xu, D.; Ma, H. Optimal layout of electric vehicle charging station locations considering dynamic charging demand. Electronics 2023, 12, 1818. [Google Scholar] [CrossRef]
- Altaf, M.; Yousif, M.; Ijaz, H.; Rashid, M.; Abbas, N.; Khan, M.A.; Waseem, M.; Saleh, A.M. PSO-based optimal placement of electric vehicle charging stations in a distribution network in smart grid environment incorporating backward forward sweep method. IET Renew. Power Gener. 2024, 18, 3173–3187. [Google Scholar] [CrossRef]
- Asghari Rad, H.; Jafari-Nokandi, M.; Hosseini, S.M. Optimal Allocation of Plug-in Electric Vehicle Parking Lots for Maximum Serviceability and Profit in the coupled distribution and transportation networks. Sci. Iran. 2024, 31, 1178–1196. [Google Scholar] [CrossRef]
- Babu, K.V.S.M.; Chakraborty, P.; Pal, M. Planning of fast charging infrastructure for electric vehicles in a distribution system and prediction of dynamic price. Int. J. Electr. Power Energy Syst. 2024, 155, 109502. [Google Scholar]
- Prajapati, S.; Fernandez, E. Solar PV parking lots to maximize charge operator profit for EV charging with minimum grid power purchase. Energy Sources Part A Recover. Util. Environ. Eff. 2025, 47, 3319–3329. [Google Scholar] [CrossRef]
- Mudgal, Y.; Tiwari, R. Residential Parking Lot Pricing Strategy Considering Scheduling of Electric Vehicles. J. Inst. Eng. (India) Ser. 2024, 106, 1129–1141. [Google Scholar] [CrossRef]
- Baherifard, M.A.; Kazemzadeh, R.; Yazdankhah, A.S.; Marzband, M. Intelligent charging planning for electric vehicle commercial parking lots and its impact on distribution network’s imbalance indices. Sustain. Energy Grids Netw. 2022, 30, 100620. [Google Scholar] [CrossRef]
- Nafeh, A.E.S.A.; Omran, A.E.F.A.; Elkholy, A.; Yousef, H.M. Optimal economical sizing of a PV-battery grid-connected system for fast charging station of electric vehicles using modified snake optimization algorithm. Results Eng. 2024, 21, 101965. [Google Scholar] [CrossRef]
- Khalid, M.; Thakur, J.; Bhagavathy, S.M.; Topel, M. Impact of public and residential smart EV charging on distribution power grid equipped with storage. Sustain. Cities Soc. 2024, 104, 105272. [Google Scholar] [CrossRef]
- Citroni, R.; Mangini, F.; Frezza, F. Efficient integration of ultra-low power techniques and energy harvesting in self-sufficient devices: A comprehensive overview of current progress and future directions. Sensors 2024, 24, 4471. [Google Scholar] [CrossRef] [PubMed]
- Junid, A.; Yap, E.H.; Ng, P.K. Electric vehicle charging at telco base station and bidirectional charging at hillslope descent technical-commercial cost-benefit study and scheduling-reservation system. In Proceedings of the 2018 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Kajang, Malaysia, 29 May–1 June 2018; pp. 137–144. [Google Scholar]
- Varone, A.; Heilmann, Z.; Porruvecchio, G.; Romanino, A. Solar parking lot management: An IoT platform for smart charging EV fleets, using real-time data and production forecasts. Renew. Sustain. Energy Rev. 2024, 189, 113845. [Google Scholar] [CrossRef]
- Sharma, S.; Niazi, K.; Verma, K.; Rawat, T. Coordination of different DGs, BESS and demand response for multi-objective optimization of distribution network with special reference to Indian power sector. Int. J. Electr. Power Energy Syst. 2020, 121, 106074. [Google Scholar] [CrossRef]
- Yadav, S.K.; Bajpai, U. Performance evaluation of a rooftop solar photovoltaic power plant in Northern India. Energy Sustain. Dev. 2018, 43, 130–138. [Google Scholar] [CrossRef]
- Quansah, D.A.; Adaramola, M.S.; Appiah, G.K.; Edwin, I.A. Performance analysis of different grid-connected solar photovoltaic (PV) system technologies with combined capacity of 20 kW located in humid tropical climate. Int. J. Hydrogen Energy 2017, 42, 4626–4635. [Google Scholar] [CrossRef]
- Jordan, D.C.; Kurtz, S.R. Photovoltaic degradation rates—An analytical review. Prog. Photovoltaics Res. Appl. 2013, 21, 12–29. [Google Scholar] [CrossRef]
- Government of India. CEA Annual Report 2022–23. 2023. Available online: https://cea.nic.in/annual-report/?lang=en (accessed on 15 May 2025).
- Kanwar, N.; Gupta, N.; Niazi, K.; Swarnkar, A. Optimal distributed generation allocation in radial distribution systems considering customer-wise dedicated feeders and load patterns. J. Mod. Power Syst. Clean Energy 2015, 3, 475–484. [Google Scholar] [CrossRef]
- Guner, S.; Ozdemir, A. Stochastic energy storage capacity model of EV parking lots. IET Gener. Transm. Distrib. 2017, 11, 1754–1761. [Google Scholar] [CrossRef]
- Anggraini, D.; Amelin, M.; Söder, L. Electric Vehicle Charging Considering Grid Limitation in Residential Areas. In Proceedings of the 2024 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 19–21 June 2024; pp. 1–6. [Google Scholar]
- Zhang, Y.; You, P.; Cai, L. Optimal charging scheduling by pricing for EV charging station with dual charging modes. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3386–3396. [Google Scholar] [CrossRef]
- Vashisth, S.; Agrawal, P.K.; Gupta, N.; Niazi, K.; Swarnkar, A. Multi-stage planning of fast charging stations for PEVs using traffic-based approach. Sustain. Energy, Grids Netw. 2022, 30, 100662. [Google Scholar] [CrossRef]
- NREL. NREL Solar Calculator. 2025. Available online: https://pvwatts.nrel.gov/ (accessed on 1 May 2025).
- Sharma, B.; Gupta, N.; Niazi, K.; Swarnkar, A. Estimating impact of price-based demand response in contemporary distribution systems. Int. J. Electr. Power Energy Syst. 2022, 135, 107549. [Google Scholar] [CrossRef]

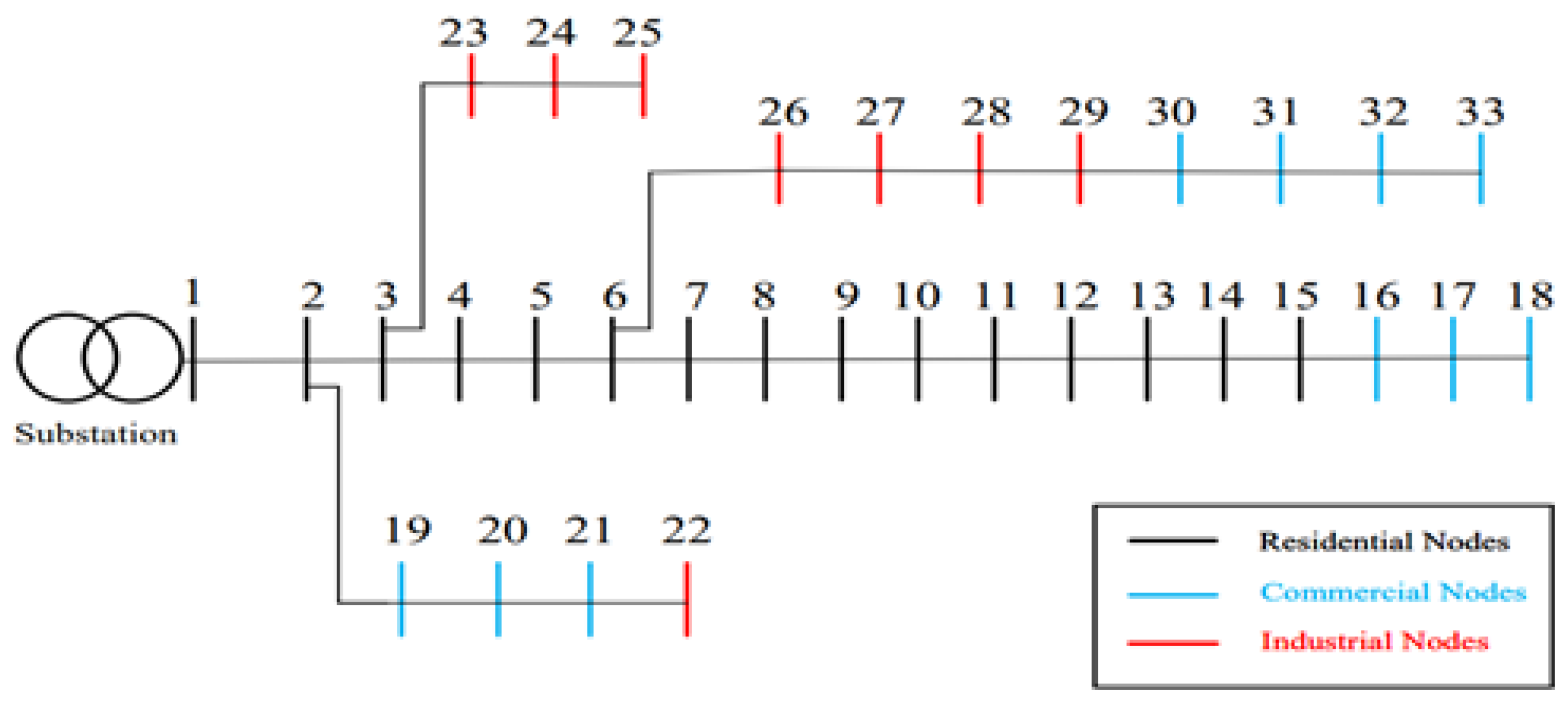

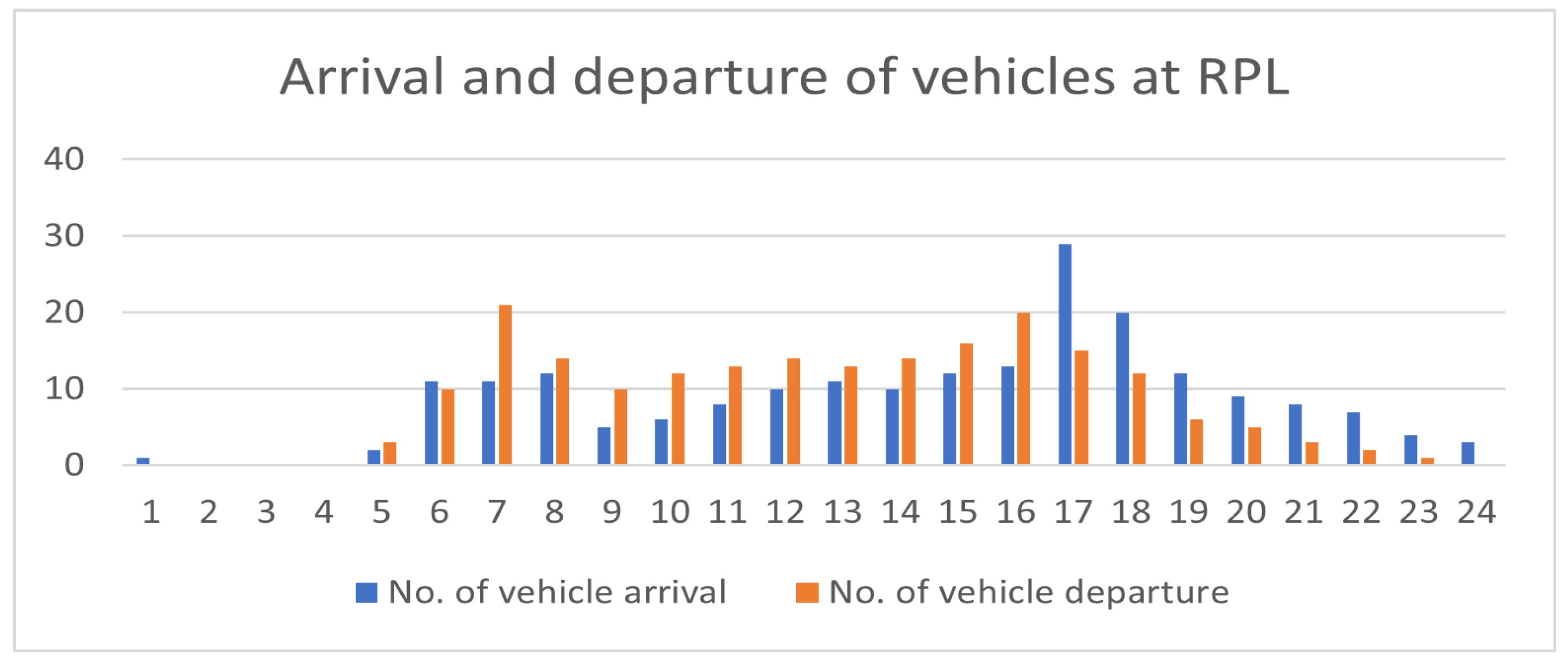
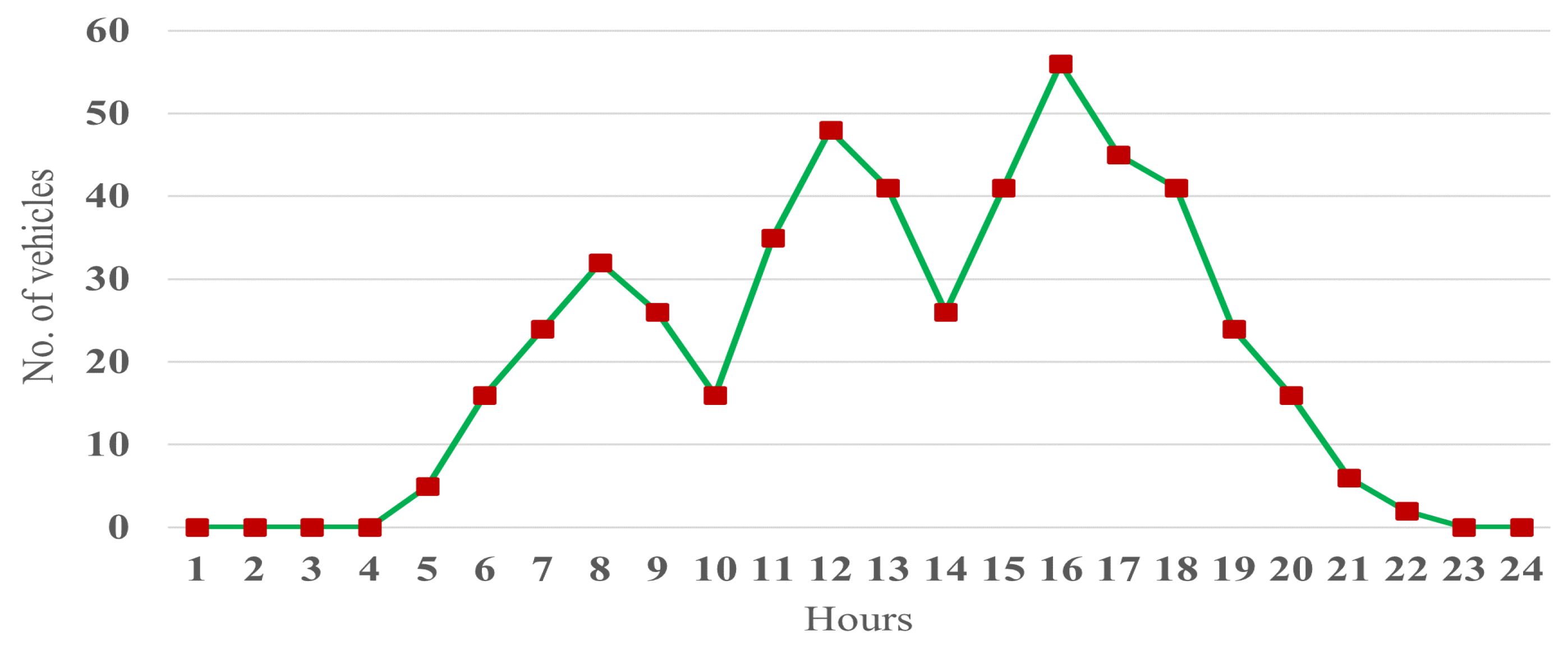
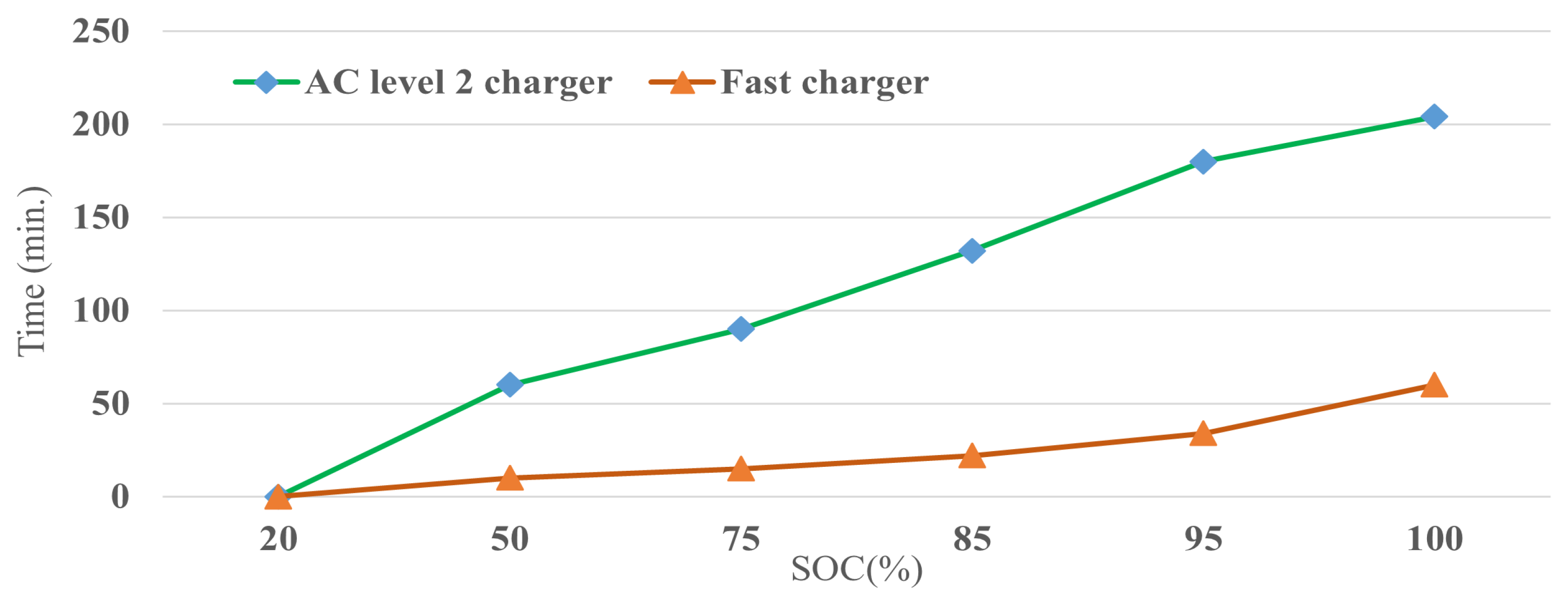




| Particular | Specification |
|---|---|
| Location | Jaipur |
| Latitude | 26.95 |
| Longitude | 75.85 |
| DC System Size (kW) | 400 |
| Module Type | Standard |
| Array Type | Fixed |
| Tilt Angle | |
| Azimuth Angle | |
| System Losses (%) | 14.08 |
| DC-to-AC Size Ratio | 1.2 |
| Type of Inverter | Grid-tied string inverter |
| Inverter Efficiency (%) | 96 |
| Class | Allocation Demand (%) | Allocation Demand (kW) | Allocated Nodes |
|---|---|---|---|
| R | 34.86 | 1295 | 1 to 15 |
| C | 29.60 | 1100 | 16 to 21, 30 to 33 |
| I | 35.54 | 1320 | 22 to 29 |
| Parameters | Value |
|---|---|
| Capacity of RPL/CPL | 200 |
| No. of vehicles at CPL | 178 |
| No. of vehicles at RPL | 204 |
| No. of vehicles at IFCS | 500 |
| No. of chargers at CPL | 35 |
| No. of chargers at RPL | 30 |
| No. of chargers at IFCS | 10 |
| Initial SOC range of vehicles at CPL | 20–50 |
| Final SOC range of vehicles at CPL | 85–95 |
| Initial SOC range of vehicles at RPL | 20–40 |
| Final SOC range of vehicles at RPL | 85–95 |
| Initial SOC range of vehicles at IFCS | 20–50 |
| Final SOC range of vehicles at IFCS | 75–85 |
| Battery capacity of vehicles at RPL | 24–40 |
| Battery capacity of vehicles at CPL | 24/30 |
| Battery capacity of vehicles at IFCS | 30/50 |
| Load | Optimum Location | Power Loss | Minimum Voltage |
|---|---|---|---|
| Base load | - | 2.38 MW | 0.9131 |
| Case study | 2, 19, 22 | 2.65 MW | 0.9125 |
| 2* Case study | 2, 19, 23 | 3.26 MW | 0.9120 |
| 3* Case study | 2, 19, 23 | 3.88 MW | 0.9110 |
| 4* Case study | 2, 19, 23 | 4.64 MW | 0.9109 |
| Optimization Method | Worst Fitness (MW) | Best Fitness (MW) | Mean Fitness | CPU Time (s) | Standard Deviation |
|---|---|---|---|---|---|
| GA | 2.6883 | 2.6746 | 2.6830 | 36.53 | 0.0054 |
| PSO | 2.6803 | 2.6659 | 2.6721 | 25.31 | 0.0053 |
| HHO | 2.6663 | 2.6518 | 2.6545 | 20.76 | 0.0048 |
| Particular | Value |
|---|---|
| Capital cost (Rs.) | 24,669,090 |
| Maintenance and repair cost (Rs.) | 3,791,716 |
| Replacement cost (Rs.) | 2,126,969 |
| Salvage cost (Rs.) | 4,118,837 |
| Life-cycle cost (Rs.) | 26,468,938 |
| Cost of electricity (Rs.⁄kWh) | 1.45 |
| System cost (Rs.⁄) | 61.67 |
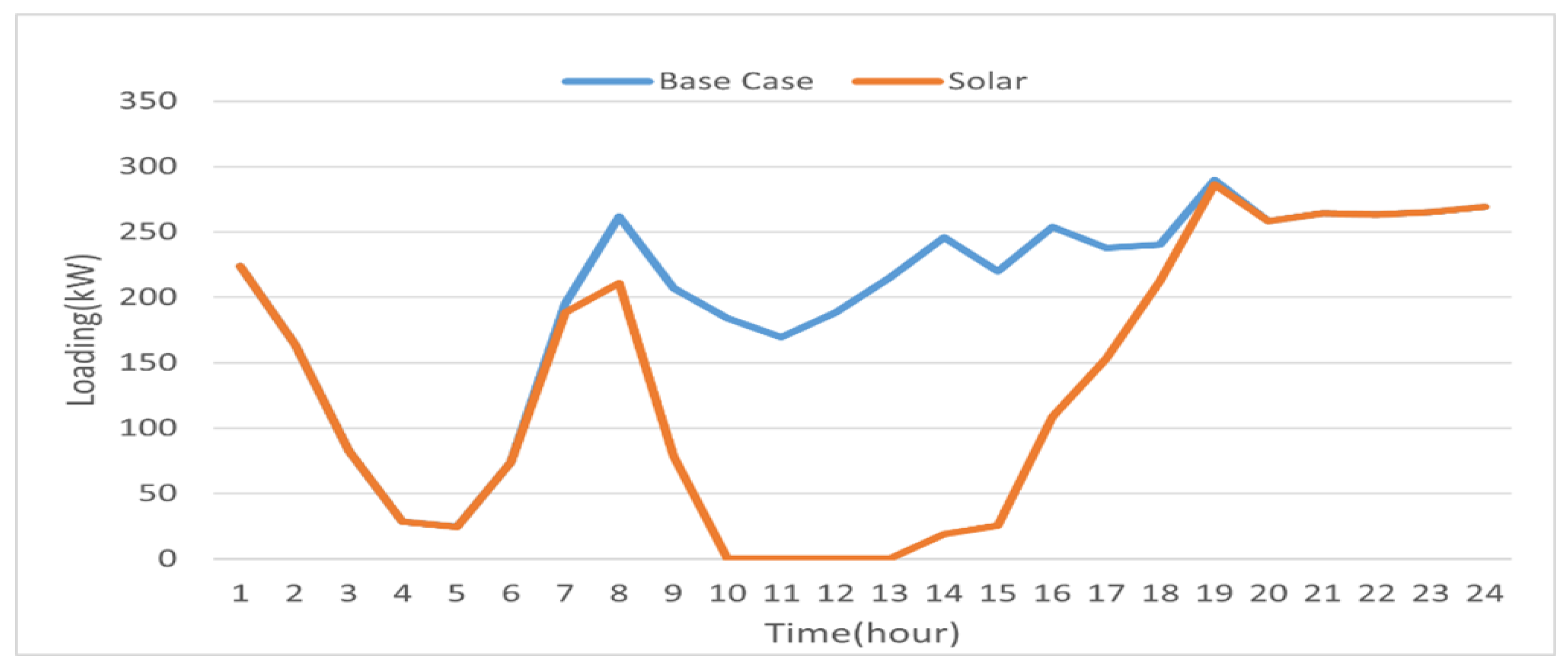
| Scenario → Cost ↓ | Before Solar | After Solar | After Solar + Scheduling |
|---|---|---|---|
| Power purchased from grid (USD/day) | 218.52 | 75.38 | 70.43 |
| Solar generation (USD/day) | - | 30.34 | 30.34 |
| Total purchasing cost (USD/day) | 218.52 | 105.72 | 100.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chopra, K.; Shah, M.K.; Niazi, K.R.; Sharma, G.; Bokoro, P.N. Optimizing Solar-Powered EV Charging: A Techno-Economic Assessment Using Horse Herd Optimization. Energies 2025, 18, 4556. https://doi.org/10.3390/en18174556
Chopra K, Shah MK, Niazi KR, Sharma G, Bokoro PN. Optimizing Solar-Powered EV Charging: A Techno-Economic Assessment Using Horse Herd Optimization. Energies. 2025; 18(17):4556. https://doi.org/10.3390/en18174556
Chicago/Turabian StyleChopra, Krishan, M. K. Shah, K. R. Niazi, Gulshan Sharma, and Pitshou N. Bokoro. 2025. "Optimizing Solar-Powered EV Charging: A Techno-Economic Assessment Using Horse Herd Optimization" Energies 18, no. 17: 4556. https://doi.org/10.3390/en18174556
APA StyleChopra, K., Shah, M. K., Niazi, K. R., Sharma, G., & Bokoro, P. N. (2025). Optimizing Solar-Powered EV Charging: A Techno-Economic Assessment Using Horse Herd Optimization. Energies, 18(17), 4556. https://doi.org/10.3390/en18174556







