Energy Management Model in Controlled Environment Agriculture: A Review
Abstract
1. Introduction
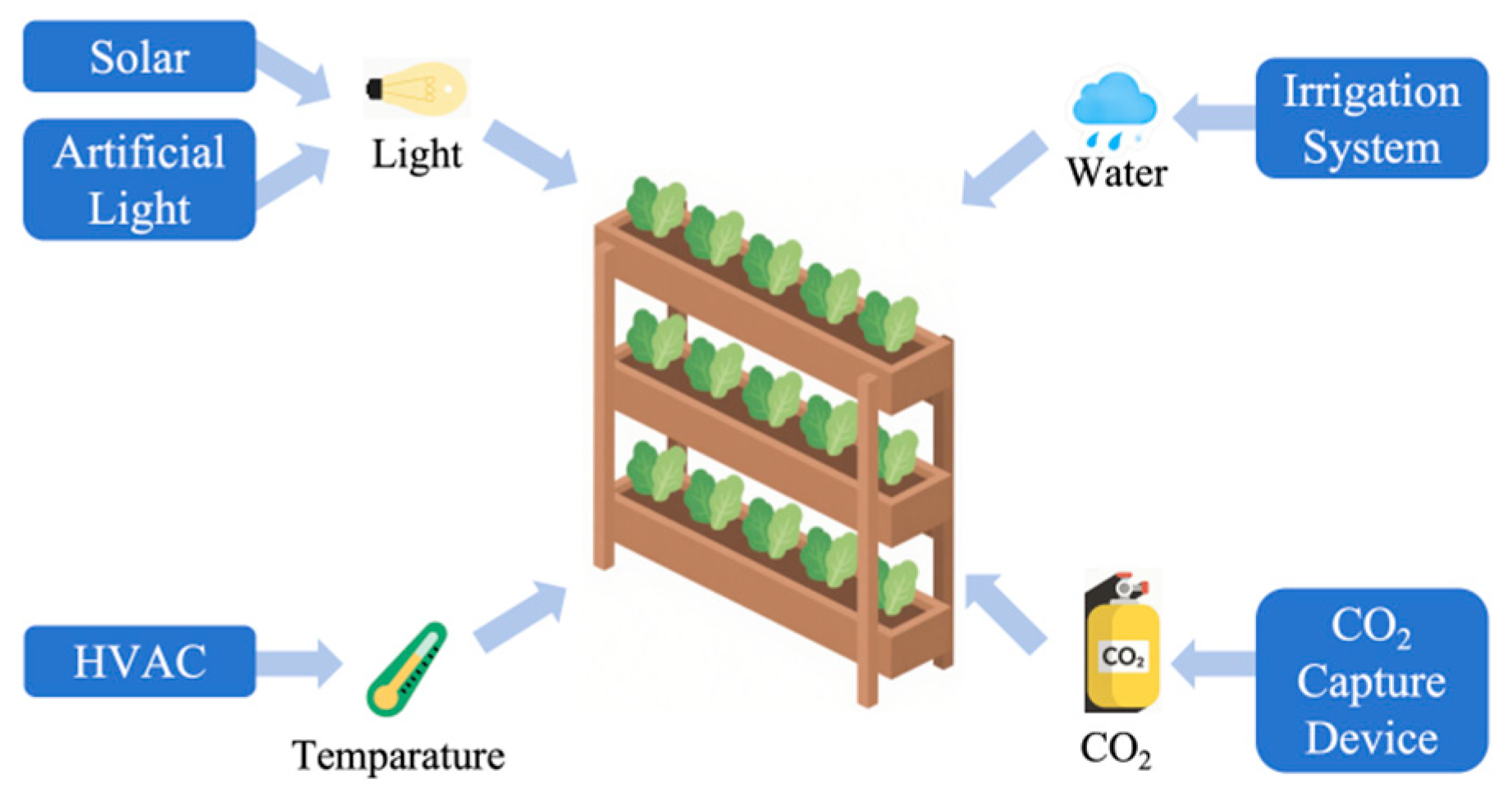
2. Environment Model in CEA
2.1. Irradiation
2.2. Temperature and Heat
2.3. Humidity and Water
2.4. Carbon Dioxide
2.4.1. Carbon Sink
2.4.2. Carbon Source
2.5. Other Environmental Models
2.5.1. Time Scale
2.5.2. Integration of Artificial Intelligence (AI)
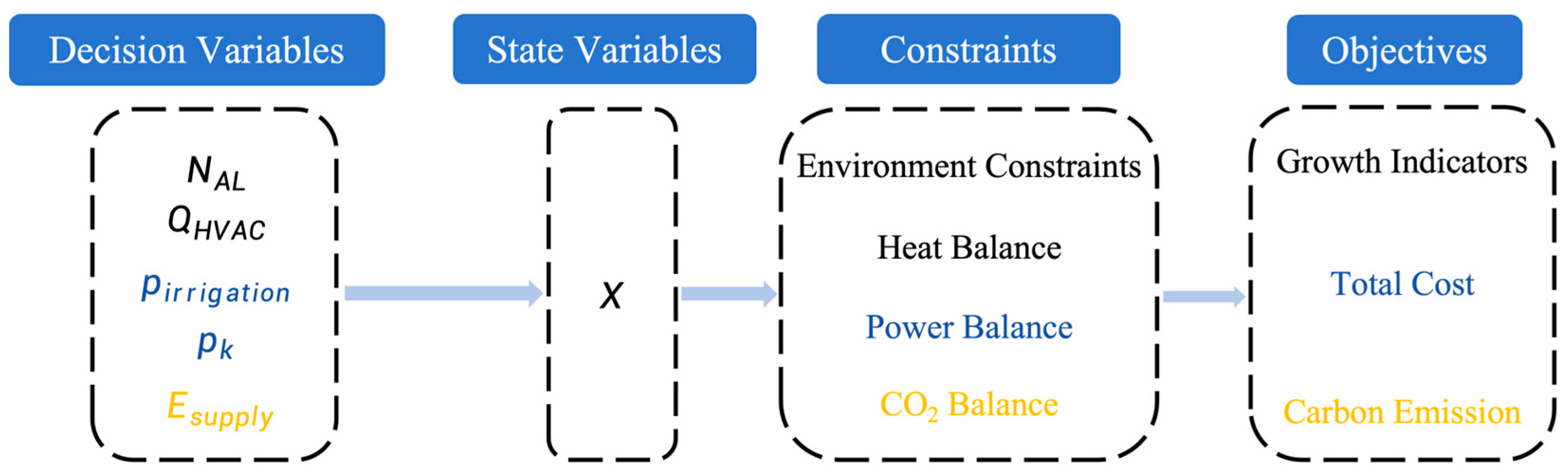
3. Multi-Disciplinary Coupling Points in Energy Management
3.1. Coupling of Plant Physiological Activities with Environmental Control
3.1.1. Environment Constraints
3.1.2. Growth Indicators
3.2. Coupling of Facility Environment and Energy
3.2.1. Electricity
3.2.2. Heat
3.3. Coupling of Plant Physiological Activities, Energy Consumption, and Carbon Emissions
4. Application
4.1. Optimal Energy Scheduling of CEA
4.2. Interaction Between CEA and Microgrids
4.3. Planning Issues
5. Future Research Directions
- (1)
- Multi-time-scale dynamic modeling of plant physiology and environment. At present, environment models of PFs mostly adopt static equations. Empirical formulas in Ref. [43] or simplified equations such as the improved Penman–Monteith equation in Ref. [23] are used to describe the physiological processes of crops, which cannot accurately reflect the dynamic impact of the environment on energy consumption. Multi-time-scale coordinated strategies considering second-level power regulation and daily growth cycle have not been fully resolved. Refs. [57,59] have considered the multi-time-scale coupling of electricity and heat, but they lack a multi-time-scale analysis of plant growth conditions. Future research can focus on the deep coupling model of environment, crop growth, and energy systems.
- (2)
- Uncertainty modeling of complex systems. In PFs, there exist exogenous uncertainties (such as random fluctuations in light intensity, changes in electricity prices, and deviations in the output of WT and PV power) and endogenous uncertainties (such as deviations in plant growth rates and errors in load demand forecasting). Most of the existing studies adopt deterministic optimization within the CEA environmental models (such as Ref. [23]) or only consider a single uncertainty factor (such as Ref. [88]). Refs. [34,89,91] adequately addressed the uncertainties within microgrids. Future research can focus on the sufficient modeling of various randomness involved in PFs.
- (3)
- DR modeling under market-oriented mechanisms. As one of the highly controllable loads, the potential of PFs in demand-side ancillary services (such as frequency regulation and reserve capacity) and the improvement in power grid resilience has not been fully tapped. Refs. [34,86] are limited to basic DR strategies, lacking a collaborative optimization model for green certificate trading, carbon tax policies, and the coupling mechanism of the long-term, medium-term, and day-ahead electricity markets. There is an urgent need to develop multi-objective energy optimization scheduling and management for PF clusters under a diversified market mechanism.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Area of the CEA system, | |
| Area of the th enclosure structure, | |
| Fitting parameters of photosynthetic rate | |
| Cumulative area cover (share of plant leaf cover in plant bed), | |
| PV coverage ratio of a PV greenhouse, | |
| PV diffuse coefficient, which equals 0.54 | |
| Thermal resistance of the th envelope structure, | |
| Air heat capacity, | |
| Thermal resistance of the ground, | |
| / | Air CO2 concentration in/outside the CEA system, |
| Respiration coefficient expressed in terms of the amount of CO2 produced, which equals | |
| Respiration coefficient, which equals 0.1/2.5 | |
| Emission intensity of the th generator, | |
| Conversion coefficient from to , which equals 4.57 | |
| Coefficient for water vapor concentration, which equals 0.2522/0.0485 | |
| Transpiration coefficient, which equals 0.408/1713/273/1.64 | |
| Unit conversion from hours to seconds, which equals 3600. | |
| Conversion coefficient from to , which equals 1.584. | |
| Mineral content in the dry matter, which equals 0.05. | |
| Plant weight coefficient, which equals 15.038/0.58/0.6/0.0029/0.1/0.64/12.683 | |
| Crop yield coefficient, which equals 0.74 | |
| PV power coefficient, which equals 0.0256 | |
| Target daily light integral, | |
| Distance coefficient of the Gauss three-point integration method at the th canopy | |
| / | Saturation/average vapor pressure |
| Evapotranspiration for the CEA system, | |
| CO2 consumed by crop photosynthetic absorption, | |
| CO2 efflux amount in soil, | |
| CO2 consumed by ventilation, | |
| CO2 produced by respiration, | |
| CO2 supplied by CO2 capture devices, | |
| Electricity emission, | |
| Photosynthetic rate of the PFAL/GH, | |
| Photosynthetic rate of the CEA system, | |
| Transpiration conductance, | |
| Ventilation rate, | |
| Condensation conductance, | |
| Standard gravity, 9.8 | |
| Growing degree-day, | |
| Absolute water vapor concentration, | |
| Air saturate humidity, | |
| Water vapor concentration outside the greenhouse, | |
| Water vapor condensation on the cover, | |
| Height of the CEA system, | |
| Pumping head of water, | |
| / | Total radiation of a PFAL/GH, |
| Total AL intensity in a CEA system, | |
| / | Total solar radiation inside a greenhouse without/with PV, |
| / | Direct/scattered radiation, |
| Total solar radiation inside a greenhouse, | |
| Total solar radiation at PV panel, | |
| Diffuse horizontal irradiance at PV panel, | |
| Light intensity of single supplemental lighting, | |
| Quantity of water per hour utilized for irrigation, | |
| Reflection coefficient | |
| Ratio of cultivated area to the total area of the CEA system | |
| Crop coefficient | |
| Temperature coefficient for PV generation | |
| Leaf area index | |
| Leaf area index between top-of-canopy at the th canopy | |
| Latent heat of evaporation of water | |
| Lettuce mass at the th period, | |
| Ventilation frequency per hour | |
| Light/dark time duration of AL in a day, | |
| Number of producing cycles throughout the year | |
| Number of ALs turned on | |
| Total power consumption for AL, | |
| Power of the th generator, | |
| Power consumption for per supplementary lighting, | |
| Power consumption of the drip irrigation system, | |
| Hourly power output from PVs, | |
| CO2 intensity released from soil at area, | |
| Actual/target photosynthetic photon flux density for the cultivation | |
| Net photosynthetic rate of the crop per unit of leaf area, | |
| Heat gain from the light not absorbed by plants, | |
| Heat generated by AL, | |
| Radiation related heat, | |
| Latent energy of plant transpiration, | |
| Heat transfer between the envelope structure and the environment, | |
| Heat loss by ventilation, | |
| Heat transfer between the CEA system and the ground, | |
| Heat generated by HVAC, | |
| PAR, | |
| PAR of the PFAL at the th canopy, | |
| PAR of the GH, | |
| Relative humidity | |
| Crop growth and development rate | |
| Temperature of indoor soil, | |
| / | Outdoor/indoor temperature, |
| Upper/lower temperature limit, | |
| Indoor temperature at the th hour, | |
| Average temperature limit in the light/dark time periods, | |
| Optimum environmental temperature, | |
| PV cell actual/reference temperature, | |
| Daily dry matter accumulation, | |
| Status of AL at the th hour | |
| Volume of the CEA system, | |
| Water vapor concentration difference at the leaf surface | |
| Lettuce dry mass, | |
| Environment variables | |
| Upper/lower environment variables | |
| Actual/reference annual crop yield, | |
| / | Proportionality factors |
| / | Direct/scattered solar transmittance value, |
| Angle between the incident direction of the sunlight and the normal angle of the PV surface, | |
| Air/water density, | |
| Slope of the vapor pressure curve | |
| Psychometric constant | |
| Conversion coefficient of converting CO2 to carbohydrate | |
| Conversion efficiency of converting carbohydrate to structural dry matter | |
| Conversion efficiency of CO2 into carbohydrates | |
| Conversion efficiency of carbohydrates into structural dry matter | |
| Efficiency of conversion of AL power to radiation | |
| Motor-pump efficiency | |
| Efficiency of PV power generation |
References
- Wang, S.; Deng, O.; Reis, S.; Zhu, Y.-G.; Xu, J.; Gu, B. Global urbanization benefits food security and nature restoration. Resour. Conserv. Recycl. 2025, 216, 108174. [Google Scholar] [CrossRef]
- van Dijk, M.; Morley, T.; Rau, M.L.; Saghai, Y. A meta-analysis of projected global food demand and population at risk of hunger for the period 2010–2050. Nat. Food 2021, 2, 494–501. [Google Scholar] [CrossRef]
- Yuan, X.; Hu, J.; Marcelis, L.F.; Heuvelink, E.; Peng, J.; Yang, X.; Yang, Q. Advanced technologies in plant factories: Exploring current and future economic and environmental benefits in urban horticulture. Hortic. Res. 2025, 12, uhaf024. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Batchelor, W.D.; Hu, K.; Han, H.; Li, J. Modeling Nitrogen Fate and Water and Nitrogen Use Efficiencies under Different Greenhouse Vegetable Production Systems Using the WHCNS-Veg Model. Plants 2024, 13, 1384. [Google Scholar] [CrossRef]
- Avgoustaki, D.D.; Xydis, G. How energy innovation in indoor vertical farming can improve food security, sustainability, and food safety? In Advances in Food Security and Sustainability; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Food and Agriculture Organization of the United Nations (FAO). The State of Food and Agriculture 2021: Making Agrifood Systems More Resilient to Shocks and Stresses; FAO: Rome, Italy, 2021. [Google Scholar] [CrossRef]
- Bashmakov, I.A.; Nilsson, L.J.; Acquaye, A.; Bataille, C.; Cullen, J.M.; de la Rue du Can, S.; Fischedick, M.; Geng, Y.; Tanaka, K. Climate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. In Lawrence Berkeley National Laboratory; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Cai, W.; Li, S.; Zha, L.; He, J.; Zhang, J.; Bao, H. Significantly enhanced energy efficiency through reflective materials integration in plant factories with artificial light. Appl. Energy 2024, 377, 124587. [Google Scholar] [CrossRef]
- Benke, K.; Tomkins, B. Future food-production systems: Vertical farming and controlled-environment agriculture. Sustain. Sci. Pract. Policy 2017, 13, 13–26. [Google Scholar] [CrossRef]
- Lu, C.; Grundy, S.; Mohmed, G.; Hardy, K. Urban Agriculture and Vertical Farming. In Encyclopedia of Sustainable Technologies, 2nd ed.; Abraham, M.A., Ed.; Elsevier: Oxford, UK, 2024; pp. 521–533. [Google Scholar] [CrossRef]
- Bu, K.; Yu, Z.; Lai, D.; Bao, H. Energy-saving effect assessment of various factors in container plant factories: A data-driven random forest approach. Clean. Energy Syst. 2024, 8, 100122. [Google Scholar] [CrossRef]
- Akram, W.; Guo, H.; Hu, W. Underground plant factory in a mine tunnel—Part 1: Conceptual design and thermal simulation. Energy Built Environ. 2025; in press. [Google Scholar] [CrossRef]
- Weidner, T.; Yang, A.; Hamm, M.W. Energy optimisation of plant factories and greenhouses for different climatic conditions. Energy Convers. Manag. 2021, 243, 114336. [Google Scholar] [CrossRef]
- Cai, W.; Bu, K.; Zha, L.; Zhang, J.; Lai, D.; Bao, H. Energy consumption of plant factory with artificial light: Challenges and opportunities. Renew. Sustain. Energy Rev. 2024, 210, 115235. [Google Scholar] [CrossRef]
- Martin, G.L.; Monfet, D. Comparison of EnergyPlus inside surfaces convective heat transfer coefficients algorithms for energy modelling of high-density controlled environment agriculture. Energy Build. 2024, 319, 114568. [Google Scholar] [CrossRef]
- Kozai, T. Resource use efficiency of closed plant production system with artificial light: Concept, estimation and application to plant factory. Proc. Jpn. Acad. 2013, 89, 447–461. [Google Scholar] [CrossRef]
- Avgoustaki, D.D.; Xydis, G. Plant factories in the water-food-energy Nexus era: A systematic bibliographical review. Food Secur. 2020, 12, 253–268. [Google Scholar] [CrossRef]
- Zou, H.; Li, C.; Zhang, A.; Zhang, X.; Chen, X.; Wang, F.; Yan, Y.; Zhang, S. Light environment control for reducing energy loss and increasing crop yield in plant factories. Sol. Energy 2023, 268, 112281. [Google Scholar] [CrossRef]
- Talbot, M.-H.; Monfet, D. Development of a crop growth model for the energy analysis of controlled agriculture environment spaces. Biosyst. Eng. 2024, 238, 38–50. [Google Scholar] [CrossRef]
- Tan, H.; Li, Z.; Wang, Q.; Mohamed, M.A. A novel forecast scenario-based robust energy management method for integrated rural energy systems with greenhouses. Appl. Energy 2023, 330, 120343. [Google Scholar] [CrossRef]
- Sun, W.; Wei, X.; Zhou, B.; Lu, C.; Guo, W. Greenhouse heating by energy transfer between greenhouses: System design and implementation. Appl. Energy 2022, 325, 119815. [Google Scholar] [CrossRef]
- Gao, Y.; Dong, J.; Isabella, O.; Santbergen, R.; Tan, H.; Zeman, M.; Zhang, G. Modeling and analyses of energy performances of photovoltaic greenhouses with sun-tracking functionality. Appl. Energy 2019, 233–234, 424–442. [Google Scholar] [CrossRef]
- Fu, X.; Zhou, Y. Collaborative Optimization of PV Greenhouses and Clean Energy Systems in Rural Areas. IEEE Trans. Sustain. Energy 2022, 14, 642–656. [Google Scholar] [CrossRef]
- Fernández, E.F.; Villar-Fernández, A.; Montes-Romero, J.; Ruiz-Torres, L.; Rodrigo, P.M.; Manzaneda, A.J.; Almonacid, F. Global energy assessment of the potential of photovoltaics for greenhouse farming. Appl. Energy 2022, 309, 118474. [Google Scholar] [CrossRef]
- Yang, Q. Plant Factory; Tsinghua University Press: Beijing, China, 2019. [Google Scholar]
- Juan, L.; Shirong, G.; Weihong, L. Simulation model for photosynthesis and dry matter accumulation in greenhouse cucumber. Trans. Chin. Soc. Agric. Eng. 2003, 19, 241–244. [Google Scholar]
- Lee, J.W.; Eom, J.N.; Kang, W.H.; Shin, J.H.; Son, J.E. Prediction of Transpiration Rate of Lettuces (Lactuca sativa L.) in Plant Factory by Penman-Monteith Model. Prot. Hortic. Plant Fact. 2013, 22, 182–187. [Google Scholar] [CrossRef]
- Baille, M.; Baille, A.; Laury, J.C. A simplified model for predicting evapotranspiration rate of nine ornamental species vs. climate factors and leaf area. Sci. Hortic. 1994, 59, 217–232. [Google Scholar] [CrossRef]
- Mauro, A.W.; Arcasi, A.; Napoli, G.; Pantaleo, A.M. Energy Cost Impact Analysis on the Total Cost of the Crop Production for Different Operating Conditions. A Salad Production Case Study. In Proceedings of the 36th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems (ECOS 2023), Las Palmas De Gran Canaria, Spain, 25–30 June 2023; pp. 2626–2636. [Google Scholar] [CrossRef]
- Chen, W.-H.; Mattson, N.S.; You, F. Intelligent control and energy optimization in controlled environment agriculture via nonlinear model predictive control of semi-closed greenhouse. Appl. Energy 2022, 320, 119334. [Google Scholar] [CrossRef]
- Akram, W.; Guo, H.; Hu, W. Numerical simulation of heat transfer through rock envelope of a plant factory in an underground mine tunnel. Energy Built Environ. 2025; in press. [Google Scholar] [CrossRef]
- Rezaei, E.; Dagdougui, H.; Ojand, K. Hierarchical Distributed Energy Management Framework for Multiple Greenhouses Considering Demand Response. IEEE Trans. Sustain. Energy 2022, 14, 453–464. [Google Scholar] [CrossRef]
- Parada, F.; Gabarrell, X.; Rufí-Salís, M.; Arcas-Pilz, V.; Muñoz, P.; Villalba, G. Optimizing irrigation in urban agriculture for tomato crops in rooftop greenhouses. Sci. Total Environ. 2021, 794, 148689. [Google Scholar] [CrossRef]
- Bozchalui, M.C.; Canizares, C.A.; Bhattacharya, K. Optimal Energy Management of Greenhouses in Smart Grids. IEEE Trans. Smart Grid 2014, 6, 827–835. [Google Scholar] [CrossRef]
- Lin, D.; Dong, Y.; Ren, Z.; Zhang, L.; Fan, Y. Hierarchical optimization for the energy management of a greenhouse integrated with grid-tied photovoltaic–battery systems. Appl. Energy 2024, 374, 124006. [Google Scholar] [CrossRef]
- Li, X.; Kang, S.; Niu, J.; Huo, Z.; Liu, J. Improving the representation of stomatal responses to CO2 within the Penman–Monteith model to better estimate evapotranspiration responses to climate change. J. Hydrol. 2019, 572, 692–705. [Google Scholar] [CrossRef]
- Choi, E.J.; Lee, D.; Lee, S.M. Comparative analysis of the performance and energy consumption of air-conditioning systems in a plant factory during a cooling season. Energy Build. 2025, 335, 115483. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.; Evans, J.; Wood, E. Impact of model structure and parameterization on Penman–Monteith type evaporation models. J. Hydrol. 2015, 525, 521–535. [Google Scholar] [CrossRef]
- Li, Z.; Liu, J.; Xiang, Y.; Zhang, X.; Chai, Y. Modeling agricultural load based on crop evapotranspiration and light integration for economic operation of greenhouse power system. CSEE J. Power Energy Syst. 2019, 7, 1113–1121. [Google Scholar] [CrossRef]
- Yang, Y.; Cui, Y.; Luo, Y.; Lyu, X.; Traore, S.; Khan, S.; Wang, W. Short-term forecasting of daily reference evapotranspiration using the Penman-Monteith model and public weather forecasts. Agric. Water Manag. 2016, 177, 329–339. [Google Scholar] [CrossRef]
- Fu, X.; Bai, J.; Sun, H.; Zhang, Y. Optimizing Agro-Energy-Environment Synergy in Agricultural Microgrids Through Carbon Accounting. IEEE Trans. Smart Grid 2024, 15, 4819–4834. [Google Scholar] [CrossRef]
- Fu, X.; Wei, Z.; Sun, H.; Zhang, Y. Agri-Energy-Environment Synergy-Based Distributed Energy Planning in Rural Areas. IEEE Trans. Smart Grid 2024, 15, 3722–3738. [Google Scholar] [CrossRef]
- Amirshekari, M.H.; Fakhroleslam, M. Impact of artificial light on photosynthesis, evapotranspiration, and plant growth in plant factories: Mathematical modeling for balancing energy consumption and crop productivity. Smart Agric. Technol. 2025, 11, 100901. [Google Scholar] [CrossRef]
- Li, W.; Zou, Y.; Yang, H.; Fu, X.; Xiang, S.; Li, Z. Two-Stage Stochastic Energy Scheduling for Multi-Energy Rural Microgrids With Irrigation Systems and Biomass Fermentation. IEEE Trans. Smart Grid 2024, 16, 1075–1087. [Google Scholar] [CrossRef]
- Fu, X.; Zhou, Y.; Wei, Z.; Wang, Y. Optimal Operation Strategy for Rural Microgrid Considering Greenhouse Load Control. CSEE J. Power Energy Syst. 2025, 11, 269–279. [Google Scholar] [CrossRef]
- Kläring, H.-P.; Hauschild, C.; Heißner, A.; Bar-Yosef, B. Model-based control of CO2 concentration in greenhouses at ambient levels increases cucumber yield. Agric. For. Meteorol. 2007, 143, 208–216. [Google Scholar] [CrossRef]
- Xu, D.; Ahmed, H.A.; Tong, Y.; Yang, Q.; van Willigenburg, L.G. Optimal control as a tool to investigate the profitability of a Chinese plant factory—Lettuce production system. Biosyst. Eng. 2021, 208, 319–332. [Google Scholar] [CrossRef]
- Wu, X.; Yang, W.; Zhang, N.; Zhou, C.; Song, J.; Kang, C. A Distributed Computing Algorithm for Electricity Carbon Emission Flow and Carbon Emission Intensity. Prot. Control Mod. Power Syst. 2024, 9, 138–146. [Google Scholar] [CrossRef]
- Ma, M.; Li, Y.; Du, E.; Jiang, H.; Zhang, N.; Wang, W.; Wang, M. Calculating Probabilistic Carbon Emission Flow: An Adaptive Regression-Based Framework. IEEE Trans. Sustain. Energy 2024, 15, 1576–1588. [Google Scholar] [CrossRef]
- Hu, J.; Jiang, C.; Cong, H.; He, Y. A low-carbon dispatch of power system incorporating active distribution networks based on locational marginal emission. IEEJ Trans. Electr. Electron. Eng. 2018, 13, 38–46. [Google Scholar] [CrossRef]
- Yu, X.; Tian, C.; Liu, W.; Jiang, X.; Yu, L.; Sun, S.; Hu, J.; Zhou, S.; Wang, X.; Jiang, C. Research on Locational Marginal Emission Based on Probabilistic Power Flow. In Proceedings of the 2019 IEEE Asia Power and Energy Engineering Conference (APEEC), Chengdu, China, 29–31 March 2019; pp. 285–290. [Google Scholar] [CrossRef]
- Liu, J.; Chai, Y.; Xiang, Y.; Zhang, X.; Grid, N.; Gou, S.; Liu, Y. Clean energy consumption of power systems towards smart agriculture: Roadmap, bottlenecks and technologies. CSEE J. Power Energy Syst. 2018, 4, 273–282. [Google Scholar] [CrossRef]
- Gu, X.; Goto, E. Evaluation of plant canopy microclimates with realistic plants in plant factories with artificial light using a computational fluid dynamics model. Build. Environ. 2024, 264, 111876. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, L.; Li, Y.; Li, D. Model predictive control and its application in agriculture: A review. Comput. Electron. Agric. 2018, 151, 104–117. [Google Scholar] [CrossRef]
- Hamidane, H.; El Faiz, S.; Guerbaoui, M.; Ed-Dahhak, A.; Lachhab, A.; Bouchikhi, B. Constrained discrete model predictive control of a greenhouse system temperature. Int. J. Electr. Comput. Eng. 2021, 11, 1223–1234. [Google Scholar] [CrossRef]
- Lin, D.; Zhang, L.; Xia, X. Hierarchical model predictive control of Venlo-type greenhouse climate for improving energy efficiency and reducing operating cost. J. Clean. Prod. 2020, 264, 121513. [Google Scholar] [CrossRef]
- Blaud, P.C.; Haurant, P.; Chevrel, P.; Claveau, F.; Mouraud, A. Multi-flow optimization of a greenhouse system: A hierarchical control approach. Appl. Energy 2023, 351, 121840. [Google Scholar] [CrossRef]
- Rosolia, U.; Zhang, X.; Borrelli, F. Data-Driven Predictive Control for Autonomous Systems. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 259–286. [Google Scholar] [CrossRef]
- Zhuang, P.; Liang, H.; Pomphrey, M. Stochastic Multi-Timescale Energy Management of Greenhouses with Renewable Energy Sources. IEEE Trans. Sustain. Energy 2018, 10, 905–917. [Google Scholar] [CrossRef]
- van Delden, S.H.; SharathKumar, M.; Butturini, M.; Graamans, L.J.A.; Heuvelink, E.; Kacira, M.; Kaiser, E.; Klamer, R.S.; Klerkx, L.; Kootstra, G.; et al. Current status and future challenges in implementing and upscaling vertical farming systems. Nat. Food 2021, 2, 944–956. [Google Scholar] [CrossRef] [PubMed]
- Kozai, T. Current Status of Plant Factories with Artificial Lighting (PFALs) and Smart PFALs. In Smart Plant Factory: The Next Generation Indoor Vertical Farms; Springer: Singapore, 2018. [Google Scholar]
- Mahmood, F.; Govindan, R.; Bermak, A.; Yang, D.; Khadra, C.; Al-Ansari, T. Energy utilization assessment of a semi-closed greenhouse using data-driven model predictive control. J. Clean. Prod. 2021, 324, 129172. [Google Scholar] [CrossRef]
- Jung, D.-H.; Kim, H.-J.; Kim, J.Y.; Lee, T.S.; Park, S.H. Model Predictive Control via Output Feedback Neural Network for Improved Multi-Window Greenhouse Ventilation Control. Sensors 2020, 20, 1756. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, F.; Govindan, R.; Bermak, A.; Yang, D.; Al-Ansari, T. Data-driven robust model predictive control for greenhouse temperature control and energy utilisation assessment. Appl. Energy 2023, 343, 121190. [Google Scholar] [CrossRef]
- Decardi-Nelson, B.; You, F. Artificial intelligence can regulate light and climate systems to reduce energy use in plant factories and support sustainable food production. Nat. Food 2024, 5, 869–881. [Google Scholar] [CrossRef]
- Ajagekar, A.; Decardi-Nelson, B.; You, F. Energy management for demand response in networked greenhouses with multi-agent deep reinforcement learning. Appl. Energy 2023, 355, 122349. [Google Scholar] [CrossRef]
- Hu, G.; You, F. AI-enabled cyber-physical-biological systems for smart energy management and sustainable food production in a plant factory. Appl. Energy 2023, 356, 122334. [Google Scholar] [CrossRef]
- Ahamed, S.; Guo, H.; Tanino, K. Energy saving techniques for reducing the heating cost of conventional greenhouses. Biosyst. Eng. 2019, 178, 9–33. [Google Scholar] [CrossRef]
- Liu, Y.M.; Wang, Y.C.; Yu, X.C.; Li, Y.S. Mathematic models of cucumber net photosynthesis rate responding to CO2 concentration, temperature, and illumination intensity. Chin. J. Appl. Ecol. 2007, 18, 883–887. [Google Scholar]
- Fu, X.; Yang, D.; Guo, Q.; Sun, H. Security analysis of a park-level agricultural energy Internet considering agrometeorology and energy meteorology. CSEE J. Power Energy Syst. 2020, 6, 743–748. [Google Scholar] [CrossRef]
- Arcasi, A.; Mauro, A.; Napoli, G.; Tariello, F.; Vanoli, G. Energy and cost analysis for a crop production in a vertical farm. Appl. Therm. Eng. 2024, 239, 122129. [Google Scholar] [CrossRef]
- Hebishima, H.; Inage, S.-I. Development of a new plant factory concept with sustainable water and energy supply. Energy Nexus 2024, 17, 100341. [Google Scholar] [CrossRef]
- Chen, D.; Mei, Y.; Liu, Q.; Wu, Y.; Yang, Z. Carbon dioxide enrichment promoted the growth, yield, and light-use efficiency of lettuce in a plant factory with artificial lighting. Agron. J. 2021, 113, 5196–5206. [Google Scholar] [CrossRef]
- Yu, H.; Wang, P.; Zhu, L.; Liu, Y.; Chen, M.; Zhang, S.; Sui, Y.; Yu, H. Optimizing light intensity and airflow for improved lettuce growth and reduced tip burn disease in a plant factory. Sci. Hortic. 2024, 338, 113693. [Google Scholar] [CrossRef]
- Eaton, M.; Shelford, T.; Cole, M.; Mattson, N. Modeling resource consumption and carbon emissions associated with lettuce production in plant factories. J. Clean. Prod. 2023, 384, 135569. [Google Scholar] [CrossRef]
- Talbot, M.-H.; Monfet, D. Analysing the influence of growing conditions on both energy load and crop yield of a controlled environment agriculture space. Appl. Energy 2024, 368, 123406. [Google Scholar] [CrossRef]
- Liang, M.H.; Chen, L.J.; He, Y.F.; Du, S.F. Greenhouse temperature predictive control for energy saving using switch actuators. IFAC-PapersOnLine 2018, 51, 747–751. [Google Scholar] [CrossRef]
- Menon, R.; Both, A.-J.; You, F. A life cycle assessment and techno-economic analysis of plant factories. J. Clean. Prod. 2025, 490, 144741. [Google Scholar] [CrossRef]
- Santini, A.; Bartolini, E.; Schneider, M.; de Lemos, V.G. The crop growth planning problem in vertical farming. Eur. J. Oper. Res. 2021, 294, 377–390. [Google Scholar] [CrossRef]
- Burg, V.; Golzar, F.; Bowman, G.; Hellweg, S.; Roshandel, R. Symbiosis opportunities between food and energy system: The potential of manure-based biogas as heating source for greenhouse production. J. Ind. Ecol. 2021, 19, 141–153. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Kotilainen, T.; Carmona-García, G.; Leip, A.; Tuomisto, H.L. Vertical farming: A trade-off between land area need for crops and for renewable energy production. J. Clean. Prod. 2022, 379, 134507. [Google Scholar] [CrossRef]
- Achour, Y.; Ouammi, A.; Zejli, D.; Sayadi, S. Supervisory Model Predictive Control for Optimal Operation of a Greenhouse Indoor Environment Coping with Food-Energy-Water Nexus. IEEE Access 2020, 8, 211562–211575. [Google Scholar] [CrossRef]
- Rutquist, P.E.; Edvall, M.M. Propt-Matlab Optimal Control Software; Tomlab optimization Inc.: Västerås, Sweden, 2010. [Google Scholar]
- Lu, M.; Liu, H.; Xu, J.; Li, H.; Gao, P.; Mao, H.; Hu, J. A hybrid approach using chained-SVR, MODE and DEA to optimize environmental control values in plant factories. Comput. Electron. Agric. 2025, 233, 110211. [Google Scholar] [CrossRef]
- Szinai, J.K.; Sheppard, C.J.; Abhyankar, N.; Gopal, A.R. Reduced grid operating costs and renewable energy curtailment with electric vehicle charge management. Energy Policy 2020, 136, 111051. [Google Scholar] [CrossRef]
- Xydis, G.; Strasszer, D.; Avgoustaki, D.D.; Nanaki, E. Mass deployment of plant factories as a source of load flexibility in the grid under an energy-food nexus. A technoeconomics-based comparison. Sustain. Energy Technol. Assess. 2021, 47, 101431. [Google Scholar] [CrossRef]
- Avgoustaki, D.D.; Xydis, G. Energy cost reduction by shifting electricity demand in indoor vertical farms with artificial lighting. Biosyst. Eng. 2021, 211, 219–229. [Google Scholar] [CrossRef]
- Khanna, T.M. Using agricultural demand for reducing costs of renewable energy integration in India. Energy 2022, 254, 124385. [Google Scholar] [CrossRef]
- Hussain, A.; Choi, I.-S.; Im, Y.H.; Kim, H.-M. Optimal Operation of Greenhouses in Microgrids Perspective. IEEE Trans. Smart Grid 2018, 10, 3474–3485. [Google Scholar] [CrossRef]
- Penuela, J.; Ben, C.; Boldyrev, S.; Gentzbittel, L.; Ouerdane, H. The indoor agriculture industry: A promising player in demand response services. Appl. Energy 2024, 372, 123756. [Google Scholar] [CrossRef]
- Seiler, J.C.; Pavlak, G.; Freihaut, J.D. Energy Dispatch Optimization at Controlled Environment Agriculture Sites with Chp: How Energy Utilization, Storage, and Market Exports Impact Operational Costs. Energy Convers. Manag. 2024, 332, 119743. [Google Scholar] [CrossRef]
- Ouammi, A. Model predictive control for optimal energy management of connected cluster of microgrids with net zero energy multi-greenhouses. Energy 2021, 234, 121274. [Google Scholar] [CrossRef]
- Esmaeli, H.; Roshandel, R. Optimal design for solar greenhouses based on climate conditions. Renew. Energy 2020, 145, 1255–1265. [Google Scholar] [CrossRef]
- Fu, X.; Zhou, Y.; Yang, F.; Ma, L.; Long, H.; Zhong, Y.; Ni, P. A Review of Key Technologies and Trends in the Development of Integrated Heating and Power Systems in Agriculture. Entropy 2021, 23, 260. [Google Scholar] [CrossRef]
- Cossu, M.; Cossu, A.; Deligios, P.A.; Ledda, L.; Li, Z.; Fatnassi, H.; Poncet, C.; Yano, A. Assessment and comparison of the solar radiation distribution inside the main commercial photovoltaic greenhouse types in Europe. Renew. Sustain. Energy Rev. 2018, 94, 822–834. [Google Scholar] [CrossRef]
- Wei, W.; Wu, D.; Wu, Q.; Shafie-Khah, M.; Catalão, J.P.S. Interdependence between transportation system and power distribution system: A comprehensive review on models and applications. J. Mod. Power Syst. Clean Energy 2019, 7, 433–448. [Google Scholar] [CrossRef]
- Vindel, J.M.; Valenzuela, R.X.; Navarro, A.A.; Zarzalejo, L.F.; Paz-Gallardo, A.; Souto, J.A.; Méndez-Gómez, R.; Cartelle, D.; Casares, J.J. Modeling Photosynthetically Active Radiation from Satellite-Derived Estimations over Mainland Spain. Remote Sens. 2018, 10, 849. [Google Scholar] [CrossRef]
- Si, Y.; Chen, L.; Zhang, X.; Chen, X.; Dan, H.; Mei, S. Optimal Capacity Allocation of Integrated Agricultural Energy Network with Enhanced Geothermal System Considering Seasonal Differences. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; IEEE: Wuhan, China, 2020; pp. 3422–3428. [Google Scholar] [CrossRef]
- Mirzamohammadi, S.; Jabarzadeh, A.; Shahrabi, M.S. Long-term planning of supplying energy for greenhouses using renewable resources under uncertainty. J. Clean. Prod. 2020, 264, 121611. [Google Scholar] [CrossRef]
- Hesaraki, A.; Holmberg, S.; Haghighat, F. Seasonal thermal energy storage with heat pumps and low temperatures in building projects—A comparative review. Renew. Sustain. Energy Rev. 2015, 43, 1199–1213. [Google Scholar] [CrossRef]
- Antoniadis, C.N.; Martinopoulos, G. Optimization of a building integrated solar thermal system with seasonal storage using TRNSYS. Renew. Energy 2019, 137, 56–66. [Google Scholar] [CrossRef]
- Yang, T.; Liu, W.; Kramer, G.J.; Sun, Q. Seasonal thermal energy storage: A techno-economic literature review. Renew. Sustain. Energy Rev. 2021, 139, 110732. [Google Scholar] [CrossRef]
- Mohebi, P.; Roshandel, R. Optimal design and operation of solar energy system with heat storage for agricultural greenhouse heating. Energy Convers. Manag. X 2023, 18, 100353. [Google Scholar] [CrossRef]

| Type | Characteristics | |
|---|---|---|
| PFAL | Vertical farming (VF) | Vertical planting layers can maximize space utilization and significantly increase the yield per unit area [10]. |
| Container PF | Modular design for easy deployment; it has high flexibility and can be used directly outdoors [11]. | |
| Underground PF | Reducing energy consumption by taking advantage of the constant temperature characteristics in the underground space [12]. | |
| GH | Closed GH | The growth of crops mainly relies on sunlight, and AL is only turned on when necessary. It is not restricted by external climatic conditions and can effectively avoid the impact of natural disasters on crops [13]. |
| Open ventilated GH | Smooth circulation with the outside air is conducive to regulating the temperature, humidity and CO2 concentration in the GH. The structure is relatively simple. Therefore, the construction and maintenance expenses are relatively low. It is greatly influenced by the natural environment [13]. | |
| PV coverage ratio (%) | 25 | 50 | 60 | 100 |
| Supplementary light intensity suggested () | 51 | 90.68 | 150.4 | 229 |
| Preferred Climate | |||
|---|---|---|---|
| Mild (basket) | 22.1 | 15.6~28 | 10.1~18.1 |
| Warm | 27 | 20.6~32.5 | 15~23 |
| Cold | 16 | 10.5~21.2 | 4~12 |
| Crop | Water Demand (mm) | ||
|---|---|---|---|
| Chengdu | Haikou | Jinan | |
| Lettuce | 3.07 | 3.83 | 3.01 |
| Cabbage | 2.95 | 3.69 | 2.90 |
| Tomato | 3.41 | 4.26 | 3.34 |
| Sweet pepper | 3.18 | 3.97 | 3.12 |
| Cucumber | 3.07 | 3.83 | 3.01 |
| Crop | Lettuce | Cabbage | Tomato | Sweet pepper | Cucumber |
| DLI | 14.51 | 17.35 | 28 | 15 | 17.5 |
| Crop | ||
|---|---|---|
| Tomatoes | 22~25 | 17~20 |
| Lettuce | 22~25 | 18~20 |
| Cucumbers | 25~30 | 20~22 |
| Bell peppers | 22~30 | 15~20 |
| References | Type | Objectives or Evaluation Indicators | Method | Characteristics or Results | Location | Energy Consumption per Lettuce Fresh Weight |
|---|---|---|---|---|---|---|
| [11] | Container PF | Data regression evaluated by the mean absolute percentage error | Data-driven random forest method | Heat transfer coefficient, the COP value of the air conditioning and the efficacy of LED have the highest contribution to the total energy consumption. | Shanghai | 4.76 kWh/kg |
| [13] | Container PF and GH | Unit energy consumption per hour | GRG non-linear engine | The energy efficiency of PFALs and GHs under different climatic conditions was compared. | Many locations around the world, taking Stockholm in winter as an example | 3.5 kWh/kg for PFAL 2.0 kWh/kg for closed GH 1.0 kWh/kg for open ventilated GH |
| [39] | Open ventilated GH | Minimize the total cost of power purchased from the external grid | Mixed-integer liner programming (MILP) | The load model of irrigation equipment was established based on the transpiration of crops. | Three cities in China, taking Sichuan as an example | |
| [47] | Closed GH | Revenue composed of the lettuce profit and the energy cost | The MATLAB function “fmincon” [83] | Adapts and calibrates a lettuce growth model and optimizes LED light intensity and CO2 supply to maximize profit | Beijing | 7.42 kWh/kg (fresh lettuce price of 34.5 RMB kg[fw]−1) |
| [77] | Open ventilated GH | The weighted minimum of temperature deviation and cost | Exhaustion approach | A temperature control system based on MPC was developed by coordinating the execution strategies of the heater and the ventilation window. | China | |
| [78] | VF | Global warming potential, acidification potential, freshwater ecotoxicity, net present value, net present value per unit, capital expenditure, total annual cost | “Farm-to-fork” life cycle assessment and techno-economic analysis | GHG reduction and energy efficiency improvement can be achieved simultaneously through the optimization of operational parameters. | Five cities in the United States | 21.21 kWh/kg |
| [79] | VF | Maximizing the demand met, minimizing the number of times shelf configurations change, minimizing the number of times crops move between shelves, minimizing the number of shelves required to meet a given demand | MILP | Adjusting the quantity of crops on different shelves to improve economy and efficiency | ||
| [84] | VF | Maximizing biomass accumulation and resource efficiency | A hybrid approach combining chained Support Vector Regression, Multi-Objective Differential Evolution, and Data Envelopment Analysis | Determine optimal light intensity and nitrogen content in nutrient solution | ||
| [59] | Open ventilated GH | Minimizing the total cost of the fast and slow scheduling cycles | An approximation method | A multi-time-scale energy management scheme considering the randomness of renewable energy is proposed. | Alberta | |
| [82] | Open ventilated GH | The differences between temperature, humidity, CO2, light, and water and the expected values are the smallest. | Model predictive control | The operation of the storage system and the reservoir around the reference value is taken into account to minimize the exchange with the main power grid, aiming to increase the use of local renewable energy production. |
| References | Type | Uncertainty | Objective of PF | Objective of Microgrid | Method |
|---|---|---|---|---|---|
| [35] | Open ventilated GH | × | Minimizing the total energy consumption of the greenhouse; minimizing energy cost minimization | Self-consumption maximization (the ratio of energy consumed within the system, sourced from PV generation and battery storage, to the total energy consumption); total cost minimization | Split into two sub-problems |
| [34] | Open ventilated GH | Electricity price, weather | Minimization of costs of energy consumption and peak demand charges | × | MILP |
| [45] | Closed GH | × | Minimizing the operating costs of the PF, such as the cost of purchasing electricity and the cost of load transfer | × | MILP |
| [66] | Open ventilated GH | × | Minimizing the total energy consumption of heating/cooling, ventilation, and irrigation systems | Maximizing the ratio of energy consumed within the system, sourced from PV generation and battery storage, to the total energy consumption; minimizing the energy cost | MILP |
| [87] | VF | × | Energy demand cost | × | A limited energy demand method |
| [88] | Not explicitly pointed out | RES | × | Minimizing operating costs of the power system | MILP |
| [89] | Open ventilated GH | RES, load | In grid-connected mode: minimizing the cost of power purchase and the cost of CHP In island mode: minimizing the penalty value for the out-of-bounds environmental parameter | × | Robust optimization |
| [90] | VF | × | The total electricity bill of the PF | × | Linear optimization |
| [91] | Closed GH | Price of electricity and carbon emissions | Minimizing energy procurement costs and emissions | × | MILP |
| [32] | Open ventilated GH | × | Minimizing the electricity purchased from the microgrid; minimizing the deviations in temperature, CO2, light, and water in the PF | Minimizing the exchange power between the PF, the reservoir, and the microgrid | Alternating direction method of multipliers |
| [92] | Open ventilated GH | × | Minimizing environmental deviation and power exchange deviation between microgrids and ES states | × | MPC-based algorithm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Wang, X.; Tan, S. Energy Management Model in Controlled Environment Agriculture: A Review. Energies 2025, 18, 4544. https://doi.org/10.3390/en18174544
Hu J, Wang X, Tan S. Energy Management Model in Controlled Environment Agriculture: A Review. Energies. 2025; 18(17):4544. https://doi.org/10.3390/en18174544
Chicago/Turabian StyleHu, Jingzhe, Xu Wang, and Shengmin Tan. 2025. "Energy Management Model in Controlled Environment Agriculture: A Review" Energies 18, no. 17: 4544. https://doi.org/10.3390/en18174544
APA StyleHu, J., Wang, X., & Tan, S. (2025). Energy Management Model in Controlled Environment Agriculture: A Review. Energies, 18(17), 4544. https://doi.org/10.3390/en18174544








