A Modular Hybrid SOC-Estimation Framework with a Supervisor for Battery Management Systems Supporting Renewable Energy Integration in Smart Buildings

Abstract

Accurate state-of-charge (SOC) estimation is crucial in smart-building energy management systems, where rooftop photovoltaics and lithium-ion energy storage systems must be coordinated to align renewable generation with real-time demand. This paper introduces a novel, modular hybrid framework for SOC estimation, which synergistically combines the predictive power of artificial neural networks (ANNs), the logical consistency of finite state automata (FSA), and an adaptive dynamic supervisor layer. Three distinct ANN architectures—feedforward neural network (FFNN), long short-term memory (LSTM), and 1D convolutional neural network (1D-CNN)—are employed to extract comprehensive temporal and spatial features from raw data. The inherent challenge of ANNs producing physically irrational SOC values is handled by processing their raw predictions through an FSA module, which constrains physical validity by applying feasible transitions and domain constraints based on battery operational states. To further enhance the adaptability and robustness of the framework, two advanced supervisor mechanisms are developed for model selection during estimation. A lightweight rule-based supervisor picks a model transparently using recent performance scores and quick signal heuristics, whereas a more advanced double deep Q-network (DQN) reinforcement-learning supervisor continuously learns from reward feedback to adaptively choose the model that minimizes SOC error under changing conditions. This RL agent dynamically selects the most suitable ANN+FSA model, significantly improving performance under varying and unpredictable operational conditions. Comprehensive experimental validation demonstrates that the hybrid approach consistently outperforms raw ANN predictions and conventional extended Kalman filter (EKF)-based methods. Notably, the RL-based supervisor exhibits good adaptability and achieves lower error results in challenging high-variance scenarios.

1. Introduction

Smart buildings are increasingly expected to act as active players in the clean-energy transition, decarbonizing their operations by maximizing on-site renewable generation and cooperative energy-sharing schemes [1,2]. In modern smart buildings, photovoltaic arrays coupled with battery storage are increasingly deployed to improve energy self-sufficiency and reduce peak load demand [3,4]. Recent work shows that battery systems act as a crucial buffer that smooths photovoltaic intermittency and delivers load-leveling and economic gains in building-scale energy hubs [5,6]. Consequently, precise SOC estimation has become crucial for building energy management systems (BEMSs) to optimally balance on-site generation and consumption. Integrating an advanced SOC-estimation framework into a BEMS can ensure that the battery is used effectively to maximize PV self-consumption and minimize grid dependence [7].

Recent trends show that battery packs coupled with on-site PV arrays are becoming standard components of a BEMS [2,8]. Accurate SOC knowledge is, therefore, not only a matter of safety but also a key variable enabling the following: (i) predictive scheduling of PV surplus into the battery; (ii) peak-shaving or time-of-use arbitrage; and (iii) health-aware dispatch that prolongs battery lifetime in buildings [9]. Consequently, an SOC estimator that is both data-driven and physically constrained, as proposed in this work, can unlock higher PV self-sufficiency ratios and lower grid-purchase costs for smart homes and commercial facilities [3,10].

Accurately estimating the state of charge (SOC) is a crucial key for the safe, efficient, and effective operation of systems using lithium-ion batteries [11]. The studies on SOC estimation primarily focus on two main methodologies, as follows: model-based and data-driven approaches. Traditional model-based frameworks, such as Coulomb counting and Kalman filtering, often demand extensive domain knowledge and need more time to implement and calibrate [12]. These methods can also struggle with the complex, non-linear dynamics and degradation effects inherent in systems that contain lithium-ion batteries, which leads to reduced accuracy under varying conditions [12].

In contrast, artificial neural network (ANN) models are increasingly utilized across various fields. These models offer a powerful alternative for SOC estimation, where they can directly learn the intricate relationships between sensor data (e.g., current, voltage, temperature) and the SOC value. The other positive aspect of ANNs is that they do not require a prior physical model or extensive domain expertise [13]. These adaptabilities make ANNs particularly interesting for real-time battery management systems (BMSs).

Other recent studies confirm this trend, covering optimal PV–battery sizing [14], multi-objective dispatch in smart homes [15], comprehensive reviews of battery-energy-storage EMS and health metrics [16], and prosumer-oriented demand-response strategies [17].

Despite the inherent success and flexibility of ANN-based frameworks in SOC estimation, their estimates can sometimes fall outside of physically applicable domain-specific constraints. For example, it may be obvious that irrational SOC values decrease during charging or unstable charging/discharging trends. Such inconsistencies both put at risk the reliability of the SOC estimation and create potential security risks. Therefore, hybrid models are being developed for more robust and secure battery management by using not only raw ANN outputs but also other models together with ANN in order not to restrict optimal battery usage within a BMS [18].

More recent works have focused on advanced hybrid estimation techniques that combine the advantages of machine learning with model-based filters and advanced rule logic. These works often combine ANNs with traditional time-series and signal processing models. For instance, Ref. [19] developed a hybrid KF-SA-Transformer model, combining Kalman filtering, sparse autoencoders, and Transformer modules to achieve reliable SOC estimations across various temperature ranges. Ref. [20] proposed a hybrid model integrating the Box–Jenkins approach with ANNs for electric vehicle applications. Ref. [21] introduced a method combining LSTM networks with attention mechanisms and Kalman filters, demonstrating strong performance under dynamic driving scenarios. Additionally, Ref. [22] presented an LSTM model coupled with squared gain extended Kalman filters. Reviews confirm that such hybrid models combining Kalman filters and neural networks generally outperform single models in terms of accuracy and generalization [23]. Kalman filters offer real-time estimation and reduced computational resources, while neural networks excel in handling nonlinear systems and uncertainty factors, making their combination beneficial [24]. However, Kalman filters are typically limited to nonlinear systems, and their accuracy can be reduced by uncertainties in real systems [25]. Similarly, ANN methods require substantial data for training.

Similarly, Ref. [26] proposed a dual-stage attention-based bidirectional recurrent neural network (RNN) with physics-informed components, achieving improved generalizability and accuracy. In the domain of reinforcement learning for battery management, recent studies have framed SOC estimation as an RL problem, leveraging architectures like proximal policy optimization (PPO) to develop robust and accurate models that adapt to diverse operating conditions [27,28]. Deep reinforcement learning has also been proposed for SOC estimation and management of nickel–metal hybrid batteries, showing high accuracy and faster convergence compared to state-of-the-art models by incorporating various parameters like route type and environmental conditions [29]. These RL-based approaches underline adaptive learning through interaction with simulated environments, and also enhance performance under various operational situations. Regarding dynamic model selection in battery applications, some studies utilize machine learning models to predict battery capacity or state of health [30,31]. Studies of hybrid models for SOC estimation demonstrate that traditional models integrated with neural networks can achieve high-precision and robust predictions under complex conditions. These hybrid systems also highlight their ability to overcome the limitations of traditional methods.

Furthermore, finite state automata (FSA) are frequently employed within BMS frameworks to manage mode transitions and enforce safety protocols. Ref. [32] proposed an FSA-based control mechanism for thermal and SOC balancing in lithium iron phosphate (LFP) battery cells using flyback converters, effectively maintaining temperature and charge stability with minimal computational cost. Other research [33] also shows the application of finite state machine control algorithms for a battery management system with a passive cell balancing algorithm.

While these rule-based systems are effective for managing transitions and security, their lack of learning capabilities can make them largely unsuitable for the continuous, nonlinear, and often unpredictable nature of SOC estimation. By their nature, they typically rely on fixed thresholds and predefined rules, which may not generalize well to new or extreme operating conditions. Combining these with ANN to monitor the output of previously learned operations offers a promising solution. Depending on this combination, FSA can derive its logical rules based on battery transitions by monitoring the ANN outputs. Thus, FSA can provide the missing prediction direction with this combination.

Considering this critical aspect, a novel modular hybrid SOC-estimation framework that addresses the advantages of ANN and FSA is proposed. The framework combines multiple ANN architectures, namely feedforward neural networks (FFNNs, long short-term memory (LSTM) networks, and 1D convolutional neural networks (1D-CNNs), with FSA-based logic correction layers. The multi-model strategy adopted in this study exploits the fact that deep artificial neural network (ANN) architectures can simultaneously encode lag-dependent (temporal) patterns and cross-signal (spatial) correlations with high fidelity, owing to their hierarchical representation capacity. Because each ANN–finite-state-automaton (FSA) pair excels under different operating regimes, a supervisory module is embedded to perform online model arbitration—at every time step, the controller analyzes the recent input trajectory and the estimators’ residuals, then activates the ANN+FSA combination predicted to minimize the forthcoming error, implementing dynamic, context-aware model selection at runtime. These dynamic selection mechanisms are defined as supervisors. These supervisors are designed to significantly increase the robustness and adaptability of SOC estimation under constantly changing battery conditions and various operational scenarios. We then augmented this supervisor using reinforcement learning (RL) via a double Deep Q-Net (DQN) for advanced model selection depending on error feedback and past decision performance. Using the supervisor allows the system to learn the optimal selection policy, thus optimizing overall predictive accuracy and system stability.

Some recent contributions show how RL is being adopted in battery management tasks. Yalçın and Herdem integrate deep Q-learning with actor–critic schemes to optimize EV charging/discharging policies [34], and Karnehm applies amortized Q-learning to control a reconfigurable pack for SOC balancing [35]. Additionally, Liu et al. use Q-learning to adaptively schedule battery energy storage in electricity markets, highlighting RL’s growing role in operational decision-making for BESS [36]. These studies leverage RL for operational control or balancing rather than for SOC estimation itself, and they do not embed a symbolic layer that enforces physically consistent SOC trajectories. In contrast, our framework uses RL in a different role—as a supervisor that arbitrates online among multiple ANN heads—while a formal FSA enforces mode-consistent transitions and safety thresholds on every estimate. To the best of our knowledge, this joint use of RL-driven multi-model arbitration with explicit symbolic (FSA) constraints for SOC estimation remains unexplored in the recent literature.

The main contributions of the proposed hybrid model and the supervisory strategies employed for model selection in this study can be summarized as follows:

• A novel module for SOC estimation is proposed, integrating the following models:

  -

  ANN-based models: data-driven neural networks with high predictive power that have recently become state-of-the-art in SOC estimation.

  -

  FSA-symbolic model: a finite-state automaton that enforces physical and logical constraints, smoothing the raw ANN output, and ensuring stable, physically plausible results.

• To ensure that selecting the correct model for new inputs will yield the lowest expected prediction error, two different supervisors are used for dynamic model selection. These are as follows:

  -

  A transparent rule-based supervisor.

  -

  An adaptive RL-based supervisor trained via double DQN.

• A comprehensive evaluation of the proposed model using an open-source NASA dataset is conducted. We compare the performance of the models and supervisors by performing a worst-case scenario.

The ANN+FSA+Supervisor framework addresses the critical problem of physically irrational SOC estimations often produced by purely data-driven methods, especially under dynamic operating conditions. While model-based approaches like the Kalman filter (KF) and its hybrid variants (e.g., ANN+KF) aim for high accuracy, they often struggle with inherent non-linearities and sensor uncertainties. Crucially, they lack a direct mechanism to enforce physical constraints, which can lead to unlikely outputs. Our proposed method explicitly fills this gap by using a unique combination of approaches. It integrates the robust learning capabilities of various ANN architectures with the logical consistency of an FSA, which directly applies physical rules to ensure valid SOC transitions and smooth noisy outputs. Furthermore, it adds an adaptive supervisor layer to dynamically select the optimal ANN+FSA model at runtime, a feature that is largely unexplored in the existing literature. This advanced, RL-based model selection distinguishes our framework from other hybrid methods and provides a robust and adaptable solution for highly accurate and reliable SOC estimation. Relative to recent RL-for-control studies [34,35,36], the novelty of the present study lies in deploying RL specifically for model selection in SOC estimation and coupling it with a symbolic FSA that guarantees physical reliability at inference.

The rest of this paper is organized as follows: Section 2 details the proposed method, including the ANN models, FSA constraints, and supervisor designs. Section 3 outlines the datasets, experimental setup, and evaluation metrics, and presents the results and analyses. Section 4 provides a comprehensive discussion of this work. Finally, Section 5 concludes this work and highlights future directions.

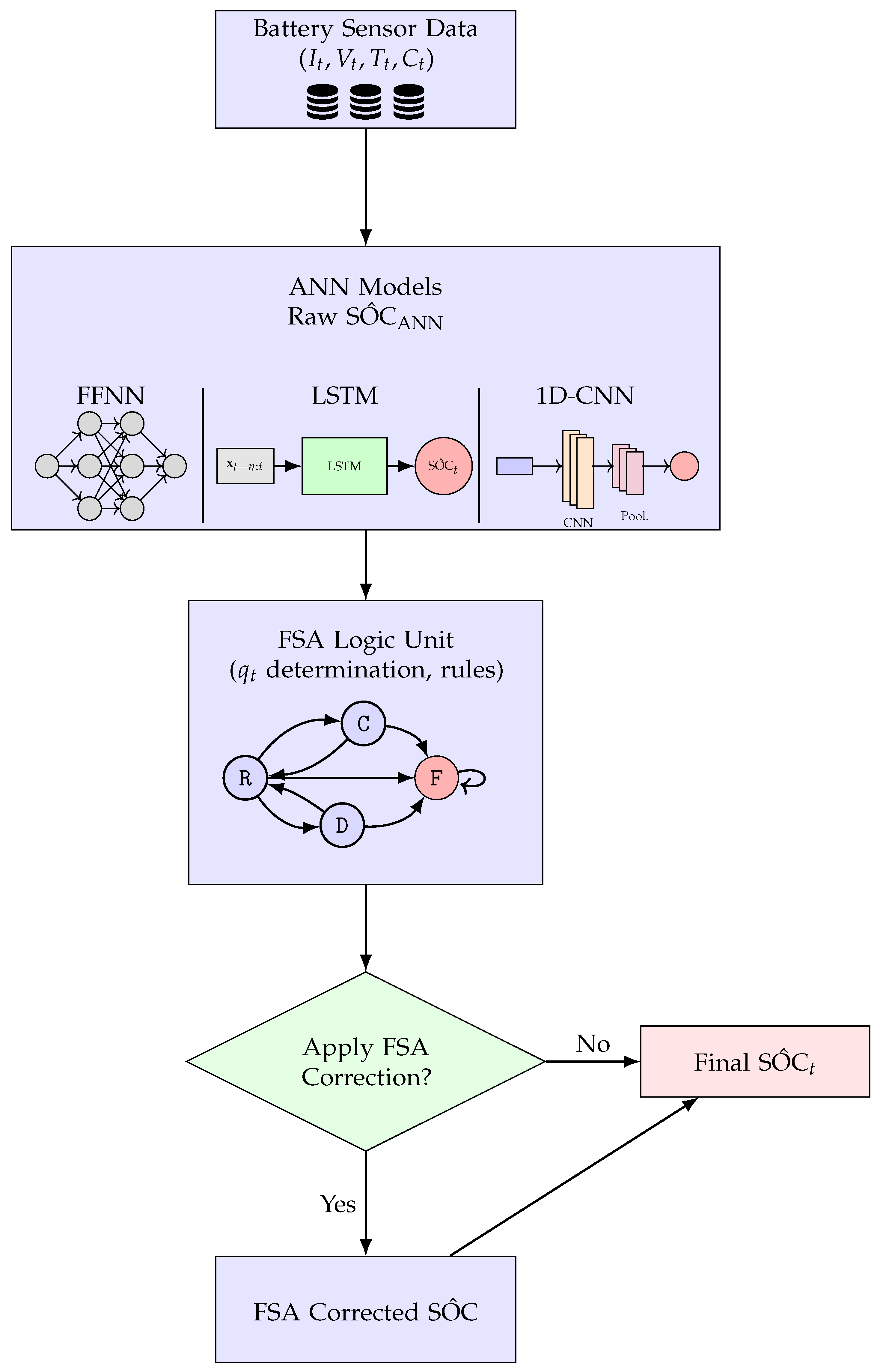
2. Materials and Methods

This section presents the detailed structure of the proposed modular hybrid SOC-estimation framework, which merges ANNs with an FSA. Furthermore, this section explains the design and operational principles of two different supervisor techniques that are rule-based and reinforcement learning (RL)-based. These supervisors are developed for clear model selection during the real-time SOC estimation process.

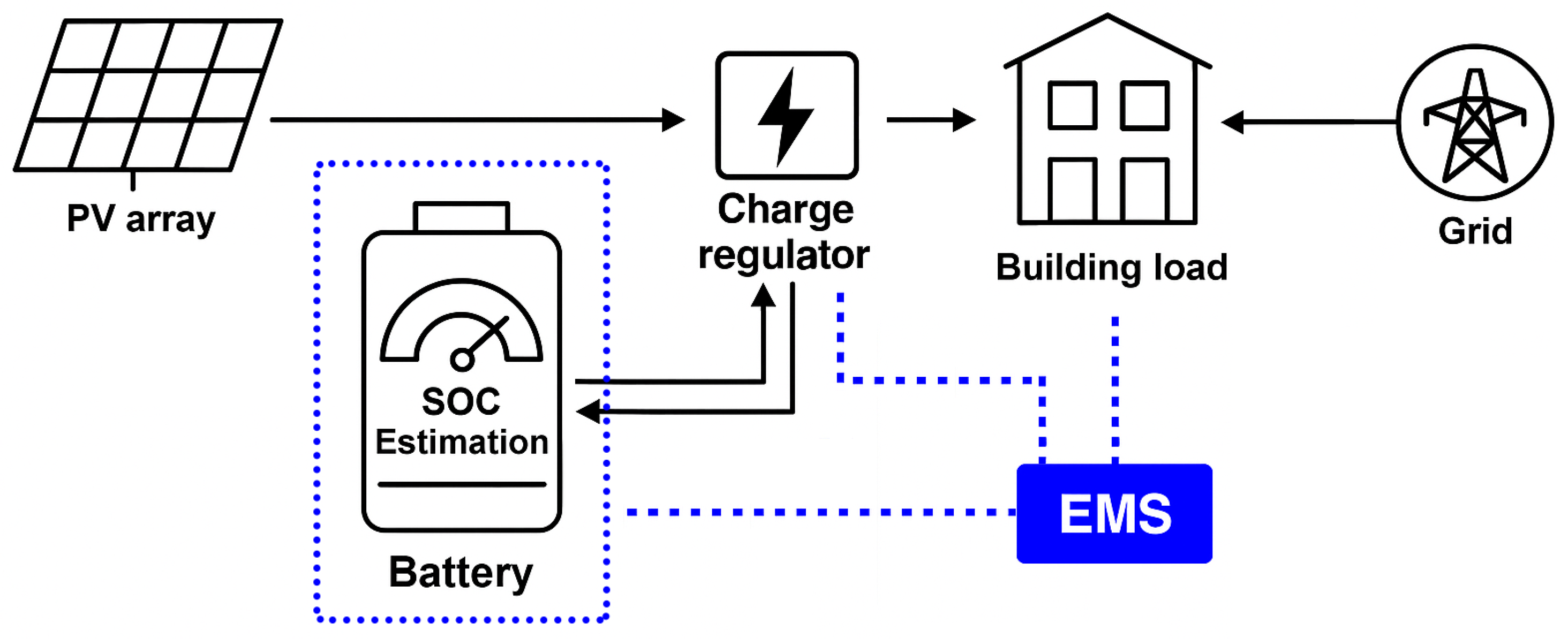
Figure 1 schematically shows how the proposed ANN-FSA state-of-charge estimator is embedded within a smart building, relaying real-time battery information to the energy management system so that rooftop PV generation, behind-the-meter storage, and grid exchange can be co-optimized.

2.1. ANN-Based SOC Estimation

ANNs are widely known and used for battery SOC estimation due to their essential capability to model highly nonlinear dependencies between input sensor data and complex battery parameters. In this work, we use three distinct and complementary ANN architectures—FFNN, LSTM, and 1D-CNN—to capture various characteristics from the input data. Each of these models offers unique strengths and allows a multifaceted approach to SOC estimation.

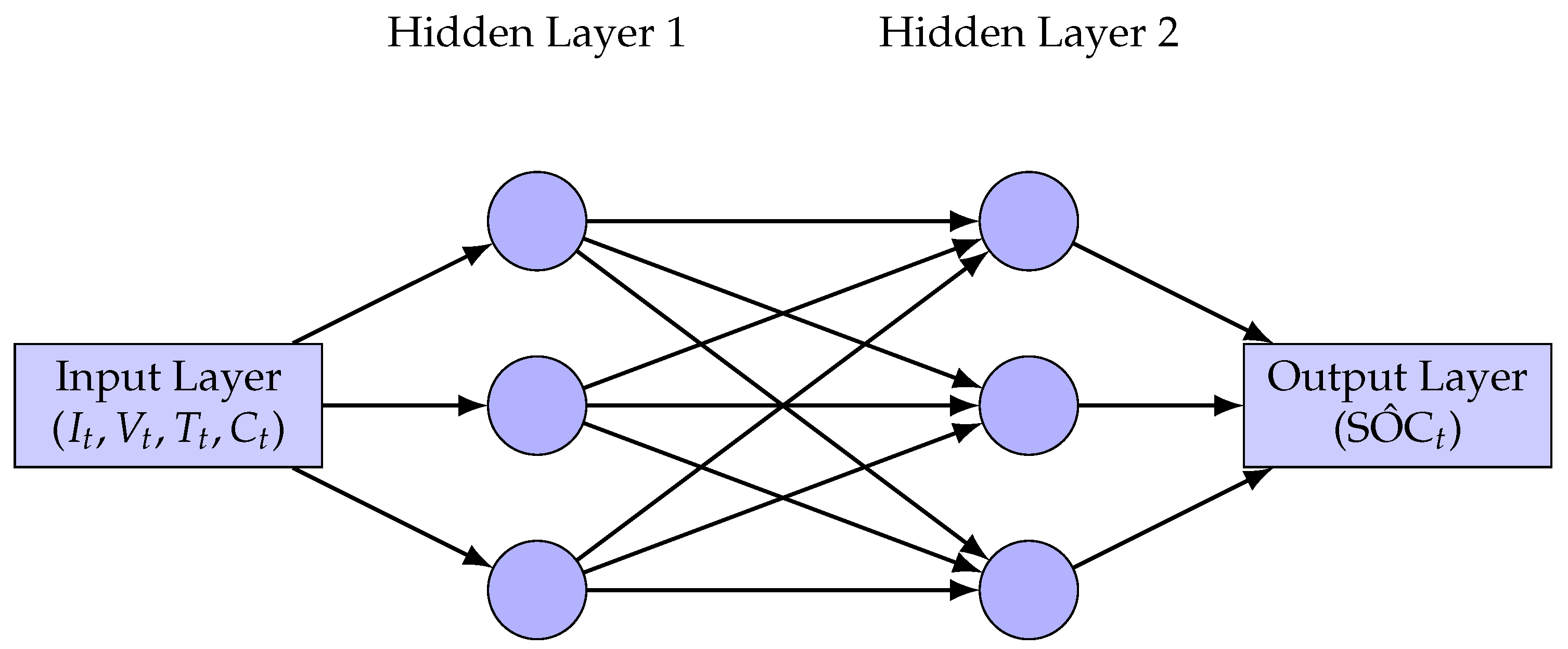
The FFNN serves as a baseline model in this framework. It was chosen for its simplicity and computational efficiency. Its architecture consists of an input layer, followed by one or more hidden layers using the rectified linear unit (ReLU) activation function, and a single output neuron to predict the SOC value (Figure 2).

The FFNN operates on a set of direct input features at time step t, which include current ($I_t$), voltage ($V_t$), temperature ($T_t$), and cycle index ($C_t$). The estimation process for FFNN is formally expressed as follows:

$${\widehat{\mathrm{SOC}}}_t^{\mathrm{FFNN}}={\mathcal{F}}_{\mathrm{FFNN}}(I_t,V_t,T_t,C_t;\theta )$$

(1)

where $\theta$ represents the optimized network parameters. It is obtained by minimizing the mean squared error (MSE) between the predicted and true SOC values during training.

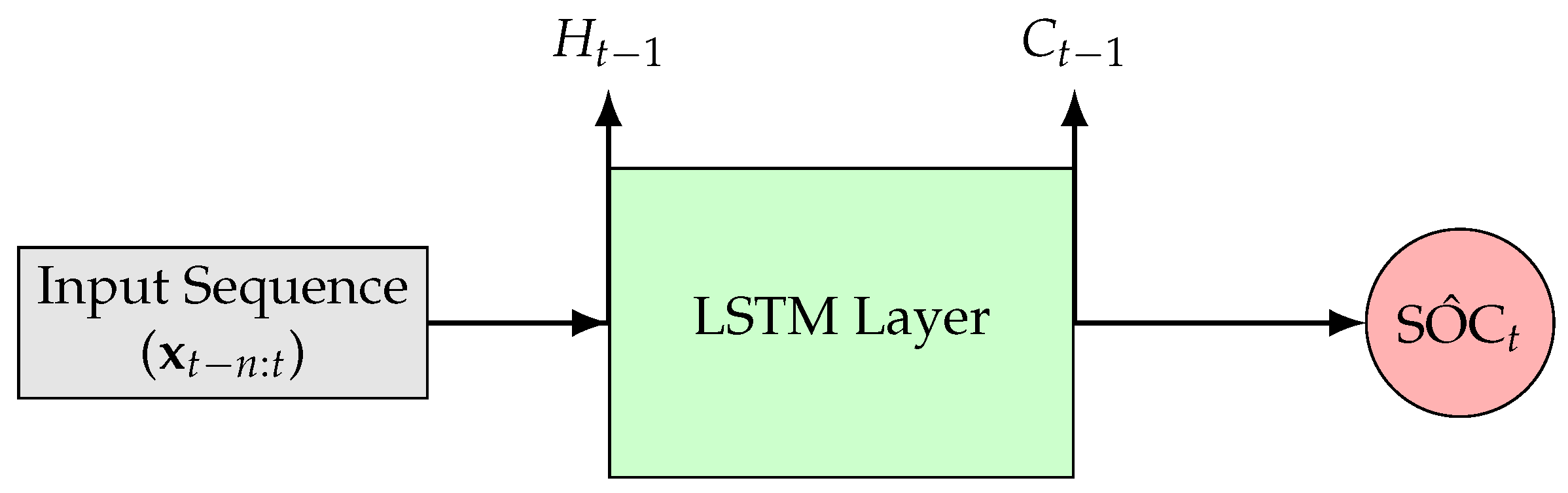
The LSTM is a specialized form of a recurrent neural network (RNN) that is specifically designed to address the vanishing gradient problem and effectively capture long-term temporal dependencies in sequential data (Figure 3) [37]. This capability is critical for SOC estimation because battery behavior shows significant time-series correlations.

Unlike the stateless FFNN, the LSTM processes a sequence of past $\{{\mathbf{x}}_{t-n},\dots ,{\mathbf{x}}_t\}$ where each ${\mathbf{x}}_i=[I_i,V_i,T_i,C_i]$ represents the input features at time i. The LSTM estimates SOC by learning from the complex temporal dynamics:

$${\widehat{\mathrm{SOC}}}_t^{\mathrm{LSTM}}={\mathcal{F}}_{\mathrm{LSTM}}({\mathbf{x}}_{t-n:t};\varphi )$$

(2)

Here, $\varphi$ denotes the learned LSTM parameters. The ability of the LSTM to retain information over long periods makes it particularly suitable for capturing the history-dependent behavior of battery charge states.

The 1D-CNN model is employed for its ability to apply convolutional filters along the temporal dimension of the input sequence (Figure 4) [38]. It enables the extraction of local patterns and main features, such as sudden voltage changes or current spikes.

This architecture is particularly capable of identifying short-term passings and characteristic signatures within the operational data of the battery. Given a multivariate time series input ${\mathbf{X}}_{t-n:t}$, the 1D-CNN executes a series of convolutional and pooling operations, followed by dense layers, to output the SOC estimate:

$${\widehat{\mathrm{SOC}}}_t^{\mathrm{CNN}}={\mathcal{F}}_{\mathrm{CNN}}({\mathbf{X}}_{t-n:t};\psi )$$

(3)

where $\psi$ denotes the CNN weights. The choice of 1D-CNN completes the LSTM by focusing on local feature extraction, which can be crucial for detecting sudden state changes.

The feasible selection of these three distinct ANN architectures (FFNN, LSTM, 1D-CNN) is based on their complementary strengths—FFNNs provide a fast and simple structure; LSTMs are talented at capturing long-term historical dependencies; and 1D-CNNs efficiently extract local, short-term patterns. Each of these models is subsequently combined with an FSA to build a robust hybrid architecture that capitalizes on these individual advantages while reducing their inherent weaknesses. This hybrid design enables logical, state-driven filtering, enhancing the robustness and interpretability of SOC predictions across multiple and challenging operational conditions.

2.2. Finite State Automaton Design

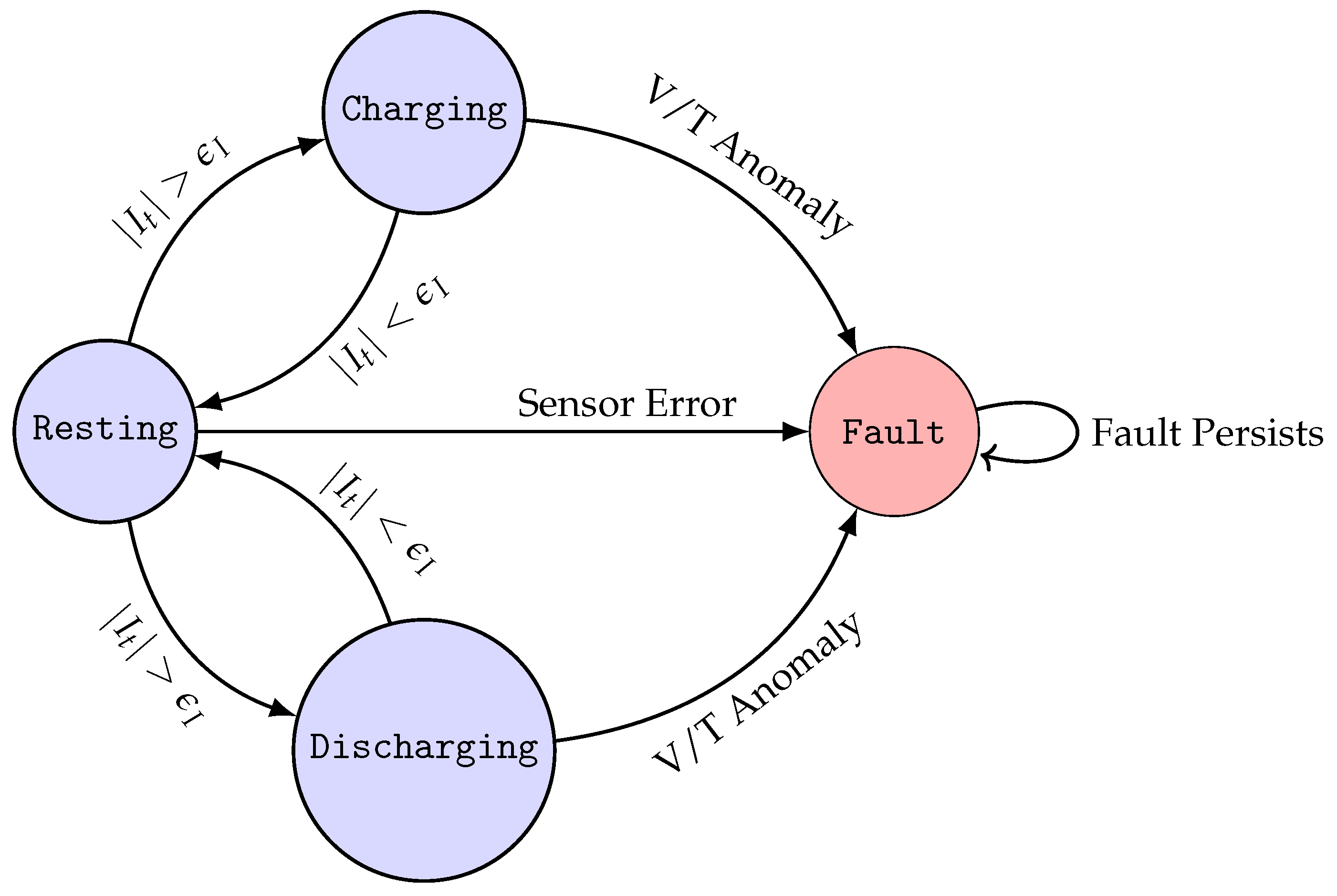
The finite state automaton (FSA) is carefully designed to model discrete battery operating modes and apply logical transitions based on predefined thresholds and physical rules (Figure 5). This deterministic behavior ensures that the SOC predictions remain within physically fair boundaries, correcting potential anomalies from the raw ANN outputs.

The FSA is formally defined by a tuple $\mathcal{A}=(Q,\Sigma ,\delta ,q_0)$, where:

• Q is the finite set of discrete battery operational states: Charging, Discharging, Resting, Fault. These states represent fundamental modes of battery operation.
• $\Sigma$ is the alphabet of input signals. It contains real-time sensor measurements such as current ($I_t$), voltage ($V_t$), and temperature ($T_t$). These inputs guide the state transitions.
• $\delta :Q\times \Sigma \to Q$ is the state transition function, which maps a current state and an input symbol to a next state. This function includes the logical rules that govern battery mode changes.
• $q_0$ is the initial state of the battery. It is typically determined at the beginning of monitoring.

The transitions between these states are governed by simple, yet physically built, rules. For instance, a transition rule to determine the Resting state is defined as follows:

$$\mathtt{Discharging}\to \mathtt{Resting}\mathrm{if}|I_t|<{ϵ}_I(\mathrm{e.g.},{ϵ}_I=0.05A)$$

This rule means that if the absolute current falls below a predefined small threshold (${ϵ}_I$), then the battery is considered to be in Resting state, where no particular charging or discharging occurs. The threshold ${ϵ}_I$ is a critical parameter that is determined experimentally from the large battery discharge characteristic analysis to accurately capture inactive periods. Other rules include state transitions to Charging (if $I_t>{ϵ}_I$), Discharging (if $I_t<-{ϵ}_I$), and Fault (e.g., if voltage or temperature exceeds safety limits, or if SOC exhibits physically impossible conditions). This clear definition of these states and transitions ensures a robust and interpretable framework for the identification of battery modes.

To ground the FSA thresholds in experimentally supported practice, we align each rule with recent Li-ion charge protocols. Resting: we detect near-zero current with $|I_t|<{ϵ}_I$ and set ${ϵ}_I=0.05,\mathrm{A}$, which lies within the common CC–CV termination band [39,40]. Charging: asserted when $I_t>{ϵ}_I$; during this state, we enforce sign consistency (SOC must increase) and a coulomb-counting rate cap $|\Delta \mathrm{SOC}|\le \left|I\right|,\Delta t/C_n$ per step [40]. Discharging: asserted when $I_t<-{ϵ}_I$ with the symmetric sign-consistency requirement (SOC must decrease) and the same rate cap [40]. Fault: triggered if the per-cell voltage exceeds the manufacturer’s charge-termination limit or if temperature departs from the safe envelope (operating within ∼0–45 °C and keeping cells below ∼45 °C during charging), as reported by recent experimental campaigns [39,41].

2.3. Hybrid ANN-FSA Integration

The core innovation in this framework lies in improving the robustness and physical consistency of SOC estimation. It is done by dynamically integrating each of the three ANN models with an FSA. The FSA continuously tracks the operational mode of the battery and applies logical consistency checks. It either modifies or validates ANN-based SOC predictions according to the current system state. This merged framework serves as a post-processing filter, ensuring that outputs stick to known physical behaviors (Figure 6).

Because a feedforward neural network (FFNN) has no internal memory, the FFNN+FSA branch derives its SOC estimate solely from the instantaneous input vector. This stateless nature makes the raw FFNN sensitive to noise and prone to overreacting to sudden, potentially false, system transitions. To handle this, when combined with an FSA, the FFNN’s raw output (${\widehat{\mathrm{SOC}}}_t^{\mathrm{FFNN}}$) is filtered or constrained. Particularly, it is done during states where instant estimates might be unreliable (e.g., such as a near-zero current Resting state). Under extreme conditions, where raw FFNN predictions might suggest an impossible SOC increase during discharge, the FSA can cap the SOC change rate or correct the value to ensure it adheres to a physically plausible trend. In such cases, the FSA can apply stability by maintaining the previous SOC value. The general hybrid calculation for FFNN is as follows:

$${\widehat{\mathrm{SOC}}}_t={\mathcal{G}}_{\mathrm{FSA}}({\widehat{\mathrm{SOC}}}_t^{\mathrm{FFNN}},q_t)$$

(4)

where ${\mathcal{G}}_{\mathrm{FSA}}$ represents the state-specific filtering function applied by the FSA. $q_t$ is the current state determined by the FSA.

LSTM+FSA models can still accumulate errors or produce physically unstable SOC jumps during sudden state changes (e.g., a rapid Charging-to-Rest transition or an unexpected discharge event). However, it is highly effective in processing temporal correlations due to its memory mechanisms. To smooth LSTM estimations and position them with physical expectations, the FSA is used to restrict or adjust predictions, especially when the raw output of LSTM suggests a physically implausible SOC change (e.g., a sudden increase in SOC during discharge). The FSA actively monitors transitions for unexpected conditions from arising, such as Charging → Fault. And also, it applies smoothing filters based on the current mode, preventing nonphysical deviations. For example, if the temperature or voltage exceeds safe limits during fast charging, the FSA immediately flags a ‘Fault‘ state and adjusts the SOC prediction, preventing potentially dangerous and physically impossible extrapolations.

The 1D-CNN+FSA model uses the 1D-CNN’s ability to capture oscillations and local patterns. However, the CNN’s sensitivity to window characteristic inputs means that long idle periods or gentle sensor noise during a Resting state could potentially trigger false alarms or unnecessary changes in its predictions. To address this issue and enhance stability, the 1D-CNN model is compatibly merged with an FSA. The FSA can halt or adjust CNN-based predictions during stable states like Resting, where SOC should rather remain constant or change very slowly. This hybrid usage explicitly applies output stability and domain-specific constraints:

The 1D-CNN+FSA model uses the 1D-CNN’s ability to capture oscillations and local patterns. However, the CNN’s sensitivity to window characteristic inputs means that long idle periods or gentle sensor noise during a Resting state could potentially trigger false alarms or unnecessary changes in its predictions. To address this issue and enhance stability, the 1D-CNN model is compatibly merged with an FSA. The FSA mitigates this by suppressing CNN-based predictions during a stable Resting state, thereby preventing noise-induced false alarms and ensuring output stability. This hybrid usage explicitly applies output stability and domain-specific constraints:

$${\widehat{\mathrm{SOC}}}_t=\left\{\begin{array}{cc}{\widehat{\mathrm{SOC}}}_t^{\mathrm{CNN}}\hfill & \mathrm{if}{q}_t\in \{\mathtt{Charging},\mathtt{Discharging}\}\hfill \\ {\widehat{\mathrm{SOC}}}_{t-1}\hfill & \mathrm{if}{q}_t=\mathtt{Resting}\hfill \end{array}\right.$$

Here, if the battery is in a Resting state, the SOC is maintained at its previous value ($\widehat{\mathrm{SOC}}t-1$), preventing false oscillations.

In substance, the hybrid structure formed by merging each ANN model with an FSA provides a robust mechanism that applies state transition logic, acts as a noise filter, and updates unsteady SOC values. This dual-layered approach significantly improves the stability and reliability of the system to estimate the SOC value. Furthermore, this design allows for the independent training of ANN models and the integration of FSA layers. The design also offers flexibility in deployment and future system enhancements.

2.4. Supervisor-Driven Model Selection

In this section, we introduce two distinct supervisory decision techniques: a rule-based supervisor and a reinforcement learning (RL)-based supervisor to enhance the robustness, adaptability, and overall energy efficiency of the proposed SOC-estimation framework. The primary responsibility of these supervisors is to intelligently and dynamically select the most feasible hybrid model (FFNN+FSA, LSTM+FSA, or 1D-CNN+FSA) at each time step. This selection is based on the characteristics of the input data and the historical performance of each candidate model. Critically, these supervisors are designed to be resilient under extreme conditions (e.g., rapid charging/discharging or significant temperature fluctuations) by leveraging signal heuristics and learned policies to choose the model best suited for maintaining physical constraints and estimation stability.

2.4.1. Rule-Based Supervisor Design

This supervisor operates on a set of predefined rules derived from wide domain knowledge and statistical heuristics of battery behavior. For each incoming observation sequence ${\mathbf{X}}_{t-n:t}$, specific statistical features are computed. These features include variance, mean gradient, and standard deviation of current (I), voltage (V), and temperature (T) signals over the observation sequence (Figure 7). The way for model selection based on these features is performed as follows:

• If $\mathrm{Var}\left(I_{t-n:t}\right)<{\epsilon }_1$ and $\mathrm{Var}\left(V_{t-n:t}\right)<{\epsilon }_2$: This condition indicates a relatively stable or Resting state with minimal current and voltage changes. In such scenarios, the FFNN+FSA model is selected due to its simplicity and efficiency, as complex temporal or spatial feature extraction may not be necessary. The thresholds ${\epsilon }_1$ and ${\epsilon }_2$ are experimentally determined based on thorough offline training data analysis to set out stable conditions.
• If strong temporal deviation or cyclical trends are detected (e.g., stable increase/decrease in I/V over time, characteristic of charging/discharging cycles): The LSTM+FSA model is selected. LSTMs are inherently designed to capture and support such long-term temporal dependencies and patterns. Thus, they provide more accurate predictions during dynamic operations. This rule is crucial for managing fast charging or discharging cycles, where the long-term memory of LSTM prevents cumulative errors and ensures a physically consistent SOC trajectory.
• If input shows frequent local spikes or short-term transients (e.g., sudden current spikes during dynamic loads or regenerative braking): The 1D-CNN+FSA model is selected. Moreover, 1D-CNNs are better at identifying and processing localized patterns and rapid changes within time-series data. This aspect is making them robust to noisy or rapidly unstable inputs. This is particularly important during scenarios with large temperature fluctuations or sudden load changes, where the 1D-CNN’s feature extraction is more effective at discerning these local anomalies.

The thresholds ${\epsilon }_1,{\epsilon }_2$ (e.g., experimentally set at 0.01 A for current variance and 0.005 V for voltage variance) are precisely determined based on comprehensive offline training data analysis and validation. Here, we aim to optimize the classification of operational states. These rules and thresholds, while fixed, serve as a first line of defense against extreme conditions by ensuring that the most suitable model for a given dynamic state is always chosen.

A meta-feedback module is integrated within this supervisor to enable a degree of non-learning-based adaptation. This module continuously saves the prediction error history of each hybrid model. At every time step t, the actual SOC value is compared with the predicted ${\widehat{\mathrm{SOC}}}_t$ of the selected model $M_t$, and the absolute error $e_t=|{\widehat{\mathrm{SOC}}}_t-{\mathrm{SOC}}_t|$ is stored. A “decreasing memory score” (exponentially weighted moving average of errors) is computed for each model. This calculation is performed as follows:

$${\overline{E}}_t^{\left(i\right)}=\alpha ·e_t^{\left(i\right)}+(1-\alpha )·{\overline{E}}_{t-1}^{\left(i\right)}$$

(5)

where $i\in \{1,2,3\}$ corresponds to the FFNN+FSA, LSTM+FSA, and 1D-CNN+FSA hybrid models, respectively. The forgetting factor $\alpha$ ($0<\alpha <1$, e.g., $\alpha =0.1$) controls the influence of recent errors versus past errors. This cumulative score guides the supervisor in selecting models that have historically exhibited a lower error rate for similar input data characteristics. In this way, an experience-based approach that has a non-learning adaptation strategy can be effectively enabled. The process of this rule-based supervisor at each step is systematically executed as follows:

(1)

Statistical feature extraction: Extract predefined statistical features (variance, mean gradient, standard deviation) from the current input signal sequence (${\mathbf{X}}_{t-n:t}$).

(2)

Rule-based condition evaluation: Evaluate the predefined rule-based conditions to identify and index the potentially suitable models for the current operating conditions.

(3)

Meta-performance score check: Consult the saved meta-performance scores (${\overline{E}}_t^{\left(i\right)}$) for the models identified in the previous step. The model with the lowest previous error score among the feasible candidates is selected as the final model.

(4)

SOC prediction: The input data is then sent into the selected hybrid model (e.g., LSTM+FSA) for SOC prediction

This design provides several advantages, as follows: (i) it keeps high modularity by separating model selection from individual model operation; (ii) it allows for interpretable decision-making, as the rules are explicitly defined; and (iii) it provides a clear guide and base for future works, including more advanced supervisors like reinforcement learning agents.

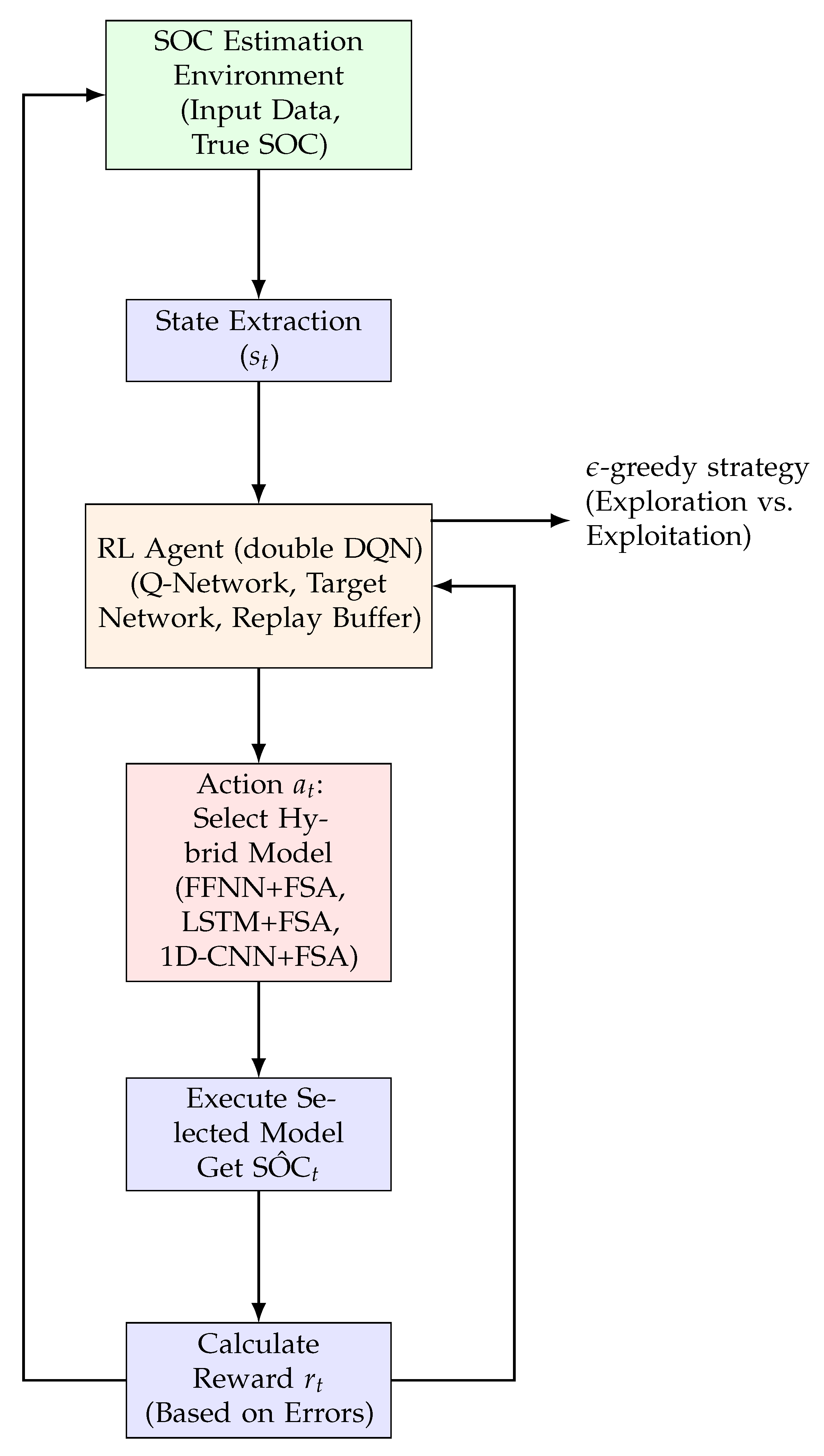
2.4.2. Reinforcement Learning-Based Supervisor Design

The second supervisor strategy is based on a reinforcement learning (RL) approach to handle the limitations of fixed rules and further enhance adaptive decision-making (Figure 8). The fundamental principle here is to enable the supervisor to learn optimal model selection policies through continuous trial-and-error relations with the dynamic SOC estimation environment. This approach is particularly powerful under extreme conditions, where fixed, heuristic rules may fail. The RL agent is not bound by pre-defined thresholds; instead, it learns from a history of errors and past actions to dynamically choose the most robust model for a given, potentially unseen, operational state. A double deep Q-network (DQN) architecture is used for training this supervisor. It was chosen for its stability and improved accuracy in estimating Q-values, reducing the overestimation bias inherent in standard DQN.

Each decision step is explained in context by a comprehensive 9-dimensional state vector ($s_t$) that summarizes critical model-specific and historical prediction errors. The state vector is precisely defined as follows:

$$s_t=[{\mathrm{MAE}}_{\mathrm{FFNN}},{\mathrm{MAE}}_{\mathrm{LSTM}},{\mathrm{MAE}}_{\mathrm{CNN}},{\mathrm{RMSE}}_{\mathrm{FFNN}},{\mathrm{RMSE}}_{\mathrm{LSTM}},{\mathrm{RMSE}}_{\mathrm{CNN}},{\mathrm{Prev}}_{\mathrm{FFNN}},{\mathrm{Prev}}_{\mathrm{LSTM}},{\mathrm{Prev}}_{\mathrm{CNN}}]$$

(6)

Here, $\mathrm{MAE}·$ and $\mathrm{RMSE}·$ represent the mean absolute error and root mean square error of each respective hybrid model over a recent past window. ${\mathrm{Prev}}_{\mathrm{FFNN}},{\mathrm{Prev}}_{\mathrm{LSTM}}$, and ${\mathrm{Prev}}_{\mathrm{CNN}}$ are one-hot encoded binary indicators specifying which model was selected in the previous time step ($t-1$). This provides the RL agent with crucial information about its rapid past actions and their impact.

The action space $A=\{0,1,2\}$ is discrete, and it corresponds to the selection of one of the three available hybrid models: 0 for FFNN+FSA, 1 for LSTM+FSA, and 2 for 1D-CNN+FSA. A carefully designed reward function is essential to guide the learning process of the RL agent towards achieving accurate and stable SOC estimations. The reward function is formulated as a negative weighted sum of two critical error metrics:

$$r_t=-\left(0.6·{\mathrm{MAE}}_t+0.4·{\mathrm{RMSE}}_t\right)$$

(7)

This formulation verifies that the agent is motivated to minimize both absolute prediction error (MAE, which provides a direct measure of average error magnitude in the same units as the target variable) and root absolute prediction error (RMSE, which penalizes larger errors more heavily). The weights (0.6 for MAE, 0.4 for RMSE) are chosen to highlight the importance of relative accuracy while also accounting for the magnitude of deviations.

${\mathrm{MAE}}_t$ and ${\mathrm{RMSE}}_t$ are computed on SOC, which is naturally bounded in [0, 1], so the two terms are commensurate without additional normalization. We set the convex weights to $0.6$ (MAE) and $0.4$ (RMSE) to reflect building-energy priorities. MAE aligns with average energy accounting in BEMS scheduling, while RMSE retains aversion to rare large spikes that can compromise safety or downstream control. Equivalently, the reward can be written as $-\left(\lambda {\mathrm{MAE}}_t+(1-\lambda ){\mathrm{RMSE}}_t\right)$ with $\lambda =0.6$. The code exposes $\lambda$ as a configuration parameter so practitioners can reproduce alternative trade-offs (e.g., more spike-averse policies with smaller $\lambda$) without changing the architecture.

The training process of the RL supervisor is managed offline. This training is done based on historical SOC estimation sequences from the NASA dataset. The double DQN network is integrated into a standard training loop for stable convergence and effective learning. The $ϵ$-greedy strategy is adopted to balance analysis (i.e., trying new actions to discover better policies) and deployment (i.e., choosing actions known to yield high rewards). The analysis rate $ϵ$ is gradually reduced from an initial value of 1.0 down to 0.05 over the training episodes. This aspect allows the agent to initially discover the environment and then filter its decision-making. The trained RL supervisor then selects the model with the highest estimated Q-value for a given state during inference. This supervisor enables a dynamic adaptation to varying signal data and demonstrates improved selection accuracy when compared with the fixed rule-based strategy. This adaptive capability is particularly valuable in high-variance or unpredictable operational scenarios. This is because the supervisor has already associated situational models, such as rapid voltage drops or high-temperature increases, with the models that performed best in the past. This ensures that the selected model maintains physical constraints and predictive stability.

To ensure reproducibility, the hyperparameter configuration of the double DQN supervisor is reported in

Table 1. Hyperparameter configuration of the double DQN supervisor.

Parameter	Value
Optimizer	Adam
Learning rate	0.001
Discount factor ($\gamma$)	0.99
Replay buffer size	10,000
Batch size	64
Target network update	Every 500 steps
Exploration ($ϵ$)	Gradually reduced from 1.0 to 0.05
Loss function	Mean Squared Error (MSE)
Gradient clipping	1.0
Training epochs	100

. The Q-network and target network each consist of two hidden layers with 64 and 32 units, respectively, using ReLU activation functions. The Adam optimizer is employed with a learning rate of 0.001. Training was conducted for 100 epochs, with an $ϵ$-greedy exploration policy decaying linearly from 1.0 to 0.05. Gradient clipping was applied at 1.0 to stabilize updates.

3. Results

In this section, we present a comprehensive analysis of the experimental setup and the quantitative results obtained from the proposed modular hybrid SOC-estimation framework. We precisely evaluate the performance of individual ANN-FSA models. Then, we illustrate the solid benefits derived from the supervisor strategy and highlight the overall contribution of the FSA under various operating scenarios.

3.1. Experimental Setup

This subsection details the experimental setup, covering the chosen datasets, feature engineering strategies, training configurations for the ANN models, and the evaluation metrics employed. The NASA battery dataset was selected for the robust evaluation of the proposed models. This publicly available dataset, widely recognized and widely used in battery health estimation research, was obtained from the NASA Prognostics Center of Excellence (PCoE) [42]. It includes long-term cycling data for lithium-ion (Li-ion) cells, which were subjected to a variety of load profiles and environmental temperatures. The measurements—current, voltage, and temperature—were sampled at a frequency of 1 Hz over extended periods, providing a rich source for dynamic SOC estimation. While this dataset provides a strong foundation for a direct comparison with numerous published works, it is important to note that it does not encompass the full spectrum of real-world variables, such as seasonal changes or varying humidity levels. However, the variety of discharge and charge cycles and thermal profiles provides a strong basis for evaluating our model’s performance and generalizability under significant operational variations.

For all ANN-based models, the input features at time step t were carefully designed to capture both real-time conditions and historical context:

$${\mathbf{x}}_t=[I_t,V_t,T_t,\Delta Q_t,C_t]$$

(8)

where $I_t$ is the real-time current, $V_t$ is the real-time voltage, $T_t$ is the real-time temperature, $\Delta Q_t$ represents the accumulated charge change from the initial state (i.e., calculated via Coulomb counting, presenting a raw estimate of charge consumed/delivered), and $C_t$ is the cycle number (i.e., indicating battery aging and capacity degrade). For the LSTM and 1D-CNN models, which fundamentally process sequential data, input windows of n = 20 time steps were constructed. This window size was statistically determined to be optimal for capturing relevant temporal dependencies and local patterns without introducing overly computational load, creating input tensors denoted as ${\mathbf{X}}_{t-n:t}$. Furthermore, findings from recent building-scale battery-EMS work suggest that comparable windows are adequate to capture the main load–storage dynamics [43].

The architectural hyperparameters for each of the three ANN models were determined empirically through a series of pilot experiments. This process aimed to balance model complexity and computational efficiency while preventing overfitting. The configurations, finalized after this exploratory phase, are as follows:

• FFNN: The network consists of two hidden layers with 64 and 32 neurons, respectively, and utilizes the ReLU activation function. The Adam optimizer with a learning rate of 0.001 was used for training.
• LSTM: This model comprises a single LSTM layer with 64 units, followed by a dense output layer. This configuration was chosen to effectively capture long-term temporal dependencies without introducing excessive model parameters. It is crucial for accurate SOC monitoring during complex discharge/charge cycles.
• 1D-CNN: This architecture includes one convolutional layer with 32 filters and a kernel size of 3, designed to capture local features. This is followed by a max pooling layer and dense regression layers. The kernel size of 3 was selected as it is a common and effective choice for extracting short-term patterns in time-series data.

Each model was subjected to training for 100 epochs. The batch size was set to 64 due to balancing training stability and computational speed. The mean squared error (MSE) was used as the loss function for guiding the models to minimize the squared difference between predicted and true SOC values. The dataset was structurally split into 80% for training and 20% for testing to ensure a fair evaluation of generalization capability. To prevent overfitting and enhance model robustness, early stopping was carefully applied based on the validation loss. Training was terminated when performance on a reserved validation set stopped improving.

The standard and robust evaluation metrics were used to extensively evaluate the performance of the proposed hybrid models and the capability of the supervisor-based selection strategy. These metrics as a whole provide findings into both prediction accuracy and system stability that are crucial for practical battery management systems.

• Root mean square error (RMSE): This metric measures the average scale of the error between the predicted (i.e., ${\widehat{\mathrm{SOC}}}_t$) and actual SOC (i.e., $SO{C}_t$) values. RMSE is particularly sensitive to large errors. This metric suppresses errors more heavily due to the squaring of differences. It is expressed as follows:

  $$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{t=1}^N{({\mathrm{SOC}}_t-\widehat{\mathrm{SOC}}t)}^2}$$

  (9)
• Mean absolute error (MAE): MAE measures the average of the absolute differences between predicted and true SOC values. It offers a straightforward and fundamental measure of overall accuracy. This metric directly reflects the average magnitude of the errors in the same units as the SOC. It is calculated as follows:

  $$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum {t=1}^N\left|{\mathrm{SOC}}_t-{\widehat{\mathrm{SOC}}}_t\right|$$

  (10)

By using these metrics, we ensure a robust and interpretable evaluation of the proposed framework.

3.2. Comparative Performance of Hybrid ANN Models with FSA Correction

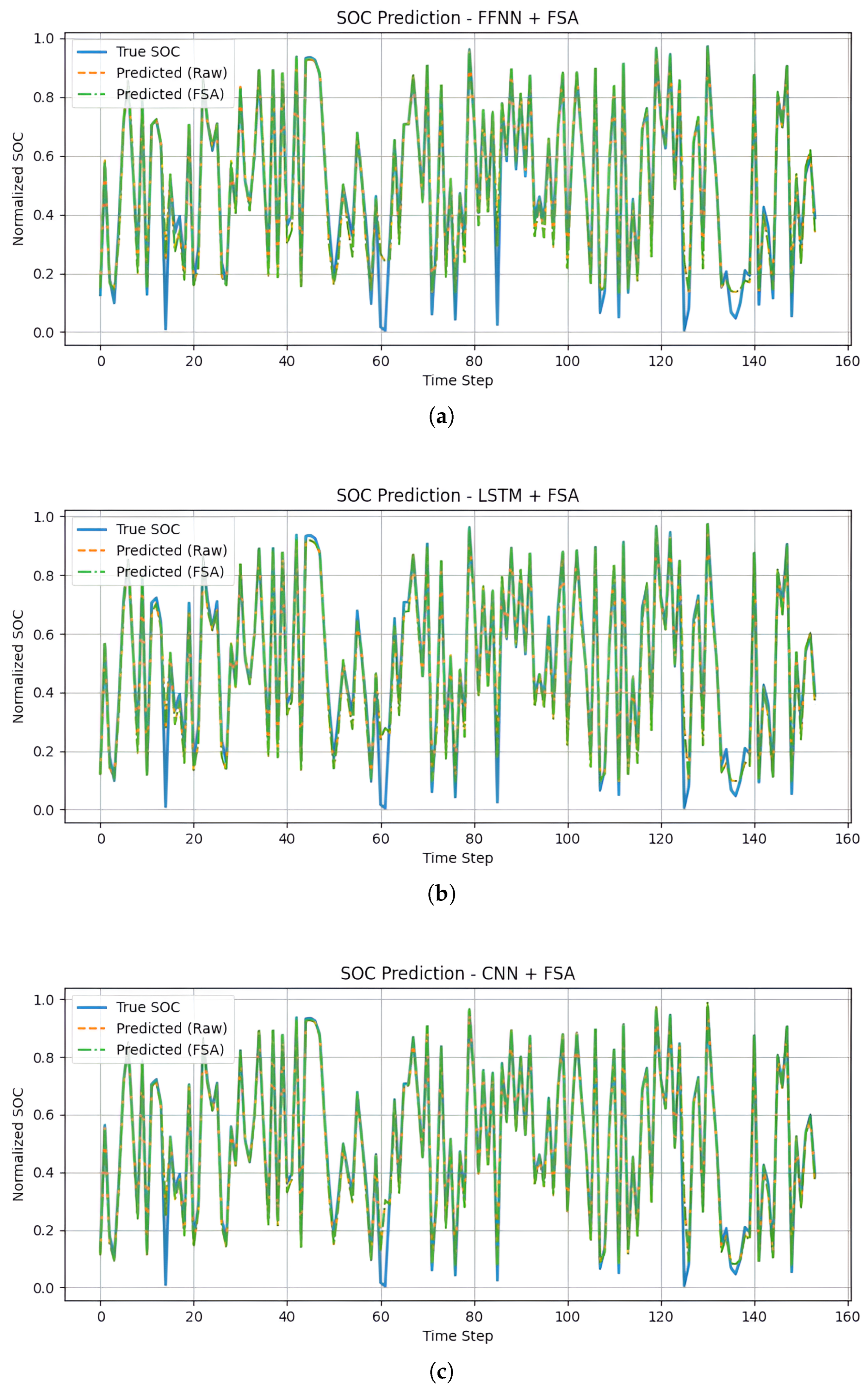
This section presents a detailed evaluation of the hybrid SOC estimation models. The integration of FSA is crucial for maintaining physical feasibility and stability in the SOC estimations. The FSA module corrects potential anomalies from raw ANN outputs. We consider three primary hybrid configurations, namely, FFNN+FSA, LSTM+FSA, and 1D-CNN+FSA.

Figure 9 provides an illustrative representation of the predicted SOC values from each hybrid model plotted against the true SOC values. Each sub-graph clearly identifies differences between the raw ANN predictions and their corresponding FSA-corrected equivalents. The visual evidence strongly indicates how the FSA correction effectively smooths sudden, non-physical transitions in the raw predictions and applies commitment to fundamental physical constraints of battery dynamics. This is particularly noticeable in regions where raw ANN outputs show unstable jumps or deviations from the true SOC trend.

Table 2. Performance metrics of raw ANN models without FSA correction.

Model	RMSE (dim.)	MAE (dim.)
FFNN	0.0598	0.0382
LSTM	0.0571	0.0337
1D-CNN	0.0482	0.0293

and

Table 3. Performance metrics of hybrid ANN models with FSA correction.

Model	RMSE (dim.)	MAE (dim.)
FFNN+FSA	0.0562	0.0318
LSTM+FSA	0.0523	0.0301
1D-CNN+FSA	0.0434	0.0185

quantitatively summarize the overall accuracy of each raw ANN model (i.e., without FSA correction) and its corresponding hybrid model (i.e., with FSA correction) using the RMSE and MAE evaluation metrics. Here, “dim.” is the abbreviation of dimensionless, as SOC is presented in normalized form and is a dimensionless value (between 0 and 1) in our analysis. The RMSE and MAE metrics are also dimensionless. Thus, we have represented the units of these error metrics accordingly.

A direct comparison between Table 2 and Table 3 shows a reliable improvement across all models with the integration of FSA. The 1D-CNN+FSA model notably achieved the lowest RMSE (0.0434) and MAE (0.0185) values among all three hybrid configurations. This hybrid model achieves the best overall accuracy and robustness in SOC estimation. This can be caused by the effectiveness of 1D-CNN in capturing complex local patterns and features. With this optimal advantage, this network results in highly refined predictions when it is combined with the logical consistency of the FSA. The LSTM+FSA model also demonstrated strong performance (RMSE: 0.0523, MAE: 0.0301), particularly better in capturing complex temporal runs due to its inherent memory capabilities. While the FFNN+FSA model showed relatively higher error rates (RMSE: 0.0562, MAE: 0.0318), it still achieved acceptable results when we especially consider its architectural simplicity and serving as a standard. These quantitative results clearly confirm the significant benefit of FSA correction in stabilizing raw ANN predictions, especially when individual ANN models produce sudden, noisy, or physically unrealistic outputs when the system is under highly dynamic current conditions. The collective analysis of both visual representations in Figure 9 and the quantitative metrics underscores the strengths and practical utility of each hybrid approach.

3.3. Supervisor Robustness and Case Analysis

In this section, we evaluate the overall estimation performance of each hybrid model under the effect of two distinct supervisory strategies: the rule-based supervisor and the reinforcement learning (RL)-based supervisor. The average error metrics, specifically MAE and RMSE, were calculated across all test data segments. The results are presented to assess the robustness and adaptability of the complete framework.

Table 4. Supervisor-wise average error comparison for each model.

Supervisor	Model	RMSE (dim.)	MAE (dim.)
Static Best Model	1D-CNN+FSA	0.0434	0.0185
Rule-based	FFNN+FSA	0.0562	0.0318
	LSTM+FSA	0.0523	0.0301
	1D-CNN+FSA	0.0434	0.0185
	Overall Performance	0.0421	0.0179
RL-based	FFNN+FSA	0.0541	0.0308
	LSTM+FSA	0.0493	0.0294
	1D-CNN+FSA	0.0412	0.0174
	Overall Performance	0.0405	0.0172

precisely outlines the combined performance metrics for each hybrid model when managed by either the rule-based or the RL-based supervisor.

Relative to the static best single model (1D-CNN+FSA; see Table 4), the RL-based supervisor reduces RMSE from 0.0434 to 0.0405 (absolute $-0.0029$, $-6.7\%$) and MAE from 0.0185 to 0.0172 (absolute $-0.0013$, $-7.0\%$). Compared to the rule-based supervisor (Table 4), RL yields $-3.8\%$ RMSE (0.0421→0.0405) and $-3.9\%$ MAE (0.0179→0.0172). The FSA correction itself contributes substantial head-wise gains versus the raw ANNs (by comparing Table 2 vs. Table 3): 1D-CNN RMSE $-10.0\%$; MAE $-36.9\%$; LSTM RMSE $-8.4\%$; MAE $-10.7\%$; FFNN RMSE $-6.0\%$; and MAE $-16.8\%$. Because SOC is normalized to [0, 1], an absolute error of $0.01$ equals one percentage point of SOC. For a battery with nominal energy $E_{\mathrm{nom}}$ (kWh), this is $0.01E_{\mathrm{nom}}$ kWh of scheduling error. Hence, the percentage reductions reported above translate linearly into proportional reductions in energy misallocation in BEMS scheduling.

The results in Table 4 provide a definitive comparison. The 1D-CNN+FSA model shows the most accurate performance (RMSE: 0.0434, MAE: 0.0185) when run statically across the entire test set. The rule-based supervisor achieves a lower overall error (RMSE: 0.0421, MAE: 0.0179), and the RL-based supervisor yields the most accurate results of all (RMSE: 0.0405, MAE: 0.0172).

This result provides strong evidence that the dynamic model selection strategy yields a superior overall performance that is demonstrably better than any single model could achieve on its own.

A critical observation from Table 4 is that the RL-based supervisor produces better performance for each individual hybrid model compared to the rule-based supervisor (e.g., 1D-CNN+FSA’s RMSE improves from 0.0434 to 0.0412). This significant improvement is likely attributed to the RL-based supervisor’s adaptive and context-aware selection framework. The optimal decisions are made by this mechanism based on real-time error feedback and decision history rather than fixed rules. This confirms that the supervisor is not a simple component, but a core strategy that enhances robustness and accuracy by dynamically adapting the framework to constantly changing conditions.

Model Selection Frequency and Bias

Analyzing the frequency with which each hybrid model is selected by the supervisor during the estimation process provides further insight into its decision biases and how different strategies focus on models under varying operational conditions. This metric implicitly reflects the supervisors’ learned or programmed preferences.

Table 5. Model selection frequency and average error metrics (RMSE, MAE) when a model is selected, for rule-based and RL-based supervisors.

Supervisor	Metric	FFNN+FSA	LSTM+FSA	1D-CNN+FSA
Rule-based	Selection Frequency (%)	22.8	37.5	39.7
	Avg. RMSE (dim.) (when selected)	0.0562	0.0523	0.0434
	Avg. MAE (dim.) (when selected)	0.0318	0.0301	0.0185
RL-based	Selection Frequency (%)	19.7	38.6	41.7
	Avg. RMSE (dim.) (when selected)	0.0541	0.0493	0.0412
	Avg. MAE (dim.) (when selected)	0.0308	0.0294	0.0174

presents both the model selection frequency distribution for both the rule-based and RL-based supervisors and the average RMSE and MAE of each model when it was selected. This combined view offers a crucial viewpoint on both the behavioral bias of each supervisor and the relative performance of the selected models.

Both supervisors exhibit a stronger preference towards the LSTM+FSA and the 1D-CNN+FSA models. This observed bias is consistent with the more effective overall performance of these models as shown in Table 4. Notably, the RL agent demonstrates an even stronger priority for the 1D-CNN+FSA hybrid model (i.e., indicated by a higher selection frequency of 1D-CNN+FSA under the RL-based supervisor), which aligns perfectly with its superior performance metrics. This suggests that the RL agent’s learning process effectively identifies and utilizes the strengths of the best-performing model while simultaneously minimizing selection errors over time. This experimental evidence further validates the effectiveness of reinforcement learning in achieving highly optimized and adaptive supervisory control for SOC estimation.

3.4. High-Error Case Analysis

While error measurements on the performance of designed models provide a positive impression, measuring their performance under challenging conditions is crucial for real-world applications. Thus, we managed a high-error case analysis by identifying the top 10 predictions with the highest absolute error for both the rule-based and RL-based supervisors. Each entry in these analyses includes the selected model, its raw prediction, the FSA-corrected output, the true SOC value, and the absolute error.

Table 6. Top 3 samples with the highest absolute error under rule-based supervision.

Time Step	Model	True SOC	Raw Pred.	FSA Corr.	Abs Err.
87	CNN	0.823	0.762	0.791	0.033
116	LSTM	0.815	0.753	0.767	0.048
132	FFNN	0.789	0.861	0.843	0.054

presents these worst-case examples under the rule-based supervisor.

Similarly,

Table 7. Top 3 samples with the highest absolute error under RL-based supervision.

Time Step	Model	True SOC	Raw Pred.	FSA Corr.	Abs Err.
87	CNN	0.823	0.766	0.798	0.026
116	LSTM	0.815	0.760	0.785	0.031
132	FFNN	0.789	0.850	0.834	0.045

presents the worst 10 estimations when managed by the RL-based supervisor.

A detailed review of both tables reveals that the most extreme errors mostly emerge during quick and highly nonlinear SOC changes or during complex transitional phases (e.g., sudden load variations, sudden charge/discharge initiations/terminations). These scenarios essentially exhibit biases in the predictions of the models used due to the rapid changes in the dynamics of battery-powered systems. Some biases persist despite the integration of the FSA. This demonstrates that individual models inherently exhibit their inherent limitations when faced with uncertain or rapidly changing conditions. However, a crucial comparative insight is observed: the RL-based supervisor generally exhibits slightly lower peak errors in these worst-case scenarios compared to the rule-based supervisor. This indicates the RL agent’s more accurate ability to adaptively select the more appropriate sequence of models, even in challenging edge cases. This adaptability is a key advantage of the learning-based supervisory strategy in mitigating extreme prediction inaccuracies.

3.5. Comparison with EKF-Based Methods

To further validate the effectiveness and superiority of the proposed hybrid ANN+FSA framework, we conducted a rigorous comparative analysis against the classical extended Kalman filter (EKF) and a hybrid EKF+ANN model. Both comparative models were evaluated on the same NASA dataset and under identical experimental conditions to ensure a fair assessment. The EKF+ANN model, a common hybrid approach, utilizes the outputs from the EKF as augmented features for a subsequent ANN regressor, aiming to combine the strengths of model-based filtering with data-driven learning.

Table 8. Comparison of ANN+FSA models with EKF and EKF+ANN.

Model	RMSE (dim.)	MAE (dim.)
EKF	0.0611	0.0349
EKF+ANN	0.0583	0.0332
FFNN+FSA	0.0562	0.0318
LSTM+FSA	0.0523	0.0301
1D-CNN+FSA	0.0434	0.0185

meticulously presents the root mean square error (RMSE) and mean absolute error (MAE) metrics for each configuration, allowing for a direct quantitative comparison.

As clearly demonstrated in Table 8, all proposed ANN+FSA hybrid models consistently outperform both the standalone EKF and the EKF+ANN hybrid in terms of both RMSE and MAE. Specifically, the 1D-CNN+FSA configuration achieves the lowest overall error among all tested models, including the EKF-based approaches. This superior performance of 1D-CNN+FSA can be attributed to its exceptional capability in capturing complex temporal dependencies inherent in battery discharge/charge profiles.

While the EKF+ANN hybrid model shows a substantial improvement over the standalone EKF, indicating the benefit of combining filtering with neural networks, it still remains less accurate than all the proposed ANN+FSA models. This clear difference highlights the distinct strength of the FSA in enforcing strict domain constraints and actively correcting unlikely SOC transitions that even feature-enhanced models like EKF+ANN may fail to robustly handle. EKF-based methods, while effective in state estimation for dynamic systems, can be sensitive to model inaccuracies and noise characteristics. This method may not inherently prevent physically impossible outputs without additional heuristic rules. The FSA, by design, provides a robust layer of physical validation.

Overall, these comparative results certainly confirm that combining data-driven ANN models with symbolic reasoning through FSA not only yields superior estimation accuracy but also critically maintains the physical validity of the SOC estimates. This framework demonstrably outperforms conventional filtering-based estimators across the key metrics. These results underscore the potential of the framework for reliable and robust battery management systems in real-world applications.

4. Discussion

Accurate real-time SOC estimation is a prerequisite for smart-building energy management systems, where battery storage must continuously buffer the stochastic output of on-site renewables and synchronize that generation with dynamic building loads. The presented hybrid methodology, integrating artificial neural networks (ANNs) with a finite state automaton (FSA) and a dynamic supervisory strategy, demonstrates promising and robust performance in the critical task of state-of-charge (SOC) estimation for lithium-ion batteries. The comprehensive results delineated in Section 3.2, Section 3.3, and Section 3.5 collectively corroborate the individual strengths of each constituent model, as well as the significant complementary improvements achieved through their strategic integration and the intelligent supervisor-driven model selection.

Our findings confirm that each ANN architecture plays a distinct role in the overall framework’s success. The feedforward neural network (FFNN) models proved most effective and efficient in stable, low-noise operating conditions, acting as a reliable baseline when battery dynamics are predictable. In contrast, long short-term memory (LSTM) networks consistently exhibited superior performance during sudden and complex transitional phases, a direct consequence of their inherent capacity to capture and leverage long-term temporal dependencies and historical context within the sequential data. The 1D convolutional neural network (1D-CNN) models, while showing strong capabilities in extracting structured local features, were observed to be susceptible to instability in highly dynamic or noisy transitional conditions if not properly managed. This vulnerability underscores the critical role of the FSA module, which consistently adds output regularization and stability. By enforcing physical constraints and reducing unrealistic estimation deviations, the FSA module significantly enhanced the physical validity and reliability of all raw ANN predictions, transforming potentially erratic outputs into robust SOC estimates.

The evolution of our supervisory strategy, from a rule-based approach to a reinforcement learning (RL)-based system, was pivotal in maximizing the framework’s adaptability. Initially, the rule-based supervisor provided a foundational and interpretable mechanism for model selection, operating on predefined heuristic thresholds and historical error trends. As detailed in Table 4 and the qualitative insights from Section 3.3, this strategic step yielded robust baseline performance and maintained clarity in decision-making. However, a significant limitation inherent to its design was its fixed decision criteria, which restricted its adaptability to unforeseen system dynamics or novel error feedback scenarios. This rigidity often meant suboptimal model selections in highly dynamic or atypical operating conditions where predefined rules might not perfectly apply.

To address this critical limitation, an RL-based supervisor, utilizing a double deep Q-network (DQN) architecture, was introduced and rigorously evaluated. This learning-based approach adaptively learned an optimal model selection policy by continuously interacting with the estimation environment, leveraging real-time error metrics and past decision outcomes. As vividly illustrated in Table 4 and further evidenced by the model selection frequency analysis (Table 5), the RL supervisor consistently demonstrated superior adaptive behavior. This supervisor exhibited an intelligent preference for the 1D-CNN+FSA model in dynamic intervals, directly correlating with its observed lowest average errors across multiple test scenarios. The ability of the RL agent to dynamically adjust its model preference, learning to exploit the strengths of the most suitable model for a given context, represents a significant leap in adaptability and overall accuracy.

The high-error case analysis (Table 6 and Table 7) further solidified the advantages of the RL-based supervisor. Even in the most challenging worst-case scenarios—typically characterized by rapid, highly nonlinear SOC changes or complex transitions—the RL supervisor maintained greater stability and exhibited slightly lower peak errors compared to its rule-based counterpart. This robust performance in outlier cases suggests that the RL agent successfully generalized its selection logic beyond fixed empirical rules, effectively utilizing prior context to make more informed decisions. This finding empirically establishes that learning-based approaches can indeed outperform fixed decision rules by dynamically adjusting to error profiles and environmental nuances. Nonetheless, it is important to acknowledge the inherent trade-offs associated with the learning-based approach, particularly its increased complexity and higher training cost. Key challenges included careful hyperparameter tuning, effective state representation design, and meticulous reward shaping to ensure stable and optimal learning. Furthermore, during initial training phases, occasional over-selection of suboptimal models (e.g., 1D-CNN in transient noisy conditions where another model might be momentarily better) was observed, indicating the need for robust exploration strategies and comprehensive training data.

A crucial aspect of our evaluation involved the comparison with conventional extended Kalman filter (EKF)-based methods, including a standalone EKF and a hybrid EKF+ANN model (Table 8). The results demonstrated that our proposed hybrid ANN+FSA models consistently outperformed both EKF and EKF+ANN across all key accuracy metrics. This highlights a fundamental advantage of integrating symbolic reasoning (i.e., FSA) with data-driven models. While EKF-based methods are powerful, they often rely on simplified linear approximations of battery dynamics and can struggle with inherent non-linearities and sensor noise without extensive tuning or additional heuristics. The FSA, conversely, provides a direct, rule-based mechanism for ensuring physical plausibility, effectively “clipping” or “correcting” outputs that deviate from realistic battery behavior, a capability not inherently present in standard EKF or even EKF+ANN models without explicit logical post-processing. This superior performance reinforces the value of incorporating explicit domain knowledge via FSA into data-driven SOC estimation.

To situate our results, we compare against two recent, application-relevant baselines. On the containerized BESS study of Zou et al.—who propose an attention-enhanced CNN–LSTM (A–CNN–LSTM)—the reported test errors are RMSE = 0.1076 and MAE = 0.0623 (SOC normalized to [0, 1]) [44]. Under the same normalization, our RL-supervised ANN+FSA achieves RMSE = 0.0405 and MAE = 0.0172, corresponding to ≈62% RMSE and ≈72% MAE reduction. In parallel, the field survey by Tian et al. emphasizes two open needs for SOC learning systems—physical constraint enforcement and online adaptivity [45]. Our design directly targets both: the FSA layer guarantees mode-consistent, physically plausible trajectories, while the double DQN supervisor adaptively switches among ANN heads, yielding lower error than any single estimator in high-variance regimes.

Concerning the computational complexity of the proposed model, it is necessary to highlight that the ANN models require computation during the prediction phase. It is worth noting that since these models are trained offline, the training cost does not directly affect the real-time performance of the system. During the prediction phase, the cost will remain low because the process involves making predictions on new data using an already-trained model. For example, FFNN has the lowest cost. LSTM and 1D-CNN, however, have a higher prediction cost compared to FFNN because they process sequential data. Nevertheless, when well-optimized and run on modern hardware, they can meet near real-time latency requirements. Additionally, since the proposed system runs only a single model selected by the supervisor instead of all ANN models simultaneously, the cost will remain at a manageable level. The FSA has the smallest computational cost within the system because it involves only a few logical rules and threshold comparisons. On the other hand, the double DQN is the component with the highest computational cost in the system. However, since its training is done offline, it does not affect the latency of the real-time system. Another explanation is that the prediction phase of a DQN model (i.e., choosing which action to take given a state vector) is generally equal to the prediction cost of a feedforward network. In summary, the prediction cost of our proposed model will be sufficient to meet the latency requirements of the SOC estimation process within the context of BMS management for smart buildings.

When considering the real-world applicability of our proposed model, it is important to note that it is a framework independent of the chemical composition of different batteries, such as Graphite Anodes [46] or Nickel-rich cathodes [47]. This is because the proposed model is not based on a physical battery model but instead relies on learning from sensor data. For example, since the ANN models in the proposed system are data-driven, they must be trained with data from different battery types to learn their unique dynamics. However, this training should not be perceived as a limitation. Instead, it is an indication of the model’s adaptability to various real-world scenarios. The FSA, independent of the battery’s chemistry, applies rule sets based on the fundamental physical constraints of all lithium-ion batteries. These constraints include, for example, the state of charge remaining between 0% and 100% and the voltage staying within a specific range. Since the supervisor’s task is to learn which ANN+FSA model yields the best result in a specific operational state, when it is trained with new battery data, it will automatically learn the best model selection policy based on the new battery’s dynamics, independent of its chemistry. In conclusion, the proposed framework is also applicable to battery types with different chemistries. However, for full implementation, the ANN models must be retrained with data from the new battery, and the FSA thresholds must be recalibrated.

In conclusion, the proposed ANN+FSA+Supervisor architecture stands out as both modular and highly adaptable. The rule-based supervisor, while offering clarity and a robust foundation, provides limited flexibility. In clear contrast, the RL-based supervisor significantly enhances adaptability and overall performance, especially in dynamic and unpredictable environments, by learning optimal model selection policies. Both supervisory mechanisms, critically, leverage the FSA layer to reduce error dissemination and ensure physical consistency, thereby contributing substantially to the robustness of the SOC estimation. This new perspective, validating the combination of statistical learning (ANN), symbolic filtering (FSA), and adaptive model selection (RL-based supervisor) for SOC estimation, underscores its significant potential applicability in complex, real-world battery management systems (BMSs).

Moreover, applying the modular SOC-estimation framework in building-integrated renewable energy systems could significantly enhance operational sustainability [48]. By enabling batteries to intelligently smooth out PV generation variability and support peak demand in a smart building, the framework helps minimize renewable energy curtailment while still meeting occupants’ energy needs. This positions the proposed approach as not only a battery management advancement but also a facilitator of greener, more resilient building energy management systems [49]. When deployed inside a building energy management system, the framework can act as the “battery intelligence” layer that coordinates PV-charging and building loads, thereby reducing renewable-energy curtailment and supporting greener, more resilient building microgrids [50,51,52].

Lastly, some limitations should be acknowledged. Our experiments rely on the publicly available NASA dataset to ensure full reproducibility. While this dataset is widely adopted in the SOC estimation literature and enables transparent benchmarking, it does not capture the full spectrum of operational conditions typical of smart buildings, such as intermittent charging due to unsteady photovoltaic availability or HVAC-driven discharging patterns. This limitation constrains the immediate external validity of our findings. To mitigate this, the authors plan an extension of validation to stationary storage datasets representative of EMS operation. In particular, such datasets would ideally capture building-integrated use cases with PV-driven charge patterns, load-following discharges, and seasonal variations. Future work will incorporate experimental campaigns on laboratory-scale stationary storage systems, or public datasets from building-integrated batteries as they become available, to validate the transferability of our approach to real smart-building environments.

For future work, integrating rule-based priors (e.g., initial policy guidance or safety constraints) with advanced learning-based adaptation could yield an even more powerful and robust hybrid approach, synergistically combining the interpretability of rules with the flexibility of learning.

5. Conclusions

This study proposed a novel hybrid state-of-charge (SOC) estimation framework designed for robust and accurate monitoring of lithium-ion batteries. By strengthening SOC accuracy under realistic operating conditions, this study advances the control toolbox needed for smart-building energy management systems that aim to maximize the self-consumption of locally produced renewable electricity. The framework’s core innovation lies in its modular integration of artificial neural networks (ANNs), a finite state automaton (FSA), and a dynamic supervisory methodology. This architecture enables diverse ANN models—specifically FFNN, LSTM, and 1D-CNN—to leverage their inherent strengths across various operating conditions, while the crucial FSA layer ensures physically valid output correction by filtering and constraining predictions within realistic bounds.

The application of two supervisory schemes to the ANN+FSA hybrids is evaluated. The rule-based supervisor implements a deterministic, interpretable policy for model selection derived from predefined performance thresholds; it exhibits stable behavior and clarifies model preferences, but its fixed heuristics limit adaptability under rapidly varying operating conditions. To address this limitation, a learning-based supervisor employing a double DQN leverages recent error signals and decision history to learn an adaptive switching policy; it consistently yields lower average errors and improved stability in challenging edge cases, demonstrating generalization beyond fixed rules. Across experiments, both supervised ANN+FSA variants outperform EKF and EKF+ANN baselines, indicating that combining symbolic consistency (FSA) with either transparent or learned arbitration enhances accuracy and preserves physical plausibility in SOC estimation.

With the FSA layer, all ANN heads show consistent gains. RMSE falls by roughly 6–10% and MAE by about 11–37% across FFNN, LSTM, and 1D-CNN (e.g., 1D-CNN MAE drops from 0.029 to 0.019). Adding the RL-based supervisor yields a further 4–7% reduction in aggregate RMSE/MAE versus both the rule-based supervisor and the static best single model. ANN+FSA configurations also outperform EKF and EKF+ANN baselines.

These improvements are practically meaningful—lower normalized SOC errors tighten energy accounting and reduce constraint violations in BEMS scheduling (e.g., PV self-consumption and peak shaving). Two key insights emerge. First, symbolic enforcement via the FSA is a necessary complement to data-driven estimators, ensuring physically consistent SOC trajectories. Second, RL-driven model arbitration delivers robust accuracy gains over fixed rules in high-variance regimes.

In essence, the proposed ANN+FSA+Supervisor architecture provides a robust and adaptable solution for high-precision SOC estimation. While the rule-based supervisor offers clarity and deterministic control, the RL-based system introduces unparalleled flexibility and adaptive optimization. Critically, both supervisory mechanisms benefit immensely from the FSA layer, which significantly reduces error dissemination and ensures the physical consistency of SOC estimates, thereby enhancing the overall reliability of the system. This novel integration of statistical learning, symbolic filtering, and adaptive model selection offers a compelling new perspective and validates its strong potential for real-world application in advanced battery management systems (BMSs).

For future work, the proposed framework will be further developed for practical deployment in embedded battery management systems (BMSs) and smart-building energy management systems (EMSs). This will involve a comprehensive assessment of computational demands, inference latency, and memory usage to ensure compatibility with resource-constrained hardware platforms. Additionally, the integration of uncertainty quantification techniques—such as Bayesian neural networks or ensemble learning—will be explored to provide confidence bounds for state-of-charge (SOC) predictions, thereby improving the reliability of decision-making in safety-critical applications. Further benchmarking against advanced hybrid and reinforcement learning-based SOC estimation approaches is planned to validate the framework against current state-of-the-art methods. Another research direction involves coupling the SOC estimator with EMS functionalities, including predictive photovoltaic (PV) charging scheduling and demand-response coordination, to evaluate its real-world benefits in smart-building environments. Finally, incorporating battery aging and state-of-health (SOH) effects into the framework is anticipated to enhance its long-term accuracy and adaptability under realistic operational conditions. This will also include validating the model using a wider variety of datasets from different operational environments to further bolster its generalizability, as well as exploring online learning techniques to enable continuous adaptation to new real-world conditions.