Optimal Placement of a Unified Power Quality Conditioner (UPQC) in Distribution Systems Using Exhaustive Search to Improve Voltage Profiles and Harmonic Distortion
Abstract
1. Introduction
1.1. Microgrid Operation Under Low and High DG Penetration
1.2. Recent Control and Optimization Directions
2. Theoretical Framework
2.1. Unified Power Quality Conditioner (UPQC)
2.1.1. Control Strategies
- UPQC−P
- UPQC−Q
2.1.2. Related Devices
2.2. Power Quality in Electrical Systems
2.2.1. Common Power Quality Problems
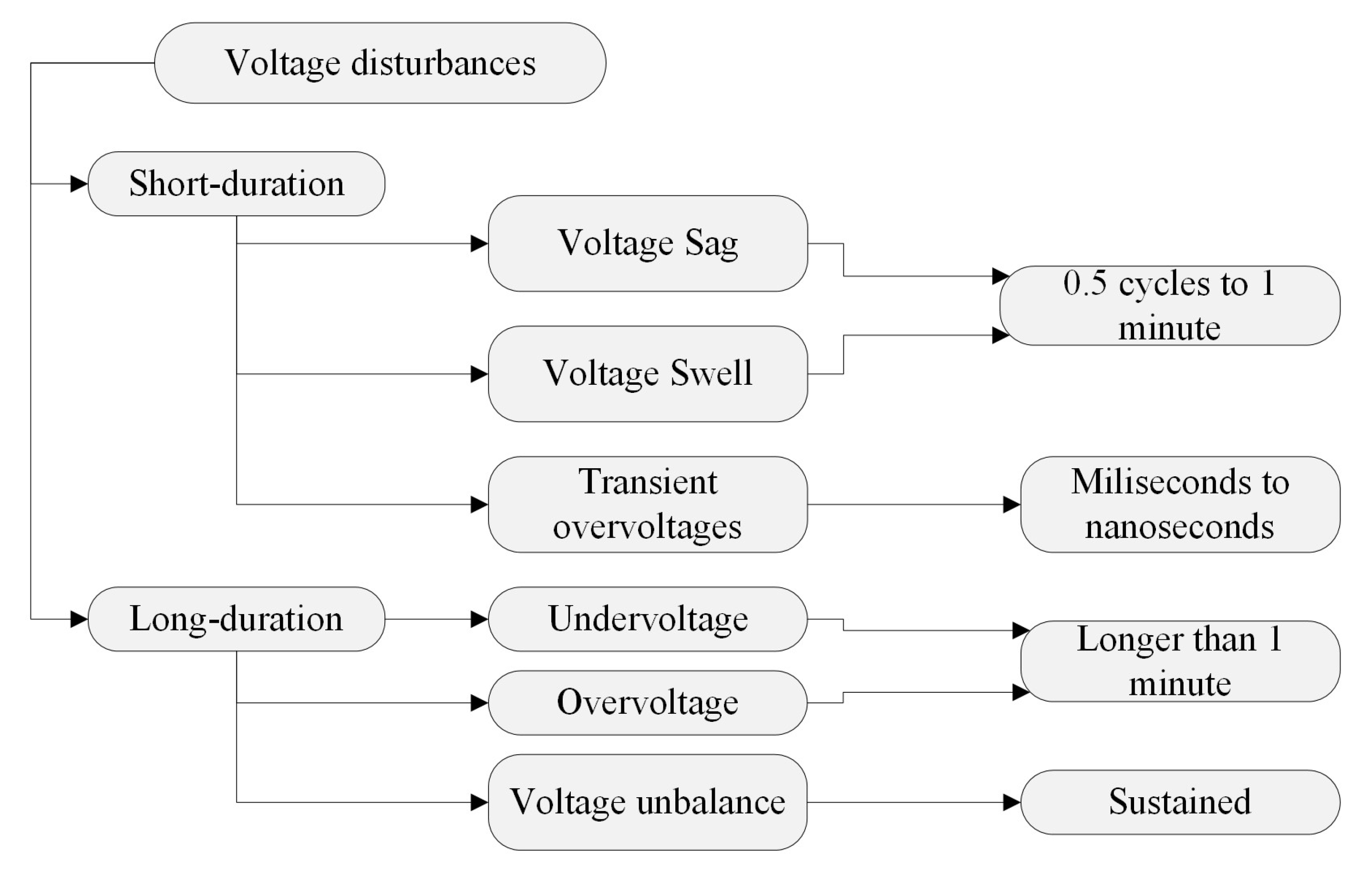
2.2.2. Voltage Disturbances
2.2.3. Voltage Deviation
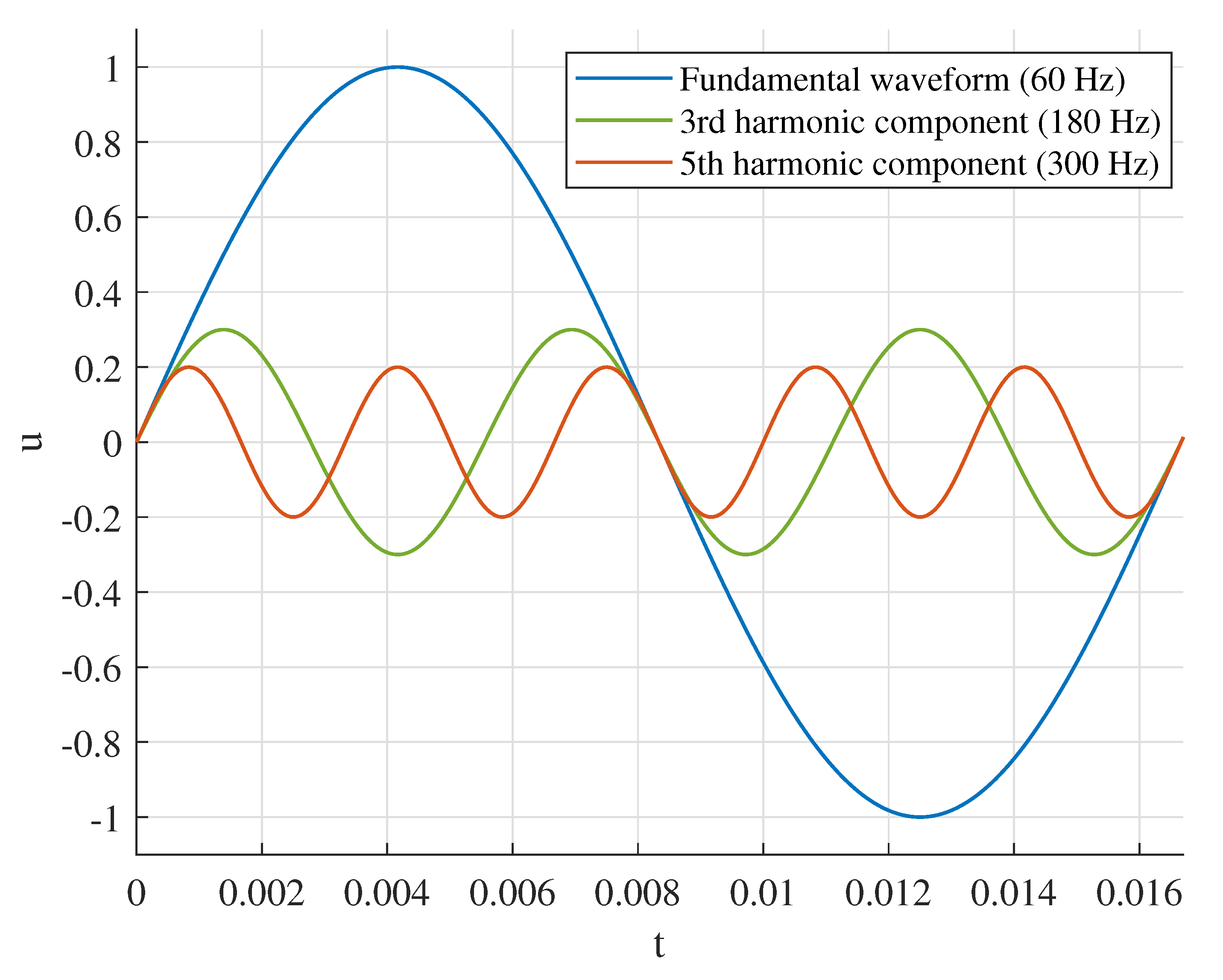
2.2.4. Total Harmonic Distortion (THD)
2.2.5. Standards and Regulations
2.3. Harmonic Order and Measurement Bandwidth
2.4. Exhaustive Search or Brute-Force Method
2.5. Related Work and Comparative Analysis
3. Methodology
3.1. Optimization Problem Statement and Candidate Node Selection
3.1.1. Decision Variables
- : binary siting variable ( if a UPQC is installed at bus i, otherwise).
- : RMS voltage magnitude at bus i (p.u.).
- : voltage THD at bus i (%).
3.1.2. Objective Function
3.1.3. Constraints
3.1.4. Assumptions and Candidate Set Rationale
3.2. Sensitivity Analysis for UPQC Location
3.3. UPQC Implementation Using Exhaustive Search
- Guarantees identification of the global optimum within the defined search space, eliminating solution variability across runs.
- Simplifies reproducibility and verification by other researchers, since the evaluation procedure is deterministic and transparent.
- Avoids the need for parameter tuning inherent to heuristic methods (e.g., population size, mutation rate, cooling schedule).
3.3.1. Extension to Multiple-UPQC Scenarios
3.3.2. Incorporating Installation and Operational Costs
- and are normalized indices of harmonic distortion and voltage deviation, respectively.
- is the normalized total cost associated with a given placement configuration.
- and are the relative weights assigned to each criterion.
- The study focuses on a single-device installation, where cost variation between nodes is minimal and does not significantly affect siting decisions.
- Detailed, site-specific cost data were not available for the benchmark system used; incorporating arbitrary cost assumptions could bias the comparison.
3.3.3. Optimization Algorithm Description
- Parameter Initialization: Initial parameters for the algorithm are defined, such as the total number of system nodes (N_total), nominal system voltage in p.u. (V_nominal), set of critical nodes (S), search space size (N_s), and importance weights for the objective function ( and ).
- Base Case Evaluation: The system is simulated without the UPQC to obtain base voltage and THDv values, and to calculate the reference metrics: local THDv (_base) and global voltage deviation (_base).
- Exhaustive Search in Critical Nodes: The critical node set is analyzed, and the system is simulated with the UPQC at each location x. For every candidate, the corresponding performance metrics ( and ) are computed.
- Analysis and Optimal Solution Selection: The minimum and maximum values for each metric are obtained to perform normalization ( and ). The scalar objective function (J) is then calculated for each location , and the solution with the minimum value (J_min) is identified.
- Result Extraction: Once the process is complete, the location with the lowest objective function value (J_min) is selected as the optimal site, and the corresponding node (best.x) is reported.
| Algorithm 1 Pseudocode of the optimization model. | |
| Optimal UPQC Placement Algorithm Based on Local THDv and Global Voltage Deviation | |
| Step 1 | Phase 0: Parameter Initialization; N_total = 33 V_Nominal = 1.0 S ← {14,19,27} N_s ← |S| |
| Step 2 | Phase 1: Initial Evaluation; (V_base, THD_base) ← SimulateSystem() (base, base) ← ComputeMetrics(V_base, THD_base) |
| Step 3 | Phase 2: Exhaustive Search in Critical Nodes result_list ← ⌀ for i = 1 to N_s do x ← S[i] (V, THD) ← SimulateSystem(x) (, ) ← ComputeMetrics(V, THD) Append results to result_list end for |
| Step 4 | Phase 3: Analysis and Optimal Solution Selection //Normalization of metrics: GetMinMax(result_list, ) GetMinMax(result_list, ) for i = 1 to N_s do r = result_list(i) ← (r. − )/( − ) ← (r. − )/( − ) r.J ← result_list(i) ← r end for //Best solution selection best ← x J_min for i = 1 to N_s do r ← result_list(i) if then J_min ← r.J best ← r end if end for |
| Step 5 | Results: Compute and display minimum cost function Display optimal placement ← best.x |
| Step 6 | End. |
3.4. Rationale for Selecting Exhaustive Search over Metaheuristic Methods
3.5. Computational Complexity and Runtime Profiling
- Per-iteration tasks: load-flow + time-domain simulation for harmonic extraction (THDv) + voltage-profile postprocessing + objective .
- Measured average wall-clock per iteration: (mean of 50 runs; std. dev. s).
| Configuration | # Iterations | Avg. Time/Iter. | Total Time |
|---|---|---|---|
| Reduced set (Case 1: no DG) | 3 | 0.42 s | 1.26 s |
| Reduced set (Case 2: with DG) | 3 | 0.42 s | 1.26 s |
| Full set (all IEEE 33-bus candidates except slack; ) † | 32 | 0.42 s | 13.44 s |
| Full set for both scenarios (no DG & with DG) | 64 | 0.42 s | 26.88 s |
3.6. Weight Selection and Sensitivity Analysis
- Case 1 (no DG): invariance of the optimum.
- Case 2 (with DG at nominal): threshold on .
3.7. Scalability and Hybrid Optimization Pathways
- (i)
- Parallel evaluation of candidates.
- (ii)
- Candidate pre-screening (pruning).
- (iii)
- Dominance filtering with lower bounds.
- (iv)
- Radial decomposition and reconciliation.
- (v)
- Greedy k-device extension with local refinement.
- (vi)
- Hybrid metaheuristic + enumeration.
- (vii)
- Stopping and robustness criteria.
3.8. UPQC Control Strategy and Series–Shunt Coordination
- Synchronous reference frame and synchronization.
- Series converter (voltage compensation).
- Shunt converter (current shaping and DC-link regulation).
- Power balance and coordination.
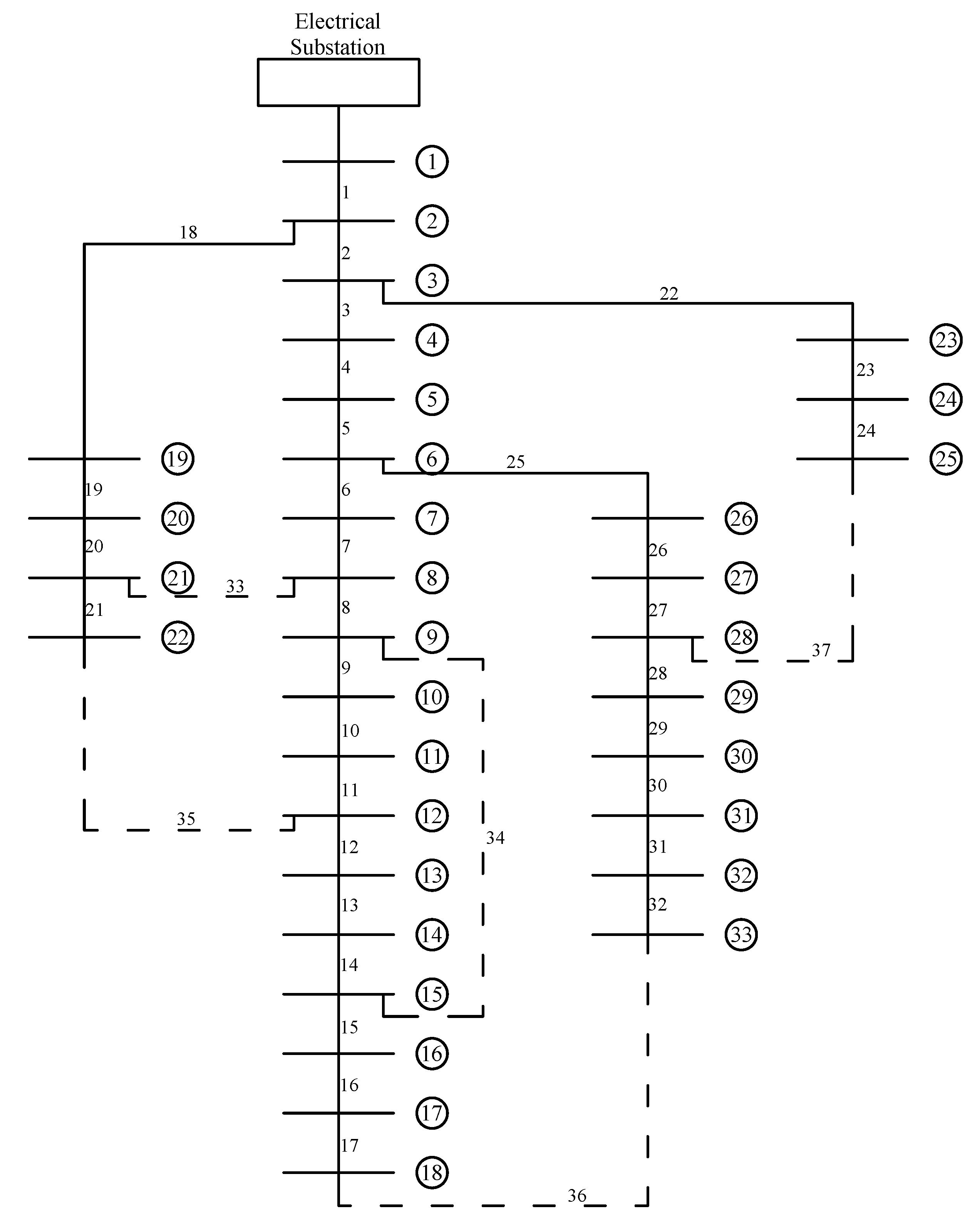
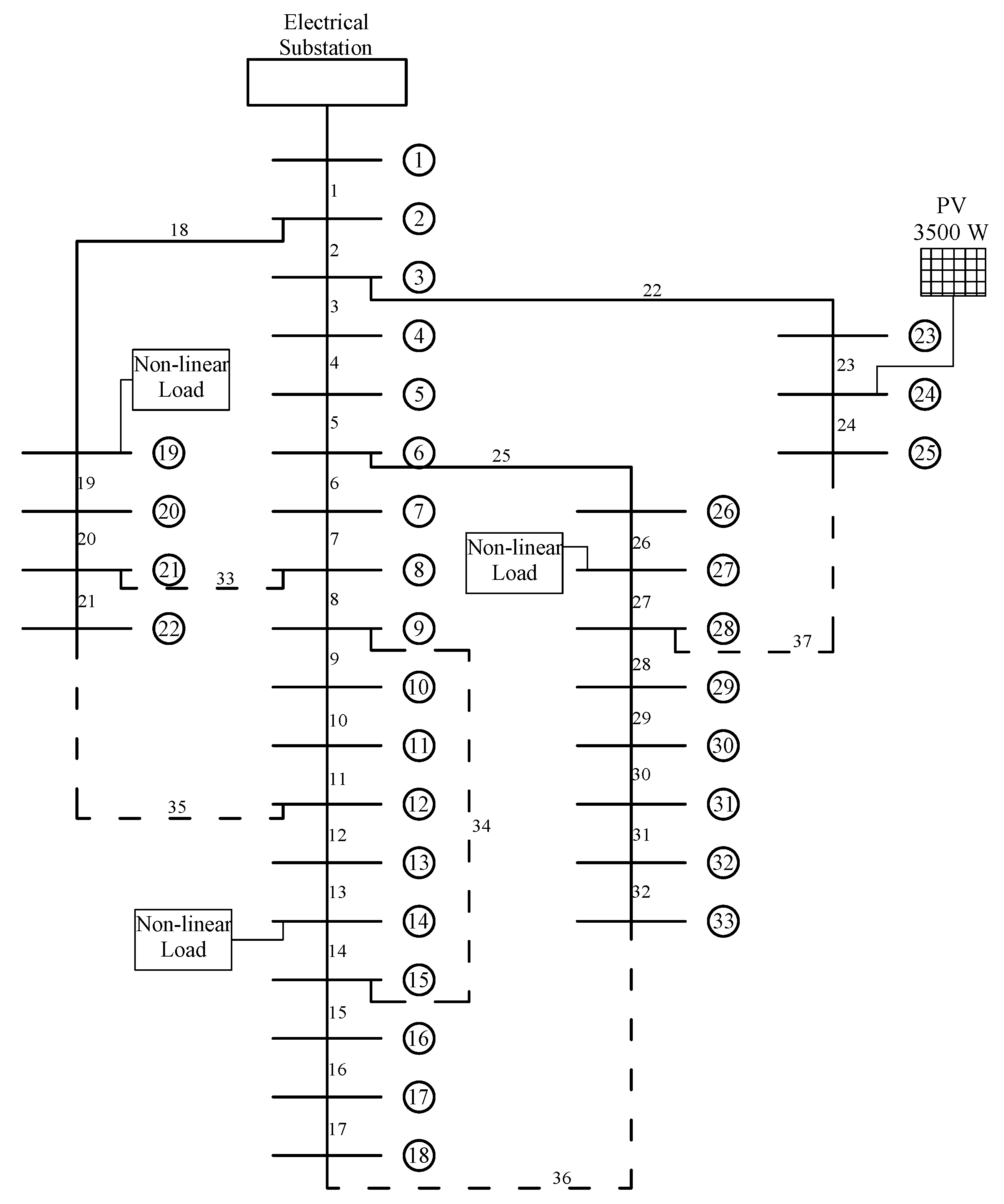
3.9. Test System
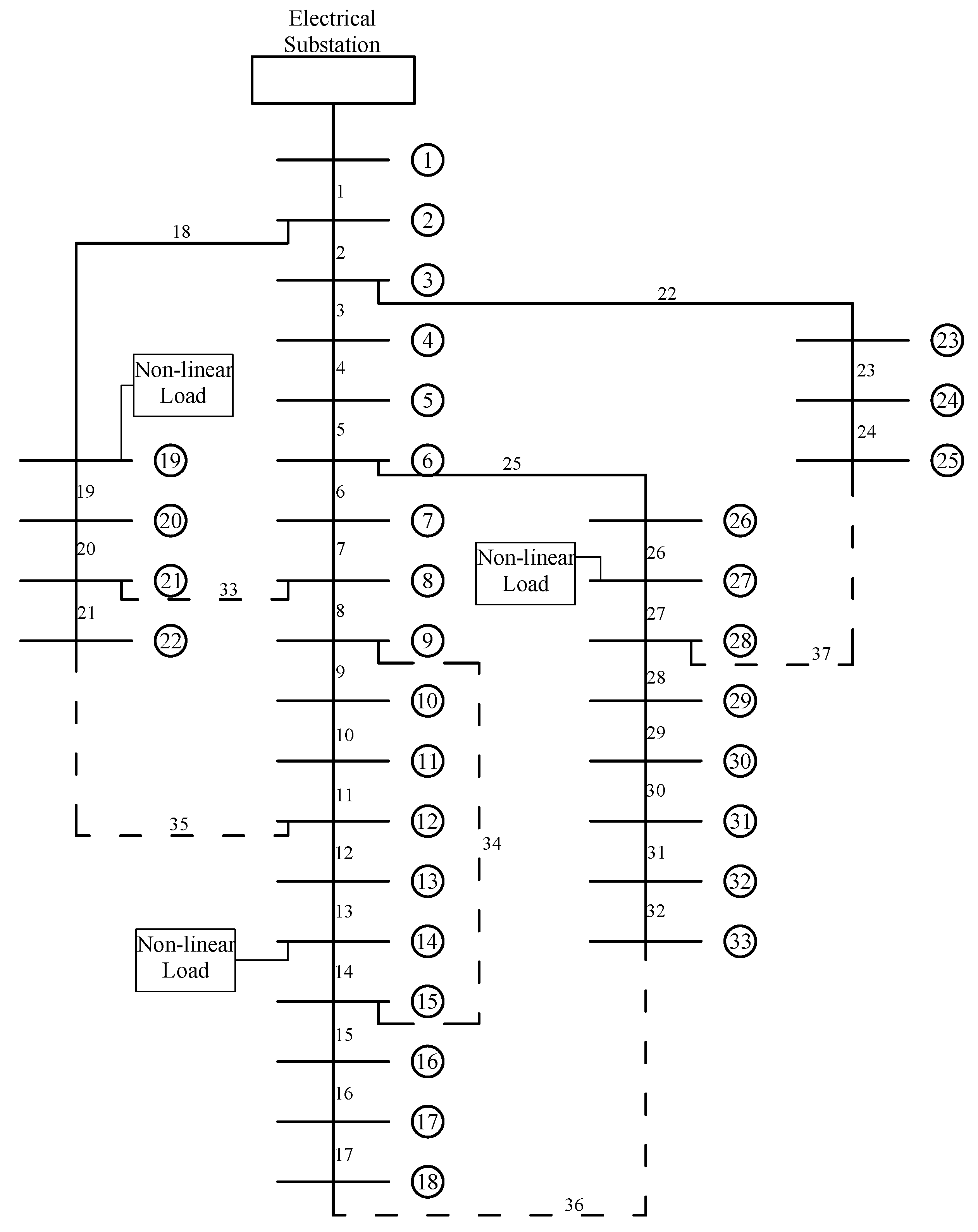
4. Case Studies
4.1. Case 1
4.2. Case 2
5. Results and Analysis
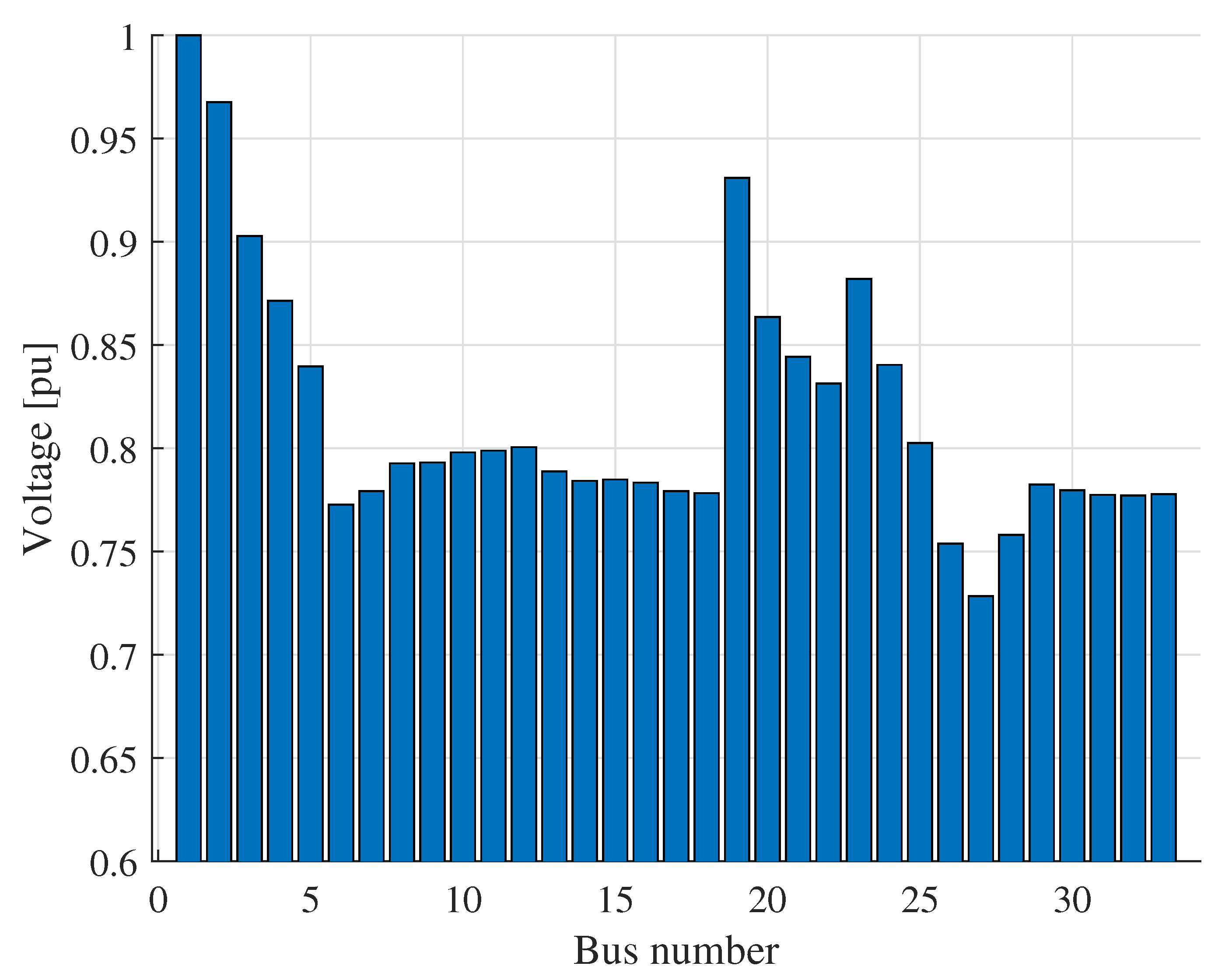
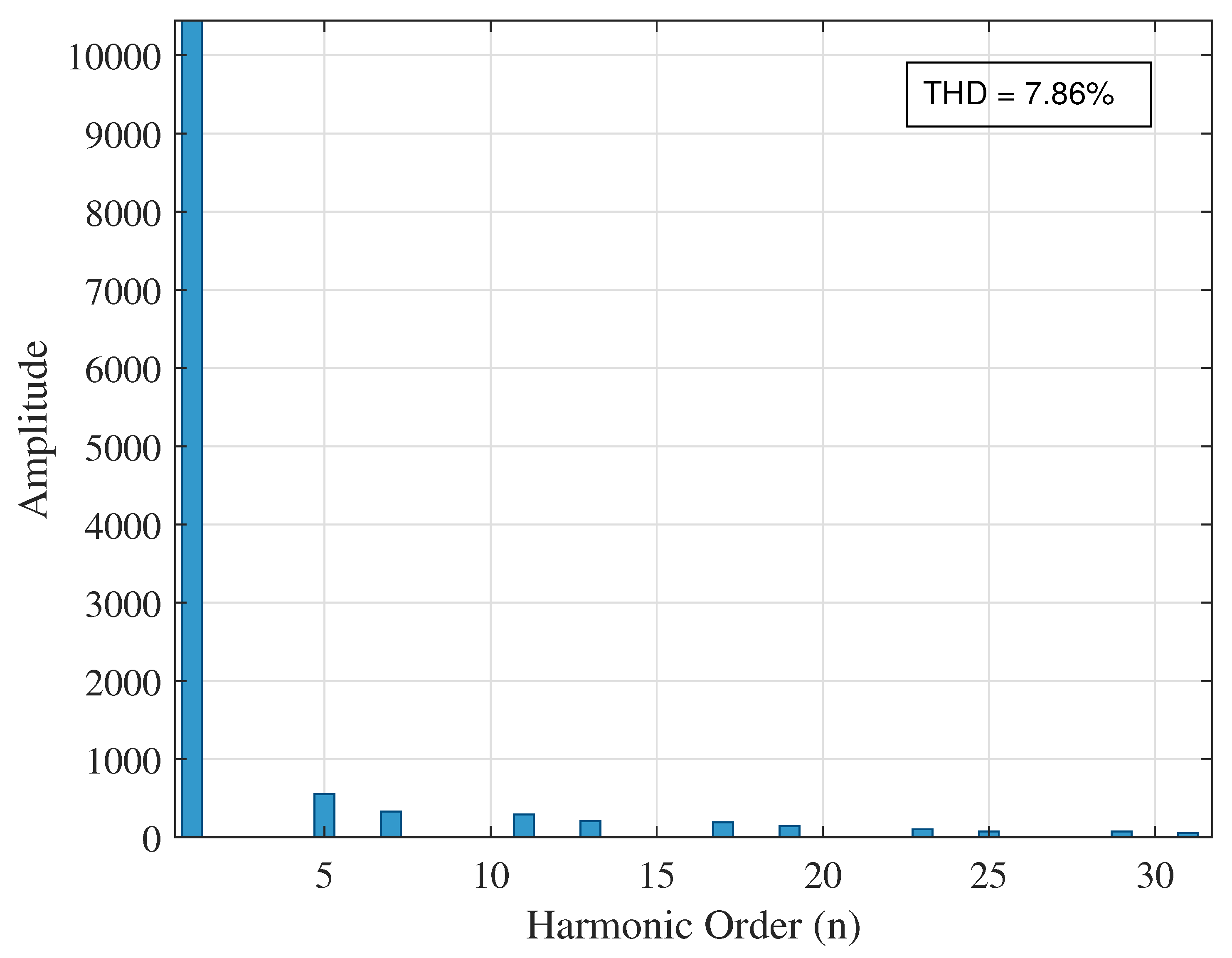
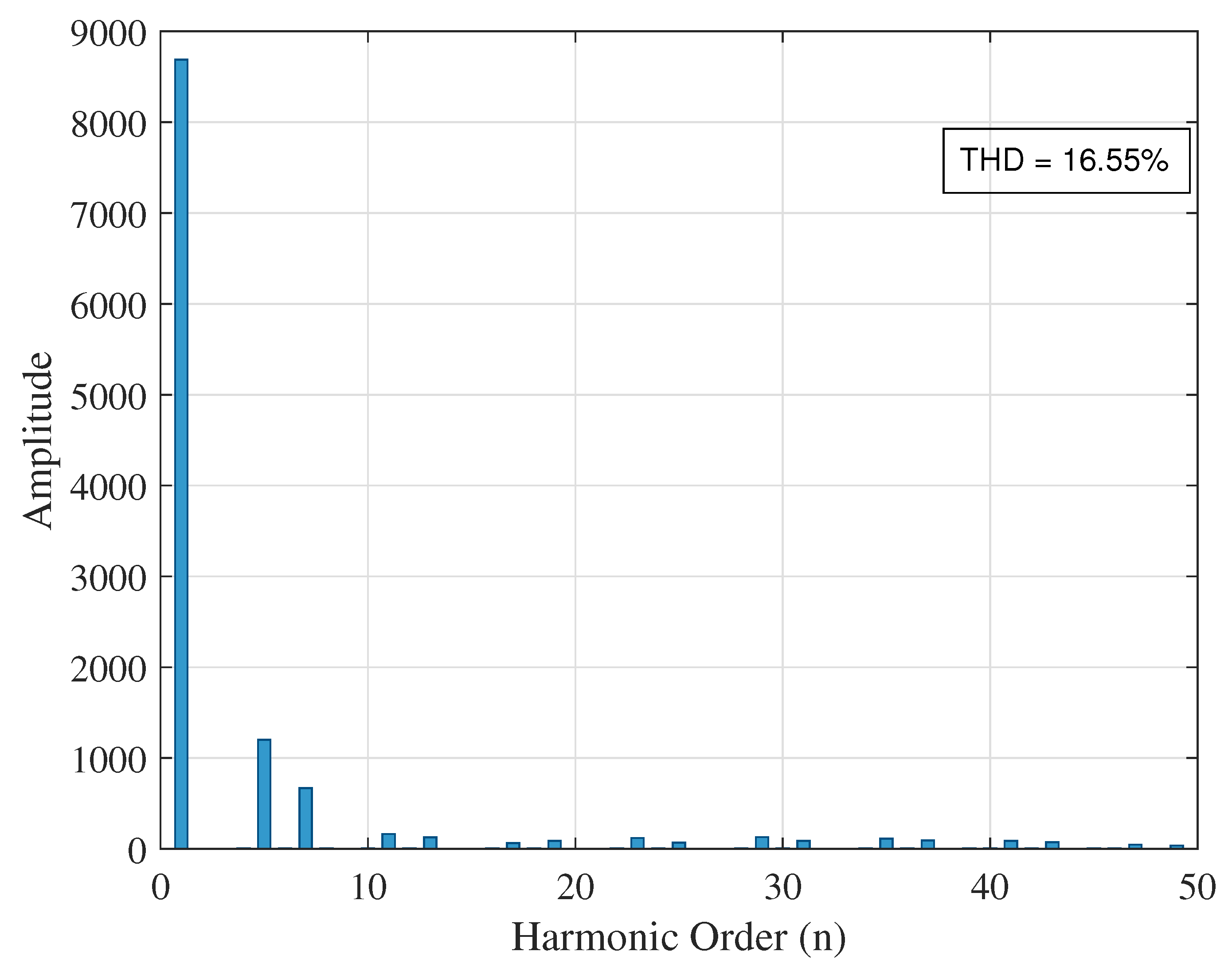
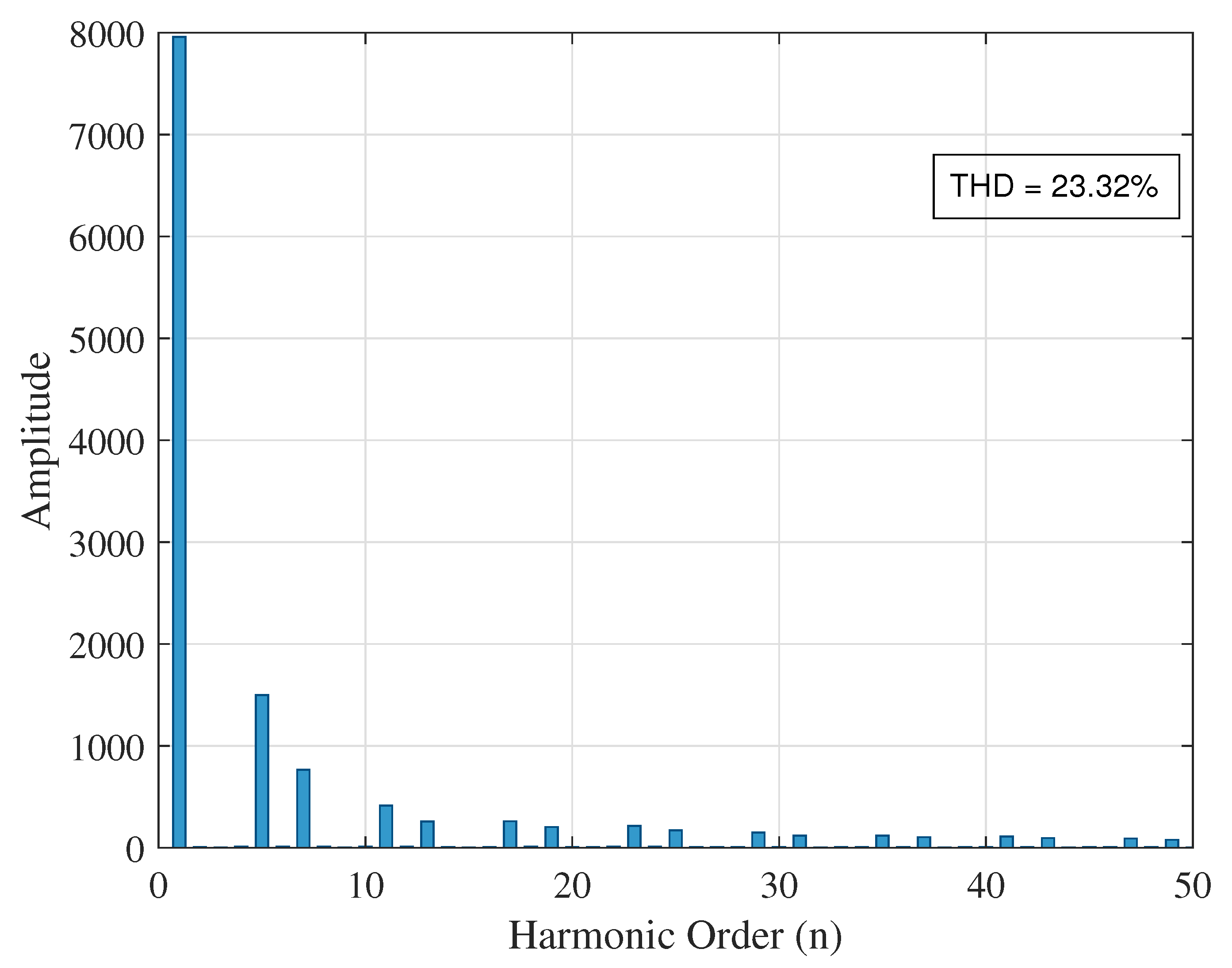
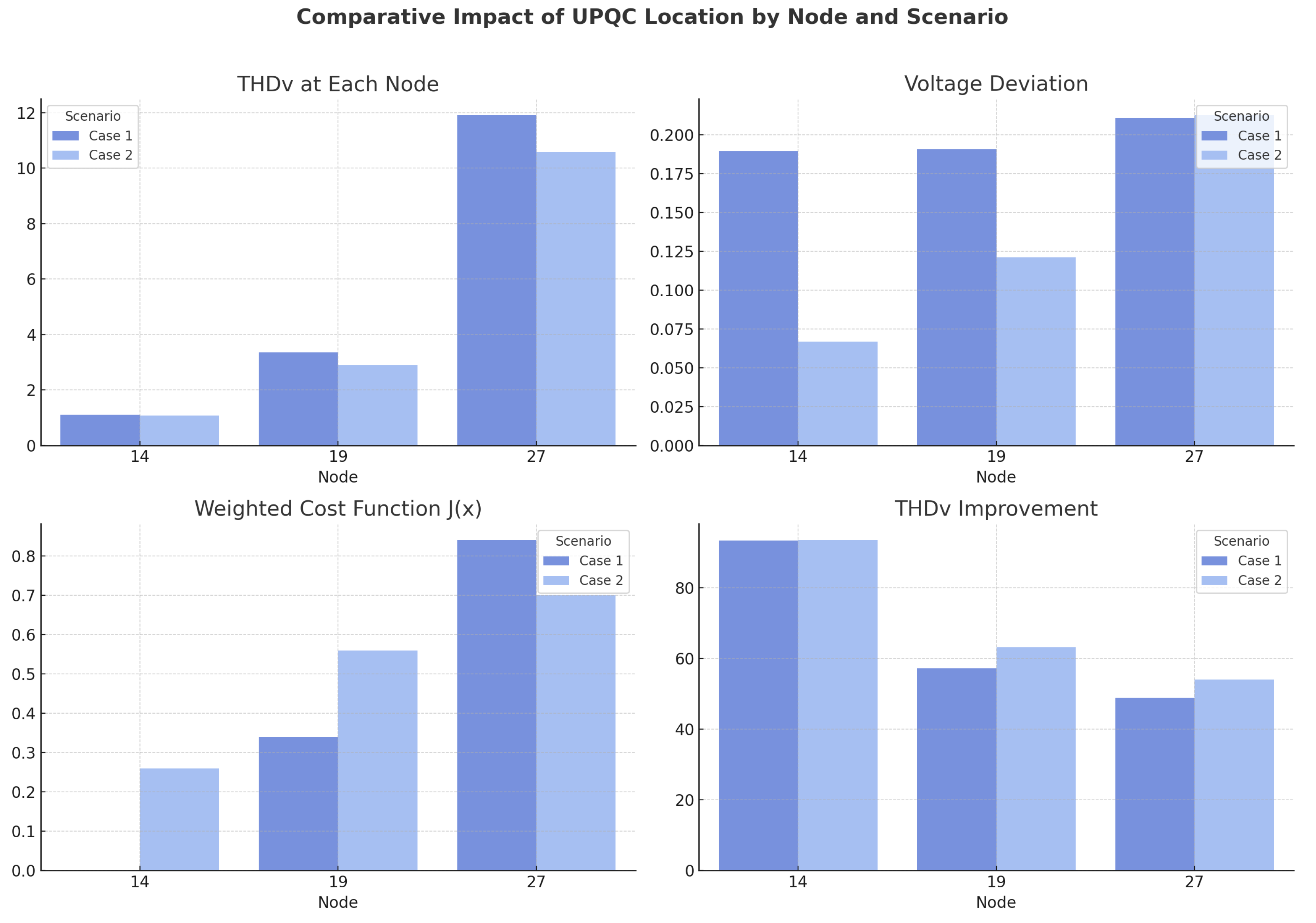
5.1. Voltage THD Summary
5.2. Case 1
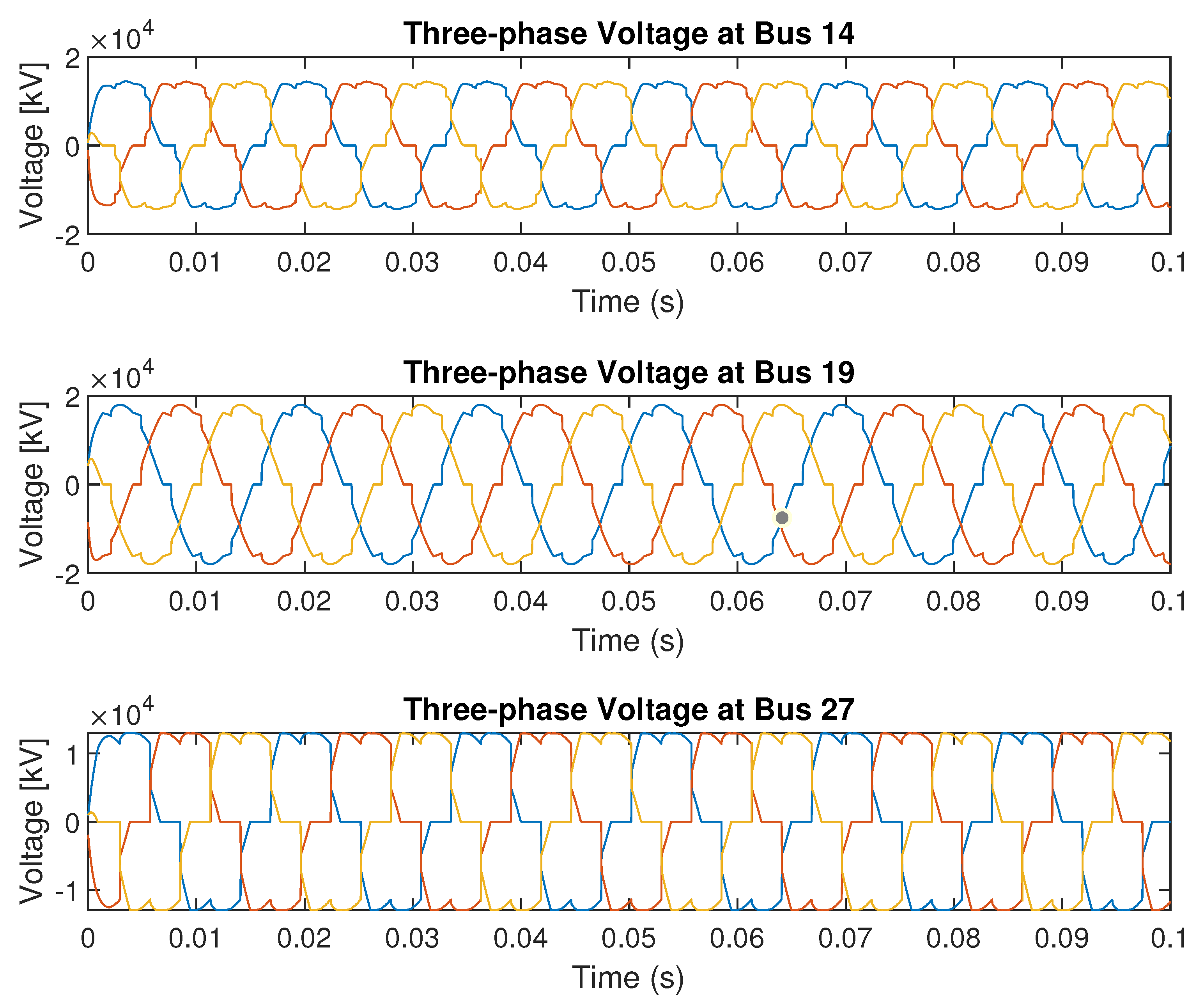
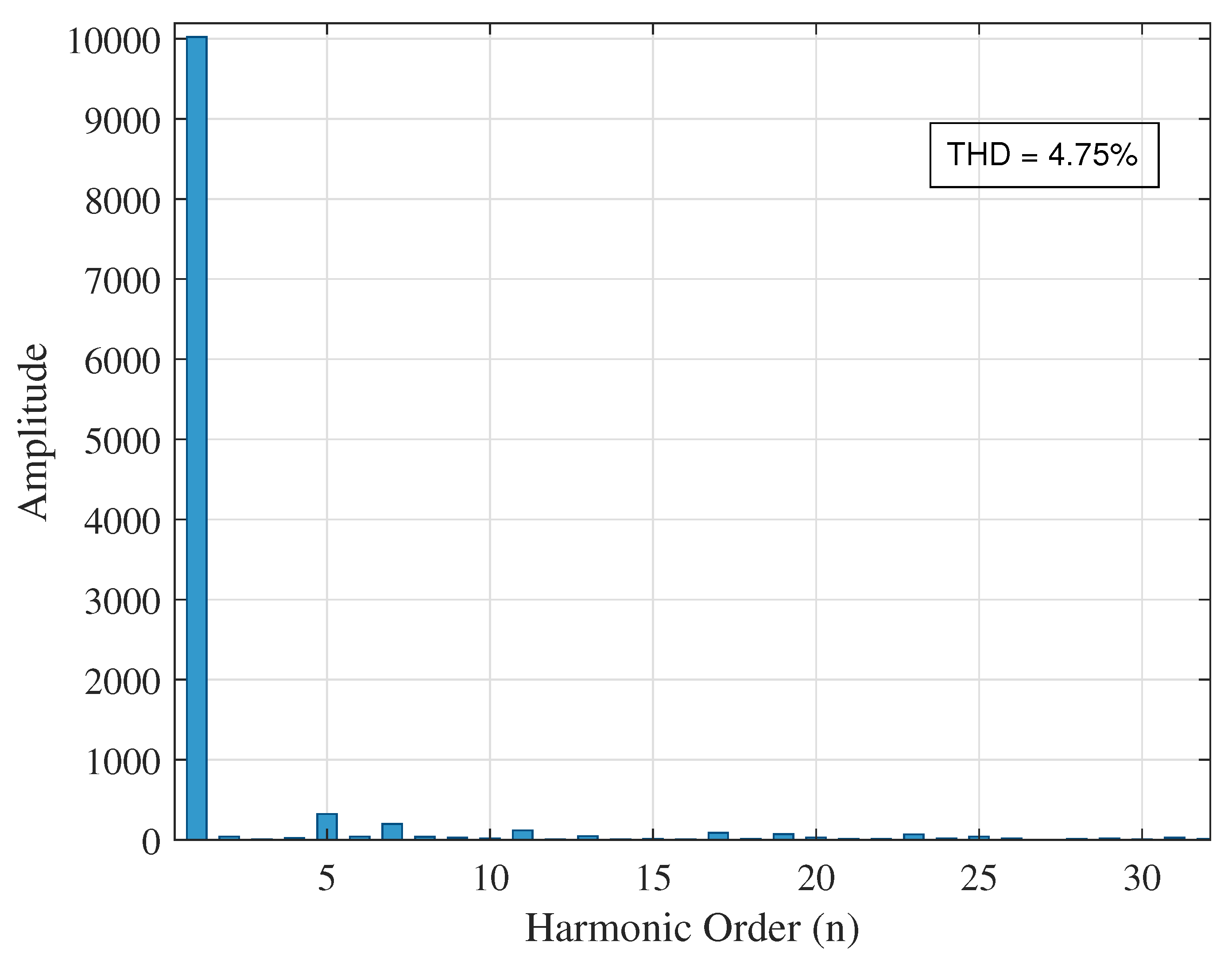
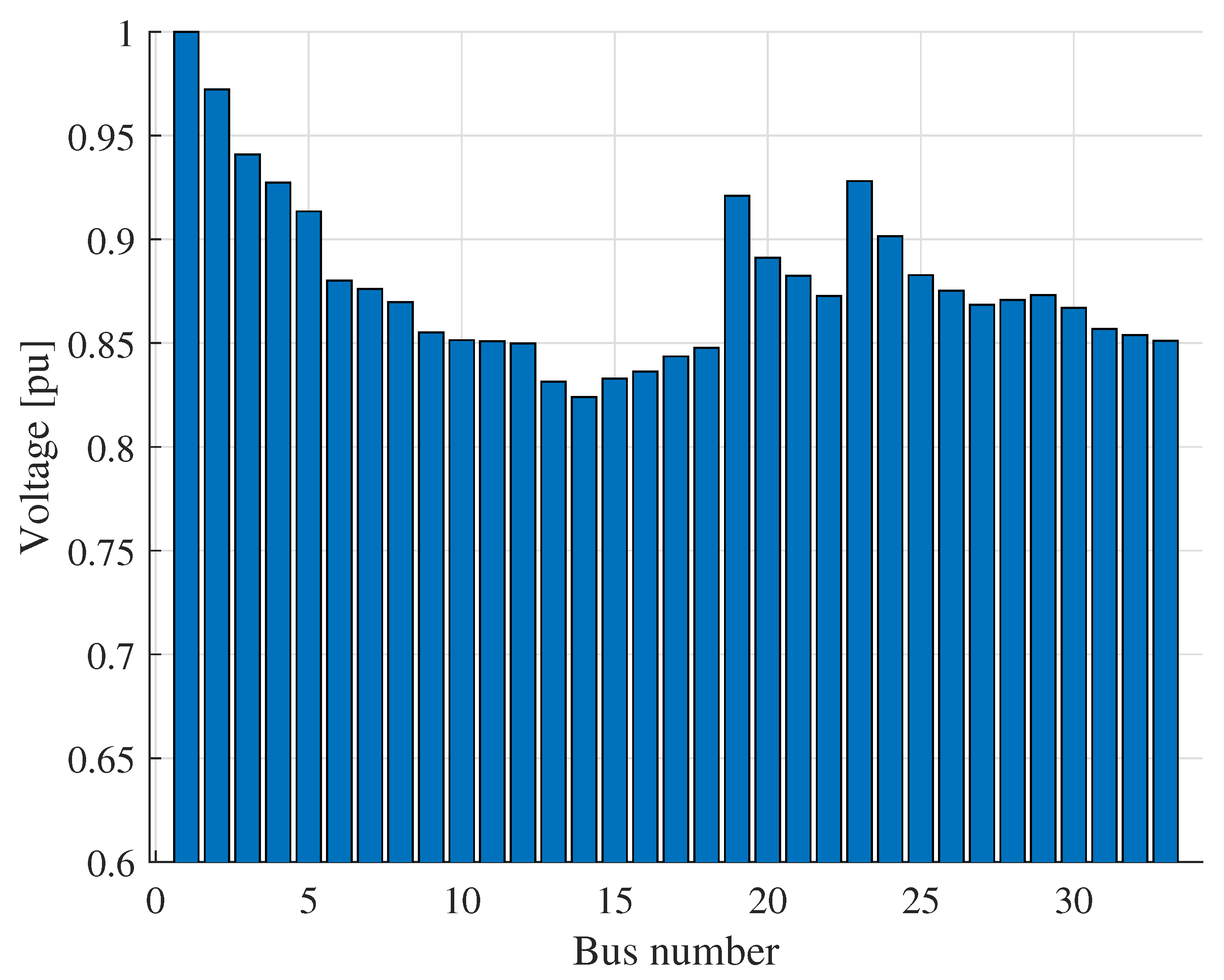
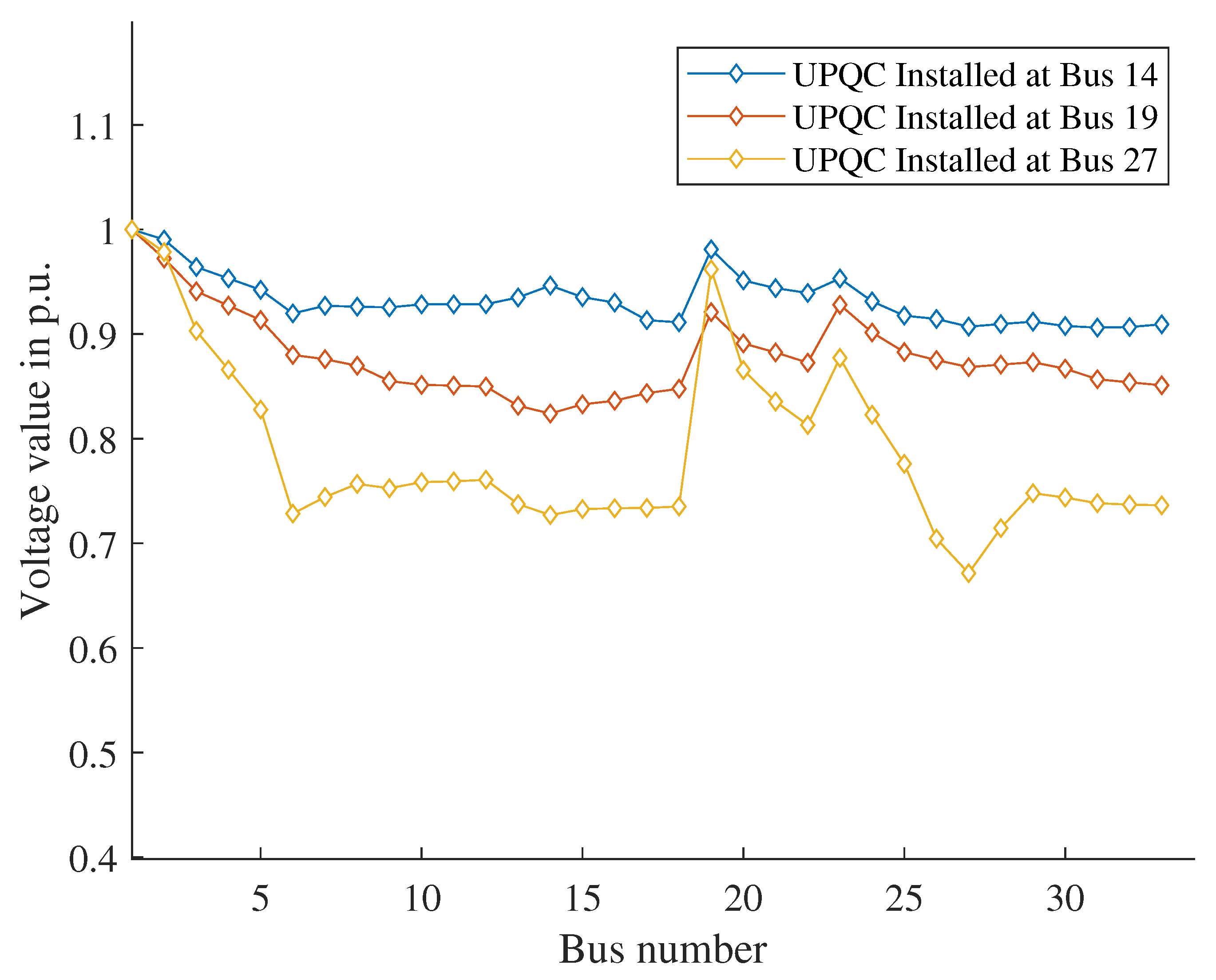
5.2.1. UPQC Installed at Bus 14
5.2.2. UPQC Installed at Bus 19
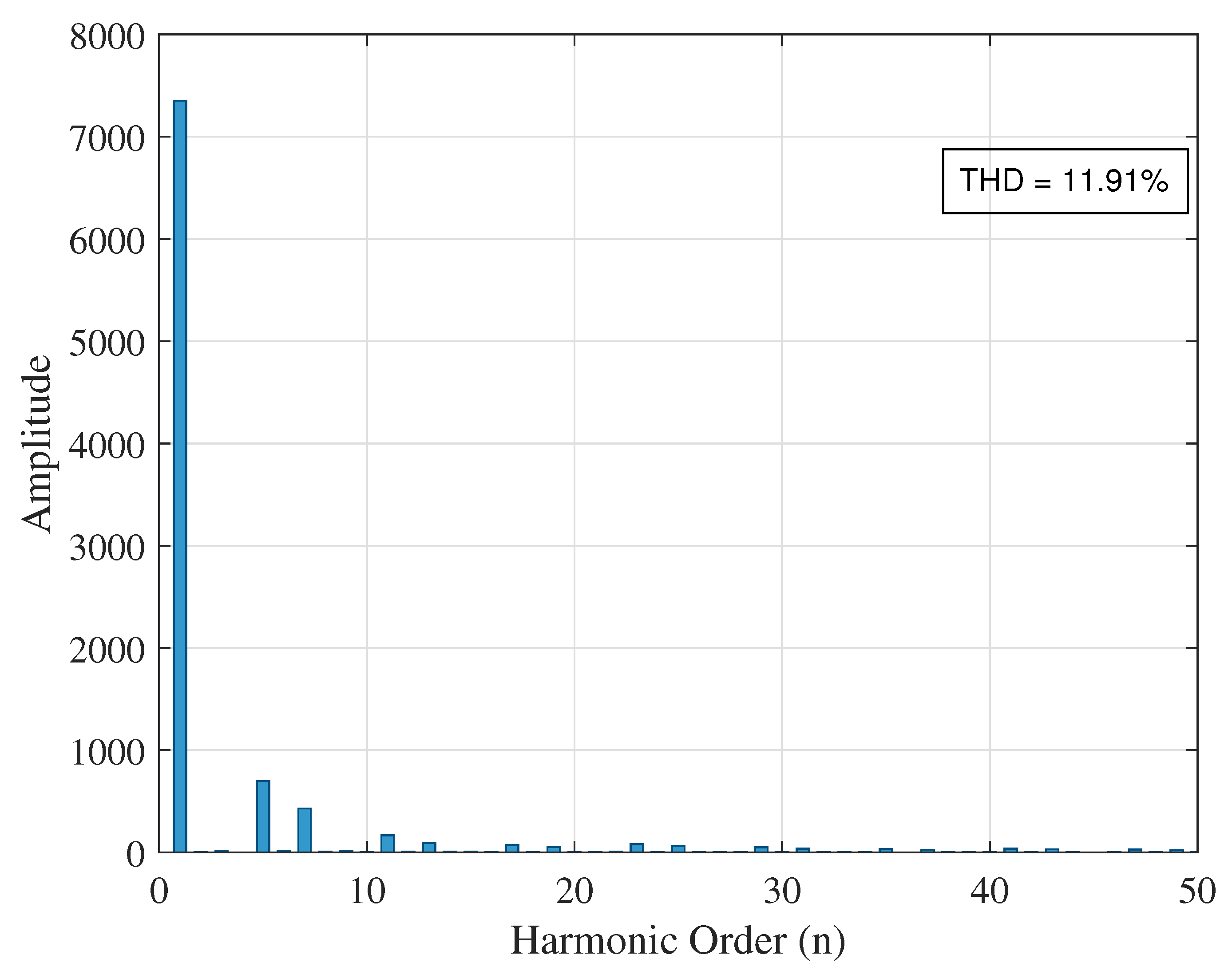
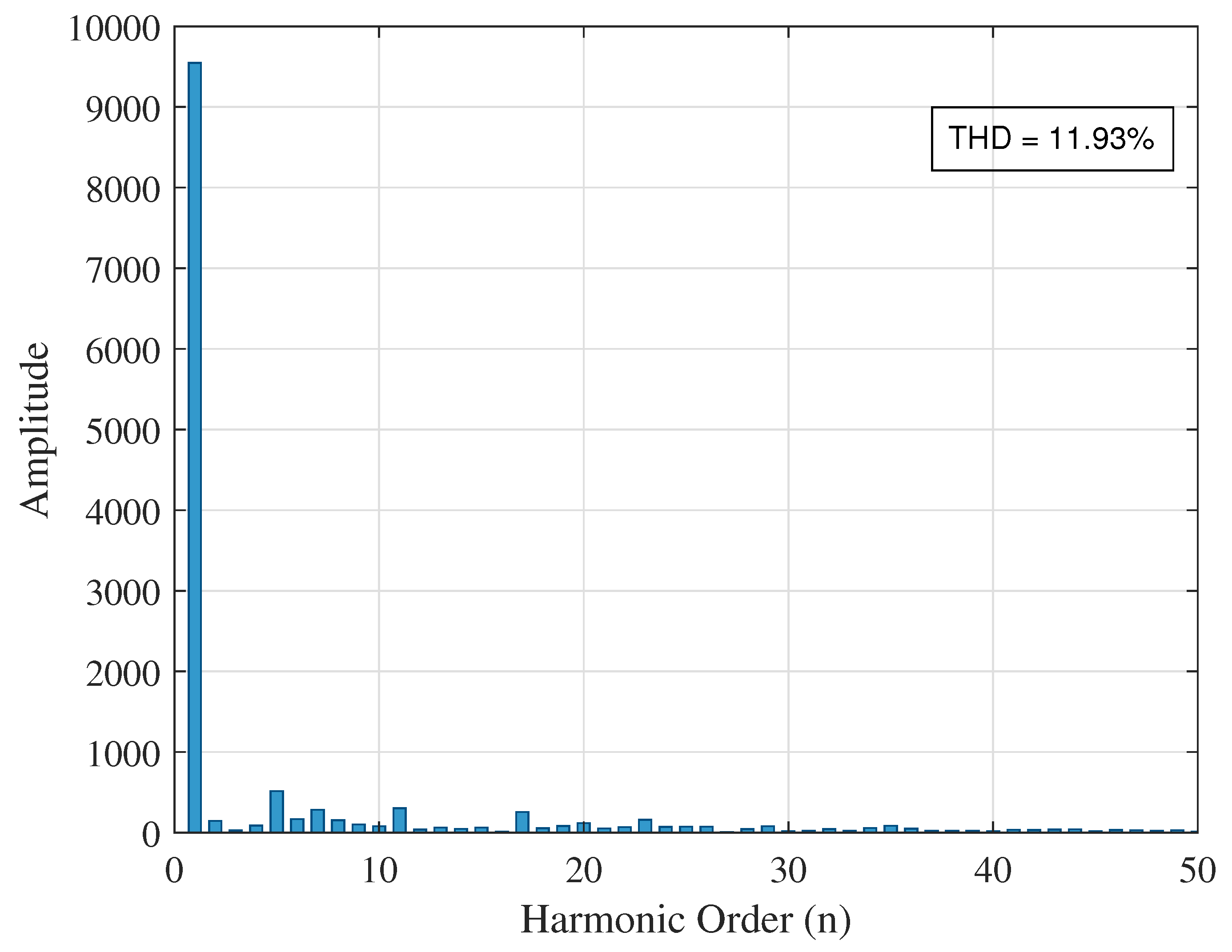
5.2.3. UPQC Installed at Bus 27
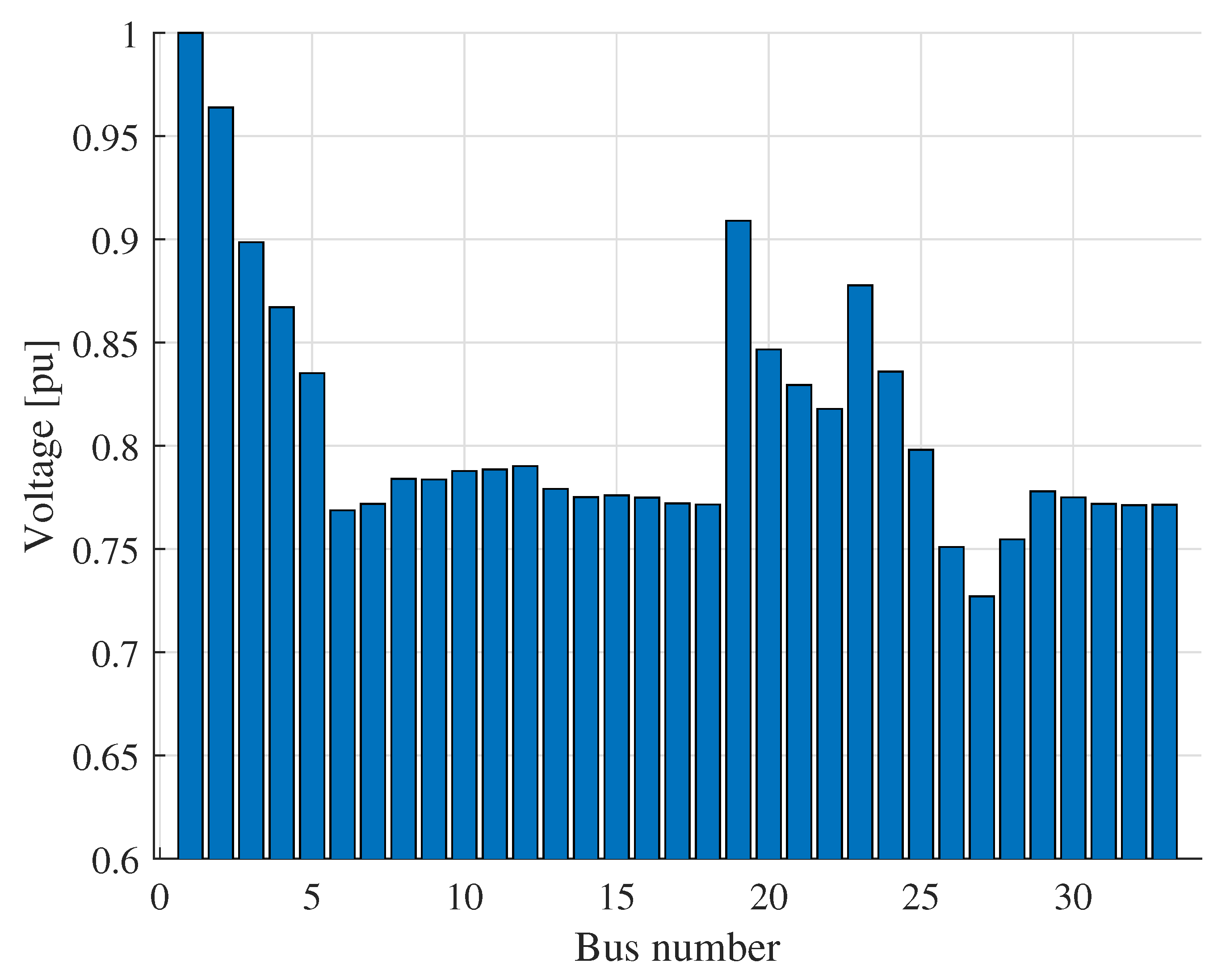
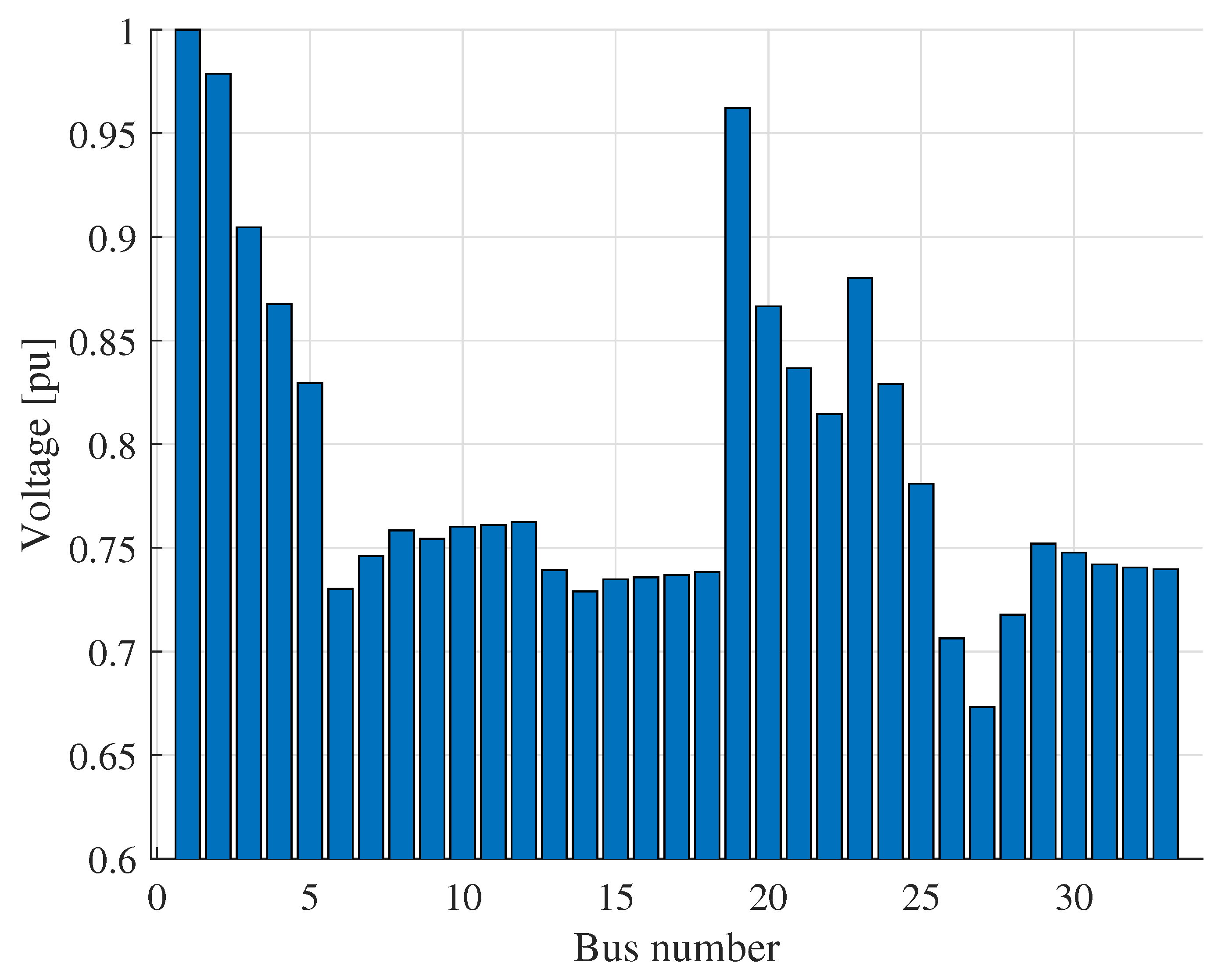
5.3. Optimal Location Analysis
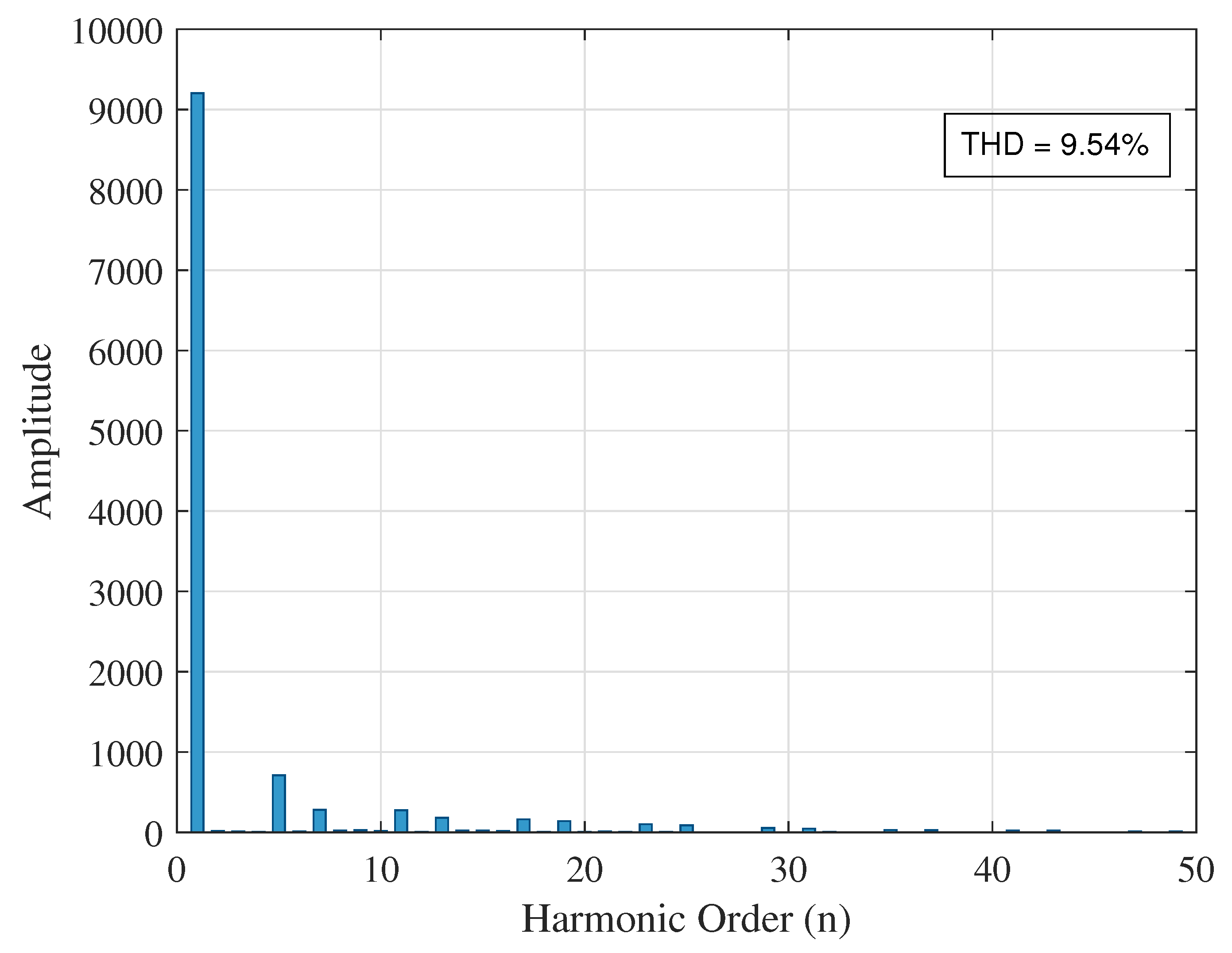
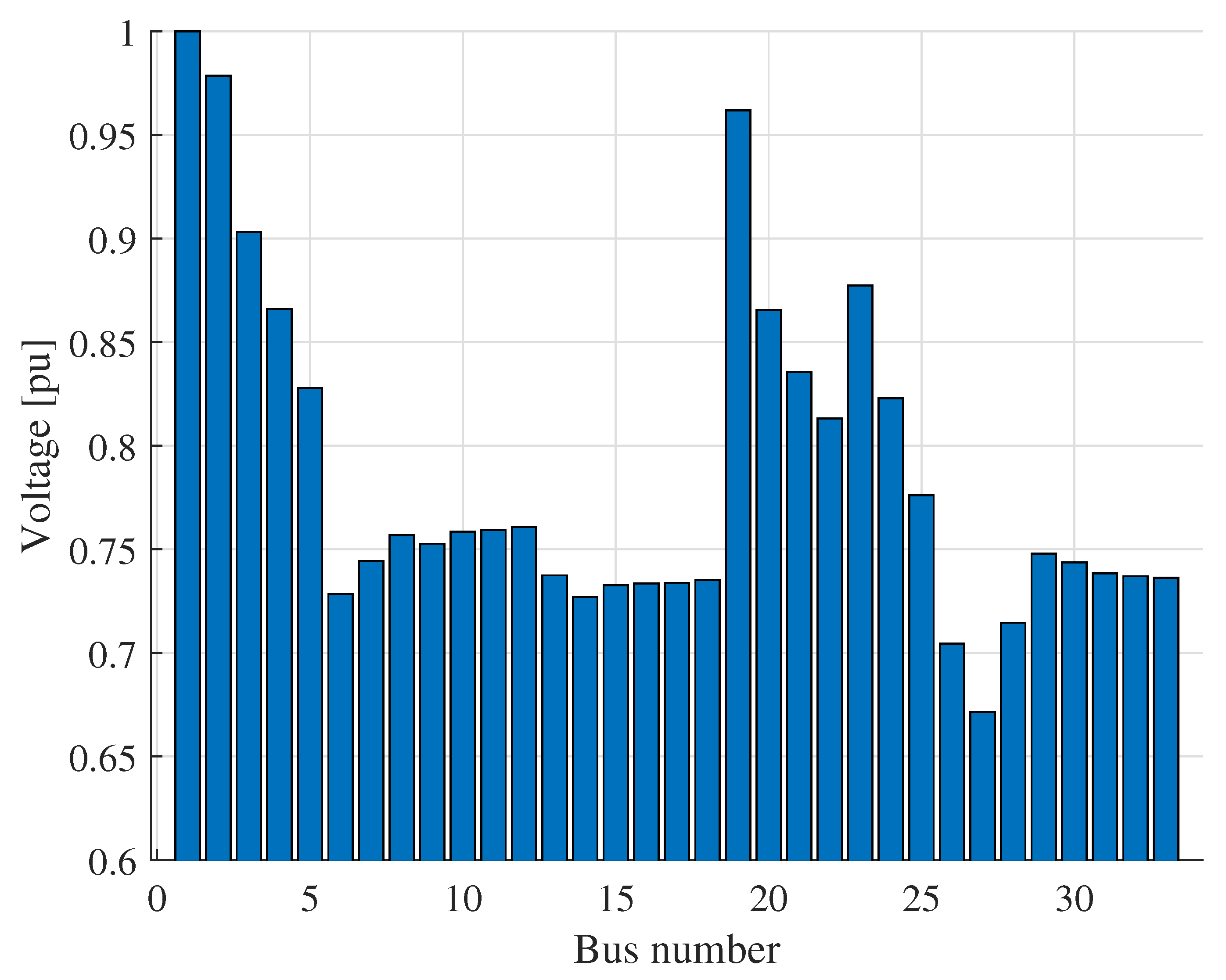
5.4. Case 2
5.5. Impact of DG Penetration on Harmonic Performance
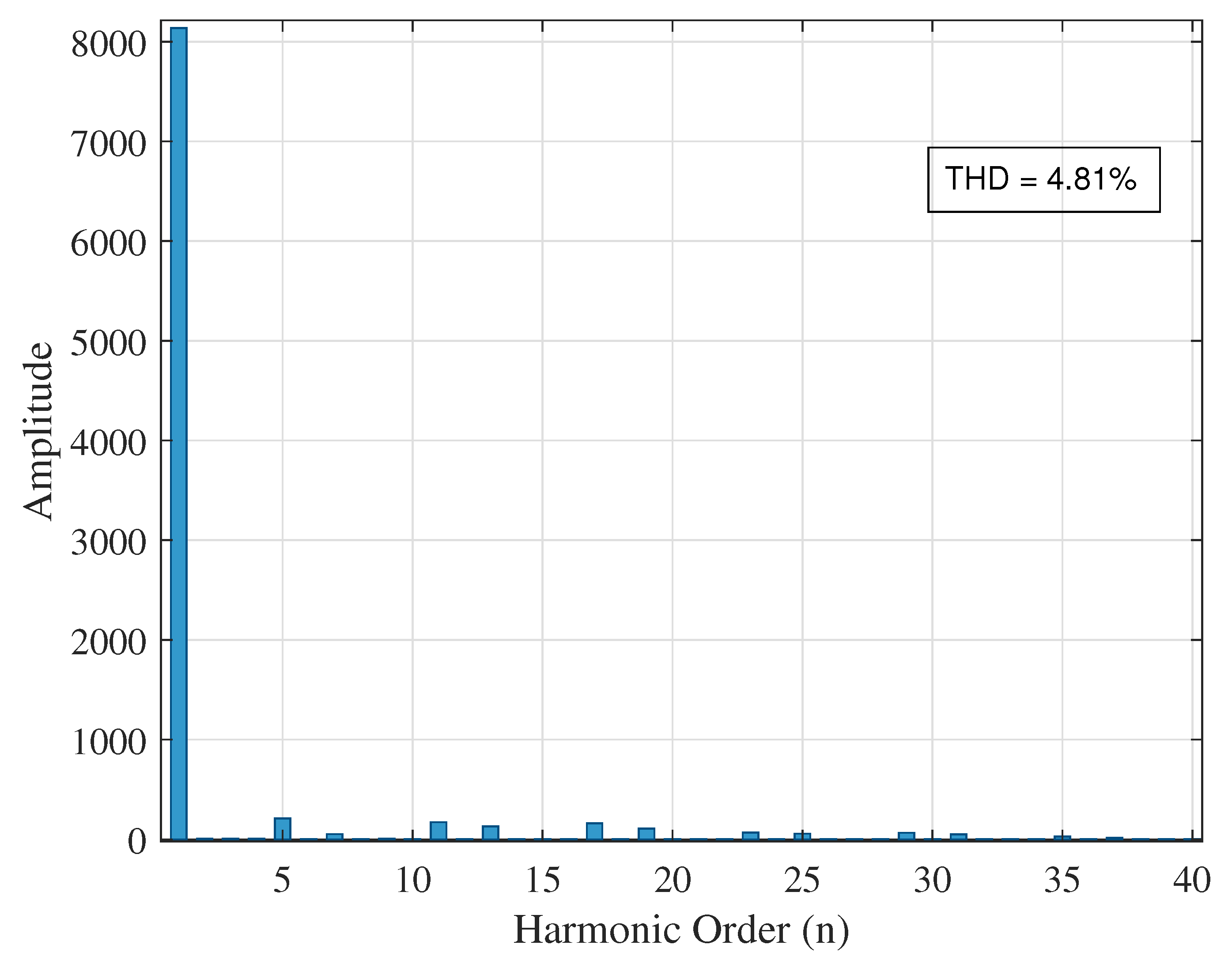
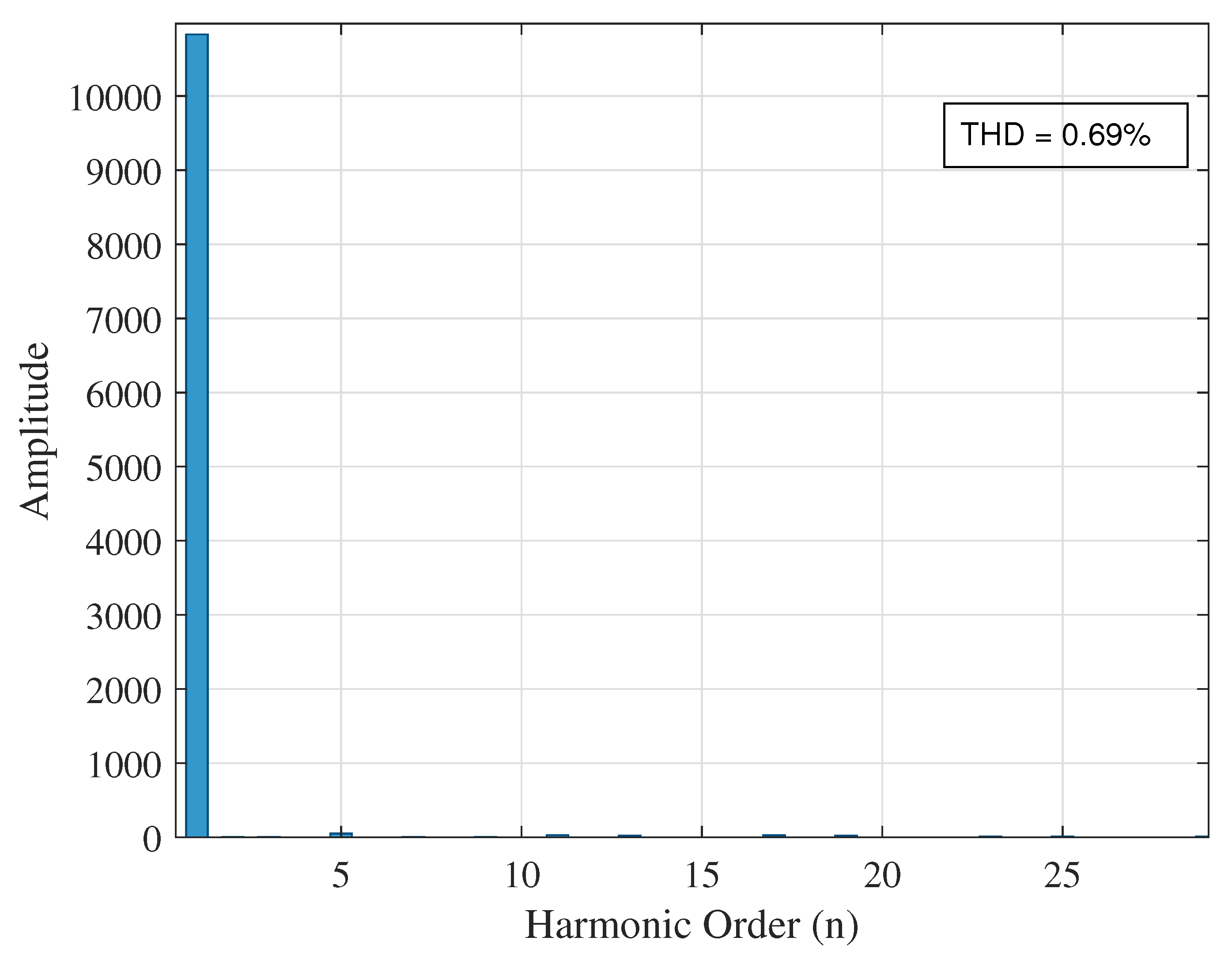
5.5.1. UPQC at Bus 14
5.5.2. UPQC at Bus 19
5.5.3. UPQC at Bus 27
5.5.4. Optimal Location Analysis
5.6. Robustness Summary and Statistical Dispersion of THDv
6. Discussion and Novelty of the Proposed Approach
- The simultaneous optimization of THDv, voltage profile, and loss minimization for UPQC placement under nonlinear load conditions.
- The application of the method to the complete network, with results confirming the dominance of nonlinear-load buses as optimal locations.
- The adaptability of the framework to extended scenarios, including multiple UPQC devices, economic evaluation, and larger network sizes.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| AC | Alternating Current |
| DC | Direct Current |
| DG | Distributed Generation |
| PV | Photovoltaic |
| UPQC | Unified Power Quality Conditioner |
| APF | Active Power Filter |
| DVR | Dynamic Voltage Restorer |
| SVC | Static Var Compensator |
| STATCOM | Static Synchronous Compensator |
| D-STATCOM | Distribution Static Compensator |
| THD | Total Harmonic Distortion |
| THDv | Voltage Total Harmonic Distortion |
| RMS | Root Mean Square |
| p.u. | Per unit |
| IEEE | Institute of Electrical and Electronics Engineers |
| IEC | International Electrotechnical Commission |
| ANSI | American National Standards Institute |
| ARCERNNR | Agencia de Regulación y Control de Energía y Recursos Naturales no Renovables |
References
- Mangalapuri, S.; Sobhan, P.V. Analysis and Improvement of the Power Quality in Grid Integrated to Distributed Generation (Solar PV System) Using UPQC. In Proceedings of the 2023 International Conference on Advanced and Global Engineering Challenges, AGEC 2023, Kakinada, India, 23–24 June 2023; pp. 20–25. [Google Scholar] [CrossRef]
- Chindris, M.; Cziker, A.; Miron, A. UPQC—The best solution to improve power quality in low voltage weak distribution networks. In Proceedings of the 2017 International Conference on Modern Power Systems, MPS 2017, Cluj-Napoca, Romania, 6–9 June 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Saliganti, K.; Papana, V.P.; Erukula, V. Performance Analysis of Solar PV-UPQC for Enhanced Power Quality. J. Eur. Syst. Autom. 2025, 58, 149–159. [Google Scholar] [CrossRef]
- Bhosale, S.S.; Bhosale, Y.N.; Chavan, U.M.; Malvekar, S.A. Power Quality Improvement by Using UPQC: A Review. In Proceedings of the 2018 International Conference on Control, Power, Communication and Computing Technologies, ICCPCCT 2018, Kannur, India, 23–24 March 2018; pp. 375–380. [Google Scholar] [CrossRef]
- Ghosh, A.; Ledwich, G. Unified Power Quality Conditioner. In Power Quality Enhancement Using Custom Power Devices; Springer Nature: New York, NY, USA, 2018; pp. 379–406. [Google Scholar] [CrossRef]
- Pathik, B.B.; Islam, S.; Akram, N.M.; Zaman, M.S.; Al-Nahian, M.A. Total Harmonic Distortion Reduction in a Power Grid: A UPQC Based Approach. In Proceedings of the International Conference on Robotics, Electrical and Signal Processing Techniques, Dhaka, Bangladesh, 7–8 January 2023; pp. 264–268. [Google Scholar] [CrossRef]
- Gu, J.; Xu, D.; Liu, H.; Gong, M. Unified power quality conditioner (UPQC): The principle, control and application. In Proceedings of the Power Conversion Conference-Osaka 2002, PCC-Osaka 2002, Osaka, Japan, 2–5 April 2006; Volume 1, pp. 80–85. [Google Scholar] [CrossRef]
- Dash, S.K.; Ray, P.K.; Ray, P. Implementation of adaptive control strategies for PV system integrated unified conditioner for optimal power quality regulation. Results Eng. 2025, 26, 105122. [Google Scholar] [CrossRef]
- Namdev, P.; Singh, R. Advances in Power Quality Enhancement: A Comprehensive Review of Custom Power Devices and Mitigation Strategies. In Proceedings of the 2023 3rd International Conference on Energy, Power and Electrical Engineering, EPEE 2023, Wuhan, China, 15–17 September 2023; pp. 761–765. [Google Scholar] [CrossRef]
- Karelia, N.; Sant, A.V.; Pandya, V. Comparison of UPQC topologies for power quality enhancement in grid integrated renewable energy sources. In Proceedings of the 2019 IEEE 16th India Council International Conference, INDICON 2019—Symposium Proceedings, Rajkot, India, 13–15 December 2019. [Google Scholar] [CrossRef]
- Chourasia, M.; Srivastava, S.P.; Panda, A. Control strategy for voltage sag/swell/harmonic/flicker compensation with conventional and fuzzy controller(UPQC). In Proceedings of the India International Conference on Power Electronics, IICPE, Nagercoil, India, 19–20 March 2015; pp. 1–6. [Google Scholar] [CrossRef]
- IEEE Std 1159; IEEE Recommended Practice for Monitoring Electric Power Quality. IEEE: Piscataway, NJ, USA, 2009; Volume 1995, pp. 1–94.
- Hernández-Mayoral, E.; Jiménez-Román, C.R.; Enriquez-Santiago, J.A.; López-López, A.; González-Domínguez, R.A.; Ramírez-Torres, J.A.; Rodríguez-Romero, J.D.; Jaramillo, O.A. Power Quality Analysis of a Microgrid-Based on Renewable Energy Sources: A Simulation-Based Approach. Computation 2024, 12, 226. [Google Scholar] [CrossRef]
- Agencia de Regulación y Control de Energía y Recursos Naturales No Renovables. Regulación Nro. ARCERNNR 002/20 (Codificada); Agencia de Regulación y Control de Energía y Recursos Naturales No Renovables: Guayaquil, Ecuador, 2023; Volume 20, pp. 1–35.
- Yadav, S.K.; Patel, A.; Mathur, H.D. Comparison of power losses for different control strategies of UPQC. In Proceedings of the PIICON 2020—9th IEEE Power India International Conference, Delhi, India, 28 February–1 March 2020; pp. 3–8. [Google Scholar] [CrossRef]
- Da Silva, S.A.; Modesto, R.A.; Sampaio, L.P.; Campanhol, L.B. Dynamic Improvement of a UPQC System Operating under Grid Voltage Sag/Swell Disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 2844–2848. [Google Scholar] [CrossRef]
- Kaur, S.; Kaur, N. Analysis of Designed Power System with Power Quality Improvement by Using UPQC. In Proceedings of the International Conference on Self Sustainable Artificial Intelligence Systems, ICSSAS 2023—Proceedings, Erode, India, 8–20 October 2023; pp. 1719–1724. [Google Scholar] [CrossRef]
- Jaiswal, P.N.; Thakre, K.; Nigam, P. Comparison of DSTATCOM, DVR and UPQC for Mitigating Voltage Sag in Distribution System. In Proceedings of the 2022 IEEE 2nd International Symposium on Sustainable Energy, Signal Processing and Cyber Security, iSSSC 2022, Gunupur, India, 15–17 December 2022; pp. 7–12. [Google Scholar] [CrossRef]
- IEC 61000-2-4; Electromagnetic Compatibility (EMC)—Part 2-4: Environment—Compatibility Levels in Power Distribution Systems in Industrial Locations for Low-Frequency Conducted Disturbances. International Electrotechnical Commission: Geneva, Switzerland, 2023; Volume 2023.
- Águila Téllez, A.; López, G.; Isaac, I.; González, J.W. Optimal reactive power compensation in electrical distribution systems with distributed resources. Review. Heliyon 2018, 4, e00746. [Google Scholar] [CrossRef] [PubMed]
- Águila, A.; Ortiz, L.; Orizondo, R.; López, G. Optimal location and dimensioning of capacitors in microgrids using a multicriteria decision algorithm. Heliyon 2021, 7, e08061. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.P.; Yan, Z. Energy Quality: A Definition. IEEE Open Access J. Power Energy 2020, 7, 430–440. [Google Scholar] [CrossRef]
- Chawda, G.S.; Shaik, A.G.; Mahela, O.P.; Padmanaban, S.; Holm-Nielsen, J.B. Comprehensive Review of Distributed FACTS Control Algorithms for Power Quality Enhancement in Utility Grid with Renewable Energy Penetration. IEEE Access 2020, 8, 107614–107634. [Google Scholar] [CrossRef]
- IEEE Standard for Harmonic Control in Electric Power Systems; IEEE: Piscataway, NJ, USA, 2022.
- International Electrotechnical Commission (IEC). IEC 61000-2-12: Electromagnetic Compatibility (EMC)—Part 2-12: Environment—Compatibility Levels for Low-Frequency Conducted Disturbances and Signalling in Public Medium-Voltage Power Supply Systems; IEC: Geneva, Switzerland, 2003. [Google Scholar]
- International Electrotechnical Commission (IEC). IEC 60038:2009+AMD1:2021 CSV—Standard Voltages; IEC: Geneva, Switzerland, 2021. [Google Scholar]
- National Electrical Manufacturers Association (NEMA). ANSI C84.1-2020: American National Standard for Electric Power Systems and Equipment—Voltage Ratings (60 Hz); NEMA/ANSI: Rosslyn, VA, USA, 2020. [Google Scholar]
- Davidrajuh, R.; Rong, C. Solving Scheduling Problems with Randomized and Parallelized Brute-Force Approach. In Proceedings of the 12th International Conference on Computer Science and Information Technologies, CSIT 2019, Barcelona, Spain, 18–20 December 2019; pp. 1–4. [Google Scholar] [CrossRef]




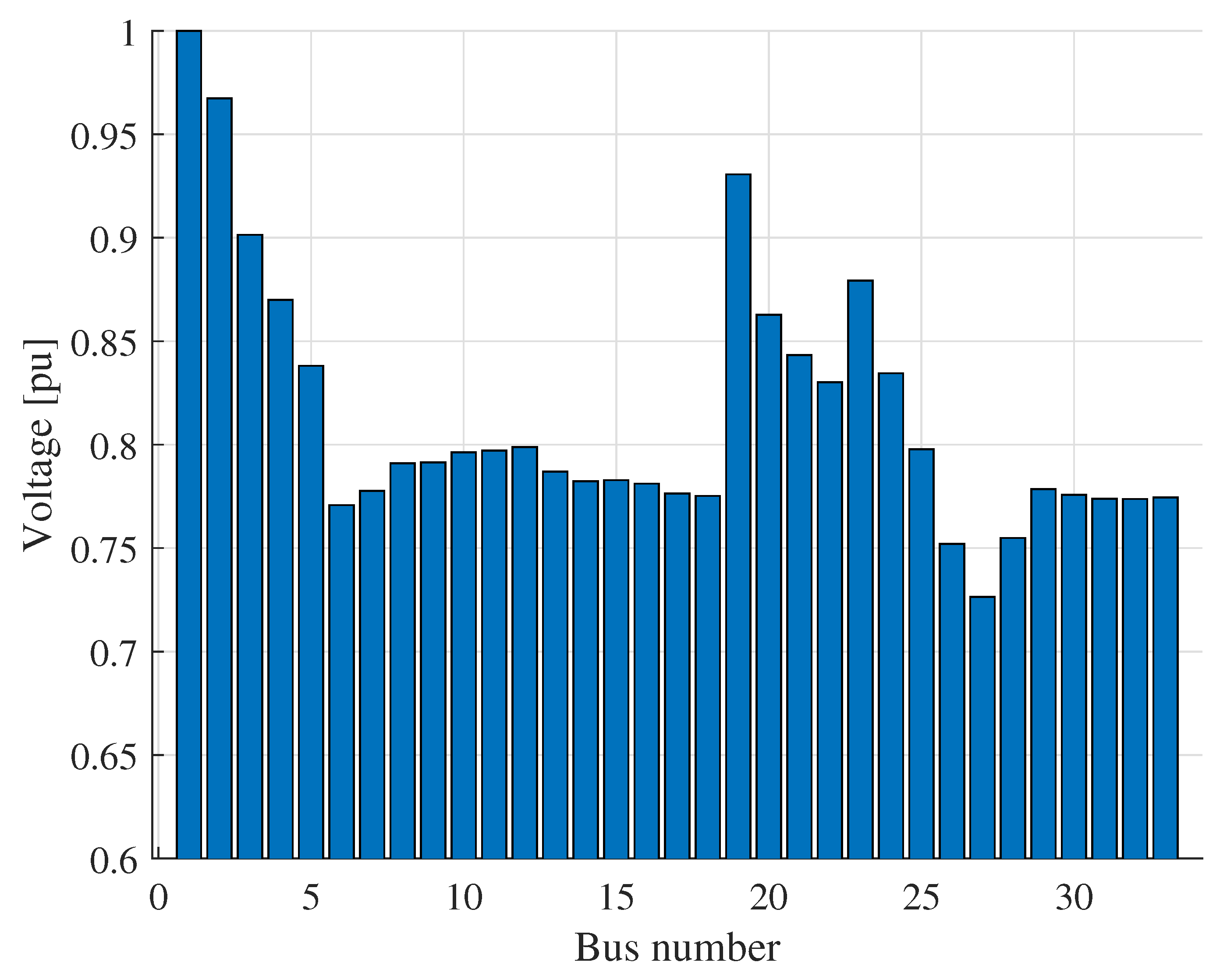

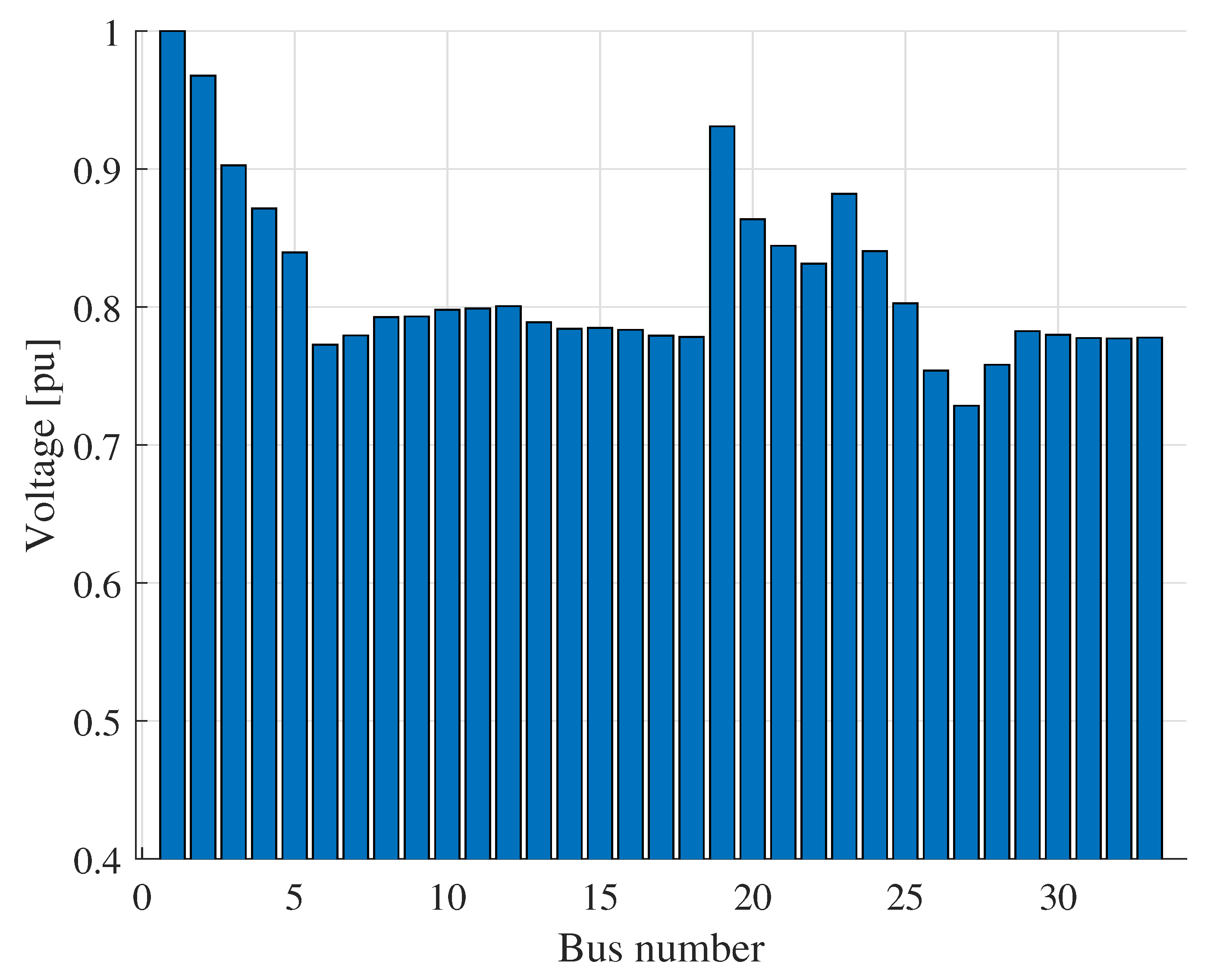










| Voltage | Current | Combined Function | |
|---|---|---|---|
| DVR | 🗸 | - | - |
| SVC | 🗸 | - | - |
| STATCOM | 🗸 | - | - |
| DSTATCOM | 🗸 | 🗸 | - |
| UPQC | 🗸 | 🗸 | 🗸 |
| Voltage Level | Individual Harmonics | THDv |
|---|---|---|
| Medium Voltage | 3% | 5% |
| Low Voltage | 5% | 8% |
| Approach/Family | Decision Scope (Typical) | Objectives (Typical) | Constraints (Typical) | Pros | Cons/Risks |
|---|---|---|---|---|---|
| Exhaustive (brute-force) search (this work) | Select UPQC bus/location over a reduced candidate set | THDv reduction, voltage deviation minimization (weighted multi-objective) | Operating limits; network feasibility | Global optimum guaranteed on small search spaces; simple, transparent; reproducible | Poor scalability with large spaces; impractical if many candidate buses or multi-device placement |
| Metaheuristics (PSO, GA/NSGA-II, ACO, DE, SA) [23] | Placement/sizing of compensation or control set-points; multi-device layouts | Multi-objective trade-offs (losses, THD, voltage profile, cost, reliability) | Device limits, voltage/current/thermal bounds; investment budgets | Handle large, nonconvex spaces; flexible with mixed/discrete variables | No global-optimality guarantees; parameter tuning needed; runs-to-run variability |
| Multicriteria/heuristic decision methods [20,21] | Placement and sizing (e.g., capacitors) in distribution networks | Combined technical indices (losses, voltage, THD) and economic criteria | Budgetary and operational constraints | Integrate technical–economic viewpoints; transparent weighting | Solution quality depends on criteria/weights and elicitation; may need ex-post feasibility checks |
| UPQC topology and control-focused works [2,4,5,7,10,11,15,17,18] | Converter topology; controller design/tuning; comparative device performance | Mitigation of sags/swells /THD, power factor, unbalance; dynamic response | Controller and device ratings; stability margins | Demonstrate mitigation efficacy and implementation aspects | Typically do not address siting as an optimization problem; limited system-level placement guidance |
| Scenario | Range | Ranking (Best → Worst) |
|---|---|---|
| Case 1 (no DG) | 14 ≺ (bus 14 always optimal) | |
| Case 2 (with DG) | 14 ≺ 19 ≺ 27 | |
| Case 2 (with DG) | 27 ≺ 19 ≺ 14 |
| Case | UPQC Location | Bus 14 | Bus 19 | Bus 27 |
|---|---|---|---|---|
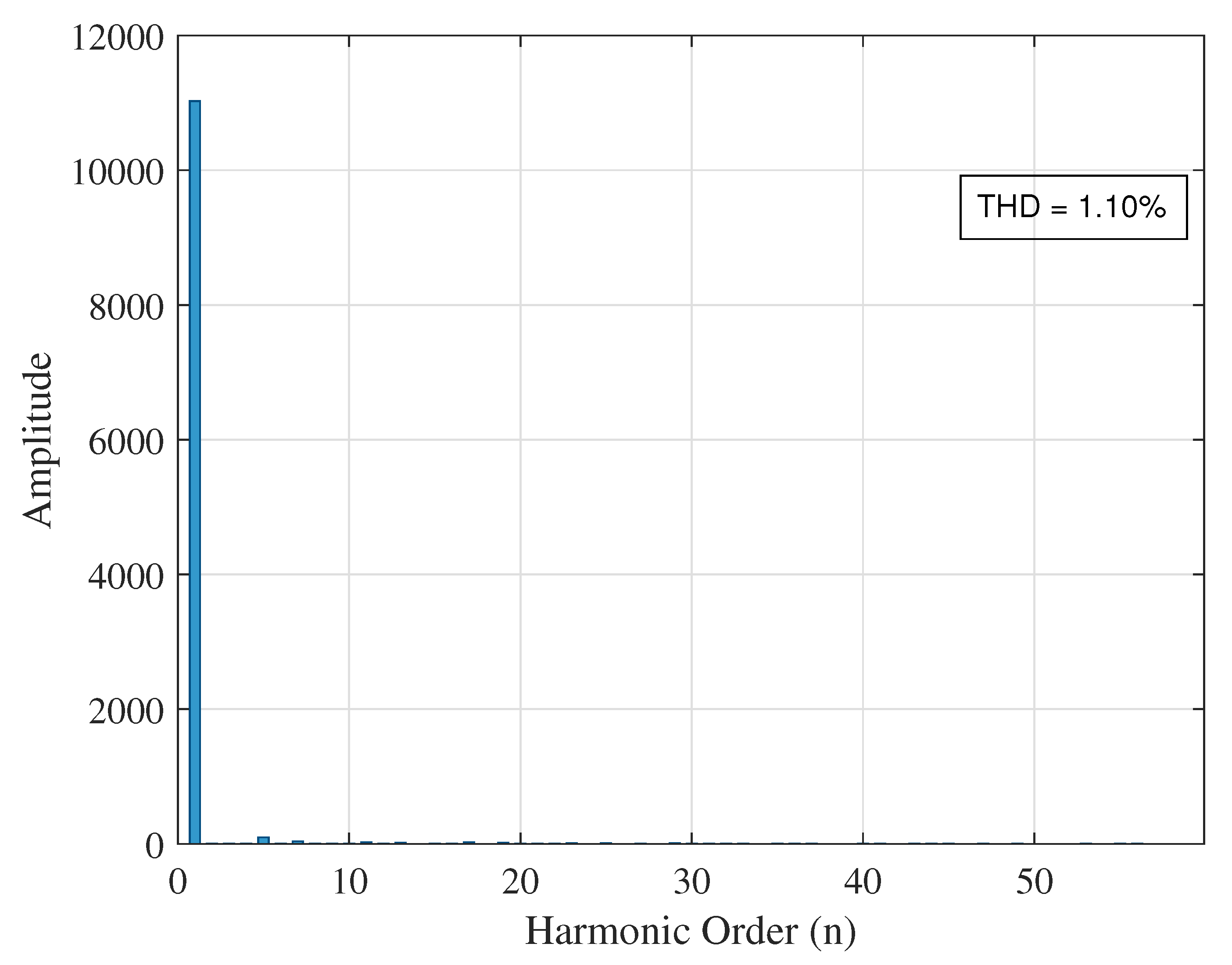
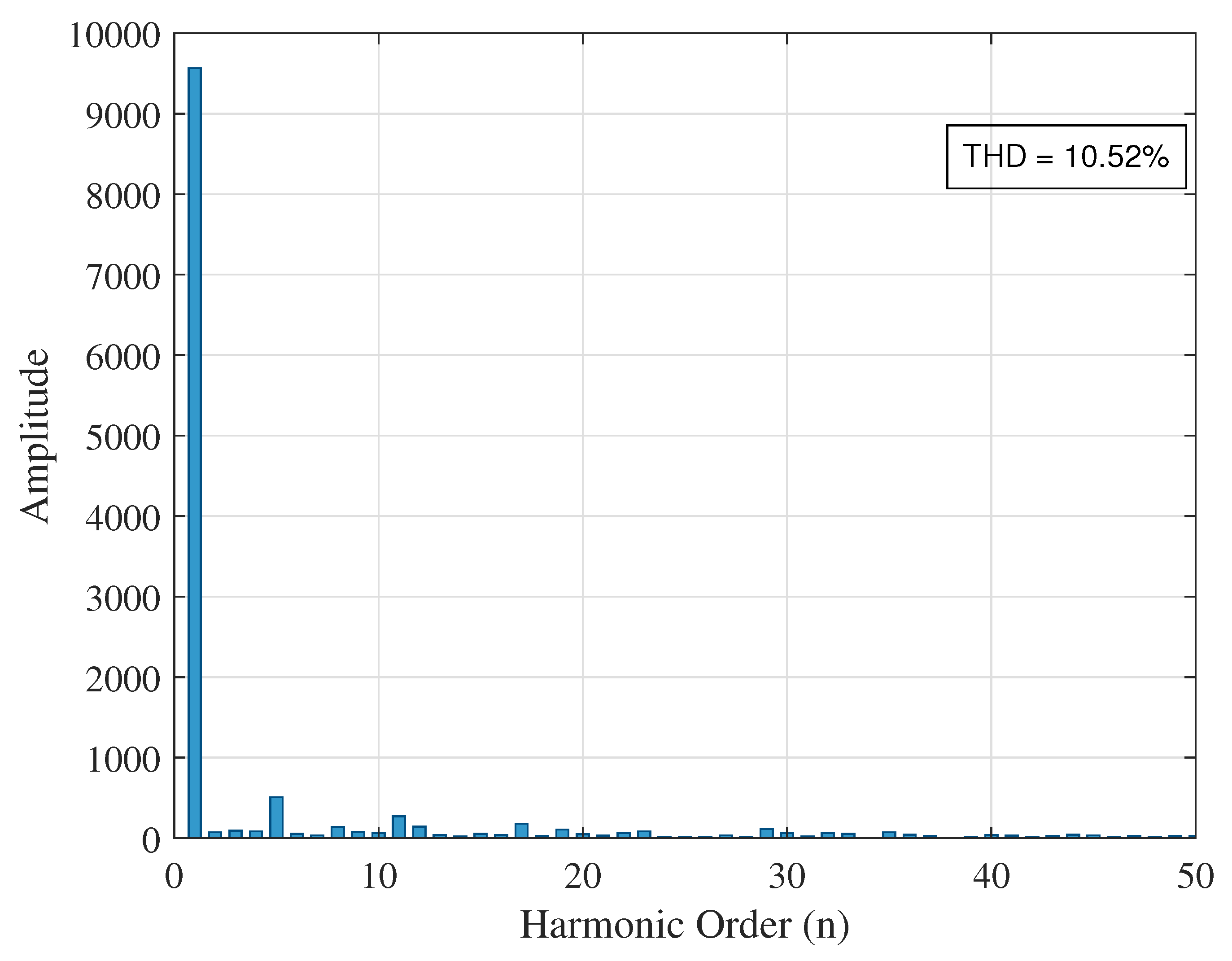
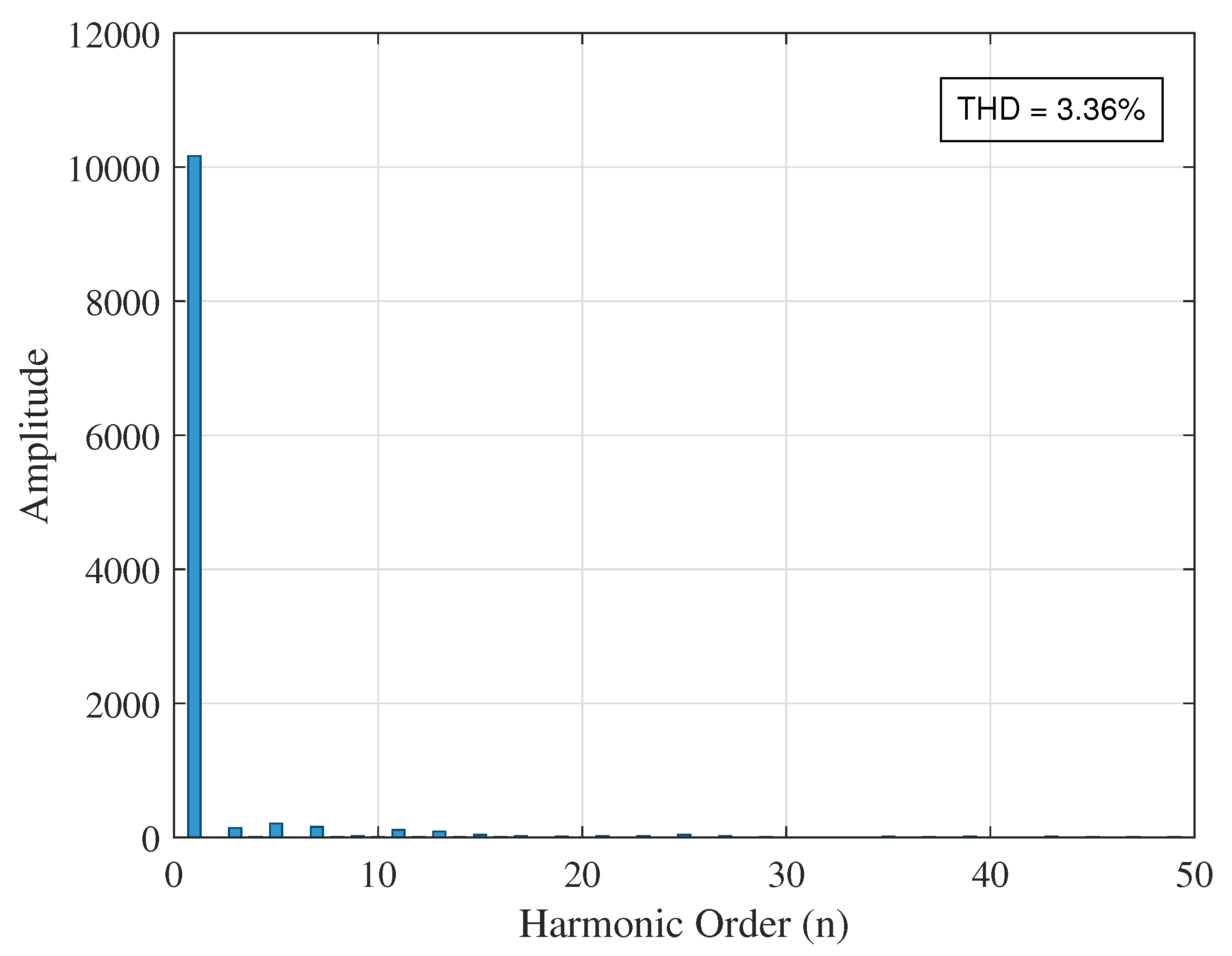
| Case 1 (No DG) | None (base) | 16.52 | 7.86 | 23.29 |
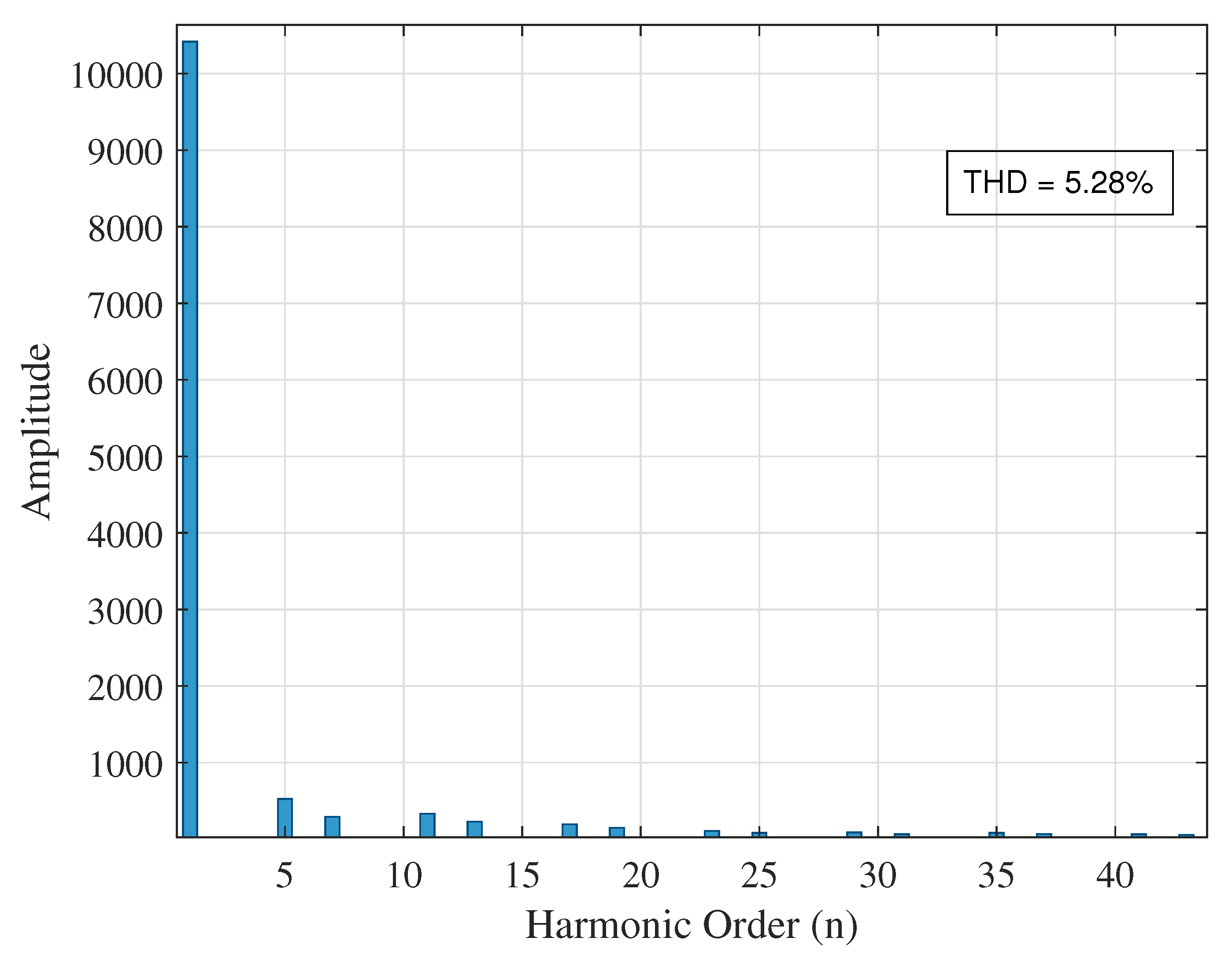
| At bus 14 | 1.10 | 4.76 | 10.52 | |
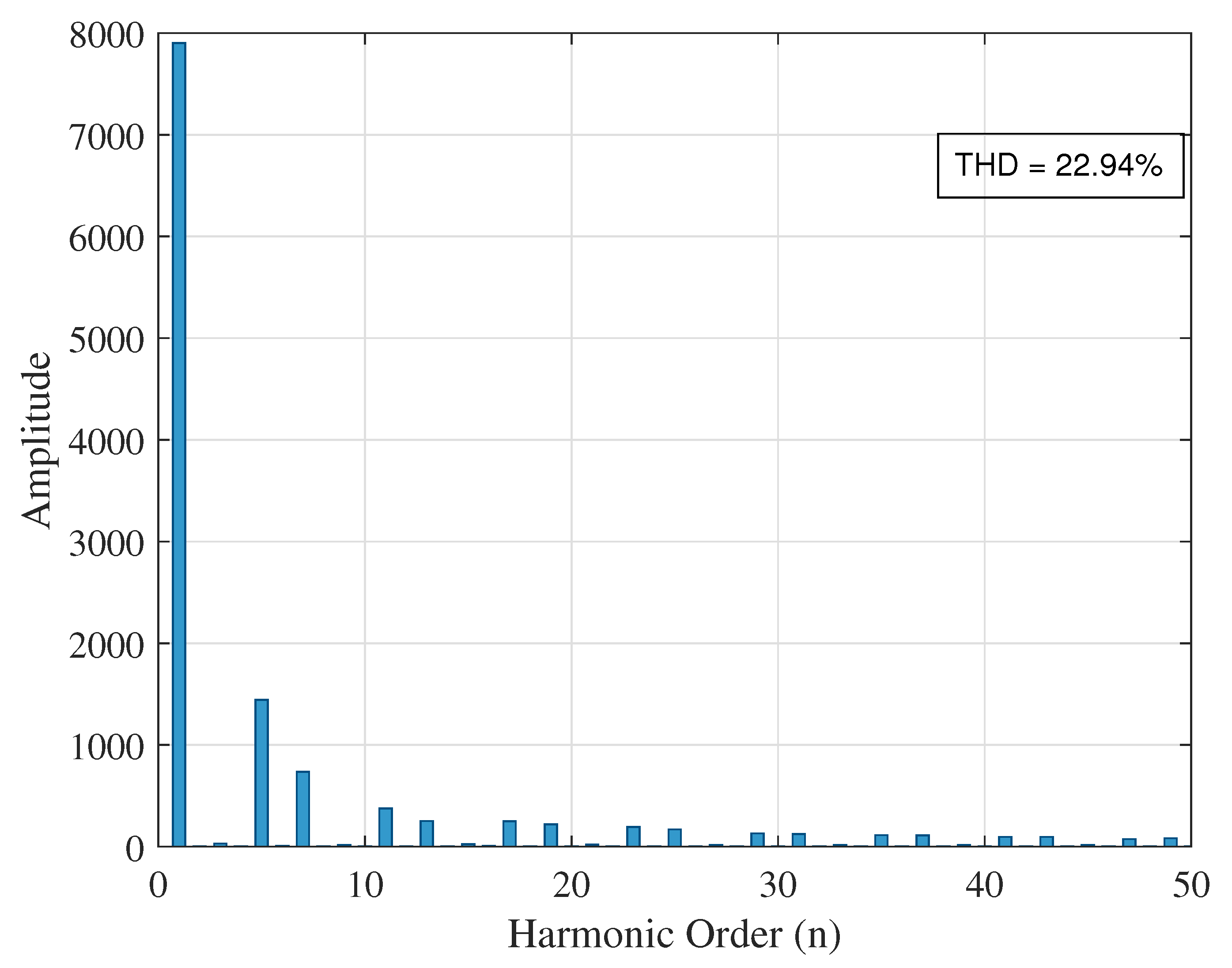
| At bus 19 | 15.01 | 3.36 | 22.94 | |
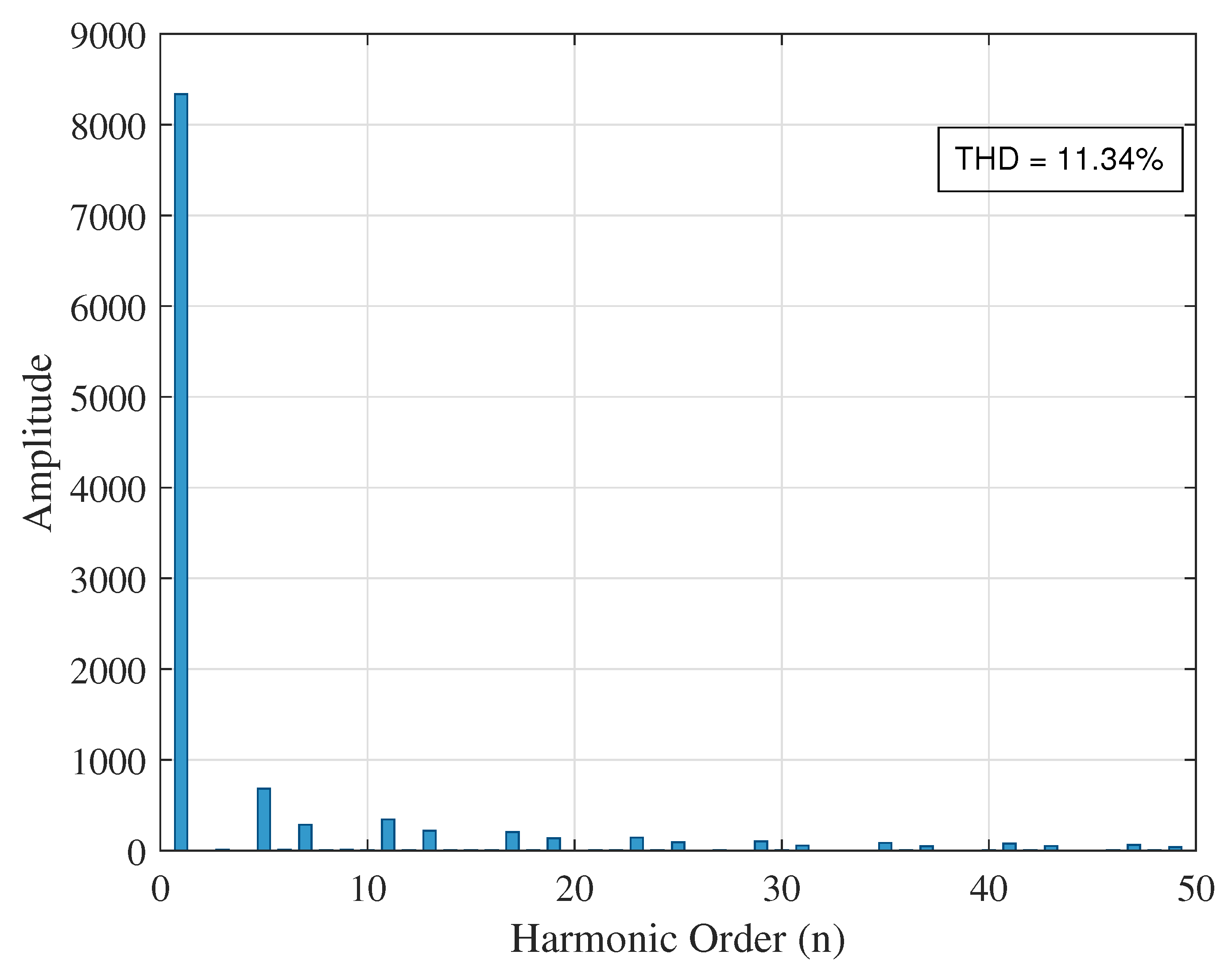
| At bus 27 | 11.34 | 5.28 | 11.91 | |
| Case 2 (With DG) | None (base) | 16.55 | 7.87 | 23.32 |
| At bus 14 | 1.08 | 4.75 | 11.39 | |
| At bus 19 | 9.54 | 2.90 | 5.53 | |
| At bus 27 | 4.81 | 0.69 | 10.57 |
| Scenario | Node | THDv (%) | Voltage Deviation (p.u.) | THDv Improvement (%) | |
|---|---|---|---|---|---|
| Case 1 (No DG) | 14 | 1.10 | 0.1896 | 0.00 | 93.34 |
| 19 | 3.36 | 0.1908 | 0.34 | 57.23 | |
| 27 | 11.91 | 0.2108 | 0.84 | 48.87 | |
| Case 2 (With DG) | 14 | 1.08 | 0.0668 | 0.26 | 93.47 |
| 19 | 2.90 | 0.1212 | 0.56 | 63.16 | |
| 27 | 10.57 | 0.2127 | 0.70 | 54.12 |
| Scenario | Condition | Mean THDv (%) | Std. Dev. (%) | Reduction vs. Base (%) |
|---|---|---|---|---|
| Case 1 (no DG) | Base (buses 14/19/27: 16.52, 7.86, 23.29) | 15.89 | 7.73 | – |
| Case 1 (no DG) | UPQC@14 (1.10, 4.76, 10.52) | 5.46 | 4.75 | 65.64 |
| Case 2 (with DG) | Base (16.55, 7.87, 23.32) | 15.91 | 7.74 | – |
| Case 2 (with DG) | UPQC@14 (1.08, 4.75, 11.39) | 5.74 | 5.23 | 63.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinosa Gutiérrez, J.S.; Aguila Téllez, A. Optimal Placement of a Unified Power Quality Conditioner (UPQC) in Distribution Systems Using Exhaustive Search to Improve Voltage Profiles and Harmonic Distortion. Energies 2025, 18, 4499. https://doi.org/10.3390/en18174499
Espinosa Gutiérrez JS, Aguila Téllez A. Optimal Placement of a Unified Power Quality Conditioner (UPQC) in Distribution Systems Using Exhaustive Search to Improve Voltage Profiles and Harmonic Distortion. Energies. 2025; 18(17):4499. https://doi.org/10.3390/en18174499
Chicago/Turabian StyleEspinosa Gutiérrez, Juan S., and Alexander Aguila Téllez. 2025. "Optimal Placement of a Unified Power Quality Conditioner (UPQC) in Distribution Systems Using Exhaustive Search to Improve Voltage Profiles and Harmonic Distortion" Energies 18, no. 17: 4499. https://doi.org/10.3390/en18174499
APA StyleEspinosa Gutiérrez, J. S., & Aguila Téllez, A. (2025). Optimal Placement of a Unified Power Quality Conditioner (UPQC) in Distribution Systems Using Exhaustive Search to Improve Voltage Profiles and Harmonic Distortion. Energies, 18(17), 4499. https://doi.org/10.3390/en18174499








