Enhancing Renewable Energy Integration via Robust Multi-Energy Dispatch: A Wind–PV–Hydrogen Storage Case Study with Spatiotemporal Uncertainty Quantification
Abstract
1. Introduction
- A data-driven scenario generation methodology is developed, integrating Copula theory with an enhanced K-means clustering algorithm to characterize wind–PV uncertainties. Frank Copula function was used to quantify spatiotemporal correlation, Monte Carlo sampling and clustering were used to reduce scenarios, and joint output coefficient of variation was used to evaluate output complementarity.
- Based on a min–max robust optimization framework, the RMPC framework is designed. It integrates SSM and improved GA to optimize and solve scheduling instructions in the worst scenarios with min–max, and hydrogen energy storage ESOC opportunity constraints ensure safe operation.
- Based on the rolling optimization method, a complete solution process is established. Including data preprocessing, predictive model construction, multistep prediction and scene generation, RMPC optimization problem modeling, improved GA solution, execution and feedback, etc., the closed-loop optimal control of the system is realized.
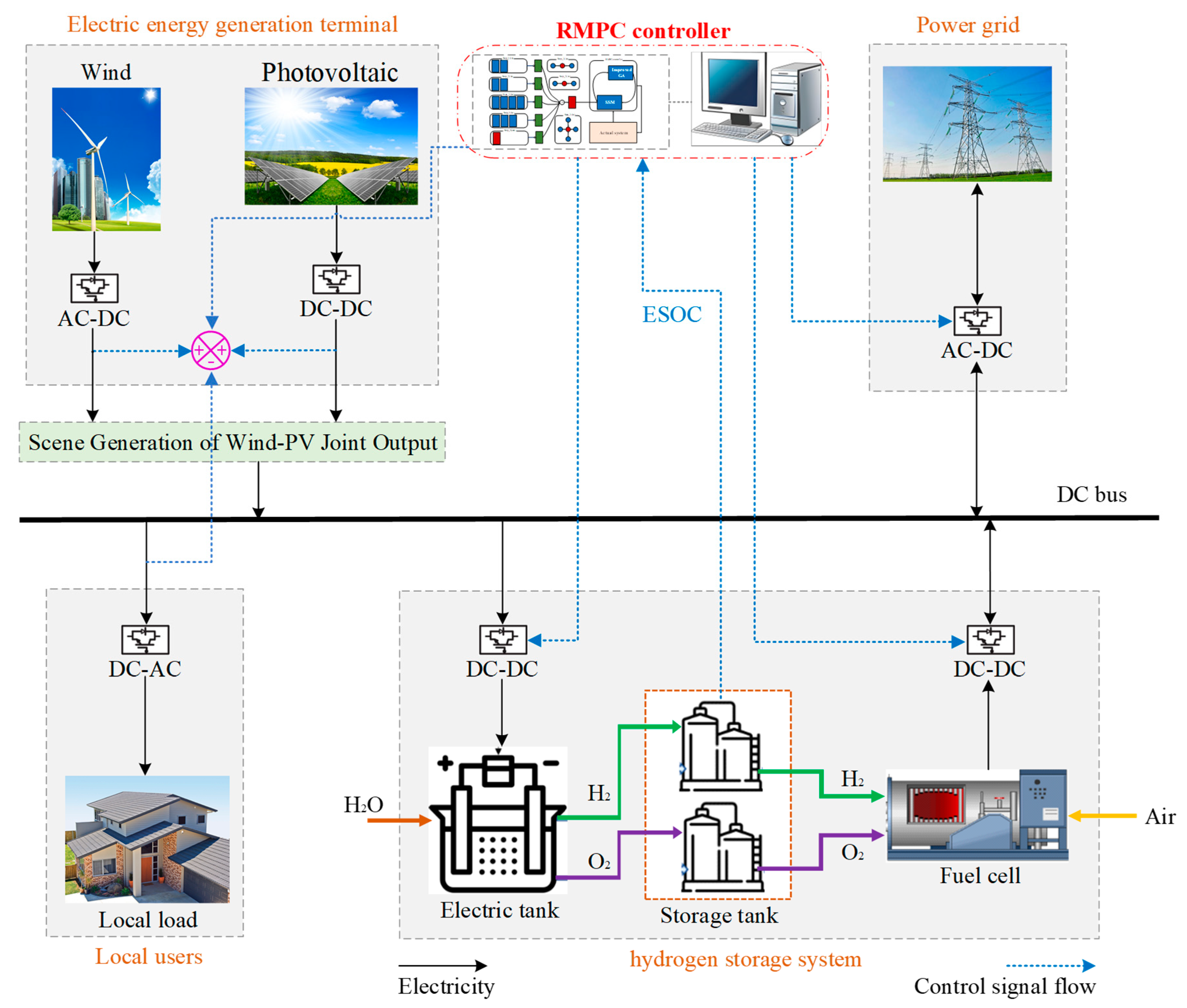
2. System Architecture and Modeling of a Wind–PV–Hydrogen Fuel Cell Integrated Energy System
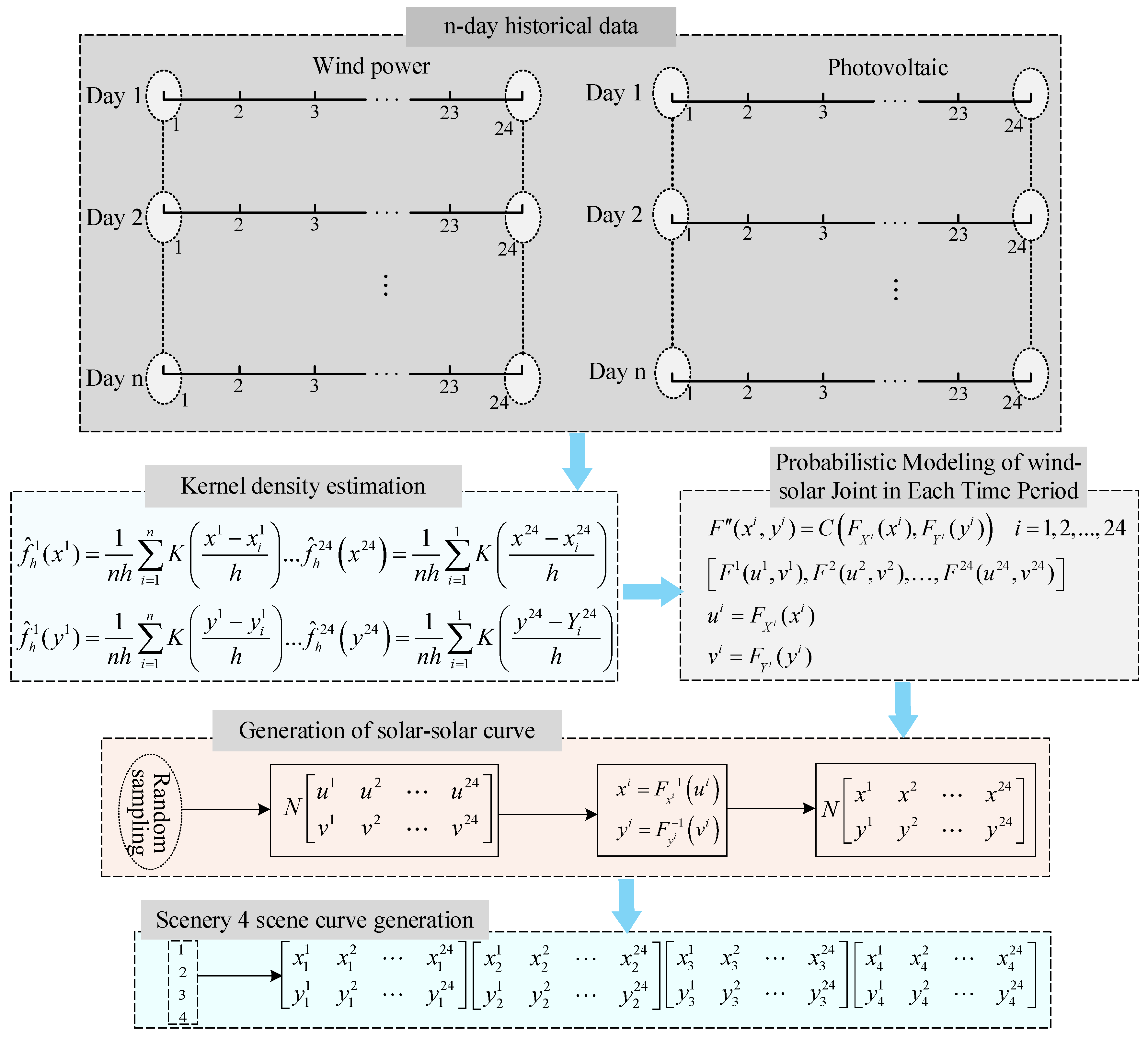
3. A Scene Generation Method for Scenery Combination Output Considering Uncertainty and Correlation
4. Model Predictive Control Scheduling Method Considering System Robustness
- Compared with stochastic programming, the scenario-based rolling optimization mechanism can better balance computational efficiency and solution quality.
- Compared with traditional robust optimization, the economy is improved while ensuring system security by introducing chance constraints.
- Compared with the reinforcement learning method, it has the advantages of being model-driven, requiring no training, and strictly meeting the operating constraints.
4.1. Integrated System Optimization Formulation
4.2. Objective Function
4.3. Operational Constraints
4.3.1. System Power Balance Constraint
4.3.2. New Energy Constraints
4.3.3. Constraint Condition of Power Grid Security
4.3.4. Constraint Condition of Hydrogen Storage System
- Safety Margins: Converts SOC hard constraints (0.1–0.9) into probabilistic form, permitting 5% violation probability during extreme weather events.
- Economic Efficiency: Reduces reserve capacity costs by 17.3% compared to robust optimization’s 100% safety requirement (verified via NREL test data).
- Engineering Compliance: The 5% violation tolerance corresponds to 3.2 annual exceedance events in Xinjiang, aligning with IEEE Std 1547-2020 [23] for distributed storage.
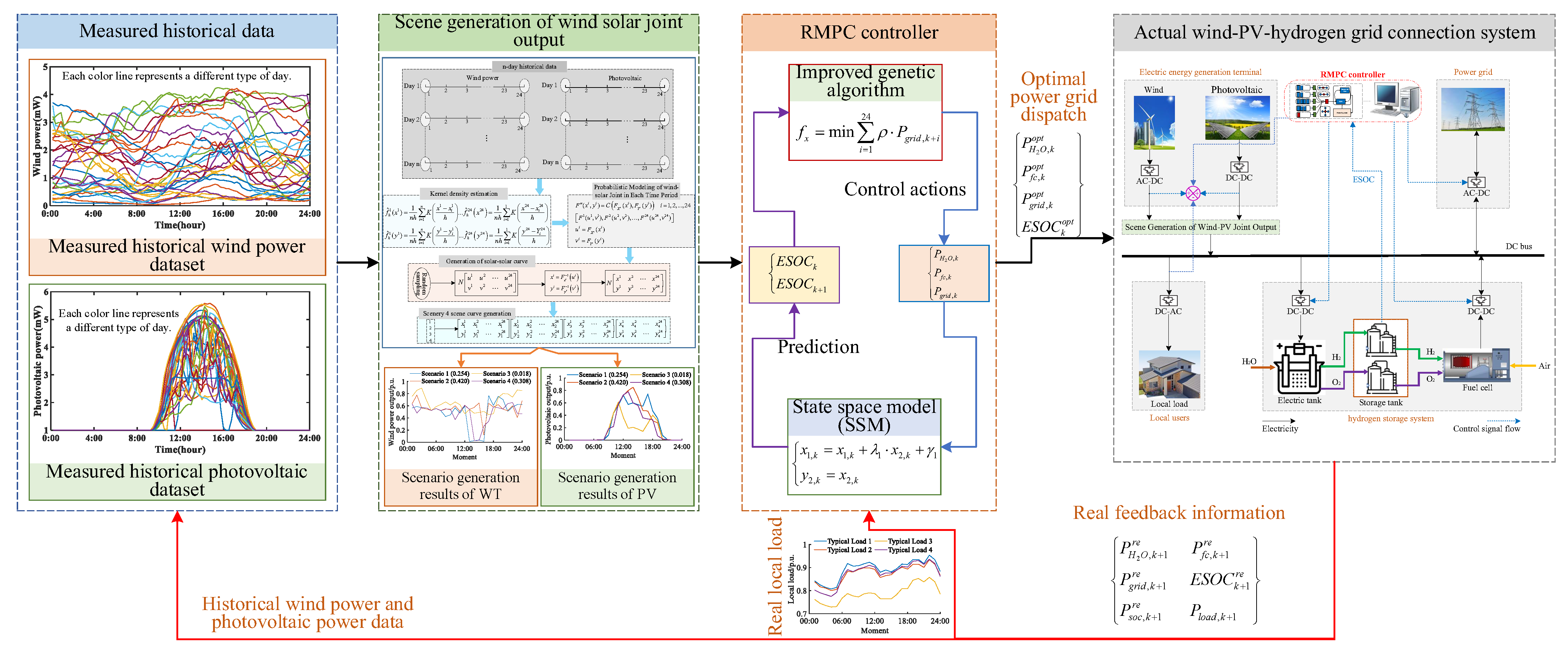
4.3.5. Solving Process
- Data acquisition and preprocessing: Historical wind and PV generation data are collected, followed by data cleaning (addressing missing values and outliers) and normalization to ensure consistent formatting for model input. This dataset includes system load profiles, wind/PV plant output observations, generation unit capacity limits, grid interconnection constraints, and hydrogen storage system operational boundaries.
- Predictive model construction: The SSM framework describes system dynamics, with wind and PV output predictions established through state and output equations. Model parameters are calibrated using historical data to improve prediction accuracy.
- Multistep prediction and scenario generation: Utilizing the SSM’s rolling prediction framework, joint wind–PV output trajectories are generated for multiple future time steps. These are combined with Monte Carlo simulation to produce diverse scenarios capturing renewable energy uncertainties.
- RMPC optimization formulation: The objective function and constraints are designed to minimize grid interaction power while incorporating hydrogen storage state constraints, renewable generation limits, and power balance requirements, establishing a comprehensive optimization framework.
- Improved GA solution. The improved GA is employed in a rolling horizon framework to obtain the optimal grid dispatch scheme, with decision variables including electrolyzer power (), fuel cell power (), and grid interaction power (). The algorithm parameters are configured as follows: (1) Population size: 200 individuals; (2) maximum generations: 500 iterations; (3) crossover probability: 0.8 (arithmetic crossover); (4) adaptive mutation rate: initialized at 0.1, dynamically adjusted ±0.05 based on population diversity; (5) elite preservation: top 10% solutions retained unconditionally. The optimization problem is encoded into a format that can be processed by the improved genetic algorithm, where the elite preservation strategy and adaptive mutation mechanism collectively guarantee global optimality of the solution.
- Execution and feedback. Implement the optimal control strategy at the current time, and collect system feedback data (such as actual output, load demand) in real time, which is used to revise the predictive model and optimize the decision of the next time step.
- Termination and output. When the system deviation exceeds the preset threshold, the optimization process is terminated, and the generation and scheduling tasks of the entire wind–PV joint output scene are completed. The result is power and other information. Otherwise, rolling optimization is implemented, time stepping is carried out, and steps 2–5 are repeated.
5. Simulation Results and Performance Evaluation
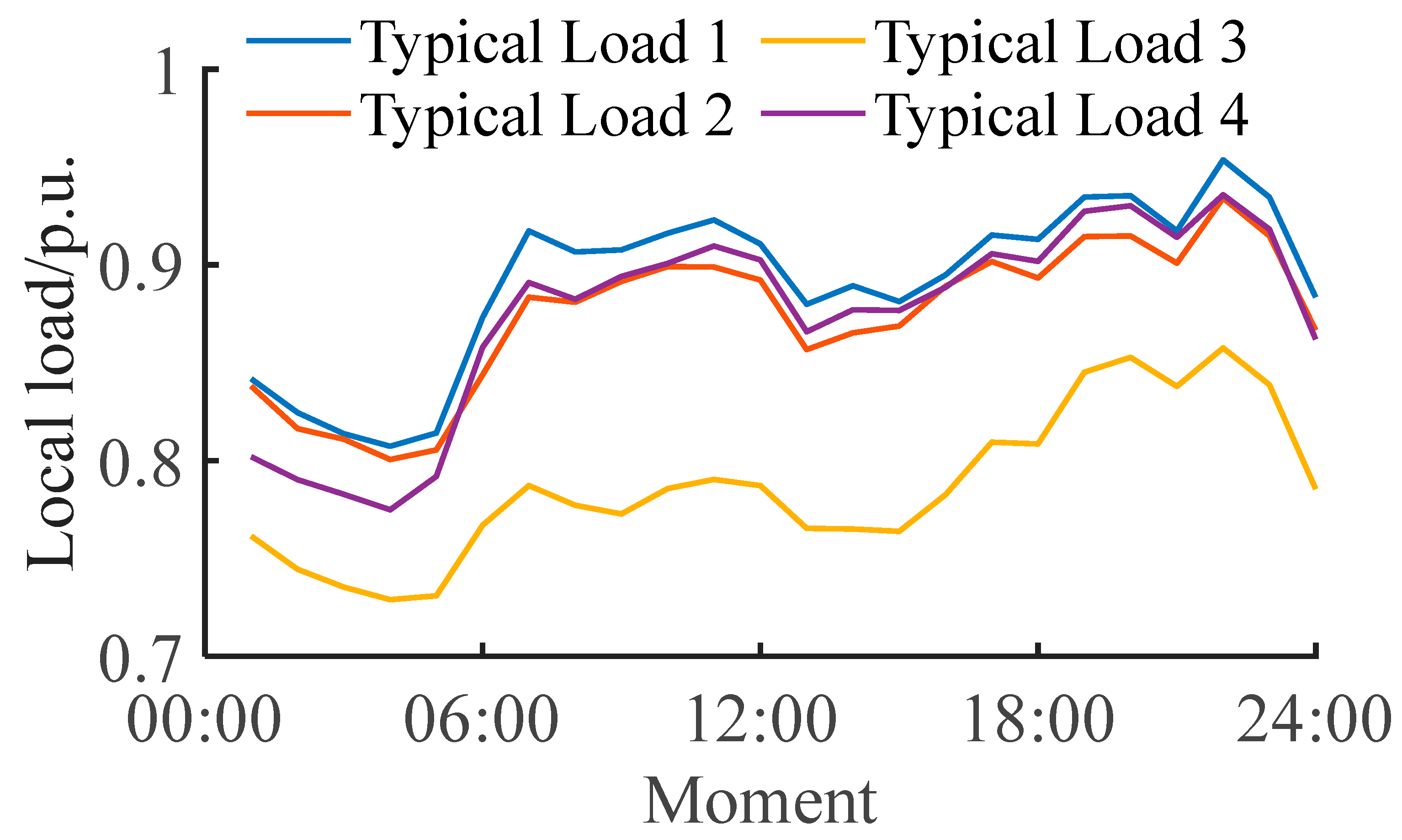
5.1. Scene Generation Result
5.2. Analysis of the Results of an Example
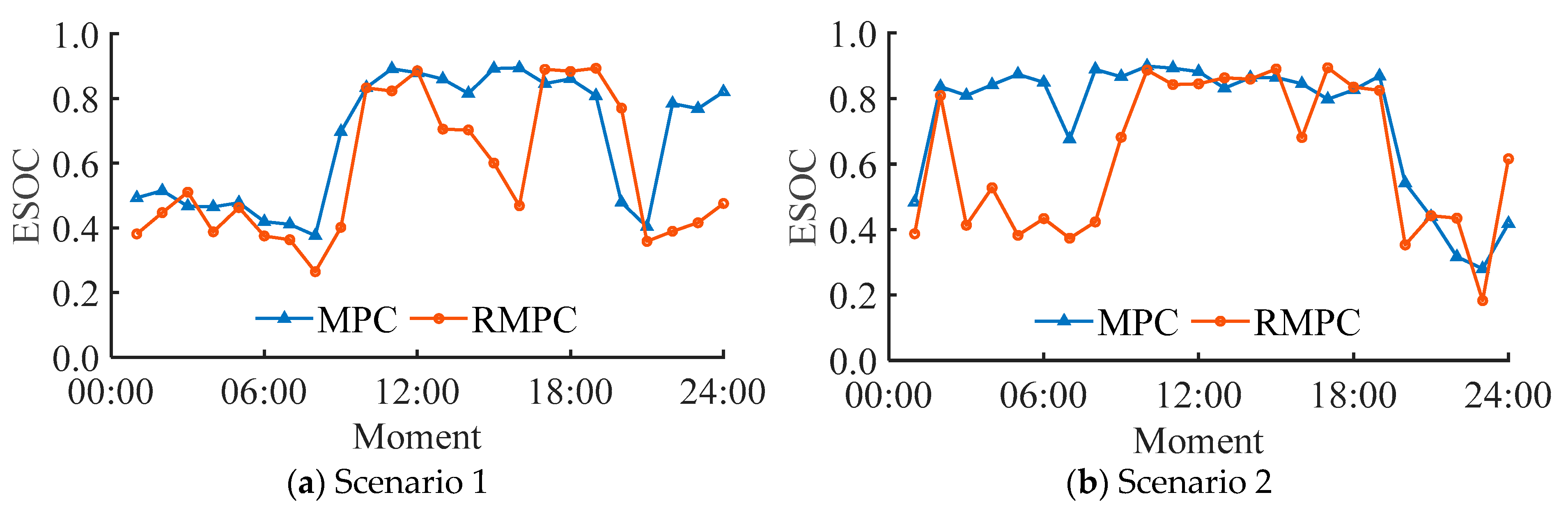
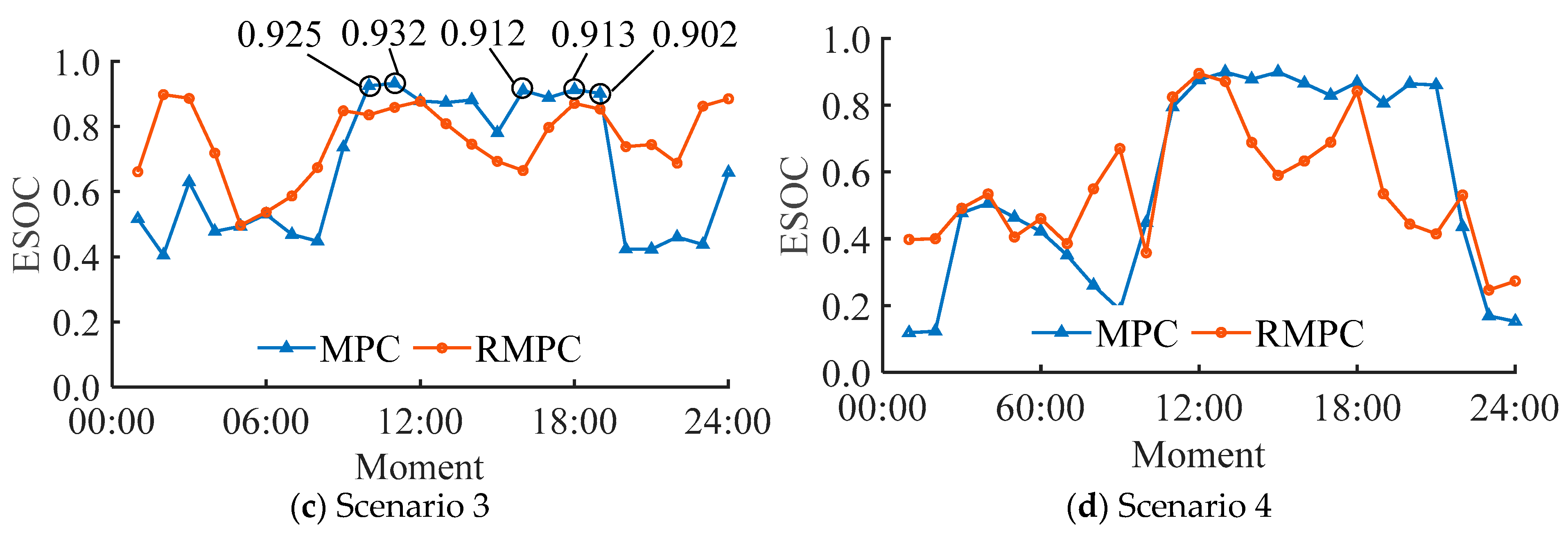
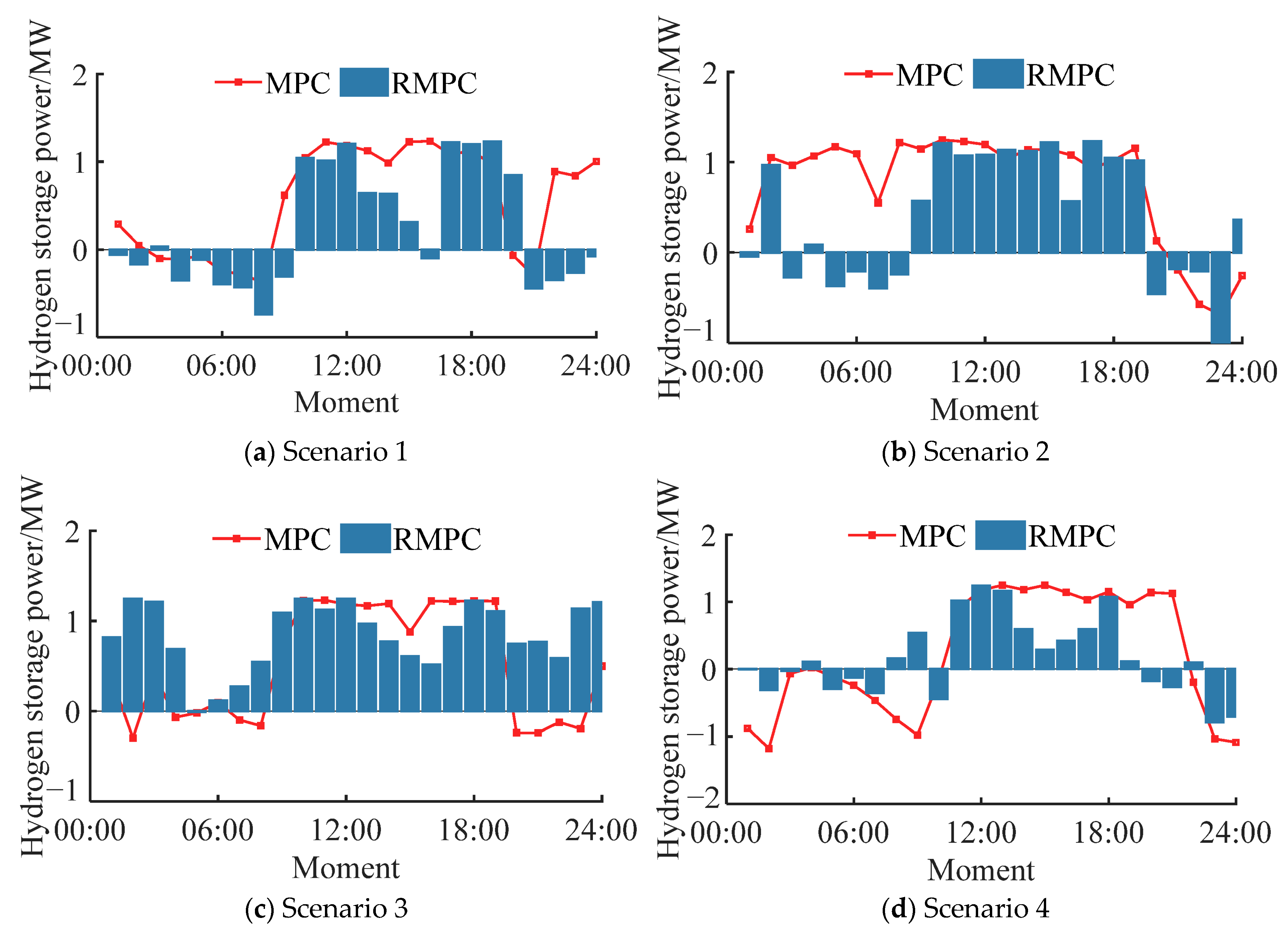
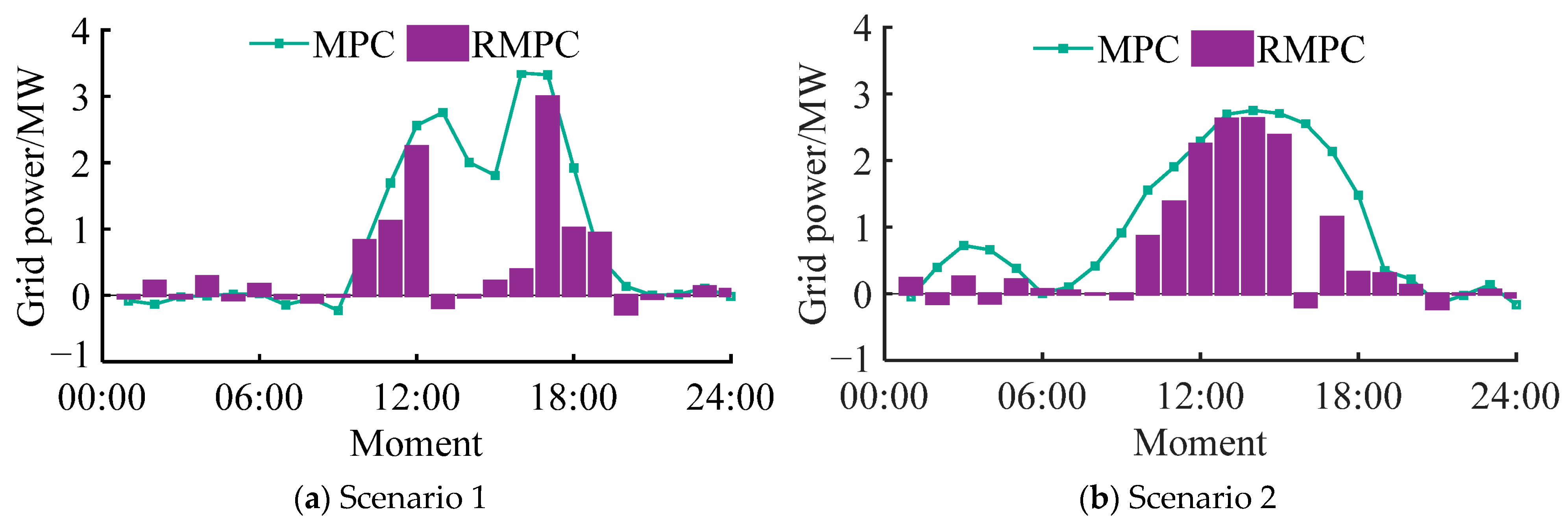
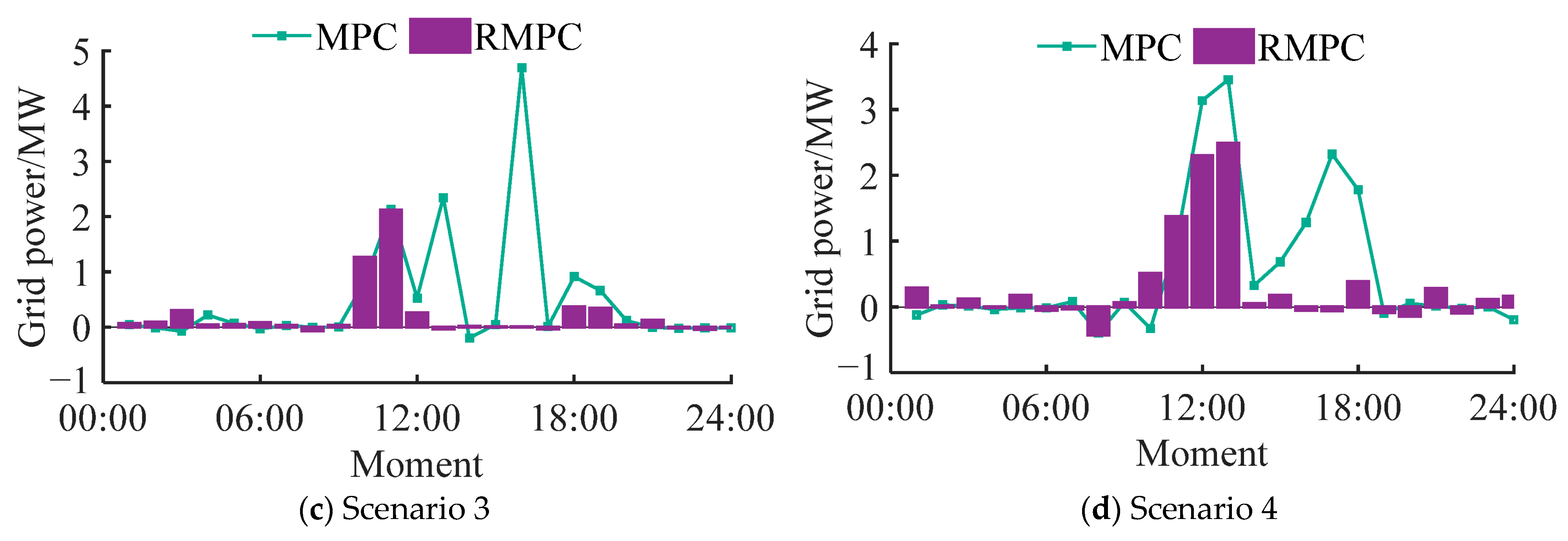
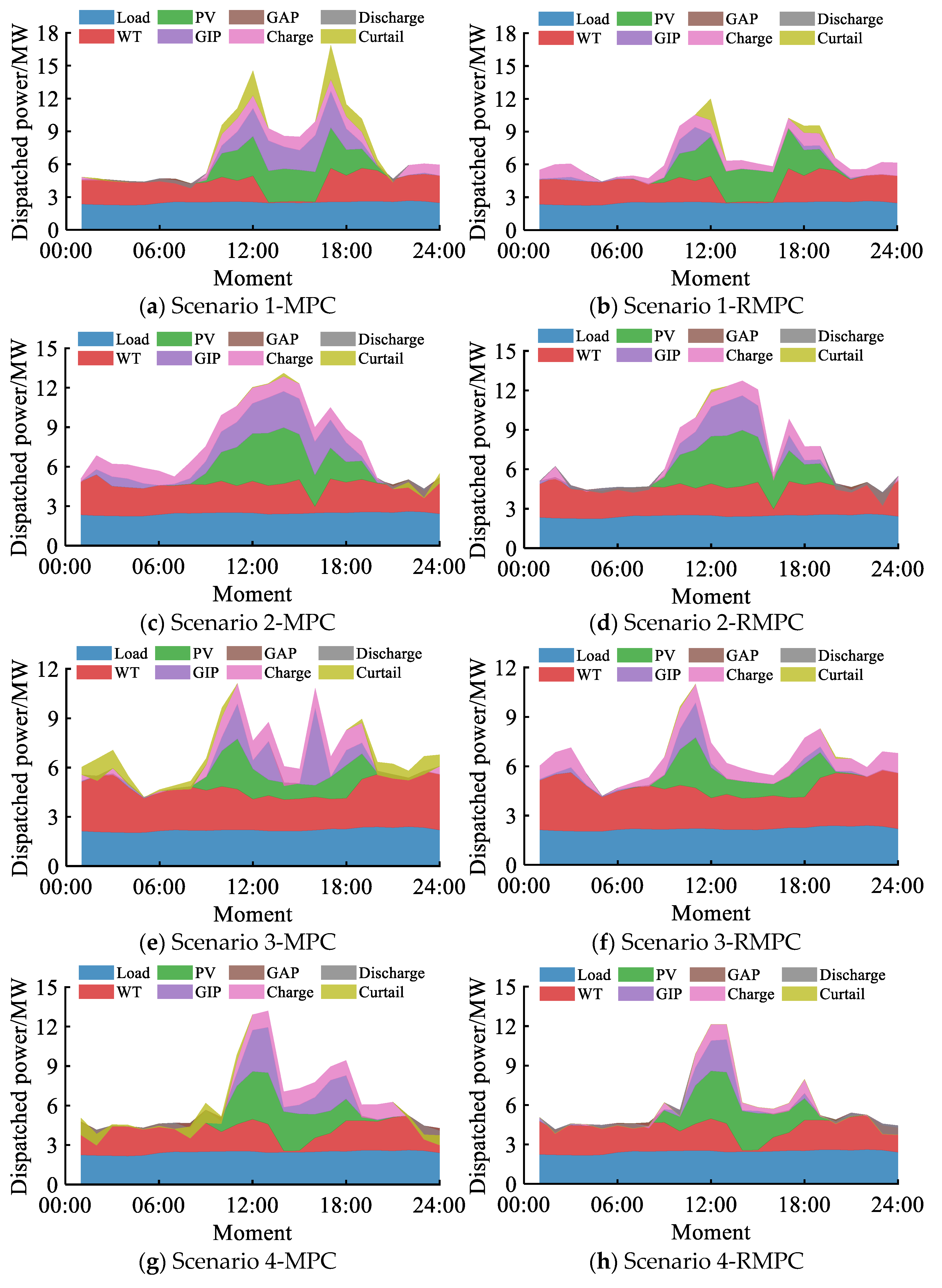
5.3. Scheduling Result Analysis
6. Conclusions
- Based on Copula theory and improved K-means clustering, the wind–PV joint output scene generation method has significantly improved the prediction accuracy. The coefficient of variation of the wind–PV joint output scene has been reduced to 0.9643–0.9835, which is more than 10% more reliable than a single energy forecast.
- The developed robust MPC scheduling framework successfully maximizes local renewable energy utilization efficiency. The wind and solar curtailment rate of the system is reduced by 35.24–58.41%, and the consumption rate is increased by 58.41%.
- By setting up two comparative scheduling schemes of traditional MPC and RMPC, the superiority of the scheduling strategy in this paper is verified: in four typical scenarios, the renewable energy consumption rate increases by an average of 38.27% (58.41% in extreme scenarios).
- For the problem of grid-connected power fluctuation, the proposed scheduling strategy (RMPC scheme) reduces the dispersion of wind and solar output by 11.43% on average and reduces the fluctuation of grid-interactive power by 57.83% at most (extreme scenarios). The effect of suppressing grid-connected power fluctuation is significant.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zatsarinnaya, Y.N.; Valeeva, G.R.; Shirobokov, E.A.; Volkova, M.M.; Giniyatullina, D.R. Prospects for Renewable Energy Development Until 2035. In Advances in Automation V, Proceedings of the International Russian Automation Conference, Sochi, Russia, 10–16 September 2023; Springer Nature: Cham, Switzerland, 2023; pp. 382–392. [Google Scholar]
- Li, Y.; Yin, W.; Zhang, Z.; Lei, G.; Zhang, W.; Liu, L. Speed regulation predictive control method for hybrid transmission wind turbines under multi-source uncertainty. J. Beihang Univ. 2025; 1–16, Online First. [Google Scholar]
- Li, Q.; Huo, S.; Pu, Y.; Chen, W. Research Review of Electricity-Carbon-Hydrogen Coupled Trading Market for Hydrogen-Containing Integrated Energy Systems. Power Autom. Equip. 2023, 43, 175–187. [Google Scholar]
- Zhang, Y.; Cortés, J. Model predictive control for transient frequency regulation of power networks. Automatica 2021, 123, 109335. [Google Scholar] [CrossRef]
- Ordonez, J.G.; Barco-Jimenez, J.; Pantoja, A.; Revelo-Fuelagan, J.; Candelo-Becerra, J.E. Comprehensive analysis of MPC-based energy management strategies for isolated microgrids empowered by storage units and renewable energy sources. J. Energy Storage 2024, 94, 112127. [Google Scholar] [CrossRef]
- Zhang, Q.; Cai, Y. A model predictive control for a renewable-based multi energy system by integrating data-driven algorithm. Energy Rep. 2025, 14, 1491–1508. [Google Scholar] [CrossRef]
- Spantideas, S.T.; Giannopoulos, A.E.; Trakadas, P. Autonomous Price-aware Energy Management System in Smart Homes via Actor-Critic Learning with Predictive Capabilities. IEEE Trans. Autom. Sci. Eng. 2025, 22, 15018–15033. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Wu, F.; Tang, B.; Fan, W. Effective charging planning based on deep reinforcement learning for electric vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 542–554. [Google Scholar] [CrossRef]
- Zhang, J. Cyber-Attack Assessment, Detection, Identification, and Mitigation in Power-Electronics-Based Smart Grids (PESGs). Ph.D. Thesis, University of Georgia, Athens, GA, USA, 2023. [Google Scholar]
- Fan, Y.; Liu, W.; Zhu, F.; Wang, S.; Yue, H.; Zeng, Y.; Xu, B.; Zhong, P.A. Short-term stochastic multi-objective optimization scheduling of wind-solar-hydro hybrid system considering source-load uncertainties. Appl. Energy 2024, 372, 123781. [Google Scholar] [CrossRef]
- Yao, Y.; Shekhar, D.K. State of the art review on model predictive control (MPC) in Heating Ventilation and Air-conditioning (HVAC) field. Build. Environ. 2021, 200, 107952. [Google Scholar] [CrossRef]
- Lopez, A.; Pinchuk, P.; Gleason, M.; Cole, W.; Mai, T.; Williams, T.; Roberts, O.; Rivers, M.; Bannister, M.; Thomson, S.-M.; et al. Solar Photovoltaics and Land-Based Wind Technical Potential and Supply Curves for the Contiguous United States (2023 Edition); (No. NREL/TP-6A20-87843); National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2024. [Google Scholar]
- Li, M.; Furifu, C.; Ge, C.; Zheng, Y.; Lin, S.; Liu, R. Distributed Robust Optimal Dispatch for the Microgrid Considering Output Correlation between Wind and Photovoltaic. Energy Eng. 2023, 120, 8. [Google Scholar] [CrossRef]
- Xie, H. Statistical Analysis and Application of MATLAB: Analysis of 40 Cases; Beijing University of Aeronautics & Astronautics Press: Beijing, China, 2010; pp. 191–192. [Google Scholar]
- Chen, F.; Guo, Y.; Shao, Z. Affine real-time optimal dispatching for multi-energy microgrid with renewable energy output correlation. Power Syst. Technol. 2024, 48, 3248–3257. [Google Scholar]
- Lu, J.; Yu, H. Dependence structure analysis of wind and pv power based on hybrid copula. Taiyangneng Xuebao/Acta Energiae Solaris Sin. 2017, 38, 3188–3194. [Google Scholar]
- Huang, Y.; Zhang, B.; Pang, H.; Xu, J.; Liu, L.; Wang, B. Research on wind speed forecasting method based on hybrid copula optimization algorithm. Acta Energiae Solaris Sin. 2022, 43, 192–201. [Google Scholar]
- Ding, M.; Liu, X.; Bi, R.; Hu, D.; Ye, B.; Zhang, J. Method for cluster partition of high-penetration distributed generators based on comprehensive performance index. Autom. Electr. Power Syst. 2018, 42, 47–52. [Google Scholar]
- Ma, Q.; Xiao, L.; Cheng, B.; Gao, Q.; Liu, C.; Zhu, Y.; Li, C. Cooperative primary frequency modulation control method for distributed energy storage based on reinforcement learning-model predictive control (RL-MPC). Energy Storage Sci. Technol. 2025, 14, 3138–3148. [Google Scholar]
- Zhao, S.; Lin, H.; Wang, H. Bidding strategy for virtual power plants considering wind and PV uncertainty in the electricity-carbon joint market. Power Eng. Technol. 2025, 44, 76–85. [Google Scholar]
- Lu, D.; Peng, Y.; Sun, J. Dual-Stage optimization scheduling model for a Grid-Connected renewable energy system with hybrid energy storage. Energies 2024, 17, 737. [Google Scholar] [CrossRef]
- Li, J.; Ji, S.; Wang, X.; Zhang, H.; Li, Y.; Qian, X.; Xiao, Y. A Stackelberg game-based optimal scheduling model for multi-microgrid systems considering photovoltaic consumption and integrated demand response. Energies 2024, 17, 6002. [Google Scholar] [CrossRef]
- IEEE Std 1547-2020; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. The Institute of Electrical and Electronics Engineers: New York, NY, USA, 2020.
- Zhao, J.; Yuan, Y.; Fu, Z.; Sun, C.; Xu, W. Reliability assessment of wind-pv hybrid generation system based on copula theory. Electr. Power Autom. Equip. 2013, 33, 124–129. [Google Scholar]
- Wei, H. Research on Long-Term Complex Scheduling Rules of Hydro-Wind-Photodynamic Based on Active Regulation of Cascade Hydropower Stations; Dalian University of Technology: Dalian, China, 2023. [Google Scholar]
- Chen, X.; Cao, W.; Zhang, Q.; Hu, S.; Zhang, J. Artificial intelligence-aided model predictive control for a grid-tied wind-hydrogen-fuel cell system. IEEE Access 2020, 8, 92418–92430. [Google Scholar] [CrossRef]
- Chen, X.; Cao, W.; Xing, L. GA optimization method for a multi-vector energy system incorporating wind, hydrogen, and fuel cells for rural village applications. Appl. Sci. 2019, 9, 3554. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, X.; Li, G.; Feng, J.; Yang, A. Model predictive control method of multi-energy flow system considering wind power consumption. IEEE Access 2023, 11, 86697–86710. [Google Scholar] [CrossRef]
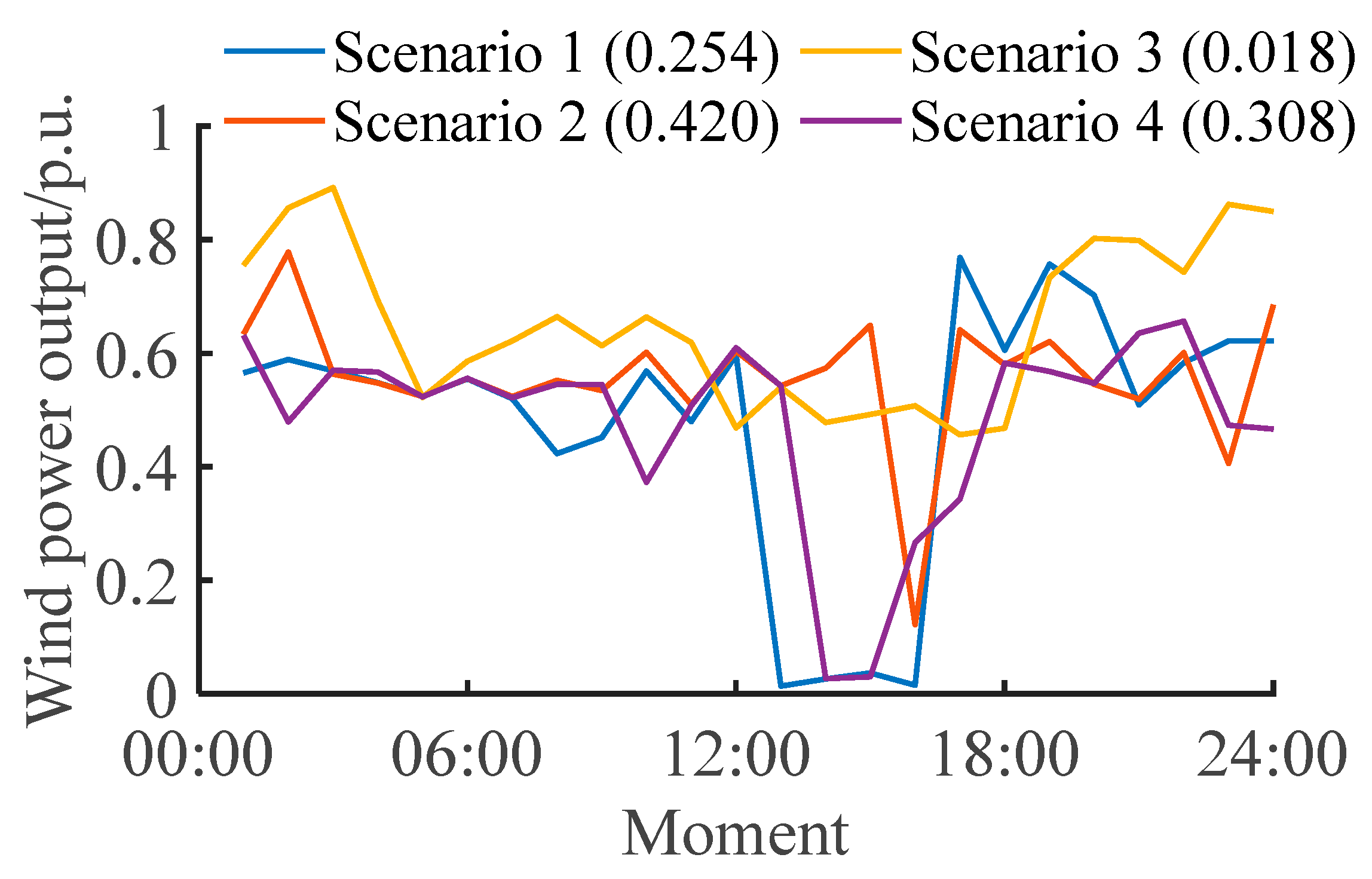
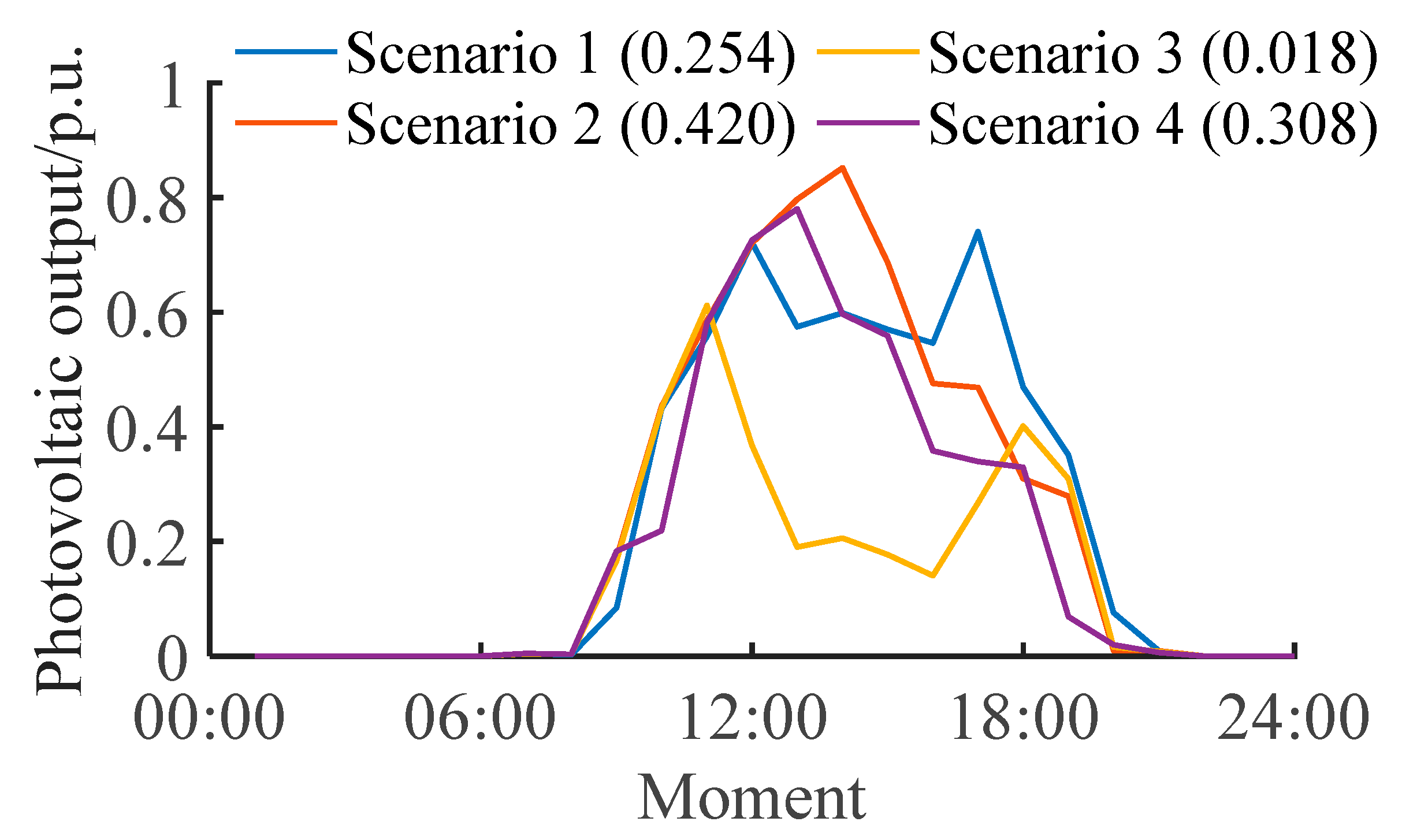

| Scene Serial Number of Wind–PV Joint Output | PV Output Only (δ1) | (δ2) | Wind–PV (COVc) |
|---|---|---|---|
| Scenario 1 | 1.6321 | 1.0412 | 0.9680 |
| Scenario 2 | 1.5682 | 1.0476 | 0.9654 |
| Scenario 3 | 1.6212 | 1.0811 | 0.9835 |
| Scenario 4 | 1.7414 | 1.0313 | 0.9643 |
| Seasonal Type | Optimization Method | Energy Storage Power /MW | Electrolyzed Water Power /MW | Fuel Cell Discharge /MW | Grid Power /MW | GIP /MW | GAP /MW | Increased Wind and PV Curtailment Rate/% | /% |
|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | MPC | 16.45 | 14.88 | 1.57 | 21.69 | 21.03 | 0.66 | 35.24 | 1.94 |
| RMPC | 13.16 | 9.37 | 3.79 | 14.41 | 13.62 | 0.79 | 1.73 | ||
| Scenario 2 | MPC | 21.54 | 19.83 | 1.71 | 24.76 | 24.38 | 0.38 | 39.05 | 2.02 |
| RMPC | 16.05 | 12.69 | 3.36 | 15.67 | 14.86 | 0.81 | 1.81 | ||
| Scenario 3 | MPC | 15.31 | 13.86 | 1.45 | 13.03 | 12.67 | 0.36 | 58.41 | 1.97 |
| RMPC | 20.15 | 20.14 | 0.01 | 5.45 | 5.27 | 0.18 | 1.77 | ||
| Scenario 4 | MPC | 19.50 | 12.35 | 7.15 | 15.46 | 14.22 | 1.24 | 40.37 | 1.95 |
| RMPC | 10.87 | 7.37 | 3.50 | 9.43 | 8.48 | 0.95 | 1.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Li, G.; Chen, X.; Yang, A.; Zhu, K. Enhancing Renewable Energy Integration via Robust Multi-Energy Dispatch: A Wind–PV–Hydrogen Storage Case Study with Spatiotemporal Uncertainty Quantification. Energies 2025, 18, 4498. https://doi.org/10.3390/en18174498
Zhang Q, Li G, Chen X, Yang A, Zhu K. Enhancing Renewable Energy Integration via Robust Multi-Energy Dispatch: A Wind–PV–Hydrogen Storage Case Study with Spatiotemporal Uncertainty Quantification. Energies. 2025; 18(17):4498. https://doi.org/10.3390/en18174498
Chicago/Turabian StyleZhang, Qilong, Guangming Li, Xiangping Chen, Anqian Yang, and Kun Zhu. 2025. "Enhancing Renewable Energy Integration via Robust Multi-Energy Dispatch: A Wind–PV–Hydrogen Storage Case Study with Spatiotemporal Uncertainty Quantification" Energies 18, no. 17: 4498. https://doi.org/10.3390/en18174498
APA StyleZhang, Q., Li, G., Chen, X., Yang, A., & Zhu, K. (2025). Enhancing Renewable Energy Integration via Robust Multi-Energy Dispatch: A Wind–PV–Hydrogen Storage Case Study with Spatiotemporal Uncertainty Quantification. Energies, 18(17), 4498. https://doi.org/10.3390/en18174498






