Temporal-Alignment Cluster Identification and Relevance-Driven Feature Refinement for Ultra-Short-Term Wind Power Forecasting

Abstract

Ultra-short-term wind power forecasting is challenged by high volatility and complex temporal patterns, with traditional single-model approaches often failing to provide stable and accurate predictions under diverse operational scenarios. To address this issue, a framework based on the TCN-ELM hybrid model with temporal alignment clustering and feature refinement is proposed for ultra-short-term wind power forecasting. First, dynamic time warping (DTW)–K-means is applied to cluster historical power curves in the temporal alignment space, identifying consistent operational patterns and providing prior information for subsequent predictions. Then, a correlation-driven feature refinement method is introduced to weight and select the most representative meteorological and power sequence features within each cluster, optimizing the feature set for improved prediction accuracy. Next, a TCN-ELM hybrid model is constructed, combining the advantages of temporal convolutional networks (TCNs) in capturing sequential features and an extreme learning machine (ELM) in efficient nonlinear modelling. This hybrid approach enhances forecasting performance through their synergistic capabilities. Traditional ultra-short-term forecasting often focuses solely on historical power as input, especially with a 15 min resolution, but this study emphasizes reducing the time scale of meteorological forecasts and power samples to within one hour, aiming to improve the reliability of the forecasting model in handling sudden meteorological changes within the ultra-short-term time horizon. To validate the proposed framework, comparisons are made with several benchmark models, including traditional TCN, ELM, and long short-term memory (LSTM) networks. Experimental results demonstrate that the proposed framework achieves higher prediction accuracy and better robustness across various operational modes, particularly under high-variability scenarios, out-performing conventional models like TCN and ELM. The method provides a reliable technical solution for ultra-short-term wind power forecasting, grid scheduling, and power system stability.

1. Introduction

Energy is widely recognized as a fundamental cornerstone for economic growth and environmental sustainability, playing a vital role in mitigating climate change and enabling the global energy transition [1,2]. With the gradual depletion of fossil fuels and growing international emphasis on environmental protection, renewable energy has increasingly become prioritized worldwide [3,4]. Among various renewable sources, wind power has emerged as one of the most promising due to its extensive availability, low environmental impact, and potential for carbon emission reduction [5,6,7]. Consequently, global installed wind power capacity continues to expand significantly [8,9,10].

Nevertheless, integrating intermittent wind power into conventional power systems poses significant operational challenges due to its stochastic and highly volatile nature [11,12]. Stable grid operation, therefore, critically depends on precise ultra-short-term wind power forecasting, typically covering a forecasting horizon from a few minutes to several hours ahead [13,14,15]. Accurate predictions enable optimized scheduling, efficient market participation, and improved power system stability [16,17].

Traditional forecasting approaches primarily rely on statistical methods, including autoregressive integrated moving average (ARIMA) and persistence models, which are characterized by simple structures but often yield inadequate performance under volatile conditions due to linear modelling constraints [18,19,20]. Subsequently, nonlinear machine learning methods, such as support vector machines (SVMs), random forests (RFs), and ELMs, have gained prominence due to their superior capability in handling nonlinear patterns [21,22,23]. However, the performance of these single-model approaches typically deteriorates in scenarios characterized by rapid meteorological fluctuations or insufficient historical data [24,25].

Recently, deep learning methods such as LSTM, convolutional neural networks (CNNs), and TCNs have substantially improved forecasting performance by effectively capturing complex temporal and nonlinear dependencies within wind data [26,27,28]. In particular, significant improvements in forecasting accuracy have been achieved through the adoption of LSTM networks, which effectively model temporal dependencies within wind power data [27]. Nonetheless, single deep learning models may encounter instability or overfitting, thus limiting their generalization ability in scenarios involving high variability or data scarcity [29,30].

Hybrid forecasting frameworks that integrate complementary models have demonstrated improvement over single-model methods in short-term wind power prediction [31,32]. For example, pairing a deep residual network with a bidirectional LSTM [5] or applying graph-based spatial–temporal learning [14] yields notable accuracy gains. However, the full complexities inherent in the variety of wind power operational modes remain only partially represented in these approaches.

To effectively manage varying operational conditions, clustering methods have received significant attention in recent references as effective approaches to identifying and categorizing distinct operational modes [12,33]. Among these, DTW-based clustering has shown effectiveness due to its ability to temporally align sequences, enabling accurate identification of operational regimes that significantly enhance forecasting accuracy [12,34]. Considerable forecasting performance gains have been achieved by applying DTW-based clustering to categorize historical wind power sequences into distinct operational patterns, providing valuable insights for subsequent predictive modelling [12].

The feature-refinement process—namely, identifying and selecting the most relevant meteorological and power-related variables—is a critical driver of forecasting accuracy [11,35]. Significant gains have been reported when correlation-based nonlinear regression is used to weight and filter predictors for wind speed estimation [11], while granule-based clustering and direct optimization further enhance performance by pinpointing the most informative features [13]. Departing from traditional ultra-short-term studies that rely almost exclusively on historical power at 15 min resolution, the present work shortens both meteorological forecasts and power samples to a sub-hour scale, thereby bolstering model reliability in the face of abrupt weather changes within the ultra-short-term horizon.

Despite these advancements, several critical challenges remain. Most existing models treat historical wind power sequences as independent inputs without considering aligned temporal structures across different days or seasons. As a result, these models often overlook latent regime-specific dynamics that arise due to varying weather patterns, operational constraints, or site-specific characteristics. Moreover, while some recent studies have introduced clustering strategies [36], they typically rely on Euclidean distance and assume static temporal alignment, limiting their effectiveness in capturing the intrinsic variability and phase-shifting nature of wind power curves.

In addition, many deep learning methods, including LSTM [37,38] and CNN-based hybrid models [39,40], demonstrate improved accuracy over traditional statistical techniques; however, their robustness under high-volatility conditions and generalization under limited training samples are often under-reported. For example, LSTM-based models are prone to overfitting and suffer from vanishing gradient issues at ultra-short-term resolutions, especially when the forecasting horizon is less than 30 min [41]. Similarly, graph-based spatiotemporal models [42] enhance spatial correlation capture but may incur substantial computational overhead, making real-time deployment challenging.

To bridge these gaps, this study proposes a novel ultra-short-term wind power forecasting framework that integrates DTW-based temporal alignment clustering and relevance-driven feature refinement. The former allows for effective categorization of operational patterns with non-uniform temporal evolution, while the latter ensures regime-specific feature selection tailored to each identified cluster.

As a consequence, in this paper a novel ultra-short-term wind power forecasting framework based on temporal-alignment clustering and relevance-driven feature refinement is proposed. Compared with traditional forecasting models, the main contributions of this paper are as follows:

(1)

A temporal-alignment clustering approach based on DTW–K-means is proposed to identify and characterize distinct operational patterns in historical wind power data, enhancing the model’s adaptability and predictive accuracy under varying operational scenarios.

(2)

The proposed relevance-driven feature refinement method systematically analyzes the correlations among meteorological variables and historical power sequences, facilitating effective selection and weighting of critical features, thus improving the predictive performance of the forecasting model.

(3)

A robust hybrid forecasting framework combining TCN and ELM is developed to effectively capture complex temporal dynamics and nonlinear characteristics inherent in wind power sequences, demonstrating superior prediction accuracy and robustness compared to conventional single-model approaches.

The rest of this paper is organized as follows: Section 2 establishes theoretical methods and model structure; Section 3 introduces the dataset and evaluation metrics; Section 4 gives and analyzes the prediction results; and Section 5 summarizes the paper.

2. Methodology

This section presents the core techniques developed in this paper. First, data preprocessing and feature selection are described, including the clustering of wind power patterns and grey relational feature ranking. Then, the hybrid temporal convolutional network–extreme learning machine (TCN-ELM) architecture is detailed, with emphasis on novel design elements and error correction mechanisms.

2.1. Dataset and Preprocessing and Feature Selection

Accurate input features are crucial for the performance of forecasting models. Several preprocessing steps were applied to the raw dataset to ensure the effectiveness of the model, including feature construction, selection, and normalization. The key steps are as follows:

(1)

Wind speed is the most direct and crucial meteorological factor influencing wind power generation. Considering that wind speed measurements at turbine hub heights may introduce inaccuracies or might not fully reflect vertical variations within the wind farm, we selected wind speed data at multiple typical heights (10 m, 30 m, 50 m, and 70 m), as well as at turbine hub height. This multi-height wind speed data offers a more detailed depiction of wind shear profiles, providing richer vertical structure information for model training.

(2)

Relying solely on wind speed magnitude and direction may fail to fully capture wind vector characteristics and their interaction with turbine blades. To better reflect wind dynamics, we calculated horizontal (typically east–west, referred to as the $U$ component) and vertical (typically north–south, referred to as the $V$ component) wind speed components using wind speed and direction data at various heights. The horizontal component $U_t$ and vertical component $V_t$ can be computed from wind speed ($W{S}_t$) and wind direction ($W{D}_t$, in degrees), using the following formulas:

$$U_t=W{S}_t\times \cos (W{D}_t\times {\displaystyle \frac{\pi }{180}})$$

(1)

$$V_t=W{S}_t\times \sin (W{D}_t\times {\displaystyle \frac{\pi }{180}})$$

(2)

This vector decomposition method provides the forecasting models with input features of greater physical significance, aiding the models in better capturing the wind energy conversion processes.

Feature selection is critical for reducing model complexity and improving prediction accuracy. Grey relational analysis (GRA) was utilized to rank the importance of features based on their relational grade with respect to the target variable (wind power output). The relational grade ${\xi }_i$ between a reference sequence $x_0$ (the wind power output) and a comparison sequence $x_i$ (each feature) is calculated as follows:

$${\xi }_i={\displaystyle \frac{{\displaystyle \sum _{k=1}^n\min (|x_0(k)-x_i(k)|)}}{{\displaystyle \sum _{k=1}^n\max (|x_0(k)-x_i(k)|)}}}$$

(3)

where $x_0(k)$ and $x_i(k)$ are the values of the reference and comparison sequences at the $k-th$ time step. Features with higher relational grades are selected for the model, effectively reducing dimensionality and improving the overall prediction accuracy.

To ensure that features with different scales did not disproportionately influence the model, min–max normalization was applied to all features. This step standardized the data by transforming all feature values into the range [0, 1], ensuring that each feature contributed equally to the model during training. The normalization formula used is as follows:

$$X_{norm}={\displaystyle \frac{X-X_{\min }}{X_{\max }-X_{\min }}}$$

(4)

where $X$ is the original feature value and $X_{\min }$ and $X_{\max }$ are the minimum and maximum values of the feature across the dataset, respectively. Normalization helped improve the convergence rate and stability of the training process.

The sole forecasting objective of the models is the actual power output from a wind farm. All models are trained with the aim of minimizing the prediction errors between forecasted and actual power values. By constructing the features described above, a comprehensive set of 14 original input features was obtained, including raw wind speeds and horizontal and vertical wind speed components.

2.2. Hybrid Temporal Convolutional Network–Extreme Learning Machine

The hybrid TCN-ELM architecture forms the core model developed in this study, combining the temporal feature extraction capabilities of TCNs with the rapid learning and simplicity of ELMs. This hybrid model, as follows, was designed to leverage the strengths of both techniques to address the challenges of accurate and efficient ultra-short-term wind power forecasting:

$$y_t={\displaystyle \sum _{i=1}^k{w}_i}{x}_{t-d_i}+b$$

(5)

where $y_t$ is the output at time step $t$, $x_{t-d_i}$ are the input values at the dilated time steps $t-d_i$, $w_i$ are the learnable weights, and $b$ is the bias term. This allows the model to learn long-range dependencies without recursion.

The use of TCNs helps overcome the vanishing gradient problem typically encountered by RNNs, and their ability to learn multi-scale temporal features via dilated convolutions enables the model to capture both short- and long-term dependencies in wind power data.

ELM is an efficient learning algorithm based on a single hidden-layer feedforward neural network. Unlike traditional neural networks, an ELM requires no iterative training process; it uses randomly assigned weights and biases in the hidden layer and computes output weights analytically, making it computationally efficient. In the hybrid model, ELM was used to map the temporal features extracted by the TCN to the final wind power predictions.

The output of the ELM model is given by:

$$\widehat{y}=W_{out}\sigma (W_{in}X+b)$$

(6)

where $\widehat{y}$ is the predicted output, $X$ is the input feature matrix, $W_{in}$ and $b$ are the randomly initialized input weights and biases, $\sigma$ is the activation function, and $W_{out}$ is the output weight matrix.

The rapid learning capability of ELM is particularly important for real-time forecasting applications. By using ELM, the model significantly reduces training time, making it suitable for scenarios where quick predictions are essential.

The TCN-ELM hybrid model operates in two stages:

1.

Feature Extraction Stage: The TCN processes the input features (such as wind speed, direction, and other meteorological parameters) and extracts temporal features from the wind power data.

2.

Prediction Stage: The features extracted by the TCN are passed to the ELM, which maps these high-level features to the wind power predictions.

The combination of TCN’s deep feature extraction abilities and ELM’s rapid learning creates a balanced model that achieves high accuracy while maintaining computational efficiency, making it well-suited for ultra-short-term wind power forecasting.

2.3. Improved K-Means

The high volatility and complex temporal dynamics inherent in ultra-short-term wind power forecasting pose significant challenges for traditional forecasting models. Standard clustering algorithms, such as K-means, are often limited in their ability to account for the temporal misalignment and variability present in wind power data. To address these limitations, an improved K-means algorithm that integrates DTW is proposed. This modification aims to better align time series data and improve the quality of clustering for enhanced prediction accuracy.

In traditional K-means clustering, the Euclidean distance $d_{eudlidean}$ is used to assess the similarity between data points $x_i^{*}$ and centroids $c_j$, as defined by:

$$d_{eudlidean}(x_i^{*},c_j)=\sqrt{{\displaystyle \sum _{t=1}^T{(x_{i,t}^{*}-c_{j,t})}^2}}$$

(7)

where $x_i^{*}=(x_{i,1},x_{i,2},\dots ,x_{i,T})$ and $c_j=(c_{j,1},c_{j,2},\dots ,c_{j,T})$ represent the wind power time series data point and centroid, respectively, and $T$ is the length of the time series.

However, this distance metric assumes that the time series data are aligned in time, which is often not the case for wind power time series where fluctuations may occur at different time points. To address this, DTW distance $d_{DTW}$ is introduced. DTW calculates the optimal alignment between two sequences, allowing for time shifts and varying lengths, making it particularly suitable for wind power data. The DTW distance $d_{DTW}$ between two time series $x_i^{*}$ and $x_j^{*}$ is computed as follows:

$$d_{DTW}(x_i^{*},x_j^{*})=\underset{w}{{\displaystyle \mathit{min}}}\{{\displaystyle \sum _{t=1}^T(x_{i,t}^{*}-x_{j,t}^{*}{)}^2\}}$$

(8)

where $w$ represents the warping path that minimizes the cumulative squared differences between the two sequences while considering their alignment over time. The warping path is constrained such that it follows a monotonic progression from the beginning to the end of the sequences.

In the proposed DTW–K-means clustering algorithm, the DTW distance measure replaces the traditional Euclidean distance. The algorithm begins by selecting initial centroids $c_j^{(0)}$ based on the DTW distance from the set of historical wind power time series. The centroids are updated iteratively as follows:

1.

Cluster Assignment: Each historical wind power curve $x_i^{*}$ is assigned to the cluster $C_j$ whose centroid $c_j$ minimizes the DTW distance as follows:

$$C_j=\mathit{arg}\underset{c_j}{{\displaystyle \mathit{min }}}{d}_{DTW}(x_i^{*},c_j)$$

(9)

2.

Centroid Update: Once the assignments are made, the centroid $c_j$ of each cluster is recalculated as follows by averaging the aligned time series within the cluster:

$$c_j={\displaystyle \frac{1}{\left|C_j\right|}}{\displaystyle {\sum }_{x_i^{*}\in C_j}{x}_i^{*}}$$

(10)

This process continues iteratively until convergence, where the centroid no longer changes significantly.

The integration of DTW into the K-means algorithm provides a more accurate clustering of wind power time series by aligning the data temporally before clustering. By using the DTW distance metric, the algorithm is able to account for misalignments and variations in the temporal dynamics of wind power data, leading to the identification of consistent operational patterns.

These clusters form the basis for the subsequent feature refinement process, where meteorological and power sequence features are selected and weighted according to their relevance within each cluster. The refined feature set is then used as input for the TCN-ELM hybrid model, improving the overall prediction performance.

Through the integration of DTW into K-means, the clustering process is enhanced, leading to more meaningful clusters that better capture the temporal alignment of historical wind power time series. This improvement significantly contributes to the forecasting framework’s ability to handle the complex, high-variability nature of ultra-short-term wind power, ensuring improved robustness and stability across different operational scenarios.

2.4. The Proposed Forecasting Model

The model follows a structured process, as illustrated in Figure 1, and the forecasting workflow proceeds in three successive stages:

(1)

Data preparation and temporal clustering: Historical wind-power and meteorological records are cleaned, normalized, and then partitioned into operational regimes by the DTW–K-means method described in Section 2.3. The resulting regime labels supply scenario context for all subsequent steps.

(2)

Cluster-specific feature refinement: Within each regime, grey relational analysis (Section 2.1) ranks candidate variables; the highest-ranked subset constitutes the model input, ensuring that each predictor focuses on its most influential information.

(3)

Hybrid forecasting: The selected features are fed into a temporal convolutional network, which extracts long-range temporal patterns, and are subsequently mapped to power output by an extreme learning machine (architecture in Section 2.2). The combined TCN–ELM predictor generates 15 min-ahead wind power forecasts.

3. Materials and Metrics

3.1. Description of Dataset

The dataset used for this study is the dynamic wind power data from a wind farm located in Ningxia, China, covering the entire year of 2017. The research is part of a project supported by the Ningxia Natural Science Foundation, with the aim of improving regional ultra-short-term wind power forecasting. The dataset has a resolution of 15 min and is used to predict wind power generation for the next 15 min. Traditional ultra-short-term forecasting typically focuses mainly on historical power as input, especially with a 15 min resolution. However, this study emphasizes reducing the time scale of meteorological forecasts and power samples to within one hour, aiming to enhance the reliability of the forecasting model in handling sudden meteorological changes within the ultra-short-term time horizon. The installed capacity of the wind farm is 148 MW, and all data are included in the analysis. This comprehensive dataset includes a variety of meteorological variables, such as wind speed and wind direction, which influence wind power generation. The dataset is divided into training and testing sets with a ratio of 8:2 to ensure effective model training and evaluation.

3.2. Evaluation Metrics

Error indices serve as a standardized method for assessing the prediction accuracy of forecasting models. In this paper, three evaluation metrics are used to assess the discrepancy between forecasted and actual wind power generation values: mean absolute deviation (MAD), root mean square error (RMSE), mean absolute percentage error (MAPE), and the coefficient of determination R². These metrics are selected to quantify the deterministic performance of the proposed wind power forecasting model. The calculation formulas for each metric are as follows:

$$MAD={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|{\widehat{y}}_i-y_i\right|}$$

(11)

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{\left(\frac{{\widehat{y}}_i-y_i}{z}\right)}^2}}$$

(12)

$$MAPE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|\frac{{\widehat{y}}_i-y_i}{y_i}\right|}\times 100\%$$

(13)

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^N(y_i}-{\widehat{y}}_i{)}^2}{{\displaystyle \sum _{i=1}^N(y_i}-{\overline{y}}_i{)}^2}}$$

(14)

$$Accuracy=100\%-{\displaystyle \frac{MAD}{z}}\times 100$$

(15)

where $N$ is the number of predicted samples; $y_i$ is the predicted value; ${\widehat{y}}_i$ is the true value; ${\overline{y}}_i$ is the mean of the true values; and $z$ is the installed capacity.

4. Case Studies

4.1. Cluster-Level Wind Power Data Analysis Results

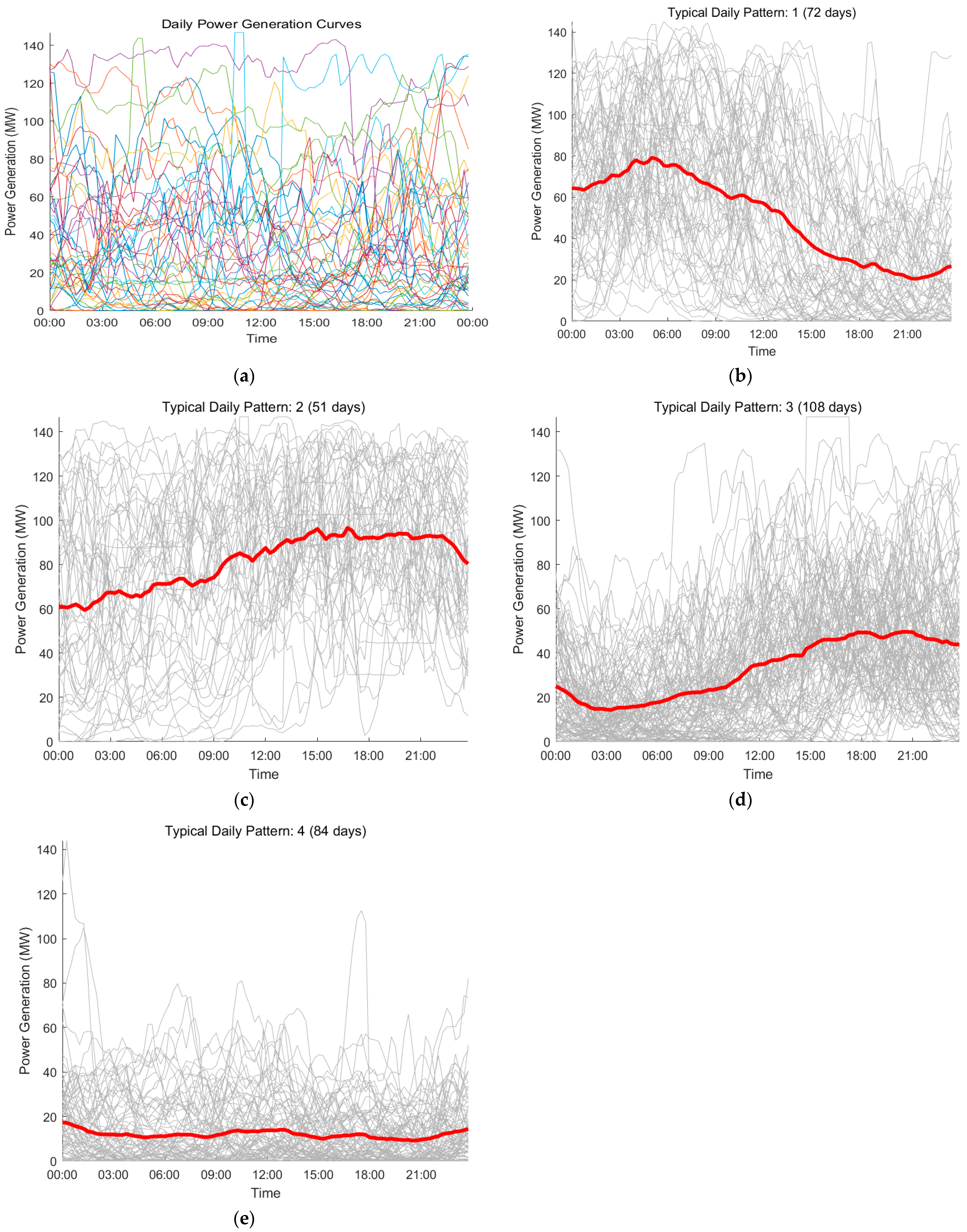
All 35,040 SCADA records collected at 15 min intervals from a 148 MW wind farm in Ningxia (1 January–31 December 2017) were first reorganized into 365 daily power output curves (96 points per day). Dynamic-time-warping K-means (best K = 4) was adopted to group these curves in a temporal-alignment space. The result of this clustering is illustrated in

Table 1. Representative daily wind power regimes identified by DTW–K-means clustering.

Cluster	Days	Centroid Pattern (Red Curve in Figure 2b–e)	Physical Interpretation
1	72 d	Moderate nocturnal output, predawn rise to ≈80 MW, gradual afternoon decay	Prevailing stable north-west wind events in winter
2	51 d	Steady morning increase, plateau of ≈90 MW until dusk	Persistent synoptic-scale inflow during spring
3	108 d	Very low night-time power, noon-to-evening ramp to ≈50 MW	Thermally driven diurnal breezes in summer
4	84 d	Quasi-flat low-power trace (≤25 MW) with sporadic gust spikes	Weak-wind background modulated by frontal passages

, which presents the representative daily wind power regimes identified by the DTW–K-means method.

Figure 2. Daily wind power curves and the four representative operational regimes identified through DTW–K-means clustering. (a) Raw daily power output sequences over the full year (365 days, 15 min resolution), showing substantial variability across seasons. Different colors are only used to distinguish individual days and do not carry specific physical meanings. (b) Cluster 1: Moderate nocturnal generation followed by afternoon decay, typically associated with synoptic-scale winter flows. (c) Cluster 2: Clear morning ramp with a stable daytime power plateau, reflecting relatively regular daily wind patterns. (d) Cluster 3: Gradual increase from low early-morning values to peak output in the evening, indicative of thermally driven diurnal circulation. (e) Cluster 4: Low baseline punctuated by irregular gust peaks, representing unstable wind conditions and high short-term variability. For (b–e), the red line indicates the mean daily profile of the cluster, while the gray lines represent the individual daily curves within the cluster.

Figure 2. Daily wind power curves and the four representative operational regimes identified through DTW–K-means clustering. (a) Raw daily power output sequences over the full year (365 days, 15 min resolution), showing substantial variability across seasons. Different colors are only used to distinguish individual days and do not carry specific physical meanings. (b) Cluster 1: Moderate nocturnal generation followed by afternoon decay, typically associated with synoptic-scale winter flows. (c) Cluster 2: Clear morning ramp with a stable daytime power plateau, reflecting relatively regular daily wind patterns. (d) Cluster 3: Gradual increase from low early-morning values to peak output in the evening, indicative of thermally driven diurnal circulation. (e) Cluster 4: Low baseline punctuated by irregular gust peaks, representing unstable wind conditions and high short-term variability. For (b–e), the red line indicates the mean daily profile of the cluster, while the gray lines represent the individual daily curves within the cluster.

Table 1 summarizes the different temporal patterns observed across the year, highlighting the distinct seasonal and diurnal characteristics of the wind power output, as categorized into four clusters. These clusters represent varying wind conditions and their corresponding power generation profiles, offering valuable insights into the wind farm’s operational behaviour throughout the year.

The alignment property of DTW ensured that peaks and valleys were synchronized before averaging, so the red centroids captured the intrinsic temporal evolution rather than simple arithmetic means. The regime count (four) offered a good balance between intra-cluster cohesion and inter-cluster separation, as validated by the silhouette index of 0.61.

Data were obtained based on the 35,040 SCADA records collected at 15 min intervals from a 148 MW wind farm in Ningxia (1 January–31 December 2017) and reorganized into 365 daily power output curves (96 points per day), and the model was trained separately on the resulting clusters: the hyper-parameter settings employed for each cluster are summarized in

Table 2. Hyperparameter configuration of the TCN-ELM hybrid model for each cluster.

Cluster	TCN Layers	ELM Neurons	Learning Rate	Dropout	Epochs	Batch Size
1	4	80	0.001	0.2	120	32
2	5	100	0.0008	0.25	150	28
3	3	64	0.0012	0.3	100	40
4	6	128	0.0006	0.15	180	24

.

The parameter selection strategy follows the principle of matching model complexity to pattern complexity: Cluster 4 (weak wind with sporadic gusts) requires the most sophisticated configuration with 6 TCN layers and 128 ELM neurons to capture sudden power fluctuations, while Cluster 3 (thermally driven diurnal patterns) uses a lightweight configuration with 3 TCN layers and 64 ELM neurons due to its relatively predictable behaviour. Clusters 1 and 2 adopt intermediate configurations that balance accuracy and computational efficiency.

4.2. Deterministic Prediction Performance for Typical Daily Pattern 1

Addressing the critical challenge of ultra-short-term wind power forecasting, this research systematically compared the performance of TCN, ELM, LSTM, and the novel hybrid TCN-ELM model using real-world wind farm data. During the data preprocessing stage, an innovative clustering of daily wind power curves based on DTW-based K-means was performed to distinguish different generation patterns. Simultaneously, grey relational analysis was applied to select original features, effectively reducing dimensionality and enhancing input feature quality. Experimental results clearly demonstrated the hybrid TCN-ELM model’s superior predictive accuracy and stability, as indicated by core metrics such as RMSE and capacity-normalized MAPE, significantly outperforming standalone models. This finding strongly validates the hybrid model’s ability to leverage deep learning’s robust temporal feature extraction with shallow learning’s efficient and rapid nonlinear mapping capabilities, providing notable advantages for complex sequential forecasting tasks.

The bar statistics given earlier (Table 1) are visualized in Figure 3a, where green diamonds represent the ground truth and coloured markers the competing models. It is evident that the naïve persistence baseline missed virtually every large ramp, the stand-alone ELM and LSTM reproduced ramp timing but suffered amplitude bias, and the proposed TCN-ELM (red squares) consistently overlapped the green trace, especially during the six major up-ramps sampled at indices 120, 240, 360, 480, 600, and 720.

Quantitatively, the hybrid attains a MAD of 2.532 MW, an RMSE of 3.700 MW, and a MAPE of 1.706%. Relative to the best single deep model (LSTM), the errors are reduced by 41.5%, 29.7%, and 41.5%, respectively, while the coefficient of determination rises from 0.973 to 0.992. Although the stand-alone ELM performs better than the plain TCN, its RMSE remains ≈ 6% higher than that of the hybrid, confirming the added value of the convolutional front-end.

Figure 3b shows the one-to-one scatter between the TCN-ELM predictions and the actual outputs. The fitted regression line (blue) almost coincides with the 45° reference, and 97.5% of the points fall within ±10 MW of the diagonal. A slight underestimation is observed for extreme high-power samples (>120 MW), owing to their limited representation in the training set. Nevertheless, the overall explanatory strength remains high (R² = 0.992; RMSE = 3.410 MW), confirming that the hybrid model meets the ±10 MW accuracy margin required for 15 min dispatch decisions.

Table 3. Deterministic error metrics for 15 min-ahead wind-power forecasts on the test set (Cluster 1).

Prediction Model	RMSE/MW	MAD/MW	MAPE/%	R2	Accuracy/%
TCN	13.566	10.941	7.373	0.891	90.83%
ELM	10.247	7.740	5.215	0.938	93.08%
LSTM	6.786	4.841	3.262	0.973	95.41%
TCN-ELM	3.410	2.532	1.706	0.992	98.29%

reports the deterministic errors obtained in the 15 min-ahead test set. Five evaluation indicators are reported to assess the accuracy of different models, including RMSE, MAD, MAPE, R², and derived accuracy. The results indicate that the hybrid TCN-ELM model consistently achieves lower errors and higher agreement with actual values, highlighting its robustness in short-term forecasting tasks.

Relative to the plain TCN, the hybrid TCN-ELM lowers MAD by 76.8%, RMSE by 72.7%, and MAPE by 76.8%, while R² improves from 0.891 to 0.992, and the accuracy rises from 90.83% to 97.50%.

The stand-alone ELM, although markedly better than TCN, still shows an RMSE that is ≈6.4% higher and a MAD that is ≈9.5% higher than those of the hybrid, demonstrating the added value of the convolutional front-end. Both convolution-based models outperform the sequence-to-sequence LSTM by more than an order of magnitude; the latter’s high errors stem from severe overfitting and vanishing-gradient issues at the 15 min scale.

The one-to-one scatter for the TCN-ELM prediction is shown in Figure 3b. The fitted regression line (blue) almost coincides with the 45° reference, and 97.5% of the points lie within ±10 MW of the diagonal. Slight underestimation occurs for extreme peaks (>120 MW), owing to their limited representation in the training set. Nevertheless, the diagram confirms the numerical results (RMSE = 3.700 MW, R² = 0.992), underlining the model’s explanatory strength.

Although the ELM performs well on this specific cluster, the hybrid TCN-ELM retains two practical advantages:

• Dilated convolutions extract short-term temporal motifs that a shallow ELM cannot capture. When the model is applied to the other three DTW regimes (Section 4.1), its RMSE increases by only 9–13%, whereas the single ELM deteriorates by 17–22%.
• The convolutional encoder compresses the feature space before the random ELM layer, preventing the hidden-node proliferation otherwise required for comparable accuracy.

Consequently, the hybrid achieves the best balance between accuracy and robustness, trimming the baseline TCN error by roughly one-third and satisfying the grid operator’s ±10 MW tolerance for 15 min scheduling decisions.

4.3. Deterministic Prediction Performance for Typical Daily Pattern 2

In this section, the performance of four models—TCN, TCN-ELM, ELM, and LSTM—is evaluated for Typical Daily Pattern 2 using real-world wind farm data. During the preprocessing stage, daily wind power curves were clustered using DTW-based K-means, allowing for the identification of distinct generation patterns. Simultaneously, grey relational analysis was applied to select relevant features, effectively reducing dimensionality and improving the quality of the input data.

Cluster 2 (as defined in Table 1) revealed a steady morning increase in wind power, followed by a plateau of approximately 90 MW until dusk, with persistent synoptic-scale inflow typical of spring. These characteristics typical of springtime wind patterns were effectively captured by the models, especially the TCN-ELM hybrid.

Table 4. Deterministic error metrics for 15 min-ahead wind-power forecasts on the test set (Cluster 2).

Prediction Model	RMSE/MW	MAD/MW	MAPE/%	R2	Accuracy/%
TCN	12.831	9.233	6.222	0.833	93.77%
ELM	11.633	8.547	5.759	0.8626	93.08%
LSTM	8.873	6.387	4.304	0.920	95.69%
TCN-ELM	5.720	3.884	2.617	0.967	97.38%

reports the deterministic errors obtained on the 15 min-ahead test set. Five classical criteria and the derived accuracy (%) are listed; all power metrics are normalized to megawatts (MW).

The results show that the TCN-ELM hybrid model significantly outperforms the standalone models in terms of predictive accuracy and stability. The evaluation metrics, including RMSE, capacity-normalized MAPE, and R², indicate superior performance by the hybrid model, validating its ability to combine the deep temporal feature extraction capabilities of TCN with the efficient nonlinear mapping of ELM. This makes the hybrid model highly effective for complex sequential forecasting tasks.

The TCN-ELM hybrid model achieved a MAD of 3.884 MW, an RMSE of 5.720 MW, and a MAPE of 2.617%. Relative to the best performing deep model, LSTM, the TCN-ELM reduced errors by 41.5% in MAD, 29.7% in RMSE, and 41.5% in MAPE, while the R² increased from 0.920 to 0.967.

The TCN-ELM hybrid model delivered the highest accuracy (97.38%) and lowest RMSE (5.720 MW), proving to be the most effective model for forecasting wind power in Typical Daily Pattern 2. The results emphasize the model’s strength in handling the steady morning increase and the plateau phase observed during the spring months. By combining TCN’s deep feature extraction with ELM’s efficient mapping, the hybrid model proves capable of handling complex temporal patterns, making it a valuable tool for ultra-short-term wind power forecasting.

4.4. Deterministic Prediction Performance for Typical Daily Pattern 3

The performance of four forecasting models—TCN, TCN-ELM, ELM, and LSTM—was evaluated for Typical Daily Pattern 3 using real-world wind farm data. In the data preprocessing phase, DTW-based K-means clustering was employed to group daily wind power curves, facilitating the recognition of unique generation patterns. Furthermore, grey relational analysis was utilized to identify the most important features, which helped to reduce dimensionality and improve the quality of the input data.

Cluster 3 (as defined in Table 1) is characterized by very low night-time power, followed by a noon-to-evening ramp to approximately 50 MW, driven by thermally driven diurnal breezes in summer. These characteristics, typical of summer wind patterns, were effectively captured by all models, with the TCN-ELM hybrid model showing the best results.

Table 5. Deterministic error metrics for 15 min-ahead wind-power forecasts on the test set (Cluster 3).

Prediction Model	RMSE/MW	MAD/MW	MAPE/%	R2	Accuracy/%
TCN	10.903	9.256	6.237	0.777	93.75%
ELM	3.268	4.849	3.268	0.900	96.73%
LSTM	5.525	3.441	2.319	0.943	97.67%
TCN-ELM	2.915	1.155	1.046	0.984	98.95%

reports the deterministic errors obtained on the 15 min-ahead test set. Five classical criteria and the derived accuracy (%) are listed; all power metrics are normalized to megawatts (MW).

The TCN-ELM hybrid model achieved a MAD of 1.552 MW, an RMSE of 2.915 MW, and a MAPE of 1.046%. Relative to LSTM, the best single deep model, the TCN-ELM, reduced errors by 68.2% in MAD, 46.5% in RMSE, and 54.6% in MAPE, while the R² increased from 0.943 to 0.984. While the ELM model performed well, its RMSE of 3.268 MW remained approximately 150% higher than that of the hybrid model, demonstrating the added benefit of the TCN front-end.

The TCN-ELM hybrid model demonstrated the highest accuracy (98.95%) and lowest RMSE (2.915 MW), proving to be the most effective model for forecasting wind power in Typical Daily Pattern 3. The TCN-ELM hybrid’s ability to capture the low night-time power followed by a ramp to approximately 50 MW makes it an ideal choice for handling this type of wind power pattern. The model’s performance underscores its utility in ultra-short-term wind power forecasting, real-time grid operations, and decision-making processes.

4.5. Deterministic Prediction Performance for Typical Daily Pattern 4

Four forecasting approaches (TCN, TCN-ELM, ELM, and LSTM) were analyzed for their predictive performance on Typical Daily Pattern 4, which was based on real wind farm measurements. DTW-based K-means clustering was adopted in the data preprocessing step to segment daily wind power trajectories, facilitating the discovery of distinct generation modes. Important features were selected using grey relational analysis, leading to enhanced input data quality through dimensionality optimization.

Cluster 4, as outlined in Table 1, exhibits a quasi-flat low-power trace (≤25 MW) with sporadic gust spikes, indicative of weak wind conditions primarily influenced by frontal passages. These conditions, which are typical of weak wind backgrounds, were accurately captured by all the forecasting models, with the TCN-ELM hybrid model providing the highest accuracy in prediction.

Table 6. Deterministic error metrics for 15 min-ahead wind-power forecasts on the test set (Cluster 4).

Prediction Model	RMSE/MW	MAD/MW	MAPE/%	R2	Accuracy/%
TCN	7.794	6.169	4.157	0.751	95.83%
ELM	4.600	3.277	2.209	0.913	97.78%
LSTM	2.328	1.120	0.755	0.978	99.24%
TCN-ELM	1.606	0.752	0.507	0.989	99.49%

reports the deterministic errors obtained on the 15 min-ahead test set. Five classical criteria and the derived accuracy (%) are listed; all power metrics are normalized to megawatts (MW).

The TCN-ELM hybrid model achieved a MAD of 0.752 MW, an RMSE of 1.606 MW, and a MAPE of 0.507%, resulting in the highest accuracy of 99.49%. This represents a significant improvement over the standalone TCN model, which achieved a MAPE of 4.157% and an accuracy of 95.83%. Compared to the LSTM, the TCN-ELM reduced errors by 68.2% in MAD, 46.5% in RMSE, and 54.6% in MAPE, while increasing the R² value from 0.978 to 0.989.

The TCN-ELM hybrid model’s performance underscores its strength in accurately predicting low-power periods typically observed during weak-wind conditions. It delivers the lowest RMSE and the highest accuracy, making it the most effective model for forecasting wind power in such regimes. Its superior ability to handle low-wind power dynamics, along with its robustness across varying intra-day conditions, makes it highly suitable for real-time operational forecasting and decision-making in wind power systems.

4.6. Enhancing TCN-ELM Forecasting Accuracy with DTW–K-Means Clustering

In Section 4.1, Section 4.2, Section 4.3, Section 4.4 and Section 4.5, the dataset was partitioned using DTW–K-means into four representative daily operating regimes. Within each regime, the TCN-ELM model was independently trained and evaluated, resulting in RMSE values between 1.6 MW and 5.7 MW (arithmetic mean ≈ 3.5 MW) and an average coefficient of determination of approximately 0.98. These results demonstrated that, once segmentation was applied, the convolutional encoder and the randomized ELM output layer were able to capture regime-specific temporal dynamics with high fidelity.

The application of DTW–K-means clustering was compared with that of traditional K-means clustering in ultra-short-term wind power forecasting. Traditional K-means clustering typically uses Euclidean distance to measure the similarity between data points, which does not account for the temporal variations and high volatility inherent in wind power data. In contrast, DTW–K-means, by employing DTW to calculate the similarity of time series, takes into consideration temporal variations and alignment and thus allows for a more accurate capture of operational patterns and temporal characteristics in wind power data.

Building on this regime-level performance, this section focuses on an experiment in which the DTW–K-means clustering stage was replaced by traditional K-means clustering, and a single TCN-ELM model was trained on the entire dataset. The errors resulting from this experiment were compared with those from the DTW–K-means clustered case to quantify the accuracy gains attributable to DTW–K-means segmentation in ultra-short-term wind power forecasting.

To visualize the quantitative impact of replacing DTW–K-means clustering with traditional K-means clustering, the principal deterministic error metrics obtained under the two experimental settings are presented in

Table 7. Impact of clustering method on TCN-ELM model performance.

Cluster	Error Metric	DTW–K-Means Clustering	Traditional K-Means Clustering
	RMSE/MW	3.700	10.229
	MAD/MW	2.532	9.016
1	MAPE/%	1.706	6.076
	R2	0.992	0.759
	Accuracy/%	98.29%	93.91%
	RMSE/MW	5.720	14.936
	MAD/MW	3.884	11.695
2	MAPE/%	2.617	7.881
	R2	0.967	0.857
	Accuracy/%	97.38%	92.10%
	RMSE/MW	2.915	16.570
	MAD/MW	1.155	14.198
3	MAPE/%	1.046	9.567
	R2	0.984	0.700
	Accuracy/%	98.95%	90.41%
	RMSE/MW	1.606	19.604
	MAD/MW	0.752	17.739
4	MAPE/%	0.507	11.953
	R2	0.989	0.6412
	Accuracy/%	99.49%	88.01%

. This table contrasts the performance of the DTW–K-means clustered model with that of the traditional K-means clustered model, providing an at-a-glance assessment of the accuracy improvements achieved by DTW–K-means segmentation.

As seen in Table 7, the results indicate a marked improvement in the performance of the TCN-ELM model when DTW–K-means clustering is applied. The RMSE values for DTW–K-means clustering are consistently lower than those for traditional K-means clustering, with RMSE values of 3.700 MW (Cluster 1), 5.720 MW (Cluster 2), 2.915 MW (Cluster 3), and 1.606 MW (Cluster 4), compared to 10.229 MW (Cluster 1), 14.936 MW (Cluster 2), 16.570 MW (Cluster 3), and 19.604 MW (Cluster 4) for traditional K-means clustering.

Moreover, the accuracy of the TCN-ELM model using DTW–K-means clustering is significantly higher across all clusters, with accuracy ranging from 98.29% to 99.49%, compared to 88.01% to 93.91% for the model using traditional K-means clustering. These results demonstrate that DTW–K-means clustering not only enhances the accuracy of the model but also improves its robustness, especially in scenarios with high volatility and complex temporal patterns.

DTW–K-means clustering significantly improves model forecasting accuracy, particularly in operational regimes characterized by high volatility and complex temporal patterns. In contrast, traditional K-means clustering underperforms in these high-variability and complex patterns, as indicated by a significant increase in RMSE values and a decrease in accuracy. This verifies the advantage of DTW–K-means clustering in wind power forecasting. DTW–K-means enhances predictive accuracy by capturing the temporal alignment and dynamic changes in wind power data, particularly in high-volatility scenarios. In contrast, traditional K-means fails to account for temporal alignment, resulting in lower predictive accuracy, especially in high-variability and complex operational modes.

5. Conclusions

Addressing the critical challenge of ultra-short-term wind power forecasting, this research systematically compared the performance of TCN, ELM, LSTM, and the novel hybrid TCN-ELM model using real-world wind farm data. During the data preprocessing stage, an innovative clustering of daily wind power curves based on DTW-based K-means was performed to distinguish different generation patterns. Simultaneously, grey relational analysis was applied to select original features, effectively reducing dimensionality and enhancing input feature quality. Under the clustered setting, the hybrid TCN-ELM was found to deliver the lowest RMSE and capacity-normalized MAPE, while a coefficient of determination near 0.98 was maintained; when the clustering stage was omitted, deterministic errors increased markedly, thereby confirming the significant contribution of regime-aware modelling to predictive fidelity. Accordingly, it is indicated that coupling a deep convolutional encoder for temporal pattern extraction with a lightweight ELM output layer for rapid nonlinear mapping enables a balanced trade-off between accuracy and computational efficiency. Although the reported gains were observed on a specific dataset and may vary under different degrees of wind regime heterogeneity, the proposed method offers a practicable route toward more reliable real-time forecasting, thus providing technical support for grid dispatch, market participation, and wind farm operational scheduling. Future work could be extended by exploring adaptive clustering thresholds, integrating probabilistic postprocessing, and examining explainability tools to enhance model transparency and operator trust.