Multiscale Evaluation of an Electrically Heated Thermal Battery for High-Temperature Industrial Energy Storage †
Abstract
1. Introduction
2. Small-Scale Analysis of Charging Brick Stack
2.1. Numerical Methodology
2.1.1. Thermal–Electric Model
Geometry and Computational Domain of the Thermal-Electric Model
Governing Equations of the Thermal-Electric Model
Boundary and Interface Conditions of the Thermal-Electric Model
2.1.2. Structural Model
Geometry and Computational Domain of the Structural Model
Governing Equations of the Structural Model
Boundary Conditions of the Structural Model
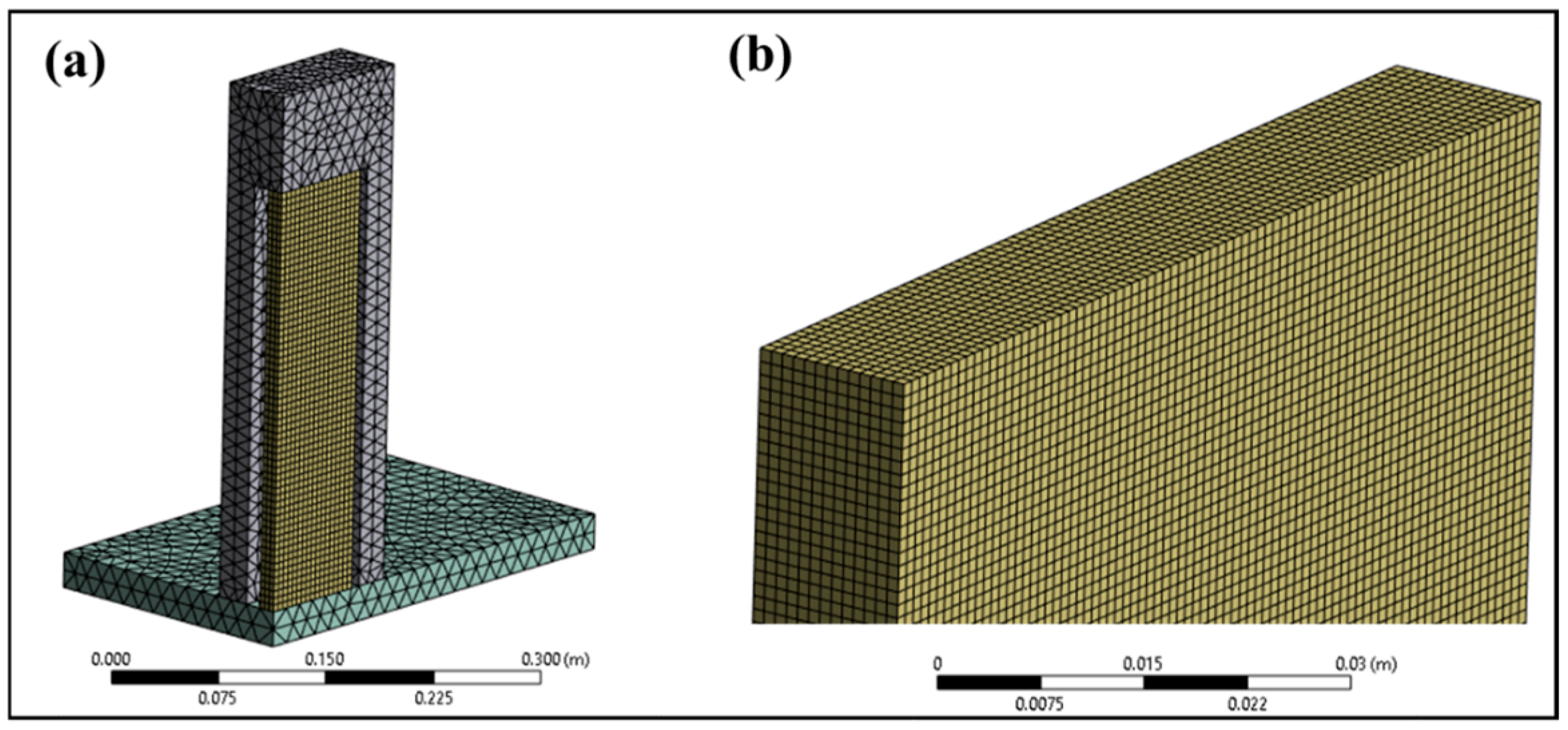
2.1.3. Meshing
2.2. Experimental Methodology
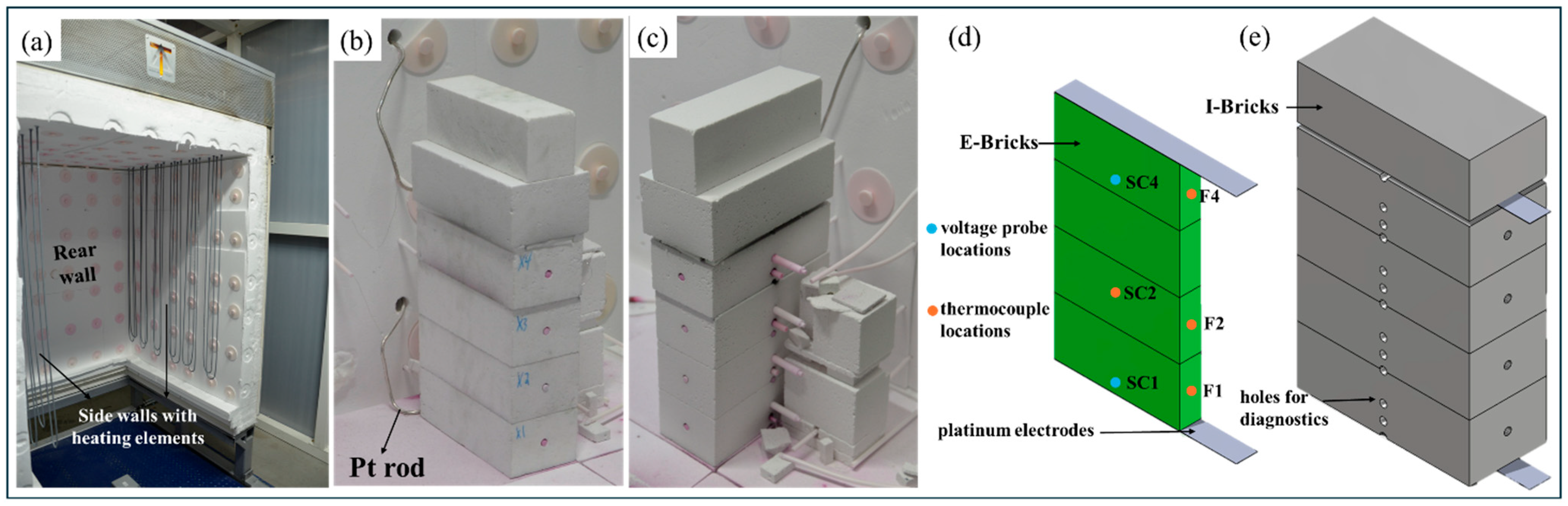
2.2.1. Experimental Setup
2.2.2. Experimental Measurement
2.2.3. Experimental Procedure
2.3. Discussion of the Small-Scale Analysis of Charging Brick Stack
2.3.1. Numerical Results
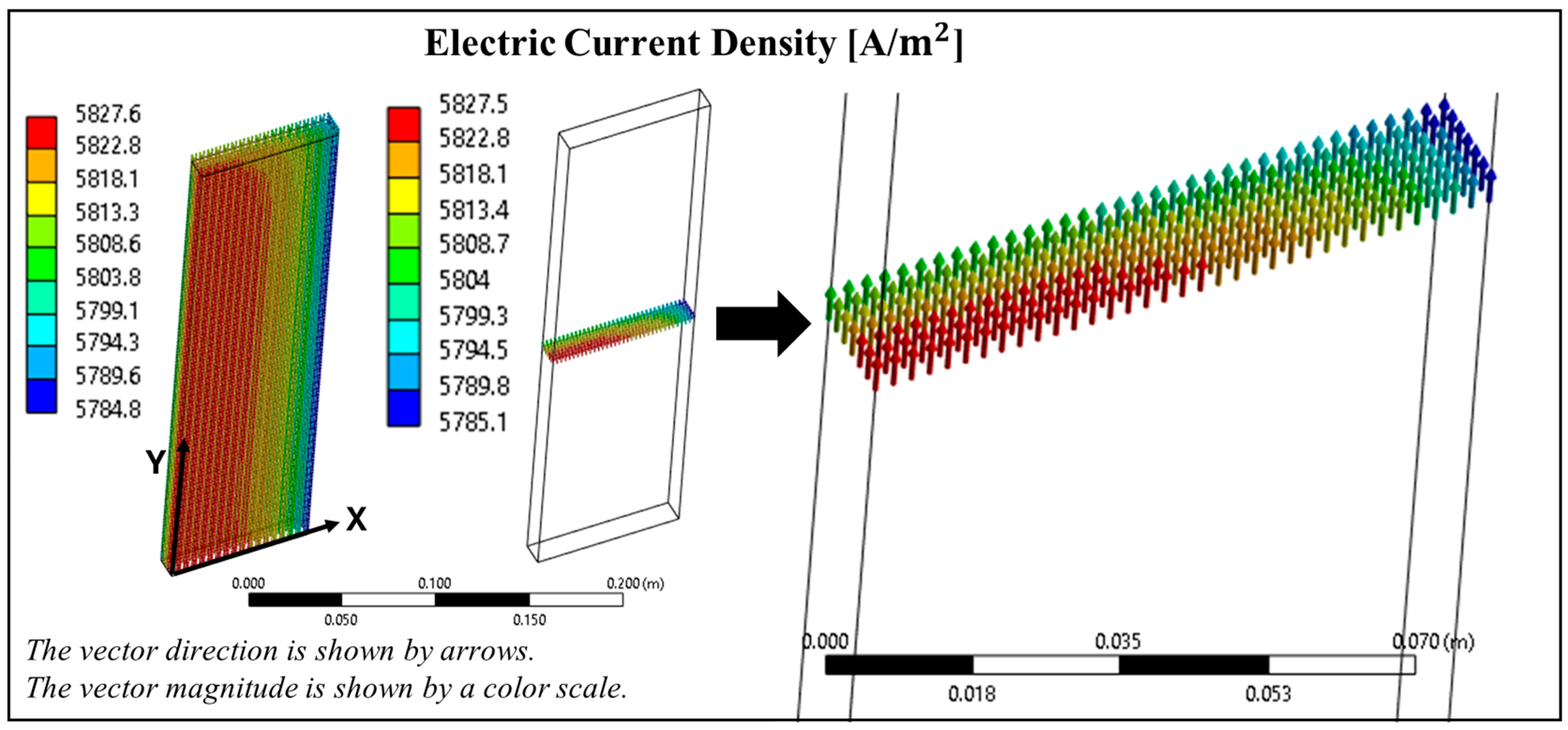
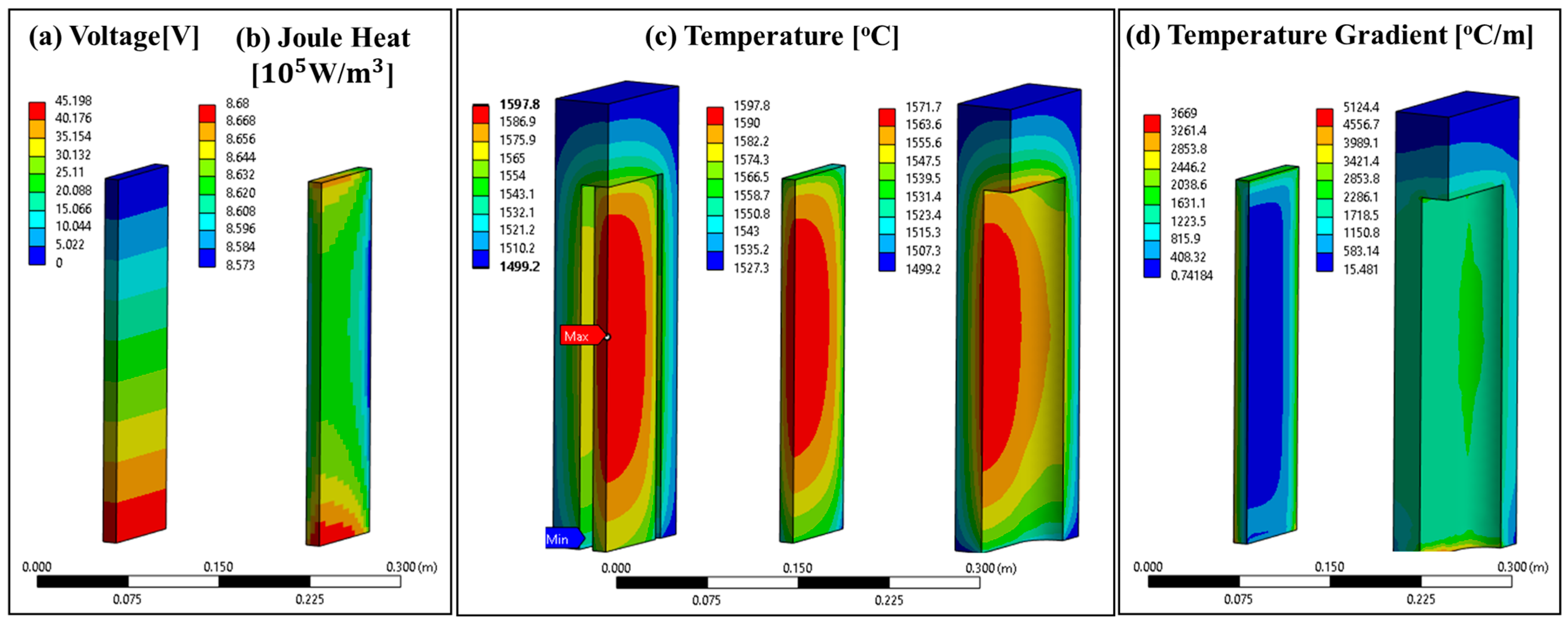
Thermal–Electric Model Results
Static Structural Model Results
2.3.2. Experimental Results and Validation of Numerical Model
Experimental Results
Numerical Model Validation with Experimental Data
3. System-Level Discharging Brick Stack
3.1. Methodology
3.1.1. Geometry and Computational Domain
3.1.2. Governing Equations
3.1.3. Initial, Boundary, and Interface Conditions
3.1.4. Operating Conditions and Parameters of the Numerical Analysis
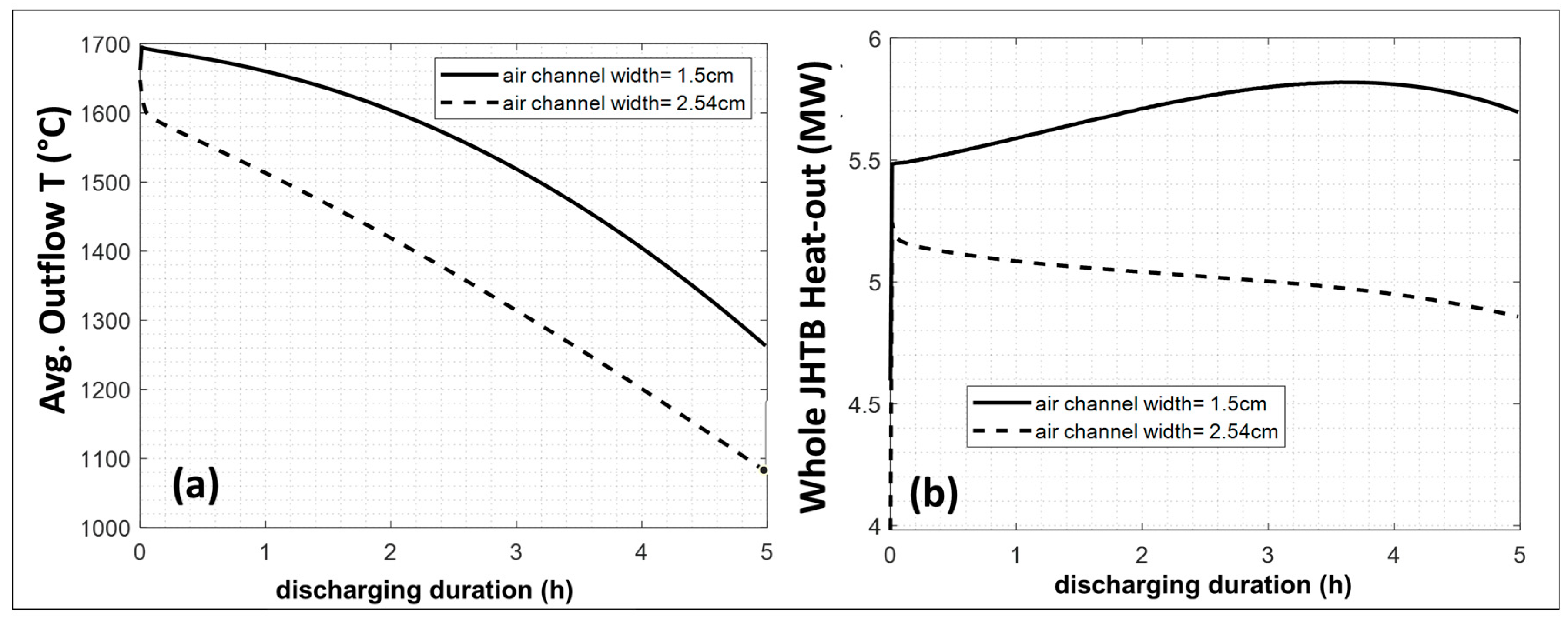
3.2. Discussion of the System-Level Discharging Brick Stack
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Area | (m2) |
| Elastic stiffness (stress–strain) matrix | (Pa) | |
| Electric field in the thermal–electric model; or Young’s Modulus in the structural model, dmissive power in radiation equations | (V/m; Pa; W/m2) | |
| View factor between surfaces i and j | (-) | |
| Shear modulus | (Pa) | |
| Generation of k due to mean velocity gradients | (kg/m/s3) | |
| Generation of | (kg/m3/s3) | |
| Convection heat transfer coefficient | (W/m2/K) | |
| Electric current density in thermal–electric equations, radiosity (in radiation), mass flux (in energy equation) | (A/m2; W/m2; (kg/m2/s)) | |
| k | Thermal conductivity or turbulent kinetic energy | (W/m2/K; m2/s2) |
| Power dissipated due to Ohmic loss | (W/m3) | |
| Energy flux | (W/m2) | |
| Net heat flux from surface i | (W/m2) | |
| Radiosity (outgoing radiative flux) flux for surface j | (W/m2) | |
| Volumetric heat generation term | (W/m3) | |
| RMS | Root mean square | (-) |
| Re | Reynolds number | (-) |
| S | Strain rate | (s−1) |
| t | Time | (s) |
| Temperature | (°C) | |
| Bulk temperature of the adjacent fluid | (°C) | |
| Absolute temperature of surface i | (K) | |
| Heat sink temperature | (°C) | |
| Surface temperature | (°C) | |
| u | Velocity | (m/s) |
| Secant coefficient of thermal expansion | (m/°C) | |
| Kronecker delta | (-) | |
| Poisson’s ratio | (-) | |
| Stress vector in structural equations | (Pa) | |
| Dissipation of k due to turbulence | (kg/m/s3) | |
| Dissipation of due to turbulence | (kg/m3/s3) | |
| Effective diffusivity | (Pa-s) | |
| Strain in the structural model | (m/m) | |
| ε | Emissivity in the thermal–electric model | (-) |
| Thermal strain vector | (m/m) | |
| Density, or electrical resistivity in thermal–electric equations, or reflectivity in radiation equations | (kg/m3;Ohm-m; -) | |
| Specific turbulent dissipation rate | (s−1) | |
| Stefan–Boltzmann Constant in radiation equations | (W/m2/K4) | |
| Visibility constant, 1 if is visible to and 0 if is not visible to | (-) | |
| Electric scalar potential | (V) | |
| Stress tensor | (Pa) | |
| Dynamic viscosity | (Pa-s) | |
| Subscripts | ||
| F# | Front face measurement location of #th brick | (-) |
| SC# | Side center measurement location of #th brick | (-) |
| x,y,z | In x, y, or z direction | (-) |
| eff | Effective | (-) |
| in | Incoming | (-) |
| k | Related to surface k | (-) |
| out | Outgoing | (-) |
| t | Turbulent | (-) |
References
- McKinsey & Company. Net-Zero Heat: Long Duration Energy Storage to Accelerate Energy System Decarbonization; LDES Council: Brussels, Belgium, 2022. [Google Scholar]
- Thiel, G.P.; Stark, A.K. To Decarbonize Industry, We Must Decarbonize Heat. Joule 2021, 5, 531–550. [Google Scholar] [CrossRef]
- Rissman, J.; Bataille, C.; Manaset, E.; Aden, N.; Morrow III, W.; Zhou, N.; Elliot, N.; Dell, R.; Heeren, N.; Huckestein, B.; et al. Technologies and Policies to Decarbonize Global Industry—Review and Assessment of Mitigation Drivers Through 2070. Appl. Energy 2020, 266, 114848. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Industrial Decarbonization Roadmap; United States Department of Energy: Washington, DC, USA, 2022.
- Vishal, S.; Renil, A.; Gaitonde, U.; Rangan, B. Performance Analysis for glass Furnace Generator. Appl. Energy 2011, 88, 4451–4458. [Google Scholar]
- Laing, D.; Zunft, S. Using Concrete and other Solid Storage Media in Thermal Energy Storate System. In Advances in Thermal Energy Storage System; Elsevier: Amsterdam, The Netherlands, 2015; pp. 65–86. [Google Scholar]
- Gasia, J.; Miro, L.; Lusia, C. Review on Systerm and Materials Requirements for High Temperature Thermal Energy Storage. Part 1: General Requirements. Renew. Sustain. Energy Rev. 2017, 75, 1320–1338. [Google Scholar] [CrossRef]
- Gil, A.; Marc, M.; Martorell, I.; Lázaro, A.; Dolado, P.; Zalba, B.; Cabez, L. State of the Art on High Temperature Thermal Energy Storage for Power Generation. Part 1—Concepts, Materials and Modellization. Renew. Sustain. Energy Rev. 2010, 14, 31–35. [Google Scholar] [CrossRef]
- Sepulveda, N.; Jenkins, J.; Edington, A.; Mallapragada, D.; Lester, R. The Design Space for Long-Duration Energy Storage in Decarbonized Power Systems. Nat. Energy 2021, 6, 505–516. [Google Scholar] [CrossRef]
- Resistance Heating Alloys and Systems for Industrial Systems. Available online: https://www.kanthal.de/globalassets/kanthal-global/downloads/resistance-heating-alloys-and-systems-for-industrial-furnaces_b_eng_lr.pdf (accessed on 1 August 2023).
- Friedmann, S.Z.; Tang, K. Low-Carbon Heat Solutions for Heavy Industry, Sources, Options and Costs Today; Columbia|SIPA Centre for Global Energy Policy: New York, NY, USA, 2019. [Google Scholar]
- IRENA. Making Breakthrough: Green Hydrogen Policies and Technology Costs; IRNEA: Abu Dhabi, United Arab Emirates, 2021. [Google Scholar]
- Stack, D. Development of High Temperature FireBrick Resistance-Heated Enery Storage (FIRES) Using Doped Ceramic Heating System. Ph.D. Thesis, MIT, Cambridge, MA, USA, 2021. [Google Scholar]
- Hensler, J.; Henry, E. Electrical Resistance of Some Refractory Oxides and Their Mixtures in the Temperature Range 600 to 1600C. J. Am. Ceram. Soc. 1953, 36, 76–83. [Google Scholar] [CrossRef]
- Stack, D.; Forsberg, C. Electrically Conductive Firebrick System. United States Patent US20220132633A1, 31 August 2021. [Google Scholar]
- IEA. The Challenge of Reaching Zero Emissions in Heavy Industry; IEA: Paris, France, 2020. [Google Scholar]
- Stack, D.; Curtis, D.; Forsberg, C. Performance of Firebrick Resistance Energy Storage for Industrial Heat Applications and Round Trip Electricity Storage. Appl. Energy 2019, 242, 782–796. [Google Scholar] [CrossRef]
- Zetterholm, J.; Ji, X.; Sundelin, B.; Martin, P.; Wang, C. Model Development of a Blast Furnace Stove. In Proceedings of the 7th International Conference on Applied Energy, Milan, Italy, 28–31 March 2015. [Google Scholar]
- Serrazina, R.; Vilarinho, P.M.; Senos, A.M.; Pereria, L.; Reaney, I.M.; Dean, J. Modelling the particle contact influence on the Joule heating and temperature distribution during FLASH sintering. J. Eur. Ceram. Soc. 2020, 40, 1205–1211. [Google Scholar] [CrossRef]
- Holland, T.; Anselmi-Tamburini, U.; Quach, D.; Tran, T.B.; Mukherjee, A.K. Effects of Local Joule Heating During the Field Assisted Sintering of Ionic Ceramics. J. Eur. Ceram. Soc. 2012, 32, 3667–3674. [Google Scholar] [CrossRef]
- Grasso, S.; Sakka, Y.; Rendtorff, N.; Hu, C.; Maizza, G.; Borodianska, H.; Vasylkiv, O. Modeling of the temperature distribution of flash sintered zirconia. J. Ceram. Soc. Jpn. 2011, 119, 144–146. [Google Scholar] [CrossRef]
- Liu, F.; Zhao, Z.; Ma, Y.G.Y.; Li, J.; Hu, X.; Ye, Z.; Dong, D. Robust Joule-heating ceramic reactors for catalytic CO oxidation. J. Adv. Ceram. 2022, 11, 1163–1171. [Google Scholar] [CrossRef]
- Ansys Mechanical, Finite Element Analysis (FEA) Software for Structural Engineering. Available online: https://www.ansys.com/products/structures/ansys-mechanical (accessed on 30 September 2024).
- Ansys Fluent Fluid Simulation Software. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 20 October 2023).
- Asar, M.E.; Stack, D.C.; Truong, B. Conjugate Heat Transfer Analysis of Discharging Joule Hive Thermal Battery. In Proceedings of the ASTFE 9th Thermal and Fluids Engineering Conference, Corvallis, OR, USA, 21–24 April 2024. [Google Scholar]
- Asar, M.E.; McKinley, D.; Truong, B.; Kabel, J. Characterizing Thermal, Electric, and Structural Responses of Electrically Charged Firebricks For Industrial Thermal Battery Applications. In Proceedings of the American Society of Thermal and Fluids Engineers (ASTFE) 10th Thermal and Fluids Engineering Conference, Washington, DC, USA, 9–12 March 2025. [Google Scholar]
- ANSYS. Theory Reference; ANSYS Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- ANSYS. Ansys Fluent Theory Guide; ANSYS Inc.: Canonburg, PA, USA, 2023. [Google Scholar]

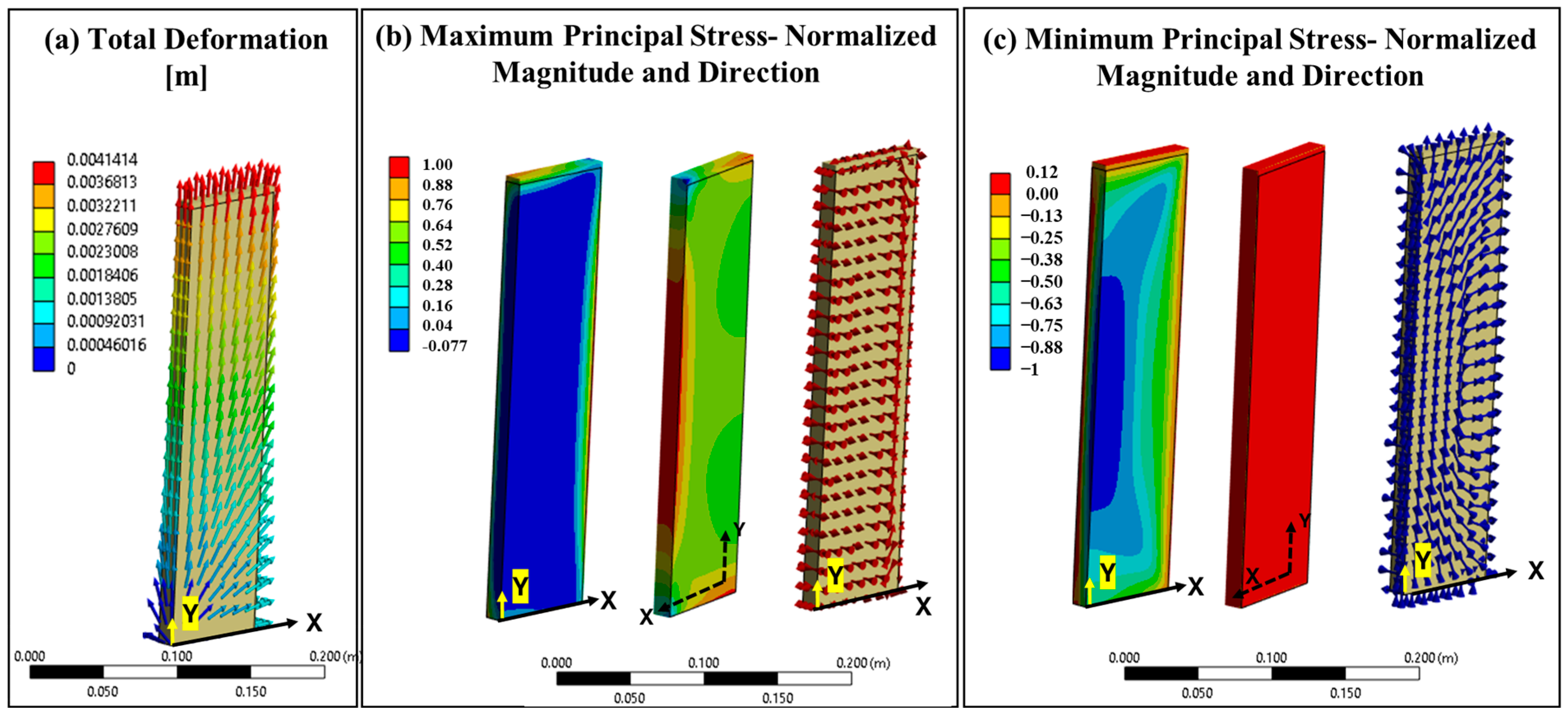


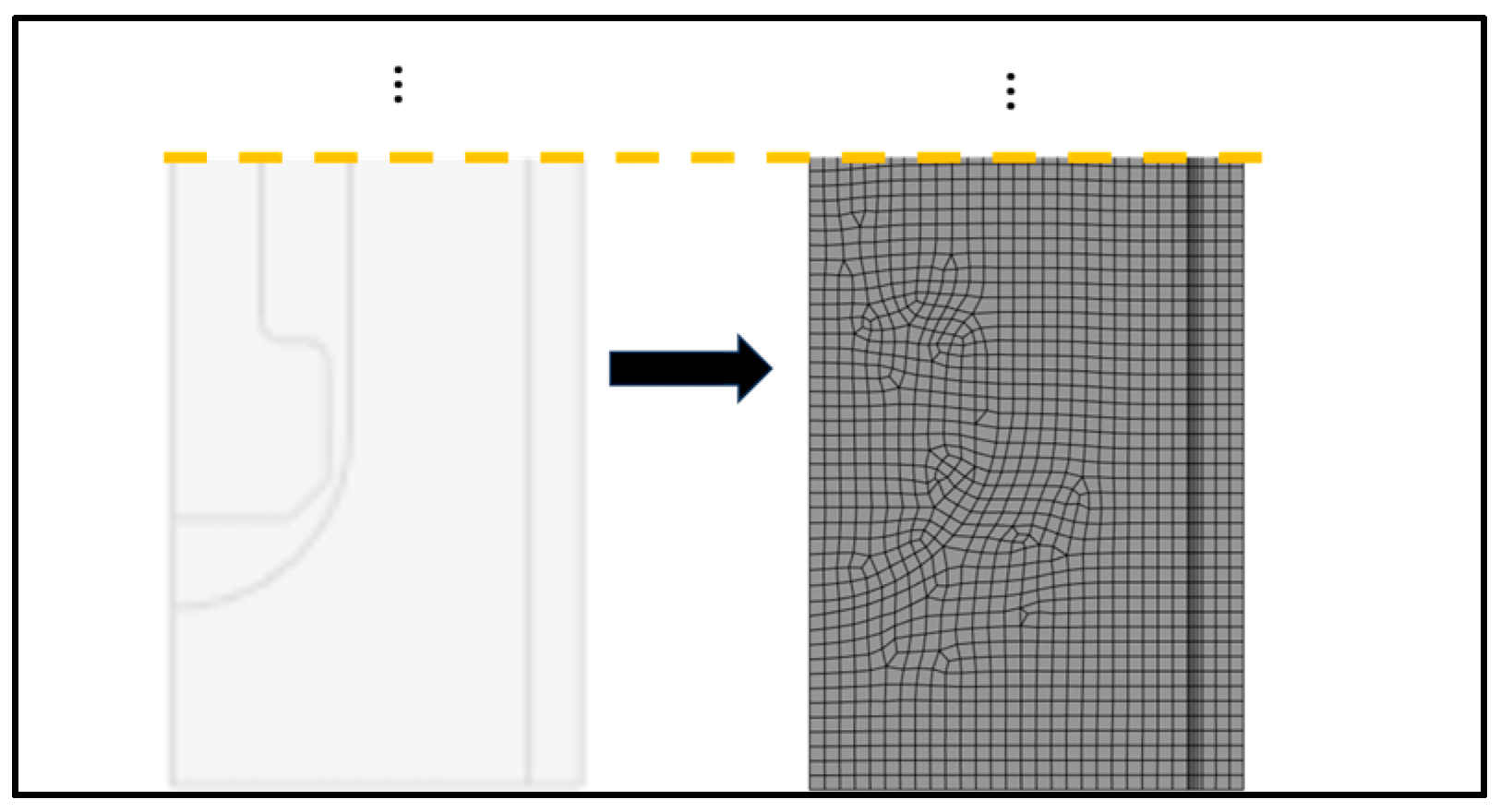
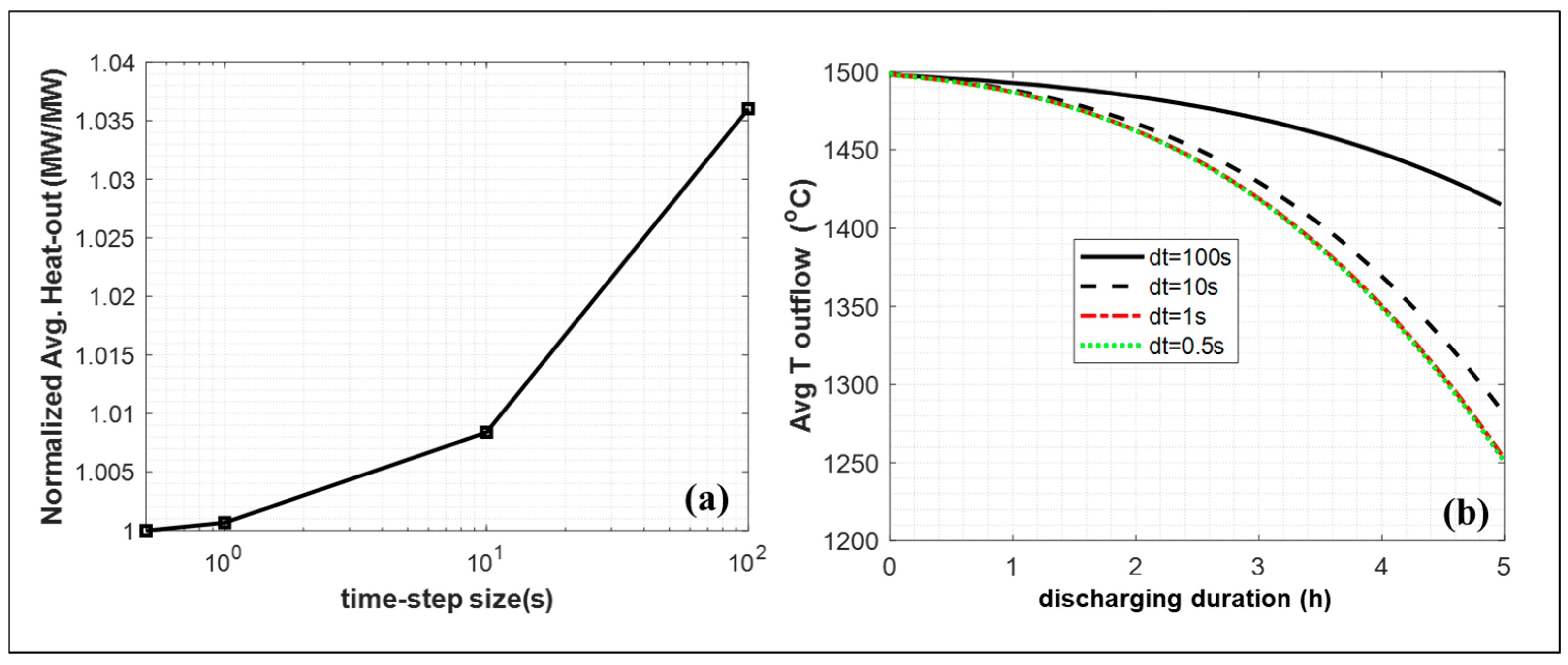
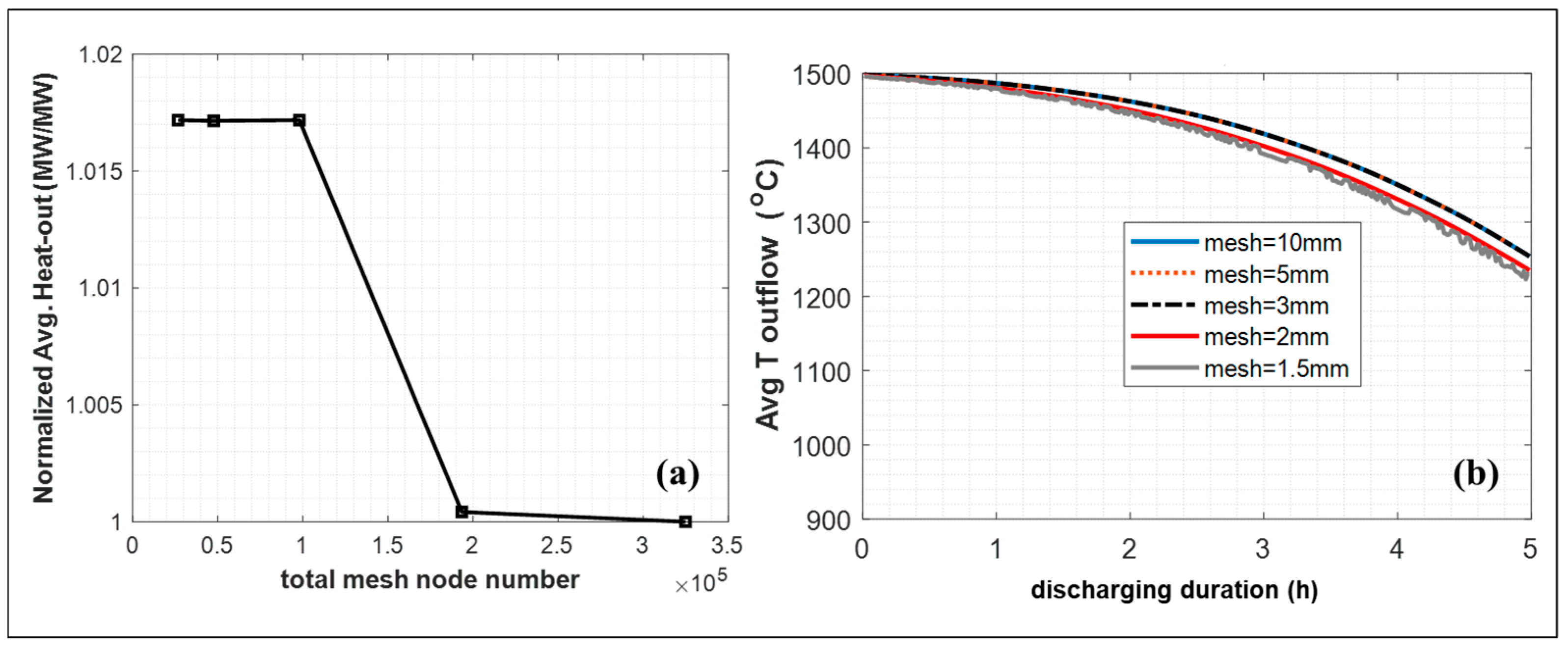

| Mesh Size | Normalized Maximum | % Difference Between the 1 mm Case | Maximum Total Deformation | % Difference Between the 1 mm Case |
|---|---|---|---|---|
| [m] | [Pa/Pa] | [m] | ||
| 0.005 | 0.9862 | 1.37% | 0.004141 | 0% |
| 0.004 | 0.9904 | 0.95% | 0.004141 | 0% |
| 0.003 | 0.9935 | 0.63% | 0.004141 | 0% |
| 0.002 | 0.9972 | 0.28% | 0.004141 | 0% |
| 0.001 | 1 | 0.004141 |
| X-Location [mm] | Y-Location [mm] | Z-Location [mm] | Experimental | Numerical | Error (num.-exp.) | |
|---|---|---|---|---|---|---|
| TF1 [°C] | 83 | 38.1 | 0 | 1545.6 ± 4.86 | 1548.6 | 3 (6.6%) |
| TF2 [°C] | 83 | 114.3 | 0 | 1555.7 ± 4.86 | 1561.6 | 5.3 (9.5%) |
| TF4 [°C] | 83 | 266.7 | 0 | 1559.5 ± 4.86 | 1557 | −2.5 (−4.2%) |
| TSC2 [°C] | 0 | 114.3 | 14.7 | 1583.0 ± 4.86 | 1576.9 | −6.1 (7.3%) |
| ΔVSC1-SC4 [V] | 0 | 12.6–241.4 | 12.7 | 33.03 ± 1.51 | 34.07 | 1.04 (3.01%) |
| Case 1 | Case 2 | |
|---|---|---|
| Air channel width | 1.5 cm | 2.54 cm |
| Total mass flow rate across all air channels in JHTB | 5 kg/s × (mass flow rate ratio) | 5 kg/s × (mass flow rate ratio) |
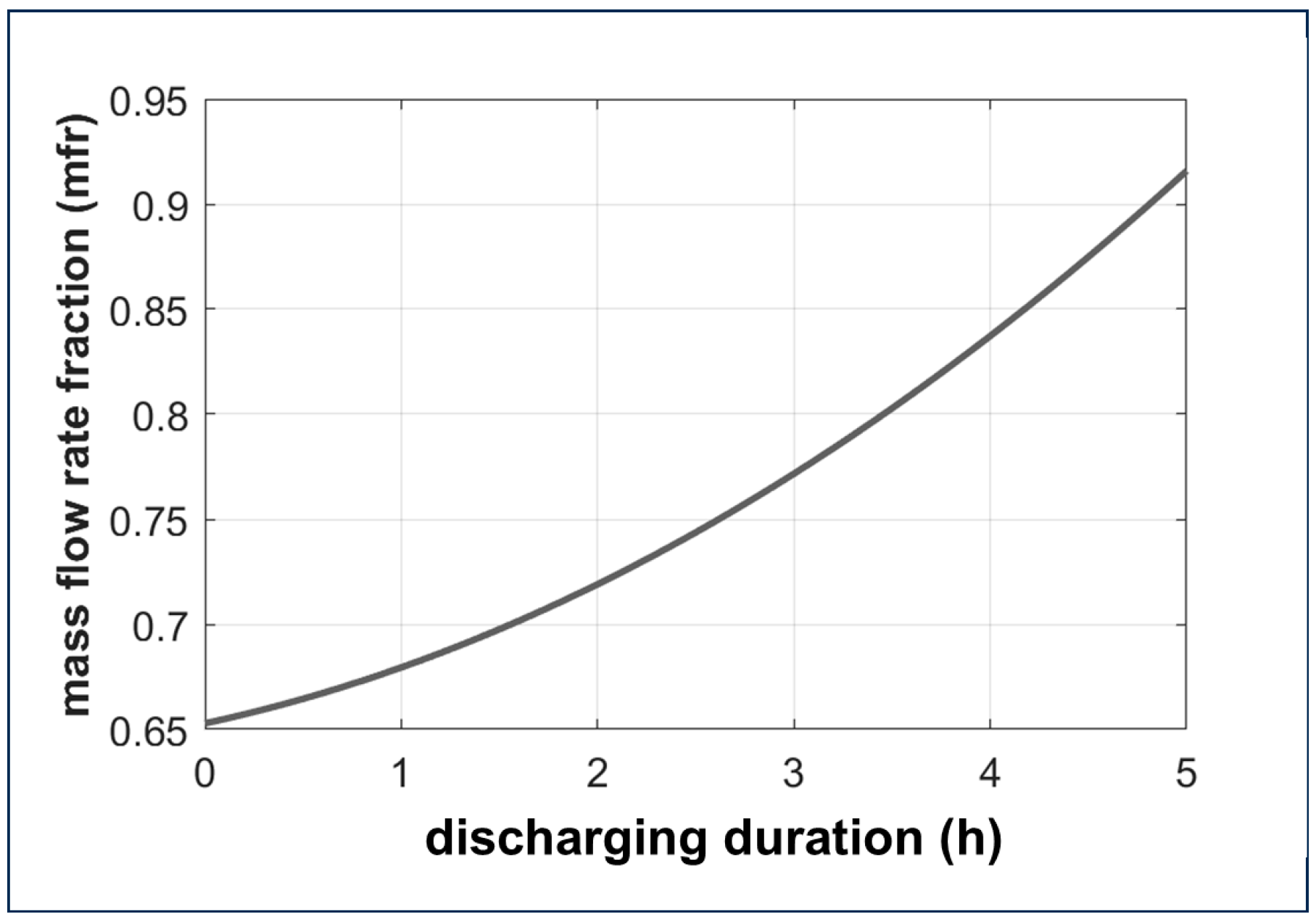
| Mass flow rate ratio | Varies from 0.6 to 0.9 as a function of time/discharge duration, see Figure 12 | Same as Case 1 |
| Tinlet,flow | 25 °C | 25 °C |
| Initial temperature of JHTB | 1700 °C | 1700 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asar, M.E.; McKinley, D.; Truong, B.; Kabel, J.; Stack, D. Multiscale Evaluation of an Electrically Heated Thermal Battery for High-Temperature Industrial Energy Storage. Energies 2025, 18, 4461. https://doi.org/10.3390/en18174461
Asar ME, McKinley D, Truong B, Kabel J, Stack D. Multiscale Evaluation of an Electrically Heated Thermal Battery for High-Temperature Industrial Energy Storage. Energies. 2025; 18(17):4461. https://doi.org/10.3390/en18174461
Chicago/Turabian StyleAsar, Munevver Elif, Daniel McKinley, Bao Truong, Joey Kabel, and Daniel Stack. 2025. "Multiscale Evaluation of an Electrically Heated Thermal Battery for High-Temperature Industrial Energy Storage" Energies 18, no. 17: 4461. https://doi.org/10.3390/en18174461
APA StyleAsar, M. E., McKinley, D., Truong, B., Kabel, J., & Stack, D. (2025). Multiscale Evaluation of an Electrically Heated Thermal Battery for High-Temperature Industrial Energy Storage. Energies, 18(17), 4461. https://doi.org/10.3390/en18174461







