Heat Exchange Effectiveness and Influence Mechanism of Coaxial Downhole in the Alpine Region of Xining City, Qinghai Province
Abstract
1. Introduction
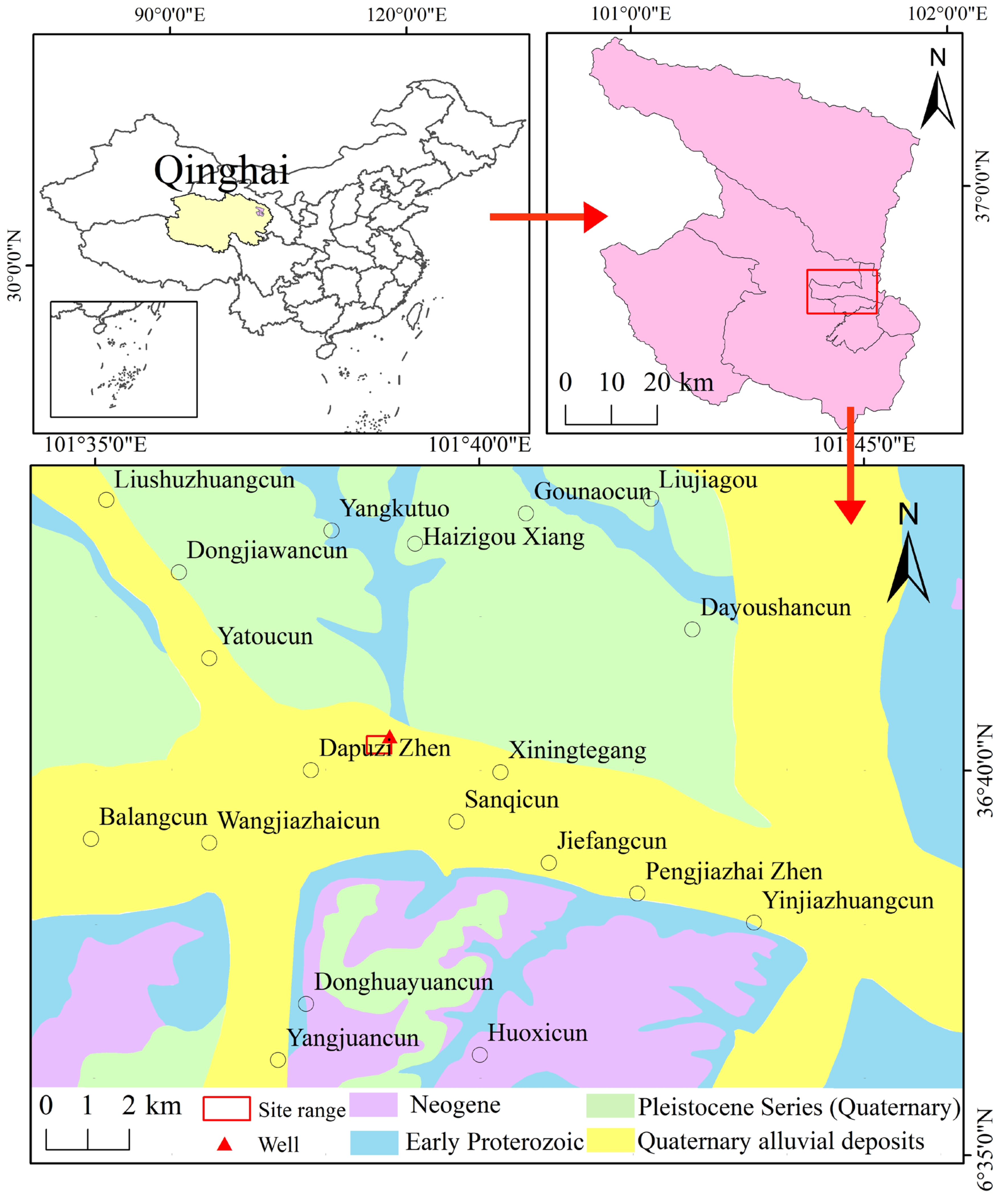
2. Overview of the Study Area
2.1. Geothermal Geological Conditions of the Site
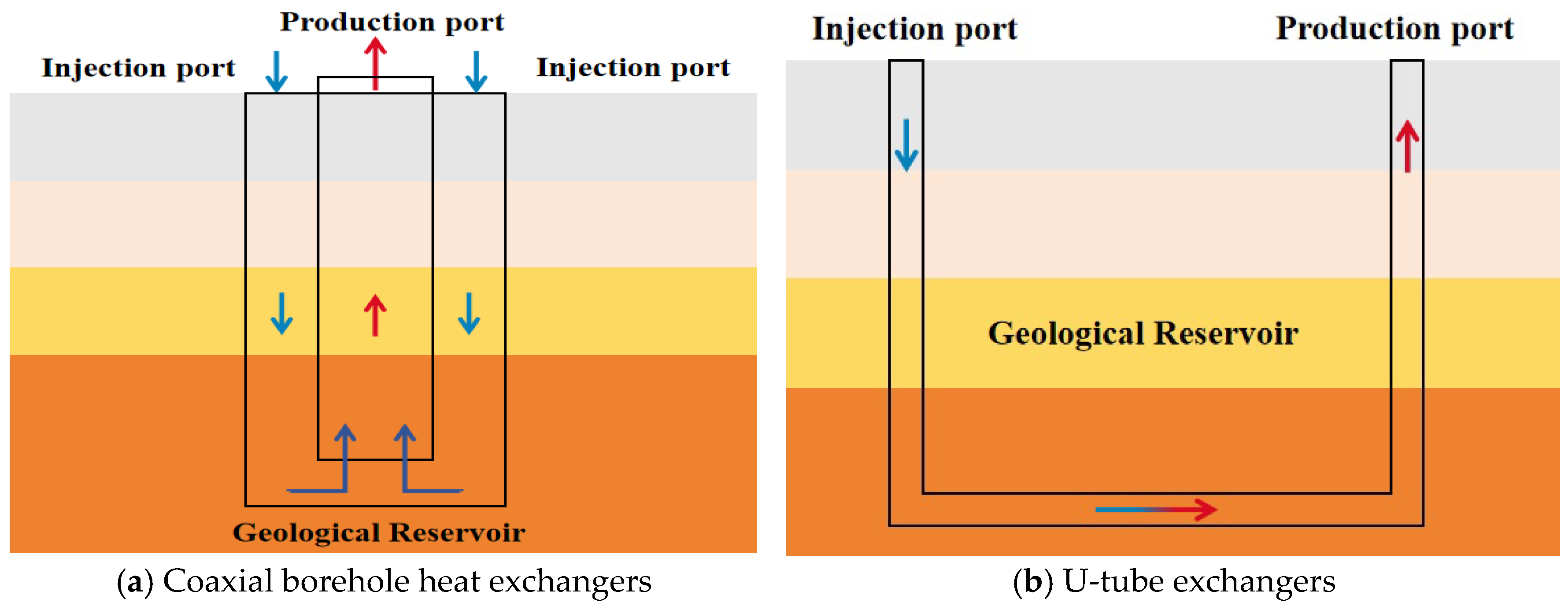
2.2. Geothermal Well Structure Model
2.3. Field Coaxial Heat Exchange Test
3. Coaxial Heat Exchange Numerical Model Construction
3.1. Model Assumptions
3.2. Heat Transfer Equation for the Thermal Storage Layer
3.3. Heat Transfer Equation in the Wellbore
3.4. Mesh Generation
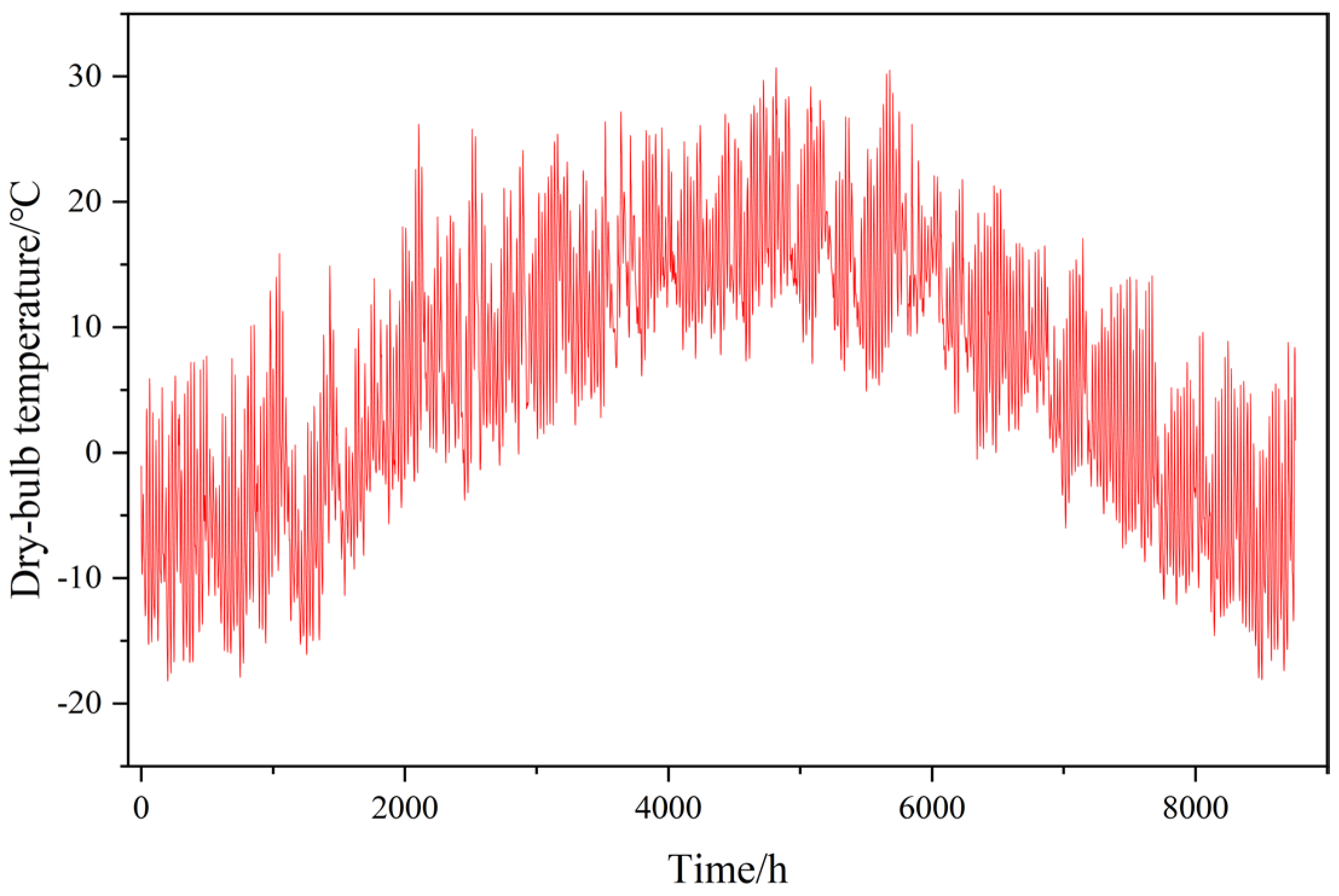
3.5. Initial and Boundary Conditions
- (1)
- Based on the average winter air temperature in Xining, the top boundary of the model was set as a constant temperature boundary:T|z=0=3 °C
- (2)
- Based on the geothermal gradient of the rock reservoir, the lateral and bottom boundaries of the model were set as geothermal gradient boundaries:
- (3)
- The inlet boundary was defined with a fixed temperature and fixed flow rate:T = Tinwhere Tin is the inlet temperature, °C; Qin is the inlet flow rate, m3/s; and A is the cross-sectional area of the pipe, m2.
- (4)
- The outlet boundary of the model was set as a thermal outflow boundary, where heat transfer occurs only in the direction of convection. The temperature gradient in the normal direction was set to zero, and radiative heat transfer was neglected:is the unit normal vector at the outlet boundary; is the temperature gradient.
- (5)
- Two general extrusion operators were used to map the temperature conditions onto the pipe wall:where (r,z) are the coordinates on the target boundary; (r′,z′), (r″,z″) are the coordinates in the source regions, which are determined using general extrusion functions. This mapping reflects the thermal coupling between the inner and outer temperature fields of the wellbore.
3.6. Solution Method
- (1)
- The model equations were spatially discretized using the finite element method (FEM). Second-order Lagrange elements, as provided by COMSOL, were selected to ensure computational accuracy.The mass conservation equation is given as follows:The energy conservation equation is given as follows:where is the fluid density, kg/m3; is the specific heat capacity at constant pressure, J/(kg·K); is the velocity vector, m/s; T is the temperature, °C; k is the thermal conductivity, W/(m·k); and Q is the volumetric heat source term. This equation describes heat conduction in solids and axial convective heat transfer in the pipe flow.
- (2)
- The Non-Isothermal Pipe Flow module in COMSOL was employed to simulate the heat transfer process within the wellbore. This module is based on the assumption of one-dimensional axial incompressible flow, and it simultaneously solves the mass and energy conservation equations to achieve a coupled solution for fluid velocity, pressure, and temperature fields. In the model, the flow velocity is assumed to exist only in the axial direction (), with no tangential or radial components, thereby simplifying the computational complexity and reflecting the dominant flow characteristics within vertical wellbores.
- (3)
- The nonlinear terms in the model were solved using the Newton–Raphson iterative method:where J is the Jacobian matrix; F is the residual vector of the equation system.
- (4)
- For temporal discretization, the implicit Backward Differentiation Formula (BDF) was employed. The maximum order was set to 2, and an adaptive time stepping scheme was used to ensure numerical stability and convergence. The time discretization is expressed as follows:
- (5)
- In the model, the wellbore flow corresponds to a high Reynolds number regime, indicating turbulent flow. Instead of using an explicit turbulence model, empirical Nusselt number correlations embedded in the Non-Isothermal Pipe Flow module were used to account for convective heat transfer under turbulent conditions. Specifically, the Gnielinski correlation, as presented in Equation (6), was applied during the simulation.
- (6)
- To ensure the convergence of the nonlinear equation system, the solver settings were configured with a relative tolerance of 0.001, an absolute tolerance factor of 1, and a maximum of 4 nonlinear iterations per time step. The convergence criterion for each time step is evaluated using the following expression:where F(x) is the fully coupled residual function; X(n) is the solution vector at the n-th iteration.
4. Results and Discussion
4.1. Analysis of Field Coaxial Heat Exchange Experiment Results
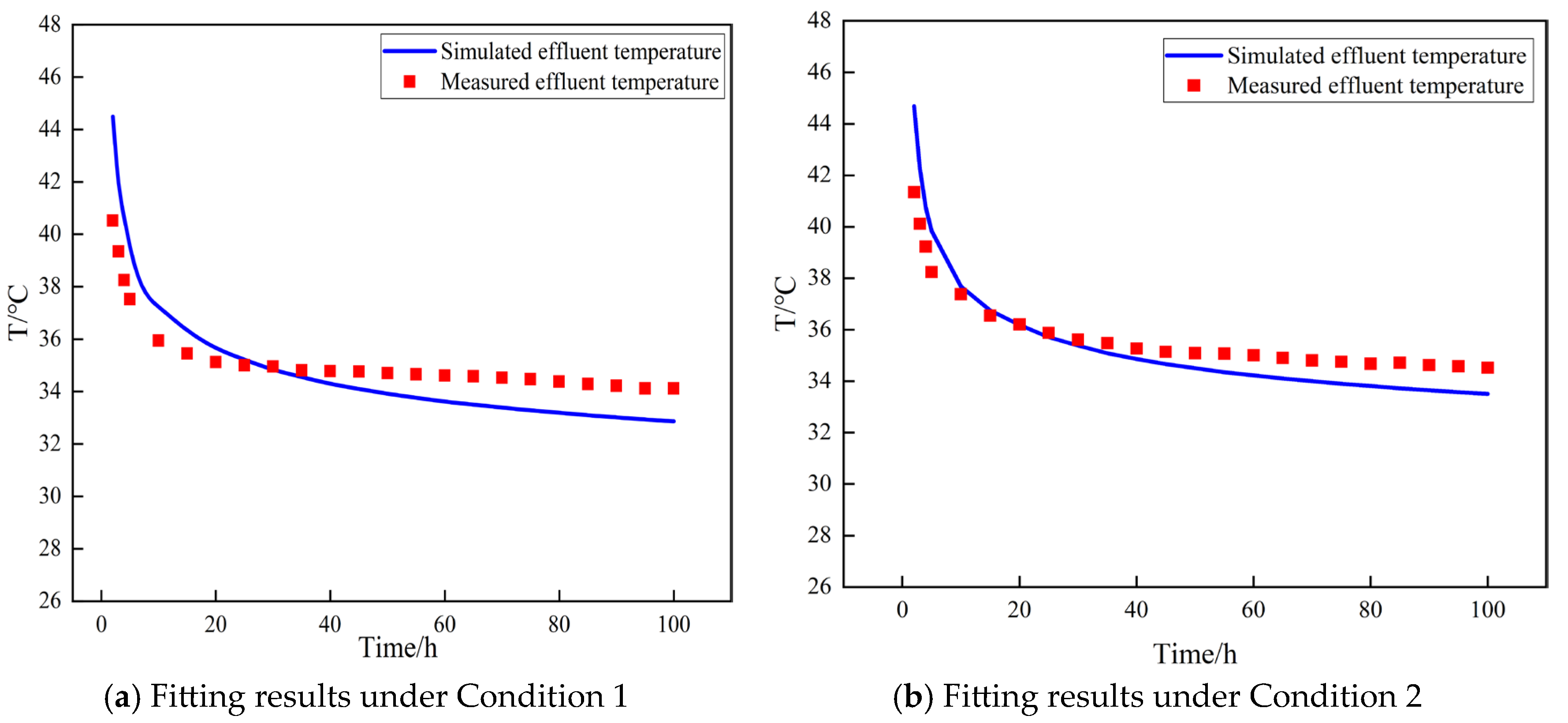
4.2. Model Identification and Validation Results and Analysis
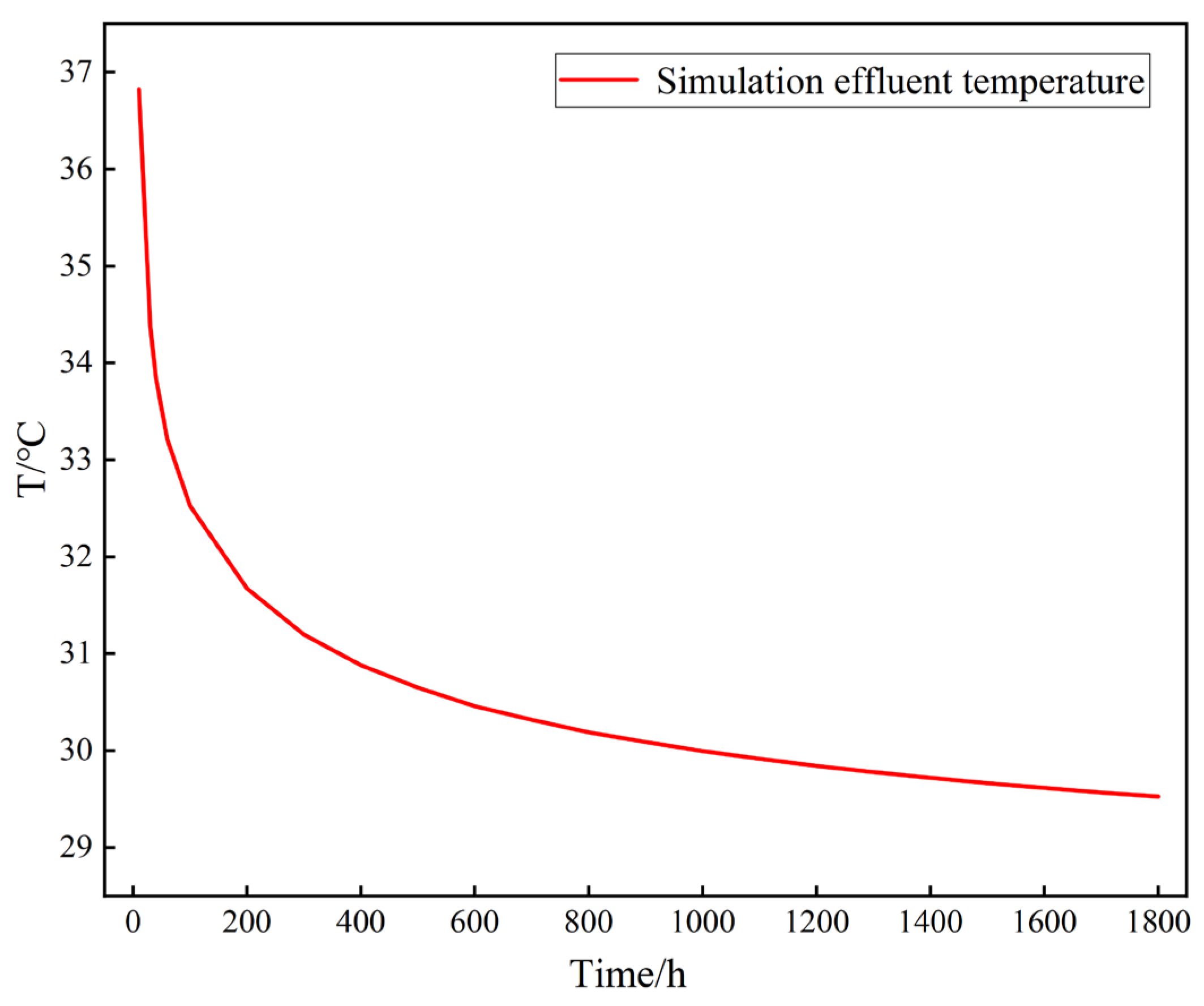
4.3. Thermal Performance Indicators
- (1)
- The heat exchange power of the well was calculated based on the inlet and outlet temperatures of the working fluid:where Q is the heat exchange power, W; is the fluid density, kg/m3; is the specific heat capacity of the fluid, J/kg °C; is the volumetric flow rate, m3/s; and and are the outlet and inlet temperatures of the fluid, respectively, °C.
- (2)
- The heat exchanger effectiveness was used to evaluate the heat exchange performance, representing the percentage ratio of the actual heat transfer to the theoretical maximum heat transfer:where Qact is the actual heat exchange power, W; Qmax is the theoretical maximum heat exchange power, W; and Tg is the initial formation temperature, °C. As the formation temperature in the model is assumed to vary linearly with depth, the weighted average temperature of the rock and soil at a depth of 2013 m was calculated to be 41.74 °C [32].
- (3)
- During the heat transfer process in a coaxial heat exchanger, thermal interaction occurs between the injected low-temperature water in the annular space and the rising high-temperature water in the inner pipe. This leads to an increase in inlet temperature and a decrease in outlet temperature, thereby reducing the overall heat exchange effectiveness. This phenomenon is referred to as thermal short-circuiting in coaxial heat exchangers. The temperature difference between the water at the bottom of the inner pipe and the outlet water is defined as the thermal short-circuit value.
4.4. Factors Affecting the Heat Transfer Performance of Heat Exchanger Wells
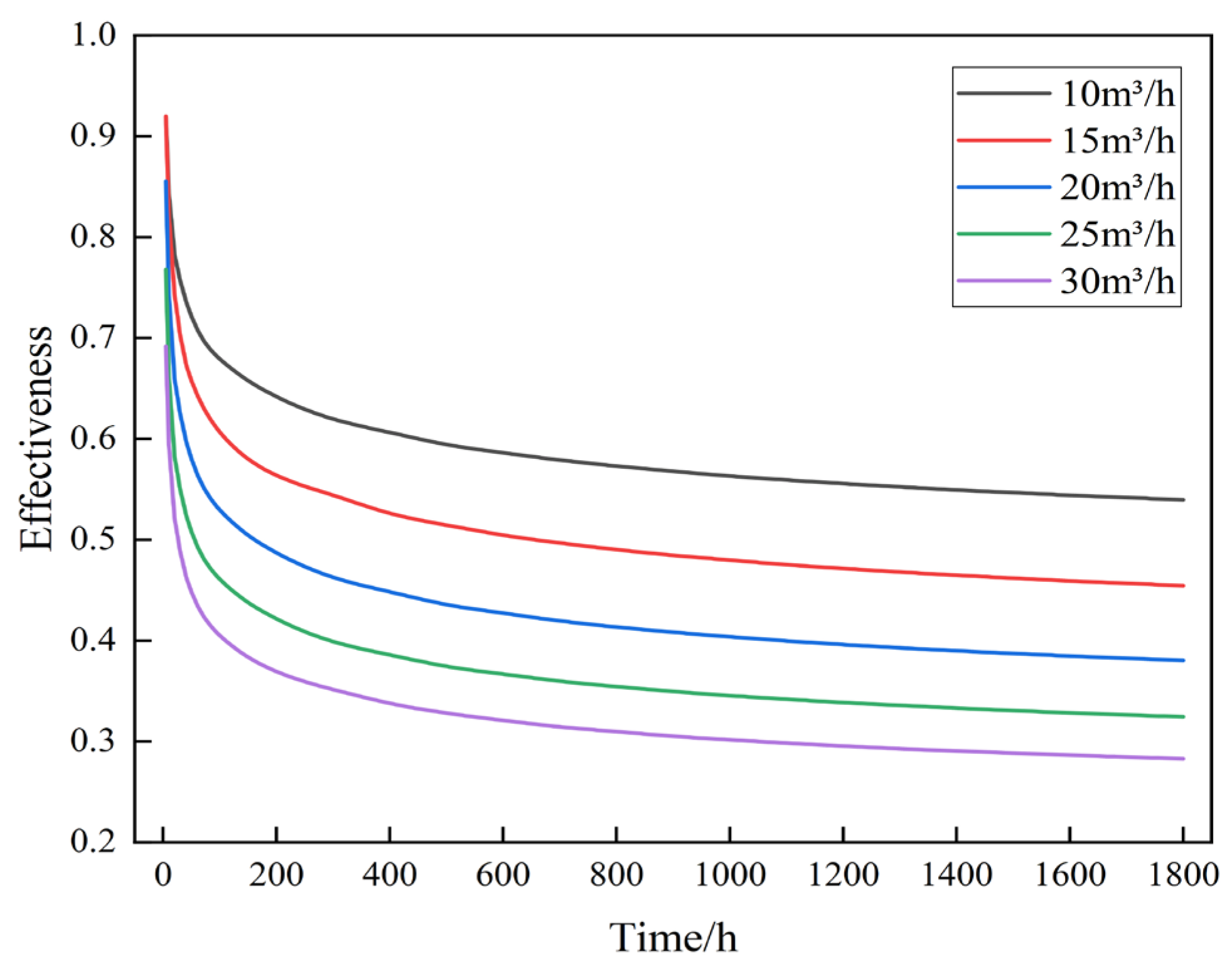
4.4.1. The Impact of Wellhead Injection Flow Rate on Heat Transfer Performance
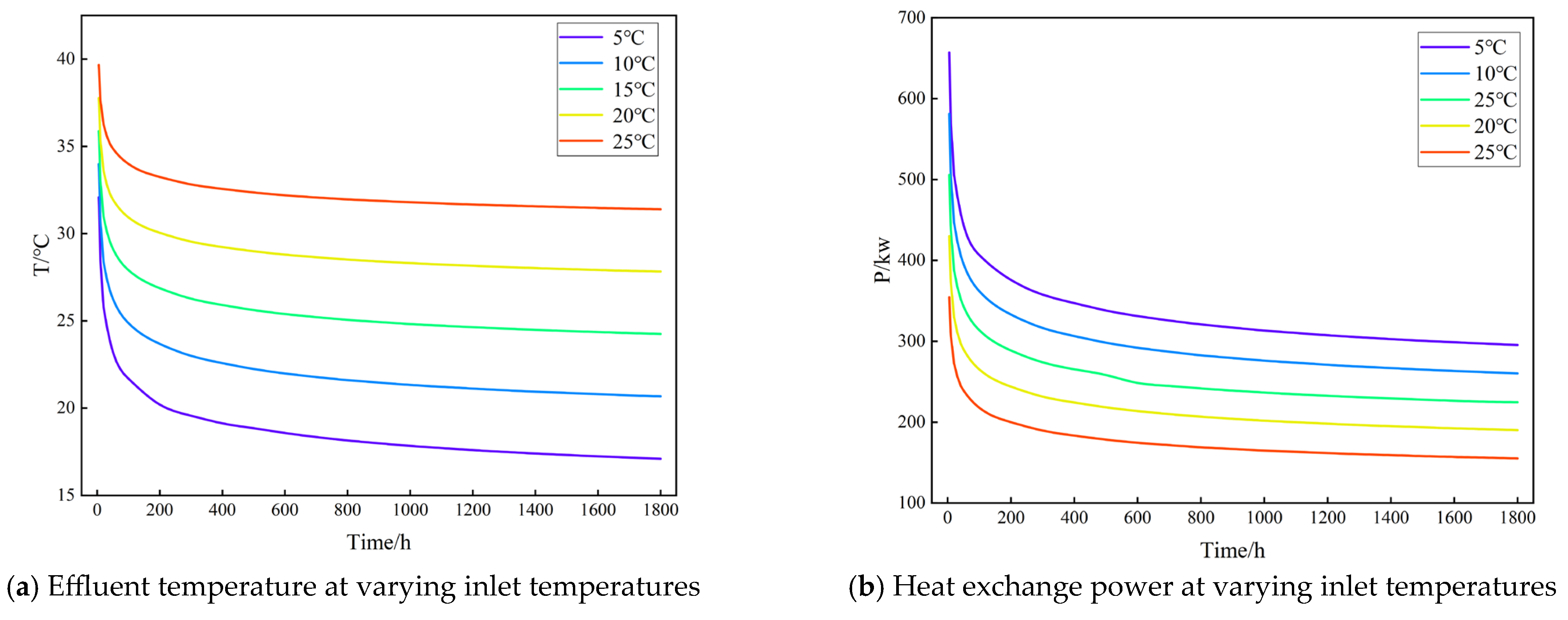
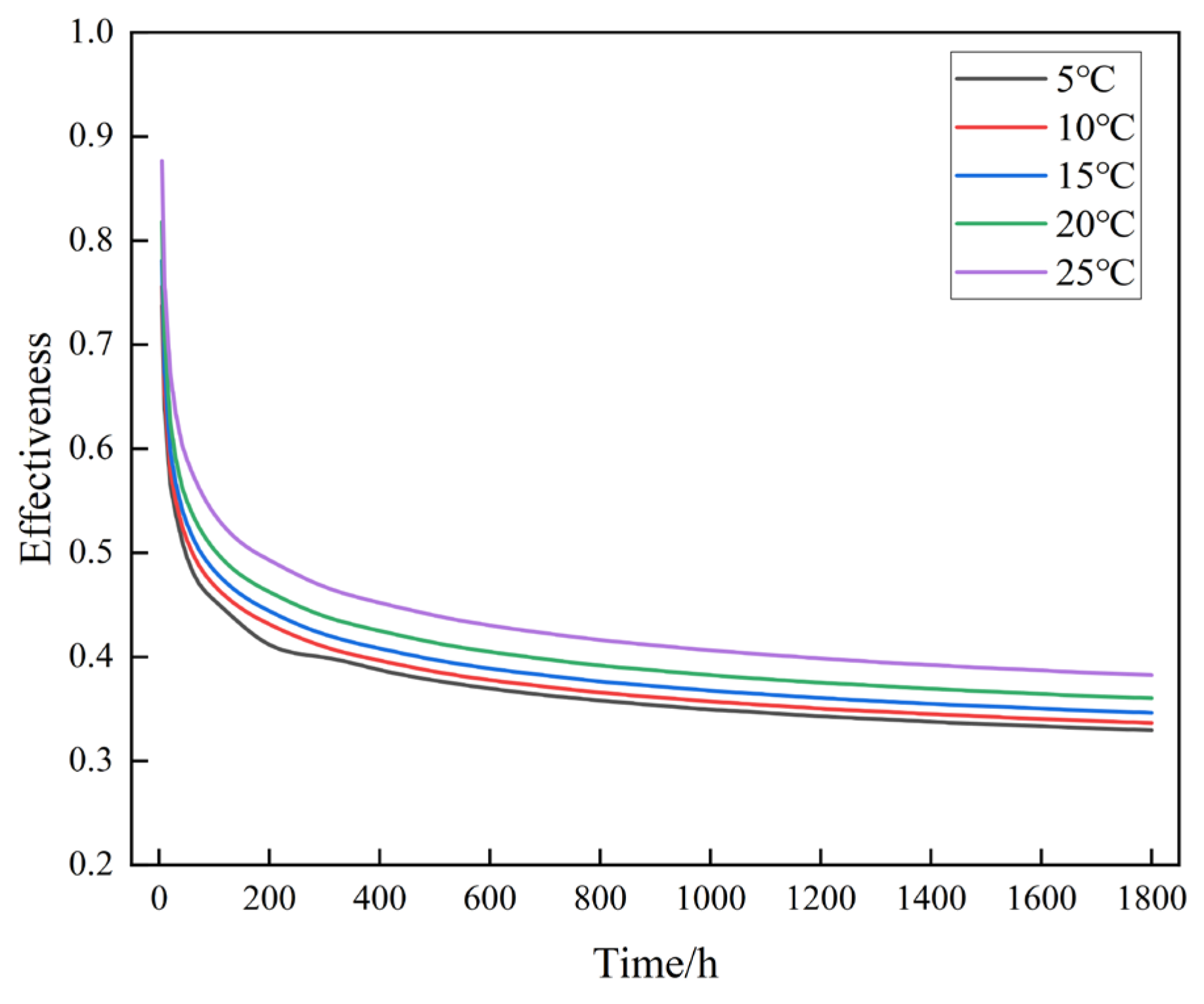
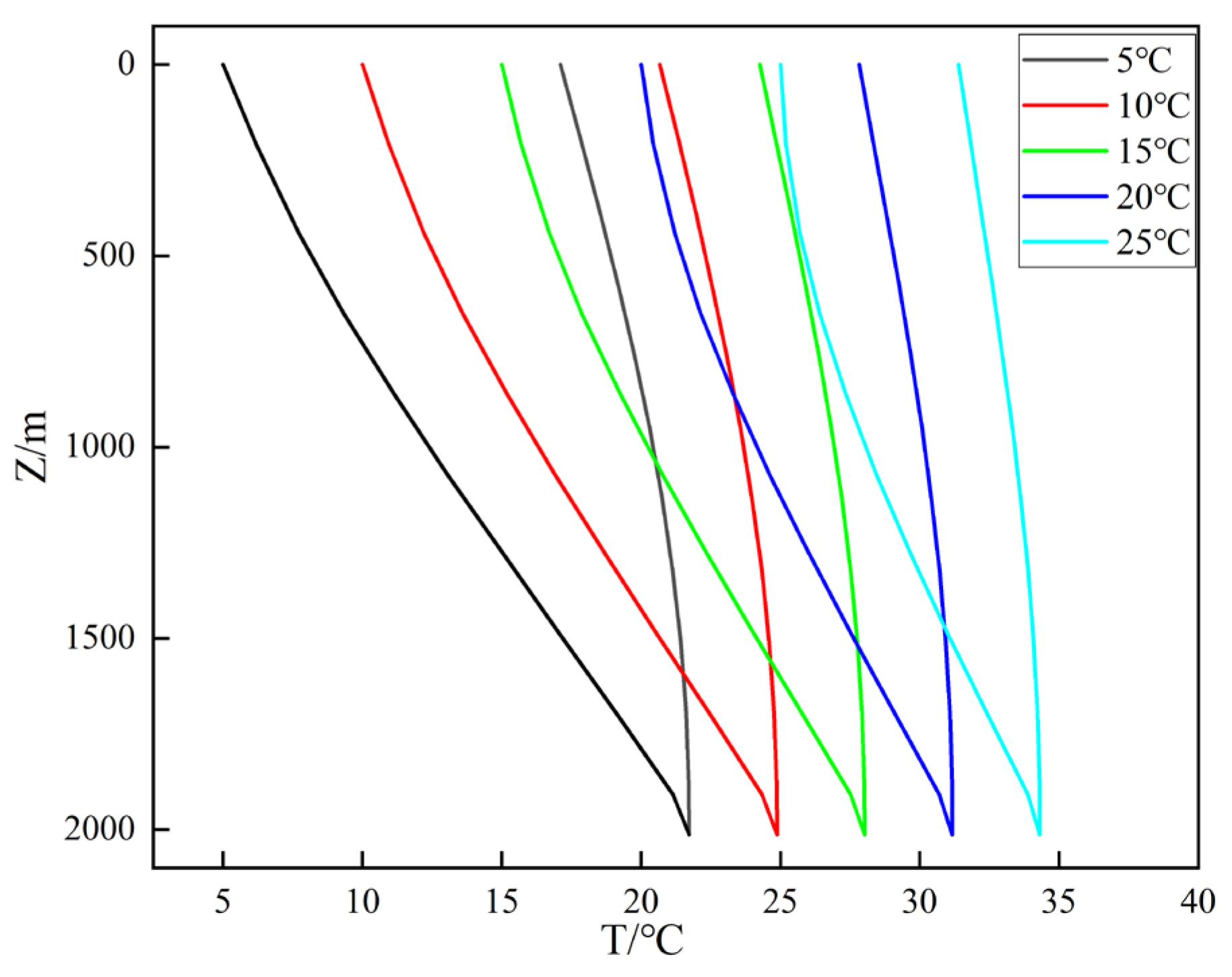
4.4.2. Influence of Inlet Water Temperature on Heat Exchange Performance
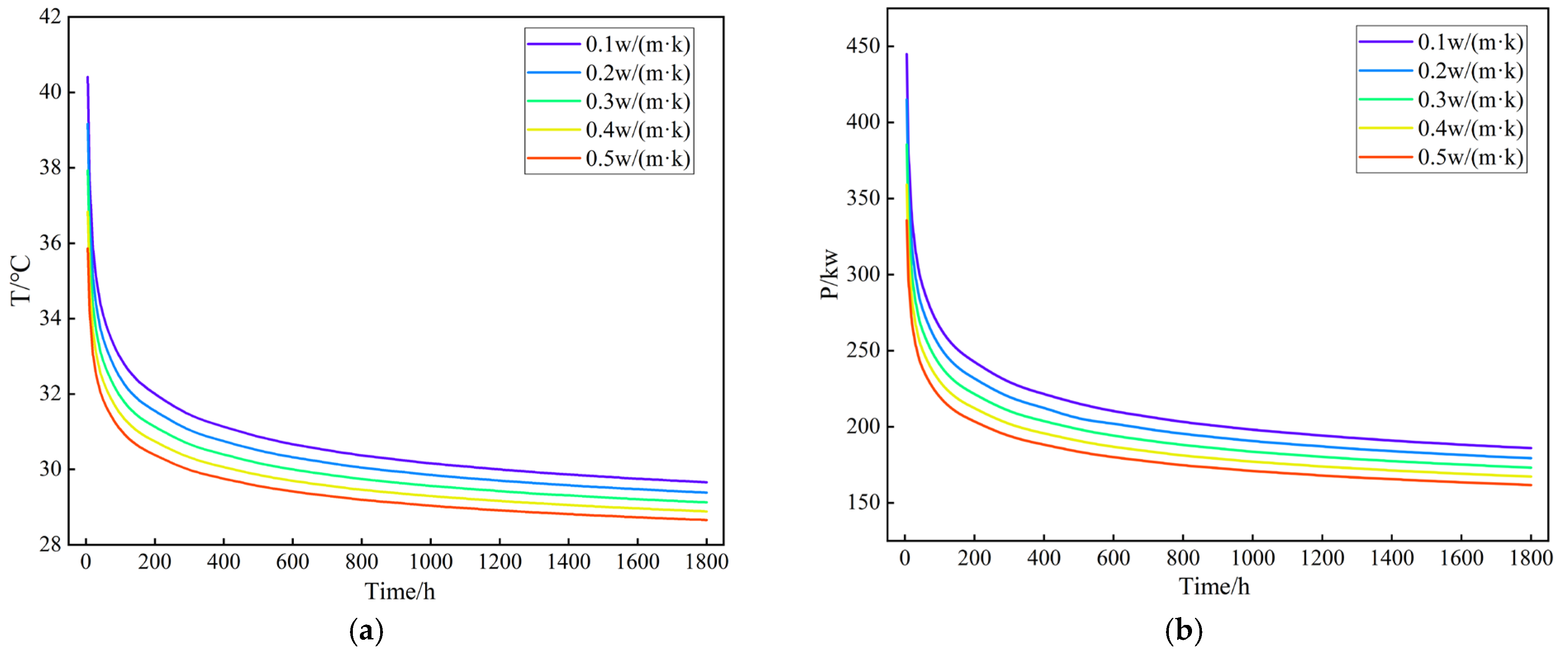
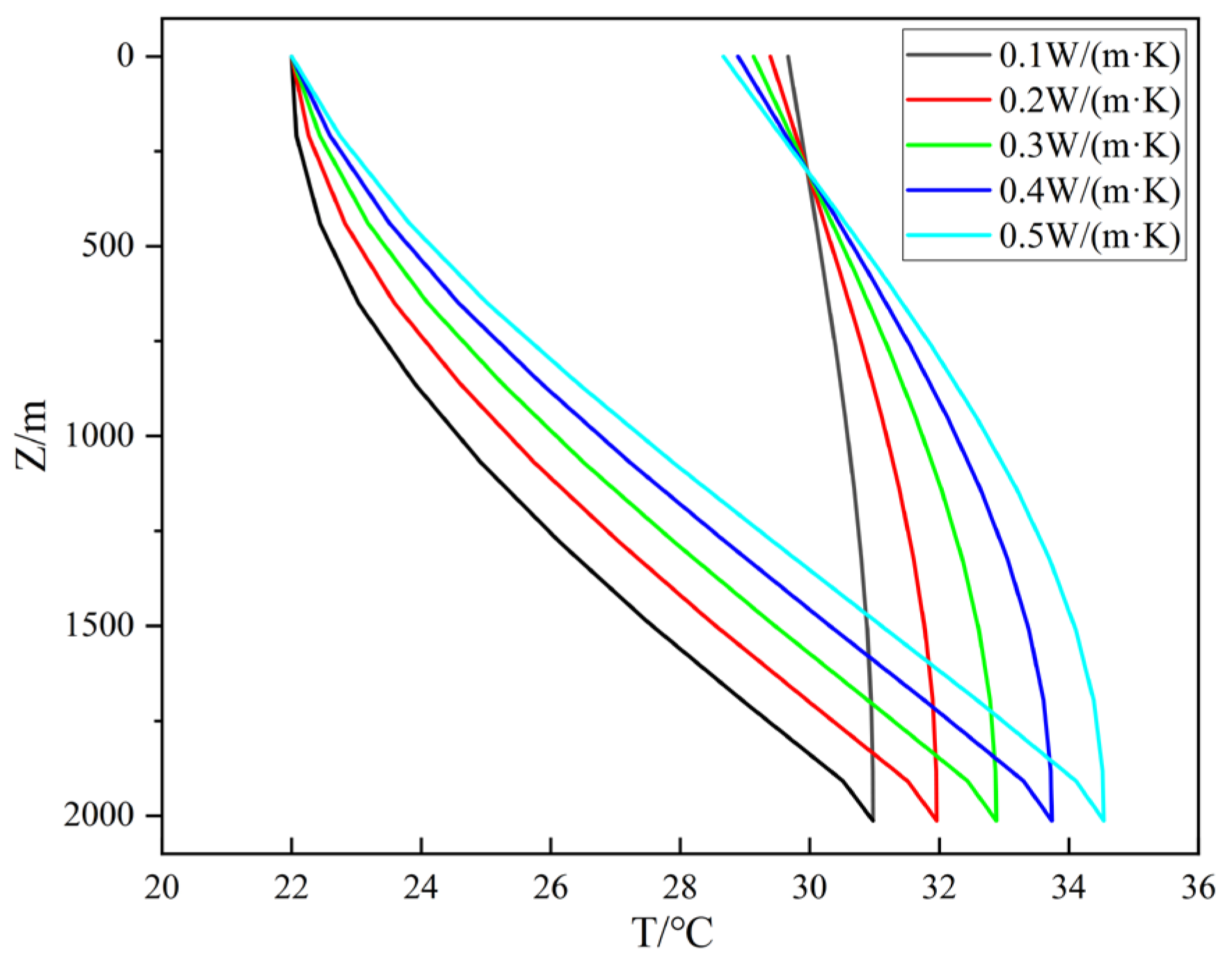
4.4.3. The Effect of the Thermal Conductivity of the Central Pipe on Heat Transfer Performance
4.5. Impact of Downhole Heat Exchange on the Temperature of the Heat Storage Layer
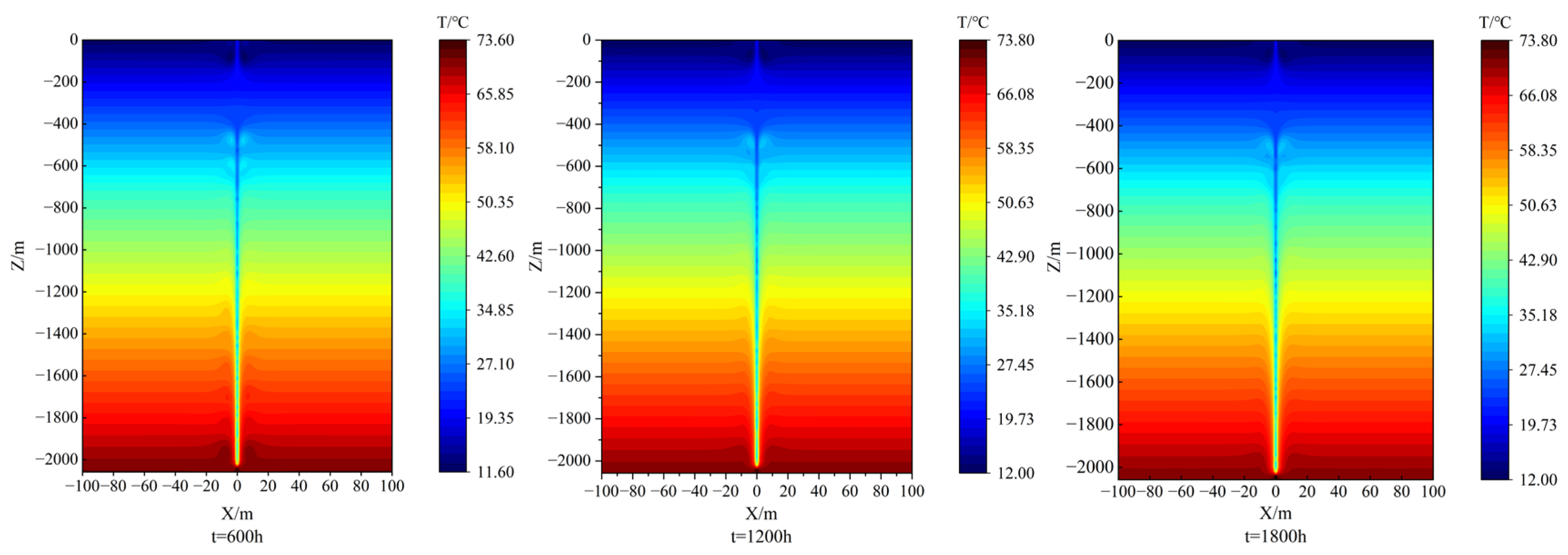
4.5.1. Impact of Downhole Heat Exchange on the Temperature Field of the Heat Storage Layer
4.5.2. Influence Radius of Geothermal Reservoir Temperature
5. Conclusions
- (1)
- Under medium–low temperature geothermal reservoir conditions in cold regions, the coaxial borehole heat exchanger demonstrates effective heat extraction performance, with a maximum average outlet temperature of 34.92 °C and a peak heat exchange power of 282.37 kW under actual operating conditions.
- (2)
- Among the three selected influencing factors, the inlet flow rate is the dominant factor affecting heat exchange power. When the inlet flow rate increases from 10 m3/h to 30 m3/h, the heat exchange power rises by 57.58%. However, due to the reduced residence time of the working fluid in the heat exchanger, both the outlet temperature and heat exchange efficiency decrease. This results in a nonlinear response characterized by “increased power–decreased temperature”.
- (3)
- The inlet water temperature primarily affects the thermal driving force and the outlet temperature. As the inlet temperature increases from 5 °C to 25 °C, the outlet temperature rises by 83.63%, while thermal short-circuiting is reduced and heat exchanger efficiency improves. However, due to the decreasing temperature difference between the formation and the fluid, the heat exchange power drops by 47.45%, indicating that excessively high inlet temperatures can weaken the system’s heat extraction capacity.
- (4)
- An increase in the thermal conductivity of the inner pipe intensifies thermal short-circuiting between the inner and outer fluid flows, thereby reducing the overall heat exchange performance. When the thermal conductivity of the inner pipe increases from 0.10 W/(m·K) to 0.50 W/(m·K), the outlet temperature decreases by 3.41%, and the heat exchange power drops by 13.7%, indicating a suppressed overall system performance.
- (5)
- Simulation of a full heating cycle shows that the outlet temperature gradually decreases to 29.53 °C, while the thermal influence radius of the reservoir expands progressively with both depth and operating time, reaching a maximum extent of 10.04 m.
- (6)
- For the coaxial borehole heat exchanger at the Dapuzi site, maintaining an inlet flow rate between 20 and 25 m3/h and an inlet temperature around 20 °C can achieve a balance between outlet temperature and heat exchange power, thereby optimizing overall heat exchange efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beier, R.A. Thermal response tests on deep borehole heat exchangers with geothermal gradient. Appl. Therm. Eng. 2020, 178, 115447. [Google Scholar] [CrossRef]
- Tang, F.; Nowamooz, H. Factors influencing the performance of shallow borehole heat exchanger. Energy Convers. Manag. 2019, 181, 571–583. [Google Scholar] [CrossRef]
- Lund, J.W.; Aniko, N.T. Direct utilization of geothermal energy 2020 worldwide review. Geothermics 2021, 90, 101915. [Google Scholar] [CrossRef]
- Yin, H.; Song, C.; Ma, L.; Gao, L.; Yang, X.; Li, W.; Zhao, J. Analysis of flow and thermal breakthrough in leaky downhole coaxial open loop geothermal system. Appl. Therm. Eng. 2021, 194, 117098. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, M.; Huang, L.; Liao, K.; Zhang, J. Review on geothermal energy development technology and numerical simulation of abandoned wells. Acta Energiae Solaris Sin. 2023, 44, 311–318. [Google Scholar]
- Cheng, N.; Zhou, C.; Luo, Y.; Shen, J.; Tian, Z.; Sun, D.; Fan, J.; Zhang, L.; Deng, J.; Rosen, M.A. Thermal behavior and performance of shallow-deep-mixed borehole heat exchanger array for sustainable building cooling and heating. Energy Build. 2023, 291, 113108. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, Y.; Jie, K.; Ren, X.; Hu, P.; Fei, L. Application of tube-in-tube type ground-source heat pump technology to hotel building. Refrig. Air-Cond. 2016, 8, 68–73. [Google Scholar]
- Luo, J.; Zhang, Y.; Liu, Q.; Li, X.; Lou, J. Numerical simulation of heat transfer performance of spiral vane reinforced medium and deep geothermal coaxial heat exchanger. World Geol. 2023, 42, 740–748. [Google Scholar]
- Wang, Y.; Liu, H.; Zhang, Q.; Zhang, L. Thermal performance analysis of a deep coaxial borehole heat exchanger with a horizontal well based on a novel semi-analytical model. Renew. Energy 2025, 239, 122073. [Google Scholar] [CrossRef]
- Li, M.; Shi, Y.; Chen, H.; Liu, C.; Li, H. Study on the heat transfer performance of coaxial casing heat exchanger for medium and deep geothermal energy in cold regions. Renew. Energy 2024, 237, 121666. [Google Scholar] [CrossRef]
- Akram, M.W.; Chen, Q.; Nortz, G.; Nortz, P. Experimental investigation and numerical modeling of an innovative horizontal coaxial ground heat exchanger (HCGHE) for geothermal heat pump applications. Appl. Therm. Eng. 2024, 257, 124492. [Google Scholar] [CrossRef]
- Guo, Z.; Dai, Y.; Zhang, J.; Gui, X.; He, Y. Improved modeling analysis on heat transfer performance of deep coaxial borehole heat exchanger with different operation modes. Energy Rep. 2024, 11, 355–368. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Y.; Luo, J.; Zheng, J.; Cheng, Y. Numerical study on heat transfer and flow characteristics of coaxial geothermal heat exchangers with helical finned inner tubes. J. Build. Eng. 2023, 65, 105752. [Google Scholar] [CrossRef]
- Zhao, J.; Tu, F.; Dai, C.; Li, X.; Zhu, Q.; Yuan, W. The experimental simulation on downhole coaxial heat exchanger in convective heat storage. Acta Energiae Solaris Sin. 2002, 6, 696–698. [Google Scholar]
- Gordon, D.; Bolisetti, T.; Ting, D.S.-K.; Reitsma, S. Experimental and analytical investigation on pipe sizes for a coaxial borehole heat exchanger. Renew. Energy 2018, 115, 946–953. [Google Scholar] [CrossRef]
- Li, P.; Zhao, G.; He, Z.; Jia, Y.; Liang, Z. Production capacity of enhanced coaxial borehole heat exchangers in horizontal wells through forced seepage. Appl. Therm. Eng. 2025, 270, 126248. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J. Enhanced heat extraction for coaxial medium-deep borehole heat exchangers by adding triangular fins on the outer tube wall. Renew. Energy 2025, 242, 122448. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, L.; Liang, Z.; Liu, Q.; Jiang, F. Thermal response analysis of a medium-deep coaxial borehole heat exchanger by circulating CO2. Geothermics 2023, 112, 102746. [Google Scholar] [CrossRef]
- Zanchini, E.; Lazzari, S.; Priarone, A. Improving the thermal performance of coaxial borehole heat exchangers. Energy 2010, 35, 657–666. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, F.; Jia, H.; Wang, L.; Klitzsch, N.; Feng, G.; Yan, C.; Ma, H.; Liu, S.; Yin, Q.; et al. Heat extraction performance of multi-level, multi-branch, closed loop coaxial horizontal borehole heat exchanger geothermal system. Appl. Therm. Eng. 2025, 269, 126045. [Google Scholar] [CrossRef]
- Niu, Q.; Ma, K.; Wang, W.; Pan, J.; Wang, Q.; Du, Z.; Wang, Z.; Yuan, W.; Zheng, Y.; Shangguan, S.; et al. Multifactor analysis of heat extraction performance of coaxial heat exchanger applied to hot dry rock resources exploration: A case study in matouying uplift, Tangshan, China. Energy 2023, 282, 128277. [Google Scholar] [CrossRef]
- Pokhrel, S.; Sasmito, A.P.; Sainoki, A.; Tosha, T.; Tanaka, T.; Nagai, C.; Ghoreishi-Madiseh, S.A. Field-scale experimental and numerical analysis of a downhole coaxial heat exchanger for geothermal energy production. Renew. Energy 2022, 182, 521–535. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, W.; Han, S.; Du, H.; Cui, P.; Ma, Z.; Feng, X.; Zhang, W. A numerical heat transfer model and performance evaluation of coaxial geothermal heat exchanger under soil freezing conditions. Appl. Therm. Eng. 2025, 266, 125538. [Google Scholar] [CrossRef]
- Gascuel, V.; Raymond, J.; Rivard, C.; Marcil, J.-S.; Comeau, F.-A. Design and optimization of deep coaxial borehole heat exchangers for cold sedimentary basins. Geothermics 2022, 105, 102504. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, F.; Zhu, R.; Zhou, X.; Liu, G.; Yuan, L.; Wang, X.; Dong, J.; Lü, H.; Li, C.; et al. A numerical study on the sustainability and efficiency of deep coaxial borehole heat exchanger systems in the cold region of northeast China. Renew. Energy 2024, 237, 121562. [Google Scholar] [CrossRef]
- Zhao, Z.; Yu, P.; Chen, H.; Luo, Y.; Zhao, D.; Bian, J. Genetic analysis and resource evaluation of the Xining geothermal field in Qinghai Province. Geol. China 2015, 42, 803–810. [Google Scholar]
- Chao, J. Study on Risk Assessment of Formation Blockage in Geothermal Water Reinjection in Xining Basin. Ph.D. Thesis, China University of Petroleum, Qingdao, China, 2021. [Google Scholar]
- Sun, H.; Wang, G.; Lin, W. Distribution characteristics and enrichment mechanism of TDS geothermal water in Xining Basin. Bull. Geol. Sci. Technol. 2022, 41, 278–287+299. [Google Scholar]
- Li, T.; Qiao, Y.; Meng, N.; Li, J.; Zhou, K.; Gao, X. Full life cycle heat extraction and power generation performance comparison of enhanced geothermal system with water and carbon dioxide as heat carrier. Appl. Therm. Eng. 2025, 269, 125997. [Google Scholar] [CrossRef]
- Hu, X.; Banks, J.; Wu, L.; Liu, W.V. Numerical modeling of a coaxial borehole heat exchanger to exploit geothermal energy from abandoned petroleum wells in Hinton, Alberta. Renew. Energy 2020, 148, 1110–1123. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, C.; Li, G.; Guo, X.; Wang, G.; Shi, Y.; Peng, C.; Tan, Y. Performance analysis of a downhole coaxial heat exchanger geothermal system with various working fluids. Appl. Therm. Eng. 2019, 163, 114317. [Google Scholar] [CrossRef]
- Li, F.; Han, E.; Liang, L.; Wu, J.; Lu, B. Long-term heat transfer performance of underground coaxial heat exchanger for medium-deep geothermal. Coal Geol. Explor. 2023, 49, 194–201. [Google Scholar]

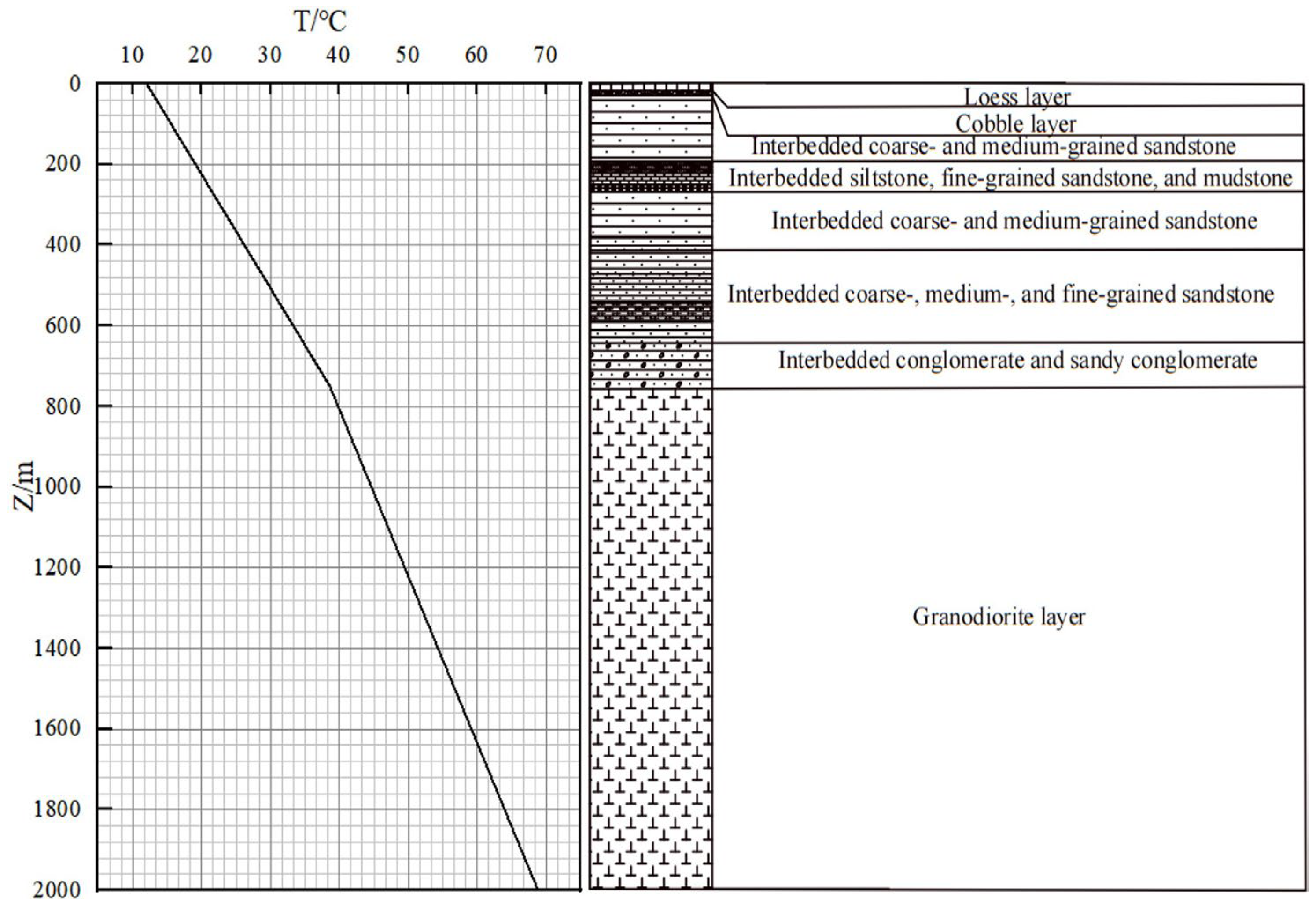



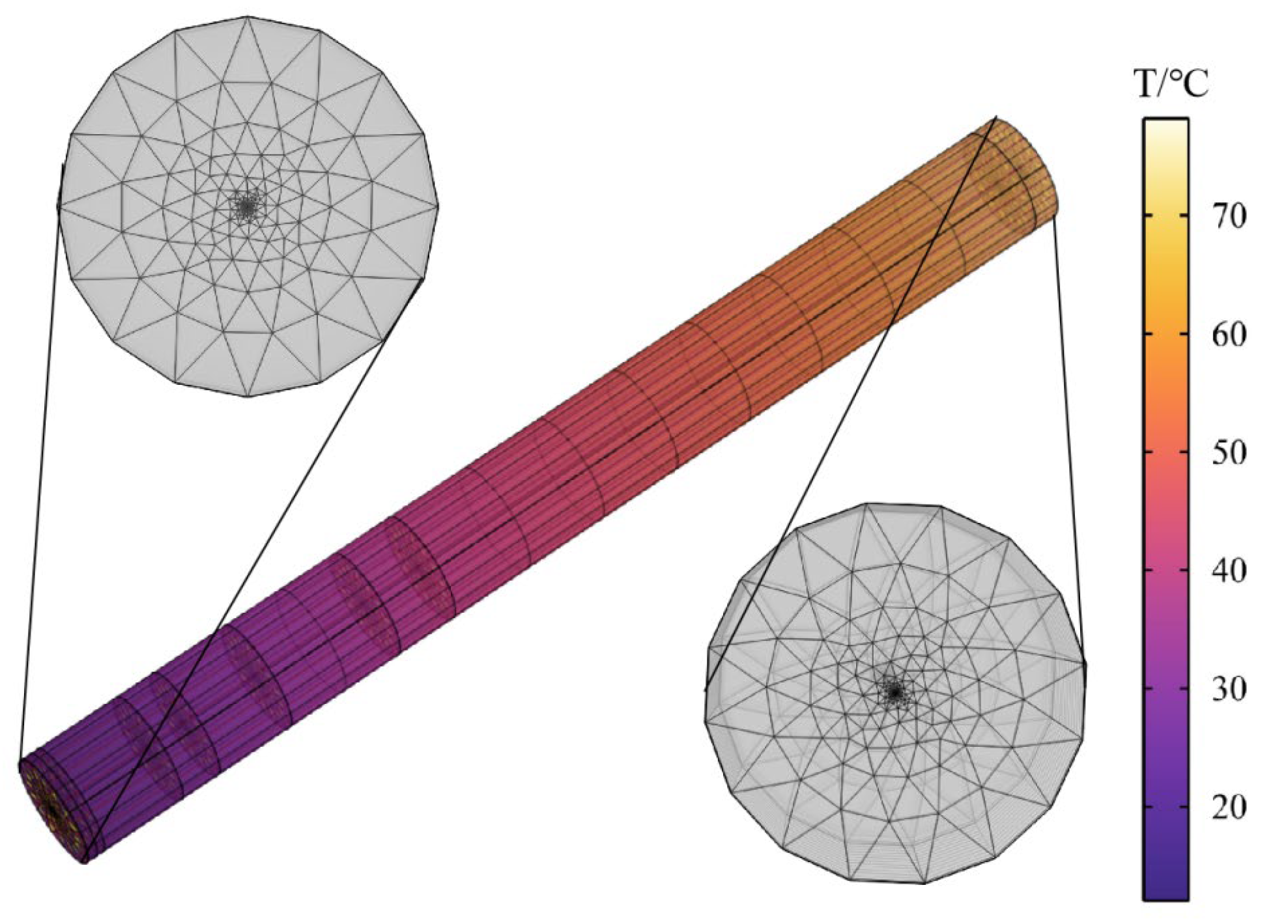






| NO. | Stratigraphic Lithology | Thickness/(m) | Thermal Conductivity (W/(m·K)) |
|---|---|---|---|
| 1 | Loess layer | 16.80 | 0.8 |
| 2 | Cobble layer | 15.50 | 2.2 |
| 3 | Interbedded coarse- and medium-grained sandstone | 158.85 | 2.8 |
| 4 | Interbedded siltstone, fine-grained sandstone, and mudstone | 75.00 | 2.2 |
| 5 | Interbedded coarse- and medium-grained sandstone | 147.25 | 2.6 |
| 6 | Interbedded coarse-, medium-, and fine-grained sandstone | 225.05 | 2.8 |
| 7 | Interbedded conglomerate and sandy conglomerate | 115.75 | 3.0 |
| 8 | Granodiorite layer | 1258.80 | 3.3 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Well Depth (m) | 2013.00 | Outer Pipe Wall Thickness (mm) | 9.20 |
| Hole Diameter (mm) | 241.30 | Inner Pipe Wall Thickness (mm) | 10.00 |
| Inner Diameter of Inner Pipe (mm) | 90.00 | Cement Grout Thermal Conductivity (W/(m·K)) | 2.0 |
| Outer Diameter of Inner Pipe (mm) | 110.00 | Outer Pipe Thermal Conductivity (W/(m·K)) | 48.00 |
| Inner Diameter of Outer Pipe (mm) | 159.40 | Inner Pipe Thermal Conductivity (W/(m·K)) | 0.25 |
| Outer Diameter of Outer Pipe (mm) | 177.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Zhan, X.; Yan, B.; Qin, G.; Yu, Y. Heat Exchange Effectiveness and Influence Mechanism of Coaxial Downhole in the Alpine Region of Xining City, Qinghai Province. Energies 2025, 18, 4451. https://doi.org/10.3390/en18164451
Zhao Z, Zhan X, Yan B, Qin G, Yu Y. Heat Exchange Effectiveness and Influence Mechanism of Coaxial Downhole in the Alpine Region of Xining City, Qinghai Province. Energies. 2025; 18(16):4451. https://doi.org/10.3390/en18164451
Chicago/Turabian StyleZhao, Zhen, Xinkai Zhan, Baizhong Yan, Guangxiong Qin, and Yanbo Yu. 2025. "Heat Exchange Effectiveness and Influence Mechanism of Coaxial Downhole in the Alpine Region of Xining City, Qinghai Province" Energies 18, no. 16: 4451. https://doi.org/10.3390/en18164451
APA StyleZhao, Z., Zhan, X., Yan, B., Qin, G., & Yu, Y. (2025). Heat Exchange Effectiveness and Influence Mechanism of Coaxial Downhole in the Alpine Region of Xining City, Qinghai Province. Energies, 18(16), 4451. https://doi.org/10.3390/en18164451






