Powering the Woods Hole X-Spar Buoy with Ocean Wave Energy—A Control Co-Design Feasibility Study
Abstract
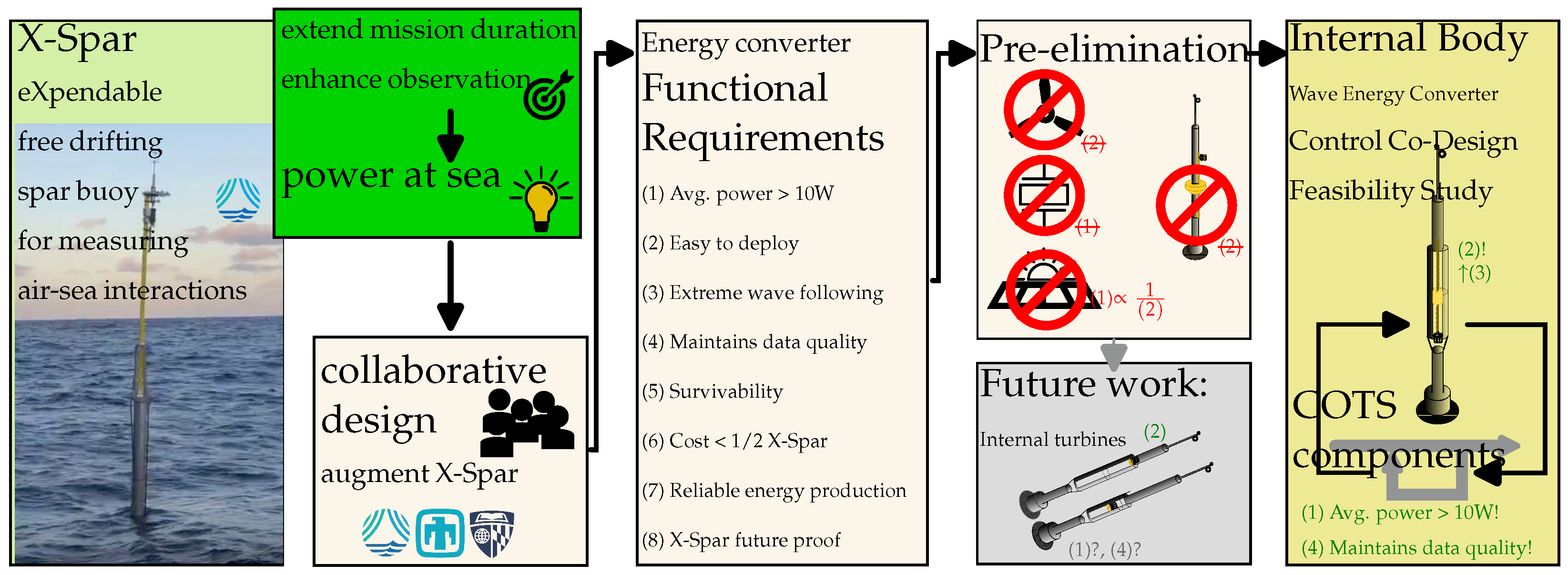
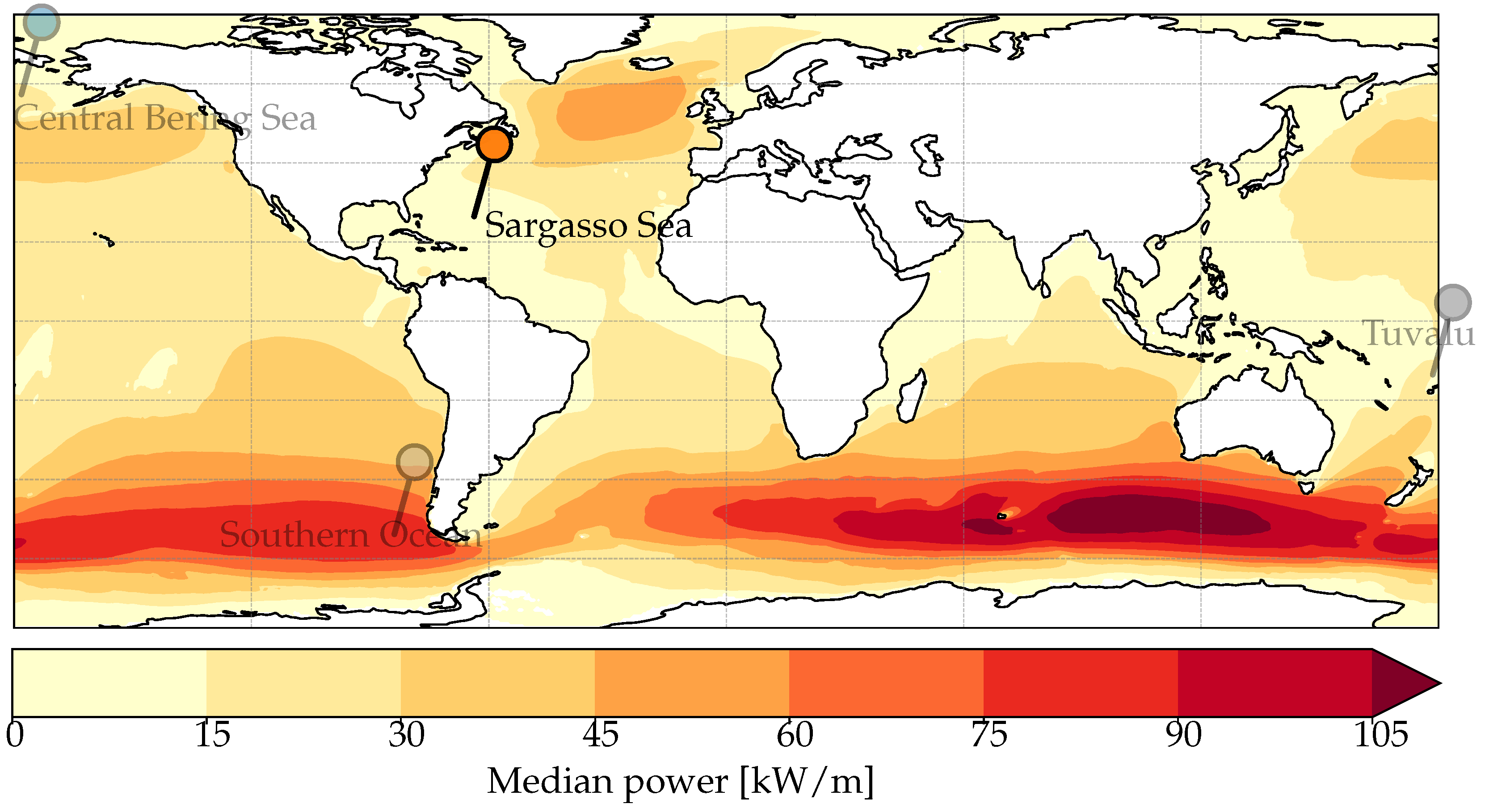
1. Introduction
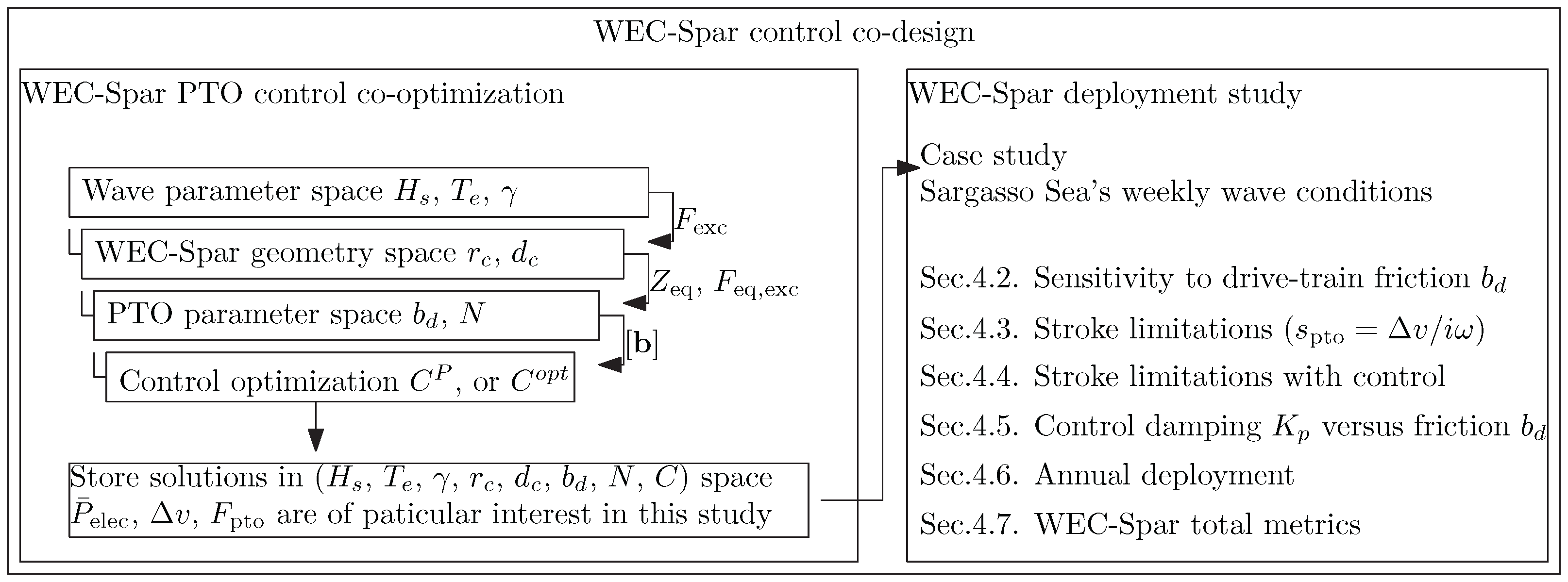
2. Collaborative Design
2.1. Functional Requirements
2.2. Pre-Elimination of Concepts
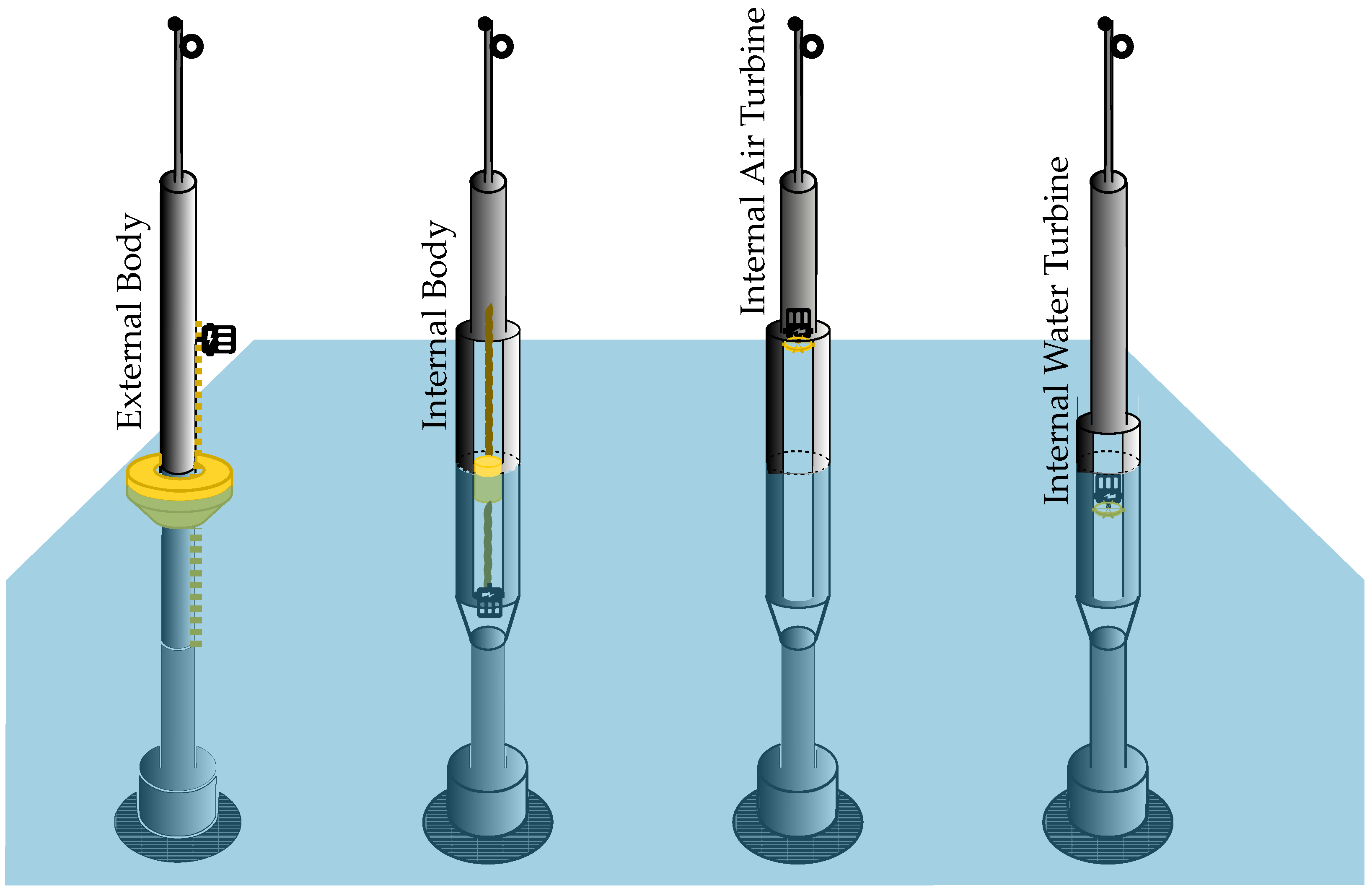
2.3. WEC Concepts to Augment the X-Spar
2.4. Design Feasibility Study
3. Internal Body WEC Control Co-Design
3.1. Dynamic Model
3.1.1. Hydrodynamic Model
- = 207.6 /, which is the SID parameter of interest.
- m = 593.3 , which is is 97.9% of the buoy’s measured dry weight of 606 .
- = 629.8 /, which under-predicts the analytical stiffness of 729.8 / by 13.7%.
3.1.2. Power Take-Off (PTO) Model
3.2. WEC-Spar PTO Multi-Port Model
3.3. Control
3.3.1. Numerically Optimal Control
3.3.2. Optimized Damping Control
3.4. Metrics
4. Results
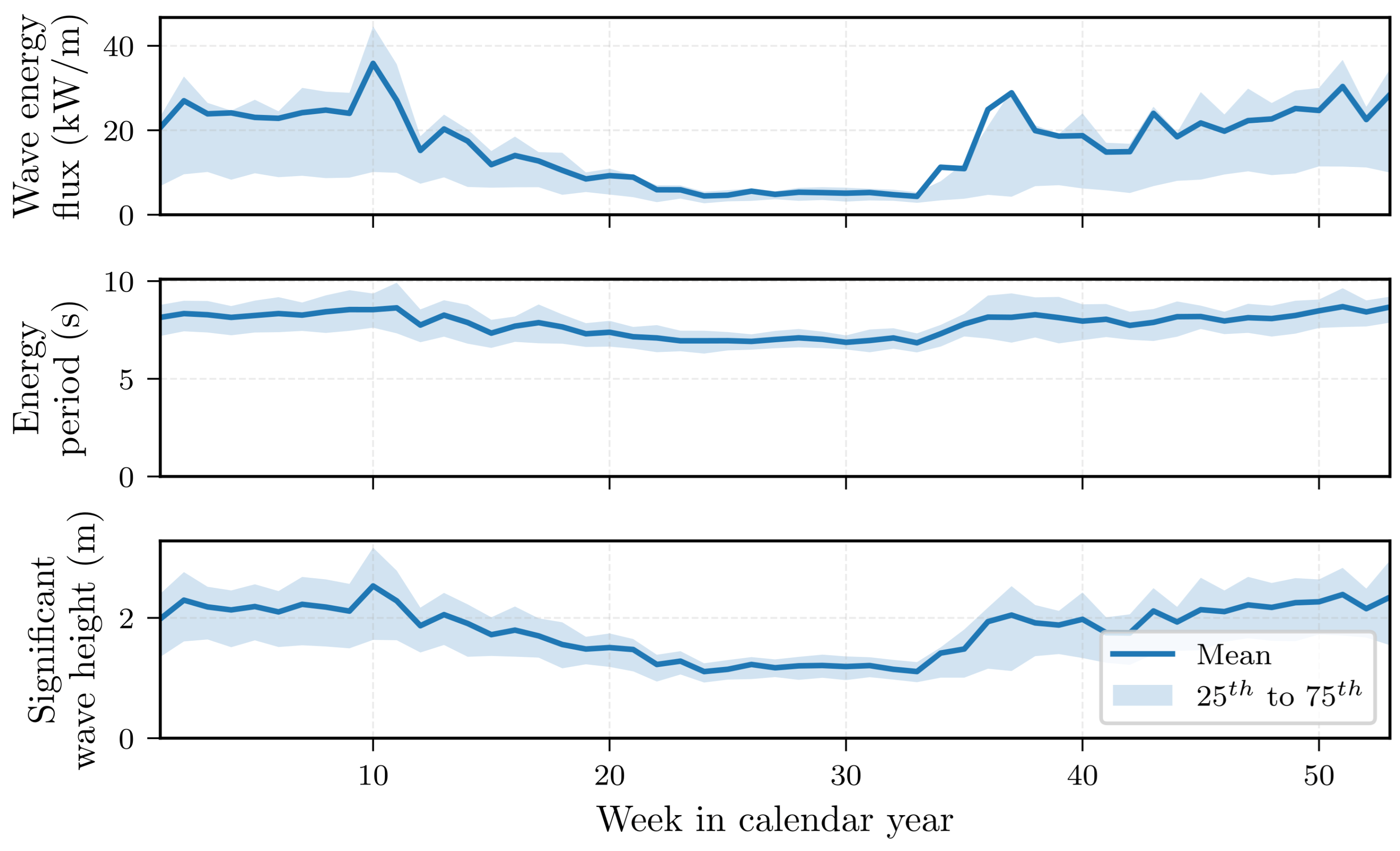
4.1. Parameter Space
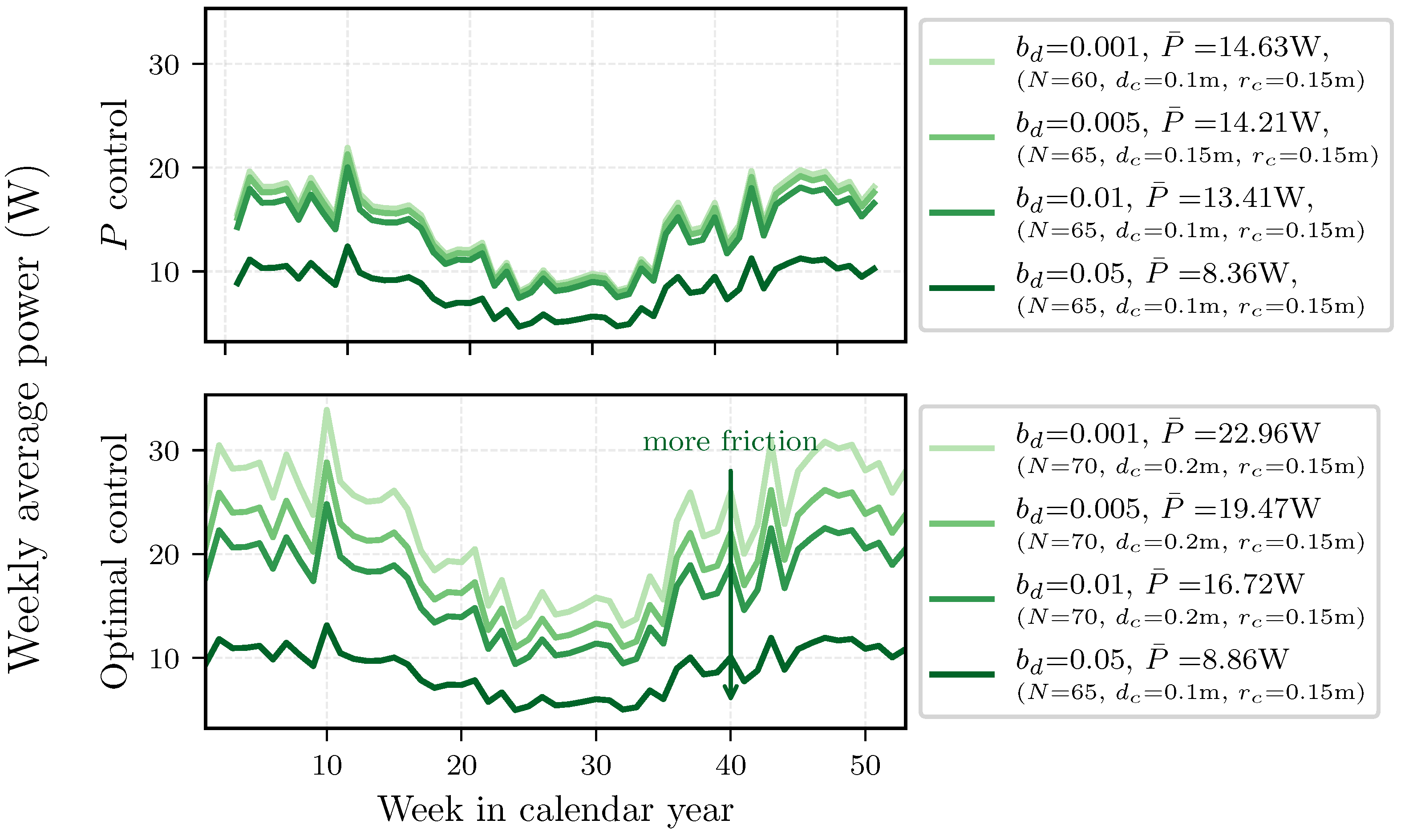
4.2. Sensitivity to Drive-Train Friction
4.3. Stroke Limitations
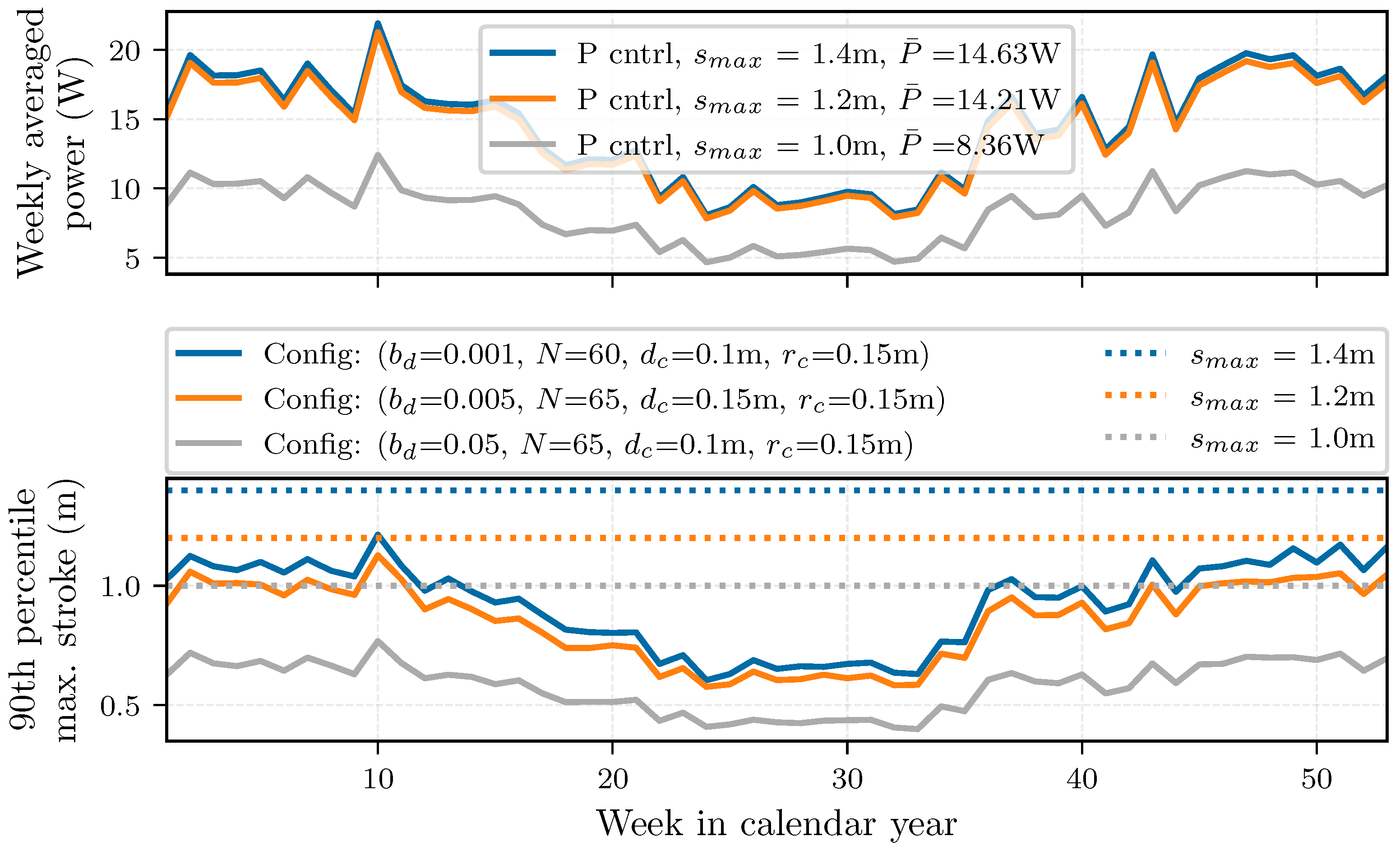
4.4. Stroke Limitations with Control
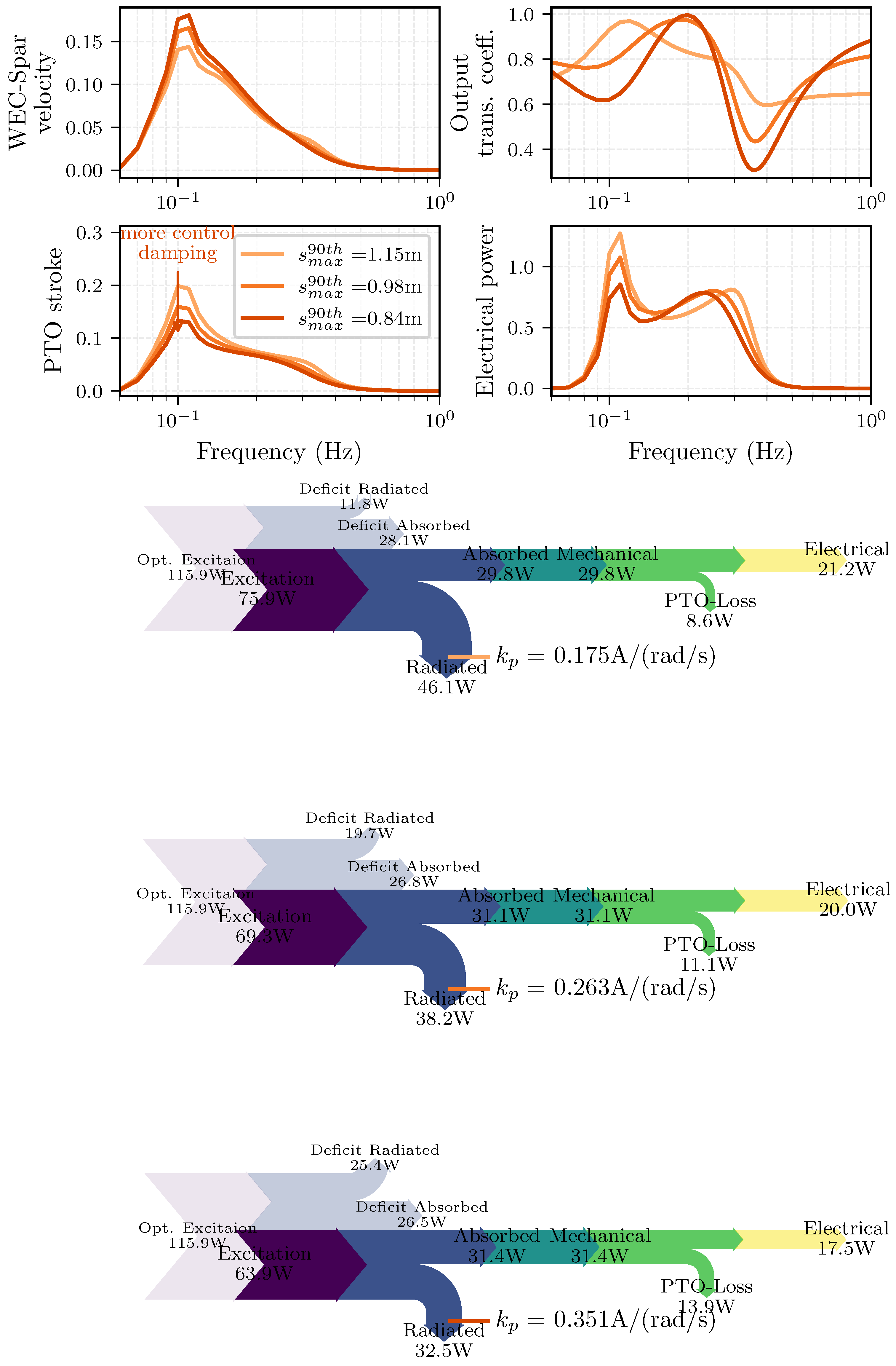
4.5. Control Damping Versus Friction
4.6. Annual Deployment
4.7. WEC-Spar Total Metrics
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Sankey Power Flow Diagram Calculations
| Optimal excitation = 2× max. absorbed | |
| Deficit absorbed | |
| Deficit radiated | |
| Excitation | |
| Radiated | |
| Absorbed | |
| Mechanical | |
| PTO-loss | |
| Electrical |
References
- Stammer, D.; Bracco, A.; AchutaRao, K.; Beal, L.; Bindoff, N.L.; Braconnot, P.; Cai, W.; Chen, D.; Collins, M.; Danabasoglu, G.; et al. Ocean Climate Observing Requirements in Support of Climate Research and Climate Information. Front. Mar. Sci. 2019, 6, 444. [Google Scholar] [CrossRef]
- Stephens, G.L.; Li, J.; Wild, M.; Clayson, C.A.; Loeb, N.; Kato, S.; L’Ecuyer, T.; Stackhouse, P.W.; Lebsock, M.; Andrews, T. An update on Earth’s energy balance in light of the latest global observations. Nat. Geosci. 2012, 5, 691–696. [Google Scholar] [CrossRef]
- Graber, H.C.; Terray, E.A.; Donelan, M.A.; Drennan, W.M.; Leer, J.C.V.; Peters, D.B. ASIS—A New Air-Sea Interaction Spar Buoy: Design and Performance at Sea. J. Atmos. Ocean. Technol. 2000, 17, 708–720. [Google Scholar] [CrossRef]
- Davis, R.E.; Talley, L.D.; Roemmich, D.; Owens, W.B.; Rudnick, D.L.; Toole, J.; Weller, R.; McPhaden, M.J.; Barth, J.A. 100 Years of Progress in Ocean Observing Systems. Meteorol. Monogr. 2019, 59, 3.1–3.46. [Google Scholar] [CrossRef]
- Clayson, C.A.; Edson, J.B.; Toole, J.M. Observing Air-Sea Exchange with a Free-Drifting Spar Buoy; Technical Report; Woods Hole Oceanographic Institution: Woods Hole, MA, USA, 2014; Available online: https://geo-prose.com/pdfs/alps/Clayson.pdf (accessed on 16 December 2024).
- Zimmerman, M.T.; Jayne, S.R.; Rainville, L.; Lee, C.M.; Toole, J.M.; Edson, J.B.; Clayson, C.A.; Ekholm, A.K.; Densmore, C.R. Observations of the Upper Ocean from Autonomous Platforms During the Passage of Extratropical Cyclone Epsilon (2020). Oceanography 2024, 37, 48–57. [Google Scholar] [CrossRef]
- Cronin, M.; Bourassa, M.; Clayson, C.; Edson, J.; Fairall, C.; Feely, R.; Harrison, D.; Josey, S.; Kubota, M.; Kumar, B.; et al. White Paper #11—Wind Stress and Air Sea Fluxes Observations: Status, Implementation and Gaps. In Report of the Tropical Pacific Observing System 2020 Workshop (TPOS 2020); Technical Report GCOS Report 184; Scripps Institution of Oceanography: La Jolla, CA, USA, 2014. [Google Scholar]
- Hara, T.; Sullivan, P.P. Wave Boundary Layer Turbulence over Surface Waves in a Strongly Forced Condition. J. Phys. Oceanogr. 2015, 45, 868–883. [Google Scholar] [CrossRef]
- Robertson, T.; Simonsen, J. Challenges and Opportunities in Contemporary Participatory Design. Des. Issues 2012, 28, 3–9. [Google Scholar] [CrossRef]
- Copping, A.; LiVecchi, A.; Spence, H.; Gorton, A.; Jenne, S.; Preus, R.; Gill, G.; Robichaud, R.; Gore, S. Maritime renewable energy markets: Power from the sea. Mar. Technol. Soc. J. 2018, 52, 99–109. [Google Scholar] [CrossRef]
- LiVecchi, A.; Copping, A.; Jenne, D.; Gorton, A.; Preus, R.; Gill, G.; Robichaud, R.; Green, R.; Geerlofs, S.; Gore, S.; et al. Powering the Blue Economy: Exploring Opportunities for Marine Renewable Energy in Maritime Markets; Technical Report; U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy: Washington, DC, USA, 2019.
- Cavagnaro, R.J.; Copping, A.E.; Green, R.; Greene, D.; Jenne, S.; Rose, D.; Overhus, D. Powering the Blue Economy: Progress Exploring Marine Renewable Energy Integration With Ocean Observations. Mar. Technol. Soc. J. 2020, 54, 114–125. [Google Scholar] [CrossRef]
- McLeod, I.; Ringwood, J.V. Powering data buoys using wave energy: A review of possibilities. J. Ocean. Eng. Mar. Energy 2022, 8, 417–432. [Google Scholar] [CrossRef]
- Lindroth, S.; Leijon, M. Offshore wave power measurements—A review. Renew. Sustain. Energy Rev. 2011, 15, 4274–4285. [Google Scholar] [CrossRef]
- Xu, R.; Wang, H.; Xi, Z.; Wang, W.; Xu, M. Recent progress on wave energy marine buoys. J. Mar. Sci. Eng. 2022, 10, 566. [Google Scholar] [CrossRef]
- Vella, N.; Foley, J.; Sloat, J.; Sandoval, A.; D’Attile, L.; Masoumi, M. A Modular Wave Energy Converter for Observational and Navigational Buoys. Fluids 2022, 7, 88. [Google Scholar] [CrossRef]
- Harms, J.; Hollm, M.; Dostal, L.; Kern, T.A.; Seifried, R. Design and optimization of a wave energy converter for drifting sensor platforms in realistic ocean waves. Appl. Energy 2022, 321, 119303. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Jiang, J. A high-efficiency wave-powered marine observation buoy: Design, analysis, and experimental tests. Energy Convers. Manag. 2022, 270, 116154. [Google Scholar] [CrossRef]
- Dizon, C.; Cavagnaro, R.J.; Robertson, B.; Brekken, T.K. Modular horizontal pendulum wave energy converter: Exploring feasibility to power ocean observation applications in the U.S. pacific northwest. IET Renew. Power Gener. 2021, 15, 3354–3367. [Google Scholar] [CrossRef]
- Li, Y.; Ma, X.; Tang, T.; Zha, F.; Chen, Z.; Liu, H.; Sun, L. High-efficient built-in wave energy harvesting technology: From laboratory to open ocean test. Appl. Energy 2022, 322, 119498. [Google Scholar] [CrossRef]
- Coe, R.; Lee, J.; Bacelli, G.; Spencer, S.; Dullea, K.; Plueddemann, A.; Buffitt, D.; Reine, J.; Peters, D.; Spinneken, J.; et al. Pioneer WEC Concept Design Report; Sandia National Laboratories: Albuquerque, NM, USA, 2023. [Google Scholar] [CrossRef]
- Lin, M.; Yang, C. Ocean observation technologies: A review. Chin. J. Mech. Eng. 2020, 33, 32. [Google Scholar] [CrossRef]
- Schofield, O.; Kohut, J.; Aragon, D.; Creed, L.; Graver, J.; Haldeman, C.; Kerfoot, J.; Roarty, H.; Jones, C.; Webb, D.; et al. Slocum gliders: Robust and ready. J. Field Robot. 2007, 24, 473–485. [Google Scholar] [CrossRef]
- Daniel, T.; Manley, J.; Trenaman, N. The Wave Glider: Enabling a new approach to persistent ocean observation and research. Ocean. Dyn. 2011, 61, 1509–1520. [Google Scholar] [CrossRef]
- Ullman, D.G. The Mechanical Design Process: Part 2; McGraw-Hill: Columbus, OH, USA, 2010. [Google Scholar]
- Weber, J.; Costello, R.; Ringwood, J.V. WEC technology performance levels (TPLs)- metric for successful development of economic WEC technology. In Proceedings of the 10th European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–5 September 2013. [Google Scholar]
- Korde, U.A.; Gish, L.A.; Bacelli, G.; Coe, R.G. Wave energy conversion using a small tubular free-floating device. J. Ocean. Eng. Mar. Energy 2024, 10, 57–69. [Google Scholar] [CrossRef]
- Bacelli, G.; Coe, R.; Patterson, D.; Wilson, D. System Identification of a Heaving Point Absorber: Design of Experiment and Device Modeling. Energies 2017, 10, 472. [Google Scholar] [CrossRef]
- Falnes, J. Wave-Energy Conversion Through Relative Motion Between Two Single-Mode Oscillating Bodies. J. Offshore Mech. Arct. Eng. 1999, 121, 32–38. [Google Scholar] [CrossRef]
- Olaru, D.; Puiu, G.C.; Balan, L.C.; Puiu, V. A New Model to Estimate Friction Torque in a Ball Screw System. In Product Engineering: Eco-Design, Technologies and Green Energy; Talabă, D., Roche, T., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 333–346. [Google Scholar] [CrossRef]
- Qiu, Y.L.; Zhou, C.G.; Feng, F.T.; Zhang, L.C. The influence of temperature rise on the friction torque of ball screw during low speed operation. Results Phys. 2023, 51, 106703. [Google Scholar] [CrossRef]
- Skrovanek, D.; Brekken, T. Impact of Biofouling on Point Absorber Wave Energy Converter Performance and Control. In Proceedings of the 2024 American Control Conference (ACC), Toronto, ON, Canada, 8–9 July 2024; pp. 3328–3333. [Google Scholar] [CrossRef]
- Coe, R.G.; Bacelli, G.; Gaebele, D.; Keow, A.; Forbush, D. Co-Design of a Wave Energy Converter Through Bi-Conjugate Impedance Matching. SSRN, 2024; preprint. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
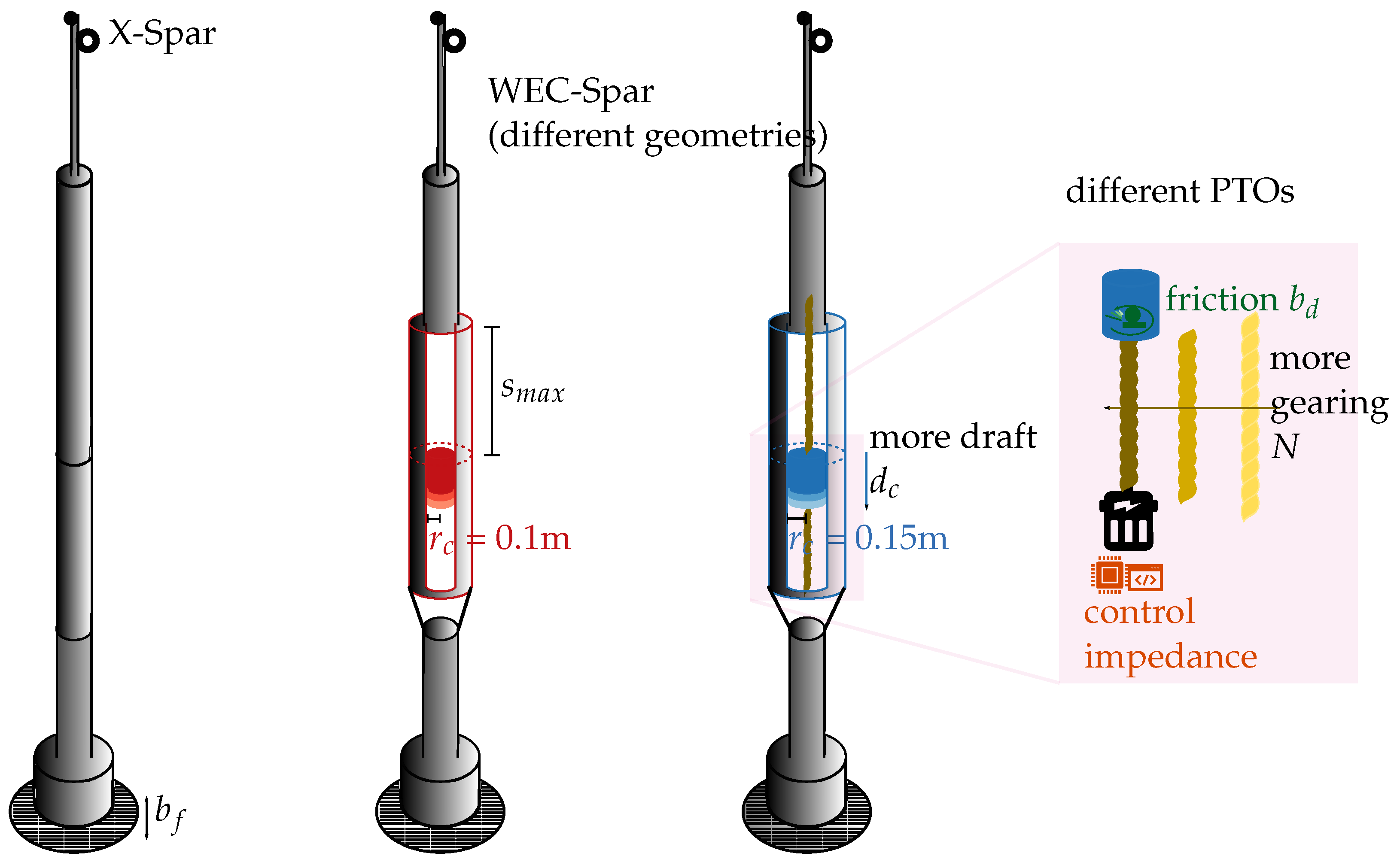
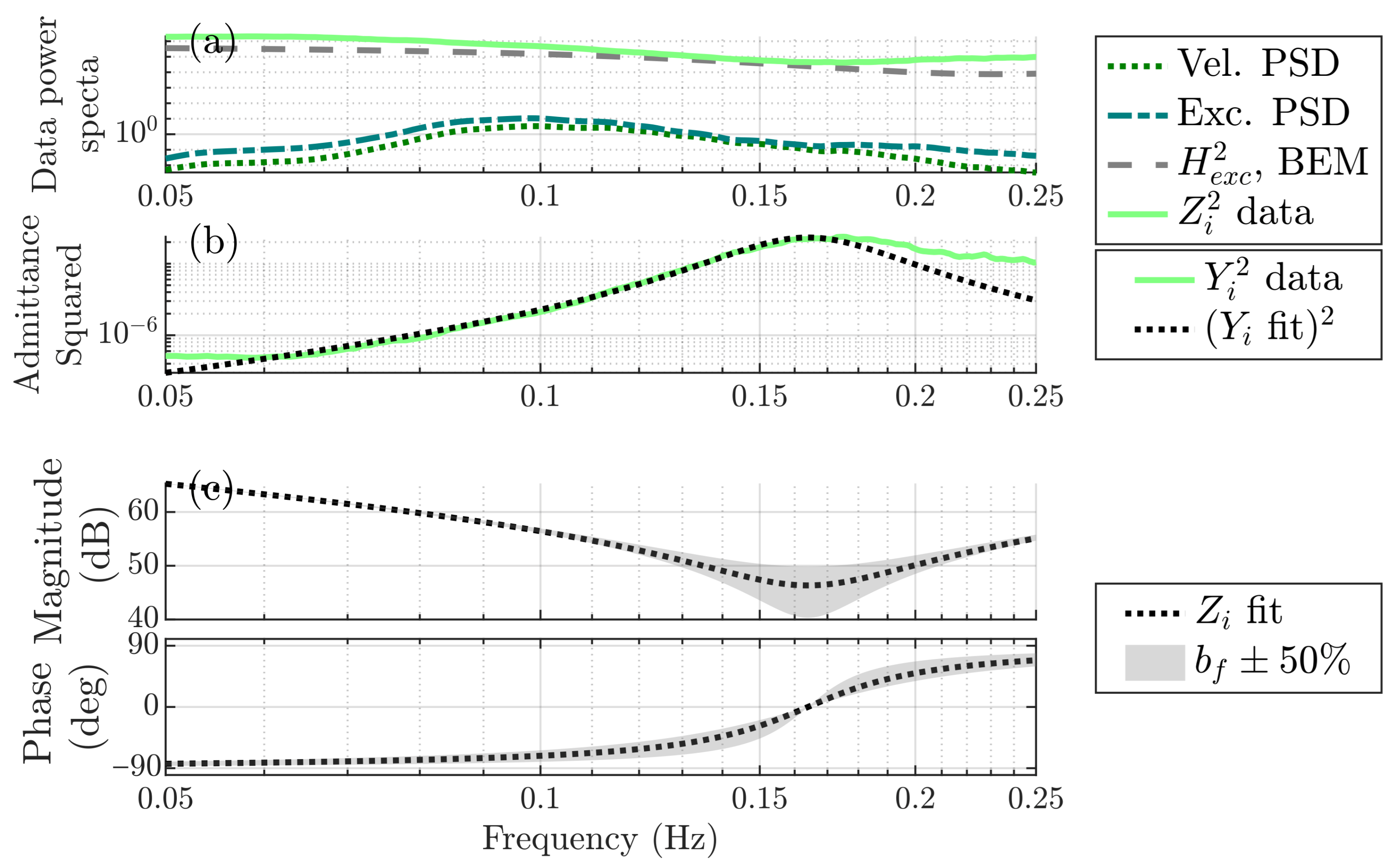
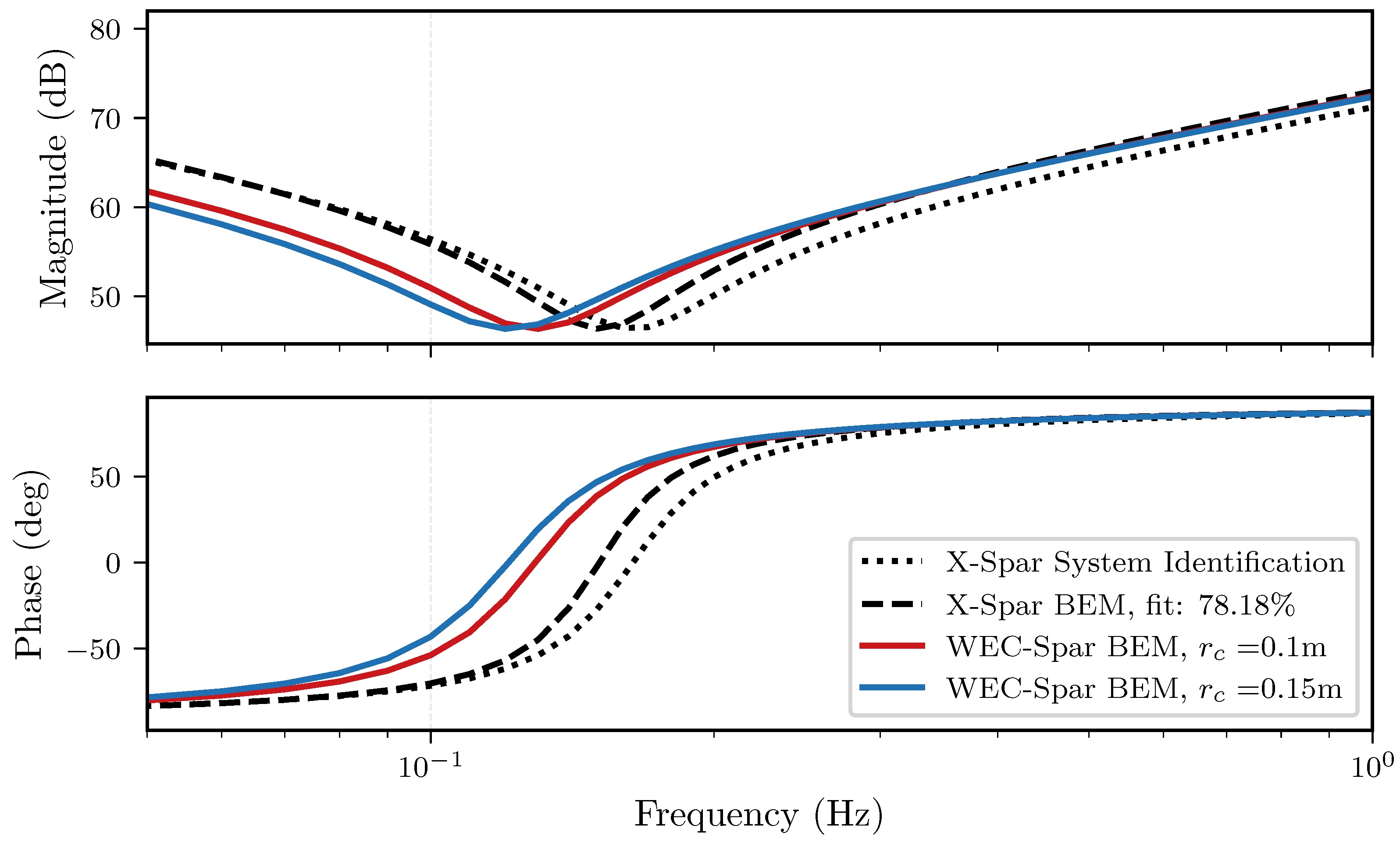
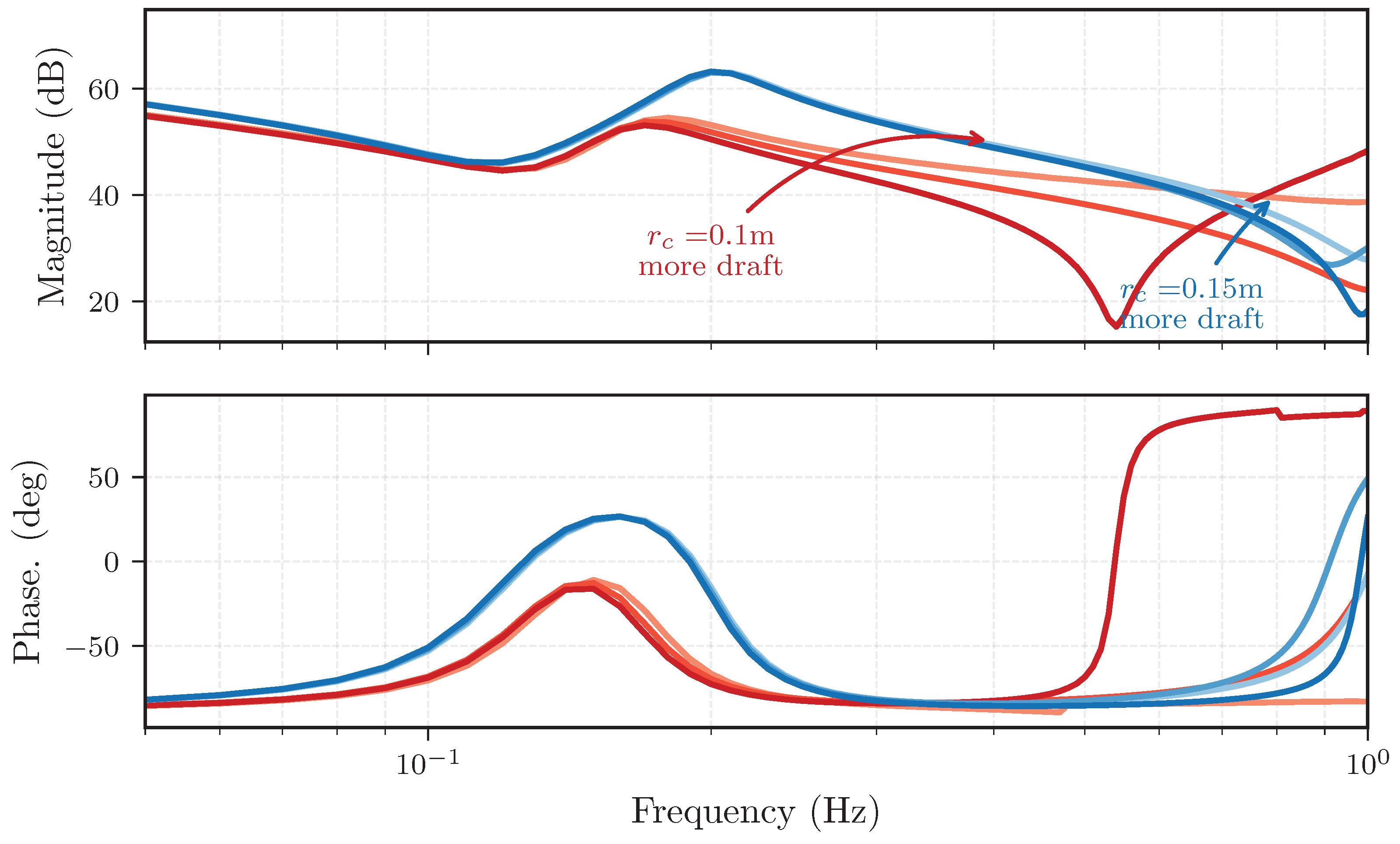
| Requirement | Importance | Requirement | Importance |
|---|---|---|---|
| (1) Produce average power above 10 watt | Very High | (5) Mechanical survivability | High |
| (2) Easy to deploy | Very High | (6) WEC cost less than 50% X-Spar CapEx | High |
| (3) Ability to follow waves in extreme seas | Very High | (7) Reliable energy production | Medium |
| (4) Does not negatively impact data quality | Very High | (8) Integrate into future X-Spar iterations | Medium |
| Follow Extreme Waves | Moving Parts | Impact CB/CG | Fatigue ( Cycles) | Stiction | |
|---|---|---|---|---|---|
| External body | Wave following if locked or actively controlled | Primary mover and drive-train | No impact | Survivability issue before fatigue | Rack and pinion issue, gear ratio trade-off between generator size and cogging force |
| Internal body | Aids wave following if locked or actively controlled | Primary mover and drive-train | No impact | Fatigue needs to be considered for design | Rack and pinion issue, gear ratio trade-off between generator size and cogging force |
| Internal air turbine | No impact | Least moving parts | Negative on CB-CG | Less issues if adequate bearings | Low stiction: same rotational direction |
| Water turbine | No impact | Depends on rectification | No or little impact | Depends on type of rectification | Low stiction: same rotational speed |
| Parameter | Value Range | |
|---|---|---|
| Radius cylinder | 0.1 and 0.15 | |
| 0.1, 0.15 and 0.2 | ||
| 0.0001, 0.005, 0.01 and 0.05 | ||
| N | 55, 60, 65 and 70 | |
| C | opt. damping or numerically optimal controller |
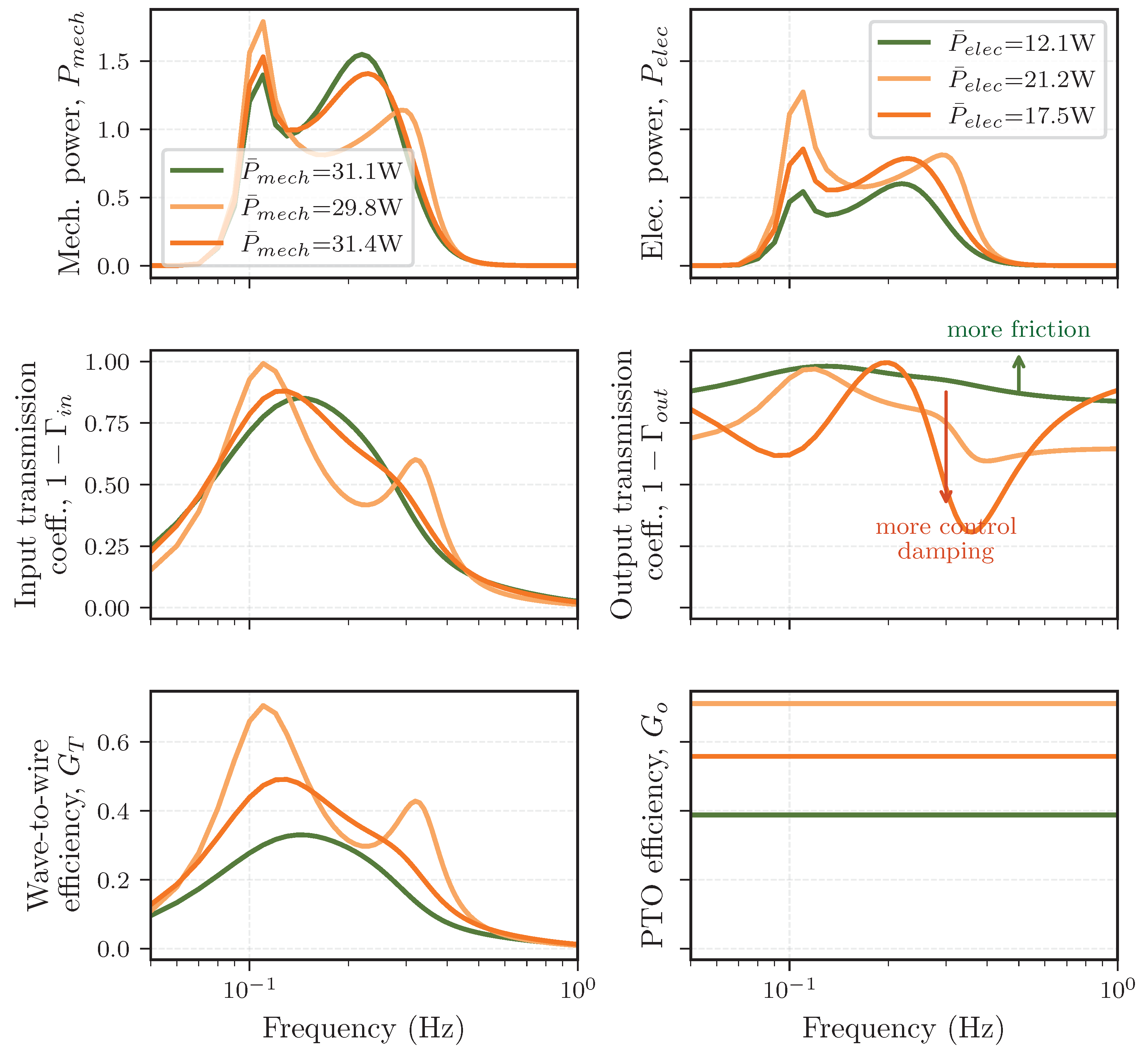
| Section 4.2 Sensitivity to drive-train friction | ||
| Figure 10 | Optimal configuration with optimized damping control: | week W |
| , , , . | ||
| Increased drive-train friction sub-optimal configuration with optimized damping control: | ||
| , , , . | ||
| Section 4.3 Stroke limitations. | ||
| Figure 11 | Configuration that is naturally within stroke limitations: | week W |
| , , , . | ||
| Section 4.4 Stroke limitations with control. | ||
| Figure 12 | Config: , , , . | week 10 |
| From optimal to decreases stroke by 27% and average power by 17%. | ||
| Section 4.5 Control damping versus friction. | ||
| Figure 13 | Config: , , , . | week 10 |
| Comparing with , and with & qualitatively. | ||
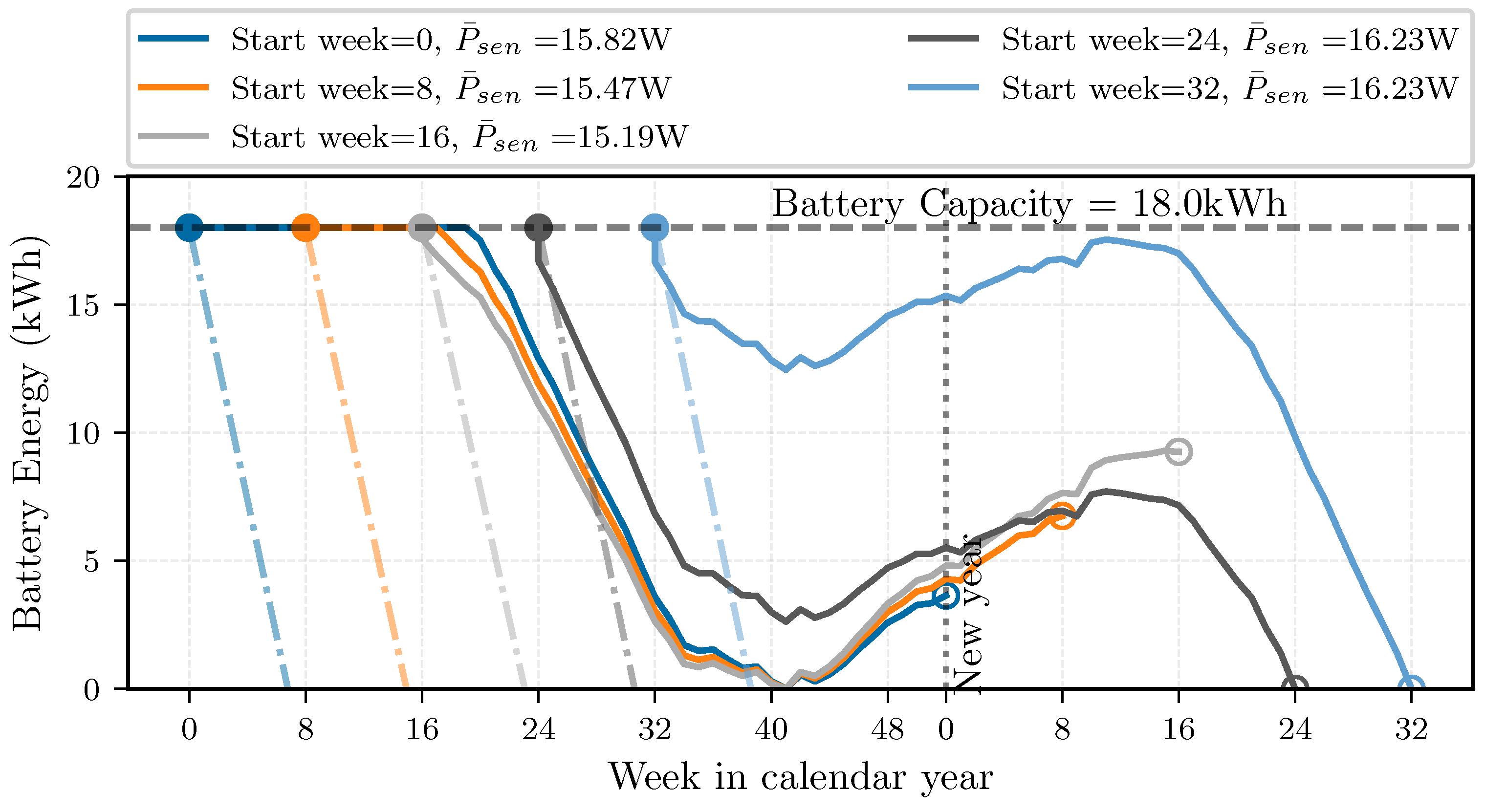
| Section 4.6 Annual deployment. | ||
| Figure 14 | , , , & . | week W |
| The sub-optimal configuration would allow an average sensor power draw between 15.2 W to 16.2 . | ||
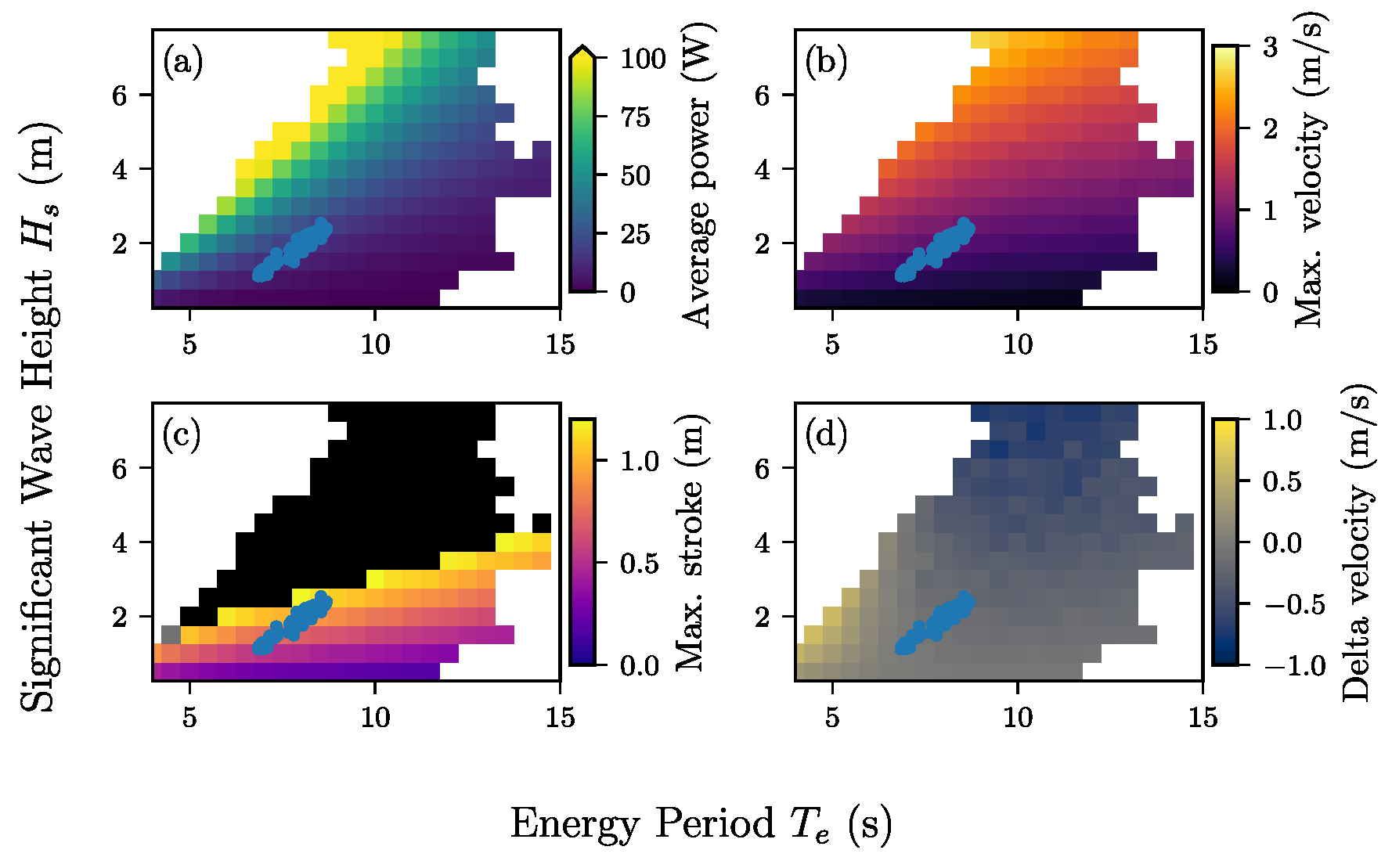
| Section 4.7 WEC-Spar total metrics. | ||
| Figure 15 | , , , & | , |
| Average power, max. velocity, max. stroke, and difference between X-Spar and WEC-Spar velocity for variable sea states. | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaebele, D.T.; Coe, R.G.; Bacelli, G.; Lanagan, T.; Fucile, P.; Korde, U.A.; Toole, J. Powering the Woods Hole X-Spar Buoy with Ocean Wave Energy—A Control Co-Design Feasibility Study. Energies 2025, 18, 4442. https://doi.org/10.3390/en18164442
Gaebele DT, Coe RG, Bacelli G, Lanagan T, Fucile P, Korde UA, Toole J. Powering the Woods Hole X-Spar Buoy with Ocean Wave Energy—A Control Co-Design Feasibility Study. Energies. 2025; 18(16):4442. https://doi.org/10.3390/en18164442
Chicago/Turabian StyleGaebele, Daniel T., Ryan G. Coe, Giorgio Bacelli, Thomas Lanagan, Paul Fucile, Umesh A. Korde, and John Toole. 2025. "Powering the Woods Hole X-Spar Buoy with Ocean Wave Energy—A Control Co-Design Feasibility Study" Energies 18, no. 16: 4442. https://doi.org/10.3390/en18164442
APA StyleGaebele, D. T., Coe, R. G., Bacelli, G., Lanagan, T., Fucile, P., Korde, U. A., & Toole, J. (2025). Powering the Woods Hole X-Spar Buoy with Ocean Wave Energy—A Control Co-Design Feasibility Study. Energies, 18(16), 4442. https://doi.org/10.3390/en18164442







