A New Model to Investigate Effect of Heat Conduction Between Tubes on Overall Performance of a Coil Absorber for Flat-Plate Solar Collectors
Abstract
1. Introduction
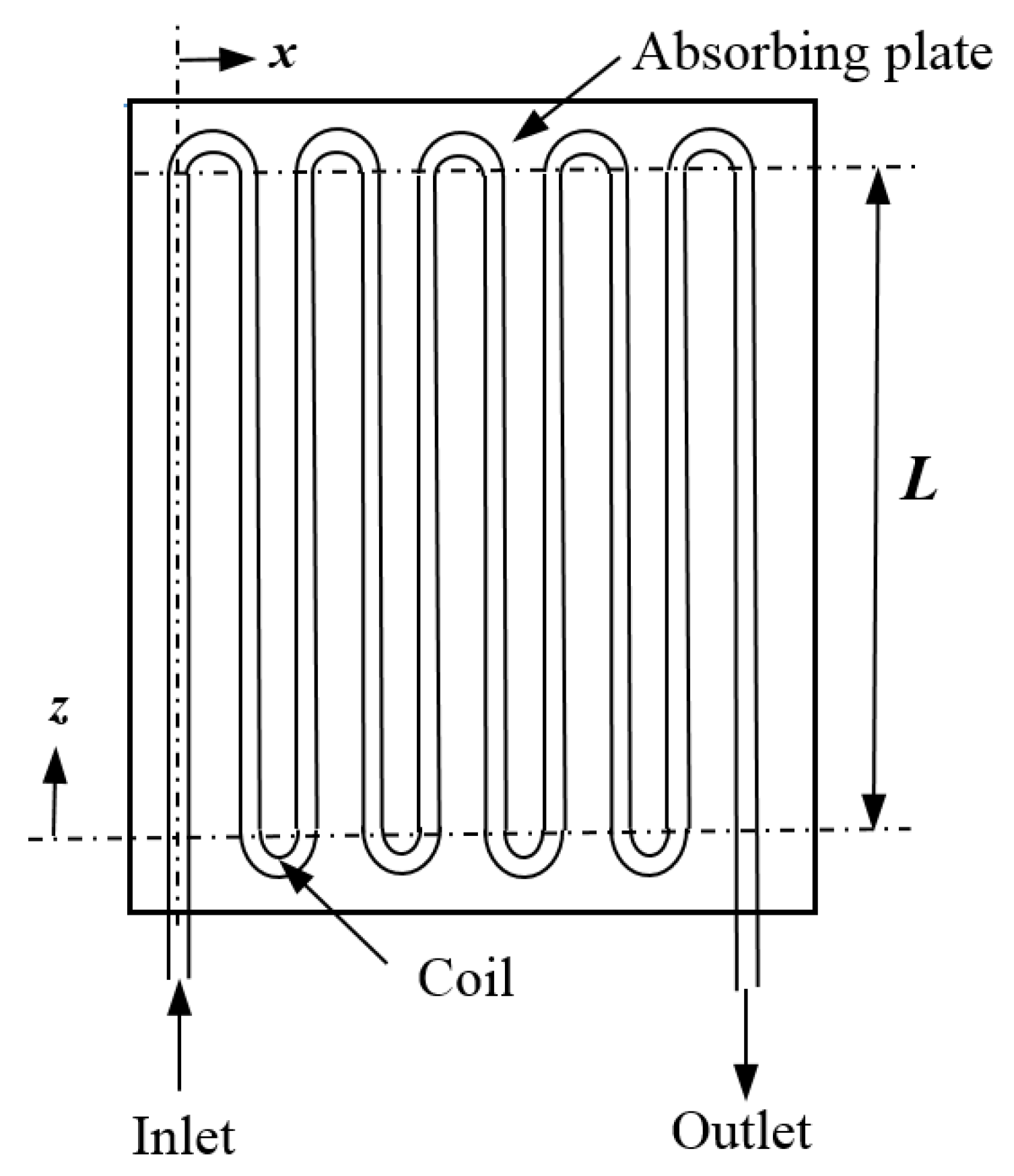
2. Collector Model and Formulation
2.1. Non-Dimensionalization
2.2. Vectorial Expression of Equations
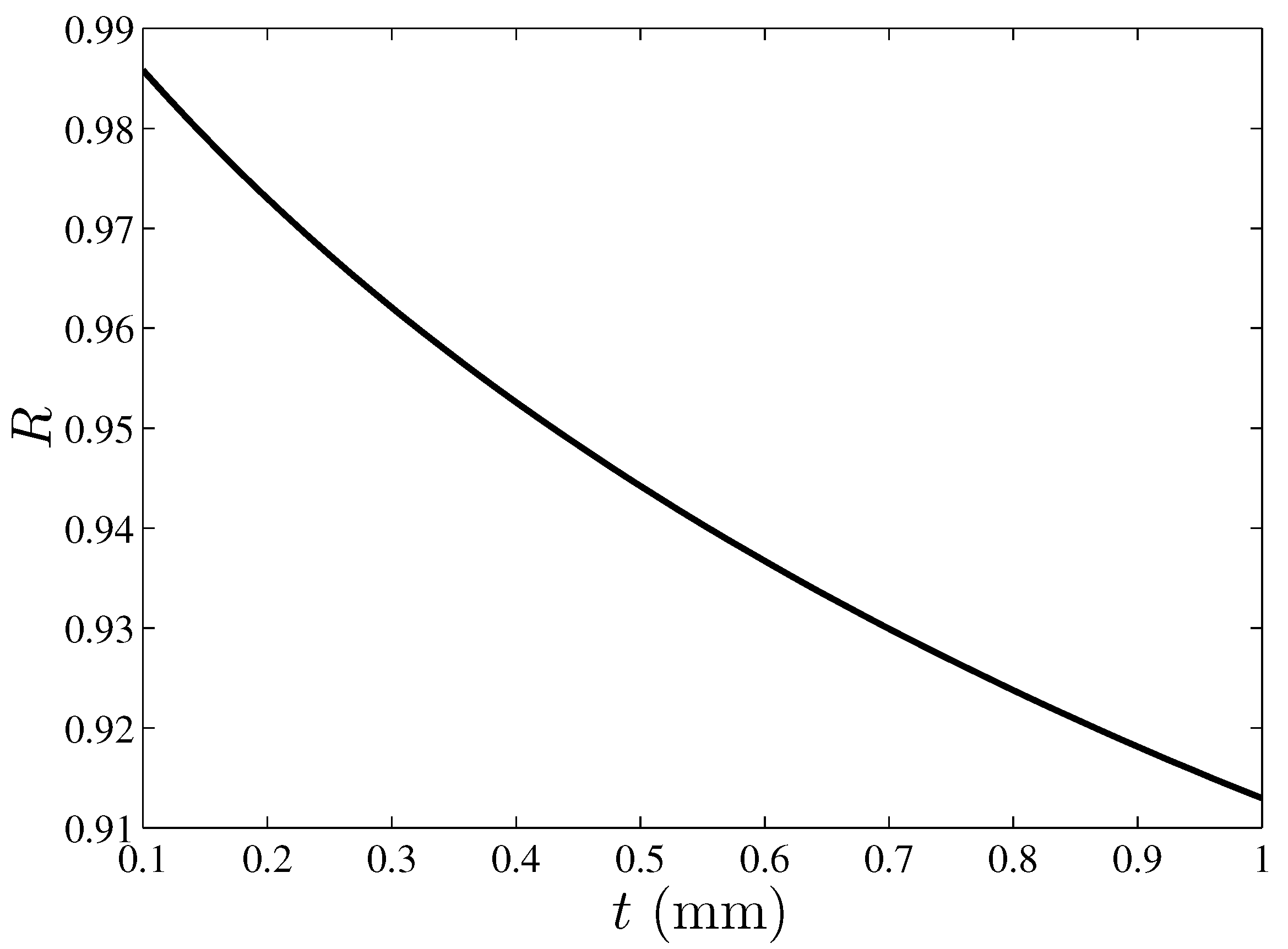
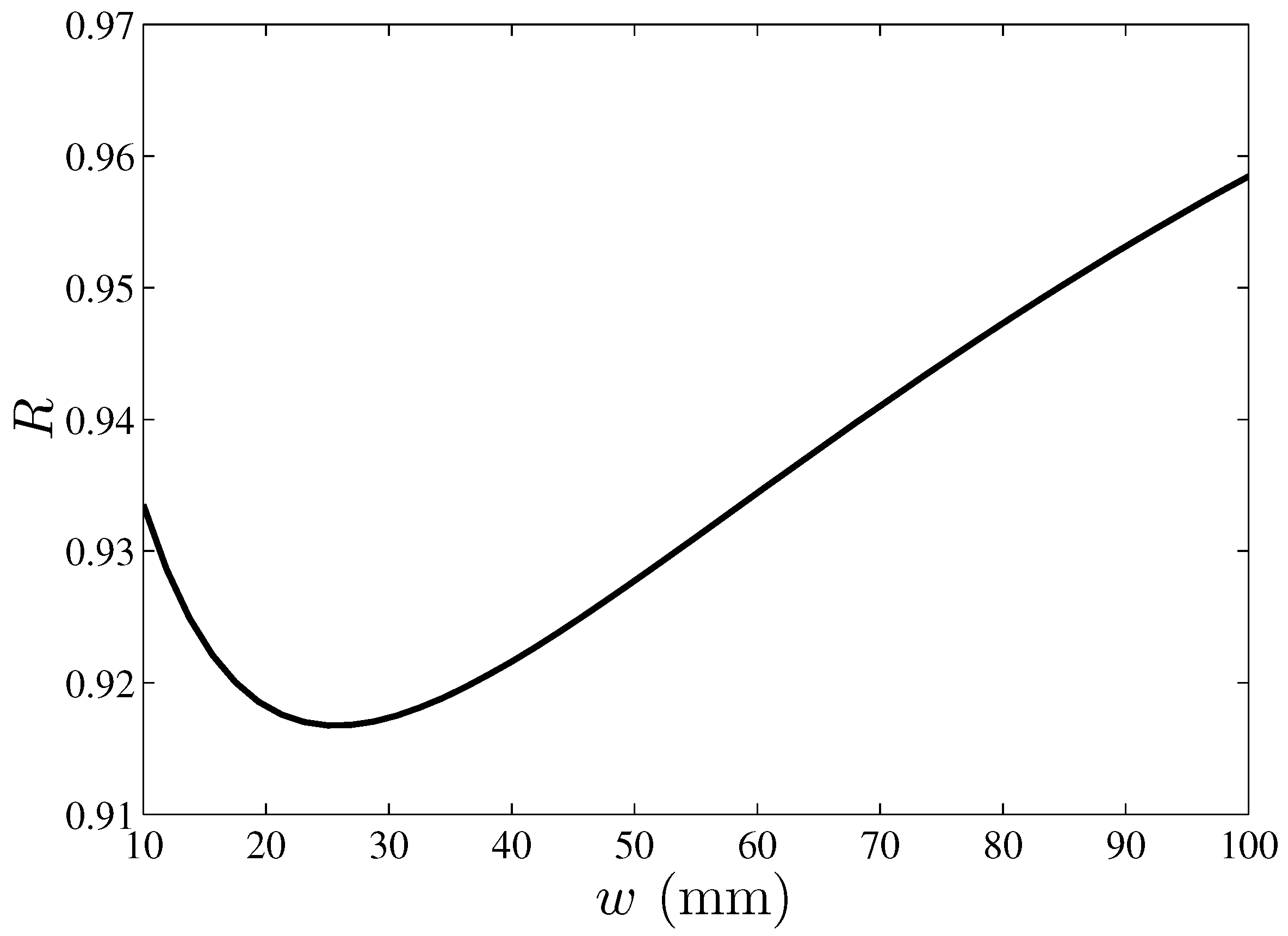
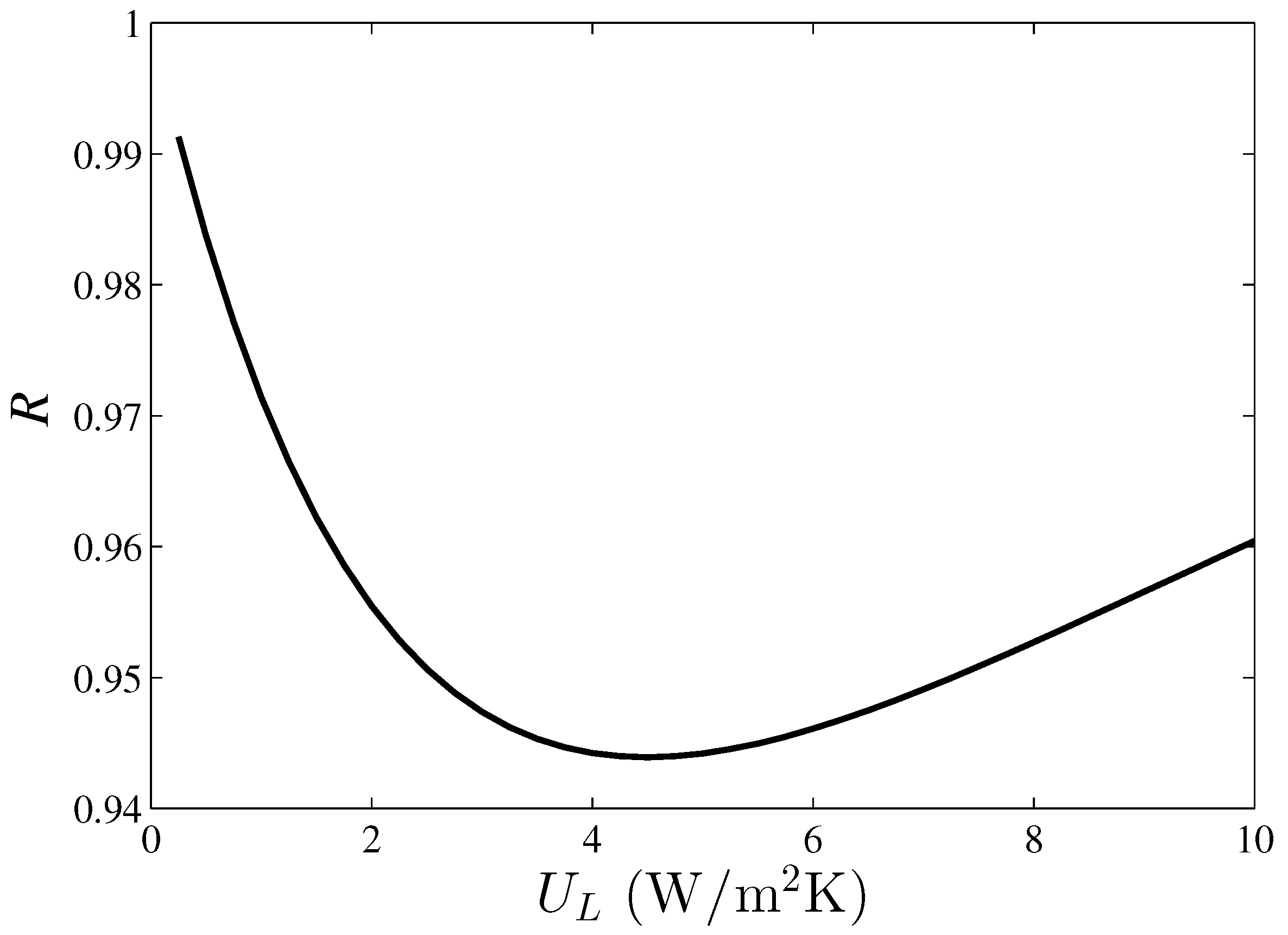
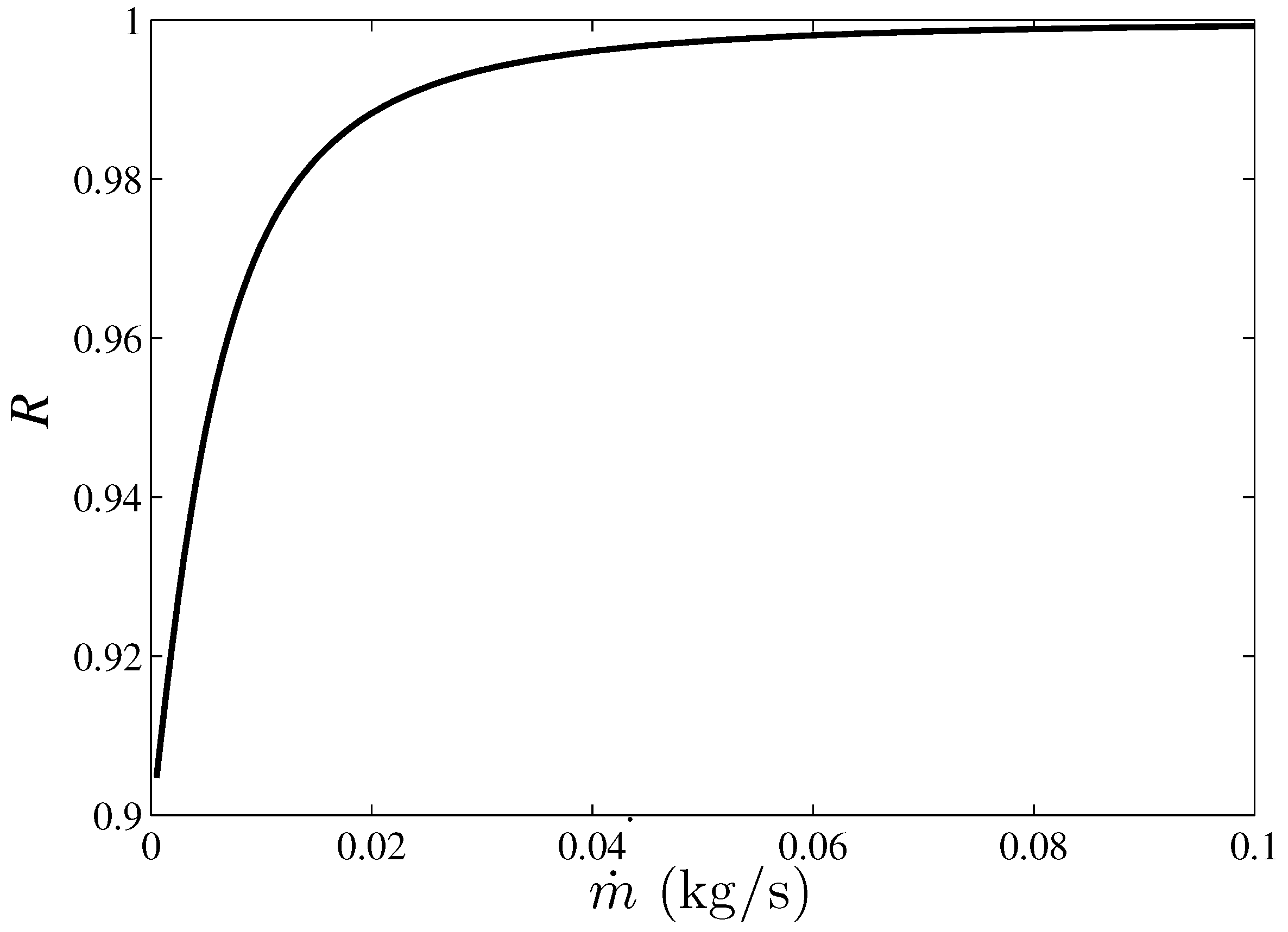
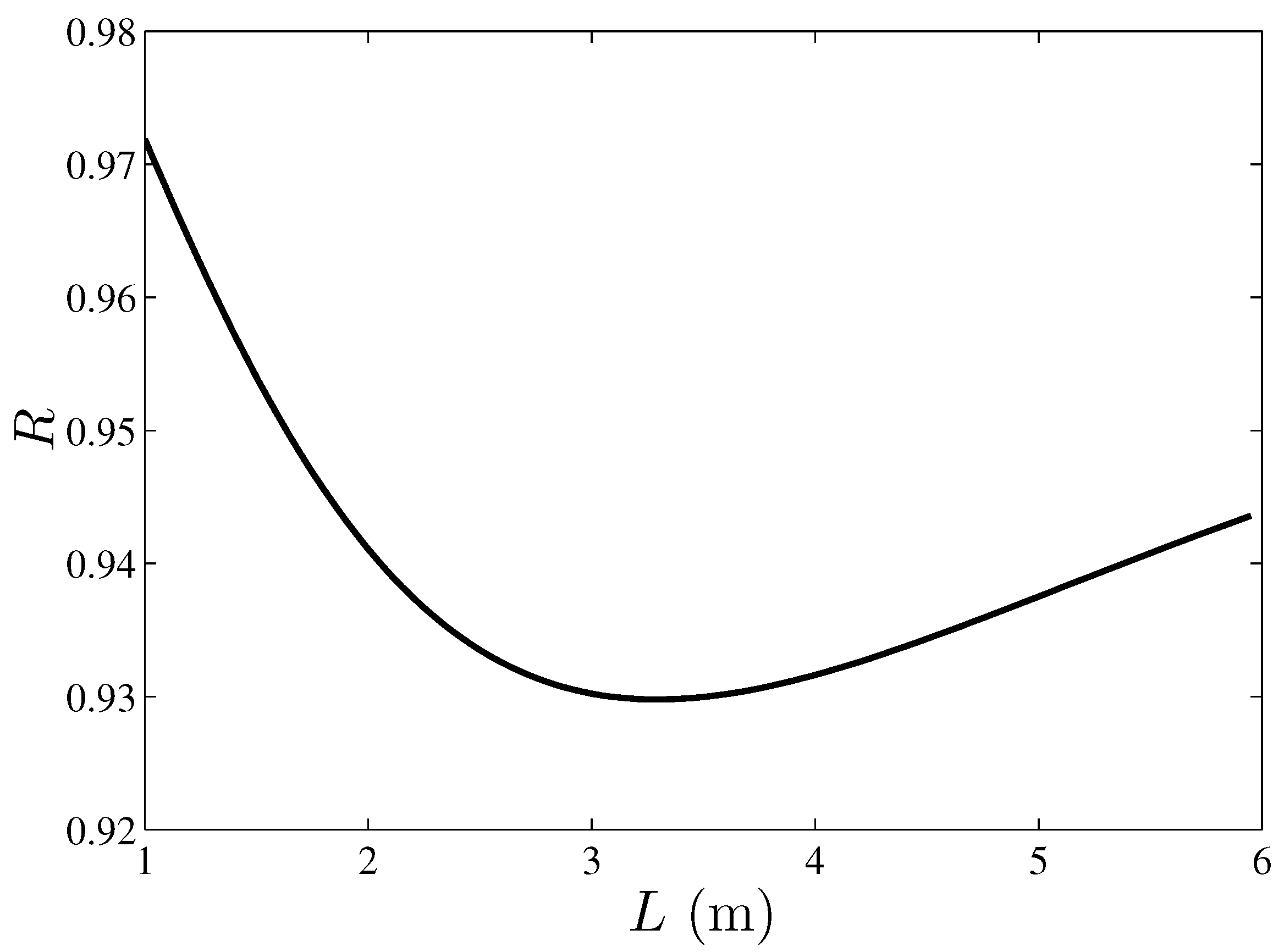
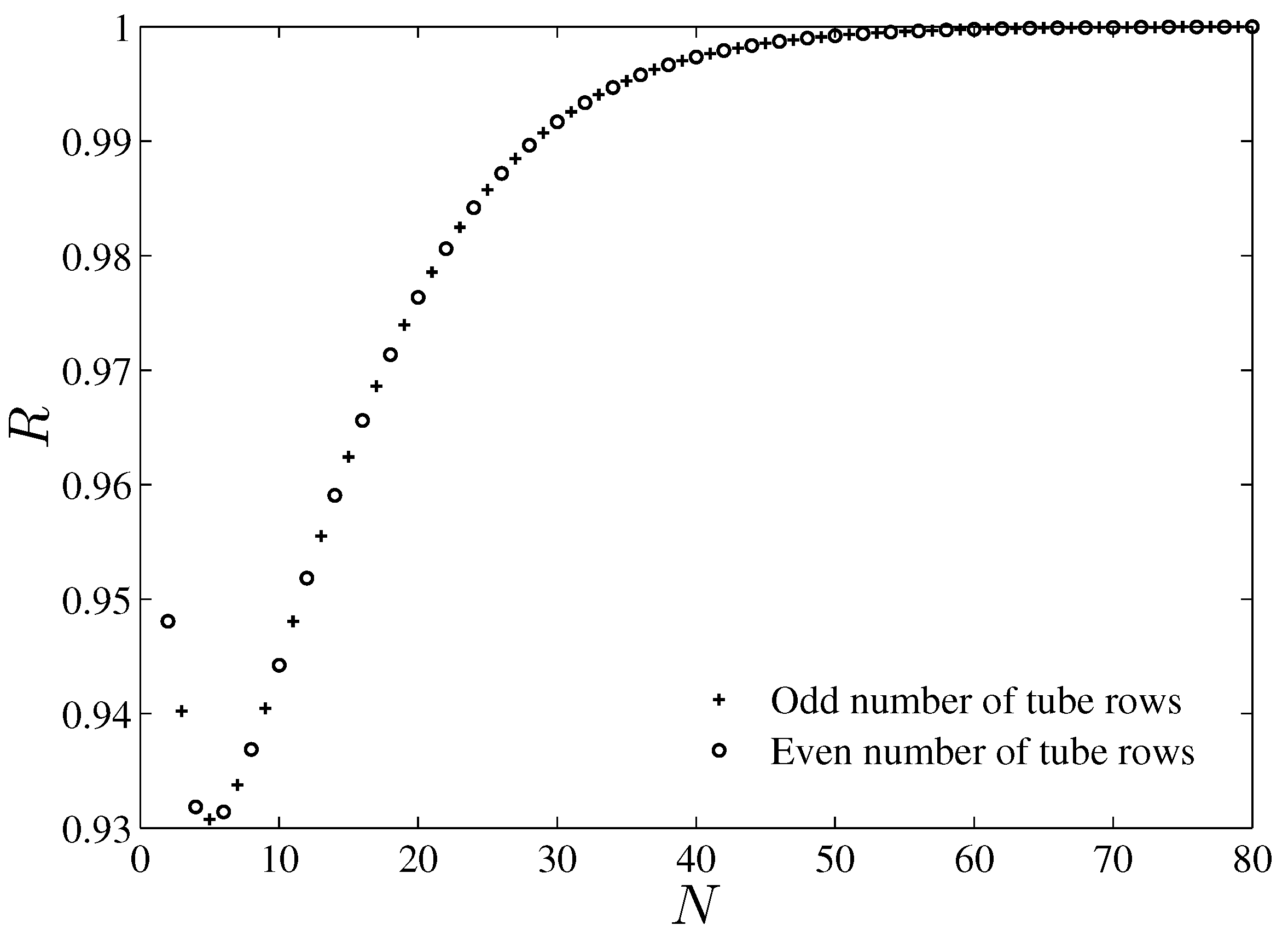
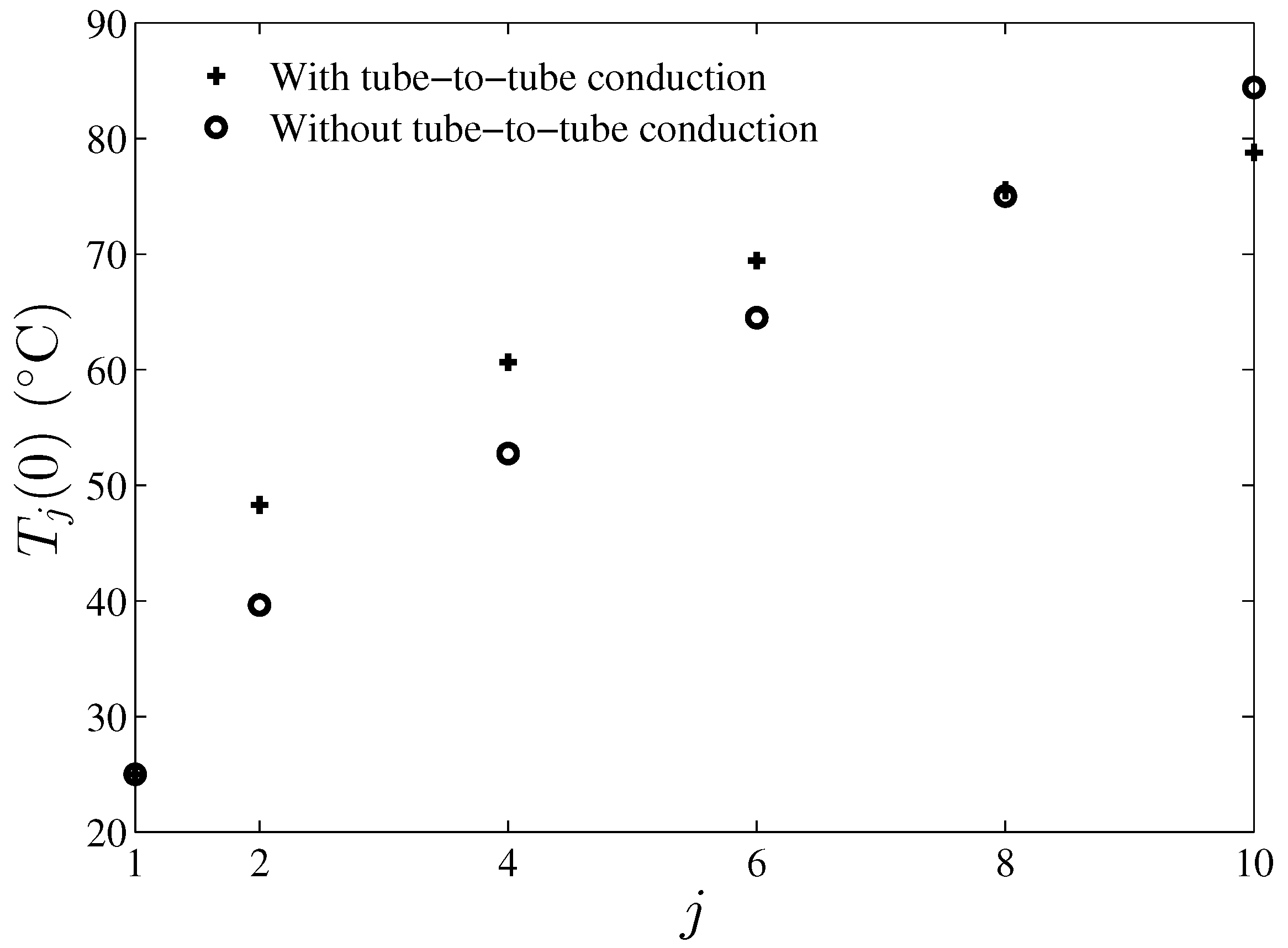
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| C | in-tube fluid specific heat (J/Kg·K) |
| collector absorber plate surface area (m2) | |
| tube inner diameter (m) | |
| tube outer diameter (m) | |
| tube differential length (m) | |
| collector heat removal factor | |
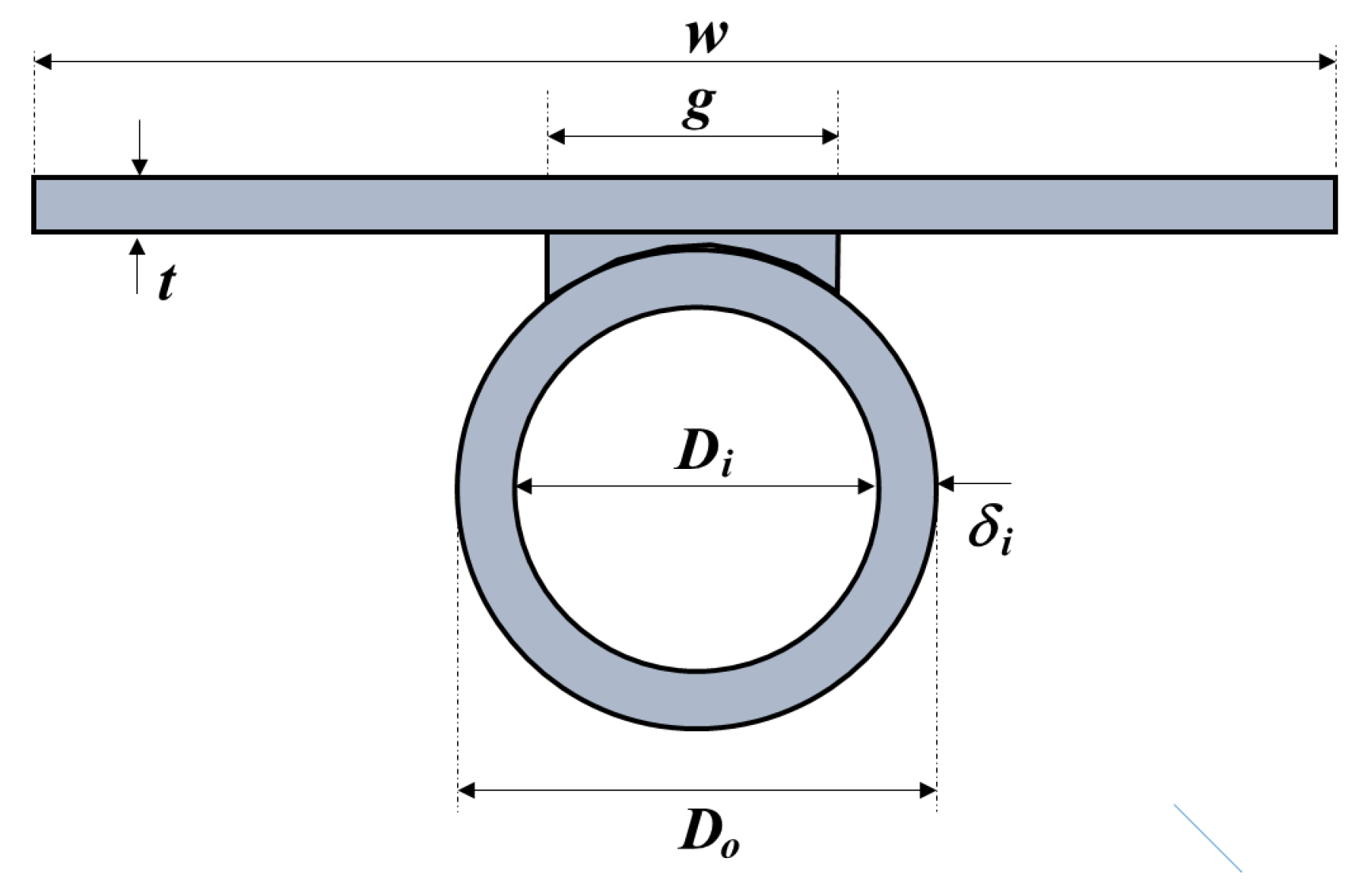
| g | length of tube–plate contact strip (m) |
| j | row number |
| in-tube convective heat transfer coefficient (W/m2·K) | |
| k | thermal conductivity of tubes and plates (W/m·K) |
| thermal conductivity of the in-tube fluid (W/m·K) | |
| L | length of each straight section of pipe (m) |
| in-tube fluid mass flow rate (kg/s) | |
| N | number of straight sections of pipe |
| Q | total heat absorbed by the in-tube fluid (W) |
| heat absorbed by the tube from adhered plate strip (W) | |
| rate of heat transfer from absorber plate to j-th tube (W) | |
| heat leaving tube j in the direction of tube (W) | |
| heat leaving tube j in the direction of tube (W) | |
| heat transferred along the plates (W) | |
| R | ratio of heat transfer rates with and without tube-to-tube conduction along the plates |
| resistance to heat transfer per unit length between the contact point of the tube–plate and the in-tube fluid (K·m/W) | |
| net solar irradiation absorbed by the plate (W) | |
| t | plate thickness (m) |
| j-th tube fluid temperature (°C) | |
| plate temperature (°C) | |
| j-th tube–plate contact strip temperature (°C) | |
| fluid inlet temperature (°C) | |
| fluid outlet temperature (°C) | |
| absorber plate overall heat transfer coefficient (W/m2·K) | |
| w | distance between adjacent tubes centerline (m) |
| z | axial position along the pipe measured from inlet (m) |
| ambient air temperature (°C) | |
| inner tube diameter-based Nusselt number | |
| inner tube diameter-based Reynolds number | |
| inner tube fluid Prandtl number | |
| f | smooth pipe Darcy–Weisbach friction factor |
| fin efficiency of pipe as extended surface | |
| j-th tube dimensionless tube–plate contact strip temperature | |
| tube thickness (m) | |
| j-th tube dimensionless fluid temperature | |
| vectorial expression of dimensionless fluid temperature | |
| vectorial expression of dimensionless tube–plate contact strip temperature | |
| kinematic viscosity of in-tube fluid (m2/s) |
References
- Tian, Y.; Zhao, C.Y. A review of solar collectors and thermal energy storage in solar thermal applications. Appl. Energy 2013, 104, 538–553. [Google Scholar] [CrossRef]
- Raja, A.; Natarajan, R.; Gaikwad, P.R.; Basil, E.; Borse, S.D.; Sundaraj, M. Heat enhancement in solar flat plate collectors—A review. J. Therm. Eng. 2024, 10, 773–789. [Google Scholar] [CrossRef]
- Merembayev, T.; Amirgaliyev, Y.; Kunelbayev, M.; Yedilkhan, D. Thermal Loss Analysis of a Flat Plate Solar Collector Using Numerical Simulation. Comput. Mater. Contin. 2022, 73, 4627–4640. [Google Scholar] [CrossRef]
- Shamsul Azha, N.I.; Hussin, H.; Nasif, M.S.; Hussain, T. Thermal performance enhancement in flat plate solar collector solar water heater: A review. Processes 2020, 8, 756. [Google Scholar] [CrossRef]
- Koholé, Y.W.; Fohagui, F.C.V.; Tchuen, G. Flat-plate solar collector thermal performance assessment via energy, exergy and irreversibility analysis. Energy Convers. Manag. 2022, 15, 100247. [Google Scholar]
- Freegah, B. Numerical and experimental analysis of the flat plate solar water heater systems’ thermal performance. Heat Transfer 2023, 52, 1118–1141. [Google Scholar] [CrossRef]
- Mokhlif, N.D.; Eleiwi, M.A.; Yassen, T.A. Experimental evaluation of a solar water heater integrated with a corrugated absorber plate and insulated flat reflectors. AIMS Energy 2023, 11, 522–539. [Google Scholar] [CrossRef]
- Hassan, Z.; Mahmood, M.; Ahmed, N.; Saeed, M.H.; Khan, R.; Abbas, M.M.; Abdelsalam, E. Techno-economic assessment of evacuated flat-plate solar collector system for industrial process heat. Energy Sci. Eng. 2023, 11, 2185–2201. [Google Scholar] [CrossRef]
- Balakrishnan, R.; Chellasamy, G.; Bojan, V.B.; Machakalai, R.K. Empirical investigation and performance evaluation of flat-plate solar water heating systems: A comparative analysis with and without heat exchangers. Z. FüR Phys. Chem. 2025, 239, 1013–1032. [Google Scholar] [CrossRef]
- Rahimi-Ahar, Z.; Khiadani, M.; Rahimi Ahar, L.; Shafieian, A. Performance evaluation of single stand and hybrid solar water heaters: A comprehensive review. Clean Technol. Environ. Policy 2023, 25, 2157–2184. [Google Scholar] [CrossRef]
- Vengadesan, E.; Gnanasekaran, K. Comprehensive performance analysis of a flat plate solar water heating system featuring a dual-inlet modified absorber. Discov. Sustain. 2025, 6, 489. [Google Scholar] [CrossRef]
- Tang, X.; Tan, C.; Liu, Y.; Sun, C.; Xu, S. Numerical Analysis on Heat Collecting Performance of Novel Corrugated Flat Plate Solar Collector Using Nanofluids. Sustainability 2024, 16, 5924. [Google Scholar] [CrossRef]
- Mahakud, J.; Kundu, B. Two-Dimensional Analysis of Absorber Plates in Solar Collectors with a Nonlinear Plate Temperature at the Tube Section. Energies 2024, 17, 5979. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 2nd ed.; Wiley Interscience: New York, NY, USA, 1991. [Google Scholar]
- Lund, K.O. General thermal analysis of serpentine-flow flat-plate solar collector absorbers. Sol. Energy 1989, 42, 133–142. [Google Scholar] [CrossRef]
- Eisenmann, W.; Vajen, K.; Ackermann, H. On the correlations between collector efficiency factor and material content of parallel flow flat-plate solar collectors. Sol. Energy 2004, 76, 381–387. [Google Scholar] [CrossRef]
- Kroeger, P.G. Performance deterioration in high effectiveness heat exchangers due to axial conduction. Adv. Cryog. Eng. 1967, 12, 363–372. [Google Scholar]
- Mondt, J.R. Correlating the effects of longitudinal heat conduction on heat exchanger performance. ASME Heat Transf. Div. 1980, 10, 123–134. [Google Scholar]
- Chiou, J.P. The effect of longitudinal heat conduction on crossflow heat exchangers. ASME J. Heat Transf. 1978, 100, 346–351. [Google Scholar] [CrossRef]
- Chiou, J.P. The advancement of compact heat exchanger theory considering the effects of longitudinal heat conduction and flow nonuniformity. ASME Heat Transf. Div. 1980, 10, 101–121. [Google Scholar]
- Heun, M.K.; Crawford, R.R. Longitudinal fin conduction in multipass cross-counterflow finned-tube heat exchangers. ASHRAE Trans. 1994, 100, 382–389. [Google Scholar]
- Romero-Méndez, R.; Sen, M.; Yang, K.T.; McClain, R.L. Effect of tube-to-tube conduction on plate-fin and tube heat exchanger performance. Int. J. Heat Mass Transf. 1997, 40, 3909–3916. [Google Scholar] [CrossRef]
- Singh, V.; Aute, V.; Radermacher, R. Numerical approach for modeling air-to-refrigerant fin-and-tube heat exchanger with tube-to-tube heat transfer. Int. J. Refrig. 2008, 31, 1414–1425. [Google Scholar] [CrossRef]
- Singh, V.; Aute, V.; Radermacher, R. Investigation of effect of cut fins on carbon dioxide gas cooler performance. HVAC&R Res. 2010, 16, 513–527. [Google Scholar] [CrossRef]
- Ding, W.K.; Fan, J.F.; He, Y.L.; Tao, W.Q.; Zheng, Y.X.; Gao, Y.F.; Song, J. A general simulation model for performance prediction of plate fin-and-tube heat exchanger with complex circuit configuration. Appl. Therm. Eng. 2011, 31, 3106–3116. [Google Scholar] [CrossRef]
- Sarfraz, O.; Bach, C.K.; Bradshaw, C.R. Discrete modeling of fin-and-tube heat exchangers with cross-fin conduction functionality. Int. J. Refrig. 2019, 104, 270–281. [Google Scholar] [CrossRef]
- Sarfraz, O.; Bach, C.K.; Bradshaw, C.R. A novel technique for computationally efficient consideration of cross-fin conduction in fin-and-tube heat exchanger models. Int. J. Refrig. 2019, 107, 73–83. [Google Scholar] [CrossRef]
- Sarfraz, O.; Bach, C.K.; Bradshaw, C.R. Validation of advanced fin-and-tube heat exchanger models with cross-fin conduction functionality. Int. J. Refrig. 2020, 116, 70–81. [Google Scholar] [CrossRef]
- Saleem, S.; Bradshaw, C.R.; Bach, C.K. Validation of a multi-circuit heat exchanger model for evaluating the effect of refrigerant circuitry on cross-fin conduction in evaporator mode. Int. J. Refrig. 2021, 131, 623–633. [Google Scholar] [CrossRef]
- Garcia, J.C.S.; Giannetti, N.; Varela, D.A.B.; Varela, R.J.; Yamaguchi, S.; Saito, K.; Berana, M.S. Design of a Numerical Simulator for Finned-Tube Heat Exchangers with Arbitrary Circuitry. Heat Transf. Eng. 2021, 43, 1675–1693. [Google Scholar] [CrossRef]
- Macchitella, S.; Colangelo, G.; Starace, G. Performance prediction of plate-finned tube heat exchangers for refrigeration: A review on modeling and optimization methods. Energies 2023, 16, 1948. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 4th ed.; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Gnielinski, V. New equations for heat and mass transfer in turbulent pipe and channel flow. Int. Chem. Eng. 1976, 16, 359–367. [Google Scholar]
- Dayan, M. High Performance in Low-Flow Solar Domestic Hot Water Systems (No. DOE/SF/15303-53). Master’s Thesis, Universty of Wisconsin, Madison, WI, USA, 1997. [Google Scholar]

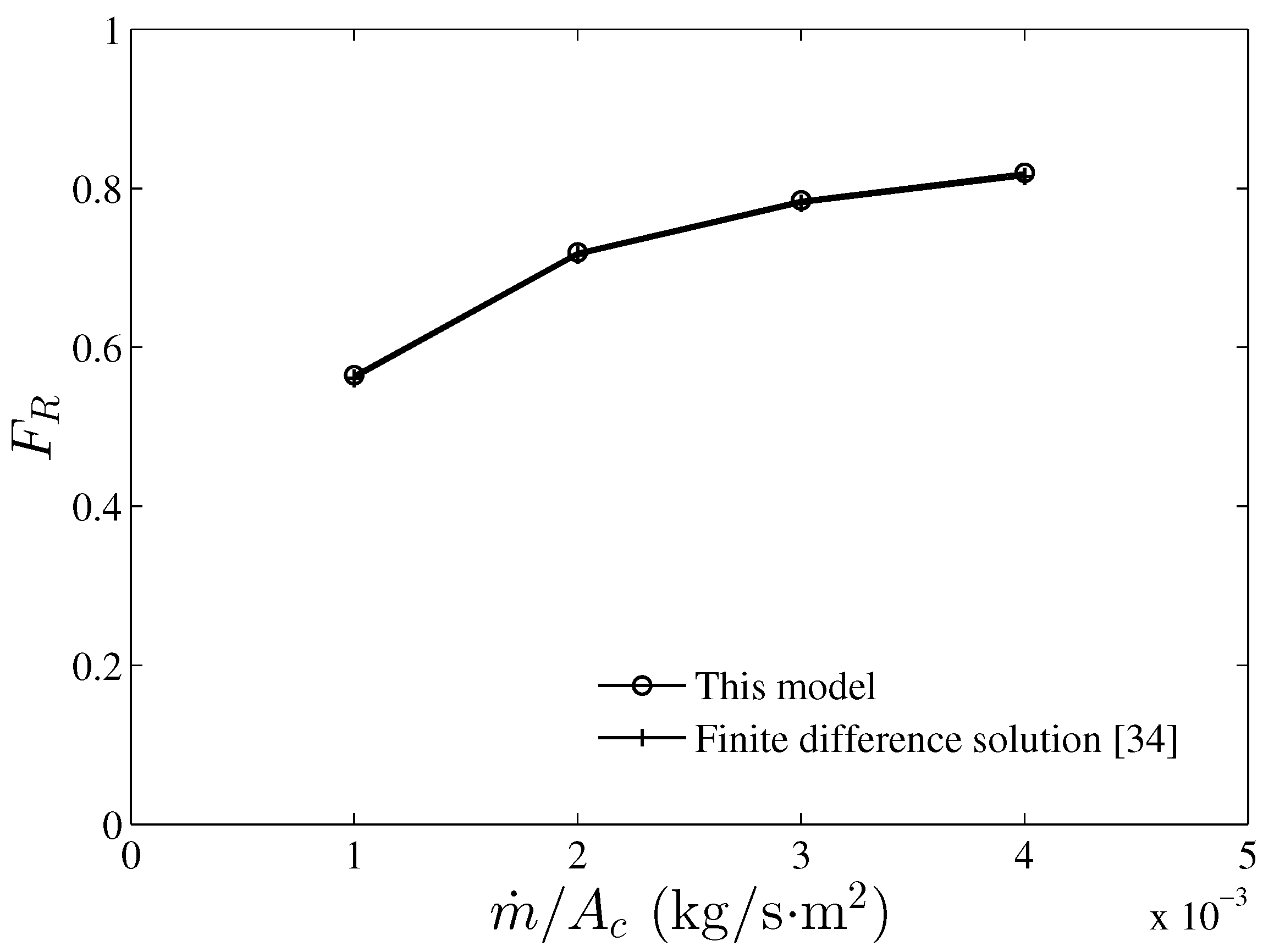
| Symbol | Description | Value | Units |
|---|---|---|---|
| Absorber plate overall heat transfer coefficient | 5.0 | W/m2· K | |
| Inner diameter of tubes | 0.0065 | m | |
| Outer diameter of tubes | 0.0075 | m | |
| L | Length of straight sections of tubes | 1.857 | m |
| t | Thickness of absorber plate | 0.0005 | m |
| w | Spacing between adjacent tubes | 0.075 | m |
| g | Plate contact length between tubes and plate | 0.00375 | m |
| N | Number of tube rows of coil | 10 | |
| k | Thermal conductivity of plates and tubes | 400 | W/m·K |
| Mass flow rate of water | 0.001 | kg/s | |
| Kinematic viscosity of water | 0.000001 | m2/s | |
| Thermal conductivity of water | 0.628 | W/m·K | |
| C | Specific heat of water | 4180 | J/kg·K |
| Net solar irradiation absorbed by the plate | 700 | W/m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Morales, E.G.; Romero-Méndez, R.; Pérez-Gutiérrez, F.G.; García-Zugasti, P. A New Model to Investigate Effect of Heat Conduction Between Tubes on Overall Performance of a Coil Absorber for Flat-Plate Solar Collectors. Energies 2025, 18, 4360. https://doi.org/10.3390/en18164360
Martínez-Morales EG, Romero-Méndez R, Pérez-Gutiérrez FG, García-Zugasti P. A New Model to Investigate Effect of Heat Conduction Between Tubes on Overall Performance of a Coil Absorber for Flat-Plate Solar Collectors. Energies. 2025; 18(16):4360. https://doi.org/10.3390/en18164360
Chicago/Turabian StyleMartínez-Morales, Elena G., Ricardo Romero-Méndez, Francisco G. Pérez-Gutiérrez, and Pedro García-Zugasti. 2025. "A New Model to Investigate Effect of Heat Conduction Between Tubes on Overall Performance of a Coil Absorber for Flat-Plate Solar Collectors" Energies 18, no. 16: 4360. https://doi.org/10.3390/en18164360
APA StyleMartínez-Morales, E. G., Romero-Méndez, R., Pérez-Gutiérrez, F. G., & García-Zugasti, P. (2025). A New Model to Investigate Effect of Heat Conduction Between Tubes on Overall Performance of a Coil Absorber for Flat-Plate Solar Collectors. Energies, 18(16), 4360. https://doi.org/10.3390/en18164360






