A Comprehensive Optimization Framework for Techno-Economic Demand Side Management in Integrated Energy Systems
Abstract
1. Introduction
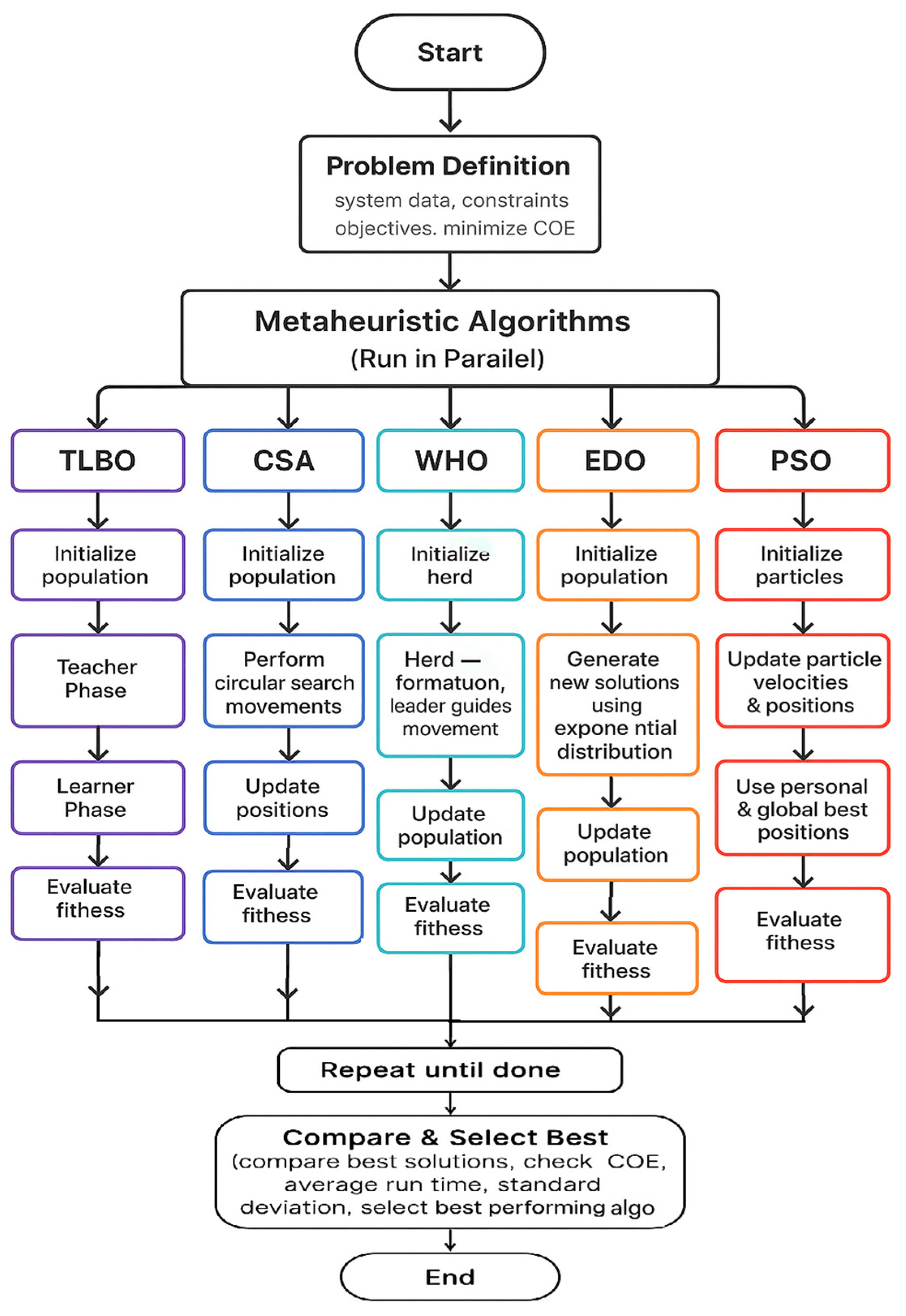
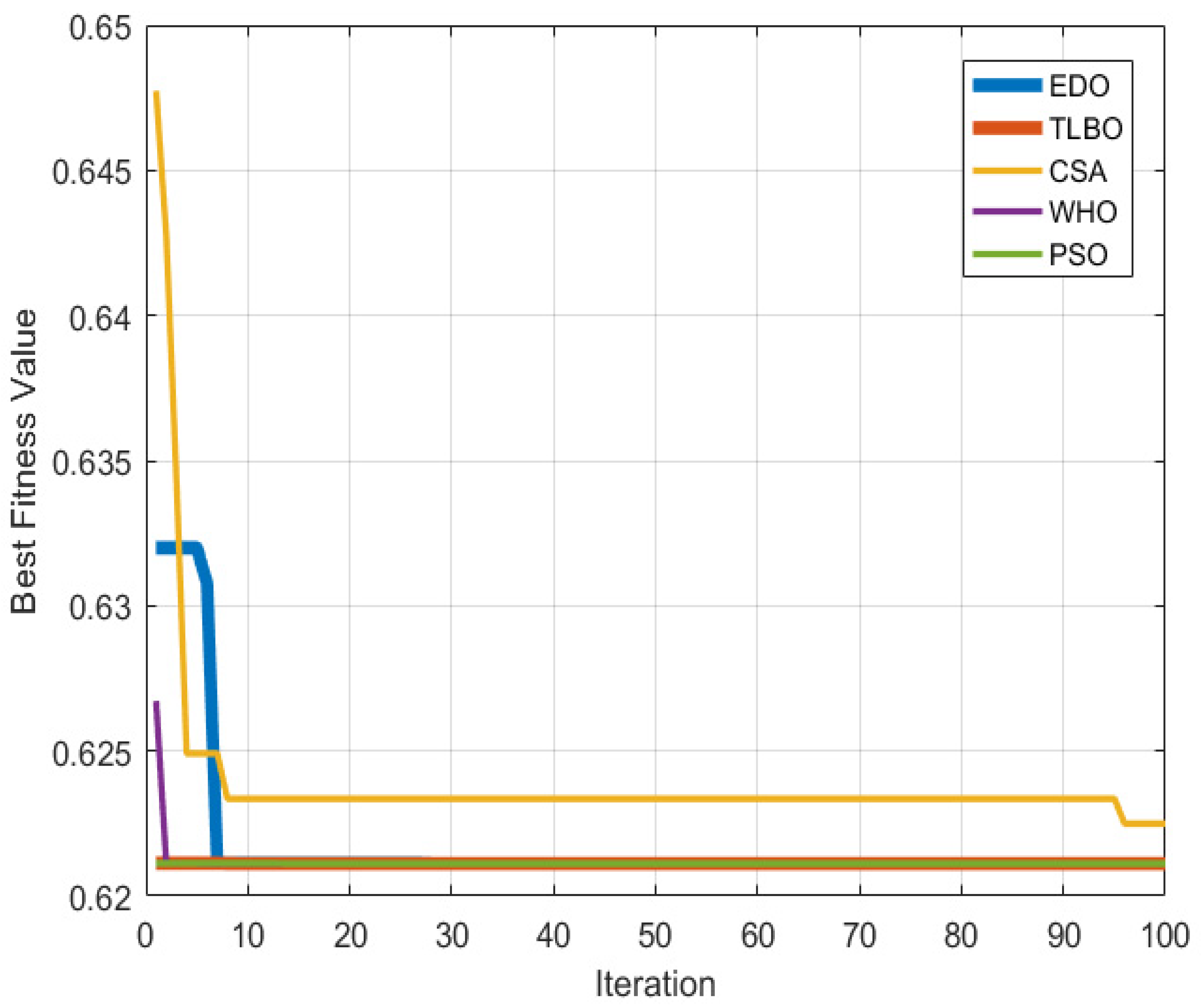
- The optimal sizing of a hybrid system configuration using multiple metaheuristic algorithms, the main one being the Exponential Distribution Optimizer (EDO) [29], to determine the optimal size for a hybrid energy system to achieve the minimum cost of energy (COE), then the results obtained from EDO were compared with that of alternative algorithms to demonstrate its effectiveness, and these algorithms include Teaching-Learning-Based Optimization (TLBO) [30], Circle Search Algorithm (CSA) [31], Wild Horse Optimizer (WHO) [32], and Particle Swarm Optimizer (PSO).
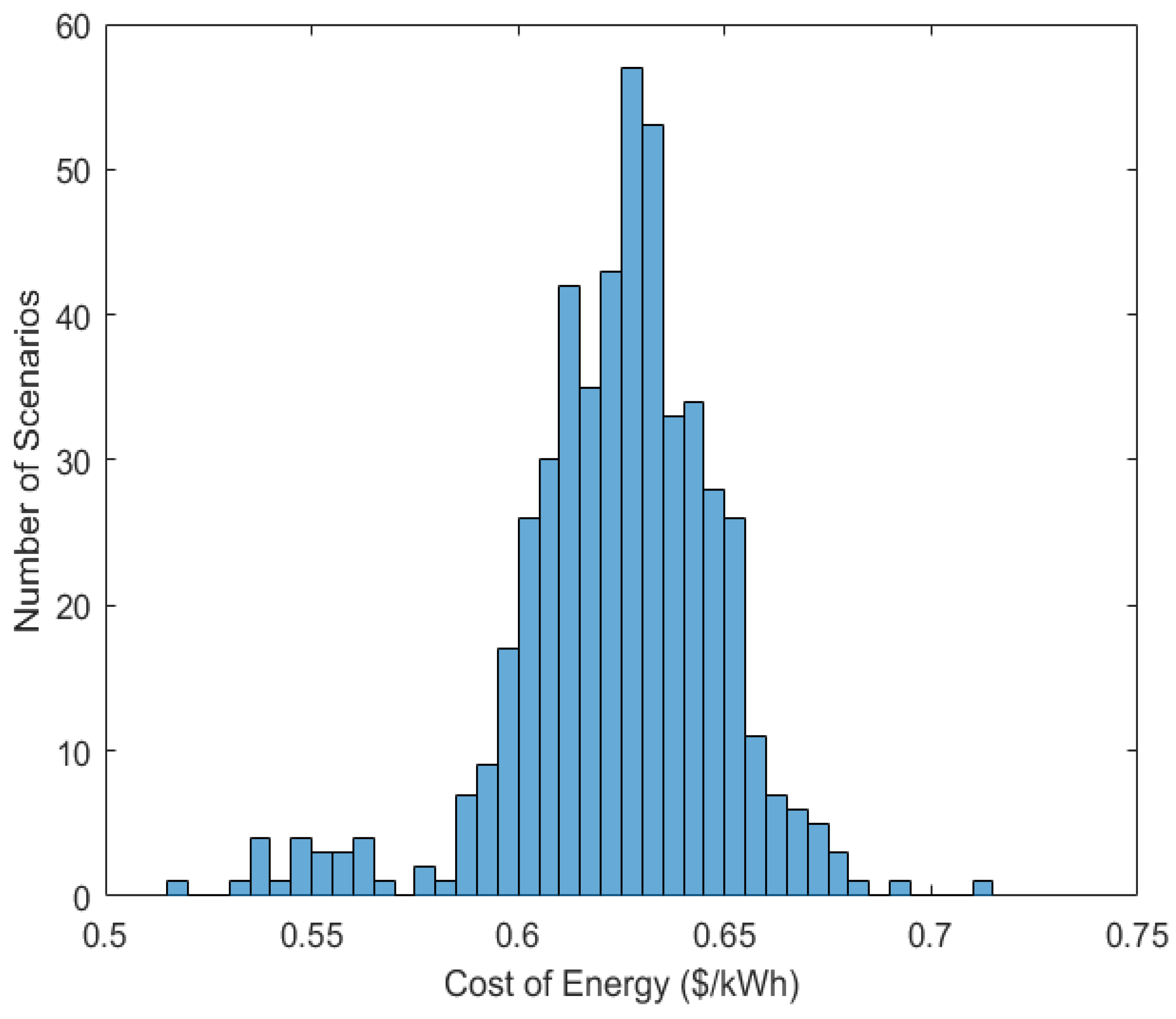
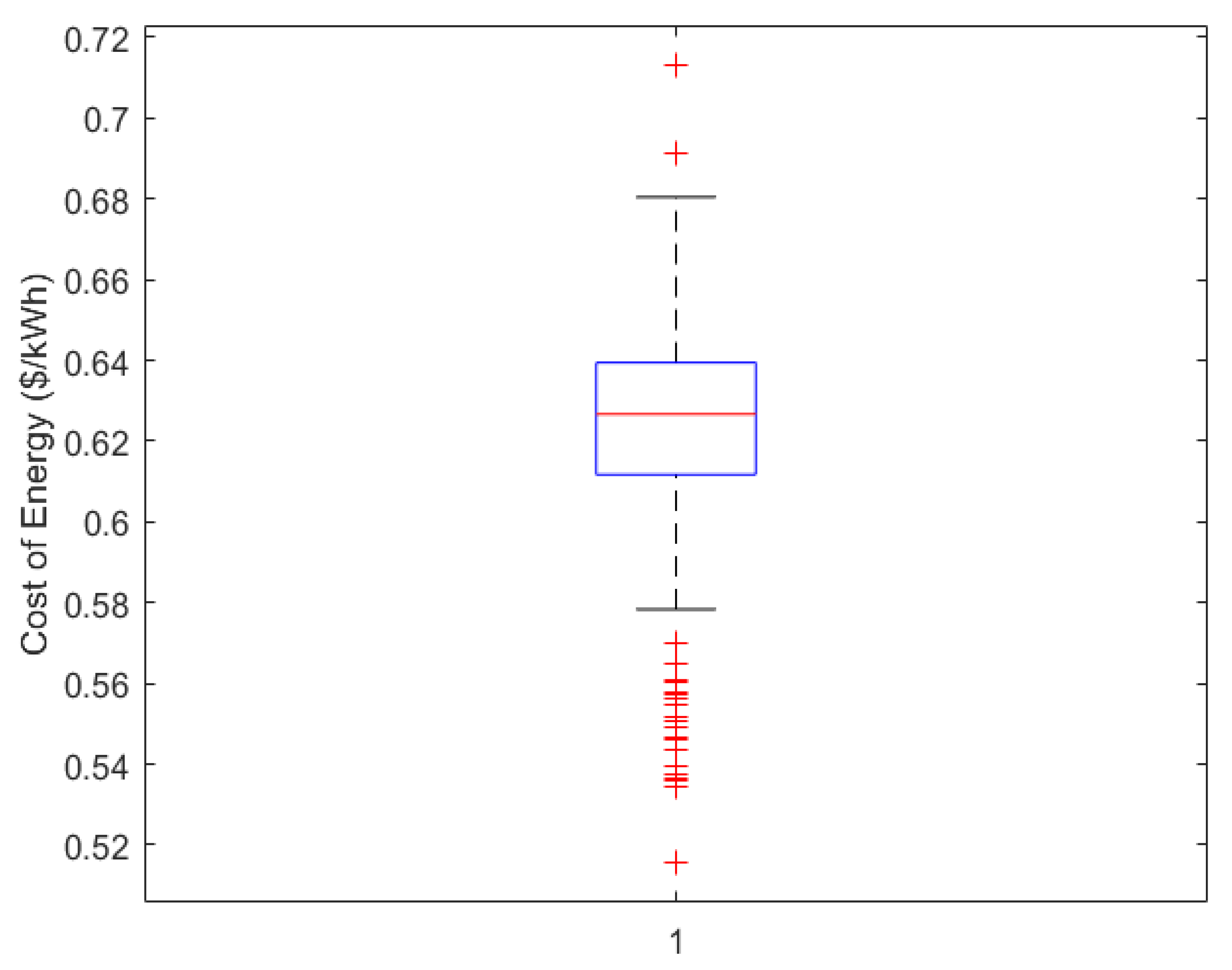
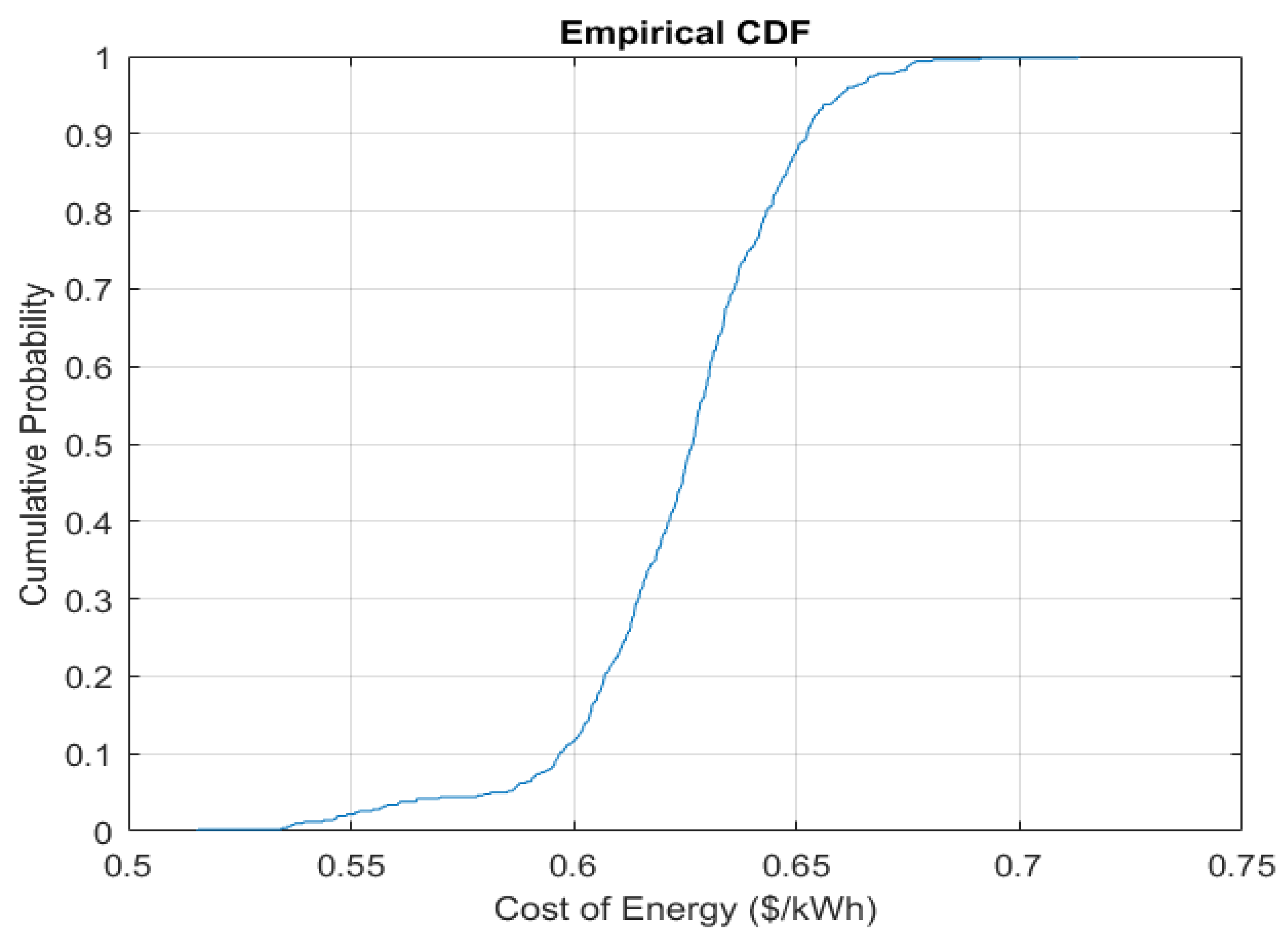
- A comprehensive Monte Carlo simulation is performed to rigorously assess the robustness of the proposed configuration under stochastic variations in solar, wind, and load demand, verifying that the system remains technically and economically viable under significant real-world uncertainty.
- Five scenarios were simulated for the optimal-sized systems, starting with a diesel-only generator and progressing to advanced hybrid systems integrating solar, wind, batteries, and Demand-Side Management (DSM) to demonstrate comparison between different configurations, and demonstrate DSM effectiveness in utilizing surplus renewable energy, reducing carbon dioxide (CO2) emissions, and stabilizing costs.
- Incorporate projected load growth over the years into the planning framework. By accounting for annual increases in energy demand, the analysis ensures that the hybrid system’s sizing and techno-economic performance remain reliable and cost-effective as consumption patterns evolve.
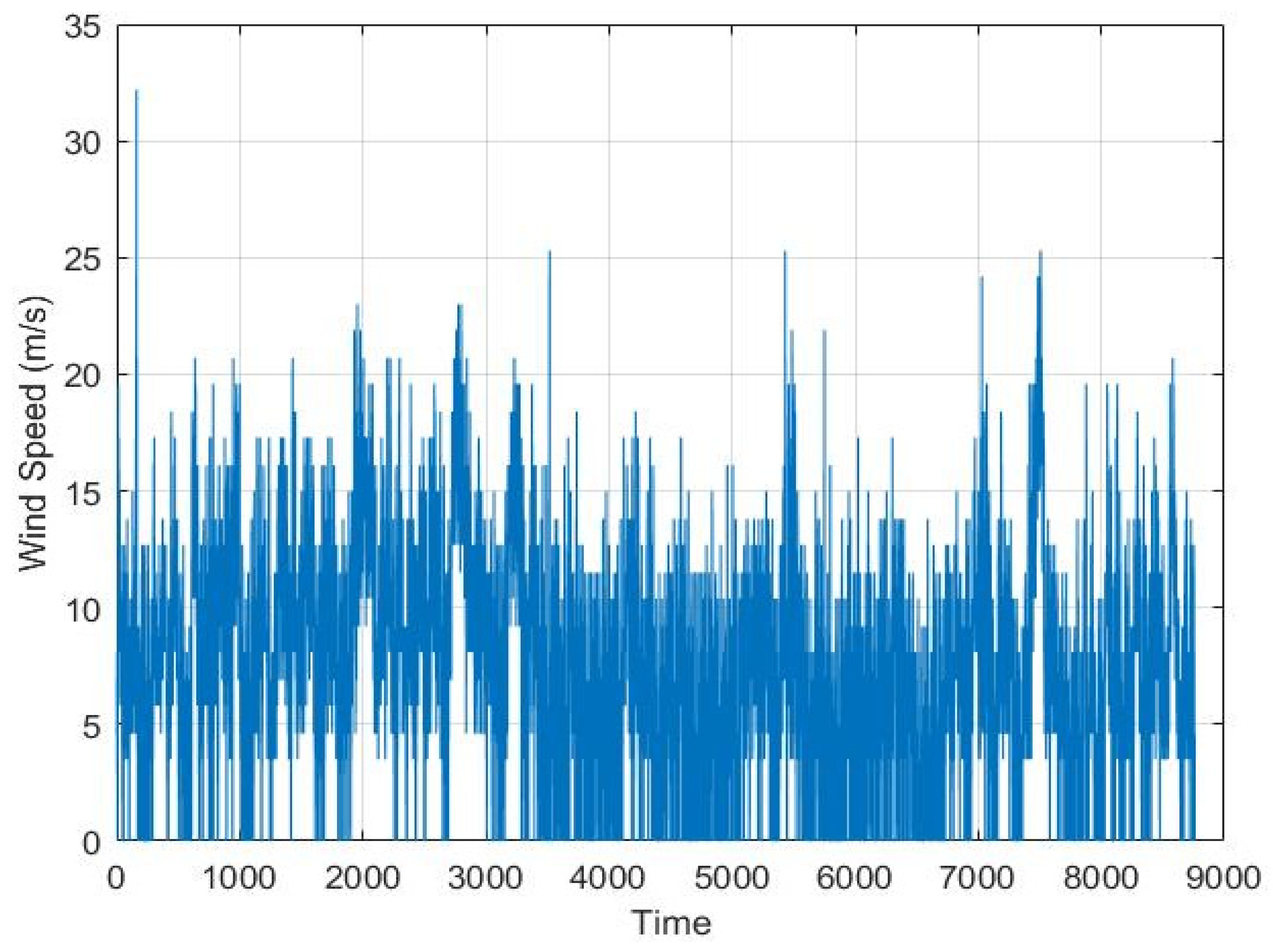
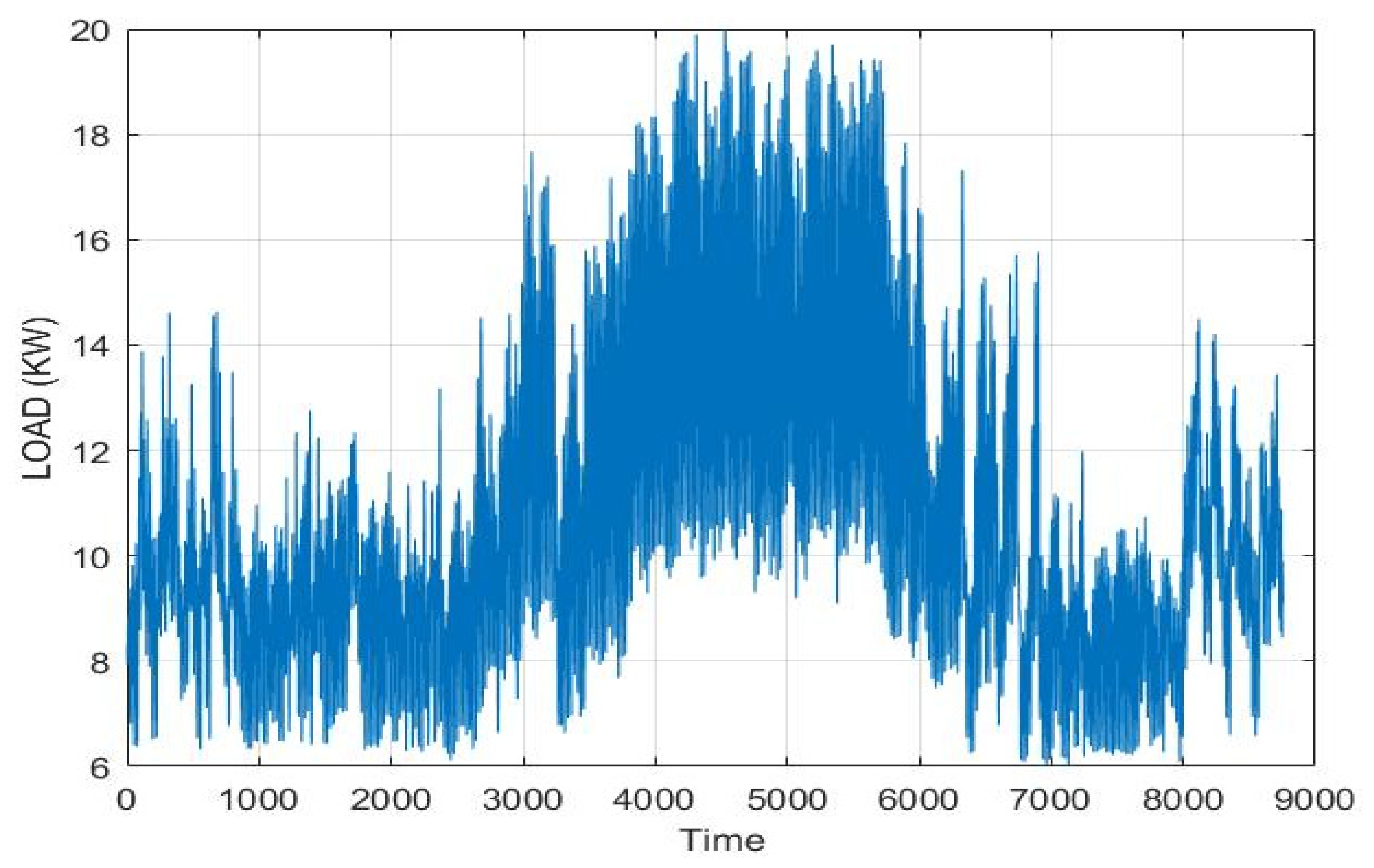
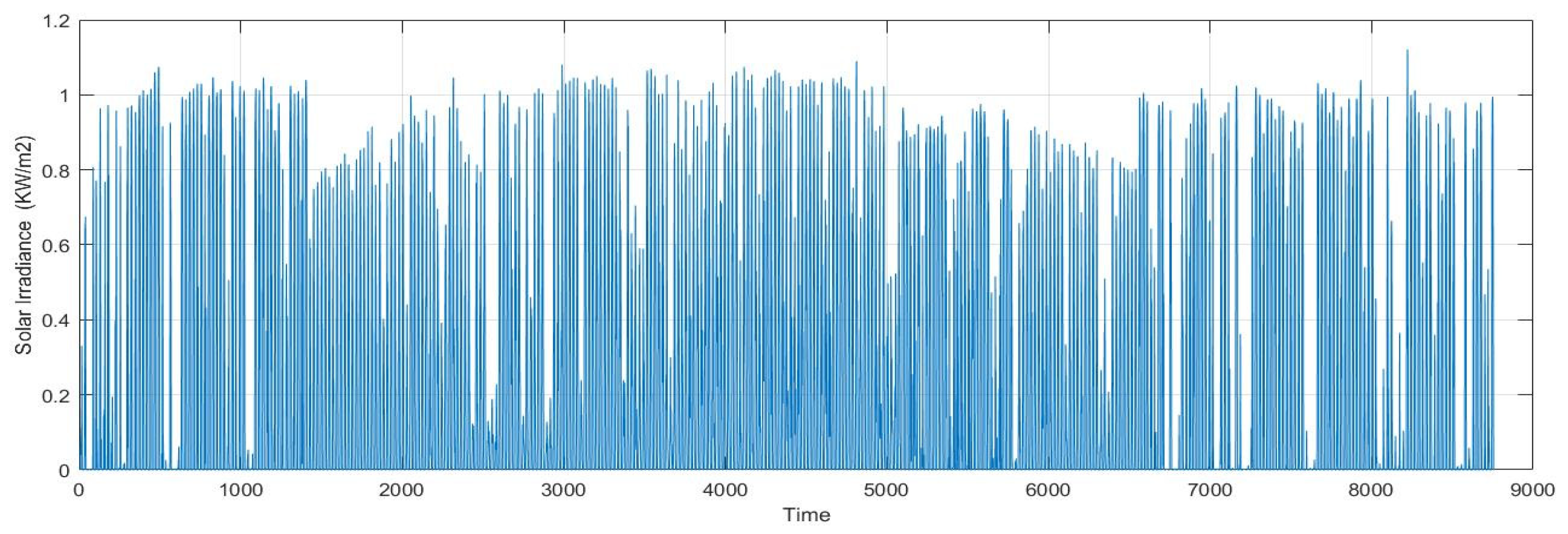
2. Meteorological Data
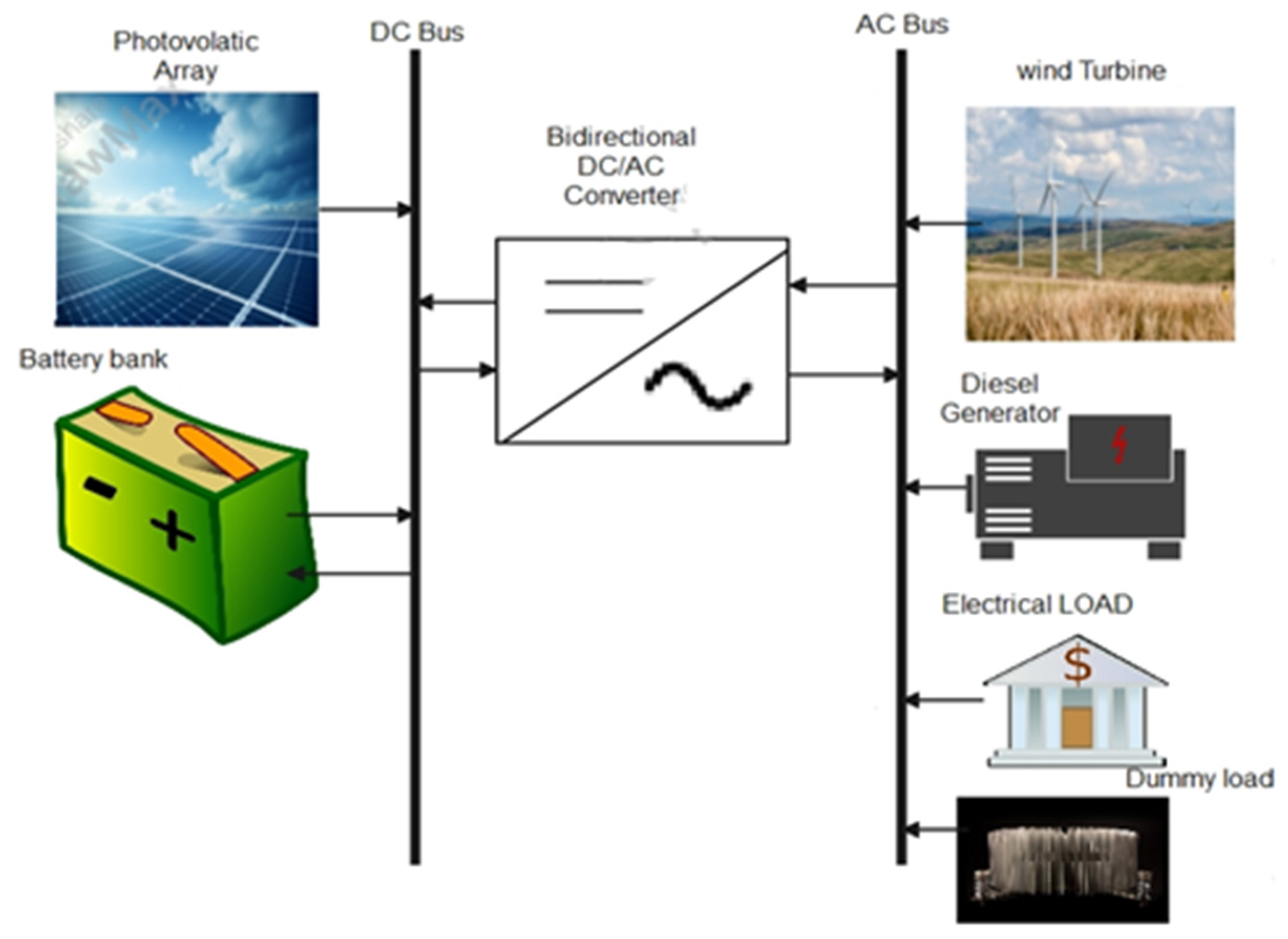
3. Configuration of the Hybrid Energy System
3.1. Photovoltaic System Mathematical Modelling
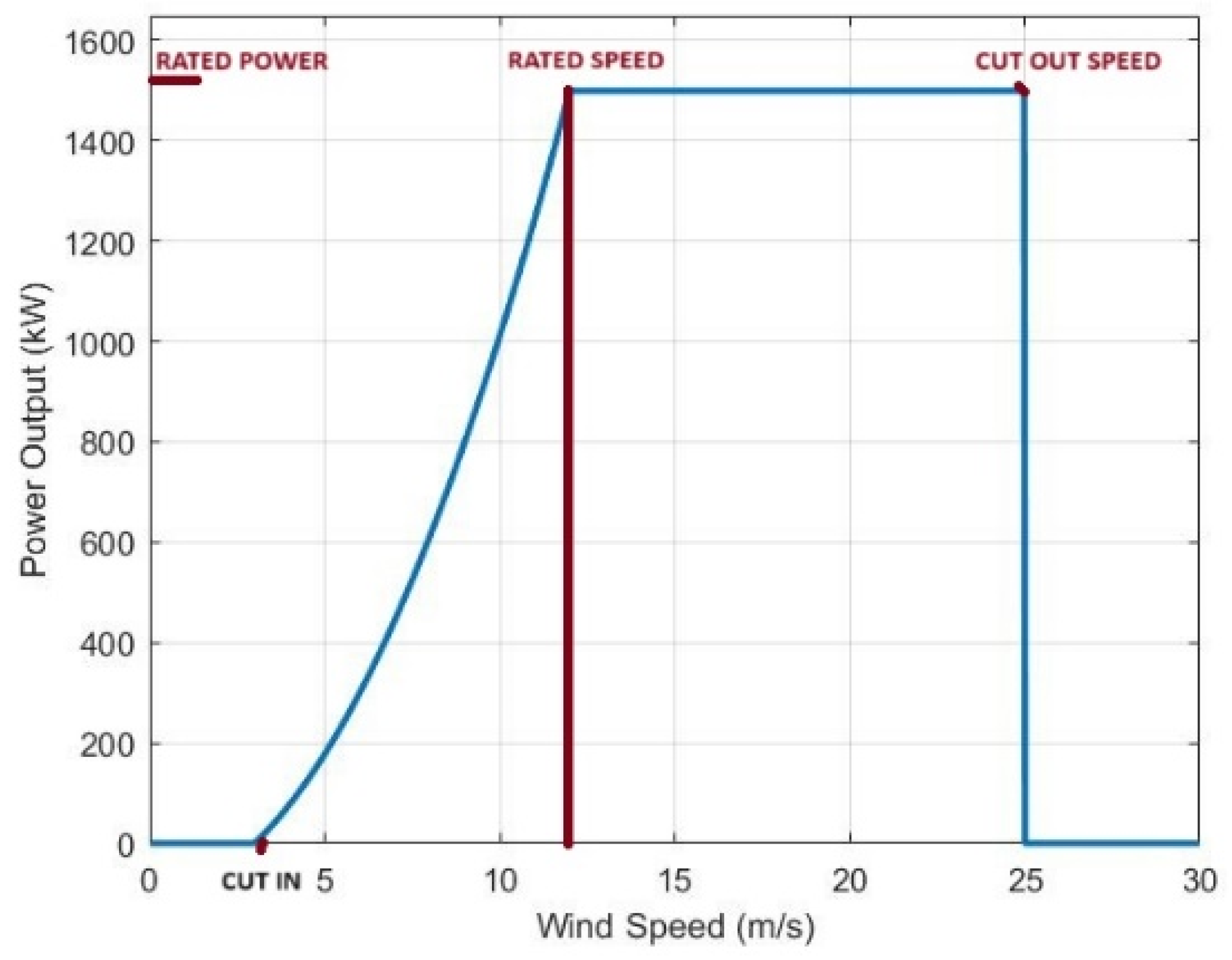
3.2. Wind Turbine Generator Mathematical Modelling
3.3. Diesel Generator Mathematical Modelling
3.4. Energy Storage System Modelling
4. Energy Management and Performance Evaluation in Hybrid Energy Systems
4.1. Power Management Strategies
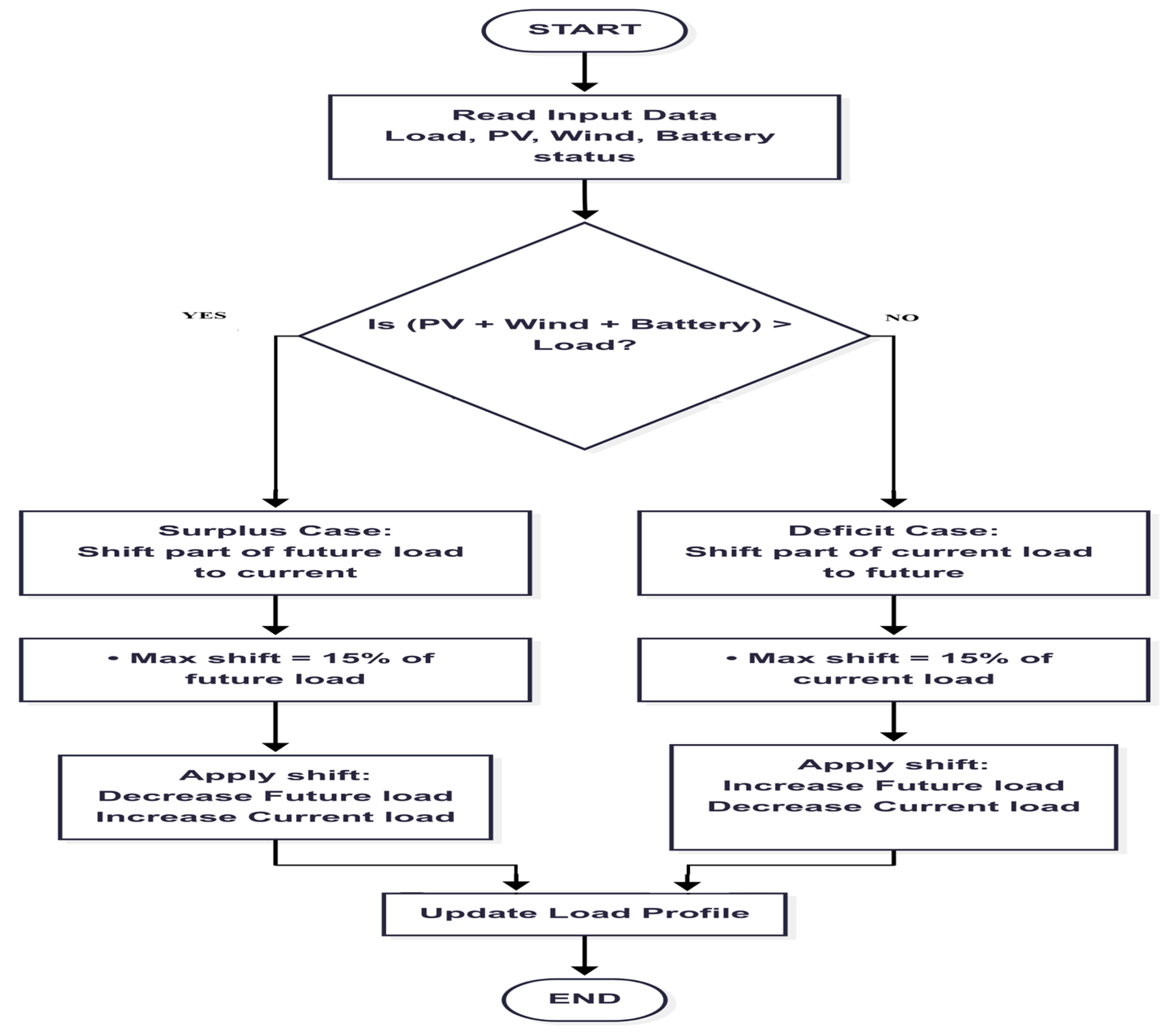
4.2. Demand Side Management
4.3. Loss of Power Supply Probability
4.4. Carbon Dioxide Saving
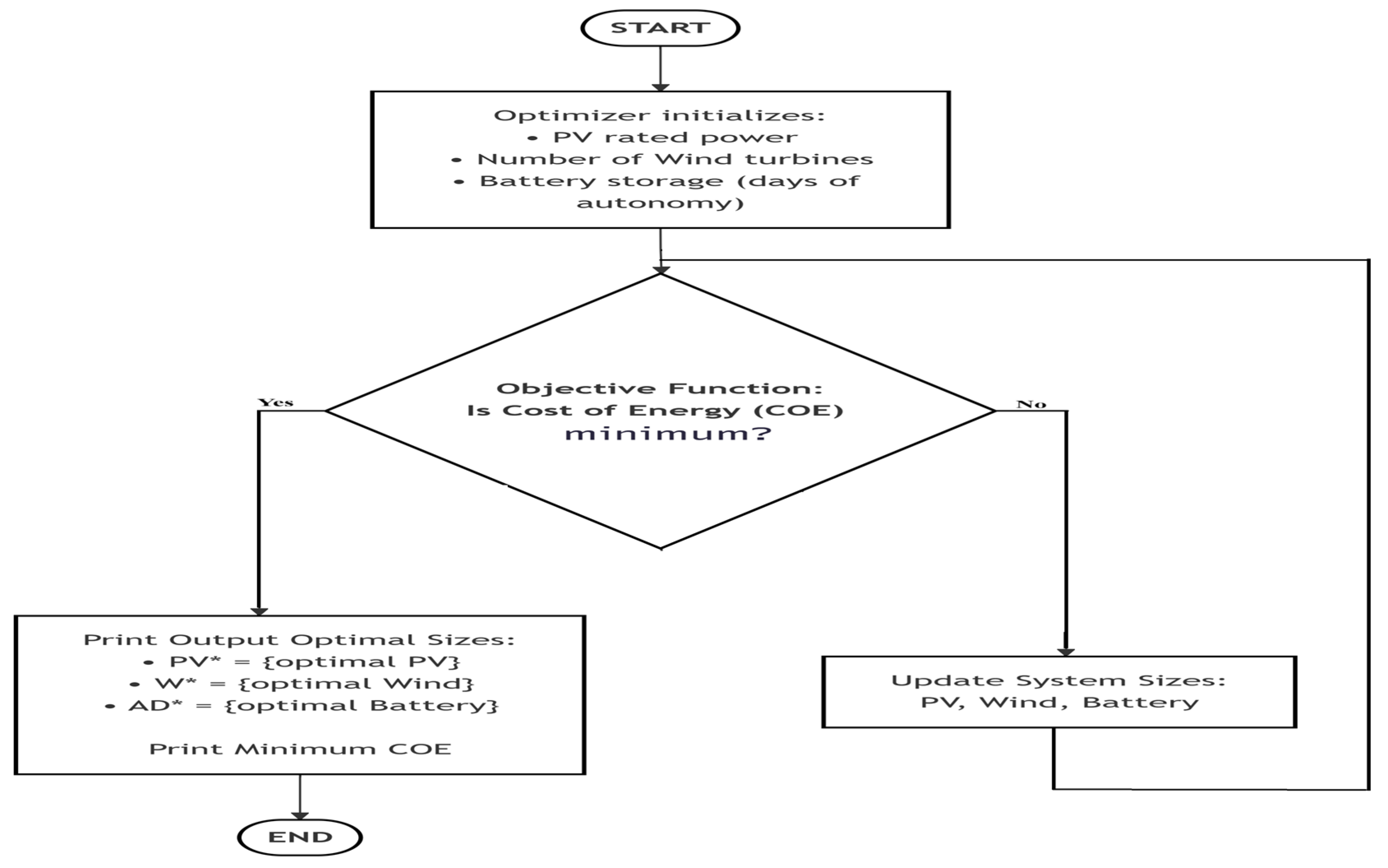
4.5. Problem Formulation
5. Exponential Distribution Optimizer
5.1. Initialization Phase
5.2. Exploitation Phase
5.3. Exploration Phase
6. Results
- Case 1: The electrical load is supplied solely by a diesel generator.
- Case 2: The load is met by renewable energy sources (RESs) without an energy storage system; the diesel generator serves as a backup when RES cannot meet the demand.
- Case 3: Identical to Case 2 but incorporates demand-side management (DSM) technology.
- Case 4: The load is primarily supplied by RES supported by an energy storage system, which is charged during periods of surplus renewable generation. The storage system has priority over the diesel generator when RES is insufficient.
- Case 5: Identical to Case 4, but with the addition of DSM technology.
6.1. Results of Optimization Techniques
6.1.1. Results of Optimization Techniques Used in Case 2
6.1.2. Robustness Analysis for Case 2
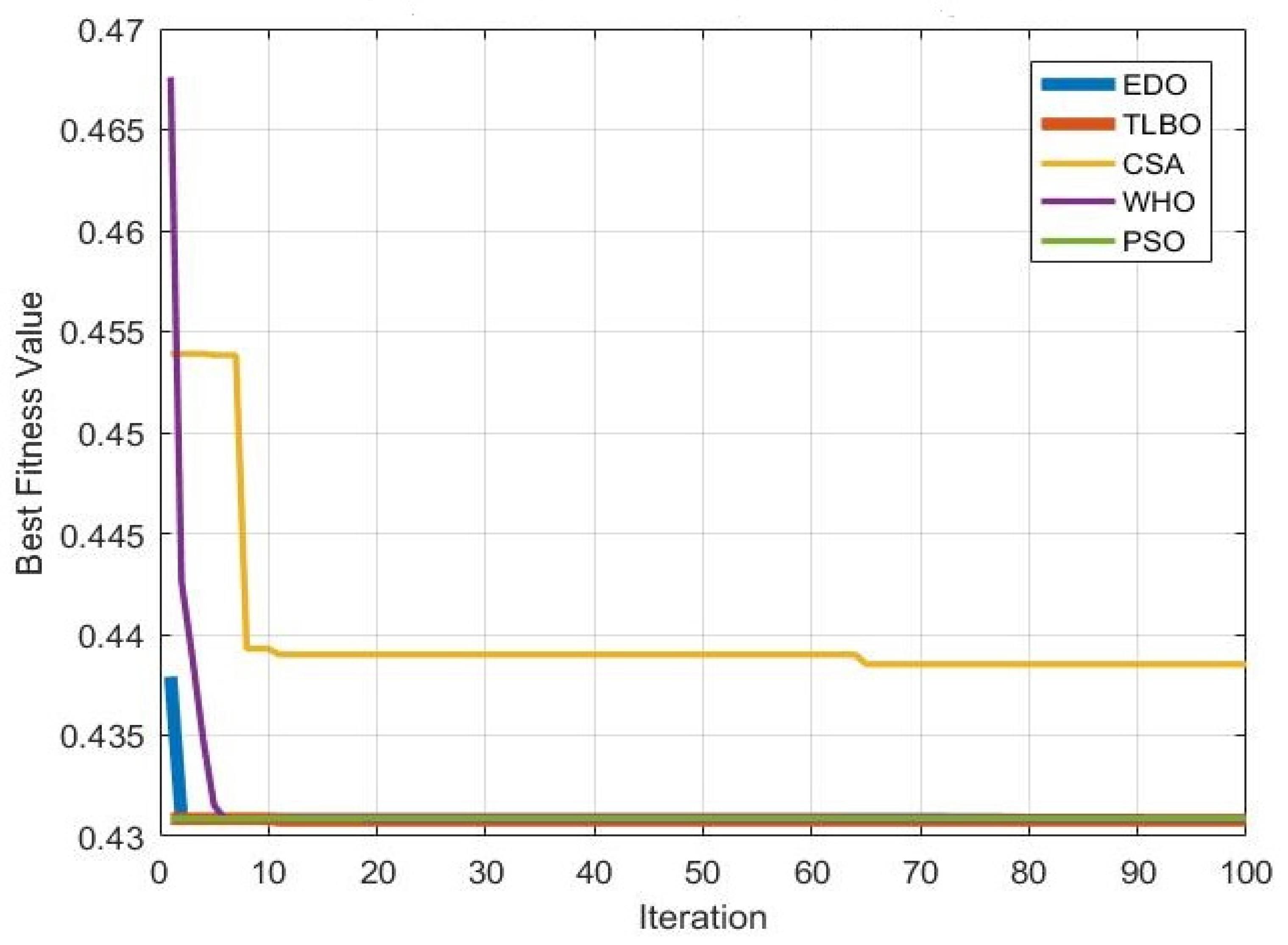
6.1.3. Results of Optimization Techniques Used in Case 4
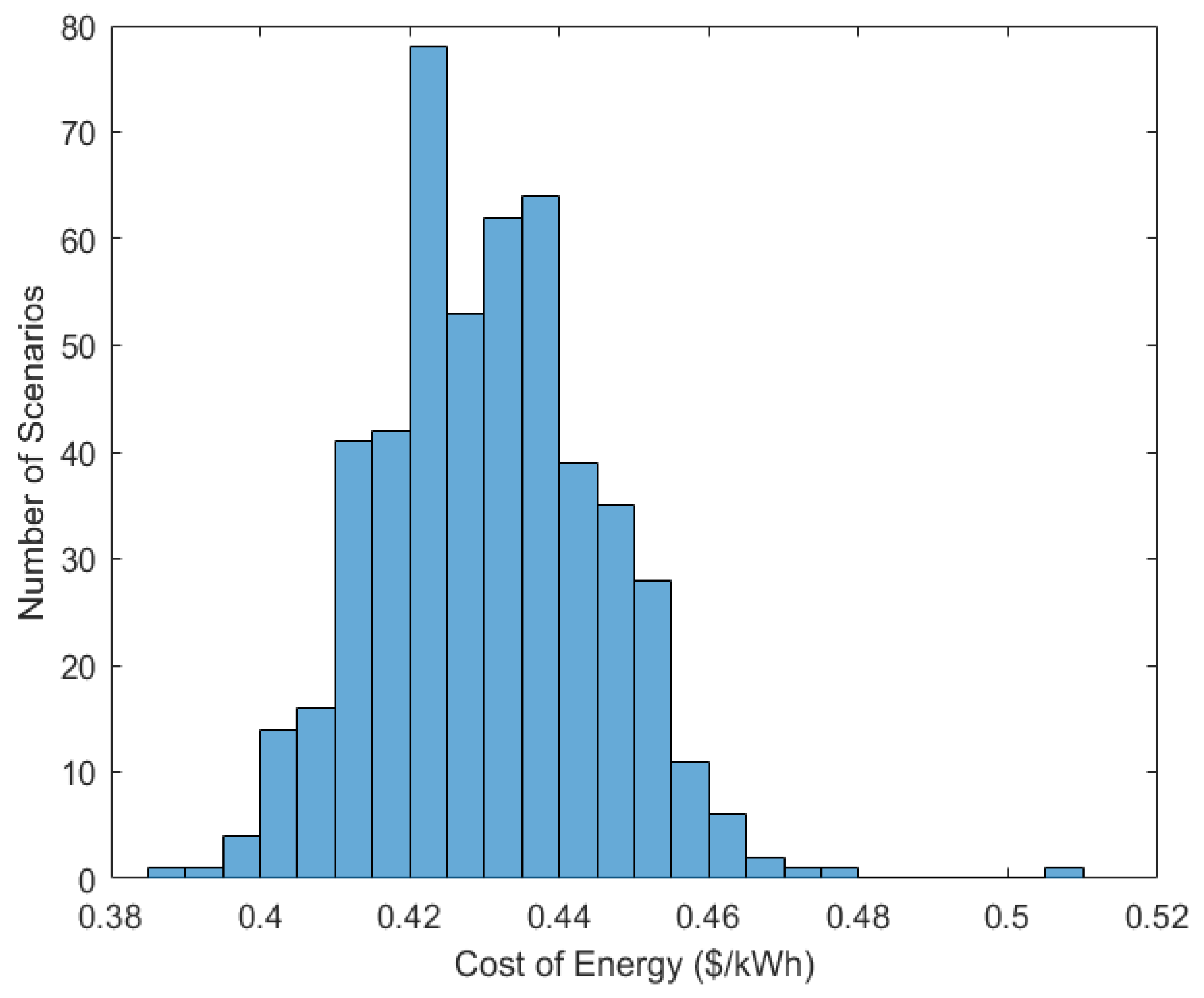
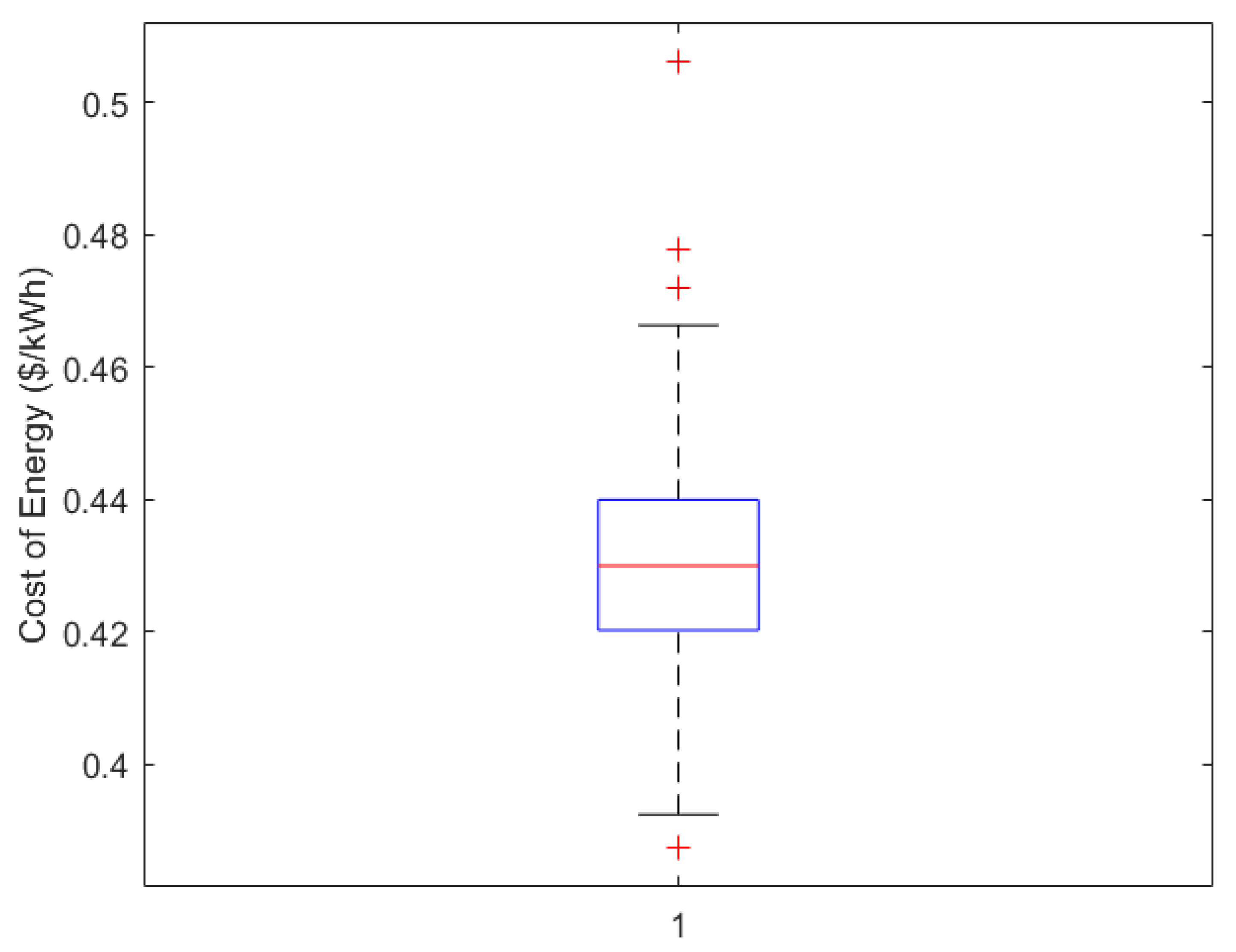
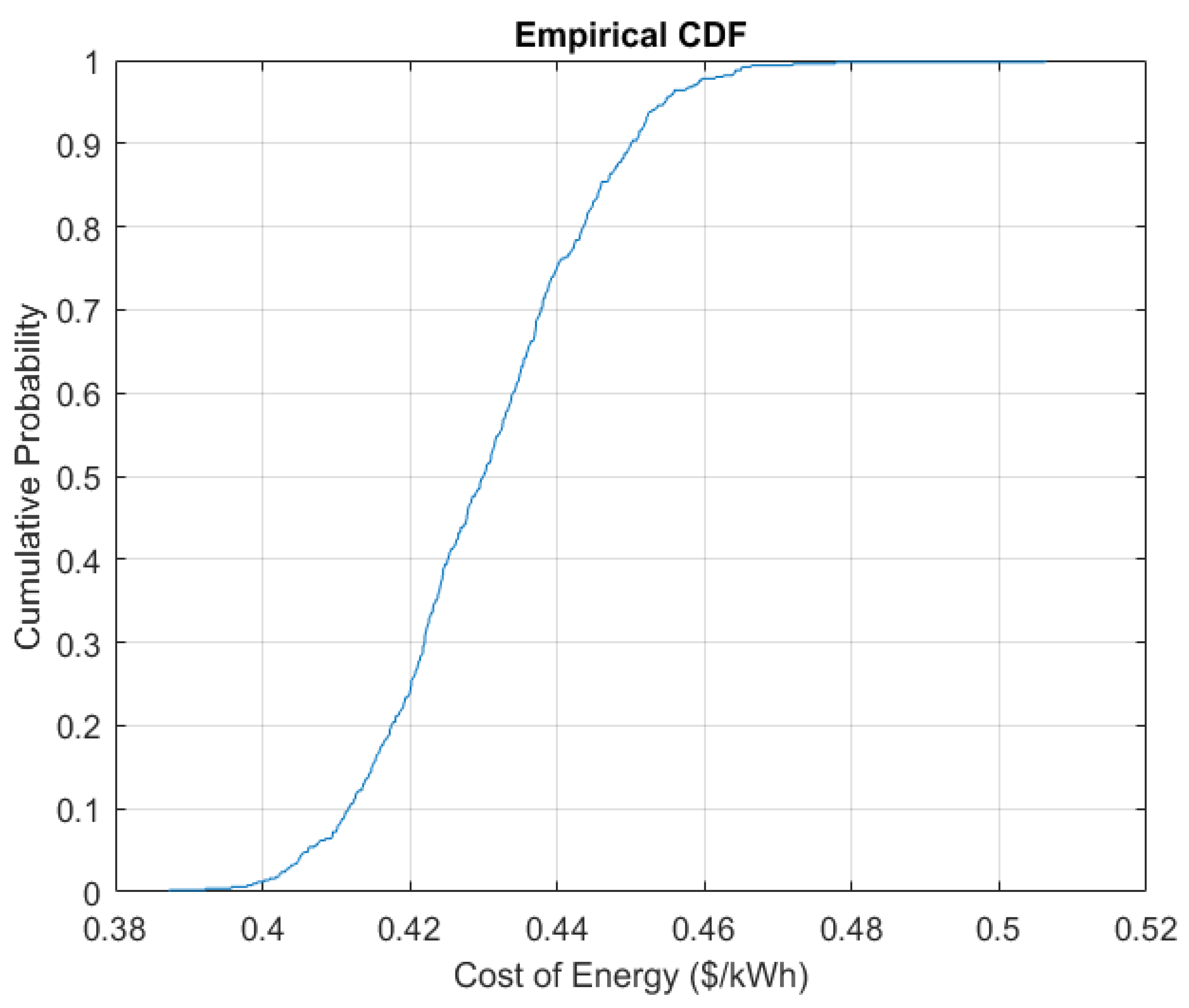
6.1.4. Robustness Analysis for Case 4
6.2. Results of Simulation of Optimal-Sized System
6.2.1. Case 1
6.2.2. Case 2
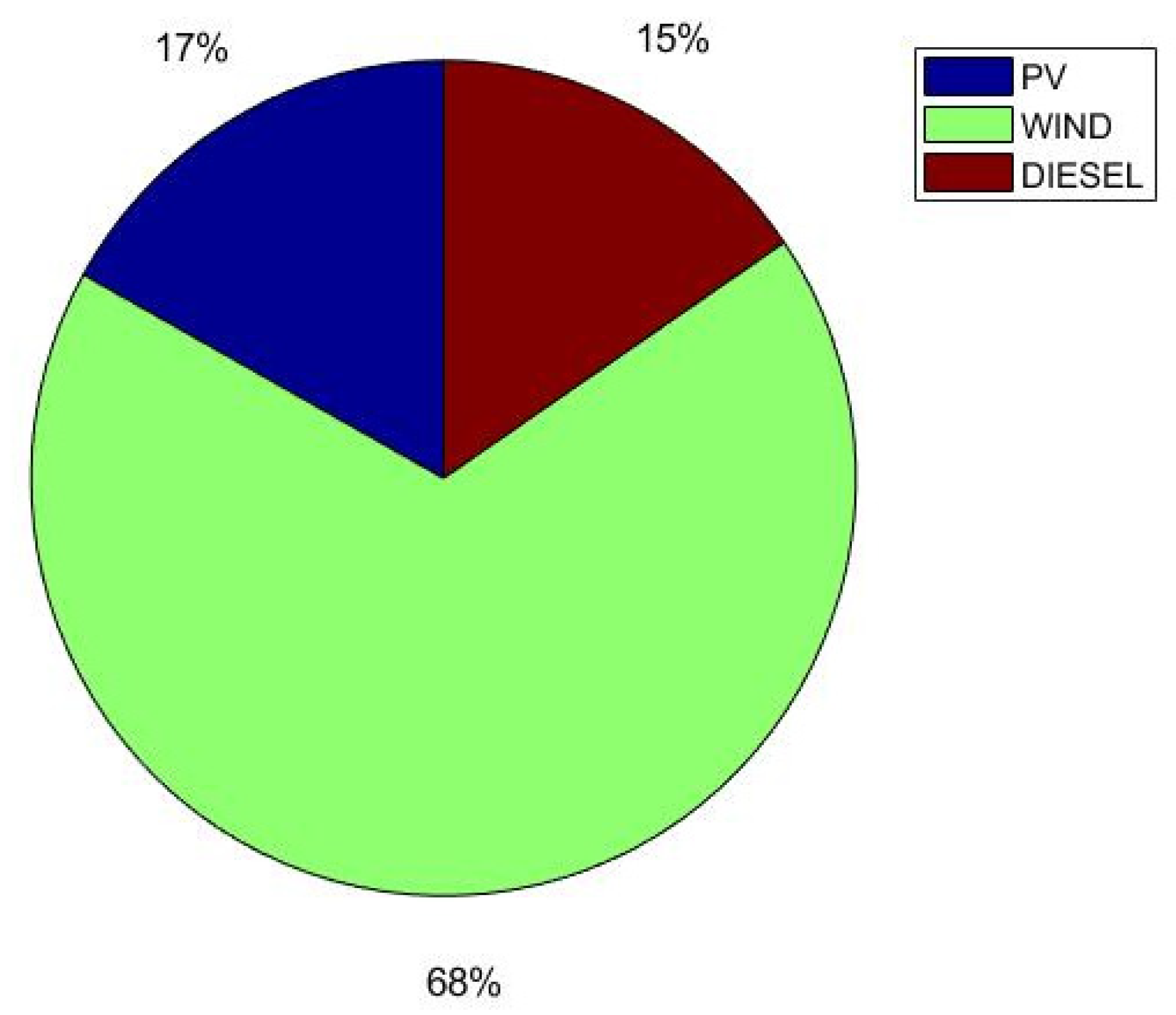
6.2.3. Case 3
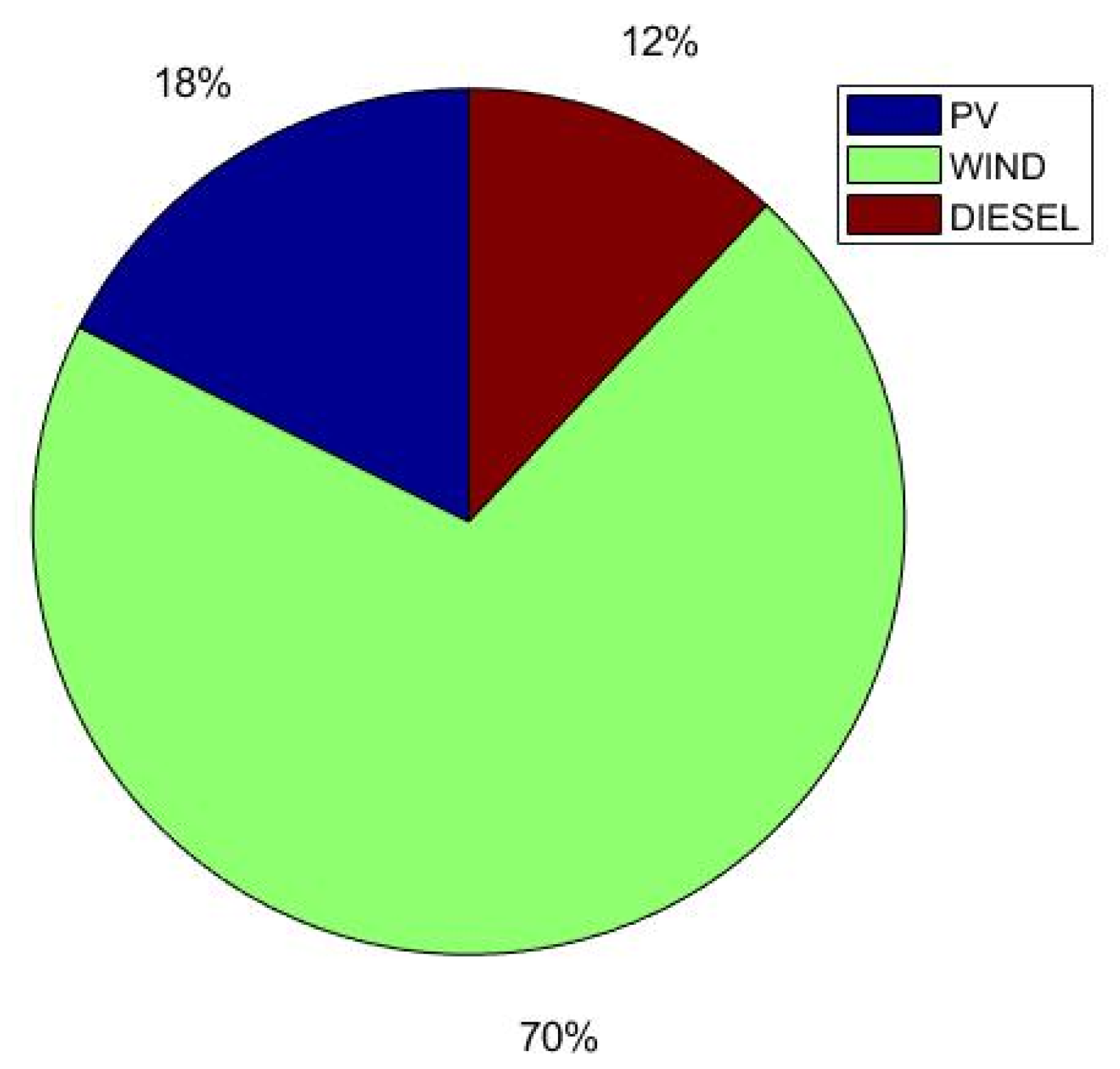
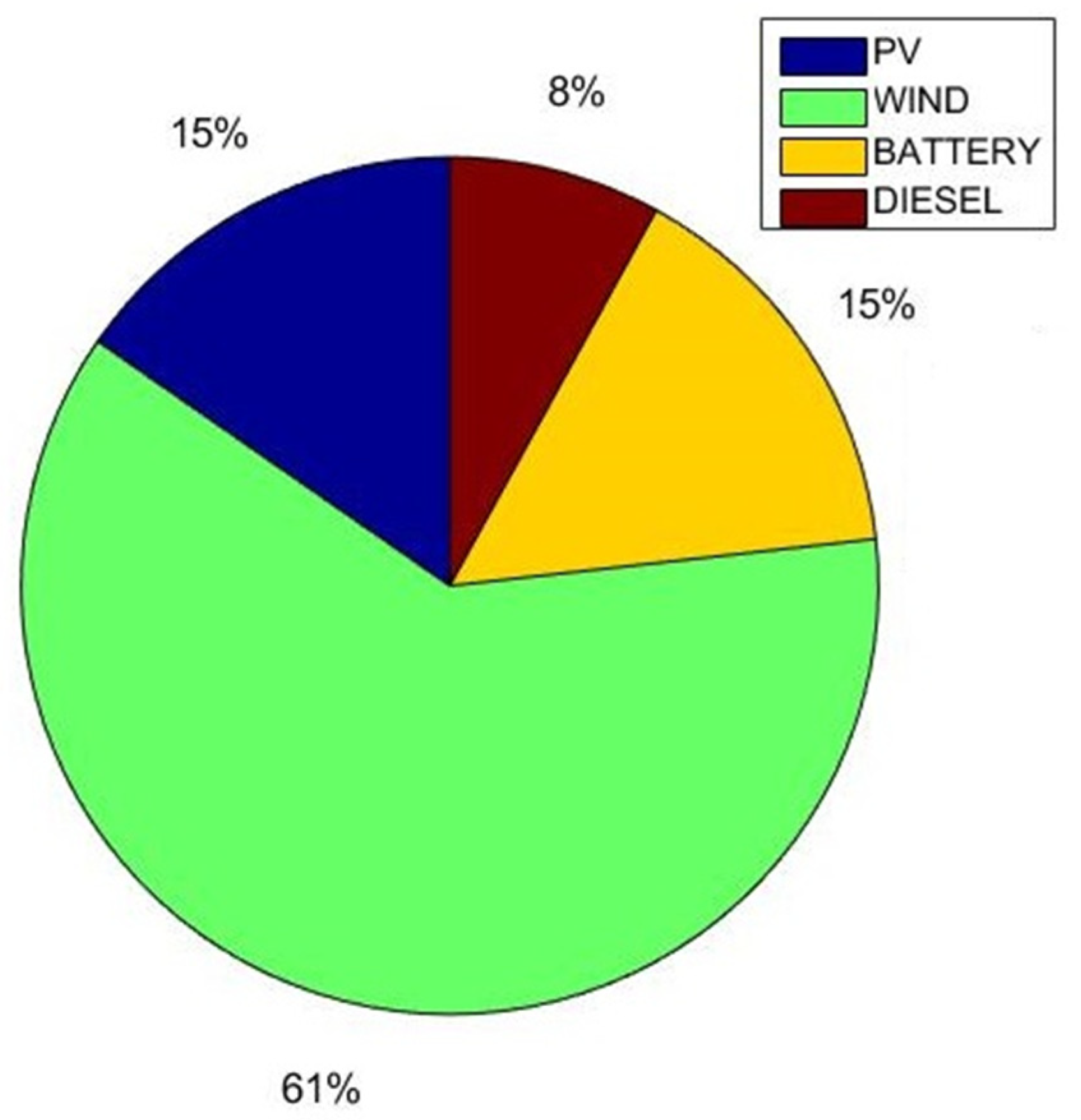
6.2.4. Case 4
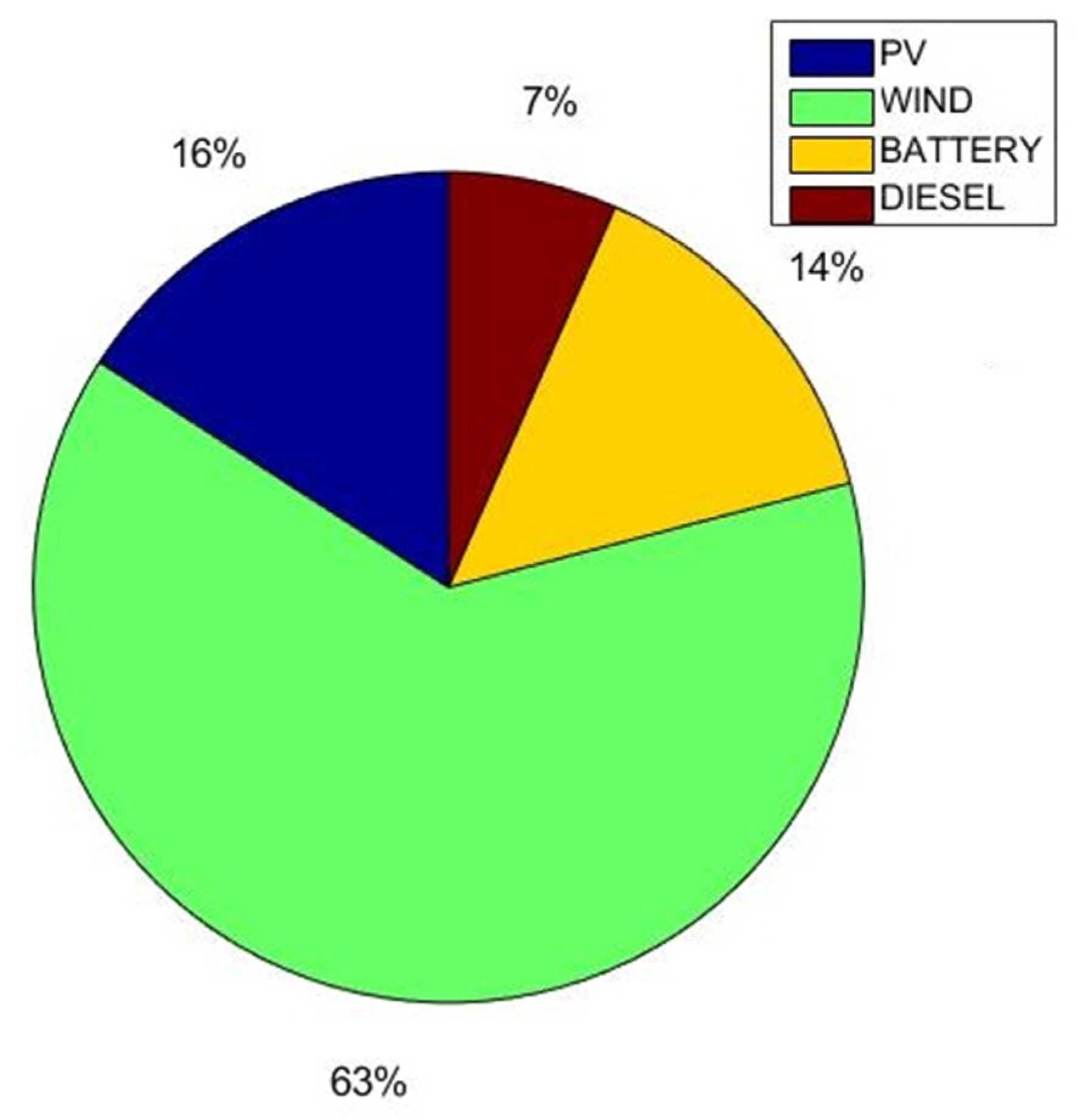
6.2.5. Case 5
6.3. Load Growth
Results of Load Growth
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, A.R.; Mahmood, A.; Safdar, A.; Khan, Z.A.; Bilal, S.; Javaid, N.A.K. Load forecasting and dynamic pricing based energy management in smart grid-a review. In Proceedings of the International Multi-topic Conference, Jamshoro, Pakistan, 11–13 February 2015. [Google Scholar]
- Clausen, L.T.; Rudolph, D. Renewable energy for sustainable rural development: Synergies and mismatches. Energy Policy 2020, 138, 111289. [Google Scholar] [CrossRef]
- Alturki, F.A.; Omotoso, H.O.; Al-Shamma’a, A.A.; Farh, H.M.; Alsharabi, K. Novel manta rays foraging optimization algorithm based optimal control for grid-connected PV energy system. IEEE Access 2020, 8, 187276–187290. [Google Scholar] [CrossRef]
- Ramesh, M.; Saini, R.P. Dispatch strategies based performance analysis of a hybrid renewable energy system for a remote rural area in India. J. Clean. Prod. 2020, 259, 120697. [Google Scholar] [CrossRef]
- Roy, A.; Kedare, S.B.; Bandyopadhyay, S. Application of design space methodology for optimum sizing of wind–battery systems. Appl. Energy 2009, 86, 2690–2703. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H. Power management of a stand-alone wind/photovoltaic/fuel cell energy system. IEEE Trans. Energy Convers. 2008, 23, 957–967. [Google Scholar] [CrossRef]
- Das, M.; Singh, M.A.K.; Biswas, A. Techno-economic optimization of an off-grid hybrid renewable energy system using metaheuristic optimization approaches–case of a radio transmitter station in India. Energy Convers. Manag. 2019, 185, 339–352. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R. Analytical strategies for renewable distributed generation integration considering energy loss minimization. Appl. Energy 2013, 105, 75–85. [Google Scholar] [CrossRef]
- Askarzadeh, A. Distribution generation by photovoltaic and diesel generator systems: Energy management and size optimization by a new approach for a stand-alone application. Energy 2017, 122, 542–551. [Google Scholar] [CrossRef]
- Ghorbani, N.; Kasaeian, A.; Toopshekan, A.; Bahrami, L.; Maghami, A. Optimizing a hybrid wind-PV-battery system using GA-PSO and MOPSO for reducing cost and increasing reliability. Energy 2018, 154, 581–591. [Google Scholar] [CrossRef]
- Tudu, B.; Roy, P.; Kumar, S.; Pal, D.; Mandal, K.K.; Chakraborty, N. Techno-economic feasibility analysis of hybrid renewable energy system using improved version of particle swarm optimization. In Proceedings of the Swarm, Evolutionary, and Memetic Computing: Third International Conference, SEMCCO 2012, Bhubaneswar, India, 20–22 December 2012; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 2012; pp. 116–123. [Google Scholar]
- Al Dawsari, S.; Anayi, F.; Packianather, M. Techno-economic analysis of hybrid renewable energy systems for cost reduction and reliability improvement using dwarf mongoose optimization algorithm. Energy 2024, 313, 133653. [Google Scholar] [CrossRef]
- Agajie, T.F.; Fopah-Lele, A.; Amoussou, I.; Ali, A.; Khan, B.; Mahela, O.P.; Nuvvula, R.S.S.; Ngwashi, D.K.; Soriano Flores, E.; Tanyi, E. Techno-Economic Analysis and Optimization of Hybrid Renewable Energy System with Energy Storage under Two Operational Modes. Sustainability 2023, 15, 11735. [Google Scholar] [CrossRef]
- Samatar, A.M.; Lekbir, A.; Mekhilef, S.; Mokhlis, H.; Tey, K.S.; Alassaf, A. Techno-economic and environmental analysis of a fully renewable hybrid energy system for sustainable power infrastructure advancement. Sci. Rep. 2025, 15, 12140. [Google Scholar] [CrossRef]
- Liao, N.; Hu, Z.; Mrzljak, V.; Nowdeh, S.A. Stochastic Techno-Economic Optimization of Hybrid Energy System with Photovoltaic, Wind, and Hydrokinetic Resources Integrated with Electric and Thermal Storage Using Improved Fire Hawk Optimization. Sustainability 2024, 16, 6723. [Google Scholar] [CrossRef]
- Amara, S.; Toumi, S.; Salah, C.B.; Saidi, A.S. Improvement of techno-economic optimal sizing of a hybrid off-grid micro-grid system. Energy 2021, 233, 121166. [Google Scholar] [CrossRef]
- Al-Sahlawi, A.A.K.; Ayob, S.M.; Tan, C.W.; Ridha, H.M.; Hachim, D.M. Optimal Design of Grid-Connected Hybrid Renewable Energy System Considering Electric Vehicle Station Using Improved Multi-Objective Optimization: Techno-Economic Perspectives. Sustainability 2024, 16, 2491. [Google Scholar] [CrossRef]
- Wang, R.; Xiong, J.; He, M.-F.; Gao, L.; Wang, L. Multi-objective optimal design of hybrid renewable energy system under multiple scenarios. Renew. Energy 2020, 151, 226–237. [Google Scholar] [CrossRef]
- Bacha, B.; Ghodbane, H.; Dahmani, H.; Betka, A.; Toumi, A.; Chouder, A. Optimal sizing of a hybrid microgrid system using solar, wind, diesel, and battery energy storage to alleviate energy poverty in a rural area of Biskra, Algeria. J. Energy Storage 2024, 84, 110651. [Google Scholar] [CrossRef]
- Jahannoush, M.; Nowdeh, S.A. Optimal designing and management of a stand-alone hybrid energy system using meta-heuristic improved sine–cosine algorithm for Recreational Center, case study for Iran country. Appl. Soft Comput. 2020, 96, 106611. [Google Scholar] [CrossRef]
- Ashraf, M.A.; Liu, Z.; Alizadeh, A.A.; Nojavan, S.; Jermsittiparsert, K.; Zhang, D. Designing an optimized configuration for a hybrid PV/Diesel/Battery Energy System based on metaheuristics: A case study on Gobi Desert. J. Clean. Prod. 2020, 270, 122467. [Google Scholar] [CrossRef]
- Makhdoomi, S.; Askarzadeh, A. Optimizing operation of a photovoltaic/diesel generator hybrid energy system with pumped hydro storage by a modified crow search algorithm. J. Energy Storage 2020, 27, 101040. [Google Scholar] [CrossRef]
- Pal, P.; Mukherjee, V. Off-grid solar photovoltaic/hydrogen fuel cell system for renewable energy generation: An investigation based on techno-economic feasibility assessment for the application of end-user load demand in North-East India. Renew. Sustain. Energy Rev. 2021, 149, 111421. [Google Scholar] [CrossRef]
- Liang, Z.; Chung, C.Y.; Zhang, W.; Wang, Q.; Lin, W.; Wang, C. Enabling High-Efficiency Economic Dispatch of Hybrid AC/DC Networked Microgrids: Steady-State Convex Bi-Directional Converter Models. IEEE Trans. Smart Grid 2025, 16, 45–61. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, G.; Zhao, D.; Tian, W. Optimal Scheduling of an Isolated Microgrid With Battery Storage Considering Load and Renewable Generation Uncertainties. IEEE Trans. Ind. Electron. 2019, 66, 1565–1575. [Google Scholar] [CrossRef]
- Cao, M.; Xu, Q.; Cai, J.; Yang, B. Optimal sizing strategy for energy storage system considering correlated forecast uncertainties of dispatchable resources. Int. J. Electr. Power Energy Syst. 2019, 108, 336–346. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand side management in smart grid using heuristic optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Kumar, S.; Kaur, T.; Upadhyay, S.; Sharma, V.; Vatsal, D. Optimal sizing of stand alone hybrid renewable energy system with load shifting, Energy Sources, Part A: Recovery. Util. Environ. Eff. 2025, 47, 1490–1509. [Google Scholar]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Exponential distribution optimizer (EDO): A novel math-inspired algorithm for global optimization and engineering problems. Artif. Intell. Rev. 2023, 56, 9329–9400. [Google Scholar] [CrossRef]
- Črepinšek, M.; Liu, S.-H.; Mernik, L. A note on teaching–learning-based optimization algorithm. Inf. Sci. 2012, 212, 79–93. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Turky, R.A.; Alghuwainem, S.; Tostado-Véliz, M.; Jurado, F. Circle search algorithm: A geometry-based metaheuristic optimization algorithm. Mathematics 2022, 10, 1626. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2022, 38 (Suppl. S4), 3025–3056. [Google Scholar] [CrossRef]
- Borhanazad, H.; Mekhilef, S.; Ganapathy, V.G.; Modiri-Delshad, M.; Mirtaheri, A. Optimization of micro-grid system using MOPSO. Renew. Energy 2014, 71, 295–306. [Google Scholar] [CrossRef]
- Omotoso, H.O.; Al-Shaalan, A.M.; Farh, H.M.H.; Al-Shamma’a, A.A. Techno-Economic Evaluation of Hybrid Energy Systems Using Artificial Ecosystem-Based Optimization with Demand Side Management. Electronics 2022, 11, 204. [Google Scholar] [CrossRef]
- Alturki, F.A.; Farh, H.M.H.; Al-Shamma’a, A.A.; AlSharabi, K. Techno-Economic Optimization of Small-Scale Hybrid Energy Systems Using Manta Ray Foraging Optimizer. Electronics 2020, 9, 2045. [Google Scholar] [CrossRef]
- Tiwari, A.N.; Dubey, N. A Methodology of Optimal Sizing for Wind Solar Hybrid System. Asian Rev. Mech. Eng. 2015, 4, 11–16. [Google Scholar] [CrossRef]
- Tiwari, V.; Dubey, H.M.; Pandit, M. Optimal Sizing and Allocation of DG in Distribution System Using TLBO. In Artificial Intelligence and Sustainable Computing; Dubey, H.M., Pandit, M., Srivastava, L., Panigrahi, B.K., Eds.; Springer: Singapore, 2022; pp. 409–421. [Google Scholar]
- Milovanović, M.; Klimenta, D.; Panić, M.; Klimenta, J.; Perović, B. An application of Wild Horse Optimizer to multi-objective energy management in a micro-grid. Electr. Eng. 2022, 104, 4521–4541. [Google Scholar] [CrossRef]
- Shaheen, M.A.M.; Ullah, Z.; Qais, M.H.; Hasanien, H.M.; Chua, K.J.; Tostado-Véliz, M.; Turky, R.A.; Jurado, F.; Elkadeem, M.R. Solution of Probabilistic Optimal Power Flow Incorporating Renewable Energy Uncertainty Using a Novel Circle Search Algorithm. Energies 2022, 15, 8303. [Google Scholar] [CrossRef]
- Ahsan, M.B.F.; Mekhilef, S.; Soon, T.K.; Usama, M.; Mubin, M.B.; Seyedmahmoudian, M.; Stojcevski, A.; Mokhlis, H.; Shrivastava, P.; Alshammari, O. Optimal sizing and cost analysis of hybrid energy storage system for EVs using metaheuristic PSO and firefly algorithms. Results Eng. 2024, 23, 102358. [Google Scholar] [CrossRef]
- Ali, Z.M.; Diaaeldin, I.M.; El-Rafei, A.; Hasanien, H.M.; Aleem, S.H.E.A.; Abdelaziz, A.Y. A novel distributed generation planning algorithm via graphically-based network reconfiguration and soft open points placement using Archimedes optimization algorithm. Ain Shams Eng. J. 2021, 12, 1923–1941. [Google Scholar] [CrossRef]
| Average | Maximum | |
|---|---|---|
| Wind speed (m/s) | 7.52 | 32 |
| Solar irradiance () | 0.2286 | 1.12 |
| Parameter | Value | Unit |
|---|---|---|
| Wind turbine generator | ||
| cut-in speed | 3 | m/s |
| cut-out speed | 25 | m/s |
| rated speed | 8 | m/s |
| rated Power | 2 | kW |
| efficiency | 95 | % |
| initial cost | 2000 | USD/kW |
| lifetime | 24 | year |
| Photovoltaic Module | ||
| initial cost | 3400 | USD/kW |
| lifetime | 24 | year |
| Inverter | ||
| efficiency | 90 | % |
| lifetime | 24 | year |
| initial cost | 2500 | USD/kW |
| Battery | ||
| efficiency | 85 | % |
| lifetime | 12 | year |
| initial cost | 280 | USD/kW |
| depth of discharge | 80 | % |
| state of charge | 20 | % |
| Diesel generator | ||
| lifetime | 24,000 | hours |
| initial cost | 1000 | USD/kW |
| fuel cost | 0.8 | USD/L |
| Economic parameters | ||
| operating, maintenance, and running cost | 20 | % |
| real interest rate | 13 | % |
| project lifetime | 24 | year |
| Optimization Technique | Optimal (COE) | Average Time | Standard Deviation |
|---|---|---|---|
| TLBO | USD 0.6211/kWh | 1604.84 s | × |
| CSA | USD 0.6288/kWh | 905.18 s | × |
| EDO | USD 0.6211/kWh | 829.83 s | × |
| WHO | USD 0.6211/kWh | 680.49 s | × |
| PSO | USD 0.6211/kWh | 818.39 s | × |
| Metric | Value |
|---|---|
| Mean COE (USD/kWh) | 0.6236 |
| Standard Deviation | ±0.0260 |
| Relative Standard Deviation (%) | 4.16% |
| Minimum COE (USD/kWh) | 0.5275 |
| Maximum COE (USD/kWh) | 0.7044 |
| Optimization Technique | Optimal (COE) | Average Time | Standard Deviation |
|---|---|---|---|
| TLBO | USD 0.43084 kWh | 1843.28 s | × |
| CSA | USD 0.44469 kWh | 903.71 s | × |
| EDO | USD 0.43092 kWh | 898.97 s | × |
| WHO | USD 0.43088/kWh | 757.33 s | × |
| PSO | USD 0.43089/kWh | 962.83 s | × |
| Metric | Value |
|---|---|
| Mean COE (USD/kWh) | 0.4304 |
| Standard Deviation | ±0.0151 |
| Relative Standard Deviation (%) | 3.51% |
| Minimum COE (USD/kWh) | 0.3873 |
| Maximum COE (USD/kWh) | 0.5063 |
| Category | Metric | Value |
|---|---|---|
| economic | net present cost (million USD) | |
| initial capital cost (million USD) | ||
| cost of energy (24 years) (USD/kWh) | ||
| total fuel consumed cost (USD/yr) | × | |
| electrical | total electricity from diesel generator (kWh/yr) | × |
| total fuel consumed (L/yr) | × | |
| emission | Carbon dioxide (kg/yr) |
| Category | Metric | Value |
|---|---|---|
| economic | net present cost (million USD) | |
| initial capital cost (million USD) | ||
| cost of energy (24 years) (USD/kWh) | 0.6211 | |
| total fuel consumed cost (USD/yr) | × | |
| electrical | total electricity production by diesel generator (kWh/yr) | × |
| total fuel consumed (L/yr) | × | |
| emission | Carbon dioxide (kg/yr) | 31,692 |
| Category | Metric | Value |
|---|---|---|
| economic | net present cost (million USD) | 0.36 |
| initial capital cost (million USD) | 0.142 | |
| cost of energy (24 years) (USD/kWh) | 0.5214 | |
| total fuel consumed cost (USD/yr) | × | |
| electrical | total electricity production by diesel generator (kWh/yr) | × |
| total fuel consumed (L/yr) | × | |
| emission | Carbon dioxide (kg/yr) | 25,882 |
| Category | Metric | Value |
|---|---|---|
| economic | net present cost (million USD) | 0.297 |
| initial capital cost (million USD) | 0.148 | |
| cost of energy (24 years) (USD/kWh) | 0.4309 | |
| total fuel consumed cost (USD/yr) | × | |
| electrical | total electricity production by diesel generator (kWh/yr) | × |
| total fuel consumed(L/yr) | × | |
| emission | Carbon dioxide (kg/yr) | 16,374 |
| Category | Metric | Value |
|---|---|---|
| economic | net present cost (million USD) | 0.28 |
| initial capital cost (million USD) | 0.148 | |
| cost of energy (24 years) (USD/kWh) | 0.4069 | |
| total fuel consumed cost (USD/yr) | × | |
| electrical | total electricity production by diesel generator (kWh/yr) | × |
| total fuel consumed(L/yr) | × | |
| emission | Carbon dioxide (kg/yr) | 14,130 |
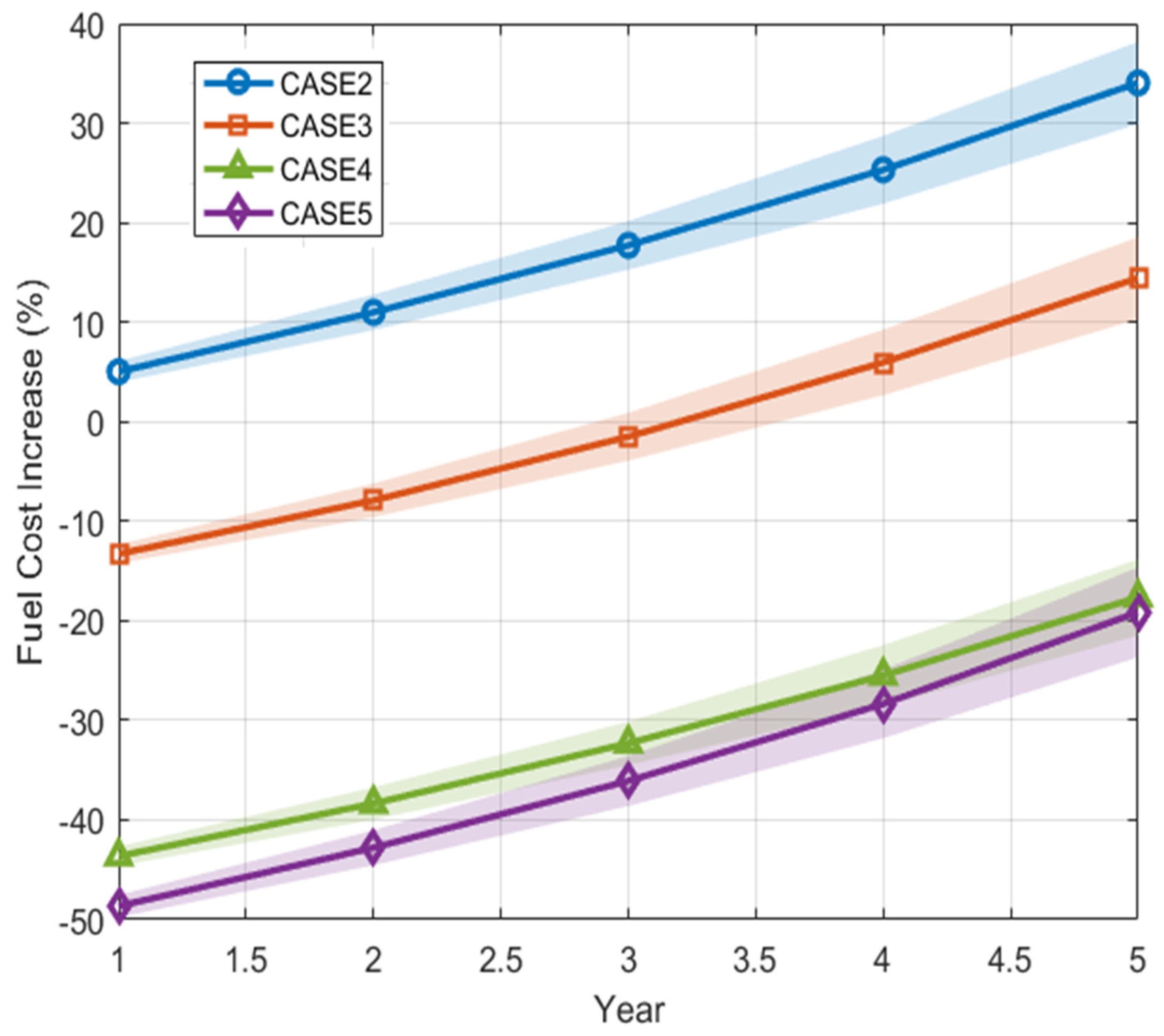
| Case | Case 2 | Case 3 | |||||
|---|---|---|---|---|---|---|---|
| Year | Mean Fuel Cost Increase (%) | ±Std | LPSP | Mean Fuel Cost Increase (%) | ±Std | LPSP | |
| 1 | 5.03 | 1.0733 | 0 | −13.29 | 0.9508 | 0 | |
| 2 | 10.99 | 1.7876 | 0 | −7.91 | 1.6862 | 0 | |
| 3 | 17.72 | 2.4488 | 0 | −1.51 | 2.4063 | 0 | |
| 4 | 25.31 | 3.4068 | 3.43 × | 5.95 | 3.2906 | 3.42 × | |
| 5 | 34.05 | 4.1465 | 1.69 × | 14.43 | 4.1349 | 1.29 × | |
| Case | Case 4 | Case 5 | |||||
|---|---|---|---|---|---|---|---|
| Year | Mean Fuel Cost Increase (%) | ±Std | LPSP | Mean Fuel Cost Increase (%) | ±Std | LPSP | |
| 1 | −43.64 | 0.9704 | 0 | −48.65 | 1.1229 | 0 | |
| 2 | −38.35 | 1.6311 | 0 | −42.79 | 1.7625 | 0 | |
| 3 | −32.31 | 2.1848 | 0 | −36.09 | 2.5247 | 0 | |
| 4 | −25.51 | 3.0550 | 3.43 × | −28.36 | 3.4400 | 3.42 × | |
| 5 | −17.66 | 3.8259 | 1.69 × | −19.16 | 4.5249 | 1.69 × | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaker, M.A.; Diaaeldin, I.M.; Attia, M.A.; Khamees, A.K.; Omar, O.A.M.; Alruwaili, M.; Elrashidi, A.; Hamed, N.M. A Comprehensive Optimization Framework for Techno-Economic Demand Side Management in Integrated Energy Systems. Energies 2025, 18, 4280. https://doi.org/10.3390/en18164280
Shaker MA, Diaaeldin IM, Attia MA, Khamees AK, Omar OAM, Alruwaili M, Elrashidi A, Hamed NM. A Comprehensive Optimization Framework for Techno-Economic Demand Side Management in Integrated Energy Systems. Energies. 2025; 18(16):4280. https://doi.org/10.3390/en18164280
Chicago/Turabian StyleShaker, Moataz Ayman, Ibrahim Mohamed Diaaeldin, Mahmoud A. Attia, Amr Khaled Khamees, Othman A. M. Omar, Mohammed Alruwaili, Ali Elrashidi, and Nabil M. Hamed. 2025. "A Comprehensive Optimization Framework for Techno-Economic Demand Side Management in Integrated Energy Systems" Energies 18, no. 16: 4280. https://doi.org/10.3390/en18164280
APA StyleShaker, M. A., Diaaeldin, I. M., Attia, M. A., Khamees, A. K., Omar, O. A. M., Alruwaili, M., Elrashidi, A., & Hamed, N. M. (2025). A Comprehensive Optimization Framework for Techno-Economic Demand Side Management in Integrated Energy Systems. Energies, 18(16), 4280. https://doi.org/10.3390/en18164280










