A Drag-Reduction Mechanism of Seagull-Inspired Curved Vortex Generators Integrating Response Surface Method and Genetic Algorithms Optimization in Compact Heat Exchangers
Abstract
1. Introduction
2. Description of the Model
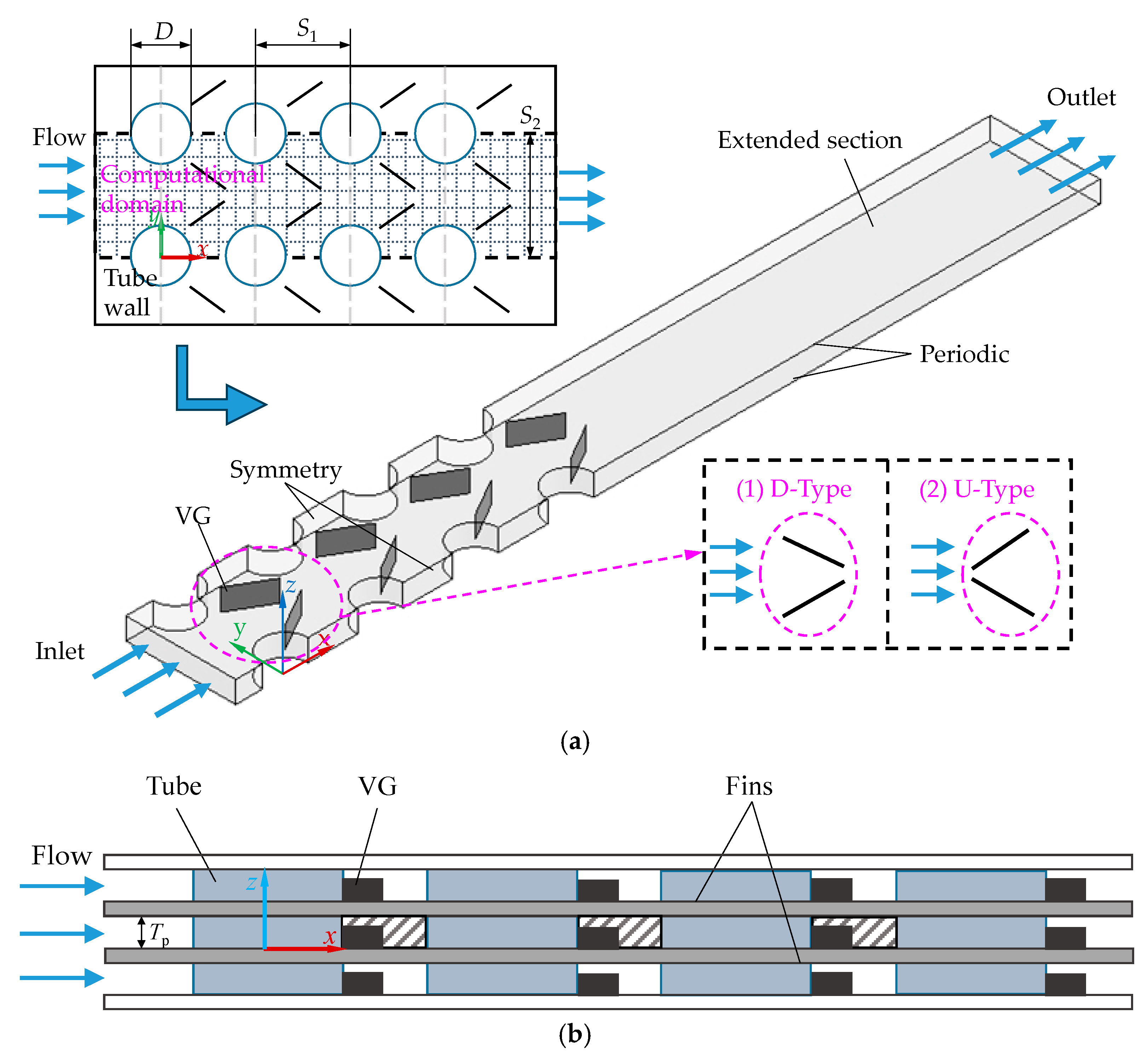
2.1. Physical Model
2.2. Governing Equations and Boundary Conditions
2.3. Parameter Definitions
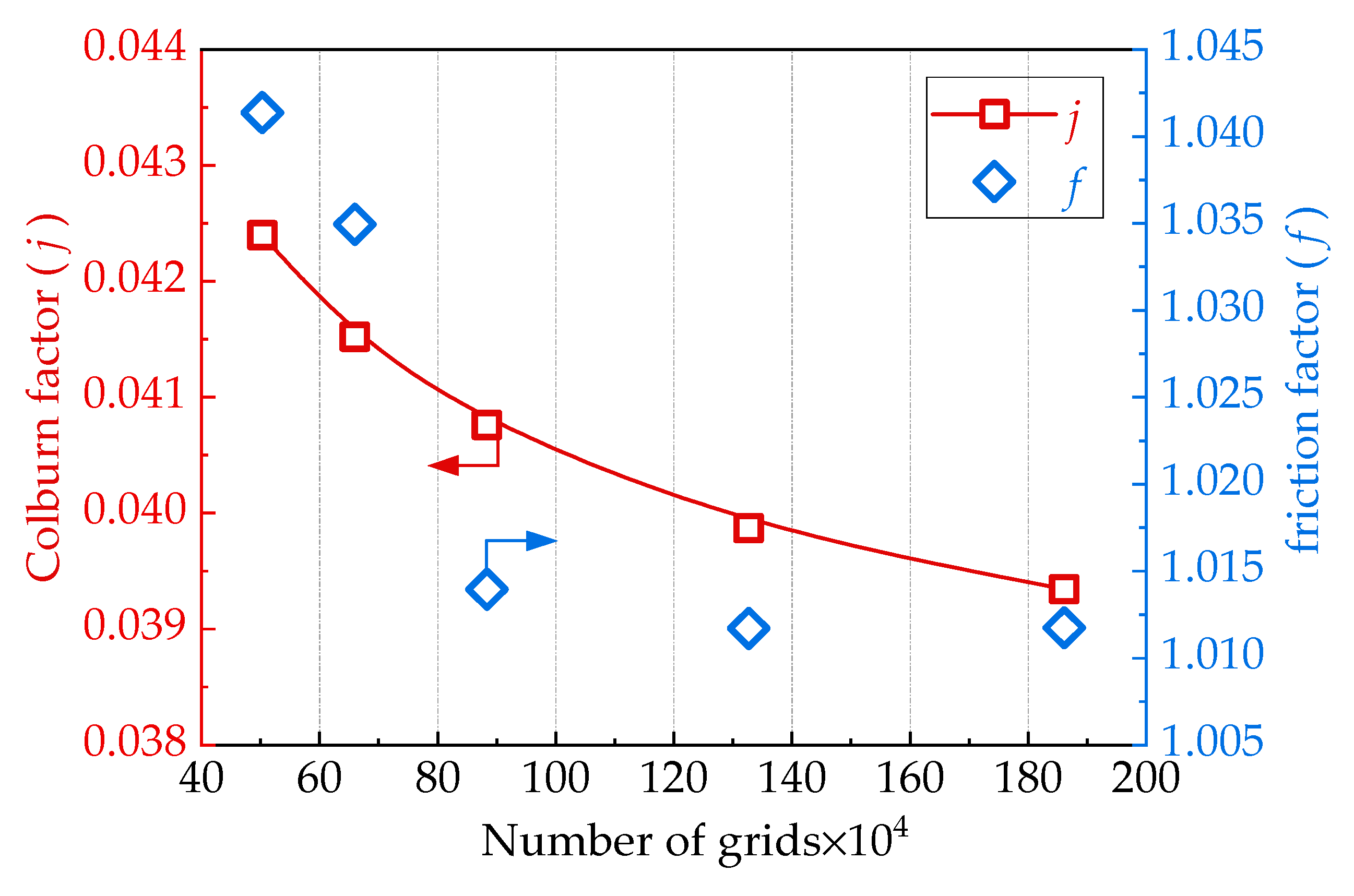
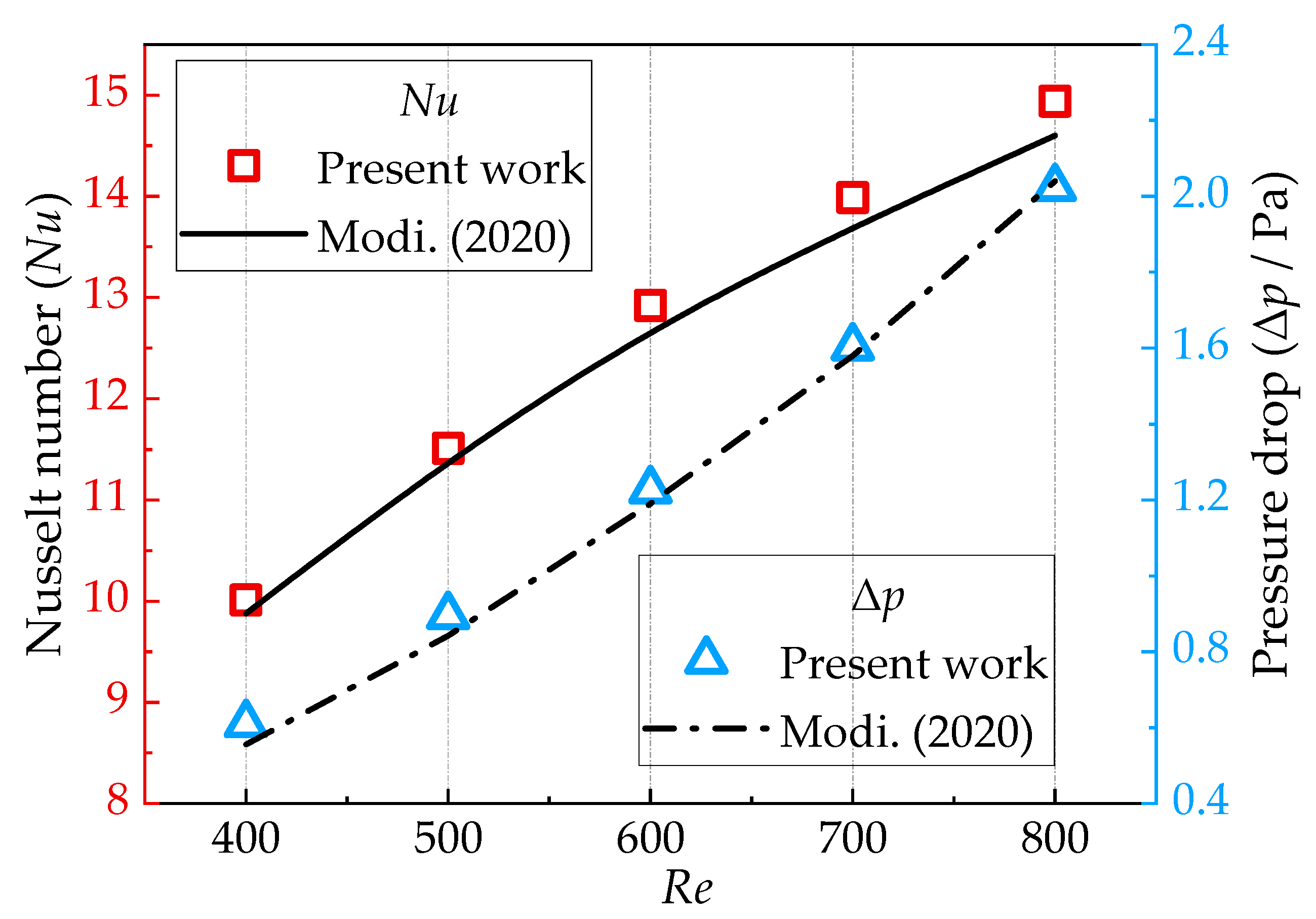
2.4. Grid Independence Test and Validation of Numerical Results
3. Methodology
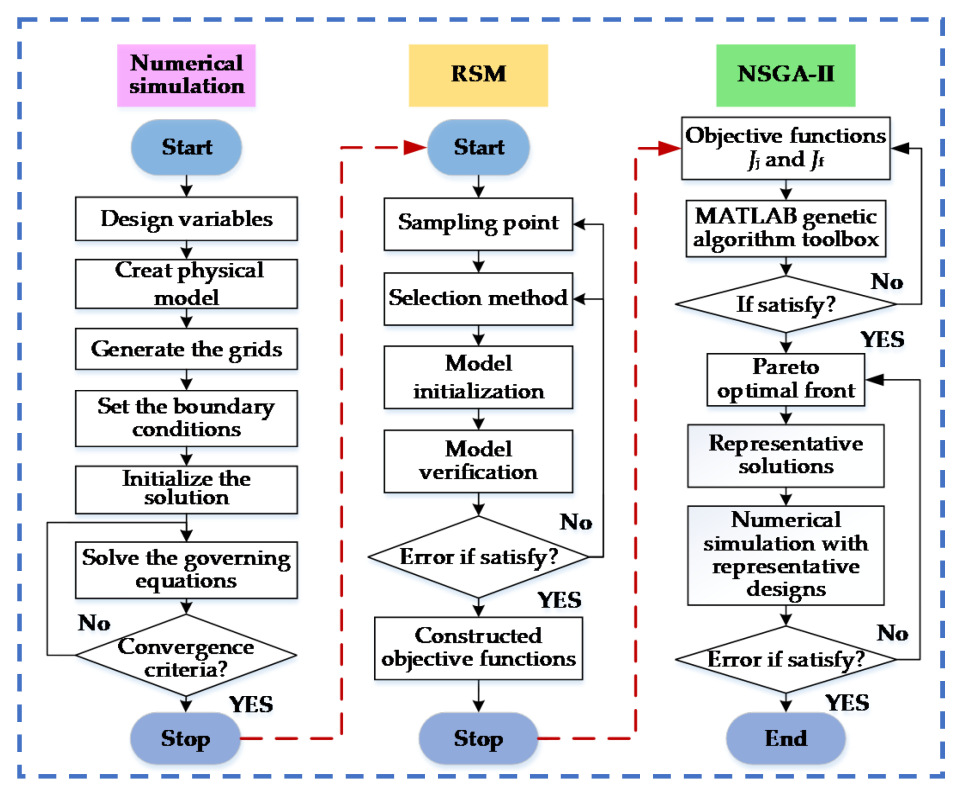
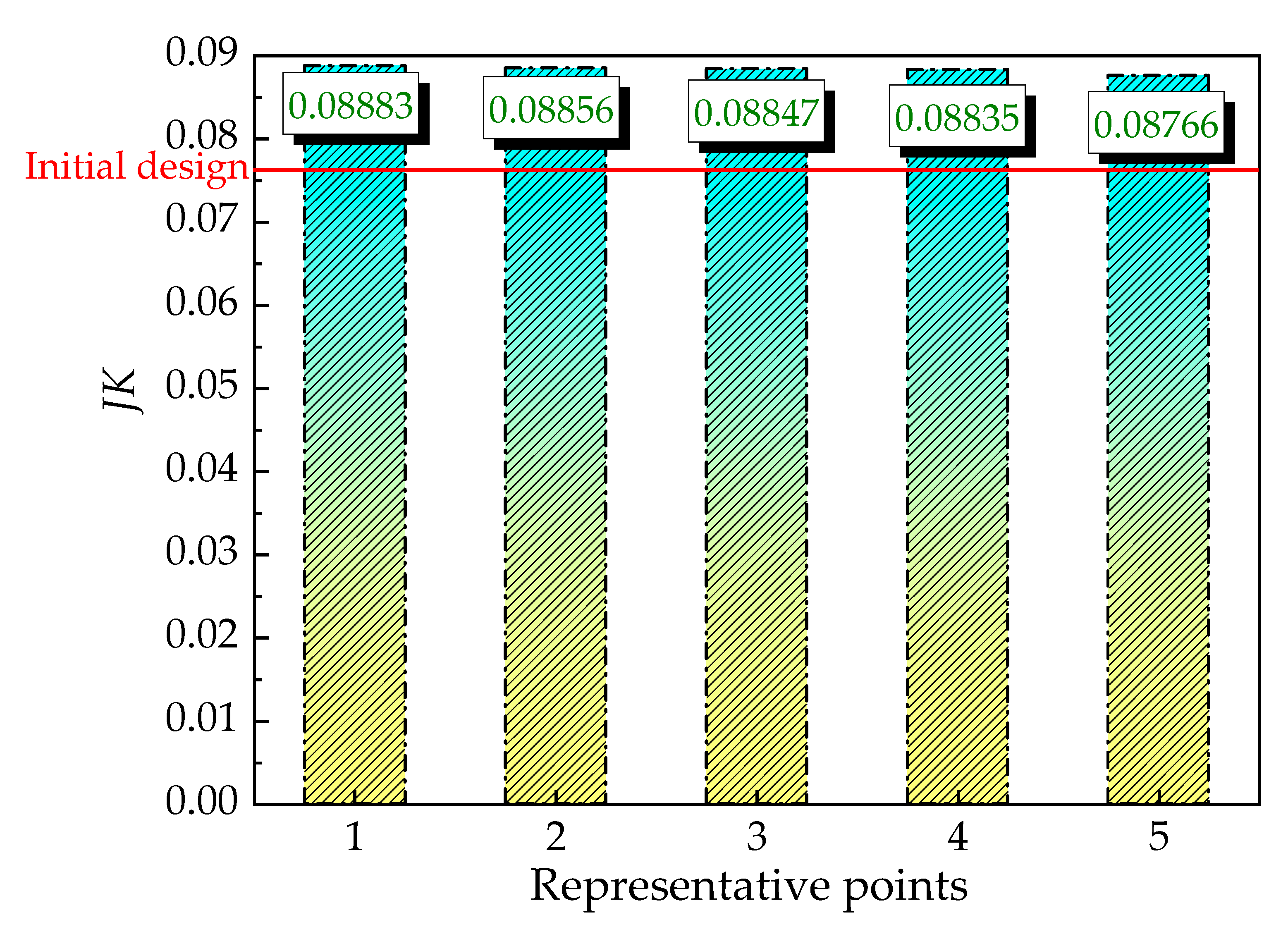
3.1. Multi-Objective Optimization Process
3.2. Design Variables and Objective Functions
3.3. Response Surface Method
4. Results and Discussions
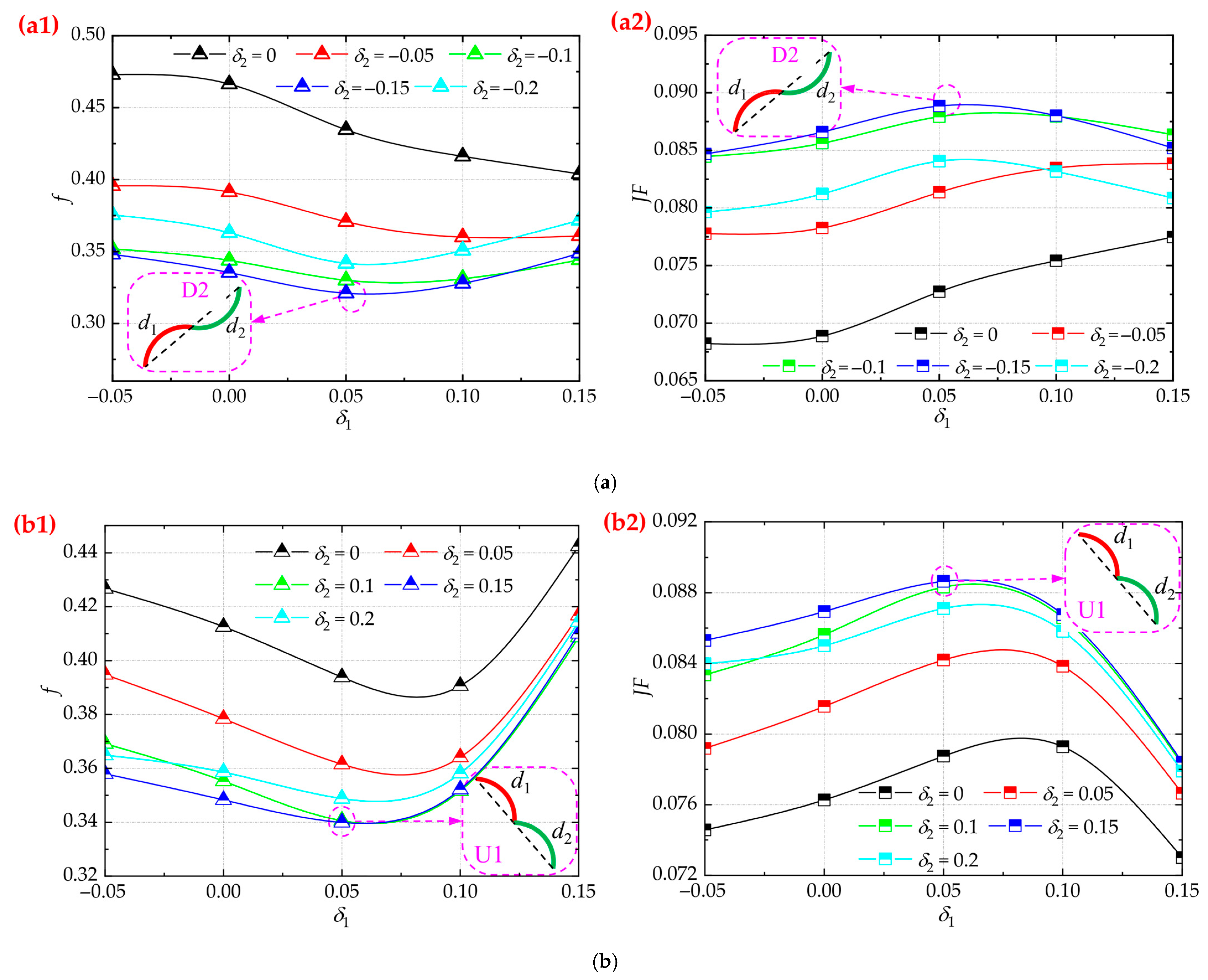
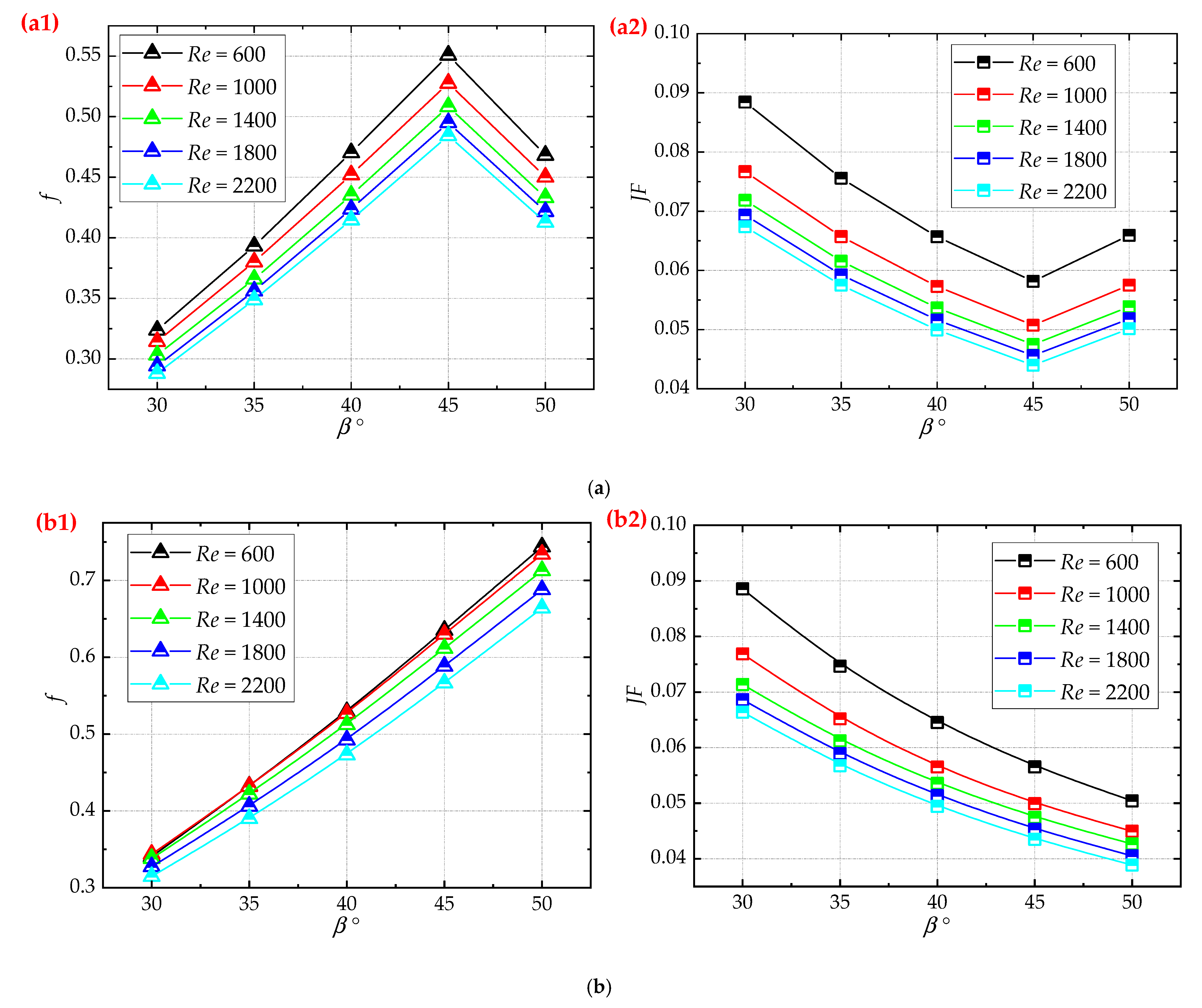
4.1. Effect of Structural Parameters on Drag Reduction Performance
4.2. Response Surface Analysis
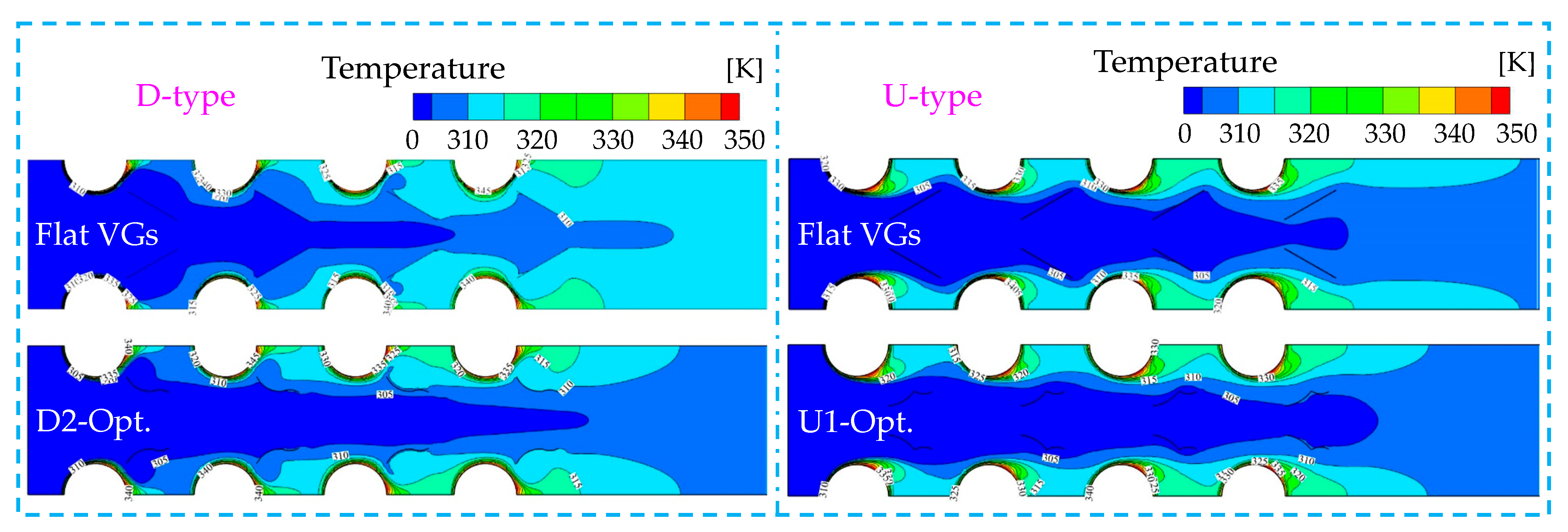
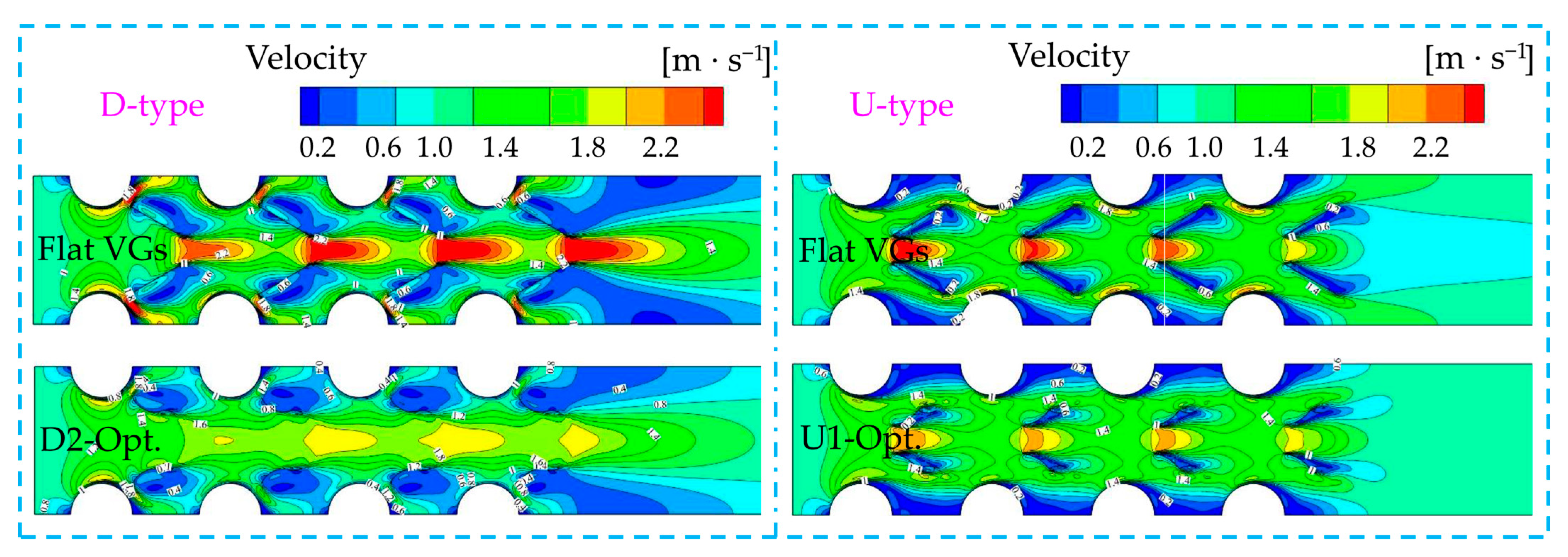
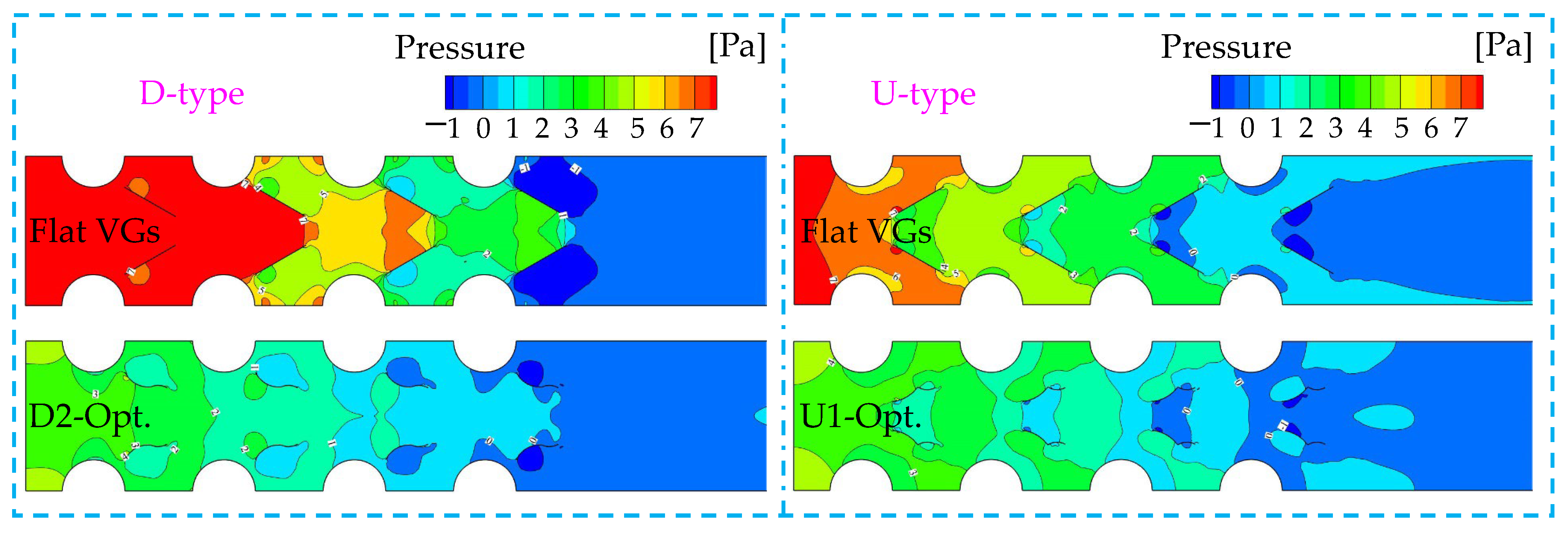
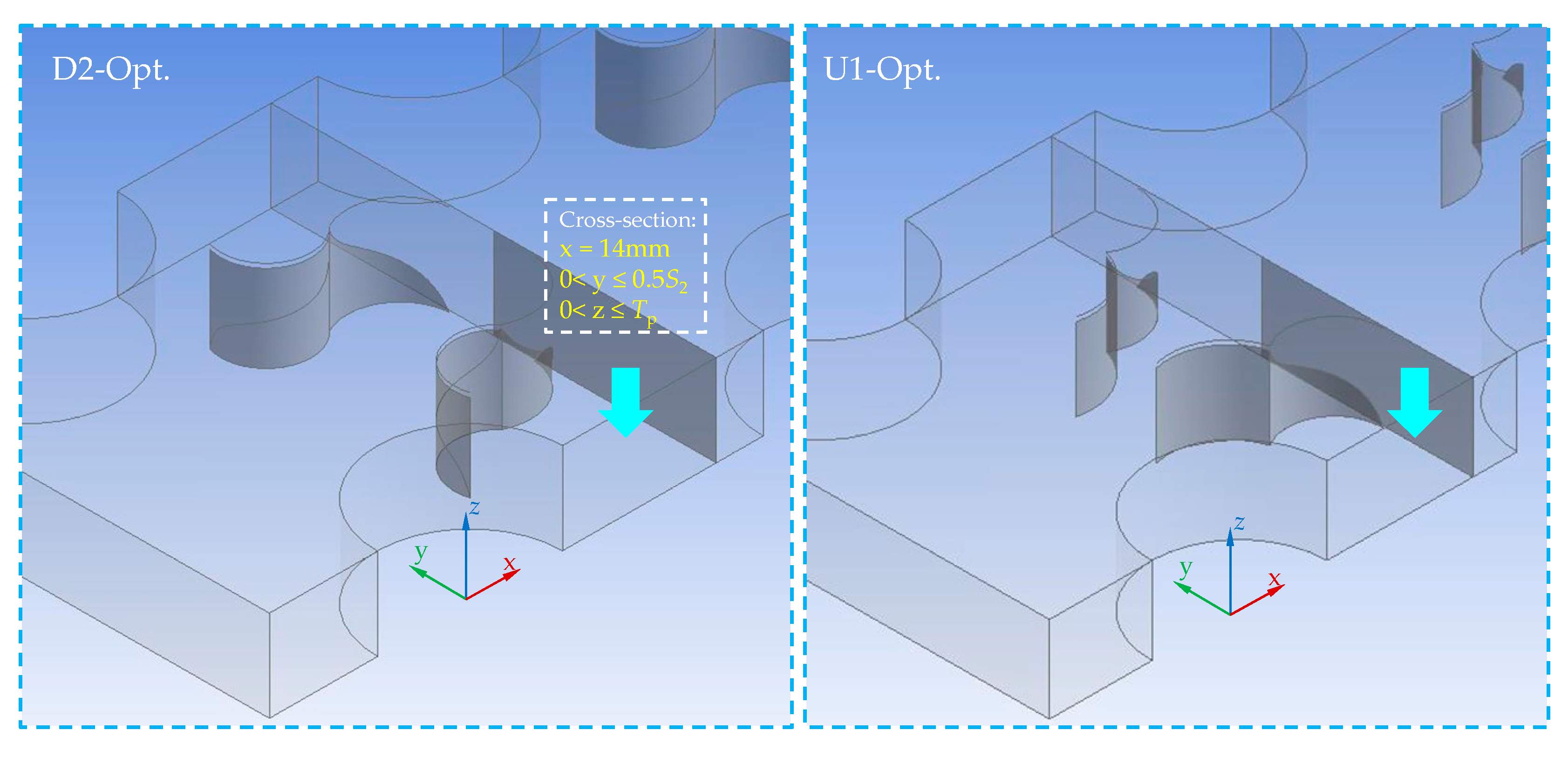
4.3. Analysis of Flow and Heat Transfer Performance of the Optimized Structure
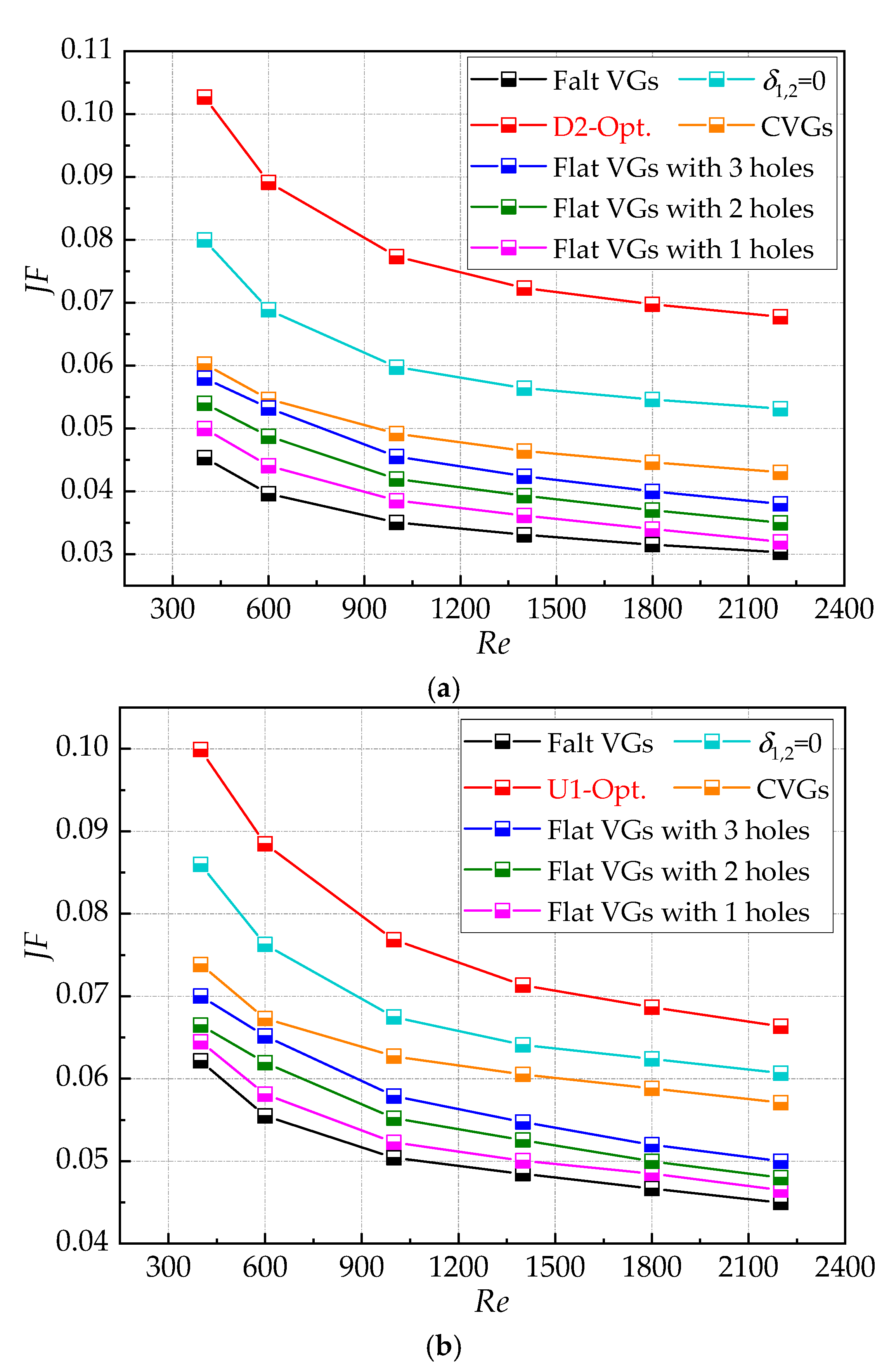
4.4. Comparisons with Other Drag-Reduction VGs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | symmetric tensor |
| B | antisymmetric tensor |
| c | midpoint |
| Cp | constant-pressure specific heat, J/(kg·K) |
| d | bending length, mm |
| DH | hydraulic diameter, mm |
| D | tube diameter, mm |
| f | friction factor |
| h | height of VGs, mm; convective heat-transfer coefficient, W/(m2·K) |
| j | Colburn factor |
| J | objective function |
| JF | comprehensive evaluation metric |
| k | turbulent kinetic energy, m2/s2 |
| l | chord length of VGs |
| m, n | constants |
| N | rows of tubes |
| Nu | Nusselt number |
| p | Pressure, Pa |
| Pr | Prandtl number |
| q | heat flux, W/m2 |
| Re | Reynolds number |
| S1, 2 | spacings between adjacent tubes, mm |
| T | temperature, K |
| Tp | spacing between adjacent fins, mm |
| Δtm | logarithmic average temperature difference, K |
| u, v, w | velocity component, m/s |
| Subscript | |
| down | bottom surface of channel |
| i | number of variables |
| in | channel inlet |
| min | minimum |
| max | maximum |
| opt | optimal value |
| out | channel outlet |
| up | top surface of channel |
| w | wall surface |
| Greek letters | |
| β | attack angle |
| δ | curvature |
| ε | turbulent dissipation rate, m2/s3 |
| λ | heat conductivity coefficient, W/(m·K) |
| μ | fluid viscosity, Pa·s |
| ρ | fluid density, kg/m3 |
| Ω | vorticity |
| Abbreviations | |
| CFD | Common-Flow-Down |
| CFU | Common-Flow-Up |
| SCVG | Seagull-Inspired Curved Vortex Generator |
| FVG | Flat VGs |
| VG | Vortex Generator |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| RSM | Response Surface Method |
| RMSE | Root Mean Square Error |
| R2 | Multivariate Statistical Coefficient |
References
- Tao, W.Q. Numerical Heat Transfer; Xi’an Jiaotong University Press: Xi’an, China, 2001. [Google Scholar]
- Luo, Y.; Li, G.; Bennett, N.S.; Luo, Z.; Munir, A.; Islam, M.S. Heat transfer enhancement in heat exchangers by longitudinal vortex generators: A review of numerical and experimental approaches. Energies 2025, 18, 2896. [Google Scholar] [CrossRef]
- Xu, L.; Li, J.; Sun, K.; Xi, L.; Gao, J.; Li, Y. Heat analysis and optimal design of fin-and-tube heat exchanger with X-truss vortex generators. Int. Commun. Heat. Mass. 2024, 152, 107248. [Google Scholar] [CrossRef]
- Demirag, H.Z.; Dogan, M.; Igci, A.A. The numerical analysis of novel type conic vortex generator and comparison with known VGs for heat transfer enhancement. Heat. Mass. Transfer. 2022, 58, 735–762. [Google Scholar] [CrossRef]
- Naik, H.; Tiwari, S.; Kim, H.D. Flow and thermal characteristics produced by a curved rectangular winglet vortex generator in a channel. Int. Commun. Heat. Mass. 2022, 135, 106103. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, X.; Zhang, Y.; Feng, Y.; Li, Y.; Meng, H.; Zhang, J.; Wu, J. Heat transfer enhancement by streamlined winglet pair vortex generators for helical channel with rectangular cross section. Chem. Eng. Process. 2020, 147, 107788. [Google Scholar] [CrossRef]
- Promvonge, P.; Skullong, S. Thermal-hydraulic performance enhancement of solar receiver channel by flapped V-baffles. Chem. Eng. Res. Des. 2022, 182, 87–97. [Google Scholar] [CrossRef]
- Modi, A.J.; Kalel, N.A.; Rathod, M.K. Thermal performance augmentation of fin-and-tube heat exchanger using rectangular winglet vortex generators having circular punched holes. Int. J. Heat. Mass. Transf. 2020, 158, 119724. [Google Scholar] [CrossRef]
- Saini, P.; Dhar, A.; Powar, S. Performance enhancement of fin and tube heat exchanger employing curved trapezoidal winglet vortex generator with circular punched holes. Int. J. Heat. Mass. Transf. 2023, 209, 124142. [Google Scholar] [CrossRef]
- Pérez, R.B.; Pérez, A.M.; Suárez, D.S. Influence of the punched holes on thermohydraulic performance and flow pattern of rectangular channels with a pair of perforated vortex generators. Int. J. Heat. Mass. Transf. 2022, 184, 122291. [Google Scholar] [CrossRef]
- Promvonge, P.; Promthaisong, P.; Skullong, S. Numerical heat transfer in a solar air heater duct with punched delta-winglet vortex generators. Case Stud. Therm. Eng. 2021, 26, 101088. [Google Scholar] [CrossRef]
- Pérez, A.M.; Altamirano, C.F.-A.; Pérez, R.B. Parametric analysis of the influence of geometric variables of vortex generators on compact louver fin heat exchangers. Therm. Sci. Eng. Prog. 2022, 27, 101151. [Google Scholar] [CrossRef]
- Oh, Y.; Kim, K. Effects of position and geometry of curved vortex generators on fin-tube heat-exchanger performance characteristics. Appl. Therm. Eng. 2021, 189, 116736. [Google Scholar] [CrossRef]
- Ramanathan, S.; Thansekhar, M.R.; Kanna, P.R.; Gunnasegaran, P. A new method of acquiring perquisites of recirculation and vortex flow in sudden expansion solar water collector using vortex generator to augment heat transfer. Int. J. Therm. Sci. 2020, 153, 106346. [Google Scholar] [CrossRef]
- Liu, L.; Ni, Z.; Tang, H.; Xu, H.; Jiang, B. Heat transfer performance and flow characteristics of a heat exchange tube with isosceles trapezoidal winglet longitudinal vortex generators. Energies. 2025, 18, 1717. [Google Scholar] [CrossRef]
- Rhakasywi, D.; Wasito, A.; Wijaya, E.P.; Rizal, R.; Adanta, D. Effect of vortex generator angle on fin and tube heat exchanger. J. Adv. Res. Numer. Heat. Transf. 2024, 16, 82–99. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, W.; Wang, P.; Jiang, J.; Luo, X. Thermal Performance of Elliptical Fin-and-Tube Heat Exchangers with Vortex Generator under Various Inclination Angles. J. Therm. Sci. 2021, 30, 257–270. [Google Scholar] [CrossRef]
- Sharma, V.R.; Sai, S.S.; Madhwesh, N.; Manjunath, M.S. Enhanced thermal performance of tubular heat exchanger using triangular wing vortex generator. Cogent Eng. 2022, 9, 2050021. [Google Scholar] [CrossRef]
- Wang, J.; Zeng, L.; He, Y. Thermal performance augmentation of microchannel using curved rectangular winglet vortex generators having rectangular perforation. Chem. Eng. Sci. 2025, 302, 120860. [Google Scholar] [CrossRef]
- İĞCİ, A.A. Enhancing heat transfer with a hybrid vortex generator combining delta wing and winglet designs: A numerical study using the GEKO turbulence model. Appl. Therm. Eng. 2025, 258, 124604. [Google Scholar] [CrossRef]
- Sharfabadi, M.M.; Mobadersani, P.; Nourpour, L. A Numerical study on heat transfer in the channel with delta winglet pair vortex generators. Int. J. Heat. Technol. 2022, 39, 1305–1312. [Google Scholar] [CrossRef]
- Shi, W.N.; Liu, T.F.; Song, K.W.; Zhang, Q.; Hu, W.L.; Wang, L.B. The optimal longitudinal location of curved winglets for better thermal performance of a finned-tube heat exchanger. Int. J. Therm. Sci. 2021, 167, 107035. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Zhang, W.; Zhao, Z. Performance optimization of plate-fin heat exchanger with curved vortex generators based on response surface method. Int. J. Therm. Sci. 2025, 210, 109659. [Google Scholar] [CrossRef]
- Dogan, M.; Erzincan, S. Experimental investigation of thermal performance of novel type vortex generator in rectangular channel. Int. Commun. Heat. Mass. 2023, 144, 106785. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, F.; Chen, X.; Zhang, Y. Performance analysis of axial air-cooling system with shark-skin bionic structure containing phase change material. Energy Convers. Manag. 2021, 250, 114921. [Google Scholar] [CrossRef]
- Wang, D.; Liu, H. A novel aerodynamic drag-reduction mechanism using dolphin-inspired ultrasonic microvibrations. Sci. Rep. 2025, 15, 13691. [Google Scholar] [CrossRef]
- Wang, Z.; Li, B.; Luo, Q.; Zhao, W. Effect of wall roughness by the bionic structure of dragonfly wing on microfluid flow and heat transfer characteristics. Int. J. Heat. Mass. Transf. 2021, 173, 121–201. [Google Scholar] [CrossRef]
- Lyu, Y.; Yu, H.; Hu, Y.; Shu, Q.; Wang, J. Bionic design for the heat sink inspired by phyllotactic pattern. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2020, 235, 3087–3094. [Google Scholar] [CrossRef]
- Li, X.J.; Zhang, J.Z.; Tan, X.M.; Zhang, Q.C.; Lu, E.H. Investigation of fluid flow and heat transfer in a narrow channel with micro barchan-dune-shaped humps. Int. J. Mech. Sci. 2022, 231, 107589. [Google Scholar] [CrossRef]
- Niu, Z.; Hao, M.; Wang, Y.; Zhang, J. Numerical simulation of enhanced heat transfer in new type of bird beak vortex generator. Acta. Energ. Sol. Sin. 2024, 45, 264–271. [Google Scholar] [CrossRef]
- Gonül, A.; Okbaz, A.; Kayaci, N.; Dalkilic, A.S. Flow optimization in a microchannel with vortex generators using genetic algorithm. Appl. Therm. Eng. 2022, 201, 117738. [Google Scholar] [CrossRef]
- Hu, D.L.; Zhang, Q.; Song, K.W.; Gao, C.; Zhang, K.; Su, M.; Wang, L.B. Performance optimization of a wavy finned-tube heat exchanger with staggered curved vortex generators. Int. J. Therm. Sci. 2023, 183, 108489. [Google Scholar] [CrossRef]
- Li, Z.; Feng, Z.; Zhang, Q.; Zhou, J.; Zhang, J.; Guo, F. Thermal-hydraulic performance and multi-objective optimization using ANN and GA in microchannels with double delta-winglet vortex generators. Int. J. Therm. Sci. 2023, 193, 108489. [Google Scholar] [CrossRef]
- Sharma, R.; Mishra, D.P.; Wasilewski, M.; Brar, L.S. Application of response surface methodology and artificial neural network to optimize the curved trapezoidal winglet geometry for enhancing the performance of a fin-and-tube heat exchanger. Energies 2023, 16, 4209. [Google Scholar] [CrossRef]
- Xie, C.; Yan, G.; Ma, Q.; Elmasry, Y.; Singh, P.K.; Algelany, A.M.; Makatar, W. Flow and heat transfer optimization of a fin-tube heat exchanger with vortex generators using Response Surface Methodology and Artificial Neural Network. Case Stud. Therm. Eng. 2022, 39, 102445. [Google Scholar] [CrossRef]
- Liang, X.; Kumar, N.B.; Mansir, I.B.; Singh, P.K.; Abed, A.M.; Dahari, M.; Nasr, S.; Albalawi, H.; Cherif, A.; Makatar, W. Management of heat transfer and hydraulic characteristics of a micro-channel heat sink with various arrangements of rectangular vortex generators utilizing artificial neural network and response surface methodology. Case Stud. Therm. Eng. 2023, 44, 102850. [Google Scholar] [CrossRef]
- Feng, Y.; Xu, R.; Cao, Y.; Wu, X.; Liang, C.; Zhang, L. Optimization of H-type finned tube heat exchangers with combinations of longitudinal vortex generator, dimples/protrusions and grooves by Taguchi method. Int. Commun. Heat. Mass. 2023, 143, 106709. [Google Scholar] [CrossRef]
- Liu, A.; Wang, G.; Wang, D.; Peng, X.; Yuan, H. Study on the thermal and hydraulic performance of fin-and-tube heat exchanger based on topology optimization. Appl. Therm. Eng. 2021, 197, 117738. [Google Scholar] [CrossRef]
- Yang, X.; Hu, J.; Fan, Y.; Min, C.; Wang, K. Enhanced heat dissipation of ribbed channels based on the coupling optimization of multiple structural parameters. Appl. Therm. Eng. 2023, 235, 121362. [Google Scholar] [CrossRef]






| Parameters | Symbol | Value |
|---|---|---|
| Rows | N | 4 |
| Chord length | l | 10 mm |
| Height | h | 5 mm |
| Attack angle | β | 30°~50° |
| Bending length | d1, d2 | −2.5~2.5 mm |
| Curvature | δ1, δ2 | −0.25~0.25 |
| Midpoint | c | 10.275 mm |
| Clustering Point | δ1 | δ2 | Pareto Front | Numerical Solution | Error% | |||
|---|---|---|---|---|---|---|---|---|
| Jj | Jf | Jj | Jf | Jj | Jf | |||
| 1 | 0.0662 | 0.1626 | −3.0292 | 3.4408 | −3.0193 | 3.3989 | 0.33 | 1.23 |
| 2 | 0.0640 | 0.1612 | −3.0265 | 3.4320 | −3.0237 | 3.4144 | 0.09 | 0.51 |
| 3 | 0.0517 | 0.1562 | −3.0151 | 3.3960 | −3.0197 | 3.4132 | 0.15 | 0.51 |
| 4 | 0.0470 | 0.1534 | −3.0116 | 3.3859 | −3.0174 | 3.4153 | 0.19 | 0.87 |
| 5 | 0.0300 | 0.1470 | −3.0050 | 3.3710 | −3.0234 | 3.4489 | 0.61 | 2.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yang, X.; Gu, X.; Liu, Y. A Drag-Reduction Mechanism of Seagull-Inspired Curved Vortex Generators Integrating Response Surface Method and Genetic Algorithms Optimization in Compact Heat Exchangers. Energies 2025, 18, 4281. https://doi.org/10.3390/en18164281
Wang Z, Yang X, Gu X, Liu Y. A Drag-Reduction Mechanism of Seagull-Inspired Curved Vortex Generators Integrating Response Surface Method and Genetic Algorithms Optimization in Compact Heat Exchangers. Energies. 2025; 18(16):4281. https://doi.org/10.3390/en18164281
Chicago/Turabian StyleWang, Zhihui, Xuguang Yang, Xiaohua Gu, and Yan Liu. 2025. "A Drag-Reduction Mechanism of Seagull-Inspired Curved Vortex Generators Integrating Response Surface Method and Genetic Algorithms Optimization in Compact Heat Exchangers" Energies 18, no. 16: 4281. https://doi.org/10.3390/en18164281
APA StyleWang, Z., Yang, X., Gu, X., & Liu, Y. (2025). A Drag-Reduction Mechanism of Seagull-Inspired Curved Vortex Generators Integrating Response Surface Method and Genetic Algorithms Optimization in Compact Heat Exchangers. Energies, 18(16), 4281. https://doi.org/10.3390/en18164281





