Physical Modelling of the Top Coal Caving Mining Method (TCC) with Hydraulic Powered Roof Support

Abstract

The efficiency of coal deposit mining using the TPC (Top Coal Caving) method strongly depends on the detailed solutions of the mining method design, which significantly affect the degree of deposit utilization, the size of losses and dilution. In order to examine the most important factors of this technology, a physical model was built that reflects the conditions of the selected lignite mine, including models of the mechanized hydraulic support walking support used in this case. Based on the research, the relationships between the thickness of the rock shelf (lignite) in the range of 4 m, 6 m and 8 m and the formation of dilution and deposit waste during the exploitation of the deposit were determined. It was shown that the most effective method of releasing lignite from under the caving is the serial-regular method with a 1.2 m advance round. Detailed relationships between individual parameters, rock material granulation, round advance and the thickness of the deposit and the layer subject to caving were given. The developed physical model of the support allows for variant analyses of various combinations of deposit parameters for any deposits in order to achieve the best efficiency of the mining method.

1. Introduction

Mining Methods with ore drawing are commonly used in global mining, primarily in ore mining [1,2,3,4,5]. Various types of mining systems are used to exploit ore and non-ferrous metal deposits. Based on many years of experience in ore mining, systems with ore drawing are also used in lignite and hard coal mining. The key problem in systems with drawing is the loss and depletion of useful mineral. A distinction is made between exploitation and non-exploitation losses. The concept of exploitation losses is understood as losses in industrial resources arising in the parts of the deposit covered by exploitation as a result of the application of a specific exploitation system and includes losses resulting from leaving the deposit in its entirety and unreleased ore located in goafs. The term non-exploitation losses means losses left as a result of the use of a specific exploitation technology resulting from unfavourable geological conditions found during mining operations. Losses in mining systems range from 16–20% [6]. The size of losses and dilution is influenced by natural factors as well as technological factors, such as in top coal caving, where various types of special sections of mechanised support are used. For the concept of mining the lignite deposit using the longwall top coal caving method in the Novaki mine in Slovakia, a physical model of the mining system was made, enabling a multi-variant study of the technological system in the context of its optimization. In comparison to the model studies with the drawing of output described in the literature [7,8], the modeling method was different in that the drawing of output was carried out from several discharge holes and the movement of the powered support section was carried out while maintaining the maximum advance step. In the case of one discharge hole, it is practically impossible to reflect the formation of the above-mentioned indicators in real conditions.

Moreover, the influence of the model walls in such a case significantly limits and disturbs the formation of areas of movement of the fragmented rock medium, which consequently gives erroneous results. In the case of releasing the ore from one discharge hole, only the mechanism of releasing the material can be presented. The model design and the method of conducting experiments allowed for a accurate reflection of the actual conditions in the analyzed mine.

Before starting the system modeling, auxiliary models were made, based on which observations were made and it was determined that the most effective way of releasing the output is the even-series method. This method allowed maintaining the contact of lignite with the waste rock at one level and obtaining the maximum volume of output from the roof shelf. In the second stage, the empirical proportionality coefficient “m” was determined, based on which the geometric parameters of the areas of movement of the fragmented rock medium in the form of ellipsoids were determined. In the third stage, the angle of inclination of the plane between the waste rock and the useful mineral in a loose state in the phase of developed exploitation was determined. In order to determine the losses and dilution of lignite, the release of a 4 m, 6 m, 8 m high lignite shelf with the take of 0.6 m, 1.2 m, 1.8 m, 2.4 m was modeled. The results obtained from the physical modeling of the longwall top coal caving system were verified by the MineCAD computer software 1.0, based on the principles of stochastic theory. This program enabled the modeling and modification of various variants of mining systems with frontal release of mined material. It has been shown that the effectiveness of the lignite deposit mining technology using the mining system, based on drawing the output as a bulk material through sections of mechanized support, is strictly dependent on the adopted method of implementing the technology and its specific parameters, which include: the size of the designed extraction, the thickness of the mined layer, and the sizes and sequences of individual portions of released output. The above-mentioned factors are of key importance in the context of the obtained values of dilution and coal losses in the mining process.

2. Top Coal Caving Mining Methods

Longwall top coal caving methods have been used since the mid-twentieth century [9,10]. Initially, the length of longwall workings did not exceed 50 m and their height was about 2.6 m, with the thickness of the roof coal shelf of up to about 5 m. Experimentally, it was found that the optimal height of the roof shelf should be in the range of 5.0–5.5 m [11]. Under varying conditions of top coal thickness, the highest top coal recovery occurs when the thickness is 4.0 m with a TCCI of 0.8 m. Additionally, when the coal seam thickness exceeds 4.0 m and the TCCI is 1.2 m, the recovery rate is maximized and the top coal caving ratio may surpass the traditional limit of 1:3 [12]. The longwall top coal caving method has been used for mining thick coal seams in China for over 30 years. The first attempts at the undermining system were made in 1982, when a powered support with a tapping window located in the caving shield was used [13]. They were also used for mining steep seams in the Yaojie Mining Buerau mine in 1990, where a seam with an inclination of 37–85° (average 61°) and a thickness of 20 m was mined. The first layer, the so-called bottom layer, was mined using a longwall system using a shearer loader, and the second layer (a 7.5 m high coal shelf) was released onto a chain conveyor behind a mechanized support [14]. In the mining area of Shenhua Group, the seams with an inclination of 60–63° (average 61.5°) and a thickness of 39 m were mined. The monthly production was 0.170 mln Mg, and the annual production was 2.040 mln Mg [15]. Wang [16] conducted an analysis on the influence of selected parameters: mining depth, coal strength parameters, coal shelf height, thickness of the overburden rock package, degree of coal and direct roof rock fragmentation on the drawing efficiency in the top coal caving system. Yasitli [9] modeling highlighted the significance of uniform fracturing of the upper coal seam to ensure continuous flow and minimize dilution. The study proposed a pre-fracture blasting strategy, utilizing finite difference modeling (FLAC3D) to analyze ground behavior and stress distribution, thereby providing a numerical simulation framework. Conversely, Wang [7] primarily examined recovery ratios influenced by factors such as seam thickness, drawing techniques, and measurement methodologies. Their approach focused on empirical and experimental methods, including field measurements, laboratory experiments, and RF-based tracking devices, without emphasizing fracturing strategies.

Based on the analysis of these parameters, he determined the index of coal tendency to collapse “y” and the coefficient of deposit utilization. Thick and steep hard coal seams are also mined in the Kuzbas Basin, the angle of inclination is more than 55°. The top coal caving systems used in hard coal mines are used in varieties with the release of output from the roof shelf to the entire height, with division into layers and with the release of output under a flexible roof [17] and with regulated release of output.

The possibility of regulating the discharge allows for a smooth outflow of the mined material, which reduces the dilution. The most modern underground mines in Europe exploiting brown coal using the underground method include the Velenje Mine in Slovenia. The exploited lignite deposit is one of the thickest in the world and reaches over 170 m [18]. The deposit has the shape of a lens, which is about 8 km long and 2.2 km wide. The thickness of the deposit ranges from 60 m to 170 m. The floor layers are formed by marly clays, sands, mudstones, dolomites and limestones. The floor layer is mined using a longwall shearer, and the coal shelf is released onto a scraper conveyor by frontally lowering the roofs of the mechanized support. In Turkey, lignite is mined in the Tuncbilek and Soma mines. The seams are classified as thick seams with thicknesses of up to 20 m. The Soma mine mines seams with thicknesses ranging from 5.5 m to 6 m [19]. According to Jangara and Ozturk [20] the required bearing capacity for the longwall cutting and top coal heights as well as the daily advance rate must be predicted for optimized coal recovery coefficient, what they found in their research.

In the Novaki mine in Slovakia, various types of room systems were used for the extraction of thick seams (>10 m), which involved two-phase mining. At the beginning of the 1980s, a decision was made to test a longwall system with the discharge of mined lignite from the upper layer. For this purpose, a special type of support was designed and constructed, equipped with a closable discharge opening. The first tests yielded very positive results. This system was successfully implemented in the Novaki mine, where seams of 10–14 m thickness were mined. The 10 m thick seams were divided into three layers. The roof and floor layers of approximately 3 m height were mined using a longwall system using a longwall shearer, leaving a protective layer of lignite of 0.4 m thickness in the roof and floor (Figure 1). The remaining roof shelf of approximately 4 m height was released through a BMV 1M type support onto a scraper conveyor.

In the Novackie Coal Basin the lignite seam is 13.20 m to 17.80 m thick (14.61 m on average) [21]. From the point of view of physical and mechanical properties, lignite is 3–5 times stronger than the surrounding rocks. The strength parameters of lignite and the rocks surrounding the deposit are presented in

Table 1. Physical and mechanical properties of lignite and the rocks surrounding the deposit [22].

Rock Properties	Clay	Upper Part of the Seam	Bottom Part of the Seam	Floor Rocks
Uniaxial compressive streghth, MPa	2.26–5.71	6.03–24.71	6.01–23.54	2.71–10.12
Tensile strength, MPa	0.6–1.28	2.15–2.26	1.03–2.06	0.95
Bending strength, MPa	2.52	5.98–6.24	3.20–5.35	0.78
Shear strength, MPa	0.85–2.93	3.85–10.70	3.13–8.87	0.68–3.93
Young modulus, MPa	311.8–571.9	395.3–853.3	502.5–871.3	225.8–661.8
Poisson’s Number, -	0.16–0.27	0.11–0.35	0.22–0.38	0.07–0.28

.

In recent years, starting from 2007, lignite has been mined using a BMV powered roof support with a discharge window, which has brought very good economic results. The mining of the base layer is carried out using a longwall shearer, and the lignite shelf is loosened by the forces of gravity and the pressure of the rock mass and by lowering and re-extending the roof of the support. The daily extraction volume and the advancement of the longwall depend on the geological and mining conditions and the degree of workability of the lignite shelf. The extraction volume as a function of the thickness of the roof shelf is illustrated in Figure 2.

In practice, there are sometimes problems related to the release of mined material, because during long downtimes, the roadways are deformed under the influence of operating pressure. The key problem is to limit the size of losses and dilution. For this purpose, an original, controlled physical model of a powered roof support was built [22], which allows for the simulation of the advancement operation and the release of mined material from the roof layer through windows made in this support, which allows for multi-variant modeling of the mining system.

3. Movement of Bulk Materials in Tanks

The specificity of mining systems with the release of the output, both in metal ore mines and mines of other minerals, is associated with the movement of crushed output masses moving with the progressing mining process. Similar issues are the subject of interest in research on the problems of storing bulk materials. The theoretical foundations of the movement of bulk material in containers were described by Kvapil [23]. These foundations are based on numerous visual observations and analyses conducted on a physical model. The model contained a bulk material placed in a tank constructed of glass walls mounted in a frame. In the lower part of the model there was a square-section opening equipped with a valve. For the tests, ground white marble was used, poured in layers separated by thin layers of black marble. After opening the opening, a certain volume of material moved, as a result of which the black layers began to move. Kvapil [23] found that primary and secondary motion occur in bulk media in reservoirs and, on this basis, introduced the concept of primary and secondary motion ellipsoids. Primary motion consists in the fact that grains move vertically under the influence of their own weight and the pressure of the overlying material, and secondary motion of grains consists in changing their position relative to the axis, deflecting the trajectory of motion and rotation. According to Kvapil [23], the volume of the primary motion ellipsoid is approximately fifteen times larger than the volume of the secondary motion ellipsoid. The movement of the material is primarily influenced by the size and shape of the grains. The shape of the grains can also vary within a wide range, from spherical to acicular. When output is discharged from the discharge hoppers, the output particles are located in the center of the discharge ellipsoid and move at different speeds in the direction of the discharge hopper inflow, and the highest speed is achieved by output particles located near the discharge hopper axis. In practice, the ore is discharged under the overlying waste rocks, the penetration of which causes its dilution [24]. When the tip of the loosening ellipsoid passes through the contact surface of the ore with the waste rocks, a funnel is formed that is symmetrical with respect to the axis of the discharge funnel. This funnel is called an inflection funnel. When an inflection funnel is formed, the ore begins to mix with the waste, which is a significant factor in dilution. The increasing volume of the loosening ellipsoid reduces losses, but at the same time the degree of ore dilution increases [25]. In the case of mining systems that involve simultaneous discharge of ore from several hoppers/discharge holes, especially those directly adjacent to each other, the efficiency of output discharge depends on the order in which these holes are activated without interruption or with an interruption until the next one is passed. The next portion is discharged after the output has been discharged from the adjacent discharge holes. Asymmetric discharge can cause a decrease in output flow and an increase in output dilution [26].

4. Physical Model for Testing the Process of Mining Output Discharge from a Single Hole and Three Sections of a Powered Roof Support with Holes

In order to determine the effect of the granulometric composition of lignite on the geometric parameters of the loosening ellipsoid, a physical model was made in a scale of 1:25 with dimensions of 27 cm × 20 cm × 56 cm (length, width, height). The adopted modelling scale (1:25) is the result of a compromise between the possibility of making original mechanical models of a powered, active support, with mechanisms enabling its movement during the experiment, with the required size of the container for crushed rock material and the size of individual grains on the one hand, and on the other hand the dimensions of the mine workings, which served as a kind of field laboratory. This model consisted of transparent walls of plexiglass plates and three sections of a mechanized support, with only the middle section having a drain hole. Model tests were carried out for lignite fractions in the range of 0.40–2 mm and 2.5–6.3 mm. The height of the lignite layer in both cases was 25 cm (in real conditions 6.25 m). Layers of clay were poured into the lignite layer in order to visually observe the formation of the loosening ellipsoid. In the case of the fraction range 0.40–2 mm, the diameter of the loosening ellipsoid was 6 cm (Figure 3), and in the case of the fraction 2.5–6.3 mm 10.5 cm (Figure 4). Based on the results of the conducted tests, it was found that with the increase in the granulometric composition of the mined material, the zone of influence of the discharge hole expands.

In the process of output drawing, it is crucial to establish the method and sequence of discharge from individual tap holes in order to limit losses and dilution of the useful mineral. In the process of ore discharge in the exploitation blocks, there is a lateral, vertical contact of the useful mineral with the waste rocks (even 2 or 3 contacts). Losses and dilution of the useful mineral begin when the discharge ellipsoid reaches the lateral contact of the useful mineral with the waste rocks. The reduction of losses and dilution can be achieved when the discharge ellipsoid simultaneously reaches vertical and horizontal contact of the useful mineral with the waste rocks. In order to determine the method of releasing lignite, a physical model was built from plexiglas plates and two models of powered support sections made in a scale of 1:25 with dimensions of 13 cm × 20 cm × 54 cm (length, width, height). Lignite in the fraction range of 4–6 mm and clay in the range of 9–12 mm were used for the tests. As part of the study, a 25 cm high layer of lignite was released. Magnesite layers were poured into the layer (Figure 5a). In the first stage of modeling, a layer of lignite was released at once (without interruption) from one tap hole until the waste rocks appeared (Figure 5b). Then, lignite was released from the adjacent section in the same way (Figure 5c).

As can be seen in the Figure 5, after the first release, the lignite is in contact with the waste rocks in two planes. After opening the tap window of the second section in the middle of the layer, dilution occurred due to the lateral contact of the lignite with the waste rocks. In the second stage, the release of lignite was started in an even-serial mode in such a way that lignite was released from both sections in appropriate doses in order to maintain the contact of the lignite with the waste rocks only in the upper part (in the roof). In the Figure 6a–l, one can observe the uniform movement of the paraboloids of rotation in the direction of the tapping hole influence. Based on the observations made, it can be stated that the most effective method of discharge in the longwall top coal caving system is the uniform-serial discharge. Using this type of discharge, one can achieve the maximum volume of mined material and limit its dilution. In the first case, the dilution occurred earlier than in the second case. The first case is permissible in block mining systems, where it is possible to determine the optimal distance between the discharge hoppers, which is impossible in the case of the longwall top coal caving system. In addition to the above-mentioned factors influencing the discharge of mined material, attention should also be paid to the degree of humidity of the mined material and its negative impact on the discharge process. With increasing humidity, with a 25% content of clay and dust, the spoil moves towards the outlet with great difficulty.

In order to determine the phenomenon occurring in the case of high humidity, a model study was conducted for lignite in the fraction range of 0.40–2 mm and 2.5–6.3 mm (Figure 7). A layer of lignite 25 cm high was poured into the model. The moisture content of lignite was determined in three tests, the average value of which was 16%. Lignite was discharged from one tap hole without the content of clay and dusty parts. At higher moisture levels, around 20%, depending on the degree of fragmentation of the excavated material, it is expected that its release will be practically impossible.

After opening the discharge window, a volume of mined material Vu was released, equal to the volume of the discharge ellipsoid Ve: Vu = Ve, (Figure 7a,b). In the next phase, a specific volume of mined material was displaced and formed a funnel on the surface (Figure 7c,d). This phenomenon often occurs when discharging bulk materials in silos and is referred to as tunnel flow. Based on model tests, it can be stated that in the case of lignite, the moisture content of which was 16%, the movement of mined material was significantly hindered. At a higher moisture content, about 20%, depending on the degree of mined material fragmentation, it is predicted that its discharge will be practically impossible.

5. Building a Physical Model of the Mining System

Physical modeling of the output drawing process, apart from analytical methods, is one of the most common methods for determining normative indicators in systems with drawing [27]. However, currently fewer and fewer scientists are involved in physical modeling due to the time-consuming nature of the research. Research on physical models, in contrast to mine research, i.e., in situ, is characterized by lower indicators related to costs and time, and it is possible to observe the release process in individual phases through transparent walls of the model, which is practically impossible in mine conditions. The difference between the results obtained in the physical model and the results from mine tests is relatively large, on the order of several percent [28]. Greater convergence of results in the case of physical modeling can be achieved by applying as closely as possible to real conditions, as well as to similarity indices. In order to obtain correct results in the process of modeling the release of ore, the methodology of functional similarity of laboratory experiments was used. When modeling the release of bulk material in the case of similarity of loosening ellipsoids and granulometric composition, the following empirical equations are used [29,30]:

$$P_1={\displaystyle \frac{q}{{\rho ·D}^{\frac{5}{2}}·g^{\frac{1}{2}}}}$$

(1)

$$P_2={\displaystyle \frac{d}{D}}$$

(2)

where:

q—speed of drawing material, kg/s;

ρ—density of bulk material, kg/cm²;

D—discharge hole diameter, m;

g—gravitational acceleration, m/s²;

d—average grain size, m.

The movement of bulk material in a confined space is also influenced by the angle of friction against the model walls ψ. The values of the coefficients of the angles of internal friction of the mined material and its friction against the model walls are dimensionless. In such a case, their values should be the same as in real conditions [31]:

$$C_{\phi }=C_{\Psi }=1$$

(3)

where:

C_φ, C_ψ—scale of coefficients of angles of internal friction and friction of the spoil against the model walls.

In practice, it is often assumed that the angles of natural repose of a bulk material of a specific granulation in the model and in nature are equal to the angles of internal friction [32].

5.1. Analysis of the Granulometric Composition of Lignite and Waste Rocks

The evaluation of the granulometric composition of the mined material was carried out in the Novaki mine in the longwall and undermining excavation using the photogrammetric method. The first stage of the work was to prepare the necessary photographic documentation. This stage is particularly important due to the direct impact on the final result of the analyses, which is due to the low level of light intensity in the excavation, air humidity and dust [33]. In the next stage, the image was scaled by placing a spherical object (ball) with a diameter of 238 mm. Photographs were taken in single sectors along the entire longwall excavation with a Canon SX130IS camera at a short distance from the mound, and the released ore was in a plane perpendicular to the camera lens (Figure 8 and Figure 9). Several dozen photographs were taken for each research sector, from which the best quality photographs were then selected.

The particle granulation of both the waste rocs and lignite was selected based on photogrammetric analysis, and the particle scaling was maintained. Due to the laboratory tests being conducted at a scale of 1:25, the dynamic similarity reflects industrial conditions only to a certain extent. In real-world conditions, vertical and horizontal stresses occur together, directly influencing the deformation patterns of individual rock mass layers. Furthermore, only a section of the rock mass was modeled in the laboratory, encompassing only a few sections of the powered support. Compared to industrial conditions, this means that the boundary conditions in the model were minimally sufficient to obtain a dissipative ellipsoid.

Fragmentation analysis was performed using CorelDraw, where the dimensions of the rock lumps (X–length, Y–height) were measured. The measured dimensions were then subjected to another analysis in Excel. The results of the analyzed lignite piles are presented in

Table 2. Lignite material parameters.

Fraction		Fraction		Fraction
Min., mm	Max., mm	Min., mm	Max., mm	Min., mm	Max., mm
0	100	100	200	200	500
Total numer of samples		Total numer of samples		Total numer of samples
320		320		320
Number of samples between: min.–max.		Number of samples between: min.–max.		Number of samples between: min.–max.
142		128		50
Contribution of fraction, %		Contribution of fraction, %		Contribution of fraction, %
44.4		40		15.6

and Figure 10, and the results of the analyzed clay piles are presented in

Table 3. Silt material parameters.

Fraction		Fraction		Fraction
Min., mm	Max., mm	Min., mm	Max., mm	Min., mm	Max., mm
0	100	100	200	200	500
Total numer of samples		Total numer of samples		Total numer of samples
92		92		92
Number of samples between: min.–max.		Number of samples between: min.–max.		Number of samples between: min.–max.
45		35		12
Contribution of fraction, %		Contribution of fraction, %		Contribution of fraction, %
56.0		31.0		13.6

and Figure 11.

$$x={\displaystyle \frac{(a_1\ast w_1+a_2\ast w_2+a_3\ast w_3+\dots +a_n\ast w_n)}{w_1+w_2+w_3+\dots {+w}_n}}$$

(4)

x = 137 mm

• where:

x—weighted average of the analyzed rock lumps;

$a_1$,$a_2$,$a_n$—average value of fraction range, mm;

$w_1$,$w_2$,$w_n$—percentage share of fractions, %.

$$x={\displaystyle \frac{(a_1\ast w_1+a_2\ast w_2+a_3\ast w_3+\dots +a_n\ast w_n)}{w_1+w_2+w_3+\dots {+w}_n}}$$

(5)

x = 249 mm

• where:

x—weighted average of the analyzed rock lumps;

$a_1$,$a_2$,$a_n$—average value of fraction range, mm;

$w_1$,$w_2$,$w_n$—percentage share of fractions, %.

Based on the analysis of the granulometric composition of lignite, it can be stated that the largest fraction share is in the range of 0–100 mm and amounts to 44.4%, while the smallest fraction share in the range of 200–500 mm is 15.6%. In the case of waste rock (clay), the smallest fractions occur in the range of 0–100 mm, while the coarsest fractions occur in the range of 200–500 mm. Based on the data obtained, the weighted average of the lump in the pile was determined for lignite and clay (Figure 12).

Particle size significantly affects the smoothness of the coal drawing. Large lumps can cause blockages, which can interrupt the drawing process. Because fine particles fill the voids between large lumps of coal, mixing coal fractions can increase efficiency. On the other hand, the risk of fine dust particles must also be considered, as they are not only explosive at certain concentrations but also have a negative impact on health.

5.2. Empirical Proportionality Coefficient “m” for Lignite

Before starting any physical modeling, regardless of the type of material used (real, equivalent), it is necessary to determine the proportionality coefficient “m”. The coefficient “m” characterizes the elongation of the ellipsoids of relaxation and discharge, as well as the properties of the relaxed material. The flow coefficient of the bulk material [34] is inversely proportional to the coefficient “m”. This coefficient is a constant value and depends on the physico-mechanical properties of the bulk material, its moisture content and degree of compaction. The parameters of the ellipsoid can be expressed by the interdependence [35]:

$$H=m·D^2$$

(6)

where:

H—ellipsoid height, m;

D—diameter of the ellipsoid, m;

m—proportionality coefficient characterizing the elongation (eccentricity) of the ellipsoids of the discharge and relaxation, m⁻¹.

The physical meaning of the m coefficient corresponds to the section of the upper part of the ellipsoid, which is expressed in units of m⁻¹ [35]. The m coefficient is not a constant value and depends on the physical properties of the output (useful mineral), its moisture content and granulometric composition. The m coefficient is determined experimentally in laboratory conditions. The experiment consists in pouring an appropriate layer of useful mineral into the model of the gangue layer lying above it. Then, the useful mineral is released until dilution occurs. Next, the volume of the mineral discharged from the model should be measured. To determine the “m” coefficient, a physical model was built in a scale of 1:25 with dimensions of 26 cm × 19 cm × 56 cm (length, width, height) (Figure 13). The dimensions of the model were selected in such a way that the model walls did not affect the formation of ellipsoids. Visual observation of the formation of ellipsoids in this case is practically impossible, although the conditions of similarity can be observed by knowing the height of the lowered shelf, the diameter and the depth of the funnel formed on the surface (Figure 14). Lignite in the fraction range of 4–6 mm and clay in the fraction range of 9–12 mm were used for the tests.

In the study, lignite layers of the following heights were released: 16 cm, 20 cm, 24 cm, 28 cm, 32 cm (in real conditions: 4 m, 5 m, 6 m, 7 m, 8 m). The height of the waste rock layer in each experiment was 5 cm. Each layer was released three times, and the average value was used for calculations. The release was carried out through one discharge hole until the waste rock (clay) appeared. The volumes (on the model scale) of released lignite are presented in

Table 4. Laboratory results obtained in determining the proportionality coefficient “m”.

Lignite Shelf Height, cm	Volume of Discharged Lignite, cm3	Coefficient “m”, m−1	Maximum (Calculated) Diameter of the Ellipsoid, cm
16	730 750 760	0.72	9.5
20	1370 1360 1340	0.62	11.4
24	1900 1970 2020	0.61	12.5
28	2560 2840 2850	0.60	13.7
32	3330 3870 3660	0.59	14.7

.

It should be noted that the volume (in real conditions) of the discharged material increases linearly depending on the height of the released layer (Figure 15). Substituting the values obtained from Table 4 into Equation (7) gives the proportionality factor “m”, (Figure 16).

$$m={\displaystyle \frac{\pi ·H^2}{6·V}}$$

(7)

where:

m—proportionality coefficient characterizing the elongation of the ellipsoids of the discharge and relaxation, m⁻¹;

H—Lignite shelf height, m;

V—volume of mined material discharged, m³.

Figure 15. Volume of mined output as a function of the thickness of the lignite shelf.

Figure 15. Volume of mined output as a function of the thickness of the lignite shelf.

Figure 16. The volume of discharged output depending on the height of the lignite shelf until the moment of dilution.

Figure 16. The volume of discharged output depending on the height of the lignite shelf until the moment of dilution.

To verify the specified coefficients, control tests were performed. Three test trials were performed, within which the discharge of lignite layers was modeled for each height of 16–32 cm (in real conditions 4–8 m). The previous physical model was used for modeling. Thin layers of clay were poured into each layer, every 5 cm. During each test, individual phases of discharge and formation of the spill figures were visually observed. When an inflection funnel formed at the boundary of the contact between lignite and waste rock, the release was stopped. Then, the maximum diameter of the ellipsoid was measured on the model (Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21). The measured diameter of the ellipsoid in the model should be consistent with the value calculated for a given coefficient. Knowing the height of the lignite shelf and the value of the coefficient “m”, the actual diameter of the ellipsoids can be determined by substituting it into Equation (8). The results are presented in Table 5.

$$D_E=\sqrt{{\displaystyle \frac{H}{m}}}$$

(8)

where:

D_E—diameter of the ellipsoid, m;

H—height of the lignite layer, m;

m—proportionality coefficient characterizing the elongation of the ellipsoids of the discharge and relaxation, m⁻¹.

Table 5. Real diameters of the ellipsoids for various heights of lignite layers.

Height of Lignite Layer, m	Coefficient m, m−1	Real Diameter of the Ellipsoid DE, m
4	0.72	2.36
5	0.62	2.84
6	0.61	3.14
7	0.60	3.42
8	0.59	3.68

Table 5. Real diameters of the ellipsoids for various heights of lignite layers.

Height of Lignite Layer, m	Coefficient m, m−1	Real Diameter of the Ellipsoid DE, m
4	0.72	2.36
5	0.62	2.84
6	0.61	3.14
7	0.60	3.42
8	0.59	3.68

Figure 17. Formation phases of the ellipsoid of extraction for a 4 m high lignite layer.

Figure 17. Formation phases of the ellipsoid of extraction for a 4 m high lignite layer.

Figure 18. Formation phases of the ellipsoid of extraction for a 5 m high lignite layer.

Figure 18. Formation phases of the ellipsoid of extraction for a 5 m high lignite layer.

Figure 19. Formation phases of the ellipsoid of extraction for a 6 m high lignite layer.

Figure 19. Formation phases of the ellipsoid of extraction for a 6 m high lignite layer.

Figure 20. Formation phases of the ellipsoid of extraction for a 7 m high lignite layer.

Figure 20. Formation phases of the ellipsoid of extraction for a 7 m high lignite layer.

Figure 21. Formation phases of the ellipsoid of extraction for a 8 m high lignite layer.

Figure 21. Formation phases of the ellipsoid of extraction for a 8 m high lignite layer.

Based on the analysis of the obtained model test results, it can be stated that the “m” coefficient changes slightly for layers 5–8 m high. With the increase of the discharged volume of mined material, this coefficient decreases. It should be noted that for a layer 4 m high, this coefficient is 1.16 times higher than for a layer 5 m high. This is due to the fact that at a shelf height of <4 m, the mined material grains move vertically at a higher speed towards the discharge opening. In the first phase, the forming discharge figures in the vertical direction quickly grow upwards, and in the second phase, these figures widen in the horizontal direction. Based on the calculations and control tests performed, it can be stated that the values of the coefficients presented in Table 5 are identical and constant for specific heights of lignite layers. It should be noted that the ellipsoid elongation coefficient decreases slightly depending on the increase of the minor and major semi-axis of the ellipsoid of relaxation.

5.3. Construction of the Physical Model

In order to analyze qualitative and quantitative extraction indicators in mining systems, physical modeling was carried out, which allows determining the formation of losses and dilution occurring in the release process. When changing geometric parameters (height of the roof shelf) and technological parameters (collection, release organization), it is possible to determine the most optimal variant of the mining system with minimal losses and dilution. The model must be constructed in such a way that it is possible to carry out tests in it several times with the possibility of visual observations necessary for documentation and analysis of the obtained results. Individual structural elements must be made so that the entire modeling process runs smoothly. A physical model in 1:25 scale was designed and built to determine lignite losses and dilution. The longwall top coal caving system model consists of: a frame measuring 155 cm × 38 cm × 52 cm (Figure 22a,c), and a tank measuring 50 cm × 36.5 cm × 90 cm (length, width, height) made of 8 mm thick Plexiglas plates, simplified 6 sections of the BMV 1Mi powered roof support (Figure 22b) made of 2 mm thick black sheet metal. The width of the section is 6 cm, the height is 12 cm, and the angle of inclination of the caving shield is 30°. Each section has a drain hole measuring 3.5 cm × 4 cm (width, height) opened by means of a steel cable with a handle attached to the end. Each section is moved independently along the entire length of the model. This is achieved by means of a rotary movement of the threaded rod, along which a nut integrated with the section moves linearly. The material released by gravity spills between the guides onto a chute directed towards a container placed on the floor. A modeling scale was adopted that guarantees the achievement of correct results, close to real conditions.

6. Experimental Studies on the Constructed Physical Model of the Longwall Top Coal Caving

The aim of laboratory experiments conducted on a physical model was to determine the value of losses and dilution occurring in the process of drawing lignite and to limit them, taking into account the factors presented below. Based on the model tests carried out on auxiliary models, it was found that the following factors have a fundamental influence on the discharge mechanism, including losses and depletion:

H—shelf height, m;

d—granulometric composition, mm;

z—advance, m;

γ—angle of inclination of the collapse shield, °;

s—dimensions of the discharge window, mm;

n—organization of drawing.

Before starting the modelling studies, the following assumptions were made:

• the longwall top coal caving mining method with the discharge of mined material should be modeled in relation to the phase of progressive exploitation,
• the discharge will take place after 2.4 and 6 cuts with the cutting drum removed by 0.6 m, taking into account the step of the powered roof support section,
• the discharge of excavated material should be carried out in individual sections.

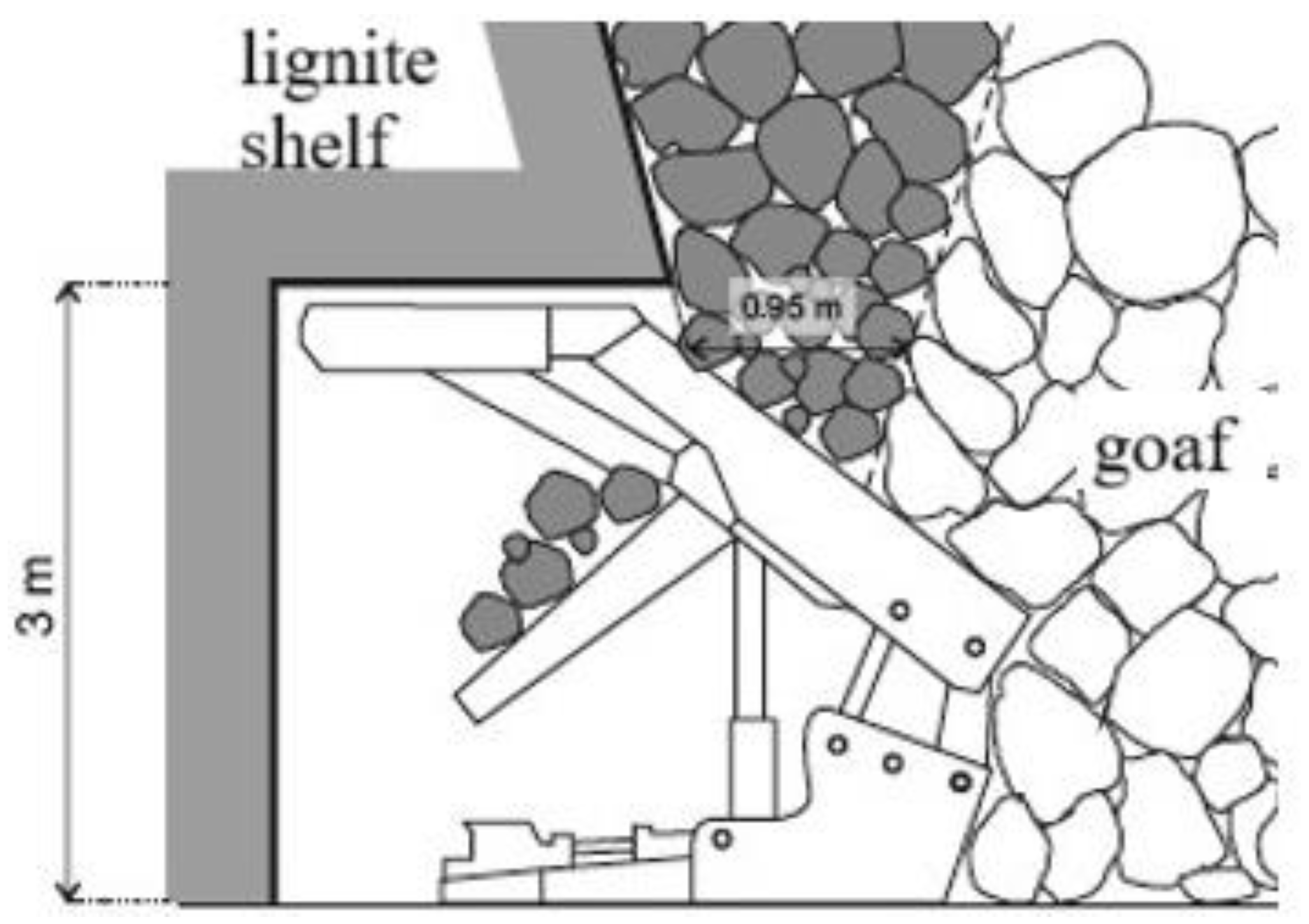
In order to obtain reliable results of the formation of losses and dilution, the process of discharge should be modeled during the normal course of exploitation, and not during the remaining phases of exploitation, i.e., during start-up and liquidation of the longwall excavation. Before starting the model tests, it was necessary to determine the angle of inclination of the plane between the waste rock and the useful mineral during the course of developed exploitation. In order to determine the angle of inclination of the plane between the waste rock and the useful mineral, an experiment was performed on a physical model in a scale of 1:25. The average height of the lignite shelf was assumed to be 24 cm, which corresponds to the thickness of the actual layer of 6 m. A layer of waste rock (clay) was piled above the lignite shelf. The powered roof support section was positioned in the model in such a way that the rear wall of the model did not affect the angle of inclination of the contact plane created during the discharge. Discharge was carried out from one discharge hole of the powered roof support section until gangue appeared in the hole. When gangue appeared in the hole, the angle between the contact of lignite and clay was measured. This angle was 10°. When the waste rock reached the discharge hole, a discharge funnel was formed on the surface, which widened in the direction of the powered roof support advance. The support was advanced after 4 cuts (every 4.8 cm) with a section step of 2.4 cm (in real conditions 0.6 m). After each advance, the angle of inclination (of the lignite shelf during discharge) was measured. This angle was constant along the entire length of the model and amounted to 10°. It is assumed that this angle will be the same for each layer in the discharge process regardless of the number of cuts. During the tests, the active zone of influence of the discharge hole was also determined (Figure 23). The width of the active zone was 0.95 m (Figure 24).

In Figure 25a–f, the waste rock gradually reached the outlet of the powered roof mechanized support. The zone of influence of the outlet is formed in the form of a paraboloid of rotation, and as the figure approaches the opening, it takes the form of a cone. In the undermining systems, the process of releasing is time-consuming and requires appropriate organization, i.e., the method and order of drawing the output. The organization of releasing can have a negative effect on the amount of losses and dilution. In the longwall top coal caving method, the technological cycle consists of several phases. In the first phase, the base layer is exploited. In the second phase, the scraper conveyor with the support moves. In the third phase, the lignite shelf is discharged. The discharge of the lignite shelf takes place simultaneously along the entire length of the longwall. During the discharge, the mining in the bottom layer is stopped, only the discharge takes place. In the case of shortwall workings, this method is most advantageous. The situation in the case of longwall workings changes slightly. Stopping the longwall face for one or two shifts has an adverse effect on maintaining the longwall workings and limits the mining process, thus limiting the progress of the longwall front. In order to improve the smoothness of exploitation and the release of output, it is assumed that in the case of a long longwall workings front, they should be divided into sections. Dividing the longwall into sections will allow the discharge of output during the mining of the solid. The number of sections depends on the length of the longwall working.

In the model tests, a section of 36 cm width was assumed, which corresponds to 9 m in real conditions and 6 sections of powered support. In the tests, lignite shelves were modeled with heights of: 16 cm, 24 cm, 32 cm (in real conditions: 4 m, 6 m, 8 m). Real material was used for the tests: lignite with granulation in the range of 4–6 mm and clay with granulation in the range of 9–12 mm. In the initial phase of modeling, the powered roof support sections were set in one line under a partition attached to the model longwalls at an angle of 10°, (Figure 26) in order to reflect the exploitation during normal exploitation. Each section had a number. First, the appropriate amount of lignite was poured into the model to the determined thickness of the lignite shelf. The ore was discharged evenly and serially, from section no. 1 to section no. 6. When the ore was discharged evenly and serially, the contact boundary of lignite with the waste rock was maintained at one level. In such a case, the output moves evenly. This excludes premature dilution of the output. The entire discharge cycle was carried out in the same order until dilution occurred. When the waste rock appeared in the discharge opening, the discharge was stopped by closing the discharge opening flap. The adopted modelling scale (1:25) is the result of a compromise between the possibility of making original mechanical models of a powered, active support (Figure 22 and Figure 26), with mechanisms enabling its movement during the experiment, with the required size of the container for crushed rock material and the size of individual grains on the one hand, and on the other hand the dimensions of the mine workings, which served as a kind of field laboratory.

Figure 27 shows an example laboratory experiment allowing for visual observation of layers in the individual phases of ore release and the discharge figures formed above each hole. The ore moved steadily towards the holes until a dilution occurred. The resulting figures took the form of a semi-ellipsoid of revolution. The apex of the ellipsoid of release (red) above the first hole reached the contact boundary between lignite and gangue.

The ellipsoids formed over the adjacent holes had approximately the same geometric parameters and their side walls were tangent. When the release from the adjacent holes is continued, the ellipsoids (yellow) will overlap. In such a case, this phenomenon causes the reduction of the so-called dead zones formed in the form of combs between the holes (Figure 28), minimizing losses between the holes.

7. Analysis of Modeling Results on the Physical Model

The modeling studies focused mainly on two key factors that largely affect the losses and dilution of the useful mineral. The first factor is the height of the lignite shelf. In the case of thick seams, the optimal shelf height can be achieved by dividing the thick seam into appropriate layers in order to obtain the lowest possible losses and dilution. The second, also important factor is the removal, i.e., moving the powered mechanized roof support section by a specified length, after performing an appropriate number of cuts. During the studies, the dependence and relationships between the above-mentioned factors were analyzed. As previously mentioned, lignite shelves of 16 cm, 24 cm, 32 cm height were released. For each lignite shelf, 4 sampling attempts were made. The powered roof support sections were moved by: 2.4 cm, 4.8 cm, 7.2 cm, 9.6 cm (in real conditions 0.6 m, 1.2 m, 1.8 m, 2.4 m), respectively. Based on research, it was determined that the optimal advance was 1.2 m. This is related to the shaping and elongation of the top of the ellipsoid of loosening. The distance between the discharge holes also has a significant impact. The first release was marked as zero (i.e., without any section displacement). In the next stage, the powered roof support sections were moved by a specified set, starting from section no. 1 to section no. 6, (Figure 29a–c). After moving the section, the first collection was discharged, Figure 29. After the discharge was completed, the section bases and guides were cleaned using special devices. The entire cycle was repeated up to the boundary of the front wall of the model, (Figure 29d–f). After each discharge, the mined material was sorted manually and using a sieve. The sorted material (lignite, clay) was weighed and documented for analysis.

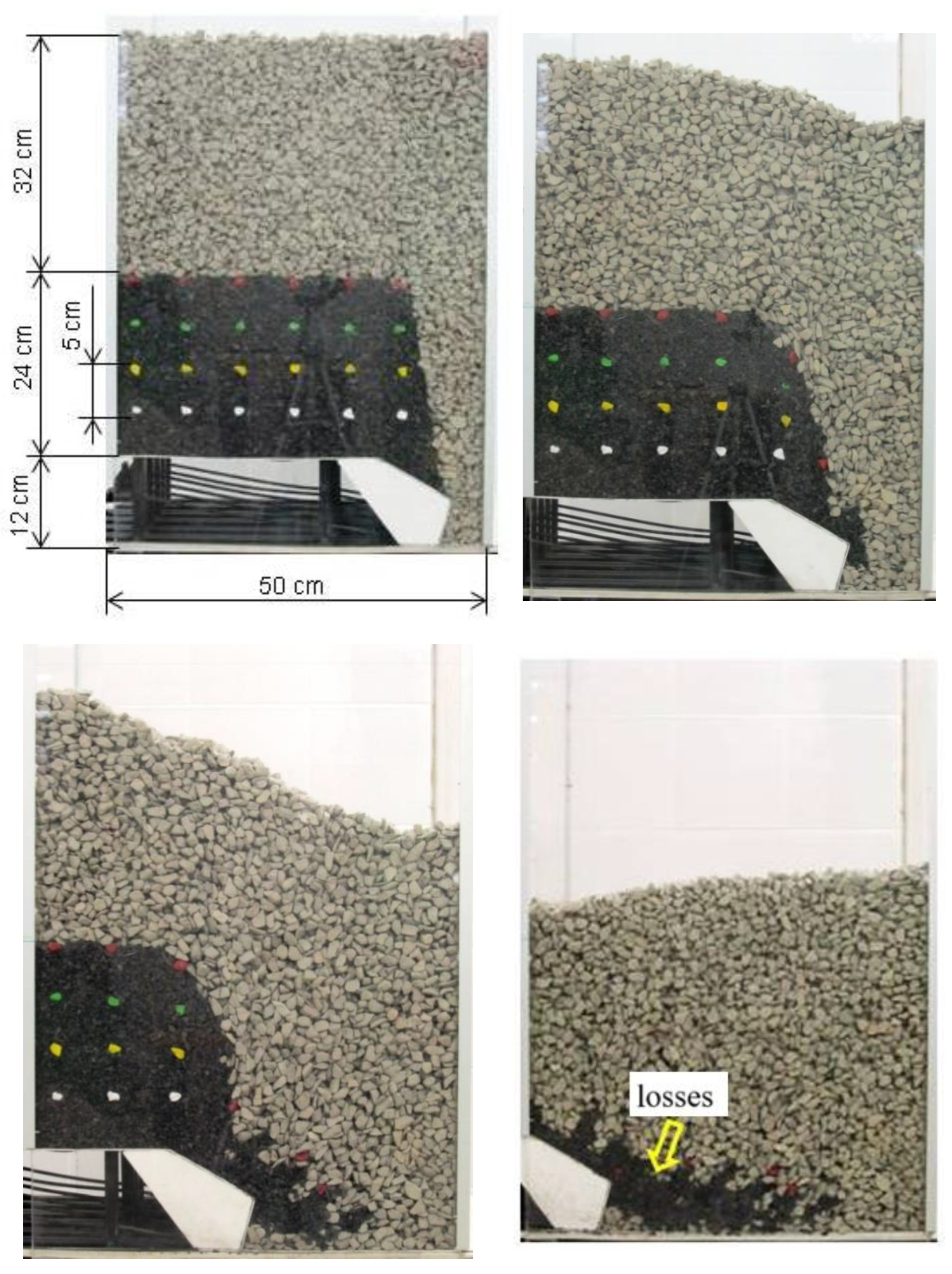
Figure 30 shows the phases of drawing a 4 m high lignite shelf. White and yellow markers were placed in the lignite layer. As the mined material was discharged, these markers gradually reached the discharge opening of the powered roof support section. One yellow marker remained in the goaf, the remaining markers were discharged through the discharge opening. Seven 4.8 cm long cuts were made during the tests. The discharge in individual cuts is shown in Figure 31. The losses visible in the figures were shaped as an irregular layer in the bottom part. In the case of drawing mined material from a 6 m high lignite shelf (Figure 32), markers in four colours (white, yellow, green, red) were placed in the layer. During the discharge, white, yellow and green markers were discharged. One green marker and 4 red markers remained in the goaf. It should be noted that after each section shift (7 cuts of 4.8 cm length) the losses formed in the shape of so-called combs. The discharge in the individual cuts is shown in Figure 33. When the 8 m high lignite shelf was discharged (Figure 34), 5 colored markers (white, yellow, green, orange, red) were placed in the layer. One orange and two red markers remained in the goaf. The losses formed in the shape of indistinct combs. In this case, attention should be paid to the trajectories of the orange and red markers. The number of removals was the same as in the previous cases. The course of the discharge of the output is shown in Figure 35. Figure 36 shows for comparison the final stages of laboratory experiments in the case of 4 m, 6 m, 8 m high lignite shelves with a 1.2 m take-off. It should be noted that in the case of the 4 m high seam almost all markers placed in the individual layers were discharged, although the yellow marker remained in the goaf. In the next experiment, i.e., the discharge of the 6 m high layer, markers were placed in the goaf in the penultimate and last layer. When the 8 m layer was discharged, the situation repeated, but the number of red markers is smaller in this case.

The next stage included model tests, which modelled the release of a 6 m high lignite shelf with cuts of 0.6 m, 1.8 m and 2.4 m. When changing the cut, one can visually observe the amount of accumulated ore in the goaf (losses) and the form of its formation. The form of the loss formation depends on the length of the cut, as well as on the height of the lignite shelf. Modelling was carried out using a cut of 0.6 m length (Figure 37). The sections of the powered roof support were moved by 2.4 cm, performing 14 cuts (Figure 38). During the release of the zero cut, all markers were discharged except for one red one, which then reached the discharge opening during the discharge of the first cut. A total of 5 cuts of 1.8 m length were made (Figure 39). Losses located in the goaf were formed in the form of distinct combs. In the goaf, 5 red markers were retained, at approximately the same height (at the top of the combs) and one green marker. As can be seen in Figure 40, the largest amount of output was discharged during the 4th cut, and the smallest amount, during the discharge of the last cut. During the discharge of the 6 m high lignite shelf, 4 cuts of 2.4 m length were made (Figure 41). In the goaf, one marker from each layer remained, including 4 red ones from the last layer. Losses were formed in the form of wide combs created after each shift of the powered roof support section. During the discharge of the third cut, the largest amount of ore was discharged (Figure 42). For comparison, the shape of losses during cuts of 0.6 m, 1.2 m, 1.8 m, 2.4 m is presented (Figure 43).

Losses arising in the release process can be analyzed in mass and volume units. The most accurate results can be achieved when considering losses in mass. Since the bulk density of the useful mineral and the gangue are different, a method based on volume measurement is used to determine depletion. The bulk density of the bulk material used for testing (lignite, clay) was determined according to the PN-EN 1097-3:2000 standard [36]. Three tests were performed for each material and the average value was calculated, which for lignite was 0.684 kg/dm³, and for clay 0.955 kg/dm³. The mass of the released useful mineral and waste rock was divided by the bulk density, then to obtain the volume, these values are substituted into the equation and we obtain the depletion of the mined material. Losses of the useful mineral were determined using the equation:

$$S={\displaystyle \frac{M_n-\sum M_w}{M_n}}·100,\%$$

(9)

where:

S—lignite losses, %;

M_n—mass of lignite in the model, kg;

∑ M_w—total mass of discharged lignite (in each advance), kg.

Dilution was defined as follows:

$$Z={\displaystyle \frac{V_{sp}}{V_{sp}+V_L}}·100,\%$$

(10)

where:

Z—dilution of the output, %;

V_sp—volume of discharged waste rock, dm³;

V_k—volume of discharged lignite, dm³.

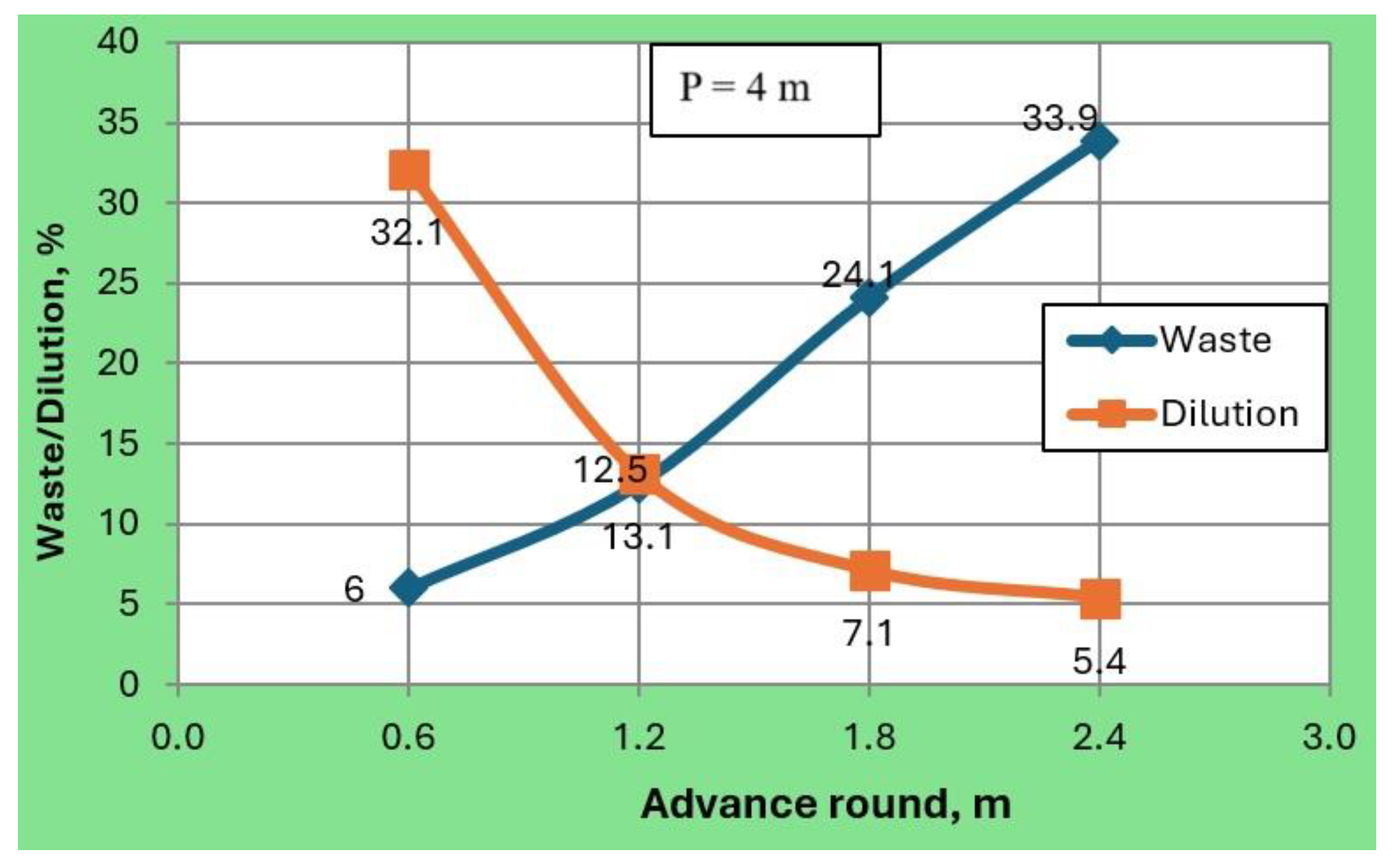
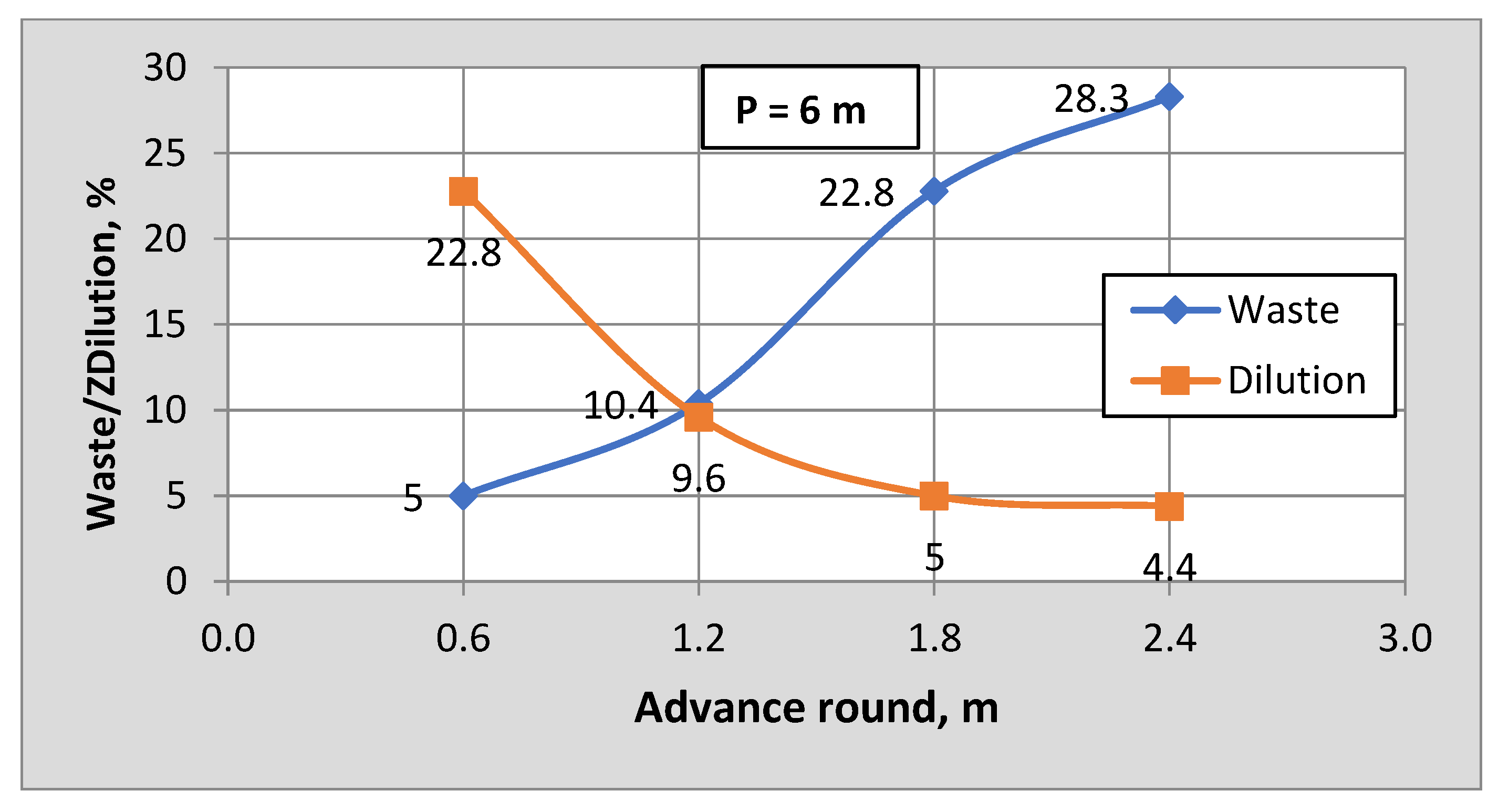
For a 4 m high shelf of lignite, losses ranged from 6–33.9%, while dilution ranged from 5.4–32.1% (Figure 44). It should be noted that for the 0.6 m advance, dilution was 32%. For the 6 m high shelf of lignite, losses ranged from 5–28.3%, dilution ranged from 4.4–22.8% (Figure 45). Losses for the 8 m shelf ranged from 4.6–30.5%. Dilution ranged from 3.9–17% (Figure 46).

Based on the cited research results, it can be stated that losses increase with the increase in the length of the cut, while the dilution decreases. Analyzing the summary graph of losses (Figure 47) resulting from the discharge of lignite shelves, it can be seen that the height of the shelf does not have a significant effect on the amount of losses. Based on the summary graph of the formation of dilution (Figure 48), it was observed that with the increase in the length of the cut, the dilution decreases. The greatest dilution was achieved in the case of a cut of 0.6 m, while the minimum was achieved in a cut of 2.4 m. Analyzing the courses of the discharge of mined material after each cut, it was found that the changes in the courses were caused by the different degree of compaction of the mined material poured into the model, which caused the loosening ellipsoid to deflect from the axis and for this reason more mined material was discharged than in the previous and next cuts.

8. Conclusions

The model tests showed that the granulometric composition of the output has a significant effect on the process and mechanism of discharge through the discharge opening. As the grain size of the ore increases, the zone of influence of the discharge opening widens, which increases the unit amount of the discharged output. The smaller the zone of influence of the opening, the greater the losses. It was shown that the shelf thickness has a slight effect on the losses and dilution of the output. The best method of discharge in the applied mining system is the even-series method. The use of this method allows for smooth movement of the output towards the discharge openings. This method excludes premature dilution from the adjacent discharge openings, because the output moves in one line of contact with the waste rock.

It was determined that in order to ensure effective and smooth discharge, the mined material should be discharged by dividing the longwall into sections. Discharge in sections limits unforeseen downtimes associated with mining and moving the support, while the displacement of the support and discharge are carried out simultaneously.

The analysis of the results of physical and numerical modeling shows that the agreement between both methods is very high, with a correlation coefficient of 0.968. In terms of the relationship between the height of the lignite shelf and the extraction index, this coefficient was 0.998, while depending on the length of the cut, it was 0.982.

In the top coal caving mining method used in the Novaky mine, losses were determined to be in the range of 6.0–33.9%, and dilution in the range of 3.9–32.1%. The greatest influence on losses and dilution is the length of the cut. With a smaller cut, losses are greater, while dilution increases significantly. With an increase in the length of the cut, losses increase, and dilution decreases significantly. With a small cut, the ellipsoid of loosening gradually reaches the vertical boundary of the contact of the ore with the waste rock, which consequently causes premature dilution.

By increasing the length of the cut, the loosening ellipsoid moves away from the vertical boundary of the contact of the output with the waste rocks, and when its maximum diameter is reached, this ellipsoid does not exceed the boundary of the contact of the output with the waste rocks. The best results were achieved with the use of a 1.2 m long cut when drawing lignite shelves with a thickness of 4 m, 6 m, 8 m, which means that with a cut of 1.2 m, minimal losses and dilution were achieved. Minimizing losses in the discharge process allows for better use of the deposit. Minimizing the dilution of output limits the amount of waste rocks extracted, which increases the costs of the system, especially the haulage and transportation of output. The optimal loss/dilution ratio depends on the economic analysis of the system costs, for which the obtained research results can be the basis.