Abstract
The evaporation dynamics of droplets on smooth and inclined micro-pillar surfaces were experimentally investigated. The surface temperature was increased from 50 °C to 120 °C, with the inclination angles being 0°, 30°, 45°, and 60° respectively. The dynamic parameters, including contact area, nucleation density, bubble stable diameter, and droplet asymmetry, were recorded using two high-speed video cameras, and the corresponding evaporation performance was analyzed. Experimental results showed that the inclination angle had a significant influence on the evaporation of micro-pillar surfaces than smooth surfaces as well as a positive correlation between the enhancement performance of the micro-pillars and increasing inclination angles. This angular dependence arises from surface inclination-induced tail elongation and the corresponding asymmetry of droplets. With definition of the one-dimensional asymmetry factor (ε) and volume asymmetry factor (γ), it was proven that although the asymmetric thickness of the droplets reduces the nucleation density and bubble stable diameter, the droplet asymmetry significantly increased the heat exchange area, resulting in a 37% improvement in the evaporation rate of micro-pillar surfaces and about a 15% increase in its enhancement performance to smooth surfaces when the inclination angle increased from 0°to 60°. These results indicate that asymmetry causes changes in heat transfer conditions, specifically, a significant increase in the wetted area and deformation of the liquid film, which are the direct enhancement mechanisms of inclined micro-pillar surfaces.
1. Introduction
With prominent heat transfer capability and advantages such as convenient arrangement, easy control, and simple operation, spray cooling has been widely adopted in high heat flux applications including solar thermal utilization [1], nuclear reactor cooling [2], and the thermal management of high-power electronic devices [3]. To optimize the heat transfer efficiency of spray cooling, various micro-pillar surfaces [4,5] have been implemented to enhance droplet evaporation, following extensive research on key influence factors such as geometric shapes [6,7], micro-pillar arrangements [8,9], surface wettability [10,11], and inclination angles [12]. Nevertheless, the inclination angle of the micro-pillar surface induces pronounced droplet asymmetry and complicates droplet evaporation. Therefore, droplet evaporation, particularly its dynamic evolution on inclined micro-pillar surfaces, still warrants further investigation to provide more in-depth insights.
The scientific investigation of droplet impact evaporation began with Worthington’s seminal work [13]. The evaporation kinetics of a droplet under low-temperature impact was generally considered to be governed by three competitive mechanisms: convective transfer at the liquid–gas interface, surface roughness effect, and wettability characteristics [14]. Researchers have systematically explored the influences of key parameters such as surface temperature [15,16,17], surface roughness [18], droplet volume [19,20], and Weber number [21,22] on droplet dynamics during vertical impact onto heated horizontal surfaces. Misyura [23,24] demonstrated that a rough copper surface had a better heat transfer performance than a smooth gold surface and a non-monotonic trend of the critical heat flux with solution concentration. Song et al. [25] demonstrated that anisotropic grooves on the surfaces strongly promoted the droplet recoil parallel to the grooves. The larger the ratio of groove area to surface, the stronger the anisotropy of the droplet. Hays et al. [26] observed that the higher the proportion of the cavity on superhydrophobic microstructures, the longer the evaporation time, and the worse the heat transfer of droplets. In fact, adding micro-structures is always accompanied by a change in wettability, which leads to a lack of the separate analysis of mechanisms. Meanwhile, the ambient medium and temperature also play a role. Gaggilla et al. [27] reported a 30% heat transfer enhancement for droplet boiling in steam compared with in air. At the same time, the temperature difference between the surface and ambiance directly affects convective transfer at the liquid–gas interface. Mollaret et al. [28] proved that the rise in surface temperature significantly altered the evaporation rate and wetting state on hydrophilic aluminum, and its effect was minimal on PTFE. However, as soon as the surface temperature rose above the Leidenfrost point, the changes in droplet diameter and thickness were almost independent of wall roughness [28,29]. Tang et al. [30] further noted that the spreading diameter increased with Weber number but decreased with wall roughness.
Compared with the above classical impact, inclined impact has been proven to have a better heat transfer performance due to the additional rolling or sliding of droplets. Wang et al. [31] observed that the heat transfer performance and cooling efficiency of inclined impact at 49° were increased by 60% compared with vertical ones. Ravikumar et al. [32] cooled a stainless-steel surface with water and obtained the best spray cooling effect at a nozzle inclination angle of 30°. Li et al. [33] proved that the cooling performance of a microelectronic maintained well with inclination angles below 50°, and once the inclination angle exceeded 50°, the cooling performance deteriorated. Silk et al. [34] experimentally demonstrated that spray cooling efficiency was 75% higher at a 30° spray angle compared with perpendicular spraying. Liu et al. [35] observed that heat transfer efficiency initially increased and then decreased as the spray angle increased from 15° to 30°, with the best heat transfer performance at 18°. Zhang et al. [36] demonstrated that for a flat surface, the cooling rates were similar for spray angles of 0° and 15° and were superior to the case of 45°. However, on rough surfaces, the spray cooling showed the best performance at a spray angle of 0°. The above research confirmed that there is an optimal spray angle for droplet evaporation on a surface, and different surfaces exhibit different optimal spray angles. At the same time, Li et al. [37] and Sani et al. [38] noted that the inclined angle of surfaces changed the droplet’s dynamic behaviors such as spreading and rebound coefficients of the droplet. Of course, in addition to the inclined angle, the dynamic behavior of droplets on an inclined wall is also closely related to the wall temperature and impact velocity [39]. Therefore, adjusting both the droplet impact angle and the inclination angle of surfaces can regulate the droplet dynamic behavior and further affect the spray cooling performance.
On micro-structured surfaces, the heat-transfer enhancement always involves modulations in droplet dynamics. Displaying the details of droplet dynamics is the foundation for revealing the enhancement mechanism. Deendarlianto et al. [40] systematically investigated the dynamic influences of key parameters on the droplet impact process on an inclined heated wall. The results showed that the higher the wall roughness, the shorter the droplet evaporation time. Although the results analyzed obvious dynamic characteristics on the inclined surface, the contact angle dynamics were not taken into account in the analysis. In the meantime, Remer et al. [41] also pointed out that the dynamics of the contact angle resulting from fluid flow more accurately reflected the surface physicochemical properties than the values obtained from static and quasi-static measurements. Following that, Pittoni et al. [42] started to use the “dynamic contact angle” to describe the interfacial motion when droplets impact walls. Ahmed et al. [43] conducted a further experiment to describe droplet morphology using the advancing and receding angles of impact droplets on inclined surfaces. In addition, Deendarlianto et al. [44] conducted micro-droplet impact on 304 steel plates with different inclination angles and captured the dynamic behaviors of contact angles corresponding to two micrometric-size droplet types, which provided experimental data for the contact angle dynamics. Although these studies revealed the significant influence of factors such as surface inclination, temperature, and morphology on droplet evaporation, there is still a lack of understanding regarding the internal dynamics of droplet evaporation on heated silicon surfaces, the actual morphologies of evaporating droplets on various inclined surfaces and microstructures.
This work studies the morphological evolution and internal dynamics of a droplet boiling on smooth, micro-pillar, and inclined heated surfaces. Nucleation density, bubble diameter, and bubble distribution were all recorded in detail through high-speed visualization techniques. Furthermore, the enhancement mechanism of micro-pillars for droplet evaporation on inclined heated substrates is discussed, which facilitates a clearer understanding of droplet boiling on inclined micro-pillar surfaces.
2. Experimental Apparatus and Procedure
The visual experiment platform mainly consisted of a droplet boiling section and the data acquisition system, as shown in Figure 1. The droplet boiling section included three parts: a droplet generator (MD, maximum error of 1.5%), a monocrystalline silicon chip, and a temperature control system. The droplet generator utilizes a stepper motor propeller and a syringe equipped with a 0.1 mm terminal diameter needle to precisely control the volume of deionized water droplets to 6 μL. The distance of the syringe from the silicon chip was controlled at 20 mm, and the Weber number of liquid droplets was calculated to be 6. Two silicon chips (size of 30 × 30 × 0.6 mm3) were used in the experiments: one had a smooth surface, the other had a micro-pillar surface with a micro-pillar size of 50 × 50 × 50 μm3 and pillar spacing of 100 μm. The static contact angles of the smooth and micro-pillar surfaces were 68° and 142°, respectively. The silicon chips were adhered to the temperature control plate using an insulating and high-thermally conductive silica-gel, in which three K-type thermocouples had been embedded in advance. An Agilent 34970A data acquisition unit (DAQ) with a sampling rate of 800 Hz was used to record and store the temperature data. The temperature control system maintained the surface temperature of the silicon chip with an error of a limit of 1 K. Boiling dynamics were captured using two high-speed cameras. A high-speed camera (Optronis CP80-4-M-500, Rocketech technology Corp., Ltd, Changsha, China; 2304 × 1720, 87,000 FPS, with macro lens) was fixed above the sample to record the evolution of the droplet outline and boiling bubbles within it, and another high-speed camera (Revealer 2F04M, Zhongke Junda Vision Technology Co., Ltd, Hefei, China; 640 × 480, 1260 FPS) was installed in front of the experimental set to capture the changes in the droplet’s side profile.
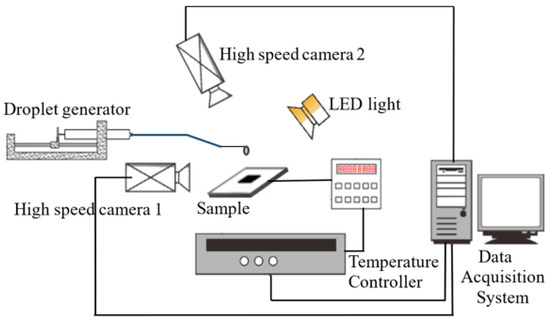
Figure 1.
Schematic of the experimental apparatus.
For the experiments, samples were rinsed with acetone, anhydrous ethanol, and deionized water in turn, then heated to the test temperature (50 °C to 120 °C), where the maximum temperature fluctuation was controlled under 1 K. The inclined angle θ was adjusted through an adjustable bracket under samples with the values of 0°, 30°, 45°, and 60°, respectively. Each experiment was repeated at least 5 times to improve the data accuracy. To reduce the influence of ambient on heat and mass transfer at the liquid–gas interface of droplets and comparatively analyze the internal boiling adjacent to the heated surface, the ambient temperature and relative humidity were maintained at 20 °C and 15% RH during all experiments.
3. Results and Discussion
3.1. Heat Transfer Performance
Figure 2 shows the droplet boiling curves on the smooth and micro-pillar array surfaces with different inclination angles, where T denotes the surface temperature and t is the droplet evaporation time. When the inclination angle of the smooth surface increased from 0°, 30°, 45° to 60°, the droplet evaporation times were 445, 417, 413, and 384 s at 50 °C; 57, 53, 51, and 41 s at 90 °C; 30, 27, 26, and 23 s at 110 °C. This means that increasing the surface inclination angle from 0° to 60° reduced the evaporation time by 14% at 50 °C, by 20% at 90 °C, and by 23% at 110 °C, while the evaporation time decreased by 94% as the surface temperature rose from 50 °C to 110 °C for the 60° inclined surface. The droplet evaporation time decreases significantly with increasing surface temperature, while the effect of the inclination angle is relatively weak on the smooth surface. When the inclination angle of the micro-pillar surface increased from 0°, 30°, 45° to 60°, the droplet evaporation times were 335, 278, 243, and 198 s at 50 °C; 37, 31, 25, and 23 s at 90 °C; and 16, 14, 11, and 10 s at 110 °C. This means that increasing the surface inclination angle from 0° to 60° significantly reduced the evaporation time by 41% at 50 °C, by 38% at 90 °C, and by 38% at 110 °C. Therefore, the effect of inclination angle cannot be ignored any further. At the same time, the surface temperature still had the main impact on the evaporation time. At θ = 60°, the evaporation time decreased by 95% as the surface temperature rose from 50 °C to 110 °C. Compared with smooth surfaces, the decrease in the droplet evaporation time on the micro-pillar surface was not only due to the increase in surface temperature, but also the inclination angle.
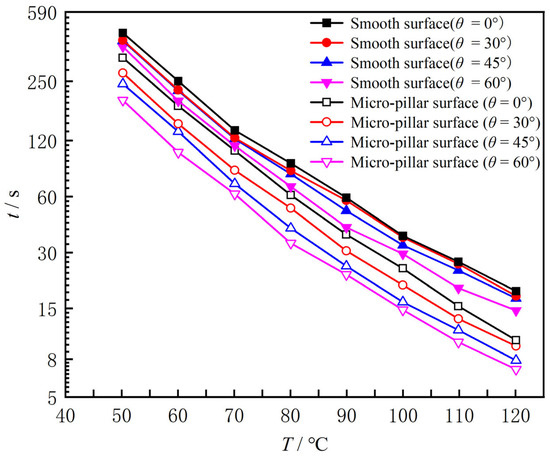
Figure 2.
Droplet boiling curves.
Compared with the smooth surfaces, all evaporation times on the micro-pillar surfaces were significantly shorter due to enhanced droplet evaporation. An enhancement factor β is defined as follows:
where ts and tp represent the droplet evaporation time on the smooth and micro-pillar surfaces, respectively, under identical surface temperature and inclination angle conditions. The fitted curves shown in Figure 3 indicate that the enhancement factor β for 0°, 30°, 45° increased monotonously without minimum values. The values of β increased by 0.12, 0.10, and 0.05, respectively, from 50 to 120 °C. It is worth noting that due to the existence of the micro-pillar structure, when droplets slide over the micro-pillars, interface oscillations at the bottom of droplets are inevitable, causing the evaporation time to vary discontinuously and be significantly dispersed compared with that on a smooth surface. Therefore, the error bar range in five experiments under certain conditions (e.g., θ = 0°, T = 70 °C) was relatively large, and even exceeded 100% of the difference captured over the entire temperature range. When the inclination angle of boiling surfaces was 60°, the enhancement factor β first decreased and then increased with the rise in surface temperature, reaching a minimum value at T = 80 °C. As shown across the whole temperature range, the average value of the enhancement factor of the micro-pillar surfaces with inclination angles of 0°, 30°, 45°, and 60° was 1.30, 1.35, 1.43, and 1.50, respectively. This means that the enhancement factor β was significantly increased by about 15% relative to the smooth surfaces when the inclination angle increased from 0°to 60°, indicating that the enhancement effect of micro-pillars on evaporation becomes more pronounced on inclined surfaces. Compared with the inclination angle, the temperature exerts a non-monotonous and more complex influence on β.
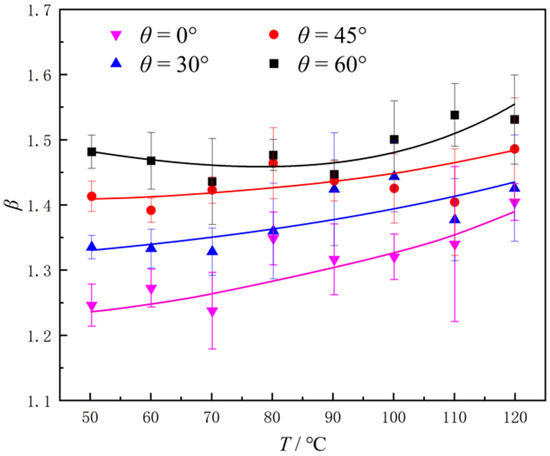
Figure 3.
Enhancement factors of heat transfer on micro-pillar structured surfaces with different inclination angles.
3.2. Classical Characters of Nucleation Boiling
3.2.1. Contact Area
When a droplet impacts on an inclined surface, it bounces and slides on a smooth surface, whereas on a micro-pillar surface, almost no bouncing occurs but it quickly enters a sliding state with an obvious tailing. At the moment of completing sliding, the droplet presents a steady morphology and then enters the evaporation process. The steady morphology of an impacting droplet on a surface is influenced by liquid properties, impacting the height, surface state, and surface inclination angle. Figure 4 presents the steady morphology of impacting droplets on smooth and micro-pillar surfaces at different inclination angles. As shown, whether viewed from the top or side, the droplet on the horizontal smooth surface is nearly a symmetrical circle. As the surface inclination angle increases, the gravitational component along the inclined surface strengthens, and the droplet gradually loses symmetry. As the inclination angle θ increases from 0° to 60°, the advancing contact angle increases by 12°, while the receding contact angle decreases by 12°. Although the hysteresis between advancing and receding angles induces a slight droplet deformation in top-view observations, the steady shape of the droplet on a smooth surface remains approximately circular. On the horizontal micro-pillar surface (θ = 0°), the droplet remains symmetrical but exhibits a smaller contact angle than that on the smooth surface due to the presence of micro-pillars. As the wall inclination angle θ increases from 0° to 60°, the receding angle of the droplet continuously decreases by 62°, and the advancing angle first increases from 65° to 72.5 ° at θ = 30° and then decreases to 45.5° at θ = 60°. On the micro-pillar surface, the surface tension at the three-phase line causes a significantly trailing tail and an elongation of the droplet, which leads to a great increase in the contact area.
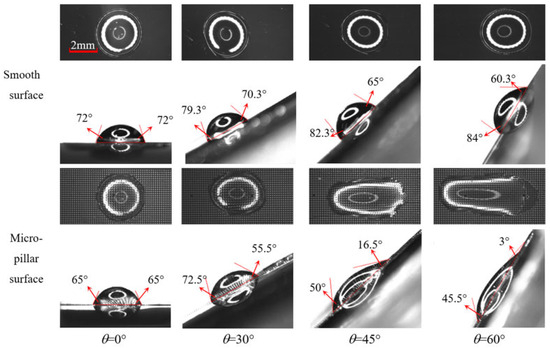
Figure 4.
Morphology of droplets after impacting and slipping on various surfaces.
Figure 5 shows a comparison of the heat transfer area of droplets. At θ = 0°, the heat transfer area on the micro-pillar surface was 1.42 times greater than that on the smooth surface. Although the trace gas was captured at the root of the micro-pillars (as a light cycle around each micro-pillar shown in Figure 6), the reduction in the micro-pillar surface by the trace amount of gas was small and negligible compared with the increased area due to the pulling of micro-pillars on the gas–liquid interface. The stable contact diameter of the droplet on the micro-pillar surface was greater than that on the smooth surface even at θ = 0°, not to mention the larger area-increase caused by the tailing and sliding on the inclined surface. As the value of θ increased from 0° to 60°, the droplet contact area on the smooth surface increased by 15.8% from 9.076 mm2 to 10.514 mm2, while the heat transfer area on the micro-pillar surface increased by 116.8% from 13.203 mm2 to 28.622 mm2. For the same inclination angle θ = 60°, the heat transfer area on the micro-pillar surface was 2.72 times larger than on the smooth surface. This means that the enhancement effect of increasing the heat transfer area can be further amplified by increasing the inclination angle on the micro-pillar surface.
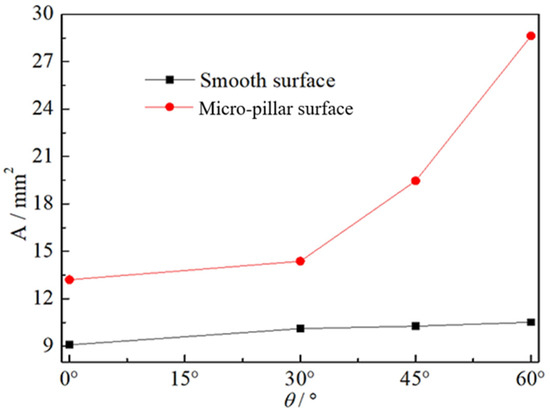
Figure 5.
Heat transfer area of droplets on surfaces with various inclination angles.
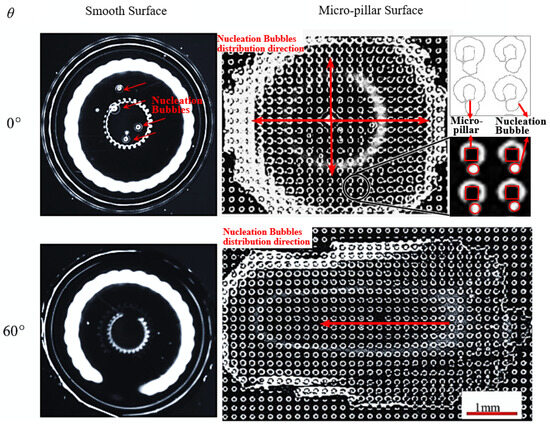
Figure 6.
Morphology of nucleation bubbles in droplets on smooth and micro-pillar surfaces (T = 90 °C).
It should be noted that both the contact area and the liquid film thickness significantly affect droplet evaporation. On smooth surfaces, the contact area and droplet thickness show a minimal change, even if droplet slippage occurs on inclined surfaces. While accompanied by the sliding and tail elongation of the droplet on inclined micro-pillar surfaces, the shape of the droplets shows an asymmetric deformation. In the thin liquid film region, the boiling bubble growth is confined [45]. The deformation of droplets and uneven thickness lead to a complex distribution in nucleation site density and bubble stable diameters.
3.2.2. Nucleation Site Density
Following the droplet impact and rebound process, trace amounts of non-condensable gas become entrapped at the droplet center, forming homogeneous nucleation sites on the smooth surface, as shown in Figure 6. However, when the droplet slides down from an inclined smooth surface, the asymmetrical contact angle facilitates non-condensable gas escape, causing most nucleation sites to dissipate. On a horizontal micro-pillar surface, the droplet impacts the surface with the liquid–gas interface sinking into the micro-pillar gaps. Trace gas shielded at each micro-pillar bottom is trapped. As shown in Figure 6, besides the large impacted bubble at the center, the micro-bubbles are radially distributed in the droplet and located at the corners of the windward sidewalls of the micro-pillars. When a droplet slips along an inclined micro-pillar surface, the droplet is extended with a thicker head and a thinner tail. The trapped micro-bubbles at the micro-pillar corners are more likely to escape, especially from the droplet tail, resulting in the volume rate of micro-bubbles in the droplet decreasing, and the distribution of micro-bubbles changing from the radial distribution to the unidirectional distribution along the droplet spreading direction.
As shown in Figure 6 and Figure 7, the bright area represents gas, and the black area represents the contact area of the solid and liquid. As a result, each black micro-pillar is surrounded by a bright circular ring, representing the trace amount of gas that surrounds the micro-pillar root, and a corresponding triggered nucleation bubble always brightly exists near it. After obtaining the phase distribution law, contour pictures are generated using the grayscale image processing method, as shown in the detailed image, and the location of nucleation sites and the diameter size of boiling bubbles can be obtained precisely. Therefore, how do we count the nucleation site density? First, the micro-pillar surface is zoned according to the distribution of the micro-pillar array as shown in Figure 7a. The sum of one micro-pillar width (50 μm) and one micro-pillar gap (100 μm) defines a unit length (150 μm). Every three units constitutes one zone with a size of 150 × 3 = 450 μm. The n represents the number of the zone from the edge of the droplet tail, and Na represents the average nucleation density, which is calculated by dividing the number of nucleation sites by the area of one zone, number/m2. As a result, Figure 7b–d shows the nucleation site distributions on the micro-pillar surface when a droplet vertically impacts a horizontal micro-pillar surface (θ = 0°), where a single large bubble forms centrally instead of dozens of micro-bubbles, and the distribution of nucleation density is symmetrical in the whole range with a minimum nucleation density at the center area. In contrast, an inclined surface exhibits reduced Na values in the tail region due to micro-bubble escape from the thin liquid film. At the same time, compared with the impact velocity, the velocity of the droplet head wrapping the micro-pillars is much lower. With a large advancing angle of droplets on the inclined surface, part of the microbubbles at the droplet head also go out during the droplet sliding process, slightly reducing the nucleation density in this region. Asymmetric distribution of nucleation density with a higher value in the middle and lower values at the two ends is formed on an inclined surface. With the increase in the wall inclination angle, the length and asymmetry of the droplet increase, and the relative position of the highest nucleation density inside the droplet also moves back to the droplet tail. This is because the droplet advance angle is bigger, and the exhaust capacity in the droplet head is higher; accordingly, the area ratio of the low nucleation density to the whole droplet area increases. Meanwhile, the nucleation density at the droplet tail is also decreased because of the thinning droplet tail with increasing inclination angle of the surface. The asymmetry of the droplet morphology causes the asymmetry of the nucleation site distribution.
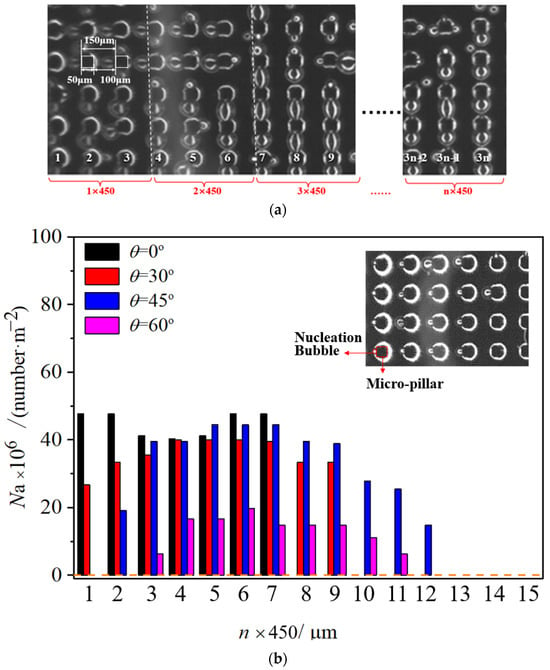
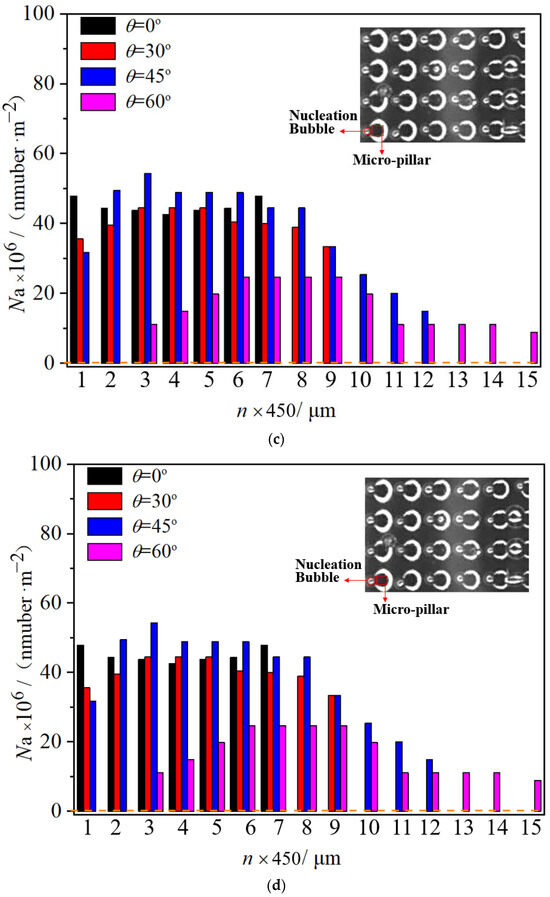
Figure 7.
Distribution of nucleation sites in droplets on micro-pillar surfaces with various inclination angles. (a) Schematic diagram of micro-pillar grouping, (b) surface temperature at 50 °C, (c) surface temperature at 70 °C, and (d) surface temperature at 90 °C.
Table 1 summarizes the average nucleation density Nav for each droplet (i.e., the total number of nucleation sites divided by the entire heat transfer area of the droplet, number/m2). It can be seen that when the smooth surface has an inclined angle, nucleation sites do not appear for droplet subcooled boiling. Compared with a smooth surface, the micro-pillar surface can significantly increase the average nucleation density of the heat transfer surface, which is also affected by the inclination and surface temperature. When the inclination angle of the micro-pillar surface is increased from 0° to 60°, the nucleation density decreases by approximately 30 × 106 at T = 50 and 70 °C. However, the nucleation density decreases by about 20 × 106 with the same inclination change when the wall temperature is 90 °C. At low surface temperatures, only one microbubble remains in each micro-pillar corner, and the nucleation site density is mainly determined by the number of micro-pillars on the surface. At T = 50, 70 °C, the nucleation site densities inside the droplet are the same, which is about 44 × 106. When the surface temperature is increased to 90 °C, multiple nucleation sites are generated around each micro-pillar, as shown in Figure 7, so the average nucleation site density increases sharply by more than 50%.

Table 1.
Nucleation site density in droplets.
3.2.3. Average Diameter of Stable Bubbles
Inside a subcooled liquid droplet, the heat transfer of a boiling bubble includes two parts: the bubble receiving heat from the substrate on the liquid–solid interface, q1, and the bubble releasing heat into the top cool liquid, q2, where q1 > 0, q2 < 0. At the beginning of bubble growth, the bubble receives more heat with a superheat on the heating wall, |q1| > |q2|. The bubble grows from a tiny volume near the heating wall. Gradually, the bubble grows out of the thermal boundary layer and extends into the subcooled liquid region. In the process, the value of |q2| increases continuously until |q1| = |q2|. The bubble remains a stable diameter R and no longer grows with the net heat flux equal to 0. If |q2| is always smaller than |q1|, the bubble continuously grows to a critical diameter and detaches from the heating wall, where the stable diameter is the same as the departure diameter for the high temperature cases. Otherwise, the bubble shrinks back to the stable diameter again when |q2| > |q1|.
Figure 8 shows the distribution of the stable diameter Rsd of boiling bubbles inside the droplet at various temperatures. Each data point of stable diameters in a zone, Rsd, was calculated from 80 to ~100 data points. Coupled with the high precision and response speed of the high-speed video camera, the error of each data point was reduced. As observed in cases with T = 50 and 70 °C in Figure 8a,b, stable bubbles primarily localize near droplet centers due to insufficient superheat and limited trapped gas at the droplet edges. When the surface temperature rises to 90 °C, the heat can provide sufficient q1 to promote the growth of microbubbles to a critical detached diameter and prevent them from disappearing. Boiling bubbles are present not only in the middle, but also in the droplet tail and head, as shown in Figure 8c, exhibiting an asymmetric distribution with a larger diameter in the middle and smaller diameters at the two ends of the droplet, the same as at the beginning of impaction. As the surface temperature was increased from 50 °C to 90 °C (θ = 0°), the maximum values of Rsd varied from 35 to 55 μm with an amplitude of 20 μm, which proves that further temperature increases induce rapid bubble growth and coalescence, intensifying boiling activity. Furthermore, as the wall inclination angle increases from 0°, 30°, 45° to 60°, the average stable bubble diameters across the entire droplet, Rav, which is calculated from the 720 to 1500 data, were measured as 33.01, 30.05, 19.09, and 16.71 μm at T = 50 °C, and 38.19, 30.36, 27.84, and 18.24 μm at T = 70 °C. These values rose significantly to 52, 49, 33, and 32 μm at T = 90 °C. The increase in the inclination angle of the wall from 0° to 60° decreased the stable diameter of boiling bubbles by about 13 to 16 μm regardless of the heating wall temperature. This is because the surface temperature mainly affects the heat transfer at the bubble interface and the corresponding growth of the bubble, both of which are relatively slow processes. In contrast, a significant change in inclination angle may instantly trigger the departure of most bubbles, leading to an abrupt transformation in the dynamic process. Thus, when θ > 30°, the stable bubble diameter decreases sharply. This indicates that besides the two parts of heat transfer, q1 and q2, another more important factor influencing the stable diameter is the inclination angle of the surface.
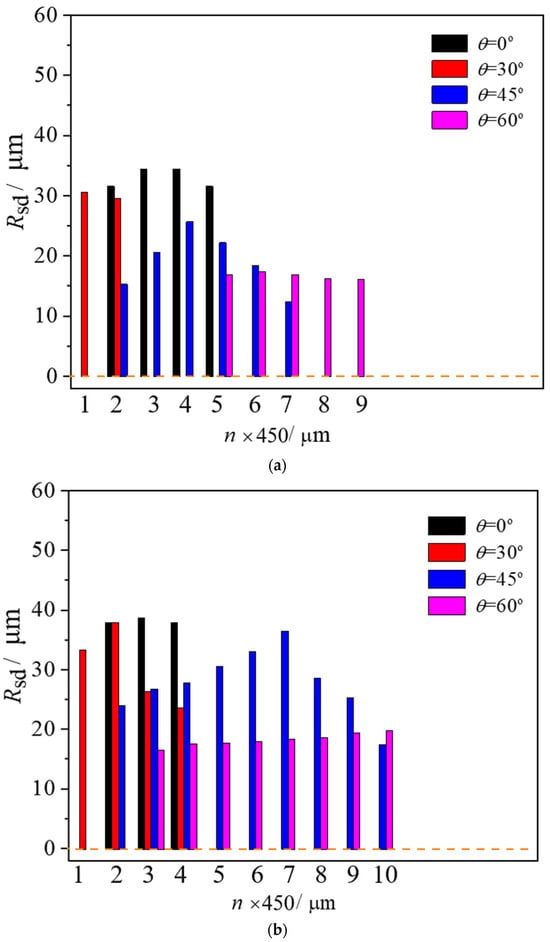
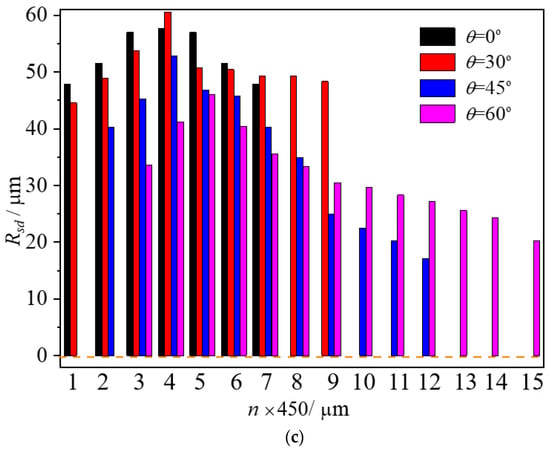
Figure 8.
Stable bubble diameters in droplets on the micro-pillar surfaces with different temperature and inclination angles: (a) T = 50 °C; (b) T = 70 °C; (c) T = 90 °C.
3.3. Analysis of Droplet Asymmetry Effect
3.3.1. Asymmetry Evaporation
As shown in Figure 9a, on a horizontal smooth surface, the volume of the droplet continuously shrinks. In the initial stage, surface tension dominates the shape of the droplet, causing it to shrink and remain circular. As the volume further decreases to small enough with the uneven friction exceeding the surface tension, the droplet easily contracts into an elliptical shape before its ultimately disappears at t = 56 s. Both the wetting perimeter and thickness decrease progressively during evaporation, yielding smooth diameter evolution curves, as shown in Figure 10. In contrast, the micro-pillar surface induces polygonal droplet profiles post-impact due to three-phase line tension effects. Its evolution shows two stages during evaporation. In the first stage, the polygon shape of the droplet becomes clear until t = 25 s. It maintains a stable polygon without size change until t = 35 s because the droplet outline is restricted in the micro-pillar arrays. During this time, evaporation only causes a decrease in the droplet thickness until its value equals the height of the micro-pillar. Entering the second stage, all wetted micro-pillars penetrate through the droplet film, and heat transfer on their side and top walls is more pronounced. The droplet outline rapidly shrinks until it completely disappears at t = 56 s. Unlike the continuous change on the smooth surface, the droplet equivalent diameter shows a cliff-like decrease, as shown in Figure 10.
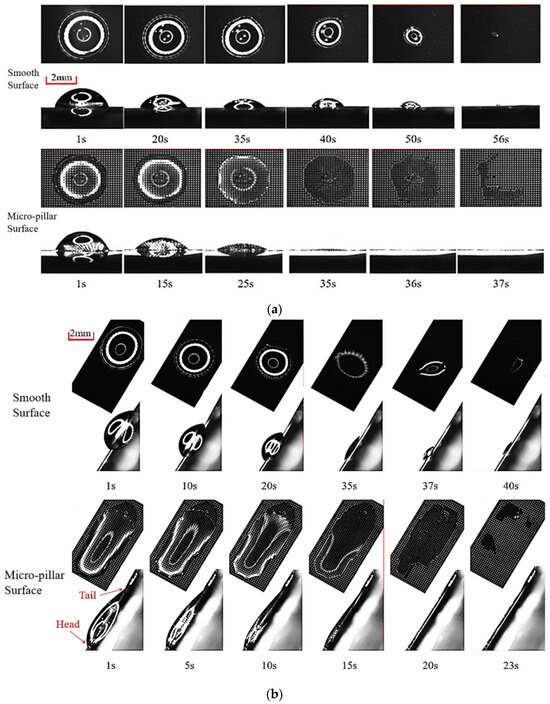
Figure 9.
Morphologic evolution of droplets in the evaporation process: (a) T = 90 °C, θ = 0°; (b) T = 90 °C, θ = 60°.
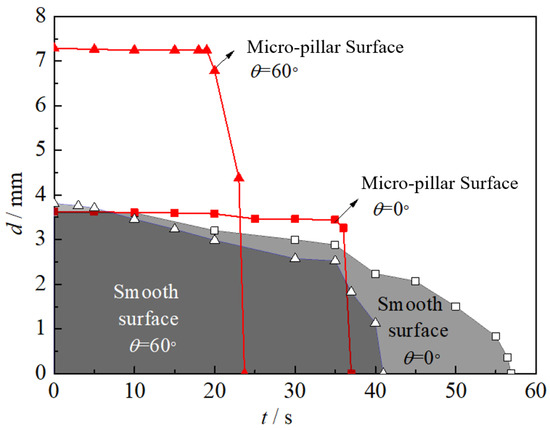
Figure 10.
Evolution of the equivalent diameter of droplets on various surfaces.
On an inclined smooth surface (θ = 60°), the droplet slides and stabilizes in a circular shape by t = 10 s, with stabilized dimensions comparable to those on a horizontal surface, as shown in Figure 9b. However, advancing and receding contact angle asymmetry induces a non-uniform liquid film thickness. The thin liquid film at the droplet tail undergoes preferential evaporation and shrinkage. This is more obvious in the late period t > 35 s, when the slope of the droplet diameter curve increases. Compared with the smooth surface, the contact area between the droplet and the heat transfer surface was significantly increased with the increase in inclination angle from 0° to 60° on the micro-pillar surface. The droplet equivalent diameter was also increased from 3.6 to 7.2 mm. Meanwhile, it can be seen from the side view in Figure 9b that the droplet showed significant asymmetry in both thickness and width when the inclination angle of the micro-pillar surface was increased, and this asymmetry of the liquid film directly caused the non-uniform distribution of the nucleation site density, which made the droplet head evaporate more rapidly. The liquid here is preferentially thinned to the height of the micro-pillar and then quickly retracted to disappear in the second stage. With the “cliff-like” decrease in the droplet equivalent diameter, the evaporation time was shortened from 37 to 23 s, and the heat transfer rate increased by about 37% with the increase in the inclination angle from 0° to 60°, as shown in Figure 10.
3.3.2. Asymmetry Factors
As stated above, the droplet asymmetry on an inclined surface shows significant effects on the contact area of heat transfer, nucleation site density, departure diameter, and even the heat transfer performance. To elucidate the enhancement mechanism of inclined micro-pillar surfaces, the quantitative characterization of droplet asymmetry is essential. Two droplet asymmetry factors and a slip distance are defined when the droplet completes slippage on an inclined surface. As shown in Figure 11, the right boundary positions of the droplets after impacting the horizontal and inclined walls are recorded as r0 and rl, respectively. The tail slip distance l on inclined surfaces can be expressed as:
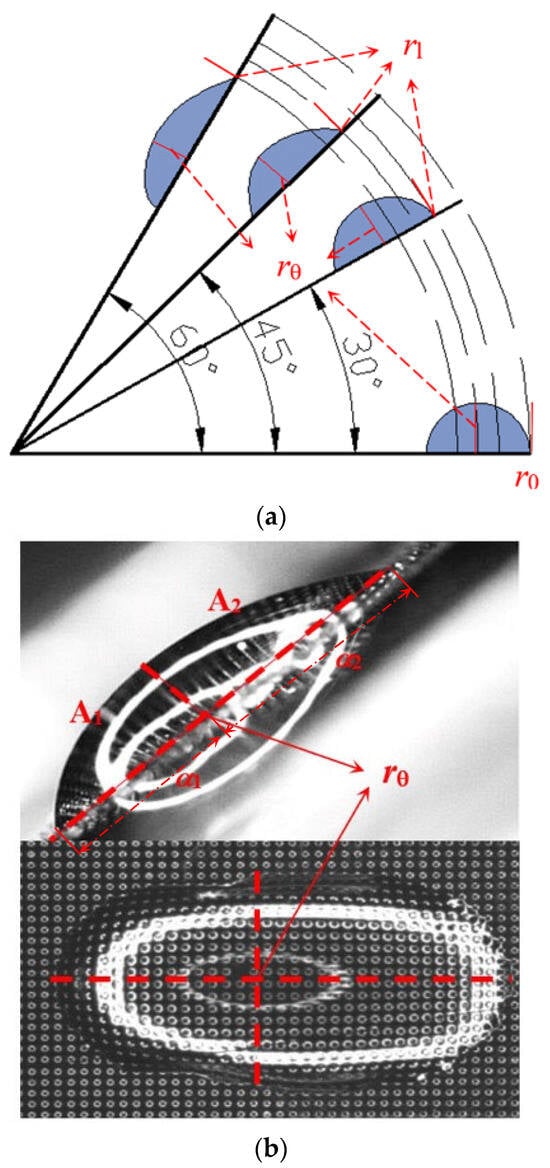
Figure 11.
Defined variables of droplets after impacting and slipping on inclined surfaces. (a) Variables on the slide distance; (b) variables on the asymmetry factors.
Meanwhile, the position corresponding to the maximum thickness of droplets is recorded as rθ. With the point rθ as the dividing site, the droplet is divided into two parts, A1 and A2. The corresponding lengths of the major axes of the two parts are α1 and α2. When a liquid droplet is symmetrical, α1 = α2. As the micro-pillar surface is tilted, a sliding droplet exhibits a tail elongation and uneven thickness, which causes the inequality of α1 and α2. Thus, a one-dimensional asymmetry factor ε is defined by the ratio of the two major axes, which is considered as a characteristic parameter representing the asymmetry of the liquid film thickness after the sliding of droplets, expressed as:
Besides the one-dimensional asymmetry factor ε, a volume asymmetry factor γ is defined as the ratio of the volumes of regions A1 and A2. The average thicknesses δ1 and δ2 and the average widths d1 and d2 of regions A1 and A2 in Figure 11 can be obtained by fitting the profiles of the side and top photographs of the droplet, and then using the area obtained by integration to divide by the length. Then, the volume asymmetry factor γ can be calculated as:
Based on the boundary layer theory of natural convection, both the temperature and viscous boundary layer thicken along the upward direction on an inclined surface, as shown in Figure 12. Increasing surface temperature further thickens the viscous boundary layer along the inclined wall, promoting larger inclination angles and extended sliding distances on high-temperature smooth surfaces. Furthermore, as soon as the droplet contacts the surface, the forces acting on the droplet also affect its spreading and sliding. As is known, accompanied by the increase in the inclination angle, the component force of the droplet gravity along the wall direction increases and lengthens the droplet sliding distance. Therefore, the sliding distance of the droplet on the smooth surface is significantly influenced by both the surface temperature and the inclination angle. In contrast, on the micro-pillar surface, micro-pillars substantially enhance sliding resistance through three-phase line tension, markedly reducing the droplet sliding distances. Although increasing the inclination angle of micro-pillar surfaces slightly elevates the sliding distances, this enhancement remains limited. Compared with that, the influence of the surface temperature on the droplet sliding distance is almost negligible. Accordingly, the values of l showed little change on the micro-pillar surface. As shown in Figure 13, the droplet sliding distance increased by 4.8 mm at T = 120 °C when the inclination angle of a smooth surface was increased from 0° to 45°. However, the sliding distances showed little change with the increase in surface temperature and inclination angle on the micro-pillar surface. As shown in Figure 13, asymmetry factors were predominantly governed by the wall inclination angle rather than surface temperature. Increasing the inclination angle from 0° to 60° elevated the one-dimensional asymmetry factor ε by 31.0% for the smooth surface and 82.3% for the micro-pillar surface. The volume asymmetry factor γ increased by 29.5% on the smooth, exhibiting weaker asymmetry than ε. This discrepancy arises because the droplet on the smooth surface maintains a near-circular profile after sliding, with a uniform width and length distributions that weaken thickness asymmetry differentiation, resulting in γ < ε. However, the droplet exhibits asymmetry in both width and length on the micro-pillar surface. The combined effect of these asymmetries results in more significant volume asymmetry than the simple one-dimensional asymmetry, thus γ > ε. The increase in γ was more significant than that of ε, by 93.9%.
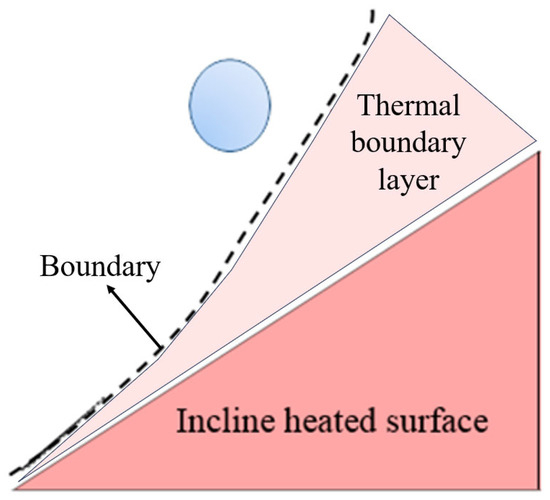
Figure 12.
Schematic of droplet impacting and slipping on an inclined heating surface.
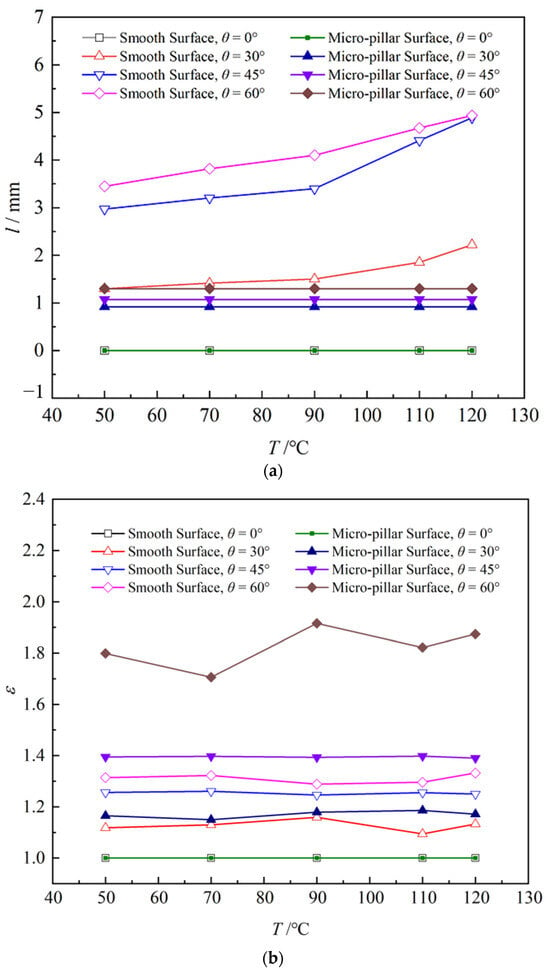
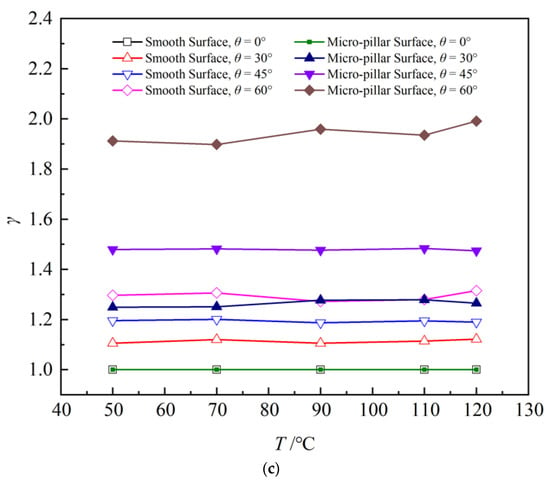
Figure 13.
Asymmetry factors of droplet on various surfaces: (a) slide distance; (b) one-dimensional asymmetry factors; (c) volume asymmetry factors.
3.4. Correlation Between Influencing Factors
Figure 14 shows the effect of inclined angles on the enhancement factors of various influencing parameters at 90 °C on micro-pillar surfaces. Here, kA, kN, kR, and kt represent the enhancement factors in heat transfer area, nucleation density, bubble stable diameter, and evaporation time of the inclined surface, respectively, while kγ and kε correspond to the enhancement factors of volume and one-dimensional asymmetry on the inclined surface, respectively. As expected, increasing the inclination angle of the micro-pillar surface intensified the droplet asymmetry, reducing the nucleation density and bubble stable diameter. kN and kR reached minimum values of 0.61 and 0.68 at a wall inclination angle of 60°. However, the droplet asymmetry triggered a 220% increase in heat exchange area, with kA reaching 2.17 times the horizontal surface value at 60°. The increase in the heat transfer area totally compensated for the diminution of parts of kN and kR. As a result, compared with the horizontal surface, the evaporation time of the droplet decreased from 37 to 23 s and the heat transfer performance was improved to nearly 137% for the inclined angle at 60°. This droplet sub-cooling boiling experiment displayed a previously unnoticed characteristic in addition to the classical boiling parameters such as constant area, nucleation density, and departure diameter, which depends largely on the combined effect of droplet asymmetry and surface micro-structure brought about by the inclined surface. This means that liquid film asymmetry is a fundamental factor, especially for the analysis of droplet or spray cooling.
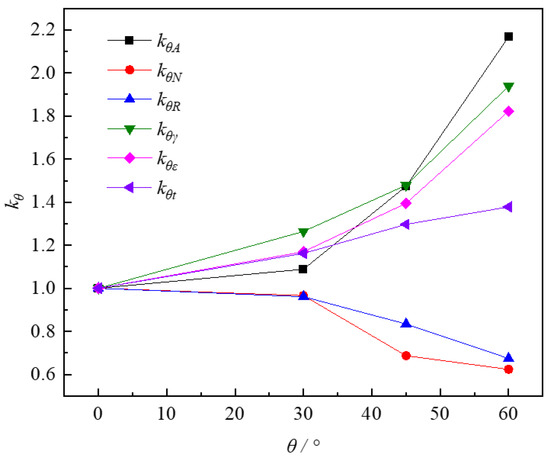
Figure 14.
Influencing factors of droplet boiling heat transfer on micro-pillar surfaces.
4. Conclusions
This paper studied subcooled droplet boiling on various inclined micro-pillar surfaces by rapidly capturing the dynamic characteristics of droplet boiling with two high-speed cameras, whose dynamic characteristics included the nucleation density and departure diameter of boiling bubbles in the droplet, the droplet contact area, and the droplet asymmetry. The following conclusions were obtained:
- (1)
- The micro-pillar structure effectively improves the heat transfer performance of subcooled boiling of liquid droplets, and the enhancement factor β increases with the surface inclination θ.
- (2)
- Micro-pillar structures on the inclined surface lengthen the droplet tail and increase the droplet asymmetry. This paper established two quantitative metrics: the volume asymmetry factor γ, and the one-dimensional asymmetry factor ε. By measuring the contact area, the droplet nucleation site, and stable diameter distribution of bubbles under different conditions, the significant influence of the droplet asymmetry on the boiling heat transfer rate was proven.
- (3)
- When increasing the surface tilt angle, the asymmetry of droplets on micro-pillar surfaces becomes more significant. Although there was a reduction in nucleation density and bubble stable diameter, the droplet asymmetry significantly increased the heat exchange area, resulting in a 37% improvement in the evaporation rate of the micro-pillar surfaces and about a 20% increase in its enhancement performance to smooth surfaces when the inclination angle increased from 0°to 60°. These results indicate that asymmetry causes changes in heat transfer conditions, specifically, a significant increase in the wetted area and deformation of the liquid film, which are the direct enhancement mechanisms of inclined micro-pillar surfaces.
Author Contributions
Conceptualization, Y.-N.Z. and G.-Q.H.; Methodology, Y.-N.Z., G.-Q.H. and L.-M.Z.; Investigation, Y.-N.Z. and G.-Q.H.; Data curation, Y.-N.Z. and G.-Q.H.; Writing—original draft preparation, Y.-N.Z.; Writing—review and editing, Y.-N.Z. and H.-X.C.; Visualization, Y.-N.Z. and L.-M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding except the National Natural Science Foundation of China (No. 52176152) and the Beijing Natural Science Foundation (No. 3222046).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
This study was supported by the National Natural Science Foundation of China (No. 52176152) and the Beijing Natural Science Foundation (No. 3222046).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| We | Weber number (-) |
| T | Surface temperature (°C) |
| t | Evaporation time of droplets (s) |
| tS | Evaporation time of droplets on smooth surface (s) |
| tP | Evaporation time of droplets on micro-pillar surface (s) |
| A | Heat transfer area between droplet and surface (mm2) |
| r0 | Right boundary position on the horizontal surface (mm) |
| rl | Right boundary position on the inclined surface (mm) |
| rθ | Maximum droplet thickness position (mm) |
| l | Droplet slip distance (mm) |
| d1 | Droplet average widths of A1 zone (mm) |
| d2 | Droplet average widths of A2 zone (mm) |
| Na | Nucleation site density (103 m−2) |
| Rsd | Average diameter of droplet (μm) |
| Surface inclined angle (°) | |
| Enhanced heat transfer factor (-) | |
| ε | One-dimensional asymmetry factor (-) |
| γ | Volume asymmetry factor (-) |
| α1 | Contact lengths between droplet and surface of A1 zone (mm) |
| α2 | Contact lengths between droplet and surface of A2 zone (mm) |
| δ1 | Droplet average thickness of A1 zone (mm) |
| δ2 | Droplet average thickness of A2 zone (mm) |
| λ | Radial distance (μm) |
References
- Chen, H.; Wang, Y.; Yang, H.; Badiei, A.; Li, G. Experimental Investigation and Exergy Analysis of a High Concentrating Photovoltaic System Integrated with Spray Cooling. Energy Convers. Manag. 2022, 268, 115957. [Google Scholar] [CrossRef]
- Bandaru, S.V.R.; Villanueva, W.; Konovalenko, A.; Komlev, A.; Thakre, S.; Skold, P.; Bechta, S. Upward-Facing Multi-Nozzle Spray Cooling Experiments for External Cooling of Reactor Pressure Vessels. Int. J. Heat Mass Transf. 2020, 163, 120516. [Google Scholar] [CrossRef]
- Chen, H.; Ruan, X.-H.; Peng, Y.-H.; Wang, Y.-L.; Yu, C.-K. Application Status and Prospect of Spray Cooling in Electronics and Energy Conversion Industries. Sustain. Energy Technol. Assess. 2022, 52, 102181. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, X.; Li, X.; Xu, J.; Qi, H.; Shan, D.; Guo, B. Enhanced Evaporation Performance on a Novel Microstructured Surface with Vertical Dimension Gradient. Int. J. Heat Mass Transf. 2022, 199, 123478. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, P.-X.; Ouyang, X.-L.; Chen, J.-N.; Christopher, D.M. Experimental Investigation of Spray Cooling on Smooth and Micro-Structured Surfaces. Int. J. Heat Mass Transf. 2014, 76, 366–375. [Google Scholar] [CrossRef]
- Li, X.; Mao, L.; Ma, X. Dynamic Behavior of Water Droplet Impact on Microtextured Surfaces: The Effect of Geometrical Parameters on Anisotropic Wetting and the Maximum Spreading Diameter. LANGMUIR 2013, 29, 1129–1138. [Google Scholar] [CrossRef]
- Misyura, S.Y. Contact Angle and Droplet Heat Transfer during Evaporation on Structured and Smooth Surfaces of Heated Wall. Appl. Surf. Sci. 2017, 414, 188–196. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, T.; Fan, J.; Sun, W.; Cao, Z. Droplet Impact Behavior on Heated Micro-Patterned Surfaces. J. Appl. Phys. 2016, 119, 114901. [Google Scholar] [CrossRef]
- Gao, L.; Lyu, J.; Zhou, Z.; Li, Y.; Gao, D.; Shi, L.; Lv, X.; Li, Y. Dynamics of Inner Bubble during Water Droplet Evaporation on Conical Micro-Pillars Surfaces. Int. Commun. Heat Mass Transf. 2022, 131, 105841. [Google Scholar] [CrossRef]
- Rymkiewicz, J.; Zapalowicz, Z. Analysis of the Evaporation Process for Water Droplet on Flat Heated Surface. Int. Commun. Heat Mass Transf. 1993, 20, 687–697. [Google Scholar] [CrossRef]
- Lu, G.; Wang, X.-D.; Yan, W.-M. Nucleate Boiling inside Small Evaporating Droplets: An Experimental and Numerical Study. Int. J. Heat Mass Transf. 2017, 108, 2253–2261. [Google Scholar] [CrossRef]
- Charitatos, V.; Pham, T.; Kumar, S. Droplet Evaporation on Inclined Substrates. Phys. Rev. Fluids 2021, 6, 084001. [Google Scholar] [CrossRef]
- Worthington, A.M. Xxviii. On the Forms Assumed by Drops of Liquids Falling Vertically on a Horizontal Plate. Proc. R. Soc. Lond. 1877, 25, 261–272. [Google Scholar] [CrossRef]
- Misyura, S.Y. Effect of Various Key Factors on the Law of Droplet Evaporation on the Heated Horizontal Wall. Chem. Eng. Res. Des. 2018, 129, 306–313. [Google Scholar] [CrossRef]
- Bernardin, J.D.; Mudawar, I.; Walsh, C.B.; Franses, E.I. Contact Angle Temperature Dependence for Water Droplets on Practical Aluminum Surfaces. Int. J. Heat Mass Transf. 1997, 40, 1017–1033. [Google Scholar] [CrossRef]
- Nikolopoulos, N.; Theodorakakos, A.; Bergeles, G. A Numerical Investigation of the Evaporation Process of a Liquid Droplet Impinging onto a Hot Substrate. Int. J. Heat Mass Transf. 2007, 50, 303–319. [Google Scholar] [CrossRef]
- Lee, H.; Cho, A.; Kim, H. Changes in Boiling Regime and Heat Transfer Effectiveness during Water Droplet Collision with a Superheated Wall. Int. J. Heat Mass Transf. 2024, 221, 125052. [Google Scholar] [CrossRef]
- Tartarini, P.; Lorenzini, G.; Randi, M. Experimental Study of Water Droplet Boiling on Hot, Non-Porous Surfaces. Heat Mass Transf. 1999, 34, 437–447. [Google Scholar] [CrossRef]
- Misyura, S.Y. Wall Effect on Heat Transfer Crisis. Exp. Therm. Fluid Sci. 2016, 70, 389–396. [Google Scholar] [CrossRef]
- Nakoryakov, V.; Misyura, S.Y.; Elistratov, S. The Behavior of Water Droplets on the Heated Surface. Int. J. Heat Mass Transf. 2012, 55, 6609–6617. [Google Scholar] [CrossRef]
- Clanet, C.; Béguin, C.; Richard, D.; Quéré, D. Maximal Deformation of an Impacting Drop. J. Fluid Mech. 2004, 517, 199–208. [Google Scholar] [CrossRef]
- Zhao, Y.; Wen, L.; Su, L.; Liu, B.; Wang, J.; Hu, L. Dynamics Behaviors of Droplets Impacting on a Heated Tailings Surface. In 12th International Symposium on High-Temperature Metallurgical Processing; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Misyura, S.Y. Nucleate Boiling in Bidistillate Droplets. Int. J. Heat Mass Transf. 2014, 71, 197–205. [Google Scholar] [CrossRef]
- Misyura, S.Y. Droplets Boiling Crisis of Ethanol Water Solution on Duralumin Substrate with Sio2 Nanoparticles Coating. Exp. Therm. Fluid Sci. 2016, 75, 43–53. [Google Scholar] [CrossRef]
- Song, D.; Song, B.; Hu, H.; Du, X.; Ma, Z. Contact Angle and Impinging Process of Droplets on Partially Grooved Hydrophobic Surfaces. Appl. Therm. Eng. 2015, 85, 356–364. [Google Scholar] [CrossRef]
- Hays, R.; Maynes, D.; Crockett, J. Thermal Transport to Droplets on Heated Superhydrophobic Substrates. Int. J. Heat Mass Transf. 2016, 98, 70–80. [Google Scholar] [CrossRef]
- Guggilla, G.; Sielaff, A.; Stephan, P. Boiling Regimes of a Single Droplet Impinging on a Superheated Surface: Effect of the Surrounding Medium. Int. J. Heat Mass Transf. 2024, 220, 124982. [Google Scholar] [CrossRef]
- Mollaret, R.; Sefiane, K.; Christy, J.R.E.; Veyret, D. Experimental and Numerical Investigation of the Evaporation into Air of a Drop on a Heated Surface. Chem. Eng. Res. Des A. 2004, 82, 471–480. [Google Scholar] [CrossRef]
- Hatta, N.; Fujimoto, H.; Takuda, H. Deformation Process of a Water Droplet Impinging on a Solid Surface. J. Fluids Eng. 1995, 117, 394–401. [Google Scholar] [CrossRef]
- Tang, C.; Qin, M.; Weng, X.; Zhang, X.; Zhang, P.; Li, J.; Huang, Z. Dynamics of Droplet Impact on Solid Surface with Different Roughness. Int. J. Multiph. Flow 2017, 96, 56–69. [Google Scholar] [CrossRef]
- Ravikumar, S.V.; Jha, J.M.; Mohapatra, S.S.; Sinha, A.; Pal, S.K.; Chakraborty, S. Experimental Study of the Effect of Spray Inclination on Ultrafast Cooling of a Hot Steel Plate. Heat Mass Transf. 2013, 49, 1509–1522. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Liu, D.; Xu, K.; Chen, Y. Experimental Study on the Effects of Spray Inclination on Water Spray Cooling Performance in Non-Boiling Regime. Exp. Therm. Fluid Sci. 2010, 34, 933–942. [Google Scholar] [CrossRef]
- Li, B.; Cader, T.; Schwarzkopf, J.; Okamoto, K.; Ramaprian, B. Spray Angle Effect during Spray Cooling of Microelectronics: Experimental Measurements and Comparison with Inverse Calculations. Appl. Therm. Eng. 2006, 26, 1788–1795. [Google Scholar] [CrossRef]
- Silk, E.A.; Kim, J.; Kiger, K. Spray Cooling of Enhanced Surfaces: Impact of Structured Surface Geometry and Spray Axis Inclination. Int. J. Heat Mass Transf. 2006, 49, 4910–4920. [Google Scholar] [CrossRef]
- Liu, N.; Zhan, T.-J.; Zhang, Y.-W.; Yin, X.-M.; Zhang, L.-X. Experimental Investigation of Comprehensive Effects of Surfactant and Inclined Mode on Spray Cooling Heat Transfer. Int. J. Therm. Sci. 2019, 136, 457–466. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, J.; Jiang, P.-X. Experimental Investigation of Spray Cooling on Flat and Enhanced Surfaces. Appl. Therm. Eng. 2013, 51, 102–111. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Ma, X.; Zhang, H. Dynamic Characteristics of Droplet Impacting on Prepared Hydrophobic/Superhydrophobic Silicon Surfaces. Surf. Coat. Technol. 2016, 307, 243–253. [Google Scholar] [CrossRef]
- LeClear, S.; LeClear, J.; Park, K.-C.; Choi, W. Drop Impact on Inclined Superhydrophobic Surfaces. J. Colloid Interface Sci. 2016, 461, 114–121. [Google Scholar] [CrossRef]
- Deendarlianto; Takata, Y.; Hidaka, S.; Indarto; Widyaparaga, A.; Kamal, S.; Purnomo; Kohno, M. Effect of Static Contact Angle on the Droplet Dynamics during the Evaporation of a Water Droplet on the Hot Walls. Int. J. Heat Mass Transf. 2014, 71, 691–705. [Google Scholar] [CrossRef]
- Deendarlianto; Takata, Y.; Kohno, M.; Hidaka, S.; Wakui, T.; Majid, A.I.; Kuntoro, H.Y.; Indarto; Widyaparaga, A. The Effects of the Surface Roughness on the Dynamic Behavior of the Successive Micrometric Droplets Impacting onto Inclined Hot Surfaces. Int. J. Heat Mass Transf. 2016, 101, 1217–1226. [Google Scholar] [CrossRef]
- Remer, M.; Psarski, M.; Gumowski, K.; Rokicki, J.; Sobieraj, G.; Kaliush, M.; Pawlak, D.; Celichowski, G. Dynamic Water Contact Angle during Initial Phases of Droplet Impingement. COLLOID Surf. A 2016, 508, 57–69. [Google Scholar] [CrossRef]
- Pittoni, P.G.; Lin, C.-H.; Yu, T.-S.; Lin, S.-Y. On the Uniqueness of the Receding Contact Angle: Effects of Substrate Roughness and Humidity on Evaporation of Water Drops. LANGMUIR 2014, 30, 9346–9354. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, G.; Sellier, M.; Jermy, M.; Taylor, M. Modeling the Effects of Contact Angle Hysteresis on the Sliding of Droplets down Inclined Surfaces. Eur. J. Mech.-B/Fluids 2014, 48, 218–230. [Google Scholar] [CrossRef]
- Deendarlianto; Takata, Y.; Widyatama, A.; Majid, A.I.; Wiranata, A.; Widyaparaga, A.; Kohno, M.; Hidaka, S.; Indarto. The Interfacial Dynamics of the Micrometric Droplet Diameters during the Impacting onto Inclined Hot Surfaces. Int. J. Heat Mass Transf. 2018, 126, 39–51. [Google Scholar] [CrossRef]
- Chaves, H.; Kubitzek, A.M.; Obermeier, F. Dynamic Processes Occurring during the Spreading of Thin Liquid Films Produced by Drop Impact on Hot Walls. Int. J. Heat Fluid Flow 1999, 20, 470–476. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).