Influence of Inclined Non-Uniform Fins on the Melting of Phase Change Materials Under Constant-Power Heating Condition
Abstract
1. Introduction
2. Description of Numerical Model
2.1. Physical Model
- (1)
- The thermophysical properties of PCM and fins are assumed as constant;
- (2)
- The PCM RT42 is considered as an incompressible fluid and is adherent to Boussinesq approximation;
- (3)
- Viscous dissipation occurring in the liquid PCM is ignored;
- (4)
- The volume variation in the phase change process is not considered;
- (5)
- The heating resistance at the heating surface is neglected.

| Property | RT42 | Copper |
|---|---|---|
| Density of solid ρs (kg/m3) | 880 | 8978 |
| Density of liquid (kg/m3) | 760 | |
| Heat capacity (J/kg·K) | 2000 | 381 |
| Latent heat (kJ/kg) | 165 | |
| Thermal conductivity k (W/m·K) | 0.2 | 387.6 |
| Dynamic viscosity (kg/m·s) | 0.0235 | |
| Melting temperature Tl (°C) | 42 | |
| Solid temperature Ts (°C) | 38 | |
| Thermal expansion coefficient β (K−1) | 0.0001 |
2.2. Governing Equations
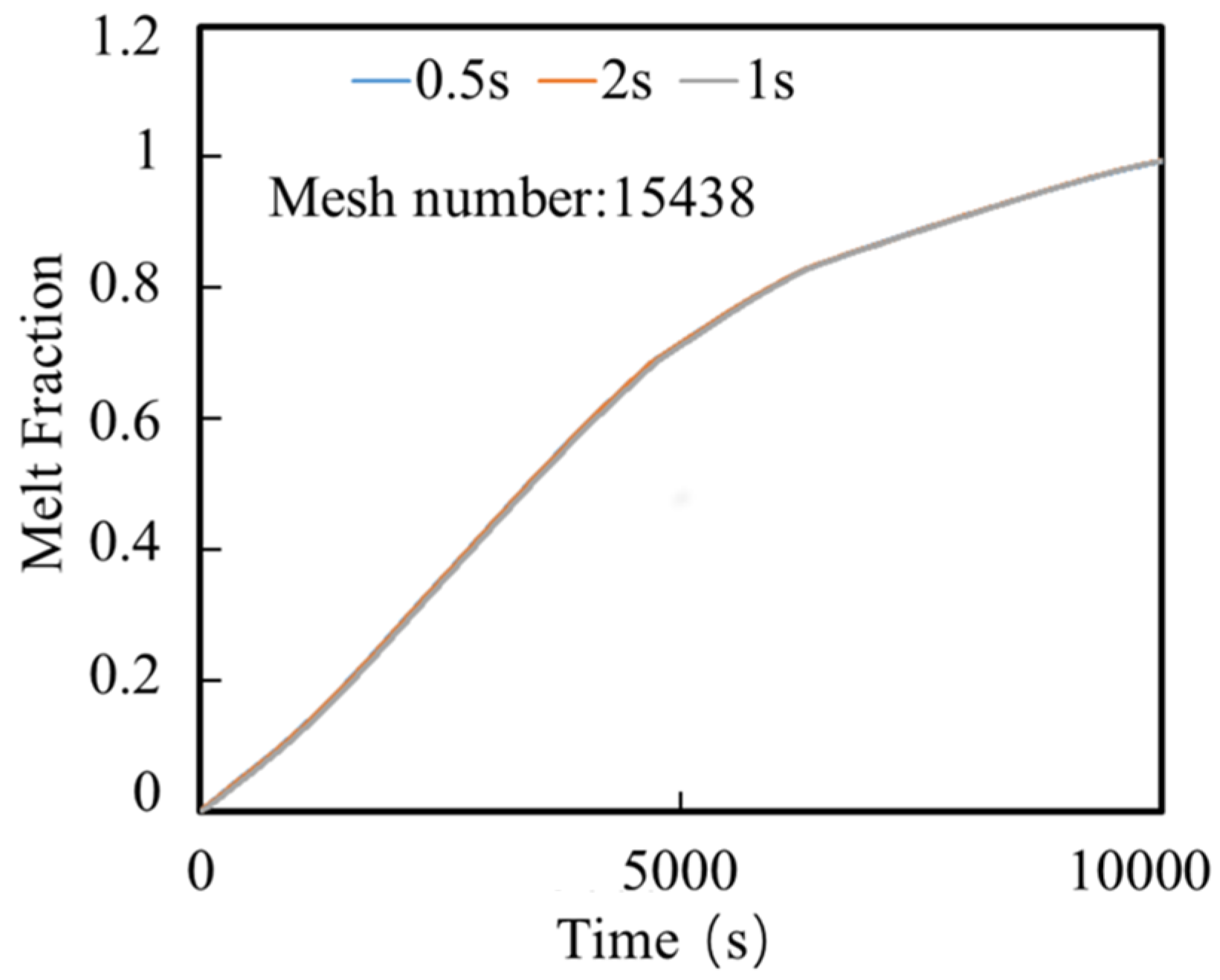
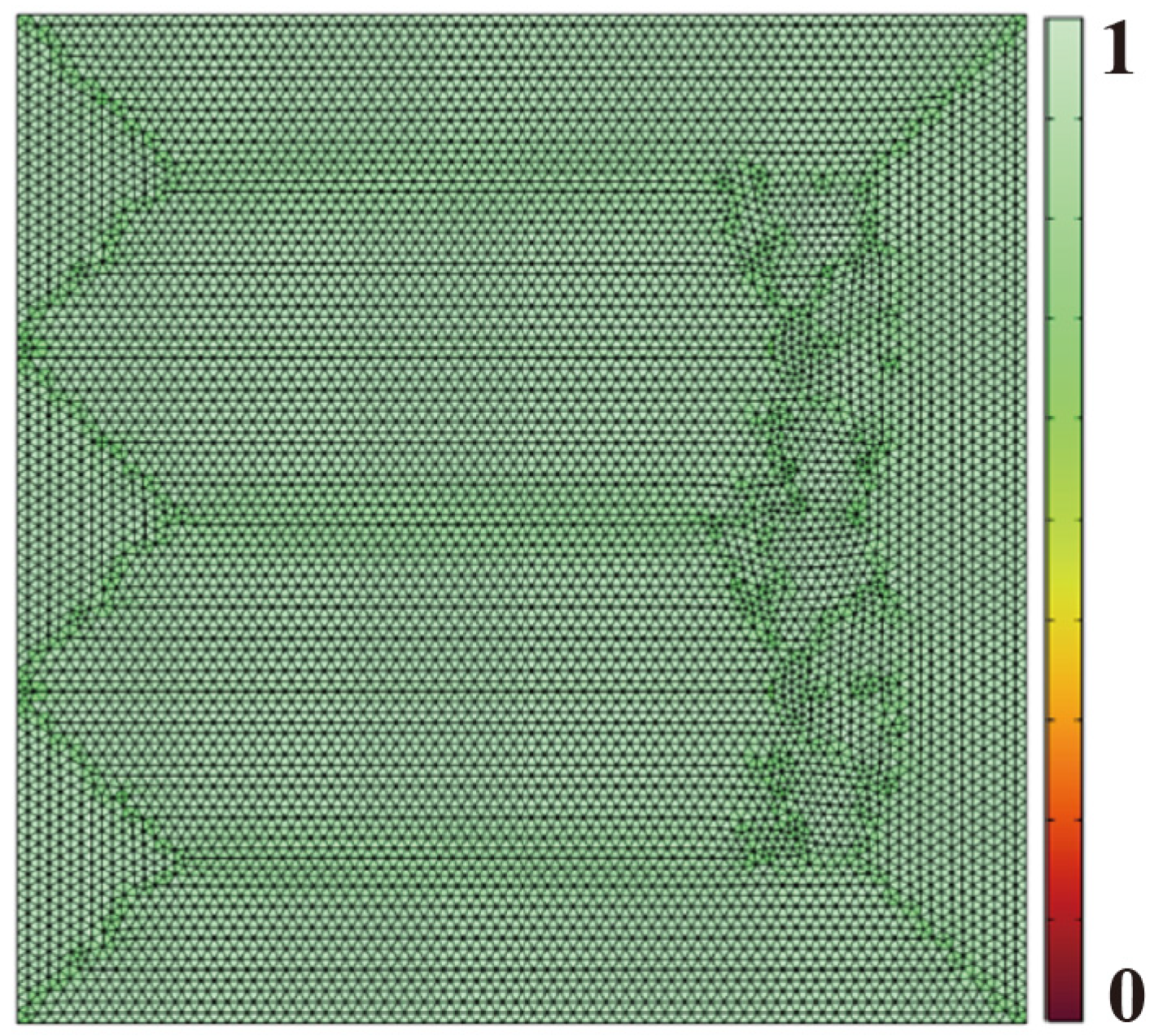
2.3. Grid and Time Step Independence Tests
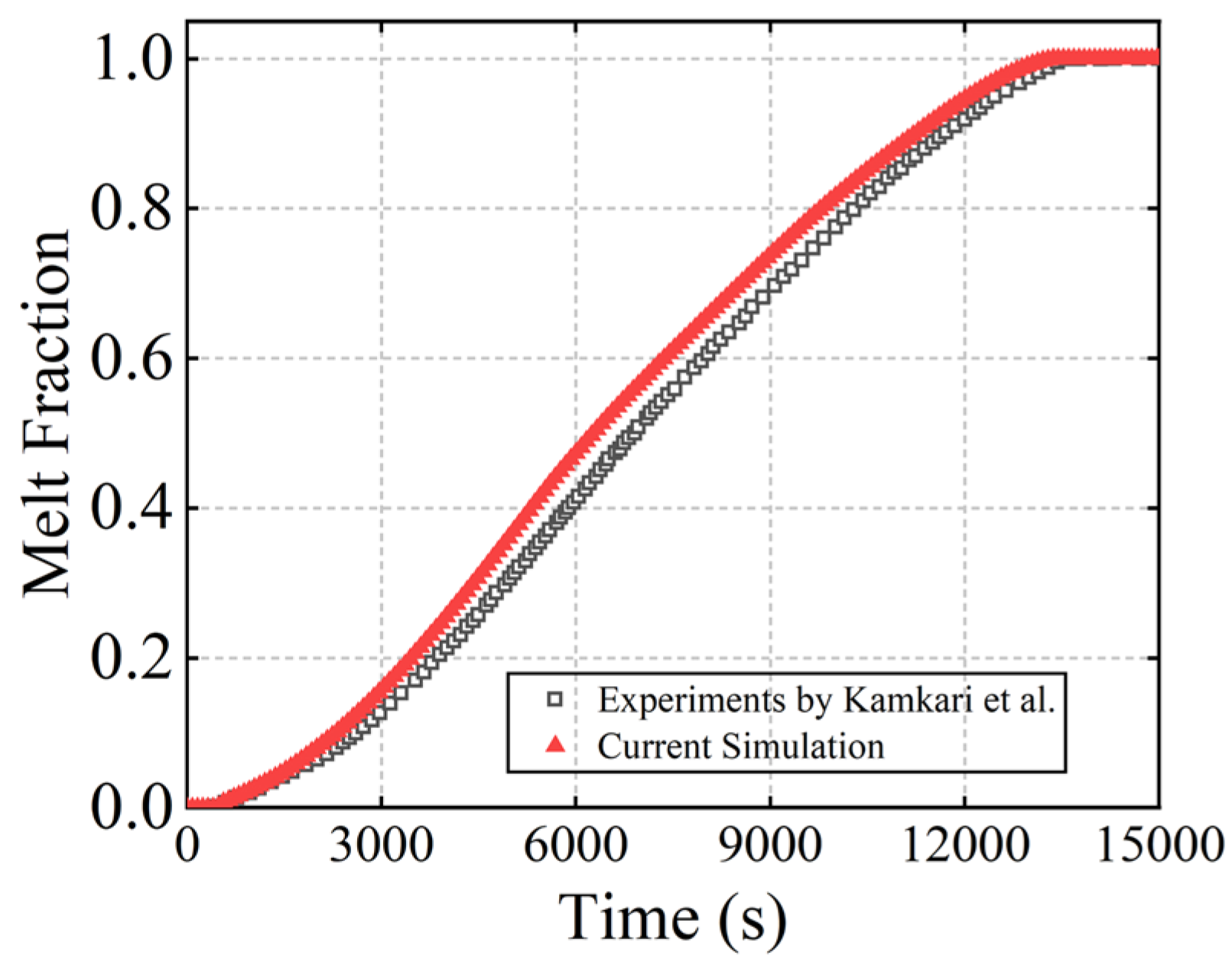
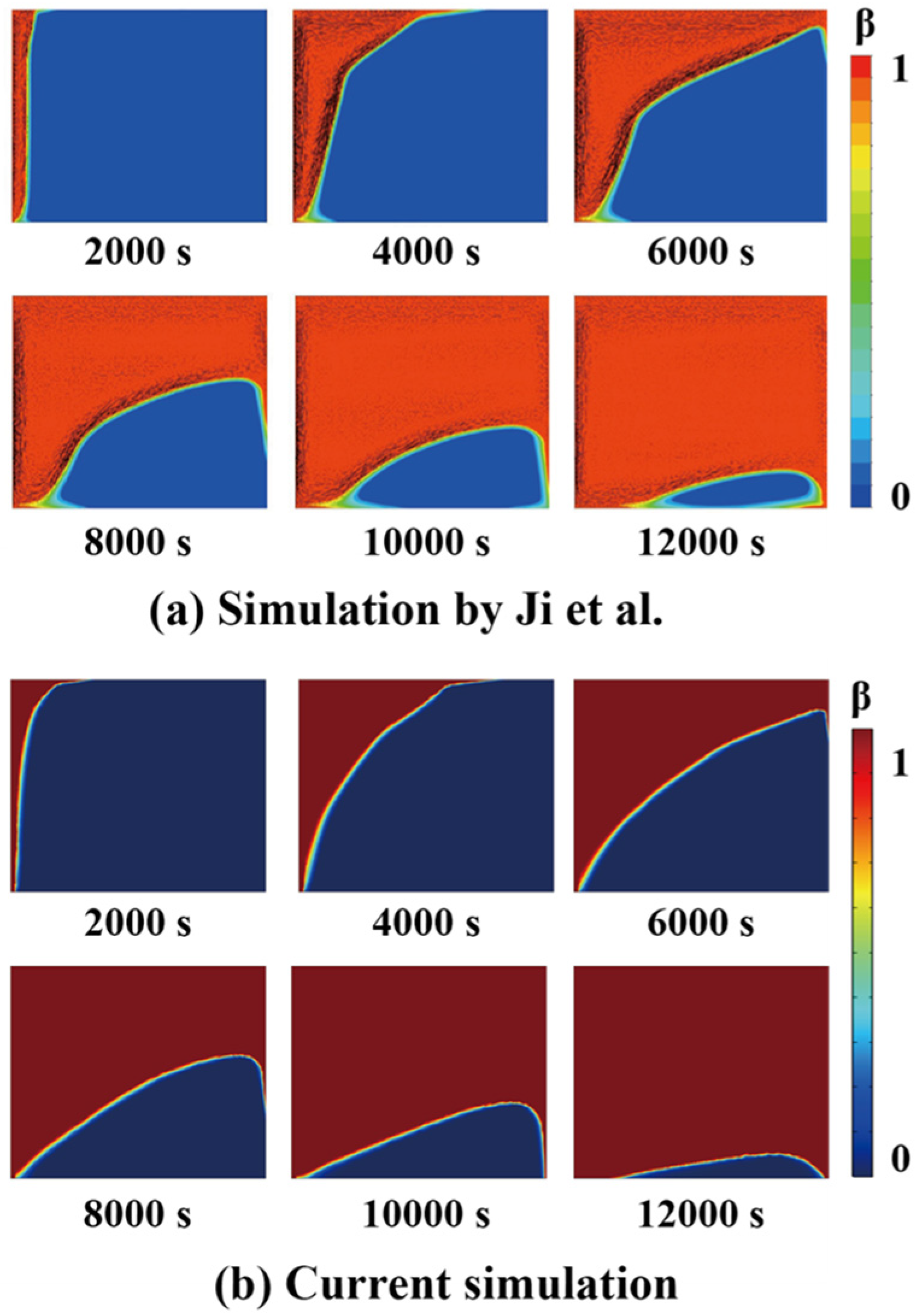
2.4. Model Verification
3. Results and Discussion
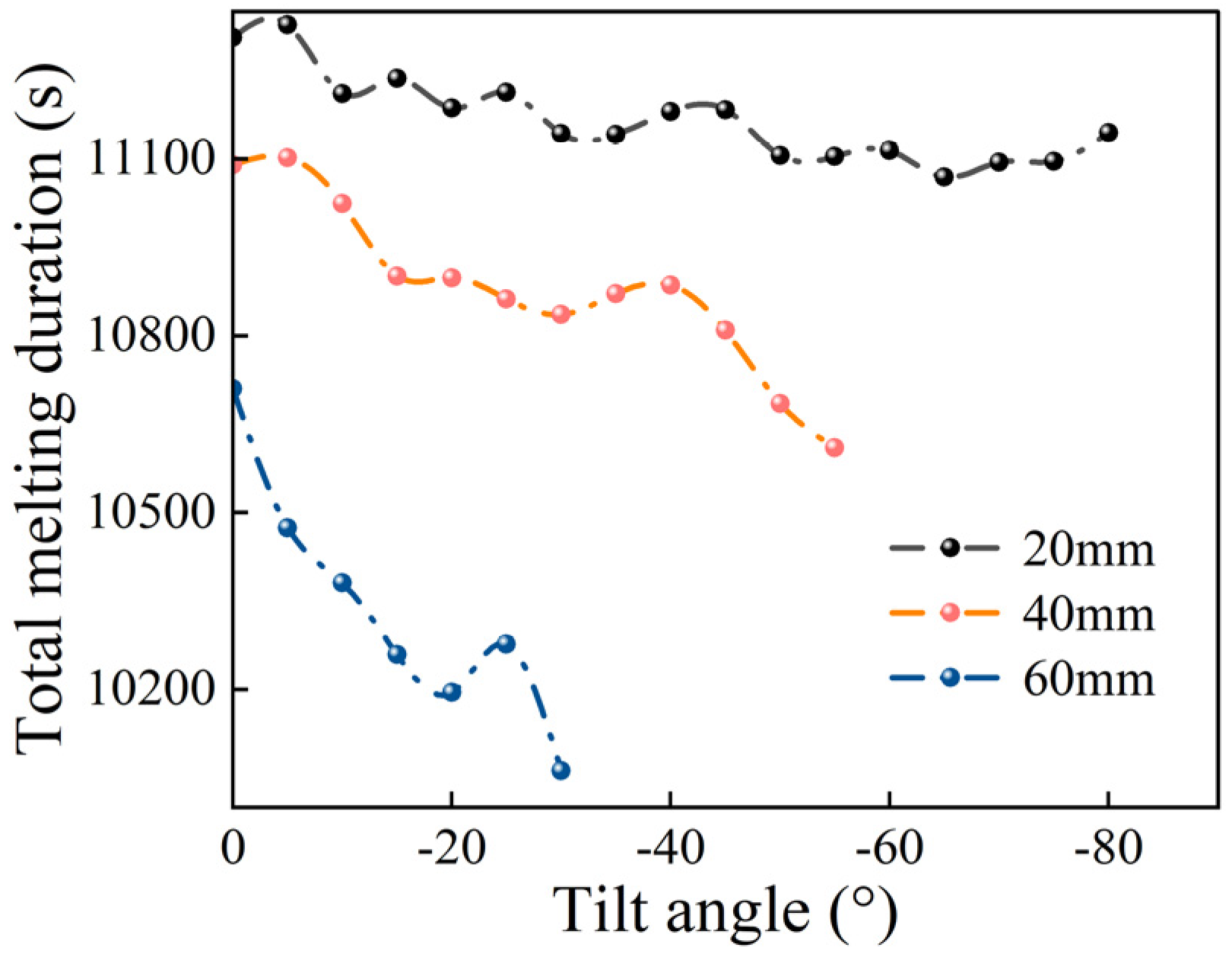
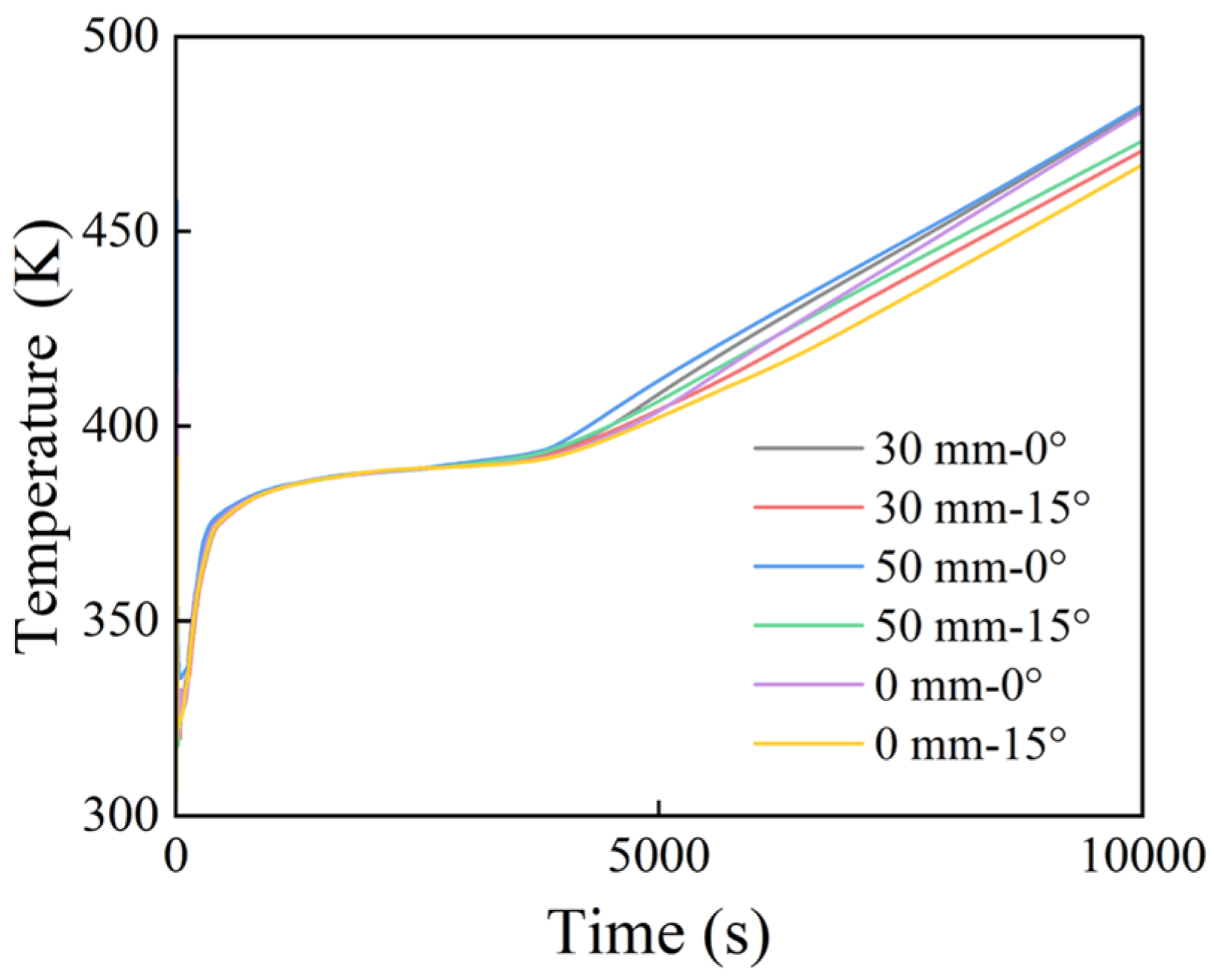
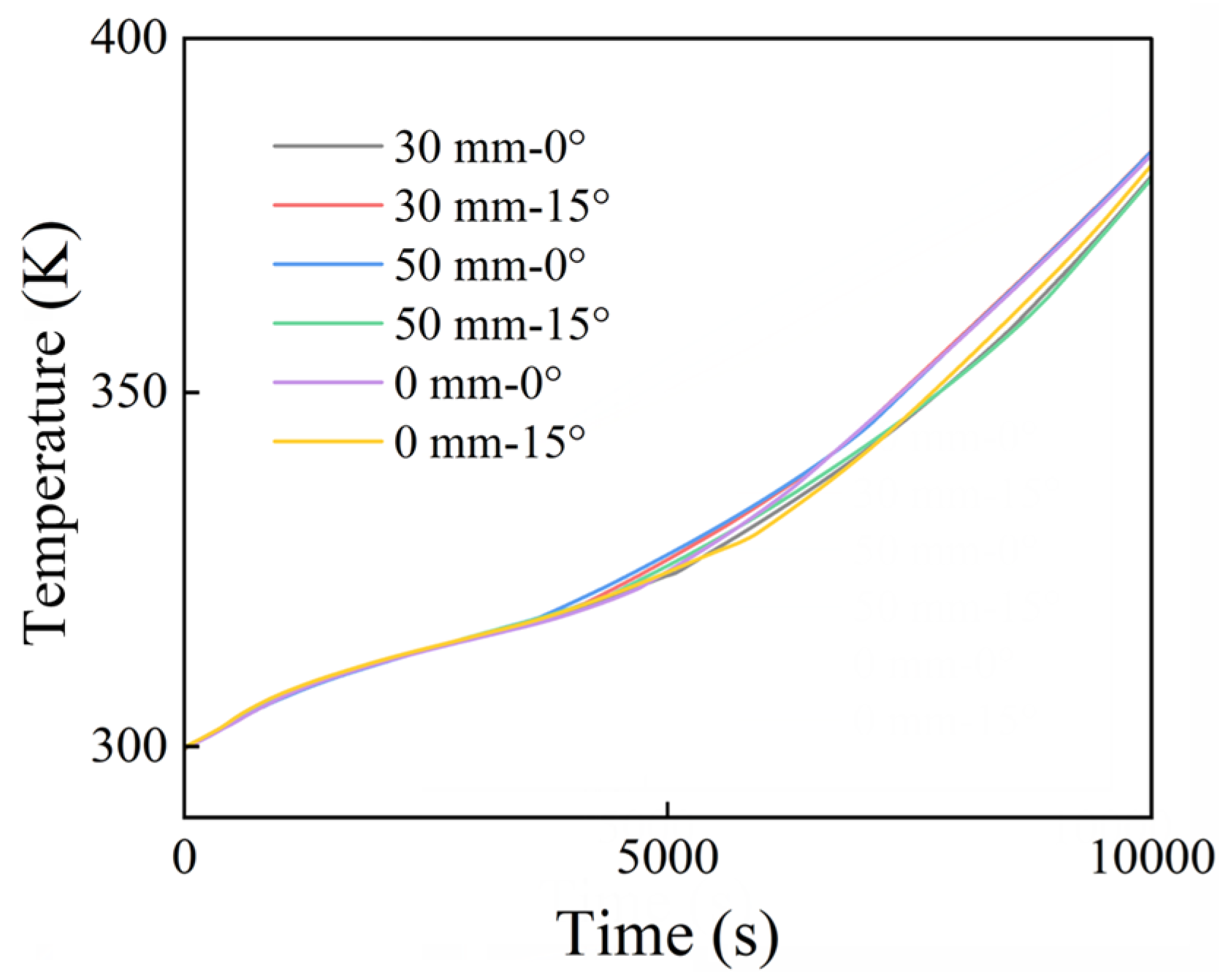
3.1. Effects of the Total Fin Length and Inclination Angle Variation
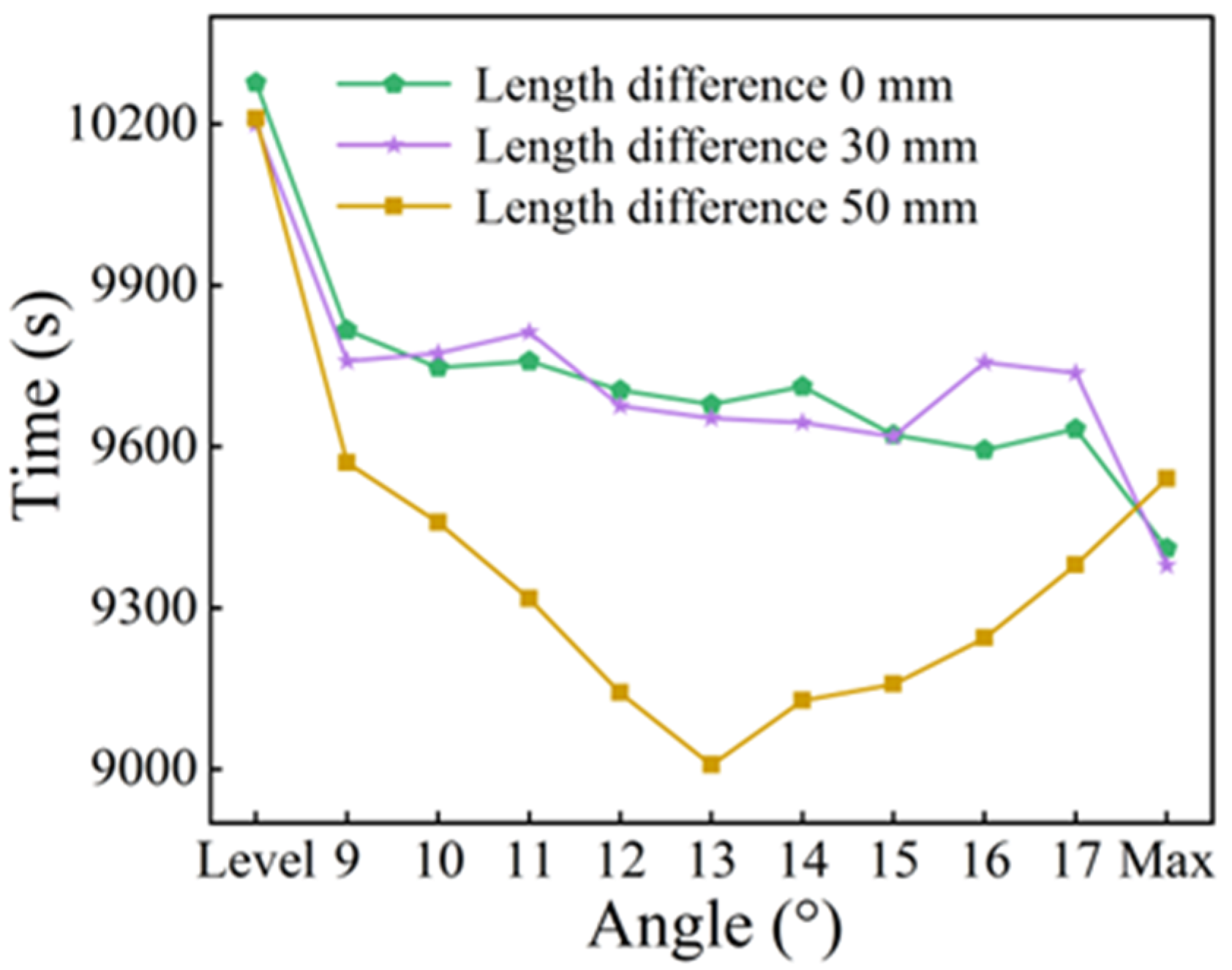
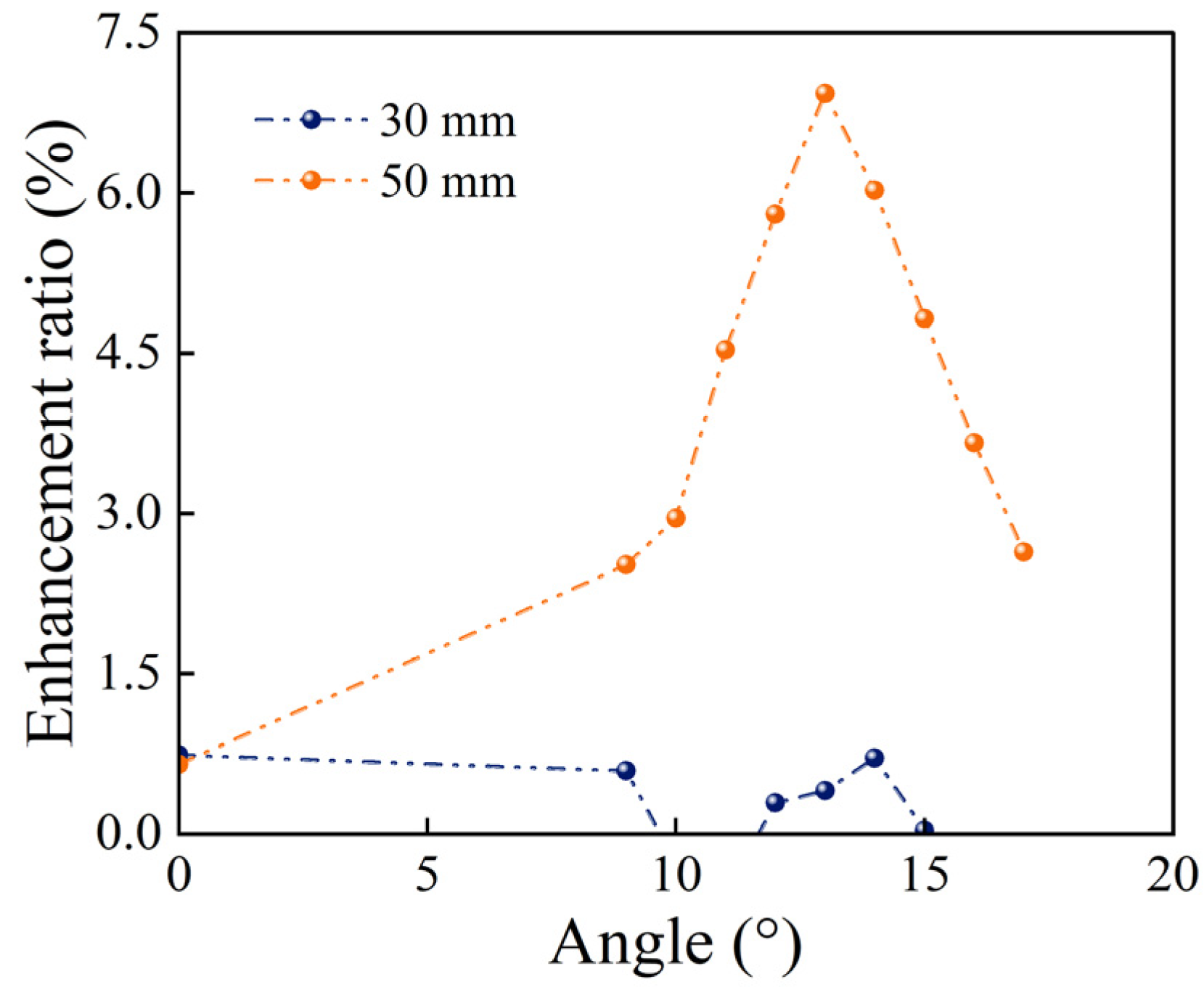
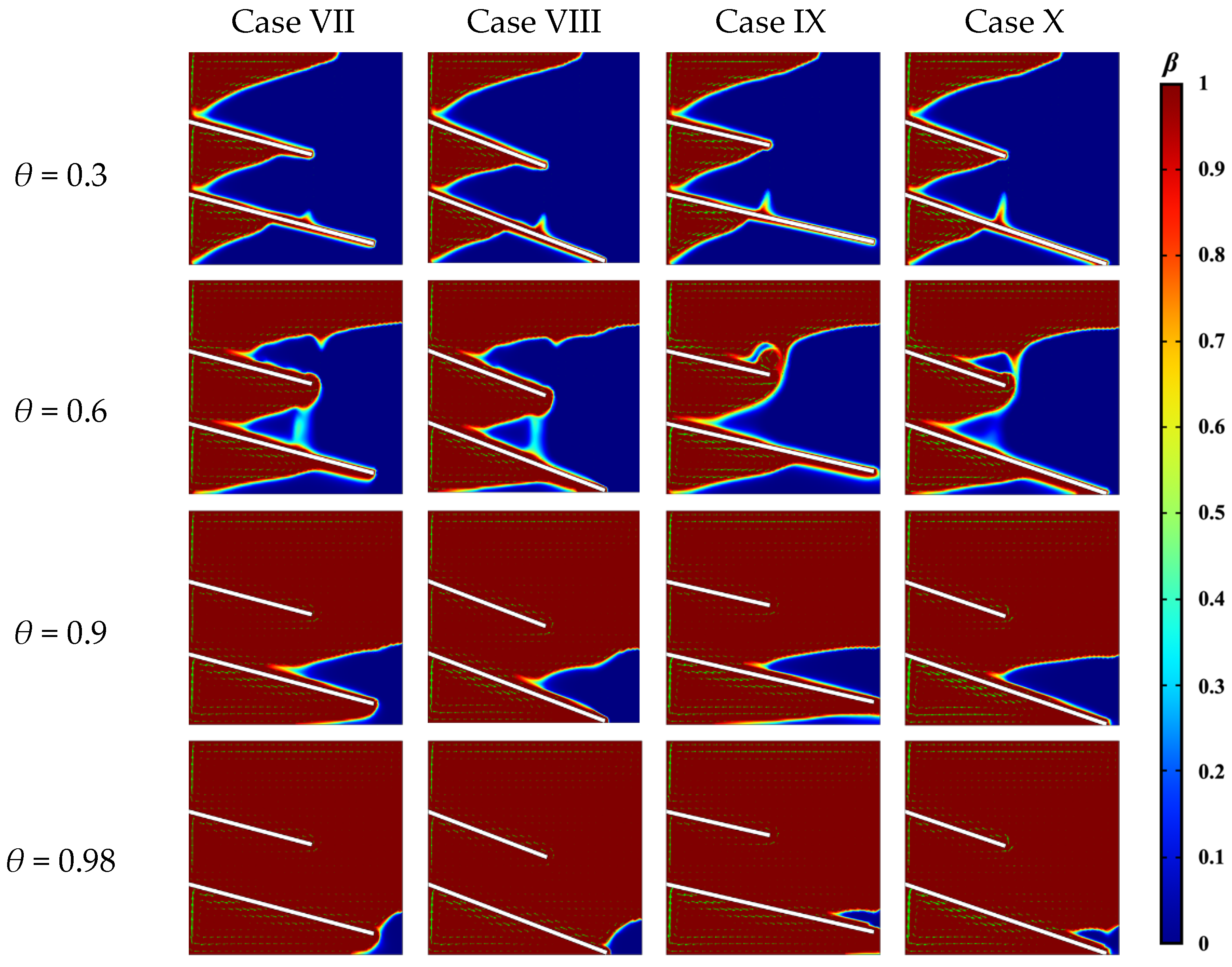
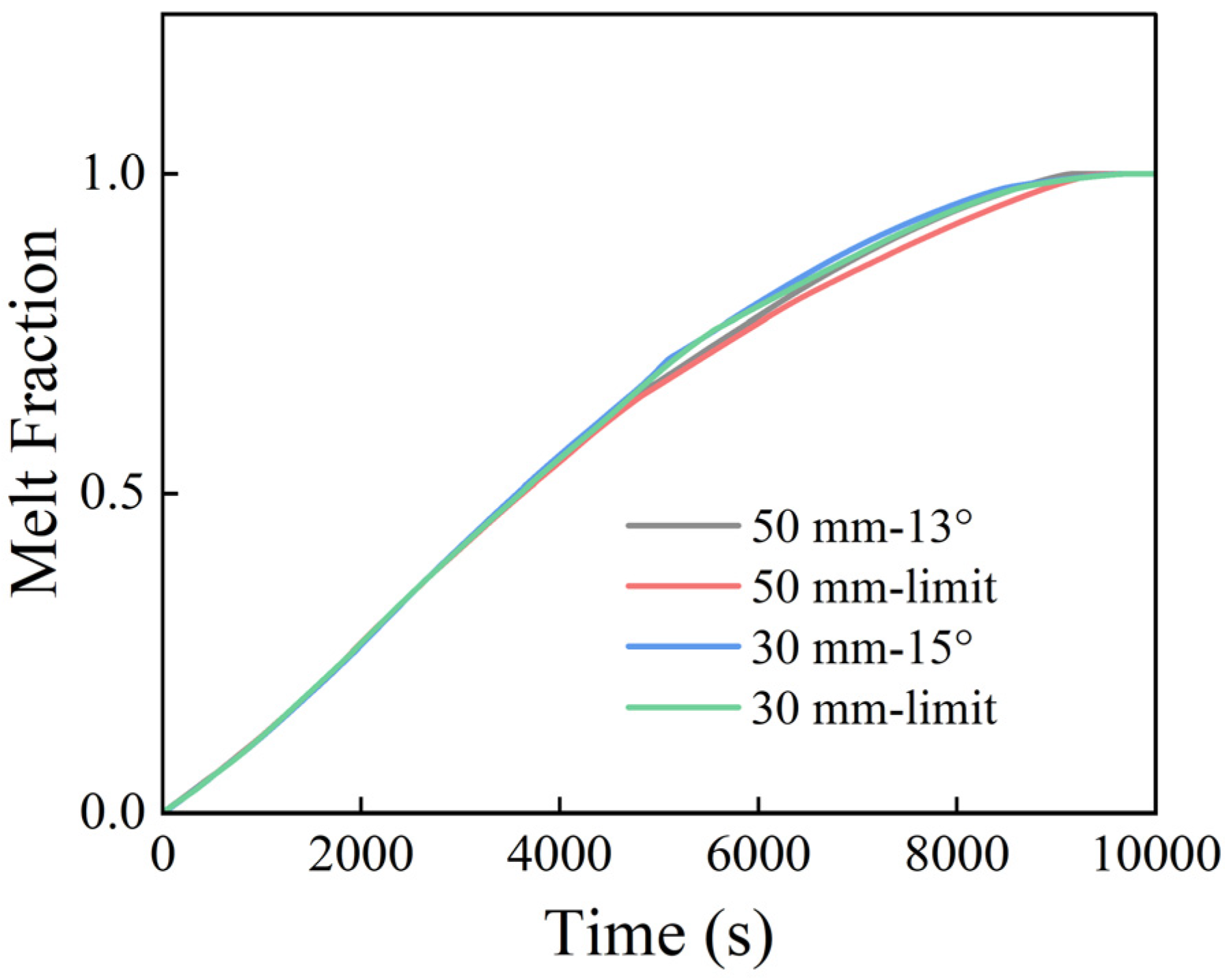
3.2. Effects of the Limit Tilt Angle on the Melting Rate
4. Conclusions
- The tilt angle of the fins significantly impacted the melting rate. When the tilt angle increased, the melting rate of the PCM in the lower regions was enhanced. This effect was particularly pronounced with longer fin configurations, and the melting rate can be enhanced by up to 6.1%.
- When the total fin length was constant, fins with a larger length difference were more effective at promoting the melting of the lower regions, especially when an appropriate tilt angle was applied. Compared with the horizontal fins of equal length, the melt duration can be reduced by 12.3%.
- When the fins tilted to the limit angle, creating an enclosed space, the flow velocity increased and the convective heat transfer was strengthened, which could reduce the overall melting time by about 2.5%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, W.; Guo, T.; Yuan, X.; Ma, H.; Liang, D.; Dong, J. Experimental study on the supercooling and heat transfer performance during the solidification of sodium acetate trihydrate composites. Sol. Energy Mater. Sol. Cells 2023, 250, 112098. [Google Scholar] [CrossRef]
- Kapsalis, V.; Karamanis, D. Solar thermal energy storage and heat pumps with phase change materials. Appl. Therm. Eng. 2016, 99, 1212–1224. [Google Scholar] [CrossRef]
- Huang, P.; Wei, G.; Cui, L.; Xu, C.; Du, X. Experimental and numerical optimization of cascaded PCM heat sink by using low melting point alloys. Energy Convers. Manag. 2022, 269, 116149. [Google Scholar] [CrossRef]
- Javani, N.; Dincer, I.; Naterer, G.F.; Yilbas, B.S. Exergy analysis and optimization of a thermal management system with phase change material for hybrid electric vehicles. Appl. Therm. Eng. 2014, 64, 471–482. [Google Scholar] [CrossRef]
- Merlin, K.; Soto, J.; Delaunay, D.; Traonvouez, L. Industrial waste heat recovery using an enhanced conductivity latent heat thermal energy storage. Appl. Energy 2016, 183, 491–503. [Google Scholar] [CrossRef]
- Xu, H.; Romagnoli, A.; Sze, J.Y.; Py, X. Application of material assessment methodology in latent heat thermal energy storage for waste heat recovery. Appl. Energy 2017, 187, 281–290. [Google Scholar] [CrossRef]
- Jaworski, M. Thermal performance of building element containing phase change material (PCM) integrated with ventilation system-an experimental study. Appl. Therm. Eng. 2014, 70, 665–674. [Google Scholar] [CrossRef]
- Rouault, F.; Bruneau, D.; Sebastian, P.; Nadeau, J.P. Use of a latent heat thermal energy storage system for cooling a light-weight building: Experimentation and co-simulation. Energy Build. 2016, 127, 479–487. [Google Scholar] [CrossRef]
- Nicolalde, J.F.; Cabrera, M.; Martínez-Gómez, J.; Salazar, R.B.; Reyes, E. Selection of a phase change material for energy storage by multi-criteria decision method regarding the thermal comfort in a vehicle. J. Energy Storage 2022, 51, 104437. [Google Scholar] [CrossRef]
- Mat, S.; Al-Abidi, A.A.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Enhance heat transfer for PCM melting in triplex tube with internal–external fins. Energy Convers. Manag. 2013, 74, 223–236. [Google Scholar] [CrossRef]
- Sangeetha, A.; Shanmugan, S.; Alrubaie, A.J.; Jaber, M.M.; Panchal, H.; Attia ME, H.; Elsheikh, A.H.; Mevada, D.; Essa, F.A. A review on PCM and nanofluid for various productivity enhancement methods for double slope solar still: Future challenge and current water issues. Desalination 2023, 551, 116367. [Google Scholar] [CrossRef]
- Shalaby, S.M.; El-Bialy, E.; El-Sebaii, A.A. An experimental investigation of a V-corrugated absorber single-basin solar still using PCM. Desalination 2016, 398, 247–255. [Google Scholar] [CrossRef]
- Tian, L.; Liu, X.; Chen, S.; Shen, Z. Effect of fin material on PCM melting in a rectangular enclosure. Appl. Therm. Eng. 2020, 167, 114764. [Google Scholar] [CrossRef]
- Rawat, P.; Ashwni, A.F.; Sherwani, A.F. A numerical study on the impact of fin length arrangement and material on the melting of PCM in a rectangular enclosure. Int. J. Heat Mass Transf. 2023, 205, 123932. [Google Scholar] [CrossRef]
- Rawat, P.; Goyal, A.; Sherwani, A.F. A comparative numerical study about the impact of rectangular and T shaped fins on melting of PCM in a rectangular enclosure. Appl. Therm. Eng. 2023, 228, 12046. [Google Scholar] [CrossRef]
- Ao, C.; Yan, S.; Hu, W.; Zhao, L.; Wu, Y. Heat transfer analysis of a PCM in shell-and-tube thermal energy storage unit with different V-shaped fin structures. Appl. Therm. Eng. 2022, 216, 119079. [Google Scholar] [CrossRef]
- Bianco, N.; Fragnito, A.; Iasiello, M.; Mauro, G.M. Design of PCM-based heat sinks through topology optimization. J. Phys. Conf. Ser. 2023, 2509, 012001. [Google Scholar] [CrossRef]
- Hosseinizadeh, S.F.; Tan, F.L.; Moosania, S.M. Experimental and numerical studies on performance of PCM-based heat sink with different configurations of internal fins. Appl. Therm. Eng. 2011, 31, 3827–3838. [Google Scholar] [CrossRef]
- Abdi, A.; Martin, V.; Chiu, J.N.W. Numerical investigation of melting in a cavity with vertically oriented fins. Appl. Energy 2019, 235, 1027–1040. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Q.; Zhang, Y.; Sun, K. Phase change material heat transfer enhancement in latent heat thermal energy storage unit with single fin: Comprehensive effect of position length. J. Energy Storage 2021, 42, 103101. [Google Scholar] [CrossRef]
- Oliveski, R.D.C.; Tacques Filho, A.D.Q.; Schroer, I.A. Melting and solidification in thermal storage: Influence of fin aspect ratio and positioning in a full charging and discharging cycle. J. Energy Storage 2022, 50, 104303. [Google Scholar] [CrossRef]
- Cui, W.; Zhang, S.; Zhang, J.; Fan, H.; Zhang, X. Numerical investigation on the melting delay of PCM top heated with a constant heat flux. Int. Commun. Heat Mass Transf. 2025, 163, 108779. [Google Scholar] [CrossRef]
- Ji, C.; Qin, Z.; Dubey, S.; Choo, F.H.; Duan, F. Simulation on PCM melting enhancement with double-fin length arrangements in a rectangular enclosure induced by natural convection. Int. J. Heat Mass Transf. 2018, 127, 255–265. [Google Scholar] [CrossRef]
- Ji, C.; Qin, Z.; Low, Z.; Dubey, S.; Choo, F.H.; Duan, F. Non-uniform heat transfer suppression to enhance PCM melting by angled fins. Appl. Therm. Eng. 2018, 129, 269–279. [Google Scholar] [CrossRef]
- Qin, Z.; Low, Z.; Ji, C.; Duan, F. Efficacy of angled metallic fins for enhancing phase change material melting. Int. Commun. Heat Mass Transf. 2022, 132, 105921. [Google Scholar] [CrossRef]
- Kamkari, B.; Shokouhmand, H.; Bruno, F. Experimental investigation of the effect of inclination angle on convection-driven melting of phase change material in a rectangular enclosure. Int. J. Heat Mass Transfer 2014, 72, 186200. [Google Scholar] [CrossRef]



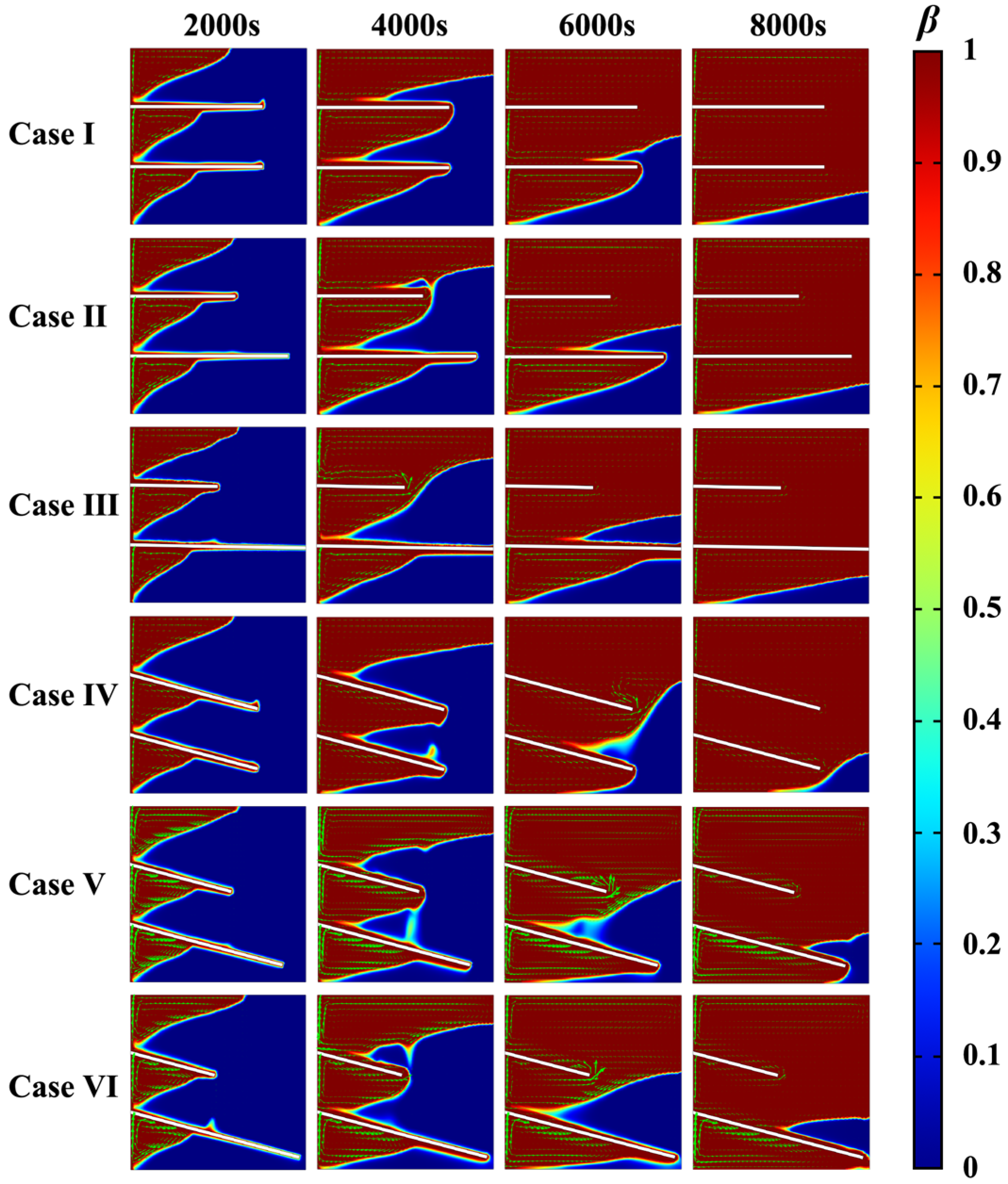

| Case No. | Fin Design | Phase Transition Time (s) |
|---|---|---|
| Case I | 75 mm–75 mm–0° | 10,277 |
| Case II | 60 mm–90 mm–0° | 10,200 |
| Case III | 50 mm–100 mm–0° | 10,189 |
| Case IV | 75 mm–75 mm–15° | 9622 |
| Case V | 60 mm–90 mm–15° | 9619 |
| Case VI | 50 mm–100 mm–0° | 9158 |
| Case VII | 60 mm–90 mm–15° | 9619 |
| Case VIII | 60 mm–90 mm–21° | 9379 |
| Case IX | 50 mm–100 mm–13° | 9008 |
| Case X | 50 mm–100 mm–19° | 9540 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Cui, W.; Yang, S.; Wu, Z.; Xiong, Z.; Zhang, S. Influence of Inclined Non-Uniform Fins on the Melting of Phase Change Materials Under Constant-Power Heating Condition. Energies 2025, 18, 1733. https://doi.org/10.3390/en18071733
Zhang X, Cui W, Yang S, Wu Z, Xiong Z, Zhang S. Influence of Inclined Non-Uniform Fins on the Melting of Phase Change Materials Under Constant-Power Heating Condition. Energies. 2025; 18(7):1733. https://doi.org/10.3390/en18071733
Chicago/Turabian StyleZhang, Xianzhe, Wenbin Cui, Shanyu Yang, Zhilu Wu, Ziyu Xiong, and Sixiang Zhang. 2025. "Influence of Inclined Non-Uniform Fins on the Melting of Phase Change Materials Under Constant-Power Heating Condition" Energies 18, no. 7: 1733. https://doi.org/10.3390/en18071733
APA StyleZhang, X., Cui, W., Yang, S., Wu, Z., Xiong, Z., & Zhang, S. (2025). Influence of Inclined Non-Uniform Fins on the Melting of Phase Change Materials Under Constant-Power Heating Condition. Energies, 18(7), 1733. https://doi.org/10.3390/en18071733





