A Review of Optimization Scheduling for Active Distribution Networks with High-Penetration Distributed Generation Access
Abstract
1. Introduction
2. Impact Analysis of Access at Different DG Penetration Rates
2.1. Analysis of the Characteristics of Distribution Network Integration Under Varying Penetration Levels of Wind and Solar Power
2.2. Laws of Influence of Different DG Penetration Rates on Node Voltage
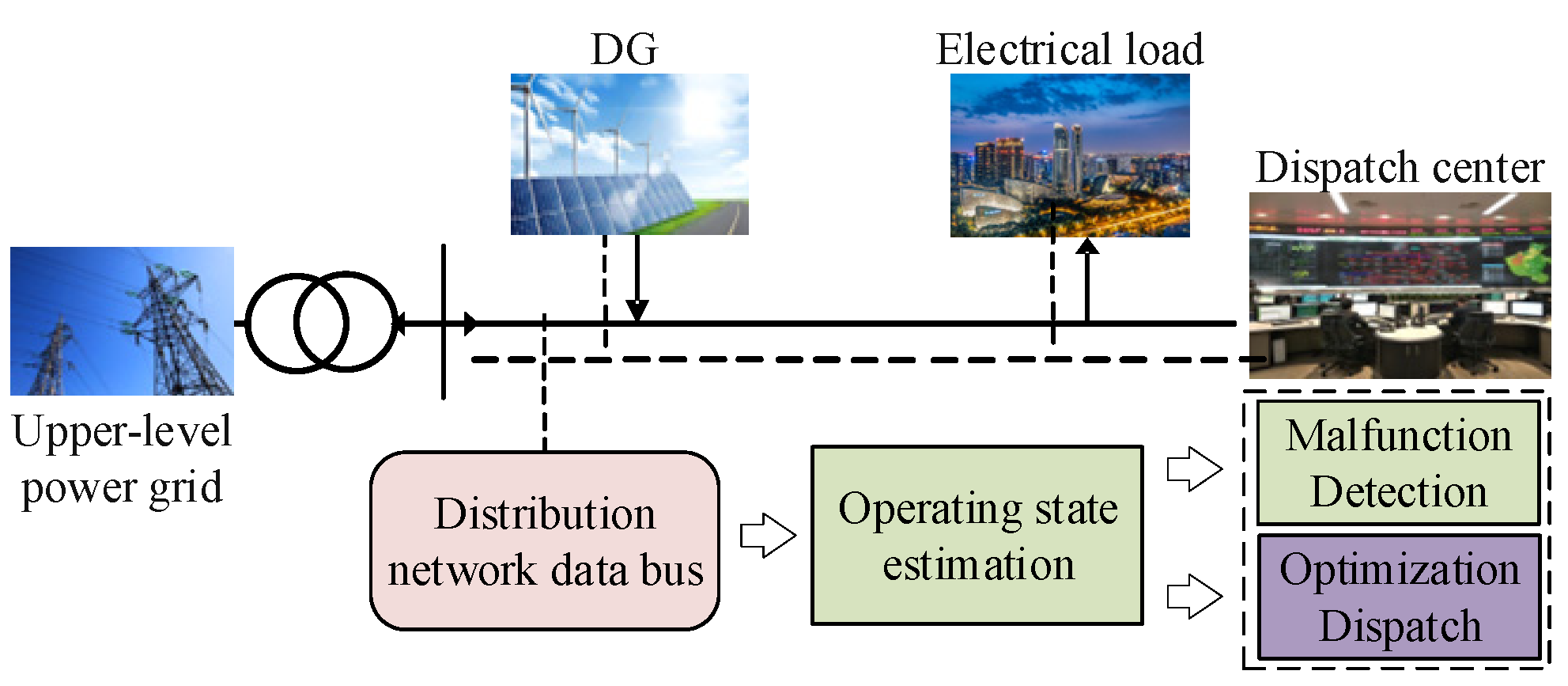
3. Optimal Scheduling Model Building and Solving
3.1. Development of an Optimal Dispatch Model for Distribution Networks
3.1.1. Control Variables
3.1.2. Objective Function
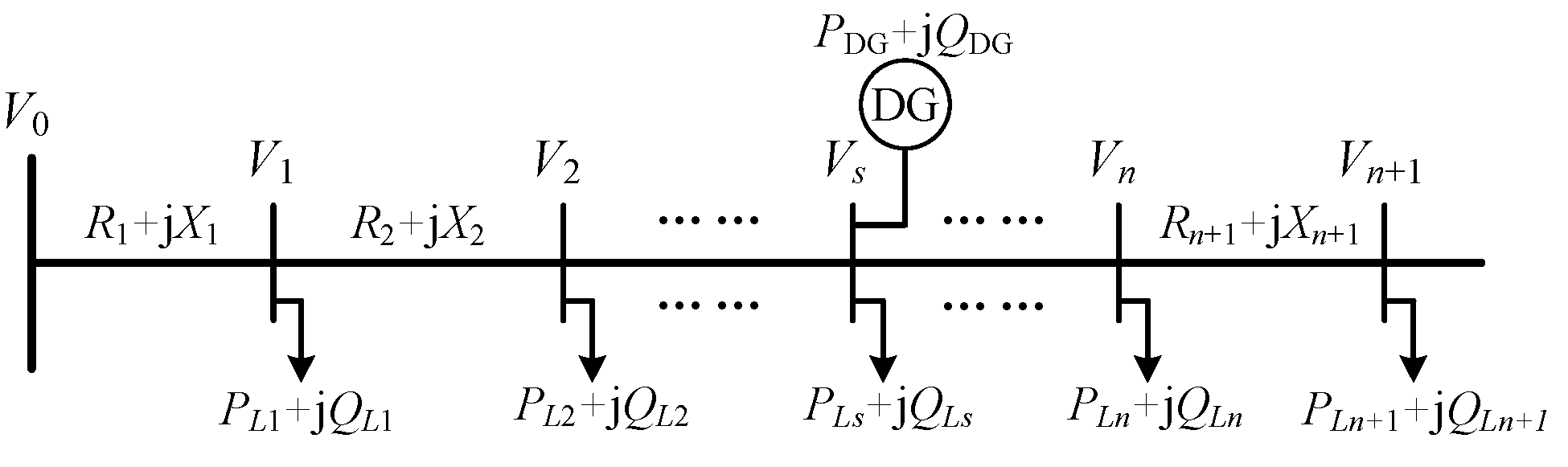
3.1.3. The Power Flow Model for Distribution Networks
3.1.4. Operational Constraints
3.2. Optimal Distribution Network Scheduling Model Solution
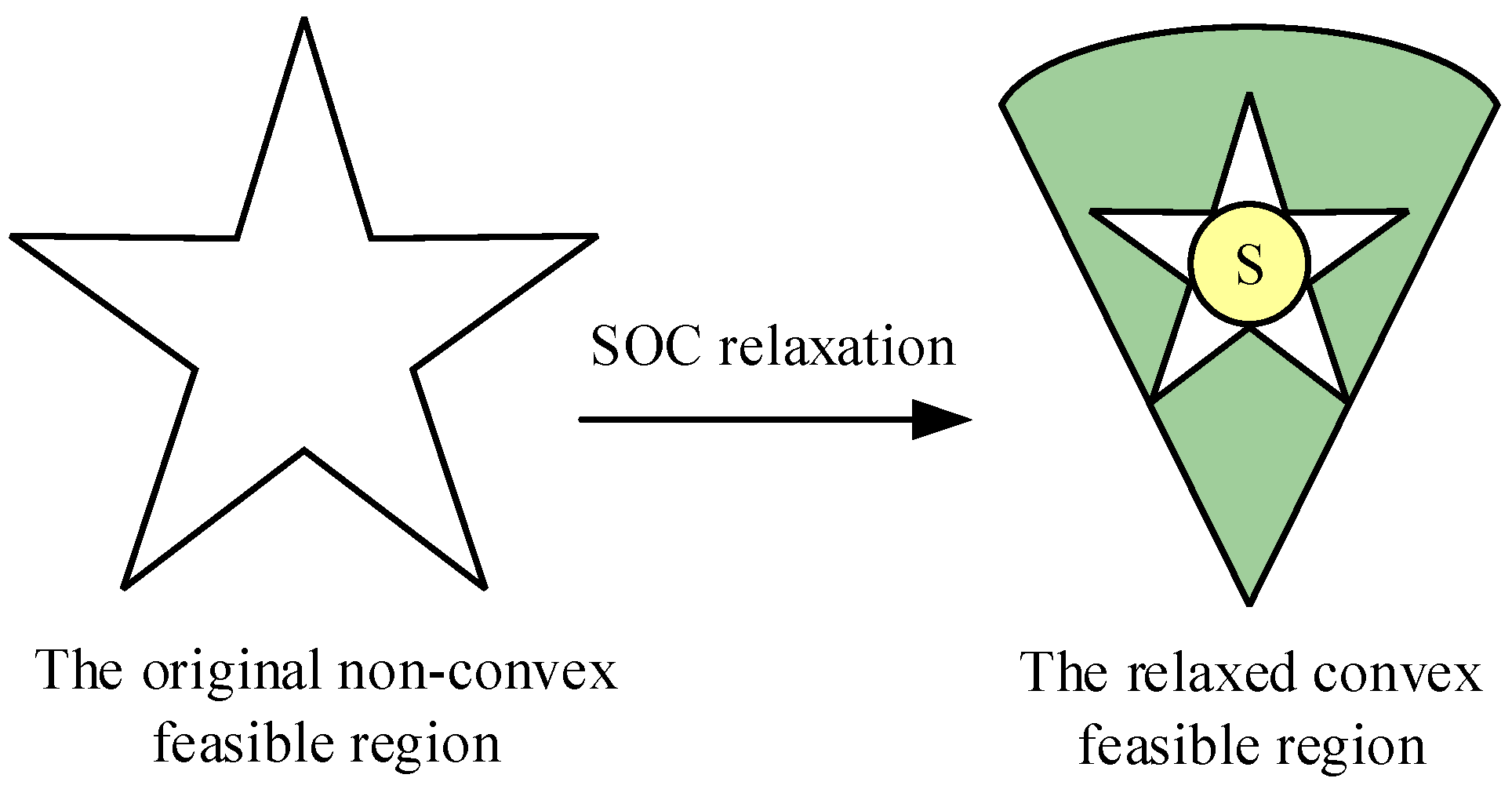
3.2.1. Mathematical Programming Methods
3.2.2. Scheduling Model Solving Algorithm
4. Study on Optimal Scheduling Strategies for High DG Penetration Rate
4.1. Stochastic Optimization Methods
4.2. Two-Stage Stochastic Optimization Method
4.3. Multi-Stage Stochastic Optimization Approach
5. Application of Artificial Intelligence Technology in Optimal Scheduling
5.1. Reinforcement Learning Methods
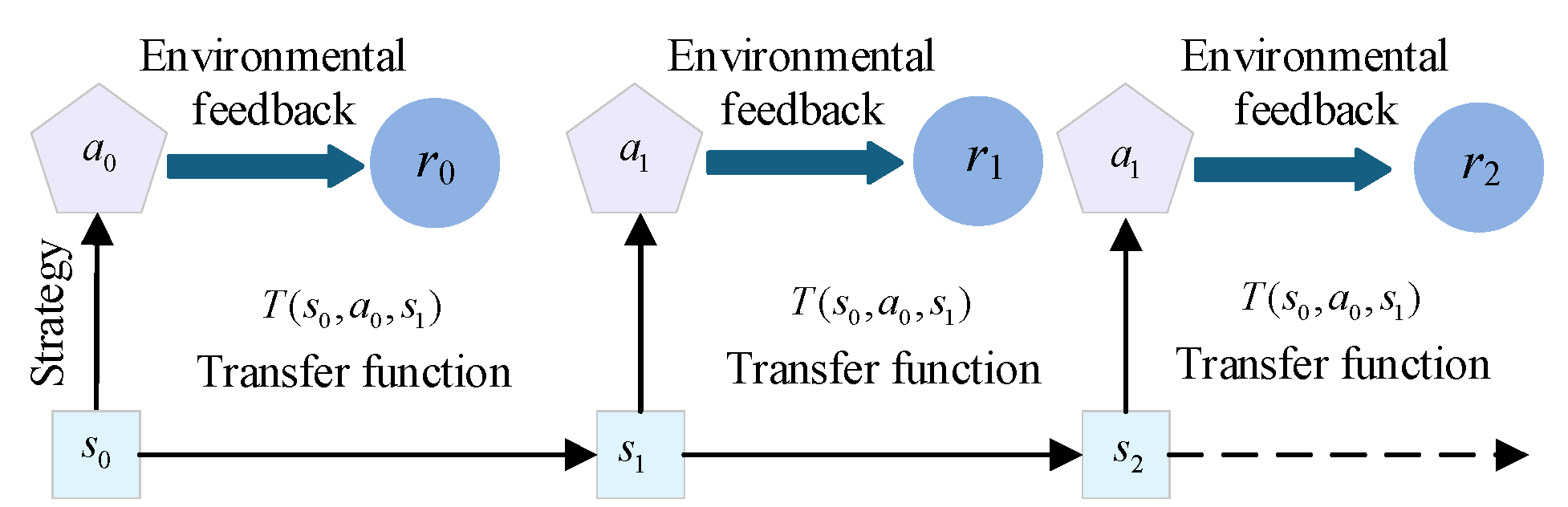
5.1.1. Markov Decision Process
- (1)
- State set: S is the set of states of the environment, where the action of the intelligent body at moment t is ;
- (2)
- Action set: A is the set of actions of an intelligent body, where the action of the intelligent body at moment t is ;
- (3)
- State transfer process: The state transfer process represents the probability that an intelligent body will perform an action in state and then transfer to the next moment state ;
- (4)
- Reward Function: The reward function is the immediate reward obtained by an intelligent body after performing the action in the state ;
5.1.2. Partially Observable Markov Decision Processes
5.2. Deep Reinforcement Learning Methods
5.3. Deep Reinforcement Learning-Based Optimal Scheduling Strategy for Distribution Networks
- (1)
- Deep reinforcement learning employs Markov decision processes (MDPs) to formalize sequential decision-making optimization problems, leveraging Bellman’s equation to systematically deconstruct these problems and enable efficient solutions for sequential control challenges.
- (2)
- Through algorithmic refinement, deep reinforcement learning achieves model-free control capabilities, mitigating the influence of distribution network modeling inaccuracies on operational strategies.
- (3)
- Integration of deep reinforcement learning with multi-agent frameworks facilitates offline training and online optimization, enabling rapid system control via localized real-time information and minimal inter-agent communication while reducing reliance on continuous data exchange.
- (4)
- Hybrid approaches combining deep reinforcement learning with traditional optimization techniques enable coordinated control of heterogeneous devices, fully leveraging power-electronics-enabled devices’ rapid-response capacities to suppress dynamic voltage fluctuations in distribution networks.
- (1)
- DRL relies on time-consuming hyperparameter tuning to optimize performance. Manual experimental parameter adjustment is only feasible for small-scale models and is difficult to scale up to large-scale scenarios.
- (2)
- Most studies overlook actual physical constraints, relying solely on penalty terms in the reward function to guide solutions, which fails to ensure feasibility. Furthermore, the decision-making mechanism of neural networks remains opaque, making it difficult to trace the reasons behind the success or failure of the model.
- (3)
- Distribution networks are characterized by their time-varying and comprehensive nature. Changes in operational conditions can alter power flow distributions, diminishing the effectiveness of offline control strategies. Existing DRL methods have not fully accounted for these dynamic characteristics, resulting in insufficient adaptability.
- (4)
- DRL typically employs historical data for offline training of agents, which are then deployed online after training. However, extreme conditions that were not encountered during the agent’s training phase may arise during system operation, making it difficult to guarantee the feasibility of solutions provided by the agent under such circumstances.
6. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Symbol List
| State variable | |
| Computed weight | |
| Decision variable | |
| Computed weight | |
| State variable | |
| Algorithm parameter |
Abbreviations
| ADN | Active Distribution Network |
| ESS | Energy Storage Systems |
| DG | Distributed Generation |
| SOCP | Second-Order Cone Programming |
| CIA | Convex Inner Approximation |
| DRL | Deep Reinforcement Learning |
| POMDP | Partially Observable MDP |
| GANs | Generative Adversarial Networks |
| PMUs | Phasor Measurement Units |
References
- Zhang, J.; Yang, K.; Wu, J.; Duan, Y.; Ma, Y.; Ren, J.; Yang, Z. Scenario simulation of carbon balance in carbon peak pilot cities under the background of the “dual carbon” goals. Sustain. Cities Soc. 2024, 116, 105910. [Google Scholar] [CrossRef]
- Nazir, M.J.; Li, G.; Nazir, M.M.; Zulfiqar, F.; Siddique, K.H.M.; Iqbal, B.; Du, D. Harnessing soil carbon sequestration to address climate change challenges in agriculture. Soil Tillage Res. 2023, 237, 105959. [Google Scholar] [CrossRef]
- Khan, I.; Tariq, M.; Alabbosh, K.F.; Rehman, A.; Jalal, A.; Khan, A.A.; Farooq, M.; Li, G.; Iqbal, B.; Ahmad, N.; et al. Soil microplastics: Impacts on greenhouse gasses emissions, carbon cycling, microbial diversity, and soil characteristics. Appl. Soil Ecol. 2024, 197, 105343. [Google Scholar] [CrossRef]
- Yan Qunmin, Qu Chenguang, Wang Lei. Research on the Source-Grid-Load-Storage Evaluation System for New Power Systems Considering the Dual Carbon Goals [J/OL]. Acta Energiae Solaris Sin. 2025, 1–11. [CrossRef]
- Yi, Z. Installed Capacity of New Energy Power Generation Surpasses That of Thermal Power for the First Time in 2024. Guangming Daily, 26 January 2025; p. 001. [Google Scholar]
- Shen, X.; Shu, H.; Cao, M.; Pan, N.; Qian, J. Influence of distributed power supply in distributed power distribution network. J. Intell. Fuzzy Syst. 2021, 40, 7803–7810. [Google Scholar] [CrossRef]
- Wang, J.; Hu, Z.; Xie, S. Expansion planning model of multi-energy system with the integration of active distribution network. Appl. Energy 2019, 253, 113517. [Google Scholar] [CrossRef]
- Zubo, R.H.; Mokryani, G.; Rajamani, H.S.; Aghaei, J.; Niknam, T.; Pillai, P. Operation and planning of distribution networks with integration of renewable distributed generators considering uncertainties: A review. Renew. Sustain. Energy Rev. 2016, 72, 1177–1198. [Google Scholar] [CrossRef]
- Yan, H.; Acquah, S.J.; Zhang, J.; Wang, G.; Zhang, C.; Darko, R.O. Overview of modelling techniques for greenhouse microclimate environment and evapotranspiration. Int. J. Agric. Biol. Eng. 2021, 14, 1–8. [Google Scholar] [CrossRef]
- Hu, Y.; Ping, L.; Amoah, A.E.; Wenye, W.; Pingping, L. Control system of a performance test-bed for frost protection wind machines. Int. J. Agric. Biol. Eng. 2016, 9, 36–43. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Yue, D.; Dou, C.; Ding, L.; Tan, D. Voltage Regulation with High Penetration of Low-Carbon Energy in Distribution Networks: A Source–Grid–Load-Collaboration-Based Perspective. IEEE Trans. Ind. Inform. 2022, 18, 3987–3999. [Google Scholar] [CrossRef]
- Gao, Y.; Ai, Q.; Yousif, M.; Wang, X. Source-load-storage consistency collaborative optimization control of flexible DC distribution network considering multi-energy complementarity. Int. J. Electr. Power Energy Syst. 2018, 107, 273–281. [Google Scholar] [CrossRef]
- Murray, W.; Adonis, M.; Raji, A. Voltage control in future electrical distribution networks. Renew. Sustain. Energy Rev. 2021, 146, 111100. [Google Scholar] [CrossRef]
- Azizivahed, A.; Arefi, A.; Ghavidel, S.; Shafie-Khah, M.; Li, L.; Zhang, J.; Catalao, J.P.S. Energy management strategy in dynamic distribution network reconfiguration considering renewable energy resources and storage. IEEE Trans. Sustain. Energy 2019, 11, 662–673. [Google Scholar] [CrossRef]
- Huang, Y.; Jiang, Y.; Wang, J. Adaptability evaluation of distributed power sources connected to distribution network. IEEE Access 2021, 9, 42409–42423. [Google Scholar] [CrossRef]
- Gao, B. Principle and implementation of current differential protection in distribution networks with high penetration of DGs. IEEE Trans. Power Deliv. 2016, 32, 565–574. [Google Scholar] [CrossRef]
- Han, C.; Song, S.; Lee, H.; Jang, G. Sensitivity model-based optimal decentralized dispatching strategy of multi-terminal DC links for the integration of distributed generations in distribution networks. IEEE Trans. Smart Grid 2021, 13, 4022–4034. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Y.; Liu, C.; Weisheng, W. The impact of distributed photovoltaic power generation on distribution network voltage and solutions to voltage violation issues. Power Syst. Technol. 2010, 34, 140–146. [Google Scholar] [CrossRef]
- Wang, Z.; Shan, Y.; Zhou, X. Analysis of distributed photovoltaic grid connection acceptance capacity considering joint benefits 2021. In Proceedings of the China Automation Congress (CAC) 2023, Chongqing, China, 17–19 November 2023; pp. 5477–5482. [Google Scholar] [CrossRef]
- Fu, J.; Han, Y.; Li, W.; Feng, Y.; Zalhaf, A.S.; Zhou, S.; Yang, P.; Wang, C. A novel optimization strategy for line loss reduction in distribution networks with large penetration of distributed generation. Int. J. Electr. Power Energy Syst. 2023, 150, 109112. [Google Scholar] [CrossRef]
- Meng, X.; Gao, J.; Sheng, W.; Gu, W.; Fan, W. A Day-ahead Two-stage Optimal Dispatching Model for Distribution Networks with Distributed Generation. Power Syst. Technol. 2015, 39, 1294–1300. [Google Scholar]
- Chen, Y.; Strothers, M.; Benigni, A. All-day coordinated optimal scheduling in distribution grids with PV penetration. Electr. Power Syst. Res. 2018, 164, 112–122. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Hasanien, H.M.; Arévalo, P.; Turky, R.A.; Jurado, F. A stochastic-interval model for optimal scheduling of PV-assisted multi-mode charging stations. Energy 2022, 253, 124219. [Google Scholar] [CrossRef]
- Xiao, G.; Yang, T.; Liu, H.; Ni, D.; Ferrari, M.L.; Li, M.; Luo, Z.; Cen, K.; Ni, M. Recuperators for micro gas turbines: A review. Appl. Energy 2017, 197, 83–99. [Google Scholar] [CrossRef]
- Mohseni-Bonab, S.M.; Rabiee, A.; Mohammadi-Ivatloo, B. Voltage stability constrained multi-objective optimal reactive power dispatch under load and wind power uncertainties: A stochastic approach. Renew. Energy 2015, 85, 598–609. [Google Scholar] [CrossRef]
- Das, C.K.; Bass, O.; Kothapalli, G.; Mahmoud, T.S.; Habibi, D. Overview of energy storage systems in distribution networks: Placement, sizing, operation, and power quality. Renew. Sustain. Energy Rev. 2018, 91, 1205–1230. [Google Scholar] [CrossRef]
- Shi, R.; Han, X.; Guo, W. Uncertain multi-objective programming approach for planning supplementary irrigation areas in rainfed agricultural regions. Irrig. Drain. 2024, 74, 1193–1214. [Google Scholar] [CrossRef]
- Pang, Y.; Li, H.; Tang, P.; Chen, C. Synchronization optimization of pipe diameter and operation frequency in a pressurized irrigation network based on the genetic algorithm. Agriculture 2022, 12, 673. [Google Scholar] [CrossRef]
- Ding, C.; Wang, L.; Chen, X.; Yang, H.; Huang, L.; Song, X. A Blockchain-Based Wide-Area agricultural machinery resource scheduling system. Appl. Eng. Agric. 2023, 39, 1–12. [Google Scholar] [CrossRef]
- Kumar, D.; Padhy, B.P. Optimal selection of voltage controlling parameter in uncertain active distribution network. IEEE Trans. Ind. Appl. 2023, 60, 1576–1588. [Google Scholar] [CrossRef]
- Pang, Y.; Li, H.; Tang, P.; Chen, C. Irrigation scheduling of pressurized irrigation networks for minimizing energy consumption. Irrig. Drain. 2022, 72, 268–283. [Google Scholar] [CrossRef]
- Macedo, L.H.; Home-Ortiz, J.M.; Vargas, R.; Mantovani, J.R.S.; Romero, R.; Catalão, J.P.S. Short-circuit constrained distribution network reconfiguration considering closed-loop operation. Sustain. Energy Grids Netw. 2022, 32, 100937. [Google Scholar] [CrossRef]
- Golari, M.; Fan, N.; Wang, J. Two-stage stochastic optimal islanding operations under severe multiple contingencies in power grids. Electr. Power Syst. Res. 2014, 114, 68–77. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhao, J.; Wei, W.; Yu, Y. Optimal charging and discharging scheme of battery energy storage system in active distribution network. Autom. Electr. Power Syst. 2016, 40, 47–53. [Google Scholar] [CrossRef]
- Ma, L.; Liu, M.; Yin, Y.; Wang, Z.; Lu, Z. Research on robust environmental-economic dispatch for multiple microgrids in active distribution networks. Acta Energiae Solaris Sin. 2020, 41, 1–10. [Google Scholar]
- Dolara, A.; Faranda, R.; Leva, S. Energy comparison of seven MPPT techniques for PV systems. J. Electromagn. Anal. Appl. 2009, 3, 152–162. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, D.; Jia, H.; Lei, Y.; Li, J. Bi-level game-based extended planning for regional integrated energy systems considering constraints of multi-energy carbon flows. Autom. Electr. Power Syst. 2023, 47, 12–22. [Google Scholar]
- Shen, W.; Qiu, J.; Meng, K.; Chen, X.; Dong, Z.Y. Low-carbon electricity network transition considering retirement of aging coal generators. IEEE Trans. Power Syst. 2020, 35, 4193–4205. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, X.; Zou, S. Capacity optimization allocation method for wind-photovoltaic-pumped storage hybrid systems considering carbon emissions. Autom. Electr. Power Syst. 2021, 45, 9–18. [Google Scholar]
- Bian, X.; Wu, S.; Zhao, J. Multi-level flexible resource planning for novel power systems considering source-load carbon responsibility allocation. Electr. Power Autom. Equip. 2024, 44, 155–164. [Google Scholar]
- Cui, Y.; Deng, G.; Zeng, P.; Zhong, W.; Zhao, Y.; Liu, X. A multi-time-scale source-load scheduling method for wind power-integrated power systems considering the low-carbon characteristics of carbon capture power plants. Proc. CSEE 2022, 42, 5869–5886+6163. [Google Scholar]
- Cui, Y.; Deng, G.; Zhao, Y.; Zhong, W.; Tang, Y.; Liu, X. Economic dispatch of wind power-integrated power systems considering the complementary low-carbon characteristics of source and load. Proc. CSEE 2021, 41, 4799–4815. [Google Scholar] [CrossRef]
- Xu, L.; Xiang, H.; Ni, L. Grain powder classification based on random forest algorithm and hardware acceleration. Comput. Appl. Res. 2022, 39, 1143. [Google Scholar] [CrossRef]
- Borghetti, A.; Bosetti, M.; Grillo, S.; Massucco, S.; Nucci, C.A.; Paolone, M.; Silvestro, F. Short-term scheduling and control of active distribution systems with high penetration of renewable resources. IEEE Syst. J. 2010, 4, 313–322. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, Y.; Zhang, S. Second-order cone programming based probabilistic optimal energy flow of day-ahead dispatch for integrated. Autom. Electr. Power Syst. 2019, 43, 25–33. [Google Scholar] [CrossRef]
- Xiao, Y.; Yu, Y.; Zhang, G. Optimal configuration of distributed power generation based on an improved sooty tern optimization algorithm. Power Syst. Prot. Control 2022, 50, 148–155. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, C.; Li, Y.; Liu, J.; Guo, Y.; Cao, Y. Multi-level reverse overloading risk assessment for distribution networks with high-penetration photovoltaic integration. High Volt. Eng. 2024, 50, 4540–4549. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, W.; Wan, H. Combing data-driven and model-driven methods for high proportion renewable energy distribution network reliability evaluation. Int. J. Electr. Power Energy Syst. 2023, 149, 108941. [Google Scholar] [CrossRef]
- Yang, B.; Tang, J.; Feng, C. Optimal Setting Method of Inverse Time Overcurrent Protection for the Distribution Networks Based on the Improved Grey Wolf Optimization. Complexity 2021, 2021, 9564583. [Google Scholar] [CrossRef]
- Wu, J.; Liu, M.; Lu, W.; Xie, K. Real-time optimization of active distribution networks with distributed energy resources participating in frequency regulation. J. Clean. Prod. 2021, 328, 129597. [Google Scholar] [CrossRef]
- Watson, J.D.; Watson, N.R.; Lestas, I. Optimized dispatch of energy storage systems in unbalanced distribution networks. IEEE Trans. Sustain. Energy 2017, 9, 639–650. [Google Scholar] [CrossRef]
- Chen, H.; Xu, Y.; Wu, W.; Sun, H. Prediction optimization fusion learning-based approach for day-ahead carbon aware scheduling in distribution network. Appl. Energy 2025, 397, 126369. [Google Scholar] [CrossRef]
- Luo, Y.; Zhu, J.; Chen, J.; Wu, R.; Huang, H.; Liu, W.; Liu, M. High-order taylor expansion-based nonlinear value function approximation for stochastic economic dispatch of active distribution network. IEEE Trans. Smart Grid 2024, 15, 4511–4521. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grisales-Noreña, L.F.; Gil-González, W. Multi-Objective battery coordination in distribution networks to simultaneously minimize CO2 emissions and energy losses. Sustainability 2024, 16, 2019. [Google Scholar] [CrossRef]
- Wang, W.; Huang, Y.; Yang, M.; Chen, C.; Zhang, Y.; Xu, X. Renewable energy sources planning considering approximate dynamic network reconfiguration and nonlinear correlations of uncertainties in distribution network. Int. J. Electr. Power Energy Syst. 2022, 139, 107791. [Google Scholar] [CrossRef]
- Tabares, A.; Muñoz-Delgado, G.; Franco, J.F.; Arroyo, J.M.; Contreras, J. Multistage reliability-based expansion planning of ac distribution networks using a mixed-integer linear programming model. Int. J. Electr. Power Energy Syst. 2022, 138, 107916. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Lu, H. Crop acreage planning for economy-resource-efficiency coordination: Grey information entropy based uncertain model. Agric. Water Manag. 2023, 289, 108557. [Google Scholar] [CrossRef]
- Weiping, W.; Zechun, H.; Yonghua, S.; Zhiwei, X. Research on OPF Hybrid Optimization Algorithm Combining Semidefinite Programming and Nonlinear Programming Models. Proc. CSEE 2016, 36, 3829–3837. [Google Scholar]
- Vittal, V. Non-Iterative Enhanced SDP Relaxations for Optimal Scheduling of Distributed Energy Storage in Distribution Systems. IEEE Trans. Power Syst. 2017, 32, 1721–1732. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, W.; Zhang, B.; Li, Z.; Li, Z. A Mixed Integer Second-order Cone Programming Based Active and Reactive Power Coordinated Multi-period Optimization for Active Distribution Network. Proc. CSEE 2014, 34, 2575–2583. [Google Scholar]
- Ji, H.; Wang, C.; Li, P.; Zhao, J.; Song, G.; Ding, F.; Wu, J. An enhanced SOCP-based method for feeder load balancing using the multi-terminal soft open point in active distribution networks. Appl. Energy 2017, 208, 986–995. [Google Scholar] [CrossRef]
- Nazir, N.; Almassalkhi, M. Grid-aware aggregation and realtime disaggregation of distributed energy resources in radial networks. IEEE Trans. Power Syst. 2021, 37, 1706–1717. [Google Scholar] [CrossRef]
- Dong, L.; Tian, A.; Yu, T. Reactive Power Optimization of Distribution Network with Distributed Generation Based on Mixed-Integer Semidefinite Programming. Autom. Electr. Power Syst. 2015, 39, 66–72. [Google Scholar]
- Farivar, M.; Low, S.H. Branch flow model: Relaxations and convexification—Part, I. IEEE Trans. Power Syst. 2013, 28, 2554–2564. [Google Scholar] [CrossRef]
- Milano, F. On the modelling of zero impedance branches for power flow analysis. IEEE Trans. Power Syst. 2015, 31, 3334–3335. [Google Scholar] [CrossRef]
- Gao, H.; Liu, J.; Wang, L.; Liu, Y. Research on optimal power flow in active distribution networks and its practical application examples. Proc. CSEE 2017, 37, 1634–1645. [Google Scholar] [CrossRef]
- Zhang, B.; Tse, D. Geometry of feasible injection region of power networks. In Proceedings of the 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 28–30 September 2011; pp. 1508–1515. [Google Scholar] [CrossRef]
- Zhang, B.; Tse, D. Geometry of injection regions of power networks. IEEE Trans. Power Syst. 2013, 28, 788–797. [Google Scholar] [CrossRef]
- Lavaei, J.; Tse, D.; Zhang, B. Geometry of power flows and optimization in distribution networks. IEEE Trans. Power Syst. 2014, 29, 572–583. [Google Scholar] [CrossRef]
- Gan, L.; Li, N.; Topcu, U.; Low, S.H. Exact Convex Relaxation of Optimal Power Flow in Radial Networks. IEEE Trans. Autom. Control 2015, 60, 72–87. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Lesieutre, B.C.; DeMarco, C.L. A Sufficient Condition for Global Optimality of Solutions to the Optimal Power Flow Problem. IEEE Trans. Power Syst. 2014, 29, 978–979. [Google Scholar] [CrossRef]
- Bernstein, A.; Wang, C.; Dall’Anese, E.; Le Boudec, J.-Y.; Zhao, C. Load Flow in Multiphase Distribution Networks: Existence, Uniqueness, Non-Singularity and Linear Models. IEEE Trans. Power Syst. 2018, 33, 5832–5843. [Google Scholar] [CrossRef]
- Zhang, B.; Lam, A.Y.S.; Domínguez-García, A.D.; Tse, D. An Optimal and Distributed Method for Voltage Regulation in Power Distribution Systems. IEEE Trans. Power Syst. 2015, 30, 1714–1726. [Google Scholar] [CrossRef]
- Stott, B.; Jardim, J.; Alsac, O. DC Power Flow Revisited. IEEE Trans. Power Syst. 2009, 24, 1290–1300. [Google Scholar] [CrossRef]
- Jabr, R.A. Optimal Power Flow Using an Extended Conic Quadratic Formulation. IEEE Trans. Power Syst. 2008, 23, 1000–1008. [Google Scholar] [CrossRef]
- Liao, X.; Zhou, Z.; Li, Z.; Huai, Q. Dynamic reconfiguration of AC/DC hybrid distribution network considering non-ideal linear BES model. Energy Rep. 2023, 9, 5628–5646. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, Y.; Mao, Z. Joint Access Planning for Soft Open Point and Distributed Energy Storage Systems. Autom. Electr. Power Syst. 2022, 46, 29–37. [Google Scholar]
- Bai, X.; Wei, H.; Fujisawa, K.; Wang, Y. Semidefinite programming for optimal power flow problems. Int. J. Electr. Power Energy Syst. 2008, 30, 383–392. [Google Scholar] [CrossRef]
- Il’in, A.V.; Fursov, A.S.; Maltseva, A.V. Generalization of the internal approximation method for the simultaneous stabilization problem. Differ. Equ. 2018, 54, 1669–1673. [Google Scholar] [CrossRef]
- Nazir, N.; Almassalkhi, M. Voltage Positioning Using Co-Optimization of Controllable Grid Assets in Radial Networks. IEEE Trans. Power Syst. 2021, 36, 2761–2770. [Google Scholar] [CrossRef]
- Ademola, A.A.; You, S.; Liu, Y. Automated two-stage conversion of hourly optimal DC flow solution to AC power flow. CSEE J. Power Energy Syst. 2023, 9, 28–36. [Google Scholar] [CrossRef]
- Yang, Z.; Bose, A.; Zhong, H.; Zhang, N.; Xia, Q.; Kang, C. Optimal Reactive Power Dispatch with Accurately Modeled Discrete Control Devices: A Successive Linear Approximation Approach. IEEE Trans. Power Syst. 2017, 32, 2435–2444. [Google Scholar] [CrossRef]
- Fang, X.; Yang, Z.; Yu, J.; Wang, Y. AC Feasibility Restoration in Market Clearing: Problem Formulation and Improvement. IEEE Trans. Ind. Inform. 2022, 18, 7597–7607. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Kong, W.; Cao, C.; Su, J.; Wang, K. Active-reactive power coordinated optimization for active distribution networks based on an improved convex inner approximation method. Proc. CSEE 2024, 44, 5528–5538. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Ren, P. Review of Theory and Key Technologies of Precision Investment in Distribution Network. Power Grid Technol. 2022, 46, 2665–2678. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Wu, L. Distributed optimization approaches for emerging power systems operation: A review. Electr. Power Syst. Res. 2017, 144, 127–135. [Google Scholar] [CrossRef]
- Bonah, E.; Huang, X.; Yi, R.; Aheto, J.H.; Osae, R.; Golly, M. Electronic nose classification and differentiation of bacterial foodborne pathogens based on support vector machine optimized with particle swarm optimization algorithm. J. Food Process Eng. 2019, 42, e13236. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, W.; Chen, Q. Evaluating aroma quality of black tea by an olfactory visualization system: Selection of feature sensor using particle swarm optimization. Food Res. Int. 2019, 126, 108605. [Google Scholar] [CrossRef]
- Adade, S.Y.-S.S.; Lin, H.; Haruna, S.A.; Johnson, N.A.N.; Barimah, A.O.; Afang, Z.; Chen, Z.; Ekumah, J.-N.; Fuyun, W.; Li, H.; et al. Multicomponent prediction of Sudan dye adulteration in crude palm oil using SERS—Based bimetallic nanoflower combined with genetic algorithm. J. Food Compos. Anal. 2023, 125, 105768. [Google Scholar] [CrossRef]
- Chang, X.; Huang, X.; Xu, W. Monitoring of dough fermentation during Chinese steamed bread processing by near-infrared spectroscopy combined with spectra selection and supervised learning algorithm. J. Food Process Eng. 2021, 44, e13783. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Tian, Y.; Wu, X.; Dai, C.; Li, B. Spectral classification of lettuce cadmium stress based on information fusion and VISSA-GOA-SVM algorithm. J. Food Process Eng. 2019, 42, e13085. [Google Scholar] [CrossRef]
- Sun, J.; Tian, Y.; Wu, X.; Dai, C.; Lu, B. Nondestructive detection for moisture content in green tea based on dielectric properties and VISSA-GWO-SVR algorithm. J. Food Process. Preserv. 2020, 44, e14421. [Google Scholar] [CrossRef]
- Majidi, M.; Zare, K. Integration of smart energy hubs in distribution networks under uncertainties and demand response concept. IEEE Trans. Power Syst. 2018, 34, 566–574. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Ma, G.; Sun, Z.; Du, M.; Huang, Y. Multi-objective Expansion Planning of Distribution Network Considering Differentiated Load Demand Response. Power Syst. Prot. Control 2022, 50, 131–141. [Google Scholar] [CrossRef]
- Sheng, S.; Fan, L.; Li, X.; Tan, X. Multi-objective Planning of Distribution Network Based on Pareto Optimality. Autom. Electr. Power Syst. 2014, 38, 51–57. [Google Scholar]
- Gao, Z.; Fan, A.; Han, J. A novel power source-load bilayer cooperative planning method for distribution networks based on adaptive ε-dominated multi-objective particle swarm algorithm. Energy Rep. 2025, 13, 1971–1979. [Google Scholar] [CrossRef]
- Dong, Z.; Xu, T.; Li, Y.; Zhu, Q. Multi-time Scale Optimal Dispatching of Active Distribution Networks Considering Source-Load-Storage Coordination. Sci. Technol. Eng. 2024, 24, 10321–10329. [Google Scholar]
- Yang, Y.; Lu, Y.; Cheng, L.; Wang, C.; Li, G.; Zhang, M. Multi-stage Robust Expansion Planning of Active Distribution Networks Considering Uncertainty in Source-Load Growth and Reliability Costs. Proc. CSEE. 2024, pp. 1–18. Available online: http://kns.cnki.net/kcms/detail/11.2107.tm.20241227.1309.008.html (accessed on 23 July 2025).
- Sanin-Villa, D.; Figueroa-Saavedra, H.A.; Grisales-Noreña, L.F. Efficient BESS scheduling in AC microgrids via Multiverse Optimizer: A Grid-Dependent and Self-Powered strategy to minimize power losses and CO2 footprint. Appl. Syst. Innov. 2025, 8, 85. [Google Scholar] [CrossRef]
- Zheng, N.; Ding, X.; Guan, Z. Active and Reactive power coordination Optimization of Distribution Network Based on Scenario Method. Power Grid Technol. 2019, 43, 1640–1651. [Google Scholar] [CrossRef]
- Bizuayehu, A.W.; de la Nieta, A.A.S.; Contreras, J.; Catalão, J.P.S. Impacts of Stochastic Wind Power and Storage Participation on Economic Dispatch in Distribution Systems. IEEE Trans. Sustain. Energy 2016, 7, 1336–1345. [Google Scholar] [CrossRef]
- Abbaspourtorbati, F.; Conejo, A.J.; Wang, J.; Cherkaoui, R. Three- or Two-Stage Stochastic Market-Clearing Algorithm? IEEE Trans. Power Syst. 2017, 32, 3099–3110. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, H.; Xing, H.; Yao, L.; Zhang, Y. Distribution network distributed power of the consideration of uncertainties in planning research review. Electr. Power Autom. Equip. 2016, 4, 1–9. [Google Scholar] [CrossRef]
- Li, P.; Jin, B.; Wang, D.; Zhang, B. Distribution System Voltage Control Under Uncertainties Using Tractable Chance Constraints. IEEE Trans. Power Syst. 2019, 34, 5208–5216. [Google Scholar] [CrossRef]
- Xu, Y.; Li, J.; Wang, Y. Consider photovoltaic park operation plan has the distribution of output uncertainty. Electr. Power Autom. Equip. 2020, 40, 85–94. [Google Scholar]
- Fu, Y.; Zhang, Z.; Li, Z.; Mi, Y. Energy Management for Hybrid AC/DC Distribution System with Microgrid Clusters Using Non-Cooperative Game Theory and Robust Optimization. IEEE Trans. Smart Grid 2020, 11, 1510–1525. [Google Scholar] [CrossRef]
- Zheng, W.; Huang, W.; Hill, D.J.; Hou, Y. An Adaptive Distributionally Robust Model for Three-Phase Distribution Network Reconfiguration. IEEE Trans. Smart Grid 2021, 12, 1224–1237. [Google Scholar] [CrossRef]
- Zhou, Y.; Shahidehpour, M.; Wei, Z.; Li, Z.; Sun, G.; Chen, S. Distributionally Robust Co-Optimization of Energy and Reserve for Combined Distribution Networks of Power and District Heating. IEEE Trans. Power Syst. 2020, 35, 2388–2398. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, X.; Zhang, Z. Data-driven decentralized optimal scheduling of AC/DC distribution networks. Power Grid Technol. 2021, 45, 4768–4778. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.; Sun, G.; Cheung, K.W.; Wang, D.; Zang, H. Adaptive Robust Day-Ahead Dispatch for Urban Energy Systems. IEEE Trans. Ind. Electron. 2019, 66, 1379–1390. [Google Scholar] [CrossRef]
- Wei, W.; Zhao, X.; Zhu, J. Ac/dc hybrid power distribution network based on robust optimization capability assessment. Electr. Power Autom. Equip. 2019, 33, 87–93. [Google Scholar]
- Ding, T.; Hu, Y.; Bie, Z. Multi-Stage Stochastic Programming with Nonanticipativity Constraints for Expansion of Combined Power and Natural Gas Systems. IEEE Trans. Power Syst. 2018, 33, 317–328. [Google Scholar] [CrossRef]
- Wei, Z.; Pei, L.; Chen, S. A Review on the Optimization Operation and Safety Analysis of High-Proportion New Energy AC/DC Hybrid Distribution Networks. Electr. Power Autom. Equip. 2021, 9, 85–94. [Google Scholar]
- Wu, Q.; Gu, J. Design and research of robot visual servo system based on artificial intelligence. Agro Food Ind. Hi-Tech 2017, 28, 125–128. [Google Scholar]
- Zhang, L.; Liao, B.; Liu, D.; Jiang, Q.; Sun, Q. Artificial Intelligence empowered evolution in medicine food homology: Innovations, Challenges, and Future Prospects. Food Biosci. 2025, 69, 106928. [Google Scholar] [CrossRef]
- El-Mesery, H.S.; Qenawy, M.; Ali, M.; Hu, Z.; Adelusi, O.A.; Njobeh, P.B. Artificial intelligence as a tool for predicting the quality attributes of garlic (Allium sativum, L.) slices during continuous infrared-assisted hot air drying. J. Food Sci. 2024, 89, 7693–7712. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, M.; Pan, Q.; Jin, X.; Wang, G.; Zhao, Y.; Hu, Y. Identification of tea plant cultivars based on canopy images using deep learning methods. Sci. Hortic. 2024, 339, 113908. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, Z.; Han, Z.; Sun, W.; He, L. A Decision-Making System for cotton irrigation based on Reinforcement learning strategy. Agronomy 2023, 14, 11. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, M.; Yu, Z.; Sun, W.; Fu, W.; He, L. Enhancing cotton irrigation with distributional actor–critic reinforcement learning. Agric. Water Manag. 2024, 307, 109194. [Google Scholar] [CrossRef]
- Liu, J.; Abbas, I.; Noor, R.S. Development of Deep Learning-Based Variable Rate Agrochemical Spraying System for targeted weeds control in strawberry crop. Agronomy 2021, 11, 1480. [Google Scholar] [CrossRef]
- Xie, F.; Guo, Z.; Li, T.; Feng, Q.; Zhao, C. Dynamic task planning for Multi-Arm harvesting robots under multiple constraints using deep reinforcement learning. Horticulturae 2025, 11, 88. [Google Scholar] [CrossRef]
- Duan, J.; Yi, Z.; Shi, D.; Lin, C.; Lu, X.; Wang, Z. Reinforcement-Learning-Based Optimal Control of Hybrid Energy Storage Systems in Hybrid AC–DC Microgrids. IEEE Trans. Ind. Inform. 2019, 15, 5355–5364. [Google Scholar] [CrossRef]
- Shang, Y.; Wu, W.; Guo, J.; Ma, Z.; Sheng, W.; Lv, Z.; Fu, C. Stochastic dispatch of energy storage in microgrids: An augmented reinforcement learning approach. Appl. Energy 2020, 261, 114423. [Google Scholar] [CrossRef]
- Bui, V.-H.; Hussain, A.; Kim, H.-M. Double Deep Q -Learning-Based Distributed Operation of Battery Energy Storage System Considering Uncertainties. IEEE Trans. Smart Grid 2020, 11, 457–469. [Google Scholar] [CrossRef]
- Ding, T.; Zeng, Z.; Bai, J.; Qin, B.; Yang, Y.; Shahidehpour, M. Optimal Electric Vehicle Charging Strategy with Markov Decision Process and Reinforcement Learning Technique. IEEE Trans. Ind. Appl. 2020, 56, 5811–5823. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.; Xu, X.; Wu, Q.; Huang, Q.; Chen, Z.; Blaabjerg, F. Deep reinforcement learning based approach for optimal power flow of distribution networks embedded with renewable energy and storage devices. J. Mod. Power Syst. Clean Energy 2021, 9, 1101–1110. [Google Scholar] [CrossRef]
- Wang, S.; Du, L.; Fan, X.; Huang, Q. Deep Reinforcement Scheduling of Energy Storage Systems for Real-Time Voltage Regulation in Unbalanced LV Networks with High PV Penetration. IEEE Trans. Sustain. Energy 2021, 12, 2342–2352. [Google Scholar] [CrossRef]
- Ji, X.; Sun, C.; Zhang, Y.; Yang, M. Transmission and Distribution Coordinated Optimal Dispatch Based on Multi-Agent and Improved Analytical Target Cascading Method. Autom. Electr. Power Syst. 2025, 49, 165–174. [Google Scholar]
- Qian, T.; Ming, W.; Shao, C.; Hu, Q.; Wang, X.; Wu, J.; Wu, Z. An edge intelligence-based framework for online scheduling of soft open points with energy storage. IEEE Trans. Smart Grid 2023, 15, 2934–2945. [Google Scholar] [CrossRef]
- Deng, Q.; Hu, D.; Cai, T. Reactive power Optimization Strategy for Distribution Network Based on Multi-Agent Deep Reinforcement Learning. New Technol. Electr. Eng. Electr. Power 2022, 41, 10–20. [Google Scholar]
- Xu, H.; Domínguez-García, A.D.; Sauer, P.W. Optimal Tap Setting of Voltage Regulation Transformers Using Batch Reinforcement Learning. IEEE Trans. Power Syst. 2020, 35, 1990–2001. [Google Scholar] [CrossRef]
- Cao, D.; Zhao, J.; Hu, W.; Ding, F.; Yu, N.; Huang, Q.; Chen, Z. Model-free voltage control of active distribution system with PVs using surrogate model-based deep reinforcement learning. Appl. Energy 2021, 306, 117982. [Google Scholar] [CrossRef]
- Liu, H.; Wu, W. Two-Stage Deep Reinforcement Learning for Inverter-Based Volt-VAR Control in Active Distribution Networks. IEEE Trans. Smart Grid 2021, 12, 2037–2047. [Google Scholar] [CrossRef]

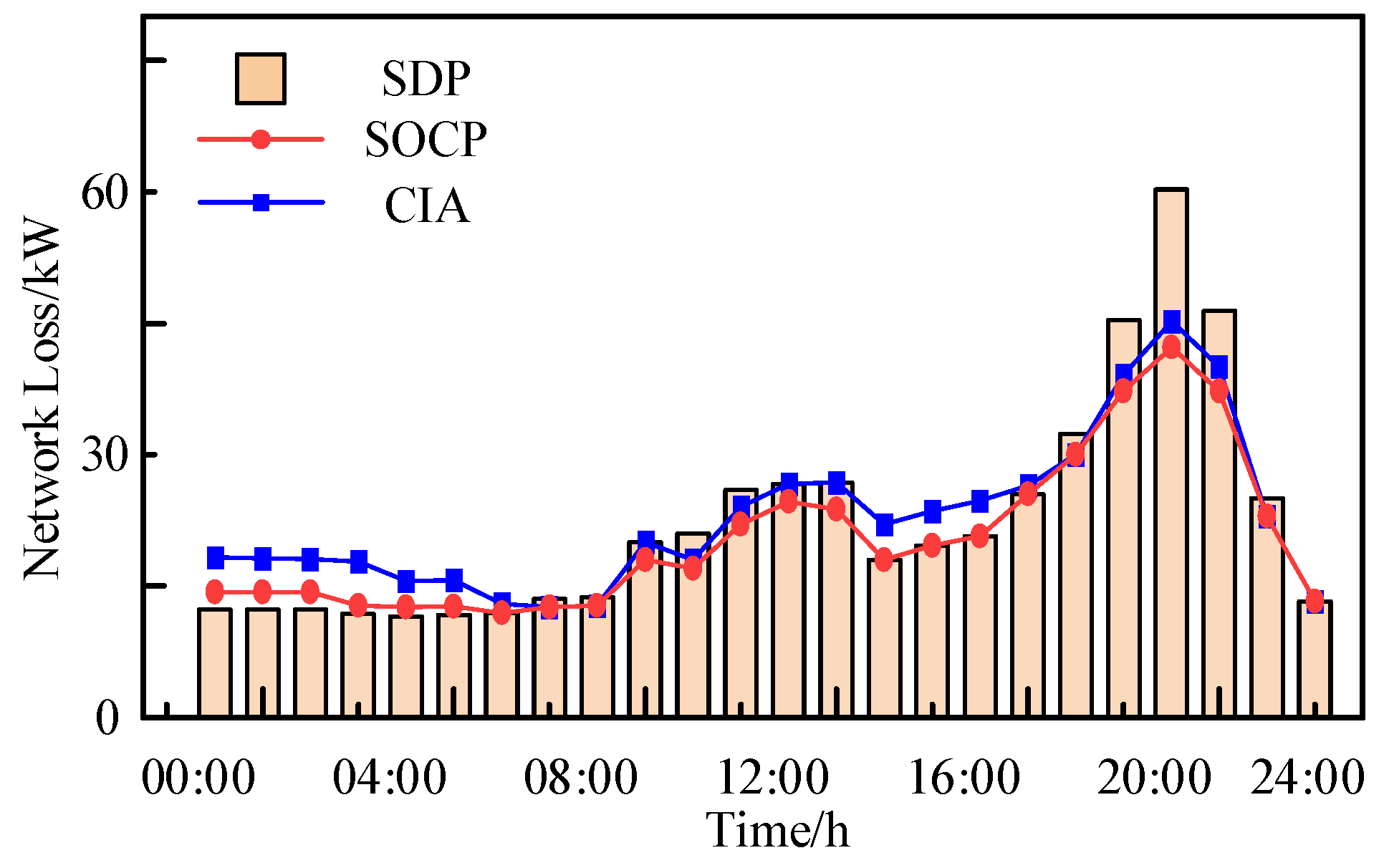
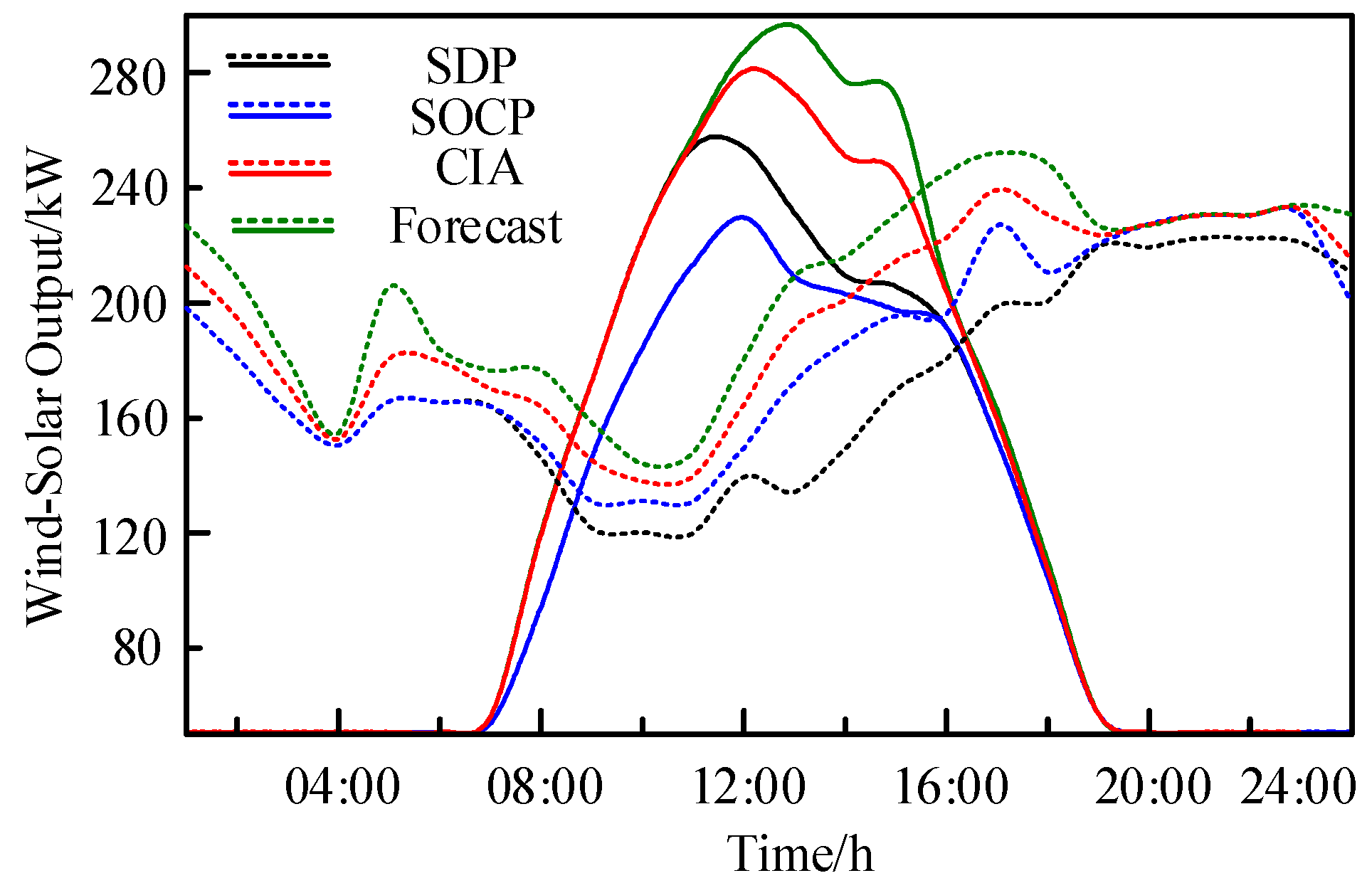
| Take | Minimum Voltage/p.u. | Maximum Voltage Variation/p.u. | Number of Nodes with Voltage Deviations |
|---|---|---|---|
| S2-1 | 0.92250 | - | 9 |
| S2-2 | 0.93621 | 0.01620 | 0 |
| S2-3 | 0.95590 | 0.03136 | 0 |
| S2-4 | 0.95601 | 0.04271 | 0 |
| S2-5 | 0.96440 | 0.05985 | 0 |
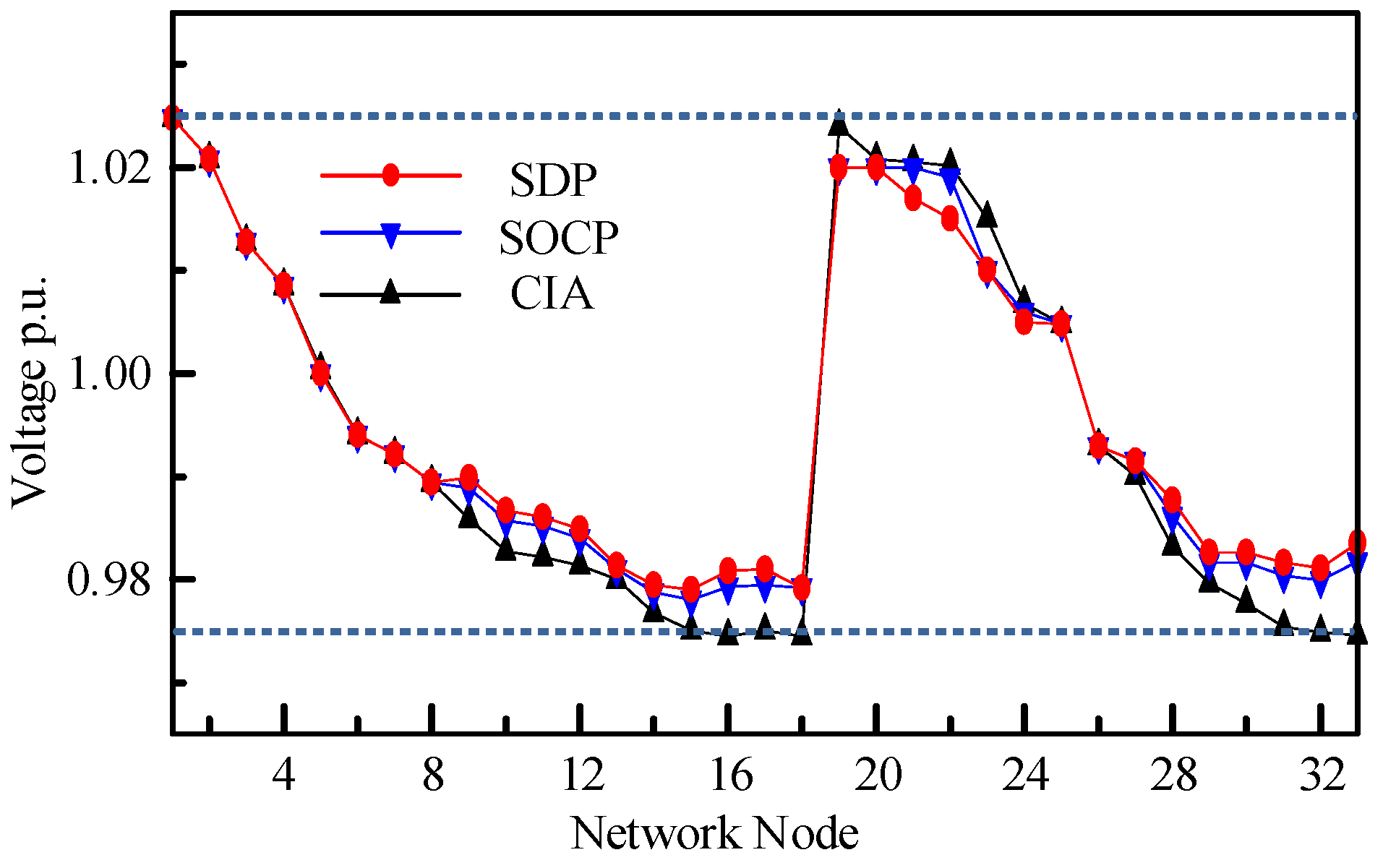
| Method | Average Value of Voltage Deviation/p.u. | Network Loss /kW | Utilization Rate of New Energy/% |
|---|---|---|---|
| SDP | 0.4218 | 537.2 | 74.9 |
| SOCP | 0.4303 | 490.7 | 85.8 |
| CIA | 0.4403 | 545.0 | 89.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Huang, Y.; Liu, Y.; Huang, T.; Zang, S. A Review of Optimization Scheduling for Active Distribution Networks with High-Penetration Distributed Generation Access. Energies 2025, 18, 4119. https://doi.org/10.3390/en18154119
Wang K, Huang Y, Liu Y, Huang T, Zang S. A Review of Optimization Scheduling for Active Distribution Networks with High-Penetration Distributed Generation Access. Energies. 2025; 18(15):4119. https://doi.org/10.3390/en18154119
Chicago/Turabian StyleWang, Kewei, Yonghong Huang, Yanbo Liu, Tao Huang, and Shijia Zang. 2025. "A Review of Optimization Scheduling for Active Distribution Networks with High-Penetration Distributed Generation Access" Energies 18, no. 15: 4119. https://doi.org/10.3390/en18154119
APA StyleWang, K., Huang, Y., Liu, Y., Huang, T., & Zang, S. (2025). A Review of Optimization Scheduling for Active Distribution Networks with High-Penetration Distributed Generation Access. Energies, 18(15), 4119. https://doi.org/10.3390/en18154119





