Multi-User Satisfaction-Driven Bi-Level Optimization of Electric Vehicle Charging Strategies
Abstract
1. Introduction
- We propose a finely stratified, hierarchical two-level optimization framework that, unlike existing uniform or heuristic models, explicitly categorizes EV users into three representative types—commuter, business, and emergency—enabling a hybrid control paradigm that bridges centralized coordination and decentralized autonomy for enhanced system responsiveness and user differentiation.
- We introduce, for the first time, a multi-objective Markov decision process that jointly models battery state of health (SOH) and user psychological anxiety, incorporating a comprehensive four-dimensional reward function encompassing charging cost, carbon emissions, battery degradation, and user satisfaction, offering a more holistic and user-aware optimization framework than prior single-objective approaches.
- We develop a context-aware dynamic hyperparameter tuning mechanism using Bayesian optimization to automatically tune network hyperparameters in response to varying operational conditions, ensuring robust and stable algorithmic performance across diverse large-scale charging scenarios—an adaptability largely overlooked in existing reinforcement learning-based methods.
2. EV Charging Environment Modeling Methods
2.1. EV Charging Model Architecture
2.2. Dual-Network Deep Reinforcement Learning
3. Bi-Level Optimization Modeling Methods
3.1. MDP Modeling
3.1.1. State Space
3.1.2. Action Space
3.1.3. State Transition Function
3.1.4. Reward Function
3.2. Two-Layer Optimization Modeling
3.2.1. Hyperparameter Optimization-Layer Model
3.2.2. User Satisfaction Layer Model
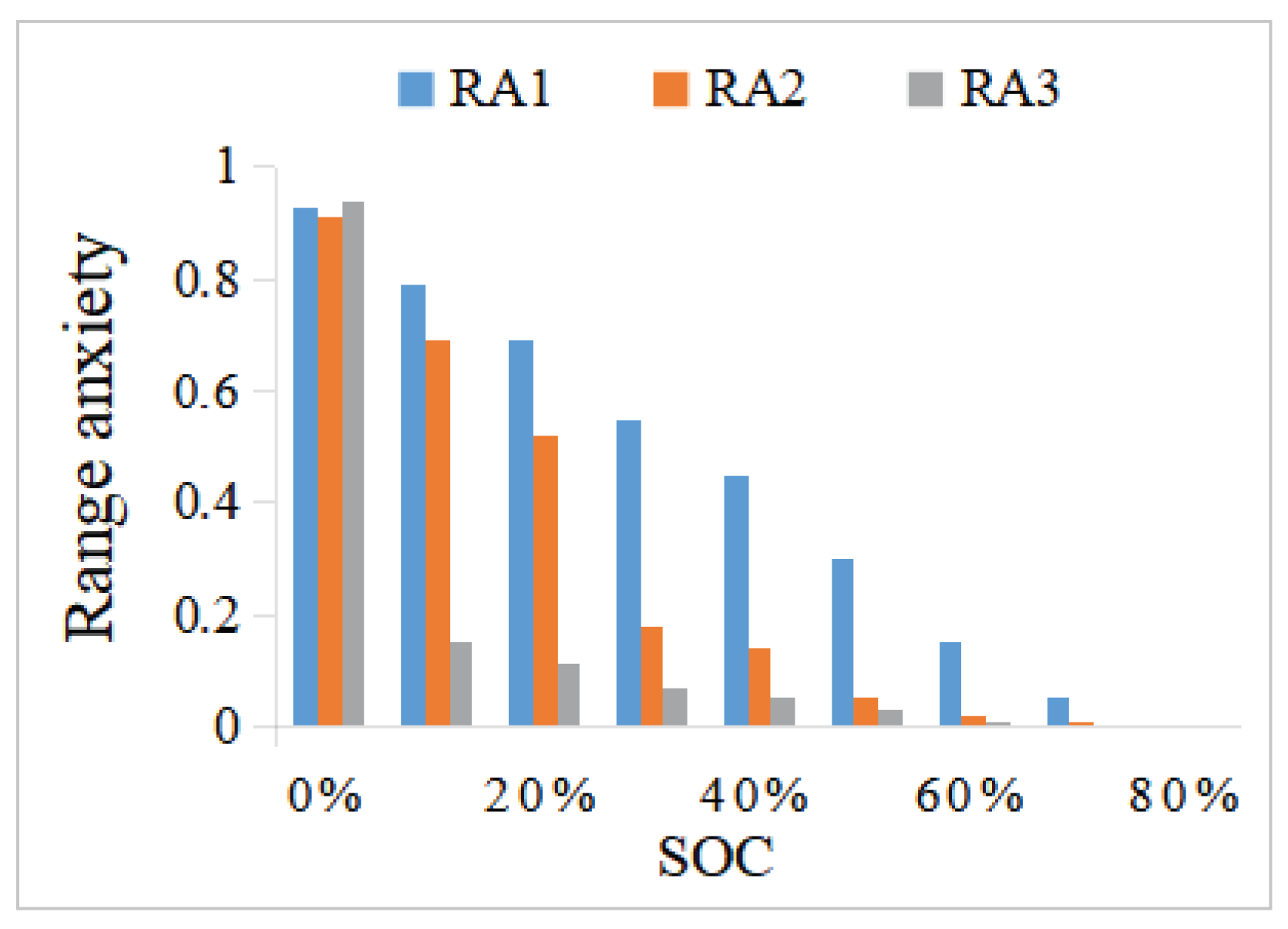
- Range Anxiety:
- Battery aging:
3.2.3. Bi-Level Optimization Model
4. Simulation Analysis
4.1. Experimental Setup
- (1)
- DDQN [29]: An improved DQN algorithm that uses two separate networks—an evaluation network and a target network—to update rewards and select actions;
- (2)
- LSTM [30]: A popular recurrent neural network that effectively captures long-term dependencies by introducing a gated mechanism and memory units to alleviate the problem of gradient disappearance and improve the sequence modeling ability;
- (3)
- Genetic Algorithm (GA) [31]: A heuristic optimization algorithm inspired by natural selection, using crossover and mutation operators to evolve solutions over generations.
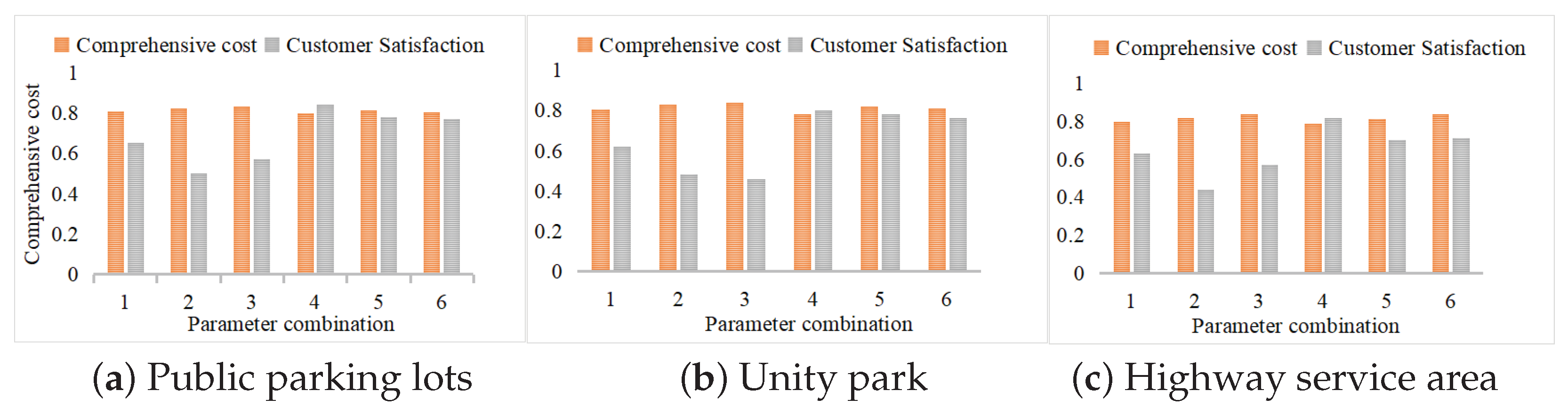
4.2. Reward Weight Combination Selection Test
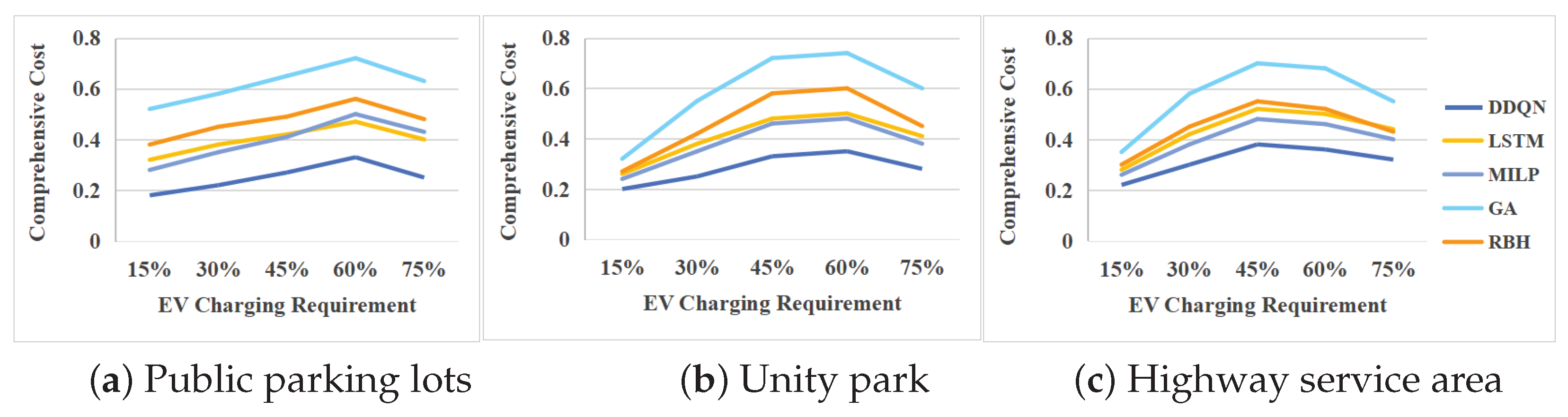
4.3. Power-Grid Scenario Adaptability Test
4.4. Parking Lot Environmental Adaptability Test
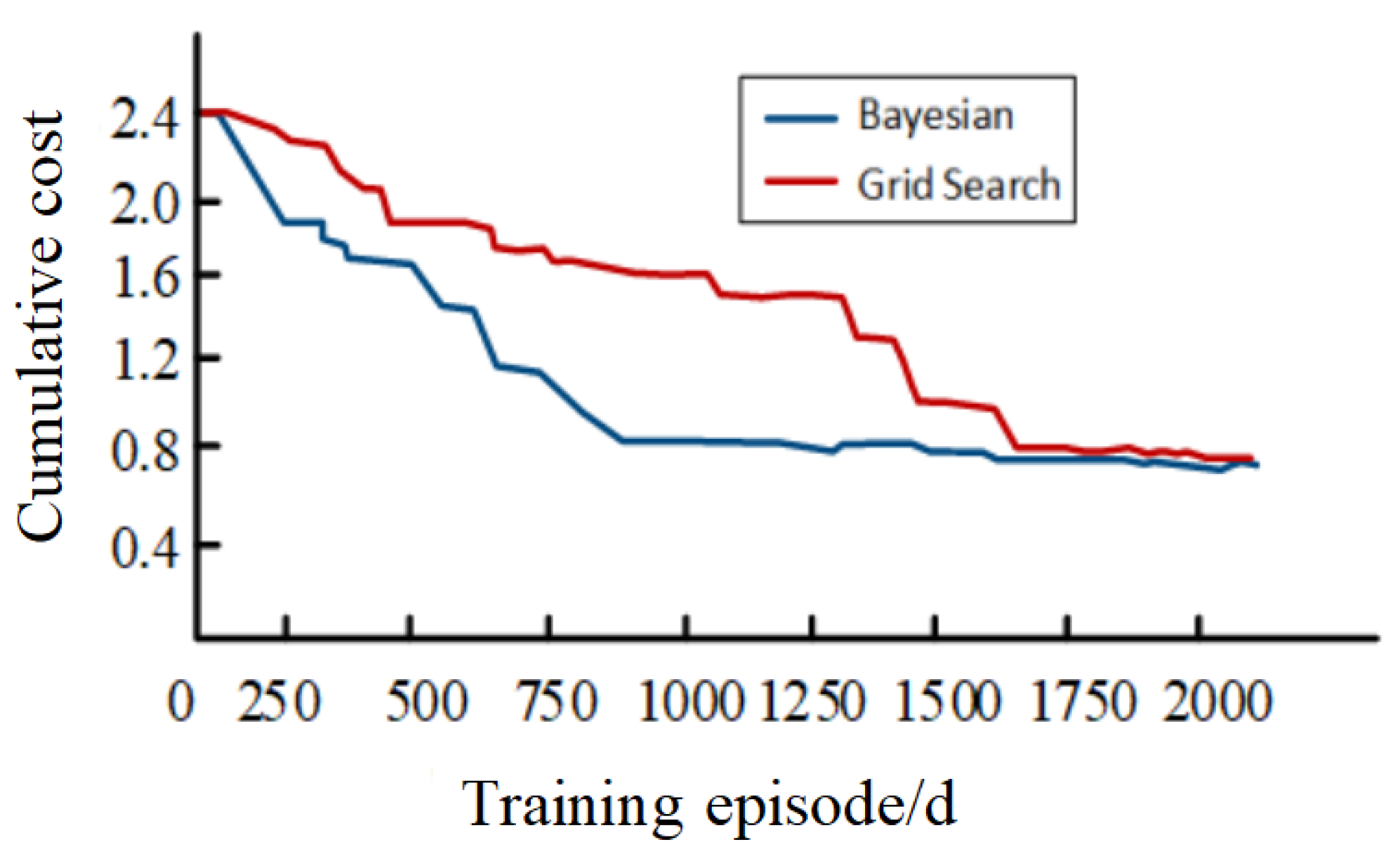
4.5. Test of Hyperparameter Optimization Results
4.6. Convergence Comparison Test of Hyperparameter Optimization Model
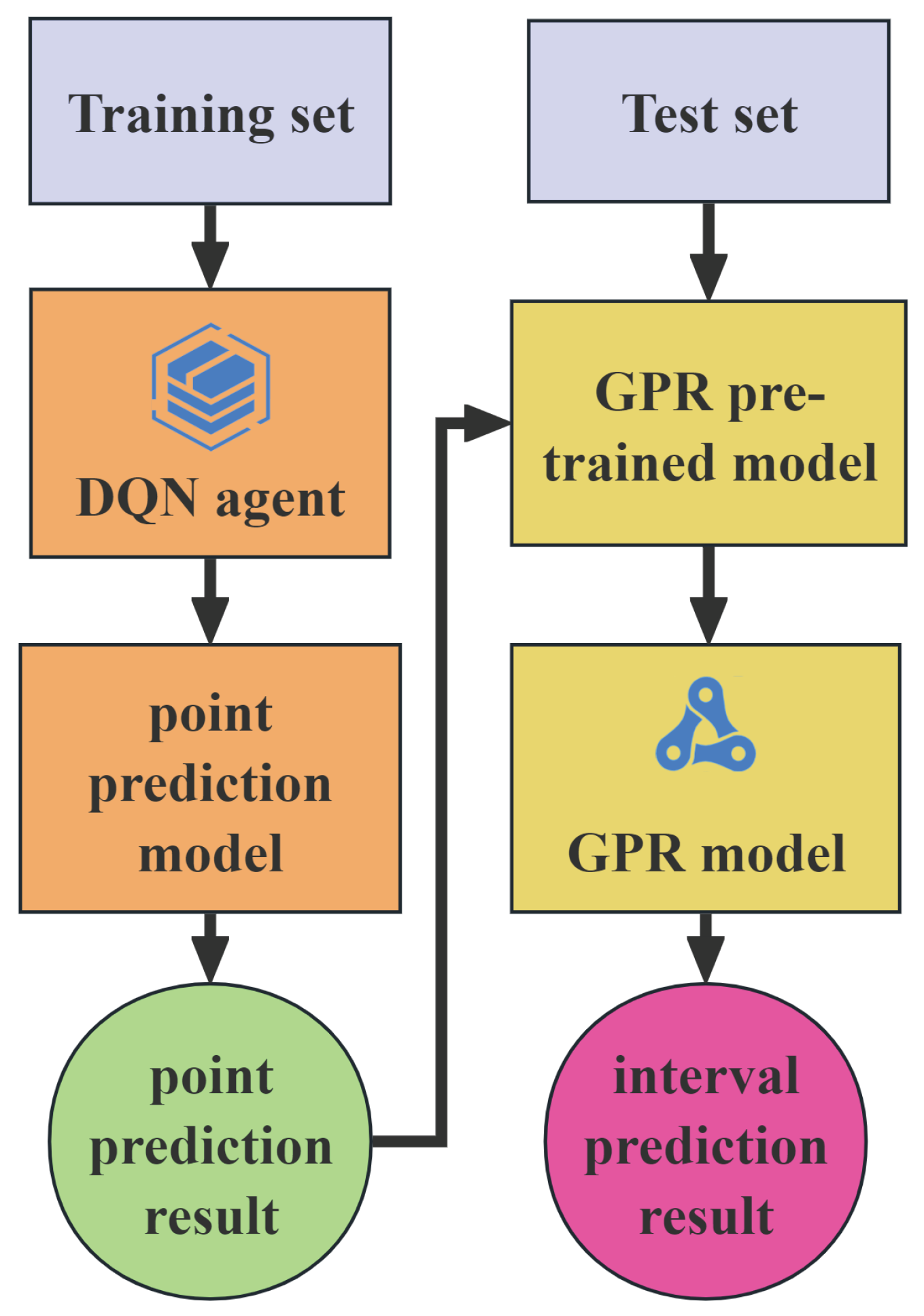
4.7. Double Optimization Model Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Szumska, E. Electric Vehicle Charging Infrastructure Along Highways in the EU. Energies 2023, 16, 895. [Google Scholar] [CrossRef]
- Vijayan, V.; Arzani, A.; Mahajan, S.M. Demand Side Management Considering Load–Voltage Interdependence and Optimal Topology Selection in Active Distribution Networks. IEEE Access 2025, 13, 49107–49120. [Google Scholar] [CrossRef]
- Tamma, W.R.; Azis Prasojo, R.; Suwarno, S. Assessment of High Voltage Power Transformer Aging Condition Based on Health Index Value Considering Its Apparent and Actual Age. In Proceedings of the 2020 12th International Conference on Information Technology and Electrical Engineering (ICITEE), Yogyakarta, Indonesia, 6–8 October 2020; pp. 292–296. [Google Scholar] [CrossRef]
- Caro, L.M.; Ramos, G.; Rauma, K.; Rodriguez, D.F.C.; Martinez, D.M.; Rehtanz, C. State of Charge Influence on the Harmonic Distortion from Electric Vehicle Charging. IEEE Trans. Ind. Appl. 2021, 57, 2077–2088. [Google Scholar] [CrossRef]
- Hu, H.; Bin, Q.; Xiao, Y.; Lin, X.; Deng, Y.; Zhang, F.; He, P.; Zhou, M. Modeling and analysis of carbon emissions throughout the entire lifecycle of electric vehicles. In Proceedings of the 2024 4th International Conference on Energy, Power and Electrical Engineering (EPEE), Wuhan, China, 20–22 September 2024; pp. 881–886. [Google Scholar] [CrossRef]
- Dahiwale, P.V.; Rather, Z.H. Centralized Multi-objective Framework for Smart EV Charging in Distribution System. In Proceedings of the 2023 IEEE PES Conference on Innovative Smart Grid Technologies—Middle East (ISGT Middle East), Abu Dhabi, United Arab Emirates, 12–15 March 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Fachrizal, R.; Munkhammar, J. Improved Photovoltaic Self-Consumption in Residential Buildings with Distributed and Centralized Smart Charging of Electric Vehicles. Energies 2020, 13, 1153. [Google Scholar] [CrossRef]
- Jarvis, P.; Climent, L.; Arbelaez, A. Smart and sustainable scheduling of charging events for electric buses. TOP 2024, 32, 22–56. [Google Scholar] [CrossRef]
- Seal, S.; Boulet, B.; Dehkordi, V.R.; Bouffard, F.; Joos, G. Centralized MPC for Home Energy Management with EV as Mobile Energy Storage Unit. IEEE Trans. Sustain. Energy 2023, 14, 1425–1435. [Google Scholar] [CrossRef]
- Zhang, J.; Che, L.; Shahidehpour, M. Distributed Training and Distributed Execution-Based Stackelberg Multi-Agent Reinforcement Learning for EV Charging Scheduling. IEEE Trans. Smart Grid 2023, 14, 4976–4979. [Google Scholar] [CrossRef]
- Ullah, Z.; Yan, L.; Rehman, A.U.; Qazi, H.S.; Wu, X.; Li, J.; Hasanien, H.M. Distributed Consensus-Based Optimal Power Sharing Between Grid and EV Charging Stations Using Derivative-Free Charging Scheduling. IEEE Access 2024, 12, 127768–127781. [Google Scholar] [CrossRef]
- Zheng, Y.; Song, Y.; Hill, D.J.; Meng, K. Online Distributed MPC-Based Optimal Scheduling for EV Charging Stations in Distribution Systems. IEEE Trans. Ind. Inform. 2019, 15, 638–649. [Google Scholar] [CrossRef]
- Saner, C.B.; Trivedi, A.; Srinivasan, D. A Cooperative Hierarchical Multi-Agent System for EV Charging Scheduling in Presence of Multiple Charging Stations. IEEE Trans. Smart Grid 2022, 13, 2218–2233. [Google Scholar] [CrossRef]
- Qian, T.; Shao, C.; Li, X.; Wang, X.; Chen, Z.; Shahidehpour, M. Multi-Agent Deep Reinforcement Learning Method for EV Charging Station Game. IEEE Trans. Power Syst. 2022, 37, 1682–1694. [Google Scholar] [CrossRef]
- Sun, F.; Diao, R.; Zhou, B.; Lan, T.; Mao, T.; Su, S.; Cheng, H.; Meng, D.; Lu, S. Prediction-Based EV-PV Coordination Strategy for Charging Stations Using Reinforcement Learning. IEEE Trans. Ind. Appl. 2024, 60, 910–919. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Wu, F.; Tang, B.; Fan, W. Effective Charging Planning Based on Deep Reinforcement Learning for Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 542–554. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, C.K.M. Dynamic Pricing for EV Charging Stations: A Deep Reinforcement Learning Approach. IEEE Trans. Transp. Electrif. 2022, 8, 2456–2468. [Google Scholar] [CrossRef]
- Chu, Y.; Wei, Z.; Fang, X.; Chen, S.; Zhou, Y. A Multiagent Federated Reinforcement Learning Approach for Plug-In Electric Vehicle Fleet Charging Coordination in a Residential Community. IEEE Access 2022, 10, 98535–98548. [Google Scholar] [CrossRef]
- Ding, T.; Zeng, Z.; Bai, J.; Qin, B.; Yang, Y.; Shahidehpour, M. Optimal Electric Vehicle Charging Strategy with Markov Decision Process and Reinforcement Learning Technique. IEEE Trans. Ind. Appl. 2020, 56, 5811–5823. [Google Scholar] [CrossRef]
- Li, H.; Wan, Z.; He, H. Constrained EV Charging Scheduling Based on Safe Deep Reinforcement Learning. IEEE Trans. Smart Grid 2020, 11, 2427–2439. [Google Scholar] [CrossRef]
- Aswantara, I.K.A.; Ko, K.S.; Sung, D.K. A centralized EV charging scheme based on user satisfaction fairness and cost. In Proceedings of the 2013 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Bangalore, India, 10–13 November 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Asna, M.; Shareef, H.; Prasanthi, A.; Errouissi, R.; Wahyudie, A. A Novel Multi-Level Charging Strategy for Electric Vehicles to Enhance Customer Charging Experience and Station Utilization. IEEE Trans. Intell. Transp. Syst. 2024, 25, 11497–11508. [Google Scholar] [CrossRef]
- Li, X.; Luo, F.; Zhang, C.; Dong, Z.Y. Stochastic EV Charging Dispatch in Unbalanced Three-Phase Networks Based on Interpretable Fuzzy Representation of User Preferences. IEEE Trans. Power Syst. 2025, 40, 1623–1635. [Google Scholar] [CrossRef]
- Zuo, W.; Li, K. Electrical vehicle charging strategy for electric road systems considering V2G technology. In Proceedings of the 2023 IEEE International Conference on Energy Technologies for Future Grids (ETFG), Wollongong, Australia, 3–6 December 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Salvatti, G.A.; Carati, E.G.; Cardoso, R.; da Costa, J.P.; de Oliveira Stein, C.M. Electric Vehicles Energy Management with V2G/G2V Multifactor Optimization of Smart Grids. Energies 2020, 13, 1191. [Google Scholar] [CrossRef]
- Pollock, J.; Chong, P.L.; Ramegowda, M.; Dawood, N.; Habibi, H.; Hou, Z.; Faraji, F.; Guo, P. Battery Electric Vehicles: A Study on State of Charge and Cost-Effective Solutions for Addressing Range Anxiety. Machines 2025, 13, 411. [Google Scholar] [CrossRef]
- Szúcs, I.; Kopják, J.; Sebestyén, G.; Wendler, M. Analyzing EV Users’ Charging Patterns for Estimating Session Parameters and Optimizing Load Management. In Proceedings of the 2025 IEEE 23rd World Symposium on Applied Machine Intelligence and Informatics (SAMI), Stará Lesná, Slovakia, 23–25 January 2025; pp. 521–526. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Q.; Li, Z.; Xiao, L.; Zhang, X. Deep Reinforcement Learning-Based Charging Pricing Strategy for Charging Station Operators and Charging Navigation for EVs. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024; pp. 1972–1978. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, S.; Chen, Y.; Zhao, L.; Chen, H.; Sun, W.; Niu, M.; Wang, H.; Wang, X. Optimal scheduling of the virtual power plant with electric vehicles using Dueling DDQN. In Proceedings of the 2024 4th International Conference on Energy, Power and Electrical Engineering (EPEE), Wuhan, China, 20–22 September 2024; pp. 1065–1070. [Google Scholar] [CrossRef]
- Xu, Z.; Cao, K.; Liu, Y.; Wang, C. Short-Term Load Prediction of EV Charging Station Based on LSTM Recursion. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024; pp. 2068–2073. [Google Scholar] [CrossRef]
- Xu, J.; Zheng, T.; Dang, Y.; Yang, F.; Li, D. Distributed Deep Reinforcement Learning for Data-Driven Water Heater Model in Smart Grid. IEEE Trans. Smart Grid 2025, 16, 2900–2912. [Google Scholar] [CrossRef]
- Loaiza-Quintana, C.; Cruz-Reyes, L.; Rangel-Valdez, N.; Gómez-Santillán, C.; Terashima-Marín, H. Iterated Local Search for the Ebuses Charging Location Problem. In Proceedings of the Parallel Problem Solving from Nature—PPSN XVII, Dortmund, Germany, 10 September 2022; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2022; Volume 13349, pp. 402–415. [Google Scholar] [CrossRef]



| Genetic Algorithm (GA) | Long Short-Term Memory (LSTM) | ||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| Gene Representation | Binary tuple (station ID, start hour, duration) | Input Representation | 24 h time series: grid price, SOC history, power constraints |
| Population Size | 200 (elite retention: top 10%) | Network Architecture | 2 × LSTM layers (128 units) → Dropout (0.3) → Dense (softmax) |
| Crossover | Two-point (p = 0.85) | Training | Epochs: 150 (early stop patience = 15), Batch: 64 |
| Mutation | Bit-flip (p = 0.02) | Optimization | Adam (lr = 0.001), Loss: weighted cross-entropy |
| Fitness Function | Weighted sum (cost, emissions, degradation) | Output | Action distribution (charge/idle/discharge per 15-min) |
| Termination | 500 gens OR < 0.1% improvement (50 gens) | Sequence | Stateful training (length = 96 = 24 h × 4 intervals) |
| Combination | Wcost | Wemission | WSOC | Wsatisfaction | Comprehensive Cost |
|---|---|---|---|---|---|
| 1 | 30% | 40% | 20% | 10% | 0.75 |
| 2 | 40% | 30% | 20% | 10% | 0.69 |
| 3 | 20% | 30% | 10% | 40% | 0.72 |
| 4 | 40% | 0% | 20% | 40% | 0.77 |
| 5 | 30% | 20% | 0% | 50% | 0.83 |
| Grid Environment | Key Characteristics | Model Adaptations |
|---|---|---|
| Hybrid Energy Grid |
|
|
| High-Carbon Grid |
|
|
| Carbon Quota-Constrained Grid |
|
|
| Scene | Private Car | Taxi | Tourist Vehicles | Scene Features |
|---|---|---|---|---|
| Public parking lots | 60% | 30% | 10% | Private cars dominate parking in residential areas/business districts |
| Unit park | 40% | 55% | 5% | Workday commuting is intensive, and taxi service is frequent |
| Highway service area | 20% | 10% | 70% | During holidays, the proportion of tourist vehicles is the highest |
| Hyperparameters/ Optimization Methods | Grid Search | Bayesian Optimization | ||||
|---|---|---|---|---|---|---|
| Combination 1 | Combination 2 | Combination 3 | Combination 4 | Combination 5 | Combination 6 | |
| Learning rate | 0.004 | 0.03 | 0.05 | 0.002 | 0.01 | 0.03 |
| Discount factor | 0.96 | 0.99 | 0.95 | 0.99 | 0.95 | 0.98 |
| Batch size | 128 | 256 | 64 | 128 | 256 | 64 |
| Explore the initial value of the rate | 1.0 | 0.99 | 0.99 | 1.0 | 0.99 | 0.99 |
| Explore the minimum value | 0.001 | 0.01 | 0.05 | 0.01 | 0.05 | 0.1 |
| Exploration rate Decay rate | 0.999 | 0.9 | 0.99 | 0.99 | 0.9 | 0.999 |
| Target network update rate | 1000 | 500 | 500 | 1000 | 1000 | 500 |
| Size of hidden layer | [256,256] | [256,256] | [128,128] | [256,256] | [256,256] | [128,128] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Xu, J.; Li, D. Multi-User Satisfaction-Driven Bi-Level Optimization of Electric Vehicle Charging Strategies. Energies 2025, 18, 4097. https://doi.org/10.3390/en18154097
Chen B, Xu J, Li D. Multi-User Satisfaction-Driven Bi-Level Optimization of Electric Vehicle Charging Strategies. Energies. 2025; 18(15):4097. https://doi.org/10.3390/en18154097
Chicago/Turabian StyleChen, Boyin, Jiangjiao Xu, and Dongdong Li. 2025. "Multi-User Satisfaction-Driven Bi-Level Optimization of Electric Vehicle Charging Strategies" Energies 18, no. 15: 4097. https://doi.org/10.3390/en18154097
APA StyleChen, B., Xu, J., & Li, D. (2025). Multi-User Satisfaction-Driven Bi-Level Optimization of Electric Vehicle Charging Strategies. Energies, 18(15), 4097. https://doi.org/10.3390/en18154097






