Optimizing Passive Thermal Enhancement via Embedded Fins: A Multi-Parametric Study of Natural Convection in Square Cavities

Abstract

Internal fins are commonly utilized as a passive technique to enhance natural convection, but their efficiency depends on complex interplay between fin design, material properties, and convective strength. This study presents an extensive numerical analysis of buoyancy-driven flow in square cavities containing a single horizontal fin on the hot wall. Over 9000 simulations were conducted, methodically varying the Rayleigh number (Ra = 10 to 10⁵), Prandtl number (Pr = 0.1 to 10), and fin characteristics, such as length, vertical position, thickness, and the thermal conductivity ratio (up to 1000), to assess their overall impact on thermal efficiency. Thermal enhancements compared to scenarios without fins are quantified using local and average Nusselt numbers, as well as a Nusselt number ratio (NNR). The results reveal that, contrary to conventional beliefs, long fins positioned centrally can actually decrease heat transfer by up to 11.8% at high Ra and Pr due to the disruption of thermal plumes and diminished circulation. Conversely, shorter fins located near the cavity’s top and bottom wall edges can enhance the Nusselt numbers for the hot wall by up to 8.4%, thereby positively affecting the development of thermal boundary layers. A U-shaped Nusselt number distribution related to fin placement appears at Ra ≥ 10³, where edge-aligned fins consistently outperform those positioned mid-height. The benefits of high-conductivity fins become increasingly nonlinear at larger Ra, with advantages limited to designs that minimally disrupt core convective patterns. These findings challenge established notions regarding passive thermal enhancement and provide a predictive thermogeometric framework for designing enclosures. The results can be directly applied to passive cooling systems in electronics, battery packs, solar thermal collectors, and energy-efficient buildings, where optimizing heat transfer is vital without employing active control methods.

1. Introduction

Natural convection plays a crucial role in various technologies, including thermal insulation in buildings, energy harvesting, electronic cooling, and phase change systems [1]. A common geometric approach involves using embedded fins, which have been utilized for years to enhance heat dissipation by increasing surface area and modifying internal flow patterns [2,3]. However, adding fins in naturally convecting enclosures creates a complex and often counterintuitive relationship among geometry, fluid characteristics, and buoyancy-driven flow [4]. In these systems, a fin’s effectiveness relies not just on its dimensions or thermal conductivity, but also on its positioning, its interaction with convective plumes, and the balance between conduction and convection in total energy transport [5].

The classic problem of natural convection in a square cavity with differentially heated vertical walls has been thoroughly investigated and frequently used as a standard for experimental and numerical validation [6,7,8]. However, despite its seeming simplicity, this configuration features a complex array of flow structures that develop in response to the Rayleigh number (Ra), Prandtl number (Pr), and thermal boundary conditions [9,10]. Introducing internal fins adds further complexity, causing blockage, localized vorticity, and thermal bridging effects [11]. Determining whether these fins improve or hinder heat transfer remains a significant challenge, especially as designs shift towards passive, maintenance-free thermal systems that function under varying ambient conditions [12,13,14]. Recent studies have also extended this problem to include latent heat effects via phase change materials, where the presence of fins continues to affect natural convection pathways and thermal storage efficiency [15].

While earlier research has focused on the individual impacts of Ra, Pr, fin length, and thermal conductivity, these studies typically evaluate these parameters in isolation, which limits our understanding of their combined effects [16,17,18]. Most existing studies either assume a fixed fin geometry or examine only a limited range of parameters [19,20,21,22,23]. Consequently, several critical questions remain unanswered: Which fin configurations achieve the most significant thermal enhancement during natural convection? How does fin performance vary between conduction- and convection-dominated regimes? Can longer conductive fins sometimes hinder heat transfer rather than enhance it? Additionally, how do fluids with low and high Prandtl numbers react differently to identical geometric obstacles?

It is both necessary and instructive to begin with the simplest case, involving a single embedded fin, to provide a controlled framework for isolating fundamental thermogeometric interactions such as flow obstruction, plume deviation, and surface conduction that are often obscured in multi-fin systems. Although many practical applications use fin arrays, this approach yields baseline insights necessary for extending to more complex configurations. A thorough parametric study on natural convection within square enclosures featuring a single embedded rectangular fin is conducted to systematically evaluate the interaction between fin geometry, fluid properties, and buoyancy across a wide range of conditions. Non-rectangular fin geometries (e.g., tapered or curved fins) were excluded to maintain consistency and isolate thermogeometric effects under controlled conditions. The study covers five orders of magnitude in Rayleigh number (10 ≤ Ra ≤ 10⁵), six Prandtl numbers (0.1 ≤ Pr ≤ 10), and a wide range of variations in fin length, thickness, position, and conductivity ratio (the ratio of fin conductivity to fluid conductivity). Each Prandtl number was implemented in dimensionless form by adjusting the ratio of kinematic viscosity to thermal diffusivity, allowing the study to represent a broad class of fluids, from liquid metals to viscous oils, without being restricted to a specific substance. More than 9000 simulations are executed to evaluate heat transfer performance on both the hot and cold walls, quantified through spatially averaged Nusselt numbers and normalized metrics, such as the Maximum Nusselt number ratio (NNR). The fin is represented as a solid insert with varying conductivity, allowing us to account for both thermally active and insulating behaviors. It is also systematically repositioned and resized to assess its geometric sensitivity. The flow is assumed to be steady, laminar, two-dimensional, and governed by the Boussinesq approximation, with incompressible Newtonian fluid and constant properties. These assumptions remain valid throughout the studied range of Ra (10–10⁵) and Pr (0.1–10), where no transition to turbulence or unsteady flow was observed. As the study focuses solely on steady-state conditions, no dimensionless time scales were introduced, and all simulations were performed using a steady-state solver.

This study provides a comprehensive thermogeometric map of fin-induced natural convection performance. It bridges the gap between canonical theoretical models and application-ready design guidance, offering new physical insights into how geometry, fluid properties, and buoyancy interact nonlinearly in finned enclosures. The outcomes can be immediately applied to the design of passive thermal devices in electronics, solar thermal collectors, battery packs, building envelopes, and microgravity heat transport systems, where optimizing heat transfer without the use of active components is critical. The novelty of this work lies in its broad yet high-resolution parametric coverage, the introduction of a normalized Nusselt number ratio (NNR) to enable fair comparisons across varying geometries, and the identification of regime-specific design principles, such as the counterintuitive performance decline of centrally positioned fins at high Rayleigh numbers. These insights, not previously reported in the literature, offer predictive guidance for future thermal management designs. This work lays the foundation for more efficient and robust thermal management solutions by elucidating the regimes in which fins enhance or impair natural convection.

2. Problem Formulation and Mathematical Model

Figure 1 illustrates the physical configuration of the problem under consideration: a two-dimensional, differentially heated square cavity with an internally mounted horizontal fin on the hot wall. The cavity width (w) and length (l) are equal, forming a square geometry (w = l). The out-of-plane depth is assumed to be sufficiently large to justify a two-dimensional approximation by minimizing three-dimensional effects.

The cavity is filled with a Newtonian incompressible fluid, which is characterized by constant properties: density (ρ), thermal diffusivity (α), kinematic viscosity (ν), and the thermal expansion coefficient (β). In such flows, pressure (P) is not an independent thermodynamic variable but rather varies as a function of temperature due to buoyancy-driven density gradients. The gravitational force acts downward along the vertical axis. The Boussinesq approximation is employed, under which density variations are neglected in all governing equations except the buoyancy term, allowing temperature differences to drive flow without significantly affecting mass conservation.

The thermal boundary conditions are defined as follows: the left vertical wall is held at a constant hot temperature (T_h), while the right wall is maintained at a uniform cold temperature (T_c). The variation in thermal boundary conditions between the cold and hot walls causes a thermal gradient in the cavity due to spatial variations in the temperature field (T). The top and bottom horizontal walls are thermally insulated, enforcing an adiabatic condition. All boundaries are treated as no-slip walls, where the x-velocity component (u) and the y-velocity component (v) are set to zero (u = v = 0).

A solid fin of finite length and thickness is attached to the hot wall, extending horizontally into the domain to modify the thermal and velocity boundary layers. The fin’s vertical placement (y_fin), thickness (w_fin), and length (l_fin) are varied parametrically to investigate the effect of the fin on boundary layers. The fin is modeled as a solid with thermal conductivity k_fin, which may differ from that of the fluid.

The governing equations are nondimensionalized using characteristic scales for length, velocity, pressure, and temperature to facilitate generalization and reduce the number of parameters in the analysis. As shown in Equation (1), the spatial coordinates x and y are normalized by the cavity width (w), while the velocity components are scaled by α/w. The pressure is nondimensionalized by ρα²/w², and the temperature field is expressed in terms of the dimensionless temperature θ, defined relative to the cold-wall and hot-wall temperatures, T_c and T_h, respectively. The geometric parameters of the embedded fin, its position, width, and length, are similarly normalized by the cavity width (w), as given in Equation (2).

$$X={\displaystyle \frac{x}{w}} Y={\displaystyle \frac{y}{w}} U={\displaystyle \frac{uw}{\alpha }} V={\displaystyle \frac{vw}{\alpha }} P={\displaystyle \frac{p{w}^2}{\rho {\alpha }^2}} \theta ={\displaystyle \frac{T-T_c}{T_h-T_c}}$$

(1)

$$Y_{fin}={\displaystyle \frac{y_{fin}}{w}} W_{fin}={\displaystyle \frac{w_{fin}}{w}} L_{fin}={\displaystyle \frac{l_{fin}}{w}}.$$

(2)

Under the Boussinesq approximation, the dimensionless governing equations include the continuity equation (Equation (3)), the momentum equations in the x- and y-directions (Equations (4) and (5)), and the energy equation (Equation (6)), where buoyancy appears as a temperature-dependent source term in the vertical momentum equation.

Continuity:

$${\displaystyle \frac{\partial U}{\partial X}}+{\displaystyle \frac{\partial V}{\partial Y}}=0$$

(3)

Momentum equations:

$$U{\displaystyle \frac{\partial U}{\partial X}}+V{\displaystyle \frac{\partial U}{\partial Y}}=-{\displaystyle \frac{\partial P}{\partial X}}+\mathit{Pr}\left({\displaystyle \frac{{\partial }^{2}U}{\partial X^2}}+{\displaystyle \frac{{\partial }^{2}U}{\partial Y^2}}\right)$$

(4)

$$U{\displaystyle \frac{\partial V}{\partial X}}+V{\displaystyle \frac{\partial V}{\partial Y}}=-{\displaystyle \frac{\partial P}{\partial Y}}+\mathit{Pr}\left({\displaystyle \frac{{\partial }^{2}V}{\partial X^2}}+{\displaystyle \frac{{\partial }^{2}V}{\partial Y^2}}\right)+Ra Pr \theta$$

(5)

Energy equation:

$$U{\displaystyle \frac{\partial \theta }{\partial X}}+V{\displaystyle \frac{\partial \theta }{\partial Y}}=\left({\displaystyle \frac{{\partial }^2\theta }{\partial X^2}}+{\displaystyle \frac{{\partial }^2\theta }{\partial Y^2}}\right)$$

(6)

The flow and temperature behavior within the cavity is governed by two dimensionless parameters: the Rayleigh number (Ra), defined in Equation (7), which quantifies the relative strength of buoyancy compared to thermal and viscous diffusion, and the Prandtl number (Pr), given in Equation (8), which represents the ratio of momentum to thermal diffusivity. Together, Ra and Pr determine the dominant heat transfer regime and influence the flow’s sensitivity to geometric modifications such as fin placement.

$$Pr={\displaystyle \frac{\nu }{\alpha }},$$

(7)

$$Ra={\displaystyle \frac{g \beta \left(T_h-T_c\right) w^3}{\nu \alpha }}.$$

(8)

To solve the governing equations, appropriate boundary conditions for velocity and temperature must be specified along all enclosure walls and fin surfaces. These conditions ensure physical consistency and enable the enforcement of no-slip and thermal constraints at solid boundaries. A detailed summary of the imposed non-dimensional boundary conditions is provided in

Table 1. Non-Dimensional Boundary Conditions.

Position	Velocity Condition	Thermal Condition
Enclosure’s top wall ($Y=1$)	U = 0 and V = 0	${\displaystyle \frac{\partial \theta }{\partial Y}}=0$
Enclosure’s bottom wall ($Y=0$ )
Enclosure’s left hot wall ($X=0$)		$\theta =1$
Enclosure’s right cold wall ($X=1$)		$\theta =0$
Fin’s top wall ($0<X<L_{fin}$ and $Y=Y_{fin}+{\displaystyle \frac{W_{fin}}{2}}$)		${\left({\displaystyle \frac{\partial \theta }{\partial Y}}\right)}_{fluid}={\displaystyle \frac{k_{fin}}{k}}{\left({\displaystyle \frac{\partial \theta }{\partial Y}}\right)}_{fin}$
Fin’s bottom wall ($0<X<L_{fin}$ and $Y=Y_{fin}-{\displaystyle \frac{W_{fin}}{2}}$)
Fin’s right wall ($Y_{fin}-{\displaystyle \frac{W_{fin}}{2}}<Y<Y_{fin}+{\displaystyle \frac{W_{fin}}{2}}$ and $X=L_{fin}$)		${\left({\displaystyle \frac{\partial \theta }{\partial X}}\right)}_{fluid}={\displaystyle \frac{k_{fin}}{k}}{\left({\displaystyle \frac{\partial \theta }{\partial X}}\right)}_{fin}$

. Thermal boundary conditions are enforced as follows: the left wall is maintained at a dimensionless temperature of θ = 1, and the right wall at θ = 0, while the horizontal walls are adiabatic, implemented as zero normal thermal flux (∂θ/∂Y = 0). All solid boundaries, including the embedded fin, satisfy the no-slip condition. At the fluid-solid interface, thermal continuity is imposed by enforcing matching heat fluxes between the solid and fluid regions.

To characterize heat transfer within the cavity, the local Nusselt number is defined at the cold wall and the heated surfaces, namely, the hot wall and the fin surfaces, as presented in Equation (9).

$$N{u}_{loc}=-{\nabla }_{\mathit{n}}\theta =-\nabla \theta \cdot \mathit{n} ,$$

(9)

where n is the unit outward normal vector on walls or fin surfaces.

The average Nusselt number on the hot and cold vertical walls is obtained by integrating the local Nusselt number along each respective wall. The expressions of average Nusselt number for the hot wall at X = 0 and the cold wall at X = 1 are given in Equation (10) and Equation (11), respectively.

$${\overline{Nu}}_{hot}=-{\displaystyle \frac{1}{W}}\underset{0}{\overset{W}{\int }}{\left.{\displaystyle \frac{\partial \theta }{\partial X}}\right|}_{X=0}dY,$$

(10)

$${\overline{Nu}}_{cold}=+{\displaystyle \frac{1}{W}}\underset{0}{\overset{W}{\int }}{\left.{\displaystyle \frac{\partial \theta }{\partial X}}\right|}_{X=1}dY.$$

(11)

When a fin is embedded on the hot wall, its surfaces contribute to additional heat transfer. The modified average Nusselt number includes these contributions by integrating along the fin’s vertical and horizontal surfaces. The corrected average Nusselt number is given by Equation (12).

$$\begin{gathered} {\overline{Nu}}_{hot}={\displaystyle \frac{1}{W+2L_{fin}}}\left[-\underset{0}{\overset{Y_{fin}-{\displaystyle \frac{W_{fin}}{2}}}{\int }}{\left.{\displaystyle \frac{\partial \theta }{\partial X}}\right|}_{X=0}dY+\underset{0}{\overset{L_{fin}}{\int }}{\left.{\displaystyle \frac{\partial \theta }{\partial Y}}\right|}_{Y=Y_{fin}-{\displaystyle \frac{W_{fin}}{2}}}dX-\underset{Y_{fin}-{\displaystyle \frac{W_{fin}}{2}}}{\overset{Y_{fin}+{\displaystyle \frac{W_{fin}}{2}}}{\int }}{\left.{\displaystyle \frac{\partial \theta }{\partial X}}\right|}_{X=L_{fin}}dY \\ -\underset{L_{fin}}{\overset{0}{\int }}{\left.{\displaystyle \frac{\partial \theta }{\partial Y}}\right|}_{Y=Y_{fin}+{\displaystyle \frac{W_{fin}}{2}}}dX-\underset{Y_{fin}+{\displaystyle \frac{W_{fin}}{2}}}{\overset{W}{\int }}{\left.{\displaystyle \frac{\partial \theta }{\partial X}}\right|}_{X=0}dY\right]. \end{gathered}$$

(12)

Since the average Nusselt number alone does not account for changes in surface area introduced by the fin, it can lead to misleading interpretations of thermal performance. To address this, Bawazeer, S.A. [24] proposed the Nusselt Number Ratio (NNR), defined in Equation (13), which normalizes heat transfer enhancement by accounting for the additional fin surface area.

$$\mathrm{N}\mathrm{N}\mathrm{R}=\left(1+{\displaystyle \frac{2L_{fin}}{W}}\right)\times {\displaystyle \frac{{\overline{Nu}}_{fin}}{{\overline{Nu}}_{no-fin}}}$$

(13)

The prefactor accounts for the added fin surface area, allowing for a fair comparison between finned and unfinned cases. An NNR greater than one indicates a net enhancement in heat transfer without severe flow obstruction, while a value below one suggests that the fin either offers minimal thermal benefit or negatively impacts flow circulation.

Finally, the stream function Ψ is introduced to describe the circulation of flow. It satisfies the Poisson equation:

$${\displaystyle \frac{{\partial }^2\Psi }{\partial X^2}}+{\displaystyle \frac{{\partial }^2\Psi }{\partial Y^2}}=-\left({\displaystyle \frac{\partial V}{\partial X}}-{\displaystyle \frac{\partial U}{\partial Y}}\right),$$

(14)

with Ψ = 0 imposed along all solid boundaries. The stream function provides a convenient tool for visualizing circulation patterns and vortex structures within the enclosure.

3. Numerical Methodology, Grid Validation, and Mesh Strategy

The numerical solution of the coupled governing equations presented in Section 2 is carried out using the finite element method (FEM) within the COMSOL Multiphysics^® 6.1 platform. The problem is treated as two-dimensional, steady, and laminar, given the range of Rayleigh numbers (10 ≤ Ra ≤ 10⁵) and Prandtl numbers (0.1 ≤ Pr ≤ 10).

The computational domain is discretized using quadratic Lagrange elements for velocity and linear elements for temperature, ensuring accurate resolution of thermal gradients and convective structures without the need for turbulence modeling. A stationary segregated solver is employed with relative tolerance set to 10⁻³. All simulations are run until residuals fall below the convergence threshold across all governing equations.

Simulations for the cavity with no fin were compared with benchmark results from de Vahl Davis [25] for air (Pr = 0.71) and Ra = 10⁴ and 10⁵ to validate the numerical model. The computed average Nusselt numbers on the hot wall (${\overline{Nu}}_{hot}$) closely matched the reported values, with relative errors of less than 0.5%, confirming the model’s reliability. Additionally, a grid independence study is performed for an enclosure filled with air (Pr = 0.71) without a fin to verify spatial accuracy. Rayleigh numbers up to Ra = 10⁵ are considered using structured meshes of increasing density: 32 × 32, 64 × 64, 128 × 128, 256 × 256, and 512 × 512. The average Nusselt number on the hot wall (${\overline{Nu}}_{hot}$) is used as the convergence metric. As summarized in

Table 2. The mean Nusselt number on the hot wall of an enclosure without a fin for different grid sizes.

Ra	Grid Sizes					% Change (256 × 256 to 512 × 512)	Convergence Status
	32 × 32	64 × 64	128 × 128	256 × 256	512 × 512
10	1.0000	1.0000	1.0000	1.0000	1.0000	0.000%	Converged
102	1.0015	1.0015	1.0015	1.0015	1.0015
103	1.1176	1.1178	1.1178	1.1178	1.1178
104	2.2402	2.2441	2.2447	2.2448	2.2448
105	4.4647	4.5121	4.5201	4.5214	4.5216	+0.004%

, the variation in ${\overline{Nu}}_{hot}$ between the two finest grids (256 × 256 and 512 × 512) is just 0.0002, amounting to a relative error of 0.004% at Ra = 10⁵, confirming the solution’s grid independence.

This analysis establishes a near-wall resolution threshold: the first inflation layer thickness near boundaries should be smaller than 1/256 ≈ 0.00391 to capture steep thermal gradients adequately. To ensure this, all finned simulations use an adaptive meshing strategy that combines structured grid refinement near solid walls with an unstructured triangular mesh in the interior.

In detail, the mesh near solid surfaces includes four inflation layers with a geometric stretching factor of 1.2. The first layer is constrained to a maximum thickness of 0.00391. In the interior, a triangular unstructured mesh is used with a maximum element size of 0.03 and a growth rate of 1.1. This hybrid approach ensures accurate prediction of boundary layer behavior while maintaining computational efficiency.

Figure 2 depicts the mesh structure for a square enclosure featuring a horizontal fin with a thickness of 0.01 and a length of 0.5, placed at Y_fin = 0.5. In Figure 2a, the complete computational grid is shown. In contrast, Figure 2b provides a detailed view of the area where the fin interfaces with the hot wall, highlighting the locally refined grid designed to address steep thermal gradients. This approach to mesh treatment is consistently employed throughout the study to ensure accurate predictions of natural convection phenomena, particularly when a fin is present.

4. Results and Discussion

A comprehensive analysis of the thermal performance of finned square cavities is presented based on 9000 numerical simulations. This number arises from a structured multi-parametric sweep involving five key physical and geometric parameters: Rayleigh number (Ra), Prandtl number (Pr), fin length (L_fin), fin vertical position (Y_fin), and fin-to-fluid thermal conductivity ratio (k_fin/k), along with an additional sub-loop over fin thickness (W_fin). Each parameter was discretized over a physically meaningful range informed by prior studies and preliminary sensitivity analysis. Specifically: Ra was varied over five values (10, 10², 10³, 10⁴, 10⁵); Pr included six values (0.1, 0.5, 0.71, 1, 5, 10); fin length used five values (0.1, 0.3, 0.5, 0.7, 0.9); vertical position covered five values (0.1, 0.3, 0.5, 0.7, 0.9); fin thickness included three values (0.001, 0.01, 0.1); and k_fin/k spanned four values (1, 10, 100, 1000). The selected conductivity ratio range (k_fin/k = 1 to 1000) captures a broad spectrum of thermal performance scenarios. While common fin materials, such as aluminum and copper, in air yield much higher ratios, typically between 7800 and 15,000, the upper bound of 1000 is sufficient to represent the onset of asymptotic behavior, allowing us to evaluate when increased conductivity no longer yields practical thermal gains.

The discussion is structured around key aspects of heat transfer behavior, including the influence of fin geometry and conductivity, regime-dependent trends in the Nusselt number, spatial sensitivity to fin placement, coupled Rayleigh-Prandtl interactions, and optimal configurations under convective conditions. Although no explicit critical Rayleigh number is reported, the progression from conduction- to convection-dominated regimes is captured qualitatively through variations in Nusselt number, flow structure, and fin sensitivity across the parametric space.

4.1. Parametric Optimization of Fin Geometry and Conductivity for Enhanced Natural Convection Flow and Heat Transfer

The analysis begins with a detailed assessment of how fin geometry and thermal conductivity influence heat transfer across varying Rayleigh and Prandtl numbers.

Table 3. Optimal Fin Geometry (Length, Position, Thickness) and Maximum Nusselt Number Ratio (NNR) for Varying Ra and Pr at k_fin/k = 1.

Ra	$$\begin{gathered} \mathbf{Maximum} \mathbf{NNR} \\ \hspace{1em}\hspace{1em}{\overline{\mathit{N}\mathit{u}}}_{\mathit{h}\mathit{o}\mathit{t}} \end{gathered}$$ (Lfin) (Yfin) (Wfin)
	Pr = 0.1	Pr = 0.5	Pr = 0.71	Pr = 1	Pr = 5	Pr = 10
10	1	1	1	1	1	1
	1.00001	1.00001	1.00001	1.00001	1.00001	1.00001
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
102	0.999984	0.999984	0.999984	0.999984	0.999984	0.999984
	1.001440	1.001441	1.001441	1.001441	1.001441	1.001441
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
103	0.999122	0.999105	0.999102	0.999100	0.999099	0.999099
	1.114984	1.116749	1.116791	1.116807	1.116807	1.116804
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
104	0.997606	0.996707	0.996632	0.996607	0.996653	0.996669
	2.120918	2.220797	2.237291	2.249079	2.265963	2.266832
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
105	0.993463	0.98922	0.989039	0.989258	0.990911	0.991147
	3.899116	4.372535	4.472169	4.550375	4.675865	4.681990
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)

presents a detailed summary of the Maximum Nusselt Number Ratio (NNR) achieved across a wide range of Rayleigh numbers (Ra = 10 to 10⁵) for six Prandtl numbers (Pr = 0.1 to 10), using a fixed fin conductivity equal to that of the fluid. This configuration isolates pure geometric effects, as the fin contributes no additional conductive advantage.

At Ra = 10, all Prandtl numbers yield an NNR of exactly 1.00001 with minimal sensitivity to Pr. This confirms that under conduction-dominated conditions, the fin is thermally passive and does not interfere with heat transport. The optimal configuration, characterized by a short fin (L_fin = 0.1), positioned near the top (Y_fin = 0.9), and very thin (W_fin = 0.001), remains consistent across all Pr values. The symmetry and thermal neutrality at this regime indicate that the fin neither perturbs the broad thermal boundary layer nor contributes to conduction enhancement.

As Ra increases to 10², the system begins transitioning into a weakly convective regime. The NNR slightly drops to 0.999984 for all Pr values, a negligible but consistent deviation. Interestingly, the associated Nusselt numbers (${\overline{Nu}}_{hot}$ ≈ 1.00144) remain near unity, reflecting that convective motion is emerging but remains symmetric and weak. Again, the optimal fin configuration remains unchanged, emphasizing that geometry still plays a passive role in this low Ra regime.

A more noticeable change occurs at Ra = 10³, where the NNR further drops to approximately 0.9991–0.99912. This ~0.09% decrease across all Pr values marks the start of performance divergence due to convective plume interaction with the fin. While the optimal geometry (short, top-aligned, thin fin) persists, ${\overline{Nu}}_{hot}$ shows a clear dependence on Prandtl number, where it increases from 1.11 at Pr = 0.1 to 1.1168 at Pr = 10. This indicates that higher-Pr fluids, which have thinner thermal boundary layers, become increasingly sensitive to local flow obstruction caused by the fin.

At Ra = 10⁴, the decline in NNR becomes more pronounced, dropping to a range of 0.9966–0.9976, representing a ~0.3% reduction in performance relative to the unfinned cavity. Here, the associated ${\overline{Nu}}_{hot}$ values show substantial growth, from 2.12 at Pr = 0.1 to 2.27 at Pr = 10, as buoyancy-driven circulation becomes dominant. Despite the increase in overall heat transfer, the embedded fin reduces relative efficiency due to distortion of the convective streamlines, particularly near mid-height. However, the table indicates that top-aligned fins still produce the best results under this neutral conductivity condition.

Finally, at Ra = 10⁵, the NNR drops further to ~0.989–0.993, indicating that the inclusion of the fin results in a clear and consistent reduction in heat transfer efficiency. This decline is most severe at Pr = 0.5, where the NNR reaches a minimum of 0.9892. However, the absolute Nusselt numbers continue to rise across all Prandtl numbers, reaching as high as ${\overline{Nu}}_{hot}$ = 4.68 at Pr = 10, signifying that while heat transfer is intensifying with Ra, the presence of a fin hinders optimal flow circulation and increases flow resistance. Notably, the same geometry, short, thin, and top-aligned, remains optimal, suggesting that only minimal fin geometries can avoid disrupting strong convection patterns.

A notable observation from the results is the consistent discrepancy between the Maximum Nusselt Number Ratio (NNR) and the average hot-wall Nusselt number (${\overline{Nu}}_{hot}$), particularly at moderate-to-high Rayleigh numbers. For instance, at Ra = 10⁵ and Pr = 10, the NNR drops below 0.991, implying a relative reduction in thermal performance due to the fin. However, the corresponding ${\overline{Nu}}_{hot}$ value exceeds 4.68. This contrast highlights a key insight that NNR is a normalized metric that compares finned performance to the unfinned baseline, accounting for added surface area. In contrast, ${\overline{Nu}}_{hot}$ reflects the absolute convective heat transfer on the hot wall. Therefore, while ${\overline{Nu}}_{hot}$ continues to rise with Ra and Pr due to more substantial buoyancy and thinner thermal boundary layers, NNR reveals the penalty introduced by the fin’s obstruction to flow, even if overall heat transfer improves. This distinction is critical for designers: a high ${\overline{Nu}}_{hot}$ does not always imply effective fin integration, NNR must be considered to assess whether the fin is enhancing or degrading relative thermal performance.

For k_fin/k = 1, the inclusion of a fin provides no enhancement and can marginally degrade performance in convective regimes. This underscores the need for careful geometric tuning or material selection (with higher conductivity) to extract thermal benefits from embedded fins in naturally convecting enclosures.

Table 4. Optimal Fin Geometry (Length, Position, Thickness) and Maximum Nusselt Number Ratio (NNR) for Varying Ra and Pr at k_fin/k = 10.

Ra	$$\begin{gathered} \mathbf{Maximum} \mathbf{NNR} \\ \hspace{1em}\hspace{1em}{\overline{\mathit{N}\mathit{u}}}_{\mathit{h}\mathit{o}\mathit{t}} \end{gathered}$$ (Lfin) (Yfin) (Wfin)
	Pr = 0.1	Pr = 0.5	Pr = 0.71	Pr = 1	Pr = 5	Pr = 10
10	1.249516	1.249516	1.249516	1.249516	1.249516	1.249516
	1.249534	1.249534	1.249534	1.249534	1.249534	1.249534
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.7)	(0.7)	(0.7)	(0.7)	(0.7)	(0.7)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
102	1.248923	1.248922	1.248922	1.248922	1.248922	1.248922
	1.250742	1.250741	1.250741	1.250741	1.250741	1.250741
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.7)	(0.7)	(0.7)	(0.7)	(0.7)	(0.7)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
103	1.178447	1.177385	1.177341	1.177319	1.177296	1.177295
	1.315104	1.316020	1.316026	1.316022	1.315999	1.315994
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
104	0.996717	0.995923	0.995863	0.995849	0.99591	0.995927
	2.119028	2.219051	2.235566	2.247368	2.264274	2.265144
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
105	0.993168	0.989038	0.988861	0.989075	0.990701	0.990935
	3.897958	4.371730	4.471363	4.549534	4.674873	4.680984
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)

presents the variation in the Maximum Nusselt Number Ratio (NNR) and associated fin geometries across a range of Rayleigh numbers (Ra = 10 to 10⁵) for six Prandtl numbers (Pr = 0.1 to 10) under a conductivity ratio of 10. This scenario introduces a moderate thermal enhancement potential, allowing the fin to act as a conductive bridge between the hot wall and the fluid, while still retaining sensitivity to convective dynamics.

At Ra = 10, the system remains in a conduction-dominated regime, yet the NNR rises to approximately 1.2495 for all Prandtl numbers, indicating a ~25% enhancement relative to the unfinned cavity. This improvement is attributed to the increased conductive capacity of the fin, which now contributes significantly to axial heat transport. The optimal geometry shifts slightly from the neutral case: the fin becomes longer (L_fin = 0.9), thicker (W_fin = 0.1), and is repositioned slightly lower (Y_fin = 0.7), reflecting a design that maximizes surface area while remaining well within the diffusive envelope of the thermal field.

As Ra increases to 10², the NNR remains nearly unchanged (~1.2489), suggesting that the system still operates predominantly under conduction with emerging convective rolls having minimal interference. Notably, the associated average hot-wall Nusselt number (${\overline{Nu}}_{hot}$) increases modestly to ~1.25 across all Pr values, reflecting incremental buoyancy effects. The optimal fin configuration remains unchanged at Ra = 10, reinforcing the idea that low-to-moderate Ra regimes benefit from large, thermally active fins, which function as extended heat exchangers with minimal flow resistance.

At Ra = 10³, the influence of convective structures becomes evident. NNR decreases by ~5.7% to values ranging from 1.1773 to 1.1784, with a more pronounced drop compared to lower Ra levels. Despite this reduction in relative performance, the absolute heat transfer continues to increase, with ${\overline{Nu}}_{hot}$ ranging from 1.31 at Pr = 0.1 to 1.316 at Pr = 10. This behavior signals the onset of a transitional regime in which the previously favorable geometry (long and thick) begins to impede vertical flow, resulting in thermal shielding or local recirculation. Nonetheless, the fin remains top-aligned (Y_fin = 0.9), indicating that high vertical placement continues to exploit rising thermal gradients.

A substantial shift occurs at Ra = 10⁴, where the NNR falls below unity for all Pr values (0.9958–0.9967), indicating that the fin now reduces relative heat transfer performance compared to a smooth cavity. Yet ${\overline{Nu}}_{hot}$ grows significantly, reaching values from 2.11 (Pr = 0.1) to 2.27 (Pr = 10). This discrepancy suggests that although the fin still transfers heat effectively due to its high conductivity, it also begins to interfere with the established convective plume, especially in fluids with higher Prandtl numbers, where boundary layers are thin and plume alignment is more critical. The optimal geometry is now dramatically reduced: the fin becomes very short (L_fin = 0.1), extremely thin (W_fin = 0.001), and remains at the top (Y_fin = 0.9), reflecting a design pivot toward minimal obstruction.

At Ra = 10⁵, this trend continues and intensifies. NNR values drop further to a range of 0.9887 to 0.9931, confirming a persistent penalty in relative heat transfer. However, the absolute Nusselt numbers continue to rise sharply, reaching as high as ${\overline{Nu}}_{hot}$ = 4.68 at Pr = 10, indicating a highly active convective regime. Interestingly, the optimal fin configuration (short, thin, and top-mounted) remains the same as for Ra = 10⁴, emphasizing that compact fins placed near high-gradient regions mitigate obstruction while preserving the conductive benefit. The data also shows that even with a tenfold conductivity contrast, enhancement diminishes at high Ra due to geometric misalignment with convective structures.

An important trend in Table 4 is the increasing divergence between the NNR and ${\overline{Nu}}_{hot}$ at higher Rayleigh numbers. For instance, at Ra = 10⁵ and Pr = 10, the NNR is only ~0.9909, indicating a slight net degradation compared to the smooth cavity, while ${\overline{Nu}}_{hot}$ exceeds 4.68, reflecting a vigorous convective regime. This contradiction underscores the dual nature of fin’s performance since ${\overline{Nu}}_{hot}$ represents total heat removal or addition, while NNR contextualizes it by comparing against the baseline and accounting for geometric cost. A fin may appear beneficial based on ${\overline{Nu}}_{hot}$ alone, but NNR reveals whether its inclusion is thermodynamically justified once the added surface area and potential flow disturbance are considered.

At moderate conductivity ratios (k_fin/k ~ 10), fin integration yields substantial thermal enhancement only in conduction-dominant regimes (Ra ≤ 10²), where large, centrally embedded fins serve as effective heat bridges. However, as convection strengthens (Ra ≥ 10³), the benefits of high conductivity become increasingly limited by geometric interference with flow. The results demonstrate that conductivity alone is insufficient to guarantee enhanced performance, as geometry must be tailored to avoid disrupting established plume structures. At higher Ra, the optimal design shifts toward short, top-aligned, and minimally intrusive fins, which balance conductive advantage with convective compatibility. This underscores the need for integrated thermogeometric optimization in passive fin-assisted heat transfer systems.

Table 5. Optimal Fin Geometry (Length, Position, Thickness) and Maximum Nusselt Number Ratio (NNR) for Varying Ra and Pr at k_fin/k = 100.

Ra	$$\begin{gathered} \mathbf{Maximum} \mathbf{NNR} \\ \hspace{1em}\hspace{1em}{\overline{\mathit{N}\mathit{u}}}_{\mathit{h}\mathit{o}\mathit{t}} \end{gathered}$$ (Lfin) (Yfin) (Wfin)
	Pr = 0.1	Pr = 0.5	Pr = 0.71	Pr = 1	Pr = 5	Pr = 10
10	1.852375	1.852375	1.852375	1.852375	1.852375	1.852375
	1.852402	1.852402	1.852402	1.852402	1.852402	1.852402
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.5)	(0.5)	(0.5)	(0.5)	(0.5)	(0.5)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
102	1.849721	1.849721	1.849721	1.849720	1.849720	1.849720
	1.852414	1.852414	1.852414	1.852414	1.852414	1.852414
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.5)	(0.5)	(0.5)	(0.5)	(0.5)	(0.5)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
103	1.679321	1.676699	1.676626	1.676594	1.676581	1.676584
	1.874062	1.874129	1.874123	1.874119	1.874107	1.874106
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.7)	(0.7)	(0.7)	(0.7)	(0.7)	(0.7)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
104	1.184570	1.174449	1.170968	1.167984	1.162925	1.162607
	2.518403	2.616831	2.628650	2.635831	2.643993	2.644244
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
105	1.031045	1.019544	1.015283	1.011088	1.003641	1.003301
	4.046618	4.506574	4.590837	4.650792	4.735933	4.739401
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)

presents the thermal performance trends in square cavities equipped with highly conductive fins (conductivity ratio = 100) across a wide range of Rayleigh numbers (Ra = 10–10⁵) and Prandtl numbers (Pr = 0.1–10). This configuration allows the fin to act as a strong axial conductor, facilitating lateral heat spreading even under weak convective motion.

At Ra = 10, the performance peaks across all cases, with NNR values consistently reaching 1.8524, independent of Pr. This represents an 85% improvement over the smooth cavity, signifying substantial conduction-driven enhancement. The optimal fin design is consistent across all fluids: a long fin (L_fin = 0.9), centered vertically (Y_fin = 0.5), and relatively thick (W_fin = 0.1). In the absence of significant flow structures, this configuration leverages direct axial conduction into the fluid core without flow interference, acting as a highly effective thermal bridge.

At Ra = 10², the NNR remains virtually unchanged (1.8497), suggesting that the transition to convection is still too weak to disrupt the fin’s conductive role. The associated Nusselt numbers (${\overline{Nu}}_{hot}$ ≈ 1.85) are nearly identical to those at Ra = 10, confirming a conduction plateau where enhancement is governed solely by material properties and geometry, rather than by buoyancy. The geometry remains unaltered, showing that mid-wall, full-length fins are still optimal in quasi-static thermal environments.

By Ra = 10³, convective activity becomes more influential. The NNR declines by ~10% to values between 1.6765 and 1.6793, marking a shift toward a mixed regime where flow begins to interact with the fin. The Nusselt numbers continue to increase (${\overline{Nu}}_{hot}$ ≈ 1.87), but the optimal fin position shifts upward (Y_fin = 0.7), indicating the fin’s role has evolved from passive conductor to an active structure that must align with thermal plume development. Although the long fin is retained, the need for repositioning suggests that early obstruction effects are beginning to emerge.

At Ra = 10⁴, a marked change occurs: NNR values fall to ~1.16–1.18, representing a further ~30% decline from the low-Ra peak. However, the absolute heat transfer continues to improve, with ${\overline{Nu}}_{hot}$ ranging from 2.51 to 2.64, depending on Pr. The optimal geometry is significantly reduced in length (L_fin = 0.1), vertically aligned at the top (Y_fin = 0.9), and much thinner (W_fin = 0.001). This transition reflects a key turning point; large, centrally located fins are no longer viable. As buoyancy strengthens, plumes become sensitive to flow blockage, and only minimal, top-mounted fins are needed to avoid disrupting convective structures. Importantly, this design pivot occurs even though the fin still has high conductivity, indicating that geometric compatibility with the flow becomes more critical than conductive capacity.

At Ra = 10⁵, NNR values drop further to approximately 1.003–1.031, approaching unity and signaling that the fin offers little to no net benefit over a finless cavity. Nonetheless, the Nusselt numbers increase significantly across all Pr values, with ${\overline{Nu}}_{hot}$ reaching approximately 4.05–4.74. This contrast highlights that the fin’s contribution becomes nearly neutralized by its interference with fully developed buoyant flow, despite its conductivity advantage. As before, the optimal fin remains short, thin, and top-aligned, demonstrating that in strong convection, only minimal geometry is required to preserve the flow structure without hindering efficiency.

A persistent trend across Table 5 is the widening gap between the NNR and ${\overline{Nu}}_{hot}$ at higher Ra. For example, at Ra = 10⁵ and Pr = 10, the system achieves a Nusselt number of 4.74; yet, the NNR is only 1.003, indicating almost no relative enhancement compared to the unfinned case. This reinforces the notion that absolute heat transfer performance can be misleading: while ${\overline{Nu}}_{hot}$ increases with Ra due to stronger convection, NNR reveals whether the fin is improving or impeding thermal performance relative to the baseline. In this regime, the fin’s conductive value is diminished by its disruptive presence, and only careful positioning and sizing can avoid performance degradation.

For high-conductivity fins (k_fin/k ~ 100), maximum thermal enhancement occurs at low Rayleigh numbers, where conduction dominates and flow remains symmetric. In these cases, long, centrally located fins serve as efficient thermal bridges. As Ra increases and convection becomes dominant, the benefit of high conductivity diminishes sharply, and fin-induced flow obstruction leads to progressively lower NNR values. Even though the overall heat transfer (${\overline{Nu}}_{hot}$) continues to rise, the relative advantage of using a fin drops nearly to zero. To retain any thermal benefit, the fin must be minimal in size, placed near the wall edge, and aligned with dominant plume trajectories. This underscores a critical design insight: in high-Ra environments, geometry and flow compatibility outweigh conductivity as the primary determinant of passive enhancement.

Table 6. Optimal Fin Geometry (Length, Position, Thickness) and Maximum Nusselt Number Ratio (NNR) for Varying Ra and Pr at k_fin/k = 1000.

Ra	$$\begin{gathered} \mathbf{Maximum} \mathbf{NNR} \\ \hspace{1em}\hspace{1em}{\overline{\mathit{N}\mathit{u}}}_{\mathit{h}\mathit{o}\mathit{t}} \end{gathered}$$ (Lfin) (Yfin) (Wfin)
	Pr = 0.1	Pr = 0.5	Pr = 0.71	Pr = 1	Pr = 5	Pr = 10
10	2.114266	2.114266	2.114266	2.114266	2.114266	2.114266
	2.114297	2.114297	2.114297	2.114297	2.114297	2.114297
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.5)	(0.5)	(0.5)	(0.5)	(0.5)	(0.5)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
102	2.111237	2.111236	2.111236	2.111236	2.111236	2.111236
	2.114311	2.114311	2.114311	2.114311	2.114311	2.114311
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.5)	(0.5)	(0.5)	(0.5)	(0.5)	(0.5)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
103	1.906475	1.903493	1.903410	1.903375	1.903362	1.903365
	2.127557	2.127626	2.127621	2.127617	2.127606	2.127604
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.7)	(0.7)	(0.7)	(0.7)	(0.7)	(0.7)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
104	1.266027	1.252565	1.248386	1.244885	1.239114	1.238770
	2.691582	2.790884	2.802443	2.809376	2.817216	2.817470
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)
105	1.074790	1.060019	1.054680	1.049521	1.040639	1.040296
	4.218307	4.685479	4.768976	4.827575	4.910520	4.914158
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)	(0.9)
	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)	(0.1)

illustrates the impact of using ultra-conductive fins, with conductivity ratios as high as 1000, on natural convection heat transfer across a broad range of Rayleigh numbers (Ra = 10² to 10⁵) and Prandtl numbers (Pr = 0.1 to 10). This regime represents a near-ideal conduction scenario, where the fin offers minimal internal thermal resistance and behaves nearly as an isothermal insert.

At Ra = 10, the NNR reaches its highest value across all conductivity cases analyzed (2.114), indicating a remarkable 111% enhancement in heat transfer relative to the unfinned cavity. The associated ${\overline{Nu}}_{hot}$ is nearly identical (~2.1143), showing that the ultra-conductive fin significantly amplifies axial energy transport in the absence of convective rolls. The optimal geometry remains long (L_fin = 0.9), centered vertically (Y_fin = 0.5), and thick (W_fin = 0.1), thereby maximizing the conductive surface area while avoiding any flow obstruction, as none exists in this diffusive regime.

At Ra = 10², NNR values remain nearly constant (~2.111), suggesting that conduction still dominates despite early buoyant instabilities. The Nusselt numbers remain unchanged from the Ra = 10 case, indicating that further increases in buoyancy have not yet altered the dominant mode of heat transfer. The optimal geometry remains unchanged, confirming that high-conductivity fins perform best when embedded in thermally quiescent or low-flow environments.

As Ra reaches 10³, a moderate shift is observed. NNR decreases to ~1.903–1.906, indicating a ~10% drop compared to the conduction plateau. However, absolute heat transfer continues to rise, with ${\overline{Nu}}_{hot}$ climbing to ~2.1276 for all Pr values. The optimal fin remains long and thick, but is now repositioned vertically to Y_fin = 0.7, reflecting the growing presence of upward-moving thermal plumes. This subtle geometric adaptation shows that even with superior conductivity, the fin must align with buoyant flow pathways to maintain its advantage.

At Ra = 10⁴, the reduction in the NNR becomes more pronounced. Values now range from 1.2388 to 1.2660, indicating that plume interference becomes a limiting factor, even for ultra-conductive fins. Despite this, ${\overline{Nu}}_{hot}$ continues to grow significantly, reaching values near 2.81–2.90, depending on Pr. The geometry adapts again, with the fin becoming shorter (L_fin = 0.1), remaining thin (W_fin = 0.001), and positioned at the top (Y_fin = 0.9), indicating that minimal intrusiveness is necessary to mitigate obstruction of increasingly structured convective rolls. At this stage, the benefit from conductivity begins to plateau, and geometric alignment becomes the key constraint.

At Ra = 10⁵, the NNR drops further to ~1.040–1.075, approaching unity. This suggests that in strongly convective environments, the advantage of ultra-conductivity is neutralized mainly by flow disruption, even when fins are small and optimally placed. However, ${\overline{Nu}}_{hot}$ values continue their upward trend, reaching ~4.21 to 4.91, a result of enhanced plume transport rather than any specific contribution from the fin. Notably, the Prandtl number influence becomes more pronounced here: high-Pr fluids (Pr = 10) see the largest ${\overline{Nu}}_{hot}$ (4.91) but the smallest NNR, highlighting that thinner boundary layers in high-Pr fluids are more sensitive to obstruction, even by minimal geometries.

The divergence between the NNR and ${\overline{Nu}}_{hot}$ becomes particularly significant in this ultra-conductive scenario. For example, at Ra = 10⁵ and Pr = 10, the Nusselt number reaches 4.914, but the NNR is just 1.040, indicating only a 4% relative gain despite the highest possible conductivity ratio. This reveals a saturation effect in which absolute heat transfer continues to rise due to convection, the relative advantage of the fin diminishes, and eventually, its benefit is marginal. Designers must therefore recognize that material enhancement without geometric or flow compatibility will yield diminishing returns, especially in high Ra, high Pr scenarios.

Ultra-conductive fins (k_fin/k ~ 1000) provide exceptional enhancement under conduction-dominated conditions (Ra ≤ 100), reaching NNR values over 2.1. However, as the system transitions to convection (Ra ≥ 10³), the benefits of high conductivity are increasingly limited by the fin’s interaction with buoyant flow structures. To avoid performance degradation, fins must become shorter, thinner, and better aligned with convective trajectories, primarily at or near wall edges. Ultimately, this study demonstrates that beyond a certain threshold, conductivity alone is insufficient for optimal performance. At high Ra, careful geometric tuning remains essential to preserve the benefits of passive thermal enhancement.

At first glance, it may seem counterintuitive that the Maximum Nusselt Number Ratio (NNR) is highest at low Rayleigh numbers (Ra) and declines as Ra increases. One might expect fins to be more effective at high Ra, where stronger natural convection enhances boundary layer activity. However, our parametric results reveal the opposite: NNR peaks under conduction-dominated conditions and steadily drops, sometimes below unity, as buoyancy-driven flow strengthens.

The dominant transport mechanism best explains this reversal. At low Ra (e.g., Ra = 10), the flow is nearly stagnant, and heat transfer occurs primarily via conduction. Under these conditions, a high-conductivity fin functions as an isothermal bridge, significantly enhancing axial heat transport without obstructing flow. Table 6 presents an NNR of 2.114 for k_fin/k = 1000 at Ra = 10, which is consistent across various Prandtl numbers.

As Ra increases, convection dominates and the role of the fin shifts. Buoyant plumes form and interact with the fin, which may now obstruct vertical circulation, flatten temperature gradients, or induce local recirculation, especially if the fin is long, thick, or poorly placed. These effects are more pronounced in high-Pr fluids due to thinner boundary layers. Consequently, the relative benefit of the fin diminishes, and NNR can fall to near or below one.

This challenges the conventional belief that fins always improve thermal performance. At high Ra, even ultra-conductive fins may degrade efficiency if misaligned with the flow. The key insight is that fin design must be tuned not only for thermal conductivity or surface area but also for compatibility with evolving flow structures. Passive enhancement is most effective in conduction-dominated regimes because fins can transfer heat without interfering with flow. In strong convection, the geometry must be designed to support rather than disrupt the natural thermal architecture.

4.2. Nusselt Number Comparison Across Low and High Rayleigh–Prandtl Number Combinations

Nusselt number variations at two limiting Rayleigh–Prandtl combinations are compared to contextualize the regime-specific performance trends identified in the parametric analysis. These representative cases, one conduction-dominated and the other convection-dominated, illustrate how fin geometry affects heat transfer under varying thermal conditions.

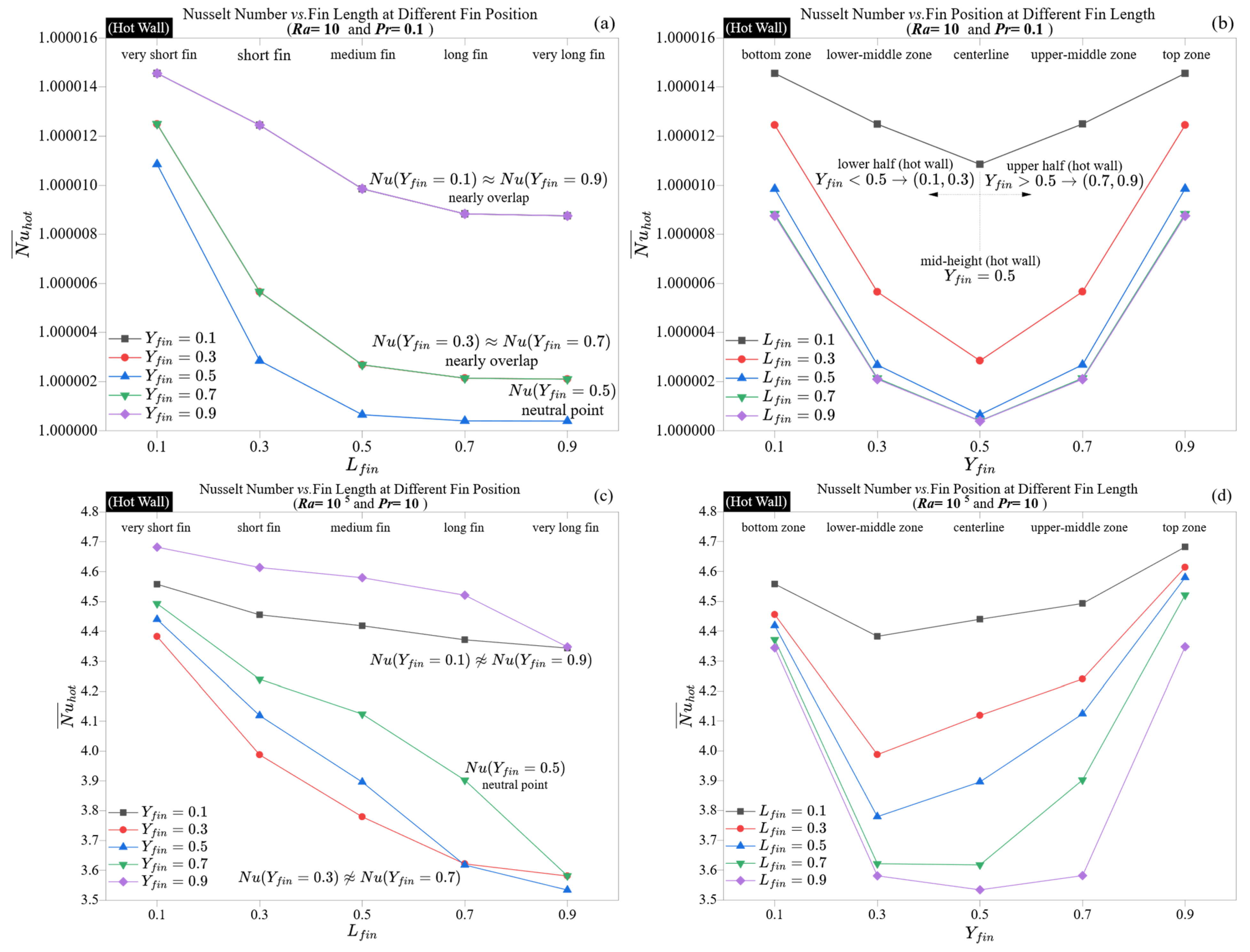
The impact of fin geometry on heat transfer from the hot wall shows clear regimes influenced by the interplay of thermal diffusion, buoyancy-driven flow, and spatial obstruction. Figure 3 illustrates how the average Nusselt number varies with fin length and position at two extreme Rayleigh–Prandtl combinations: Ra = 10, Pr = 0.1, as shown in Figure 3a,b, and Ra = 10⁵, Pr = 10, as shown in Figure 3c,d.

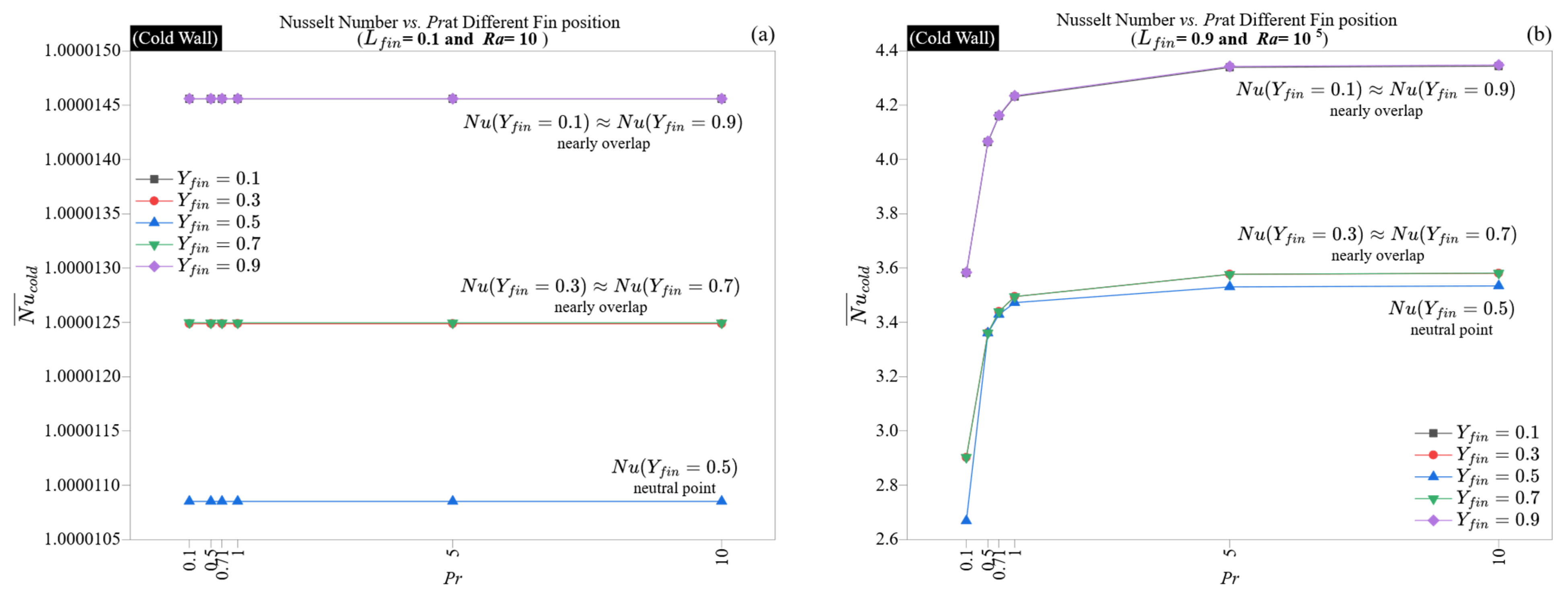
At Ra = 10, the flow remains primarily diffusion-dominated with minimal convective circulation. As indicated in Figure 3a,b, Nusselt numbers show slight variation across different geometric configurations, fluctuating within ±1.5 × 10⁻⁵ around unity. The length of the fin has a negligible effect, and the vertical placement, from the bottom to the top wall, results in only slight curvature. Notably, the lowest values consistently appear when the fin is centered (position ≈ 0.5), implying that the wall-normal thermal gradient peaks at mid-height, rendering this area somewhat more responsive to obstruction, even without flow. These findings confirm that when conduction dominates transport, fin geometry behaves in a thermally passive manner.

In contrast, the situation changes significantly at Ra = 10⁵, Pr = 10, where convective currents become dominant. Figure 3c,d show that the length and placement of fins substantially impact hot-wall Nusselt numbers, which vary from 3.53 to 4.68. Short fins located near the top wall (e.g., L_fin = 0.1 at Y_fin = 0.9) achieve the highest heat transfer by aligning with the upward thermal plume near its detachment region. Conversely, long fins positioned centrally (e.g., L_fin = 0.9 at Y_fin = 0.5) significantly lower ${\overline{Nu}}_{hot}$ by disrupting the core convective flow, effectively splitting the plume and flattening the vertical temperature gradient. These turning points in Nusselt number trends identify critical fin lengths at which the benefits of conduction are outweighed by plume disruption, particularly in high Ra convection-dominated regimes.

The difference in alignment between bottom- and top-aligned fins is significant: fins placed higher enhance plume continuation, while those positioned lower can disrupt early development stages. This geometric selectivity is intensified by the high Prandtl number, which results in narrow thermal boundary layers, making the system particularly susceptible to vertical disturbances. At Ra = 10⁵, the Nusselt number variation exceeds 30%, in sharp contrast to the less than 0.002% range at Ra = 10. This shift from geometric neutrality to thermal susceptibility exemplifies a critical regime change: in systems dominated by diffusion, fin geometry is irrelevant, whereas in convection-dominated scenarios, it is crucial.

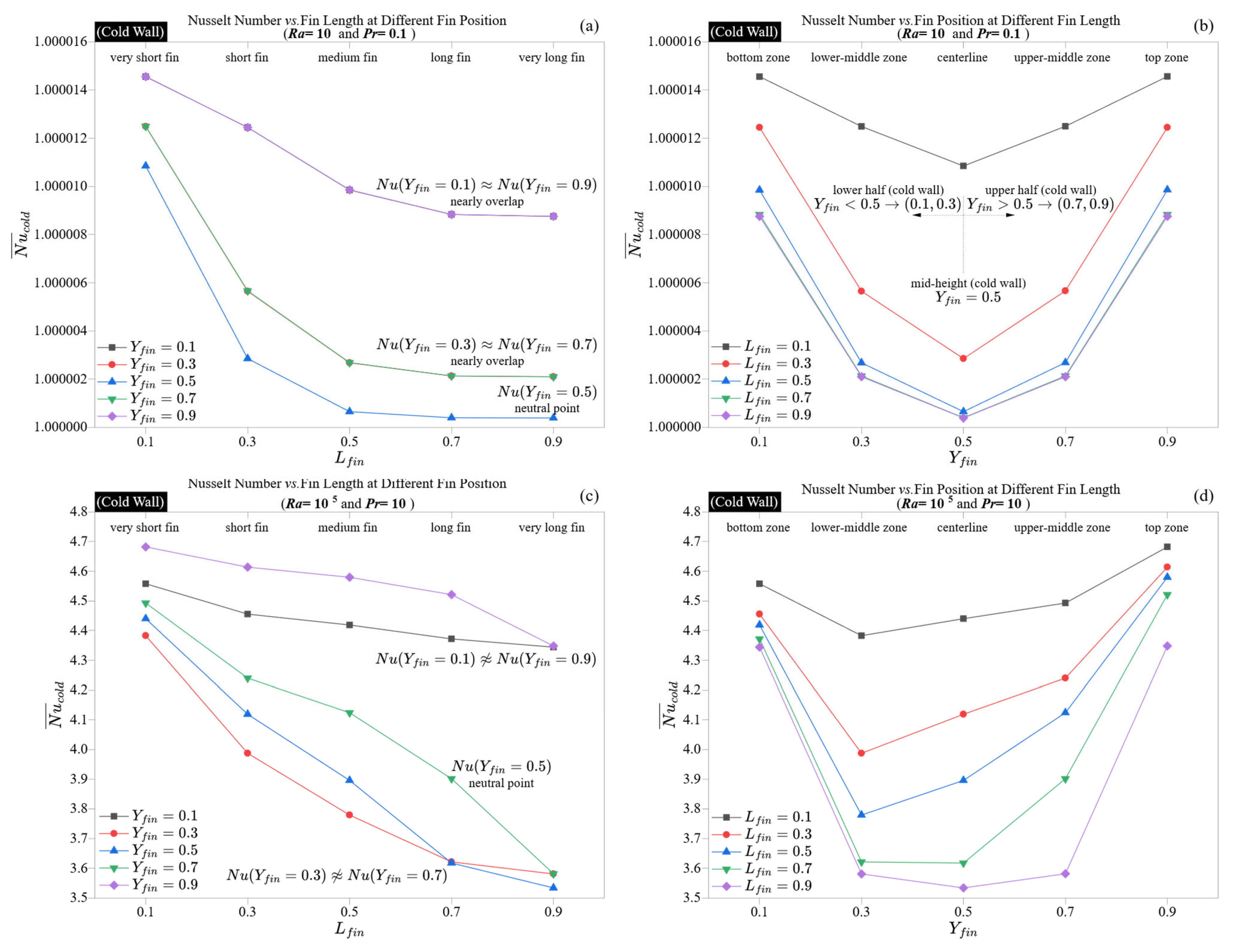
The cold wall contributes a complementary yet distinctly dynamic role to the thermal structure of natural convection within the cavity. In contrast to the hot wall, which uses fins to modulate thermal input, the cold wall focuses primarily on thermal absorption and wake recovery. Its Nusselt number trends therefore signify the downstream effects of plume interaction, flow recirculation, and thermal diffusion. Figure 4 illustrates this behavior within the same Rayleigh-Prandtl boundaries applied earlier, at Ra = 10, Pr = 0.1 (Figure 4a,b), and Ra = 10⁵, Pr = 10 (Figure 4c,d).

In the diffusive regime, as shown in Figure 4a,b, the distribution of the Nusselt number closely resembles that of the hot wall, aligning to within six significant digits. This symmetry is due to the system being in a quasi-static state, where there is no significant flow; conduction solely governs the thermal field, resulting in nearly uniform temperature gradients within the cavity. Acceptable variations on either wall cause minimal disruption to isotherm curvature, resulting in identical thermal metrics on both sides. Consequently, there is an entirely symmetric conduction profile.

However, under high Rayleigh and Prandtl conditions, the behavior of the cold wall diverges subtly yet significantly from that of the hot wall. Figure 4c,d illustrate that the average Nusselt number on the cold wall peaks at 4.68 and dips to a low of 3.53, closely reflecting the hot wall’s values but with slight positional variations. The cold wall’s response to the post-plume thermal wake, influenced by deflections caused by upstream fins, generates a delayed effect: fins obstructing hot wall plumes upstream inadvertently reduce convective intensity on the cold wall.

The trends illustrated in Figure 4c indicate that longer fins typically lead to a decrease in Nusselt number, particularly at mid-height. In contrast, the cold wall shows somewhat greater tolerance to geometric obstructions compared to the hot wall. For example, the Nusselt number difference between L_fin = 0.1 and L_fin = 0.9 at central positions is generally smaller, usually under 0.9, while the hot side often experiences differences greater than 1.1. This implies that although fins on the hot wall influence core energy injection, the thermal energy that survives the convective path to reach the opposite boundary primarily dictates cold-wall transfer. This performance reduction at mid-height placement is specific to square cavities with symmetric vertical plumes; generalizing this effect to other geometries would require careful analysis of how plume dynamics shift with boundary shape and aspect ratio.

Position-dependent trends, as shown in Figure 4d, further validate these findings. The lowest Nusselt number is again observed at mid-wall fin positions, but this minimum is less distinct. This subtle minimum results from diminished convective coherence: by the time the fluid hits the cold wall, it has become partially mixed and slowed down, which strengthens the thermal boundary layer against lateral fin disturbances. Additionally, the overall profile is somewhat flatter, indicating that the cold-wall Nusselt number is less concentrated and more shaped by the accumulated behavior upstream.

Unlike the hot wall, where the optimal fin placement enhances vertical alignment with buoyant flow, effective cold-wall designs focus on reducing wake interference and ensuring ample lateral access for incoming fluid. This highlights an important design distinction: thermal input and thermal recovery depend on different fin placement strategies, and no single fin geometry can optimize both types of walls simultaneously.

4.3. Spatial Control of Wall Heat Transfer: Role of Fin Length and Position

After establishing the regime sensitivity of fin performance, the analysis now shifts toward understanding how fin length and vertical position affect localized wall heat transfer. These spatial factors play a decisive role in shaping boundary layer behavior and energy distribution in naturally convecting enclosures.

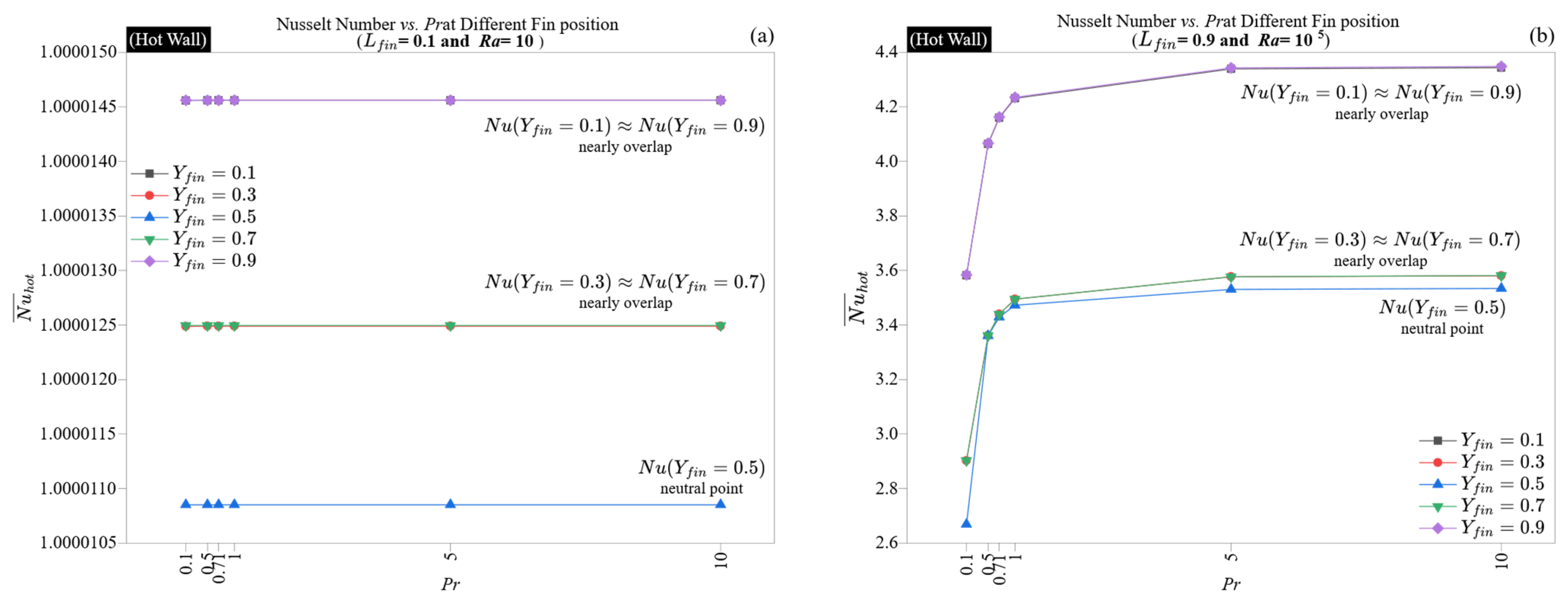
Figure 5 and Figure 6 illustrate the influence of the Prandtl number on the thermal behavior of finned cavities, showing the average wall Nusselt number plotted against fin position for two sample fin lengths (L_fin = 0.1 and L_fin = 0.9) across six Pr values, ranging from 0.1 to 10. In Figure 5a and Figure 6a, the diffusion-dominated regime (Ra = 10) is depicted, whereas Figure 5b and Figure 6b focus on the convective regime (Ra = 10⁵).

When the Rayleigh number is low, changes in the Prandtl number have little effect. Figure 5a and Figure 6a show that all Nusselt numbers remain nearly constant and equal to their conduction limit (≈1.0000146 for short fins and ≈1.0000004 for long fins at the mid-position). This constancy emphasizes that, under minimal thermal forcing, the interaction between momentum and thermal diffusion is negligible; there is no flow or thermal stratification, and both walls maintain thermal symmetry, regardless of the Prandtl number. This consistency persists even with variations in fin position, reinforcing that, under pure conduction, the Prandtl number has no impact.

In the convective case at Ra = 10⁵, there is a clear and increasingly nonlinear sensitivity to the Prandtl number. Both walls exhibit this sensitivity, particularly the hot wall, as shown in Figure 5b. As the Prandtl number increases from 0.1 to 10, the Nusselt number significantly rises, from 2.67 to 4.35 at mid-height (Y_fin = 0.5) and from 3.58 to 4.35 at the wall edges (Y_fin = 0.1 and 0.9). This pattern is closely linked to the thickness of the thermal boundary layer, which decreases as Pr increases. Higher Prandtl numbers hinder thermal diffusion, resulting in steeper gradients near the walls and sharper plume boundaries, thereby enhancing wall-normal heat transport.

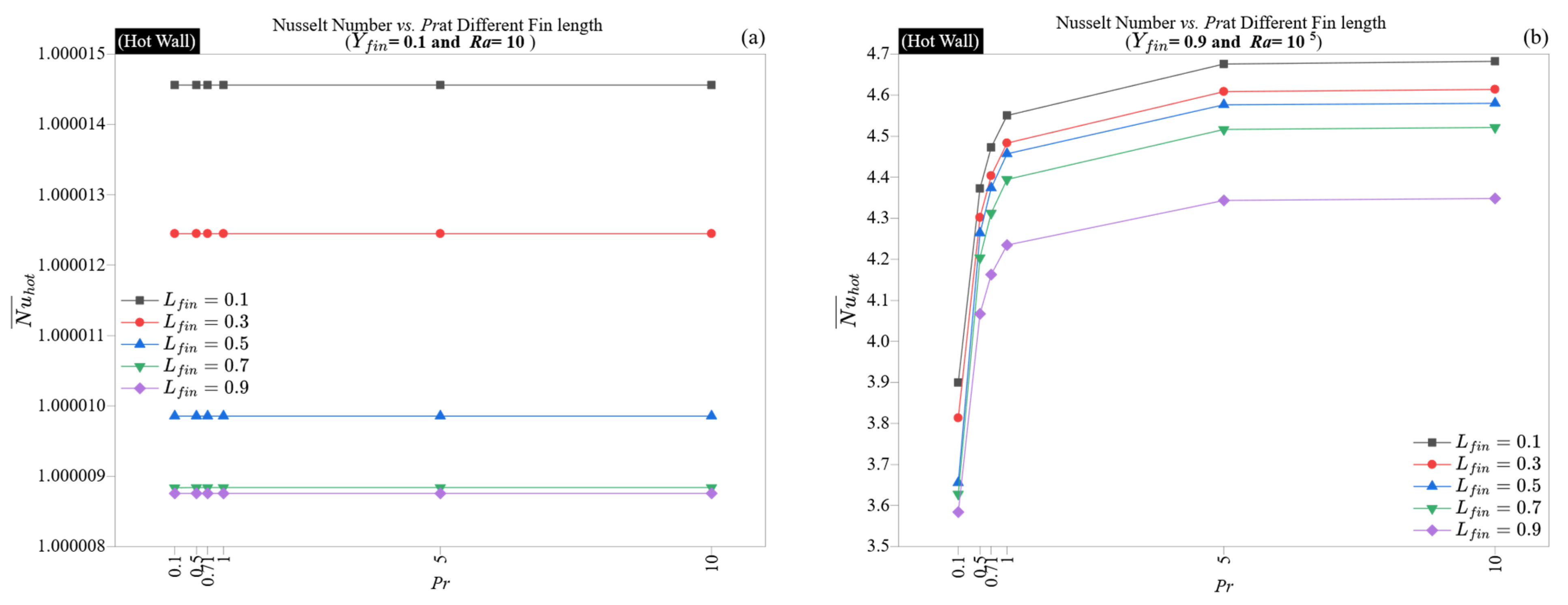
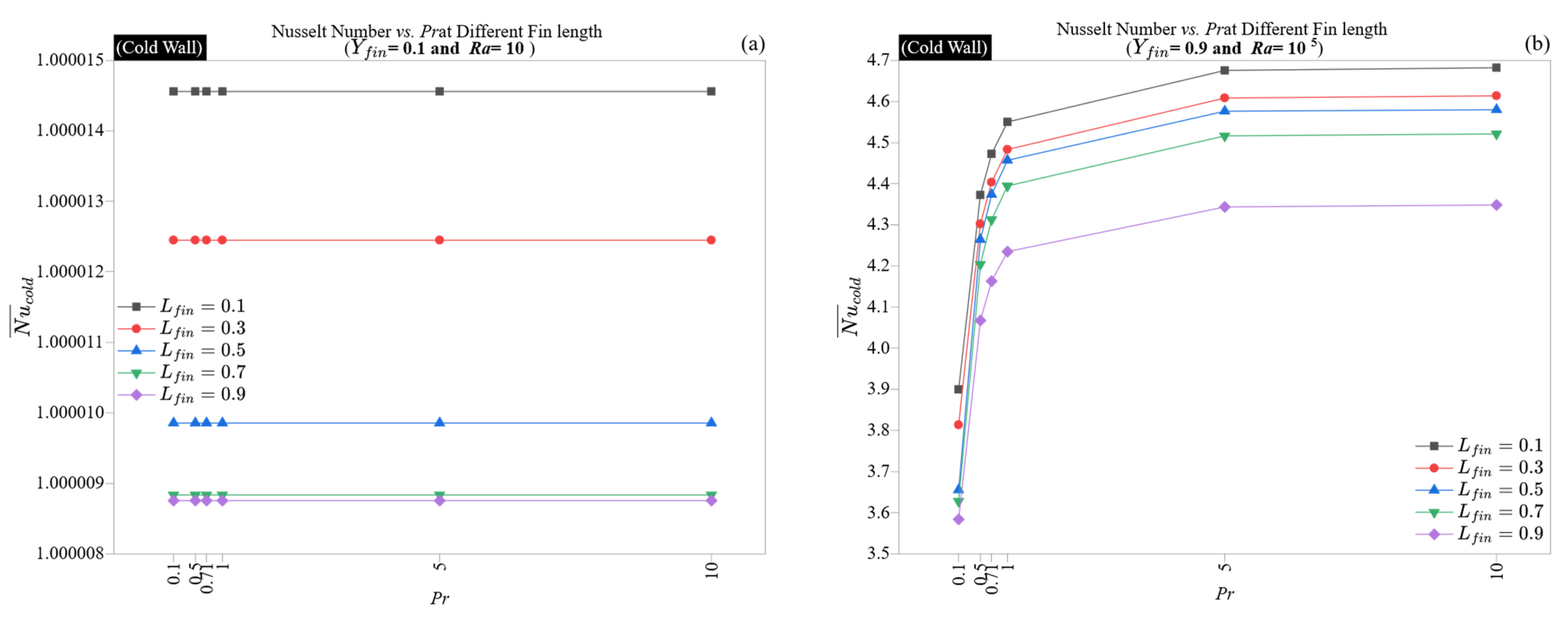
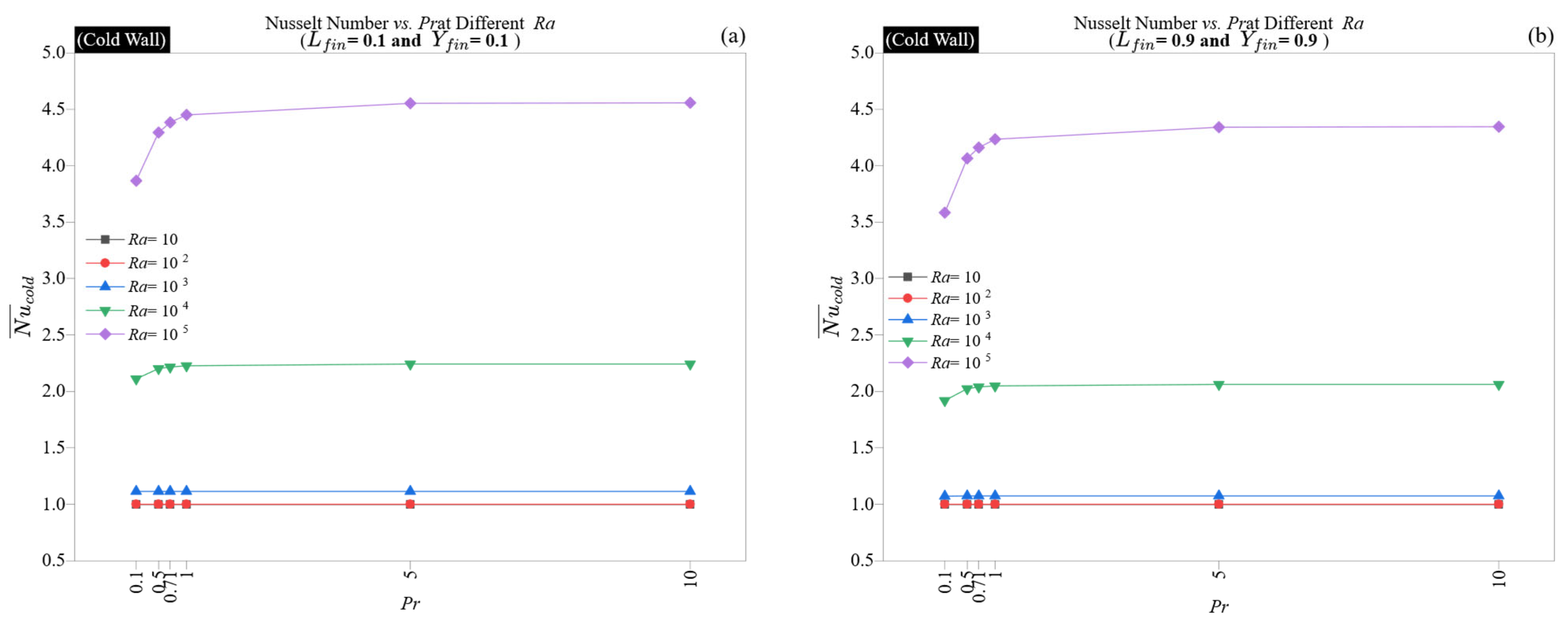
Interestingly, the advantages of high Pr are not evenly distributed throughout the wall. While all locations exhibit an increase in Nusselt number with Pr, the most significant improvement occurs at mid-wall positions, where fins impede flow. For example, at Y_fin = 0.5 and L_fin = 0.9, the Nusselt number rises from 2.67 (Pr = 0.1) to 3.53 (Pr = 10), which is approximately a 32% increase. This indicates that fluids with a higher Prandtl number are more resistant to geometric disruptions, as their confined plumes are less prone to being flattened by nearby obstacles. Fins positioned at the top continue to yield the highest Nusselt number values across varying Pr, thanks to their placement in line with the terminal convective surge zone.

The cold wall reflects these trends with somewhat decreased sensitivity, as shown in Figure 6b. The maximum Nusselt number still occurs near Y_fin = 0.9, and the values closely follow those of the hot wall. However, the gap between low and high Pr cases is narrower, particularly for long fins, suggesting that thermal reception at the cold wall is more stable, influenced by the integrated plume structure formed upstream. This supports the notion that cold-wall performance results from downstream effects, determined more by convective quality than by initiation conditions.

This analysis shows that the Prandtl number is a secondary factor in conduction but a primary influence in convection. Its effect increases in geometrically confined areas and is particularly significant for fin designs that would typically hinder low-Prandtl flows. Therefore, the Prandtl number serves as a thermal “buffer,” improving the system’s capacity to dissipate heat even in less than ideal geometric configurations.

Figure 7 and Figure 8 examine how the Prandtl number affects the distribution of the Nusselt number for fixed fin locations under two different Rayleigh conditions. This analysis focuses on the performance of five fin lengths (0.1–0.9 m) at the lower fin position (Y_fin = 0.1) for Ra = 10, and the upper fin position (Y_fin = 0.9) for Ra = 10⁵, observing the Prandtl response at both thermal boundaries.

At a low Rayleigh number (Ra = 10), conduction primarily governs the heat transfer regime Figure 7a and Figure 8a illustrate that the Nusselt number is constant across all Prandtl numbers and fin lengths, settling close to unity (1.0000146 for short fins and 1.0000088 for long fins). This lack of sensitivity indicates that, in still thermal conditions, changes in the relative diffusivities of momentum and energy do not affect the wall-normal gradient. Furthermore, the uniformity of the Nusselt number along both walls underscores the symmetry within the conduction regime. The slight decline in Nusselt number with longer fin lengths is merely geometric, not influenced by transport.

In contrast, at Ra = 10⁵ and Y_fin = 0.9, as shown in Figure 7b and Figure 8b, the Prandtl number has a significant impact on the results. For the hot wall, the Nusselt number increases from 3.58 (Pr = 0.1) to 4.68 (Pr = 10) for short fins, and from 3.65 to 4.58 for long fins. A comparable increase occurs on the cold wall, although with slightly lower absolute values. This improvement is nonlinear and levels off at higher Pr values, demonstrating the contraction of the thermal boundary layer, which minimizes diffusive losses and enhances the rate of heat extraction from the wall.

A key observation is that the performance advantage of increasing Pr diminishes as the fin length increases. At Pr = 10, the Nusselt number decreases by approximately 0.33 units when transitioning from short to long fins (4.68 to 4.35), while at Pr = 0.1, this change results in a decrease of only about 0.3 units (3.90 to 3.58). This indicates that in high-Pr conditions, longer fins can more significantly hinder plume exit, thus moderating the convective advantage. The cold wall exhibits a similar suppression, reinforcing that long fins positioned near the plume termination point create a distributed drag that slightly counteracts the benefits from sharper boundary layers.

Overall, the findings suggest that with strong convective forcing, the Prandtl number plays a crucial role in thermal optimization, provided that fin placement allows access to plume-rich areas. Fins positioned near the top wall exhibit higher thermal gradients and effectively take advantage of Pr-induced enhancements, whereas longer fins may partially obscure this benefit. Therefore, for optimal system performance, using high-Pr fluids in combination with short, top-aligned fins creates a synergistic configuration that maximizes convective throughput.

4.4. Coupled Rayleigh–Prandtl Effects Under Geometrical Extremes

The influence of Rayleigh and Prandtl number interactions on fin performance is examined through two contrasting geometric configurations. By analyzing extreme cases of fin length and vertical placement, the results highlight the nonlinear coupling between fluid properties and geometric obstruction in determining convective heat transfer efficiency.

Figure 9 and Figure 10 offer a detailed look at how the Rayleigh number (Ra) and Prandtl number (Pr) together influence thermal transport in fin-assisted cavities across a five-order-of-magnitude range of Ra. We analyze two distinct fin configurations: a short fin positioned near the cavity base (L_fin = 0.1, Y_fin = 0.1) and a long fin located near the top boundary (L_fin = 0.9, Y_fin = 0.9). These scenarios reveal variations in heat transfer behavior due to the relative alignment (or lack thereof) between the fin and the prevailing thermal plume structure.

At low Ra (10–100), heat transfer is dominated by diffusion, with Nusselt numbers remaining near unity for all Pr and both walls. In this range, thermal gradients are minimal, velocity magnitudes are low, and the formation of convective cells is inhibited. The Prandtl number and fin location do not significantly affect the temperature field, resulting in consistently flat Nusselt number profiles in Figure 9a,b, as well as in Figure 10a,b. This plateau indicates the asymptotic approach to the conduction limit, regardless of fluid viscosity or wall positioning.

A notable shift occurs as Ra exceeds 10³. For the lower-positioned short fin (Figure 9a and Figure 10a), Nusselt numbers experience a sharp increase with Ra, further intensified by higher Pr. At Ra = 10⁵, Nusselt number values vary between 3.87 and 4.56, influenced by Pr. In this scenario, the fin’s position aligns with the base of the buoyant plume, allowing it to capture the rising fluid at the onset of circulation. Fluids with higher Pr, characterized by narrower thermal boundary layers, support steeper wall gradients and greater convective throughput, thereby improving wall heat transfer.

In contrast, the long fin, positioned against the top wall (Figure 9b and Figure 10b), exhibits limited growth in the Nusselt number. Although the top location is theoretically superior for thermal extraction, the considerable length of the fin creates a notable obstruction, especially under high-Ra conditions. Consequently, Nusselt number values at Ra = 10⁵ peak at just below 4.35, even with Pr = 10, which is approximately 0.22 lower than what is observed in the short-fin scenario. Additionally, the rate of Nusselt number increase with Ra is more gradual. This decline in performance highlights the interference penalty faced by long fins placed in areas with fully developed plume outflow, a situation that becomes increasingly significant as convective strength escalates.

The cold wall trends closely follow those of the hot wall, with consistent downward offsets. At Ra = 10⁵, the Nusselt number for the cold wall varies from 3.58 to 4.35 across different Prandtl numbers (Pr), depending on the geometry. This slight delay is due to the indirect heating of the cold wall: it gains thermal energy only after plume transport, making it more responsive to upstream fin-induced redirection. Still, the proportional increase in Nusselt number with Pr is similar to that of the hot wall, emphasizing that the Prandtl number influences boundary layer compression. In contrast, the Rayleigh number (Ra) determines the degree of global convection.

These findings support the notion that high Pr improves wall heat transfer, but only when the fin design enables effective plume development. Short fins located close to the flow origin (bottom wall) leverage thermal entrainment, facilitating the natural evolution of vertical plumes. In contrast, long fins positioned at the top often hinder plume ascent and create areas of partial stagnation, resulting in suppression of the Nusselt number, even in high Pr fluids. Therefore, the optimal thermal configuration in high Ra and high Pr conditions is the one that minimizes obstruction while strategically positioning elements near the plume initiation point.

4.5. Fin Position and Length Optimization Under Convective Flow Conditions

A focused analysis of fin position and length is presented here to determine optimal configurations in convection-dominated regimes. Emphasis is placed on identifying spatial arrangements that align with buoyant flow patterns and enhance heat transfer without introducing significant flow resistance.

Figure 11 and Figure 12 illustrate how the position of the fin affects wall heat transfer across five Rayleigh numbers (Ra = 10 to 10⁵) in two contrasting thermal configurations: a short fin at a low Prandtl number (Pr = 0.1), as shown in Figure 11a and Figure 12a, and a long fin at a high Prandtl number (Pr = 10), illustrated in Figure 11b and Figure 12b. These boundary cases were selected to demonstrate how thermal performance is spatially sensitive to fin placement in both conduction-dominated and convection-dominated scenarios.

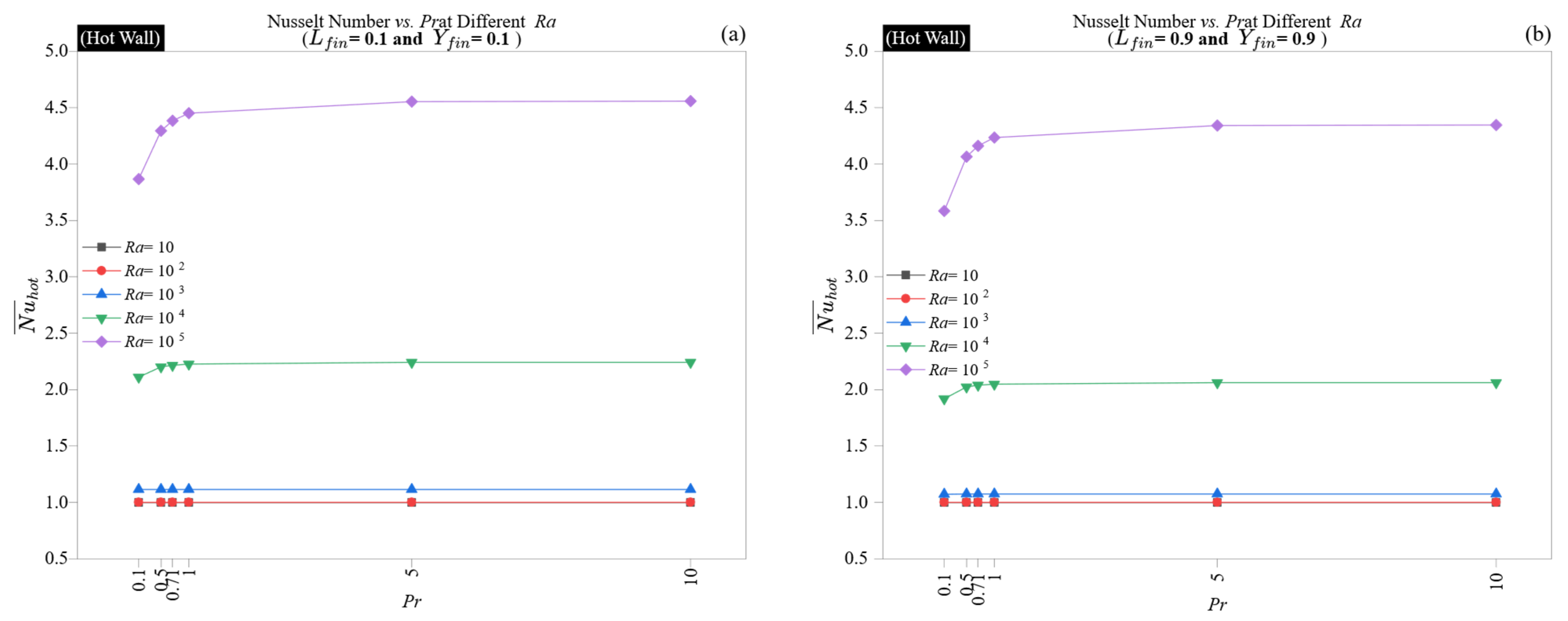
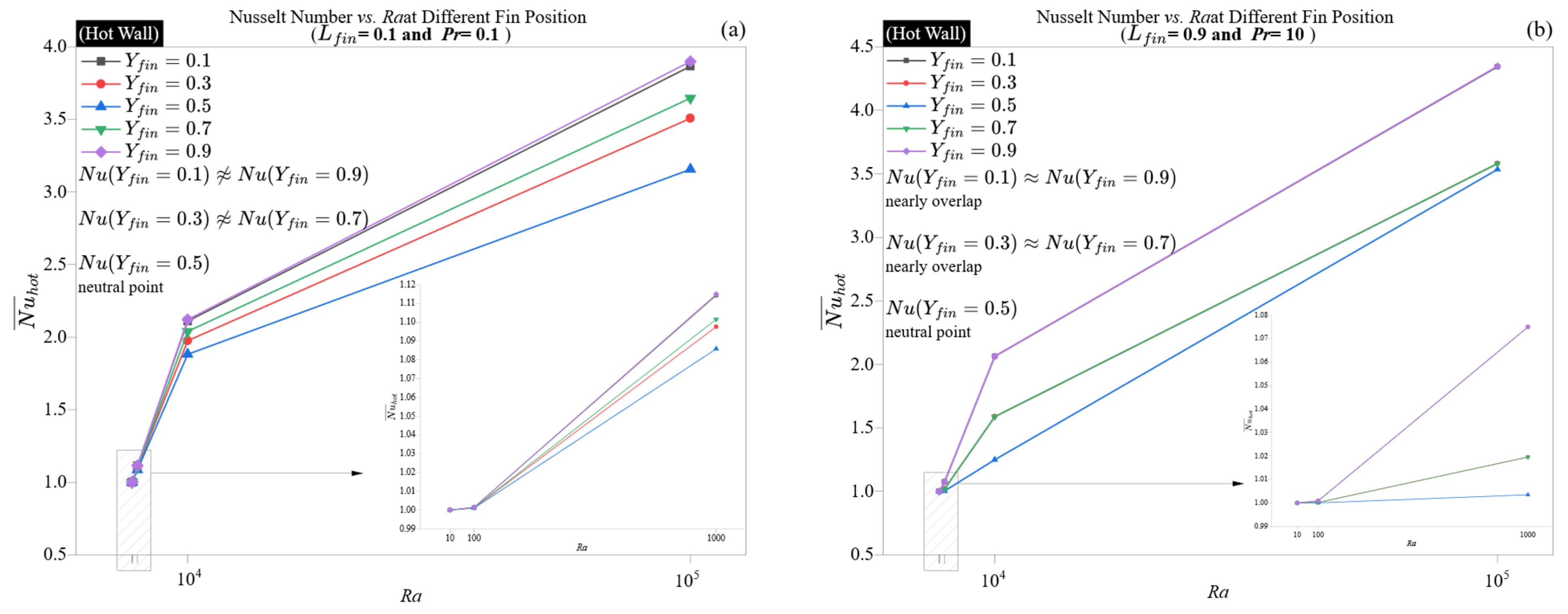
At low Rayleigh numbers (Ra = 10), the Nusselt numbers for both the hot and cold walls stay close to one, independent of fin position or fluid characteristics. This consistent behavior, observed in all panels, underscores the prevalence of conductive transport and the lack of sensitivity of thermal gradients to geometric changes in these conditions.

As Ra increases to 10² and 10³, the Nusselt number starts to display spatial variation. In conditions with low Prandtl numbers and short fins, as shown in Figure 11a and Figure 12a, peak Nusselt number values are observed near the vertical boundaries (Y_fin = 0.1 and 0.9). In contrast, the centerline positioned fin (Y_fin = 0.5) consistently shows lower values. At higher Rayleigh numbers, the Nusselt number demonstrates a clear U-shaped dependence on fin position, especially in the Pr = 10, long-fin scenario, as shown in Figure 11b. For example, at Ra = 10⁵, the Nusselt number achieves a maximum of 4.35 at the cavity edges (Y_fin = 0.1 and 0.9) but falls to a minimum of 3.53 at the center (Y_fin = 0.5). This pattern indicates a gradual restriction of convective movement to the sidewalls, as the central plume becomes more obstructed by long fins, while outer positions retain better thermal accessibility. This trend is characteristic of natural convection systems with steep thermal gradients and slender boundary layers. The center-mounted fins disrupt the symmetry of the plume, causing stagnation and a decrease in the Nusselt number. In contrast, edge-aligned fins align with the main upwash and either contribute positively or remain neutral.

The pattern becomes more pronounced at Ra = 10⁴ and 10⁵. In the high-Pr, long-fin scenario (Figure 11b and Figure 12b, the hot wall displays a steep Nusselt number gradient from mid-position (Y_fin = 0.5: $\overline{Nu}$ ≈ 3.53) to the bottom and top edges (Y_fin = 0.1 or 0.9: $\overline{Nu}$ ≈ 4.34). This variation of 22.5% suggests that, in conditions of strong buoyancy and thin thermal layers, the placement of the fin is a crucial factor in controlling the outcome. By positioning a long fin at the centerline, a considerable obstruction is created for the vertical plume core, thereby decreasing the Nusselt number, even with favorable fluid characteristics. Conversely, the edge-aligned fin enhances the boundary layer’s curvature, facilitating localized extraction and maintaining the flow’s coherence.

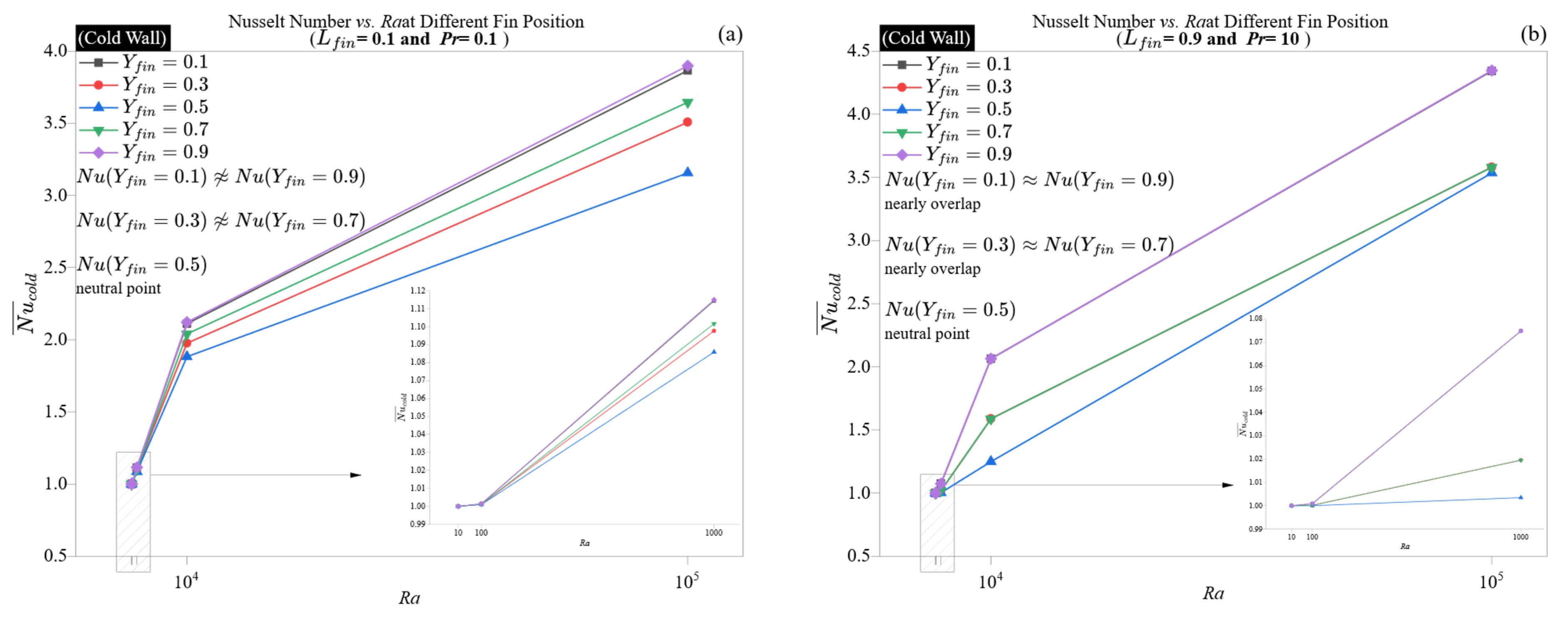
The cold wall (Figure 12a,b) closely reflects these dynamics; however, the peak Nusselt number values are slightly lower, and the U-shaped trend is somewhat less pronounced. This asymmetry arises from the cold wall receiving pre-conditioned, upward-moving fluid. Although the upstream fin location still impacts the Nusselt number at the cold wall, its effect is somewhat moderated by the plume’s downstream inertia. Nevertheless, the correlation between hot and cold wall behavior, particularly at high Ra and Pr, illustrates that the fin position determines convective accessibility, independent of the thermal boundary orientation.

A significant nonlinear effect noted at high Ra is the reversal of geometric penalty in long-fin, high-Pr setups. Although longer fins usually reduce the Nusselt number due to flow obstruction, careful positioning near edges can completely recover or even surpass central values seen in short-fin, low-Pr configurations. For example, at Ra = 10⁵, Pr = 10, and Y_fin = 0.9, the hot wall reaches a $\overline{Nu}$ of 4.35, exceeding the value of 3.87 that is obtained in the short-fin scenario at Pr = 0.1, Y_fin = 0.1. This illustrates the crucial role of aligning high thermal gradients with low-obstruction geometries to enhance fin performance.

In conclusion, these findings indicate that the position of fins becomes a vital design factor only when convective transport is well established, particularly at Ra ≥ 10³ and Pr ≥ 1. In such scenarios, fins located close to the wall boundaries (either top or bottom) take advantage of the flow’s natural curvature, whereas fins situated at mid-height may disrupt vertical consistency and diminish thermal efficiency. Consequently, the interaction between Pr, Ra, and Y_fin establishes a geometric-performance framework for optimizing thermal design in natural convection systems.

Figure 13 and Figure 14 provide a detailed analysis of how fin length (L_fin = 0.1 to 0.9) affects the Nusselt number on both hot and cold walls. This is examined at fixed fin positions and two thermophysical extremes: a low Prandtl number with a bottom-aligned fin (Figure 13a and Figure 14a) and a high Prandtl number with a top-aligned fin (Figure 13b and Figure 14b).

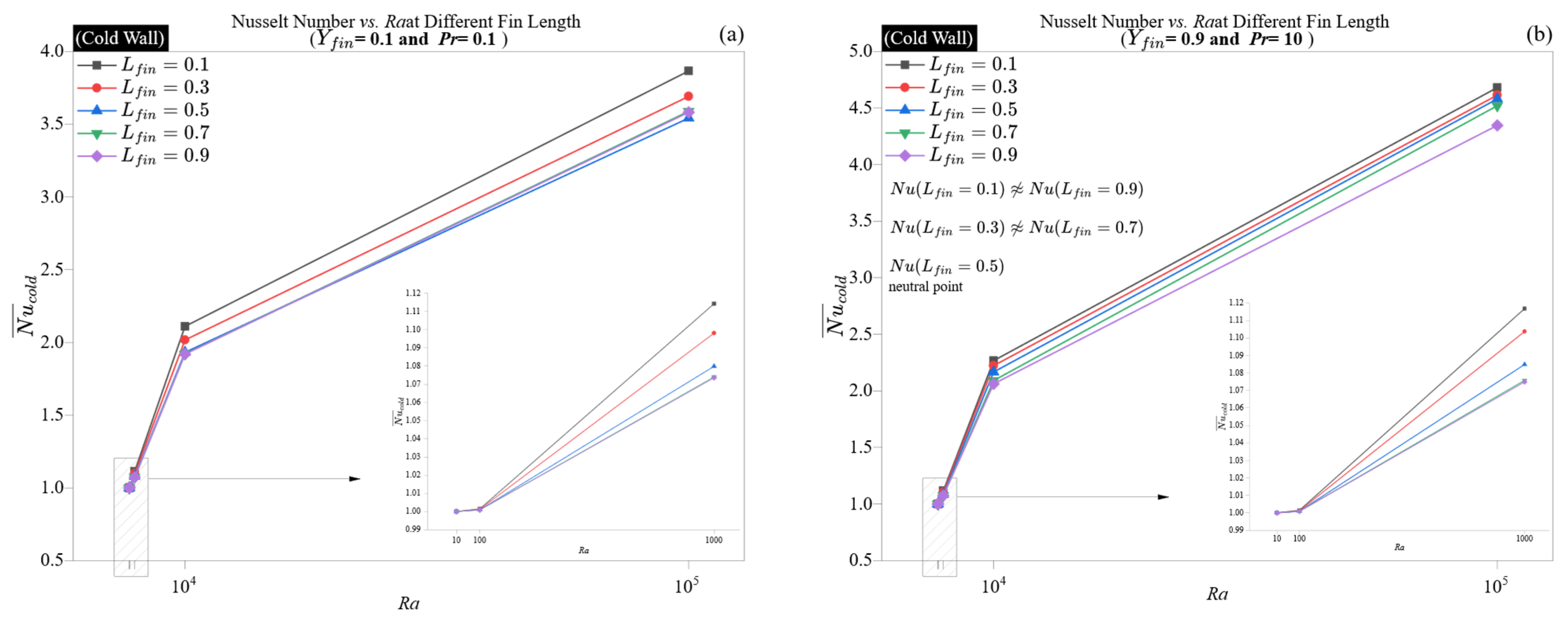
At a low Rayleigh number (Ra = 10), the Nusselt number stays close to one for all fin lengths, indicating that the system is primarily conduction-dominated and unaffected by geometric variations, regardless of thermal diffusivity. This is illustrated by the behavior of both hot and cold walls, where the Nusselt number changes by less than 0.001 between fin _lengths of 0.1 and 0.9 for Pr = 0.1.

As Ra increases to 100 and 1000, a non-monotonic pattern starts to appear, especially at Pr = 10. For instance, in Figure 13b, at Ra = 1000, the Nusselt number for the hot wall peaks at shorter lengths (L_fin = 0.1: ${\overline{Nu}}_{hot}$ ≈ 1.1168) and then decreases for intermediate lengths (L_fin = 0.5: ${\overline{Nu}}_{hot}$ ≈ 1.0848), while it slightly recovers at the longest length (L_fin = 0.9: ${\overline{Nu}}_{hot}$ ≈ 1.0748). This indicates that intermediate-length fins create a disruption zone that neither fully engages with nor avoids the primary convective streamlines, resulting in localized recirculation or thermal shadowing. Conversely, short fins cause minimal interference, whereas very long fins, situated near the thermal boundary (Y_fin = 0.9), align more effectively with the curvature of the boundary layer and prevent central blockage.

At elevated buoyancy forces (Ra = 10⁴ and 10⁵), the Nusselt number increases significantly with Ra across all fin lengths, with sensitivity to fin length becoming distinctly pronounced. In the high-Pr scenario (Figure 13b, the Nusselt number values range from 2.27 (L_fin = 0.1) to 2.06 (L_fin = 0.9) at Ra = 10⁴ and from 4.68 to 4.35 at Ra = 10⁵. This 7–10% reduction demonstrates how excessively long fins can hinder wall-normal momentum transfer, particularly in regions where the thermal plume rises most intensely. The behavior observed at the cold wall, as shown in Figure 14b, exhibits a similar trend but with slightly reduced magnitudes, further confirming the secondary thermal influence of the downstream boundary.

Conversely, at Pr = 0.1, the impact of fin length is significantly milder. In Figure 13a, even when Ra = 10⁵, the Nusselt number only slightly decreases from 3.87 at L_fin = 0.1 to 3.58 at L_fin = 0.9. This suggests that in low-Pr fluids, the thicker thermal boundary layers reduce the obstructive effects of fin geometry, enabling longer fins to work alongside vertical transport without causing significant flow bifurcations.

A detailed examination shows that mid-length fins (L_fin = 0.5) create local minima in the Nusselt number on both hot and cold walls, regardless of the Pr values. This indicates that L_fin = 0.5 disrupts the plume core most effectively, failing to skim the wall or deeply realign flow trajectories. This optimal point for disruption aligns with previous findings about fin position but is now emphasized in the axial (vertical) direction.

Overall, the findings indicate that fin length is a crucial design factor mainly at intermediate-to-high Rayleigh numbers and elevated Prandtl numbers. In these scenarios, long fins can cause significant interference if they are not properly placed. In contrast, in low-Pr fluids or under low Rayleigh number conditions, thermal diffusion prevails, reducing the effects of geometrical extension.

4.6. Summary of Design Implications for Passive Thermal Enhancements

A detailed parametric investigation into the Rayleigh number, Prandtl number, fin geometry, and material conductivity reveals several essential design principles for enhancing passive thermal performance in natural convection settings.

Initially, the efficiency of fin-based enhancements is significantly influenced by the flow regime. At low Rayleigh numbers (Ra ≤ 10²), variations in fin geometries result in minimal changes to the Nusselt number, regardless of the Prandtl number or fin positioning. This consistency demonstrates that conductive regimes do not respond to geometric alterations, indicating that incorporating fins is thermally unnecessary unless radiative or transient effects are predominant.

In comparison, at moderate-to-high Rayleigh numbers (Ra ≥ 10³), the relationship between fin placement and convective plume development becomes crucial. Fins located close to the bottom (Y_fin = 0.1) enhance upward thermal entrainment and benefit from organized flow development, especially in high-Prandtl fluids. On the other hand, fins positioned at mid-height (Y_fin = 0.5) consistently hinder heat transfer across all fin lengths, with reductions of up to 22% compared to edge-aligned configurations. This is due to the disturbance of core plumes, the splitting of recirculating cells, and the thickening of the thermal boundary layer around the obstruction.

The analysis indicates that fin length does not consistently enhance or diminish performance. Short fins (L = 0.1) offer slight improvements by causing localized plume separation without significant blockage. Mid-length fins (L = 0.5) typically align with the thermal plume’s core and serve as partial barriers, particularly under strong buoyancy. Long fins (L = 0.9) can improve performance if situated near the sidewalls, taking advantage of the flow path’s curvature, but become harmful when positioned centrally.

The thermal conductivity ratio between the fin and the fluid influences whether the fin serves as a thermal bridge or an insulator. When k_fin/k ≤ 1, fins slightly hinder global heat transfer by redirecting flow but do not enhance thermal conduction. Conversely, if the fin’s conductivity is significantly higher (k_fin/k ≥ 10), it aids in heat extraction, provided it does not significantly disrupt the geometry.

Collectively, these findings indicate that effective high-performance passive designs should utilize short or tapered fins made of materials with high thermal conductivity, positioned near vertical boundaries where flow gradients are the steepest. Steering clear of mid-wall placements and excessive fin length reduces convective interference while maintaining the advantages of surface extension. These principles remain effective across a broad spectrum of fluid properties and natural convection strengths, offering a practical framework for geometrically simple yet thermally efficient passive enhancements.

5. Conclusions

This study presents a detailed numerical analysis of the interaction between fin geometry, fluid characteristics, and the strength of natural convection in square enclosures. More than 9000 simulations were performed to derive a predictive understanding of heat transfer behavior by systematically varying the Rayleigh number (10 ≤ Ra ≤ 10⁵), Prandtl number (0.1 ≤ Pr ≤ 10), and fin attributes, including length, position, thickness, and thermal conductivity ratio. The analysis focused on both average and local Nusselt numbers, as well as a Nusselt Number Ratio (NNR), to assess the thermal enhancement or suppression effects resulting from the embedded fins.

The main findings of the study are as follows:

• Geometry-Convection Coupling: In conditions of weak convection (Ra ≤ 10²), the design of the fins has little effect, and heat transfer is primarily governed by conduction and symmetry. However, when convection becomes the dominant factor (Ra ≥ 10³), the configuration and length of the fins have a significant impact on thermal effectiveness. Short, edge-aligned fins can boost hot-wall Nusselt numbers by as much as 8.4%. In contrast, long fins positioned centrally may decrease heat transfer by up to 11.8%, primarily due to plume bifurcation and the disruption of vertical circulation.
• U-Shaped Sensitivity: The research found a strong U-shaped trend in heat transfer sensitivity related to fin position, especially at elevated Rayleigh numbers. Fins positioned near the top or bottom edges consistently perform better than those set at mid-height, and this outcome is consistent across all Prandtl numbers and conductivity ratios.
• Material Conductivity Effects: Although fins made of materials with high thermal conductivity (like k_fin/k = 100 or 1000) offer excellent heat conduction paths initially (for instance, achieving an NNR of up to 2.11 at Ra = 10), their advantages significantly decrease as Ra increases because of disruption in buoyant flow structures. This indicates that conductivity alone is insufficient for optimization, as geometric compatibility becomes the limiting factor.
• Prandtl Number Influence: Fluids with a higher Prandtl number, characterized by thinner thermal boundary layers, demonstrate increased sensitivity to fin design. They benefit significantly from optimal arrangements, but they also face greater drawbacks from flow disturbances due to improperly positioned fins.
• Design Recommendations: To achieve substantial passive enhancement, the most effective approach involves using short, highly conductive fins placed close to top or bottom boundaries. These areas typically exhibit steep thermal gradients and coherent convective plumes. Mid-height and long fins should generally be avoided, especially in high Ra and high Pr environments, as they tend to block core convective currents and create thermal stagnation zones.

Quantitatively, the benefits of high-conductivity fins (k_fin/k ≥ 100) diminish at high Rayleigh numbers due to geometric interference with buoyant structures, with performance asymptotically saturating around k_fin/k ≈ 1000. Although the current study considers a single horizontal fin, the qualitative insights, such as the sensitivity to placement, the performance decline at mid-height, and the dominance of geometry over conductivity at high Ra, are expected to extend to multi-fin systems, especially when fins are spaced to avoid hydrodynamic interference.

This research offers a thermogeometric design map that enables more informed decisions when integrating passive fins into natural convection systems. The research findings also highlight a practical trade-off between maximizing total heat transfer and optimizing geometric efficiency. The present study shows that fin placement near the top or bottom of the cavity enhances absolute heat transfer by aligning with dominant convective pathways and avoiding central plume disruption. However, as demonstrated in previous work [24], mid-height fin placement may offer better thermal performance relative to added surface area, as quantified by the Nusselt Number Ratio (NNR). This suggests that in large-scale or high-power systems, edge-aligned fins are advantageous for maximizing total thermal output. In contrast, in constrained or miniaturized systems where surface area or material use must be minimized, mid-height fins may offer a more efficient use of geometric additions. Designers should select fin configurations based on whether the objective is to maximize raw thermal throughput or to optimize heat transfer per unit of fin geometry. For instance, these findings can be applied directly to the optimization of heat transfer in electronics cooling, solar thermal collectors, battery packs, and passive building envelopes.

While the present study focuses on steady-state, two-dimensional enclosures, the qualitative trends, such as plume interference, edge-aligned fin superiority, and diminishing returns of high-conductivity fins at high Ra, are expected to hold in three-dimensional and transient extensions. Future work should explore multi-fin configurations, transient thermal loads, and three-dimensional geometries to extend these insights into more complex or practical applications.