Methods for Measuring and Computing the Reference Temperature in Newton’s Law of Cooling for External Flows
Abstract
1. Introduction
- should equal where and vice versa (referred to as Requirement A). If this requirement is not satisfied at any location on the solid’s surface (i.e., but ), then will be undefined at those locations.
- should be continuous across (referred to as Requirement B). For Requirement B to be met, the limit of must approach the same value as approaches from higher or lower temperatures. Note that Requirements A and B are connected because if Requirement A is satisfied, then Requirement B is satisfied and vice versa.
- The method for measuring or computing and should yield a unique and a unique at each location on the cooled or heated surface (referred to as Requirement C).
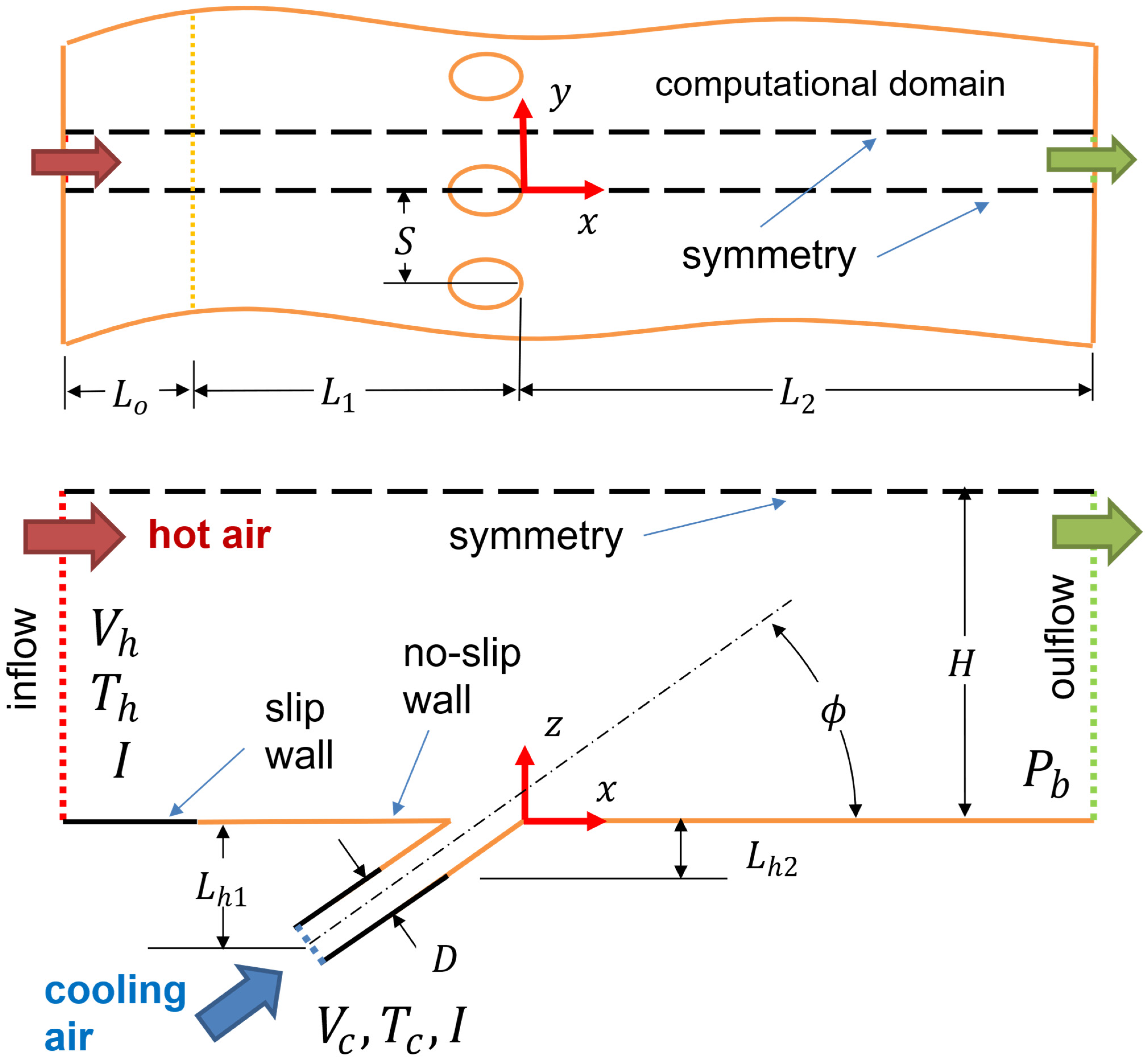
2. Problem Description
3. Problem Formulation and Numerical Method of Solution
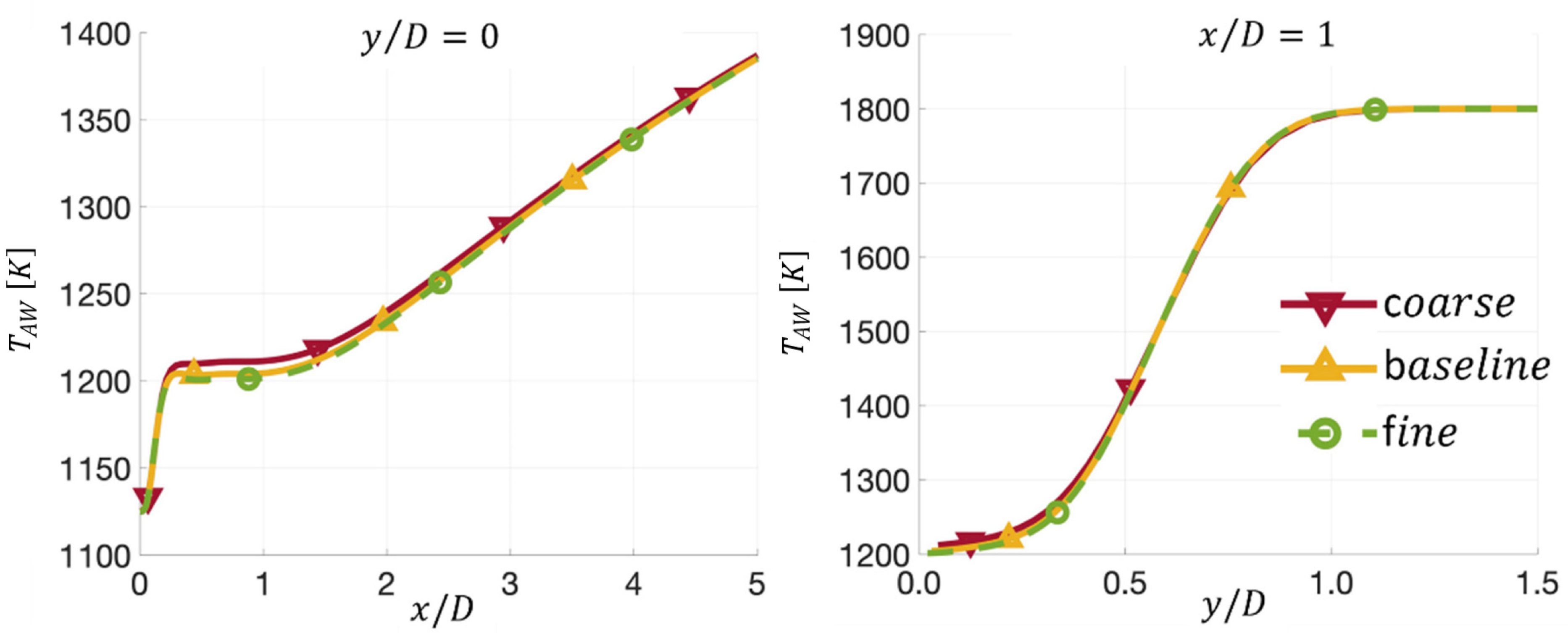
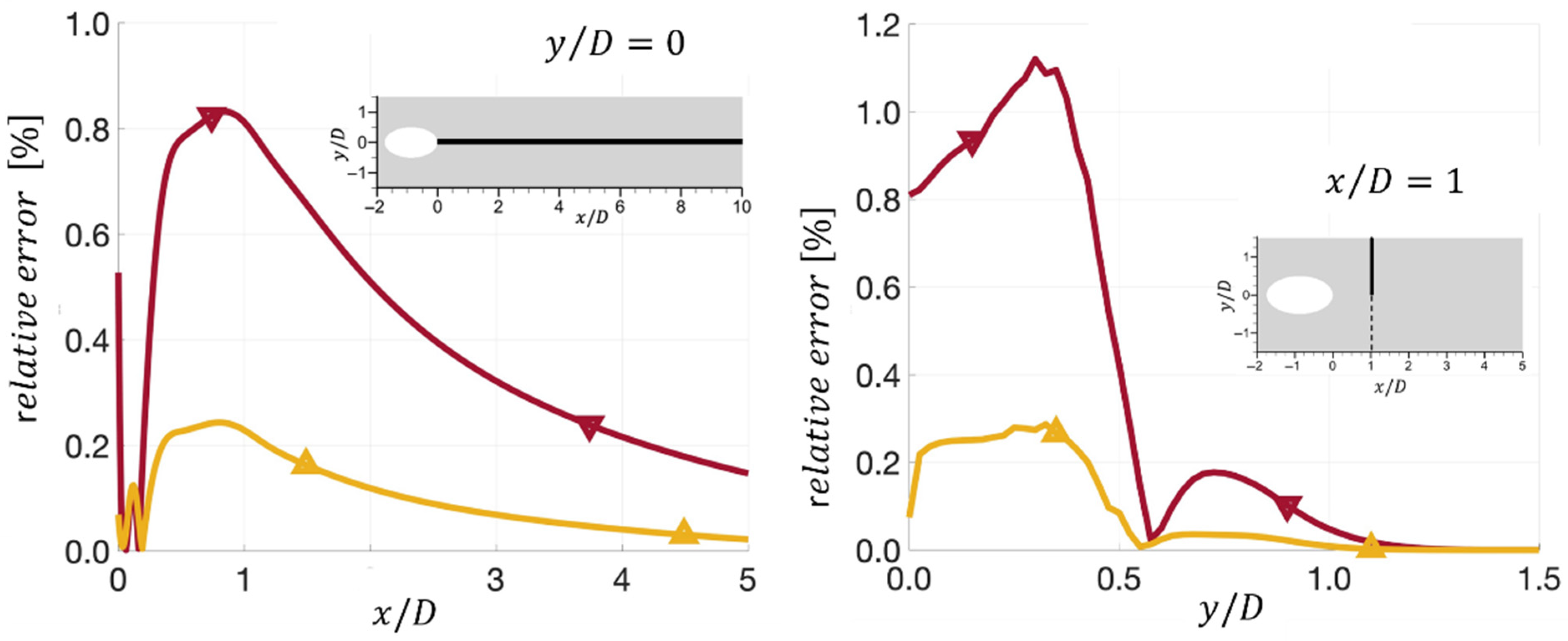
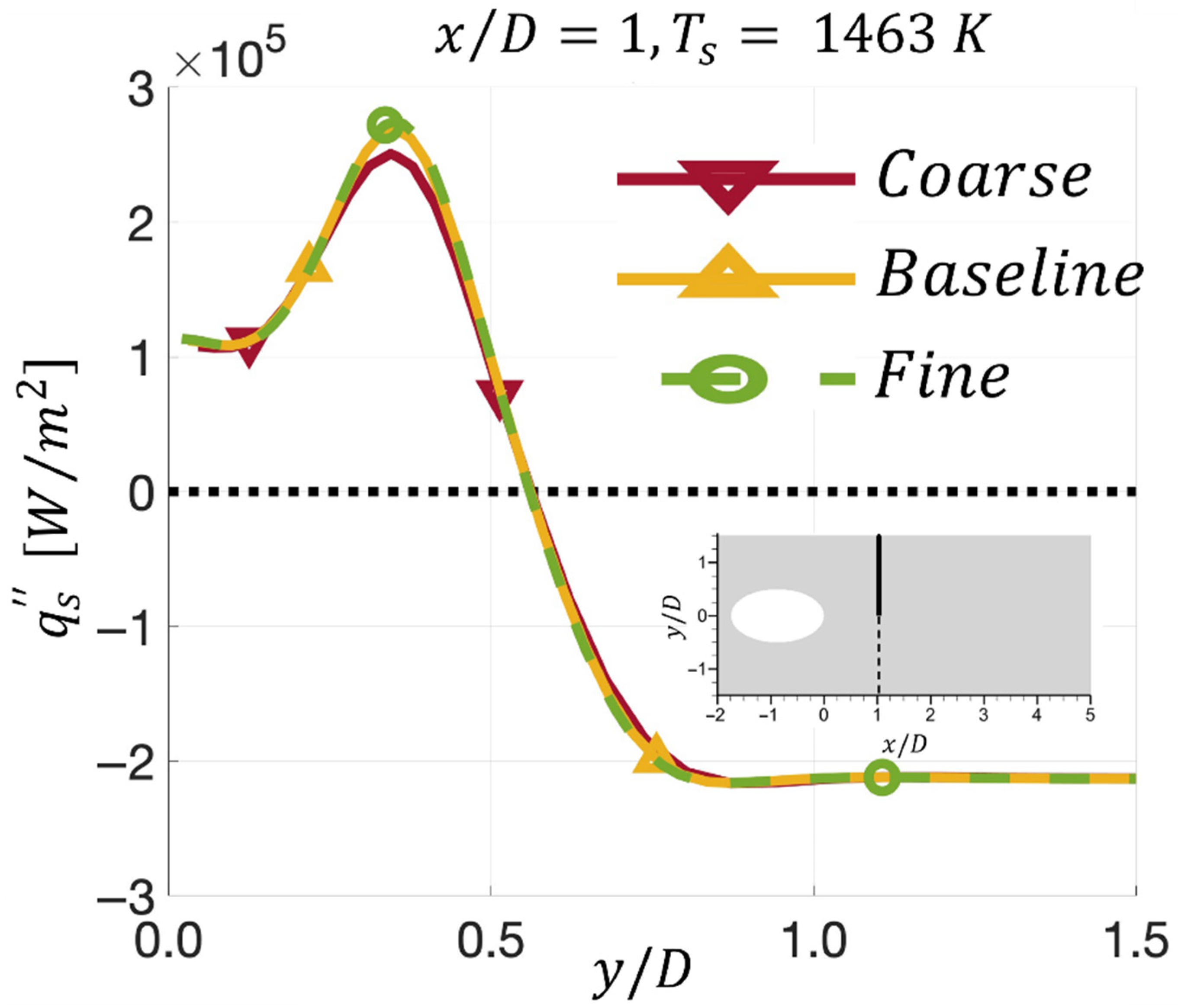
4. Grid Sensitivity Study
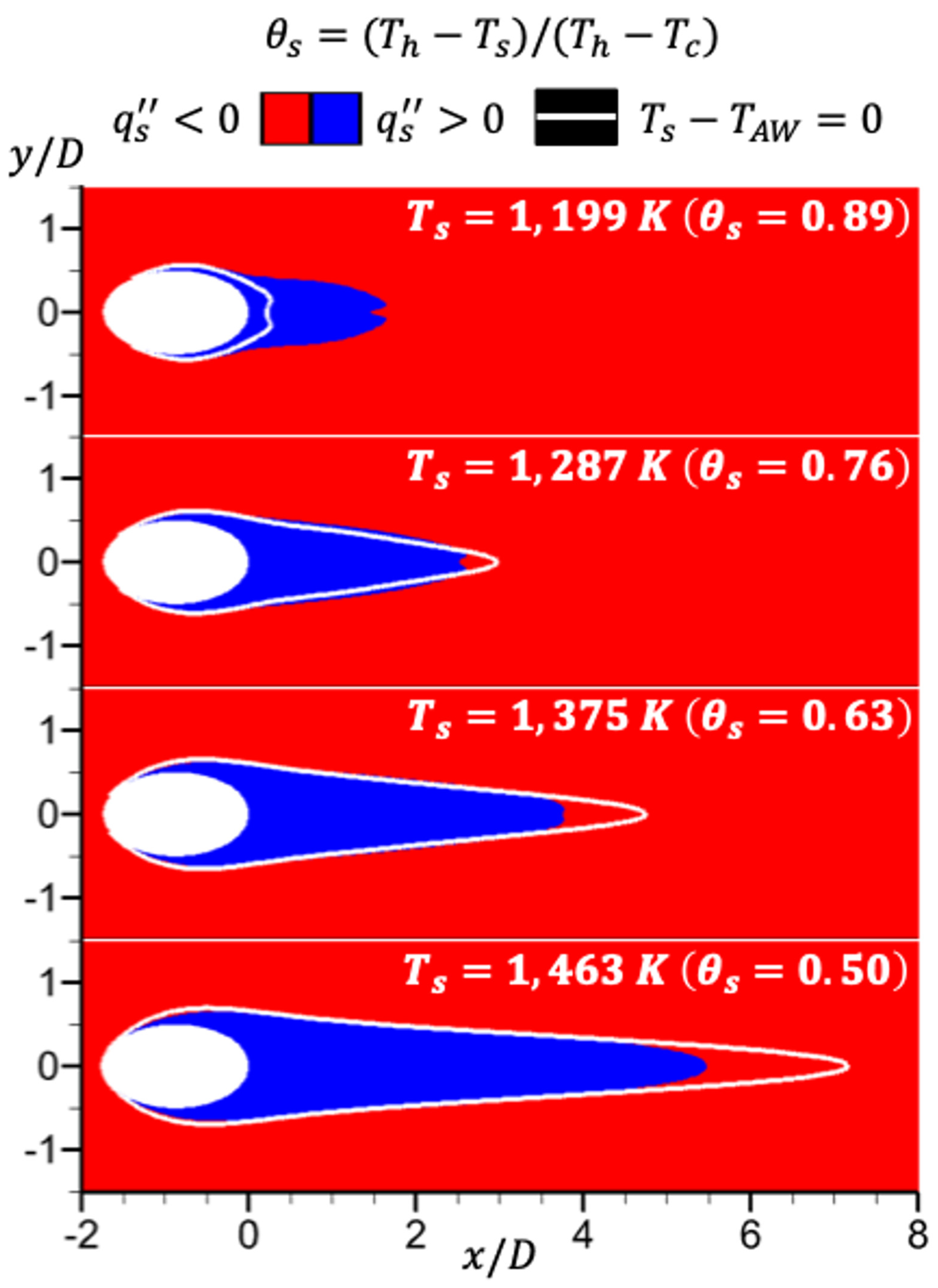
5. Results
5.1. Obtained by the Adiabatic-Wall (AW) Method
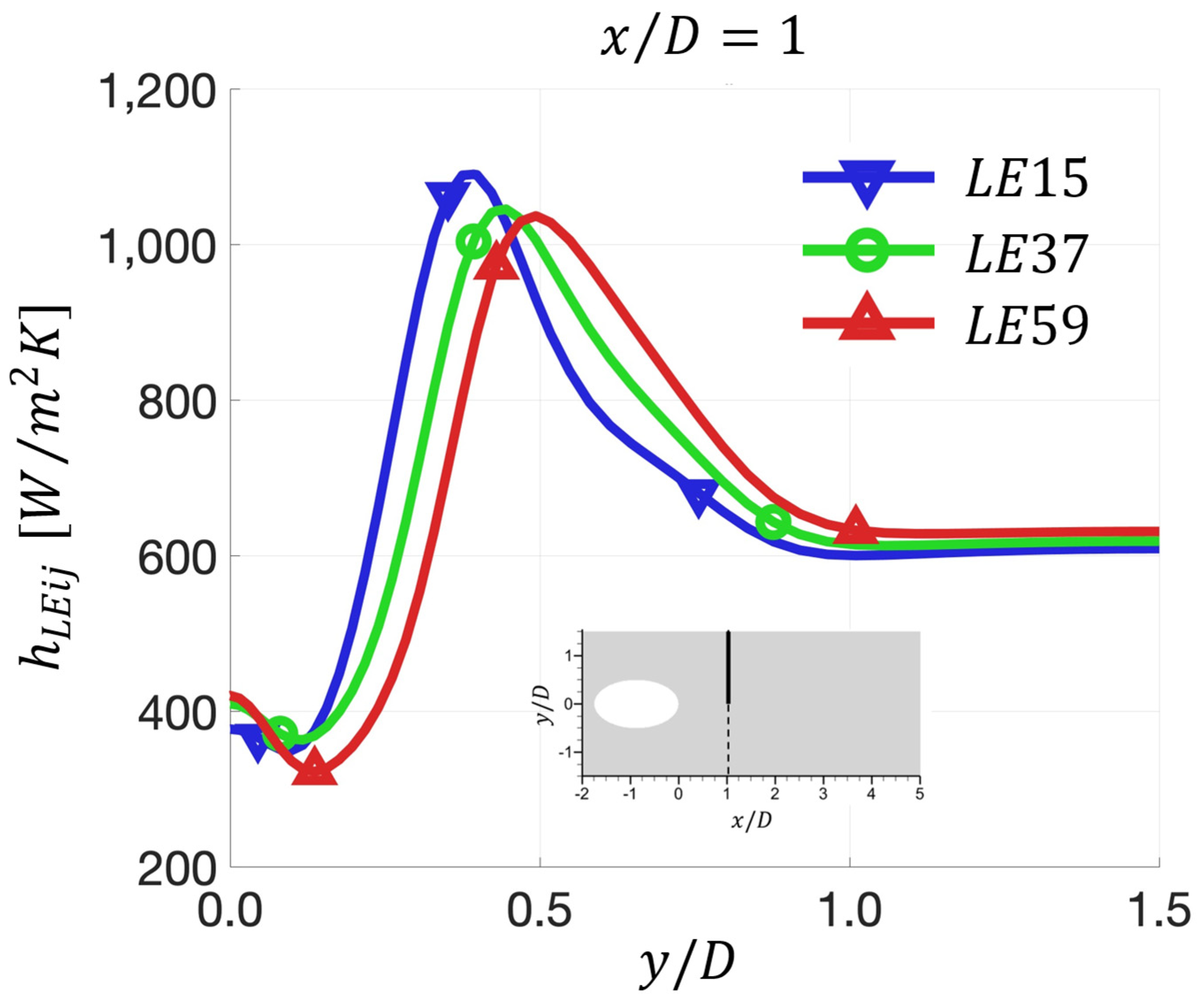
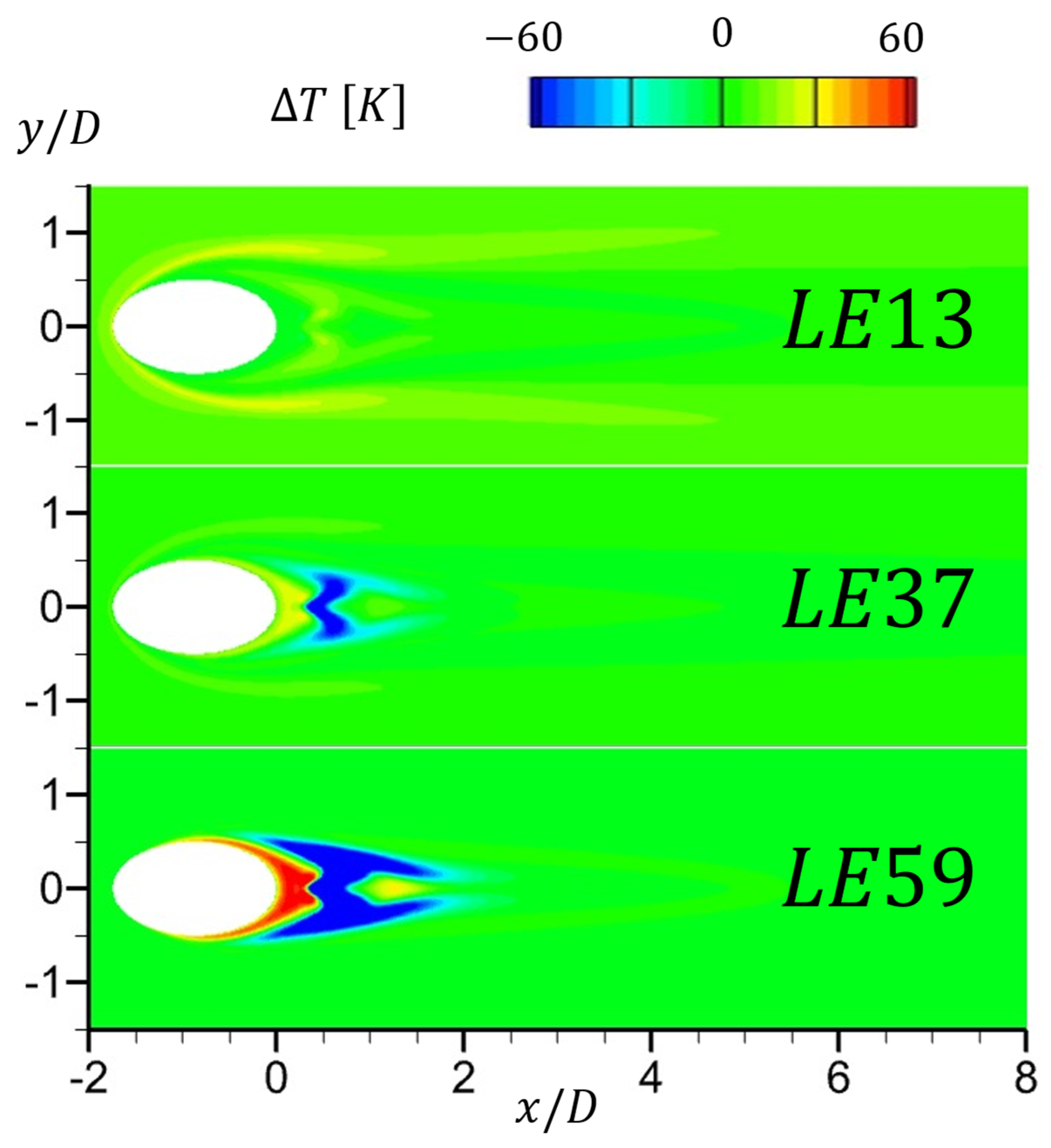
5.2. Obtained by the Linear-Extrapolation (LE) Method
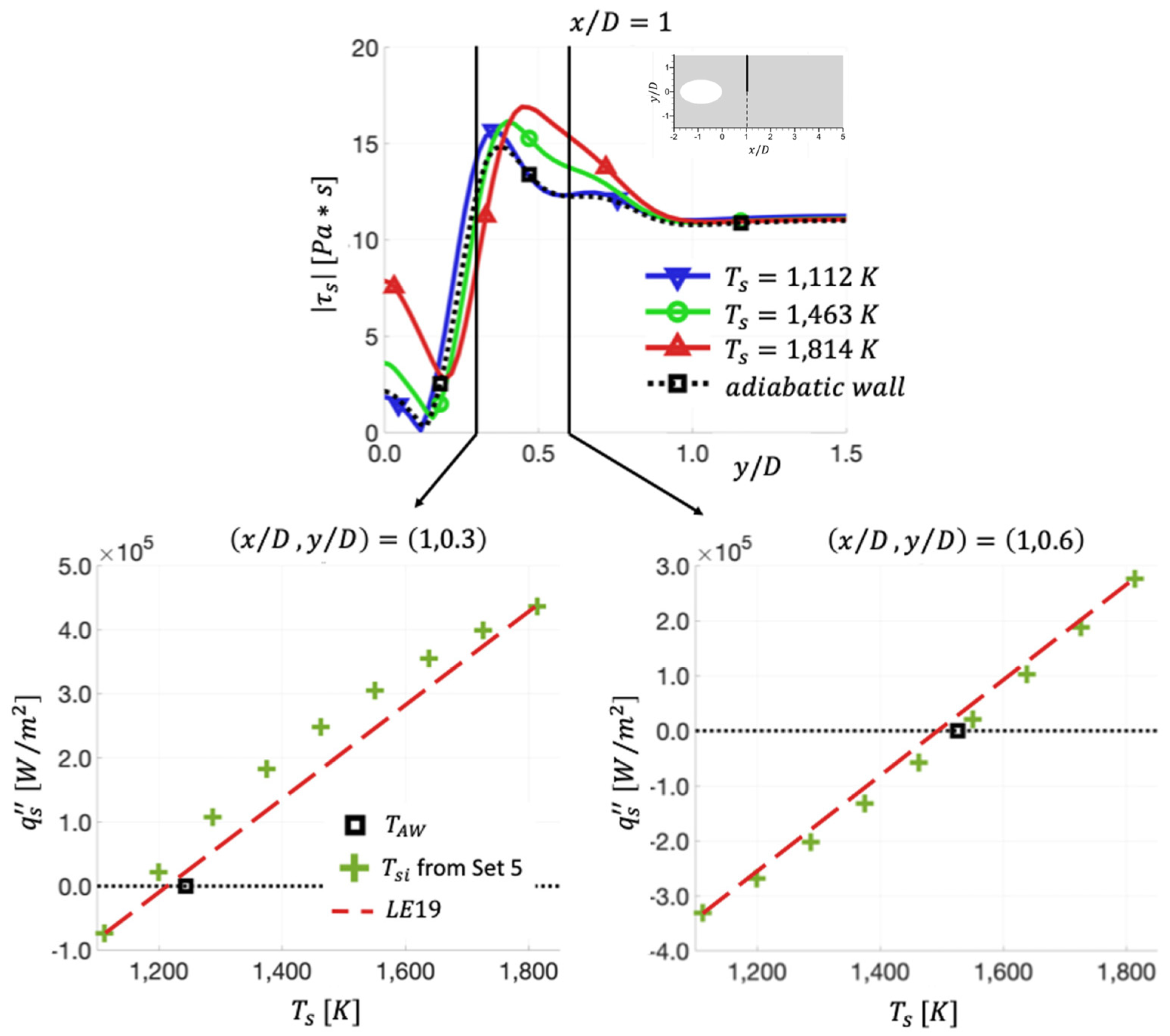
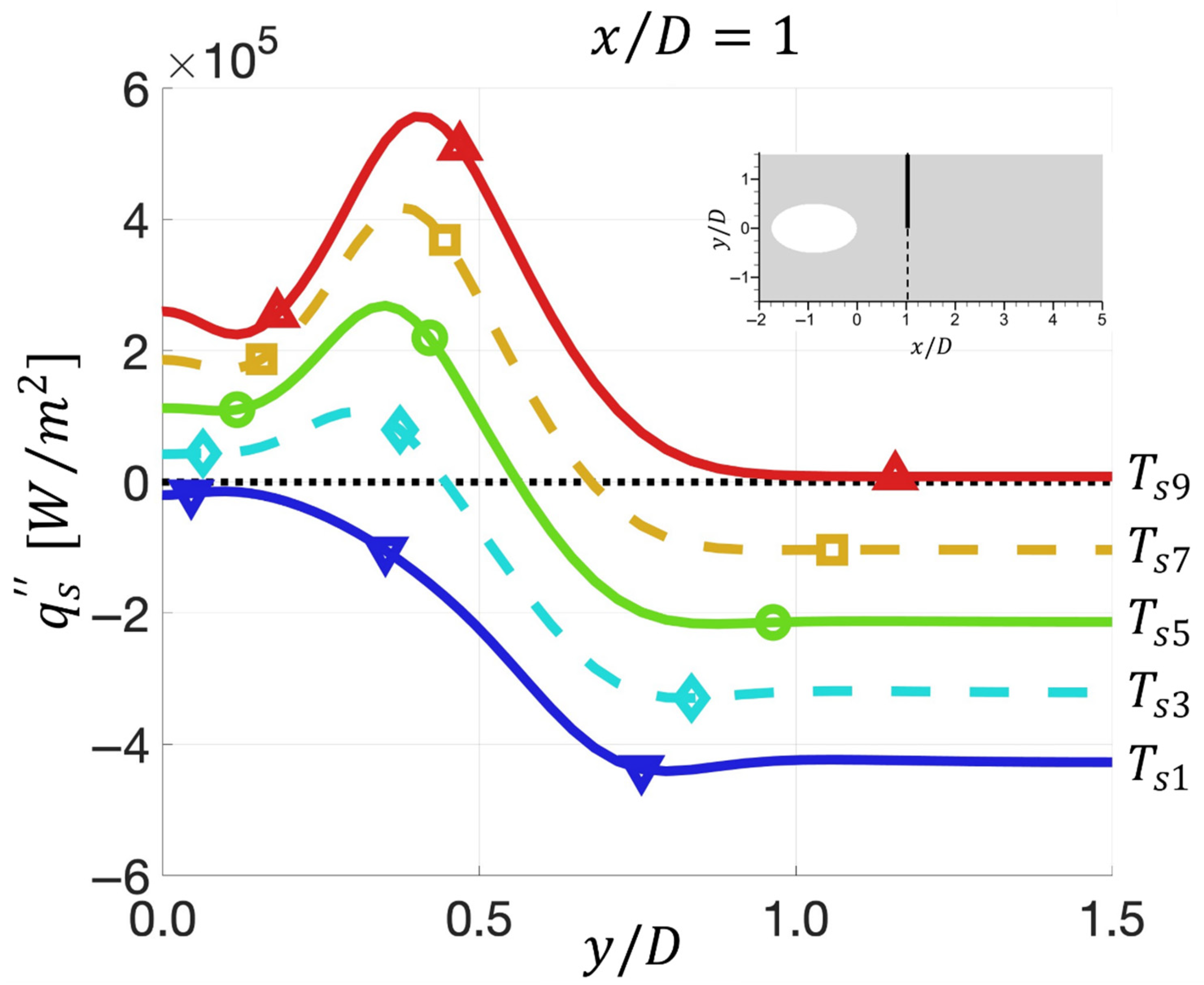
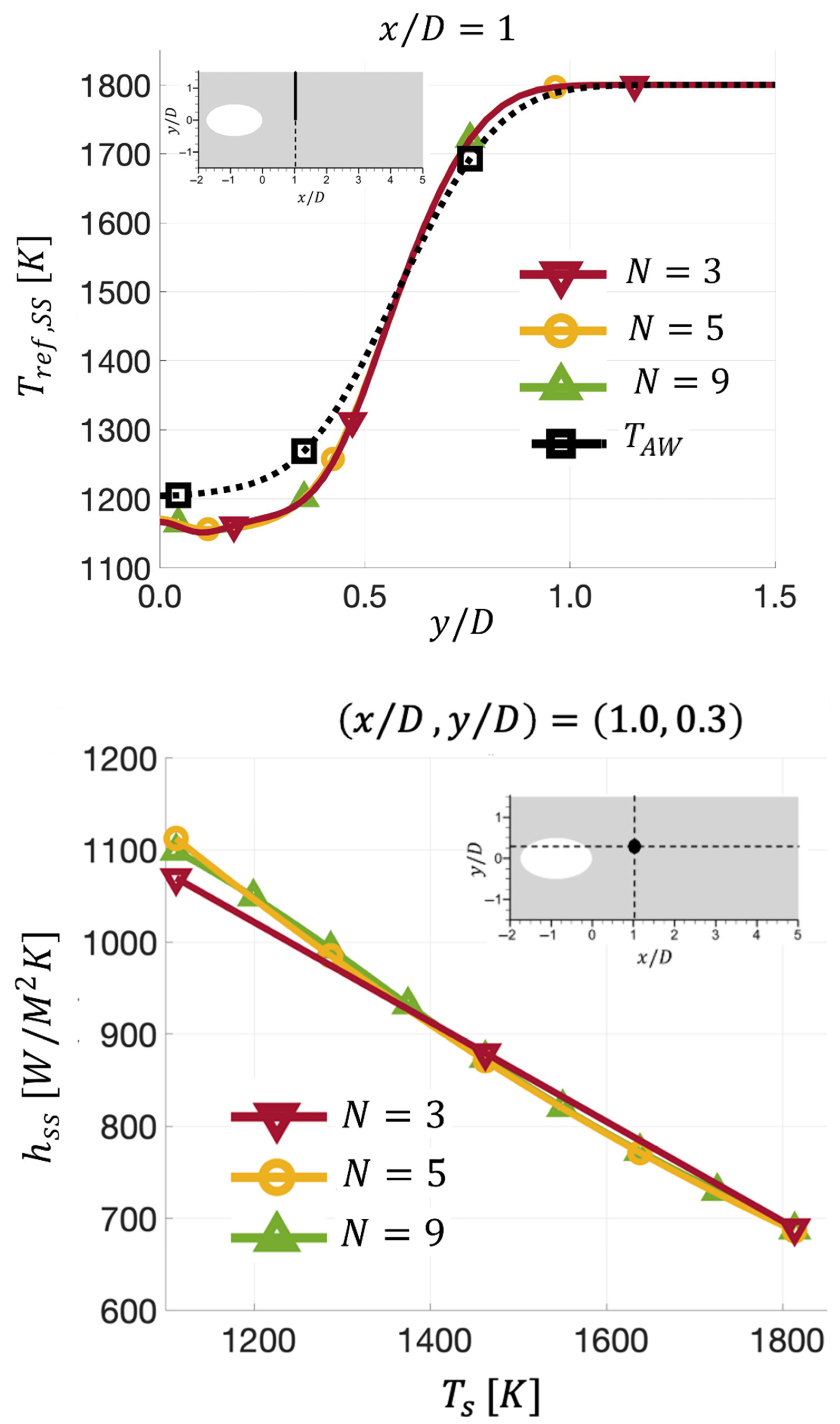
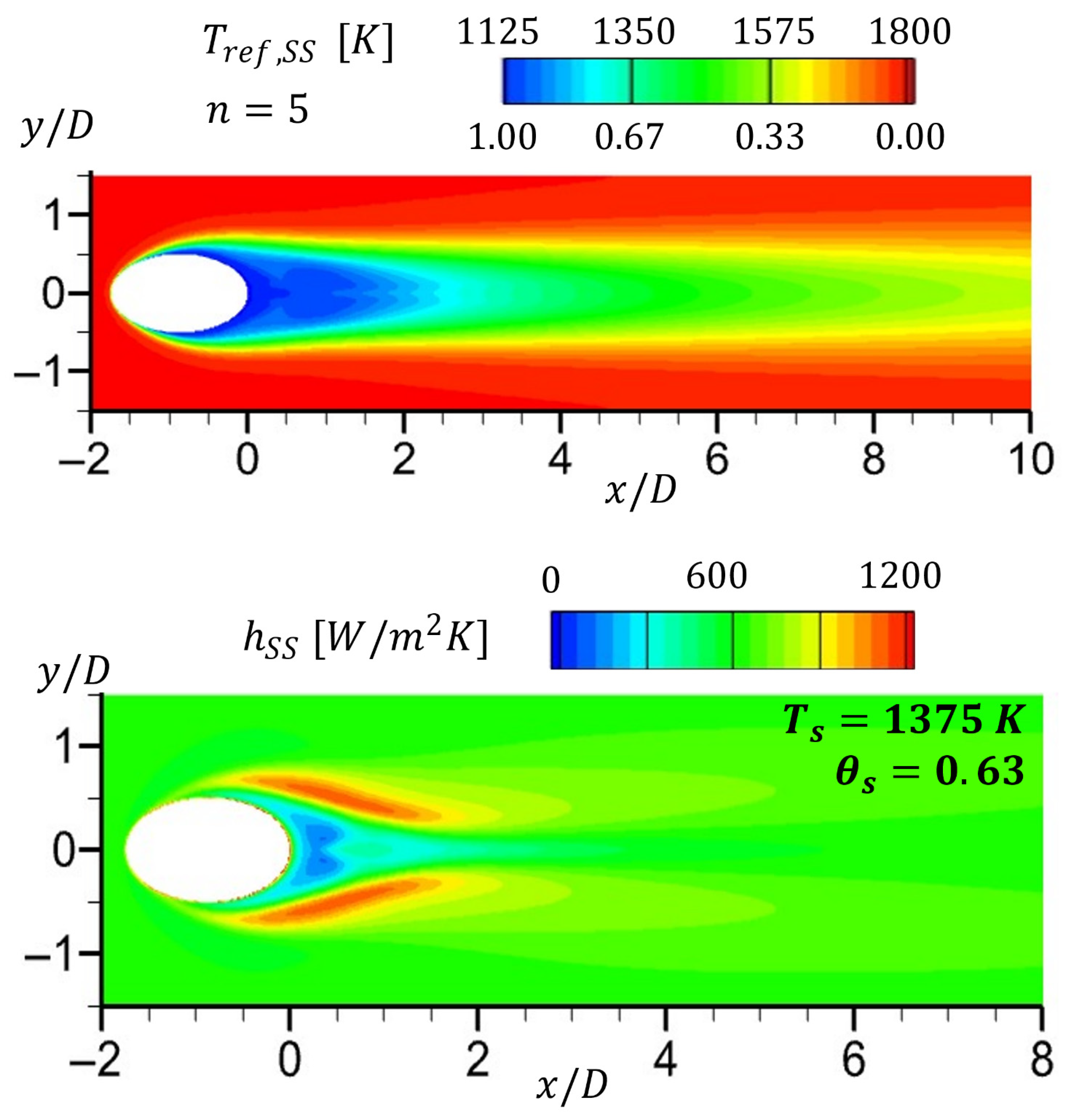
5.3. Obtained by the State-Space (SS) Method
- 1.
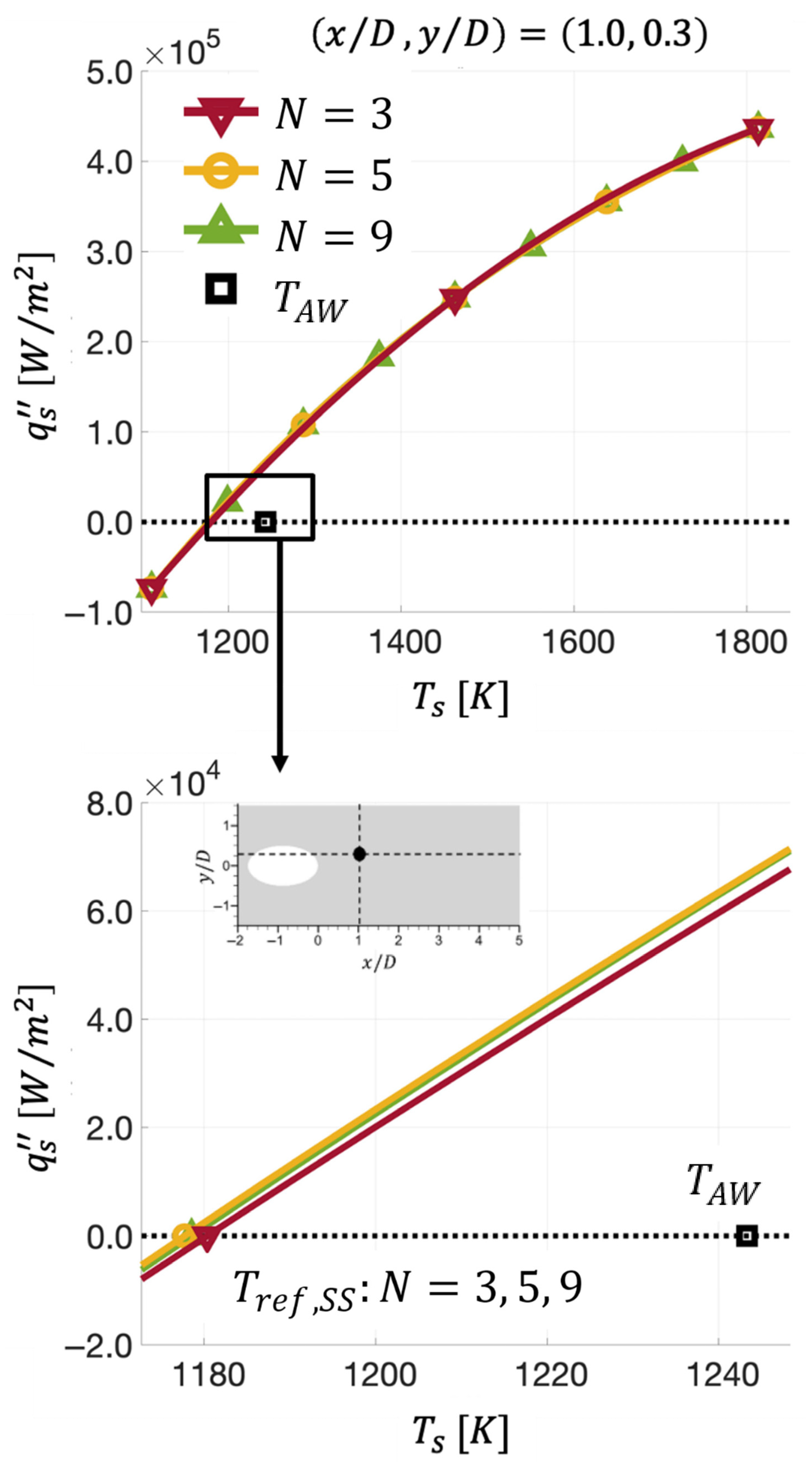
- The first step is to discretize in Equation (9) to produce isothermal-wall temperature states, denoted as , where . The states chosen must include one temperature lower than the lowest temperature in the flow field (i.e., ) and one temperature higher than the highest temperature in the flow field (i.e., ) to ensure that the entire state space is accounted for. In this study, Equation (9) was discretized as follows:where , , and . Note that , which is lower than , and , which is higher than Equation (11) with includes all values given in Table 1.
- 2.
- The second step is to compute or measure at every point on the surface of the film-cooled plate with isothermal wall temperature denoted as . Repeat for . If there are uncertainties in the measurements, then multiple measurements should be made for each , and the averaged and should be used in subsequent steps.
- 3.
- The third step is to perform a transfinite interpolation of , at , generated in Step 2, to construct a function G. In this study, cubic spline interpolation was used with the third derivative at and set to the third derivative at adjacent points, corresponding to the “Not-a-Knot” end condition [52].
- 4.
- The fourth step is to use a root-finding routine for the function, G, to find the at every point on the surface that makes . The that makes at is denoted as .
- 5.
- The fifth step is to assign the temperature obtained in Step 4, namely, at , as .
- 6.
- The sixth step is to calculate at every point on the film-cooled surface by using Equation (1). At all locations where , . At locations where and , apply L’Hospital’s Rule so that .
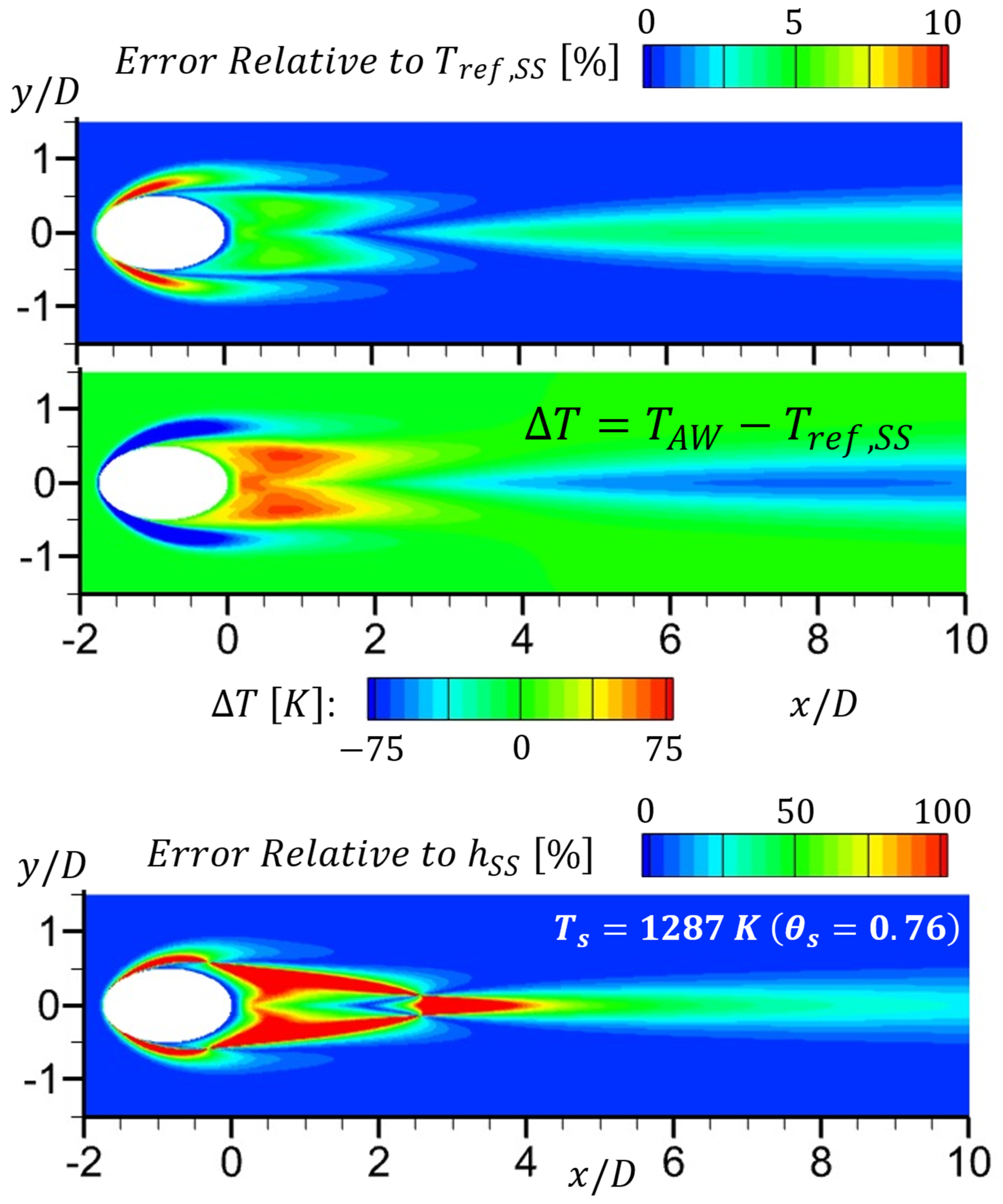
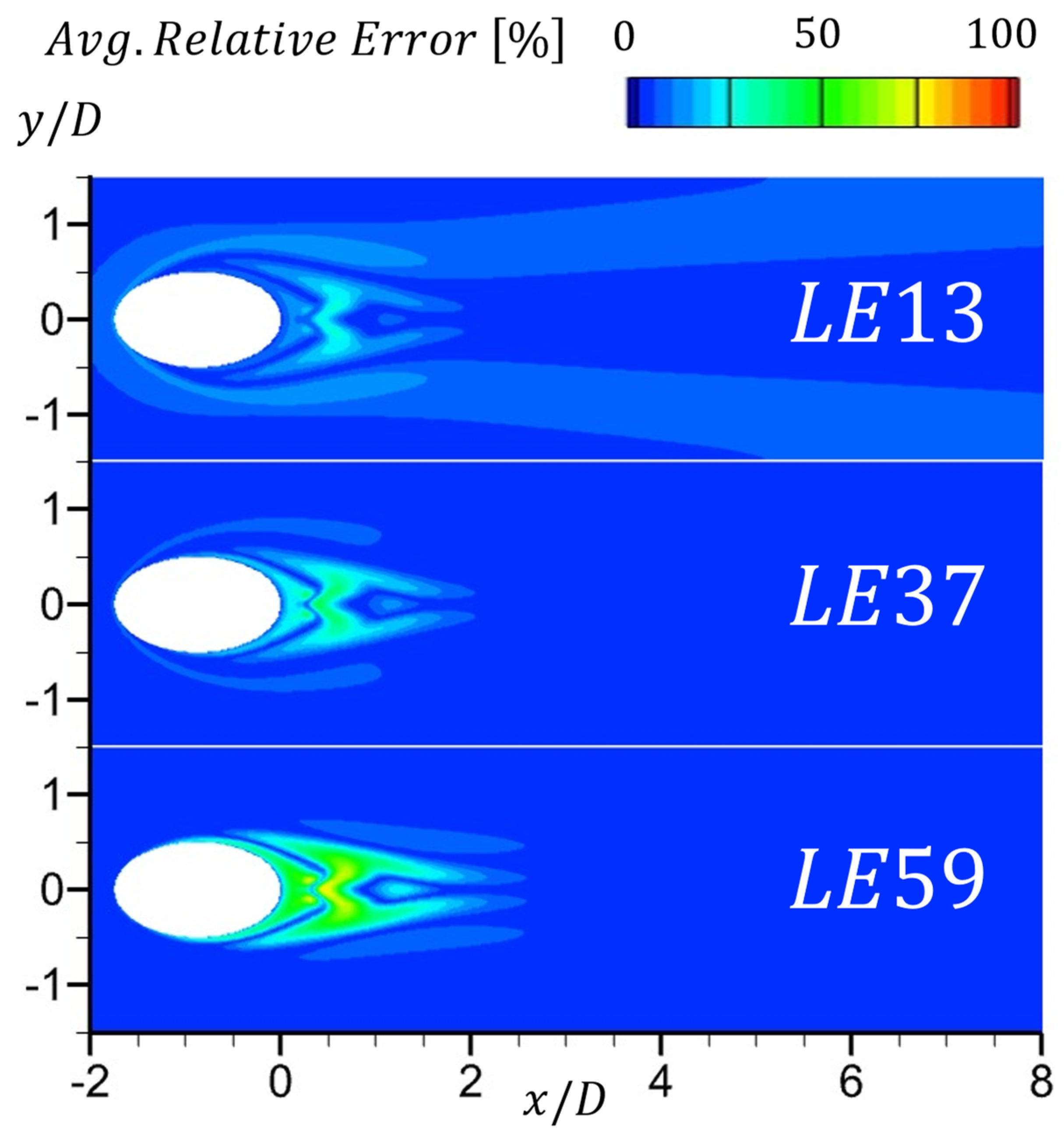
5.4. Errors in Obtained by the AW and LE Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| specific heat at constant pressure | |
| diameter of film-cooling hole | |
| and pair used in the LE method | |
| height of computational domain | |
| heat-transfer coefficient | |
| thermal conductivity | |
| dimensions of the film-cooled flat plate in Figure 2 | |
| static pressure | |
| laminar, turbulent Prandtl number | |
| heat flux on surface exposed to convection | |
| spacing between film-cooling holes | |
| temperature, T of cooling air, T of hot air | |
| adiabatic wall temperature | |
| reference temperature in Newton’s law of cooling | |
| temperature on surface exposed to convection | |
| coordinate axes | |
| non-dimensional : | |
| laminar viscosity | |
| shear stress | |
| film-cooling hole angle with respect to flat plate | |
| variable used to span the state space of |
References
- Kays, W.M.; Crawford, M.E. Convective Heat and Mass Transfer, 2nd ed.; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Goldstein, R.J. Film Cooling. Adv. Heat Transf. 1971, 7, 321–379. [Google Scholar]
- Lin, Y.L.; Shih, T. I-P. Film Cooling of a Semi-Cylindrical Leading Edge with Injection through Rows of Compound-Angled Holes. ASME J. Heat Transf. 2001, 123, 645–654. [Google Scholar] [CrossRef]
- Nastasi, R.; Rosafio, N.; Salvadori, S.; Misul, D.A. Evaluation of Film Cooling Adiabatic Effectiveness and Net Heat Flux Reduction on a Flat Plate Using Scale-Adaptive Simulation and Stress-Blended Eddy Simuylation Approaches. Energies 2024, 17, 2782. [Google Scholar] [CrossRef]
- Ethridge, M.I.; Cutbirth, J.M.; Bogard, D.G. Scaling of Performance for Varying Density Ratio Coolants on an Airfoil with Strong Curvature and Pressure Gradient Effects. ASME J. Turbomach. 2001, 123, 231–237. [Google Scholar] [CrossRef]
- Gritsch, M.; Baldauf, S.; Martiny, M.; Schulz, A.; Wittig, S. The Superposition Approach to Local Heat Transfer Coefficient in High Density Ratio Film Cooling Flows; ASME 99-GT-168; ASME: New York, NY, USA, 1999. [Google Scholar]
- Popp, O.; Smith, D.E.; Bubb, J.V.; Grabowski, H.C., III; Diller, T.E.; Schetz, J.A.; Ng, T.E. Investigation of Heat Transfer in a Film Cooled Transonic Turbine Cascade, Part I: Steady Heat Transfer; ASME Paper 2000-GT-199; ASME: New York, NY, USA, 2000. [Google Scholar]
- Dittmar, J.; Schulz, A.; Wittig, S. Adiabatic Effectiveness and Heat Transfer Coefficient of Shaped Film Cooling Holes on a Scaled Guide Vane Pressure Side Model. Int. J. Rotating Mach. 2004, 10, 345–354. [Google Scholar] [CrossRef]
- Pinilla, V.; Solano, J.P.; Paniagua, G.; Anthony, R.J. Adiabatic Wall Temperature Evaluation in a High Speed Turbine. ASME J. Heat Transf. 2012, 134, 091601. [Google Scholar] [CrossRef]
- Sousa, J.; Villafane, L.; Paniagua, G. Thermal Analysis and Modelling of Surface Heat Exchangers Operating in the Transonic Regime. Energy 2014, 64, 961–969. [Google Scholar] [CrossRef]
- Baldauf, S.; Schulz, S.; Wittig, S. High-Resolution Measurements of Local Heat Transfer Coefficients From Discrete Hole Film Cooling. J. Turbomach. 2001, 123, 749–757. [Google Scholar] [CrossRef]
- Eckert, E. Survey on Heat Transfer at High Speeds; WADC Tech Report; Wright Air Development Center, Air Research and Development Command, United States Air Force: Washington, DC, USA, 1954. [Google Scholar]
- Sommer, S.C.; Short, B.J. Free-Flight Measurements of Turbulent-Boundary-Layer Skin Friction in the Presence of Severe Aerodynamic Heating at Mach Numbers from 2.8 to 7.0; NACA Technical Note 3391; NACA: Hampton, VA, USA, 1955. [Google Scholar]
- van Driest, E.R. The Problem of Aerodynamic Heating. Aeronaut. Eng. Rev. 1956, 15, 26–41. [Google Scholar]
- Coles, D.E. The Turbulent Boundary Layer in a Compressible Fluid. Phys. Fluids 1962, 7, 1403–1423. [Google Scholar] [CrossRef]
- Higgins, K. Comparison of Engineering Correlations for Predicting Heat Transfer in Zero-Pressure-Gradient Compressible Boundary Layers with CFD and Experimental Data; DSTO Defence Science and Technology Organization: Victoria, OC, Canada, 2008. [Google Scholar]
- Neal, L.; Bertram, M.H. Turbulent-Skin-Friction and Heat-Transfer Charts Adapted from the Spalding and Chi Method; NASA-TN-D-3969; NASA: Washington, DC, USA, 1967. [Google Scholar]
- Fitt, A.D.; Forth, C.J.P.; Robertson, B.A.; Jones, T.V. Temperature ratio effects in compressible turbulent boundary layers. Int. J. Heat Mass Transf. 1986, 29, 159–164. [Google Scholar] [CrossRef]
- Moffat, R.A. What’s New in Convective Heat Transfer. Int. J. Heat Fluid Flow 1998, 19, 90–101. [Google Scholar] [CrossRef]
- Arvizu, D.; Moffat, R.J. Use of Superposition in Calculating Cooling Requirements for Circuit Cards Containing Arrays of Electronic Components; Stanford University: Stanford, CA, USA, 1983. [Google Scholar]
- Ortega, A.; Moffat, R.J. Heat Transfer from an Array of Simulated Electronic Components: Experimental Results for Free Convection with and without a Shrouding Wall. ASME Heat Transf. Electron. Equip. 1985, 48, 5–15. [Google Scholar]
- Anderson, A.; Moffat, R.J. The Adiabatic Heat Transfer Coefficient and the Superposition Kernel Function: Part I—Data for Arrays of Flatpacks for Different Flow Conditions. J. Electron. Packag. 1992, 11, 14–21. [Google Scholar] [CrossRef]
- Anderson, A.; Moffat, R.J. The Adiabatic Heat Transfer Coefficient and the Superposition Kernel Function: Part II—Modelling Flatpack Data as a Function of Turbulence. J. Electron. Packag. 1992, 114, 22–28. [Google Scholar] [CrossRef]
- Hacker, J.M.; Eaton, J.K. Measurements of Heat Transfer in a Separated and Reattaching Flow with Spatially Varying Thermal Boundary Conditions. Int. J. Heat Fluid Flow 1997, 18, 131–141. [Google Scholar] [CrossRef]
- He, L. Spectral Heat Transfer Coefficient for Thermal Design Analysis—Part 1: Augmenting the Cooling Law for Non-Isothermal Wall. ASME J. Turbomach. 2025, 147, 061001. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 5th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Beck, J.V.; St Claire, C.R.; Blackwell, B. Inverse Heat Conduction; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Eckert, E.R.; Goldstein, R.J. Measurements in Heat Transfer, 2nd ed.; Hemispshere: Washington, DC, USA, 1976. [Google Scholar]
- Han, J.-C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology; Taylor and Francis: New York, NY, USA, 2000. [Google Scholar]
- Shih, T.I.-P.; Yang, V. (Eds.) Turbine Aerodyanamics, Heat Transfer, Materials, and Mechanics; Progress in Astronautics and Aeronautics; AIAA: Reston, VA, USA, 2014. [Google Scholar]
- Ligrani, P.M.; Camci, C. Adiabatic Film Cooling Effectiveness from Heat Transfer Measurements in Compressible, Variable Property Flow. J. Heat Transf. 1985, 107, 313–320. [Google Scholar] [CrossRef]
- Camci, C.; Kim, K.; Hippensteele, S.A. A New Hue Capturing Technique for the Quantitative Interpretation of Liquid Crystal Images Used in Convective Heat Transfer Studies. J. Turbomach. 1992, 114, 765–775. [Google Scholar] [CrossRef]
- Chyu, M.K.; Ding, H.; Downs, J.P.; Soechting, F.O. Determination of Local Heat Transfer Coefficient Based on Bulk Mean Temperature Using a Transient Liquid Crystal Technique. J. Exp. Therm. Fluid Sci. 1998, 18, 142–149. [Google Scholar] [CrossRef]
- Lin, M.; Wang, T. A Transient Liquid Crystal Method Using a 3-D Inverse Transient Conduction Scheme. Int. J. Heat Mass Transf. 2002, 45, 3491–3501. [Google Scholar] [CrossRef]
- Owen, J.M.; Newton, P.J.; Lock, G.D. Transient Heat Transfer Measurements Using Thermochromic Liquid Crystal. Part 2: Experimental Uncertainties. Int. J. Heat Fluid Flow 2003, 24, 23–28. [Google Scholar] [CrossRef]
- Kassab, A.J.; Divo, E.; Kapat, J.S.; Chyu, M.K. Retrieval of Multi-Dimensional Heat Transfer Coefficient Distributions Using an Inverse-BEM-Based Regularized Algorithm: Numerical and Experimental Examples. Eng. Anal. 2005, 29, 150–160. [Google Scholar]
- Bons, J. Transient Method for Convective Heat Transfer Measurement with Lateral Conduction—Part 1: Application to a Deposit-Roughened Gas Turbine Surface. J. Heat Transf. 2009, 131, 011301. [Google Scholar] [CrossRef]
- Bons, J.; Fletcher, D.; Borchert, B. Transient Method for Convective Heat Transfer Measurement with Lateral Conduction—Part II: Application to an Isolated Spherical Roughness Element. J. Heat Transf. 2009, 131, 011302. [Google Scholar] [CrossRef]
- Nishida, S.; Murata, A.; Saito, H.; Iwamoto, K. Compensation of Three-Dimensional Heat Conduction Inside Wall in Heat Transfer Measurement of Dimpled Surface by Using Transient Technique. J. Enhanc. Heat Transf. 2012, 19, 331–341. [Google Scholar] [CrossRef]
- Shih, T.I.-P.; Ramachandran, S.G.; Ames, R.; Dennis, R.A. CFD Conjugate Analysis of Transient Measurements of the Heat-Transfer Coefficient in a Duct with Pin Fins. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Expo-sition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar]
- Shih, T.I-P.; Gomatam-Ramachandran, S.; Chyu, M.K. Time Accurate CFD Conjugate Analysis of Transient Measurements of the Heat-Transfer Coefficient in a Channel with Pin Fins. J. Propuls. Power Res. 2013, 2, 10–19. [Google Scholar] [CrossRef][Green Version]
- Sathyanarayanan, S.K.; Shih, T.I-P. Time-Accurate Conjugate Analysis of Transient Measurements of Heat-Transfer Coefficients. AIAA J. Thermophys. Heat Transf. 2017, 31, 527–537. [Google Scholar] [CrossRef]
- Peck, J.; Liu, J.; Bryden, K.M.; Shih, T.I.-P. Method for Measuring and Computing the Adiabatic Wall Temperature; ASME Paper GT2020-14169; ASME: London, UK, 2020. [Google Scholar]
- Umana, E.M.; Yang, X. Review of Film Cooling Techniques for Aerospace Vehicles. Energies 2025, 18, 3085. [Google Scholar] [CrossRef]
- Kuo, K.K. Principles of Combustion; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat & Mass Transfer, 7th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Shih, T.-H.; Liou, W.; Shabbir, A.; Zhu, J. A New Eddy Viscosity Model for High Reynolds Number Turbulent Flow—Model Development and Validation. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Chen, H.C.; Patel, V.C. Near-Wall Turbulence Modles for Complex Flows Including Separation. AIAA J. 1988, 26, 641–648. [Google Scholar] [CrossRef]
- Wolfshtein, M. The Velocity and Temperature Distribution in One-Dimensional Flow with Turbulence Augmentation and Pressure Gradient. Int. J. Heat Mass Transf. 1969, 12, 301–318. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys® Academic Research Fluent, Release 2021 R2; Help System, Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Rhie, C.M.; Chow, W.L. Numerical Study of Turbulent Flow Past and Airfoild with Trailing Edge Separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Uri, M.A.; Grief, C. Chapter 11—Piecewise Polynomial Interpolation. In A First Course in Numerical Computing; Estep, D., Ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2011; pp. 311–359. [Google Scholar]
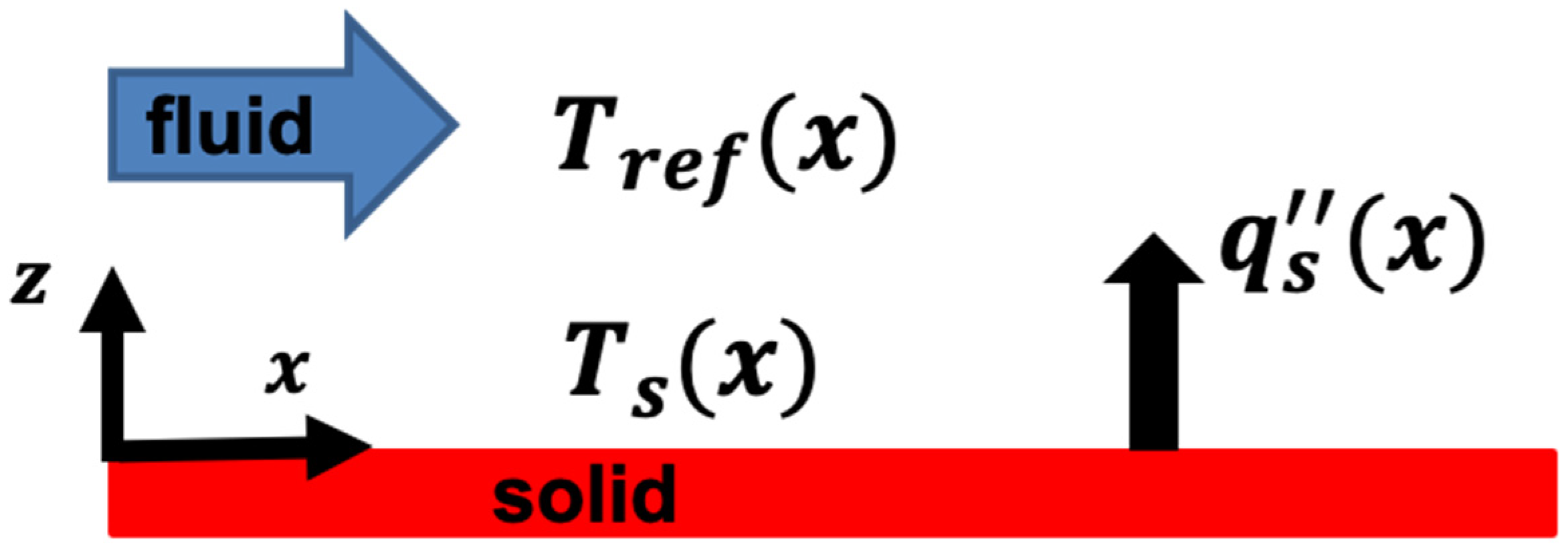
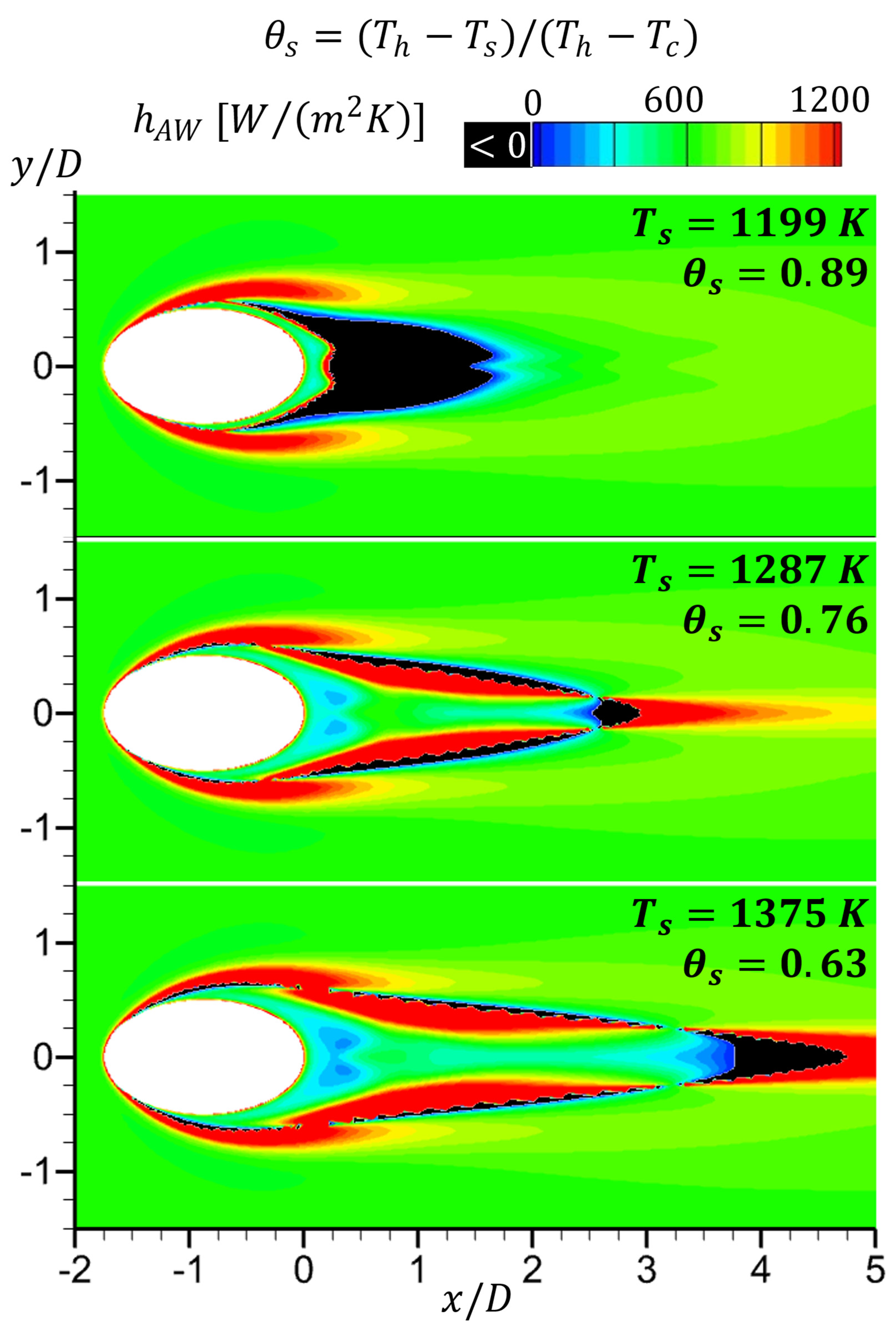
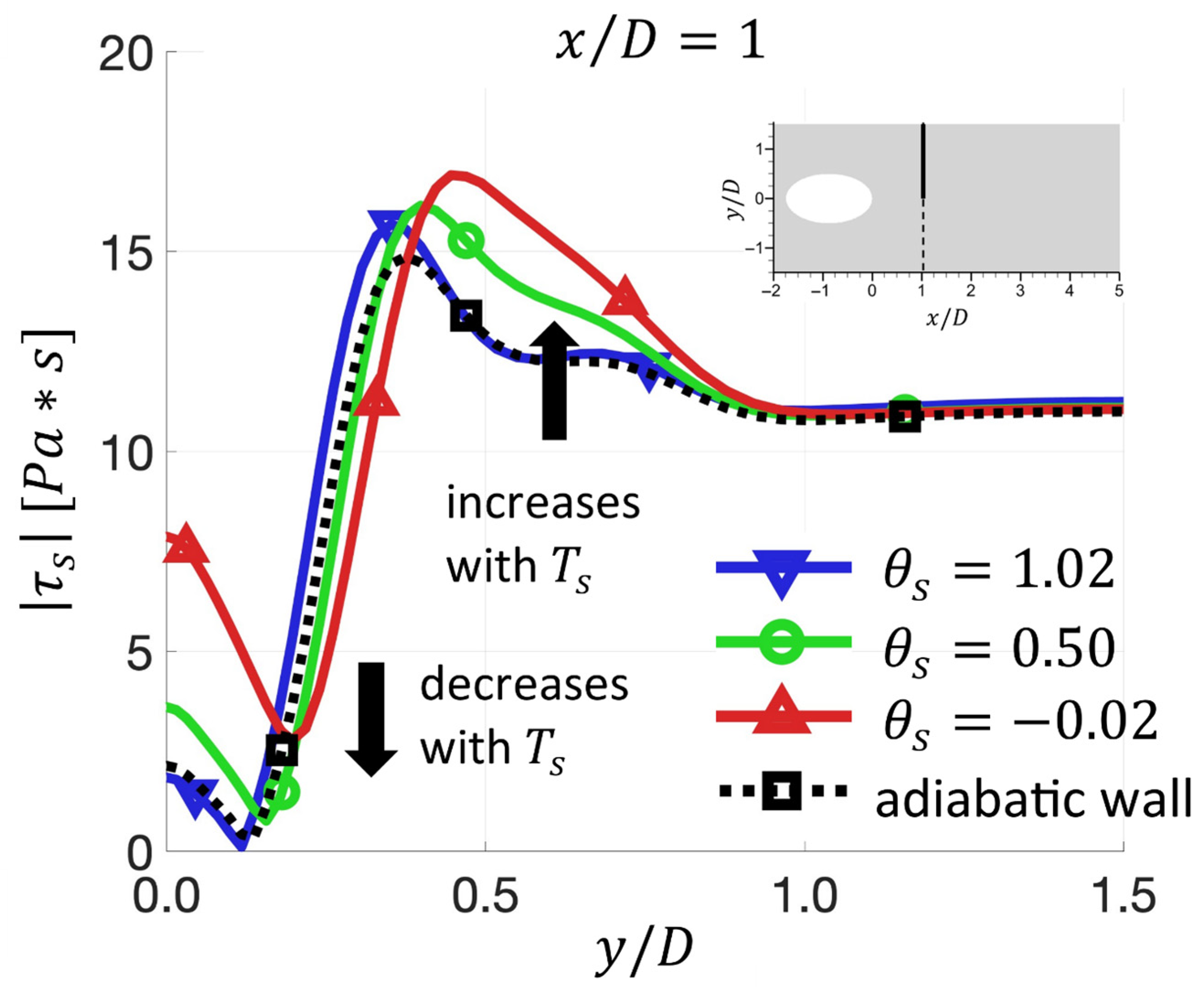
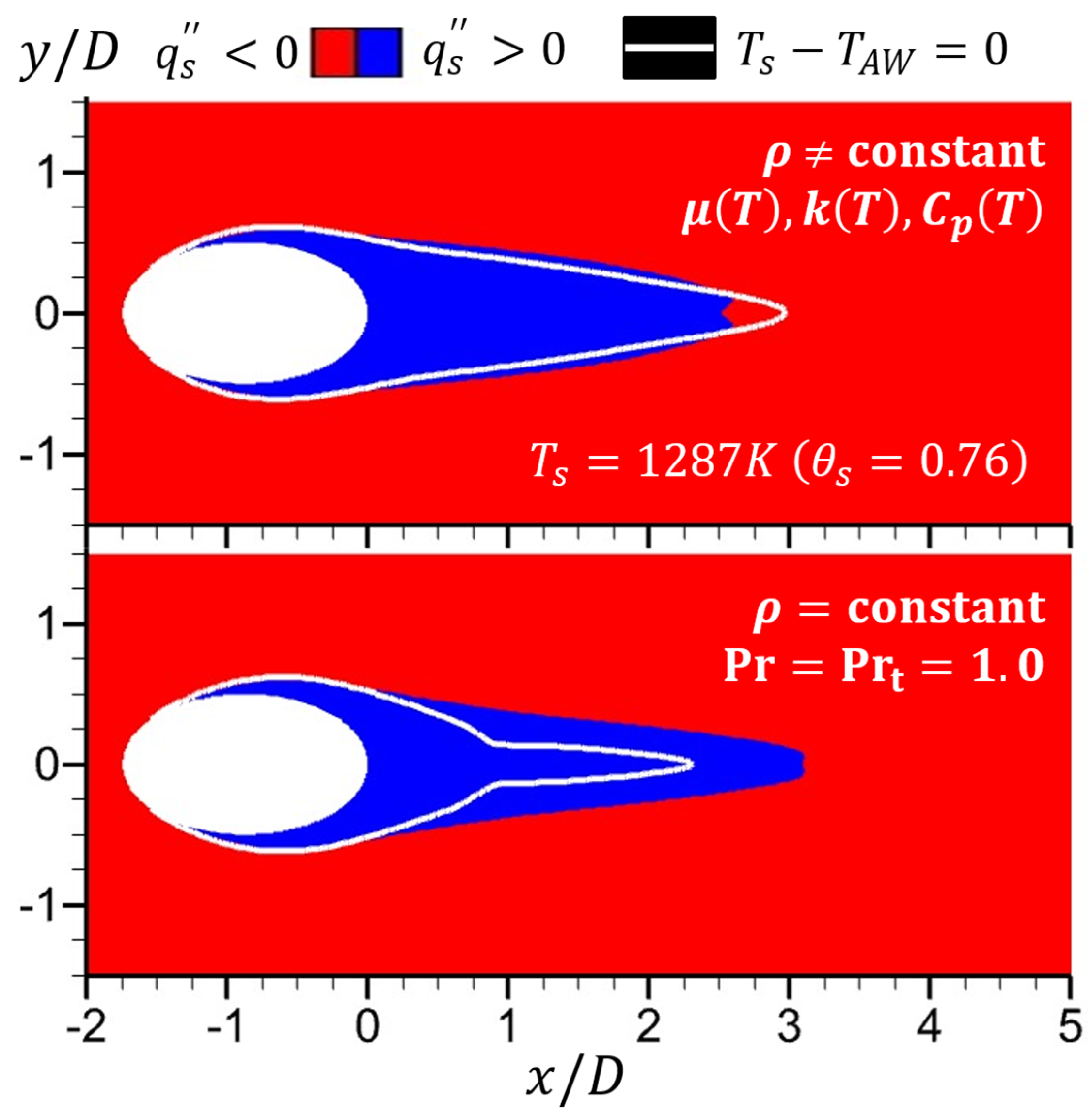
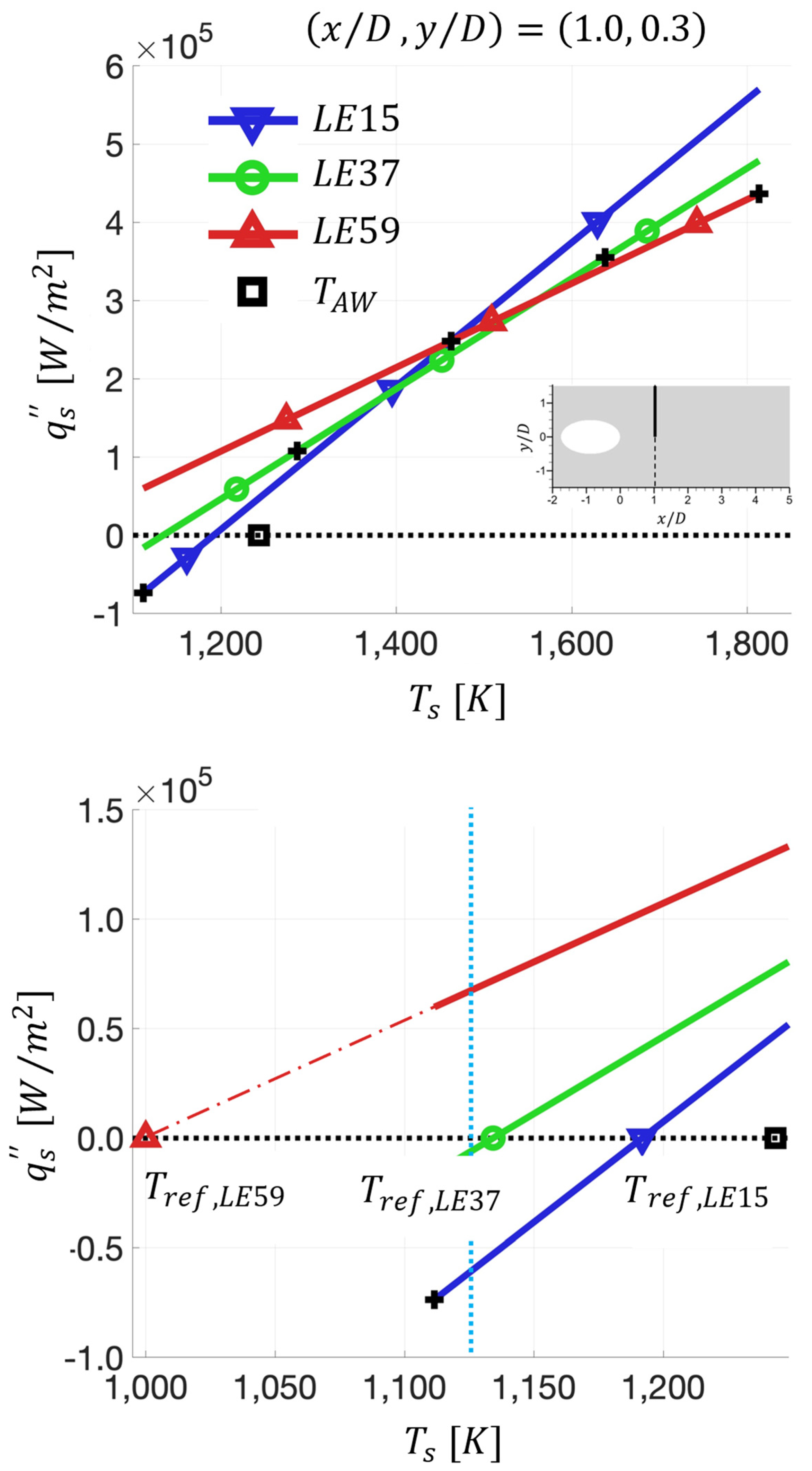
| Set Number | |
|---|---|
| 1: AW method | 1199, 1287, 1375, 1463 |
| 2: LE method | 1112, 1287, 1463, 1638, 1814 |
| 3: SS method | 1112, 1463, 1814 |
| 4: SS method | 1112, 1287, 1463, 1638, 1814 |
| 5: SS method | 1112, 1199, 1287, 1375, 1463, 1550, 1638, 1726, 1814 |
| Grid | Total No. of Cells (Million) | No. of Grid Points on Hole Circumference |
|---|---|---|
| coarse | 1.72 | 112 |
| baseline | 5.70 | 172 |
| fine | 20.3 | 264 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peck, J.; Shih, T.I.-P.; Bryden, K.M.; Crane, J.M. Methods for Measuring and Computing the Reference Temperature in Newton’s Law of Cooling for External Flows. Energies 2025, 18, 4074. https://doi.org/10.3390/en18154074
Peck J, Shih TI-P, Bryden KM, Crane JM. Methods for Measuring and Computing the Reference Temperature in Newton’s Law of Cooling for External Flows. Energies. 2025; 18(15):4074. https://doi.org/10.3390/en18154074
Chicago/Turabian StylePeck, James, Tom I-P. Shih, K. Mark Bryden, and John M. Crane. 2025. "Methods for Measuring and Computing the Reference Temperature in Newton’s Law of Cooling for External Flows" Energies 18, no. 15: 4074. https://doi.org/10.3390/en18154074
APA StylePeck, J., Shih, T. I.-P., Bryden, K. M., & Crane, J. M. (2025). Methods for Measuring and Computing the Reference Temperature in Newton’s Law of Cooling for External Flows. Energies, 18(15), 4074. https://doi.org/10.3390/en18154074





