Multi-Dimensional Feature Perception Network for Open-Switch Fault Diagnosis in Grid-Connected PV Inverters
Abstract
1. Introduction
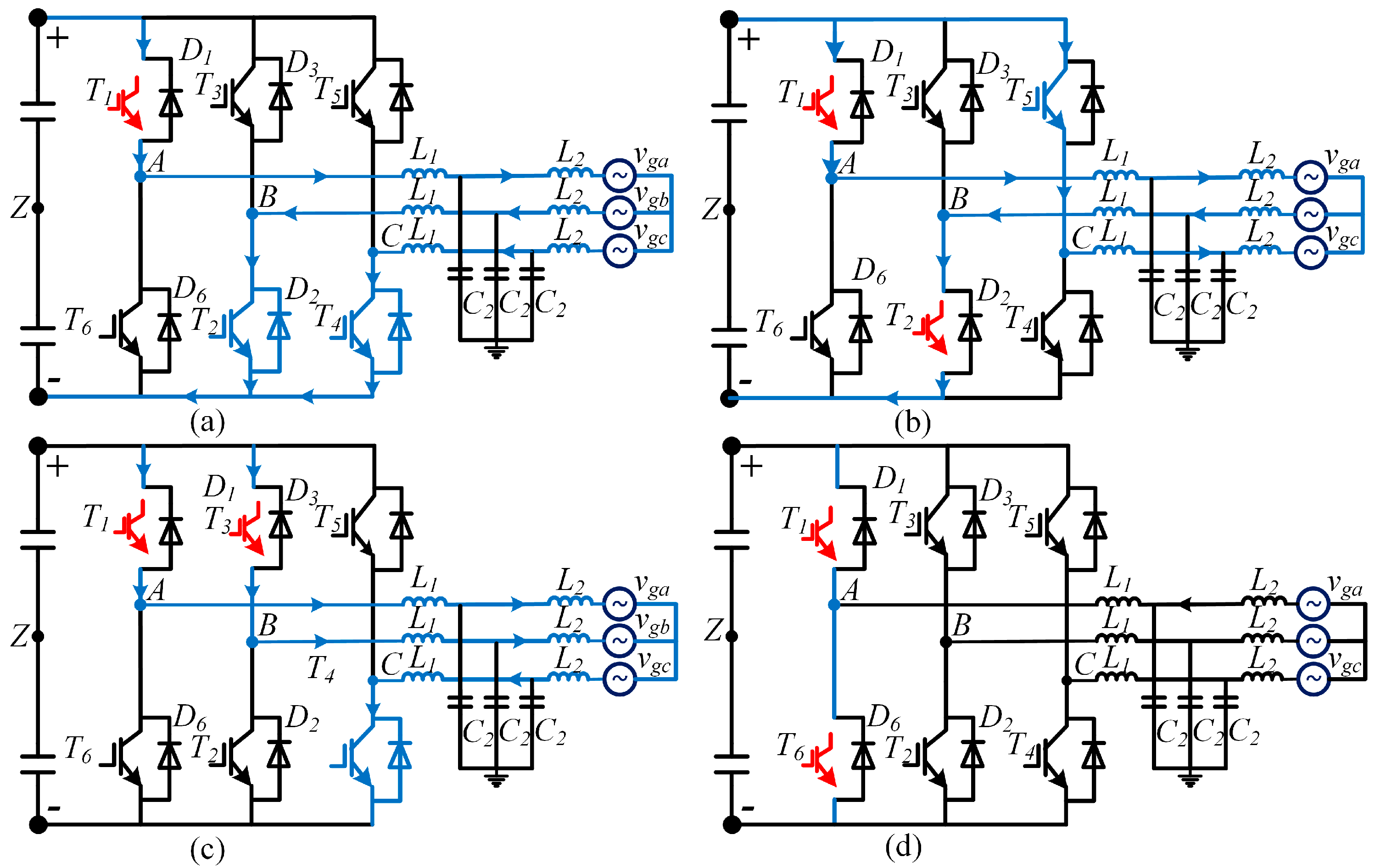
2. Open-Switch Fault Analysis of PV Grid-Connected Inverter
3. Methods
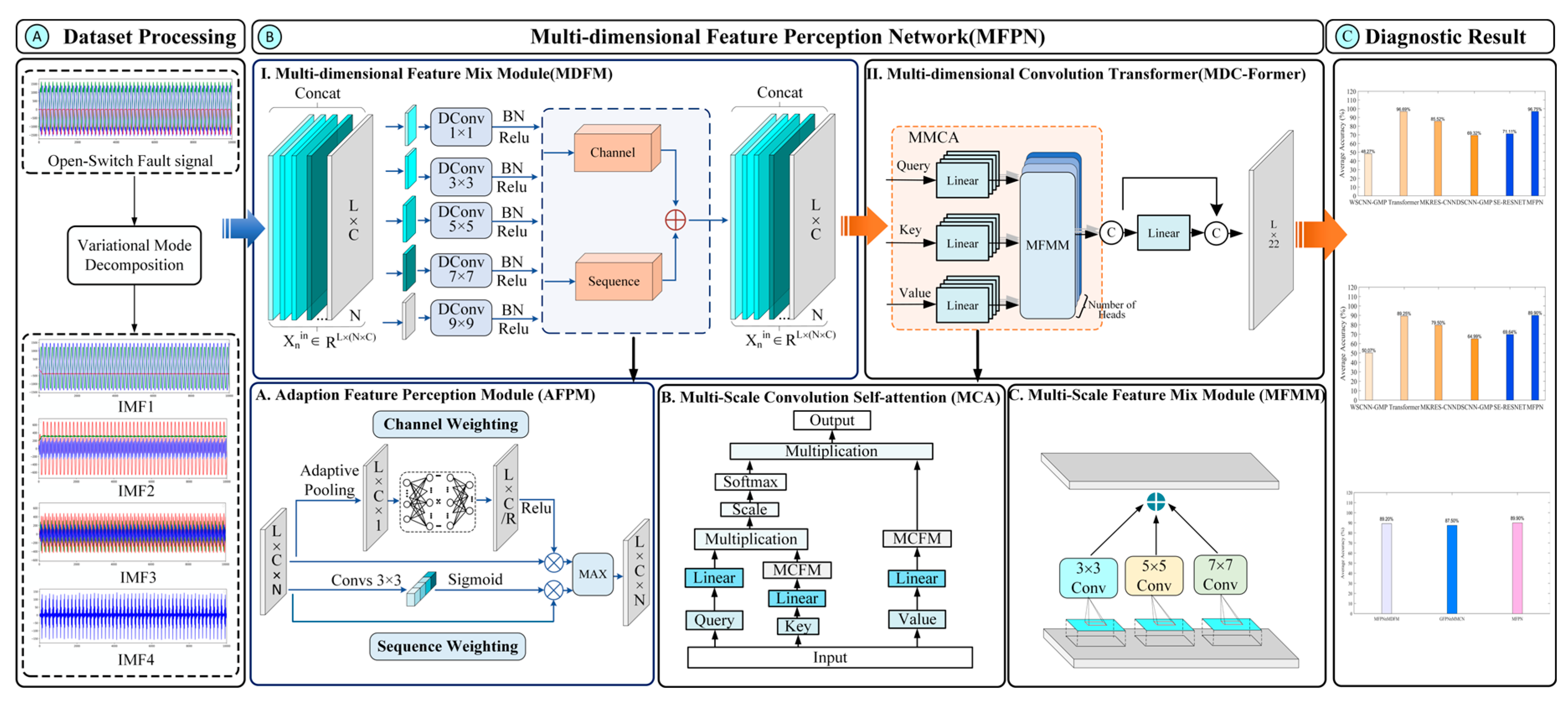
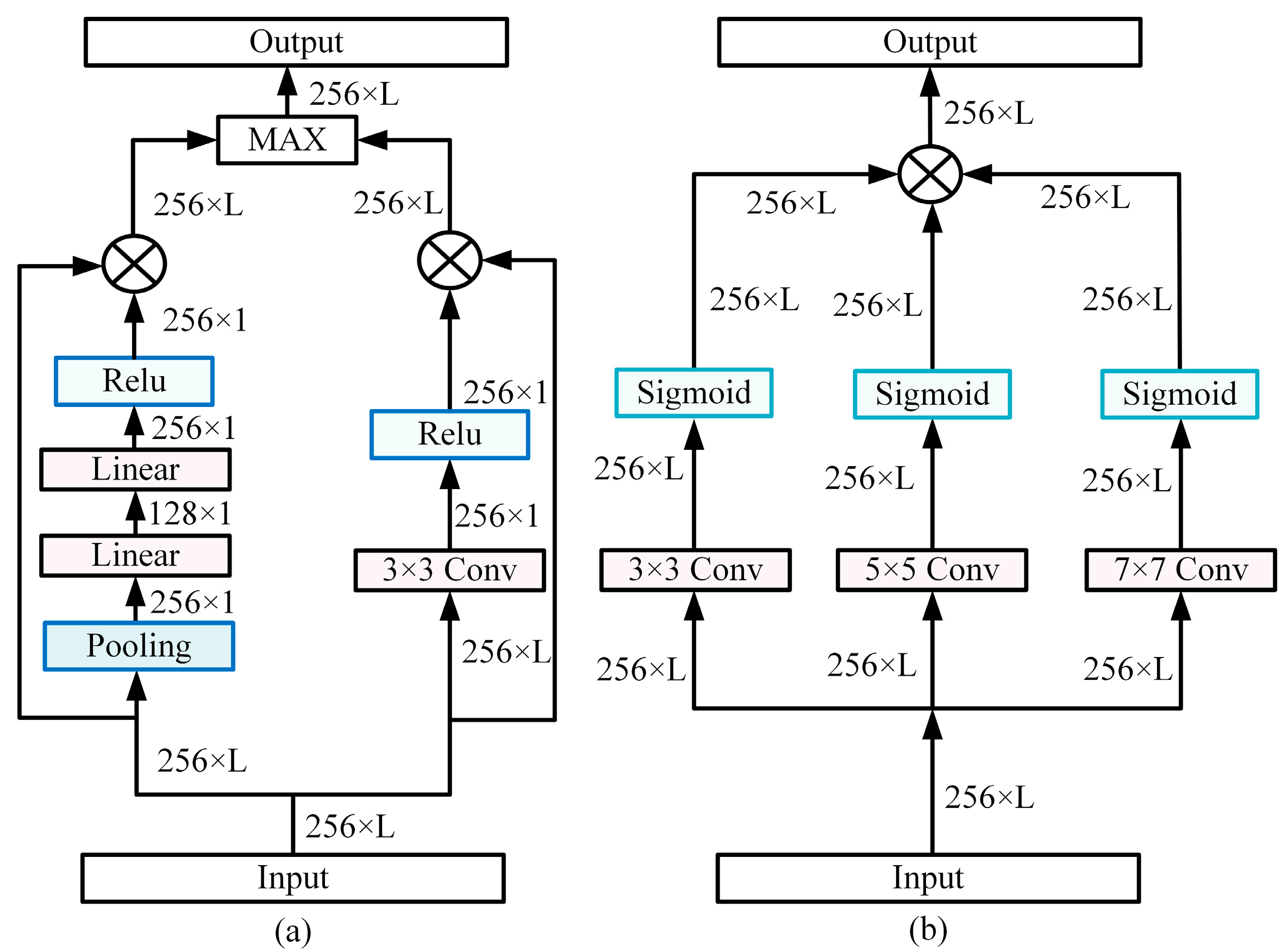
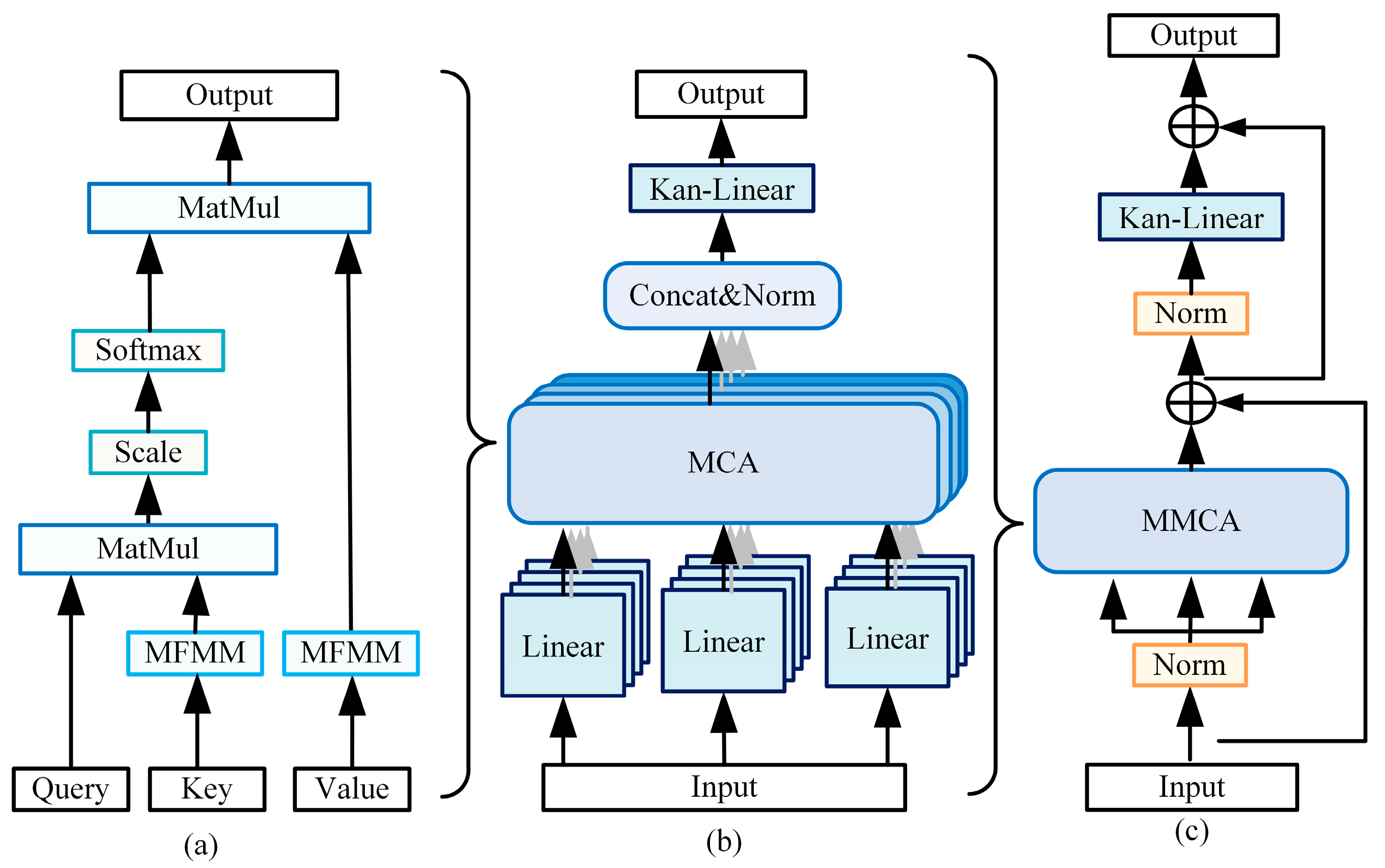
3.1. Fault Diagnosis Algorithm Based on Multi-Dimensional Feature Perception Network
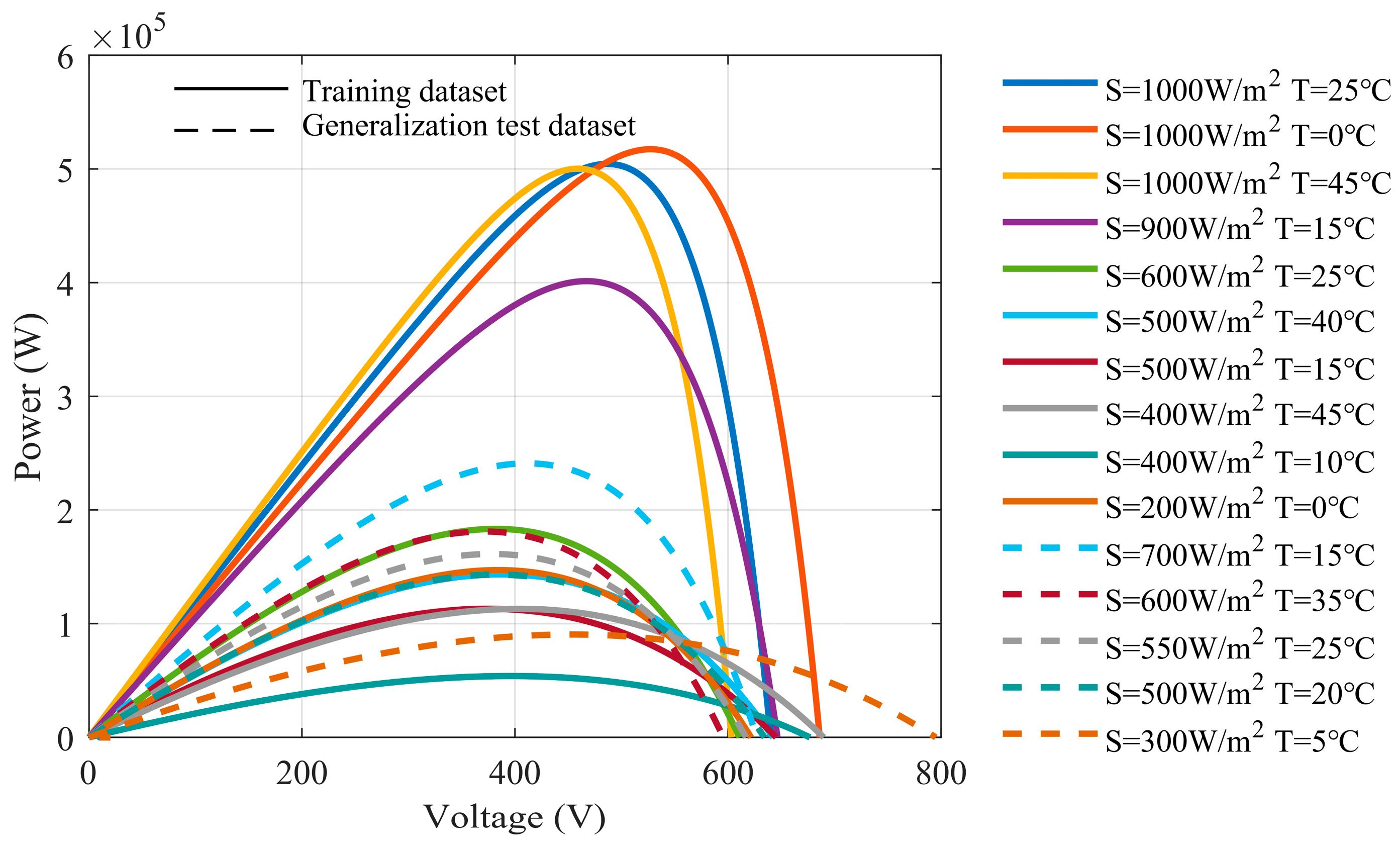
3.2. Hardware in the Loop Platform Dataset
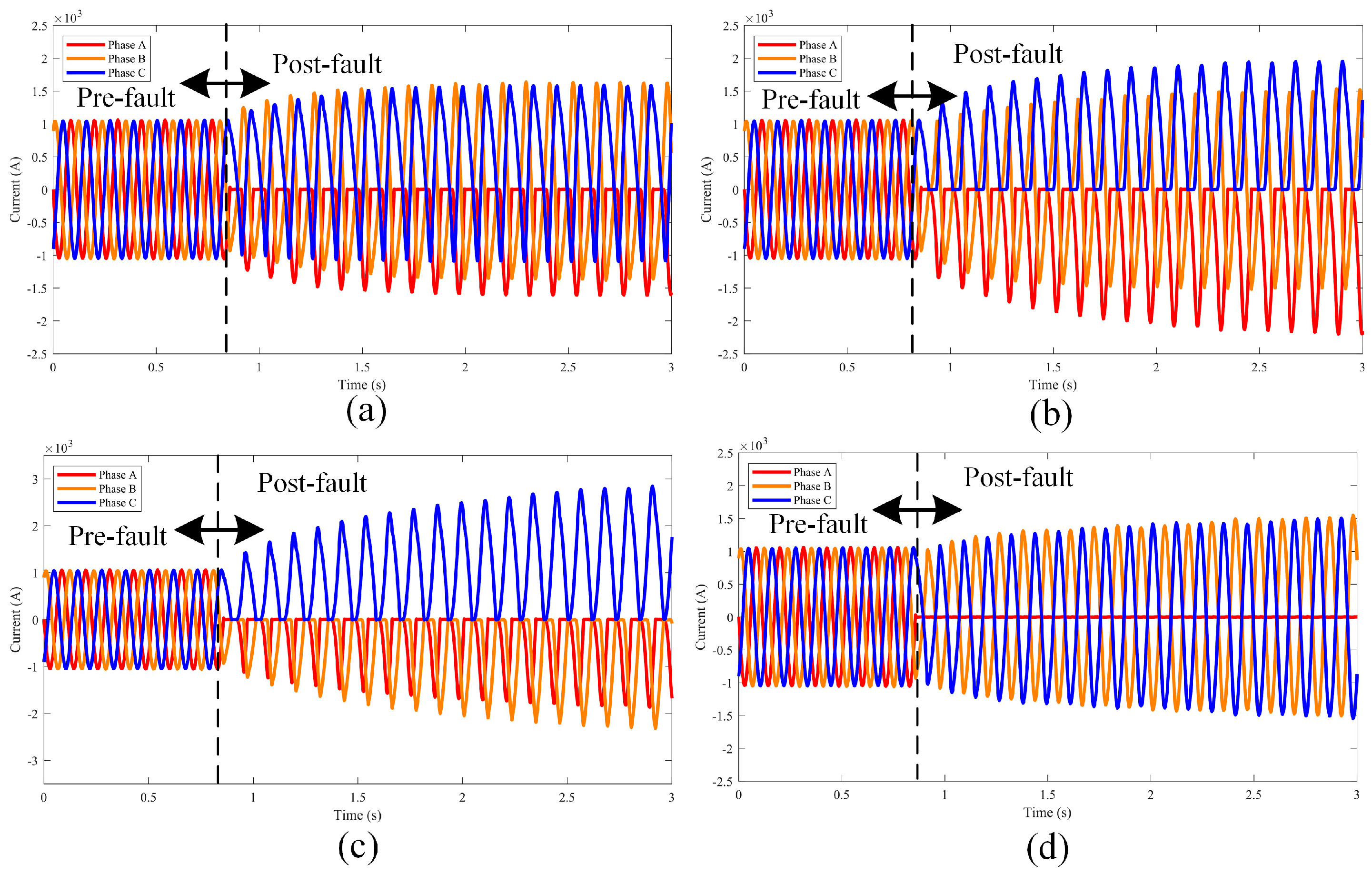
4. Results and Discussion
4.1. Configuration Settings
- (1)
- WSCNN-GMP [31]: WSCNN-GMP is an improved convolutional neural network-based method specifically designed for inverter fault diagnosis under varying load conditions;
- (2)
- TRANSFORMER [32]: The Transformer algorithm is a self-attention-based method developed for tasks involving long-range sequence processing;
- (3)
- MKRES-CNN [33]: MKRES-CNN is an algorithm based on a multiscale residual convolutional neural network designed explicitly for fault diagnosis of the motor;
- (4)
- DSCNN-GMP [33]: DSCNN-GMP is an algorithm based on depth-wise separable convolution with global max pooling, designed explicitly for open-circuit fault diagnosis of neutral-point clamped (NPC) inverters;
- (5)
- SE-ResNet [34]: SE-ResNet is an improved neural network algorithm based on ResNet, used for open-circuit fault diagnosis in photovoltaic inverters.
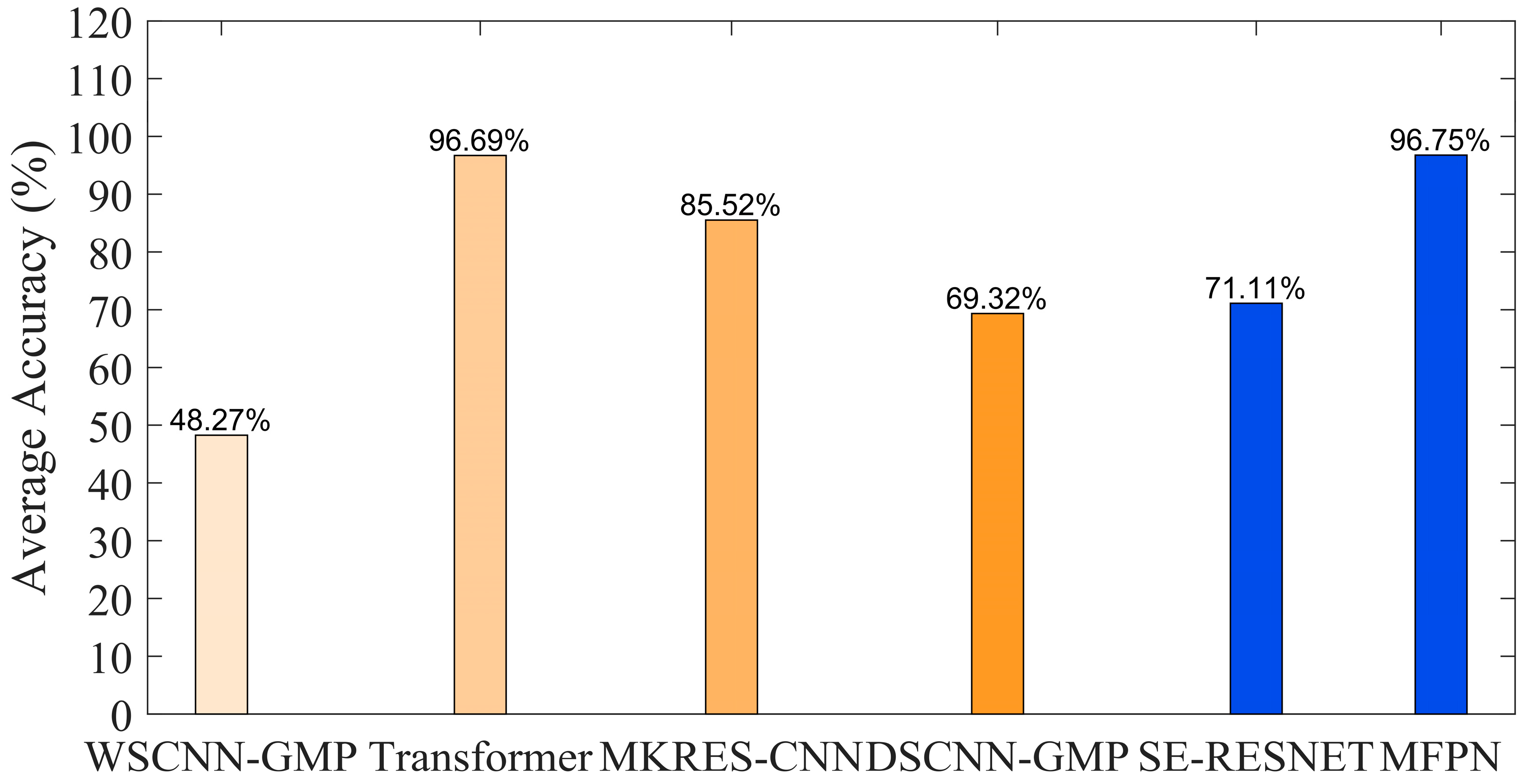
4.2. Comparison with Other Algorithm
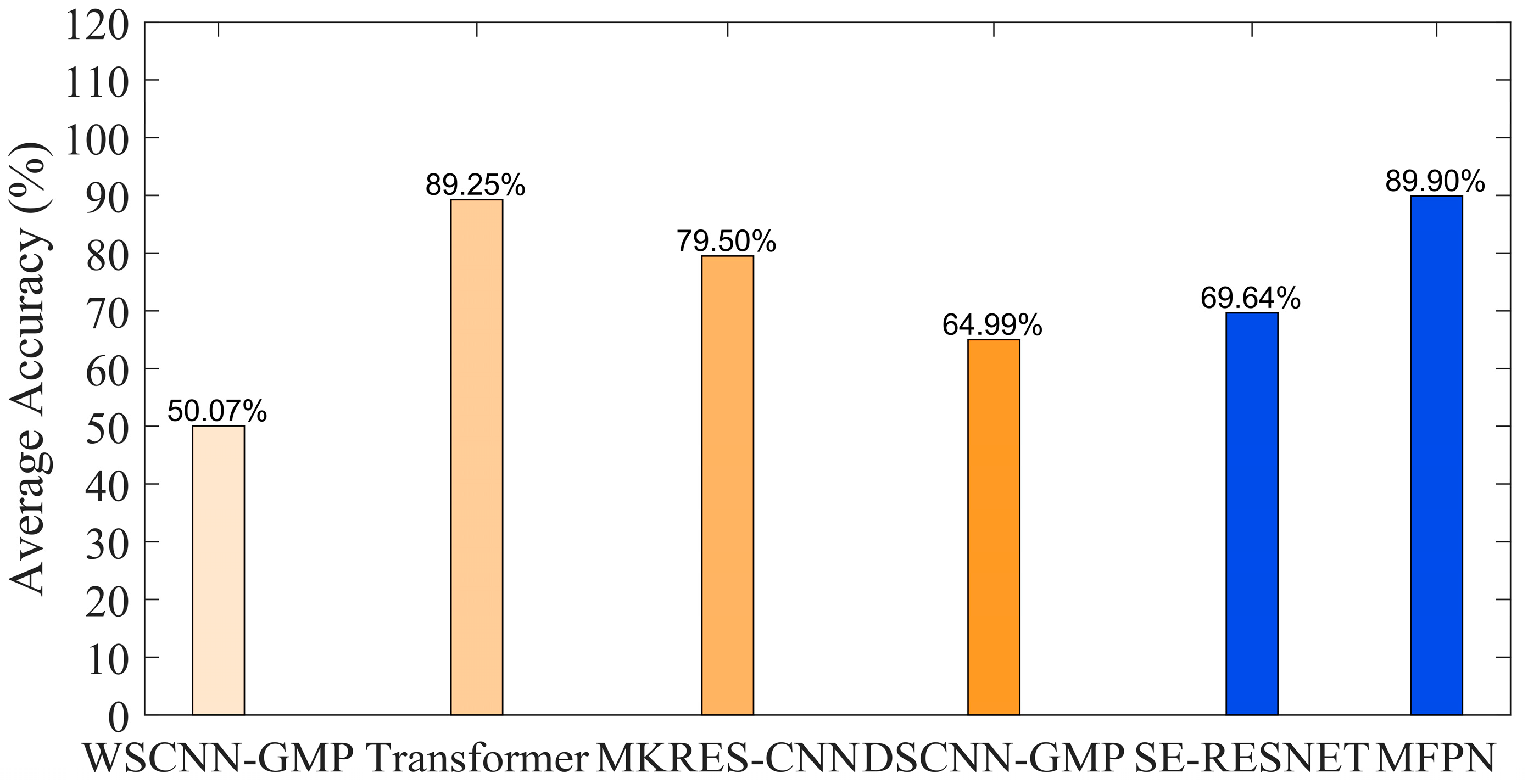
4.3. Robustness AGAINST Generalization Test
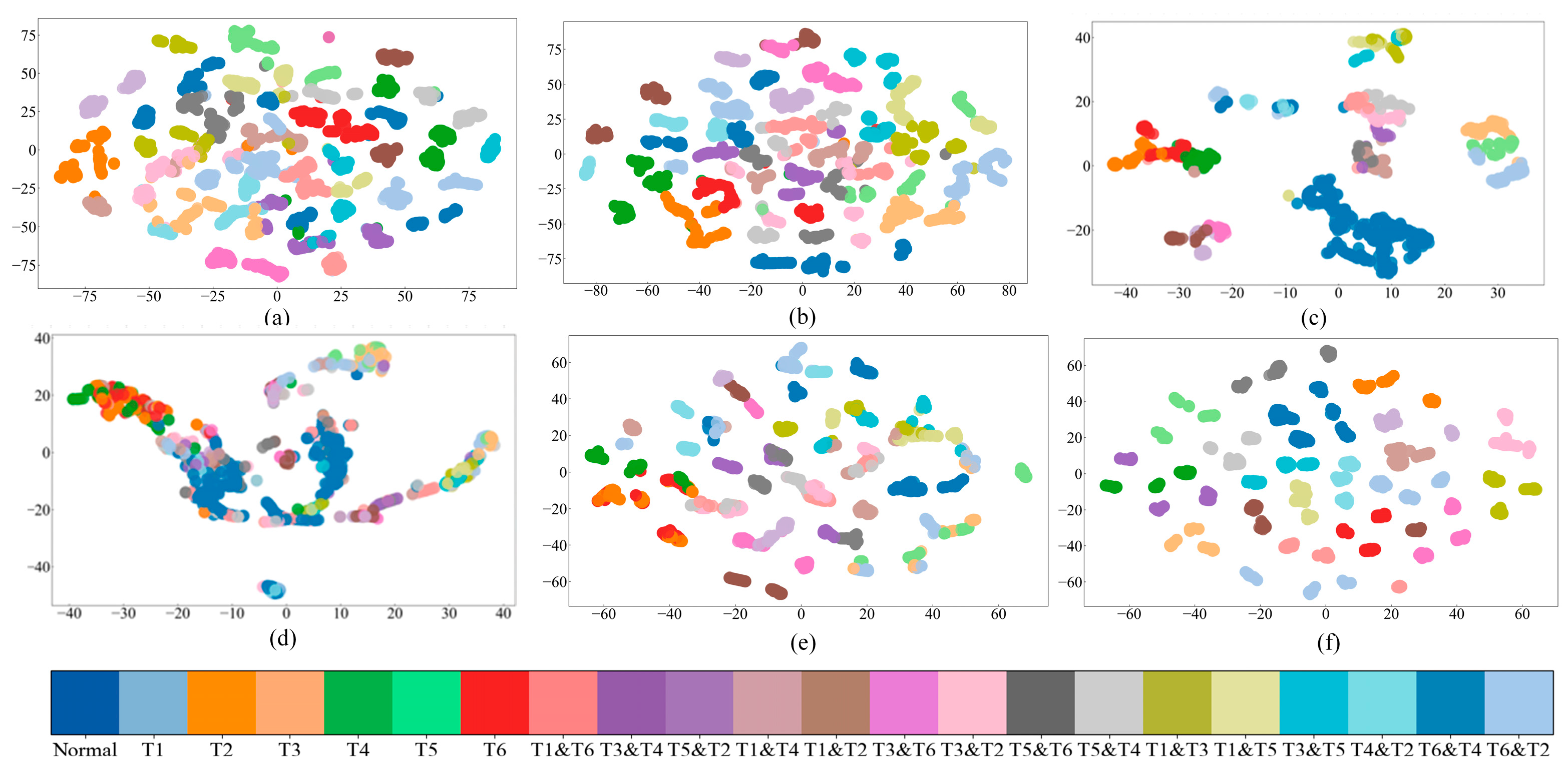
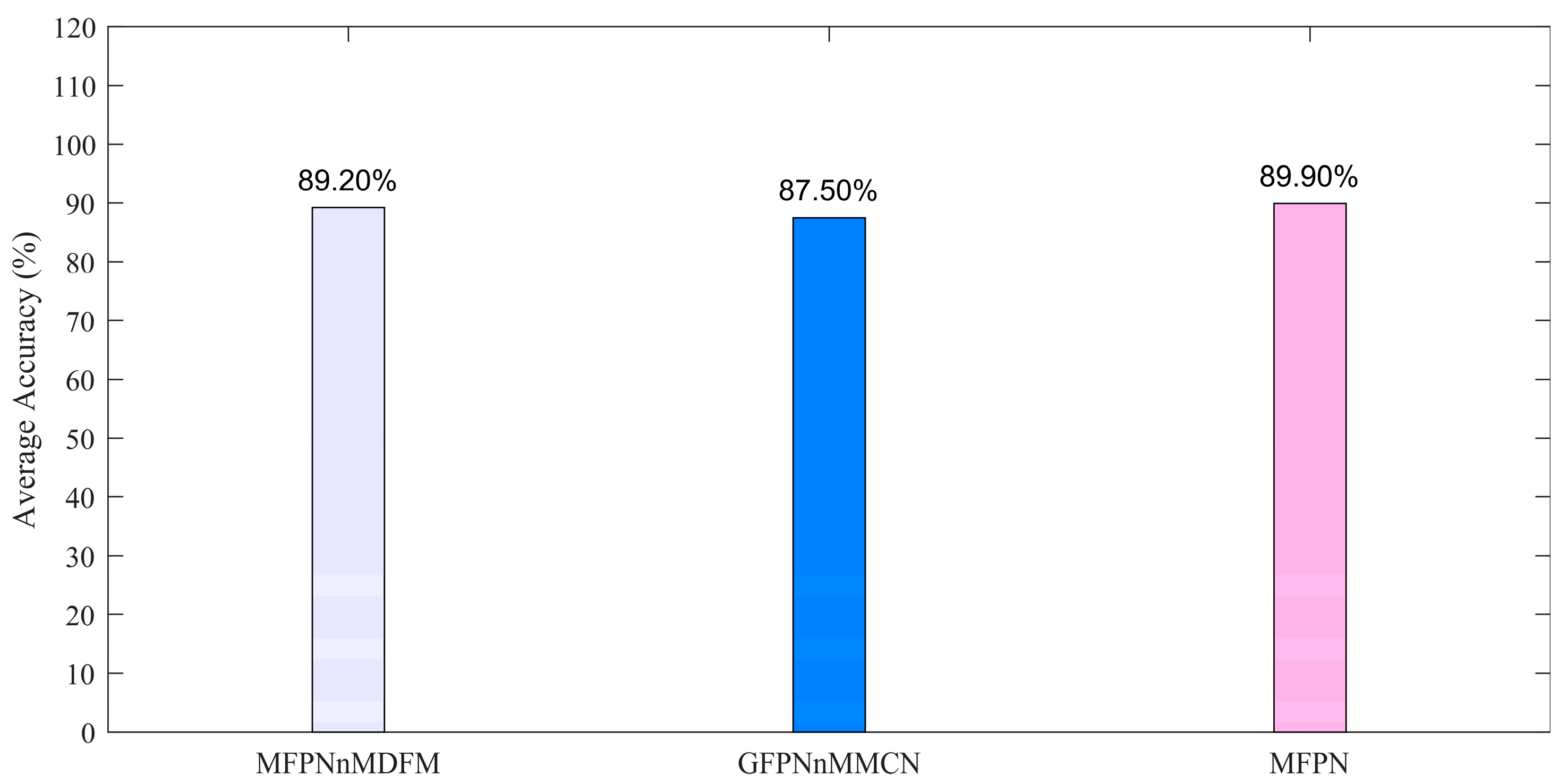
4.4. Ablidation Studies
4.5. Training Time, Inference Time, and Resource Usage Cost of the Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, B.; Wang, Z.; Chen, J. Shaping the Solar Future: An Analysis of Policy Evolution, Prospects and Implications in China’s Photovoltaic Industry. Energy Strategy Rev. 2024, 54, 101474. [Google Scholar] [CrossRef]
- De Almeida, J.O.M.B.; Torres, A.G.; Cupertino, A.F.; Pereira, H.A. Three-Phase Photovoltaic Inverters during Unbalanced Voltage Sags: Comparison of Control Strategies and Thermal Stress Analysis. In Proceedings of the 2016 12th IEEE International Conference on Industry Applications (INDUSCON), Curitiba, Brazil, 20–23 November 2016. [Google Scholar]
- Meral, M.E.; Çelik, D. Minimisation of Power Oscillations with a Novel Optimal Control Strategy for Distributed Generation Inverter under Grid Faulty and Harmonic Networks. IET Renew. Power Gener. 2020, 14, 3010–3022. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Z.; Chen, Z. Fast Diagnosis and Location Method for Open-Circuit Fault in Inverter Based on Current Vector Character Analysis. Trans. China Electrotech. Soc. 2018, 33, 883–891. [Google Scholar]
- Bandyopadhyayi, P.; Purkait, P.; Koley, C. A SVM-Based Classifier for Identification of Spurious Resistance Fault Involving IGBTs in VSI-Based Induction Motor Drive. In Proceedings of the 2018 IEEE Applied Signal Processing Conference (ASPCON), Kolkata, India, 7–9 December 2018; pp. 9–13. [Google Scholar] [CrossRef]
- Hu, K.; Meng, X.; Liu, Z.; Xu, J.; Lin, G.; Tong, L. Flux-Based Open-Switch Fault Diagnosis and Fault Tolerance for IM Drives with Predictive Torque/Flux Control. IEEE Trans. Transp. Electrif. 2022, 8, 4595–4606. [Google Scholar] [CrossRef]
- Jlassi, I.; Estima, J.O.; El Khil, S.K.; Bellaaj, N.M.; Cardoso, A.J.M. Multiple Open-Circuit Faults Diagnosis in Back-to-Back Converters of PMSG Drives for Wind Turbine Systems. IEEE Trans. Power Electron. 2015, 30, 2689–2702. [Google Scholar] [CrossRef]
- Campos-Delgado, D.U.; Espinoza-Trejo, D.R. An Observer-Based Diagnosis Scheme for Single and Simultaneous Open-Switch Faults in Induction Motor Drives. IEEE Trans. Ind. Electron. 2011, 58, 671–679. [Google Scholar] [CrossRef]
- Espinoza-Trejo, D.R.; Campos-Delgado, D.U. Detection and Isolation of Actuator Faults for a Class of Nonlinear Systems with Application to Electric Motors Drives. IET Control Theory Appl. 2009, 3, 1317–1329. [Google Scholar] [CrossRef]
- Champa, P.N.; Deshpande, A.A. Effect of LSPWM at Variable and Fixed Switching Frequency on Cascaded Multilevel Inverter. In Proceedings of the 2024 International Conference on Advances in Modern Age Technologies for Health and Engineering Science (AMATHE), Shivamogga, India, 16–17 May 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Shi, T.; He, Y.; Wang, T.; Tong, J.; Li, B.; Deng, F. An Improved Open-Switch Fault Diagnosis Technique of a PWM Voltage Source Rectifier Based on Current Distortion. IEEE Trans. Power Electron. 2019, 34, 12212–12225. [Google Scholar] [CrossRef]
- Nzekwu, C.N. Fault Diagnosis of Inverter Power Switches Using Signal-Data Based Machine Learning. Doctoral Thesis, Glasgow Caledonian University, Glasgow, UK, 2024. [Google Scholar]
- Martins, J.F.; Pires, V.F.; Lima, C.; Pires, A.J. Fault Detection and Diagnosis of Grid-Connected Power Inverters Using PCA and Current Mean Value. In Proceedings of the IECON 2012—38th Annual Conference of the IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 5185–5190. [Google Scholar] [CrossRef]
- Khomfoi, S.; Tolbert, L.M. Fault Diagnosis and Reconfiguration for Multilevel Inverter Drive Using AI-Based Techniques. IEEE Trans. Ind. Electron. 2007, 54, 2954–2968. [Google Scholar] [CrossRef]
- Ali, M.; Din, Z.; Solomin, E.; Cheema, K.M.; Milyani, A.H.; Che, Z. Open Switch Fault Diagnosis of Cascade H-Bridge Multi-Level Inverter in Distributed Power Generators by Machine Learning Algorithms. Energy Rep. 2021, 7, 8929–8942. [Google Scholar] [CrossRef]
- Sun, Q.; Yu, X.; Li, H.; Fan, J. Adaptive Feature Extraction and Fault Diagnosis for Three-Phase Inverter Based on Hybrid-CNN Models under Variable Operating Conditions. Complex Intell. Syst. 2022, 8, 29–42. [Google Scholar] [CrossRef]
- Li, B.; Lu, W.; Xie, Z. Open-Circuit Fault Diagnosis Method of ANPC Three-Level Inverter Based on Joint Optimized Echo State Network. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 1912–1915. [Google Scholar] [CrossRef]
- Li, J.; Tao, J.; Ding, W.; Zhang, J.; Meng, Z. Period-Assisted Adaptive Parameterized Wavelet Dictionary and Its Sparse Representation for Periodic Transient Features of Rolling Bearing Faults. Mech. Syst. Signal Process. 2022, 169, 108796. [Google Scholar] [CrossRef]
- Fu, Y.; Ji, Y.; Meng, G.; Chen, W.; Bai, X. Three-Phase Inverter Fault Diagnosis Based on an Improved Deep Residual Network. Electronics 2023, 12, 3460. [Google Scholar] [CrossRef]
- Jiang, W.; Tashakor, N.; Pourhadi, P.; Koehler, A.; Wang, H.; Goetz, S.M. Optimizing PV–Battery Hybrid Systems: A Reconfigurable Approach with Module-Level Maximum-Power-Point Tracking and Load Sharing. IEEE Trans. Power Electron. 2024, 40, 2327–2341. [Google Scholar] [CrossRef]
- Feng, X.; Yan, Z.; Chen, N.; Zhang, Y.; Ma, Y.; Liu, X.; Fan, Q.; Wang, L.; Huang, W. The Synthesis of Shape-Controlled MnO2/Graphene Composites via a Facile One-Step Hydrothermal Method and Their Application in Supercapacitors. J. Mater. Chem. A1 2013, 1, 12818–12825. [Google Scholar] [CrossRef]
- Li, Y.; Dai, W.; Zhang, W. Bearing Fault Feature Selection Method Based on Weighted Multidimensional Feature Fusion. IEEE Access 2020, 8, 19008–19025. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Wu, L.; Sarkar, S.; Jiang, D. An Adaptive Spatiotemporal Feature Learning Approach for Fault Diagnosis in Complex Systems. Mech. Syst. Signal Process. 2019, 117, 170–187. [Google Scholar] [CrossRef]
- Liu, H.; Xu, Q.; Han, X.; Wang, B.; Yi, X. Attention on the Key Modes: Machinery Fault Diagnosis Transformers through Variational Mode Decomposition. Knowl.-Based Syst. 2024, 289, 111479. [Google Scholar] [CrossRef]
- Yan, X.; Li, Z.; Meng, L.; Qi, Z.; Wu, W.; Li, Z.; Meng, X. Empowering Vision Transformers with Multi-Scale Causal Intervention for Long-Tailed Image Classification. arXiv 2025, arXiv:2505.08173. [Google Scholar]
- Mao, J.; Jain, A.K. Artificial Neural Networks for Feature Extraction and Multivariate Data Projection. IEEE Trans. Neural Netw. 1995, 6, 296–317. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Lee, C.-H. Real-Time Data-Driven Method for Bolt Defect Detection and Size Measurement in Industrial Production. Actuators 2025, 14, 185. [Google Scholar] [CrossRef]
- Urrea, C. Hybrid Fault-Tolerant Control in Cooperative Robotics: Advances in Resilience and Scalability. Actuators 2025, 14, 177. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, Z. A Generalized Center-Aligned High-Resolution Pulse Width Modulator Implementation Using an Output Serializer in Field Programmable Gate Arrays. Actuators 2025, 14, 181. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, F. Research on Sensorless Technology of a Magnetic Suspension Flywheel Battery Based on a Genetic BP Neural Network. Actuators 2025, 14, 174. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, R.; Si, Y.; Wang, L. An Improved Convolutional Neural Network for Three-Phase Inverter Fault Diagnosis. IEEE Trans. Instrum. Meas. 2022, 71, 3510915. [Google Scholar] [CrossRef]
- Lv, H.; Chen, J.; Pan, T.; Zhang, T.; Feng, Y.; Liu, S. Attention Mechanism in Intelligent Fault Diagnosis of Machinery: A Review of Technique and Application. Measurement 2022, 199, 111594. [Google Scholar] [CrossRef]
- Xie, F.; Tang, X.; Xiao, F.; Luo, Y.; Shen, H.; Shi, Z. Online Diagnosis Method for Open-Circuit Fault of NPC Inverter Based on 1D-DSCNN-GMP Lightweight Edge Deployment. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 6054–6067. [Google Scholar] [CrossRef]
- Lin, P.; Qian, Z.; Lu, X.; Lin, Y.; Lai, Y.; Cheng, S.; Chen, Z.; Wu, L. Compound Fault Diagnosis Model for Photovoltaic Array Using Multi-Scale SE-ResNet. Sustain. Energy Technol. Assess. 2022, 50, 101785. [Google Scholar] [CrossRef]


| Item | Parameters | Values |
|---|---|---|
| PV Array | Short-circuit current | isc = 1200 A |
| Open-circuit voltage | voc = 640 V | |
| MPPT current | imppt = 1000 A | |
| MPPT voltage | vmppt = 502 V | |
| DC-DC Boost Converter | Switch frequency | fsw = 10 kHz |
| DC-side capacitance (C, C1) | (3 × 10−3 F, 4.7 × 10−2 F) | |
| DC-side inductor | L = 1 × 10−2 H | |
| DC-AC Grid-Connected Inverter | Switch frequency | fsw = 10 kHz |
| Current control loop (KPi, KIi) | (500, 1000) | |
| Power control loop (KPw, KIw) | (500, 1000) | |
| AC-side reference power | Pref = 500 kW | |
| AC-side reference active power | Qref = 0 kVA | |
| LCL Filter | Grid-side inductor (L1, L2) | (1 × 10−3 H, 2.64 × 10−5 H) |
| Grid-side capacitance | C2 = 1.5 × 10−7 F | |
| Power Grid | Grid-side voltage | 800 V |
| Class | Illustration | Training Data | Test Data | Total Data |
|---|---|---|---|---|
| 0 | Healthy Status | 1080 | 720 | 1800 |
| 1 | T1 Failure | 1080 | 720 | 1800 |
| 2 | T2 Failure | 1080 | 720 | 1800 |
| 3 | T3 Failure | 1080 | 720 | 1800 |
| 4 | T4 Failure | 1080 | 720 | 1800 |
| 5 | T5 Failure | 1080 | 720 | 1800 |
| 6 | T6 Failure | 1080 | 720 | 1800 |
| 7 | T1&T6 Failure | 1080 | 720 | 1800 |
| 8 | T3&T4 Failure | 1080 | 720 | 1800 |
| 9 | T5&T2 Failure | 1080 | 720 | 1800 |
| 10 | T1&T4 Failure | 1080 | 720 | 1800 |
| 11 | T1&T2 Failure | 1080 | 720 | 1800 |
| 12 | T3&T6 Failure | 1080 | 720 | 1800 |
| 13 | T3&T2 Failure | 1080 | 720 | 1800 |
| 14 | T5&T6 Failure | 1080 | 720 | 1800 |
| 15 | T5&T4 Failure | 1080 | 720 | 1800 |
| 16 | T1&T3 Failure | 1080 | 720 | 1800 |
| 17 | T1&T5 Failure | 1080 | 720 | 1800 |
| 18 | T3&T5 Failure | 1080 | 720 | 1800 |
| 19 | T4&T2 Failure | 1080 | 720 | 1800 |
| 20 | T6&T4 Failure | 1080 | 720 | 1800 |
| 21 | T6&T2 Failure | 1080 | 720 | 1800 |
| 0 | Healthy Status | 1080 | 720 | 1800 |
| Classifier | Training Time (s) | Inference Time (s) | FLOPs |
|---|---|---|---|
| WSCNN-GMP | 35 | 0.176 | 3.40 × 109 |
| Transformer | 1320 | 0.215 | 29.2 × 109 |
| MKRES-CNN | 91 | 0.197 | 2.05 × 109 |
| CNN-GAP | 531 | 0.377 | 4.25 × 109 |
| SE-RESNET | 28 | 0.247 | 13.6 × 109 |
| MFPN | 1470 | 1.210 | 1.32 × 109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; He, Y.; Zhan, Y.; Chang, Q.; Hu, K.; Wang, H. Multi-Dimensional Feature Perception Network for Open-Switch Fault Diagnosis in Grid-Connected PV Inverters. Energies 2025, 18, 4044. https://doi.org/10.3390/en18154044
Xie Y, He Y, Zhan Y, Chang Q, Hu K, Wang H. Multi-Dimensional Feature Perception Network for Open-Switch Fault Diagnosis in Grid-Connected PV Inverters. Energies. 2025; 18(15):4044. https://doi.org/10.3390/en18154044
Chicago/Turabian StyleXie, Yuxuan, Yaoxi He, Yong Zhan, Qianlin Chang, Keting Hu, and Haoyu Wang. 2025. "Multi-Dimensional Feature Perception Network for Open-Switch Fault Diagnosis in Grid-Connected PV Inverters" Energies 18, no. 15: 4044. https://doi.org/10.3390/en18154044
APA StyleXie, Y., He, Y., Zhan, Y., Chang, Q., Hu, K., & Wang, H. (2025). Multi-Dimensional Feature Perception Network for Open-Switch Fault Diagnosis in Grid-Connected PV Inverters. Energies, 18(15), 4044. https://doi.org/10.3390/en18154044





